在现行基于承载力的抗震设计方法中,刚度被假定为截面的基本属性,即对于给定几何形状和尺寸的构件,认为其截面屈服曲率与屈服弯矩成正比。然而对于梁、柱以及剪力墙的研究发现[1―3],在截面强度随轴压比和抗弯钢筋配筋率发生变化时,刚度事实上是随着强度近似成比例变化的。如果无法准确估算结构构件的有效刚度,则会影响结构固有周期的计算精度,进一步导致构件间的内力分配出现偏差,因此采用基于承载力的抗震设计方法设计出的结构无法保证其在不同水平地震作用下达到预定的性能要求。反观,屈服曲率在给定的截面尺寸和材料特性下是一个相对稳定的参数,以屈服曲率为基础建立起的基于位移的抗震设计方法,能确保不同构件在地震作用下具有充分的弹塑性变形能力,也是实现结构理想屈服机制和损伤模式的有效途径。而截面的变形参数(屈服曲率、极限曲率及延性)是应用基于位移的抗震设计方法的关键和基础,因此,有必要研究不同类型构件截面变形参数的计算方法。
目前国内外对于剪力墙截面变形参数的研究主要集中于矩形截面剪力墙。其中对于屈服曲率的研究主要有两种方法,其一是以Priestley等[3]、Paulay[4]、Tjen等[5]、赵花静等[6]、Massone等[7]为代表,采用弯矩-曲率分析法,考察轴压比、配筋率、混凝土强度以及钢筋屈服应力等参数对屈服曲率的影响,并通过回归分析建立屈服曲率的经验计算公式;其二是以钱稼茹等[8]为代表,根据剪力墙的试验结果,建立截面屈服时受压边缘混凝土应变的计算公式,进而依据平截面假定得到屈服曲率的计算公式。对于极限曲率的研究也主要有两种方法,其一是以Priestley等[3]和Hu等[9]为代表,采用弯矩-曲率分析法,寻找出影响极限曲率的相关参数,并通过参数拟合求出极限曲率的经验计算公式;其二是以钱稼茹等[8]和张松等[10]为代表,通过截面受压区外侧纤维混凝土的极限压应变与受压区高度的比值来求得极限曲率,其关键在于约束混凝土本构的选取。
然而高层建筑结构中矩形墙较少单独出现,其通常被组合成了不同截面形式的带翼缘剪力墙,通过作者前期完成的T形和L形墙的抗震性能试验研究发现[11],非对称截面带翼缘剪力墙在不同受力方向下的承载力、刚度、延性存在显著差异。对于翼缘受压方向,受压区高度较小,剪力墙具有较强的变形能力;而对于翼缘受拉方向,受压区高度较大,将导致腹板自由端发生脆性破坏,变形能力较差,同时该方向的截面刚度也相对较大。因此在进行带翼缘剪力墙截面设计前,有必要了解其不同受力方向下截面变形参数的差异性。但国内外关于带翼缘剪力墙截面变形参数却鲜有研究,仅Smyrou等[12]对T形墙进行了弯矩-曲率分析,考察了轴压比,纵筋配筋率以及腹板高度与翼缘宽度比对屈服曲率和极限曲率的影响,经回归分析建立了相应的经验计算公式。但该研究所考虑的影响因素及取值范围有限,未能全方位地反应此类构件的截面变形特性,同时建立的公式只适用于特定工况,且计算结果离散性较大。因此针对带翼缘剪力墙特别是T形、L形等非对称截面剪力墙,有必要通过大量的数值运算,建立一种兼顾精度和效率的截面变形参数计算方法。
为此,本文对非对称截面带翼缘剪力墙进行弯矩-曲率分析,分别针对翼缘受拉和翼缘受压方向,研究不同影响因素对其截面屈服曲率和极限曲率的影响,通过对数值计算结果的回归分析,建立屈服曲率、极限曲率以及延性的简化计算公式。
1 屈服曲率的分析与计算
1.1 屈服曲率的定义
屈服曲率大致有两种定义方式,其中赵花静等[6]和钱稼茹等[8]均以最外侧受拉钢筋屈服时的截面曲率作为屈服曲率,即构件的初始屈服曲率,然而Priestley等[3]提出的有效屈服曲率对于设计更有意义,其定义为由坐标原点经过初始屈服点的直线与通过峰值弯矩点的M-φ曲线切线的交点。通过有效屈服曲率可将M-φ曲线近似为双折线模型,该双折线模型由于其简便性和足够的精确性在设计中得到了广泛的应用。考虑到软化段切线取法具有一定的主观性,本文参考文献[13]采用图1所示的方法来计算有效屈服曲率,即:
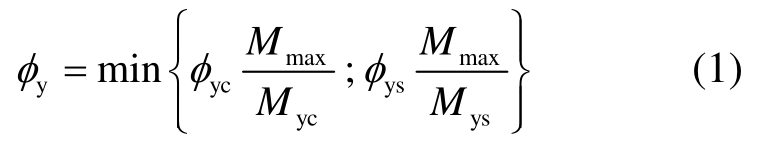
式中:φyc和Myc分别为非约束混凝土达到峰值应变ε0时对应的曲率和弯矩;φys和Mys分别为纵筋达到屈服应变εy时对应的曲率和弯矩。在低轴压时,纵筋通常率先屈服,因此φys作为控制因素;而在高轴压时,特别是对于翼缘受拉方向,受压区边缘混凝土率先达到峰值应变,φyc成为控制因素。
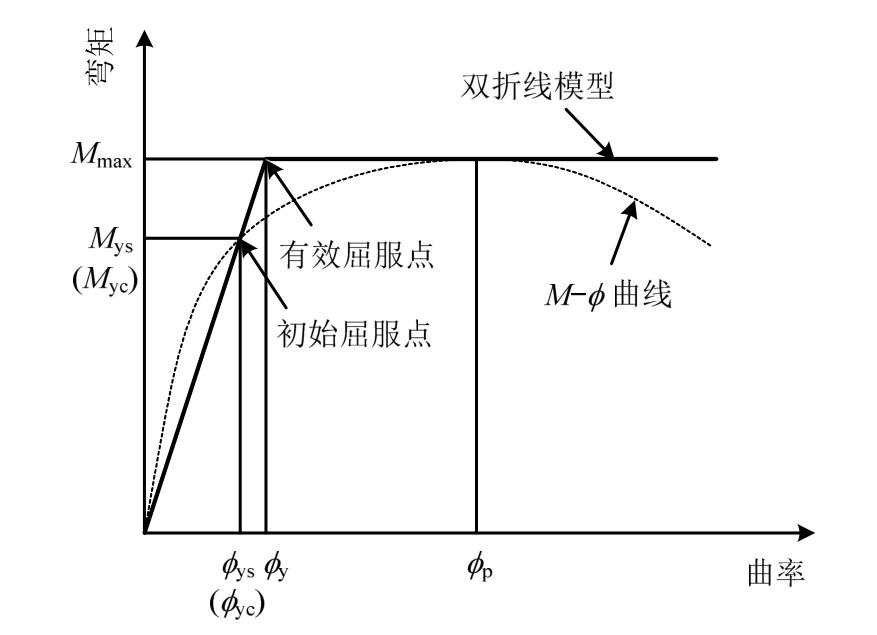
图1 屈服曲率的定义
Fig.1 Definition of yield curvature
1.2 弯矩-曲率分析
利用非线性钢筋混凝土构件截面分析软件XTRACT对RC带翼缘剪力墙进行弯矩-曲率分析。该软件是将截面离散成多个单元,利用平截面假定求得每个时刻的单元应变,再利用应力-应变关系求得单元应力,进而得到截面内力。该分析方法不仅满足应变的协调性,同时通过迭代运算来满足截面的平衡方程,也可引入非线性本构关系对约束区和非约束钢筋混凝土进行分析。
对作者在文献[11]中完成的T形截面带翼缘剪力墙试验模型进行截面弯矩-曲率分析,腹板和翼缘截面厚度均为100 mm,腹板截面高度为1000 mm,翼缘截面宽度为900 mm。混凝土本构关系选用Mander等[14]提出的约束混凝土本构模型,钢筋采用双折线模型,强化段弹性模量取初始弹性模量的1%[15]。分析时首先施加轴向压力,然后逐步增加曲率,计算中止的条件为纵筋达到极限拉应变或约束混凝土达到破坏应变。其中纵筋极限拉应变按《混凝土结构设计规范》(GB50010―2010)[16]取0.075;约束混凝土破坏应变取为箍筋断裂时对应的混凝土应变,具体是根据能量原理,通过箍筋屈服应力、配箍率以及箍筋极限拉应变来计算约束混凝土破坏应变[14]。
鉴于试验未对截面曲率进行相关测量,为了验证XTRACT分析结果的有效性,将其计算得到的弯矩-曲率曲线通过塑性铰模型转化成荷载-弯曲变形曲线,并与试验测得的骨架曲线进行对比,如图2所示,具体的计算过程见文献[17]。可以看出计算结果与试验吻合良好,验证了XTRACT模型及其参数选取的准确性。
以文献[11]的试验试件TW-1为原型(如图3),通过改变其设计参数,研究带翼缘剪力墙屈服曲率随不同影响因素的变化规律,所选取的影响因素及其取值范围见表1。

图2 计算与试验荷载-弯曲变形骨架曲线对比图
Fig.2 Comparison of load-flexural deformation skeleton curves between experimental and analytical results
表1 影响因素的取值
Table 1 Value ranges of influential factors
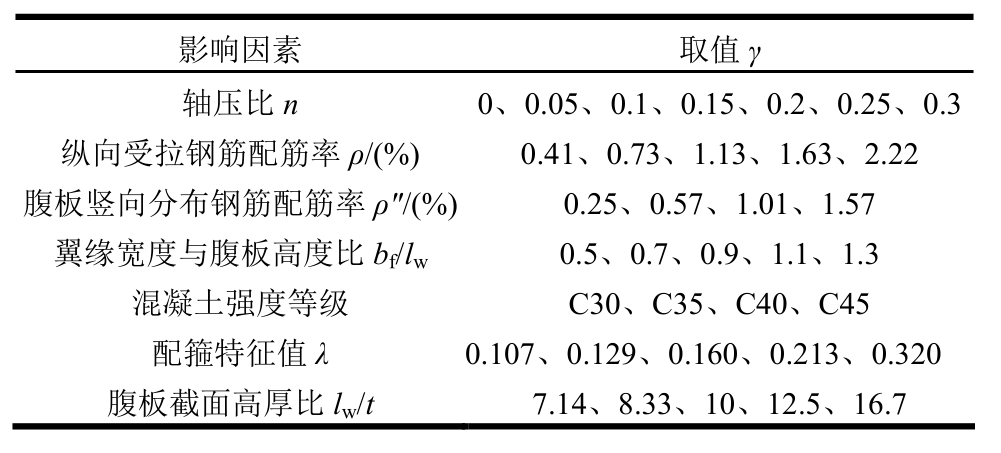
影响因素 取值γ轴压比n 0、0.05、0.1、0.15、0.2、0.25、0.3纵向受拉钢筋配筋率ρ/(%) 0.41、0.73、1.13、1.63、2.22腹板竖向分布钢筋配筋率ρ"/(%)0.25、0.57、1.01、1.57翼缘宽度与腹板高度比bf/lw 0.5、0.7、0.9、1.1、1.3混凝土强度等级 C30、C35、C40、C45配箍特征值λ 0.107、0.129、0.160、0.213、0.320腹板截面高厚比lw/t 7.14、8.33、10、12.5、16.7
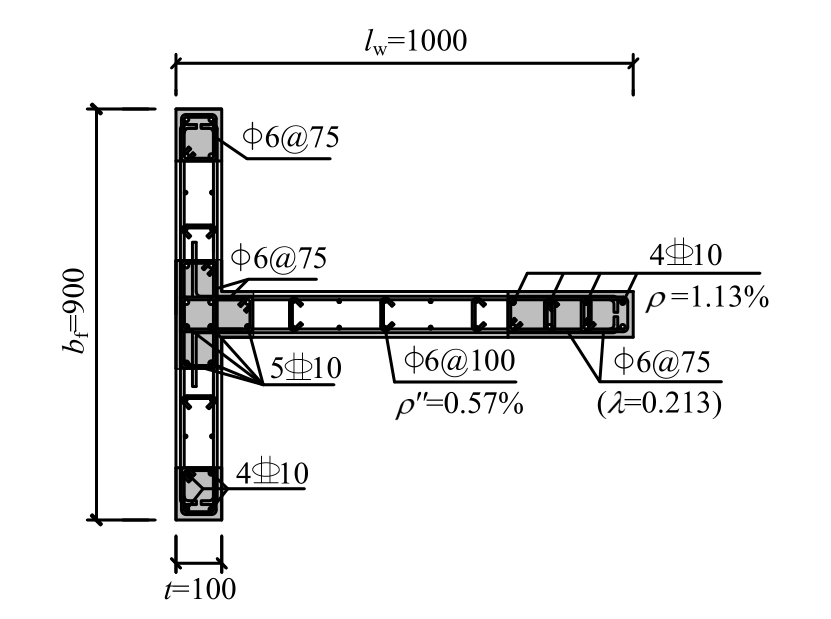
图3 T形墙截面尺寸及配筋图
Fig.3 Dimensions and reinforcement details of T-shaped wall cross-section
计算轴压比时取材料强度的平均值,C30、C35、C40、C45混凝土轴心抗压强度分别取28.41 MPa、33.14 MPa、37.88 MPa、42.18 MPa。纵筋采用HRB400级钢筋,分布钢筋采用HRB335级钢筋,不同钢筋的屈服强度依据文献[11]试验测得的材料特性取值。纵向受拉钢筋直径分别取6 mm、8 mm、10 mm、12 mm、14 mm,相应的纵筋配筋率为0.41%、0.73%、1.13%、1.63%、2.22%;腹板竖向分布钢筋直径分别取4 mm、6 mm、8 mm、10 mm,相应的分布钢筋配筋率为0.25%、0.57%、1.01%、1.57%;箍筋间距分别取50 mm、75 mm、100 mm、125 mm、150 mm,相应的配箍特征值为0.320、0.213、0.160、0.129、0.107。翼缘宽度与腹板高度比的变化是通过改变翼缘宽度实现的,而腹板截面高厚比的变化是通过改变截面厚度实现的,这样通过上述两个参数即可反映翼缘宽度。腹板高度以及截面厚度这三个几何参数的相对取值对屈服曲率的影响。
由文献[12]关于屈服曲率的研究可知,屈服曲率与钢筋的屈服应变εy成正比,与腹板截面高度lw成反比,为了便于分析,本节引入无量纲屈服曲率系数ky来表征不同参数对屈服曲率的影响:
对表1中所考察的7个参数逐一进行分析。每次考察其中一个参数,计算时其余参数依据文献[11]中的试验模型取固定值。为了能够清楚地阐明屈服曲率随各参数变化的原因,图4给出了屈服曲率、受压区高度以及屈服应变三者间的关系。由图4(a)可以看出,受拉钢筋作为屈服的控制因素时,受压区高度的增大使得屈服曲率相应增大,而由图4(b)可知,受压混凝土作为屈服的控制因素时,受压区高度的增大反而使得屈服曲率相应减小。因此屈服曲率随不同参数变化的根本原因在于不同屈服控制因素下受压区高度的变化。
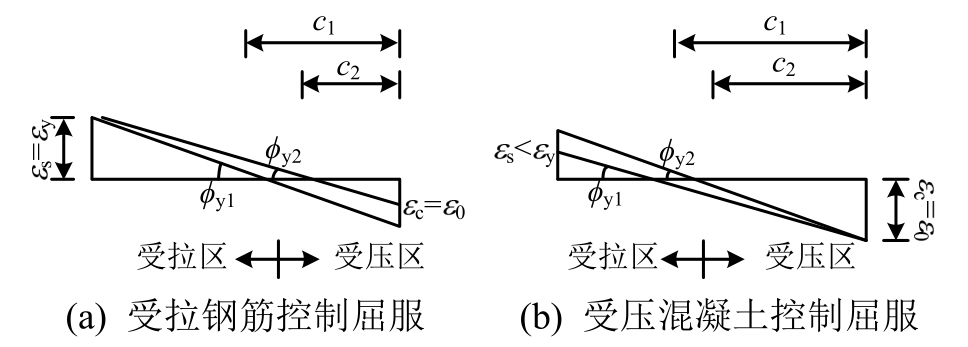
图4 屈服曲率、受压区高度与屈服应变间的关系
Fig.4 Relationships between yield curvature, depth of compressive zone and yield strain
经过计算,图5~图10分别给出了不同参数影响下翼缘受拉和翼缘受压方向屈服曲率系数随轴压比的变化关系图。图中空心符号表示截面屈服是由受拉钢筋控制的;实心符号表示截面屈服是由受压混凝土控制的。可以看出,带翼缘剪力墙在翼缘受拉方向和翼缘受压方向截面达到屈服时的控制因素及屈服曲率的取值各有不同。在翼缘受拉方向,对于轴压比小于0.1的情况,截面屈服大部分是由受拉纵筋控制;而当轴压比大于等于0.1时,由于受压区高度较大,截面屈服基本是由受压混凝土控制。在翼缘受压方向,翼缘的存在迫使受压区高度相对较小,截面屈服全部由受拉纵筋控制。同时也发现,翼缘受拉方向和翼缘受压方向屈服曲率随不同参数的变化规律也存在明显的差异,以下针对各因素逐一进行分析。
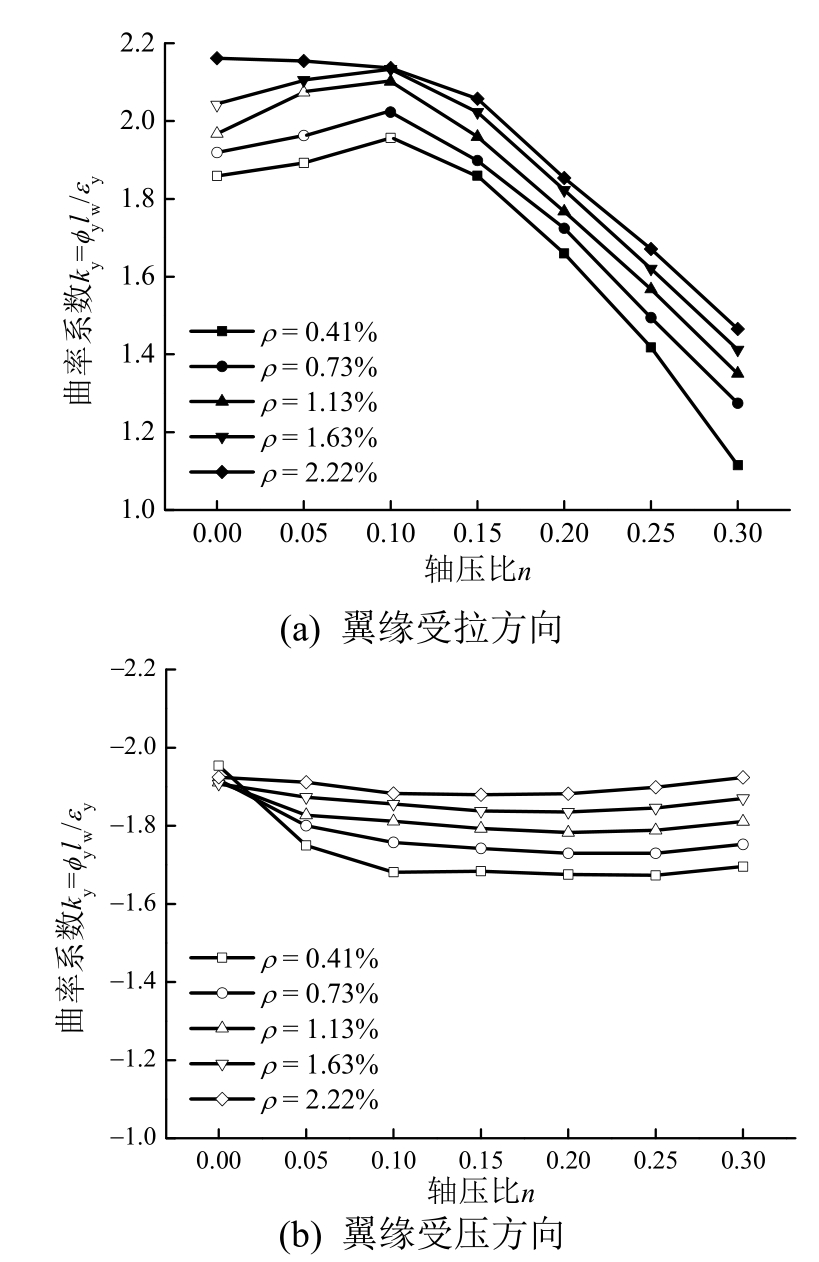
图5 纵筋配筋率对屈服曲率的影响
Fig.5 Effect of longitudinal reinforcement ratio on yield curvature
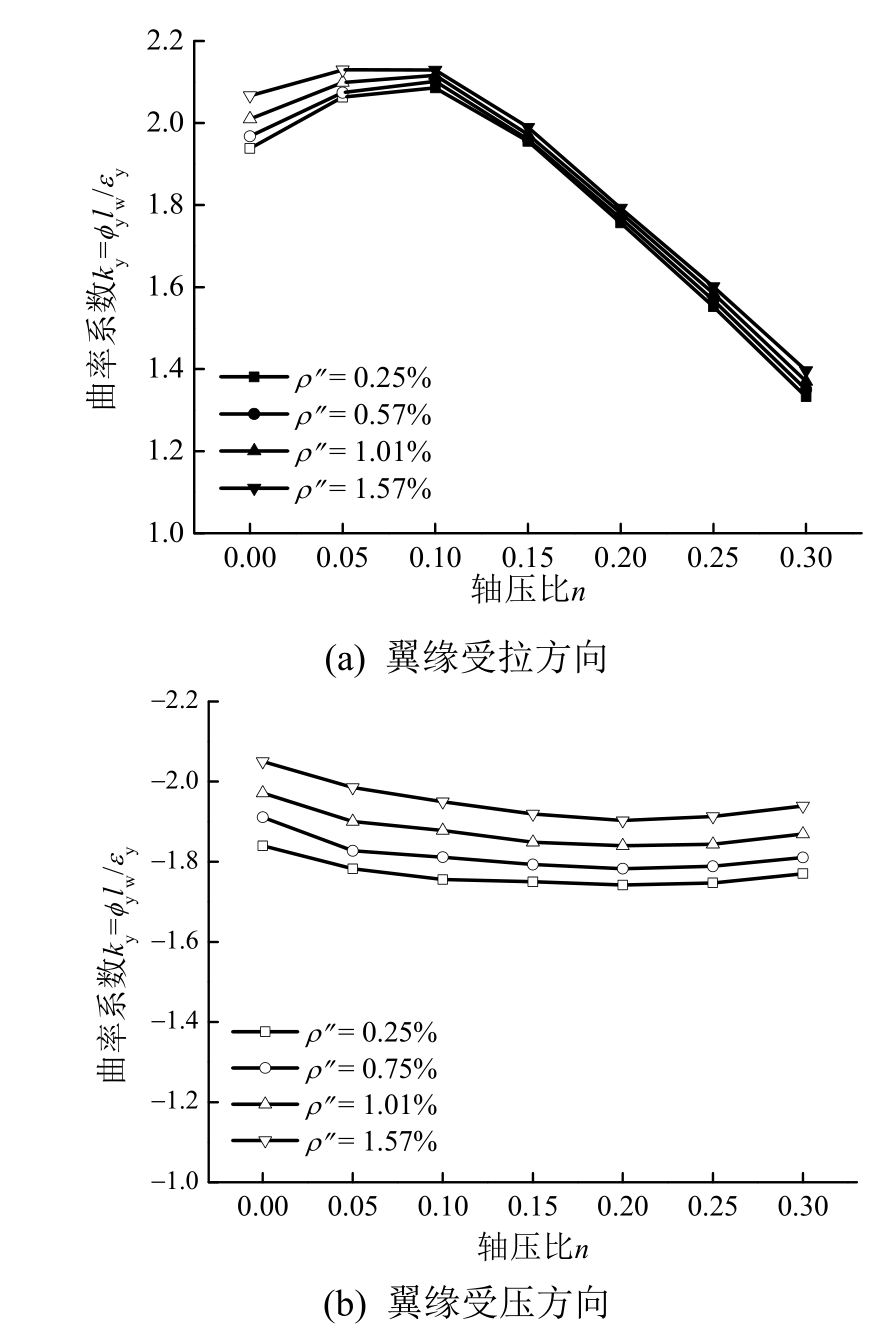
图6 腹板竖向分布钢筋配筋率对屈服曲率的影响
Fig.6 Effect of web distributed vertical reinforcement ratio on yield curvature
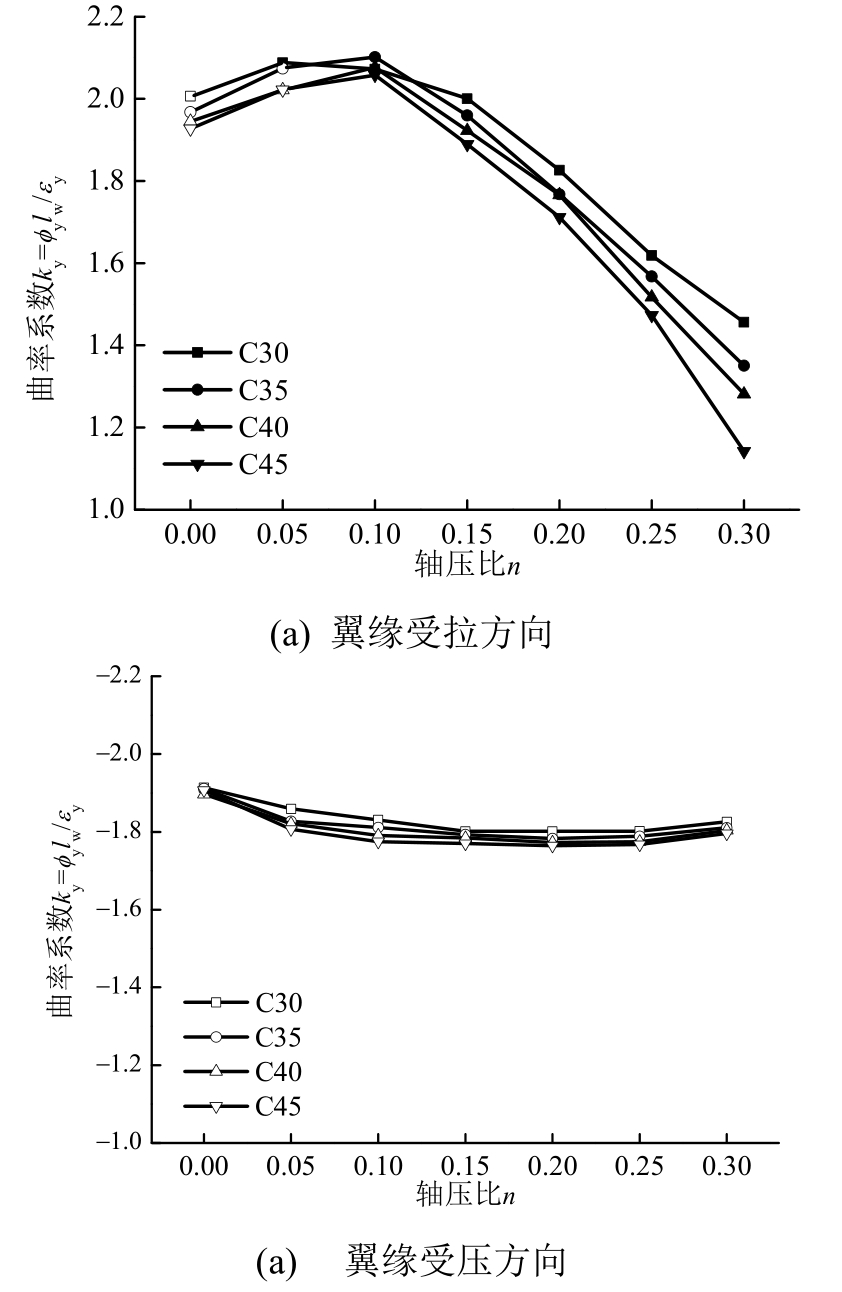
图7 混凝土强度对屈服曲率的影响
Fig.7 Effect of concrete strength on yield curvature
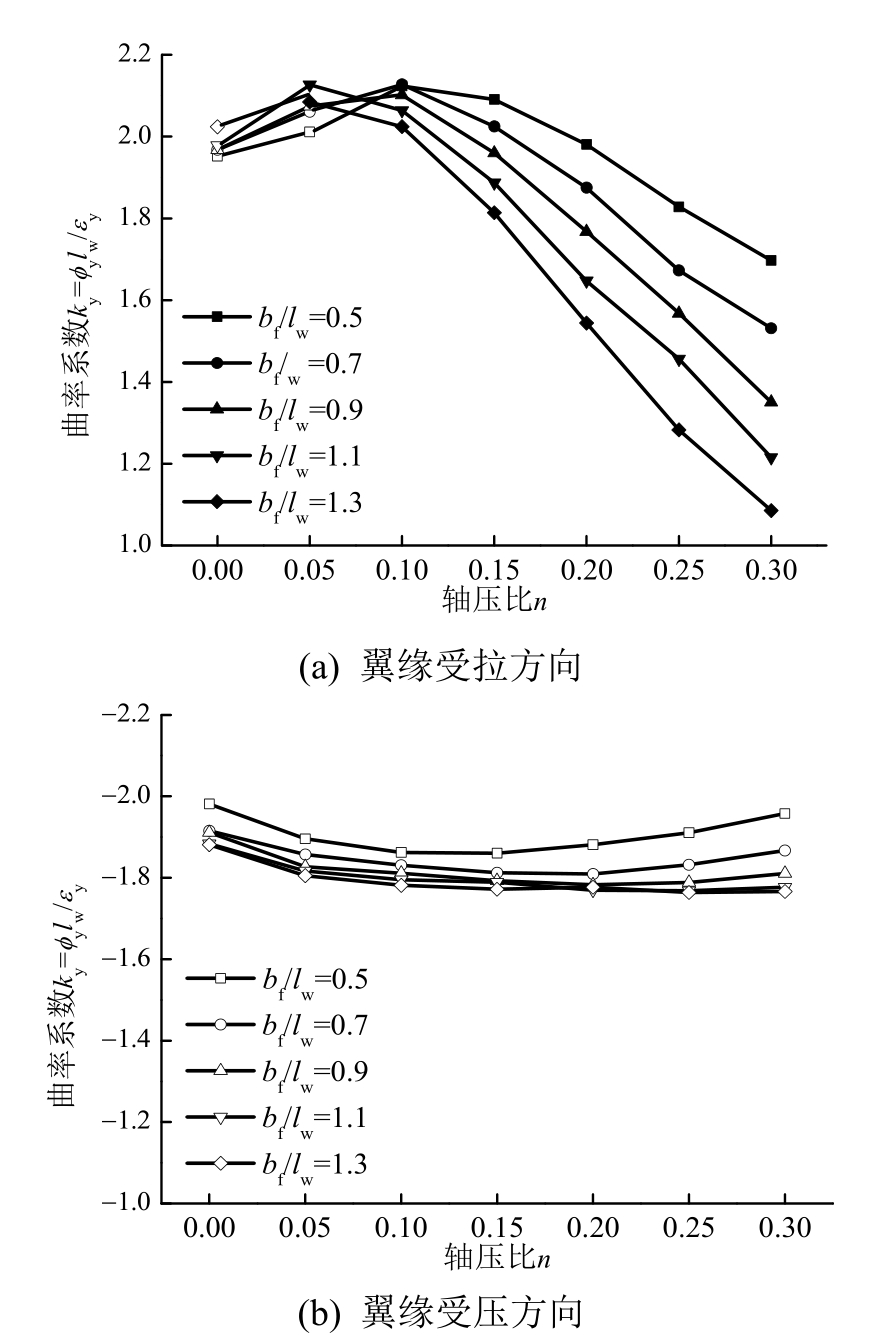
图8 翼缘宽度与腹板高度比对屈服曲率的影响
Fig.8 Effect of flange width to web height ratio on yield curvature
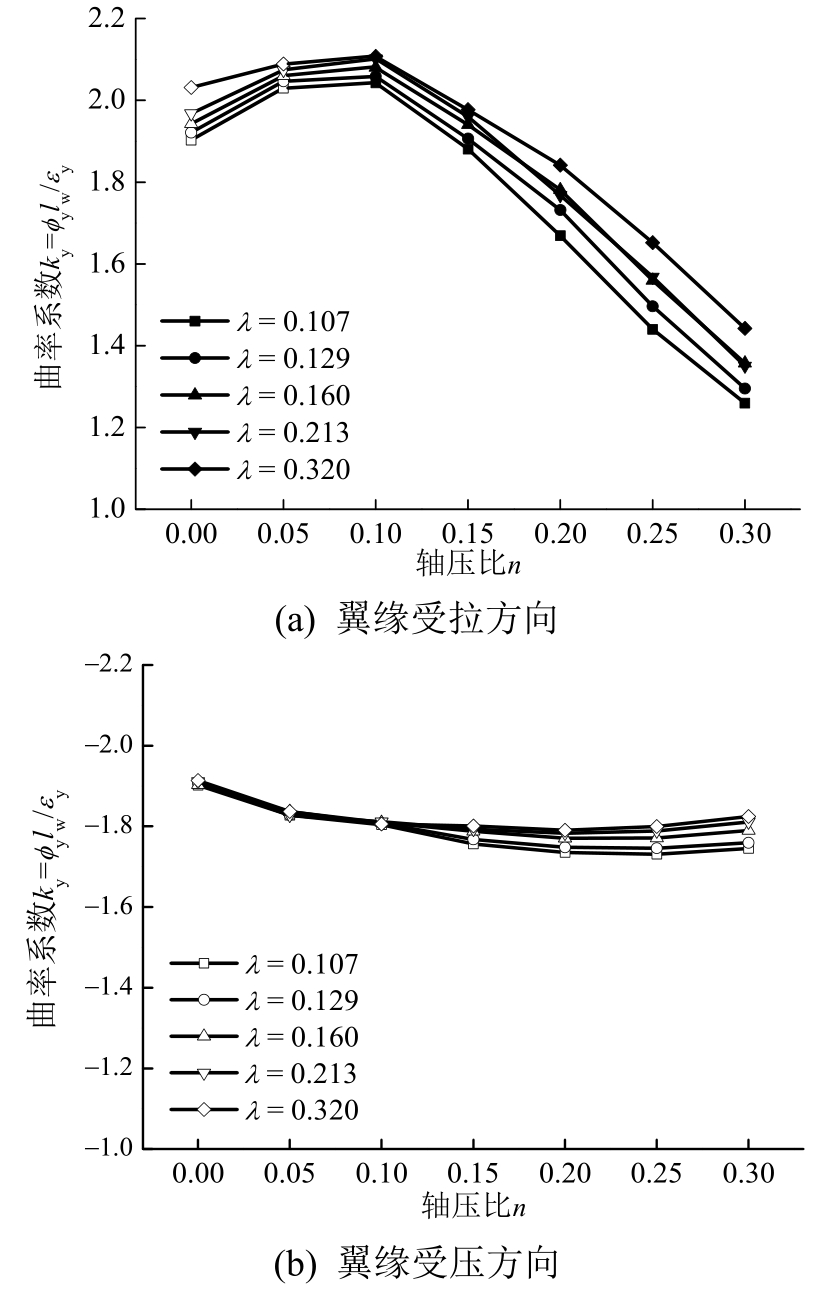
图9 配箍特征值对屈服曲率的影响
Fig.9 Effect of stirrup characteristic value on yield curvature
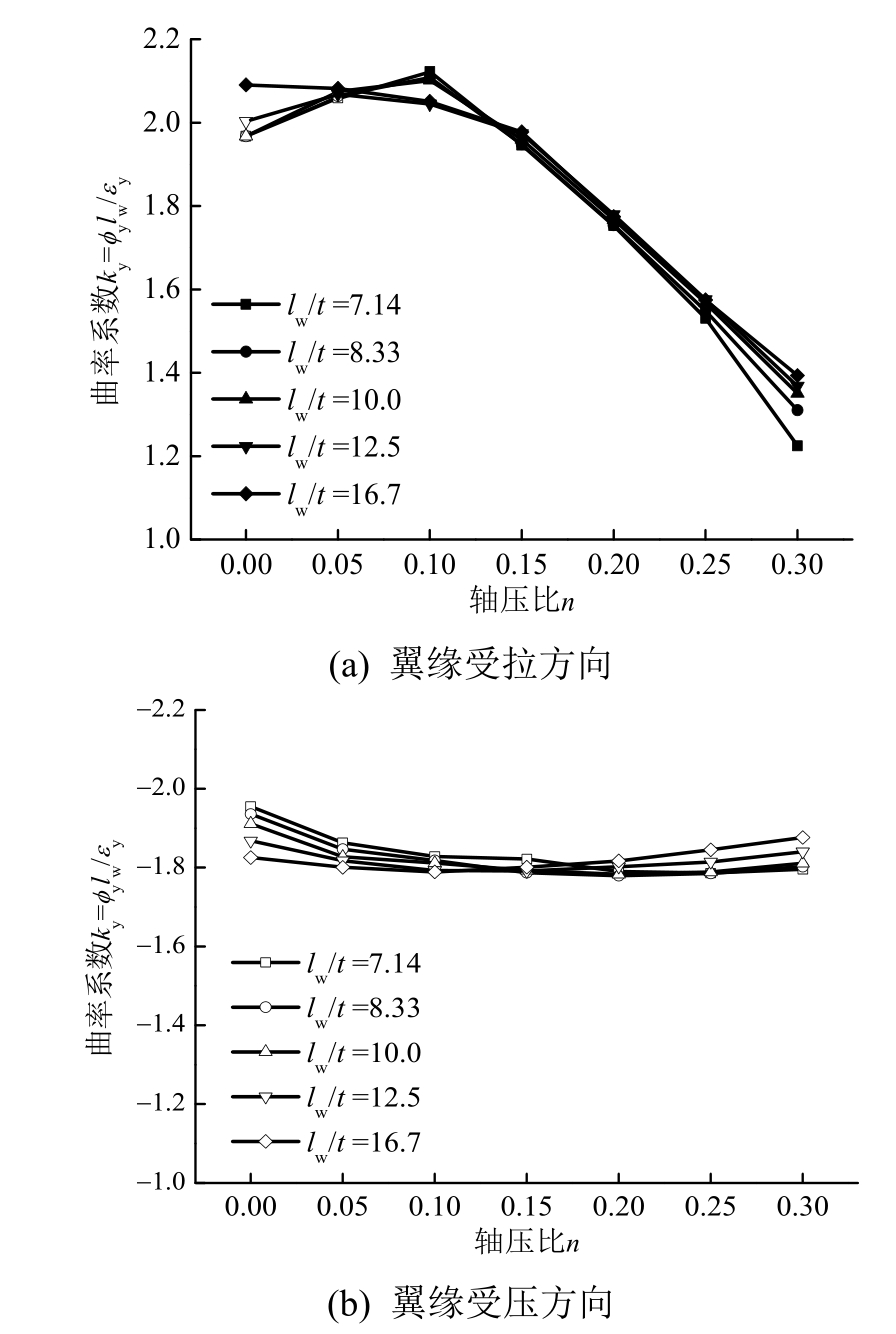
图10 腹板截面高厚比对屈服曲率的影响
Fig.10 Effect of web height to thickness ratio on yield curvature
1) 轴压比
综合图5~图10屈服曲率系数随轴压比的变化关系可以看出,对于翼缘受拉方向,在轴压比较小受拉钢筋作为屈服的控制因素时,屈服曲率随着轴压比的增大而增大。这是因为轴压力的增大使得截面受压区高度得以增加,从而屈服曲率也相应增大。从另一角度看,也是因为增大的轴压力抵消了一部分的钢筋应力,从而延缓了截面的屈服。当轴压比较大受压混凝土成为屈服的控制因素后,屈服曲率随着轴压比的增大而减小,这同样归因于截面受压区高度的增大,加剧了混凝土应变的增大。对于翼缘受压方向,总体来看屈服曲率随轴压比的增大变化不明显。分析是因为翼缘受压方向截面的屈服始终是由受拉钢筋控制的,同时由于翼缘面积较大,轴压力的增大对受压区高度的提升贡献不大,因此屈服曲率也变化不大。
2) 纵筋配筋率
从图5(a)可以看出,对于翼缘受拉方向,无论是受拉钢筋还是受压混凝土控制截面屈服,屈服曲率均随着纵筋配筋率的增大而增大,特别是在轴压比较小时其增大程度更为明显。分析原因发现:纵筋配筋率的增大对截面受拉区和受压区的应力及其合力均有提高,当轴压比较小时,截面受压区高度较小,此时纵筋配筋率的提高对受拉区合力的贡献更大,从而需要更大的受压区高度来平衡拉力。因此在受拉纵筋控制屈服时,屈服曲率随着纵筋配筋率的增大而增大。当轴压比较大时,截面受压区高度较大,此时纵筋配筋率的提高对受压区合力的贡献更大,从而需要更小的受压区高度来平衡拉力。因此在受压混凝土控制屈服时,屈服曲率也随着纵筋配筋率的增大而增大。从图5(b)可以看出,对于翼缘受压方向,屈服曲率随着纵筋配筋率的增大也有明显的增大。这说明纵筋配筋率的提升可有效延缓带翼缘剪力墙的屈服,避免构件过早进入塑性状态。
3) 腹板竖向分布钢筋配筋率
从图6(a)可以看出,对于翼缘受拉方向,在轴压比的变化范围内,屈服曲率随着腹板竖向分布钢筋配筋率的增大而增大,但其对屈服曲率的影响程度较小,特别是在受压混凝土作为屈服控制因素后,当ρ''从0.25%增大到1.57%时,屈服曲率的变化不超过5%。从图6(b)可以看出,对于翼缘受压方向,屈服曲率随着腹板竖向分布钢筋配筋率的增大有明显的增大,这是因为,ρ''的增大显著提高了了该方向的受压区高度,从而屈服曲率得以增大。
4) 混凝土强度
从图7(a)可以看出,对于翼缘受拉方向,无论是受拉钢筋还是受压混凝土控制截面屈服,屈服曲率均随着混凝土强度的增大而减小。分析发现:随着混凝土强度的增大,其在相同应变下可承担的压应力增大,从而减小了截面的受压区高度;但从另一方面看,混凝土强度增大的同时,在相同轴压比下截面承受的轴压力也增大,所以截面的受压区高度又相应增大,但两者哪一个是主要因素还需进一步分析。通过观察截面屈服时的中和轴位置可以发现,当轴压比为0和0.05即受拉钢筋控制截面屈服时,混凝土强度越高受压区高度就越小,因此屈服曲率就越小;而轴压比大于0.05后,受压混凝土控制截面屈服。此时混凝土强度越高受压区高度越大,所以屈服曲率越小。从图7(b)可以看出,对于翼缘受压方向,随着混凝土强度的增大,截面的屈服曲率略有减小,但变化程度有限。
5) 翼缘宽度与腹板高度比
从图8(a)可以看出,对于翼缘受拉方向,在轴压比较小受拉钢筋作为屈服的控制因素时,屈服曲率随着翼缘宽度与腹板高度比的增大而增大,而当轴压比较大受压混凝土成为屈服的控制因素后,屈服曲率随着翼缘宽度与腹板高度比的增大而减小,这是由于翼缘宽度的增大迫使截面受压区高度增大导致的。从图8(b)可以看出,对于翼缘受压方向,随着翼缘宽度与腹板高度比的增大,屈服曲率略有减小,但变化程度也较小。
6) 配箍特征值
从图9(a)可以看出,对于翼缘受拉方向,无论是受拉钢筋还是受压混凝土控制截面屈服,屈服曲率都随着配箍特征值的增大而增大,在轴压比较大时其增大程度相对明显。从图9(b)可以看出,对于翼缘受压方向,屈服曲率随着配箍特征值的增大略有增大。这说明配箍特征值的提升同样可以延缓带翼缘剪力墙的屈服,但其对屈服曲率的提升相比纵筋配筋率效果甚微。
7) 腹板截面高厚比
从图10可以看出,无论翼缘受拉还是翼缘受压方向,不同腹板截面高厚比下屈服曲率系数随轴压比的变化曲线几乎重合,说明截面厚度的改变对屈服曲率几乎没有影响。
总体来看,影响翼缘受拉方向屈服曲率大小的主要因素是轴压比、纵筋配筋率和翼缘宽度与腹板高度比,而影响翼缘受拉方向屈服曲率大小的主要因素是纵筋配筋率和腹板竖向分布钢筋配筋率,因此下文将基于以上参数对屈服曲率的计算公式进行拟合。
1.3 屈服曲率的简化计算
通过1.2节的参数分析找出了影响屈服曲率的主要因素,为了得到更为精确的回归结果,在上述正交分析的基础上需要进一步对这些主要因素影响下的屈服曲率进行变参数的补充计算。本节对翼缘受拉方向屈服曲率的三个主要影响因素分别按照表1取值,采用全面分析法对轴压比的7个水平,纵筋配筋率的5个水平以及翼缘宽度与腹板高度比的5个水平共进行了(7×5×5)175个工况的分析。同样对翼缘受压方向屈服曲率的两个主要影响因素按照表1取值,采用全面分析法对纵筋配筋率的5个水平和竖向分布钢筋配筋率的4个水平共进行了(5×4)20个工况的分析。由于计算工况较多,此处不再逐一列出各工况下屈服曲率计算值。
分析发现:对于翼缘受拉方向,轴压比大于等于0.1时,屈服曲率系数与各影响因素均近似呈线性关系,可采用多元线性函数进行回归;而当轴压比小于0.1时,屈服曲率随各参数的变化程度相对较小,且规律性不强,整体来看略小于轴压比为0.1时的取值。同时考虑到在实际结构中底部剪力墙轴压比的取值普遍大于0.1,为便于计算,本文对于轴压比小于0.1时的屈服曲率按轴压比为0.1的计算结果取值。对于翼缘受压方向,屈服曲率系数与各影响因素也均近似呈线性关系,同样采用多元线性函数进行回归。
经回归分析,得出带翼缘剪力墙翼缘受拉方向屈服曲率系数的计算表达式:
式中:下标y表示屈服状态(yield);下标FiT表示翼缘受拉(Flange in Tension);n为轴压比;ρ为纵筋配筋率;bf为翼缘宽度;lw为腹板截面高度。
将式(3)代入式(2)即可得到翼缘受拉方向屈服曲率的计算公式:
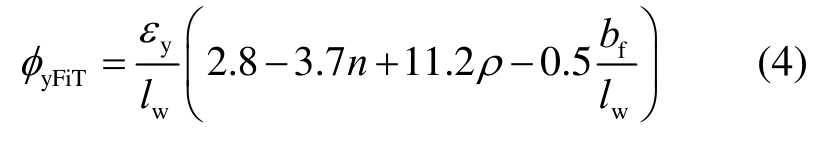
同样回归得到翼缘受压方向屈服曲率系数的计算表达式:
式中:下标FiC表示翼缘受压(Flange in Compression);ρ′为腹板竖向分布钢筋配筋率。
代入式(2)即可得到翼缘受压方向屈服曲率的计算公式:
基于以上195个工况的计算数据拟合式(3)和式(5)的相关系数分别为0.93和0.91,表明数据相关度较高,采用多元线性函数进行回归是合理的。本文得出的屈服曲率的计算公式相较前述研究成果,不仅将翼缘受拉和翼缘受压状态进行了区分,还将更多的影响因素考虑其中。公式的建立是以大量数值计算为基础,公式形式相对简单,确保了公式的准确性和简便性,便于工程设计的应用。
1.4 试验验证
通过屈服曲率计算出的屈服位移与国内外T形墙的试验结果进行比对,以验证屈服曲率计算公式的准确性。本节将屈服位移定义为剪力墙底部截面弯曲屈服时的顶部位移,对于顶部作用一集中荷载的情况,底部截面屈服时可认为曲率沿高度方向呈线性分布。在不考虑剪切变形和纵筋滑移变形贡献的前提下,通过积分可得到剪力墙顶点屈服位移与屈服曲率的关系:
式中,H为剪力墙的总高度。针对文献[11]和文献[18]中7片发生弯曲破坏的T形墙试验模型,分别按照式(4)和式(6)计算出翼缘受拉和翼缘受压方向的屈服曲率,再依据式(7)计算出屈服位移。对比结果见表2。
表2 屈服位移计算结果对比
Table 2 Comparison of yield displacement results
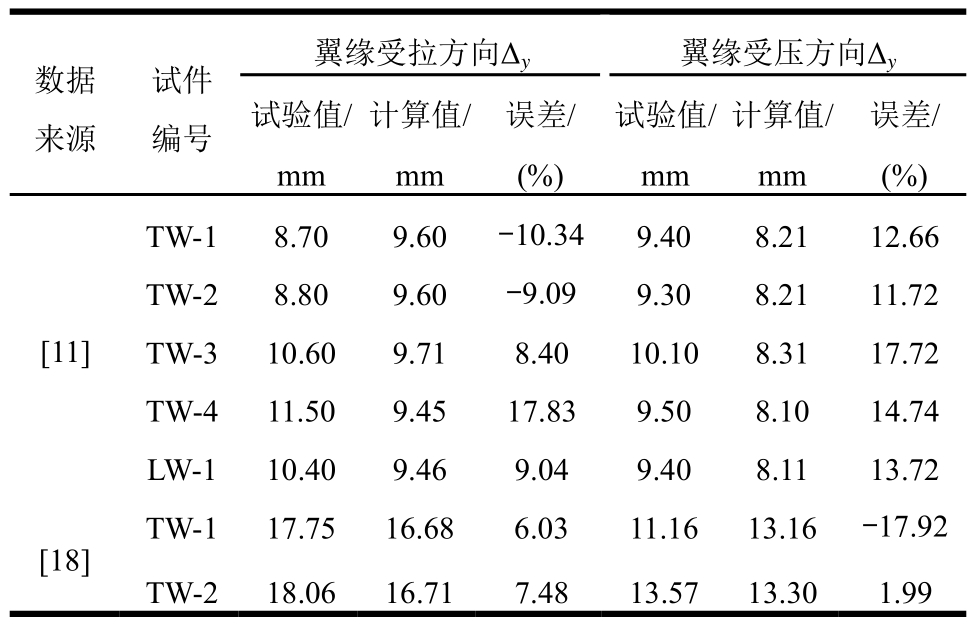
数据来源翼缘受拉方向Δy 翼缘受压方向Δy试件编号 试验值/mm计算值/mm误差/(%)试验值/mm计算值/mm误差/(%)TW-1 8.70 9.60 -10.34 9.40 8.2112.66[11]TW-2 8.80 9.60 -9.09 9.30 8.2111.72 TW-3 10.60 9.71 8.40 10.10 8.3117.72 TW-4 11.50 9.45 17.83 9.50 8.1014.74 LW-1 10.40 9.46 9.04 9.40 8.11 13.72 TW-1 17.75 16.68 6.03 11.16 13.16-17.92[18]TW-2 18.06 16.71 7.48 13.57 13.301.99
由表2可以看出,除个别情况外,本文公式计算出的屈服位移普遍小于试验值。这是因为按式(7)计算屈服位移时,只考虑了截面弯曲变形的影响,而忽略了截面剪切变形以及支座处纵筋滑移引起的位移。对于翼缘受拉方向,除试件TW-4外,其余试件误差基本在10%以内,试件TW-4试验屈服位移较大的原因在于加载初期基础表面产生了少许裂缝,但该裂缝在构件屈服后并未继续扩展,从而导致试验屈服位移偏大。对于翼缘受压方向,试验屈服位移普遍超过计算值10%,这是因为该方向剪切变形所占比重相对较大,忽略剪切变形计算出的屈服位移也就与试验值相差较多。但总体来看,试验值与计算值基本接近。两者间的误差基本控制在15%以内,验证了屈服曲率计算的准确性,也为曲率延性的计算提供依据。
2 极限曲率的分析与计算
2.1 极限曲率的定义
对不同配筋、尺寸和受不同轴压力的截面来说,其极限状态通常由不同因素控制,本文将极限曲率定义为以下四类情况所对应曲率的较小值:
1) 截面的抗弯能力下降到最大弯矩的85%;
2) 核心混凝土达到极限压应变,依据文献[12]取极限压应变εccu=0.018;
3) 受拉纵筋达到极限拉应变,依据文献[12]取极限拉应变εsu=0.06;
4) 受压纵筋达到压屈应变,依据文献[19]按式(8)计算。
式中,s和d分别为箍筋的间距和纵筋直径。由带翼缘剪力墙的试验研究可知[9],条件2)和条件3)分别为翼缘受拉和翼缘受压方向的控制因素,而条件4)对于横向约束较好时不起控制作用。
2.2 影响因素分析
沿用1.2节的弯矩-曲率分析方法,按照表1的参数取值对带翼缘剪力墙进行非线性截面分析。为了便于研究,同样引入无量纲极限曲率系数ku:
经过计算,图11~图16分别给出了不同参数影响下翼缘受拉和翼缘受压方向极限曲率系数随轴压比的变化关系图。
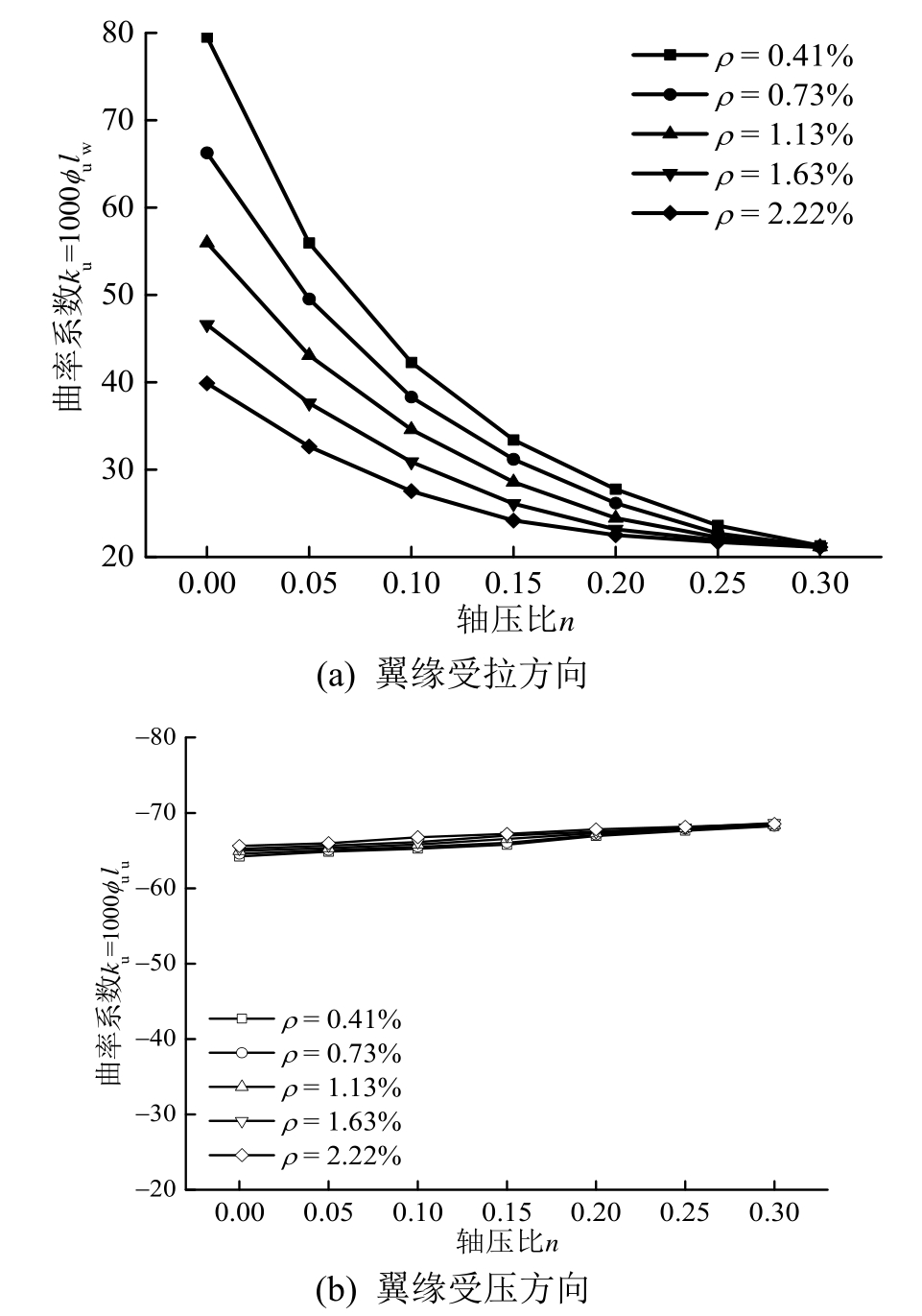
图11 纵筋配筋率对极限曲率的影响
Fig.11 Effect of longitudinal reinforcement ratio on ultimate curvature
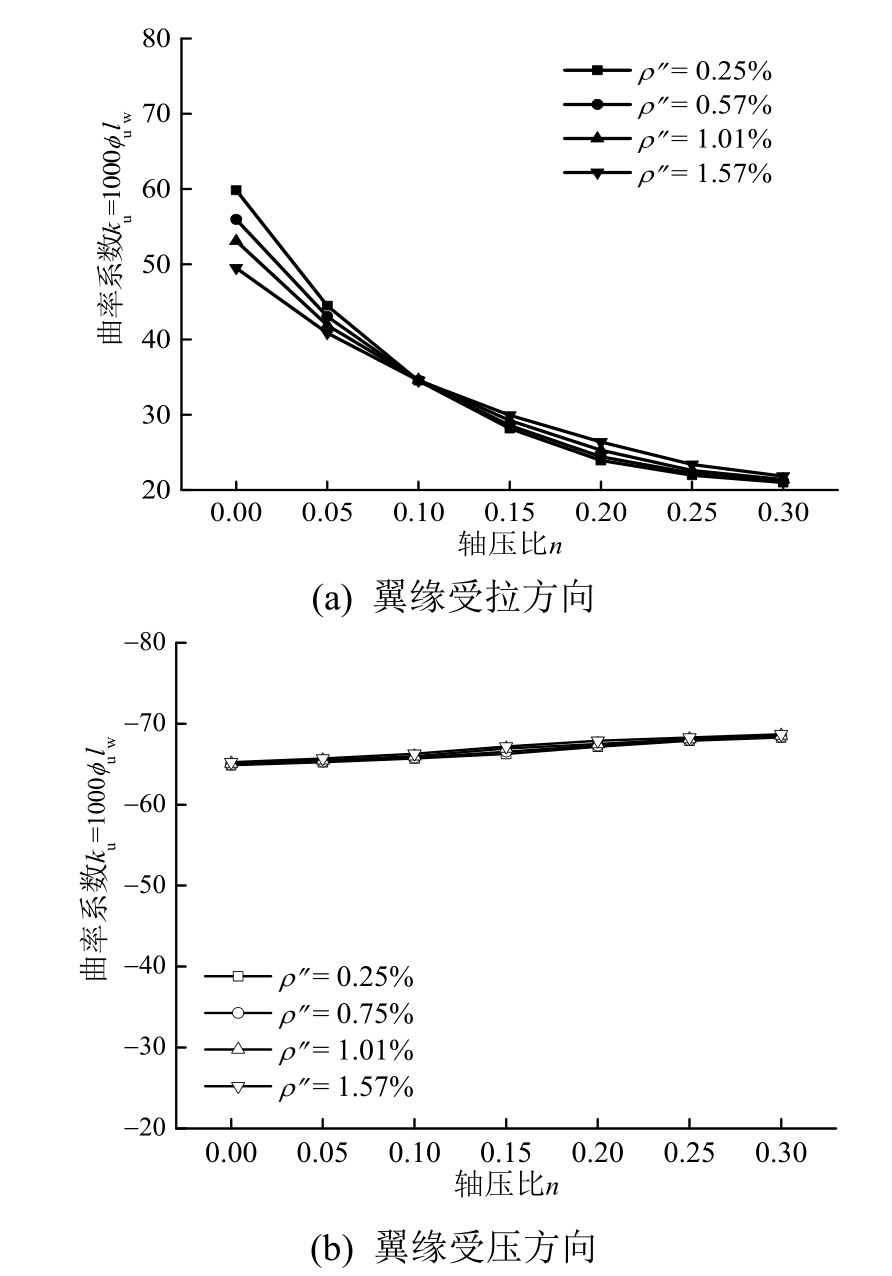
图12 腹板竖向分布钢筋配筋率对极限曲率的影响
Fig.12 Effect of web distributed vertical reinforcement ratio on ultimate curvature
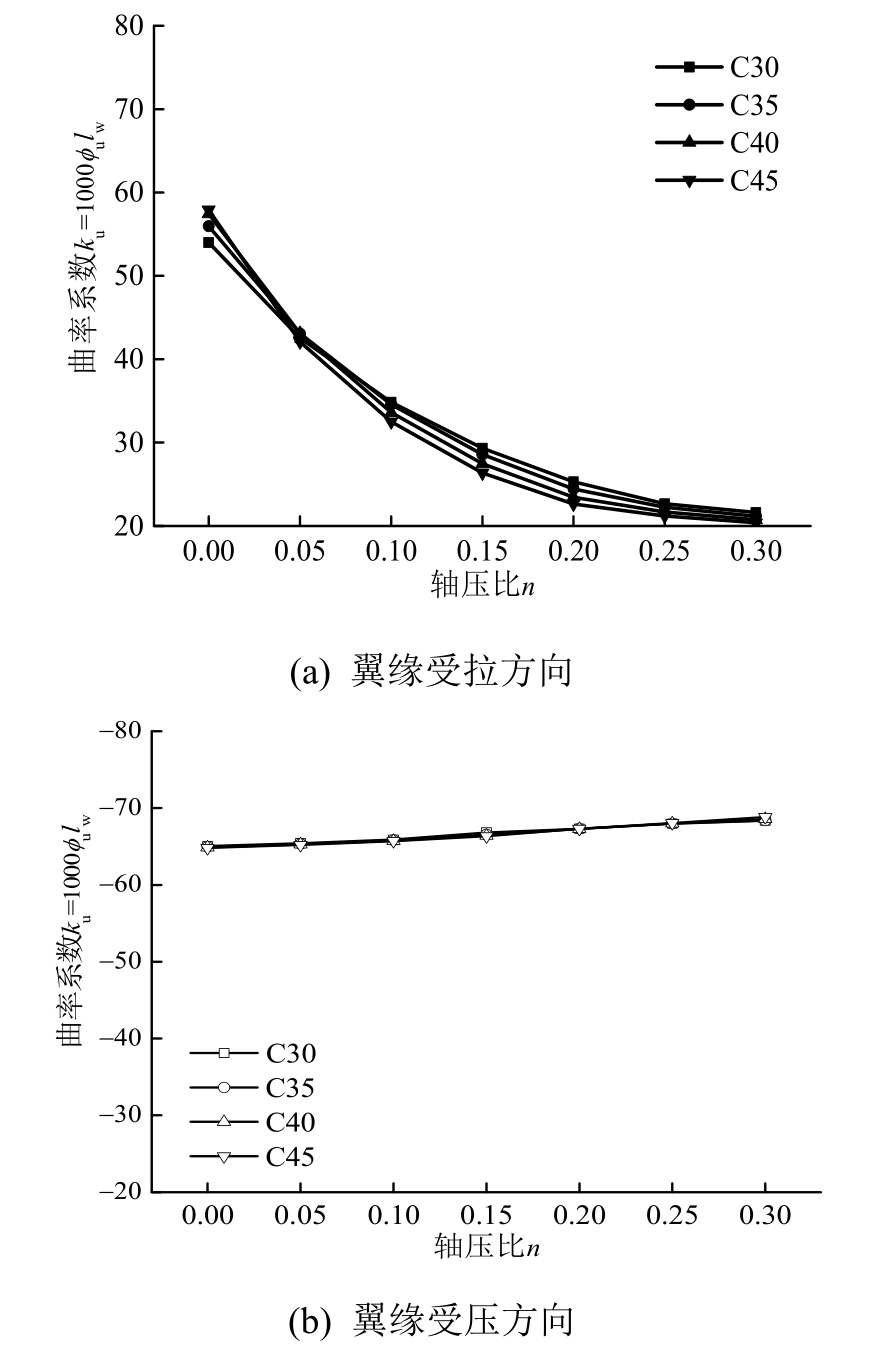
图13 混凝土强度对极限曲率的影响
Fig.13 Effect of concrete strength on ultimate curvature

图14 翼缘宽度与腹板高度比对极限曲率的影响
Fig.14 Effect of flange width to web height ratio on ultimate curvature
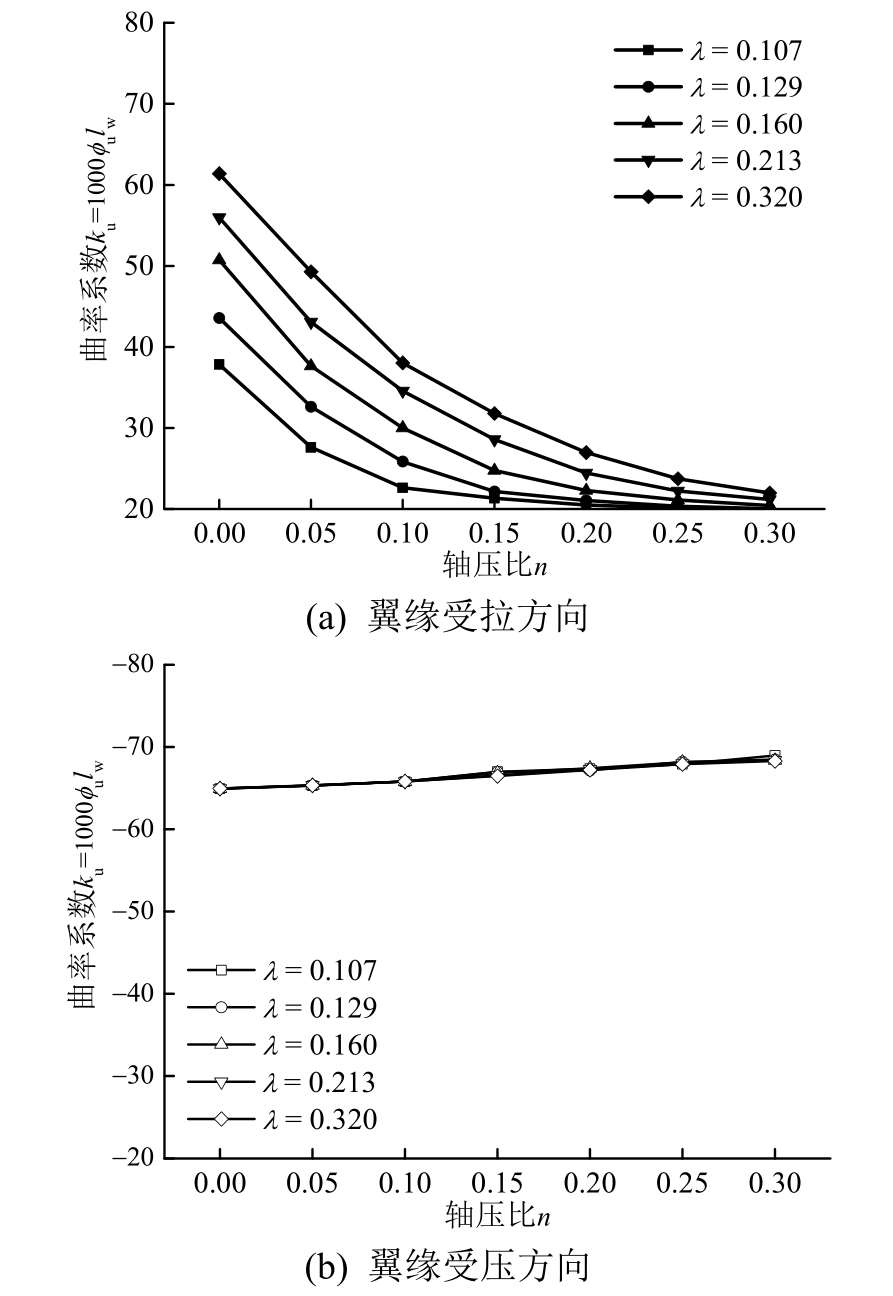
图15 配箍特征值对极限曲率的影响
Fig.15 Effect of stirrup characteristic value on ultimate curvature

图16 腹板截面高厚比对极限曲率的影响
Fig.16 Effect of web height to thickness ratio on ultimate curvature
从图11~图16可以看出,带翼缘剪力墙翼缘受压方向各参数对极限曲率的影响较小,其中轴压比、翼缘宽度与腹板高度比和腹板截面宽厚比的影响相对突出。随着轴压比的增大,极限曲率相应增大,这同样可以用图4不同控制因素下受压区高度的变化来解释。分析可知翼缘受压方向的破坏始终是由腹板端部纵筋拉断导致的,轴压力的增大使得截面受压区高度得以增加,从而增大了极限曲率。由图14可以看出,极限曲率随着翼缘宽度与腹板高度比的增大而减小,这是由翼缘宽度的增大迫使截面受压区高度减小导致的。由图16可以看出,极限曲率随着腹板截面高厚比的增大而减小,这因为腹板截面高厚比的增大是由截面厚度减小所致,进而受压区高度也相应减小,特别是在轴压比较大中和轴位于腹板内时,其变化更为明显。
翼缘受拉方向的破坏是由腹板端部混凝土达到极限压应变控制的,由各图可以看出翼缘受拉方向极限曲率在不同参数下的取值范围较广,且变化规律各有不同。总体来看,除了腹板竖向分布钢筋配筋率和混凝土强度外,其余参数对极限曲率的影响均较为显著。极限曲率随着轴压比、纵筋配筋率、翼缘宽度与腹板高度比以及腹板截面高厚比的增大明显减小;这都是由受压区高度增大,混凝土更早达到极限压应变所致;同时极限曲率随着配箍特征值的增大而增大,这是因为配箍特征值的增大提高了混凝土的极限压应变,延缓了截面的破坏。
2.3 极限曲率的简化计算
通过2.2节的参数分析找出了影响极限曲率的主要因素,为了得到更为精确的回归结果,同样在上述正交分析的基础上进一步对这些主要因素影响下的极限曲率进行变参数的补充计算。本节对翼缘受拉方向极限曲率的五个主要影响因素分别按照表1取值,采用全面分析法对轴压比的7个水平,纵筋配筋率的5个水平、翼缘宽度与腹板高度比的5个水平、配箍特征值的5个水平以及腹板截面高厚比的5个水平共进行了(7×5×5×5×5)4375个工况的分析。同样对翼缘受拉方向极限曲率的三个主要影响因素按照表1取值,采用全面分析法对对轴压比的7个水平,翼缘宽度与腹板高度比的5个水平以及腹板截面高厚比的5个水平共进行了(7×5×5)175个工况的分析。
分析各组数据发现,对于翼缘受拉方向,随着轴压比的增大,极限曲率的减小呈现先快后缓的趋势,符合指数函数的曲线特征,而极限曲率与其余影响因素均近似呈线性关系,因此可采用多元线性函数与指数函数的组合进行回归。而对于翼缘受压方向,极限曲率与各影响因素也均近似呈线性关系,同样可采用多元线性函数进行回归。经回归分析,得到带翼缘剪力墙翼缘受拉方向极限曲率系数的计算表达式:
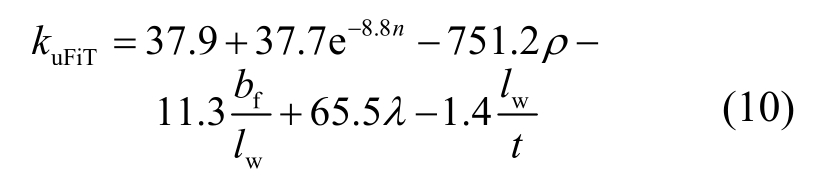
式中,下标u表示极限状态(ultimate)。
将式(10)代入式(9)即可得到翼缘受拉方向极限曲率的计算公式:
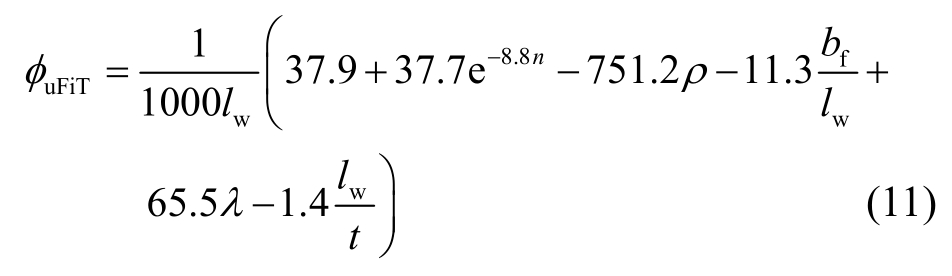
同样回归得到翼缘受压方向极限曲率系数的计算表达式:
代入式(9)即可得到翼缘受压方向极限曲率的计算公式:
式中:λ为配箍特征值;t为截面厚度。拟合式(10)和式(12)的相关系数均达到0.9,数据相关度较高,说明采用上述函数类型进行回归是合理的。
3 带翼缘剪力墙延性计算方法
前述分析分别建立了带翼缘剪力墙截面屈服曲率和极限曲率的计算方法,通过上述计算公式可得到翼缘受拉方向曲率延性的计算公式:

以及翼缘受压方向曲率延性的计算公式:
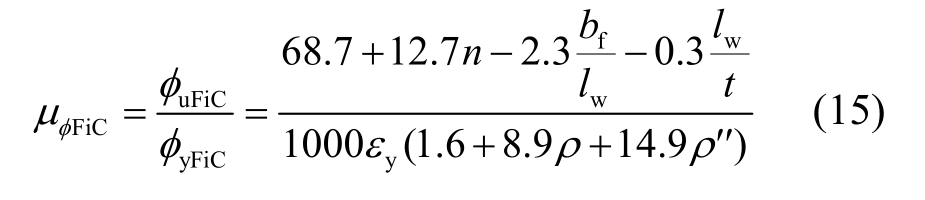
在忽略剪切变形和纵筋滑移变形影响的前提下,基于上述曲率延性计算式,采用Park等[20]提出的关系式可计算剪力墙的位移延性,即:
式中:he为墙肢有效高度,对于受集中荷载的剪力墙取荷载作用点至墙底的距离;lp为塑性铰区高度,依据文献[20]取lp=(0.2lw+0.044H),H为墙肢总高度。依据上述方法分别计算了文献[11]和文献[18]中7片发生弯曲破坏的T形墙试验试件的位移延性,将结果汇总于表3,并与试验结果进行对比。
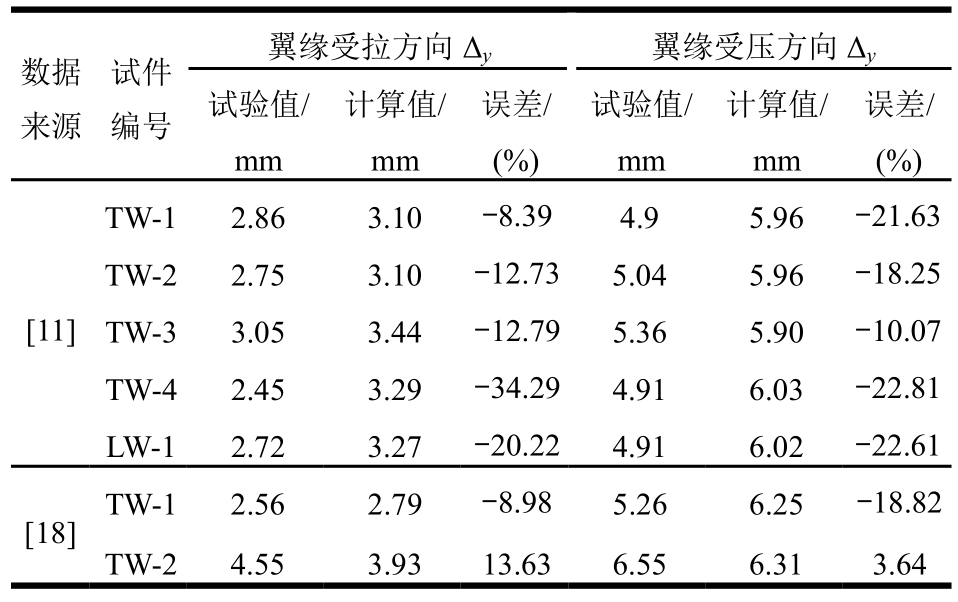
由表3可以看出,除个别情况外,本文公式计算得到的位移延性普遍大于试验值,特别是在翼缘受压方向计算值超过试验值达到20%左右,这首先是因为本文方法计算得到的是弯曲延性,而带翼缘剪力墙剪切变形可达到总变形的10%以上,势必会减小试件的位移延性。其次对于翼缘受压方向,其破坏是由腹板自由端压屈后的纵筋拉断导致的,而文本采用的单调加载无法准确考虑纵筋压屈对其极限拉应变的减小,从而一定程度上高估了翼缘受压方向的变形能力。另一方面文献[18]试验结束时翼缘受压方向的性能并未退化到计算设定的极限状态,个别试件甚至还未达到承载力极限状态,因此翼缘受压方向的计算结果普遍大于试验值。总体来看依照文本计算方法可较好地估算出带翼缘剪力墙的位移延性,可为变形能力计算以及基于位移的抗震设计提供依据。
表3 位移延性计算结果对比
Table 3 Comparison of displacement ductility results
数据来源翼缘受拉方向Δy 翼缘受压方向Δy试件编号试验值/mm计算值/mm误差/(%)试验值/mm计算值/mm误差/(%)TW-12.86 3.10 -8.39 4.9 5.96 -21.63[11]TW-22.75 3.10 -12.73 5.04 5.96 -18.25 TW-33.05 3.44 -12.79 5.36 5.90 -10.07 TW-42.45 3.29 -34.29 4.91 6.03 -22.81[18]TW-24.55 3.93 13.63 6.55 6.31 3.64 LW-12.72 3.27 -20.22 4.91 6.02 -22.61 TW-12.56 2.79 -8.98 5.26 6.25 -18.82
4 结论
(1)影响带翼缘剪力墙翼缘受拉方向屈服曲率的主要因素是轴压比、纵筋配筋率和翼缘宽度与腹板高度比。在轴压比较小受拉钢筋作为屈服的控制因素时,屈服曲率随着轴压比和翼缘宽度与腹板高度比的增大而增大;当轴压比较大受压混凝土成为屈服的控制因素后,屈服曲率随着轴压比和翼缘宽度与腹板高度比的增大而减小;屈服曲率始终随着纵筋配筋率的增大而增大。影响翼缘受压方向屈服曲率的主要因素是纵筋配筋率和腹板竖向分布钢筋配筋率。屈服曲率均随着纵筋配筋率和腹板竖向分布钢筋配筋率的增大而增大。
(2)影响带翼缘剪力墙翼缘受拉方向极限曲率的因素较多且取值范围较广。极限曲率随着轴压比、纵筋配筋率、翼缘宽度与腹板高度比以及腹板截面高厚比的增大明显减小;随着配箍特征值的增大而增大。翼缘受压方向各参数对极限曲率的影响较小,其中轴压比、翼缘宽度与腹板高度比和腹板截面宽厚比对其影响相对突出。极限曲率随着轴压比的增大而增大;随着翼缘宽度与腹板高度比和腹板截面高厚比的增大而减小。
(3)通过对4941个工况下计算结果的回归分析,建立了带翼缘剪力墙截面屈服曲率和极限曲率的简化计算公式、并进一步推导了曲率延性和位移延性的计算公式。通过与试验结果的比对,验证了计算公式的准确性。本文所建立公式不仅将翼缘受拉和翼缘受压状态进行了区分,并择取了影响截面曲率的关键因素,公式形式也相对简单,可为带翼缘剪力墙的变形能力计算以及基于位移的抗震设计提供依据。
[1]徐明雪, 梁兴文, 于婧, 等.UHPC梁短期刚度理论与试验研究[J].工程力学, 2019, 36(1): 146―154, 164.Xu Mingxue, Liang Xingwen, Yu Jing, et al.Theoretical and experimental investigation on immediate stiffness of UHPC beams [J].Engineering Mechanics, 2019, 36(1):146―154, 164.(in Chinese)
[2]李义柱, 曹双寅, 许鹏杰, 等.600 MPa级钢筋混凝土柱抗震性能试验研究[J].工程力学, 2018, 35(11):181―189.Li Yizhu, Cao Shuangyin, Xu Pengjie, et al.Experimental study on aseismic behavior of reinforced concrete columns with grade 600 MPa steel bars [J].Engineering Mechanics, 2018, 35(11): 181―189.(in Chinese)
[3]Priestley M J N, Kowalsky M J.Aspects of drift and ductility capacity of rectangular cantilever structural walls [J].Bulletin of the New Zealand National Society for Earthquake Engineering, 1998, 31(2): 73―85.
[4]Paulay T.An estimation of displacement limits for ductile systems [J].Earthquake Engineering and Structural Dynamics, 2002, 3l(10): 583―599.
[5]Tjen N T, Mark A A, John W W.Yield displacement estimates for displacement-based seismic design of ductile reinforced concrete structural wall buildings [C].13th World Conference on Earthquake Engineering,Vancouver B C, Canada, 2004: 1―15.
[6]赵花静, 梁兴文, 宋璨.高强混凝土剪力墙屈服位移计算方法[J].土木建筑与环境工程, 2014, 36(3): 80―85.Zhao Huajing, Liang Xingwen, Song Can.Yield displacement calculation method of high-strength concrete shear wall [J].Journal of Civil, Architectural & Environmental Engineering, 2014, 36(3): 80―85.(in Chinese)
[7]Massone L M , Alfaro J I.Displacement and curvature estimation for the design of reinforced concrete slender walls [J].Structural Design of Tall and Special Buildings,2016, 25(16): 823―841.
[8]钱稼茹, 吕文, 方鄂华.基于位移延性的剪力墙抗震设计[J].建筑结构学报, 1999, 20(3): 42―48.Qian Jiaru, Lü Wen, Fang Ehua.Displacement ductility-based aseismic design for shear walls [J].Journal of Building Structures, 1999, 20(3): 42―48.(in Chinese)
[9]Hu H S, Nie J G, Eatherton M R.Deformation capacity of concrete-filled steel plate composite shear walls [J].Journal of Constructional Steel Research, 2014, 103(1):148―158.
[10]张松, 吕新林, 章红梅.钢筋混凝土剪力墙构件极限位移的计算方法及试验研究[J].土木工程学报, 2009,42(4): 10―16.Zhang Song, Lü Xilin, Zhang Hongmei.Experimental and analytical studies on the ultimate displacement of RC shear walls [J].China Civil Engineering Journal, 2009,42(4): 10―16.(in Chinese)
[11]史庆轩, 王斌, 何伟锋, 等.带翼缘钢筋混凝土剪力墙抗震性能试验研究[J].建筑结构学报, 2017, 38(1):106―115.Shi Qingxuan, Wang Bin, He Weifeng, et al.Experimental research on seismic behavior of reinforced concrete shear walls with flange [J].Journal of Building Structures, 2017, 38(1): 106―115.(in Chinese)
[12]Smyrou E, Sullivan T, Priestley N, et al.Sectional response of T-shaped RC walls [J].Bulletin of Earthquake Engineering, 2013, 11(4): 999―1019.
[13]Sheikh M N, Tsang H H, Lam A.Estimation of yield curvature for direct displacement-based seismic design of RC columns [C].Australian Earthquake Engineering Conference, Victoria, Australia, 2008: 1―12.
[14]Mander J B, Priestley M J N, Park R.Theoretical stress-strain model for confined concrete [J].Journal of Structure Engineering, 1988, 114(8): 1804―1826.
[15]田建勃, 史庆轩, 刘云贺, 等.PRC连梁-混合联肢剪力墙抗震性能分析[J].工程力学, 2018, 35(11): 53―67.Tian Jianbo, Shi Qingxuan, Liu Yunhe, et al.Research on aseismic performance of PRC coupling beam-hybrid coupled shear wall system [J].Engineering Mechanics,2018, 35(11): 53―67.(in Chinese)
[16]GB 50010―2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB 50010―2010, Code for design of concrete structures[S].Beijing: Architecture Industry Press, 2010.(in Chinese)
[17]Brueggen B L.Performance of T-shaped reinforced concrete structural walls under multi-directional loading[D].America: University Of Minnesota, 2009.
[18]Thomsen J H, Wallace J W.Displacement-Based design of slender reinforced concrete structural walls—experimental verification [J].Journal of Structure Engineering, 2004, 130(4): 618―630.
[19]曹祖同, 陈云霞, 王玲勇, 等.钢筋陶粒砼压弯构件强度、延性和滞回性能的研究[J].建筑结构学报, 1998,9(6): 2―16.Cao Zutong, Chen Yunxia, Wang Lingyong, et al.Study on strength, ductility and hysteretic behavior of reinforced ceramsite concrete members subjected to axial load and flexural [J].Journal of Building Structures,1998, 9(6): 2―16.(in Chinese)
[20]Park R, Paulay T.Reinforced concrete structures [M].America: John Wiley & Sons, 1995.