悬索桥桥面系采用钢-混凝土组合桥面系是一种新的尝试,组合桥面系通过剪力连接件将混凝土板和钢梁组合在一起,能够发挥钢和混凝土两种材料的优势,实现力学性能的最优化[1-2],且具有施工便捷、承载性能优越等特点[3]。
在连续组合桥面系中负弯矩区混凝土容易受拉开裂[4],降低结构的整体承载力及耐久性,许多学者也对此开展了系列试验研究,聂建国等[5]开展了承受负弯矩作用的简支组合梁静力性能试验;Ansourian等[6]则开展了一批钢-混凝土连续组合梁试验。组合桥面系负弯矩区开裂传统的解决方法是施加预应力[7],但由于预应力损失、施工困难等问题导致预应力方案往往较少在大跨桥梁中采用。大跨桥梁中一种方法是采用简支方案架设桥面系以避免负弯矩区的出现,同时在支座处安装伸缩缝以达到受力和变形要求[8],但这种方法存在转角过大及耐久性不足的劣势,因此有必要研究新的方法解决组合桥面系负弯矩问题。
聂建国等[9]提出了一种新型抗拔不抗剪T型连接件(T型连接件)来改善连续组合桥面系负弯矩区的受力性能。T型连接件具有纵向不抗剪的特性,能有效释放钢-混凝土界面的剪力,进而降低负弯矩区混凝土板的拉应力;同时T型连接件也保留了传统栓钉抗混凝土板掀起的功能。针对这种T型连接件,聂建国等[10-11]开展了一系列实验,研究了连接件的抗拔性能及滑移性能,验证了其抗拔不抗剪的力学特性,并提出了模拟其滑移效应的滞回模型及抗拔承载力设计公式[12-13]。
目前针对T型连接件的试验全部集中在连接件层面,有必要进行体系层面的研究,探究T型连接件对组合桥面系力学性能的影响。而针对钢-混凝土桥面的现有试验大多为梁式试验[14-15],桥面系的试验研究较为缺乏;同时悬索桥桥面系与连续组合梁的受力模式存在差异,通过梁式试验来模拟悬索桥桥面系的力学性能存在一定误差。因此,本文开展了钢-混凝土组合桥面系的悬吊试验研究,探究T型连接件在组合桥面系中的实用性能,并基于试验情况建立了有限元模型进行进一步分析。基于构件变形特征、关键点应变等结果,重点分析了T型连接件对混凝土应力、桥面系抗弯刚度、扭转刚度等力学性能的影响;结合有限元分析结果,针对T型连接件塑料泡棉厚度、钢结构防屈曲设计等设计要点进行了总结。相关结论可为T型连接件在组合桥面系中的应用和后续研究提供参考;此外本文设计的悬吊系统加载方式能较好的反映出悬索桥受力特性,该方法可为悬索桥后续试验研究提供借鉴。
1 试验概况
1.1 试件设计
以某悬索桥初步设计方案的参数为基础,进行了试验构件设计;沿桥纵向及截面高度方向试件缩尺比为1∶5;考虑到试验场地限制,将截面宽度方向试件的缩尺比调整为1∶8。在此基础上,考虑到实验室提供的钢材板厚及加工条件限制,将钢结构的尺寸进行了调整,调整前后组合截面的抗弯惯性矩、钢结构截面的抗弯惯性矩分别保持一致。
试件采用双工字型组合截面,缩尺后试件长度为8.0 m、宽度为4.0 m、高度为0.425 m,其中钢梁高0.375 m,混凝土板厚50 mm;工字钢截面的上翼缘、腹板、下翼缘截面尺寸分别为160 mm×10 mm、353 mm×12 mm、300 mm×12 mm。构件共3跨,每跨2.5 m,此外在边跨吊点处各外延0.25 m;每个吊点处设置连接装置,用于吊杆和桥面系的连接。试件设计尺寸可参见图1。
在试件连接件的布置中,为研究不同界面性能对组合截面构件的影响,试件南侧采用传统栓钉连接件,栓钉直径6 mm、高40 mm,横向双排布设,纵向间距为50 mm。试件北侧采用T型连接件,T型连接件由T型钢板及外覆塑料泡棉组成,如图2所示。T型钢板中翼板沿桥纵向长20 mm,腹板高36 mm;翼板及腹板沿桥横向宽30 mm,板厚4 mm。为实现T型连接件纵向不抗剪的特性,在T型钢板外覆盖塑料泡棉,塑料泡棉厚5 mm。其中翼板处塑料泡棉能避免混凝土与T型钢板翼板接触,释放此处界面(混凝土与T型钢板翼板界面)粘结传递的剪力;腹板处塑料泡棉能为钢梁及混凝土板的界面滑移提供滑移空间[13]。基于聂建国等[13]的研究成果,塑料泡棉提供的有效滑移空间略大于其厚度的1/3。T型连接件采用单列布置,纵向间距为200 mm。
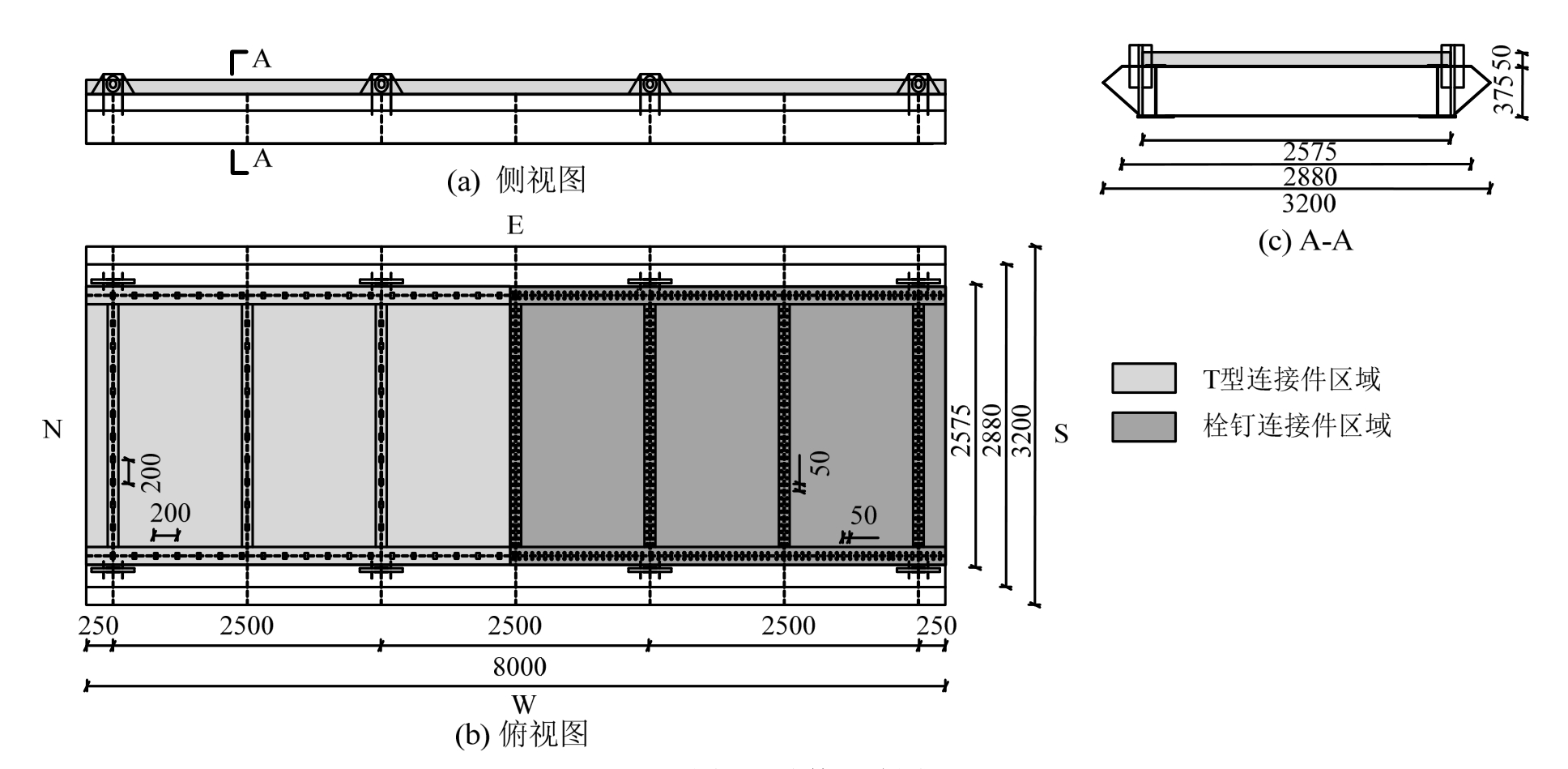
图1 试件尺寸图 /mm
Fig.1 Overall view of the specimen
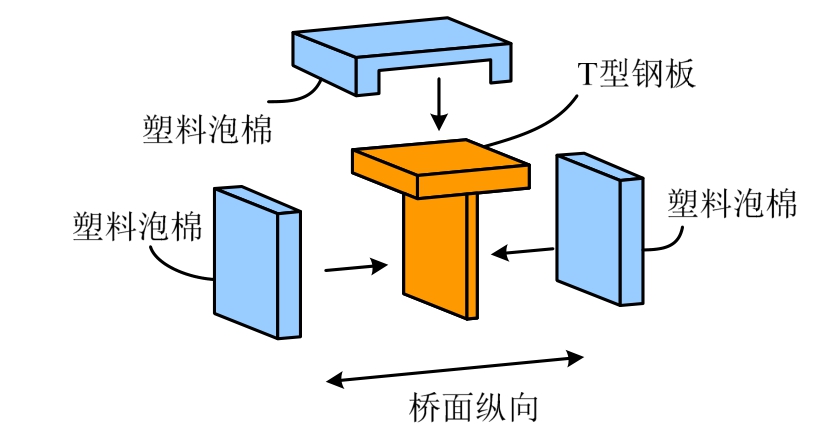
图2 T型连接件构造图
Fig.2 Dimensions for the URSP-T connector
试验悬吊装置的轴测图见图3,采用8个钢结构柱做支承,在柱子相应高度悬臂伸出一个梁段,并在悬臂梁对应位置开竖向孔,8根吊杆穿过该竖向孔固定在悬臂梁上;吊杆下端则与桥面板进行连接,形成三跨连续悬索桥桥面系受力体系。
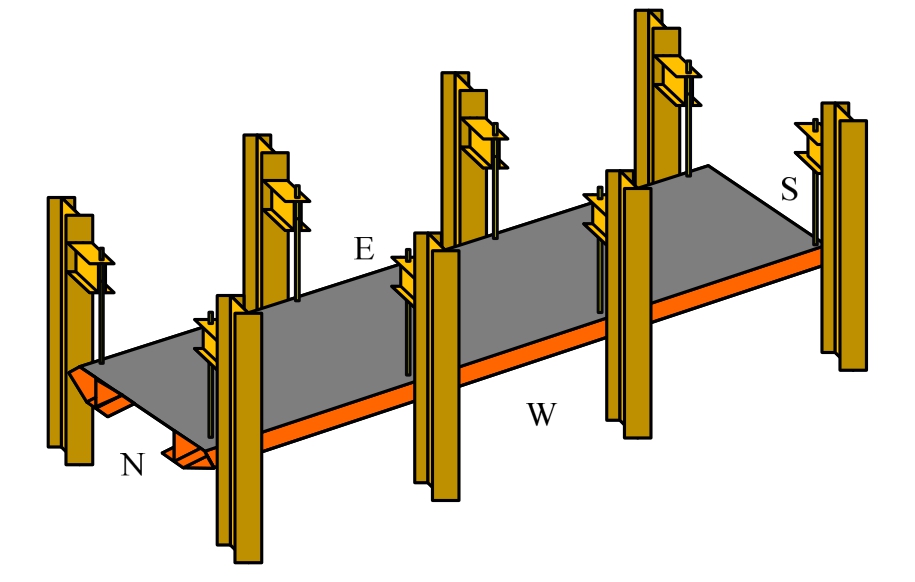
图3 试验吊装装置设计图
Fig.3 Schematic diagram of the test set up
1.2 试件制作及吊装
试件制作包括钢结构加工、连接件安装、混凝土浇筑等。进行T型连接件安装时,首先需将T型钢板焊接到预定位置,然后制作预定尺寸的塑料泡棉,并将其贴于T型钢板的外侧及顶部,见图4。
试验的布置安装见图5。试件通过8根吊杆吊装在相应的柱子上。南、北两侧分别设置2个千斤顶用于加载,两个大刚性梁作为千斤顶的反力支承安置在反力架上。

图4 T型连接件安装图
Fig.4 URSP-T connector installation

图5 试验布置安装图
Fig.5 A general view of the test set-up
在吊装过程中,按照预先计算的各吊杆分布力情况调整吊杆内力;吊杆自身安装调整装置,其吊杆内力通过设置在吊杆顶端的力传感器传输到电脑进行调整。吊杆和桥面系的连接采用插入扣装置;竖向传力板由桥面系底部贯穿伸出并在顶部留有孔洞,吊杆底部伸出装置亦留出孔洞,通过钢块插入两者共同的孔洞完成传力连接,见图6。

图6 吊杆桥面连接细部图
Fig.6 Detail of hanger and bridge deck connection
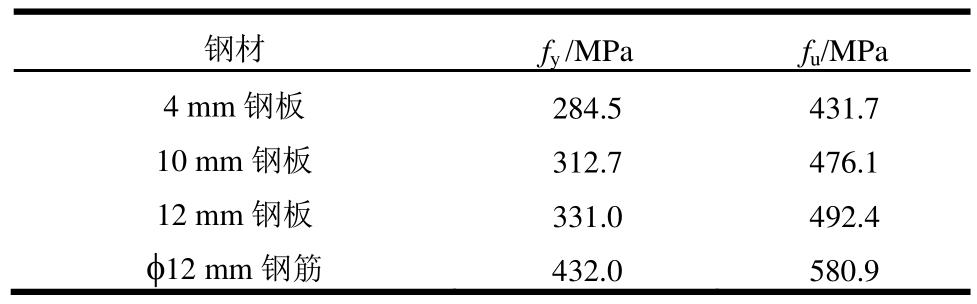
试验所采用的混凝土受压材性件为150 mm立方体,其受压强度为fcu=38.19 MPa。试验中钢板、钢筋的的材料性质见表1。
表1 钢材材性表
Table 1 Material properties of steel
钢材 fy /MPa fu/MPa 4 mm钢板 284.5 431.7 10 mm钢板 312.7 476.1 12 mm钢板 331.0 492.4 φ12 mm钢筋 432.0 580.9
1.3 加载方案
本试验拟采用不同方案进行加载,分为三部分:弹性工况加载、扭转工况加载和极限工况加载。针对不同的加载工况采用不同的加载方案。
1.3.1 弹性工况
弹性工况的加载方案见图7,采用千斤顶对相应跨的跨中进行加载。弹性阶段采用4个工况,分别为工况1:西侧(W)加载;工况2:北侧(N)加载;工况3:南侧(S)加载;工况4:南北侧(SN)加载。弹性工况加载时各千斤顶加载至30 t停止加载。
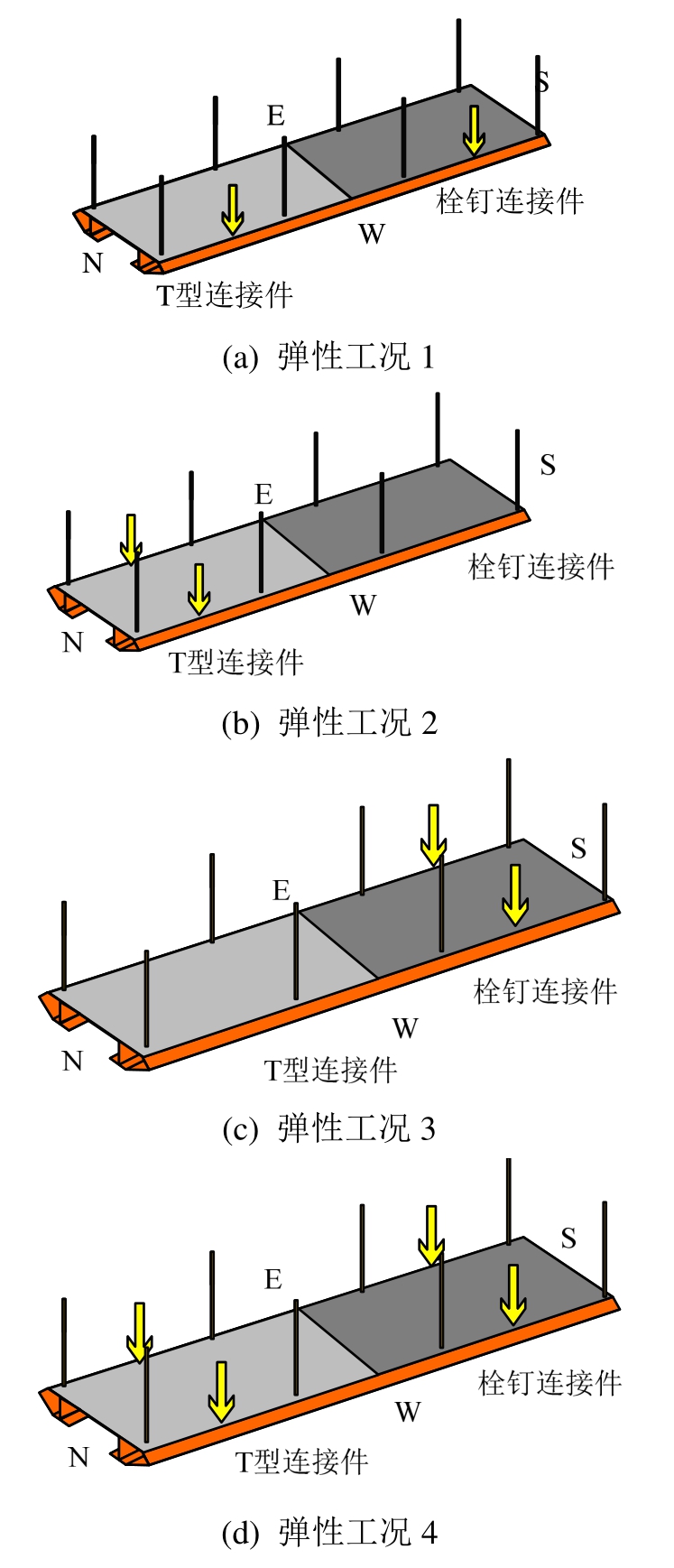
图7 弹性加载方案
Fig.7 Elastic working conditions
1.3.2 扭转工况
扭转工况加载方案见图8,采用中跨单侧加载的方式进行扭转加载,千斤顶加载至30 t时停止加载。
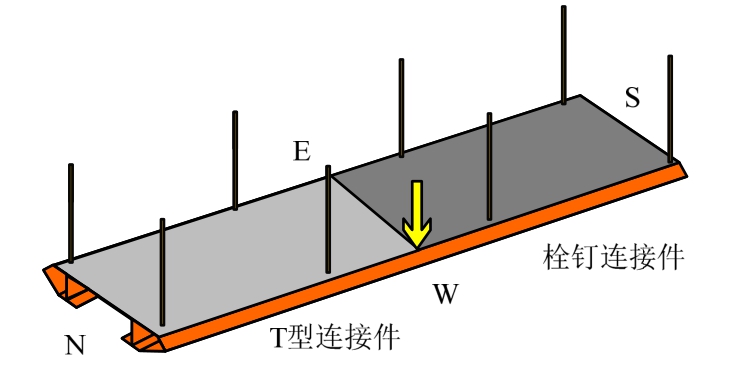
图8 扭转加载方案
Fig.8 Torsional working condition
1.3.3 极限工况
极限工况加载方案见图9,加载时去掉中跨两对吊杆,并在跨中施加集中荷载,直至试件破坏。
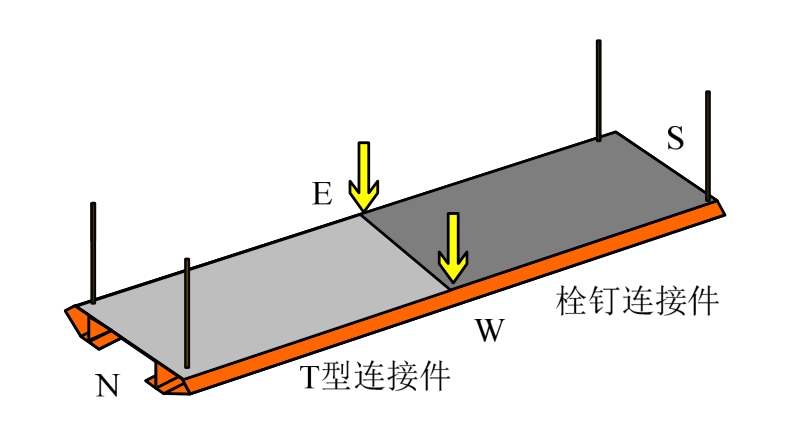
图9 极限加载方案
Fig.9 Ultimate working condition
1.4 量测方案
试验的量测方案包括力的量测、变形的量测及应变的量测。其中对力的量测包括加载千斤顶反力的量测及吊杆力的量测。
变形的量测分为三部分,第一部分是各跨跨中的竖向挠度;第二部分是各吊杆底部处的竖向变形。由于吊杆都有各自的刚度,第一部分测得的竖向挠度实际包含了吊杆的变形,因此需要对每个吊杆进行竖向变形的量测,基于这两部分的量测结果可以推测桥面系的实际竖向变形。第三部分是监测位移计,安置于南北侧东西水平向和南北水平向,用于检测桥面系水平面内的整体平动和转动,一旦有过大变形便停止加载。
应变的量测包括两部分,第一部分是钢结构应变,着重量测钢梁底部的纵向应变;第二部分是混凝土应变,着重量测顶板的纵向应变。钢结构及混凝土应变片主要布设在图10所示的5个截面上,图中a1、a3、a5为各跨跨中截面,a2、a4为中吊杆所在截面。在每个截面混凝土顶板均匀布设5个混凝土应变片,工字钢底板、横隔 板底板布设钢结构应变片。后续试验结果描述中,a1~a5截面混凝土应变结果依次用编号1~5表明其位置,钢结构应变结果依次用编号6~10表明其位置。
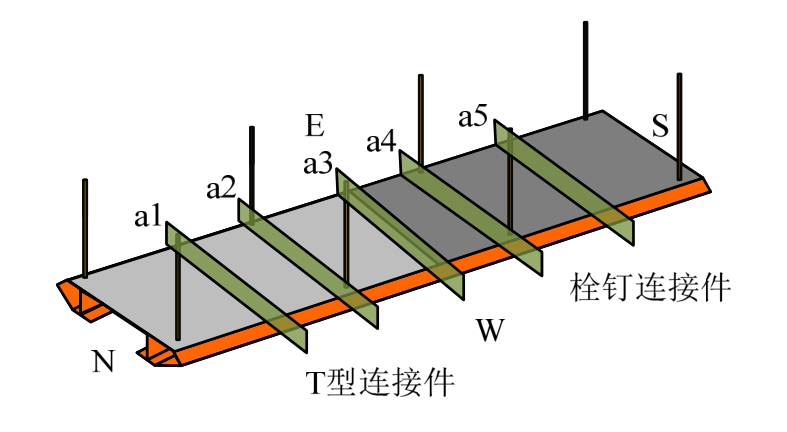
图10 应变片布置情况
Fig.10 Strain gauge arrangement of the test
2 试验现象和结果
2.1 弹性工况试验结果
将弹性工况的相关试验结果进行汇总,并选取有代表性的工况进行具体分析。总体来说,弹性工况下,桥面系仍处在正常使用阶段,加载过程中栓钉一侧发现裂缝的时间早于T型连接件一侧,此外栓钉一侧裂缝宽度也大于T型连接件一侧。
2.1.1 竖向变形
以工况1的结果为例,图11(a)表示量测直接得到的加载点挠度结果,当加载到30 t时,北侧(T件侧)量测挠度为6.95 mm,南侧(栓钉侧)量测挠度为6.78 mm。
本文悬吊加载的构件本质为弹性支撑连续结构,吊杆可视为弹簧支座,桥面系可视为主梁,由于吊杆的变形会使得桥面系存在一定的整体变形(可视为刚体位移),为更直观的反映桥面系的变形情况,将剔除整体变形后的竖向位移结果称为有效变形。有效变形能反映出吊杆刚度及桥面系刚度的特征。图11(b)即为有效变形结果,北侧有效挠度为1.74 mm,南侧有效挠度为1.47 mm,表明T件侧的结构刚度低于栓钉侧的结构刚度。
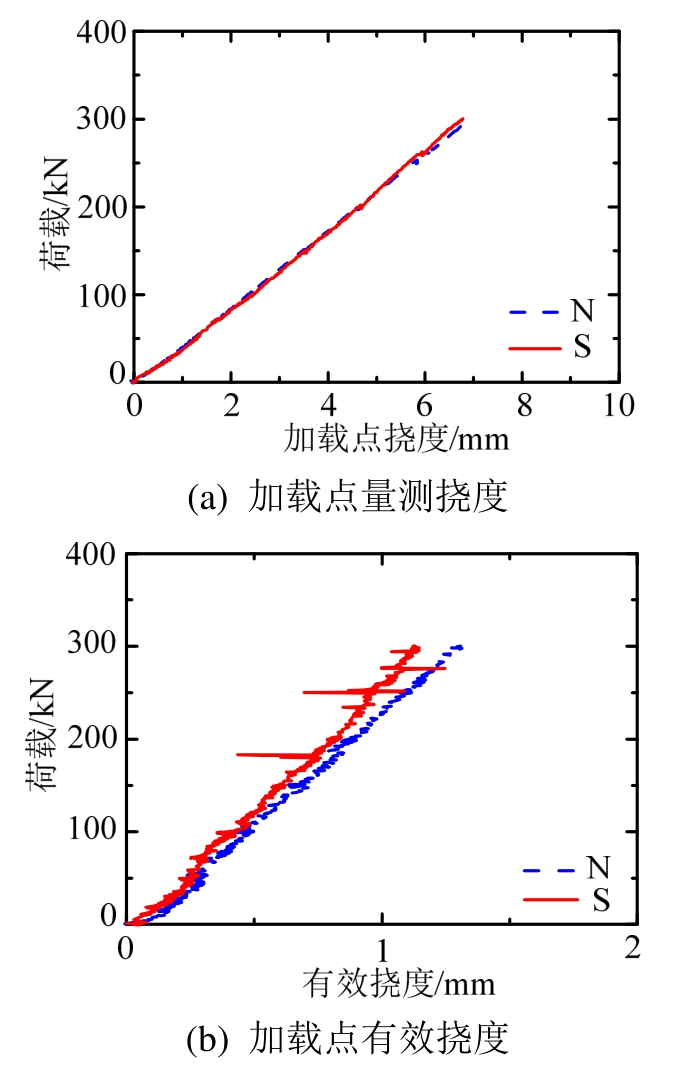
图11 竖向变形:工况1
Fig.11 Vertical deflection of working condition I
表2汇总了弹性工况下(各千斤顶加载到30 t时)加载点处构件的竖向变形。分析对比表中数据,主要有以下特点:
1) 在所有工况下,北侧有效挠度均大于南侧有效挠度,表明T型连接件的使用虽然缓解了混凝土负弯矩开裂问题,但在一定程度上降低了组合结构截面弯曲刚度。
表2 弹性工况竖向变形结果
Table 2 Vertical deflection of elastic working conditions

工况号 加载点 加载点量测挠度/mm 加载点有效挠度/mm N S N S 1 西侧边跨跨中 6.95 6.78 1.74 1.47 2 北侧边跨跨中 7.77 ― 2.73 ―3 南侧边跨跨中 ― 7.44 ― 2.49 4 南北侧边跨跨中 7.44 7.10 2.14 1.86
2) 对比量测挠度和有效挠度,结果表明由于吊杆具有一定竖向刚度,桥面系的有效挠度仅为量测挠度的一部分,其比例与吊索系统的竖向刚度和桥面系的竖向刚度比例相关。对于悬索桥,随着跨度的增大,吊索系统的竖向刚度在总刚度中比例迅速增大,因此桥面系刚度的比重迅速降低,这明显区别于传统连续梁体系。本文开展的悬吊试验也有力地验证了悬索桥的变形特点。
2.1.2 关键点应变
工况1为西侧加载,工况4为南北侧加载,两种工况的应变结果呈现出相似的规律。以工况4结果为例,图12为关键点应变的分布图,对比南、北两侧应变,发现北侧钢结构受拉应变值大于南侧,而北侧混凝土拉应变小于(或压应变大于)南侧。结果也表明了T型连接件一方面会降低混凝土拉应变,另一方面会导致正弯矩下底部钢结构应变变大。
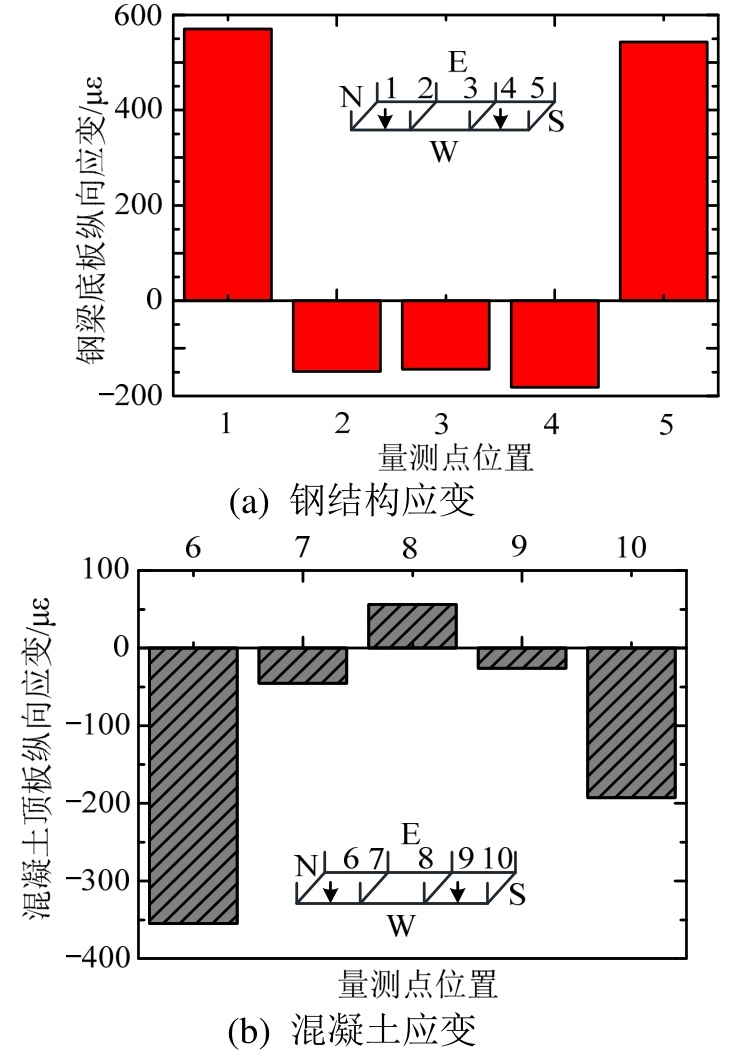
图12 应变结果:工况4
Fig.12 Strain results of working condition IV
工况2为北侧加载,工况3为南侧加载,两种工况的应变结果呈现出相似的规律。以工况2结果为例,图13为关键点应变的分布图,可以看出钢结构应变呈现由北向南逐渐减小的趋势,在位置4处降低到最大值;混凝土应变由压应变向南逐步变为拉应变,在位置9处达到最大值。该现象与传统连续梁有明显不同,连续梁会在相邻跨产生正、负弯矩的转换,但该试验中在接近隔一跨位置正弯矩才逐渐转换为负弯矩,原因为试验中构件是进行悬吊加载,而吊杆有一定的竖向刚度,此为真实悬索桥桥面系内力状态与连续梁内力状态的差异。通过采用悬吊试验的方式将这一特征展现,更接近悬索桥桥面系实际受力状态,是本试验的一个亮点。
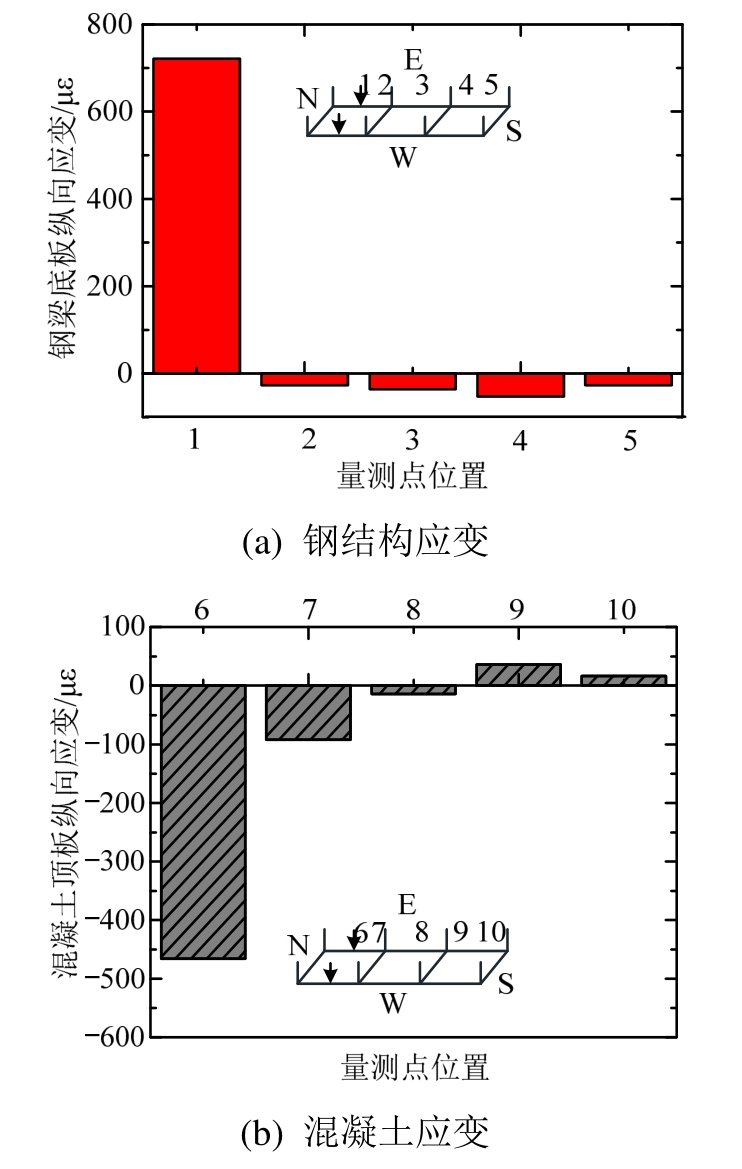
图13 应变结果:工况2
Fig.13 Strain results of working condition II
2.2 扭转工况试验结果
构件采用中跨跨中加载的方式进行扭转加载。通过每个吊杆的内力变化,可计算得到扭矩的大小;通过各吊点处的竖向位移计,可以计算得到各吊杆截面的转角;这样便可以计算得到该处截面的扭转刚度,其计算公式为:
式中:φ表示扭转角;T表示扭矩;dl表示计算长度;GI表示扭转刚度。
采用上述加载方式,得到构件的扭转角-扭矩关系曲线,如图14所示。曲线相对线性,但抖动比较大,原因主要为试验是中跨跨中加载,边跨吊杆受力较小,发生微小抖动就会造成吊杆内力值的跳动,引发不稳定的结果。构件刚度计算的结果如表3所示。
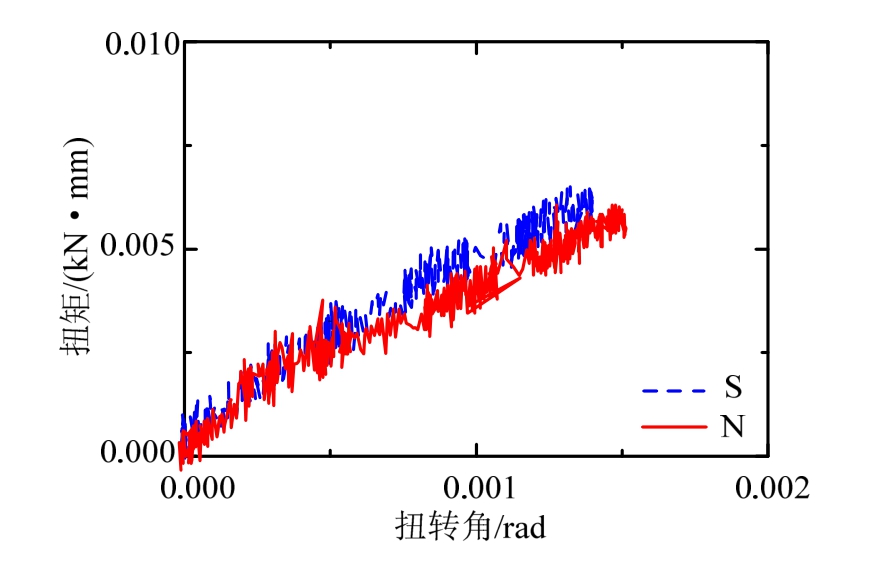
图14 扭转角-扭矩曲线
Fig.14 Curve of the rotational angle and the torque
表3 构件扭转刚度计算结果 /(kN·mm2/rad)
Table 3 Torsional stiffness of test specimens
位置(北侧/南侧) N S扭转刚度 3.66×1010 4.07×1010
结果表明相较于北侧扭转刚度,构件南侧扭转刚度更大一些。T型连接件的使用会使得桥面系扭转刚度(横桥向刚度)有一定程度降低,但降低幅度不大(约10%)。基于T型连接件的构造,初步分析可认为T型连接件外包的塑料泡棉会使得横桥向刚度产生一定程度降低,故需要进一步探究T型连接件对横桥向刚度的影响。
2.3 极限工况试验结果
进行极限工况加载时去掉中跨的4根吊杆,采用中跨千斤顶进行加载,在此加载模式下,跨径变成之前状态的3倍,相同荷载下构件变形会迅速增大,破坏荷载也会提前。极限工况下中跨跨中位置(即图10所示的a3截面)的荷载-位移曲线如图15所示。极限工况下试验现象如下:在荷载15 t之前,荷载-位移曲线呈线性;当加载到20 t时,跨中混凝土的板底发生开裂;底部钢结构在荷载施加到27.46 t时屈服,构件达到屈服荷载,此时对应的跨中最大挠度为46.15 mm;在30 t附近,钢混凝土交界面开始出现明显的纵向滑移,南侧(栓钉)不明显,在北侧(T件侧)有明显错动痕迹;当加载到37.8 t时,由于滑移的存在,混凝土与吊杆处加劲肋发生挤压,产生混凝土开裂;加载到41.8 t时达到最大荷载,对应的挠度为181.21 mm,此后荷载开始下降;当荷载降至40.0 t时,混凝土大面积脱落,中间顶部混凝土压溃,顶板钢板压屈,加载停止。
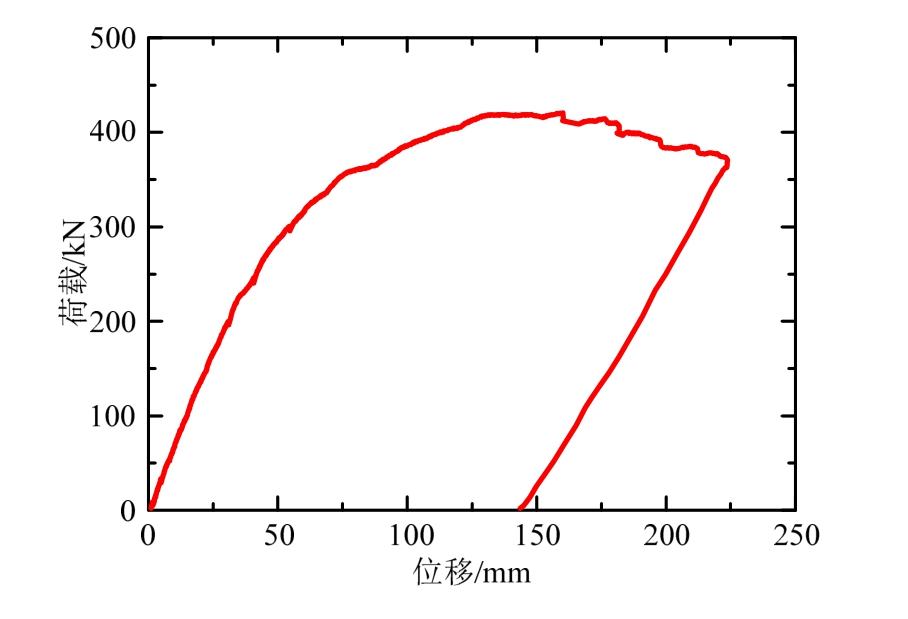
图15 极限工况下跨中位置荷载-位移曲线
Fig.15 Curve of load and vertical displacement in the middle span under ultimate working condition
图16所示为构件破坏后的局部形态。图16(a)为跨中混凝土压溃形态;图16(b)为T型连接件一侧的端部滑移情况,破坏状态下最大滑移接近20 mm;图16(c)和图16(d)为T型连接件的残余变形,用工具剔除混凝土后发现T型连接件产生很大的残余变形,从T型连接件的残余变形可看出其纵向刚度很弱,具有纵向不抗剪的特性。考虑到T型连接件同时具有抗掀起的作用,在正常使用阶段应尽量避免T型钢板受到显著的剪力作用,即设计时连接件两侧的塑料泡棉厚度应满足正常使用阶段界面的滑移量要求。

图16 破坏形态(极限工况)
Fig.16 Failure morphology (ultimate working condition)
为了更明晰地对比T型连接件一侧和栓钉一侧刚度,将北侧及南侧边跨跨中位置(即图10所示的a1、a5截面)的荷载-位移曲线进行作图,见图17所示。实线代表栓钉一侧,虚线代表T型连接件一侧。从图中可明显观察到在屈服荷载之前,两条曲线几乎重合;达到屈服荷载后,出现一定差异;在达到最大荷载后试验中观察到明显滑移时,两条曲线差距迅速变大。数据表明T型连接件可以保证正常使用阶段正弯矩下的桥面系刚度,而在屈服荷载后会发生界面滑移而导致刚度降低。
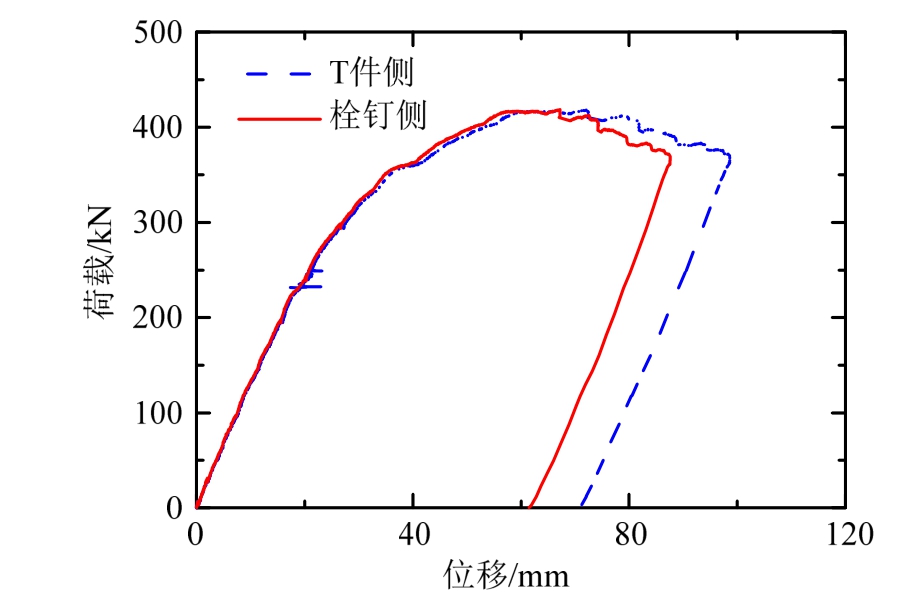
图17 T件侧与栓钉侧荷载-位移曲线对比
Fig.17 Curves of load and vertical displacement fo r symmetric points between the URSP-T connector side and stud side
3 有限元分析
3.1 有限元模型
为进一步研究T型连接件的力学性能,基于通用有限元软件ANSYS建立了组合桥面系的精细有限元模型,并与试验结果进行对比,对其受力特性展开分析。
有限元模型中混凝土采用SOLID65单元模拟,采用Rüsch曲线[16]作为单轴混凝土本构。钢梁采用SHELL181单元模拟,钢材的应力-应变采用四折线本构。为准确模拟不同连接件的受力性能,采用非线性弹簧单元COMBIN39建立混凝土板和钢梁之间的连接。针对栓钉的剪力滑移曲线,选用Ollgaard等[17]的研究成果;针对T型连接件的剪力滑移曲线,采用聂建国等[13]提出的三折线模型,并基于试验中T型连接件尺寸及材性进行相关参数标定。吊杆单元亦采用弹簧单元COMBIN39模拟。
基于试验边界条件,有限元模型中吊杆顶端采用全自由度约束,吊杆底端直接连接在桥面系吊杆处。为防止构件侧向及纵向变形过大,对一侧的吊杆底端点约束其侧向位移,对垂直一侧的吊杆底端点约束其纵向位移。有限元加载采用与试验相同的加载方案,分为三部分:弹性加载、扭转加载和极限加载,有限元模型如图18所示。
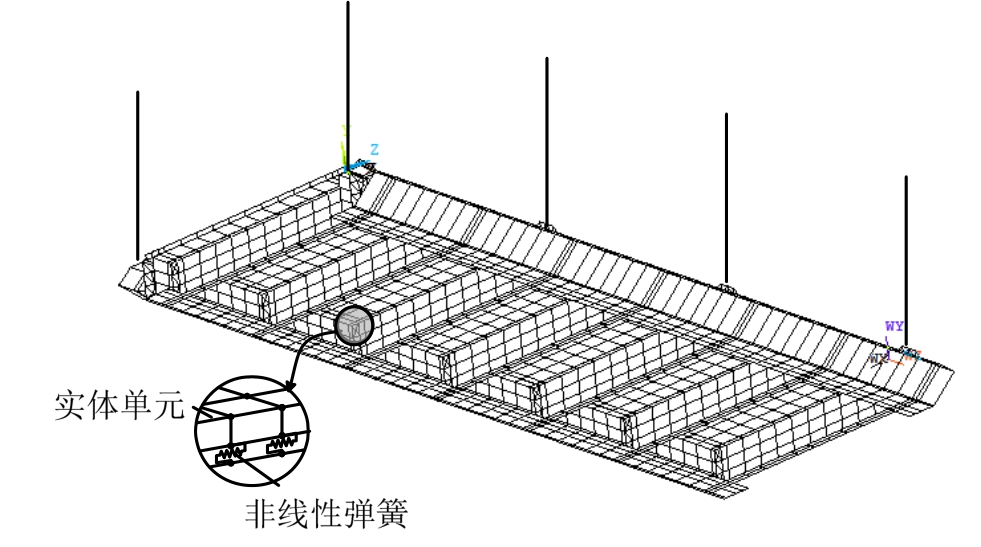
图18 试验的有限元模型
Fig.18 FEA model of the test
3.2 弹性工况
表4为弹性工况下构件加载点变形的对比结果,有限元计算的竖向位移及有效变形结果与试验结果吻合良好,计算平均误差为2%以内。在竖向位移对比中,有限元结果略高于试验结果,这可能是吊杆刚度的数据在试验量测中偏小所致。而对于实际变形,有限元结果与试验结果吻合精度高,验证了有限元模型的有效性。
表4 弹性工况变形对比
Table 4 Elastic results of the deflection
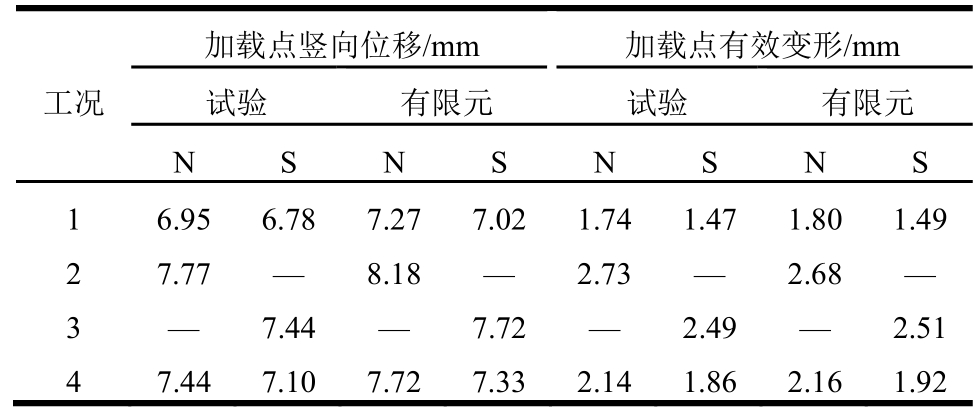
加载点竖向位移/mm 加载点有效变形/mm工况试验 有限元 试验 有限元N S N S N S N S 1 6.956.787.277.02 1.74 1.47 1.801.49 2 7.77— 8.18— 2.73 — 2.68—3 — 7.44— 7.72 — 2.49 — 2.51 4 7.447.107.727.33 2.14 1.86 2.161.92
图19为关键点钢结构和混凝土应变对比结果,图中有限元结果和试验结果两者总体吻合。总体来说,钢结构底板的应变误差相对较小,而混凝土应变误差相对较大。这是因为混凝土应变的试验量测受到加载装置的影响,由于局部承压等效应导致量测结果不够准确,有限元模拟则不会产生上述问题,不过总体来说混凝土应变误差大小在可接受范围内。此外,对比工况2北侧加载点(位置1/位置6)与工况3南侧加载点(位置5/位置10)的应变结果,可看出在T件侧加载时(工况2)混凝土顶板压应变更大,钢结构底板拉应变也相应更大。该结果表明相较于传统的栓钉,T型连接件的使用降低了截面的组合作用,也验证了T型连接件不抗剪的特性。

图19 弹性工况应变对比
Fig.19 Elastic results of the stress
3.3 扭转工况对比
有限元采用与试验相同的加载方式进行扭转工况加载,荷载施加在西侧中跨跨中位置。将有限元计算得到的加载点荷载-位移曲线与试验曲线进行对比,如图20所示。在300 kN集中荷载作用下,有限元算得到的加载点挠度为7.30 mm,与试验结果误差为0.1%。
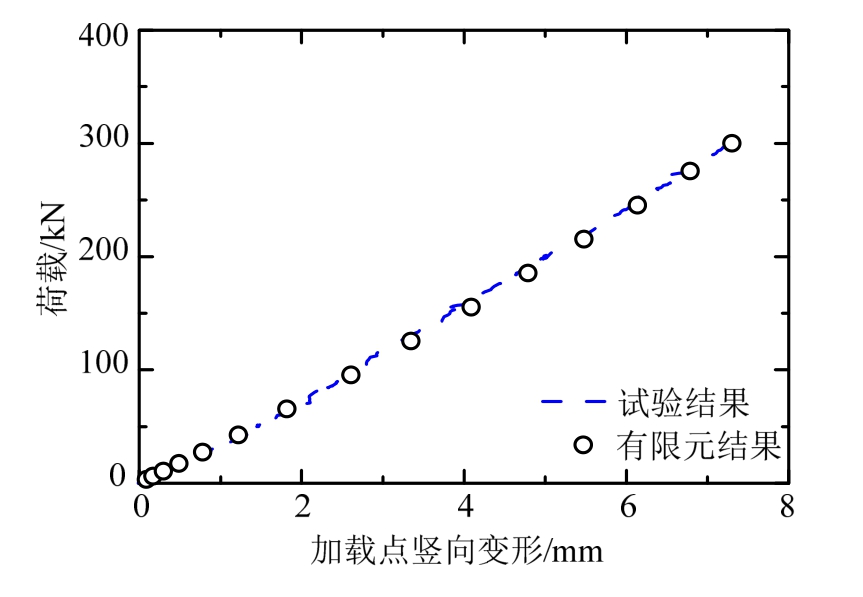
图20 扭转工况荷载-位移对比
Fig.20 Load- displacement curve under torsional condition
3.4 极限工况对比
极限工况下,将有限元计算得到的中跨跨中位置荷载-位移曲线与试验曲线进行对比,如图21所示。从图中可看出有限元模型在初始刚度和屈服强度方面精度可靠,但计算的极限强度偏高,这是因为ANSYS模型中对于混凝土开裂模拟不够准确,需要更精细的开裂模型才能得到更合理的结果。
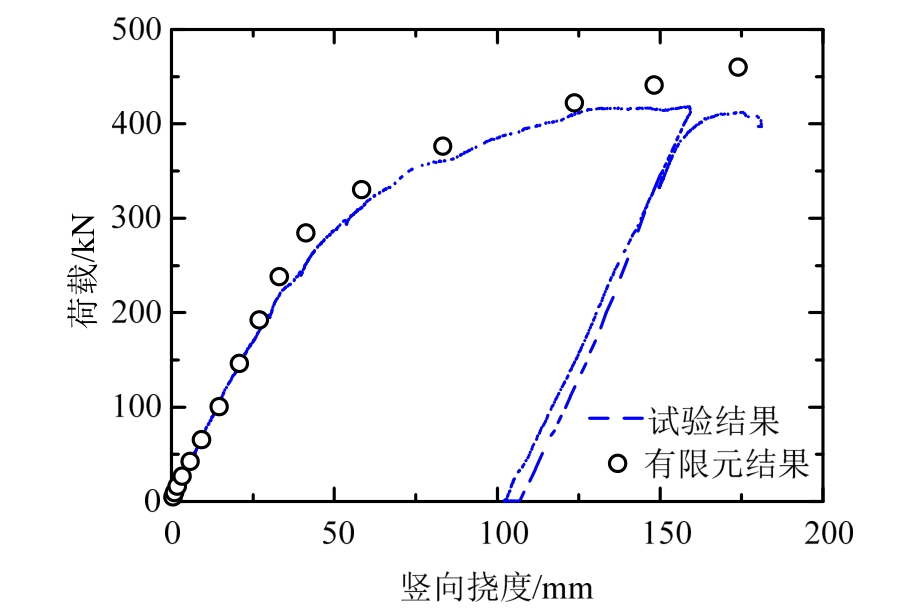
图21 极限工况荷载-位移曲线对比)
Fig.21 Load-displacement curve under ultimate condition
图22所示为试件关键截面的竖向应变分布。从有限元模型中提取两组对称位置的截面进行分析,图22(a)为边跨跨中截面沿着高度方向的应变,图22(b)为中间吊杆处截面沿着高度方向的应变分布。图中黑色实线代表T件侧,虚线代表栓钉侧。从图22可看出顶板处混凝土压应变在T件侧更大,但混凝土底板拉应变也增大。由于T型连接件对界面的削弱,钢结构的顶板压应变和底板拉应变也都比栓钉一侧大,符合T型连接件降低截面刚度引起的应变分布特点。而在弯矩更大的位置,T件侧与栓钉侧应变差距会有所提高,如图22(b)所示。实际设计使用中,应避免T型连接件应用在弯矩较大的正弯矩区,避免混凝土底部较大的拉应变以及钢梁顶板较大的压应变。

图22 极限工况截面应变分布
Fig.22 Strain distribution of cross-section under ultimate condition
4 结论
本文设计并开展了钢-混凝土组合桥面系悬吊加载的试验,试验构件对称布设新型抗拔不抗剪T型连接件和栓钉以探究T型连接件对桥面系力学性能的影响。同时建立了有限元模型,并将试验结果与有限元结果进行分析对比。基于试验现象及相关分析结果,主要结论如下:
(1)T型连接件能有效降低混凝土拉应变,在缓解负弯矩混凝土开裂方面效果显著。但同时由于T型连接件降低了组合作用,一定程度上增大了钢结构的应力,在负弯矩中使用T型连接件应注意钢结构受压应力的控制以及防屈曲的设计。
(2)基于极限工况结果,正常使用阶段T型连接件对桥面系刚度影响较小;在屈服荷载后才会因显著的界面滑移导致刚度下降,使得极限承载力也略有下降;此外扭转工况表明,T型连接件也会一定程度降低桥面系扭转刚度。
(3)有限元模型中T型连接件的剪力-滑移曲线采用聂建国等[13]提出的三折线模型进行模拟,相应的有限元计算结果与试验吻合良好。表明三折线模型能够准确模拟出T型连接件的受力特性。
(4)本文开展的悬吊试验有力地验证了悬索桥的变形特点,试验结果也体现出悬索桥桥面系与连续梁受力状态的差异,基于悬吊系统的试验方法可为悬索桥试验研究提供借鉴。
[1]聂建国, 余志武.钢-混凝土组合梁在我国的研究及应用[J].土木工程学报, 1999, 32(2): 3―8.Nie Jianguo, Yu Zhiwu.Research and practice of composite steel-concrete beams in China [J].China Civil Engineering Journal, 1999, 32(2): 3―8.(in Chinese)
[2]钟新谷, 舒小娟, 郑玉国, 等.钢箱-混凝土组合梁正截面承载力的初步研究[J].土木工程学报, 2002, 35(6):73―78.Zhong Xingu, Shu Xiaojuan, Zheng Yuguo, et al.Research on bearing capacity of steel box-concrete composite beams[J].China Civil Engineering Journal, 2002, 35(6): 73―78.(in Chinese)
[3]Viest I M.Investigation of stud shear connectors for composite concrete and steel T-beams [J].Journal of the American Concrete Institute, 1956, 27(8): 875―891.
[4]张彦玲, 樊健生, 李运生.连续组合梁桥裂缝发展规律分析及裂缝宽度计算[J].工程力学, 2011, 28(7): 84―90.Zhang Yanling, Fan Jiansheng, Li Yunsheng.Law of crack development and calculation of crack width of continuous composite beams [J].Engineering Mechanics, 2011, 28(7):84―90.(in Chinese)
[5]聂建国, 李法雄, 樊健生, 等.不同翼板形式组合梁受弯性能试验研究[J].公路交通科技, 2009, 26(10): 53―58.Nie Jianguo, Li Faxiong, Fan Jiansheng, et al.Experimental study on flexural behavior of composite beams with different styles of concrete flange [J].Journal of Highway and Transportation Research and Development, 2009, 26(10): 53―58.(in Chinese)
[6]Ansourian P.Experiments on continuous composite beams[C]// Proceedings of the Institution of Civil Engineers.Sydney: School of Civil Engineering, University of Sydney, 1981: 25―71.
[7]胡少伟, 叶祥飞.预应力连续组合梁负弯矩区抗弯承载力分析[J].工程力学, 2013, 30(11): 160―165.Hu Shaowei, Ye Xiangfei.Analysis on the bending capacity of the negative moment region in prestressed continuous composite beams.[J].Engineering Mechanics,2013, 30(11): 160―165.(in Chinese)
[8]王忠彬, 杨进, 周平.鹦鹉洲长江大桥钢-混结合梁悬索桥方案研究[J].桥梁建设, 2010, 2010(4): 52―56.Wang Zhongbin, Yang Jin, Zhou Ping.Study of steel and concrete composite girder suspension bridge scheme for Yinwuzhou Changjiang River Bridge [J].Bridge Construction, 2010, 2010(4): 52―56.(in Chinese)
[9]聂建国, 陶慕轩, 聂鑫, 等.抗拔不抗剪连接新技术及其应用[J].土木工程学报, 2015, 48(4): 7―14, 58.Nie Jianguo, Tao Muxuan, Nie Xin, et al.New technique and application of uplift-restricted and slip-permitted connection [J].China Civil Engineering Journal, 2015,48(4): 7―14, 58.(in Chinese)
[10]聂建国, 李一昕, 陶慕轩, 等.新型抗拔不抗剪连接件抗拔性能试验[J].中国公路学报, 2014, 27(4): 38―45.Nie Jianguo, Li Yixin, Tao Muxuan, et al.Experimental research on uplift performance of a new type of uplift restricted-slip free connector [J].China Journal of Highway and Transport, 2014, 27(4): 38―45.(in Chinese)
[11]聂建国, 马原.抗拔不抗剪栓钉连接件抗拔性能试验研究[J].特种结构, 2015, 32(3): 6―12.Nie Jianguo, Ma Yuan.Experimental study on uplift restricted-slip free connector [J].Special Structures, 2015,32(3): 6―12.(in Chinese)
[12]聂建国, 李一昕, 陶慕轩.新型抗拔不抗剪连接件的滑移性能及其滞回模型[J].工程力学, 2014, 31(11): 46―52.Nie Jianguo, Li Yixin, Tao Muxuan.Slip performance and hysteresis model of a new type of uplift restricted-slip free connectors [J].Engineering Mechanics, 2014, 31(11): 46―52.(in Chinese)
[13]Nie J G, Li Y X, Tao M X, et al.Uplift-restricted and slip-permitted T-shape connectors [J].Journal of Bridge Engineering, 2014, 20(4): 04014073.
[14]Nie J G, Zhu Y J, Tao M X, et al.Optimized prestressed continuous composite girder bridges with corrugated steel webs [J].Journal of Bridge Engineering, 2016, 22(2):04016121.
[15]Jiang Y, Hu X, Hong W, et al.Experimental study and theoretical analysis of partially encased continuous composite beams [J].Journal of Constructional Steel Research, 2016, 117: 152―160.
[16]Rusch H.Researches toward a general flexural theory for structural concrete [J].Journal of the American Concrete Institute, 1960, 57(1): 1―28.
[17]Ollgaard J G, Slutter R G, Fisher J W.Shear strength of stud connectors in lightweight and normal-weight concrete[J].AISC Engineering Journal, 1971, 8(2): 55―64.