地震模拟振动台试验是研究工程结构地震反应和破坏机理最有效的方法之一[1]。该方法是依据模型相似理论设计一定比例的结构模型并固定于振动台台面之上，将实际采集或者人工合成的地震波按照相似理论进行缩放，利用振动台实现地震波再现来对模型结构进行地震模拟振动台试验[2]。地震模拟振动台试验理论基础为相似理论，即为使模型试验结果能尽量真实地反映原型结构，必须考虑原型与模型的相似关系[3]。
振动台模型相似主要包括应变失真模型相似、忽略重力模型相似、拟真实模型相似和人工质量模型相似[4]。应变失真模型是指应变相似系数Sε不等于1，在相似关系推导中所有由应变决定的物理量均乘以关于应变的一次幂，因此，其可以考虑模型和原型的材料非线性影响，但不能很好的模拟几何非线性关系。重力忽略模型仅适用于重力可以忽略的情况。拟真实模型可以实现模型与原型的完全相似，但要求模型材料具备弹性模量低和密度大的特点，而这通常难以实现，且由于材料不同，也不能真实地反映原型结构。人工质量模型是在模型上附加非结构效应的大密度材料以满足重力与惯性力的相似模型，即用人工配重来实现模型材料密度大的要求。人工质量相似因能同时满足重力和水平惯性力的相似条件而获得广泛的应用，也是最能真实地反映原型结构的一种相似。但是，由于振动台的承载能力有限，对于大型结构的缩尺模型或采用大缩尺比例的模型，完全人工质量(满配重)的设置难以实现，因而实际应用时常采用未完全人工质量(欠配重)模型。
当前，地震振动台模型试验绝大多数采用的是欠人工质量模型相似。吕西林等[5－10]是国内较早开展欠人工质量模型相似理论的研究，并基于人工质量模型相似建立了混合模型理论，其选择了长度、弹性模量和质量作为基本物理量，其它物理量的相似系数根据相似第二定量由基本物理量的相似系数线性表示。张敏政[11]推导了欠人工质量模型的一致相似律，其选择了长度、弹性模量和质量密度为基本物理量。黄维平等[12－13]研究了砌体结构配重不足时的动力试验模型与原型相似关系。林皋等[14]在大量振动台模型试验的基础上提出了大坝及土体结构动力模型的相似技巧。宋二祥等[15]则对地基土与结构相互作用振动台模型试验中相似比的实现问题进行了探讨。陈星烨等[16]分析了大型结构试验模型的相似理论。迟世春等[17]以两个几何比尺为2的有机玻璃模型的试验，验证了动力模型的弹性相似律和重力相似律。Tabatabaiefar等[18]通过对高层建筑结构模型侧向位移数值模拟和振动台试验结果的对比，验证了大比例缩尺模型的有效性和合理性。
不过，欠人工质量模型由于存在重力失真的影响，不能较准确的反映结构的抗震能力。甚至有的研究为了尽可能追求振动台试验模型的大缩尺、大尺寸结构，难以设置足够的人工质量，从而使这些模型存在显著的重力失真[19－22]。为此，一些学者开展了欠人工质量模型的重力失真影响研究，分析了重力失真度与地震响应的影响关系。Anderson等[23]认为重力对结构的地震反应有重要影响，且重力失真对结构相似性的影响是通过重力的结构效应的变化来反应的。Dancygier[24]通过数值分析指出重力荷载的参与会增加水平地震作用下无支撑钢框架的上部梁和下部柱的延性要求。郑伟[25]以模型重力失真度为变量，给出了重力失真度的计算公式，并就砌体房屋模型动力极限强度试验中的重力失真效应进行修正。陈以一等[26]研究了重力失真度对振动台模型试验相似性的影响，并基于混合模型理论的双参数判据法开展了三层单跨平面钢框架的重力失真影响研究。赵作周等[27]提出了基于振动台试验的欠人工质量缩尺结构模型不同配筋设计方法下试验结果的差异，分析了欠质量程度对欠人工质量模型承载力的影响。
上述文献表明，忽略重力失真会过高估计结构的抗震性能和抗倒塌能力。不过，这些文献大都是通过理论探讨重力失真对相似模型的影响，虽有开展少量欠人工质量模型振动台试验研究，但在这些试验研究中，并未开展完全人工质量(满配重)模型试验，研究结果还缺乏验证，因而还有待进一步的深入研究。为此，本文基于人工质量的混合模型相似理论，以缩尺比为1∶10的钢管混凝土单圆管拱结构为试验模型[28－29]，通过设置各种欠人工质量来实现不同重力失真度，如0.5倍模型配重、1.5倍模型配重、4.5倍模型配重以及9倍模型配重(满配重)等，开展不同地震波及人工波作用下重力失真度对该相似模型动力性能和地震反应影响的试验研究。
1 模型相似设计
对于该钢管混凝土单圆管拱结构的地震反应，各主要参量可表述为如下函数关系：
式中：σ为结构的动力响应应力；l为结构构件尺寸；Ε为结构构件的弹性模量；δ为结构响应位移；ν为结构响应速度；g为重力加速度；ε为结构的动应变响应；ζ为阻尼比；ρi为结构构件人工配重后的质量密度；ti为时间；ai为结构响应加速度；ωi为结构自振圆频率；ηi为重力失真度。其中，ηi可表示为：
式中：Sl为几何相似系数；Sρi为密度相似系数；下标i为对应不同失真度的物理量，i=1,2,…,5。
本文取前3个物理量l、E和ρ作为基本量，对应的量纲和量纲相似比分别为SL=[L]、SE=[E]和Sρ=[ρ]，那么其余各参量的量纲相似比都可表示为这3个量的单项式。本模型的SL=1/10=0.1。由于采用原型材料，因此，本模型的SE=1.0。
由式(2)可知，0≤ηi＜1.0，本次试验以重力失真度ηi为参数设计了5组试验，其重力失真度ηi分别为0(表示没有失真的模型)，0.45、0.65、0.75和0.85。通过式(2)计算可知Sρi：
Sρi计算结果如表1第3行所示，分别为10.0、5.5、3.5、2.5和1.5，也即需设置9倍配重、4.5倍配重、2.5倍配重、1.5倍配重和0.5倍配重，如表1所示。表1也给出了该模型其它物理相似系数的关系式和比值，同时也给出了0倍配重(无配重，也即忽略重力模型)时的比值。
表1 模型相似系数
Table 1 Similarity coefficients
注：“－”表示无相似比系数。
相似系数比值模型特征 物理量 量纲相似关系 9倍配重(η5=0)4.5倍配重(η4=0.45)2.5倍配重(η3=0.65)1.5倍配重(η2=0.75)几何特性 线位移δ S [L]S=0.1 LL线尺寸l SL [L]SL=0.1 0.5倍配重(η1=0.85)0倍配重(η0=0.9)密度ρi Sρ [ρ] Sρ5=10.0 Sρ4=5.5 Sρ3=3.5 Sρ2=2.5 Sρ1=1.5 Sρ0=1.0材料特性SE=1.0应力σ Sσ [E]Sσ=SESε=1.0应变ε Sε — Sε=1.0模型自重m0 Sm0 [ρL3]Sm0=Sρ弹性模量E SE [E]S=0.001人工质量ma Sma [EL-2]-[ρL3]Sma=0.009Sma=0.0045Sma=0.0025Sma=0.0015 Sma=0.0005 Sma=0 3L模型总重mi Sm0+Sma 0.01 0.0055 0.0035 0.0025 0.0015 0.001加速度a Sa [Eρ-1L-1]Sa=1.0 Sa=1.8 Sa=2.9 Sa=4 Sa=6.7 Sa=10动力特性重力加速度g Sg —Sg=1.0时间t ST [E-0.5ρ0.5L]ST=10/10=ST=5.5/10=ST=3.5/10=ST=2.5/10=ST=1.5/10=ST=1.0/10=0.316 0.235 0.187 0.158 0.122 0.1自振频率ω Sω [E0.5ρ-0.5L-1]Sω=1/ST =Sω=1/ST =Sω=1/ST =Sω=1/ST =Sω=1/ST =Sω=1/ST =3.16 4.26 5.35 6.33 8.20 10阻尼比ζ Sζ — Sζ=1.0刚度k Sk [EL]Sk=SESL=0.1
2 试验简介
钢管混凝土拱结构试验模型按几何缩尺比例1∶10设计制作，模型净跨径L为4.6 m，净矢高f为1.53 m，矢跨比ϑ(ϑ=f/L)为1/3，拱轴线为二次抛物线。通过沿模型拱轴线方向每隔20 cm焊设与之垂直的长度为48 cm的钢杆来固定配重，并通过施加不同的配重块来实现不同的欠人工质量模型，以实现不同的重力失真度。人工质量的设置如图1所示，其中，图1(a)是1.5倍模型配重时的照片，图1(b)是满配重时的照片，为了节省篇幅，其它配重模型照片未给出。为了使模型固定在振动台台面上，加工制作了2块长宽为1.0 m×1.0 m、厚为35 mm的固定铁板，使该模型的两拱脚通过设置三角撑焊接在铁板上，再在铁板上开螺孔，然后通过高强螺栓连接使铁板锚固于振动台台面上。
图1 不同配重的模型照片
Fig.1 Photos of models with complementary artificial mass
拱结构模型截面为单圆管截面，外径D和壁厚t分别为76 mm和3.8 mm。模型钢材采用Q345钢，钢材的平均屈服强度fs为320 MPa、抗拉强度fu为540 MPa、弹性模量Es为2.00×105 MPa、泊松比μs为0.283。混凝土采用C30，混凝土28 d立方体抗压强度fcu为45.6 MPa、弹性模量Ec为3.65×104 MPa、泊松比μ为0.245，试验模型介绍详见文献[28]所述。
该拱结构模型在福州大学地震模拟振动台三台阵设备上进行试验。加速度传感器为东华公司生产的DH610型号。试验过程中主要对该模型的加速度、位移和应变进行测量，各传感器的布置方式与文献[28―29]完全一致，其中，应变片布置了36个，包括轴向应变和环向应变；加速度计布置了23个，同时布置了2个LVDT位移传感器。
3 试验加载
3.1 地震波输入介绍
试验输入的3种地震波激励与文献[28―29]的基本相同，分别为E1、E2人工波以及ELCentro波。其中，ELCentro波的PGA为0.34 g。不过，这三种波的时程曲线并不完全与文献[28―29]的一致。其中，文献[28―29]输入的地震波为按满配重时的时间相似压缩并经重采样后频率为256 Hz的地震波，而本文输入的地震波时程和采样频率分别与模型的重力失真度ηi(不同配重)相关。
福州大学地震模拟振动台三台阵系统的最高使用频率为50 Hz。由于该系统要求输入的地震波采样频率f必须为2n(n为自然数，FFT变换)，而采样频率一般不小于2倍的使用频率，即n＞6(f ＞100 Hz)。因此，该振动台输入的地震波采样频率最低一般为128 Hz，最高一般不超过2048 Hz。
表2给出了ELCentro地震波的采样频率f0(50Hz)与重力失真度ηi的对应关系。由表2可知，对于不同配重模型，由f0通过理论频率比Sωi计算可得到这些模型的采样频率fi，分别为158 Hz、213 Hz、267 Hz等。由于fi不是2n，因此需要进行重采样，如对于ELCentro原型波，其采样频率f0为50 Hz，为了能输入到该振动台系统中，可通过重采样把f0转换为256 Hz，并以此作为基准频率fα。
表2 ELCentro地震波采样频率与重力失真度
Table 2 Sample frequencies of El-Centro wave and degrees of gravity distortion
名称 原型9倍配重4.5倍配重2.5倍配重1.5倍配重0.5倍配重重力失真度ηi — η5=0η4=0.45 η3=0.65 η2=0.75η1=0.85理论频率比Sωi1.03.1624.264 5.345 6.3258.165采样频率fi/Hz50 158213 267 316 408重采样频率256(基准频率)fα/Hz
为了分析时间压缩对不同失真度模型地震响应的影响，以fα(256 Hz)为基准频率，以频率比Ki为参数，对每一种重力失真度的模型，均设计了5种频率比参数，分别为0.5、1.0、2.0、4.0和8.0。其中，Ki可表示为：
式中：fri为重采样频率；fα为基准频率；下标i为对应不同重采样频率的物理量，i=1, 2, …, 5。
表3以重力失真度为0.85的(0.5倍配重)模型为例，给出了输入频率比Ki的变化。根据频率比及式(4)计算可得到重采样频率fri，计算结果如表3第4行所示，即需要输入5种不同重采样频率的地震波。
按不同频率比压缩后的ELCentro地震波时程曲线如图2所示。
表3 ELCentro地震波频率比参数
Table 3 Frequency ratio parameters of ElCentro wave
名称 0.5倍配重(η1=0.85)基准频率fi/Hz 256输入频率比Ki 0.5 1.0 2.0 4.0 8.0重采样频率fri/Hz 128 256 512 10242048
图2 输入ELCentro地震波时程曲线
Fig.2 Time-history curves of input ElCentro waves
3.2 卓越频率峰值平台Smax
卓越频率峰值平台Smax定义详见文献[28]所示，图3给出了与Ki对应的5种不同时间压缩的ELCentro波的峰值加速度Smax反应谱曲线。
由图3可知，5种不同时间压缩的ELCentro波的峰值加速度平台均约为7.0 m/s2。当K1=0.5时，ELCentro波的卓越频率峰值平台Smax对应的频率范围约为1.0 Hz～4.0 Hz；K2=1.0时，约为2.0 Hz～8.5 Hz；K3=2.0时，约为4.0 Hz～17.0 Hz；K4=4.0时，约为8.0 Hz～34.0 Hz；K5=8.0时，约为16.0 Hz～68.0 Hz。可见，Ki每增加一倍，ELCentro波的卓越频率峰值平台Smax对应的起始频率以及频率范围也相应的增加一倍，二者具有较好的线性增长关系。
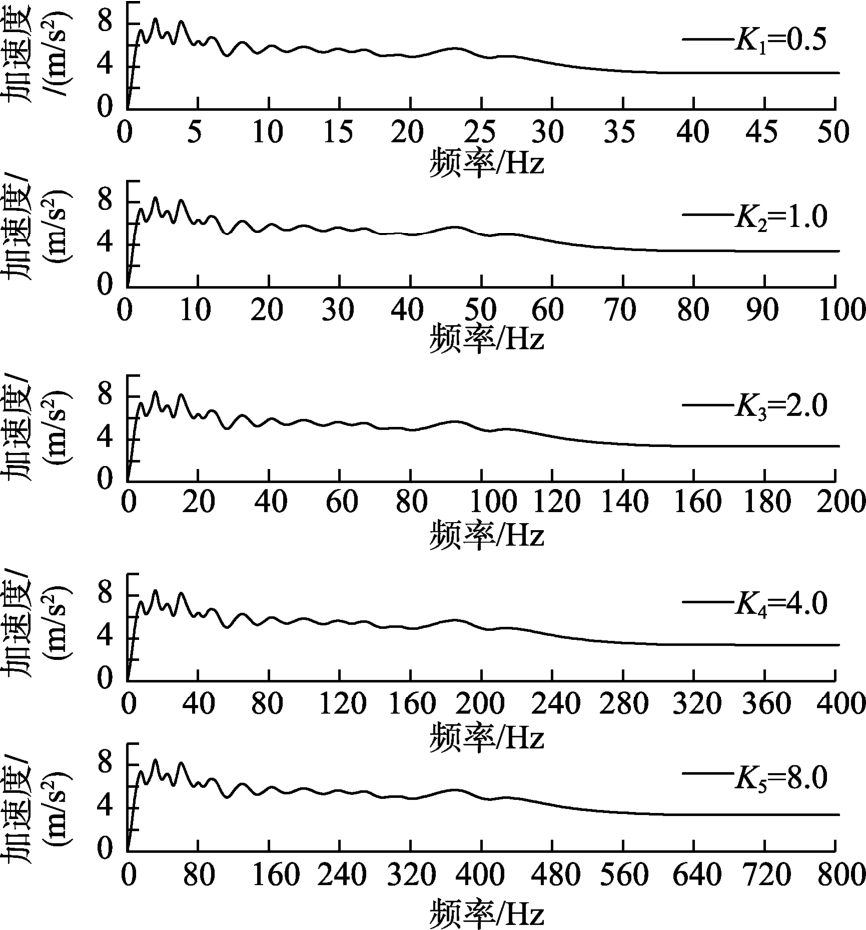
图3 ELCentro波反应谱曲线对比
Fig.3 Comparison of different frequency response spectrum (FRS) curves of ElCentro wave
3.3 试验工况
试验工况主要是正弦扫频激励、白噪声激励和地震波激励，地震波激励为一致激励，输入方向主要考虑了X向(纵向)、Y向(横向)和X向+Y向。对于ELCentro波，共计50种试验工况，如表4所示，为了节约篇幅，E1和E2波未给出。此外，由于正弦波激励和白噪声激励只是用来测试模型的基本动力特性、检测系统是否正常工作、试验模型是否安装可靠、传感测量装置是否有效等，因此，正弦波激励和白噪声激励等也未列入表4的试验工况中。
表4 台阵试验工况
Table 4 Cases of shake table test
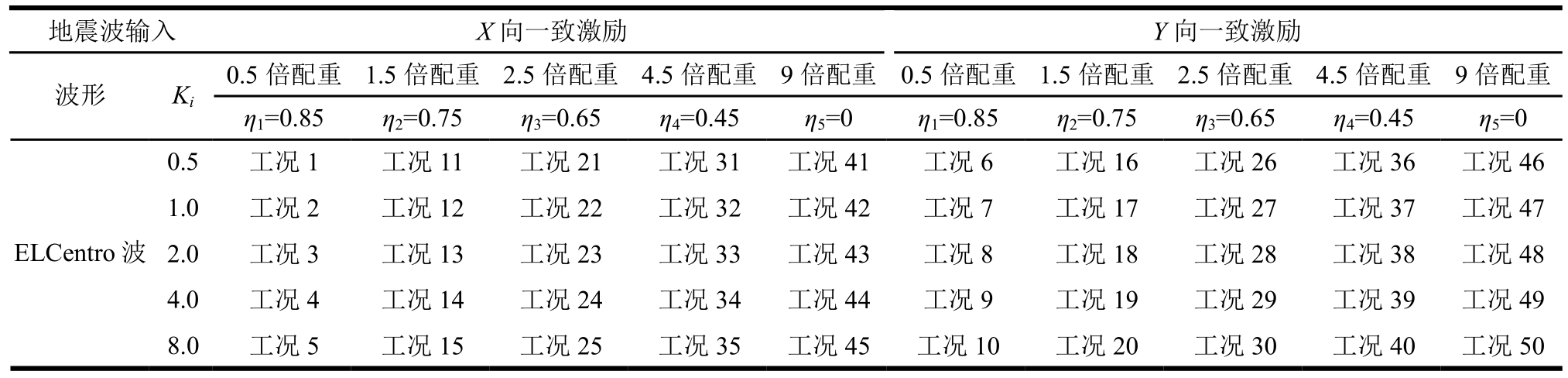
注：X为纵(桥)向；Y为横(桥)向。
地震波输入 X向一致激励Y向一致激励波形 Ki η=0.85 η=0.75 η=0.65 η=0.45 η=0 η=0.85 η=0.75 η=0.65 η=0.45 η=0 1234512345 0.5倍配重 1.5倍配重 2.5倍配重 4.5倍配重9倍配重0.5倍配重1.5倍配重2.5倍配重 4.5倍配重9倍配重0.5 工况1 工况11 工况21 工况31工况41工况6 工况16工况26 工况36工况46 ELCentro波1.0 工况2 工况12 工况22 工况32工况42工况7 工况17工况27 工况37工况47 2.0 工况3 工况13 工况23 工况33工况43工况8 工况18工况28 工况38工况48 4.0 工况4 工况14 工况24 工况34工况44工况9 工况19工况29 工况39工况49 8.0 工况5 工况15 工况25 工况35工况45工况10工况20工况30 工况40工况50
4 试验结果与分析
4.1 动力特性
本文中每个工况试验前都进行了相应加速度峰值的白噪声扫描，扫描时间不少于60 s。通过白噪声激励可测得钢管混凝土拱结构模型的加速度响应时程曲线，然后进行FFT变换和模态参数识别得到结构的前几阶模态和自振频率。测得各个配重模型的前几阶失稳模态均分别是面外对称侧倾失稳、面内反对称竖向失稳、面外反对称失稳(侧扭)以及面内对称竖向失稳，也即重力失真度不会影响模型的失稳模态。不同失真度的模型频率相似系数理论值如表1第14行所示，分别为3.16(η5=0)，4.26(η4=0.45)等，其中计算公式为：
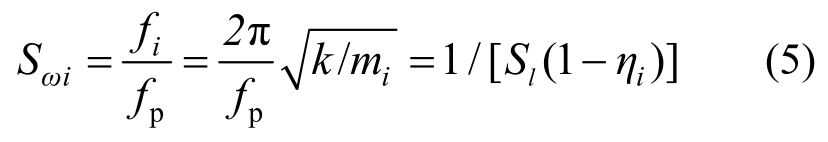
式中：Sωi为模型第一阶频率相似系数理论值；fp=0.66 Hz为原型桥第一阶频率；fi为各配重模型的第一阶频率，i=1, 2, …, 5；mi为各配重模型的总质量，即模型自重与各人工配重之和，即：
式中：m0为模型自重；ma为各人工配重质量；ni为模型配重质量与模型自重的比值；Sl为几何相似系数；ηi为重力失真度。
根据式(5)可计算不同失真度模型的第一阶频率相似系数，如图4的黑色曲线和表5(第1行)所示。同时，也在图4和表5(第2行)中给出了试验实测值。
由图4可知，随着重力失真度的增加，模型第一阶固有频率及其相似系数也增加；同时，试验实测频率相似系数要大于理论相似系数，即失真模型的刚度更大。不过，随着重力失真度的减小，二者误差逐渐减小，满配重时，模型与原型第一阶固有频率表现出较好的相似性。因此，比较可知，重力失真对拱结构模型第一阶频率相似有较大的影响，配重不足时，由试验结果反推原型存在一定的误差，误差最大超过20%，重力失真的影响不可忽略。
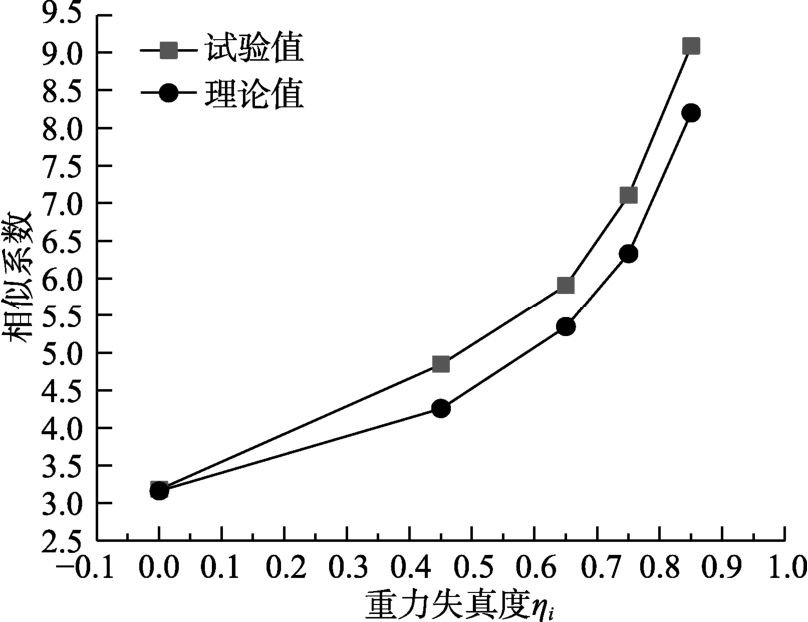
图4 第一阶频率相似系数
Fig.4 Similarity coefficients of first frequency
为了减小重力失真的影响，定义配重放大系数βi为：
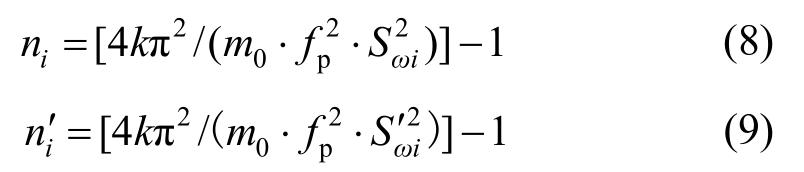
式中：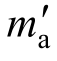
为模型实际配重质量；ma为模型理论配重质量；
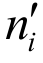和ni为模型配重质量与模型自重的比值，可由式(8)和式(9)计算得出，
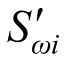为模型第一阶频率相似系数试验实测值，i=1, 2, …, 5。
配重放大系数计算结果如表5所示。计算表明，失真度越大、配重放大系数也越大。通过调整式(7)的配重放大系数，可减小由模型重力失真产生的误差。
表5 配重放大系数计算结果
Table 5 Amplification coefficients of complementary artificial mass
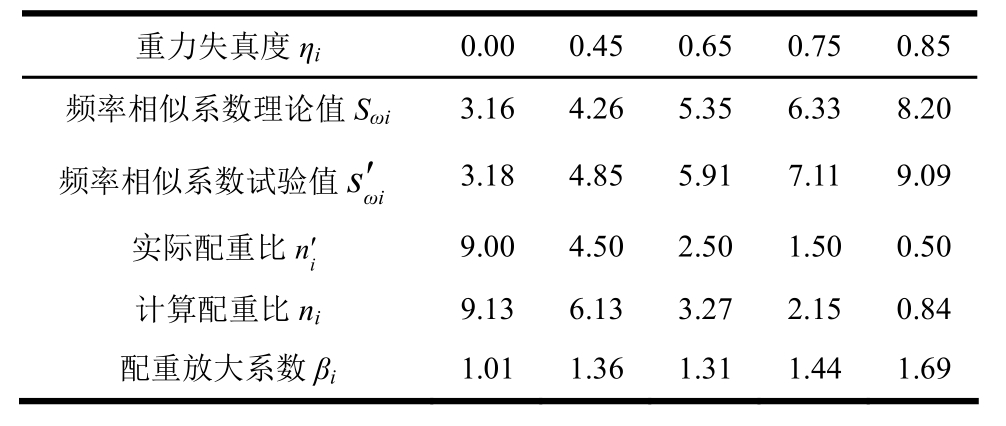
重力失真度ηi 0.00 0.45 0.65 0.750.85频率相似系数理论值Sωi 3.16 4.26 5.35 6.338.20频率相似系数试验值sω′i 3.18 4.85 5.91 7.119.09实际配重比ni ′ 9.00 4.50 2.50 1.500.50计算配重比ni 9.13 6.13 3.27 2.150.84配重放大系数βi 1.01 1.36 1.31 1.441.69
4.2 加速度响应时程曲线
限于篇幅，本文仅给出ELCentro波的试验工况和结果，同时，仅给出频率比K1=0.5和K2=1.0激励下，模型拱关键截面处的加速度响应时程曲线。其中纵向(X向)激励时，给出的是L/4截面处的，如图5所示；横向(Y向)激励时，给出的是L/2截面处的，如图6所示。其它频率比和其它截面处的时程曲线图形未给出。另外，为方便表示，只给出了具代表性时间段(0 s～40 s)的时程曲线。
4.2.1 纵向(X向)激励
由图5可知，频率比K1=0.5和K2=1.0时，不同重力失真度ηi的拱结构模型X向加速度时程具有较明显的不同，重力失真度越小、加速度时程越饱满，模型拱动力响应也越大，加速度峰值出现的时间也延后越明显。另外，满配重(无重力失真，η=0)时的加速度响应明显大于其它失真模型的加速度响应。
4.2.2 横向(Y向)激励
由图6可知，Y向激励时，不同重力失真度η的拱结构模型加速度响应也不同，即重力失真度越小，加速度时程越饱满，模型拱动力响应也越大，加速度峰值时间也越延后。重力失真度η为0(满配重)时的加速度响应明显大于其它失真度的。
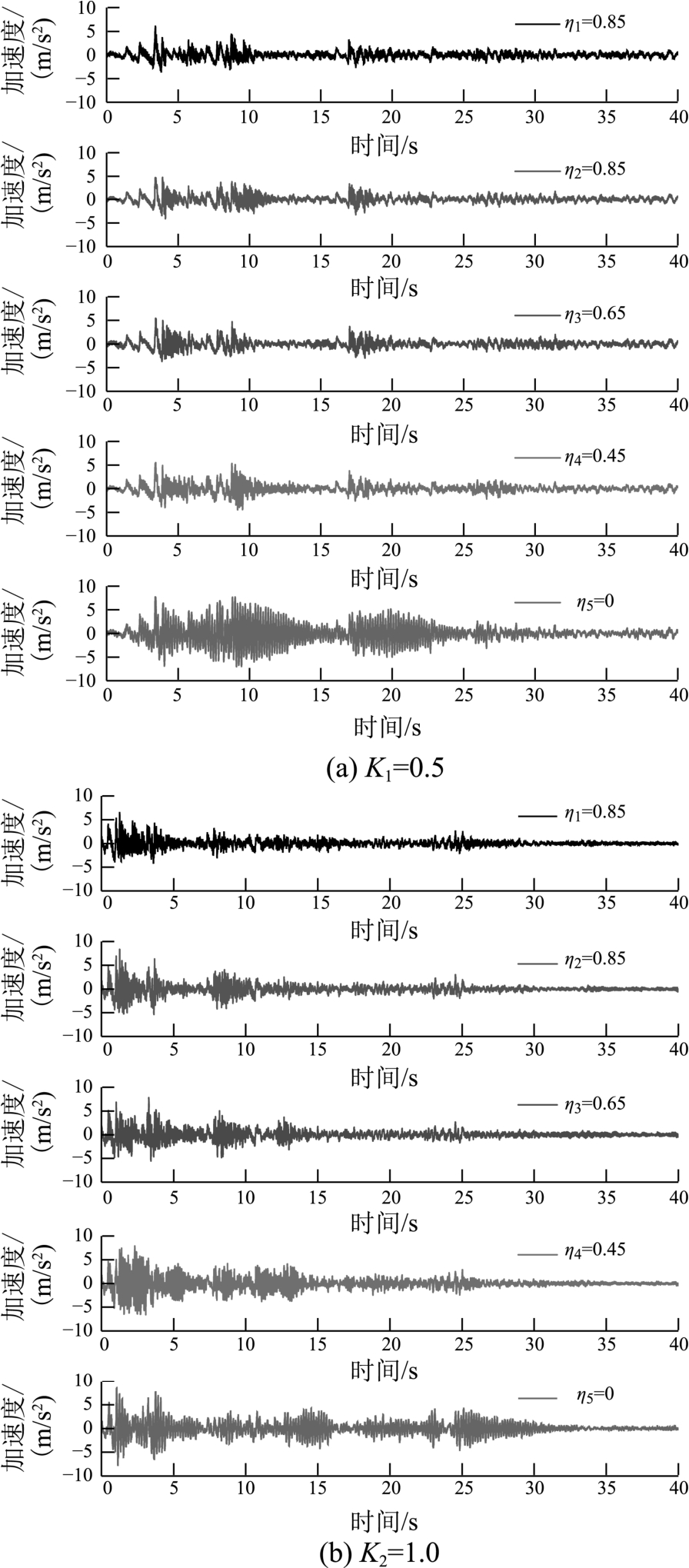
图5 模型拱X向加速度响应时程曲线
Fig.5 Acceleration time-history curves in X direction
比较图6与图5可知，Y向激励时的加速度响应明显大于X向的，加速度响应峰值时间也延长了很多，前者的时程曲线也更加饱满。
4.3 加速度放大系数
4.3.1 加速度放大系数与重力失真度关系
为了分析配重对拱结构模型加速度响应的影响，图7给出了模型X向和Y向加速度响应放大系数与重力失真度的关系曲线。其中X向激励时给出的是L/4截面处的，Y向激励时给出的是L/2截面处的。
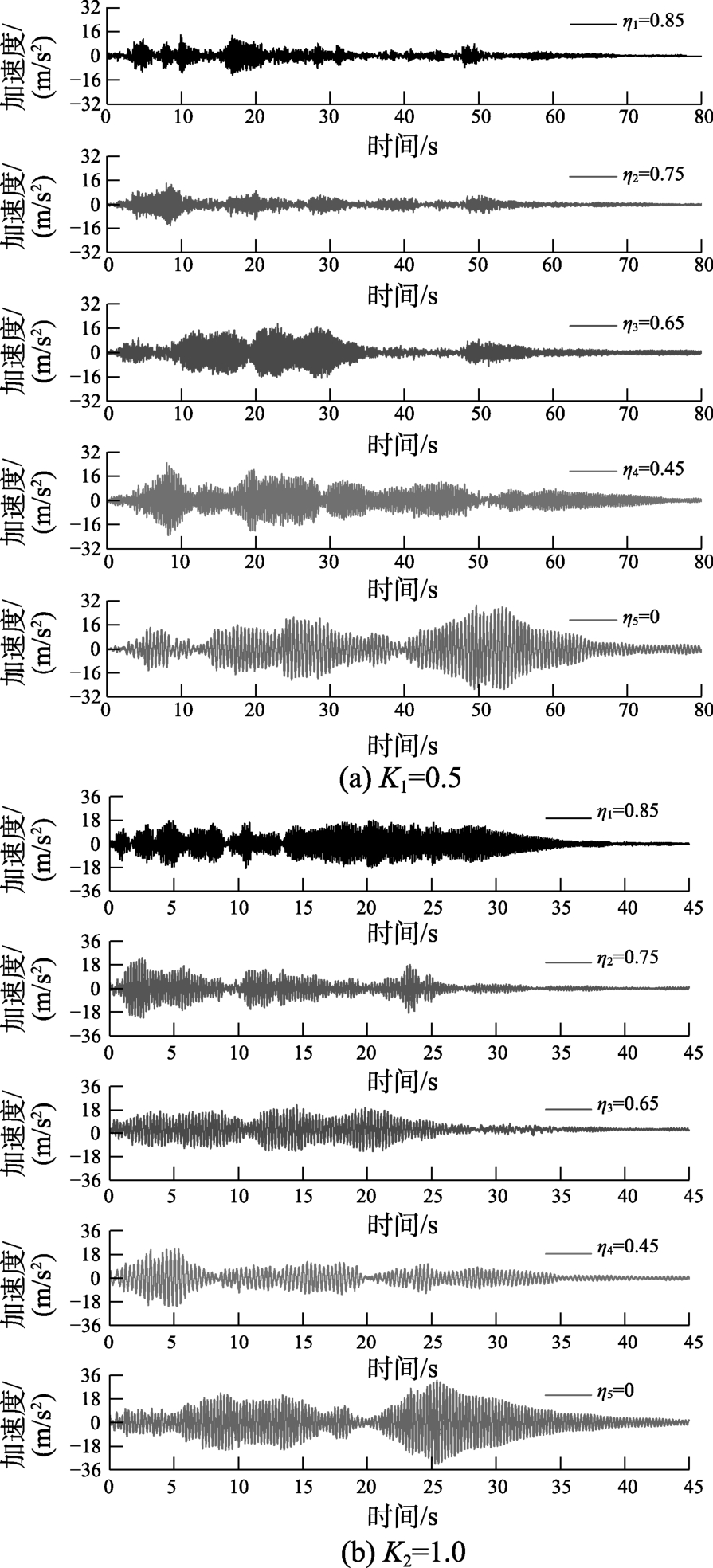
图6 模型拱Y向加速度响应时程曲线
Fig.6 Acceleration time-history curves in Y direction
由图7(a)可知，当频率比为K1=0.5和K2=1.0时，X向加速度放大系数随着失真度的增加而减小。频率比K3=2.0时，重力失真度的影响不明显，X向加速度放大系数基本相同，约放大2.5倍。当频率比K4=4.0和K5=8.0时，X向加速度放大系数随着重力失真度的增加呈现增大的趋势。这是因为重力失真越小的模型，基频也越小，激振频率越高、相应响应也越小。
由图7(b)可知，频率比K1=0.5和K2=1.0时，Y向加速度放大系数随着失真度的增加而减小。而其他频率比时，失真度越大，模型Y向加速度放大系数也越大。
对比图7(a)和图7(b)可知，激励波频率较低时，模型X向和Y向加速度放大系数均以满配重(无重力失真，η=0)时最大；激励波频率较高时，模型X向和Y向加速度放大系数均以配重最少(失真度η=0.85)时最大。不同的是，Y向加速度放大系数明显大于X向，且随着失真度的改变，前者加速度放大系数变化幅度明显，说明Y向加速度放大系数受重力失真度的影响比X向较大。
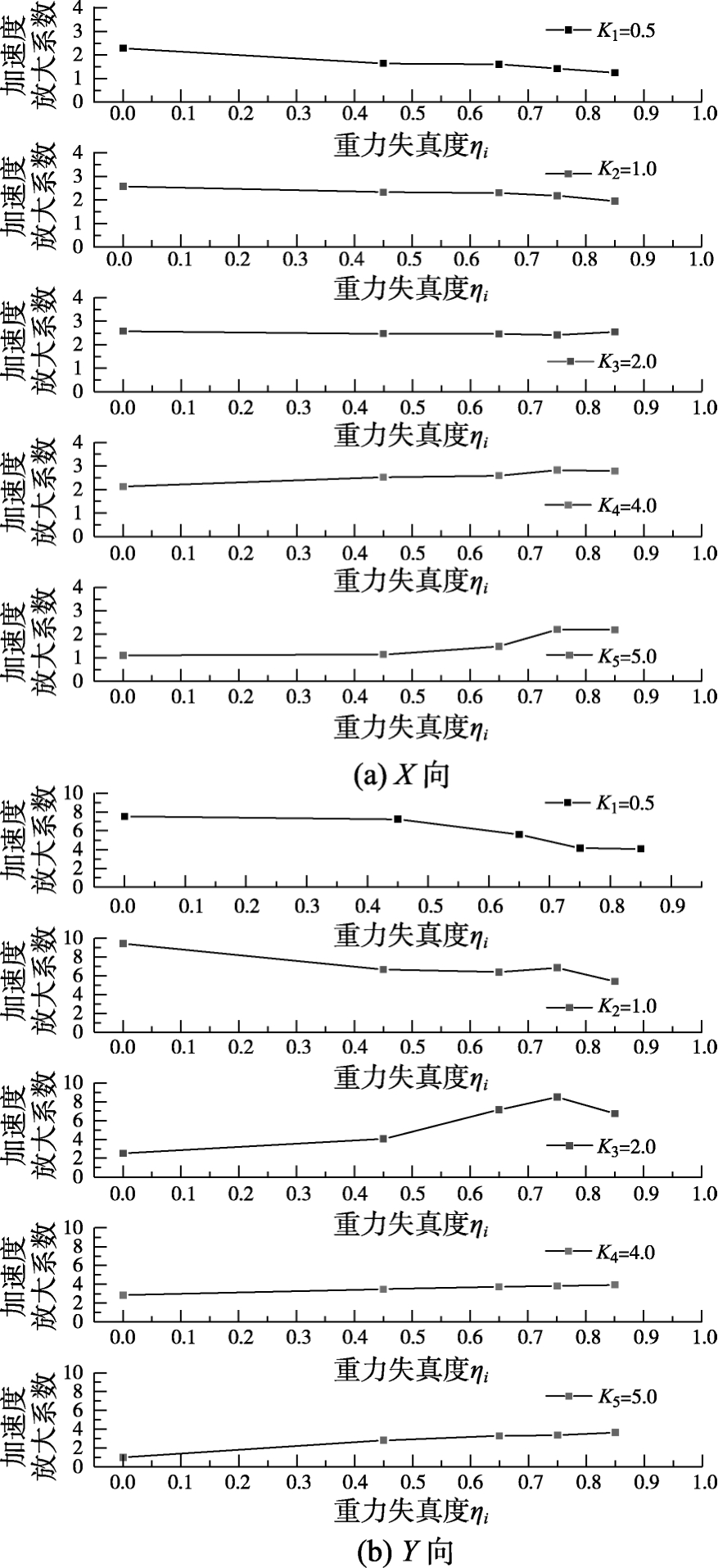
图7 加速度放大系数与重力失真度关系
Fig.7 Acceleration amplification coefficients and gravity distortion
4.3.2 加速度放大系数与频率比关系
为了分析时间压缩对不同失真度模型加速度响应的影响，图8给出了模型X向和Y向加速度响放大系数与频率比的关系曲线，其中X向激励时，给出的是L/4截面处的，Y向激励时，给出的是L/2截面处的。由图8(a)可知，对于不同失真度的拱结构模型，随着激励波频率比的增加，其X向加速度放大系数基本呈现先增加后减小的趋势。失真度较小的模型(η1=0和η2=0.45)基本以频率比K2=1.0和K3=2.0时的加速度放大系数最大、频率比K5=8.0时的加速度放大系数最小。失真度较大的模型基本以频率比K4=4.0时的加速度放大系数最大、频率比K1=0.5时的加速度放大系数最小。
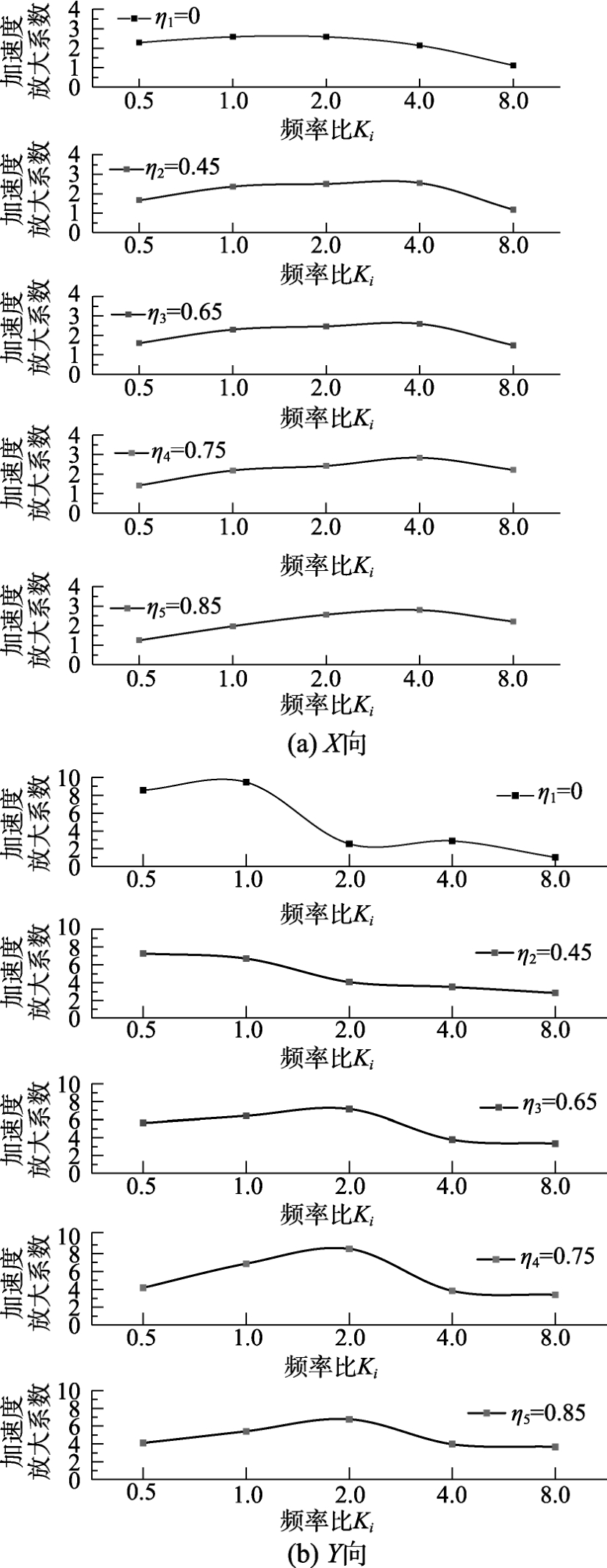
图8 加速度放大系数与频率比关系
Fig.8 Acceleration amplification coefficients and frequency ratio
由图8(b)可知，对于失真度较小的拱结构模型，其Y向加速度放大系数随着激励波频率比的增加而减小，其中当频率比K1=0.5时加速度放大系数最大，放大了约9倍、频率比K5=8.0时的加速度放大系数最小。而失真度较大的模型基本以频率比K3=2.0时的加速度放大系数最大、频率比K5=8.0时的加速度放大系数也最小。
对比图8(a)和图8(b)可知，随着激励波频率比的改变，模型Y向加速度放大系数变化幅度明显大于X向，说明Y向加速度放大系数受输入波频率比的影响比X向较大。
总之，重力失真对钢管混凝土单圆管拱结构模型加速度响应的影响因输入波频率比的不同有较大的差异，可通过调整模型配重及输入波的频率比减小加速度响应由于模型重力失真产生的影响。
6 结论
通过不同失真度的钢管混凝土单圆管拱结构模型振动台试验，研究了不同配重、不同输入波频率比对该相似模型动力特性及加速度响应的影响。研究结果表明：
(1)重力失真对钢管混凝土单圆管拱结构模型第一阶频率相似有较大的影响，配重不足时，由试验结果反推原型误差最大超过20%，通过调整配重放大系数，可减小由模型重力失真产生的误差。
(2)模型重力失真度越小，加速度时程越饱满，动力响应也越大，加速度峰值时间也越延后。无重力失真时的模型加速度响应明显大于失真模型的加速度响应。
(3)重力失真度和输入波的频率比对该拱结构模型横向(Y向)加速度放大系数的影响要大于对纵向(X向)的。
(4)重力失真对钢管混凝土单圆管拱结构模型加速度响应的影响因输入波频率比的不同有较大的差异，可通过调整模型配重及输入波的频率比减小模型重力失真对加速度响应产生的影响。
[1]邱法维, 钱稼茹, 陈志鹏.结构抗震实验方法[M].北京: 科学出版社, 2000.Qiu Fawei, Qian Jiaru, Chen Zhipeng.The structural seismic testing method [M].Beijing: Science Press, 2000.(in Chinese)
[2]黄浩华.地震模拟振动台的设计及其应用技术[M].北京: 科学出版社, 2008.Huang Haohua.The design and technical application of earthquake similitude of shaking tables [M].Beijing:Science Press, 2008.(in Chinese)
[3]Meng QingLi, Zhang MinZheng.Nonlinear Performance Simulation of RC Structures with Small-Scaled Model in Earthquake Simulation Test [J].In Advanced Materials Research, 2011, 243: 3717―3729.
[4]Sabnis G M, Harris H G, White R N.et al.Structural modeling and experimental techniques [M].Boca Raton:Chemical Rubber Company Press, 1983.
[5]Lu Xilin.Application of identification methodology to shaking table tests on reinforced concrete columns [J].Engineering Structures, 1995, 17(7): 505―511.
[6]吕西林, 周德源.砌体结构墙体模型振动台试验及其动力相似关系[J].工程抗震, 1993, 9(3): 12―16.Lu Xilin, Zhou Deyuan.Dynamic similitude law of wall model on test of shaking table for masonry structures[J].Earthquake Resistant Engineering and Retrofitting, 1993,9(3): 12―16.(in Chinese)
[7]吕西林, 程海波.钢筋混凝土框架结构的动力相似关系研究[J].地震工程与工程振动, 1997, 17(1): 140―147.Lv Xilin, Cheng Haibo.Study on dynamic similitude theory of reinforced concrete frame structure [J].Earthquake Engineering and Engineering Vibration,1997, 17(1): 140―147.(in Chinese)
[8]吕西林, 陈跃庆.结构-地基相互作用体系的动力相似关系研究[J].地震工程与工程振动, 2001, 21(3): 85―92.Lv Xilin, Chen Yueqin.Study on dynamic similitude theory of soil-structure interaction system [J].Earthquake Engineering and Engineering Vibration, 2001, 21(3):85―92.(in Chinese)
[9]Lv Xilin, Zhou Ying, Lu Wensheng, et al.Shaking table model test on Shanghai World Financial Center Tower [J].Earthquake Engineering Structure of Dynamic, 2007,36(4): 439―457.
[10]鲁亮, 吕西林.振动台模型试验中一种消除重力失真效应的动力相似关系研究[J].结构工程师, 2001, 17(4):45―48.Lu Liang, Lv Xilin.Study of Dynamic similitude law for the shaking table test to cancel the gravity distortion effect [J].Structural Engineers, 2001, 17(4): 45―48.(in Chinese)
[11]张敏政.地震模拟实验中相似律应用的若干问题[J].地震工程与工程振动, 1997, 17(2): 52―58.Zhang Minzheng.Study on similitude laws for shaking table tests [J].Earthquake Engineering and Engineering Vibration, 1997, 17(2): 52―58.(in Chinese)
[12]黄维平, 邬瑞锋, 张前国.配重不足时的动力试验模型与原型相似关系问题的探讨[J].地震工程与工程振动,1994, 14(4): 64―71.Huang Weiping, Wu Ruifeng, Zhang Qianguo.Study on the analogy between scale models with less ballast and their prototypes under shaking table test [J].Earthquake Engineering and Engineering Vibration, 1994, 14(4):64―71.(in Chinese)
[13]黄维平, 王连广.人工质量在砖混结构振动台试验中的作用[J].地震工程与工程振动, 2001, 21(3): 99―103.Huang Weiping, Wang Lianguang.Effects of ballast on test of shaking table for masonry structures [J].Earthquake Engineering and Engineering Vibration,2001, 21(3): 99―103.(in Chinese)
[14]林皋, 朱彤, 林蓓.结构动力模型试验的相似技巧[J].大连理工大学学报, 2000, 40(1): 1―8.Lin Gao, Zhu Tong, Lin Bei.Similarity technique for dynamic structural model test [J].Journal of Dalian University of Technology, 2000, 40(1): 1―8.(in Chinese).
[15]宋二祥, 武思宇, 王宗纲.地基-结构系统振动台模型试验中相似比的实现问题探讨[J].土木工程学报,2008, 41(10): 87―92.Song Er-xiang, Wu Si-yu, Wang Zong-gang.A tentative solution for similitude realization in shaking table tests of SSI systems [J].China Civil Engineering Journal, 2008,41(10): 87―92.(in Chinese)
[16]陈星烨, 马晓燕, 宋建中.大型结构试验模型相似理论分析与推导[J].长沙交通学报学报, 2004, 20(1): 11―14.Chen Xingye, Ma Xiaoyan, Song Jianzhong.The comparability analysis and deduction of a large structure test model [J].Journal of Changsha Communications University, 2004, 20(1): 11―14.(in Chinese)
[17]迟世春, 林少书.结构动力模型试验相似理论及其验证[J].世界地震工程, 2004, 20(4): 11―19.Chi Shichun, Lam Siushu.Validation of similitude laws for dynamic structural model test [J].World Earthquake Engineering, 2004, 20(4): 11―20.(in Chinese)
[18]Tabatabaiefar H R, Mansoury B.Detail design, building and commissioning of tall building structural models for experimental shaking table tests [J].Structural Design of Tall & Special Buildings, 2016, 25(8): 357―374.
[19]吴庆雄, 黄育凡, 陈宝春.钢管混凝土组合桁梁-格构墩轻型桥梁振动台阵试验研究[J].工程力学, 2014,31(9): 89―96.Wu Qingxiong, Huang Yufan, Chen Baochun.Shaking tables testing study of lightweight bridge with CFST composite truss girder and lattice pier [J].Engineering Mechanics, 2014, 75(9): 73―86.(in Chinese)
[20]闫维明, 李晰, 陈彦江, 李勇, 顾大鹏.钢管混凝土拱桥台阵试验研究:场地条件的影响[J].工程力学, 2013,30(6): 116―123.Yan Weiming, Li Xi, Chen Yanjiang, Li Yong, Gu Dapeng.Shaking table research on a CFST arch bridge model: effect of site condition [J].Engineering Mechanics, 2013, 30(6): 116―123.(in Chinese)
[21]陈彦江, 张德义, 李晰, 贾宏宇, 闫维明.空间变化地震作用下钢管混凝土拱桥的抗震分析[J].工程力学,2013, 30(12): 99―106.Chen Yanjiang, Zhang Deyi, Li Xi, Jia Hongyu, Yan Weiming.Stochastic seismic analysis of a CFST arch bridge under spatially varying ground motions.[J].Engineering Mechanics, 2013, 30(12): 99―106.(in Chinese)
[22]Goto Y, Ebisawa T, Obata M, et al.Ultimate behavior of steel and CFT piers in two-span continuous elevated-girder bridge models tested by shake-table excitations [J].Journal of Bridge Engineering, 2017,22(5): 04017001.
[23]Anderson J C, Bertero V V.Effects of gravity loads and vertical ground acceleration on the seismic response of multistory frames [J].Earthquake Engineering Structure Dynamic, 2003(30): 175―184.
[24]Dancygier A N, Quantitative evaluation of effect of gravity on small-scale modeling [J].Journal of Engineering Mechanics, 1995, 13(8): 773―777.
[25]郑伟.关于动力极限强度模型试验中失真效应及其修正准则的探讨[J].工程抗震, 1992(3): 39―43.Zheng Wei.Discussion on distortion effect and its correction criteria in dynamic ultimate strength model test [J].Earthquake Resistant Engineering and Retrofitting,1992(3): 39―43.(in Chinese)
[26]陈以一, 张大照, 卢文胜等.承载开闭钢屋盖的预应力混凝土看台结构抗震性能研究[J].土木工程学报,2007, 40(8): 22―28.Chen Yiyi, Zhang Dazhao, Lu Wensheng, et at.Seismic performance of a prestressed concrete stadium structure supporting a retractable steel roof [J].Journal of Civil Engineering, 2007, 40(8): 22―28.(in Chinese)
[27]赵作周, 管桦, 钱稼茹.欠人工质量缩尺振动台试验结构模型设计方法[J].建筑结构学报, 2010, 31(7): 78―85.Zhao Zuozhou, Guan Hua, Qian Jiaru.Design method of small scaled shaking table test structural model lacking artificial mass [J].Journal of Building Structures, 2010,31(7): 78―85.(in Chinese)
[28]黄福云, 李建中, 陈宝春, 等.钢管混凝土单圆管拱结构振动台阵试验研究[J].工程力学, 2014, 31(4):82―92.Huang Fuyun, Li Jianzhong, Chen Baochun, et al.Shaking tables testing of concrete filled steel tubular arc rib model [J].Engineering Mechanics, 2014, 31(4): 82―92.(in Chinese)
[29]黄福云, 陈宝春, 李建中,等.钢管混凝土单圆管拱结构罕遇地震作用下振动台阵试验研究[J].工程力学,2015, 32(7): 64―73.Huang Fuyang, Chen Baochun, Li Jianzhong, et al.Shaking tables testing of concrete filled steel tubular single arch rib model under the excitation of rare earthquakes [J].Engineering Mechanics, 2015, 32(7):64―73.(in Chinese)