混凝土作为一种多相复合的准脆性材料,其破坏与断裂机理非常复杂,因而对其断裂性能的研究就显得十分必要。而目前应用于研究混凝土断裂性能的一个重要的模型为我国学者徐世烺与Reinhardt[1―3]提出的双K断裂模型。该模型首次提出用起裂断裂韧度![]() 监控结构是否开裂,用失稳断裂韧度
监控结构是否开裂,用失稳断裂韧度![]() 判断结构的裂缝扩展是否稳定。应该说,
判断结构的裂缝扩展是否稳定。应该说,![]() 的提出,对于高混凝土坝、输水结构及核安全壳等对裂缝有严格要求的结构的抗裂性能有重要参考价值[4]。目前,学者们大多基于三点弯曲梁[5―14]、紧凑拉伸[15―16]和楔入劈拉[17―20]试件研究混凝土的双K断裂参数。
的提出,对于高混凝土坝、输水结构及核安全壳等对裂缝有严格要求的结构的抗裂性能有重要参考价值[4]。目前,学者们大多基于三点弯曲梁[5―14]、紧凑拉伸[15―16]和楔入劈拉[17―20]试件研究混凝土的双K断裂参数。
三点弯曲梁试件虽制作相对简单,但尺寸较大且搬运中易损坏,而紧凑拉伸和楔入劈拉试件较小 ,但加载装置较复杂,近几年来,很多学者采用了新的试件形式。文献[21―24]基于中央带穿透裂缝的立方体劈拉试件研究了混凝土的双K断裂参数。Wu等[25]采用圆柱体楔入劈拉试件研究了大骨料粒径的大坝混凝土的真实的双K断裂参数。Xu等[26]指出半圆形三点弯曲梁试件所得的双K断裂参数受试件尺寸及强度影响较大。李庆华等[27]基于改进的圆形紧凑拉伸试件比较了双G断裂参数转化得到与实测的双K断裂参数。
考虑到三点弯曲梁在裂缝扩展路径出现偏斜时会出现剪力作用导致的ΙΙ型断裂分量[28―30]的影响,文献[31―33]基于跨中截面带缝的四点弯曲梁研究了纤维混凝土的断裂性能。对于四点弯曲梁,因其跨中裂缝截面附近处于纯弯区段,故该种试验方式从理论上更符合Ι型断裂模式,因而可以得到更接近真实的断裂参数。基于此,本文通过开展四点弯曲梁试验研究了混凝土的双K断裂性能,并通过将荷载作用下的四点弯曲梁纯弯曲段等效为纯弯曲梁,基于线性叠加原理给出了计算混凝土四点弯曲梁有效裂缝长度![]() 的计算公式,并研究了不同初始缝高比对其断裂性能的影响。
的计算公式,并研究了不同初始缝高比对其断裂性能的影响。
试验共设计了初始缝高比为0.2、0.3、0.4、0.5及0.6的5组四点弯曲梁,每组试件浇筑4个,试件尺寸为L×B×H=1000 mm×120 mm×200 mm,支座间跨度为800 mm。试验用一级配混凝土由饮用水,P·O42.5级水泥,经20 mm筛孔的筛子筛过的石灰岩碎石,天然河砂,配合比为水泥∶水∶砂∶石子=0.470∶1∶1.369∶2.780制成。试件的预制裂缝由厚度为3 mm钢板制作,并在用于预制裂尖的钢板一侧制作成15°尖角,以符合裂缝尖端形态。试件浇筑时,钢板预先涂上脱模剂,混凝土浇筑约4 h后拔出钢板。所有试件24 h后拆模,试件拆模后均用潮湿的土工布覆盖,并在室温下养护28 d。混凝土标准立方块28 d龄期抗压强度为40.78 MPa,弹性模量为32.46 GPa。
在试件表面距预制缝处约10 mm的位置对称粘贴一对长为20 mm的应变片[6―7],用以测定起裂荷载Pini。试验在200 kN的万能试验机上开展,两个跨中加载点距支座距离均为200 mm,加载速率由跨中挠度控制,所有试件均为0.05 mm/min。加载装置如图1所示。

图1 试验装置
Fig.1 Test device
使用量程为2mm的夹式引伸仪测量裂缝张口位移(CMOD)。试验过程中的荷载P、裂尖的应变值ε以及裂缝开口位移CMOD用动态应变测试系统进行采集。
本文采用应变片监控起裂[6―7,10],四点弯曲梁中典型的荷载-应变(P-ε)曲线如图2(a)所示。由图2(a)可知,在初始加载阶段,预制缝尖端受拉,裂尖两侧应变片的应变值ε基本呈线性增加;当荷载达到Pini时,裂缝尖端处混凝土因受拉产生应力集中而开裂,积蓄的应变能释放,P-ε曲线上应变值达到最大;随着荷载的进一步增加,裂尖处应变逐渐减小,故P-ε曲线转折点对应的荷载即试件的Pini[19]。最大荷载Pmax由荷载-裂缝张开口位移(P-CMOD)曲线测得,试件中典型的P-CMOD曲线如图2(b)所示,即P-CMOD曲线峰值点荷载即为该试件的最大荷载Pmax。

图2 Pini及Pmax的确定
Fig.2 Determination of Pini and Pmax
四点弯曲梁试件形式如图3所示。其中B、H、S和D分别为试件厚度、高度、支座间跨度及加载点到支座的距离,试件跨高比S/H =4且D=H。
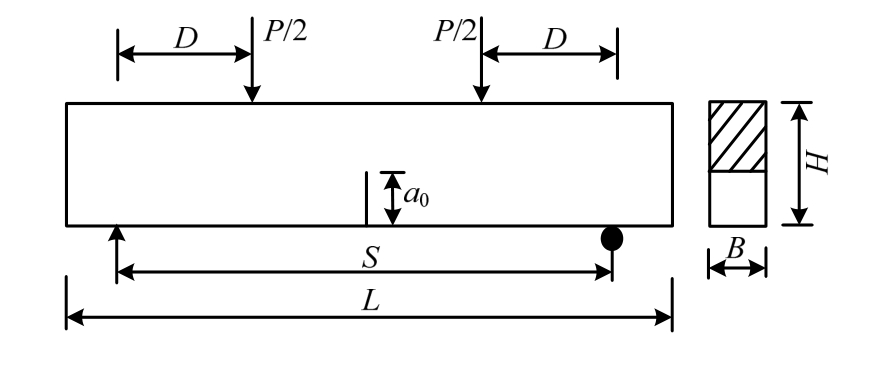
图3 四点弯曲梁试件形式
Fig.3 Dimensions of FPB specimen
由线性渐进叠加假定[2]可知,虽然混凝土裂尖存在断裂过程区,线性叠加原理仍适用,故四点弯曲梁CMOD和断裂韧度,可以分解为荷载作用下的四点弯曲梁和自重作用下的三点弯曲梁的CMOD和断裂韧度值之和。
由图4所示的四点弯曲梁受力状态可知,对于荷载作用下的四点弯曲梁,跨中裂缝截面附近处于试件的纯弯段,故将荷载作用下的四点弯曲梁纯弯曲段等效为纯弯曲梁,由线性渐进叠加假定[2],外荷载引起的裂缝的有效裂缝长度为[34]:
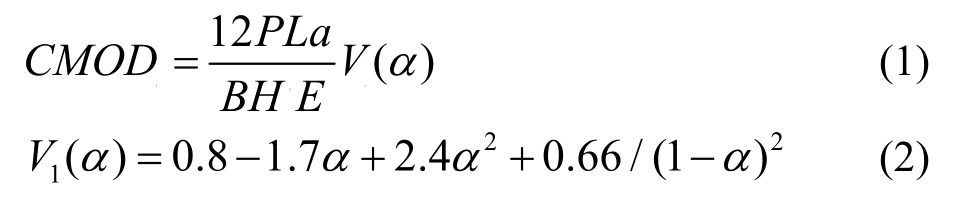
式中:CMOD1为荷载引起的CMOD;P为荷载值;E为试件计算弹性模量;α=(a+h)/(H+h),a为任意荷载下的裂缝长度;h为装置夹式引伸计的薄钢片厚度。
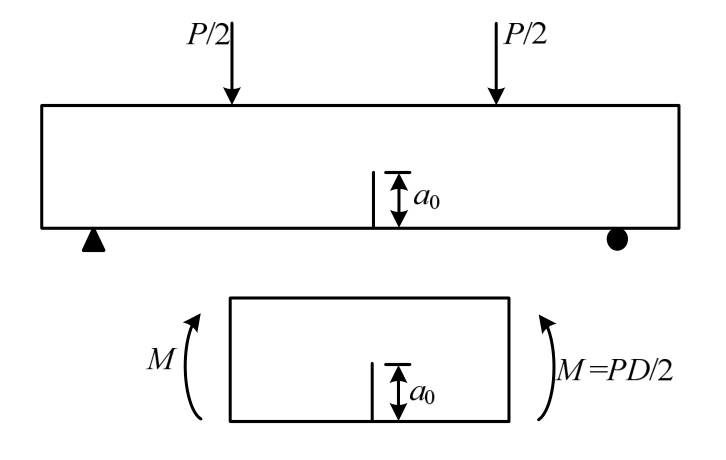
图4 四点弯曲梁试件受力状态
Fig.4 Stress state of FPB specimen
此时,外荷载引起的断裂韧度值![]() 为[34]:
为[34]:
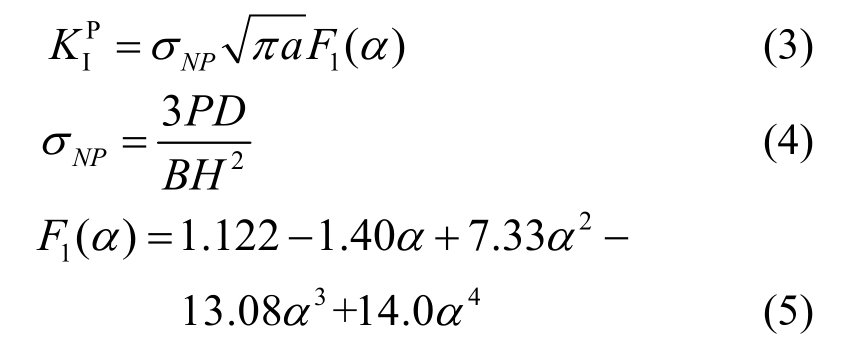
式中,σNP为外荷载作用下的裂缝截面名义应力。
自重作用下的有效裂缝长度为[34]:
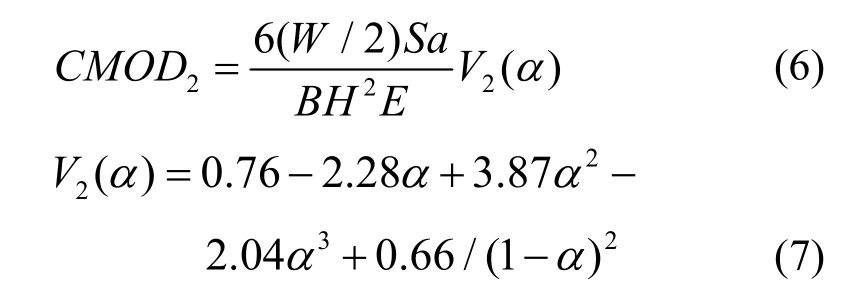
式中:CMOD2为自重引起的CMOD;W为试件支座间跨度范围内自重,就本试验,所有试件W均取平均值,即W=0.480 kN。
自重引起的断裂韧度![]() 为[34]:
为[34]:
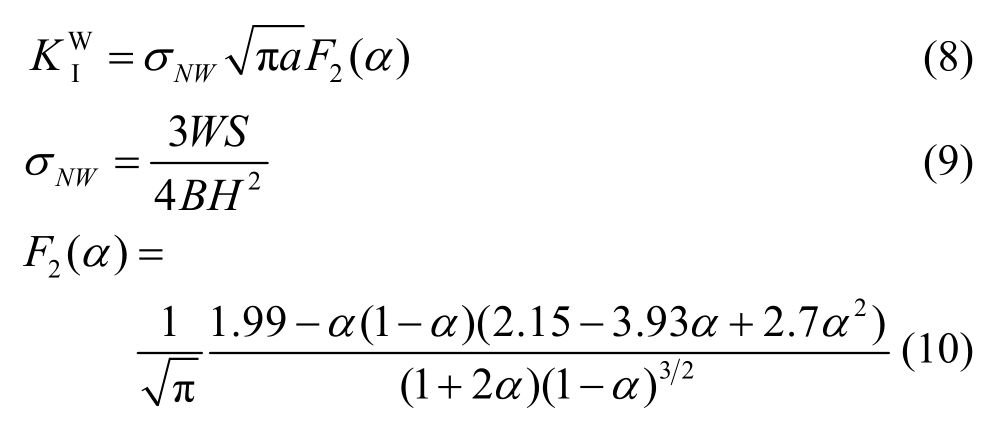
式中,σNW为外荷载作用下的裂缝截面名义应力。
由上述知,四点弯曲梁ac可由其CMOD即由式(1)和式(6)叠加而得:
试件的E可由下式计算[35]:
式中:α0=(a0+h)/(H+h),a0为初始裂缝长度;Ci为实测的P-CMOD曲线初始段柔度。
四点弯曲梁断裂韧度由式(3)和式(8)叠加得到:
由此,四点弯曲梁的双K断裂参数计算过程如下:1) 据式(12)确定混凝土计算弹性模量E;2) 将求得的弹性模量E、最大荷载Pmax、临界裂缝张开口位移CMODc代入式(11),通过数值计算的方式求解临界有效裂缝长度ac;3) 将起裂荷载Pini、初始裂缝长度a0代入式(13)便可得到起裂断裂韧度![]() 4) 将最大荷载Pmax、临界有效裂缝长度ac代入式(13)便可得到失稳断裂韧度
4) 将最大荷载Pmax、临界有效裂缝长度ac代入式(13)便可得到失稳断裂韧度![]()
图5给出了每组初始缝高比典型试件的P-CMOD曲线。由图5可知,在四点弯曲梁试验过程中观察到了与三点弯曲梁、楔入劈拉及紧凑拉伸试件类似的现象[1―3],即四点弯曲梁的断裂过程也可以分为三个阶段:在初始加载阶段,可以认为试件处于弹性变形阶段,P-CMOD曲线表现为线性增长;当荷载增至Pini时,裂尖附近开始出现微小裂缝,随着荷载的进一步增大,裂尖附近的微小裂缝不断发展连通,此时,试件裂缝处于稳定扩展阶段直至达到Pmax,表明由于混凝土的黏聚力作用,试件裂尖存在一个稳定扩展的断裂过程区;当荷载达到Pmax后,裂缝继续扩展并且扩展速度较Pmax前快。就本试验而言,除初始缝高比为0.2及0.3的试件由于混凝土材料的脆性特性及积蓄的应变能过大而在峰值荷载后的软化段出现了荷载的陡降而后又缓慢降低的现象外,其他试件均能得到稳定的下降段。最后,试件因微裂缝连通而形成的宏观裂缝沿竖直方向穿过整个试件截面而破坏。试验过程中同样观察到个别试件裂缝扩展路径上因需绕开强度较大的粗骨料而出现少量的偏斜现象,但由于跨中裂缝所在截面附近处于纯弯段,因此,即使裂缝出现了少量偏斜,仍可以认为裂尖因剪力作用导致的ΙΙ型断裂分量很小。

图5 典型试件的 P-CMOD曲线
Fig.5 P-CMOD curves of typical specimens
由上述3.1可知,初始缝高比为0.2及0.3的试件P-CMOD曲线未测到完整的下降段,但双K断裂参数的计算所需要测定的试验参数较少,故即使试件P-CMOD曲线的软化段不完整也不影响其双K断裂参数的计算[2]。因此,据1.3中所述方法测得的试件Pini及Pmax如表1所示。图6给出了Pini、Pmax及Pini/Pmax随初始缝高比的变化情况。
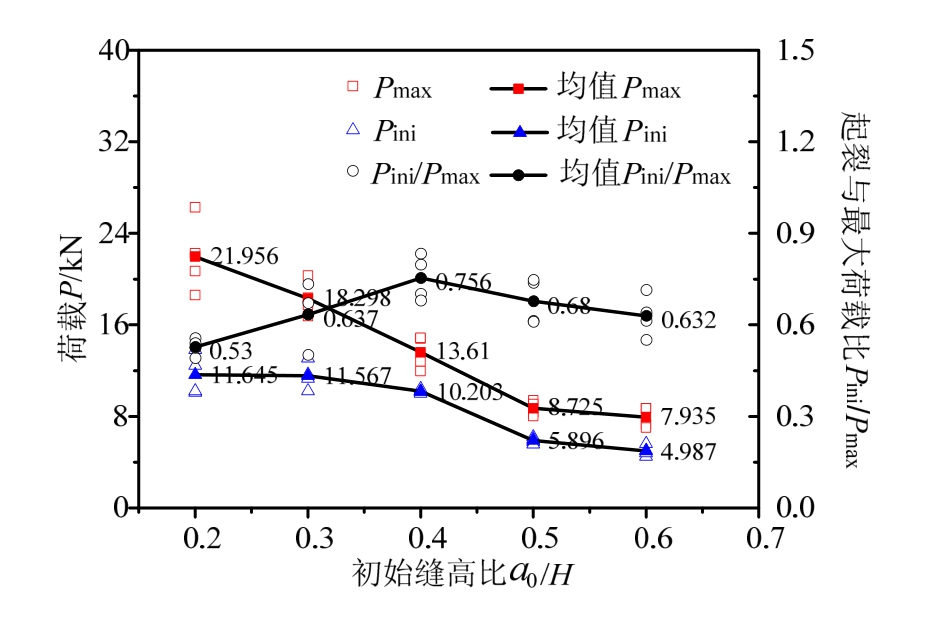
图6 Pini及Pmax与初始缝高比关系
Fig.6 Variation of Pini and Pmax with initial crack-depth ratio
由图6可知,四点弯曲梁的Pini及Pmax表现出了与三点弯曲梁相同的变化趋势[7],即均随着初始缝高比的增大而减小,其中,Pini及Pmax分别由初始缝高比为0.2时的11.645 kN和21.956 kN降为初始缝高比为0.6时的4.987 kN和7.935 kN,分别降低了57.2%和63.9%。Pini/Pmax则先从初始缝高比为0.2时的0.530增至初始缝高比为0.4时的0.756而后减小至初始缝高比为0.6时的0.632,可见初始缝高比为0.4的试件起裂最晚。
表1 试验数据及参数计算
Table 1 Experimental data and parameter calculations
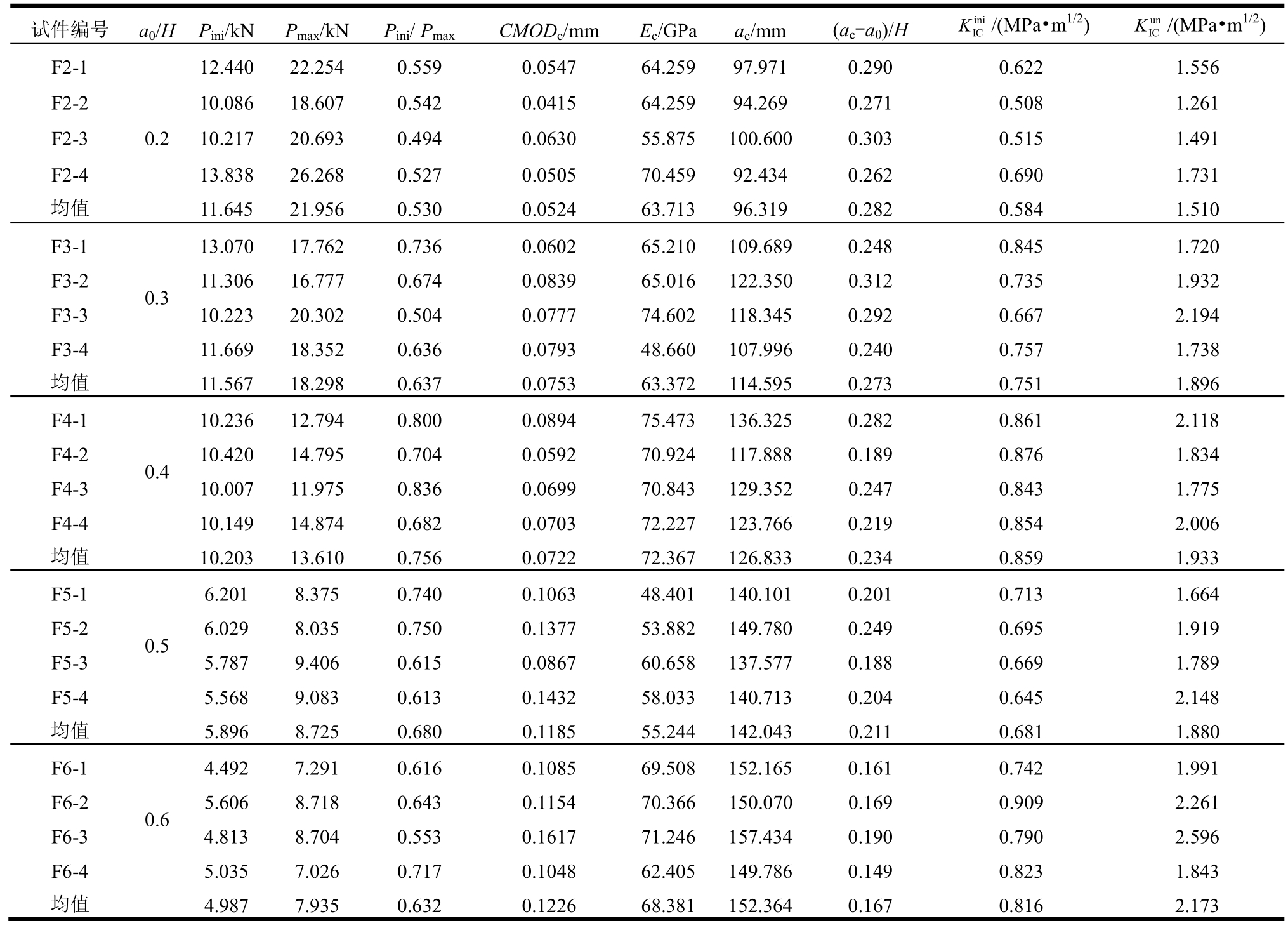
注:Fx-xx中F代表四点弯曲梁,x代表试件初始缝高比为0.x,xx代表该组试件个数。
试件编号 a0/H Pini/kN Pmax/kN Pini/ Pmax CMODc/mm Ec/GPaac/mm (ac-a0)/H ini K/(MPa·m1/2) un IC K/(MPa·m1/2)IC F2-112.440 22.254 0.559 0.0547 64.25997.971 0.290 0.622 1.556 F2-2 10.086 18.607 0.542 0.0415 64.25994.269 0.271 0.508 1.261 F2-3 10.217 20.693 0.494 0.0630 55.875100.6000.303 0.515 1.491 F2-4均值0.2 F3-2 11.306 16.777 0.674 0.0839 65.016122.3500.312 0.735 1.932 F3-3 10.223 20.302 0.504 0.0777 74.602118.3450.292 0.667 2.194 F3-4 11.669 18.352 0.636 0.0793 48.660107.9960.240 0.757 1.738均值 11.567 18.298 0.637 0.0753 63.372114.5950.273 0.751 1.896 F4-1 0.4 1.731 1.510 F3-1 0.3 13.838 11.645 26.268 21.956 0.527 0.530 0.0505 0.0524 70.459 63.713 92.434 96.319 0.262 0.282 0.690 0.584 13.070 17.762 0.736 0.0602 65.210109.6890.248 0.845 1.720 10.236 12.794 0.800 0.0894 75.473136.3250.282 0.861 2.118 F4-2 10.420 14.795 0.704 0.0592 70.924117.8880.189 0.876 1.834 F4-3 10.007 11.975 0.836 0.0699 70.843129.3520.247 0.843 1.775 F4-4 10.149 14.874 0.682 0.0703 72.227123.7660.219 0.854 2.006均值 10.203 13.610 0.756 0.0722 72.367126.8330.234 0.859 1.933 F5-1 0.5 6.201 8.375 0.740 0.1063 48.401140.1010.201 0.713 1.664 F5-2 6.029 8.035 0.750 0.1377 53.882149.7800.249 0.695 1.919 F5-3 5.787 9.406 0.615 0.0867 60.658137.5770.188 0.669 1.789 F5-4 5.568 9.083 0.613 0.1432 58.033140.7130.204 0.645 2.148均值 5.896 8.725 0.680 0.1185 55.244142.0430.211 0.681 1.880 F6-1 0.6 4.492 7.291 0.616 0.1085 69.508152.1650.161 0.742 1.991 F6-2 5.606 8.718 0.643 0.1154 70.366150.0700.169 0.909 2.261 F6-3 4.813 8.704 0.553 0.1617 71.246157.4340.190 0.790 2.596 F6-4 5.035 7.026 0.717 0.1048 62.405149.7860.149 0.823 1.843均值 4.987 7.935 0.632 0.1226 68.381152.3640.167 0.816 2.173
不同于三点弯曲梁[2],对于四点弯曲梁由表1可知,式(12)计算的弹性模量E基本为试验实测值的两倍左右。分析原因发现,在裂尖产生相同的拉应力时,四点弯曲梁所需的外荷载为三点弯曲梁的两倍,而此时两种试件形式所产生的CMOD值基本相同,使得四点弯曲梁实测的P-CMOD曲线初始段柔度Ci为三点弯曲梁的二分之一,从而导致了由式(12)计算的弹性模量E为试验实测值的两倍左右。
临界有效裂缝长度ac反映了试件失稳破坏时的裂缝扩展长度。据实测的Pini及Pmax,结合式(11)计算了试件的ac如表1所示。为了更好的比较不同初始缝高比试件裂缝的扩展情况,定义一个无量纲参数即试件的相对临界有效裂缝扩展长度(ac-a0)/H。图7给出了(ac-a0)/H随试件初始缝高比的变化情况。
由图7可知,随着初始缝高比的增大,(ac-a0)/H从初始缝高比为0.2时的0.282逐渐减小至初始缝高比为0.6时的0.167,减小了40.8%。分析原因,可能是边界效应[36―41]导致,即当裂缝扩展到试件的上边界附近时,上边界会对裂缝的扩展起到一定的限制作用,且试件初始缝高比越大,这种约束作用越强,从而导致(ac-a0)/H随初始缝高比的增大而减小。

图7 (ac-a0)/H与初始缝高比关系
Fig.7 Variation of (ac-a0)/H with initial crack-depth ratio
由式(13)计算所得的![]() 如表1所示,图8给出了
如表1所示,图8给出了![]() 随试件初始缝高比的变化情况。由图8可知,基于四点弯曲梁测得的
随试件初始缝高比的变化情况。由图8可知,基于四点弯曲梁测得的![]() 先由初始缝高比为0.2时的0.584 MPa·m1/2逐渐增大至初始缝高比为0.4时的0.859 MPa·m1/2,而后减小至初始缝高比为0.5时的0.681 MPa·m1/2,最后又增大至初始缝高比为0.6时的0.816 MPa·m1/2,可见
先由初始缝高比为0.2时的0.584 MPa·m1/2逐渐增大至初始缝高比为0.4时的0.859 MPa·m1/2,而后减小至初始缝高比为0.5时的0.681 MPa·m1/2,最后又增大至初始缝高比为0.6时的0.816 MPa·m1/2,可见![]() 随初始缝高比的变化不大;
随初始缝高比的变化不大;![]() 则从初始缝高比为0.2时的1.510 MPa·m1/2增大至初始缝高比为0.3时的1.896 MPa·m1/2,而当初始缝高比由0.3逐渐增至0.5时,
则从初始缝高比为0.2时的1.510 MPa·m1/2增大至初始缝高比为0.3时的1.896 MPa·m1/2,而当初始缝高比由0.3逐渐增至0.5时,![]() 基本保持在1.900 MPa·m1/2不变,但当初始缝高比为0.6时,又观察到少量增大,即从1.880 MPa·m1/2增至2.173 MPa·m1/2。考虑到混凝土材料的离散型及不可避免的试验误差,可以认为四点弯曲梁测得的
基本保持在1.900 MPa·m1/2不变,但当初始缝高比为0.6时,又观察到少量增大,即从1.880 MPa·m1/2增至2.173 MPa·m1/2。考虑到混凝土材料的离散型及不可避免的试验误差,可以认为四点弯曲梁测得的![]() 不随初始缝高比变化,分别为0.738 MPa·m1/2和1.879 MPa·m1/2,与文献[19]的结果基本相同。
不随初始缝高比变化,分别为0.738 MPa·m1/2和1.879 MPa·m1/2,与文献[19]的结果基本相同。
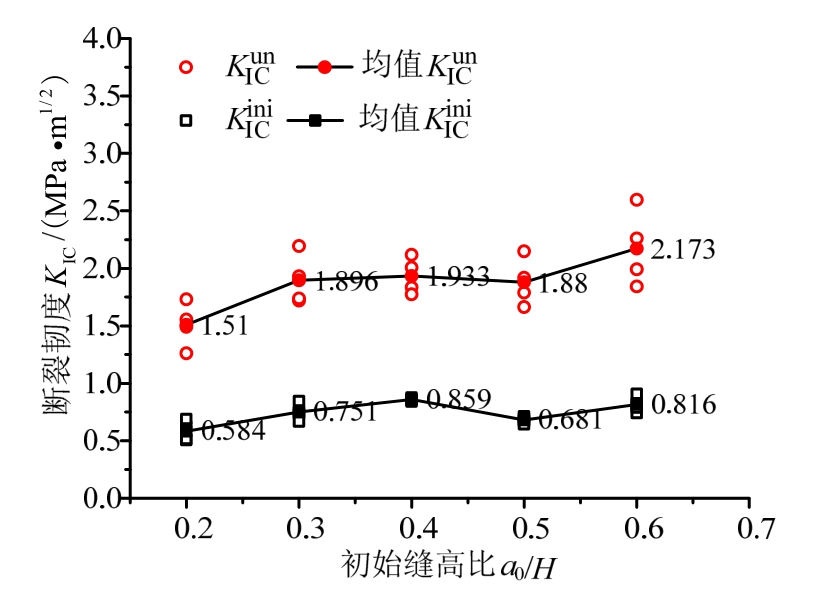
图8 双K断裂参数与初始缝高比关系
Fig.8 Variation of double-K fracture parameters with initial crack-depth tio
对于四点弯曲梁,因其跨中裂缝截面附近处于纯弯曲段,而能减小裂缝扩展路径出现偏折而引起的剪力作用的影响,故从理论上更符合I型断裂模式。基于此,本文采用四点弯曲梁研究了混凝土的断裂性能,通过将四点弯曲梁等效为纯弯曲梁,给出了计算混凝土四点弯曲梁有效裂缝长度ac、起裂断裂韧度![]() 和失稳断裂韧度
和失稳断裂韧度![]() 的计算公式,并研究了不同初始缝高比对四点弯曲梁试件断裂参数的影响,得到以下结论:
的计算公式,并研究了不同初始缝高比对四点弯曲梁试件断裂参数的影响,得到以下结论:
(1)与三点弯曲梁类似,四点弯曲梁测得的Pini及Pmax随初始缝高比的增大而减小,分别由初始缝高比为0.2时的11.645 kN和21.956 kN降为初始缝高比为0.6时的4.987 kN和7.935 kN,分别降低了57.2%和63.9%,并且发现初始缝高比为0.4的试件起裂最晚。
(2)由于边界效应的影响,计算所得的四点弯曲梁相对裂缝扩展长度(ac-a0)/H随初始缝高比的增大而减小,从初始缝高比为0.2时的0.282逐渐减小至初始缝高比为0.6时的0.167,减小了40.8%。
(3)随着初始缝高比的增大,试验测得的![]() 及
及![]() 整体变化不大。考虑到混凝土材料的离散型及不可避免的试验误差,可以认为四点弯曲梁测得的
整体变化不大。考虑到混凝土材料的离散型及不可避免的试验误差,可以认为四点弯曲梁测得的![]() 不随初始缝高比的增大而改变,分别为0.738 MPa·m1/2和1.879 MPa·m1/2。
不随初始缝高比的增大而改变,分别为0.738 MPa·m1/2和1.879 MPa·m1/2。
(4)由上述可知,四点弯曲梁可以用于研究混凝土的双K断裂参数。
应该指出,本文仅研究了不同初始缝高比对四点弯曲梁双K断裂参数的影响,关于不同试件尺寸及不同加载跨度即剪跨比对四点弯曲梁双K断裂参数的影响有待进一步研究。
[1]Xu S L, Reinhardt H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture Part I: Experimental investigation of crack propagation[J].International Journal of Fracture, 1999, 98(2): 111―149.
[2]Xu S L, Reinhardt H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams [J].International Journal of Fracture, 1999, 98(2): 151―177.
[3]Xu S L, Reinhardt H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture Part III: Compact tension specimens and wedge splitting specimens [J].International Journal of Fracture, 1999,98(2): 179―193.
[4]Kumar S, Barai S V.Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function [J].Engineering Fracture Mechanics, 2009, 76(7): 935―948.
[5]Kumar S, Barai S V.Determining the double-K fracture parameters for three-point bending notched concrete beams using weight function [J].Fatigue & Fracture of Engineering Materials & Structures, 2010, 33(10):645―660.
[6]李晓东, 董伟, 吴智敏, 等.小尺寸混凝土试件双K断裂参数试验研究[J].工程力学, 2010, 27(2): 166―171.Li Xiaodong, Dong Wei, Wu Zhimin, et al.Experimental investigation on double-K fracture parameters of small size specimens of concrete [J].Engineering Mechanics,2010, 27 (2): 166―171.(in Chinese)
[7]荣华, 董伟, 吴智敏, 等.大初始缝高比混凝土试件双K断裂参数的试验研究[J].工程力学, 2012, 29(1):162―167.Rong Hua, Dong Wei, Wu Zhimin, et al.Experimental investigation on double-K fracture parameters for large crack-depth ratio in concrete [J].Engineering Mechanics,2012, 29 (1): 162―167.(in Chinese)
[8]胡少伟, 米正祥.标准钢筋混凝土三点弯曲梁双K断裂特性试验研究[J].建筑结构学报, 2013, 34(3): 152―157.Hu Shaowei, Mi Zhengxiang.Experimental study on double-K fracture characteristics of standard reinforced concrete three-point beams [J].Journal of Building Structures, 2013, 34(3): 152―157.(in Chinese)
[9]Dong W, Wu Z M, Zhou X M.Calculating crack extension resistance of concrete based on a new crack propagation criterion [J].Construction & Building Materials, 2013, 38(2):879―889.
[10]徐世烺, 余秀丽, 李庆华.电测法确定低强混凝土裂缝起裂和等效裂缝长度[J].工程力学, 2015, 32(12): 84―89.Xu Shilang, Yu Xiuli, Li Qinghua.Determination of crack initiation and equivalent crack length of low strength concrete using strain gauges [J].Engineering Mechanics, 2015, 32(12): 84―89.(in Chinese)
[11]王璀瑾, 董伟, 王强, 等.混凝土Ⅰ型裂缝扩展准则比较研究[J].工程力学, 2016, 33(5): 89―96.Wang Cuijin, Dong Wei, Wang Qiang, et al.A comparative study on propagation criterion of concrete model Ⅰ crack [J].Engineering Mechanics, 2016, 33(5):89―96.(in Chinese)
[12]Yu K Q, Yu J T, Lu Z D, et al.Fracture properties of high-strength/high-performance concrete (HSC/HPC)exposed to high temperature [J].Materials and Structures,2016, 49(11): 4517―4532.
[13]赵燕茹, 王磊, 韩霄峰, 等.冻融条件下玄武岩纤维混凝土断裂韧度研究[J].工程力学, 2017, 34(9): 92―101.Zhao Yanru, Wang Lei, Han Xiaofeng, et al.Fracture toughness of basalt-fiber reinforced concrete subjected to cyclic freezing and thawing [J].Engineering Mechanics,2017, 34(9): 92―101.(in Chinese)
[14]Rong H, Dong W, Zhang X, et al.Size effect on fracture properties of concrete after sustained loading [J].Materials and Structures, 2019, 52(1): 16―27.
[15]Kumar S, Barai S V.Influence of specimen geometry on determination of double-K fracture parameters of concrete: A comparative study [J].International Journal of Fracture, 2008, 149(1): 47―66.
[16]Qing L B, Li Q B.A theoretical method for determining initiation toughness based on experimental peak load [J].Engineering Fracture Mechanics, 2013, 99(1): 295―305.
[17]徐世烺, 张秀芳, 郑爽.小骨料混凝土双K断裂参数的试验测定[J].水利学报, 2006, 37(5): 543―553.Xu Shilang, Zhang Xiufang, Zheng Shuang.Experimental measurement of double-K fracture parameters of concrete with small size aggregate [J].Journal of Hydraulic Engineering, 2006, 37(5): 543―553.(in Chinese)
[18]Kumar S, Barai S V.Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function [J].Engineering Fracture Mechanics, 2009, 76(7): 935―948.
[19]Zhang X F, Xu S L.A comparative study on five approaches to evaluate double-K fracture toughness parameters of concrete and size effect analysis [J].Engineering Fracture Mechanics, 2011, 78(10): 2115―2138.
[20]陆洲导, 俞可权, 苏磊, 等.高温后混凝土断裂性能研究[J].建筑材料学报, 2012, 15(6): 836―840.Lu Zhoudao, Yu Kequan, Su Lei, et al.Residual fracture behaviors of concrete subjected to elevated temperatures[J].Journal of Building Materials, 2012, 15(6): 836―840.(in Chinese)
[21]Ince R.Determination of the fracture parameters of the double-K model using weight functions of split-tension specimens [J].Engineering Fracture Mechanics, 2012,96(18): 416―432.
[22]胡晓威, 张秀芳, 徐世烺.采用立方体劈拉试件测定混凝土双K断裂参数[J].水利学报, 2012, 43(增刊1):98―109.Hu Xiaowei, Zhang Xiufang, Xu Shilang.Determination of double-K fracture parameters of concrete using split-tension cubes [J].Journal of Hydraulic Engineering,2012, 43(Suppl 1): 98―109.(in Chinese)
[23]Hu S W, Zhang X F, Xu S L.Effects of loading rates on concrete double-K fracture parameters [J].Engineering Fracture Mechanics, 2015, 149(17): 58―73.
[24]Qing L B, Dong M W, Guan J F.Determining initial fracture toughness of concrete for split-tension specimens based on the extreme theory [J].Engineering Fracture Mechanics, 2018, 189(3): 427―438.
[25]Wu Y, Xu S L, Li Q H, et al.Estimation of real fracture parameters of a dam concrete with large size aggregates through wedge splitting tests of drilled cylindrical specimens [J].Engineering Fracture Mechanics, 2016,163(13): 23―36.
[26]Xu S L, Malik M A, Li Q H, et al.Determination of double-K fracture parameters using semi-circular bend test specimens [J].Engineering Fracture Mechanics,2016 , 152(2): 58―71.
[27]李庆华, 种法澄, 张麒, 等.改进的圆形紧凑拉伸法研究混凝土双G断裂参数[J].水利学报, 2018, 49(4):474―482.Li Qinghua, Zhong Facheng, Zhang Qi, et al.Study of double-G fracture parameters using modified round compact tension method [J].Journal of Hydraulic Engineering, 2018, 49(4): 474―482.(in Chinese)
[28]Carpinteri A, Fortese G, Ronchei C, et al.Mode I fracture toughness of fibre reinforced concrete [J].Theoretical and Applied Fracture Mechanics, 2017, 91(5): 66―75.
[29]Dong W, Yang D, Zhou X, et al.Experimental and numerical investigations on fracture process zone of rock-concrete interface [J].Fatigue & Fracture of Engineering Materials & Structures, 2017, 40(5): 820―835.
[30]Vantadori S, Carpinteri A, Guo L P, et al.Synergy assessment of hybrid reinforcements in concrete [J].Composites Part B Engineering, 2018, 147(16): 197―206.
[31]Caggiano A, Cremona M, Faella C, et al.Fracture behavior of concrete beams reinforced with mixed long/short steel fibers [J].Construction & Building Materials, 2012, 37(3): 832―840.
[32]Bencardino F, Rizzuti L, Spadea G, et al.Implications of test methodology on post-cracking and fracture behaviour of steel fibre reinforced concrete [J].Composites Part B Engineering, 2013, 46(3): 31―38.
[33]Leone M, Centonze G, Colonna D, et al.Fiber-reinforced concrete with low content of recycled steel fiber: Shear behavior [J].Construction & Building Materials, 2018,161(5): 141―155.
[34]Tada H, Paris P C, Irwin G R.The stress analysis of cracks handbook [M].New York: ASME Press, 2000.
[35]RILEM Technical Committee 50-FMC.Determination of fracture parameters (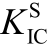 and CTODc) of plain concrete using three-point bend tests [J].Materials & Structures,1990, 23(6): 457―460.
and CTODc) of plain concrete using three-point bend tests [J].Materials & Structures,1990, 23(6): 457―460.
[36]Hu X Z, Duan K.Size effect and quasi-brittle fracture:The role of FPZ [J].International Journal of Fracture,2008, 154(1/2): 3―14.
[37]Hu X Z, Guan J F, Wang Y S, et al.Comparison of boundary and size effect models based on new developments [J].Engineering Fracture Mechanics, 2017, 175(7):146―167.
[38]管俊峰, 王强, Hu Xiaozhi, 等.考虑骨料尺寸的混凝土岩石边界效应断裂模型[J].工程力学, 2017, 34(12):22―30.Guan Junfeng, Wang Qiang, Hu Xiaozhi, et al.Boundary effect fracture model for concrete and granite considering aggregate size [J].Engineering Mechanics, 2017, 34(12):22―30.(in Chinese)
[39]Guan J F, Hu X Z, Yao X H, et al.Fracture of 0.1 and 2 m long mortar beams under three-point-bending [J].Materials & Design, 2017, 133(11): 363―375.
[40]徐平, 胡晓智, 张敏霞, 等.考虑骨料体积含量影响的混凝土准脆性断裂预测模型及应用[J].工程力学,2018, 35(10): 75―84.Xu Ping, Hu Xiaozhi, Zhang Mingxia, et al.Quasi-brittle fracture model and application on concrete considering aggregate volume content effect [J].Engineering Mechanics, 2018, 35(10): 75―84.(in Chinese)
[41]管俊峰, 姚贤华, 白卫峰, 等.由小尺寸试件确定混凝土的断裂韧度与拉伸强度[J].工程力学, 2019, 36(1):70―79.Guan Junfeng, Yao Xianhua, Bai Weifeng, et al.Determination of fracture toughness and tensile strength of concrete using small specimens [J].Engineering Mechanics, 2019, 36(1): 70―79.(in Chinese)
STUDY OF THE DOUBIE-K FRACTURE PARAMETERS OF CONCRETE BASED ON EQUIVALENT PURE BENDING BEAMS
尹阳阳(1991―),男,河南开封人,博士生,主要从事混凝土断裂力学研究(E-mail: yinyy1991@hhu.edu.cn);
范 冰(1989―),男,河南郑州人,博士生,主要从事混凝土断裂力学研究(E-mail: fanbing1989@126.com);
张 润(1994―),男,安徽六安人,硕士生,主要从事混凝土断裂力学研究(E-mail: hhuzhangrun@163.com).