地震作用会引起坝与库水的相互作用,由此产生的动水压力在坝体抗震性能的评价中是不可忽视的关键因素之一。目前,在地震条件下坝前动水压力作用的数值计算与实验方面已有许多的研究成果[1―18],其研究范围涵盖了拱坝、重力坝以及面板坝3种重要坝型,所采用的数值计算方法包括解析法、边界元法(BEM)、有限元法(FEM)和近年出现的比例边界有限元法(SBFEM)。
由Wolf和Song[19]提出的比例边界有限元方法已经被广泛地应用于大坝的静、动力分析[4―7,15,20―21]。对于坝前动水压力的数值计算,SBFEM具有其特殊的优势[4],即仅对流固交界面进行离散,就可以模拟半无限域库水,节省了节点自由度个数,具有较高效率;而且该方法可以考虑不同方向的地震激励、迎水坝面的倾角以及复杂河谷形状等影响。孔宪京等[7,15]采用SBFEM模拟库水,实现了面板坝与库水动力非线性耦合时域分析,该方法具有较高的计算精度,而且忽略动水压力可能使面板动应力产生明显的误差(超过20%)[7];此外,对于具有倾斜坝面的面板堆石坝,传统的Westergaard集中附加质量方法对面板动应力所造成的误差不可忽视(误差超过40%)[15];考虑到较薄的防渗面板对于水库安全运行的重要性,采用精确的动水压力方法来计算面板地震响应是十分重要的。
由于在坝-库动力相互作用分析中,采用SBFEM、FEM或BEM等数值方法处理动水压力时得到的附加质量阵为满阵,当耦合系统自由度数达到一定的规模时,尤其对于具有较强非线性(弹塑性)的数值计算,求解方程消耗了大量的计算时间。针对这个问题,本文提出了一种基于FEM-SBFEM的坝-库水动力流固耦合简化分析方法,并且将其应用在面板坝的非线性动力计算中,通过对比动水压力的分布规律、面板动应力响应以及计算耗时的差异,验证了该简化方法的计算精度和效率。
1 基于FEM-SBFEM的动力耦合计算方法的改进
采用SBFEM离散坝前半无限不可压缩库水[4](令水中波速c=∞,激振频率ω=0)计算出动水压力附加质量阵,采用FEM离散面板堆石坝,现将动力耦合方法以及相应的改进简述如下。
1.1 基于SBFEM的坝前动水压力求解
假定库水为无粘性、不可压缩、小扰动理想流体,地震条件下,坝前动水压力满足拉普拉斯方程:
库水自由表面边界条件:
坝与库水交界面上的边界条件:
水库与基岩(河谷和岸坡)界面上边界条件:
式中:∇2为Laplace算子;p为动水压力;ρ为库水密度;n为界面的法向;![]() 分别为坝库交界面与库水基岩交界面的法向加速度。由于SBFEM离散了坝前半无限域库水,库尾无穷远处辐射条件是自动满足的。
分别为坝库交界面与库水基岩交界面的法向加速度。由于SBFEM离散了坝前半无限域库水,库尾无穷远处辐射条件是自动满足的。
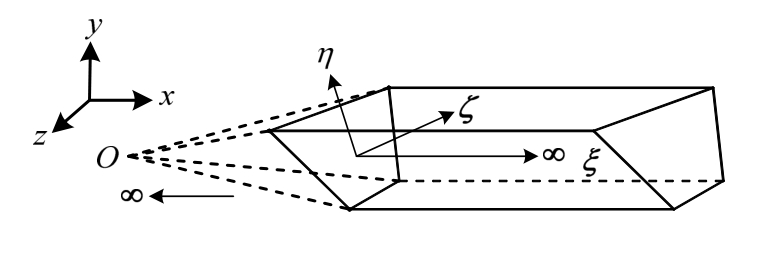
图1 坝前库水域比例边界有限单元示意
Fig.1 Local coordinate system of reservoir in SBFEM
如图1所示,将相似中心O置于库水下游无限远处,则根据比例边界有限元思想只需在坝体迎水面离散库水,将三维问题转化为二维问题;可直接利用坝体迎水面的有限元网格自动生成一些由坝面(ξ=0)延伸至库水上游无穷远处(ξ=+∞)的棱柱状水体单元(ξ为径向坐标),水域内任一点的整体坐标(x,y,z)与局部坐标(ξ,η,ζ)可以通过插值函数[N(η, ζ)]联系在一起,如下所示:
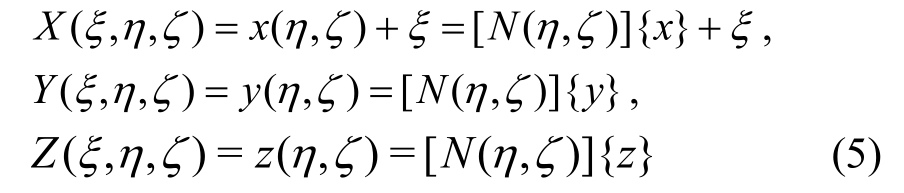
式中,(x,y,z)为坝水交界面上节点的整体坐标。采用加权余量法对动水压力的控制方程和边界条件进行求解,并利用比例边界坐标变换可得到频域动水压力控制方程式(6)和边界条件式(7):
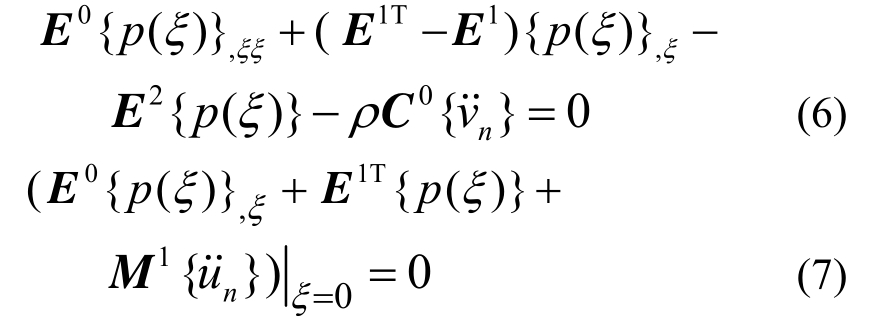
其中,式(6)为关于径向坐标ξ的二阶线性常微分方程,并且E0、E1、E2、C0、M1等系数矩阵只与坝体迎水面的有限元网格相关,与ξ无关。最后,由式(6)和式(7)可以解得由于地震荷载而引起的坝面上的动水压力为:
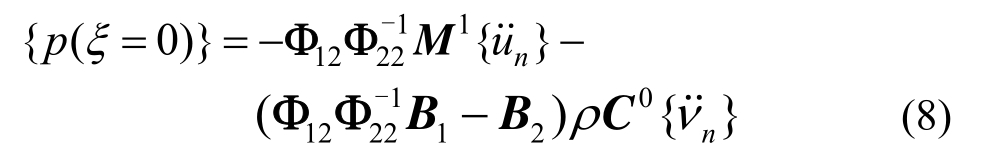
动水压力包含两个分量:前者表示由坝体迎水面的法向加速度激励![]() 所引起的分量,而后者表示由河谷与岸坡的加速度激励
所引起的分量,而后者表示由河谷与岸坡的加速度激励![]() 所引起的分量。
所引起的分量。
1.2 坝与库水动力耦合计算方法
式(9)~式(11)列出由式(8)计算而得的动水压力附加质量矩阵。式中,L1与为整体坐标方向与坝面法向的转换矩阵,L2为整体坐标方向与河谷岸坡法向的转换矩阵,mu和mv分别为与坝体迎水面加速度和河谷基岩迎水面加速度相关的附加质量阵。只要将附加质量阵Mp叠加到坝体有限元动力方程的质量阵中,即可考虑不同方向地震动输入时的动水压力作用。
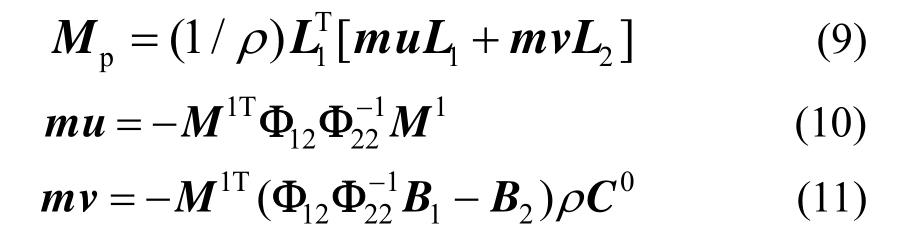
计算而得的附加质量阵mu是满阵,所有元素都是非零的,即在计算坝体迎水面激振所引起的动水压力时,坝面某一节点的动水压力与坝面所有节点的加速度激励![]() 都相关。而在计算基岩河谷激振所引起的动水压力时,坝面某一节点的动水压力仅与坝面与河谷交界线上的节点加速度激励
都相关。而在计算基岩河谷激振所引起的动水压力时,坝面某一节点的动水压力仅与坝面与河谷交界线上的节点加速度激励![]() 相关,因此附加质量阵mv是非常稀疏的矩阵,包含大量的零元素。显然,由于质量阵mu的存在,使得附加质量阵Mp为满阵,使得动力分析中的等效刚度矩阵求解消耗时间大幅提升。
相关,因此附加质量阵mv是非常稀疏的矩阵,包含大量的零元素。显然,由于质量阵mu的存在,使得附加质量阵Mp为满阵,使得动力分析中的等效刚度矩阵求解消耗时间大幅提升。
1.3 附加质量的物理意义与分布特点
由以上分析可知,只需化简mu即可降低附加质量阵Mp的节点自由度相关性。当附加质量阵mu为n阶时(即坝体迎水面的水位线以下有n个结点),其元素muij的物理意义为迎水面结点j对库水的单位法向加速度激励所引起的作用于结点i上的动水压力。选取mu中的第i行,即mui1, mui2,…, muii,…,muin,则该行元素给出了坝体迎水面(水位线以下)所有结点对结点i动水压力贡献。
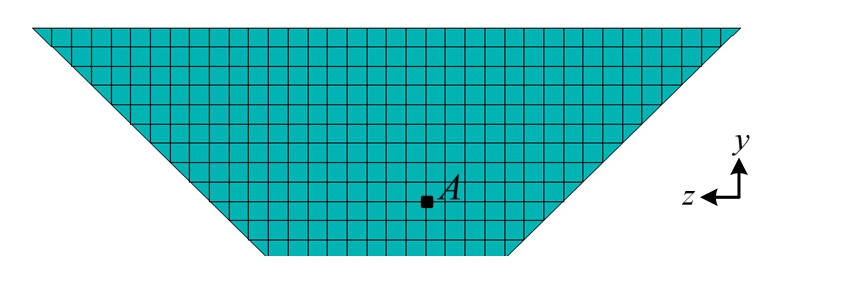
图2 坝体迎水面网格
Fig.2 Mesh of dam face
选取在等腰梯形河谷中的垂直迎水坝面来分析动水压力附加质量阵mu的分布特点,迎水面高200 m,上下底边宽度分别为600 m和200 m,其网格划分情况见图2,坝前水深为200 m(满库情况)。提取附加质量阵mu中与迎水面结点A(图2)相对应的那一行元素,并且在图3中绘制了坝面所有结点在单位面板法向加速度激励下对结点A动水压力的影响(归一化的相对值);如图3所示,结点A对自己的影响是最大的,而且离结点A越近的结点对其动水压力影响越大。迎水面其他结点也是类似的规律,故不再赘述。
对于附加质量阵mu,在第i行所有的元素中,有的元素相对较小,是可以忽略的;因此,当计算作用于结点i上的动水压力时,只需要留下在结点i附近的影响相对较大的元素,其它元素可直接取零。
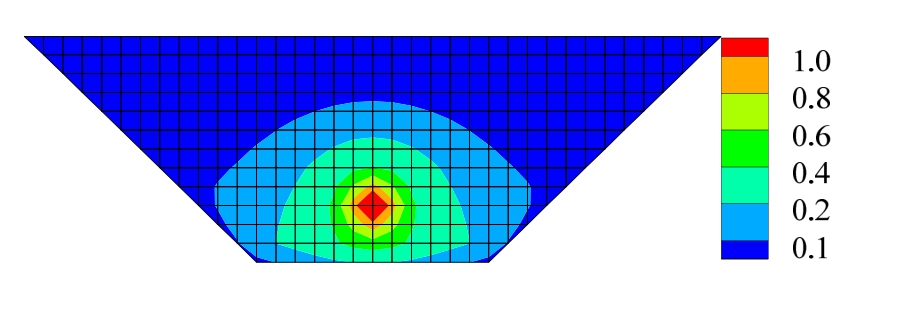
图3 坝面所有结点对结点A的动水压力影响
Fig.3 Effect of all dam face nodes on node A
1.4 理论分析
根据附加质量阵mu各个元素的物理意义,采用按行处理的方式,提出了一种简单、易行的化简方法,现简述如下:
1) 提取动水压力附加质量阵mu的i行元素,按元素数值从大到小排列,并且对该行元素进行累加求和Sumi。2) 在排好序的该行元素中,保留下前面的较大元素、舍掉后边较小的元素,由此需要选定保留系数β(0≤β≤1.0),使得β=SumLefti /Sumi ,其中SumLefti为该行保留下来的元素之和,未留下来的元素直接取零。3) 按照此方法,从第一行开始处理,直到最后一行。
该化简方法仅需提供一个保留系数β,即可实现不同程度的化简,简单易行。β=1.0表示附加质量阵完全保留,没有化简;而β=0表示附加质量阵完全删除,不考虑动水压力。显然,保留系数β的取值决定了附加质量阵化简之后的计算精度和效率:当β取值减小时,可降低动力耦合计算的精度,提高计算效率。面对计算精度和效率之间的矛盾,以下基于面板坝的非线性动力流固耦合分析,对保留系数β的取值进行了敏感性分析。
2 面板坝算例验证与结果讨论
采用FEM-SBFEM方法,进行地震条件下面板堆石坝与库水的动力流固耦合计算,通过选取不同的附加质量阵保留系数β,分析面板动应力结果,讨论了计算效率和精度之间的平衡关系以及保留系数β的取值范围。
2.1 面板坝有限元模型与地震动输入
计算模型采用275 m高的典型面板坝(见图4),共包含单元37860个;棱柱形半无限域库水网格由面板坝迎水面网格自动生成,如图5所示。面板坝的上游面坡度为1∶1.4,下游面坡度为1∶1.6,两岸坡度为1∶1,河谷宽95 m,库区水深265 m,面板厚度为0.3m +0.0035H(H为坝高,单位m)。图6为Koyna地震波,两向地震波采用一致输入方法同时输入,顺河向地震波的加速度峰值均为1.5 m/s2,竖向地震加速度峰值为1.0 m/s2。
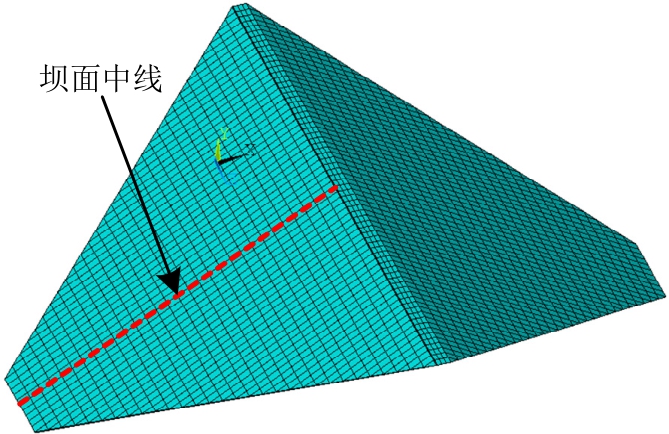
图4 面板坝网格
Fig.4 Finite element mesh of CFRD

图5 库水网格示意
Fig.5 Sketch of reservoir mesh
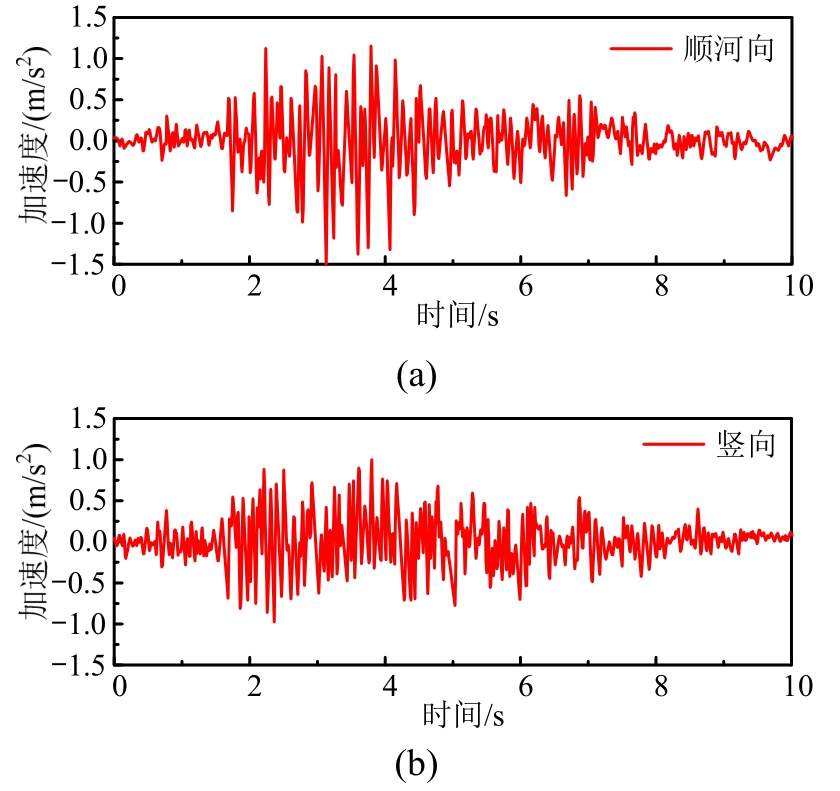
图6 Koyna地震波时程
Fig.6 Time history of Koyna earthquake
2.2 面板坝材料本构模型及参数
筑坝堆石料的动静力本构具有较强的非线性[22―27],本文采用改进的广义塑性模型[22],该模型包含的17个材料参数,其取值详见表1。混凝土面板采用线弹性模型,弹性模量E=30 GPa,泊松比ν=0.167。堆石体与混凝土面板均采用等参元。周边缝以及竖缝单元的法向压缩与拉伸刚度分别取为25 GPa/m和5 MPa/m,切向刚度为1 MPa/m,各参数均采用文献[28]的建议值。面板与垫层之间的接触面采用Goodman单元模拟,其动力本构模型为理想弹塑性模型[29],参数选取如表2所示。
表1 堆石料广义塑性模型参数
Table 1 Parameters of rockfill materials
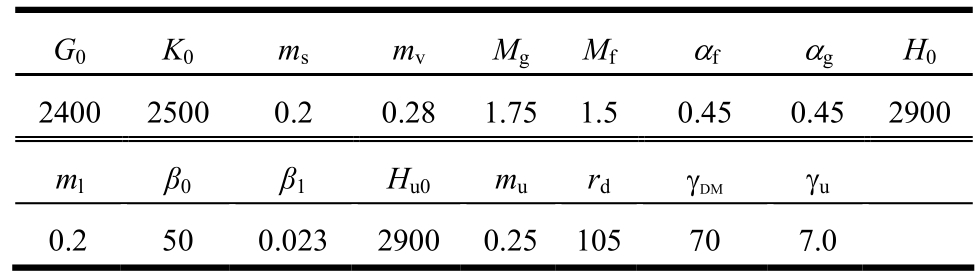
G0 K0 ms mv Mg Mf αf αg H0 240025000.2 0.281.75 1.5 0.45 0.452900 ml β0 β1 Hu0 mu rd γDM γu 0.2 50 0.02329000.25 105 70 7.0
表2 理想弹塑性接触面模型参数
Table 2 Parameters of ideal elasto-plastic interface model
k1 k2/(kPa·m-1) n φ/(°) c/kPa 300 1×107 0.8 41.5 0
2.3 附加质量阵化简效果
选取动水压力附加质量阵保留系数β=1.0、β=0.8、β=0.6、β=0.4共4种工况。本算例中,面板迎水面水位线下有2329个结点,则附加质量阵mu包含2329×2329=5424241个元素。表3列出了不同保留系数条件下,留下的附加质量阵的元素的个数及其占总量的比重(保留率);图7则给出了保留率与保留系数的关系曲线。可见,当1.0<β<0.8时,保留率降低速度很快;当0.0<β<0.6时,保留率降低速度很慢;当保留系数取较小值时,可以节省很多由附加质量阵所占用的内存。
表3 附加质量阵化简效果
Table 3 Simplification of added mass matrix

保留系数 β=1.0 β=0.8 β=0.6 β=0.4留下元素(个) 5424241 888242 380948 148384保留率/(%) 100.0 16.4 7.0 2.7
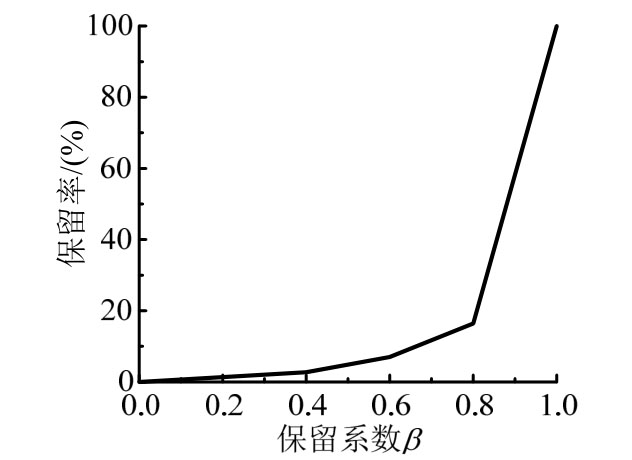
图7 保留率与保留系数的关系曲线
Fig.7 Retention coefficient and retention rate
2.4 动水压力分布差异
地震激振下的动水压力绝对值沿迎水坝面中线(图4)的二维分布包络见图8,随着保留系数的降低,动水压力逐渐减小,而且动水压力包络基本保持类似的形状。动水压力的最大值出现在坝基,在该处附近不同的工况下动水压力相差不大。

图8 坝面中线动水压力包络
Fig.8 Envelope of hydrodynamic pressure
2.5 面板动应力与计算效率
研究了不同保留系数(β=1.0、β=0.8、β=0.6、β=0.4)的动水压力附加质量阵对面板动应力极值(最大值)及其分布和计算耗时的影响;计算面板动应力的误差时,以未化简的附加质量阵(β=1.0)的计算结果为基准。
2.5.1 面板动应力精度
表4和表5分别列出了不同的保留系数条件下,面板顺坡向和坝轴向动应力最大值及其误差。从表4可知,随着保留系数β的降低,面板的动应力误差逐渐增大,保留系数对面板的顺坡向动应力影响较大,而对坝轴向动应力影响较小。图9为保留系数不同取值时的面板顺坡向动拉应力极值分布,可见随着保留系数β的降低,面板动应力的高应力区范围逐渐减小,但变化并不明显,计算精度缓慢降低,β=0.6时面板动应力最大值误差不到5%(表5)。
表4 面板动应力极值
Table 4 Maximal stress of slab
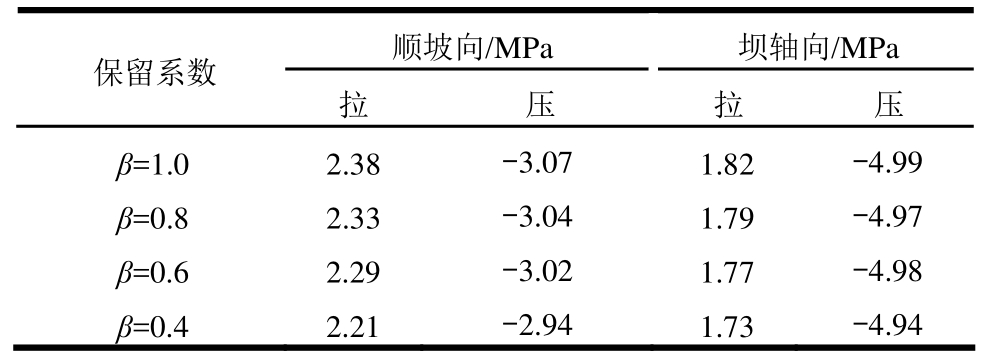
保留系数顺坡向/MPa 坝轴向/MPa拉 压 拉 压β=1.0 2.38 -3.07 1.82 -4.99 β=0.8 2.33 -3.04 1.79 -4.97 β=0.6 2.29 -3.02 1.77 -4.98 β=0.4 2.21 -2.94 1.73 -4.94
表5 面板动应力极值的误差
Table 5 Error of maximal stress of slab
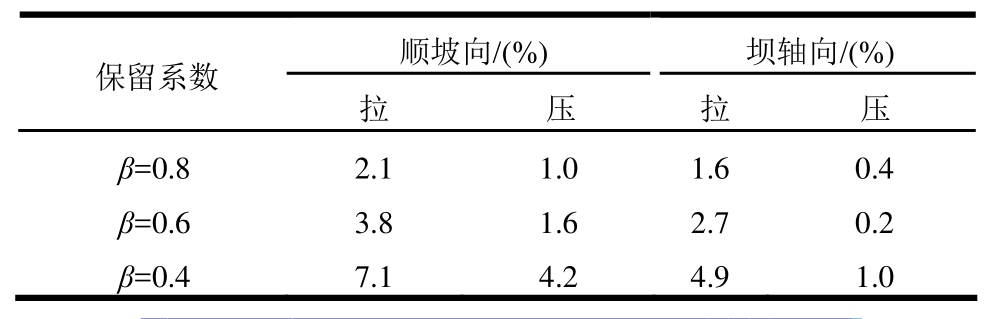
保留系数 拉 压 拉 压顺坡向/(%) 坝轴向/(%)β=0.8 2.1 1.0 1.6 0.4 β=0.6 3.8 1.6 2.7 0.2 β=0.4 7.1 4.2 4.9 1.0
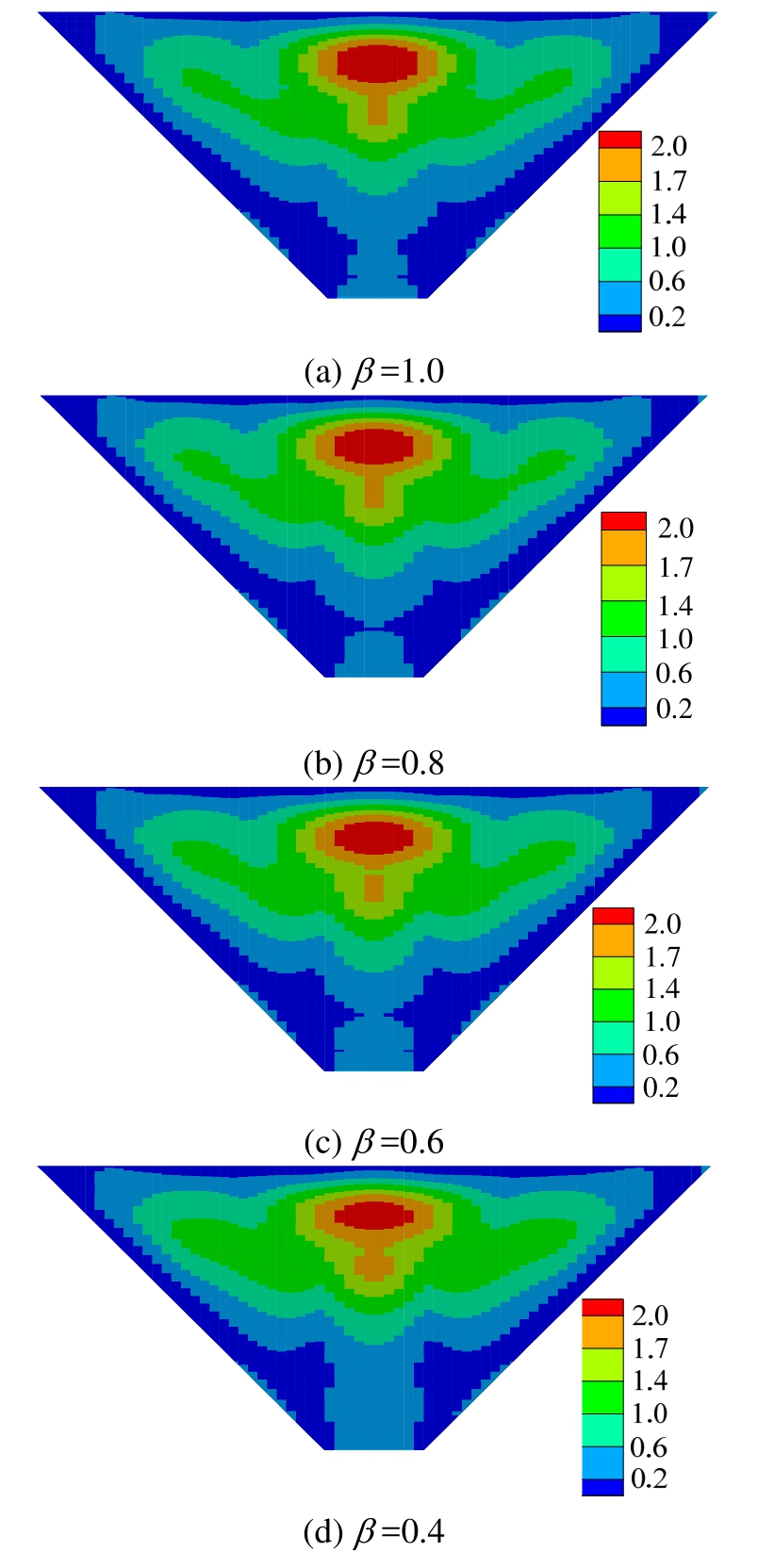
图9 面板顺坡向动拉应力极值分布 /MPa
Fig.9 Maximal slope direction dynamic tensile stress of slab
2.5.2 计算效率讨论
数值计算所用台式计算机的CPU型号为Intel(R)Xeon(R) CPU E5-2697 V2,主频2.7 GHz。表6列出了不同保留系数工况下,面板坝-库水流固耦合动力计算的消耗时间及其所占比率(以β=1.0工况的计算耗时为基准)和对应的面板动应力的最大误差。由表6可见,随着保留系数的降低,耦合计算的消耗时间大幅度地降低,而精度也随之降低,误差最大为7.1%。采用未化简的动水压力附加质量阵时(β=1.0)计算消耗时间最多,保留系数β=0.4时所需的计算耗时仅为其13.3%,由此可见附加质量阵对动力耦合计算效率的影响非常大。联合表5和表6可知:当保留系数β=0.8时,计算时间节省了原来的2/3以上,而计算精度没有明显降低,保留系数β≈0.8适应于计算自由度规模相对较小情况。当动力耦合计算的自由度规模相对较大时,保留系数β可在0.6附近取值,此时耦合计算消耗时间还不到原来的1/5,也可保证计算误差不会太大。
表6 面板动应力极值的最大误差
Table 6 Maximal error of maximal stress of slab

保留系数 β=1.0 β=0.8 β=0.6 β=0.4计算耗时/min 1490.2 434.4 271.4 198.9耗时比率/(%) 100.0 29.2 18.2 13.3应力最大误差/(%) ― 2.1 3.8 7.1
3 结论
本文得到以下结论:
(1)提出了一种基于FEM-SBFEM的坝-库水动力流固耦合简化分析方法,并且将其应用在面板坝的非线性动力耦合计算中;该方法根据附加质量阵的物理意义与分布特点,通过化简动水压力附加质量阵,在保证具有良好精度的前提下,大幅降低计算消耗时间、提高计算效率。
(2)仅需提供一个保留系数β(0≤β≤1.0)即可实现不同程度的化简,简单易行;当保留系数取较小值时,尤其对于计算规模较大的算例,可以节省很多内存,提高计算效率,计算精度会相应降低。
(3)随着保留系数β的降低,坝前动水压力逐渐减小,面板的动应力误差逐渐增大,耦合计算的消耗时间大幅度地降低。采用未化简的动水压力附加质量阵时(β=1.0)计算消耗时间最多,保留系数β=0.4时所需的计算耗时仅为其13.3%,可见附加质量阵对动力耦合计算效率的影响非常大。
(4)保留系数β≈0.8适应于计算自由度规模相对较小情况,计算精度没有明显降低;当计算的自由度规模相对较大时,保留系数β可在0.6附近取值,可保证计算误差不会太大。此外,本文提供的坝库动力耦合分析中的附加质量阵化简方法也适用于其他数值方法(FEM等)计算出的动水压力附加质量,也可应用于混凝土坝的分析。
[1]李俊杰, 马恒春.蓄水期面板堆石坝动力特性研究[J].岩土工程学报, 1995, 17(4): 20―27.Li Junjie, Ma Hengchun.Research on dynamic property of CFRD in the period of water storage [J].Chinese Journal of Geotechnical Engineering, 1995, 17(4): 20―27.(in Chinese)
[2]王铭明, 陈健云, 徐强, 等.不同高度重力坝动水压力分析及Westergaard修正公式研究[J].工程力学, 2013,30(12): 65―70, 84.Wang Mingming, Chen Jianyun, Xu Qiang, et al.Study on diffrerent height gravity hydrodynamic pressure and westergaard correction formula [J].Engineering Mechanics, 2013, 30(12): 65―70, 84.(in Chinese)
[3]陈国荣, 姜弘道.边界单元法在动水压力分析中的应用[J].河海大学学报, 1989, 17(2): 19―25.Chen Guorong, Jiang Hongdao.Boundary element method for the hydrodynamic pressure [J].Journal of Hohai University, 1989, 17(2): 19―25.(in Chinese)
[4]Lin G, Wang Y, Hu Z.An efficient approach for frequency-domain and time-domain hydrodynamic analysis of dam-reservoir systems [J].Earthquake Engineering & Structural Dynamics, 2012, 41(13):1725―1749.
[5]王翔, 金峰.动水压力波高阶双渐近时域平面透射边界I: 理论推导[J].水利学报, 2011, 42(7): 839―847.Wang Xiang, Jin Feng.High-order doubly asymptotic time-domain plane transmitting boundary for hydrodynamic pressure I: Theoretical derivation [J].Journal of Hydraulic Engineering, 2011, 42(7): 839―847.(in Chinese)
[6]李上明, 吴连军.基于连分式与有限元法的坝库耦合瞬态分析方法[J].工程力学, 2016, 33(4): 9―16.Li Shangming, Wu Lianjun.Dam-reservoir interaction transient-method based on continued fraction formulation and FEM [J].Engineering Mechanics, 2016, 33(4): 9―16.(in Chinese)
[7]孔宪京, 许贺, 邹德高, 等.不同激振方向下动水压力对高面板坝面板动应力的影响[J].水利学报, 2016,47(9): 1153―1159.Kong Xianjing, Xu He, Zou Degao, et al.Effects of hydrodynamic pressure on dynamic stress of slab of high concrete faced rock fill dam under excitation of different directions [J].Journal of Hydraulic Engineering, 2016,47(9): 1153―1159.(in Chinese)
[8]陈厚群.水坝抗震的实验研究[J].工程抗震与加固改造, 1986(2): 20―24, 46.Chen Houqun.Study on dam experiments of earthquake resistance [J].Journal of Seismic Engineering and Reinforcement and Reconstruction, 1986(2): 20―24, 46.(in Chinese)
[9]阎承大, 张楚汉.规则河谷中计算水坝动水压力的解析方法[J].清华大学学报: 自然科学版, 1990, 30(5):15―21.Yan Chengda, Zhang Chuhan.Analytical solution for evaluation of hydrodynamic pressures for dam-reservoirs on some regular canyons [J].Journal of Tsinghua University: Science and Technology, 1990, 30(5): 15―21.(in Chinese)
[10]王进廷, 杜修力, 张楚汉.重力坝-库水-淤砂-地基系统动力分析的时域显式有限元模型[J].清华大学学报:自然科学版, 2003, 8: 1112―1115.Wang Jinting, Du Xiuli, Zhang Chuhan.Explicit finite element model for dynamic analysis of dam-reservoirsediment-foundation system [J].Journal of Tsinghua University: Science and Technology, 2003, 8: 1112―1115.(in Chinese)
[11]陈厚群, 杨大伟.地震条件下拱坝库水相互作用的试验研究[J].水利学报, 1989(7): 29―39.Chen Houqun, Yang Dawei.Study on arch dam-reservoir water interaction under earthquake condition [J].Journal of Hydraulic Engineering, 1989(7): 29―39.(in Chinese)
[12]Kartal M E, Bayraktar A.Non-linear earthquake response of CFR DAM-reservoir-foundation systems [J].Mathematical and Computer Modelling of Dynamical Systems, 2013, 19(4): 353―374.
[13]迟世春, 顾淦臣.面板堆石坝坝水系统自振特性研究[J].河海大学学报, 1995, 23(6): 104―107.Chi Shichun, Gu Ganchen.Study on natural vibration characteristics of CFRD-reservoir system[J].Journal of Hohai University, 1995, 23(6): 104―107.(in Chinese)
[14]岑威钧, 张自齐, 袁丽娜, 等.库水对高面板堆石坝动力反应的影响[J].武汉大学学报: 工学版, 2015, 48(4):441―446.Cen Weijun, Zhang Ziqi, Yuan Lina, et al.Study of influence of reservoir water on response of high concrete face rockfill dynamic dams [J].Engineering Journal of Wuhan University , 2015, 48(4): 441―446.(in Chinese)
[15]Xu H, Zou D, Kong X, et al.Error study of Westergaard's approximation in seismic analysis of high concrete-faced rockfill dams based on SBFEM [J].Soil Dynamics and Earthquake Engineering, 2017, 94: 88―91.
[16]Karalar M, Cavusli M.Assessing 3D seismic damage performance of a CFR dam considering various reservoir heights [J].Earthquakes and Structures, 2019, 16(2):221―234.
[17]Karalar M, Cavusli M.Evaluation of 3D Nonlinear earthquake behaviour of the ilsu CFR dam under far-fault ground motions [J].Advances in Civil Engineering, 2019,2019: 1―15..
[18]Sotoudeh P, Ghaemian M, Mohammadnezhad H.Seismic analysis of reservoir-gravity dam-massed layered foundation system due to vertically propagating earthquake [J].Soil Dynamics and Earthquake Engineering, 2019, 116: 174―184.
[19]Wolf J P, Song C.The scaled boundary finite-element method-a primer: derivations [J].Computers & Structures,2000, 78(1): 191―210.
[20]孔宪京, 陈楷, 邹德高, 等.一种高效的FE-PSBFE耦合方法及在岩土工程弹塑性分析中的应用[J].工程力学, 2018, 35(6): 6―14.Kong Xianjing, Chen Kai, Zou Degao, et al.An efficient FE-PSBFE coupled method and application to the elasto-plastic analysis of geotechnical engineering structures [J].Engineering Mechanics, 2018, 35(6): 6―14.(in Chinese)
[21]钟红, 林皋, 李红军.坝基界面在非线性水压力驱动下的非线性断裂过程模拟[J].工程力学, 2017, 34(4):42―48.Zhong Hong, Lin Gao, Li Hongjun.Nonlinear fracture simulation of dam-foundation interface driven by nonlinear water pressure [J].Engineering Mechanics,2017, 34(4): 42―48.(in Chinese)
[22]Xu B, Zou D, Liu H.Three-dimensional simulation of the construction process of the Zipingpu concrete face rockfill dam based on a generalized plasticity model [J].Computers and Geotechnics, 2012, 43: 143―154.
[23]Ling H I, Liu H.Pressure-level dependency and densification behavior of sand through generalized plasticity model [J].Journal of Engineering Mechanics,2003, 129(8): 851―860.
[24]刘萌成, 高玉峰, 刘汉龙.堆石料剪胀特性大型三轴试验研究[J].岩土工程学报, 2008(2): 205―211.Liu Mengcheng, Gao Yufeng, Liu Hanlong.Study on shear dilatancy behaviors of rockfills in large-scale triaxial tests [J].Chinese Journal of Geotechnical Engineering, 2008(2): 205―211.(in Chinese)
[25]张凌凯, 王睿, 张建民, 等.不同应力路径下堆石料的动力变形特性试验研究[J].工程力学, 2019, 36(3):114―120, 130.Zhang Lingkai, Wang Rui, Zhang Jianmin, et al.Experimental study on dynamic deformation characteristics of rock fill materials under different stress paths [J].Engineering Mechanics, 2019, 36(3): 114―120,130.(in Chinese)
[26]王蕴嘉, 周梦佳, 宋二祥.考虑颗粒破碎的堆石料湿化变形特性离散元模拟研究[J].工程力学, 2018, 35(增刊): 217―222.Wang Yunjia, Zhou Mengjia, Song Erxiang.Dem simulation of wetting deformation characteristics of rock fill considering particle breakage [J].Engineering Mechanics, 2018, 35(Suppl): 217―222.(in Chinese)
[27]金德海, 徐明.考虑围压对粗粒土蠕变特性影响的Burgers模型参数修正方法研究[J].工程力学, 2016,33(12): 135―142.Jin Dehai, Xu Ming.Parameter correction method of burgers model for coarse-grained soil considering confining pressure [J].Engineering Mechanics, 2016,33(12): 135―142.(in Chinese)
[28]邹德高, 尤华芳, 孔宪京, 等.接缝简化模型及参数对面板堆石坝面板应力及接缝位移的影响研究[J].岩石力学与工程学报, 2009, 28(增刊1): 3257―3263.Zou Degao, You Huafang, Kong Xianjing, et al.Research on joint simplified model and effects of joint parameters on panel stress and joint displacements of faced rockfill dam [J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl 1): 3257―3263.(in Chinese)
[29]Zou D, Xu B, Kong X, et al.Numerical simulation of the seismic response of the Zipingpu concrete face rock fill dam during the Wenchuan earthquake based on a generalized plasticity model [J].Computers and Geotechnics, 2013, 49: 111―122.