有限元法是求解微分方程比较有效的数值计算方法，具有数值稳定性好、通用性强的特点。计算机的出现，使得有限元法得到了快速发展和广泛应用。有限元法使得许多大型工程计算得以实现，对科学和工程的发展起到了巨大的推动作用。
有限元的求解精度依赖于网格和单元次数：网格越密，单元次数越高，计算精度就越高。因此，为了提高结果精度就需要加密网格或提高单元次数，这相应导致有限元求解的计算量快速增加。为了在比较小的计算代价下有效提高有限元解的精度，国内外学者对超收敛计算开展了大量研究，提出了一些超收敛计算方法，其中代表性的有SPR法[1-2]、REP法[3]、PEM法[4]、RCP法[5]、NPF-based法[6]、单元正交分析法[7]、EEP法[8-11]等。
Douglas和Dupont[12]最早对二阶线性常微分方程边值问题提出了p型超收敛算法的思想，并给出了数学证明。本文作者所在的课题组对该方法进行了推广，取得了较好的效果。文献[13]用该法作了一维有限元自适应分析，文献[14]将该法拓展至结构自由振动分析，文献[15]将该法应用于平面曲梁静力分析，文献[16]将该法应用于旋转壳和薄壁曲梁的静力分析，文献[17]将该法应用于平面曲梁面内自由振动分析，文献[18]将该法应用于Euler梁弹性稳定分析。本文力图将该法推广应用于非线性常微分方程边值问题的分析中。
一些专家学者对非线性边值问题有限元解的超收敛性进行了研究。陈传淼[19]证明线性问题的超收敛结论对非线性椭圆问题的有限元解仍然成立，熊之光和杨喜陶[20]证明了非线性椭圆问题矩形有限元的超收敛性，Chow和Carey[21]证明了非线性两点边值问题有限元解中结点位移的超收敛性质。除此之外，文献[22]提出一种非线性有限元解的误差估计方法，文献[23]将EEP法应用于一维非线性有限元的自适应分析。基于非线性两点边值问题有限元解答中结点位移的超收敛性，本文将p型超收敛算法推广至非线性两点边值问题的有限元求解中。
1 模型问题及有限元解
本文考虑一类如下形式的非线性两点边值问题：
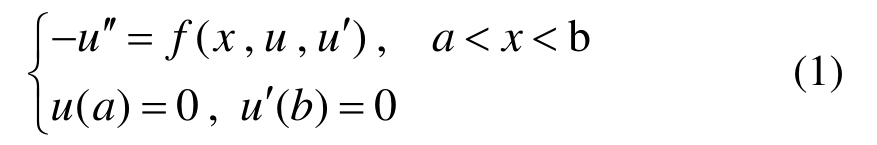
式中：u=u(x)为待求函数；()′=d()/dx ，()′=d2()/dx2。对该问题建立弱形式：
式中，v为检验函数。经分部积分引进边界条件后弱形式如式(3)所示：
利用上述弱形式可对该非线性边值问题进行有限元求解。首先对结构进行离散，如图1所示。记单元个数为ne，结点坐标为xj (j=1,2，…,ne+1)，单元尺寸为he (e=1,2,…,ne)。
图1 有限元网格
Fig.1 FE mesh
有限元网格尺寸定义为：
有限元将解答用分片多项式离散为：
式中：N为有限元基函数矩阵[24]；Δh为整体自由度向量。对检验函数v亦进行类似的分片多项式离散：
将试探函数与检验函数代入弱形式可得有限元刚度矩阵K和荷载向量P(Δh)：
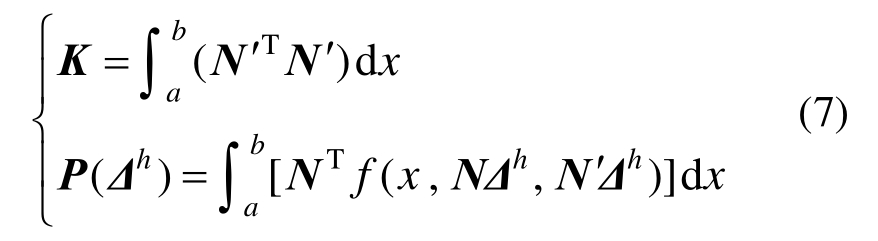
对本文的非线性问题，荷载向量P(Δh)是整体自由度Δh的非线性函数关系，因此该方程组是一个非线性方程组，需进行迭代求解。本文采用Newton法进行迭代求解，具体求解过程如下。记：
则有：
式中，F′(Δh )=∂F(Δh)/∂Δh是F(Δh)的Jacobi矩阵，具体计算如下：
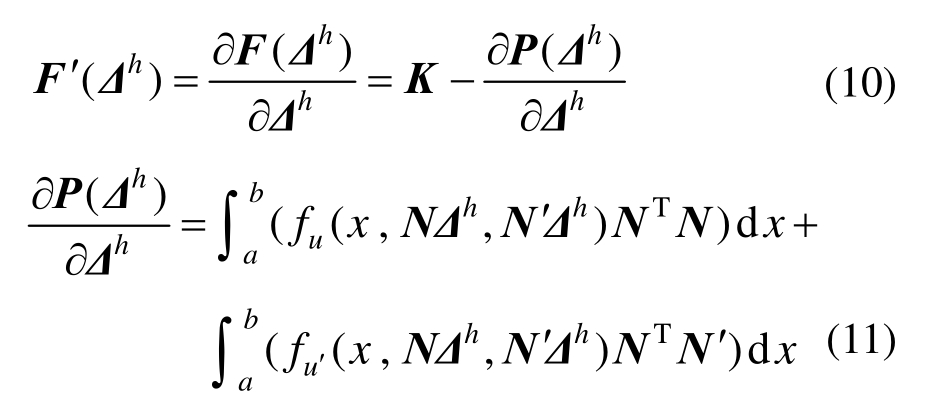
式中：()u=∂()/∂u ，()u′=∂()/∂u′。
由Newton迭代求解出Δh，代入式(5)即得有限元解uh。记有限元解的误差：
文献[21]证明有限元解具有如下收敛阶：
式中，m为有限元计算所采用的单元次数。有限元导数解由函数解求导得到，精度降低一阶：
文献[21]证明有限元解uh在结点处具有更好的收敛性：
当单元次数m＞1时，结点解的收敛阶高于单元内点解的收敛阶，具有超收敛性。因此在网格加密过程中，结点解将比单元内点解更快地向精确解收敛，其误差将远小于单元内点解的误差。结点解的超收敛性是本文构造p型超收敛算法的基础。
2 超收敛求解思路
对于原问题在任意单元(e)上的精确解u，应满足如下的非线性常微分方程边值问题：
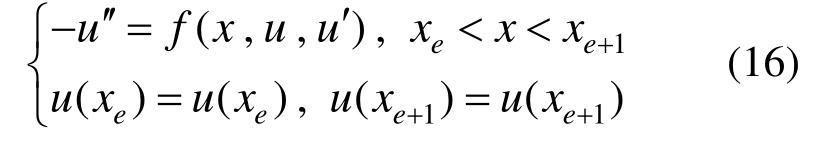
由式(15)知，有限元结点解具有O(h2m)的超收敛性，在网格加密过程中，结点解将比单元内点解更快地收敛到精确解，故当网格足够密时，近似有：
因此单元(e)上的解答u将近似于如下边值问题的解答：
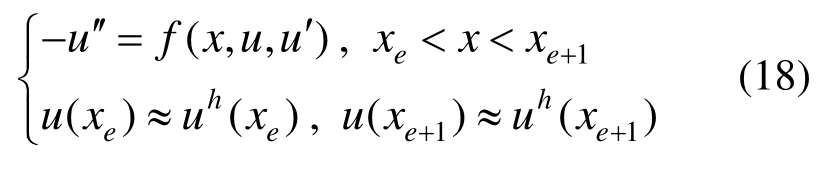
采用更高次单元求解该边值问题可获得单元上的超收敛解。但该边值问题仍是非线性的，需迭代求解，为避免迭代求解，对方程右边项f(x,u,u′)在有限元解答处作Taylor展开，有：
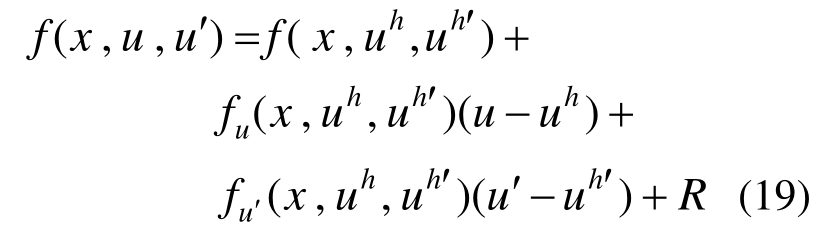
式中，R是展开的残余项，为：
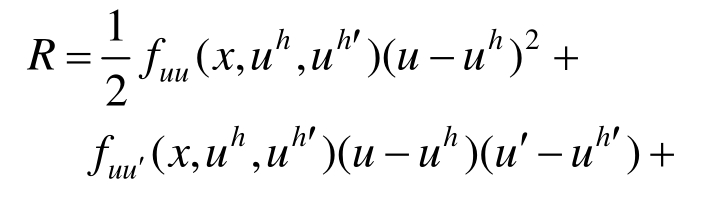
记：
则有：
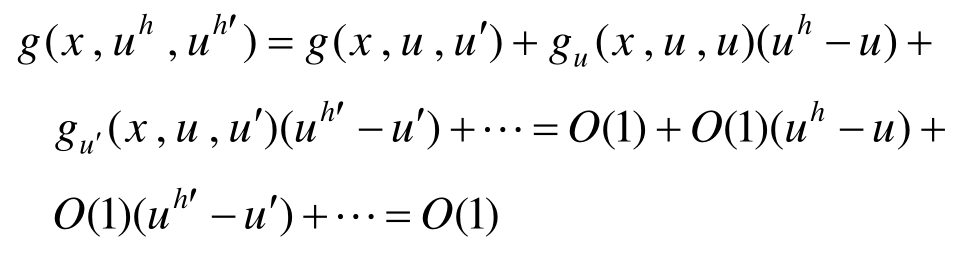
即：
同理，可证：
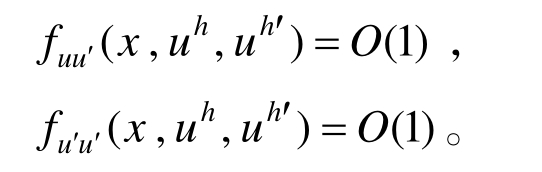
引入式(13)、式(14)的误差估计，可得：
至此，可将式(18)中的非线性边值问题近似为如下线性边值问题：
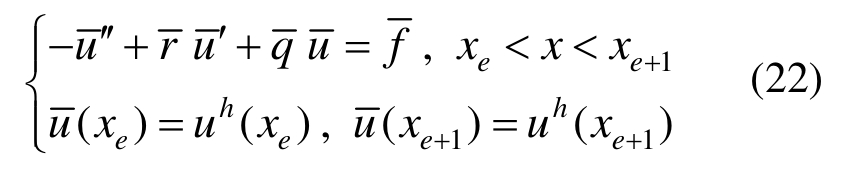
式中：
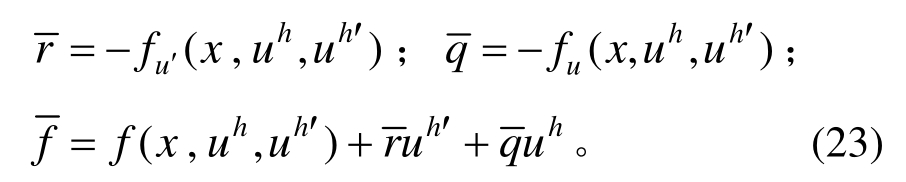
本文通过求解该线性边值问题获得单元(e)上的超收敛解，对该边值问题，本文直接采用一个高次单元进行求解。设单元次数为
单元(e)上的超收敛解为：
式中：
为次数为
的形函数矩阵；
为在单元(e)上的自由度向量。下标b、c分别对应单元端部自由度和单元内部自由度。其中
在单元(e)上进行超收敛计算时的刚度矩阵
和荷载向量为
分别为：
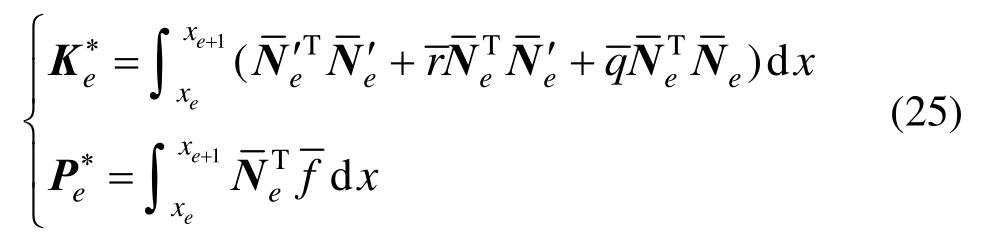
该边值问题的有限元方程为：
式中：
分别为单元刚度矩阵中端部自由度和内部自由度对应的子矩阵；
为单元荷载向量中内部自由度对应的子向量。由该方程可求得内部自由度解
为：
从而得到单元(e)上的超收敛解：
3 超收敛误差估计
记超收敛解的误差为：
式中：
单元上
次有限元解，由文献[12]的估计：
由式(16)和式(22)相减，得：
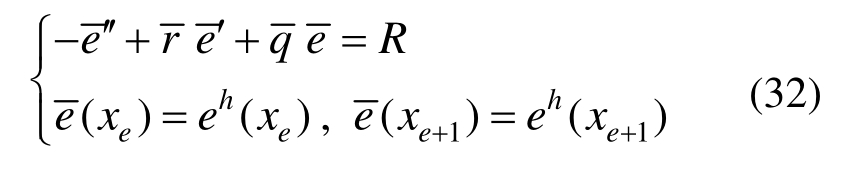
由式(15)、式(21)知，式(32)中R=O(h2m)，eh (xe)=O(h2m )，eh(xe+1)=O(h2m )，故当网格足够密时，有：
从而可得超收敛解的误差为：
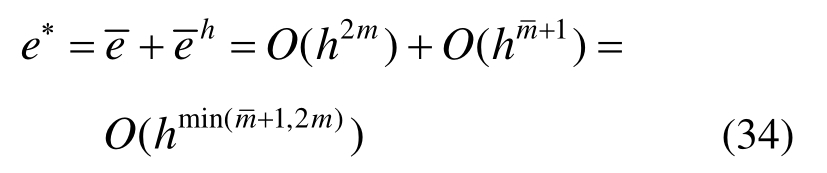
有限元解的误差如式(13)所示。易见，m＞1时，min(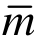
+1,2m)＞m +1，u*收敛阶高于uh ，u*具有超收敛性。数值算例显示，这样求得的u*′也有超收敛性。
4 数值算例
本文算法已编制成Fortran程序。大量数值试验表明本文方法高效、可靠，能有效提高解答的精度和收敛阶。本节给出若干数值算例，用以展示其效果。为考察收敛阶，本文选取误差模为最大模。
例1.半无限长膜问题
图2所示为半无限长膜问题[25]。当荷载和结构对称时，取一半结构进行分析，其控制微分方程为：
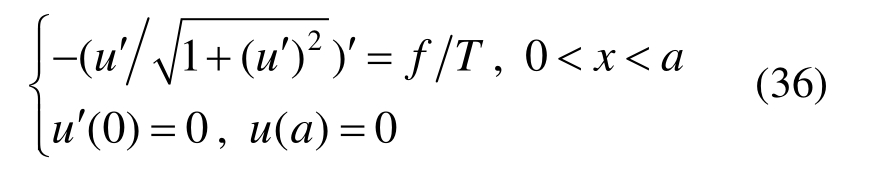
式中：u为半无限长膜的挠度；f为横向均布荷载；T为薄膜张力。上述微分方程可以进一步等价转换为如下形式：
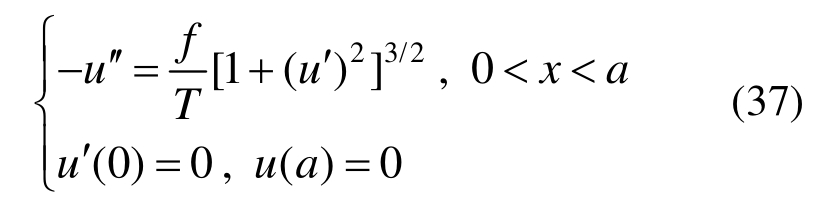
上述微分方程的精确解为：
本例取参数a=1，T=1，f=0.6进行计算。
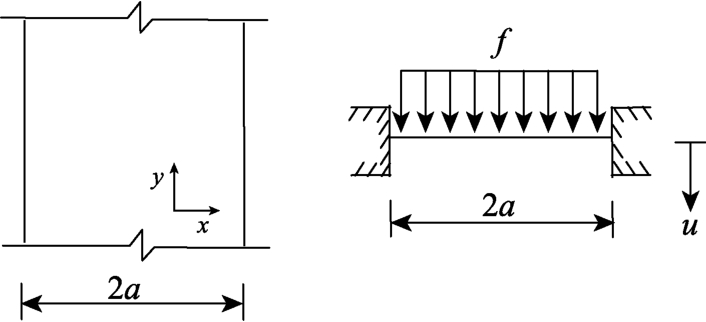
图2 例1中的物理模型
Fig.2 Model problem in Example 1
为考察本文方法的精度修复效果，将求解域均分为2个单元和不均匀分为3个单元(结点坐标依次为x=0 , 0.5 , 0.8 , 1.0)，采用线性元(m=1)进行有限元计算，采用二次元(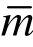
=2)进行超收敛修复，有限元解、超收敛解与精确解的对比如图3所示。易见，无论是均匀网格还是非均匀网格，本文方法的修复效果均非常显著。
为考察本文方法的收敛阶，采用三次元(m=3)进行有限元计算，依次采用四次元(
=4)、五次元(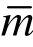=5)、六次元(
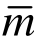=6)、七次元(
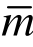=7)进行超收敛修复，计算结果如图4和表1所示。易见，相对于有限元解，超收敛解的精度和收敛阶有显著提升。本例中，当
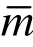=5时，位移达到最佳收敛阶(有限元求解一维C0问题时，若解答足够光滑，m次单元端结点解具有h2m的超收敛特性，该收敛阶一般被认为是最佳的[7-8]，不能再提高，故称“最佳”)；当
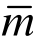=6时，位移的一阶导数也达到最佳收敛阶(2m)；而由六次元(
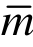=6)升到七次元(
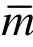=7)时，位移和位移的一阶导数的收敛阶不再提高。超收敛解呈现出如下的超收敛规律：超收敛计算次数
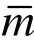每提高一次，位移和位移的一阶导数的收敛阶提高一阶，直到最佳收敛阶(2m)为止。
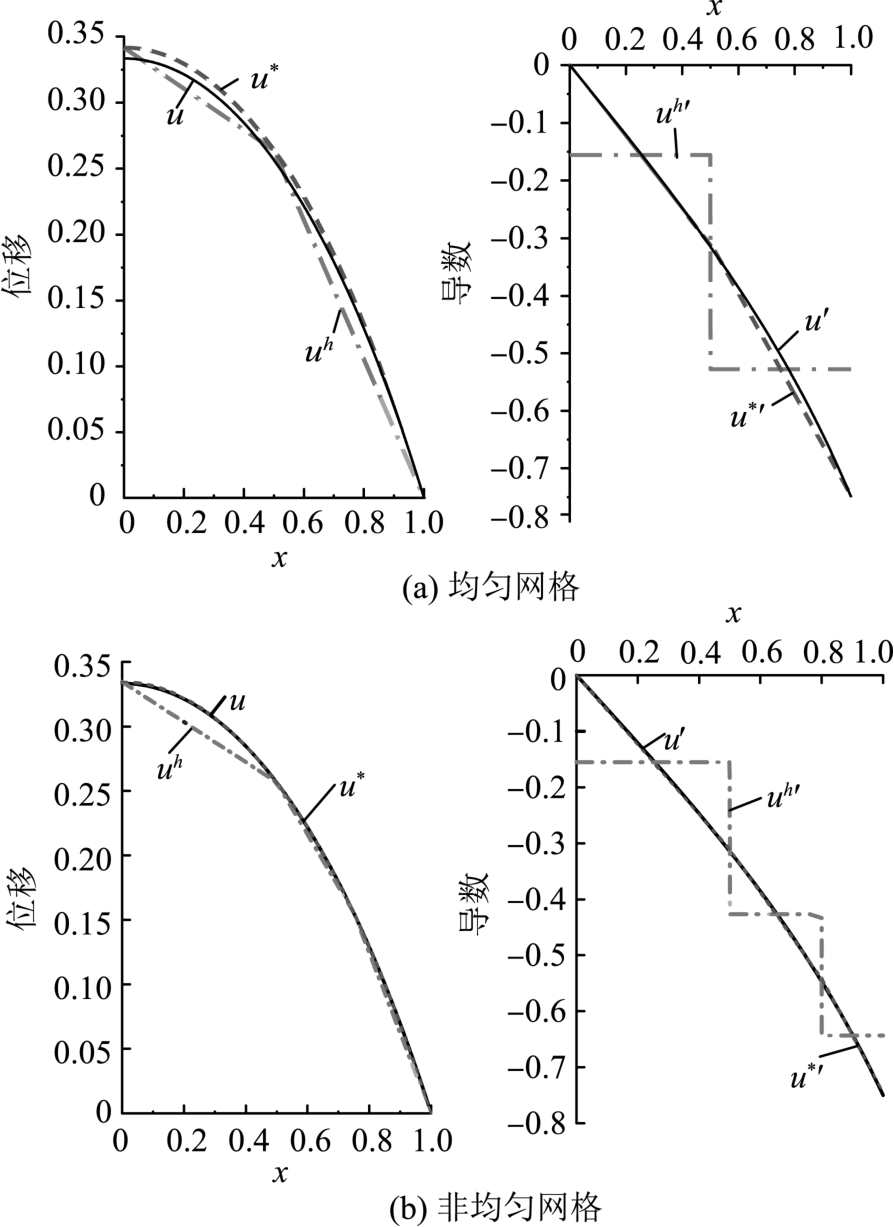
图3 例1有限元解与超收敛解的对比
Fig.3 The comparison of the FE solution with the recovered solution in Example 1
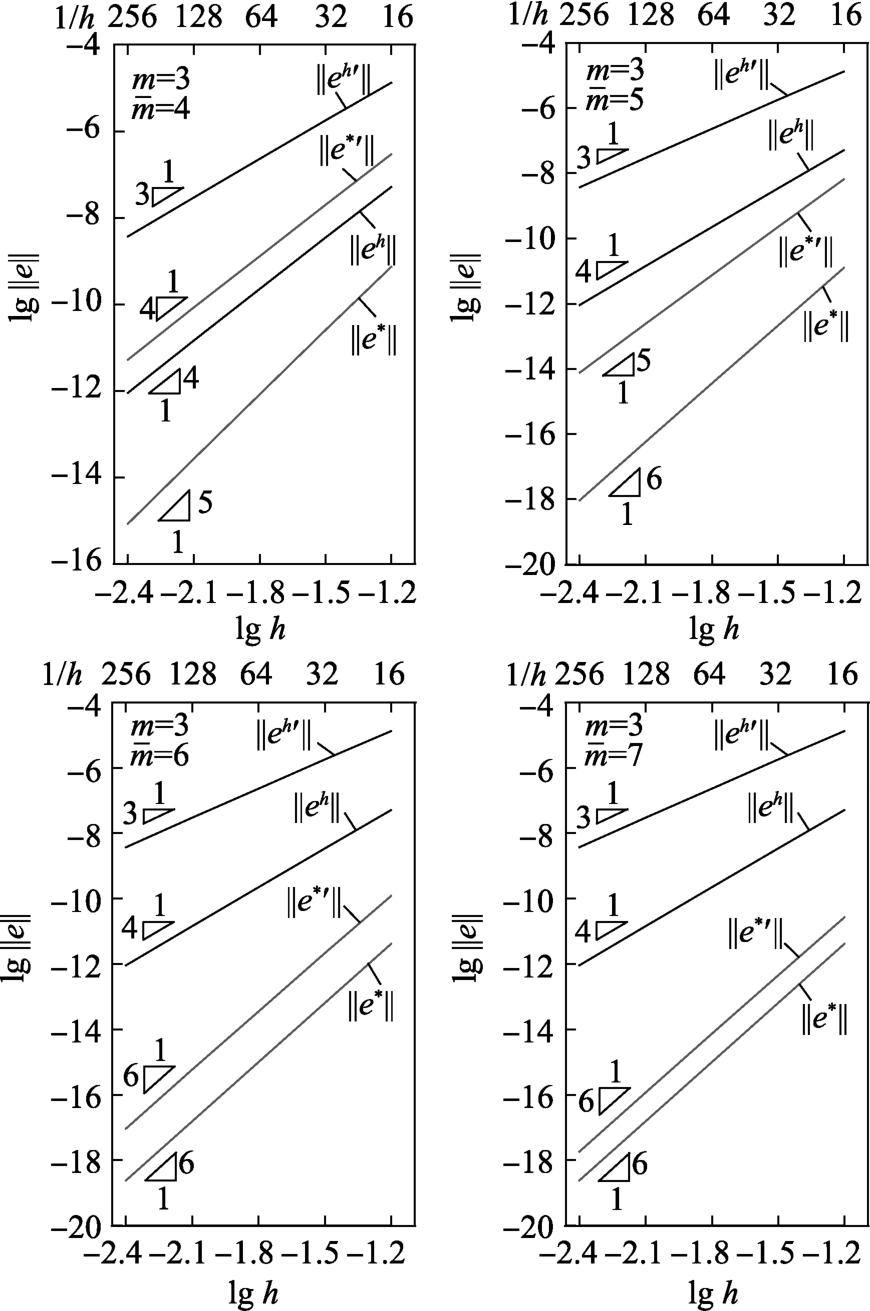
图4 例1有限元解和超收敛解的收敛阶
Fig.4 Rate of convergence of the FE solutions and recovered solutions in Example 1
表1 例1有限元解和超收敛解的误差与收敛阶
Table 1 Error and convergence rate of FE solutions and recovered solutions in Example 1
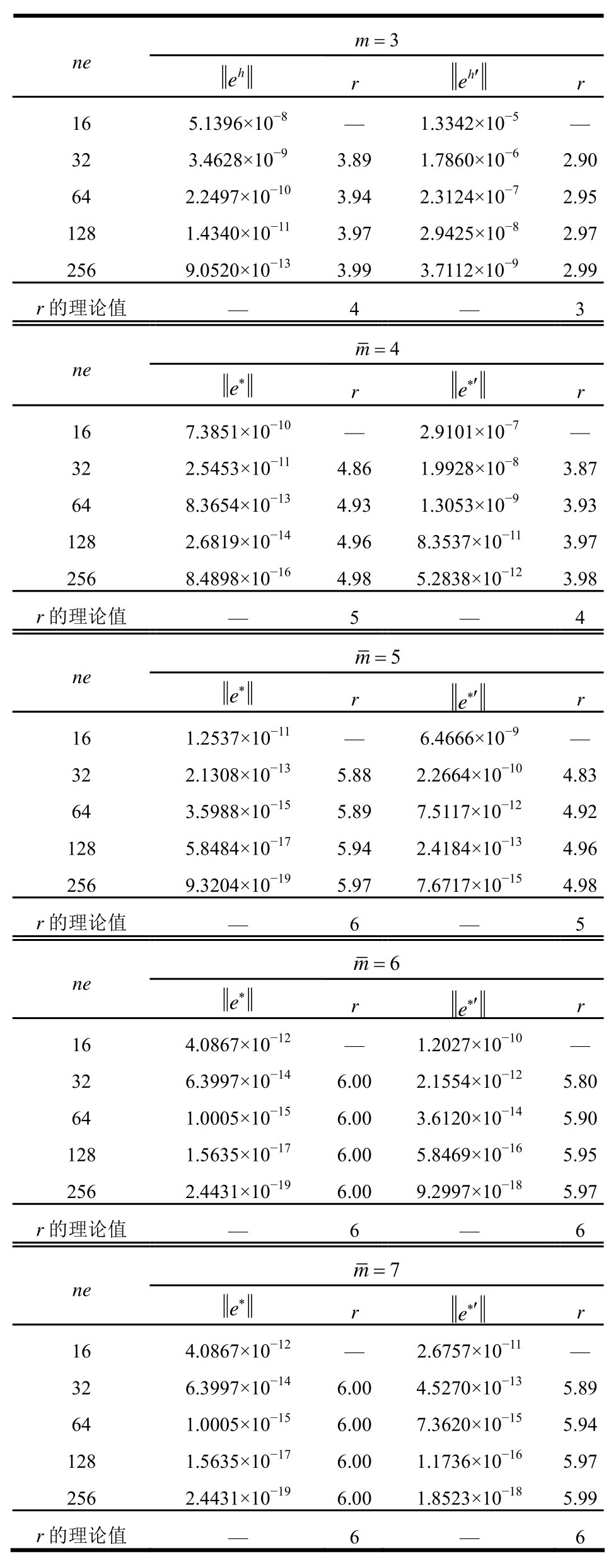
m=3 ne e r h e′ r h 16 5.1396×10-8 — 1.3342×10-5 —32 3.4628×10-9 3.89 1.7860×10-6 2.90 64 2.2497×10-10 3.94 2.3124×10-7 2.95 128 1.4340×10-11 3.97 2.9425×10-8 2.97 256 9.0520×10-13 3.99 3.7112×10-9 2.99 r的理论值 — 4 — 3 m=4 ne e* r e*′ r 16 7.3851×10-10 — 2.9101×10-7 —32 2.5453×10-11 4.86 1.9928×10-8 3.87 64 8.3654×10-13 4.93 1.3053×10-9 3.93 128 2.6819×10-14 4.96 8.3537×10-11 3.97 256 8.4898×10-16 4.98 5.2838×10-12 3.98 r的理论值 — 5 — 4 m=5 ne e* r e*′ r 16 1.2537×10-11 — 6.4666×10-9 —32 2.1308×10-13 5.88 2.2664×10-10 4.83 64 3.5988×10-15 5.89 7.5117×10-12 4.92 128 5.8484×10-17 5.94 2.4184×10-13 4.96 256 9.3204×10-19 5.97 7.6717×10-15 4.98 r的理论值 — 6 — 5 ne m=6 e* r e*′ r 16 4.0867×10-12 — 1.2027×10-10 —32 6.3997×10-14 6.00 2.1554×10-12 5.80 64 1.0005×10-15 6.00 3.6120×10-14 5.90 128 1.5635×10-17 6.00 5.8469×10-16 5.95 256 2.4431×10-19 6.00 9.2997×10-18 5.97 r的理论值 — 6 — 6 ne m=7 e* r e*′ r 16 4.0867×10-12 — 2.6757×10-11 —32 6.3997×10-14 6.00 4.5270×10-13 5.89 64 1.0005×10-15 6.00 7.3620×10-15 5.94 128 1.5635×10-17 6.00 1.1736×10-16 5.97 256 2.4431×10-19 6.00 1.8523×10-18 5.99 r的理论值 — 6 — 6
例2.化学反应问题
化学反应问题[26]是一类非线性微分方程边值问题，其控制微分方程为：
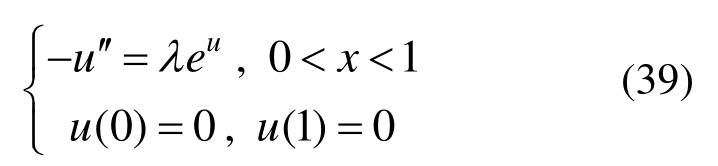
式中，λ＞0。该非线性微分方程具有如下形式的理论解：
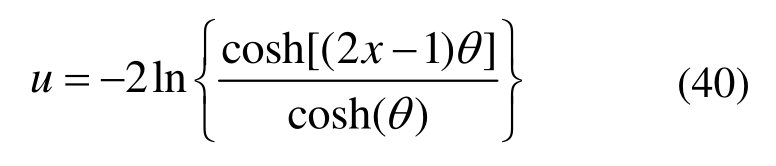
式中，θ由以下条件确定：
由该条件可知：存在一个大于0的临界值λ*，使得当0＜λ＜λ*时，控制微分方程有2个解；当λ=λ*时，控制微分方程有唯一解；当λ＞λ*时，控制微分方程无解。
解答关于x=1/2对称。利用对称性还可将问题简化到半域：
为验证本文算法在非线性问题存在多解时的修复效果，取λ=1进行计算，此时系数θ的2个解为：
对该非线性问题迭代求解时，若初始解取为u0=0，有限元解收敛到解1：
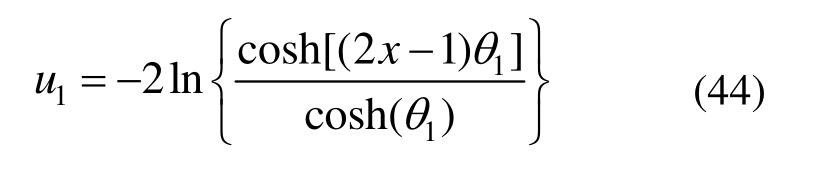
若初始解取为u0=4x，有限元解收敛到解2：
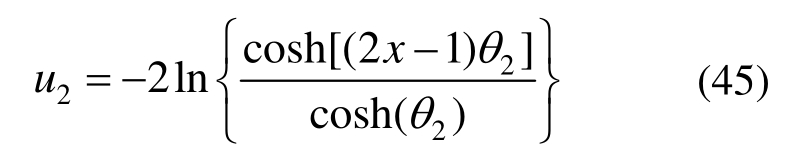
解1和解2在半域分布如图5所示。
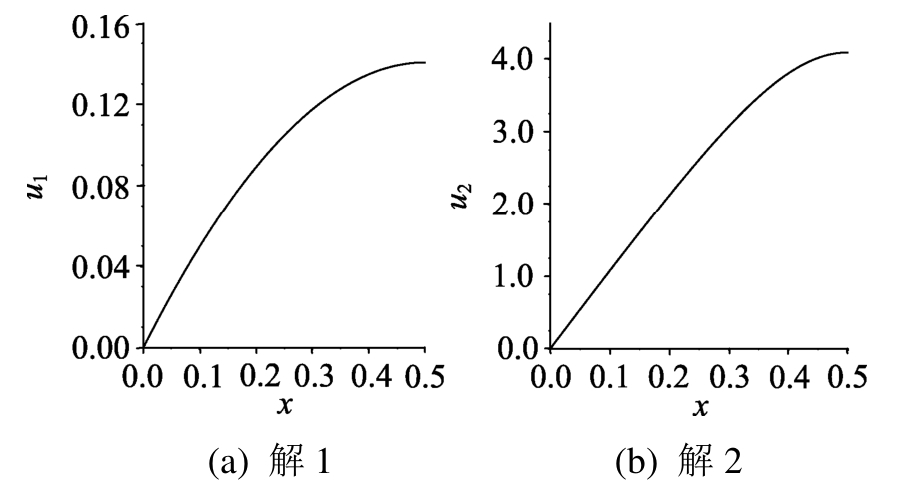
图5 例2的2个解
Fig.5 The two solutions in Example 2
对该问题采用二次元(m=2)进行有限元计算，取不同初始解使解答分别收敛到解1分支和解2分支后，取三次元(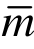
=3)、四次元(
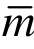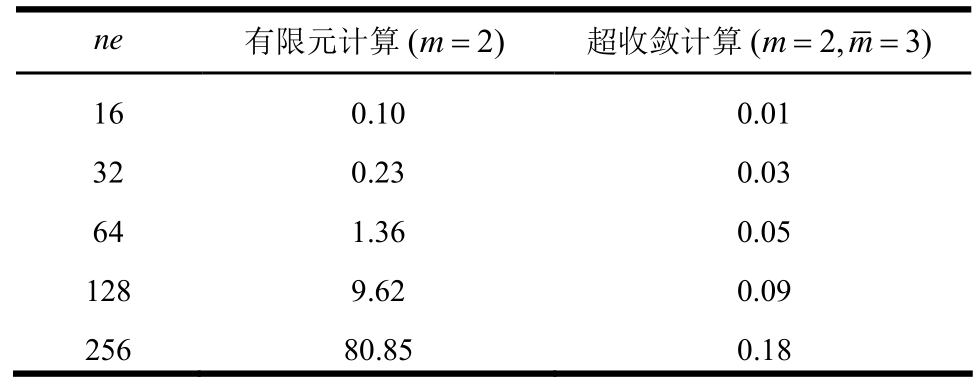
=4)进行超收敛计算，计算结果如图6、图7和表2、表3所示。易见，对于非线性问题多解的情形，不管对于哪个解答分支，本文方法均能进行有效修复。表4列出了解1分支用二次元(m=2)求解和三次元(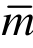
=3)作p型超收敛计算所用时间。易见，相对于有限元求解所用时间，p型超收敛计算所用时间非常微小，几可忽略。由表2可见，32个二次元网格经用三次元(
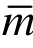=3)作p型超收敛计算后，导数精度已经超过256个二次元网格的导数精度，但总的计算时间只有后者的0.26/80.85≈1/311，可见本文p型超收敛计算对精度和计算效率的提升是非常显著的，是一高效算法。
以上算例充分表明本文方法稳定、高效，能够在有限元解的基础上，显著提高解答的精度、质量和收敛阶。数值算例表明，本文超收敛解答具有如表5所示的收敛规律。
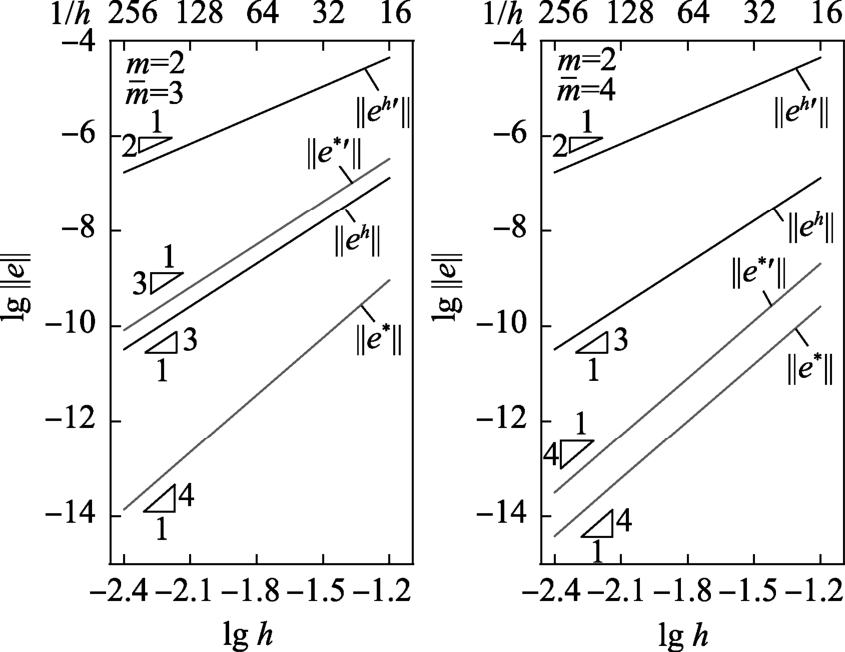
图6 例2解1有限元解和超收敛解的收敛阶
Fig.6 Rate of convergence of the FE solutions and recovered solutions on the first solution in Example 2
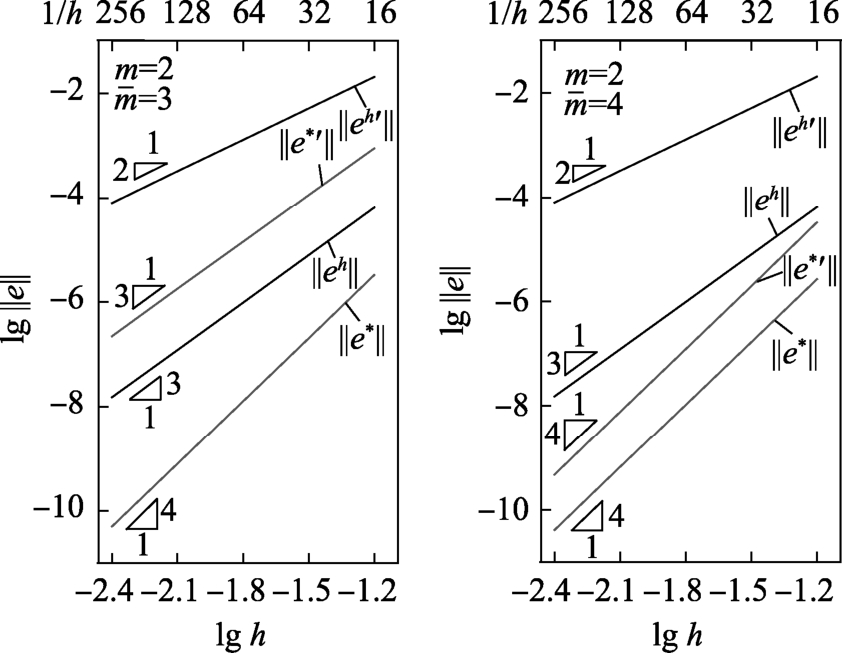
图7 例2解2有限元解和超收敛解的收敛阶
Fig.7 Rate of convergence of FE solutions and recovered solutions on the second solution in Example 2
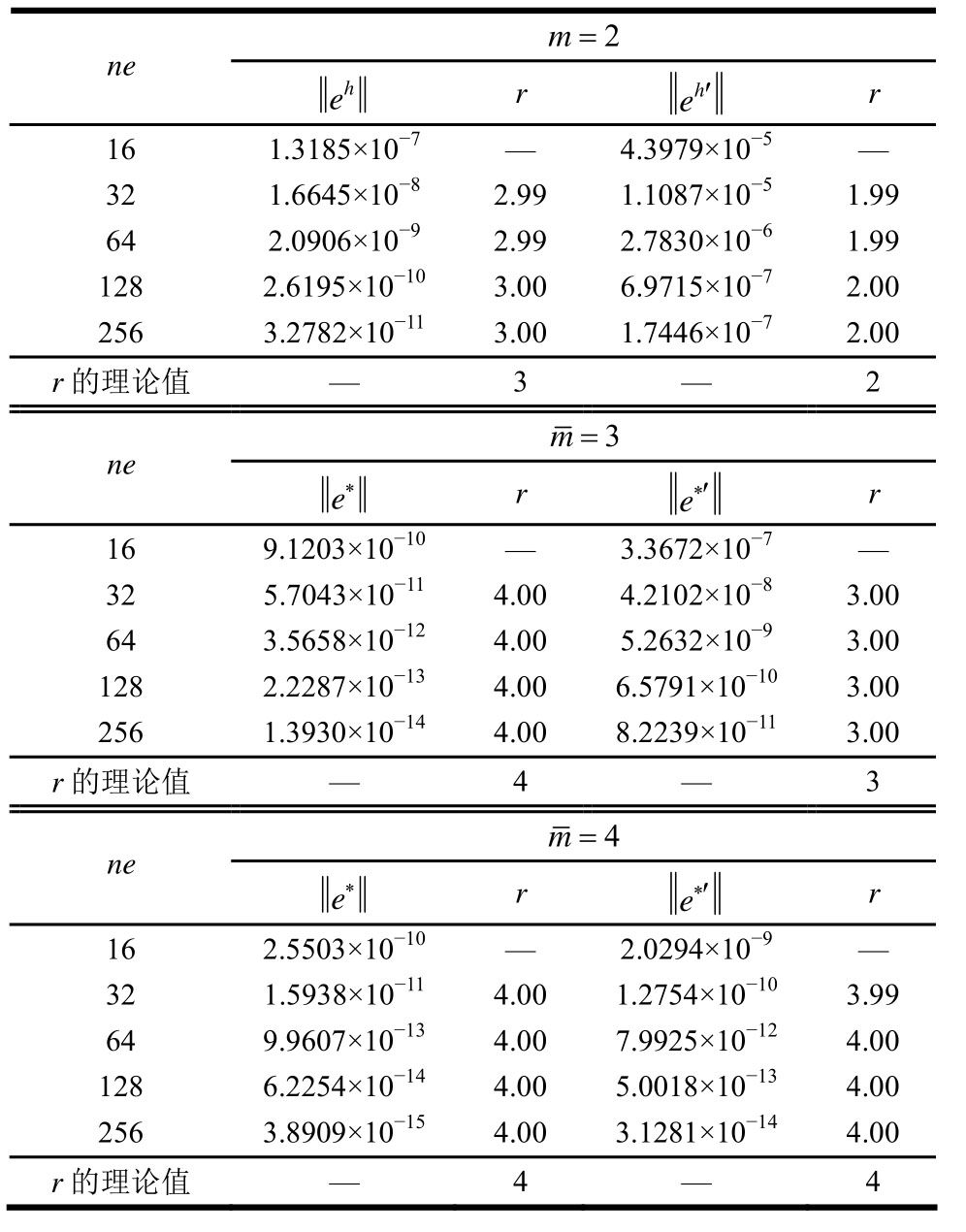
表2 例2解1有限元解和超收敛解的误差与收敛阶
Table 2 Error and convergence rate of FE solutions and recovered solutions on the first solution in Example 2
2 ne m=e r h e′ r h 16 1.3185×10-7 — 4.3979×10-5 —32 1.6645×10-8 2.99 1.1087×10-5 1.99 64 2.0906×10-9 2.99 2.7830×10-6 1.99 128 2.6195×10-10 3.00 6.9715×10-7 2.00 256 3.2782×10-11 3.00 1.7446×10-7 2.00 r的理论值 — 3 — 2 ne m=3 e* r e*′ r 16 9.1203×10-10 — 3.3672×10-7 —32 5.7043×10-11 4.00 4.2102×10-8 3.00 64 3.5658×10-12 4.00 5.2632×10-9 3.00 128 2.2287×10-13 4.00 6.5791×10-10 3.00 256 1.3930×10-14 4.00 8.2239×10-11 3.00 r的理论值 — 4 — 3 ne m=4 e* r e*′ r 16 2.5503×10-10 — 2.0294×10-9 —32 1.5938×10-11 4.00 1.2754×10-10 3.99 64 9.9607×10-13 4.00 7.9925×10-12 4.00 128 6.2254×10-14 4.00 5.0018×10-13 4.00 256 3.8909×10-15 4.00 3.1281×10-14 4.00 r的理论值 — 4 — 4
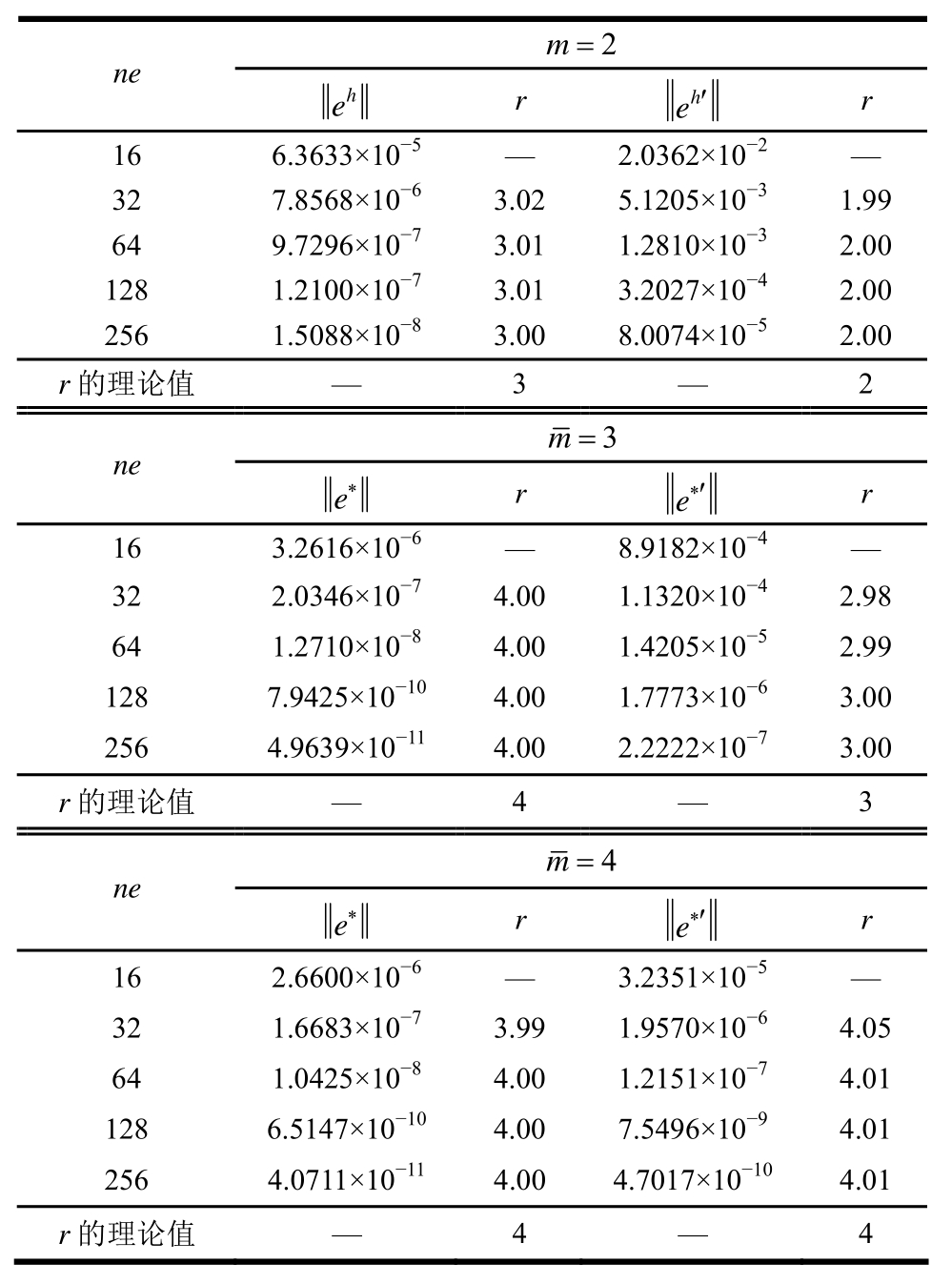
表3 例2解2有限元解和超收敛解的误差与收敛阶
Table 3 Error and convergence rate of FE solutions and recovered solutions on the second solution in Example 2
2 ne m=e r h e′ r h 16 6.3633×10-5 — 2.0362×10-2 —32 7.8568×10-6 3.02 5.1205×10-3 1.99 64 9.7296×10-7 3.01 1.2810×10-3 2.00 128 1.2100×10-7 3.01 3.2027×10-4 2.00 256 1.5088×10-8 3.00 8.0074×10-5 2.00 r的理论值 — 3 — 2 ne m=3 e* r e*′ r 16 3.2616×10-6 — 8.9182×10-4 —32 2.0346×10-7 4.00 1.1320×10-4 2.98 64 1.2710×10-8 4.00 1.4205×10-5 2.99 128 7.9425×10-10 4.00 1.7773×10-6 3.00 256 4.9639×10-11 4.00 2.2222×10-7 3.00 r的理论值 — 4 — 3 ne m=4 e* r e*′ r 16 2.6600×10-6 — 3.2351×10-5 —32 1.6683×10-7 3.99 1.9570×10-6 4.05 64 1.0425×10-8 4.00 1.2151×10-7 4.01 128 6.5147×10-10 4.00 7.5496×10-9 4.01 256 4.0711×10-11 4.00 4.7017×10-10 4.01 r的理论值 — 4 — 4
表4 例2解1计算时间 /s
Table 4 Computation time on the first solution in Example 2
ne 有限元计算(m=2) 超收敛计算(2,3)m=m=16 0.10 0.01 32 0.23 0.03 64 1.36 0.05 128 9.62 0.09 256 80.85 0.18
表5 超收敛解的收敛阶
Table 5 Convergence order of recovered solutions
u* u*′r min(1,2)m+mmin(m,2m)
5 结论
本文将p型超收敛算法成功拓展应用于非线性常微分方程边值问题的有限元超收敛计算。泰勒展开是本文的关键技术和核心创新，该技术将单元解近似满足的非线性常微分方程边值问题线性化为线性常微分方程边值问题，避免了超收敛计算中的迭代运算，有效提高了超收敛求解的效率。一方面由于本文算法是利用高次元的高收敛性进行精度修复，超收敛求解的单元次数须高于有限元求解的次数(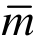
≥m+1)；另一方面，由于本文算法是基于结点解的超收敛性进行修复，内点解的收敛阶不可能超过结点解的收敛阶，因此超收敛求解的单元次数
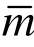不宜超过结点解的收敛阶，即
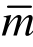≤2m。在此范围内(m+1≤
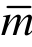≤2m )，超收敛求解的单元次数越高，超收敛修复得到的解答精度也越高。若采用更高次单元(
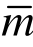＞2m)进行修复，所得解答与采用2 m次单元修复得到解答的精度相当，收敛阶相同，函数和导数均为最高阶(O(h2m))。数值算例表明，本文的超收敛算法高效、可靠、计算代价小、实施方便，是一个颇具潜力的方法，值得进一步推广应用。
[1]Zienkiewicz O C, Zhu J Z.The superconvergent patch recovery and a posteriori error estimates.Part 1: The recovery technique [J].International Journal for Numerical Methods in Engineering, 1992, 33(7):1331―1364.
[2]Zienkiewicz O C, Zhu J Z.The superconvergent patch recovery and a posteriori error estimate.Part 2: Error estimates and adaptivity [J].International Journal for Numerical Methods in Engineering, 1992, 33(7):1365―1382.
[3]Boroomand B, Zienkiewicz O C.Recovery by equilibrium in patches (REP) [J].International Journal for Numerical Methods in Engineering, 1997, 40(1):137―164.
[4]Stein E, Ohnimus S.Equilibrium method for postprocessing and error estimation in the finite element method [J].Computer Assisted Mechanics and Engineering Sciences, 1997, 4(3―4): 645―666.
[5]Ubertini F.Patch recovery based on complementary energy [J].International Journal for Numerical Methods in Engineering, 2004, 59(11): 1501―1538.
[6]Payen D J, Bathe K J.The use of nodal point forces to improve element stresses [J].Computers & Structures,2011, 89(5): 485―495.
[7]陈传淼.有限元超收敛构造理论[M].长沙: 湖南科学技术出版社, 2002: 29―37.Chen Chuanmiao.Structure theory of superconvergence of finite elements [M].Changsha: Hunan Science and Technology Press, 2002: 29―37.(in Chinese)
[8]袁驷, 王旭, 邢沁妍, 等.具有最佳超收敛阶的EEP法计算格式:Ⅰ算法公式[J].工程力学, 2007, 24(10): 1―5.Yuan Si, Wang Xu, Xing Qinyan, et al.A scheme with optimal order of super-convergence based on EEP method: I formulation [J].Engineering Mechanics, 2007,24(10): 1―5.(in Chinese)
[9]袁驷, 邢沁妍, 王旭, 等.具有最佳超收敛阶的EEP法计算格式:Ⅱ数值算例[J].工程力学, 2007, 24(11): 1―6.Yuan Si, Xing Qinyan, Wang Xu, et al.A scheme with optimal order of super-convergence based on EEP method: II Numerical results [J].Engineering Mechanics,2007, 24(11): 1―6.(in Chinese)
[10]袁驷, 赵庆华.具有最佳超收敛阶的EEP法计算格式:Ⅲ数学证明[J].工程力学, 2007, 24(12): 1―5, 13.Yuan Si, Zhao Qinghua.A scheme with optimal order of super-convergence based on EEP method: III Mathematical proof [J].Engineering Mechanics, 2007,24(12): 1―5, 13.(in Chinese)
[11]袁驷, 吴越, 徐俊杰, 等.基于EEP法的三维有限元超收敛计算初探[J].工程力学, 2016, 33(9): 15―20.Yuan Si, Wu Yue, Xu Junjie, et al.Exploration on super-convergent solutions of 3d FEM based on EEP method [J].Engineering Mechanics, 2016, 33(9): 15―20.(in Chinese)
[12]Douglas J, Dupont T.Galerkin approximations for the two point boundary problems using continuous piecewise polynomial spaces [J].Numerical Mathematics, 1974,22(2): 99―109.
[13]钟博, 叶康生, 袁驷.基于p型超收敛计算的一维有限元自适应分析[J].工程力学, 2016, 33(增刊1): 23―28.Zhong Bo, Ye Kangsheng, Yuan Si.One dimensional finite element adaptive analysis based on a p-type superconvergent recovery scheme [J].Engineering Mechanics, 2016, 33(Suppl 1): 23―28.(in Chinese)
[14]叶康生, 曾强.结构自由振动问题有限元新型超收敛算法研究[J].工程力学, 2017, 34(1): 45―50, 68.Ye Kangsheng, Zeng Qiang.A new superconvergent recovery method for FE analysis on structural free vibration problems [J].Engineering Mechanics, 2017,34(1): 45―50, 68.(in Chinese)
[15]叶康生, 姚葛亮.平面曲梁有限元静力分析的p型超收敛算法[J].工程力学, 2017, 34(11): 26―33, 58.Ye Kangsheng, Yao Geliang.A p-type superconvergent recovery method for FE static analysis of planar curved beams [J].Engineering Mechanics, 2017, 34(11):26―33, 58.(in Chinese)
[16]刘胜来.旋转壳和薄壁曲梁静力问题的有限元新型超收敛算法研究[D].北京: 清华大学, 2017.Liu Shenglai.A study on new superconvergence recovery method for static problems of axisymmetric shells and thin planary curved beams [D].Beijing: Tsinghua University, 2017.(in Chinese)
[17]叶康生, 殷振炜.平面曲梁内自由振动有限元分析的p型超收敛算法[J].工程力学, 2019, 36(5): 28―36, 52.Ye Kangsheng, Yin Zhenwei.A p-type superconvergent recovery method for FE analysis of in-plane free vibration of planar curved beams [J].Engineering Mechanics, 2019, 36(5): 28―36, 52.(in Chinese)
[18]叶康生, 殷振炜.Euler梁弹性稳定分析的有限元p型超收敛算法[J].力学与实践, 2018, 40(6): 647―652.Ye Kangsheng, Yin Zhenwei.A p-type superconvergent recovery method for FE elastic stability analysis of Euler beams [J].Mechanics in Engineering, 2018, 40(6):647―652.(in Chinese)
[19]Chen C M.Superconvergence of finite element approximations to nonlinear elliptic problems [C]//Proceedings of the China-France Symposium on Finite Element Methods, Beijing, 1982: 622―640.
[20]熊之光, 杨喜陶.非线性椭圆问题矩形有限元的超收敛性[J].桂林工学院学报, 2004, 24(1): 97―99.Xiong Zhiguang, Yang Xitao.Superconvergence of rectangular finite element method for nonlinear elliptic problem [J].Journal of Guilin Institute of Technology,2004, 24(1): 97―99.(in Chinese)
[21]Chow S S, Carey G F.Superconvergence phenomena in nonlinear two-point boundary-value problems [J].Numerical Methods for Partial Differential Equations,1993, 9(5): 561―577.
[22]Verfürth R.A posteriori error estimates for nonlinear problems.Finite element discretization of elliptic equations [J].Mathematics of Computation, 1994,62(206): 445―475.
[23]Yuan S, Du Y, Xing Q, et al.Self-adaptive one-dimensional nonlinear finite element method based on element energy projection method [J].Applied Mathematics and Mechanics, 2014, 35(10): 1223―1232.
[24]Strang G, Fix G J.An analysis of the finite element method [M].Englewood Cliffs, NJ: Prentice-Hall, 1973:216―240.
[25]Yuan S.The finite element methods of lines: Theory and applications [M].Beijing: Science Press, 1993: 387―388.
[26]Kubíček M, laváček V.Numerical solution of nonlinear boundary value problems with applications[M].Englewood Cliffs, NJ: Prentice-Hall, 1983.