钢筋混凝土(RC)柱的剪切破坏属于脆性破坏，具有耗能能力差、位移延性低和承载能力退化迅速等缺点[1]，对工程结构的安全性造成严重威胁，甚至会引起工程结构发生坍塌。因此，准确分析RC柱的抗剪承载力，对于工程结构的抗震设计和安全性评估具有重要意义。
RC柱抗剪承载力的影响因素众多，包括混凝土抗压强度和钢筋屈服强度等材料参数，截面尺寸、剪跨比、钢筋直径和混凝土保护层厚度等几何参数，以及配箍率和轴压比等其他因素[2―3]。由于混凝土材料的非均质特性以及施工偏差等因素的影响，上述影响因素具有显著的客观不确定性[2, 4―10]。同时，由于RC柱的抗剪机理复杂，不同的RC柱抗剪承载力分析模型引入了不同的模型假定，比较经典的包括桁架模型[11]、修正压力场模型[12―14]、强度退化理论模型[15]和桁架-拱模型[16]等。由于不同模型所考虑的影响因素、引入的模型假定和选用的试验数据等方面有所差异，不同的RC柱抗剪承载力分析模型受主观不确定性的影响[2, 4-10]。然而，目前国内外规范中传统的RC柱抗剪承载力模型[13, 17-21]均属于确定性模型，不仅无法合理考虑RC柱的材料参数和几何参数等存在的客观不确定性，而且无法考虑模型建立过程中由于考虑因素不全面或引入模型假定等因素引起的主观不确定性。对此，文献[22]在确定性抗剪承载力模型的基础上利用基本设计参数构造经验性的误差修正项来考虑不确定性的影响，建立了RC柱的概率抗剪承载力模型，但是所引入的误差修正项缺乏明确的力学机制，不仅涉及模型比选问题，而且计算较为繁琐。
鉴于此，本文基于桁架-拱模型，结合贝叶斯理论和马尔科夫链蒙特卡洛(MCMC)法，研究建立了一种能够综合考虑力学机制和不确定性影响的RC柱概率抗剪承载力模型，并利用试验数据验证了该概率模型的有效性。
1 基于力学机制的概率抗剪承载力模型表达式
根据桁架-拱模型[16]，RC柱的抗剪承载力Vn由混凝土、箍筋和拱作用的抗剪承载力贡献组成：
式中：Vc和Vs分别为桁架模型中混凝土压杆和横向钢筋(箍筋)的抗剪承载力贡献；Va为拱模型的抗剪承载力贡献。其中，混凝土压杆的抗剪承载力贡献Vc为[16]：
式中：b和h0分别为柱截面的宽度和有效高度；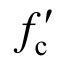
为混凝土抗压强度；α为混凝土的抗剪承载力贡献系数，其计算表达式为[13, 23]：
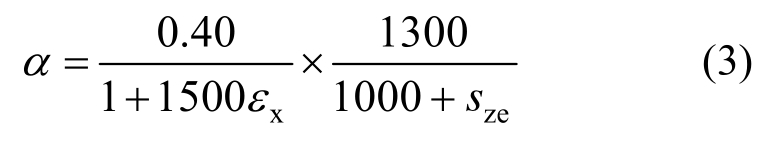
式中：sze为尺寸效应因子，定义为RC构件的有效裂缝间距，文献[13]建议取sze=300mm ；εx为应变效应因子，定义为RC柱截面中点处的纵向应变，计算公式为[13]：
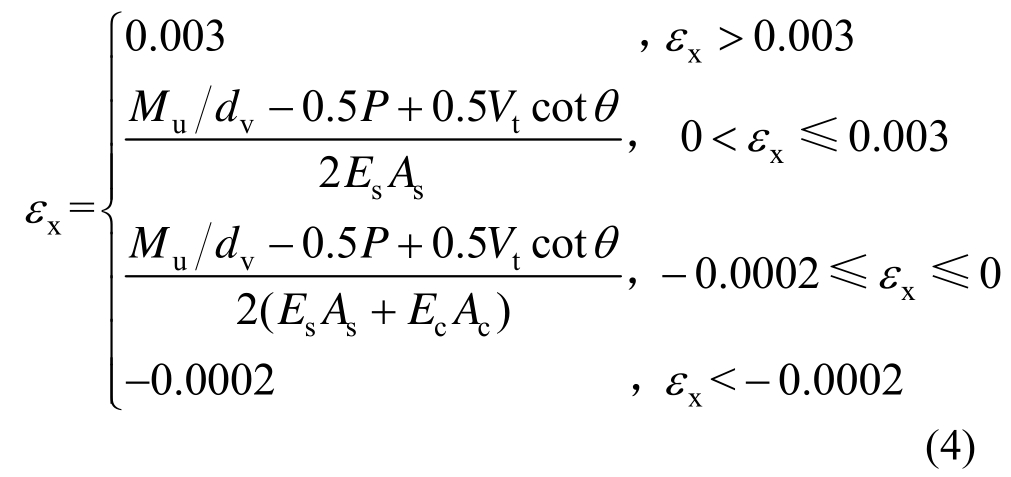
式中：Mu=VtL/ζ1；Vt=Vc+Vs 为桁架模型的抗剪承载力贡献；L为柱高；ζ1为约束条件系数，一端固定一端铰接时取ζ1=1，两端固定时取ζ1=2；dv为在柱截面受剪方向两侧纵筋截面形心之间的距离；P为轴压力；Es和Ec分别为纵筋和混凝土的弹性模量；As和Ac分别为纵筋面积和柱截面的混凝土面积；θ为临界斜裂缝倾角，计算公式为[24]：
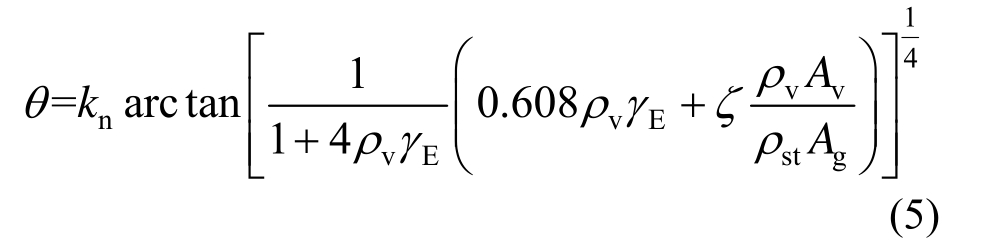
式中：ρv为配箍率；ρst为配筋率；Ag=bh为柱的截面积，其中h为RC柱截面高度；Av=bh0为柱的有效抗剪截面积；kn=1.80n2-2.25n+1.54为轴压比修正系数[24]；γE为钢筋和混凝土的弹性模量比；ζ为RC柱的边界条件系数，两端固定时取ζ=0.57，一端固定一端铰接时取ζ=1.57。
在式(1)中，桁架模型中箍筋的抗剪承载力贡献Vs为[16]：
式中：Asv和fyv分别为箍筋的截面积和屈服强度；s为箍筋的间距。
在式(1)中，拱模型的抗剪承载力贡献Va为[16]：
式中，η为拱模型的抗剪承载力贡献系数，计算公式为：
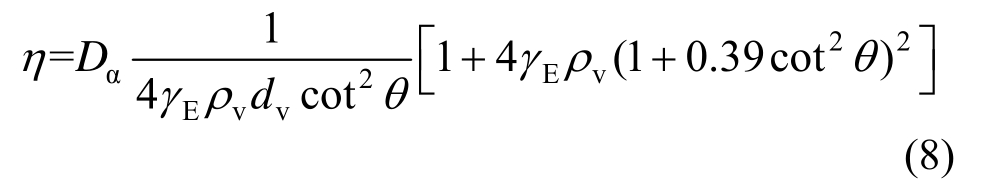
式中：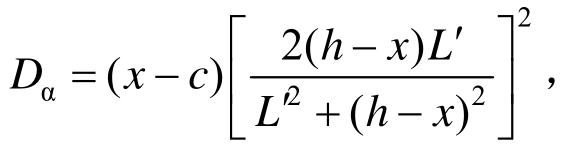
其中x为RC柱截面的中性轴高度，c为混凝土保护层厚度，L′为柱的有效计算长度。
结合式(2)、式(6)和式(7)可知，RC柱的抗剪承载力模型可以描述为：
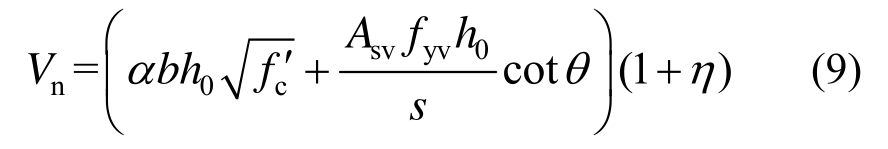
由式(3)和式(4)可知，α的取值需要根据εx的大小进行计算，而当-0.0002≤εx ≤0.003时，α需要利用式(2)～式(6)对εx进行迭代分析才可以确定，计算过程较为繁琐。同时，由式(6)和式(8)可知，临界斜裂缝倾角θ和拱模型的抗剪承载力贡献系数η的计算公式也较为复杂。因此，式(9)所描述的RC柱抗剪承载力模型的计算公式过于复杂，不便于工程应用。为了克服上述缺陷，本文从文献[16, 25―37]中收集了58组剪切破坏型RC柱的试验数据，见表1。表中，Vtest为RC柱抗剪承载力的实测值，μ为位移延性系数；fyt纵筋屈服强度，FF表示两端约束，FP表示一端约束一端简支，“—”表示无临界斜裂缝倾角实测值。由于表1中的前38组试验数据给出了临界斜裂缝倾角θ的测试值，所以可以基于这38组试验数据对α、cotθ和η的取值进行统计分析，如图1所示。由图1可知，α、η和cotθ的取值均具有一定的随机性，其变异系数分别为0.250、0.323和0.667。因此，传统的确定性抗剪承载力模型将上述三个参数选取为确定性参数不合理。
鉴于此，本文将α、cotθ和η分别描述为概率模型参数β1、β2和β3，同时考虑模型误差的影响，从而建立了综合考虑力学机制和不确定性影响的RC柱概率抗剪承载力模型的表达式：
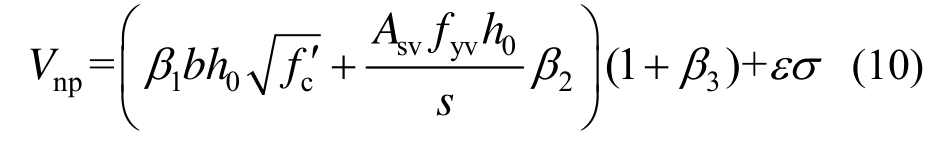
式中：Vnp为RC柱抗剪承载力的概率预测值；β=[β1,β2,β3]T为概率模型参数向量；εσ为概率模型的模型误差[38]，且εσ～N(0,σ2)，其中ε为标准正态随机变量，σ为模型误差的标准差。
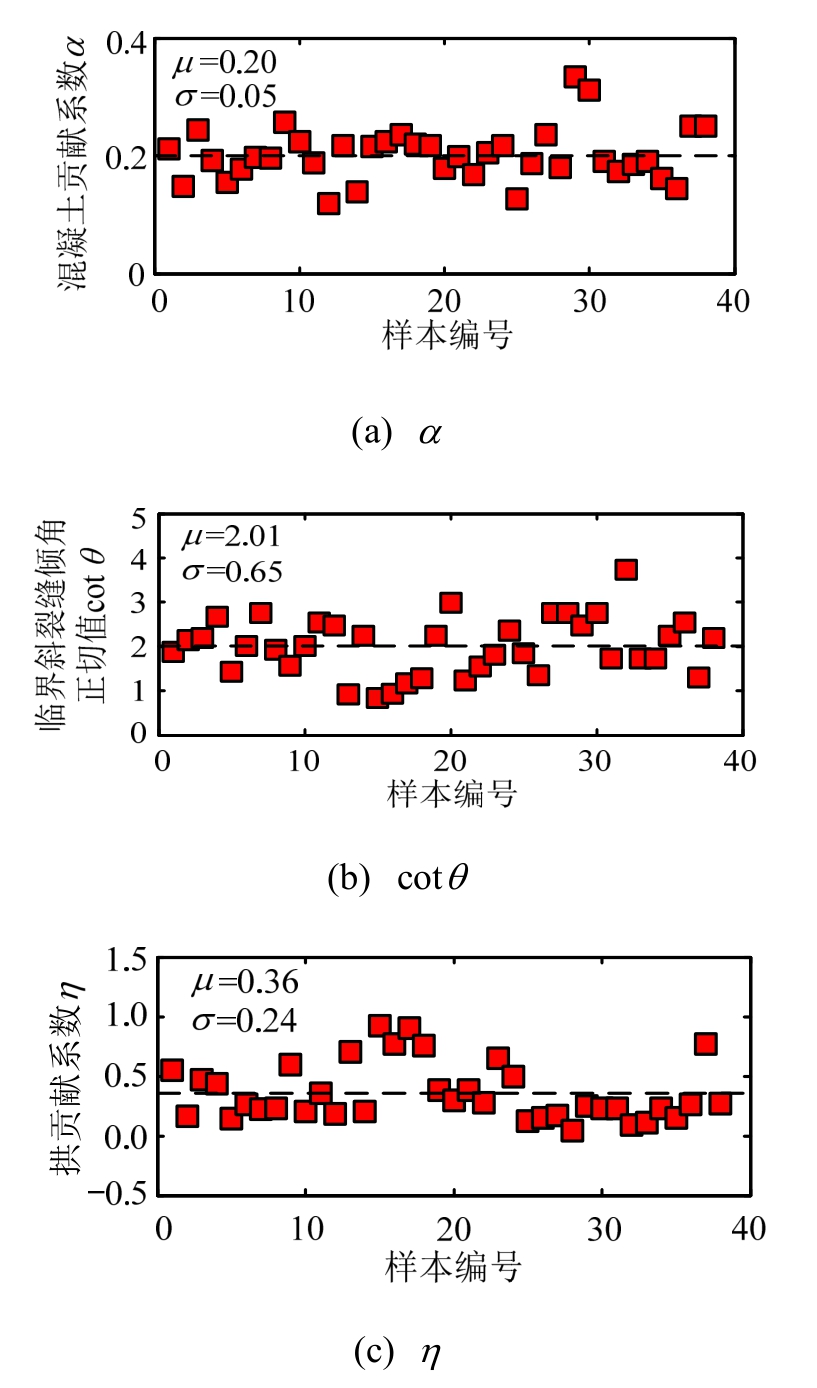
图1 α、cotθ和η的概率信息
Fig.1 Probabilistic information of α, cotθ and η
表1 RC柱的基本参数和抗剪承载力试验数据
Table 1 Basic parameters and experimental data for shear strength of RC columns
images/BZ_198_233_418_361_510.pngimages/BZ_198_358_418_486_510.png images/BZ_198_483_418_611_510.png images/BZ_198_608_418_736_510.png images/BZ_198_733_418_860_510.png images/BZ_198_857_418_984_510.png images/BZ_198_981_418_1090_510.pngimages/BZ_198_1087_418_1234_510.pngimages/BZ_198_1231_418_1358_510.png images/BZ_198_1355_418_1461_510.pngimages/BZ_198_1458_418_1612_510.png images/BZ_198_1609_418_1737_510.pngimages/BZ_198_1737_418_1833_464.pngimages/BZ_198_1737_464_1833_510.pngimages/BZ_198_1830_418_1965_510.pngimages/BZ_198_1962_418_2120_510.png images/BZ_198_2117_418_2245_510.pngimages/BZ_198_233_513_361_558.pngimages/BZ_198_358_513_486_558.pngimages/BZ_198_483_513_611_558.pngimages/BZ_198_608_513_736_558.pngimages/BZ_198_733_513_860_558.pngimages/BZ_198_857_513_984_558.pngimages/BZ_198_981_513_1090_558.pngimages/BZ_198_1087_513_1234_558.pngimages/BZ_198_1231_513_1358_558.pngimages/BZ_198_1355_513_1461_558.pngimages/BZ_198_1458_513_1612_558.pngimages/BZ_198_1609_513_1737_558.pngimages/BZ_198_1734_513_1833_558.png images/BZ_198_1830_513_1965_558.pngimages/BZ_198_1962_513_2120_558.pngimages/BZ_198_2117_513_2245_558.pngimages/BZ_198_233_559_361_604.pngimages/BZ_198_358_559_486_604.pngimages/BZ_198_483_559_611_604.pngimages/BZ_198_608_559_736_604.pngimages/BZ_198_733_559_860_604.pngimages/BZ_198_857_559_984_604.pngimages/BZ_198_981_559_1090_604.pngimages/BZ_198_1087_559_1234_604.pngimages/BZ_198_1231_559_1358_604.pngimages/BZ_198_1355_559_1461_604.pngimages/BZ_198_1458_559_1612_604.pngimages/BZ_198_1609_559_1737_604.pngimages/BZ_198_1734_559_1833_604.png images/BZ_198_1830_559_1965_604.pngimages/BZ_198_1962_559_2120_604.pngimages/BZ_198_2117_559_2245_604.pngimages/BZ_198_233_604_361_650.pngimages/BZ_198_358_604_486_650.pngimages/BZ_198_483_604_611_650.pngimages/BZ_198_608_604_736_650.pngimages/BZ_198_733_604_860_650.pngimages/BZ_198_857_604_984_650.pngimages/BZ_198_981_604_1090_650.pngimages/BZ_198_1087_604_1234_650.pngimages/BZ_198_1231_604_1358_650.pngimages/BZ_198_1355_604_1461_650.pngimages/BZ_198_1458_604_1612_650.pngimages/BZ_198_1609_604_1737_650.pngimages/BZ_198_1734_604_1833_650.png images/BZ_198_1830_604_1965_650.pngimages/BZ_198_1962_604_2120_650.pngimages/BZ_198_2117_604_2245_650.pngimages/BZ_198_233_650_361_696.pngimages/BZ_198_358_650_486_696.pngimages/BZ_198_483_650_611_696.pngimages/BZ_198_608_650_736_696.pngimages/BZ_198_733_650_860_696.pngimages/BZ_198_857_650_984_696.pngimages/BZ_198_981_650_1090_696.pngimages/BZ_198_1087_650_1234_696.pngimages/BZ_198_1231_650_1358_696.pngimages/BZ_198_1355_650_1461_696.pngimages/BZ_198_1458_650_1612_696.pngimages/BZ_198_1609_650_1737_696.pngimages/BZ_198_1734_650_1833_696.png images/BZ_198_1830_650_1965_696.pngimages/BZ_198_1962_650_2120_696.pngimages/BZ_198_2117_650_2245_696.pngimages/BZ_198_233_696_361_742.pngimages/BZ_198_358_696_486_742.pngimages/BZ_198_483_696_611_742.pngimages/BZ_198_608_696_736_742.pngimages/BZ_198_733_696_860_742.pngimages/BZ_198_857_696_984_742.pngimages/BZ_198_981_696_1090_742.pngimages/BZ_198_1087_696_1234_742.pngimages/BZ_198_1231_696_1358_742.pngimages/BZ_198_1355_696_1461_742.pngimages/BZ_198_1458_696_1612_742.pngimages/BZ_198_1609_696_1737_742.pngimages/BZ_198_1734_696_1833_742.png images/BZ_198_1830_696_1965_742.pngimages/BZ_198_1962_696_2120_742.pngimages/BZ_198_2117_696_2245_742.pngimages/BZ_198_233_742_361_788.pngimages/BZ_198_358_742_486_788.pngimages/BZ_198_483_742_611_788.pngimages/BZ_198_608_742_736_788.pngimages/BZ_198_733_742_860_788.pngimages/BZ_198_857_742_984_788.pngimages/BZ_198_981_742_1090_788.pngimages/BZ_198_1087_742_1234_788.pngimages/BZ_198_1231_742_1358_788.pngimages/BZ_198_1355_742_1461_788.pngimages/BZ_198_1458_742_1612_788.pngimages/BZ_198_1609_742_1737_788.pngimages/BZ_198_1734_742_1833_788.png images/BZ_198_1830_742_1965_788.pngimages/BZ_198_1962_742_2120_788.pngimages/BZ_198_2117_742_2245_788.pngimages/BZ_198_233_788_361_833.pngimages/BZ_198_358_788_486_833.pngimages/BZ_198_483_788_611_833.pngimages/BZ_198_608_788_736_833.pngimages/BZ_198_733_788_860_833.pngimages/BZ_198_857_788_984_833.pngimages/BZ_198_981_788_1090_833.pngimages/BZ_198_1087_788_1234_833.pngimages/BZ_198_1231_788_1358_833.pngimages/BZ_198_1355_788_1461_833.pngimages/BZ_198_1458_788_1612_833.pngimages/BZ_198_1609_788_1737_833.pngimages/BZ_198_1734_788_1833_833.png images/BZ_198_1830_788_1965_833.pngimages/BZ_198_1962_788_2120_833.pngimages/BZ_198_2117_788_2245_833.pngimages/BZ_198_233_834_361_879.pngimages/BZ_198_358_834_486_879.pngimages/BZ_198_483_834_611_879.pngimages/BZ_198_608_834_736_879.pngimages/BZ_198_733_834_860_879.pngimages/BZ_198_857_834_984_879.pngimages/BZ_198_981_834_1090_879.pngimages/BZ_198_1087_834_1234_879.pngimages/BZ_198_1231_834_1358_879.pngimages/BZ_198_1355_834_1461_879.pngimages/BZ_198_1458_834_1612_879.pngimages/BZ_198_1609_834_1737_879.pngimages/BZ_198_1734_834_1833_879.png images/BZ_198_1830_834_1965_879.pngimages/BZ_198_1962_834_2120_879.pngimages/BZ_198_2117_834_2245_879.pngimages/BZ_198_233_879_361_925.pngimages/BZ_198_358_879_486_925.pngimages/BZ_198_483_879_611_925.pngimages/BZ_198_608_879_736_925.pngimages/BZ_198_733_879_860_925.pngimages/BZ_198_857_879_984_925.pngimages/BZ_198_981_879_1090_925.pngimages/BZ_198_1087_879_1234_925.pngimages/BZ_198_1231_879_1358_925.pngimages/BZ_198_1355_879_1461_925.pngimages/BZ_198_1458_879_1612_925.pngimages/BZ_198_1609_879_1737_925.pngimages/BZ_198_1734_879_1833_925.png images/BZ_198_1830_879_1965_925.pngimages/BZ_198_1962_879_2120_925.pngimages/BZ_198_2117_879_2245_925.pngimages/BZ_198_233_925_361_971.pngimages/BZ_198_358_925_486_971.pngimages/BZ_198_483_925_611_971.pngimages/BZ_198_608_925_736_971.pngimages/BZ_198_733_925_860_971.pngimages/BZ_198_857_925_984_971.pngimages/BZ_198_981_925_1090_971.pngimages/BZ_198_1087_925_1234_971.pngimages/BZ_198_1231_925_1358_971.pngimages/BZ_198_1355_925_1461_971.pngimages/BZ_198_1458_925_1612_971.pngimages/BZ_198_1609_925_1737_971.pngimages/BZ_198_1734_925_1833_971.png images/BZ_198_1830_925_1965_971.pngimages/BZ_198_1962_925_2120_971.pngimages/BZ_198_2117_925_2245_971.pngimages/BZ_198_233_971_361_1017.pngimages/BZ_198_358_971_486_1017.pngimages/BZ_198_483_971_611_1017.pngimages/BZ_198_608_971_736_1017.pngimages/BZ_198_733_971_860_1017.pngimages/BZ_198_857_971_984_1017.pngimages/BZ_198_981_971_1090_1017.pngimages/BZ_198_1087_971_1234_1017.pngimages/BZ_198_1231_971_1358_1017.pngimages/BZ_198_1355_971_1461_1017.pngimages/BZ_198_1458_971_1612_1017.pngimages/BZ_198_1609_971_1737_1017.pngimages/BZ_198_1734_971_1833_1017.png images/BZ_198_1830_971_1965_1017.pngimages/BZ_198_1962_971_2120_1017.pngimages/BZ_198_2117_971_2245_1017.pngimages/BZ_198_233_1017_361_1063.pngimages/BZ_198_358_1017_486_1063.pngimages/BZ_198_483_1017_611_1063.pngimages/BZ_198_608_1017_736_1063.pngimages/BZ_198_733_1017_860_1063.pngimages/BZ_198_857_1017_984_1063.pngimages/BZ_198_981_1017_1090_1063.pngimages/BZ_198_1087_1017_1234_1063.pngimages/BZ_198_1231_1017_1358_1063.pngimages/BZ_198_1355_1017_1461_1063.pngimages/BZ_198_1458_1017_1612_1063.pngimages/BZ_198_1609_1017_1737_1063.pngimages/BZ_198_1734_1017_1833_1063.png images/BZ_198_1830_1017_1965_1063.pngimages/BZ_198_1962_1017_2120_1063.pngimages/BZ_198_2117_1017_2245_1063.pngimages/BZ_198_233_1063_361_1108.pngimages/BZ_198_358_1063_486_1108.pngimages/BZ_198_483_1063_611_1108.pngimages/BZ_198_608_1063_736_1108.pngimages/BZ_198_733_1063_860_1108.pngimages/BZ_198_857_1063_984_1108.pngimages/BZ_198_981_1063_1090_1108.pngimages/BZ_198_1087_1063_1234_1108.pngimages/BZ_198_1231_1063_1358_1108.pngimages/BZ_198_1355_1063_1461_1108.pngimages/BZ_198_1458_1063_1612_1108.pngimages/BZ_198_1609_1063_1737_1108.pngimages/BZ_198_1734_1063_1833_1108.png images/BZ_198_1830_1063_1965_1108.pngimages/BZ_198_1962_1063_2120_1108.pngimages/BZ_198_2117_1063_2245_1108.pngimages/BZ_198_233_1109_361_1154.pngimages/BZ_198_358_1109_486_1154.pngimages/BZ_198_483_1109_611_1154.pngimages/BZ_198_608_1109_736_1154.pngimages/BZ_198_733_1109_860_1154.pngimages/BZ_198_857_1109_984_1154.pngimages/BZ_198_981_1109_1090_1154.pngimages/BZ_198_1087_1109_1234_1154.pngimages/BZ_198_1231_1109_1358_1154.pngimages/BZ_198_1355_1109_1461_1154.pngimages/BZ_198_1458_1109_1612_1154.pngimages/BZ_198_1609_1109_1737_1154.pngimages/BZ_198_1734_1109_1833_1154.png images/BZ_198_1830_1109_1965_1154.pngimages/BZ_198_1962_1109_2120_1154.pngimages/BZ_198_2117_1109_2245_1154.pngimages/BZ_198_233_1154_361_1200.pngimages/BZ_198_358_1154_486_1200.pngimages/BZ_198_483_1154_611_1200.pngimages/BZ_198_608_1154_736_1200.pngimages/BZ_198_733_1154_860_1200.pngimages/BZ_198_857_1154_984_1200.pngimages/BZ_198_981_1154_1090_1200.pngimages/BZ_198_1087_1154_1234_1200.pngimages/BZ_198_1231_1154_1358_1200.pngimages/BZ_198_1355_1154_1461_1200.pngimages/BZ_198_1458_1154_1612_1200.pngimages/BZ_198_1609_1154_1737_1200.pngimages/BZ_198_1734_1154_1833_1200.png images/BZ_198_1830_1154_1965_1200.pngimages/BZ_198_1962_1154_2120_1200.pngimages/BZ_198_2117_1154_2245_1200.pngimages/BZ_198_233_1200_361_1246.pngimages/BZ_198_358_1200_486_1246.pngimages/BZ_198_483_1200_611_1246.pngimages/BZ_198_608_1200_736_1246.pngimages/BZ_198_733_1200_860_1246.pngimages/BZ_198_857_1200_984_1246.pngimages/BZ_198_981_1200_1090_1246.pngimages/BZ_198_1087_1200_1234_1246.pngimages/BZ_198_1231_1200_1358_1246.pngimages/BZ_198_1355_1200_1461_1246.pngimages/BZ_198_1458_1200_1612_1246.pngimages/BZ_198_1609_1200_1737_1246.pngimages/BZ_198_1734_1200_1833_1246.png images/BZ_198_1830_1200_1965_1246.pngimages/BZ_198_1962_1200_2120_1246.pngimages/BZ_198_2117_1200_2245_1246.pngimages/BZ_198_233_1246_361_1292.pngimages/BZ_198_358_1246_486_1292.pngimages/BZ_198_483_1246_611_1292.pngimages/BZ_198_608_1246_736_1292.pngimages/BZ_198_733_1246_860_1292.pngimages/BZ_198_857_1246_984_1292.pngimages/BZ_198_981_1246_1090_1292.pngimages/BZ_198_1087_1246_1234_1292.pngimages/BZ_198_1231_1246_1358_1292.pngimages/BZ_198_1355_1246_1461_1292.pngimages/BZ_198_1458_1246_1612_1292.pngimages/BZ_198_1609_1246_1737_1292.pngimages/BZ_198_1734_1246_1833_1292.png images/BZ_198_1830_1246_1965_1292.pngimages/BZ_198_1962_1246_2120_1292.pngimages/BZ_198_2117_1246_2245_1292.pngimages/BZ_198_233_1292_361_1338.pngimages/BZ_198_358_1292_486_1338.pngimages/BZ_198_483_1292_611_1338.pngimages/BZ_198_608_1292_736_1338.pngimages/BZ_198_733_1292_860_1338.pngimages/BZ_198_857_1292_984_1338.pngimages/BZ_198_981_1292_1090_1338.pngimages/BZ_198_1087_1292_1234_1338.pngimages/BZ_198_1231_1292_1358_1338.pngimages/BZ_198_1355_1292_1461_1338.pngimages/BZ_198_1458_1292_1612_1338.pngimages/BZ_198_1609_1292_1737_1338.pngimages/BZ_198_1734_1292_1833_1338.png images/BZ_198_1830_1292_1965_1338.pngimages/BZ_198_1962_1292_2120_1338.pngimages/BZ_198_2117_1292_2245_1338.pngimages/BZ_198_233_1338_361_1384.png images/BZ_198_233_1383_361_1429.pngimages/BZ_198_358_1338_2120_1429.pngimages/BZ_198_2117_1338_2245_1384.png images/BZ_198_2117_1383_2245_1429.pngimages/BZ_198_233_1429_361_1475.pngimages/BZ_198_358_1429_486_1475.pngimages/BZ_198_483_1429_611_1475.pngimages/BZ_198_608_1429_736_1475.pngimages/BZ_198_733_1429_860_1475.pngimages/BZ_198_857_1429_984_1475.pngimages/BZ_198_981_1429_1090_1475.pngimages/BZ_198_1087_1429_1234_1475.pngimages/BZ_198_1231_1429_1358_1475.pngimages/BZ_198_1355_1429_1461_1475.pngimages/BZ_198_1458_1429_1612_1475.pngimages/BZ_198_1609_1429_1737_1475.pngimages/BZ_198_1734_1429_1833_1475.png images/BZ_198_1830_1429_1965_1475.pngimages/BZ_198_1962_1429_2120_1475.pngimages/BZ_198_2117_1429_2245_1475.pngimages/BZ_198_233_1475_361_1521.pngimages/BZ_198_358_1475_486_1521.pngimages/BZ_198_483_1475_611_1521.pngimages/BZ_198_608_1475_736_1521.pngimages/BZ_198_733_1475_860_1521.pngimages/BZ_198_857_1475_984_1521.pngimages/BZ_198_981_1475_1090_1521.pngimages/BZ_198_1087_1475_1234_1521.pngimages/BZ_198_1231_1475_1358_1521.pngimages/BZ_198_1355_1475_1461_1521.pngimages/BZ_198_1458_1475_1612_1521.pngimages/BZ_198_1609_1475_1737_1521.pngimages/BZ_198_1734_1475_1833_1521.png images/BZ_198_1830_1475_1965_1521.pngimages/BZ_198_1962_1475_2120_1521.pngimages/BZ_198_2117_1475_2245_1521.pngimages/BZ_198_233_1521_361_1567.pngimages/BZ_198_358_1521_486_1567.pngimages/BZ_198_483_1521_611_1567.pngimages/BZ_198_608_1521_736_1567.pngimages/BZ_198_733_1521_860_1567.pngimages/BZ_198_857_1521_984_1567.pngimages/BZ_198_981_1521_1090_1567.pngimages/BZ_198_1087_1521_1234_1567.pngimages/BZ_198_1231_1521_1358_1567.pngimages/BZ_198_1355_1521_1461_1567.pngimages/BZ_198_1458_1521_1612_1567.pngimages/BZ_198_1609_1521_1737_1567.pngimages/BZ_198_1734_1521_1833_1567.png images/BZ_198_1830_1521_1965_1567.pngimages/BZ_198_1962_1521_2120_1567.pngimages/BZ_198_2117_1521_2245_1567.pngimages/BZ_198_233_1567_361_1613.pngimages/BZ_198_358_1567_486_1613.pngimages/BZ_198_483_1567_611_1613.pngimages/BZ_198_608_1567_736_1613.pngimages/BZ_198_733_1567_860_1613.pngimages/BZ_198_857_1567_984_1613.pngimages/BZ_198_981_1567_1090_1613.pngimages/BZ_198_1087_1567_1234_1613.pngimages/BZ_198_1231_1567_1358_1613.pngimages/BZ_198_1355_1567_1461_1613.pngimages/BZ_198_1458_1567_1612_1613.pngimages/BZ_198_1609_1567_1737_1613.pngimages/BZ_198_1734_1567_1833_1613.png images/BZ_198_1830_1567_1965_1613.pngimages/BZ_198_1962_1567_2120_1613.pngimages/BZ_198_2117_1567_2245_1613.pngimages/BZ_198_233_1613_361_1659.png images/BZ_198_233_1658_361_1704.pngimages/BZ_198_358_1613_2120_1704.pngimages/BZ_198_2117_1613_2245_1659.png images/BZ_198_2117_1658_2245_1704.pngimages/BZ_198_233_1704_361_1750.pngimages/BZ_198_358_1704_486_1750.pngimages/BZ_198_483_1704_611_1750.pngimages/BZ_198_608_1704_736_1750.pngimages/BZ_198_733_1704_860_1750.pngimages/BZ_198_857_1704_984_1750.pngimages/BZ_198_981_1704_1090_1750.pngimages/BZ_198_1087_1704_1234_1750.pngimages/BZ_198_1231_1704_1358_1750.pngimages/BZ_198_1355_1704_1461_1750.pngimages/BZ_198_1458_1704_1612_1750.pngimages/BZ_198_1609_1704_1737_1750.pngimages/BZ_198_1734_1704_1833_1750.png images/BZ_198_1830_1704_1965_1750.pngimages/BZ_198_1962_1704_2120_1750.pngimages/BZ_198_2117_1704_2245_1750.pngimages/BZ_198_233_1750_361_1796.pngimages/BZ_198_358_1750_486_1796.pngimages/BZ_198_483_1750_611_1796.pngimages/BZ_198_608_1750_736_1796.pngimages/BZ_198_733_1750_860_1796.pngimages/BZ_198_857_1750_984_1796.pngimages/BZ_198_981_1750_1090_1796.pngimages/BZ_198_1087_1750_1234_1796.pngimages/BZ_198_1231_1750_1358_1796.pngimages/BZ_198_1355_1750_1461_1796.pngimages/BZ_198_1458_1750_1612_1796.pngimages/BZ_198_1609_1750_1737_1796.pngimages/BZ_198_1734_1750_1833_1796.png images/BZ_198_1830_1750_1965_1796.pngimages/BZ_198_1962_1750_2120_1796.pngimages/BZ_198_2117_1750_2245_1796.pngimages/BZ_198_233_1796_361_1842.pngimages/BZ_198_358_1796_486_1842.pngimages/BZ_198_483_1796_611_1842.pngimages/BZ_198_608_1796_736_1842.pngimages/BZ_198_733_1796_860_1842.pngimages/BZ_198_857_1796_984_1842.pngimages/BZ_198_981_1796_1090_1842.pngimages/BZ_198_1087_1796_1234_1842.pngimages/BZ_198_1231_1796_1358_1842.pngimages/BZ_198_1355_1796_1461_1842.pngimages/BZ_198_1458_1796_1612_1842.pngimages/BZ_198_1609_1796_1737_1842.pngimages/BZ_198_1734_1796_1833_1842.png images/BZ_198_1830_1796_1965_1842.pngimages/BZ_198_1962_1796_2120_1842.pngimages/BZ_198_2117_1796_2245_1842.pngimages/BZ_198_233_1842_361_1888.pngimages/BZ_198_358_1842_486_1888.pngimages/BZ_198_483_1842_611_1888.pngimages/BZ_198_608_1842_736_1888.pngimages/BZ_198_733_1842_860_1888.pngimages/BZ_198_857_1842_984_1888.pngimages/BZ_198_981_1842_1090_1888.pngimages/BZ_198_1087_1842_1234_1888.pngimages/BZ_198_1231_1842_1358_1888.pngimages/BZ_198_1355_1842_1461_1888.pngimages/BZ_198_1458_1842_1612_1888.pngimages/BZ_198_1609_1842_1737_1888.pngimages/BZ_198_1734_1842_1833_1888.png images/BZ_198_1830_1842_1965_1888.pngimages/BZ_198_1962_1842_2120_1888.pngimages/BZ_198_2117_1842_2245_1888.pngimages/BZ_198_233_1888_361_1934.png images/BZ_198_233_1933_361_1979.pngimages/BZ_198_358_1888_2120_1979.pngimages/BZ_198_2117_1888_2245_1934.png images/BZ_198_2117_1933_2245_1979.pngimages/BZ_198_233_1979_361_2025.pngimages/BZ_198_358_1979_486_2025.pngimages/BZ_198_483_1979_611_2025.pngimages/BZ_198_608_1979_736_2025.pngimages/BZ_198_733_1979_860_2025.pngimages/BZ_198_857_1979_984_2025.pngimages/BZ_198_981_1979_1090_2025.pngimages/BZ_198_1087_1979_1234_2025.pngimages/BZ_198_1231_1979_1358_2025.pngimages/BZ_198_1355_1979_1461_2025.pngimages/BZ_198_1458_1979_1612_2025.pngimages/BZ_198_1609_1979_1737_2025.pngimages/BZ_198_1734_1979_1833_2025.png images/BZ_198_1830_1979_1965_2025.pngimages/BZ_198_1962_1979_2120_2025.pngimages/BZ_198_2117_1979_2245_2025.pngimages/BZ_198_233_2025_361_2071.pngimages/BZ_198_358_2025_486_2071.pngimages/BZ_198_483_2025_611_2071.pngimages/BZ_198_608_2025_736_2071.pngimages/BZ_198_733_2025_860_2071.pngimages/BZ_198_857_2025_984_2071.pngimages/BZ_198_981_2025_1090_2071.pngimages/BZ_198_1087_2025_1234_2071.pngimages/BZ_198_1231_2025_1358_2071.pngimages/BZ_198_1355_2025_1461_2071.pngimages/BZ_198_1458_2025_1612_2071.pngimages/BZ_198_1609_2025_1737_2071.pngimages/BZ_198_1734_2025_1833_2071.png images/BZ_198_1830_2025_1965_2071.pngimages/BZ_198_1962_2025_2120_2071.pngimages/BZ_198_2117_2025_2245_2071.pngimages/BZ_198_233_2071_361_2117.pngimages/BZ_198_358_2071_486_2117.pngimages/BZ_198_483_2071_611_2117.pngimages/BZ_198_608_2071_736_2117.pngimages/BZ_198_733_2071_860_2117.pngimages/BZ_198_857_2071_984_2117.pngimages/BZ_198_981_2071_1090_2117.pngimages/BZ_198_1087_2071_1234_2117.pngimages/BZ_198_1231_2071_1358_2117.pngimages/BZ_198_1355_2071_1461_2117.pngimages/BZ_198_1458_2071_1612_2117.pngimages/BZ_198_1609_2071_1737_2117.pngimages/BZ_198_1734_2071_1833_2117.png images/BZ_198_1830_2071_1965_2117.pngimages/BZ_198_1962_2071_2120_2117.pngimages/BZ_198_2117_2071_2245_2117.pngimages/BZ_198_233_2117_361_2163.pngimages/BZ_198_358_2117_486_2163.pngimages/BZ_198_483_2117_611_2163.pngimages/BZ_198_608_2117_736_2163.pngimages/BZ_198_733_2117_860_2163.pngimages/BZ_198_857_2117_984_2163.pngimages/BZ_198_981_2117_1090_2163.pngimages/BZ_198_1087_2117_1234_2163.pngimages/BZ_198_1231_2117_1358_2163.pngimages/BZ_198_1355_2117_1461_2163.pngimages/BZ_198_1458_2117_1612_2163.pngimages/BZ_198_1609_2117_1737_2163.pngimages/BZ_198_1734_2117_1833_2163.png images/BZ_198_1830_2117_1965_2163.pngimages/BZ_198_1962_2117_2120_2163.pngimages/BZ_198_2117_2117_2245_2163.pngimages/BZ_198_233_2163_361_2209.png images/BZ_198_233_2208_361_2254.pngimages/BZ_198_358_2163_2120_2254.pngimages/BZ_198_2117_2163_2245_2209.png images/BZ_198_2117_2208_2245_2254.pngimages/BZ_198_233_2254_361_2300.pngimages/BZ_198_358_2254_486_2300.pngimages/BZ_198_483_2254_611_2300.pngimages/BZ_198_608_2254_736_2300.pngimages/BZ_198_733_2254_860_2300.pngimages/BZ_198_857_2254_984_2300.pngimages/BZ_198_981_2254_1090_2300.pngimages/BZ_198_1087_2254_1234_2300.pngimages/BZ_198_1231_2254_1358_2300.pngimages/BZ_198_1355_2254_1461_2300.pngimages/BZ_198_1458_2254_1612_2300.pngimages/BZ_198_1609_2254_1737_2300.pngimages/BZ_198_1734_2254_1833_2300.png images/BZ_198_1830_2254_1965_2300.pngimages/BZ_198_1962_2254_2120_2300.pngimages/BZ_198_2117_2254_2245_2300.pngimages/BZ_198_233_2300_361_2346.pngimages/BZ_198_358_2300_486_2346.pngimages/BZ_198_483_2300_611_2346.pngimages/BZ_198_608_2300_736_2346.pngimages/BZ_198_733_2300_860_2346.pngimages/BZ_198_857_2300_984_2346.pngimages/BZ_198_981_2300_1090_2346.pngimages/BZ_198_1087_2300_1234_2346.pngimages/BZ_198_1231_2300_1358_2346.pngimages/BZ_198_1355_2300_1461_2346.pngimages/BZ_198_1458_2300_1612_2346.pngimages/BZ_198_1609_2300_1737_2346.pngimages/BZ_198_1734_2300_1833_2346.png images/BZ_198_1830_2300_1965_2346.pngimages/BZ_198_1962_2300_2120_2346.pngimages/BZ_198_2117_2300_2245_2346.pngimages/BZ_198_233_2346_361_2392.pngimages/BZ_198_358_2346_486_2392.pngimages/BZ_198_483_2346_611_2392.pngimages/BZ_198_608_2346_736_2392.pngimages/BZ_198_733_2346_860_2392.pngimages/BZ_198_857_2346_984_2392.pngimages/BZ_198_981_2346_1090_2392.pngimages/BZ_198_1087_2346_1234_2392.pngimages/BZ_198_1231_2346_1358_2392.pngimages/BZ_198_1355_2346_1461_2392.pngimages/BZ_198_1458_2346_1612_2392.pngimages/BZ_198_1609_2346_1737_2392.pngimages/BZ_198_1734_2346_1833_2392.png images/BZ_198_1830_2346_1965_2392.pngimages/BZ_198_1962_2346_2120_2392.pngimages/BZ_198_2117_2346_2245_2392.pngimages/BZ_198_233_2392_361_2438.pngimages/BZ_198_358_2392_486_2438.pngimages/BZ_198_483_2392_611_2438.pngimages/BZ_198_608_2392_736_2438.pngimages/BZ_198_733_2392_860_2438.pngimages/BZ_198_857_2392_984_2438.pngimages/BZ_198_981_2392_1090_2438.pngimages/BZ_198_1087_2392_1234_2438.pngimages/BZ_198_1231_2392_1358_2438.pngimages/BZ_198_1355_2392_1461_2438.pngimages/BZ_198_1458_2392_1612_2438.pngimages/BZ_198_1609_2392_1737_2438.pngimages/BZ_198_1734_2392_1833_2438.png images/BZ_198_1830_2392_1965_2438.pngimages/BZ_198_1962_2392_2120_2438.pngimages/BZ_198_2117_2392_2245_2438.pngimages/BZ_198_233_2438_361_2484.pngimages/BZ_198_358_2438_486_2484.pngimages/BZ_198_483_2438_611_2484.pngimages/BZ_198_608_2438_736_2484.pngimages/BZ_198_733_2438_860_2484.pngimages/BZ_198_857_2438_984_2484.pngimages/BZ_198_981_2438_1090_2484.pngimages/BZ_198_1087_2438_1234_2484.pngimages/BZ_198_1231_2438_1358_2484.pngimages/BZ_198_1355_2438_1461_2484.pngimages/BZ_198_1458_2438_1612_2484.pngimages/BZ_198_1609_2438_1737_2484.pngimages/BZ_198_1734_2438_1833_2484.png images/BZ_198_1830_2438_1965_2484.pngimages/BZ_198_1962_2438_2120_2484.pngimages/BZ_198_2117_2438_2245_2484.pngimages/BZ_198_233_2484_361_2529.pngimages/BZ_198_358_2484_486_2529.pngimages/BZ_198_483_2484_611_2529.pngimages/BZ_198_608_2484_736_2529.pngimages/BZ_198_733_2484_860_2529.pngimages/BZ_198_857_2484_984_2529.pngimages/BZ_198_981_2484_1090_2529.pngimages/BZ_198_1087_2484_1234_2529.pngimages/BZ_198_1231_2484_1358_2529.pngimages/BZ_198_1355_2484_1461_2529.pngimages/BZ_198_1458_2484_1612_2529.pngimages/BZ_198_1609_2484_1737_2529.pngimages/BZ_198_1734_2484_1833_2529.png images/BZ_198_1830_2484_1965_2529.pngimages/BZ_198_1962_2484_2120_2529.pngimages/BZ_198_2117_2484_2245_2529.pngimages/BZ_198_233_2529_361_2575.pngimages/BZ_198_358_2529_486_2575.pngimages/BZ_198_483_2529_611_2575.pngimages/BZ_198_608_2529_736_2575.pngimages/BZ_198_733_2529_860_2575.pngimages/BZ_198_857_2529_984_2575.pngimages/BZ_198_981_2529_1090_2575.pngimages/BZ_198_1087_2529_1234_2575.pngimages/BZ_198_1231_2529_1358_2575.pngimages/BZ_198_1355_2529_1461_2575.pngimages/BZ_198_1458_2529_1612_2575.pngimages/BZ_198_1609_2529_1737_2575.pngimages/BZ_198_1734_2529_1833_2575.png images/BZ_198_1830_2529_1965_2575.pngimages/BZ_198_1962_2529_2120_2575.pngimages/BZ_198_2117_2529_2245_2575.pngimages/BZ_198_233_2575_361_2621.pngimages/BZ_198_358_2575_486_2621.pngimages/BZ_198_483_2575_611_2621.pngimages/BZ_198_608_2575_736_2621.pngimages/BZ_198_733_2575_860_2621.pngimages/BZ_198_857_2575_984_2621.pngimages/BZ_198_981_2575_1090_2621.pngimages/BZ_198_1087_2575_1234_2621.pngimages/BZ_198_1231_2575_1358_2621.pngimages/BZ_198_1355_2575_1461_2621.pngimages/BZ_198_1458_2575_1612_2621.pngimages/BZ_198_1609_2575_1737_2621.pngimages/BZ_198_1734_2575_1833_2621.png images/BZ_198_1830_2575_1965_2621.pngimages/BZ_198_1962_2575_2120_2621.pngimages/BZ_198_2117_2575_2245_2621.pngimages/BZ_198_233_2621_361_2667.pngimages/BZ_198_358_2621_486_2667.pngimages/BZ_198_483_2621_611_2667.pngimages/BZ_198_608_2621_736_2667.pngimages/BZ_198_733_2621_860_2667.pngimages/BZ_198_857_2621_984_2667.pngimages/BZ_198_981_2621_1090_2667.pngimages/BZ_198_1087_2621_1234_2667.pngimages/BZ_198_1231_2621_1358_2667.pngimages/BZ_198_1355_2621_1461_2667.pngimages/BZ_198_1458_2621_1612_2667.pngimages/BZ_198_1609_2621_1737_2667.pngimages/BZ_198_1734_2621_1833_2667.png images/BZ_198_1830_2621_1965_2667.pngimages/BZ_198_1962_2621_2120_2667.pngimages/BZ_198_2117_2621_2245_2667.pngimages/BZ_198_233_2667_361_2713.pngimages/BZ_198_358_2667_486_2713.pngimages/BZ_198_483_2667_611_2713.pngimages/BZ_198_608_2667_736_2713.pngimages/BZ_198_733_2667_860_2713.pngimages/BZ_198_857_2667_984_2713.pngimages/BZ_198_981_2667_1090_2713.pngimages/BZ_198_1087_2667_1234_2713.pngimages/BZ_198_1231_2667_1358_2713.pngimages/BZ_198_1355_2667_1461_2713.pngimages/BZ_198_1458_2667_1612_2713.pngimages/BZ_198_1609_2667_1737_2713.pngimages/BZ_198_1734_2667_1833_2713.png images/BZ_198_1830_2667_1965_2713.pngimages/BZ_198_1962_2667_2120_2713.pngimages/BZ_198_2117_2667_2245_2713.pngimages/BZ_198_233_2713_361_2759.pngimages/BZ_198_358_2713_486_2759.pngimages/BZ_198_483_2713_611_2759.pngimages/BZ_198_608_2713_736_2759.pngimages/BZ_198_733_2713_860_2759.pngimages/BZ_198_857_2713_984_2759.pngimages/BZ_198_981_2713_1090_2759.pngimages/BZ_198_1087_2713_1234_2759.pngimages/BZ_198_1231_2713_1358_2759.pngimages/BZ_198_1355_2713_1461_2759.pngimages/BZ_198_1458_2713_1612_2759.pngimages/BZ_198_1609_2713_1737_2759.pngimages/BZ_198_1734_2713_1833_2759.png images/BZ_198_1830_2713_1965_2759.pngimages/BZ_198_1962_2713_2120_2759.pngimages/BZ_198_2117_2713_2245_2759.pngimages/BZ_198_233_2759_361_2804.pngimages/BZ_198_358_2759_486_2804.pngimages/BZ_198_483_2759_611_2804.pngimages/BZ_198_608_2759_736_2804.pngimages/BZ_198_733_2759_860_2804.pngimages/BZ_198_857_2759_984_2804.pngimages/BZ_198_981_2759_1090_2804.pngimages/BZ_198_1087_2759_1234_2804.pngimages/BZ_198_1231_2759_1358_2804.pngimages/BZ_198_1355_2759_1461_2804.pngimages/BZ_198_1458_2759_1612_2804.pngimages/BZ_198_1609_2759_1737_2804.pngimages/BZ_198_1734_2759_1833_2804.png images/BZ_198_1830_2759_1965_2804.pngimages/BZ_198_1962_2759_2120_2804.pngimages/BZ_198_2117_2759_2245_2804.pngimages/BZ_198_233_2804_361_2850.pngimages/BZ_198_358_2804_486_2850.pngimages/BZ_198_483_2804_611_2850.pngimages/BZ_198_608_2804_736_2850.pngimages/BZ_198_733_2804_860_2850.pngimages/BZ_198_857_2804_984_2850.pngimages/BZ_198_981_2804_1090_2850.pngimages/BZ_198_1087_2804_1234_2850.pngimages/BZ_198_1231_2804_1358_2850.pngimages/BZ_198_1355_2804_1461_2850.pngimages/BZ_198_1458_2804_1612_2850.pngimages/BZ_198_1609_2804_1737_2850.pngimages/BZ_198_1734_2804_1833_2850.png images/BZ_198_1830_2804_1965_2850.pngimages/BZ_198_1962_2804_2120_2850.pngimages/BZ_198_2117_2804_2245_2850.pngimages/BZ_198_233_2850_361_2896.pngimages/BZ_198_358_2850_486_2896.pngimages/BZ_198_483_2850_611_2896.pngimages/BZ_198_608_2850_736_2896.pngimages/BZ_198_733_2850_860_2896.pngimages/BZ_198_857_2850_984_2896.pngimages/BZ_198_981_2850_1090_2896.pngimages/BZ_198_1087_2850_1234_2896.pngimages/BZ_198_1231_2850_1358_2896.pngimages/BZ_198_1355_2850_1461_2896.pngimages/BZ_198_1458_2850_1612_2896.pngimages/BZ_198_1609_2850_1737_2896.pngimages/BZ_198_1734_2850_1833_2896.png images/BZ_198_1830_2850_1965_2896.pngimages/BZ_198_1962_2850_2120_2896.pngimages/BZ_198_2117_2850_2245_2896.pngimages/BZ_198_233_2896_361_2942.pngimages/BZ_198_358_2896_486_2942.pngimages/BZ_198_483_2896_611_2942.pngimages/BZ_198_608_2896_736_2942.pngimages/BZ_198_733_2896_860_2942.pngimages/BZ_198_857_2896_984_2942.pngimages/BZ_198_981_2896_1090_2942.pngimages/BZ_198_1087_2896_1234_2942.pngimages/BZ_198_1231_2896_1358_2942.pngimages/BZ_198_1355_2896_1461_2942.pngimages/BZ_198_1458_2896_1612_2942.pngimages/BZ_198_1609_2896_1737_2942.pngimages/BZ_198_1734_2896_1833_2942.png images/BZ_198_1830_2896_1965_2942.pngimages/BZ_198_1962_2896_2120_2942.pngimages/BZ_198_2117_2896_2245_2942.pngimages/BZ_198_233_2942_361_2988.pngimages/BZ_198_358_2942_486_2988.pngimages/BZ_198_483_2942_611_2988.pngimages/BZ_198_608_2942_736_2988.pngimages/BZ_198_733_2942_860_2988.pngimages/BZ_198_857_2942_984_2988.pngimages/BZ_198_981_2942_1090_2988.pngimages/BZ_198_1087_2942_1234_2988.pngimages/BZ_198_1231_2942_1358_2988.pngimages/BZ_198_1355_2942_1461_2988.pngimages/BZ_198_1458_2942_1612_2988.pngimages/BZ_198_1609_2942_1737_2988.pngimages/BZ_198_1734_2942_1833_2988.png images/BZ_198_1830_2942_1965_2988.pngimages/BZ_198_1962_2942_2120_2988.pngimages/BZ_198_2117_2942_2245_2988.pngimages/BZ_198_233_2988_361_3034.pngimages/BZ_198_358_2988_486_3034.pngimages/BZ_198_483_2988_611_3034.pngimages/BZ_198_608_2988_736_3034.pngimages/BZ_198_733_2988_860_3034.pngimages/BZ_198_857_2988_984_3034.pngimages/BZ_198_981_2988_1090_3034.pngimages/BZ_198_1087_2988_1234_3034.pngimages/BZ_198_1231_2988_1358_3034.pngimages/BZ_198_1355_2988_1461_3034.pngimages/BZ_198_1458_2988_1612_3034.pngimages/BZ_198_1609_2988_1737_3034.pngimages/BZ_198_1734_2988_1833_3034.png images/BZ_198_1830_2988_1965_3034.pngimages/BZ_198_1962_2988_2120_3034.pngimages/BZ_198_2117_2988_2245_3034.pngimages/BZ_198_233_3034_361_3079.pngimages/BZ_198_358_3034_486_3079.pngimages/BZ_198_483_3034_611_3079.pngimages/BZ_198_608_3034_736_3079.pngimages/BZ_198_733_3034_860_3079.pngimages/BZ_198_857_3034_984_3079.pngimages/BZ_198_981_3034_1090_3079.pngimages/BZ_198_1087_3034_1234_3079.pngimages/BZ_198_1231_3034_1358_3079.pngimages/BZ_198_1355_3034_1461_3079.pngimages/BZ_198_1458_3034_1612_3079.pngimages/BZ_198_1609_3034_1737_3079.pngimages/BZ_198_1734_3034_1833_3079.png images/BZ_198_1830_3034_1965_3079.pngimages/BZ_198_1962_3034_2120_3079.pngimages/BZ_198_2117_3034_2245_3079.pngimages/BZ_198_233_3079_361_3125.pngimages/BZ_198_358_3079_486_3125.pngimages/BZ_198_483_3079_611_3125.pngimages/BZ_198_608_3079_736_3125.pngimages/BZ_198_733_3079_860_3125.pngimages/BZ_198_857_3079_984_3125.pngimages/BZ_198_981_3079_1090_3125.pngimages/BZ_198_1087_3079_1234_3125.pngimages/BZ_198_1231_3079_1358_3125.pngimages/BZ_198_1355_3079_1461_3125.pngimages/BZ_198_1458_3079_1612_3125.pngimages/BZ_198_1609_3079_1737_3125.pngimages/BZ_198_1734_3079_1833_3125.png images/BZ_198_1830_3079_1965_3125.pngimages/BZ_198_1962_3079_2120_3125.pngimages/BZ_198_2117_3079_2245_3125.pngimages/BZ_198_233_3125_361_3171.pngimages/BZ_198_358_3125_486_3171.pngimages/BZ_198_483_3125_611_3171.pngimages/BZ_198_608_3125_736_3171.pngimages/BZ_198_733_3125_860_3171.pngimages/BZ_198_857_3125_984_3171.pngimages/BZ_198_981_3125_1090_3171.pngimages/BZ_198_1087_3125_1234_3171.pngimages/BZ_198_1231_3125_1358_3171.pngimages/BZ_198_1355_3125_1461_3171.pngimages/BZ_198_1458_3125_1612_3171.pngimages/BZ_198_1609_3125_1737_3171.pngimages/BZ_198_1734_3125_1833_3171.png images/BZ_198_1830_3125_1965_3171.pngimages/BZ_198_1962_3125_2120_3171.pngimages/BZ_198_2117_3125_2245_3171.png
2 概率模型参数的后验分布信息
2.1 贝叶斯理论和基于DRAM算法的MCMC法
由式(10)可知，要确定RC柱的概率抗剪承载力模型，首先需要确定概率模型参数β的统计信息。本文利用贝叶斯理论来确定β的后验分布：
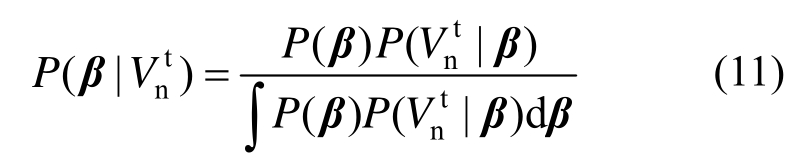
式中：
的后验分布概率密度函数，其中
为RC柱抗剪承载力的试验测试值；P(β)为β的先验分布概率密度函数；
为似然函数；
为正则化因子。由式(11)可知，随着试验数据量的增加，可以不断更新β的后验分布信息。然而，在运用式(11)确定β的后验分布时，正则化因子
的求解往往涉及多维积分，计算比较困难。鉴于此，本文采用马尔科夫链蒙特卡洛(MCMC)法来确定β的后验分布信息，进而确定RC柱的概率抗剪承载力模型。
MCMC法的基本原理是基于β的先验分布信息构造一条马尔科夫链，当马尔科夫链达到平稳状态时对其抽样产生后验分布的样本，进而通过对样本进行统计分析确定β的后验分布信息。为了保证抽样方法的收敛性和样本的遍历性，同时兼顾抽样精度和效率，本文采用基于DRAM算法[39-40]的MCMC法确定β的后验分布信息，基本步骤如下：
1) 选定β的初始值β0，构造建议分布q(·)，给定样本容量m。本文选取β的先验分布均值作为初始值β0。
2) 给定初始(第1层)建议的协方差矩阵
本文假定概率模型参数之间相互独立，并根据β的先验分布标准差构造初始协方差矩阵。同时设置非适应阶段的迭代步数N0，在非适应阶段无需更新协方差矩阵，当超过非适应段时按式(12)更新协方差矩阵[39-40]：
式中：υ为较小的正数，常取10-5以保证Cj的非奇异性；sd为比例因子，通常取sd=5.76M，M为概率模型参数的维数；cov(β0,β1,...,βj-1)为历史样本的协方差矩阵；Id为M维的单位矩阵。
3) 重复以下过程，直到产生满足遍历性、非周期性、回返性和不可约束性的马尔科夫链。
a) 设当前参数为βj-1(j≥1)，则从当前建议分布q(βj-1,·)中随机抽取一个模型参数候选值β*，其中黑点代表建议分布的变量；
b) 计算第1层的接受概率p1(βj-1,β*)：
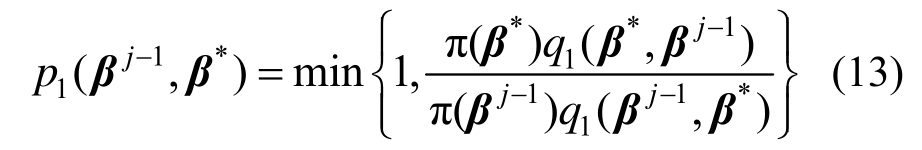
式中：π(β)为平稳分布，其中
c) 从[0,1]均匀分布中产生随机数u，若满足u≤p1(βj -1,β*)，则接受模型参数候选值β*，即令βj=β*，然后进入步骤e)；否则进入步骤d)；
d) 根据抽样的历史参数调整建议分布协方差矩阵，同时从第N(N≥2)层建议分布q(βj-1,β*,·)中抽取新的模型参数候选值βN*，并利用新的建议分布根据式(14)计算第N层接受概率，然后对模型参数候选值βN*进行第N层判断，从[0,1]均匀分布中产生随机数u，若满足u≤pN(βj -1,β*,...,βN*)，则接受模型参数候选值βN*，即令βj=βN *，然后进入步骤e)；否则令N=N+1重复步骤d)；
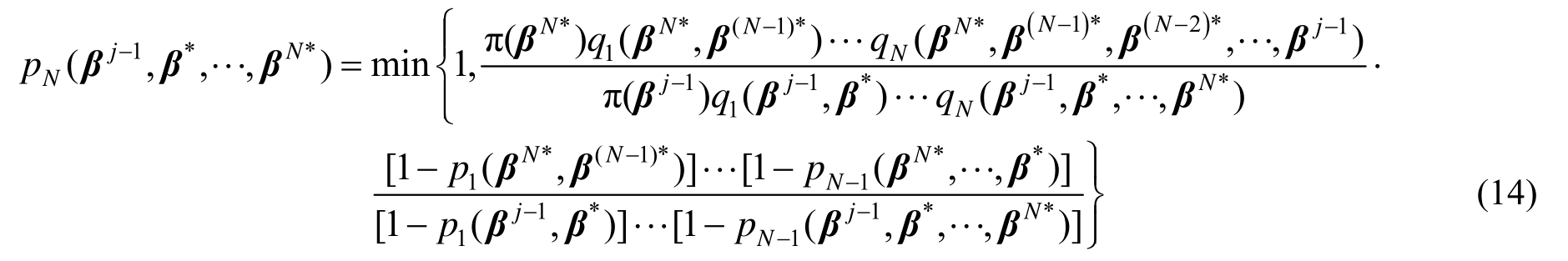
e) 若j＞m则停止，否则增加迭代次数返回步骤a)，其中βj为当前变量。
2.2 先验分布信息和更新批次对模型更新的影响
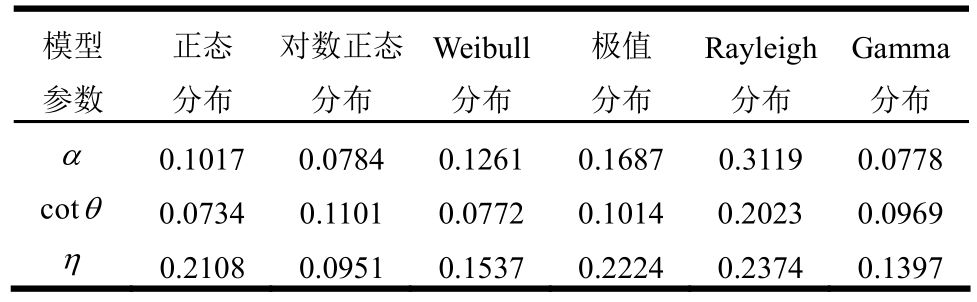
由式(11)可知，要确定β的后验分布信息，首先需要确定β的先验分布信息(包括均值、标准差、分布类型、相关系数等)。基于表1中前38组试验数据的基本参数，利用式(3)、式(5)和式(8)可以分别计算得到参数α、cotθ和η的38组数据，进而根据Kolmogorov-Smirnov(K-S)检验可以确定上述参数的先验分布，K-S统计量见表2。
表2 模型参数的K-S统计量
Table 2 Statistics of K-S tests of model parameters
模型参数正态分布对数正态分布Weibull分布极值分布Rayleigh分布Gamma分布α 0.1017 0.0784 0.1261 0.1687 0.3119 0.0778 cotθ 0.0734 0.1101 0.0772 0.1014 0.2023 0.0969 η 0.2108 0.0951 0.1537 0.2224 0.2374 0.1397
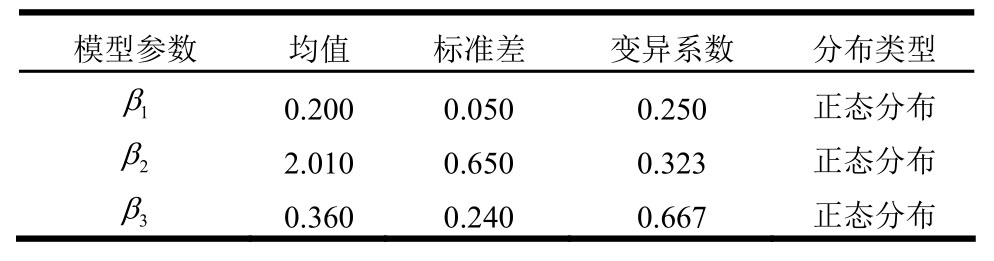
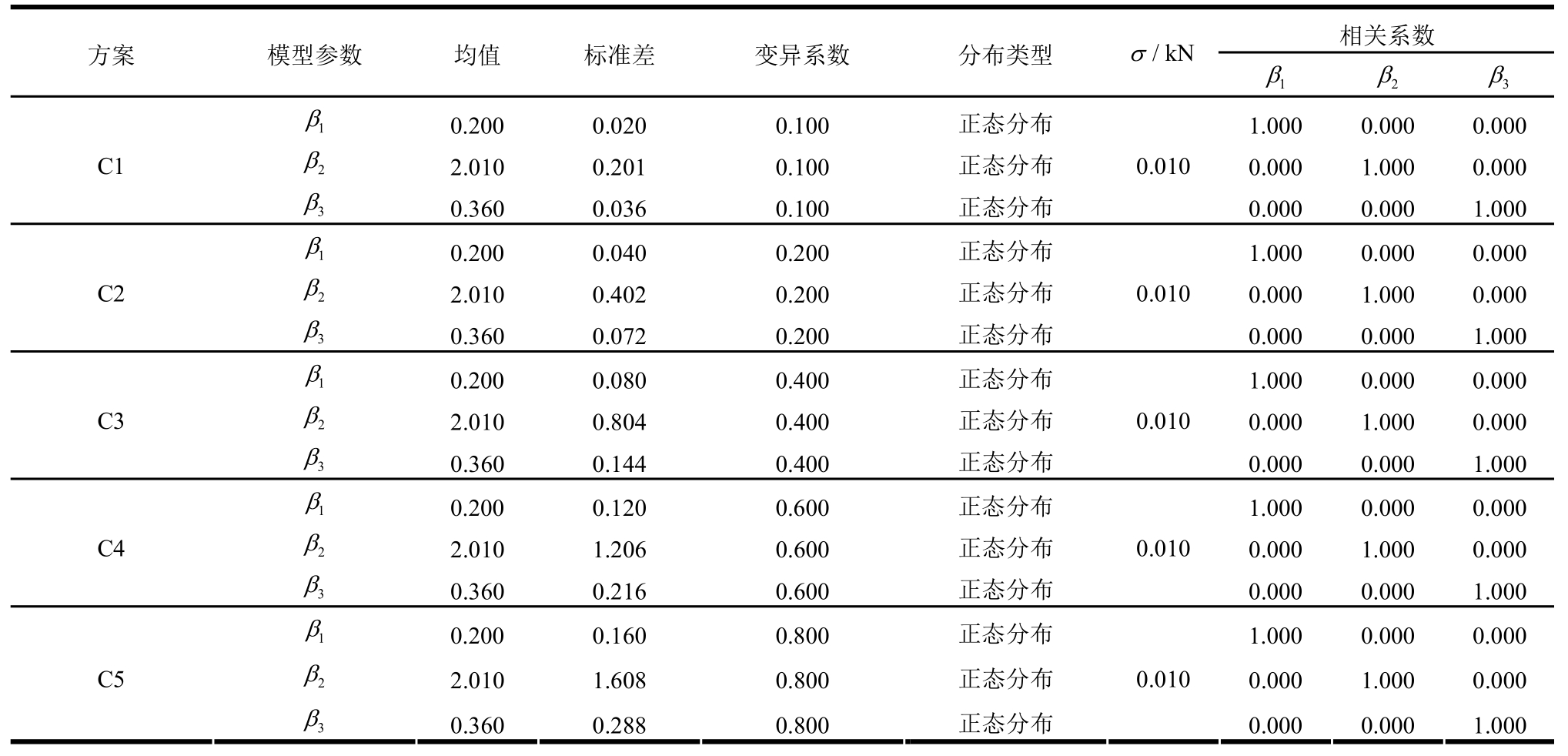
当显著性水平取0.05、样本容量为38时，K-S检验临界值为0.2206。由表2可知，参数α、cotθ和η均不拒绝服从正态分布、对数正态分布、Weibull分布和Gamma分布。考虑到正态分布更加方便使用，故本文假定上述参数的先验分布均服从正态分布。结合第2节所确定的参数α、cotθ和η的均值、标准差和变异系数，可以确定概率模型参数β的先验分布信息，见表3。为了避免由于统计数据过少造成先验分布的变异系数过小而引起计算误差，本文根据表3确定概率模型参数β的均值和先验分布类型，假定各概率模型参数之间相互独立、模型误差的标准差为0.01 kN，分别考虑β的先验分布变异系数取0.10、0.20、0.40、0.60和0.80五种情况，见表4。
表3 基于38组试验数据确定的β先验信息
Table 3 Prior distribution of β based on 38 sets of experimental data
模型参数 均值 标准差 变异系数 分布类型β1 0.200 0.050 0.250 正态分布β2 2.010 0.650 0.323 正态分布β3 0.360 0.240 0.667 正态分布
表4 先验分布统计信息的5种方案
Table 4 Five cases for statistical characteristics of prior distribution
相关系数方案 模型参数 均值 标准差 变异系数 分布类型 σ/kN β1 β2 β3 β1 0.200 0.020 0.100 正态分布 1.000 0.000 0.000 C1β2 2.010 0.201 0.100 正态分布 0.000 1.000 0.000 0.010 β3 0.360 0.036 0.100 正态分布0.000 0.000 1.000 β1 0.200 0.040 0.200 正态分布 1.000 0.000 0.000 C2β2 2.010 0.402 0.200 正态分布 0.000 1.000 0.000 0.010 β3 0.360 0.072 0.200 正态分布0.000 0.000 1.000 β1 0.200 0.080 0.400 正态分布 1.000 0.000 0.000 C3β2 2.010 0.804 0.400 正态分布 0.000 1.000 0.000 0.010 β3 0.360 0.144 0.400 正态分布0.000 0.000 1.000 β1 0.200 0.120 0.600 正态分布 1.000 0.000 0.000 C4β2 2.010 1.206 0.600 正态分布 0.000 1.000 0.000 0.010 β3 0.360 0.216 0.600 正态分布0.000 0.000 1.000 β1 0.200 0.160 0.800 正态分布 1.000 0.000 0.000 C5β2 2.010 1.608 0.800 正态分布 0.000 1.000 0.000 0.010 β3 0.360 0.288 0.800 正态分布0.000 0.000 1.000
同时，为了分析试验数据量(即更新批次)对概率模型参数后验分布信息的影响，将表1中58组试验数据分为3批(前18组数据为第一批、前38组数据为第二批、全部58组数据为第三批)，分别根据表4中的5种先验分布信息方案更新概率模型参数的后验分布信息。需要说明的是，各方案第一批更新时的先验信息见表4，第二批和第三批更新时的先验分布信息取前一批更新确定的后验分布均值及相应方案下的变异系数，并假定β均服从正态分布，且各概率模型参数之间相互独立，模型误差的标准差为0.01 kN。基于贝叶斯公式(Bayes rules)，利用MCMC法可以得到各方案下不同批次更新后各概率模型参数的后验分布均值、标准及对应的模型误差标准差，见表5～表7。由表5～表7可知，在更新批次相同的情况下，随着先验分布变异系数的增加，各概率模型参数的后验分布(包括均值、标准和模型误差标准差)呈现逐渐收敛的趋势；在先验分布变异系数相同的情况下，随着参与更新的试验数据量(即更新批次)的增加，β的后验分布呈现不断更新且逐渐收敛的趋势；此外，模型误差的标准差基本不受先验分布的影响，而主要与参与更新的试验数据的离散程度有关。
对不同先验分布方案和不同更新批次下概率模型参数的样本点进行K-S检验及相关性分析可知，各概率模型参数的后验分布均不拒绝服从正态分布，模型参数之间具有一定的相关性且均为负相关性，其相关系数的对比分析见图2。由图2可知，随着先验分布变异系数和更新批次的增加，β1和β3以及β2和β3之间的相关系数的绝对值呈现逐渐增大且收敛的趋势，同时β1和β2之间的相关系数也逐渐趋于收敛；当更新批次不小于2次、先验分布的变异系数不小于0.6时，概率模型参数之间的相关系数基本趋于稳定。由此可见，为了保证概率模型参数之间相关系数的准确性，概率模型参数的先验分布变异系数不宜过小，且参与更新的数据量也不能太少。
表5 先验分布和更新批次对后验分布均值的影响
Table 5 Influences of prior distribution and number of updates on mean values of posterior distribution
更新批次C1 C2 C3 C4 C5 β1 β2 β3 β1 β2 β3 β1 β2 β3 β1 β2 β3 β1 β2 β3第一批 0.208 1.646 0.340 0.244 1.458 0.343 0.2831.2480.350 0.2991.1840.341 0.305 1.1360.350第二批 0.230 1.509 0.340 0.257 1.349 0.3350.2691.3160.3210.2721.3360.302 0.268 1.3270.316第三批 0.236 1.381 0.334 0.251 1.302 0.3220.2581.3250.2940.2641.3560.266 0.260 1.3370.284
表6 先验分布和更新批次对后验分布标准差的影响
Table 6 Influences of prior distribution and number of updates on standard deviations of posterior distribution
更新批次C1 C2 C3 C4 C5 β1 β2 β3 β1 β2 β3 β1 β2 β3 β1 β2 β3 β1 β2 β3第一批 0.012 0.067 0.027 0.014 0.078 0.038 0.0210.1090.057 0.0270.1410.076 0.029 0.1490.084第二批 0.010 0.066 0.026 0.016 0.101 0.0490.0230.1320.0760.0210.1220.068 0.023 0.1300.076第三批 0.010 0.069 0.028 0.017 0.110 0.0550.0190.1160.0680.0180.1090.058 0.019 0.1120.064
表7 先验分布和更新批次对模型误差标准差的影响
Table 7 Influences of prior distribution and number of updates on standard deviations of model error
更新批次 C1 C2 C3 C4 C5第一批 61.998 kN 60.229 kN 59.216 kN 59.273 kN 59.286 kN第二批 62.994 kN 62.469 kN 62.597 kN 62.583 kN 62.627 kN第三批 60.920 kN 60.950 kN 60.977 kN 60.941 kN 60.956 kN
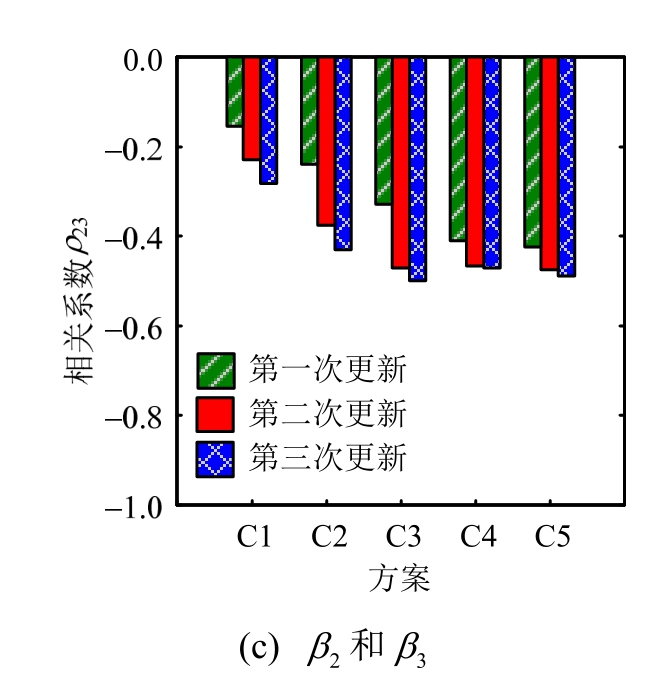
图2 不同方案和更新批次下概率模型参数之间的相关性
Fig.2 Comparison of the correlation between probability model parameters under different schemes and update batches
以第三批次更新后的概率模型参数的后验分布信息为例，概率模型参数先验分布的变异系数对模型参数后验分布概率密度函数(Probability density function, PDF)的影响，如图3所示。由图3可知，随着变异系数的增加，概率模型参数的后验分布概率密度(Probability density, PD)逐渐趋于稳定，且在先验分布变异系数大于等于0.60时更为明显，说明概率模型参数的先验分布变异系数不能选取太小。为了保证概率模型参数后验分布的稳定性，本文建议将概率模型参数先验分布的变异系数选取为0.60。
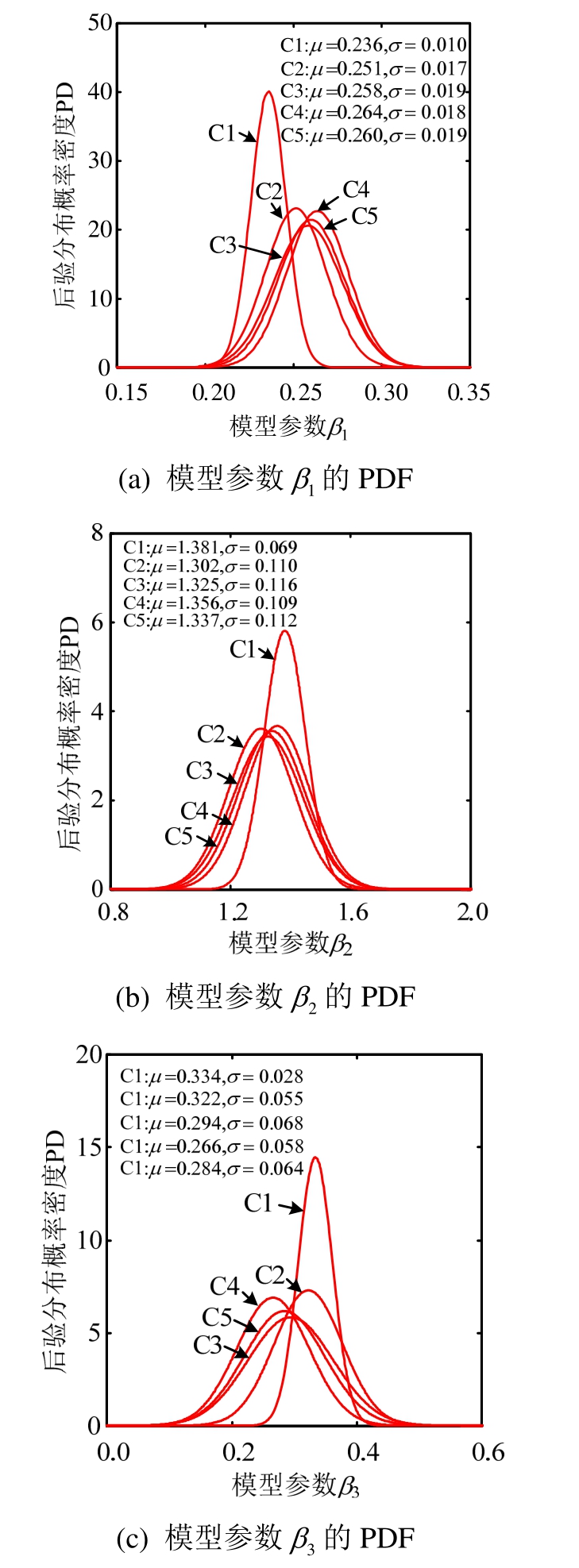
图3 概率模型参数的先验分布变异系数对后验分布概率密度的影响
Fig.3 Influence of coefficient of variation of prior distribution on probability density of posterior distribution
以概率模型参数先验分布变异系数取0.60(即C4)为例，更新批次对概率模型参数后验分布概率密度的影响如图4所示。由图4可知，随着试验数据量(即更新批次)的增加，概率模型参数后验分布概率密度逐渐趋于稳定，说明随着数据量的增加，概率模型参数可以实现不断更新。
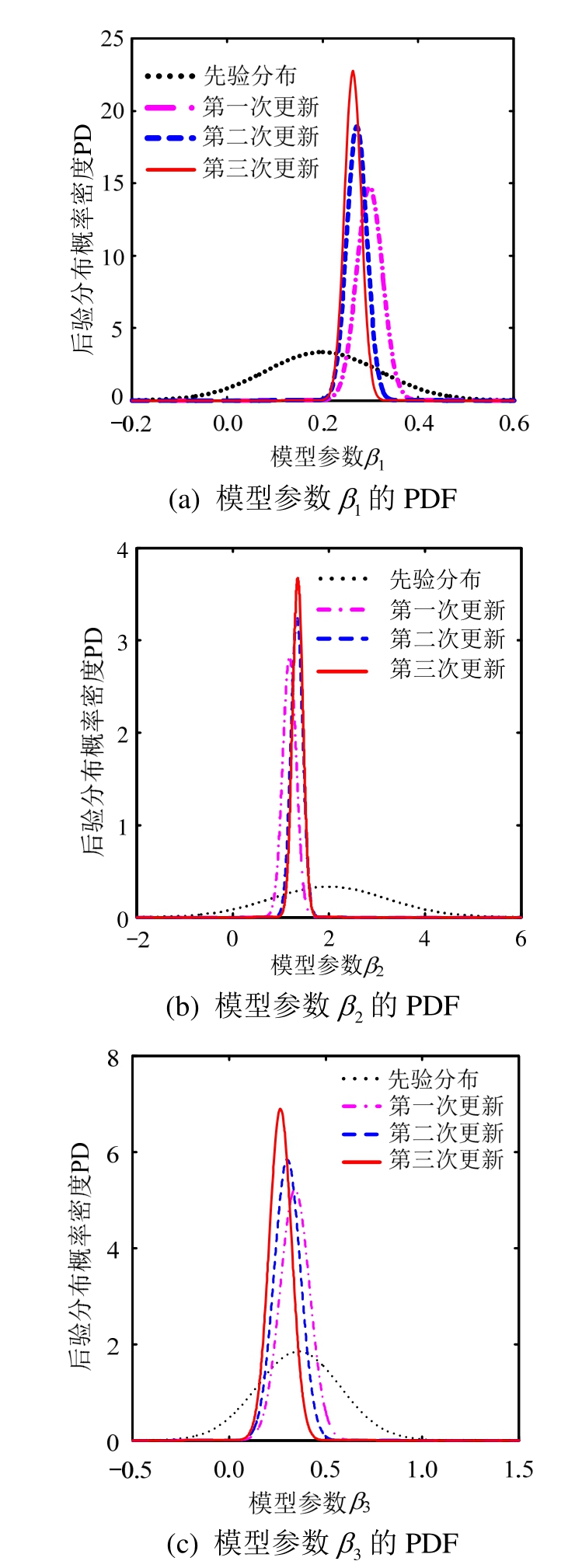
图4 更新批次对概率模型参数后验分布概率密度的影响
Fig.4 Influence of number of updates on probability density of posterior distribution
3 对比分析与验证
3.1 抗剪承载力的概率特征值
假定概率模型参数β与模型误差εσ之间相互独立，根据式(10)所定义的RC柱概率抗剪承载力模型以及C4方案下第三批次确定的后验分布信息，利用一般函数的近似矩方法[41]，可以确定概率抗剪承载力Vnp的均值(μV)和标准差(σV)的解析表达式分别为：
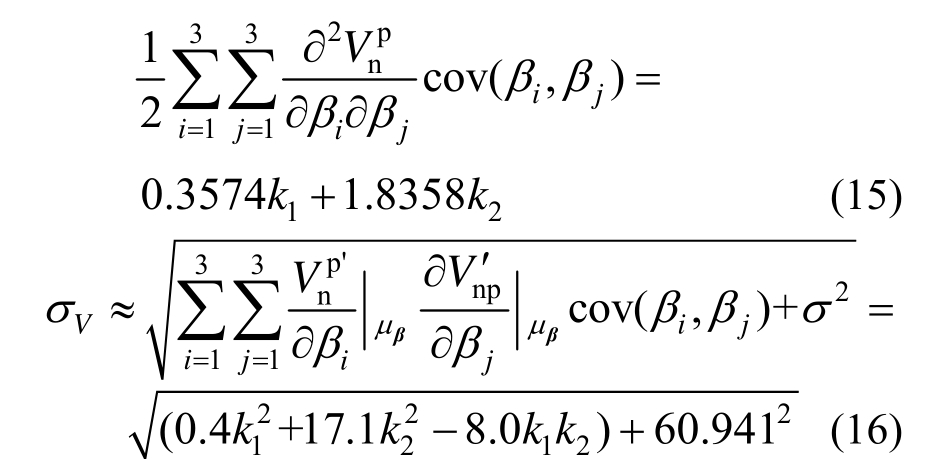
式中，
为概率模型参数
为βi和βj之间的协方差，其中ρij为βi和βj之间的相关系数，σβi和σβj分别为βi和βj的标准差；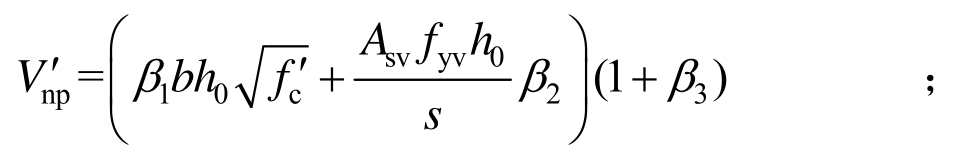
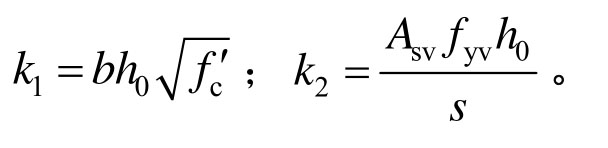
基于表1中的58组试验数据，可以验证由式(15)所描述的概率抗剪承载力均值模型的计算精度，如图5所示。由图5可知，式(15)的计算值与实测值的散点大多落在±30%线范围内，且均匀地分布在等值线附近，说明式(15)具有良好的计算精度。
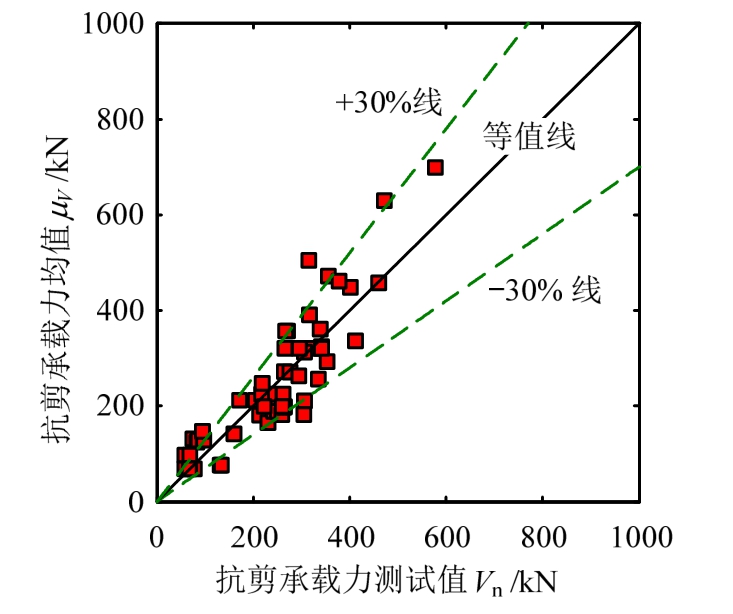
图5 均值模型计算值与试验测试值的对比分析
Fig.5 Comparison between tested and calculated shear strengths
3.2 抗剪承载力的置信区间
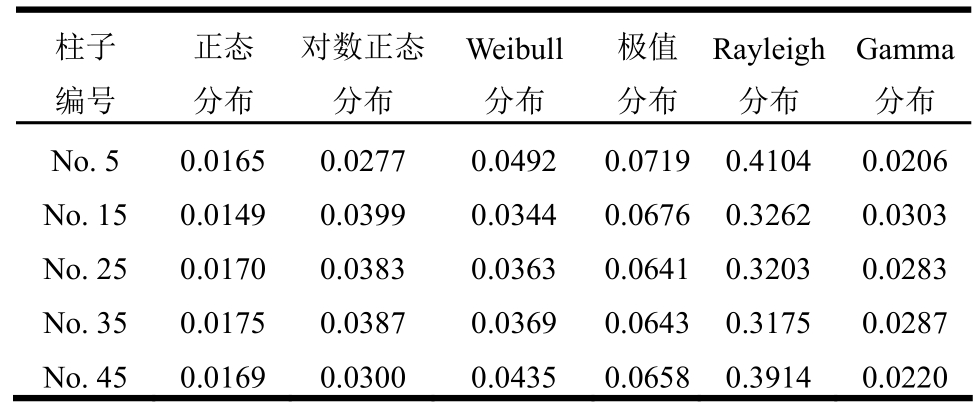
结合式(10)所描述的RC柱概率抗剪承载力模型和概率模型参数β的后验分布信息，采用蒙特卡洛法(MCS)可以产生大量RC柱抗剪承载力的随机样本，进而对随机样本进行K-S检验，从表1中任意选取5条RC柱(以第5、15、25、35和45条柱为例)，K-S检验结果见表8。当显著性水平取0.05、样本容量为1000时，K-S检验临界值为0.0430。由表8可知，RC柱的抗剪承载力不拒绝服从正态分布、对数正态分布和伽马分布。考虑到RC柱的抗剪承载力为非负值，且对数正态分布比伽马分布更加方便使用，所以本文选取对数正态分布作为RC柱抗剪承载力的经验概率分布类型。
表8 RC柱抗剪承载力的K-S统计量
Table 8 Statistics of K-S tests of shear strength for RC columns
柱子编号正态分布对数正态分布Weibull分布极值分布Rayleigh分布Gamma分布No.5 0.0165 0.0277 0.0492 0.0719 0.4104 0.0206 No.150.0149 0.0399 0.0344 0.0676 0.3262 0.0303 No.250.0170 0.0383 0.0363 0.0641 0.3203 0.0283 No.350.0175 0.0387 0.0369 0.0643 0.3175 0.0287 No.450.0169 0.0300 0.0435 0.0658 0.3914 0.0220
结合式(15)和式(16)所确定的均值和标准差，进而可以确定RC柱概率抗剪承载力的概率密度函数fV (Vnp )和累积分布函数FV(Vnp )：
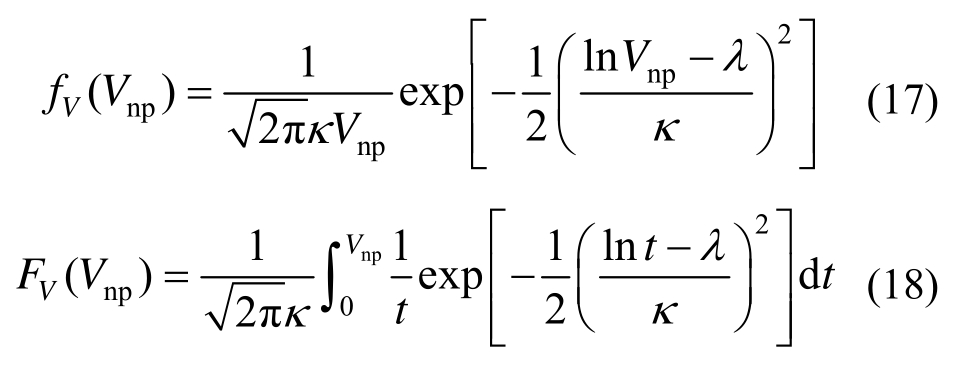
式中：λ和κ为对数正态分布函数的分布参数，与Vnp的均值μV和标准差σV之间的关系为：
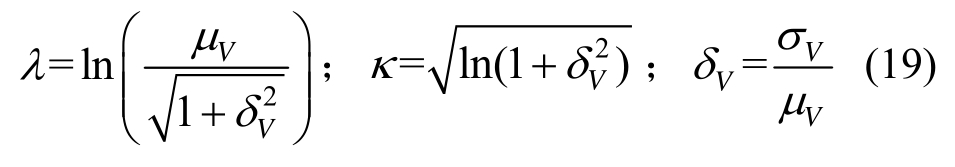
基于式(18)，可以计算给定置信水平1-α时RC柱概率抗剪承载力的双侧置信区间
其中，置信上限
和置信下限
分别为：
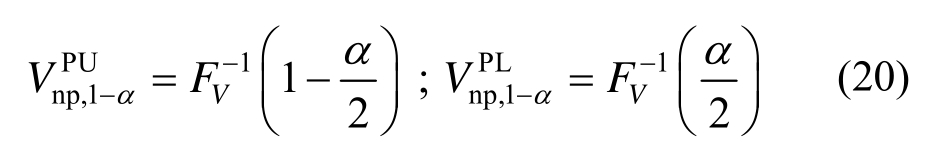
选取置信水平1-α分别为0.50和0.95，可以分别计算RC柱概率抗剪承载力的50%和95%双侧置信区间。表1中的58组试验数据在50%和95%双侧置信区间的分布情况如图6所示。由图6可知，约1/2的试验数据落在50%置信区间内，几乎全部试验数据落在95%置信区间内，说明所建立的RC柱概率抗剪承载力模型可以较好地描述RC柱抗剪承载力的概率分布特性。
基于上述RC柱概率抗剪承载力的置信区间，可以对现有国内外设计规范[13, 17-21]中RC柱确定性抗剪承载力模型的计算精度进行校准分析，如图7的均值所示。由图7可知，CSA A23.3―04模型[13]、FEMA 273模型[17]、ACI 318模型[18]和SL 191―2008模型[19]的计算值大部分位于95%置信下限和50%置信下限之间，表明上述模型普遍低估RC柱抗剪承载力；CEN―2005模型[20]的计算值约1/2数据落在50%置信区间内，其余大部分的数据落入95%置信下限和50%置信下限之间，说明该模型略微低估RC柱抗剪承载力；GB 50010―2010模型[21]的计算值几乎全部落在了95%置信区间内，且绝大部分落在了50%置信区间内，表明该模型预测精度相对较好。
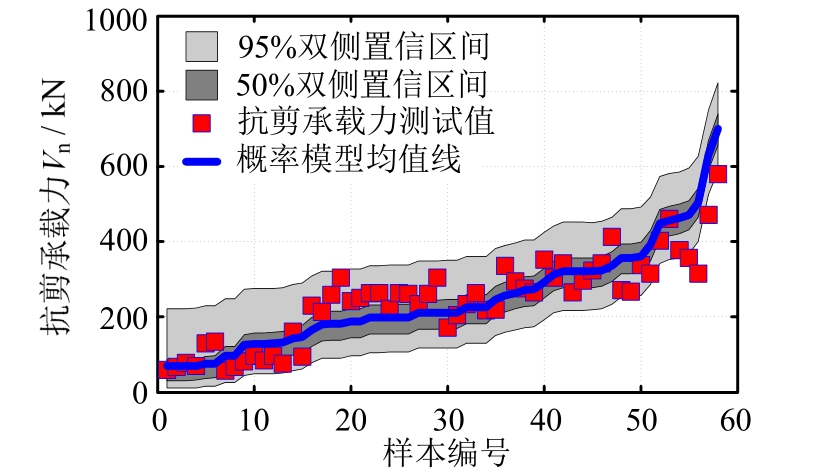
图6 试验测试值在50%和95%双侧置信区间的分布情况
Fig.6 Distribution of test values in the two-sided confidence intervals of 50% and 95%
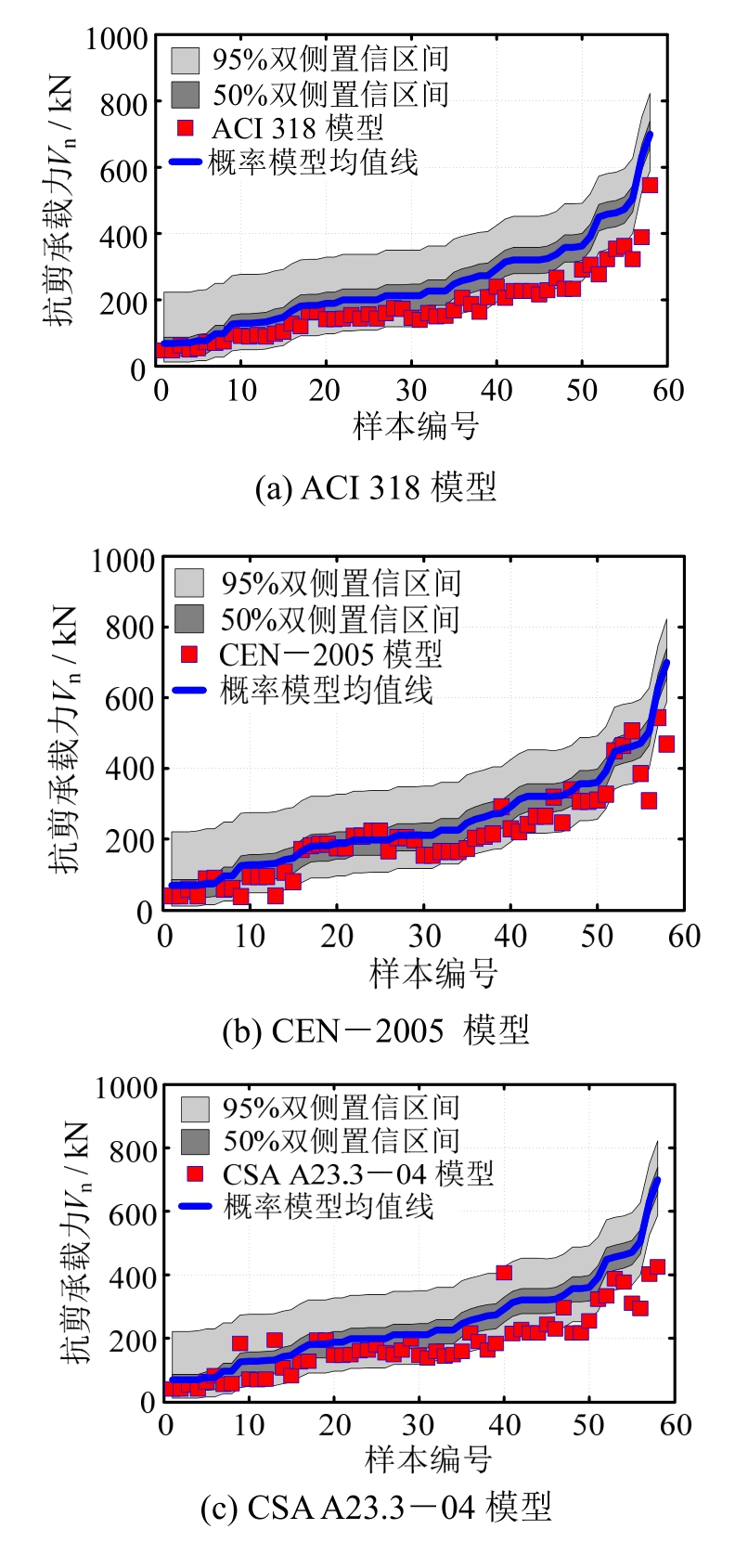
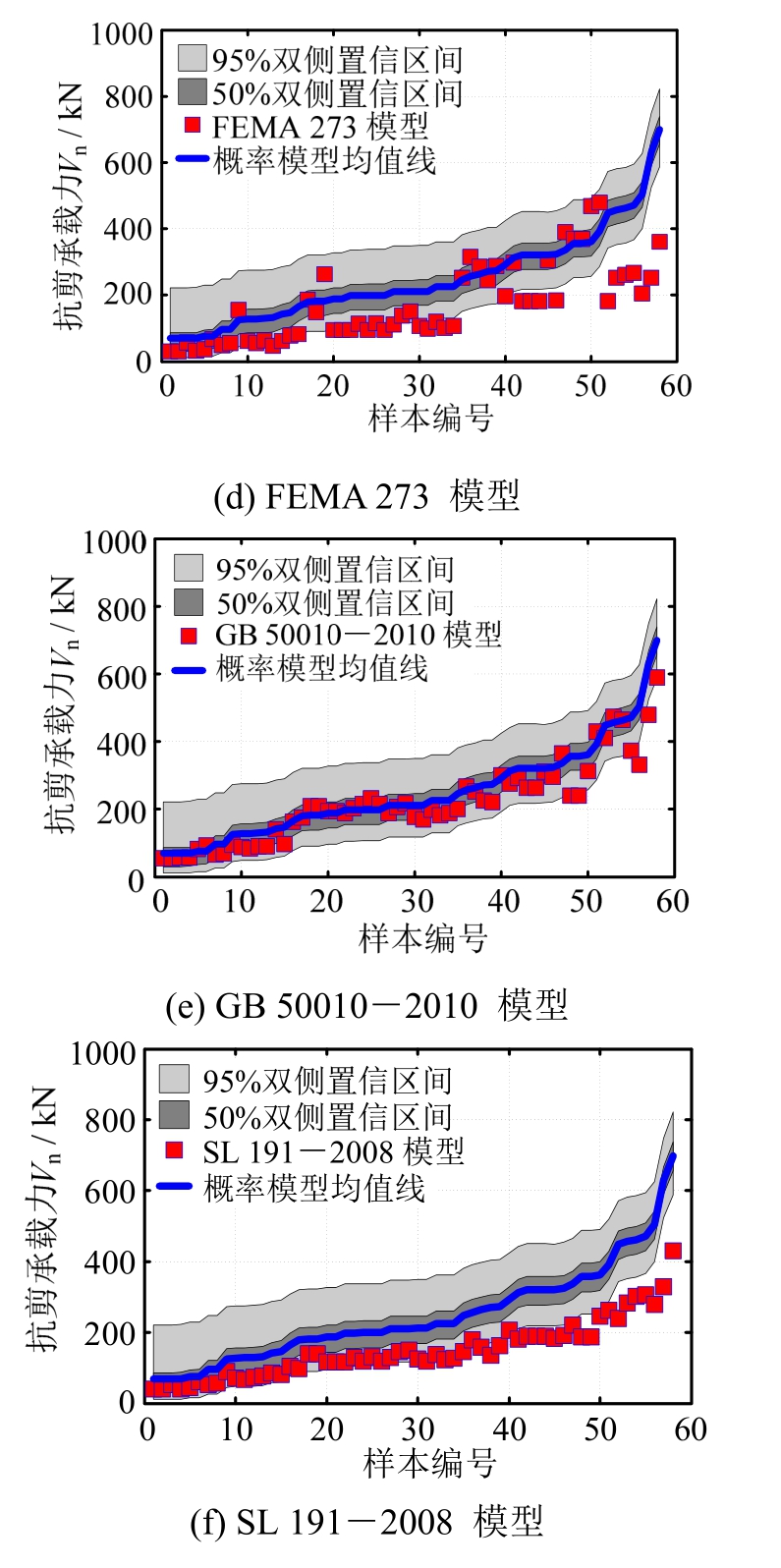
图7 基于95%和50%置信区间校准分析确定性抗剪承载力模型的计算精度
Fig.7 Calibration of accuracy of deterministic shear strength models based on confidence intervals of 95% and 50%
4 结论
(1) 基于桁架-拱模型，结合贝叶斯公式(Bayes rules)和马尔科夫链蒙特卡洛(MCMC)法，建立了一种能够综合考虑力学机制和不确定性影响的RC柱概率抗剪承载力模型。该概率模型不仅具有清晰的力学机制和较为严密的理论基础，而且随着试验数据的增加可以不断更新其后验分布。
(2) 为了保证概率模型参数后验分布的稳定性和收敛性，概率模型参数先验分布的变异系数不宜过小(建议不小于0.60)，且参与更新的数据量也不能太少。
(3) 基于RC柱的概率抗剪承载力模型所确定的抗剪承载力置信区间，不仅可以合理描述RC柱抗剪承载力的概率分布特性，而且可以校准分析传统确定性抗剪承载力模型的计算精度。
[1]张勤, 王娜, 贡金鑫.钢筋混凝土柱地震破坏模式及考虑剪切变形的抗震性能研究进展[J].建筑结构学报,2017, 38(8): 1-13.Zhang Qin, Wang Na, Gong Jinxing.State of the art of seismic performance including shear effects and failure modes of reinforced concrete columns [J].Journal of Building Structures, 2017, 38(8): 1-13.(in Chinese)
[2]余波, 陈冰, 吴然立.剪切型钢筋混凝土柱抗剪承载力计算的概率模型[J].工程力学, 2017, 34(7): 136-145.Yu Bo, Chen Bing, Wu Ranli.Probabilistic model for shear strength of shear-critical reinforced concrete columns [J].Engineering Mechanics, 2017, 34(7): 136-145.(in Chinese)
[3]邓明科, 张阳玺, 胡红波.高延性混凝土加固钢筋混凝土柱抗剪承载力计算[J].工程力学, 2018, 35(3): 159-166.Deng Mingke, Zhang Yangxi, Hu Hongbo.Experimental study and calculation of the shear capacity of RC columns strengthened with high ductile concrete [J].Engineering Mechanics, 2018, 35(3): 159-166.(in Chinese)
[4]Armen D K, Ditlevsen O.Aleatory or epistemic? Does it matter? [J].Structural Safety, 2009, 31(2): 105-112.
[5]Murphy C, Gardoni P, Harris C E.Classification and moral evaluation of uncertainties in engineering modeling [J].Science and Engineering Ethics, 2011,17(3): 553-570.
[6]余波, 陈冰.锈蚀钢筋混凝土梁抗剪承载力计算的概率模型[J].工程力学, 2018, 35(11): 115-124.Yu Bo, Chen Bing.Probabilistic model for shear strength of corroded reinforced concrete beams [J].Engineering Mechanics, 2018, 35(11): 115-124.(in Chinese)
[7]余波, 陶伯雄, 刘圣宾.一种箍筋约束混凝土峰值应力的概率模型[J].工程力学, 2018, 35(9): 135-144.Yu Bo, Tao Boxiong, Liu Shengbin.A probabilistic model for peak stress of concrete confined by ties [J].Engineering Mechanics, 2018, 35(9): 135-144.(in Chinese)
[8]Chen J B, Wan Z Q.A compatible probabilistic framework for quantification of simultaneous aleatory and epistemic uncertainty of basic parameters of structures by synthesizing the change of measure and change of random variables [J].Structural Safety, 2019,78: 76-87.
[9]Yu B, Tang R K, Li B.Probabilistic calibration for development length models of reinforcing bar [J].Engineering Structures, 2019, 182: 279-289.
[10]Yu B, Liu S B, Li B.Probabilistic calibration for shear strength models of reinforced concrete columns [J].Journal of Structural Engineering, 2019, 145(5):04019026-1-04019026-14.
[11]Ritter W.Die bauweise hennebique [J].Chweizerische Bauzeitung, 1899, 33(7): 59-61.
[12]Vecchio F J, Collins M P.The modified compressionfield theory for reinforced concrete elements subjected to shear [J].ACI Structural Journal, 1986, 83(2): 219-231.
[13]CSA A23.3-04, Design of concrete structures [S].Mississauga, Ontario, Canada: Canadian, Canadian Standards Association, 2004.
[14]魏巍巍, 贡金鑫.钢筋混凝土构件基于修正压力场理论的受剪承载力计算[J].工程力学, 2011, 28(2): 111-117.Wei Weiwei, Gong Jinxin.Shear strength of reinforced concrete members based on modified compression field theory [J].Engineering Mechanics, 2011, 28(2): 111-117.(in Chinese)
[15]Biskinis D E, Roupakias G K, Fardis M N.Degradation of shear strength of reinforced concrete members with inelastic cyclic displacements [J].ACI Structural Journal,2004, 101(6): 773-783.
[16]Pan Z, Li B.Truss-arch model for shear strength of shear-critical reinforced concrete columns [J].Journal of Structural Engineering, 2013, 139(4): 548-560.
[17]FEMA273, NEHRP guidelines for the seismic rehabilitation of buildings [S].Washington, D C: Federal Emergency Management Agency, 1997.
[18]ACI 318-11, Building code requirements for structural concrete and commentary [S].Farmington Hills:American Concrete Institute, 2011.
[19]SL 191―2008, 水工混凝土结构设计规范[S].北京:中国水利水电出版社, 2008.SL 191―2008, Design code for hydraulic structures [S].Beijing: China Water & Power Press, 2008.(in Chinese)
[20]EN-1998-3, CEN.Design of structures for earthquake resistance - Part 3: Assessment and retrofitting of buildings [S].Eurocode 8.Brussell: European Committee for Standardization, 2005.
[21]GB 50010―2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2015.GB 50010―2010, Code for design of concrete structures[S].Beijing: China Architecture & Building Press, 2015.(in Chinese)
[22]吴涛, 刘喜, 邢国华.基于贝叶斯理论的钢筋混凝土柱受剪承载力计算[J].工程力学, 2013, 30(5): 195-201, 206.Wu Tao, Liu Xi, Xing Guohua.Study on the shear capacity of reinforced concrete column based on Bayesian theory [J].Engineering Mechanics, 2013,30(5): 195-201, 206.(in Chinese)
[23]魏巍巍.基于修正压力场理论的钢筋混凝土结构受剪承载力及变形研究[D].大连: 大连理工大学, 2011.Wei Weiwei.Study on shear capacity and deformation for reinforced concrete structure based on modified compression field theory [D].Dalian: Dalian University of Technology, 2011.(in Chinese)
[24]余波, 吴然立, 陈冰.剪切型钢筋混凝土柱临界斜裂缝倾角的概率模型[J].计算力学学报, 2017, 34(5):547-554.Yu Bo, Wu Ranli, Chen Bing.Probabilistic model for critical diagonal crack angle of shear-critical reinforced concrete columns [J].Chinese Journal of Computational Mechanics, 2017, 34(5): 547-554.(in Chinese)
[25]Umehara H, Jirsa J O.Shear strength and deterioration of short reinforced concrete columns under cyclic deformations [R].Washington, D C: National Science Foundation, 1982.
[26]Bett B J, Klingner R E, Jirsa J O.Behavior of strengthened and repaired reinforced concrete columns under cyclic deformations [R].Washington, D C:National Science Foundation, 1985.
[27]Yalçin.Seismic evaluation and retrofit of existing reinforced concrete bridge columns [D].Canada:University of Ottawa, 1998.
[28]Xiao Y, Martirossyan A.Seismic performance of high-strength concrete columns [J].Journal of Structural Engineering, 1998, 124(3): 241-251.
[29]Lynn A C.Seismic evaluation of existing reinforced concrete building columns [D].Berkeley: University of California, 2001.
[30]Nakamura T, Yoshimura M.Gravity load collapse of reinforced concrete columns with brittle failure modes[J].Journal of Asian Architecture and Building Engineering, 2002, 1(1): 21-27.
[31]Lam S S E, Wang Z Y, Liu Z Q, et al.Drift capacity of rectangular reinforced concrete columns with low lateral confinement and high-axial load [J].Journal of Structural Engineering.2003, 129(6): 733-742.
[32]Yoshimura M, Takaine Y, Nakamura T.Axial collapse of reinforced concrete columns [C]// 13th World Conference on Earthquake Engineering, Vancouver, B C, Canada,2004: 1-11.
[33]Ousalem H, Kabeyasawa T, Tasai A.Evaluation of ultimate deformation capacity at axial load collapse of reinforced concrete columns [C]// 13th World Conference on Earthquake Engineering, Vancouver, B C,Canada, 2004: 1-11.
[34]Tran C T N.Experimental and analytical studies on the Seismic behavior of reinforced concrete columns with light transverse reinforcement [D].Singapore: Nangyang Technological University, 2010.
[35]Wibowo A, Wilson J L, Lam N T K, et al.Drift capacity of lightly reinforced concrete columns [J].Australian Journal of Structural Engineering, 2011, 15(2): 131-150.
[36]Pham T P, Li B.Seismic performance of reinforced concrete columns with plain longitudinal reinforcing bars[J].ACI Structural Journal, 2014, 111(3): 561-572.
[37]Li Y A, Huang Y T, Hwang S J.Seismic response of reinforced concrete short columns failed in shear [J].ACI Structural Journal, 2014, 111(4): 945-954.
[38]Gardoni P, Der Kiureghian A, Mosalam K M.Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations [J].Journal of Engineering Mechanics,2002, 128(10): 1024-1038.
[39]Haario H, Laine M, Mira A, et al.DRAM: Efficient adaptive MCMC [J].Statistics & Computing, 2006,16(4):339-354.
[40]刘纲, 罗钧, 秦阳, 等.基于改进MCMC方法的有限元模型修正研究[J].工程力学, 2016, 33(6): 138-145.Liu Gang, Luo Jun, Qin Yang, et al.A finite element model updating method based on improved MCMC method [J].Engineering Mechanics, 2016, 33(6): 138-145.(in Chinese)
[41]Melchers R E.Structural reliability analysis and prediction [M].Chichester: John Wiley and Sons, 2002.