预应力混凝土空心板梁桥受力明确、构造简单、施工方便,是中小跨径桥梁中应用最广的桥型之一[1],但由于早期空心板小铰缝等相对薄弱的横向构造,导致空心板梁桥在修建或运营过程发生很多病害。相关研究者[2]在对全国13个省市的1200座混凝土桥梁进行重点调查时发现,空心板梁桥病害主要是板底纵向裂缝和铰缝破坏[3-6],造成铰缝破坏的原因主要有车辆荷载作用下铰缝受力状态与空心板不一致、铰缝协同工作性能差、铰缝连接方式不当等[7-9]。另外,一些学者还对空心板梁桥的疲劳破坏等病害进行了研究[10],提出空心板试验梁三阶段疲劳损伤破坏特征。相关研究者在对江西昌樟高速公路的药湖大桥的监测中,发现约有20块板在跨中附近出现横向裂缝,605块板端头出现纵向裂缝;在浙江、广西的多座空心板梁桥也均发现了不同程度的纵向裂缝和横向裂缝病害[11]。上述空心板病害分析大多停留在强度分析阶段,而对其开裂机理缺少深入研究。
在混凝土梁桥开裂行为模拟方面,冷艳玲等[12]采用ABAQUS分析了装配式空心板梁桥铰缝开裂对跨中截面荷载横向分布的影响。聂建国等[13-14]对ABAQUS中的塑性损伤模型、弥散开裂模型和混凝土本构模型中影响结构静力行为的关键因素进行了研究,表明采用ABAQUS塑性损伤模型可以较好模拟混凝土结构开裂,并通过现场试验数据验证了结果的正确性。此外,ABAQUS在模拟结构承载力和抗冲击性等方面也具有广泛应用[15-16]。而引起混凝土梁开裂的应力集中相关研究中,目前大多集中在U型切槽或腹部开孔混凝土梁的力学性能方面[17-18]。而由于空心板和护栏固结后的不合理分缝引起尖端另外一侧应力集中的相关研究未见报道。
2016年5 月,浙江省台缙高速公路东延段杨司高架桥出现43片空心板梁开裂事故。与传统抗弯抗剪受力裂缝及粘结裂缝不同,上述43片梁绝大部分都出现的是横向非贯穿的L型裂缝,且裂缝均位于边板上,与混凝土护栏分缝位置一一对应,该现象暗示护栏分缝与空心板开裂存在密切联系。鉴于此,本研究首先对空心板开裂现场进行了调研取证,然后采用ABAQUS建立综合考虑钢筋和预应力的弹性模型和塑性损伤有限元模型,通过现场调研和数值分析相互验证[19-20],系统研究空心板边板中L型裂缝的开裂原因。
1 案例桥事故信息
1.1 设计资料
杨司高架位于台州临海杜桥,起止桩号K18+576.48~K22+102.52,全长3526 m,分为左右两幅,单幅每跨10片预应力混凝土空心板连续梁,以20 m跨径为主。下部结构采用桩柱式桥墩台,钻孔灌注桩基础。全桥按双向四车道标准建设,设计时速100 km/h。桥梁的平面图、立面图和典型断面图如图1所示。

图1 桥梁平面图、立面图和典型断面图 /cm
Fig.1 Elevation, plan and views and typical section
边板尺寸及预应力筋布置如图2所示,混凝土强度等级为C50,采用抗拉强度标准值fpk=1860 MPa的高强度低松弛的钢绞线,控制张拉应力σcon为1395 MPa,有效预应力σpe为1116 MPa。根据规范[21]及设计图纸信息得出,扣除全部预应力损失后的预加力在构件抗裂验算边缘产生的混凝土预压应力σpc为10.48 MPa。综合考虑预压应力和正常使用期间荷载产生的拉应力,仅将混凝土护栏作为均布荷载加在空心板上时,采用桥梁结构设计软件,空心板全截面受压,最小压应力为1.268 MPa。
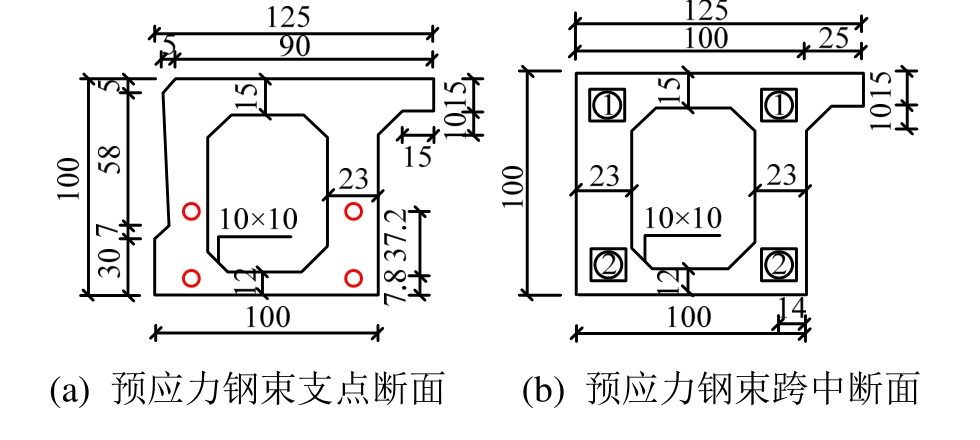
图2 预应力混凝土空心板边板截面尺寸 /cm
Fig.2 Cross section of a prestressed concrete side hollow slab
防撞护栏和混凝土空心板边板现浇成整体,护栏跨中分缝深度和护栏高度一致,为1.2 m,宽度为0.02 m。护栏与边板连接如图3所示。
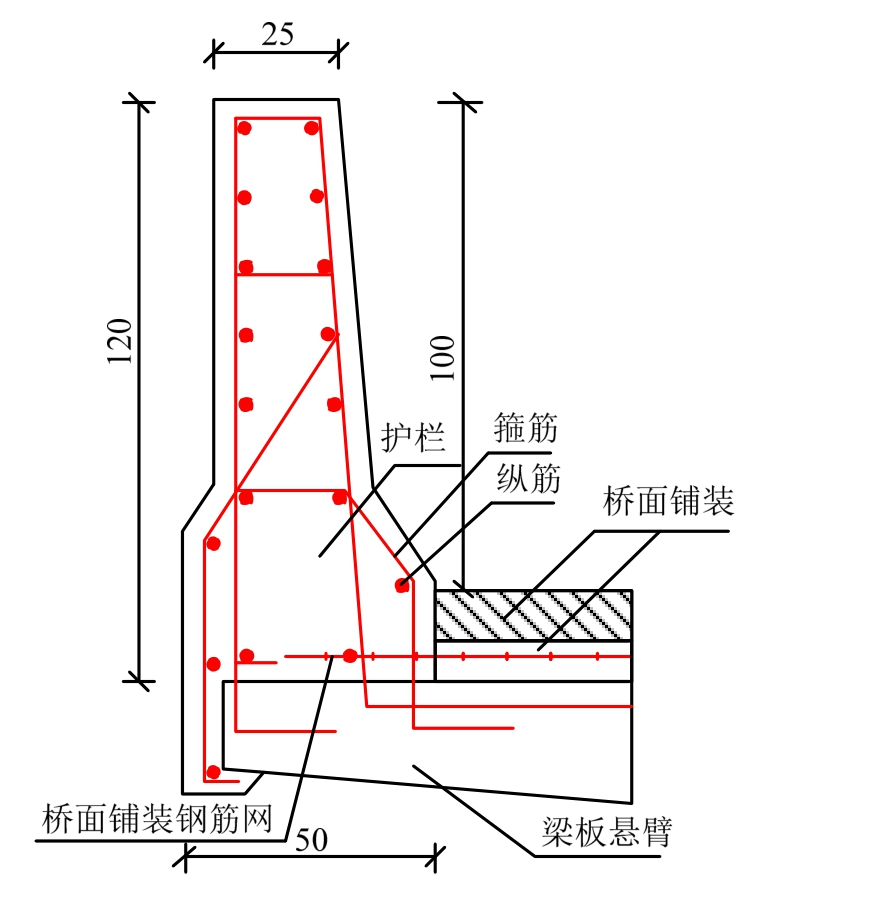
图3 护栏边板连接示意图 /cm
Fig.3 Connection between safety barrier and side hollow slab
1.2 事故现场调研
在2016年3月~6月进行的桥梁竣工检测中,发现杨司高架桥43片梁板出现结构裂缝,其中33片梁在护栏跨中分缝(图4(a))正下方腹板存在一条延伸至底板呈L型的裂缝(图4(b));5片梁腹板存在一条竖向裂缝但未在底板横向延伸(图4(c));2片梁底板存在一条横向裂缝且未延伸至腹板(图4(d));腹板存在两条竖向裂缝,一条延伸至底板并横向延伸另外一条仅延伸至底板的空心板共2片(图4(e));腹板存在三条竖向裂缝均未延伸至底板的空心板共1片(图4(f))。裂缝尺寸、数量信息如图5所示,L型裂缝如图6所示。


图4 现场空心板裂缝照片
Fig.4 Crack photos of hollow slab
与空心板传统裂缝相比,杨司高架空心板裂缝有以下显著特征:1) 仅在边板外侧腹板发生延伸到底板的L型裂缝,边板内侧几乎无裂缝;2) 大多事故梁有且仅有一条裂缝;3) 裂缝位置与防撞护栏分缝的位置一一对应。

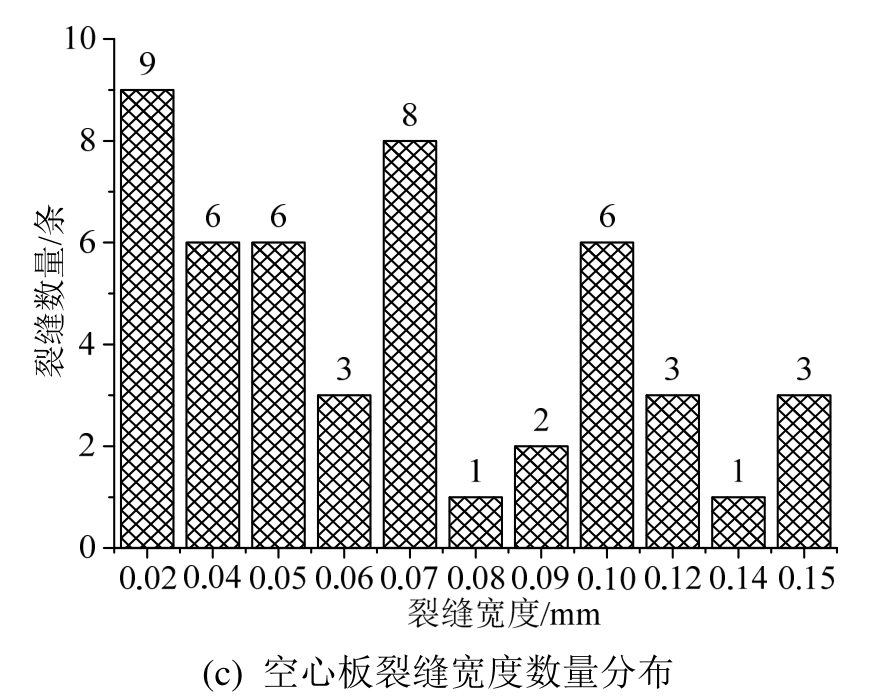
图5 边空心板裂缝数量分布
Fig.5 Distribution of side hollow slab crack quantity
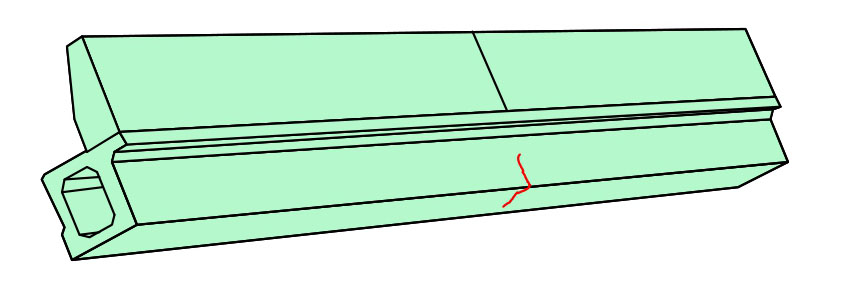
图6 L型裂缝示意图
Fig.6 Schematic diagram of L-type crack
上述开裂特征与施工和疲劳因素引起的裂缝不同。如果是疲劳或施工因素,在汽车荷载作用最大的空心板上更易发生裂缝,而实际工程中,裂缝发生在非机动车道汽车荷载相对较小的边梁,因此,推断不是疲劳或施工因素引起的开裂。目前,尚未发现国内外有关于符合上述特征的空心板裂缝的相关研究报道。
2 案例桥有限元分析
分别建立ABAQUS空心板全桥和单梁模型,研究分缝对边板应力分布影响,在验证护栏分缝会引起边板底部应力集中及单梁模型可以较好地表达上述应力集中的基础上,建立单梁塑性损伤模型和弹性模型,从模型分缝尺寸及分缝位置两方面,开展空心板开裂影响因素分析。
在分析分缝尺寸影响时,采用图7中a、b分别代表分缝深度和宽度,L代表边板长度。在分缝底部施加12.7 kN/m线荷载模拟混凝土护栏重力,保证不同分缝宽度情况下各工况有同样重力(图7(a));为确保分缝深度不同时截面有效高度一致(图7斜线部分),缝深和护栏的高度一致,采用调整护栏高度模拟分缝深度的影响,并通过在护栏上施加线性荷载补偿各工况间护栏高差引起自重荷载的区别,保证不同高度护栏有同样的重力(图7(b))。同时,在a=0 m、b=0 m(护栏无缝)时,护栏重力等效成线荷载施加在空心板上,确保截面有效高度一致(图7(c))。
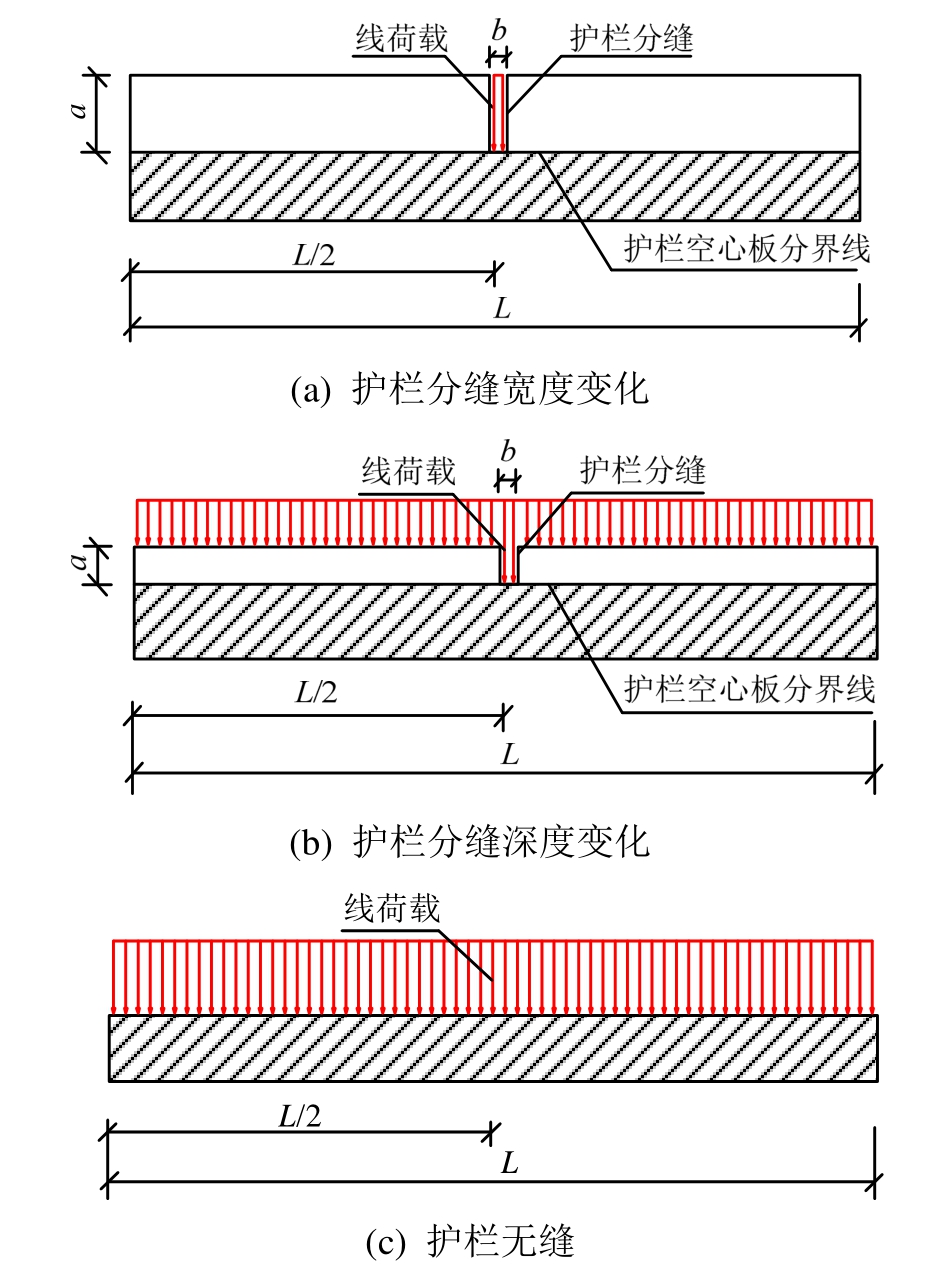
图7 空心板截面示意图
Fig.7 Cross section of hollow slab
模型工况如表1所示,模型中不同种类荷载分别在不同分析步中施加,模型边界条件为简支。模型中护栏跨中分缝,边板护栏之间绑定模拟两者固结;护栏不分缝,边板护栏之间不绑定,护栏等效成线荷载施加在边板上。
2.1 材料参数
有限元模型中主梁、铰缝及护栏均采用实体C3D8R单元,预应力筋及普通钢筋采用桁架T3D2单元。混凝土强度等级为C50,混凝土采用表2计算参数并参考混凝土规范[22]给出的应力-应变曲线方程,预应力筋和普通钢筋采用表3计算参数。
2.2 弹性模型
根据表1工况建立ABAQUS空心板全桥及单梁弹性模型,空心板构造尺寸见图1和图2。铰缝和桥面板之间采用接触模块中面面接触[23]来实现,550 kN标准车辆[24]布置在桥面应急车道内侧相邻车道且跨中弯矩最不利处。采用约束中的内置区域Embedded将预应力钢筋及普通钢筋嵌入混凝土中[25]。预应力筋的预应力通过降温法施加,本文预应力下的等效降温值为ΔT=-596.17 ℃。
表1 模型工况
Table 1 Conditions of model

注:1) 全桥与单梁弹性模型对比,比较二者应力集中效应异同;2) 参考实际设计习惯,根据最大应力与全桥模型等效原则,计算单梁模型的车道荷载分布系数,确定单梁模型的一级车道荷载;3) (0~1.2,+0.2)表示a从0逐步递增到1.2,单次增幅为0.2,(0.02,0.2~1.2,+0.2)表示b最小值为0.02,然后从0.02逐步递增到1.2,单次增幅为0.2。
编号 类型 钢筋和预应力 范围及分缝位置 分缝尺寸(a m×b m) 荷载1 弹性模型 不考虑全桥、跨中 0×0 自重和550 kN标准车辆荷载1.2×0.02考虑 单梁、跨中 1.2×0.02 2 塑性损伤模型1.2×0.02单梁、跨中 0×0不考虑 单梁、跨中 1.2×0.02考虑 单梁、跨中 (0~1.2,+0.2)×(0.02,0.2~1.2,+0.2)考虑 单梁、跨中1/4和3/4 1.2×0.02自重和考虑横向分布系数的公路一级车道荷载
表2 混凝土计算参数
Table 2 Calculation parameters of concrete

质量密度 弹性模量 抗压强度 抗拉强度 泊松比 线膨胀系数 单元类型2600 kg/m3 3.45×1010 Pa 3.24×107 Pa 2.65×106 Pa0.167 1×10-5 C3D8R
表3 预应力钢筋和空心板纵向钢筋的计算参数
Table 3 Calculation parameters of prestressed reinforcement and longitudinal reinforcement in hollow slabs

材料 直径 弹性模量 泊松比 膨胀系数 单元类型预应力筋 15.24 mm 1.95×1011 Pa 0.3 1.2×10-5 T3D2普通钢筋 12.8 mm 1.95×1011 Pa 0.3 1.2×10-5 T3D2
2.3 塑性损伤模型
ABAQUS提供的混凝土本构模型有弥散裂缝模型、塑性损伤模型。混凝土塑性损伤(CDP)模型因收敛性好,常被用于各类钢筋混凝土构件的受力分析[26]。本文混凝土模型选择混凝土损伤模型,根据表1工况建立单梁塑性损伤模型并与单梁弹性模型对比,本构关系按照混凝土参考混凝土规范[22]给出的应力-应变曲线方程选取。
3 数值计算结果
3.1 弹性模型分析
单梁弹性模型计算结果应力云图和全桥模型相似,因此,取全桥模型梁板底部、边板外应力云图如图8所示。
从图8(a)和图8(c)可以看出,护栏跨中有分缝时,边板跨中底板区域有明显应力集中(图中圆圈所示),图8(b)和图8(d)护栏等效成线荷载时,边板则没有应力集中。根据计算结果按如下三种方法取应力曲线:1) 取全桥模型在自重和车辆荷载共同作用下如图8(a)和图8(b)箭头所示方向梁板底部沿横向的应力分布,x代表所取单元位置,D代表空心板宽度总和,应力分布如图9所示;2) 取全桥、单梁模型在自重作用下如图8(c)和图8(d)箭头所示方向边板底部沿纵向的应力分布,x代表所取单元位置,L代表边板长度,应力分布如图10所示;3) 取全桥模型在仅有自重作用以及同时有自重和车辆荷载作用时如图8(c)和图8(d)箭头所示方向边板底部沿纵向的应力分布,应力分布如图11所示。应力分布中负值代表压应力,正值代表拉应力。
由图9可知:在自重和车辆荷载作用下,护栏跨中分缝,全桥模型护栏所在边板跨中底部区域应力与其他空心板相比突然增大,达到6.91 MPa,护栏等效成线荷载时应力和其他空心板接近,仅有2.19 MPa,护栏跨中分缝边板跨中底部最大应力较护栏等效成线荷载时增大4.72 MPa。
由图10可知:在自重作用下,护栏跨中分缝时,全桥模型和单梁模型边板底部沿纵向的应力均在x/L=0.4~0.6区域突然增大,跨中位置达到最大,全桥模型边板跨中底部最大应力为5.59 MPa,单梁模型为6.77 MPa;护栏等效为线荷载时,两种模型应力曲线比较平滑,全桥模型边板跨中底部最大应力为1.83 MPa,单梁模型为2.68 MPa。上述结果说明,无论是全桥模型还是单梁模型,护栏跨中分缝时二者边板底板存在应力集中,应力分布趋势一致。在护栏等效成线荷载时,单梁模型和全桥模型的跨中底部最大应力相差0.84 MPa,而分缝时,差值达到1.18 MPa,且全桥模型护栏分缝时边板跨中底部区域最大应力较无缝时增大3.76 MPa,单梁模型护栏分缝时增大4.09 MPa,说明对于单梁模型,横向分布效应会导致应力集中效应较全桥模型更明显。
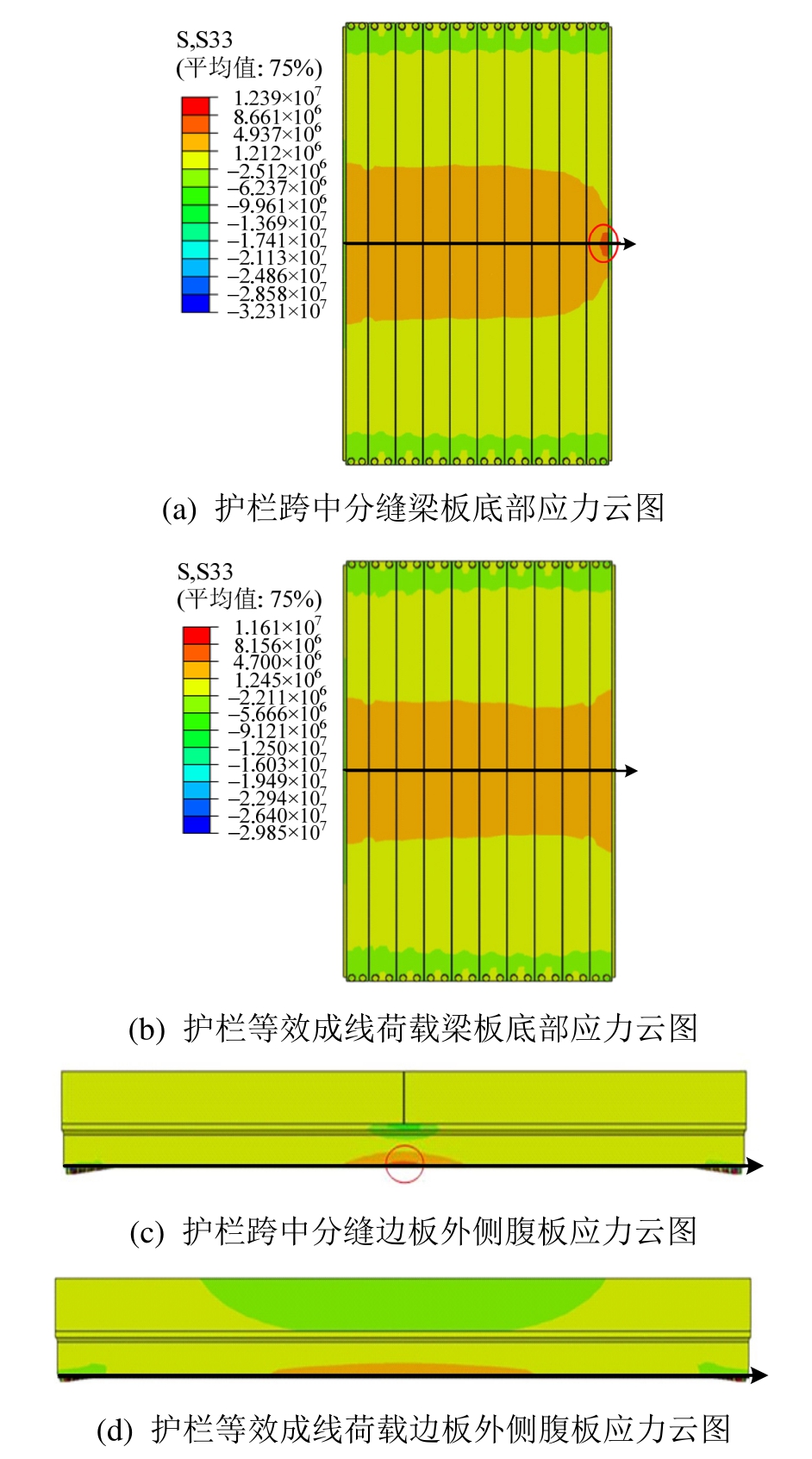
图8 空心板应力云图
Fig.8 The stress of hollow slab
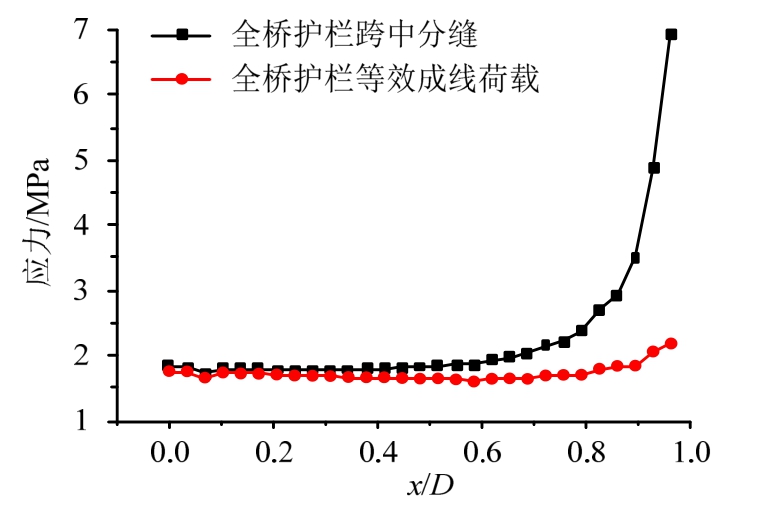
图9 全桥模型底板沿横向应力分布
Fig.9 Lateral stress distribution along the bottom plate
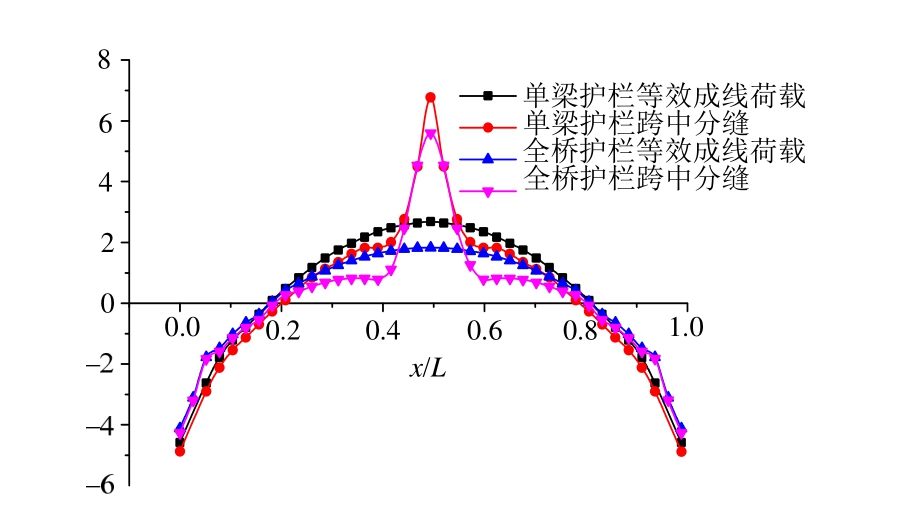
图10 全桥和单梁模型在自重作用下边板底部沿纵向应力分布对比
Fig.10 Comparison of vertical stress distribution along the bottom plate of the side beam in full bridge model and single beam model under the action of gravity
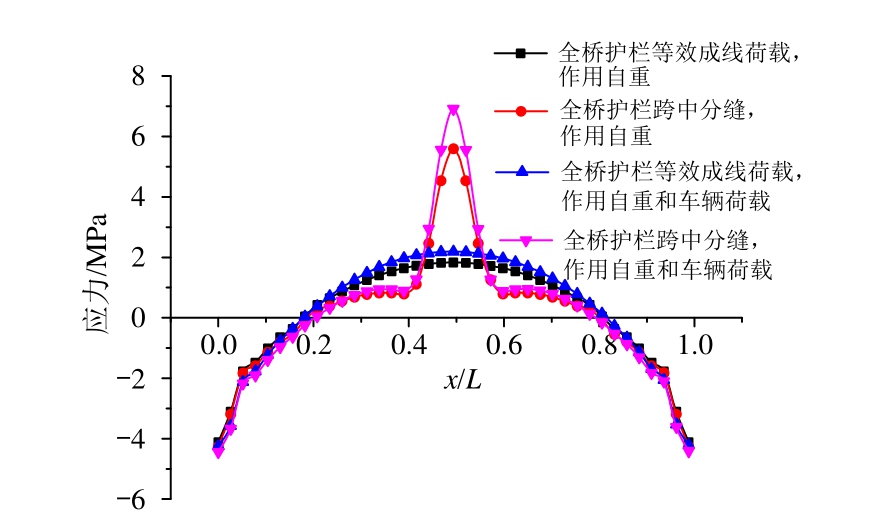
图11 全桥模型有无车辆荷载边板底部沿纵向应力分布对比
Fig.11 Comparison of vertical stress distribution along the bottom plate of the side beam in full bridge model with and without vehicle load
由图11可知:护栏跨中分缝时,有汽车荷载时边板跨中底部区域最大应力达到6.91 MPa,无汽车荷载作用时为5.59 MPa,两者相差1.32 MPa。护栏等效成线荷载时,有汽车荷载比纯自重作用应力增幅为0.36 MPa。说明综合考虑汽车荷载后,应力集中效应会加剧,其增长速度大于横向分布导致应力的增加速度。
上述研究表明,单梁模型的应力分布趋势与全桥模型一致,相对而言自重作用下的应力集中更加显著,因此,采用单梁模型是可以表达应力集中效应的。本文采用单梁模型分析应力集中影响因素分析。
3.2 影响因素分析
3.2.1 不同有限元模型结果对比
假定应力超过C50混凝土抗拉强度标准值2.65 MPa时,混凝土开裂。为找出混凝土中最大拉应力达到2.65 MPa时对应的临界开裂荷载,取根据表1所建单梁模型计算结果中跨中底部区域最大应力达到2.65 MPa时空心板底部沿纵向的应力分布,如图12所示。
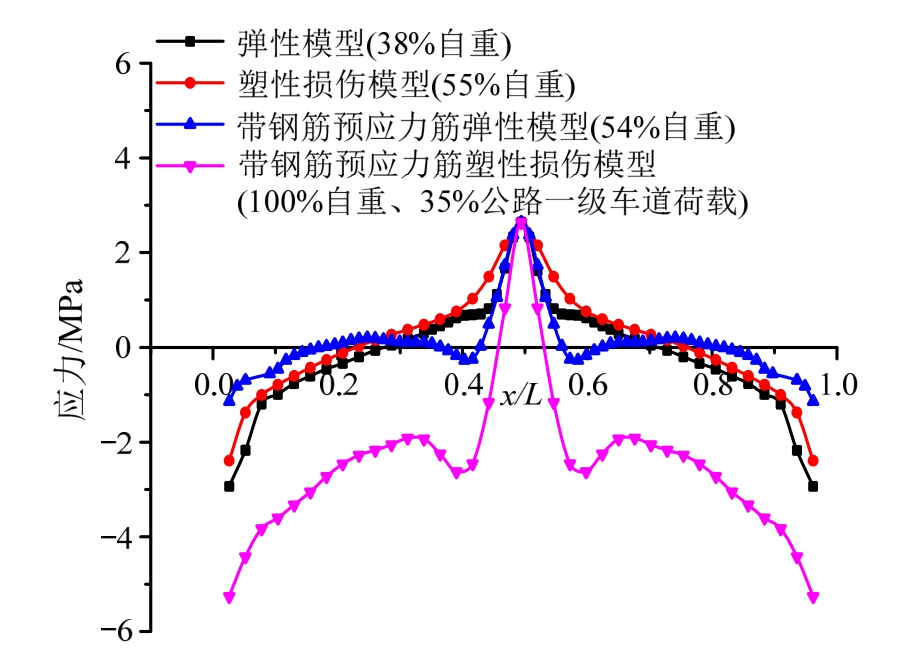
图12 不同材料边板底部沿纵向应力分布
Fig.12 Vertical stress distribution along the bottom of the side beam with different materials
混凝土护栏分缝后,四种模型均出现不同程度的应力集中。由图12可知:要使空心板底部最大应力达到2.65 MPa,弹性模型所需荷载最小,只需施加38%自重,塑性损伤模型需施加55%自重,带钢筋及预应力筋弹性模型需施加54%自重,塑性损伤模型需施加100%自重和35%公路一级车道荷载。说明相较于弹性模型,塑性损伤模型计算出的临界开裂荷载较大,考虑钢筋和预应力作用后,计算出的临界开裂荷载也较大。
3.2.2 分缝深度和宽度的影响
在图12中,带钢筋和预应力筋的塑性损伤模型跨中底板应力达到2.65 MPa时临界开裂荷载为100%自重和35%公路一级车道荷载,为方便对比,各工况均施加该临界开裂荷载。边板底部沿纵向应力分布如图13所示。
由图13可知:由于预应力的作用,护栏无缝的底板最大应力是压应力,为-1.07 MPa,护栏分缝时在x/L=0.4~0.6区域应力会先下降再上升,在跨中位置达到最大。由图13(a)可知:裂缝深度a=1.2 m保持不变,随着裂缝宽度b由0.02 m增大到1.2 m,应力从2.65 MPa减小到0.06 MPa。由图13(b)可知:裂缝宽度b=0.02 m保持不变,随着分缝深度a由0 m增大到1.2 m,应力从-1.07 MPa增大到2.65 MPa,说明分缝深度越大、宽度越小,应力集中效应就越明显。
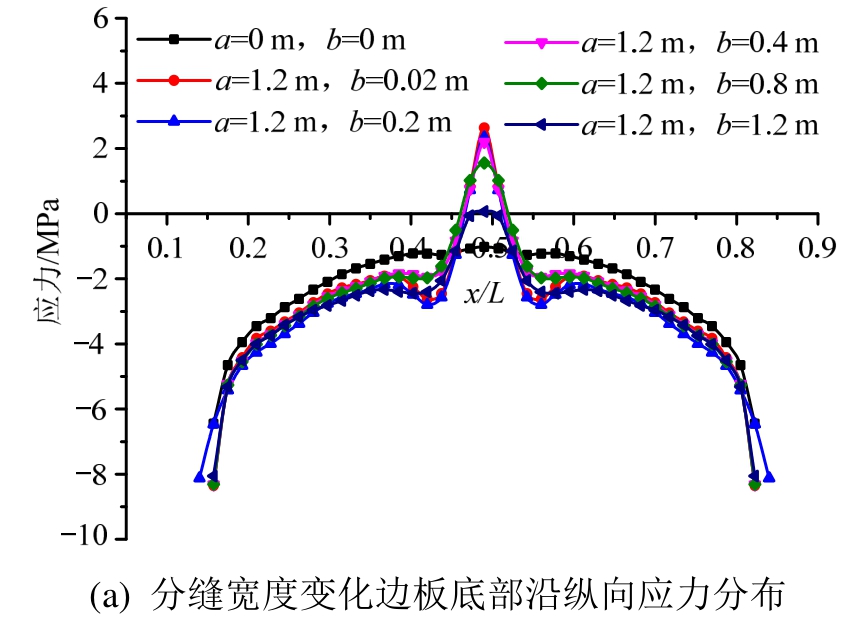
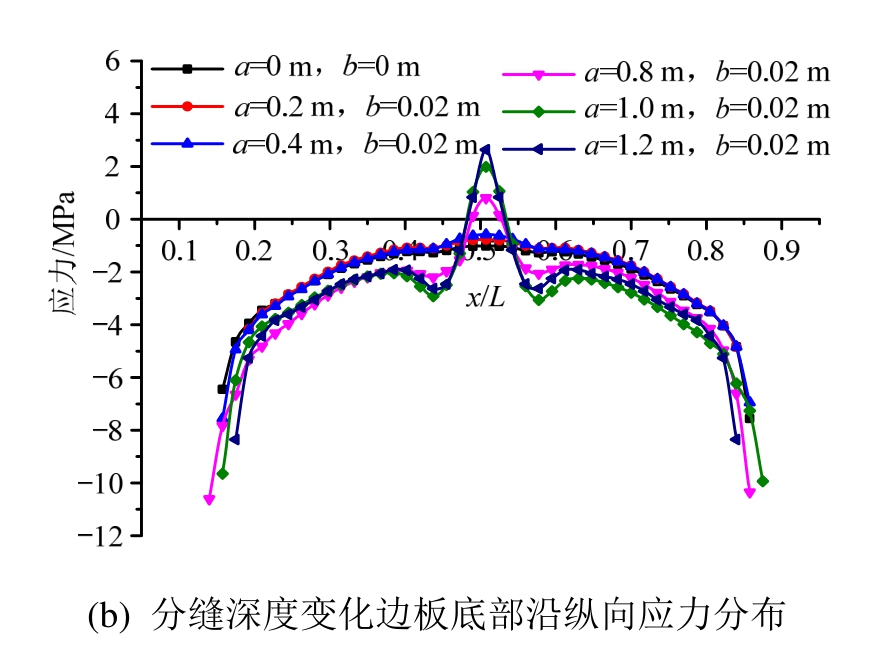
图13 分缝深度宽度变化边板底部沿纵向应力分布
Fig.13 Vertical stress distribution along the bottom of the side beam with the change of parting-line’s depth and width
3.2.3 分缝位置的影响
为方便对比分析,各工况均施加考虑钢筋和预应力筋的塑性损伤模型在a=1.2 m、b=0.02 m时跨中底板应力达到2.65 MPa的临界开裂荷载。边板底部沿纵向应力分布如图14所示。
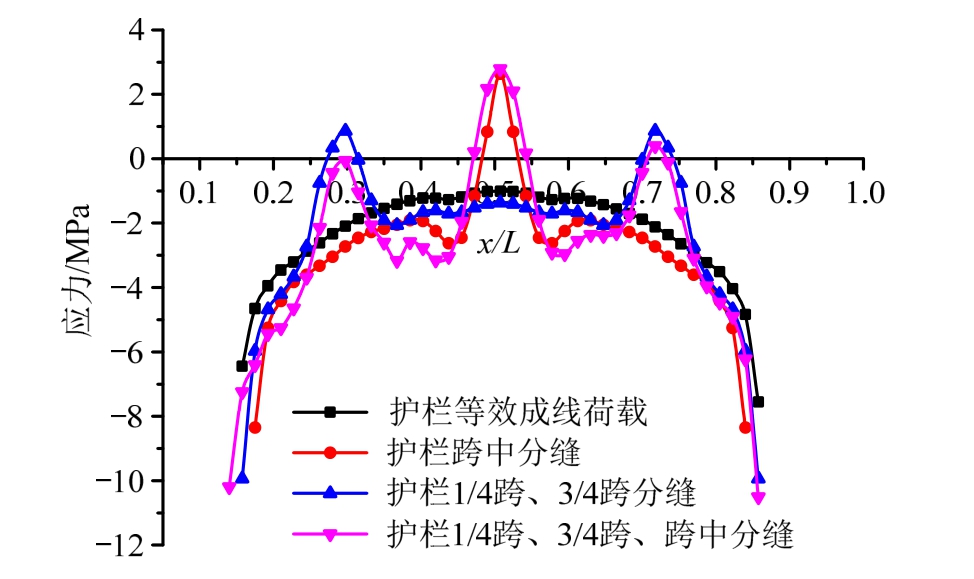
图14 分缝位置不同边板底部沿纵向应力分布
Fig.14 Vertical stress distribution along the bottom of the side beam with different parting-line’s positions
从图14可知:在跨中有分缝的同时在1/4跨和3/4跨分缝,不仅没有降低跨中混凝土应力集中效应,而且在1/4跨和3/4跨也出现了应力集中,但其峰值应力相对较小,为0.87 MPa,不会导致混凝土开裂。因此,为避免类似病害的发生,护栏跨中不能分缝,如果有分缝需要,可以在1/4跨、3/4跨分缝。
4 结论
通过对空心板现场进行调查取证,并与有限元数值分析结果二者相互验证,得出以下结论:
(1) 在边板护栏和空心板固结的情况下,由于混凝土护栏偏置在空心板上,不恰当的跨中混凝土护栏分缝将引起刚度突变,导致应力集中,诱发出现穿过传统中和轴的L型裂缝;
(2) 随着跨中空心板上护栏预留缝宽度增大,边板模型跨中底部应力逐渐减小;随着跨中空心板上护栏预留缝深度增加,边板模型跨中底部应力逐渐增大;
(3) 采用单梁弹性模型和塑性损伤模型均可以较好地模拟应力集中现象,模拟结果与现场实际裂缝出现位置一致,其中带钢筋和预应力钢筋的塑性损伤模型与现场较为接近。
(4) 空心板跨中位置承受弯矩最大,在以后护栏设计施工过程中要避免在此位置分缝,或采用开“假缝”等方式避免护栏分缝后出现刚度突变,降低应力集中的强度,从而避免应力集中后的空心板开裂。
[1]姚玲森.桥梁工程[M].第2版.北京: 人民交通出版社, 2003: 70.Yao Lingsen.Bridge engineering [M].2nd ed.Beijing:China Communications Press, 2003: 70.(in Chinese)
[2]交通运输部公路科学研究院.国省道干线公路混凝土梁式桥损伤调查与分析报告[R].北京: 交通运输部公路科学研究院, 2011.Beam bridges on national and provincial arterial road[R].Beijing: Research Institute of Highway of MOT,2011.(in Chinese)
[3]邵旭东, 周里鸣, 李立峰.薄壁空心板纵向裂缝的畸变分析与试验研究[J].公路, 2007(3): 59-64.Shao Xudong, Zhou Liming, Li Lifeng.Distortion analysis and experimental research on longitudinal cracks of thin-walled hollow slab [J].Highway, 2007(3):59-64.(in Chinese)
[4]谭晟.高等级公路桥梁空心板开裂原因分析研究[D].重庆: 重庆交通大学, 2008.Tan Sheng.Highway hollow plate analysis of the reasons for cracking [D].Chongqing: Chongqing Jiaotong University, 2008.(in Chinese)
[5]Clay Naito, Lawrence Jones, Lan Hodgson.Development of flexural strength rating procedures for adjacement prestressed concrete box girder bridges [J].Journal of Bridge Engineering, 2011, 16(5): 662-670.
[6]赵卫国, 薛文.先张法预应力混凝土空心板梁纵向裂缝分析[J].公路, 2006(10): 52-53.Zhao Weiguo, Xue Wen.Analysis on longitudinal cracks of prestressed concrete hollow plate beam [J].Highway,2006(10): 52-53.(in Chinese)
[7]王渠, 吴庆雄, 陈宝春.装配式空心板桥铰缝破坏模式试验研究[J].工程力学, 2014, 31(增刊1): 115-120.Wang Qu, WU Qingxiong, Chen Baochun.Experimental study on failure mode of hinged joint in assembly voided slab bridge [J].Engineering Mechanics, 2014, 31(Suppl 1):115-120.(in Chinese)
[8]Scott D Porter, Julander J Logan, Marvin W Halling, et al.Flexural testing of precast bridge deck panel connections [J].Journal of Bridge Engineering, 2011,16(3): 422-430.
[9]Scott D Porter, Julander J Logan, Marvin W Halling,et al.Shear testing of precast bridge deck panel transverse connections [J].Journal of Performance of Constructed Facilities, 2012, 26(4): 462-468.
[10]朱红兵, 余志武, 姜天华.钢筋混凝土空心板梁疲劳损伤试验研究[J].桥梁建设, 2013, 43(3): 42-47.Zhu Hongbing, Yu Zhiwu, Jiang Tianhua.Test study of fatigue damage of reinforced concrete hollow slab beams[J].Bridge Construction, 2013, 43(3): 42-47.(in Chinese)
[11]易汉斌, 李传习, 吴后选, 等.既有预应力宽幅空心板受力性能的破坏性试验[J].长安大学学报(自然科学版), 2018, 38(4): 64-70, 118.Yi Hanbin, Li Chuanxi, Wu Houxuan, et al.Destructive test on mechanical behavior of existing prestressed wide hollow slabs [J].Journal of Chang’an University (Natural Science Edition), 2018, 38(4): 64-70, 118.(in Chinese)
[12]冷艳玲, 张劲泉, 程寿山, 等.装配式混凝土空心板梁桥单板受力问题的数值解析[J].公路交通科技, 2013,30(5): 63-66, 73.Leng Yanling, Zhang Jinquan, Cheng Shoushan, et al.Numerical analysis on single plate loading effect of precast hollow plate girder bridge [J].Journal of Highway and Transportation Research and Development,2013, 30(5): 63-66, 73.(in Chinese)
[13]聂建国, 王宇航.ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J].工程力学, 2013,30(4): 59-67, 82.Nie Jianguo, Wang Yuhang.Comprison study of consititutive model of concrete in ABAQUS for static analysis of structures [J].Engineering Mechanics, 2013,30(4): 59-67, 82.(in Chinese)
[14]Vidya Sagar Ronanki, David I.Burkhalte, Sriram Aaleti,et al.Richardson.Experimental and analytical investigation of end zone cracking in BT-78 girders [J].Engineering Structures, 2017(151): 503-517.
[15]唐琼, 李易, 陆新征, 等.多螺箍筋柱轴压承载力研究[J].工程力学, 2018, 35(增刊1): 166-171.Tang Qiong, Li Yi, Lu Xinzheng, et al.Study on axial compression capacity of multi-spiral hoops confined concrete columns [J].Engineering Mechanics, 2018,35(Suppl 1): 166-171.(in Chinese)
[16]朱翔, 陆新征, 杜永峰, 等.新型复合柱抗冲击试验研究及有限元分析[J].工程力学, 2016, 33(8): 158-166,220.Zhu Xiang, Lu Xinzheng, Du Yongfeng, et al.Experimental study and finite element analysis of impact resistance of novel composite columns [J].Engineering Mechanics, 2016, 33(8): 158-166, 220.(in Chinese)
[17]王启智, 汪坤.U形切槽三点弯曲梁的应力集中系数[J].四川大学学报(工程科学版), 2007, 39(3): 1-6.Wang Qizhi, Wang Kun.Stress concentration factors for three point bending beam with single-edge U-shaped notch [J].Journal of Sichuan University(Engineering Science Edition), 2007, 39(3): 1-6.(in Chinese)
[18]黄泰赟, 蔡健.腹部开有矩形孔的钢筋混凝土简支梁在集中荷载下的试验研究[J].土木工程学报, 2009,42(10): 36-45.Huang Taiyun, Cai Jian.Experimental study on simply supported reinforced concrete beams with rectangular web openings [J].China Civil Engineering Journal, 2009,42(10): 36-45.(in Chinese)
[19]王兵见, 赵航, 彭卫兵, 等.独柱墩梁桥横向稳定计算理论与验证[J].中国公路学报, 2017, 30(9): 93-100.Wang Bingjian, Zhao Hang, Peng Weibing, et al.Lateral stability calculation theory and verification of single-column gider bridge [J].China Journal of Highway and Transport, 2017, 30(9): 93-100.(in Chinese)
[20]彭卫兵, 徐文涛, 陈光军, 等.独柱墩梁桥抗倾覆承载力计算方法[J].中国公路学报, 2015, 28(3): 66-72.Peng Weibing, Xu Wentao, Chen Guangjun, et al.Calculation method for anti-overturning capacity of single column pier gider bridge [J].China Journal of Highway and Transport, 2015, 28(3): 66-72.(in Chinese)
[21]JTG 3362―2018, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京: 人民交通出版社, 2018.JTG 3362―2018, Code for design of reinforced concrete and prestressed concrete bridges and culverts on highways [S].Beijing: China Communications Press,2018.(in Chinese)
[22]GB 50010―2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB 50010―2010, Code for design of concrete structures[S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[23]刘沛林.装配式钢筋混凝土简支板梁桥铰缝受力性能研究[D].北京: 清华大学, 2010.Liu Peilin.Study on behaviors of hinge joints for fabricated reinforced concrete simply-supported plate girder bridges [D].Beijing: Tsinghua University, 2010.(in Chinese)
[24]JTG D60―2015, 公路桥涵设计通用规范[S].北京:人民交通出版社, 2015.JTG D60―2015, General code for design of highway bridges and culverts [S].Beijing: China Communications Press, 2015.(in Chinese)
[25]Dassault Systèmes Simulia Corporation.Abaqus analysis user’s manual (6.12) [M].Providence (RI, USA):Dassault Systèmes, 2012.
[26]黄正, 吕志涛, 涂永明.基于扰动应力场模型的ABAQUS二次开发及其与塑性损伤模型的比较[J].土木工程学报, 2016, 49(5): 40-49.Huang Zheng, Lv Zhitao, Tu Yongming.Secondary development of ABAQUS based on disturbed stress field model (DSFM) and its comparison with damage plasticity model [J].China Civil Engineering Journal,2016, 49(5): 40-49.(in Chinese)