场地动力响应的估计是正确分析工程结构抗震性能的一个重要环节，也是岩土动力学中一个重要的研究问题。在实际分析中，通常假设地震波从远场波源垂直入射到广义结构，这种假定对于一般工程和距离波源较远时是合理的，但是对于隧道、地下管线等大型结构，斜入射引起的地面运动对结构的非一致效应是不可忽略的[1-4]。因此，在自由场地的动力响应分析中考虑斜入射问题是有必要的。
近年来，随着海洋工程的发展，水下地基场地地震动问题逐渐受到重视。由于海底地震动记录的缺乏，一些学者尝试用数值或解析方法分析水下地基场地地震动问题。朱镜清和李金成[5]利用频域波动法对海水-海床耦合系统进行了地震动分析，采用参数研究法，改变了水深、土层厚度及组成情况，认为在50 m水深范围内，海水可以作为不可压缩流体。席仁强等[6]基于任意拉格朗日-欧拉法，推导了时变区域上的流体运动方程，提出了能够分析地震作用下覆水场地流固耦合的计算方法。但将水下饱和土层假定为单相介质。Stoll和Kan[7]基于Biot饱和多孔介质理论[8]，推导了水层和饱和土层交界处振幅关系式，研究了渗透系数、入射角等因素对反射与透射系数的影响规律。Li等[9]将海水层的动力刚度矩阵引入地基场地总刚度矩阵中，对比研究了陆地与海底地震动差别，研究结果表明，海底地震动竖向分量在P波与海水层的共振频率范围内显著降低。Wang等[10-11]分别建立了P波和SV波作用下深水地基场地波动问题的解，考虑了饱和多孔介质的饱和度、渗透系数和入射角对动水压力的影响。张奎等[12]基于单相弹性介质、流体饱和多孔介质和理想流体弹性波动理论，推导了平面P波和SV波入射下，深水地基场地波动问题的解析解，重点分析了土层刚度、饱和度及入射角变化时水深对位移响应的影响规律。上述工作表明，海底地震动与陆地情况差异较大，且入射角度对海底地震动的影响不容忽视，有必要深入研究并建立合理方法以解决斜入射下水下结构地震动分析的输入问题。
近年来，地震波斜入射下陆地场地地震动输入方法的研究取得了很大进展，尤其是能够考虑土体非线性行为，且方便应用于大型软件分析的时域数值方法。李山有等[4]采用固定有限元网格，根据Snell定理[13]结合入射侧边界结点的内插公式和内结点位移的位移公式，实现了单相介质中体波斜入射的时步数值模拟。刘晶波和王艳[1]根据Snell定律建立了边界结点的内插公式，和内结点位移计算公式相结合，将二维运动方程转化为一维方程，并采用在竖直向任意网格尺寸和水平向由时步和水平视波速确定网格尺寸的有限元划分形式，从而将斜入射的二维问题转化为一维问题；刘晶波和王艳[14]又在计算区域的基底设置了粘性人工边界，将输入地震动转化为作用于人工边界上的等效荷载，结合集中质量有限元方法和中心差分法建立结点运动方程组，水平方向相邻结点的运动用该结点相邻时刻的运动表示，求解的二维结点运动方程组化为一维方程组，从而可以确定自由波场。赵密等[15-16]针对文献[14]的粘性边界在P-SV波以大角度入射时自由场的计算精度会降低的问题，提出了一种精确模拟半空间辐射阻尼的人工边界条件，提高了计算精度。李鹏和宋二祥[17]将一维化时域算法扩展到了三维自由场计算中，并实现了隧道纵向非一致地震反应的三维地震反应。卓卫东等[18-19]在一维化时域算法的基础上，利用Rayleigh阻尼考虑了阻尼对成层介质动力响应的影响。李伟华等[20]将单相介质的一维化算法推广到了饱和介质场地中，建立了地震波斜入射下成层饱和场地地震动输入的计算方法。由以上研究成果可知，现有研究成果多针对成层单相介质和饱和介质，对于水下地基场地地震动响应的研究成果还较少。赵成刚等[21]采用解耦的技术，建立了流体-饱和介质-单相弹性介质耦联的显式有限元法方程，该方法不需要组装总的刚度方程和求解联立方程组，极大地提高了计算效率，但只适用于垂直入射的情况。
综上所述，水下地基场地地震动研究亟待深入，相应的地震动输入方法仍不完善。本文旨在建立一种考虑平面波斜入射的水下地基场地地震动的时域有限元分析方法。该方法依据Snell定理，在已建立的饱和介质一维化时域算法[20]的基础上，首先建立水层的一维化有限元方程组，将斜入射下水层波动的空间二维问题转化为简单的一维问题，然后通过考虑水层与饱和多孔介质层间、不同饱和多孔介质交界面以及基岩与饱和多孔介质层间的边界条件，将已有的成层饱和土的一维化有限元方程与水层的一维化有限元方程组装，采用精确人工边界条件模拟基岩半空间的截断效应和输入特征，形成了水下地基场地地震动分析的整体一维化时域有限元方程，将中心差分法和Newmark法相结合建立了地震波斜入射下水下地基场地节点位移和加速度响应的数值解，通过与傅里叶变换得到的理论解和现有的文献进行了对比，验证了本文方法的计算精度和有效性。
1 水下地基场地分析模型
分析模型如图1所示，基岩上覆盖一定厚度的土层，其上有一定深度的水层。假定基岩为单相弹性介质，土层为水饱和的多孔介质，水层为理想可压缩流体。采用整体坐标系xOz。坐标原点O在水层表面。设水层深度为h1，饱和土层厚度为h2。水层编号为第0层；饱和土层共有N层，从上至下编号分别为第1层，第2层，…，第N层；基岩编号为第N+1层。r结点、tl(l=1, 2 ,…, N+1)结点和n结点分别代表水与饱和土、饱和土与饱和土以及饱和土与基岩的交界点。其中，饱和土层层厚为h21, h22, …, h2N。平面P或SV波分别以入射角θ或β从基岩入射。
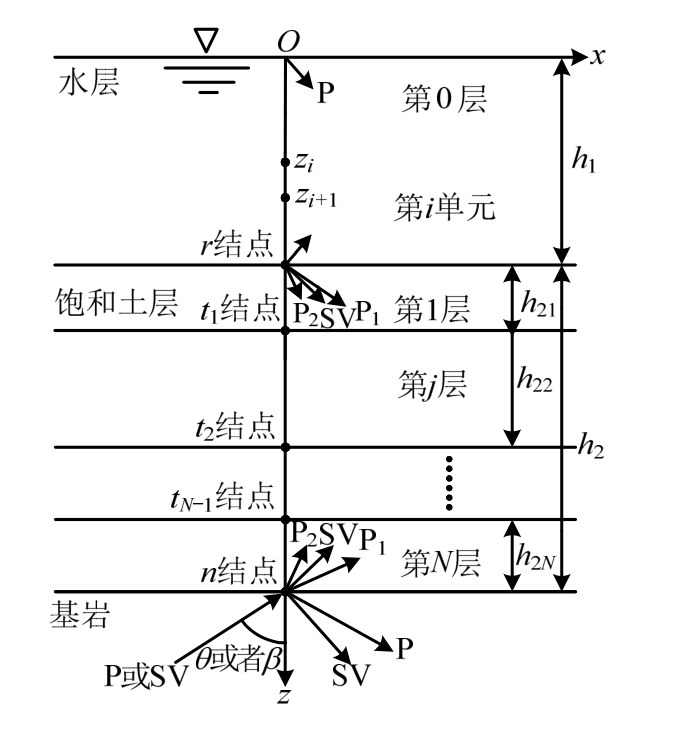
图1 水下地基场地模型
Fig.1 The model of underwater site
根据理想流体波动理论[13]，其波动方程表达式为(符号w代表水层)：
式中：上标..表示对时间t的二阶导数；ρw为水的密度；Kw为水的体积模量；uw为水的位移。
根据理想流体的本构理论，有以下关系式成立：
式中，pw为水的压力。
Biot饱和多孔介质理论[8]给出了饱和土层的波动方程(符号s和f分别代表土层固相和液相)：
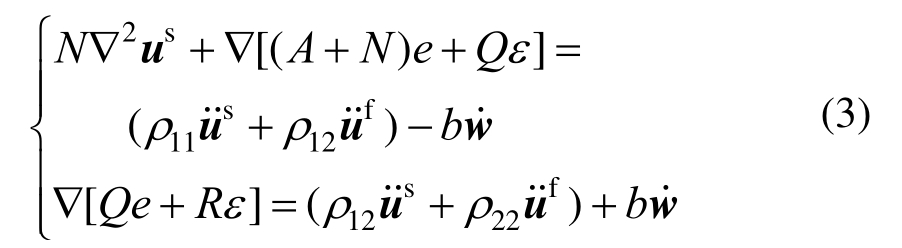
式中：e=divus、ε=divuf，us和uf分别为固相和液相位移向量；w为相对位移，w=n(uf-us)，n为孔隙度；b为耗散参数，b=ηn2/kp，η为液相粘滞系数，kp为渗透系数；ρ11=(1―n)ρs，ρ22=nρf，ρ12=0，ρs、ρf为固相和流体密度；A、N、Q、R为刚度参数，可以用土骨架的Lame常数λ、μ以及土颗粒、土骨架和孔隙流体的体积模量Ks、Kb和Kf表示为：
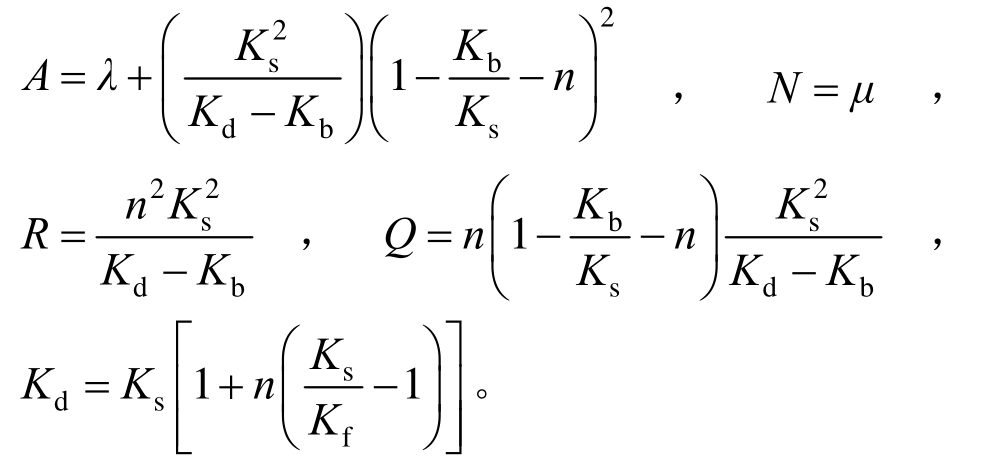
基于Biot的饱和多孔介质本构理论，有以下关系式成立：
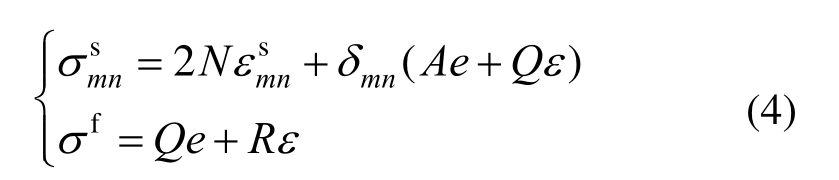
式中：
为饱和土固相应力；σf为液相应力，
代表孔隙水压力。
2 一维化时域方法的建立
一维化方法主要是通过Snell定律，将二维运动方程转化为一维方程，并采用在竖直向任意网格尺寸和水平向由时步和水平视波速确定网格尺寸的有限元划分形式，将斜入射的二维问题转化为一维问题。本节将详细介绍水层和饱和土层一维化有限元方程的建立过程。
2.1 水层的空间一维化方程
将理想流体波动方程式(1)改写为矩阵形式：
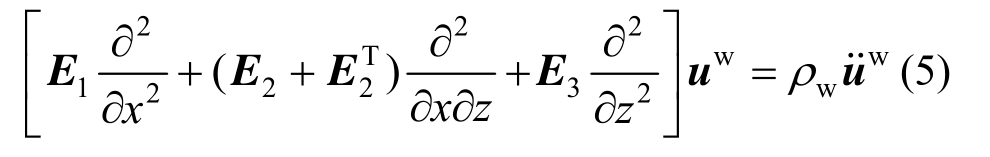
式中，E1、E2、E3为水的刚度参数矩阵，表达式为：
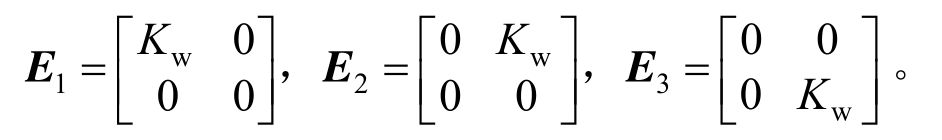
将本构关系表达式(2)改写为矩阵形式：
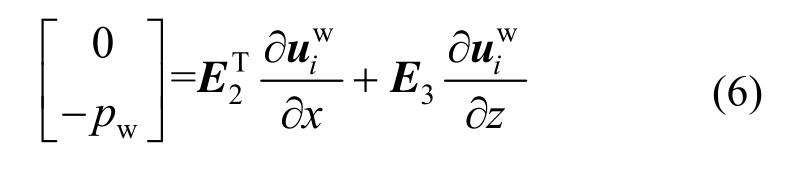
为计算水层波场，需要将水层沿竖向离散为一定数量的两结点有限单元，将所有水层单元和结点自上而下进行编号，对于编号为i的有限单元，其上、下结点坐标分别为zi和zi+1(如图1所示)，水层中结点位移向量为
其形式为：
位移插值形式为：
式中：N为单元形函数矩阵，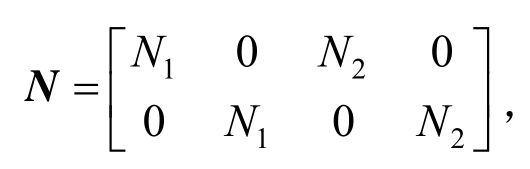
其中，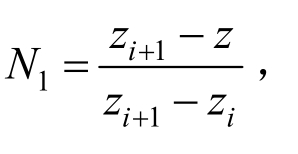
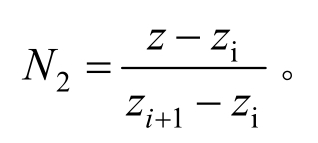
取权函数
将波动方程式(5)、本构表达式(6)和位移插值式(7)代入Galerkin弱积分形式，最后得到表达式：
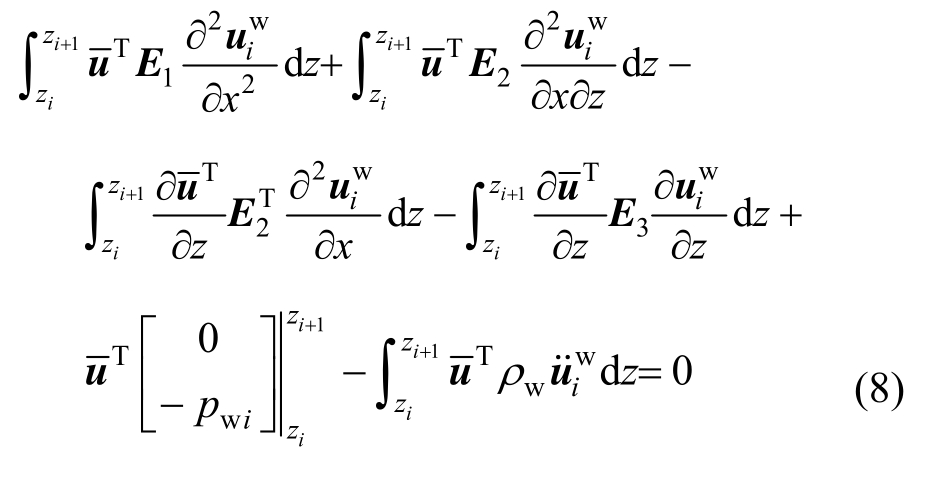
根据Snell定理，水平成层介质x方向视波速相等，因此有微分算子：
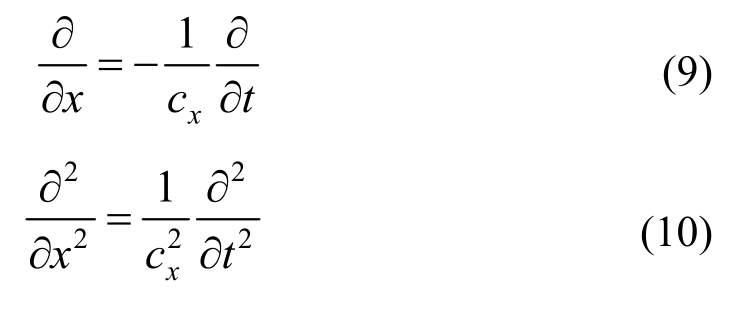
式中，cx为视波速，当P波入射时，cx=cP/sin θ，cP为入射P波的波速；当SV波入射时，cx=cS/sin β，cS为入射SV波的波速。
将微分算子式(9)和式(10)代入式(8)，得到一维方程：
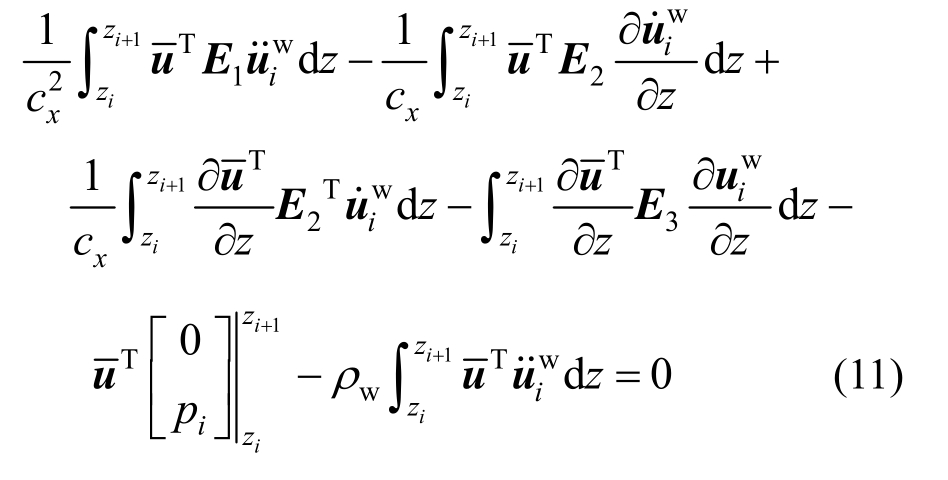
利用
的任意性，整理式(11)便得到水层一维化有限元方程式，具体形式如下：
式中，
分别是水的单元集中质量、阻尼和刚度矩阵，具体形式分别为(忽略零元素)：
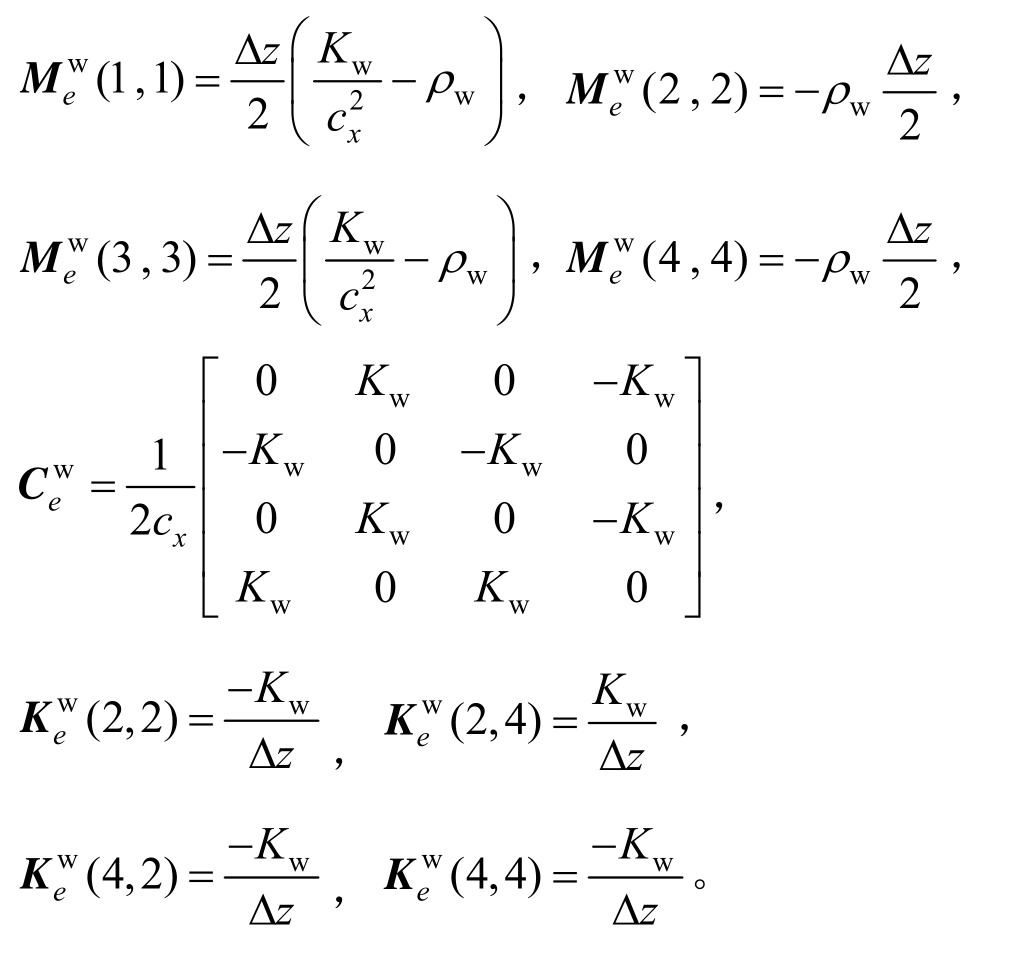
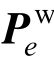是水的荷载矩阵，具体形式为：
2.2 饱和土层的空间一维化方程
按照水层一维化有限元方程组的建立过程，可以得到饱和多孔介质一维化有限元方程组：
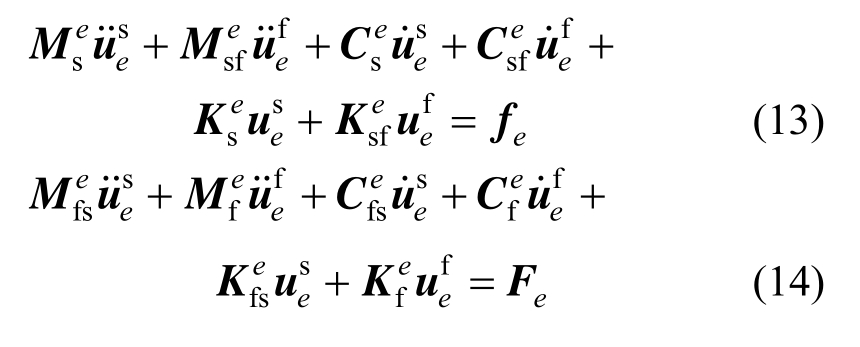
式中：
为单元集中质量矩阵；
为单元阻尼矩阵；
为单元刚度矩阵；fe和Fe为单元荷载列阵，表达式详见文献[20]。
2.3 边界条件
水下地基场地的动力响应是一个复杂的问题，由于波场包含多种介质，不同介质的交界面处必然存在不同的边界条件。
2.3.1 水层自由面边界条件
水层表面法向应力为零：
2.3.2 水层和饱和土层交界面
1) 水层和土层法向位移连续：
2) 土骨架切应力为零：
3) 水层和土层法向应力连续：
4) 水层和土层液相法向应力成比例：
2.3.3 饱和土层和饱和土层交界面
1) 土骨架法向位移连续：
2) 土骨架切向位移连续：
3) 流体法向相对位移连续：
4) 土骨架切向应力连续：
5) 法向总应力连续：
6) 孔隙水压力连续：
2.3.4 基岩和饱和土层交界面
1) 基岩与土骨架固相切向位移连续：
2) 基岩与固相和液相法向位移连续：
3) 基岩与土骨架切应力连续：
4) 基岩与土层法向总应力连续：
2.4 整体有限元方程的叠加
在同一介质中，单元的有限元方程可以直接按照常规的“对号入座”法叠加成整体方程组，但在不同介质交界面处，例如水土交界面，不同性质土层交界面，由它们各自的边界条件可知，水平方向位移不存在连续性条件，常规的叠加方法不能适用于该问题，因此需要进行特殊的处理。
2.4.1 对水层单元的处理
对于水层单元的有限元方程，节点位移向量个数与饱和土层单元中不同。为了便于与饱和土层单元有限方程组成整体方程组，需要对水层单元方程组进行处理。
首先将水层的有限元方程(式(12))整理成规范化的形式，即：
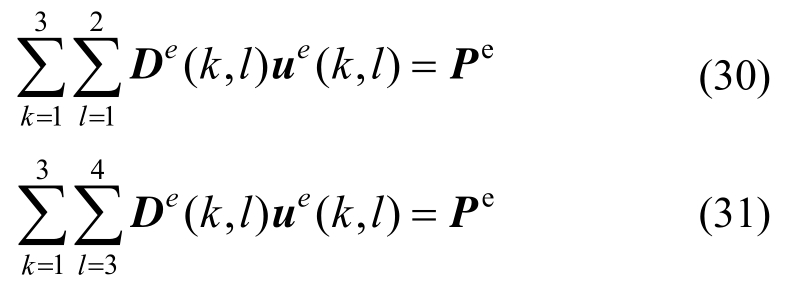
式中：
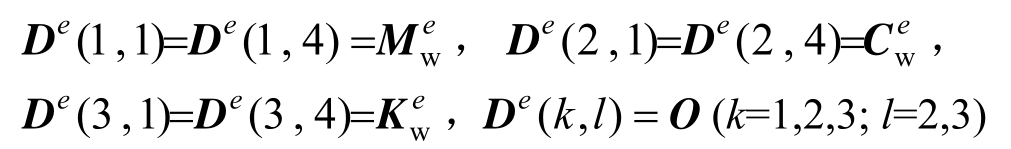
(O为四阶零矩阵)，
其次，根据水土交界面的边界条件，将交界面处水层单元方程的规范化形式重新整理如下：
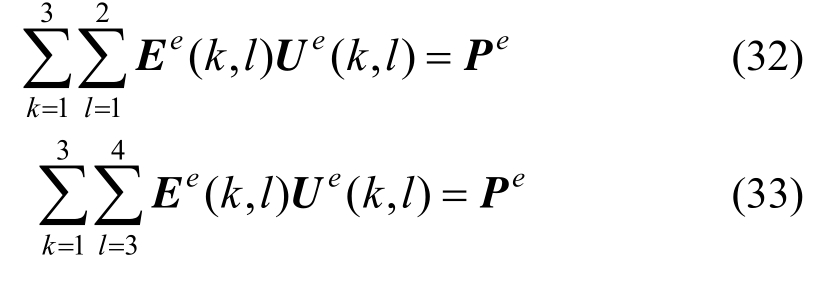
式中：
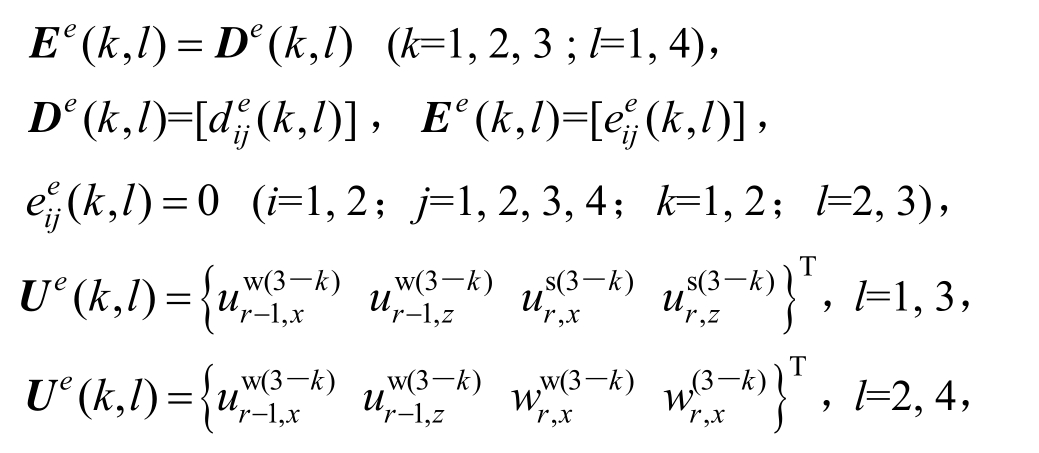
上标(3-k)表示该变量对时间的3-k阶导数。
最后，当水土交界面的2个单元进行叠加时，将水土交界面r结点处的位移、速度、加速度矩阵各增加一个维度，并保证等式恒成立。则水土交界面的两个单元叠加结果可以表示为：
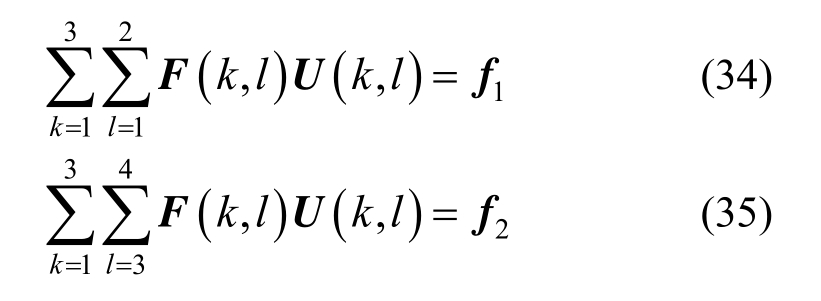
式中：
其中，
是饱和土层的质量、阻尼、刚度矩阵用相对位移和孔隙率处理过的元素，具体形式详见文献[20]；U(k,l)为单元叠加后得到的加速度(速度、位移)列阵；f1和f2为单元叠加后得到的荷载列阵。
2.4.2 对饱和土层单元的处理
饱和土层交界面的边界条件含有相对位移项we和孔压项pf，为了便于应用边界条件，同样需要对饱和土层单元有限元方程组作特殊处理，则不同土层交界面两个单元叠后的结果可以表示为：
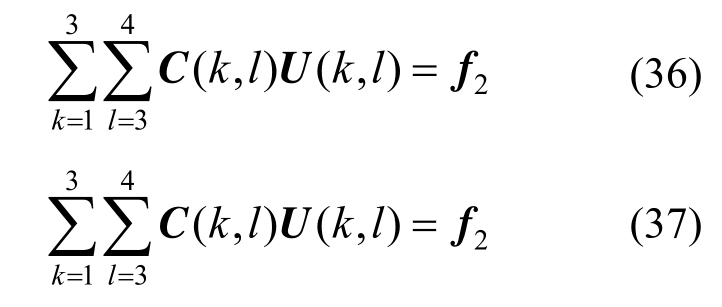
式中：C(k , l)为单元叠加后得到的质量(阻尼、刚度)矩阵，具体形式详见文献[20]。
2.4.3 底部人工边界及输入
为了模拟基岩的截断效应和输入特征，采用赵密等[15]提出的精确人工边界条件，该边界条件由未知散射波的吸收边界条件和已知入射波的输入边界条件组成：
式中：σj 为基岩的应力；S为散射阻抗；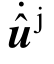
为人工边界结点上的入射波速度矢量，与入射波的速度时程
有关，当P波入射时，
当SV波入射时，
2.4.4 整体有限元方程
将精确人工边界条件式(38)结合饱和土层单元方程式(30)、式(31)和水层单元方程式(36)、式(37)以及各边界条件表达式(15)～式(29)，叠加成整体方程，最终形式为：
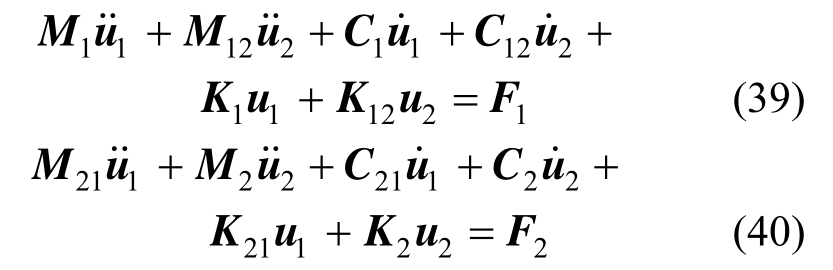
式中：M1、M12、M21和M2，C1、C12、C21和C2，K1、K12、K21和K2与固相、固液耦合、液固耦合、液相的整体集中质量、阻尼、刚度矩阵的关系为
(最后一列除最末元素为1外，其他均为0)，
(最后一列均为0)，
(最后一列均为0)，
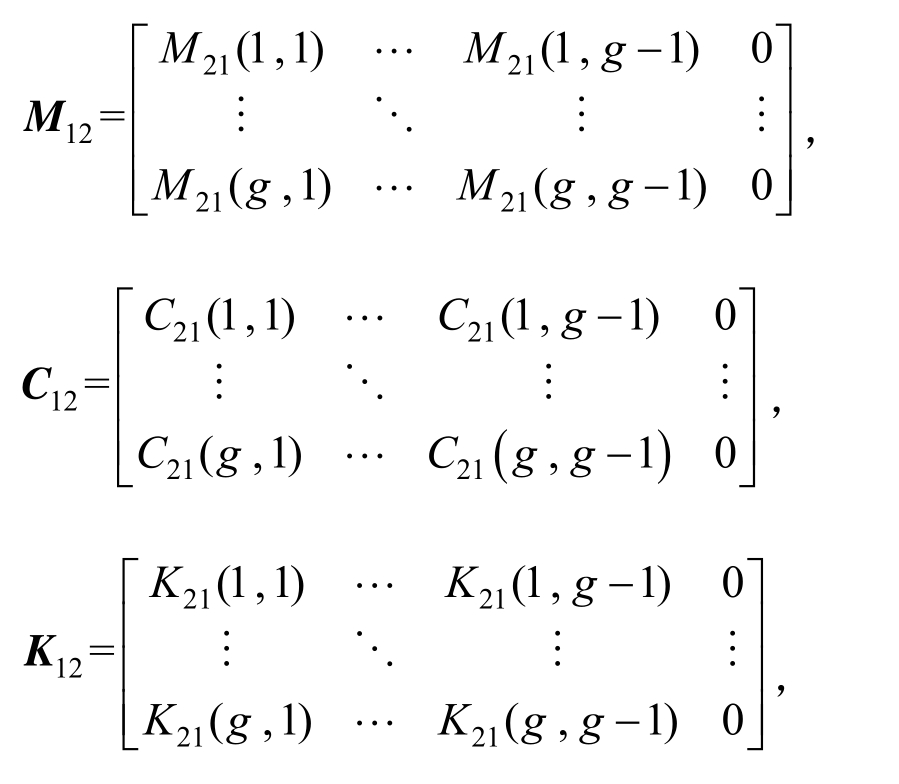
CB(g,g)=-S；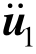
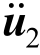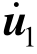和
，
和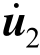
，u1和u2分别为整体第一和第二加速度、速度、位移列阵，具体形式分别为：
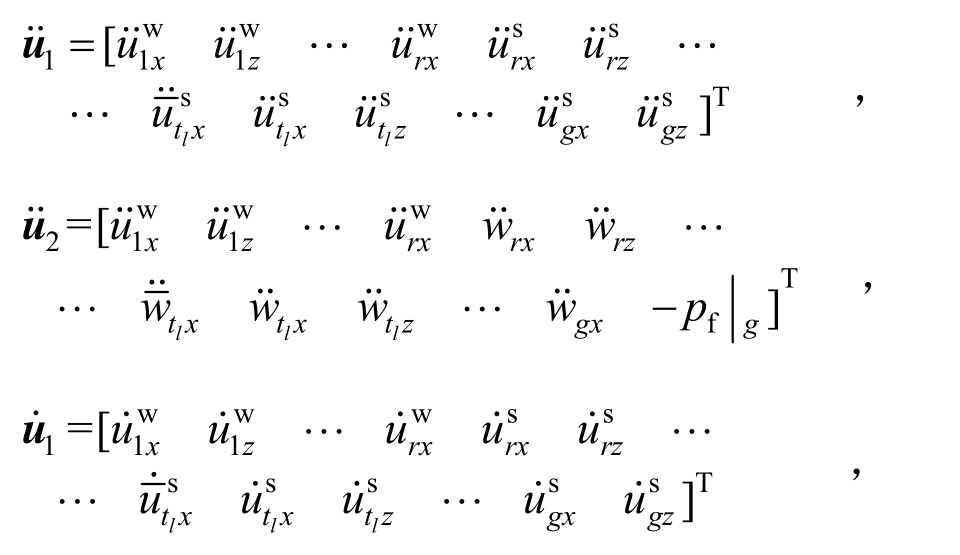
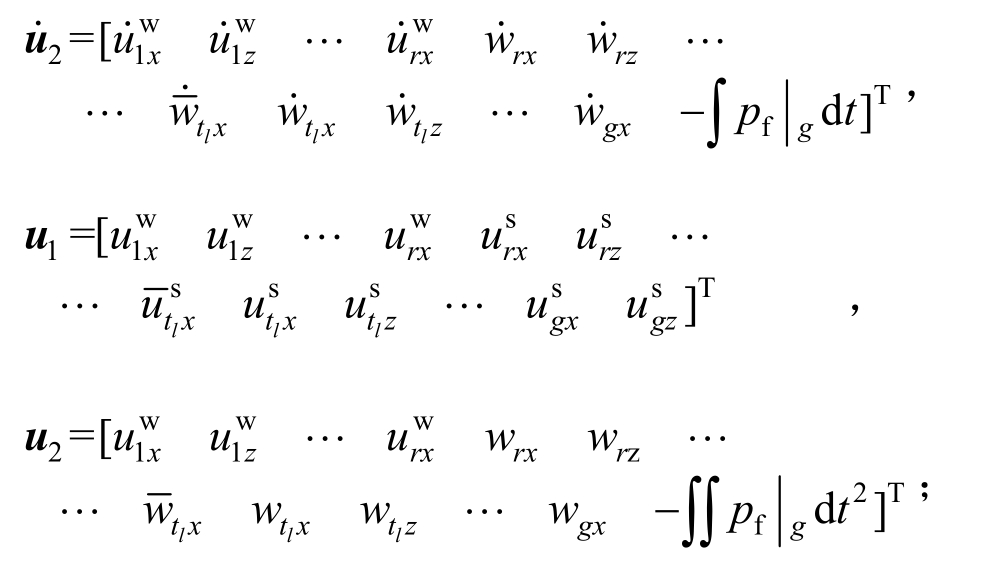
F1和F2分别表示整体第一荷载列阵和整体第二荷载列阵，具体表达式为
F2=[0...0]T。值得注意的是，经过上述处理后的整体矩阵的阶数变为g=2h+N，其中h为结点总数。
3 结点动力响应表达式
为了求解结点动力响应表达式，可以将中心差分法与Newmark平均加速度近似格式相结合形式[22]。该方法具有二阶精度和良好的稳定性，具体内容本文将不再赘述。
联立解式(39)和式(40)可以求得，在t=pΔt时刻下加速度响应表达式：
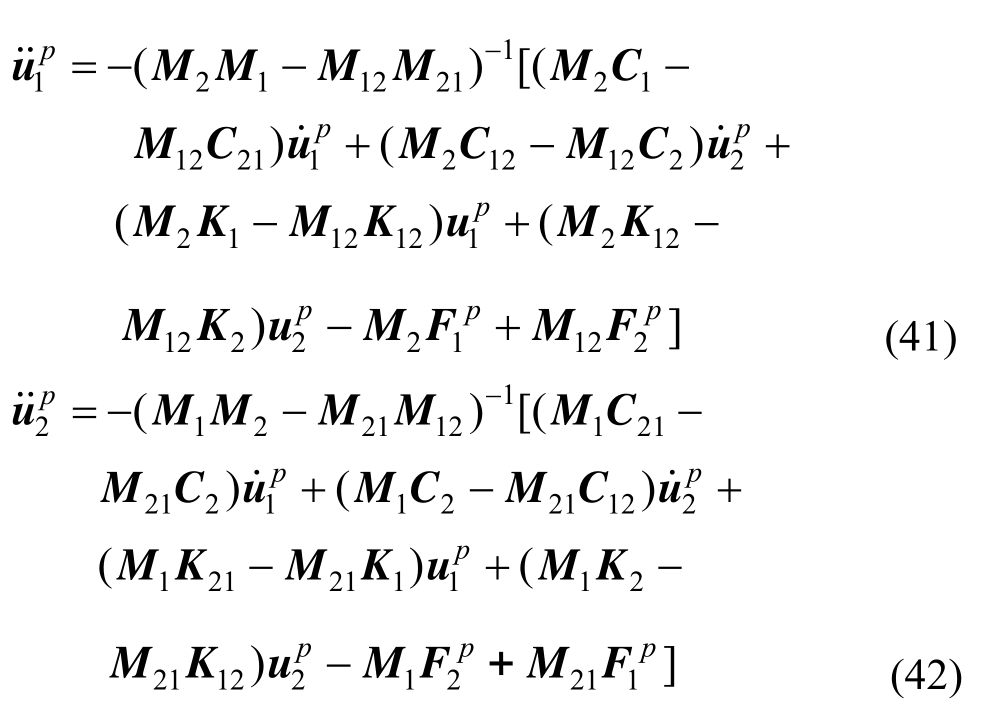
速度响应表达式从略，利用时间变量的中心差分法，可得t=(p+1)Δt 时刻下位移响应表达式：
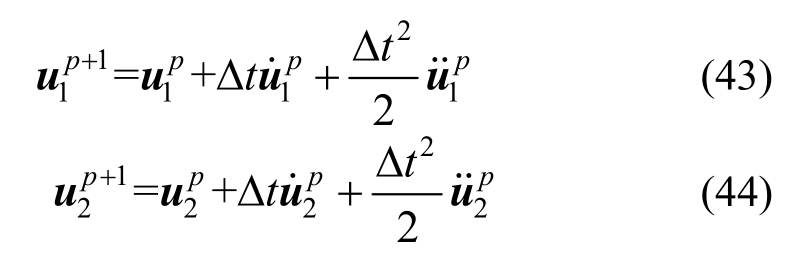
将式(41)～式(43)得到的水层和饱和土层的加速度、速度和位移响应，分别代入式(13)、式(14)，可以得到水层和饱和土层中单元的应力响应。
4 算例验证与分析
为验证本文方法的计算精度和有效性，以下对两个算例进行计算和分析。
算例1：由于可供验证的水下地基场地的文献资料较少，将一维化时域算法退为成层单相半空间场地与文献[16]进行对比验证。
算例2：将一维化时域算法得到的数值结果，与文献[12]的方法结合傅里叶变换得到的理论解进行对比验证。入射波选用峰值A=0.1 m，持时T=0.3 s的脉冲波，其位移时程曲线如图2所示。
4.1 算例1的验证与分析
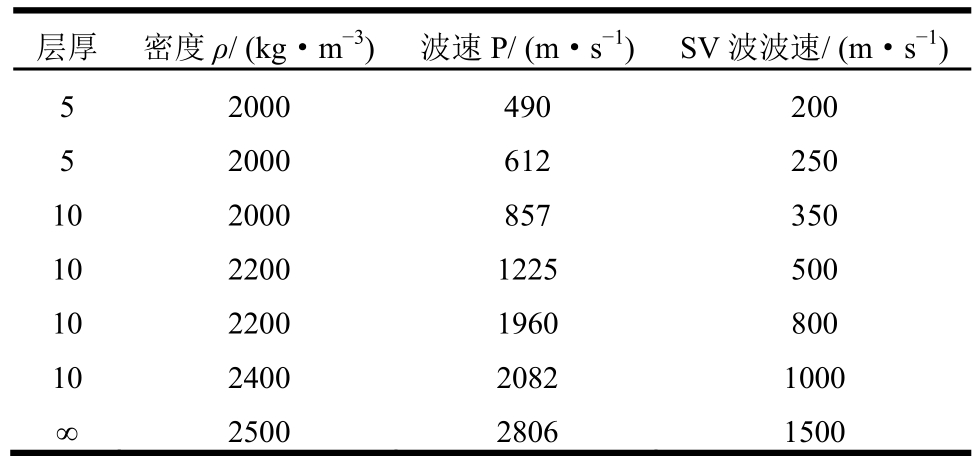
将水层深度取为0 m，饱和介质的孔隙度取为0.001，孔隙流体密度取为0.001 kg·m-3，则水下地基场地可退化为成层单相半空间场地，以此验证和分析本文不同土层交界面单元方程处理方法的合理性和有效性。算例取自文献[16]中的Leibstadt场地，该场地共6层土，总厚h2=50 m(为考虑基岩的影响，将人工边界条件设在60 m处)，每层土层厚度和土性参数详见表1。竖直方向的空间步距为1 m，满足数值稳定性条件的时间步距为0.00001 s。
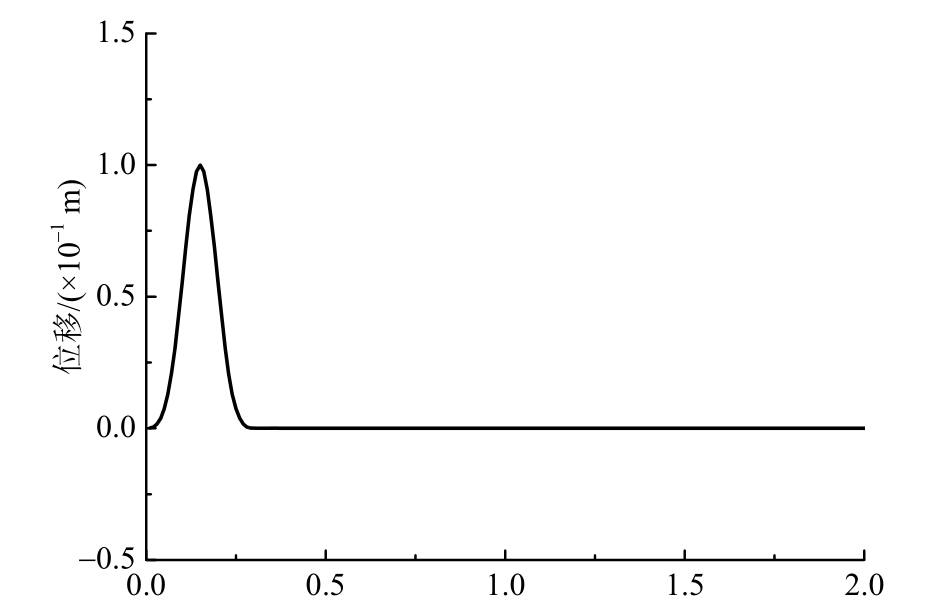
图2 位移时程曲线
Fig.2 The time-history curve of displacement
表1 瑞士Leibstadt场地土性参数
Table 1 The constants of Leibstadt site in Swizeland
层厚 密度ρ/ (kg·m-3) 波速P/ (m·s-1) SV波波速/ (m·s-1)5 2000 490 200 5 2000 612 250 10 2000 857 350 10 2200 1225 500 10 2200 1960 800 10 2400 2082 1000∞ 2500 2806 1500
平面P波和SV波均以30°入射，利用本文方法求解土层表面的加速度，分别与文献[16]中图4(b)和图6(b)进行对比验证；求解沿饱和土层深度分布的最大水平及竖向加速度分别与文献[16]中图4(d)和图6(d)进行对比验证。
图3给出了P波30°入射时，本文一维化时域方法得到的土层表面的水平和竖向加速度以及沿土层深度分布的最大加速度与文献[16]中图4(b)和图4(d)的对比。图4给出了SV波30°入射时，本文一维化时域方法得到的土层表面的水平和竖向加速度和沿土层深度分布的最大加速度与文献[16]中图6(b)和图6(d)的对比。从图3和图4可以看到，在平面P波和SV波入射下，本文方法得到的土层表面加速度和最大加速度沿土深分布的曲线与文献[16]的相关结果吻合较好，整体误差小于3%，精度较高，证明了本文方法的计算精度和有效性。
图3 P波作用下本文计算结果与文献[16]的对比
Fig.3 Comparison of calculation results obtained in this paper with those in the Ref.[16]due to P-wave incidence
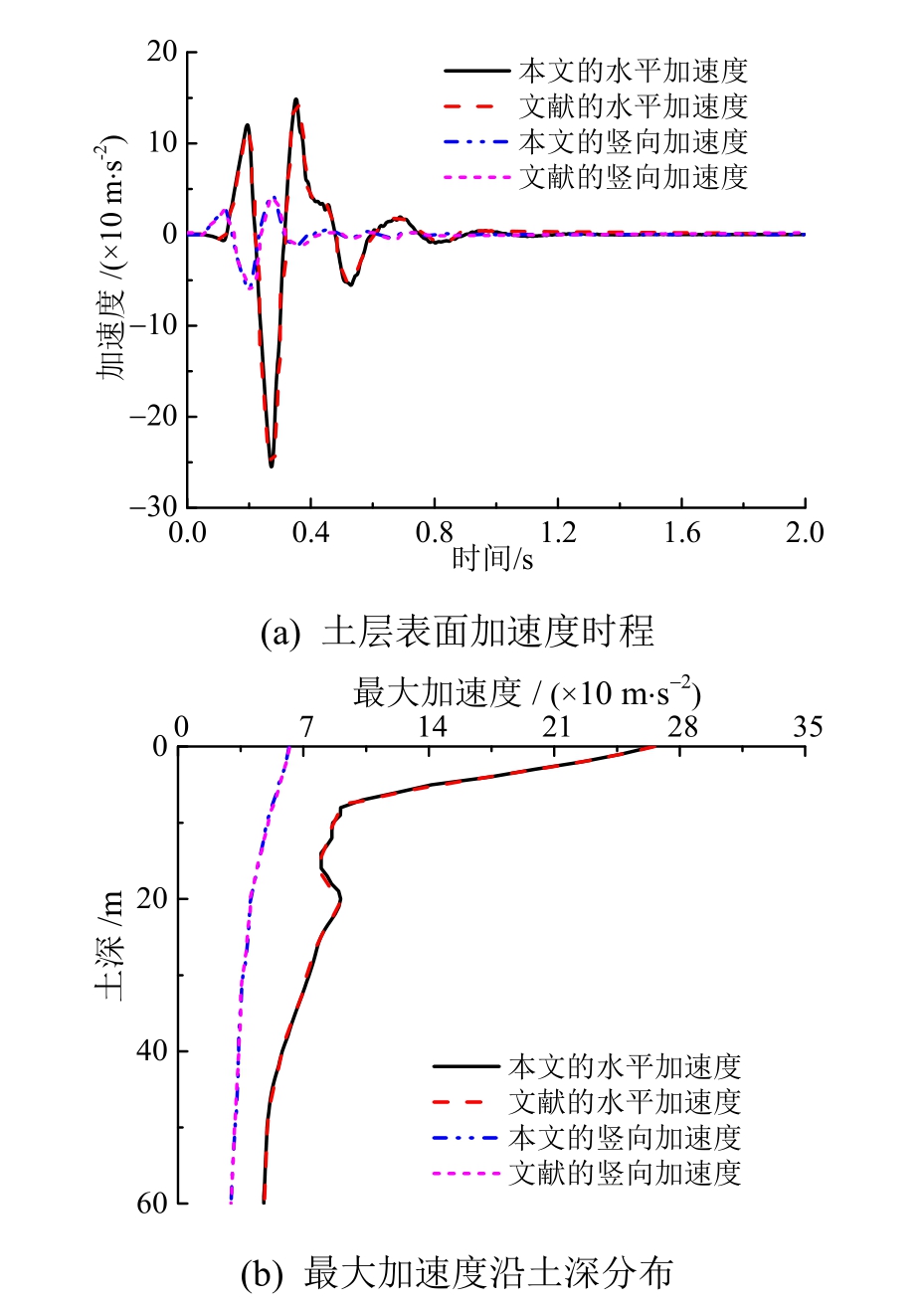
图4 SV波作用下本文计算结果与文献[16]的对比
Fig.4 Comparison of calculation results obtained in this paper with those in the Ref.[16]due to SV-wave incidence
4.2 算例2的验证与分析
算例1采用了地震波斜入射下成层介质的对比结果，由于在计算过程中未能验证水层、饱和土层单元及两者交界面的处理方法的合理性，因此选取水层深度h1=50 m，单层饱和土层厚度h2=50 m的算例。其中，水的体积模量Kw=2.0 GPa、密度ρw=1000 kg/m3；基岩的拉梅常数λb=15.633 GPa和Gb=15.633 GPa，密度ρb=2385 kg/m3；饱和土层土颗粒体积模量Ks=36 GPa，液相体积模量Kf=2 GPa，流固两相耦合质量ρ12=0，渗透系数k=10-10 m2。其余的计算参数见表2。将人工边界条件设在土与基岩交界面处。竖直方向的空间步距为1 m，满足数值稳定性条件的时间步距为0.00001 s。
表2 饱和土层的材料参数
Table 2 The material parameters of saturated soil
固相密度ρs/ (kg·m-3)液相密度ρf/ (kg·m-3)拉梅常数λ/ MPa拉梅常数μ/MPa孔隙度n粘滞系数η 2700 1000 22.0 22.0 0.6 0.001
平面P波和SV波分别以θ=60°和β=30°入射，利用本文方法求解水土交界面处水平及竖向固相位移和相对位移，分别与文献[12]的方法结合傅里叶变换得到的理论解进行对比验证。
图5和图6分别给出了P波60°及SV波30°斜入射时，本文一维化时域方法得到的水土交界面处的水平及竖向固相位移和相对位移与文献[12]的方法结合傅里叶变换得到的理论解的对比结果。由图5和图6可知，在平面P波和SV波入射下，本文方法得到的固相位移和相对位移与文献[12]的方法结合傅里叶变换得到的理论解吻合较好，整体误差小于2%，精度较高，同样验证了本文方法的计算精度和有效性。
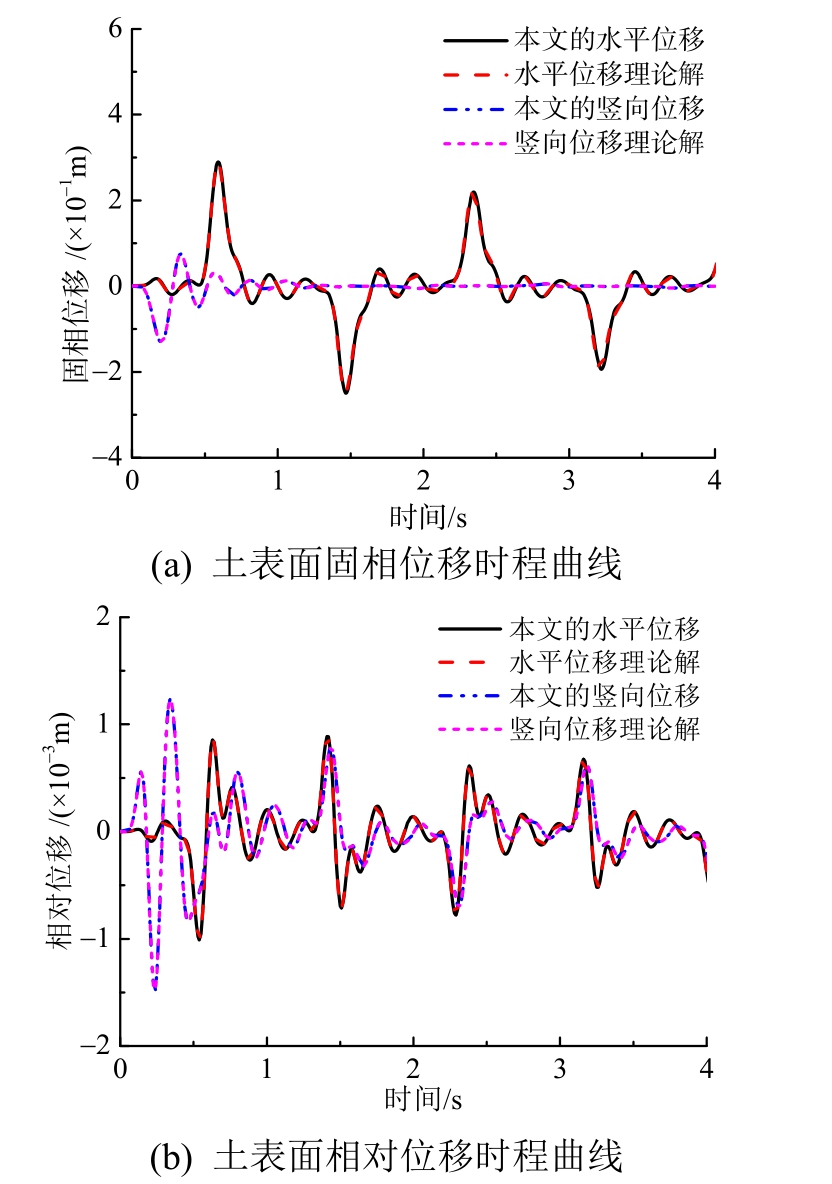
图5 P波作用下本文计算结果与文献[12]的对比
Fig.5 Comparison of calculation results obtained in this paper with those in the Ref.[12]due to P-wave incidence
图6 SV波作用下本文计算结果与文献[12]的对比
Fig.6 Comparison of calculation results obtained in this paper with those in the Ref.[12]due to SV-wave incidence
5 结论
本文依据Snell定理，推导了水层一维化单元有限元方程，将斜入射下水层波动的空间二维问题转化为简单的一维问题，通过考虑水层与饱和多孔介质层间、不同饱和多孔介质交界面以及基岩与饱和多孔介质层间的边界条件，以及基岩处的精确人工边界条件，将已有的成层饱和土的一维化有限元方程与水层的一维化有限元方程组装成整体有限元方程。将中心差分法和Newmark法相结合建立了地震波斜入射下水下地基场地节点位移和加速度响应的数值解。通过2个典型算例，初步验证了本文时域算法是有效性的，并且具有较高的计算精度。
本文研究重点是地震斜入射下水下地基场地地震反应分析方法，限于篇幅，基于此方法得到的水下地基场地动力响应将另文介绍。由于计算算法的局限性，该方法不能应用于平面SV波大于临界入射角的斜入射情况，后续的研究重点也是改进算法、扩大适用范围。
[1]刘晶波, 王艳.成层半空间出平面自由波场的一维化时域算法[J].力学学报, 2006, 38(2): 219―225.Liu Jingbo, Wang Yan.A 1D time-domain method for 2-D wave motion in elastic layered half-space by anti-plane wave oblique incidence [J].Acta Mechanic Sinica, 2006, 38(2): 219―225.(in Chinese)
[2]Takahiro S, Kazuhiko K.Estimation of earthquake motion incident angle flat-rock site [C]// Proceedings of 12th World Conference Earthquake Engineering, New Zealand, 2000: 9―56.
[3]黄景琦, 杜修力, 田志敏, 等.斜入射 SV 波对地铁车站地震响应的影响[J].工程力学, 2014, 31(9): 81―88,103.Huang Jingqi, Du Xiuli, Tian Zhimin, et al.Effect of the oblique incidence of seismic SV waves on the seismic response of subway station structure [J].Engineering Mechanics, 2014, 31(9): 81―88, 103.(in Chinese)
[4]李山有, 廖振鹏, 周正华.大型结构地震反应数值模拟中的波动输入[J].地震工程与工程振动, 2001, 6(2):1―5.Li Shanyou, Liao Zhenpeng, Zhou Zhenghua.Wave motion input in numerical simulation of seismic response for large-scale structure [J].Earthquake Engineering and Engineering Vibration, 2001, 6(2): 1―5.(in Chinese)
[5]朱镜清, 李金成.海水对海底地震动的影响问题[C]//中国地震学会第四次学术大会论文摘要集.北京: 中国地震学会, 1992: 61.Zhu Jingqing, Li Jincheng.Problem of effects of seawater on undersea ground seismic motion [C]// Proc.of China Seismological Society of the 4th Academic Conference.Beijing: Seismological Society of China, 1992: 61.(in Chinese)
[6]席仁强, 陈国兴, 王志华.覆水场地地震反应分析[J].防灾减灾工程学报, 2009, 29(6): 610―617.Xi Renqiang, Chen Guoxing, Wang Zhihua.Seismic response of underwater site [J].Journal of Disaster Prevention and Mitigation Engineering, 2009, 29(6):610―617.(in Chinese)
[7]Stoll R D, Kan T K.Reflection of acoustic waves at a water-sediment interface [J].Journal of the Acoustical Society of America, 1981, 69(1): 149―156.
[8]Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid [J].The Journal of the Acoustical Society of America, 1956, 28(2): 168―191.
[9]Li C, Hao H, Li H, et al.Theoretical modeling and numerical simulation of seismic motions at seafloor [J].Soil Dynamics and Earthquake Engineering, 2015, 77:220―225.
[10]Wang J T, Zhang C H, Jin F.Analytical solutions for dynamic pressures of coupling fluid-solid-porous medium due to P wave incidence [J].Earthquake Engineering and Engineering Vibration, 2004, 3(2): 263―271.
[11]Wang J T, Zhang C H, Jin F.Analytical solutions for dynamic pressures of coupling fluid-porous medium-solid due to SV wave incidence [J].International Journal for Numerical and Analytical Methods in Geomechanics,2009, 33(12): 1467―1484.
[12]张奎, 李伟华, 赵成刚.平面波入射下深水地基场地动力响应分析[J].岩土工程学报, 2018, 40(6): 1066―1074.Zhang Kui, Li Weihua, Zhao Chenggang.Dynamic responses of an underwater site subjected to plane P- or SV-wave incidence [J].Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1066―1074.(in Chinese)
[13]Achenbach J D.弹性固体中波的传播[M].徐植信, 洪锦如, 译.上海: 同济大学出版社, 1992.Achenbach J D.Wave propagation in elastic solids [M].Translated by Xu Zhixin , Hong Jinru.Shanghai: Tongji University Press, 1992.(in Chinese)
[14]刘晶波, 王艳.成层介质中平面内自由波场的一维化时域算法[J].工程力学, 2007, (24)7: 16―22.Liu Jingbo, Wang Yan.A 1D time domain method for in-plane wave motion of free field in layered media [J].Engineering Mechanics, 2007, (24)7: 16―22.(in Chinese)
[15]赵密, 杜修力, 刘晶波, 等.P-SV波斜入射时成层半空间自由场的时域算法[J].地震工程学报, 2013, (35)1:84―90.Zhao Mi, Du Xiuli, Liu Jingbo, et al.Time-domain method for free field in layered half space under P-SV waves of Oblique Incidence [J].China Earthquake Engineering Journal, 2013, (35)1: 84―90.(in Chinese)
[16]Zhao M, Yin H, Du X, et al.1D finite element artificial boundary method for layered half space site response from obliquely incident earthquake [J].Earthquakes &Structures, 2015, 9(1): 173―194.
[17]李鹏, 宋二祥.隧道纵向非一致地震反应的三维数值分析[J].地震工程与工程振动, 2014, 34(增刊): 274―280.Li Peng, Song Erxiang.Three-dimensional numerical analysis for longitudinal asynchronous seismic response of tunnels [J].Earthquake Engineering and Engineering Dynamics, 2014, 34(Suppl): 274―280.(in Chinese)
[18]卓卫东, 高智能, 谷音.P-SV波斜入射时有阻尼成层介质自由波场的一维化时域算法[J].水利与建筑工程学报, 2016, 14(16): 18―24.Zhuo Weidong, Gao Zhineng, Gu Yin.A 1 D time-domain method for in-plane wave motion of free field in layered media with damping under obliquely incident P-SV waves [J].Journal of Water Resources and Architectural Engineering, 2016, 14(16): 18―24.(in Chinese)
[19]高智能, 卓卫东, 谷音.SH波斜入射时有阻尼成层介质自由场的一维化时域算法[J].振动与冲击, 2017,36(16): 37―43.Gao Zhineng, Zhuo Weidong, Gu Yin.A 1D time-domain method for free field motion in layered media with damping under obliquely incident SH wave [J].Journal of Vibration and Shock, 2017, 36(16): 37―43.(in Chinese)
[20]李伟华, 夏佩林, 张奎, 等.成层饱和介质平面波斜入射问题的一维化时域方法[J].力学学报, 2018, 50(2):349―361.Li Weihua, Xia Peilin, Zhang Kui, et al.1-D time-domain method for free field in layered saturated poroelastic media by plane wave oblique incidence [J].Chinese Journal of Theoretical and Applied Mechanics, 2018,50(2): 349―361.(in Chinese)
[21]赵成刚, 李伟华, 王进廷, 等.三种介质耦联系统动力反应分析的显式有限元法及其应用[J].地震学报, 2003,25(3): 262―271.Zhao Chenggang, Li Weihua, Wang Jinting, et al.An explicit finite element method for dynamic analysis in three-medium coupling system and its application [J].Acta Seismologica Sinica, 2003, 25(3): 262―271.(in Chinese)
[22]李小军, 廖振鹏, 杜修力.有阻尼体系动力问题的一种显式差分解法[J].地震工程与工程振动, 1992(4): 74―80.Li Xiaojun, Liao Zhenpeng, Du Xiuli.An explic it finite difference method for viscos-elastic dynamic problem [J].Earthquake Engineering and Engineering Vibration,1992(4): 74―80.(in Chinese)