现实工程结构中，由于结构自身材料，边界条件或是外部荷载的不确定性(如混凝土的弹性模量，结构安装误差和地震荷载、风荷载)，导致结构的响应(如内力和位移)会具有随机性，采用含随机参数的建模会更贴合实际情况。随机结构的静力响应分析是一项基础而重要的工作，其结果可直接应用于结构的可靠性分析中。目前，国内外用于求解随机结构的静力响应问题的方法主要分为基于抽样(sampling-based)和非基于抽样(non-sampling-based)的方法。
基于抽样的方法中应用最为广泛的是蒙特卡洛模拟法(Monte-Carlo simulation method)[1]，该方法反复利用随机变量的样本进行确定性的有限元分析，再对求得的结果样本进行统计得到响应的概率特性，缺点是如果想要保证求解结果具有较好的精度和收敛性，就需要大量的计算样本，在结构可靠性分析中尤其如此；另外对于现实中复杂的大型结构，采用蒙特卡洛模拟法所需的计算量也是难以承受的。还有拟蒙特卡洛法(Quasi-Monte Carlo simulation)[2]和重要抽样法(importance sampling)[3]，这两种方法是在蒙特卡洛模拟法基础上的改进，其计算效率较蒙特卡洛模拟法有一定的提高。
非基于抽样的方法一般是试图以某种含随机变量的显式表达式来描述随机结构的响应量，常见的有摄动法，Neumann展开法和谱方法。摄动法通常采用低阶摄动，如结构的随机位移向量表达式只取至1阶、2阶项[4]，在随机参数波动范围较小的情况下，低阶摄动法具有很高的计算效率和精度。Kamiński[5]推导了高阶摄动法，表达式可取到6阶～10阶项，用来获得响应的前四阶矩。Neumann[6]展开法是将结构刚度矩阵的逆矩阵用Neumann级数展开来表示，进而获得响应的表达式，近期，王相玉在Neumann展开法的基础上提出了广义的Neumann展开法，其计算效率有了明显提高，并给出了表达式的先验误差估计[7-8]。Ghanem和Spanos[9]提出的谱方法是把随机响应在一组正交基上做投影，各个基向量的坐标系数可以通过随机Galerkin法来计算，谱方法有严格的误差估计，若取适当数目的基向量，该方法将有很高的计算精度，但是当随机变量的数目较多或所取的基向量数目增加时，计算量会急剧增加。最近，李烨君和黄斌等[10]提出了一种混合摄动伽辽金法，该方法在高阶摄动的基础上通过随机Galerkin法来获得级数中各阶项的修正系数，以改进高阶摄动的计算精度。除了以上方法之外，还有许多重要的随机有限元方法，如随机因子法[11-12]、降维法[13]和响应面法[14-15]等。这些方法的目的都是在保证计算精度的前提下用尽可能少的计算耗时来求解随机结构静力响应的统计特性，而且允许结构系统中有较多的随机变量，随机变量的变化范围也不局限于小变异情况。
同伦分析方法是由廖世俊[16]提出的一种可以用于求解强非线性微分方程的解析近似方法，该方法克服了传统摄动法对小参数的依赖性，其在非线性力学、流体力学和金融学等领域都有成功的应用。目前，利用同伦分析方法来求解随机结构系统的文献还很少，吉猛等[17]利用同伦分析方法对汽车车架结构进行了可靠性分析；笔者最近利用同伦分析方法成功地对随机特征值问题进行了求解[18]，在随机参数变异性较大的情况下仍能够获得较精确的计算结果，且计算效率也不错。
本文力求将同伦分析方法的思想应用于随机结构的静力响应分析中，首先将结构的控制方程重新进行同伦构造获得零阶变形方程，通过对零阶变形方程中的参数p求导可获得结构位移响应的同伦级数解的表达式，同时，文章提出两种降维策略用于大幅度降低该位移表达式的计算工作量。数值算例表明新方法较传统的摄动法有更大的收敛范围，和正交多项式展开法相比，在计算精度相当的情况下，新方法的计算耗时明显更少，另外，此方法还可方便的应用于几何非线性结构的静力分析中。
1 随机结构静力控制方程
对于一具有N个自由度的确定性结构，其弹性刚度矩阵
是应变与单元节点位移关系矩阵，D为弹性矩阵，V是结构单元体积。当结构承受静力外荷载F时，结构的位移控制方程可表示如下：
式中，U为节点位移向量。当考虑结构材料、截面尺寸或者外荷载的随机性时，刚度矩阵和荷载向量将成为随机变量的函数，因而，结构的位移向量也相应的可视为随机参数的函数。
假设结构的弹性模量为一连续随机场，目前常见的离散随机场的方法包括中心点法、形状函数法、最优线性估计、权重积分法和Karhunen-Loéve展开法等，对于这些方法的具体探讨和比较可参考文献[19]。若选择用Karhunen-Loéve展开来离散此弹性模量随机场，具体表示方法如下：设含r个随机变量ξ={ξ1,ξ2,…,ξr }的弹性模量可表示为E(X,ξ)，其中X代表空间坐标。将弹性模量的自协方差函数记作C(x1,x2)，那么利用Karhunen-Loéve展开离散后的弹性模量随机场可表示为：
式中：λi和Ei (X)分别是自协方差函数C(x1,x2)的特征值和特征向量，符号
表示求期望。那么随机弹性矩阵D(X,ξ)可表示为：
将式(3)代入
后整理可得随机刚度矩阵的表达式：
其中，
另一方面，设外荷载包含s个随机变量，那么有：
式中：F0和Fi分别为等效节点荷载向量F的均值和随机部分的确定性向量；n为整个结构系统总的随机变量个数。
2 随机响应的同伦级数解
2.1 随机静力控制方程的同伦构造
廖世俊在同伦思想的基础上提出了同伦分析方法来求解非线性问题，根据同伦分析方法的思想，本文试图在确定性结构和随机参数波动后的结构之间建立一个同伦关系：由于此时的结构位移向量必然是系统随机变量ξ的函数，故设想构造这样一个函数Ψ(ξ,h,p)，当p=0时，Ψ(ξ,h,0)=U0；当p=1时，Ψ(ξ,h,1)=U(ξ,h)。U0为一初始解，由于结构的响应在随机参数波动前后的变化并不是十分巨大，故完全有理由选择随机参数取均值时结构的响应作为初始解，即
同时，构造如下方程来寻求最终解U(ξ,h)与U0之间的关系：
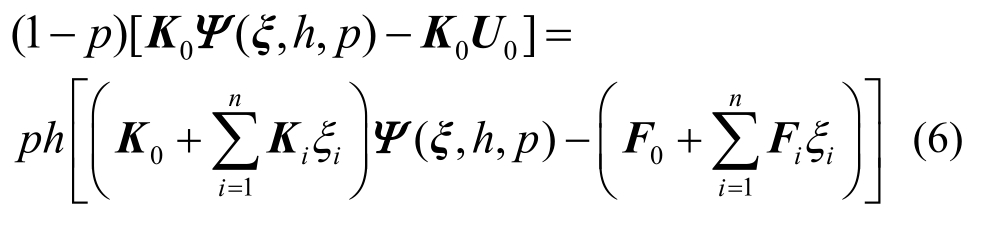
式中，h≠0，当i=1, 2,…,r时，Ki为非零矩阵，当i=r+1, r+2,…,n时，Ki=0；当i=1,2,…,r时，Fi=0，当i=r+1,r+2,…, n时，Fi为非零矩阵。通过式(6)容易观察到当p=0时，Ψ(ξ,h,0)=U0；当p=1时，Ψ(ξ,h,1)=U(ξ,h)。因此式(6)就构造了从U0到U(ξ,h)的同伦，称式(6)为零阶变形方程。
在构造了零阶变形方程后，根据已知信息，若将Ψ(ξ,h,p)做关于参数p的麦克劳林展开有：
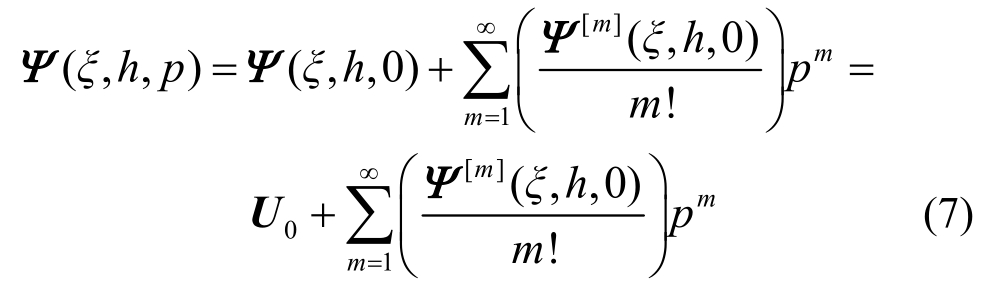
式中，Ψ[m](ξ,h,0)代表Ψ(ξ,h,p)在p=0处关于p的m阶偏导数，其具体形式可以通过将零阶变形式(6)对参数p求m次偏导后，再令p=0得到。详细步骤如下。
首先将零阶变形式(6)对p求一次偏导得到：
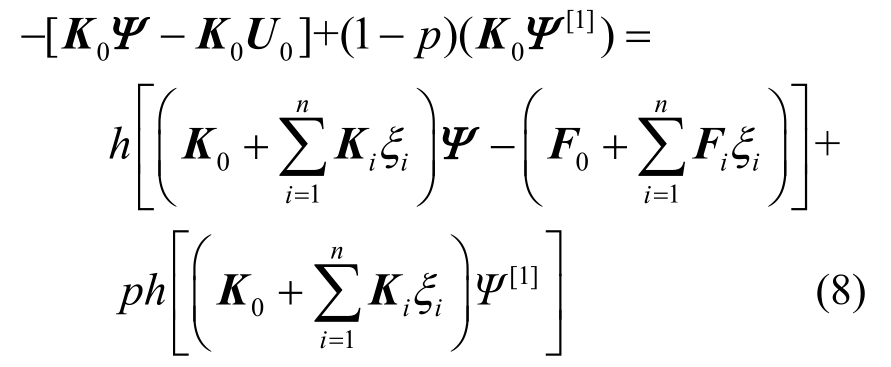
为方便起见，式(8)中将Ψ(ξ,h,p)简写为Ψ。式(8)称作1阶变形方程，令式(8)中的p=0可得：
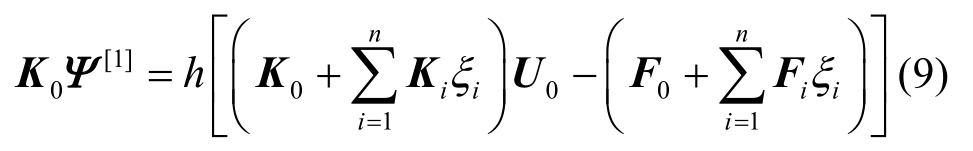
由于K0U0-F0=0，则有：
其中，
这样就得到了麦克劳林展式(7)中的
若继续将1阶变形式(8)对p求一次偏导可得2阶变形式(11)。
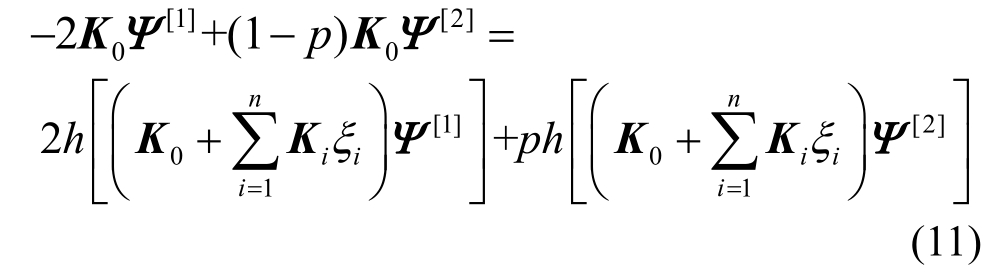
令式(11)中的p=0，有：
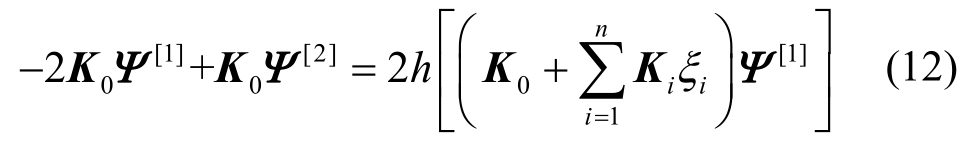
整理可得：
其中：
式中，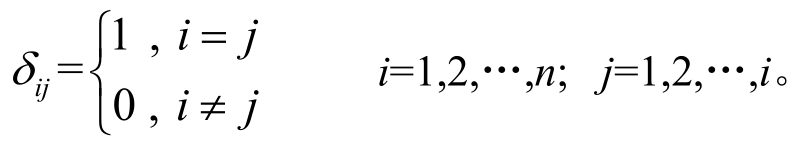
以此类推，通过将零阶变形方程对参数p求m阶偏导，可得到Ψ[m]。将所得到的Ψ[m]代入式(7)，然后令p=1，整理后有如下表达式：
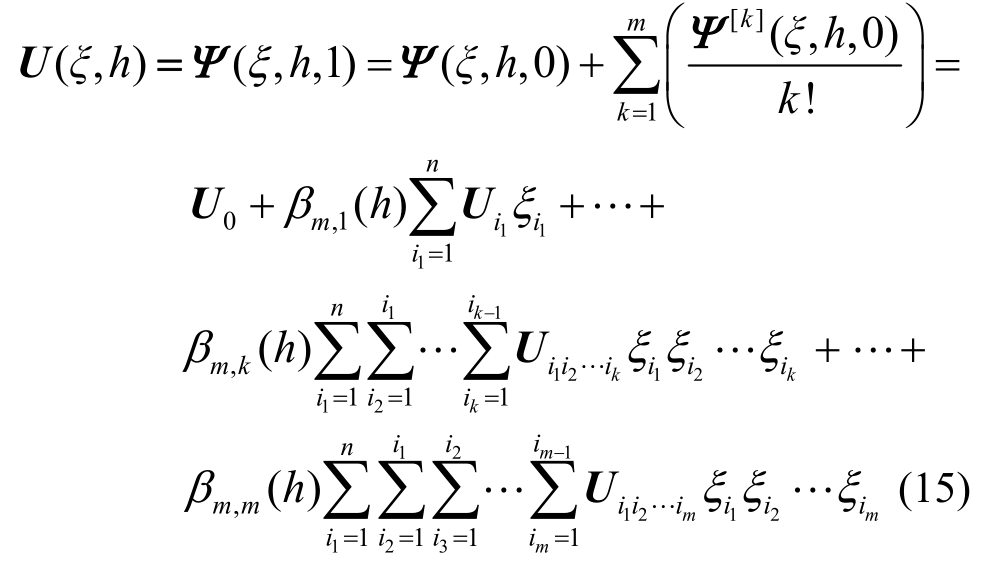
式中，βm,k(h)为：
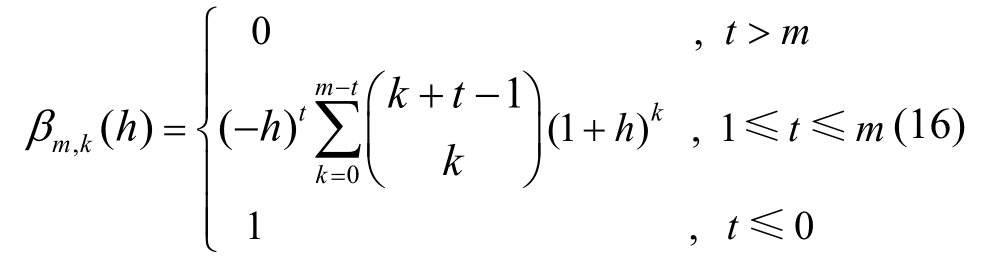
βm,k(h)称作趋近函数，此函数中含有一待定参数h，其取值在-2～0，在同伦分析方法中，此趋近函数可直接影响到表达式(15)的收敛范围，具体收敛性质和证明可参见文献[18,20]。
2.2 同伦级数表达式的降维策略
通过2.1节的方法得到随机结构的同伦级数表达式，理论上可以取到无穷多阶，但在实际工程问题的求解中，考虑到计算成本，只能取有限项作为近似解，同时考虑到当结构随机参数的数量很多时，高阶项的交叉项数目会急剧增加，也会引起难以承受的计算工作量，故本节提出了一种可以显著提高计算效率同时又尽可能保证结果精度的降维策略。
对于一含n个随机变量ξ={ξ1,ξ2,…,ξn}的系统，对于其静力位移响应的同伦级数表达式(15)，此级数表达式中除零阶项U0以外的任意一项均可表示为
的形式，其中Γ（h）为趋近函数和一确定性向量的乘积。li(i=1,2,…,n)是任意自然数，定义当l1,l2,…,ln中有q个不为0，其余均为0时，称此时的
为q维交叉项。例如，当q=1时，其形式为
只含一个随机变量；当q=2时，其形式为
只含两个随机变量。倘若在同伦级数表达式(15)中只保留q=1维的交叉项，所得到的级数形式称为单变量同伦级数解(HSFEM-1)；倘若在同伦级数表达式(15)中只保留q≤2维的交叉项，所得到的级数形式称为双变量同伦级数解(HSFEM-2)，以此类推，当取q≤n时为完整的同伦级数表达式。
考虑到实际的可操作性，式(15)只取到有限展开阶数，用符号
代表同伦级数解，下标m代表级数的展开阶数，上标q表示级数中至多包含q维的交叉项，那么这样就不可避免地产生近似误差，而此误差可以通过趋近函数中适当的h值来尽可能减小。
2.3 趋近函数中参数h值的确定
在获得降维的同伦级数表达式后，表达式中只有趋近函数βm,k(h)中的参数h的值是未知的，采用如下方式来确定h的取值并同时使该同伦级数解尽可能逼近真实值。
对于一含有N个自由度，n个随机参数{ξ1,ξ2,...,ξn }的静力响应系统，设这些随机参数对应的均值和均方差分别为{μ1,μ2,...,μn }和{σ1,σ2,...,σn}。在这n个变量所组成的随机样本空间内选取n个样本，其样本坐标分别为ξ1=[ησ1,0,...,0]，ξ2=[0,ησ2,...,0]，…，ξn=[0,0,...,ησn ]。η是处于2.5～3的一常数，这n个样本点的确定性节点位移向量d(ξi),i=1,2,…,n ,可以通过式(1)直接得到，它们也是这些样本点的精确值。另一方面，对于这n个样本点，也可以将其坐标代入到同伦级数表达式中得到n个近似解
注意到这些近似解在代入样本坐标后均为只含一个未知参数h的N维向量函数。对于第j自由度，做目标函数
分别对应于
的第j个自由度的位移。通过优化目标函数zj(h)便可找到一合适的h值令同伦级数近似解与真实解的误差尽可能地小。
总结来说，通过同伦分析方法来求解随机结构的静力响应可按照以下步骤来进行：
1) 构造形如式(4)的随机刚度矩阵，例如采用Karhunen-Loéve展开来离散结构的弹性模量随机场；采用式(5)来表示随机外荷载；
2) 利用式(6)构造零阶变形方程，并按照2.1节中的方法推导得到结构位移响应的同伦级数表达式中的各阶确定性向量系数，并按2.2节方法进行降维和降阶处理，一般取单变量同伦级数(HSFEM-1)和双变量同伦级数(HSFEM-2)；
3) 按照2.3节中的方法通过寻找目标函数zj(h)的最小值来确定趋近函数中的参数h的取值；
4) 通过同伦级数近似解来计算响应的概率统计特性，如前四阶矩和概率密度曲线。
3 算例分析
算例1.如图1所示，一6 m长的变截面悬臂梁，AB和BC两段长均为3 m，在梁的端部有一随机集中力荷载F。考虑梁抗弯刚度和梁端集中力的随机性，AB和BC两段抗弯刚度以及集中荷载的具体表达形式如式(17)：
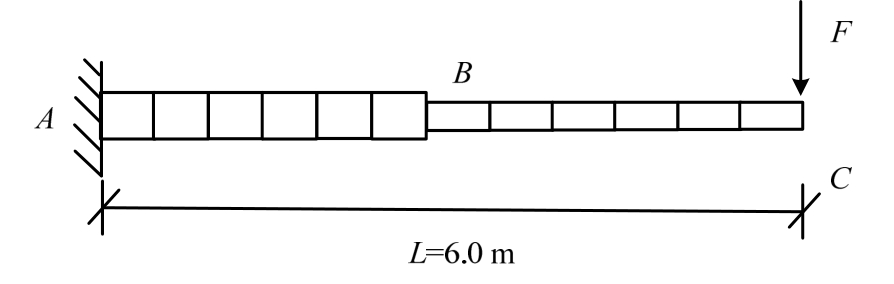
图1 变截面悬臂梁端
Fig.1 Variable cross-section cantilever beam
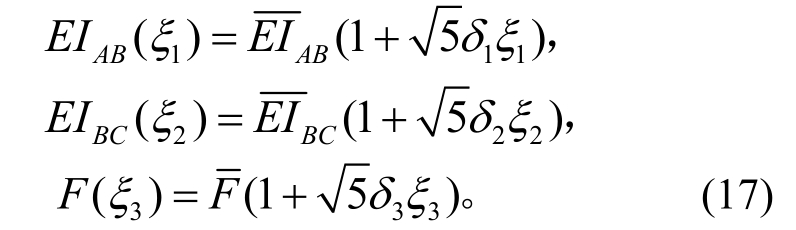
其中，
三个随机变量ξi(i=1,2,3)均服从贝塔分布，其概率密度函数为
是相应于两段抗弯刚度及外荷载的变异系数。本算例中假设这三个变异系数均为0.2。该悬臂梁模型被划分为12个单元，每个单元节点考虑挠度和转角两个自由度。本算例采用广义的正交多项式展开法(GPC)，展开阶数分别取2阶和4阶；本文的双变量同伦分析方法(HSFEM-2)，展开阶数分别取2阶～6阶，来求解悬臂梁端点的竖向挠度，并以采用20万样本的直接蒙特卡洛法的结果作为参照，来说明所提方法的精度和计算效率。
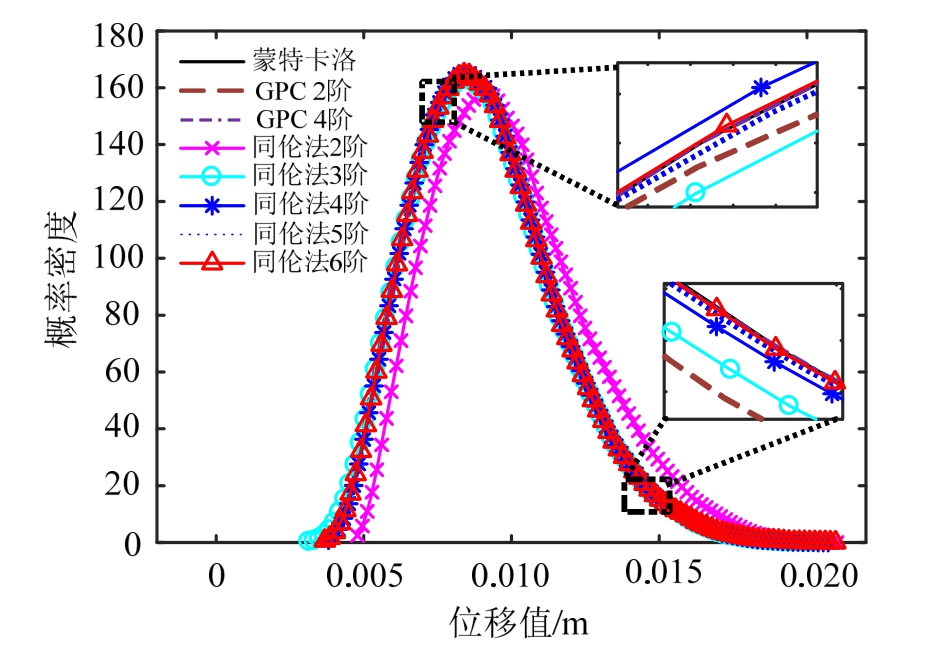
图2 悬臂梁端点位移的概率密度图
Fig.2 PDFs of the displacement at the end of the cantilever beam
图2为利用各方法获得的悬臂梁端点挠度的概率密度曲线，通过与蒙特卡洛的结果相比较发现：本文方法的2阶展开在变异系数较大的情况下存在一定的误差，3阶展开式便可以获得较满意的结果，4阶以上的展开式就可以获得十分高的计算精度，越高阶展开的结果就越逼近蒙特卡洛的结果。为了进一步比较本文方法与GPC法的计算精度，表1列出了各种方法求解端点位移值的前4阶矩值，即均值、均方差、偏度和峰度。可以看出，同伦法3阶展开与GPC 2阶展开精度相当，同伦法6阶展开与GPC 4阶展开精度相当，这也可以在图1的局部放大图中得以证实。为了比较各方法的计算效率，图3列出了两种方法不同展开阶数的求解时间，所有计算时间均除以同伦分析法2阶展开的求解时间，转化成其倍数。可以发现在本算例中，即使同伦分析法6阶展开的计算时间也少于GPC法2阶展开。考虑当计算精度相当时，GPC 2阶展开约为同伦法3阶展开的7倍，GPC 4阶展开约为同伦法6阶展开的20倍，同时，同伦法6阶展开的计算时间仅为蒙特卡洛模拟法的1/550，由此可知，利用本文方法在求解随机结构静力响应时，在保证较高计算精度时仍有很好的计算效率。
表1 悬臂梁端点位移的前四阶统计矩
Table 1 First four moments of the displacement at the end of the cantilever beam
统计矩 蒙特卡洛 GPC 2阶展开 GPC 4阶展开 同伦法2阶展开同伦法3阶展开同伦法4阶展开 同伦法5阶展开 同伦法6阶展开均值 0.0092 0.0092 0.0092 0.0100 0.0091 0.0092 0.0092 0.0092均方差 0.0025 0.0025 0.0025 0.0026 0.0025 0.0025 0.0025 0.0025偏度 0.6123 0.5569 0.6116 0.6203 0.5430 0.6098 0.6031 0.6125峰度 3.2621 3.0057 3.2565 3.0867 3.1274 3.2298 3.2435 3.2580
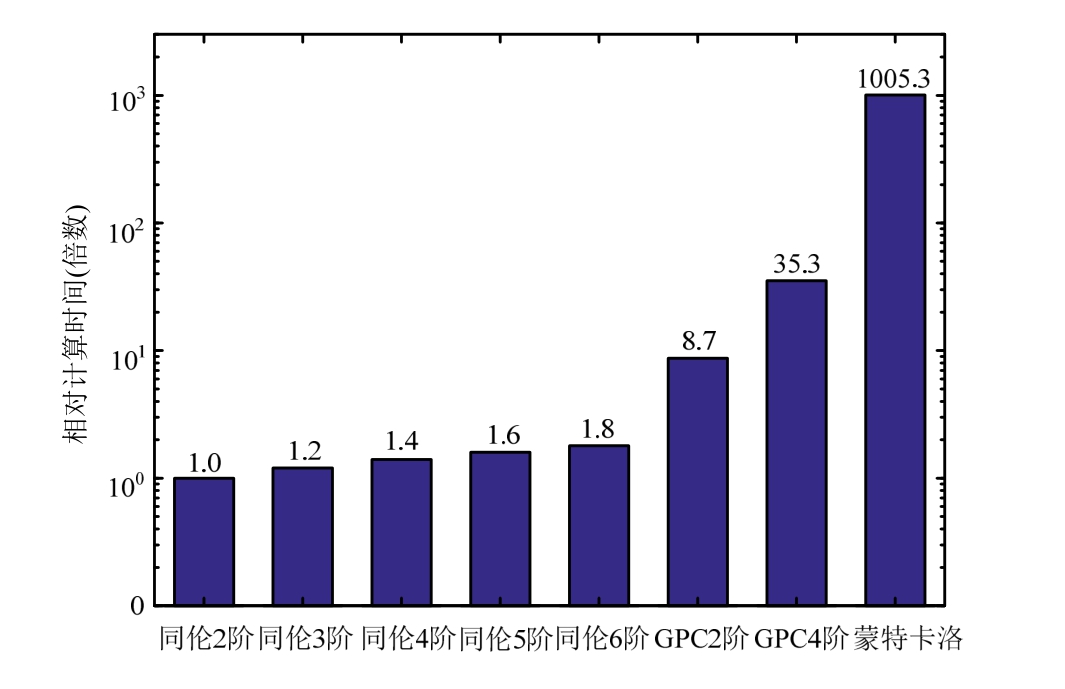
图3 不同方法的计算时间比较
Fig.3 Comparison of the calculating time by different methods
算例2. 本算例中将考虑同伦分析方法在随机结构几何非线性分析中的应用，考虑如图4所示的一平面桁架拱结构，拱径为R=100 m，共有41根杆件，杆件截面面积均为0.15 m2，拱角28.08°，径向杆件长2 m，在桁架中间的顶点处有一大小为100 kN的集中力。桁架的弹性模量的分为中间四跨和其余部分两个区(见图5)，其值分别为E1和E2。考虑弹性模量的随机性，假设E1和E2均服从贝塔分布，均值都为1×105 kN/m2，以桁架拱中点的竖向挠度值为目标进行统计分析。首先对弹性模量取均值时的确定性桁架拱中点位移进行分析，图6画出了此种情况下中点挠度的荷载位移曲线，可以看到该结构位移与荷载呈明显的非线性关系，当集中荷载值为100 kN时对应的挠度值为1.908 m。
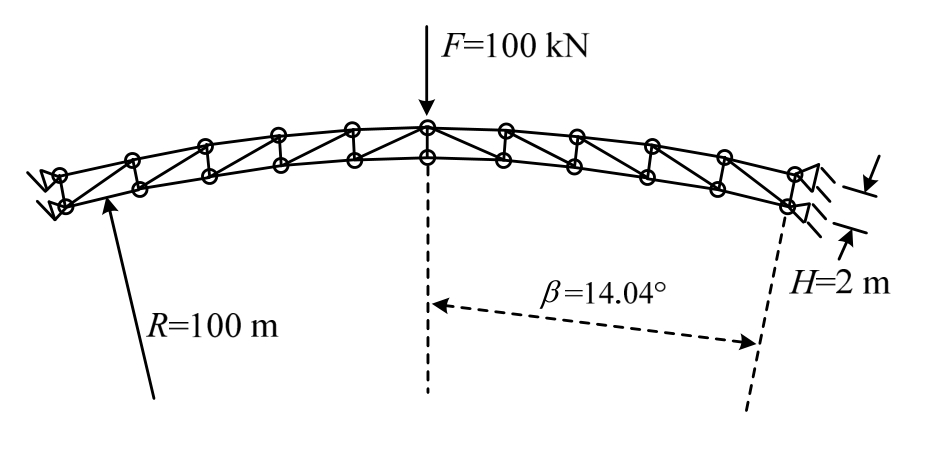
图4 静力荷载作用下的桁架拱结构
Fig.4 Plane truss arch under static load
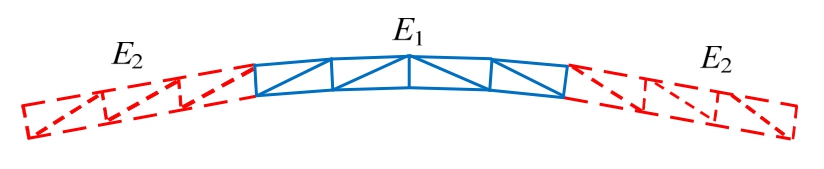
图5 桁架拱结构的弹性模量分区
Fig.5 Partition of the random elastic modulus
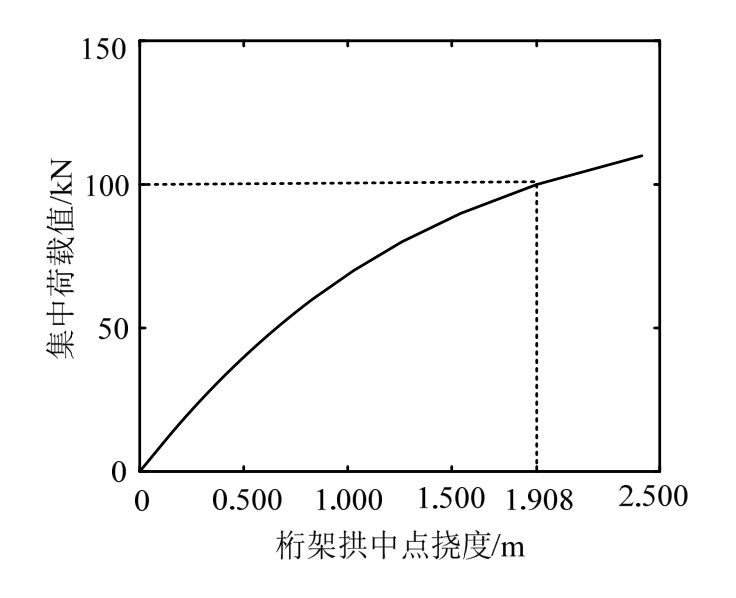
图6 确定性桁架拱结构中点的荷载位移曲线
Fig.6 Deterministic deflection at the center of the truss arch
设δ1和δ2分别是弹性模量E1和E2的变异系数，取δ1=0.05，δ2分别取0.05、0.10、0.15和0.20，采用6阶展开的单变量同伦分析法，6阶展开的双变量同伦分析法、蒙特卡洛模拟法(100000样本)三种方法来求解挠度的前4阶统计矩。其中同伦分析方法表达式中的各阶确定性系数可以参考文献[21]采用相同的方法获得，即同伦级数表达式中各阶的确定性系数的递推形式与文献中的递推随机有限元方法相同，然后在此基础上将本文中的趋近函数乘在各阶系数前即可得到最终表达式。表2～表5分别列出了利用各方法算得的桁架拱中点挠度值的均值、均方差、偏度和峰度。表2中均值为负值代表位移值向下。
表2 桁架拱中点挠度的均值(δ1=0.05)
Table 2 Mean of the deflection at the central point of the truss arch (δ1=0.05)
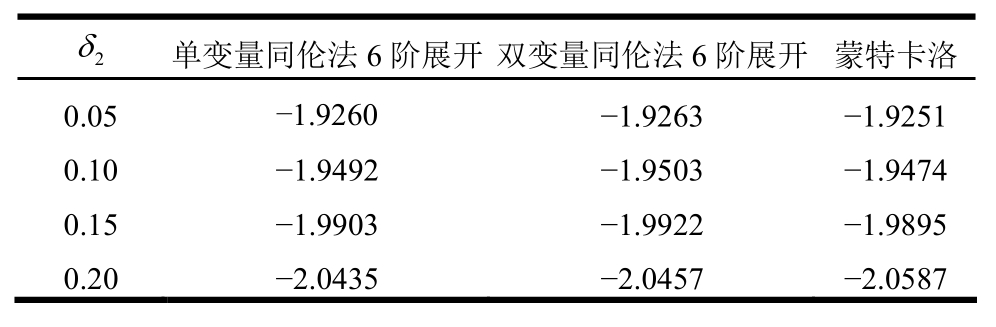
2δ 单变量同伦法6阶展开双变量同伦法6阶展开蒙特卡洛0.05 -1.9260 -1.9263 -1.9251 0.10 -1.9492 -1.9503 -1.9474 0.15 -1.9903 -1.9922 -1.9895 0.20 -2.0435 -2.0457 -2.0587
表3 桁架拱中点挠度的均方差(δ1=0.05)
Table 3 Standard deviation of the deflection at the central point of the truss arch (δ1=0.05)
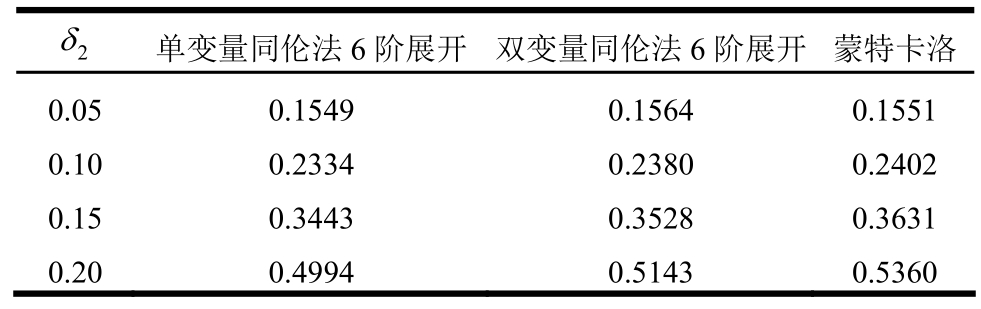
2δ 单变量同伦法6阶展开 双变量同伦法6阶展开蒙特卡洛0.05 0.1549 0.1564 0.1551 0.10 0.2334 0.2380 0.2402 0.15 0.3443 0.3528 0.3631 0.20 0.4994 0.5143 0.5360
表4 桁架拱中点挠度的偏度(δ1=0.05)
Table 4 Skewness of the deflection at the central point of the truss arch (δ1=0.05)
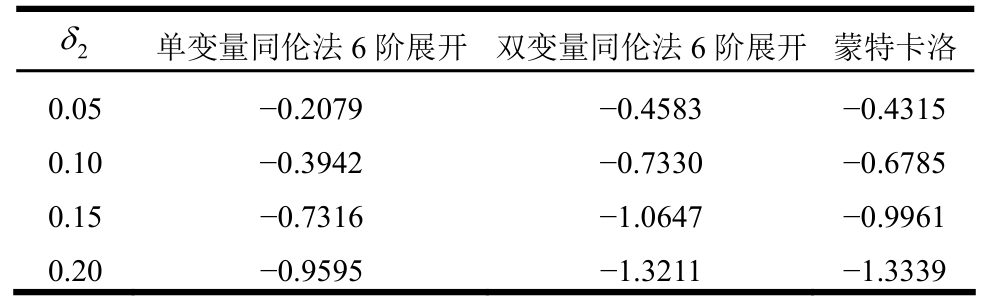
2δ 单变量同伦法6阶展开 双变量同伦法6阶展开蒙特卡洛0.05 -0.2079 -0.4583 -0.4315 0.10 -0.3942 -0.7330 -0.6785 0.15 -0.7316 -1.0647 -0.9961 0.20 -0.9595 -1.3211 -1.3339
表5 桁架拱中点挠度的峰度(δ1=0.05)
Table 5 Kurtosis of the deflection at the central point of the truss arch (δ1=0.05)
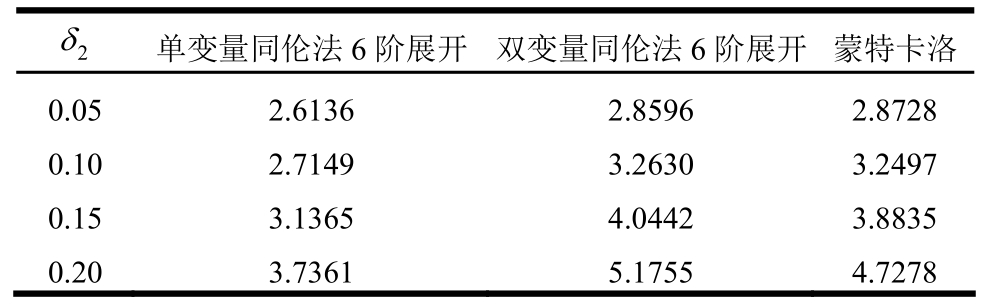
2δ 单变量同伦法6阶展开 双变量同伦法6阶展开蒙特卡洛0.05 2.6136 2.8596 2.8728 0.10 2.7149 3.2630 3.2497 0.15 3.1365 4.0442 3.8835 0.20 3.7361 5.1755 4.7278
通过表2～表5的结果可见，随着变异系数的增大，中点挠度均值较均值点的确定性位移有增大的趋势；单变量同伦法，在均值和均方差结果上都很好，对偏度和峰度的拟合随着变异系数的增大会有明显的误差，尤其是偏度，即使在δ2=0.05时也没有得到满意的结果。对双变量同伦法而言，在变异系数较大的情况下前四阶矩结果也都很好，与蒙特卡洛的结果相比，其前四阶矩最大误差分别为0.6%、4.1%、8.0%和9.4%。在计算效率上，三种方法的计算时间分别为2.61 s、6.88 s和6563.7 s，由于几何非线性分析时对每一个样本进行确定性有限元法求解时都涉及迭代，所以蒙特卡洛的计算时间远远超过本文方法，约为双变量同伦法的1000倍，可见本文方法在处理较大变异性下的几何非线性问题时仍可获得较好的结果和很高的计算效率。
4 结论
本文利用同伦分析方法重新构造含随机参数结构的静力位移方程，获得了含随机变量和趋近函数的结构位移的同伦级数解，并进一步通过降维策略来大幅减少表达式的求解工作量。数值算例表明，双变量同伦法三阶展开的计算精度与GPC法二阶展开相当，前者计算时间约为后者的1/7；双变量同伦法六阶展开的计算精度与GPC法四阶展开相当，前者计算时间约为后者的1/20。
同时，本文方法也可方便的应用于随机结构的几何非线性分析中，在随机参数变异性较大的情况下仍能有较好的计算精度，而且具有很高的计算效率。由于本方法推导过程简便且易于编程，也可进一步应用于材料非线性分析中去。总而言之，本文为随机结构的静力响应分析提供了一种可选择的新的高效求解方法。
[1]Stefanou G.The stochastic finite element method: Past,present and future [J].Computer Methods in Applied Mechanics & Engineering, 2009, 198(9): 1031―1051.
[2]Niederreiter H, Spanier J.Monte carlo and quasi-monte carlo methods [M].Berlin: Springer, 2000: 10―26.
[3]Melchers R E.Importance sampling in structural system[J].Structural Safety, 1989, 6(1): 3―10.
[4]Kleiber M, Hien T D.The stochastic finite element method [M].Chichester: John Wiley, 1992: 47―53.
[5]Kamiński M.On the dual iterative stochastic perturbation-based finite element method in solid mechanics with Gaussian uncertainties [J].International Journal for Numerical Methods in Engineering, 2015, 104(11):1038―1060.
[6]Yamazaki F, Shinozuka M, Dasgupta G.Neumann expansion for stochastic finite element analysis [J].Journal of Engineering Mechanics, 1988, 114(8): 1335―1354.
[7]王相玉.随机有限元方程的解法与误差及随机介质的形态描述研究[D].北京: 清华大学, 2015.Wang Xiangyu.Research on solution methods, error estimations for stochastic finite element equation and morphology descriptions of random media [D].Beijing:Tsinghua University, 2015.(in Chinese)
[8]Wang X Y, Cen S, Li C F, et al.A priori error estimation for the stochastic perturbation method [J].Computer Methods in Applied Mechanics & Engineering, 2015, 286(3): 1―21.
[9]Ghanem R G, Spanos P D.Stochastic finite elements: A spectral approach [M].New York: Springer-Verlag, 1992:47―59.
[10]Li Y J, Huang B, Li C Q.Hybrid perturbation-Galerkin methods for structural reliability analysis [J].Probabilistic Engineering Mechanics, 2017, 48: 59―67.
[11]Gao W, Kessissoglou N J.Dynamic response analysis of stochastic truss structures under non-stationary random excitation using the random factor method [J].Computer Methods in Applied Mechanics & Engineering, 2007,196(25): 2765―2773.
[12]陈建军, 马洪波, 马娟, 等.基于随机因子的结构分析方法[J].工程力学, 2012, 29(4): 15―23.Chen Jianjun, Ma Hongbo, Ma Juan, et al.Structural analysis method based on random factor [J].Engineering Mechanics, 2012, 29(4): 15―23.(in Chinese)
[13]Rahman S, Xu H.A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics [J].Probabilistic Engineering Mechanics,2004, 19(4): 393―408.
[14]Falsone G, Impollonia N.A new approach for the stochastic analysis of finite element modelled structures with uncertain parameters [J].Computer Methods in Applied Mechanics & Engineering, 2002, 191(44):5067―5085.
[15]杨绿峰, 李朝阳.结构随机分析的向量型层递响应面法[J].工程力学, 2012, 29(11): 58―64.Yang Lüfeng, Li Zhaoyang.Vectorial cooperative response surface method for stochastic analysis of structures [J].Engineering Mechanics, 2012, 29(11):58―64.(in Chinese)
[16]Liao Shijun.Numerically solving non-linear problems by the homotopy analysis method [J].Computational Mechanics, 1997, 20(6): 530―540.
[17]吉猛, 姜潮, 韩硕.一种基于同伦分析的结构可靠性功能度量法 [J].计算力学学报, 2015, 32(2): 149―153.Ji Meng, Jiang Chao and Han Shuo.A performance measure approach of structural reliability based on homotopy analysis [J].Chinese Journal of Computational Mechanics, 2015,32(2): 149―153.(in Chinese)
[18]Huang B, Zhang H, Phoon K K.Homotopy approach for random eigenvalue problem [J].International Journal for Numerical Methods in Engineering, 2018, 113(3): 450―478.
[19]Li C C.Optimal discretization of random fields [J].Journal of Engineering Mechanics, 1993, 119(6): 1136―1154.
[20]廖世俊.广义泰勒原理: “同伦分析方法”之有效性的一个数理逻辑证明[J].应用数学和力学, 2003, 24(1):47―54.Liao Shijun.On a generalized Taylor theorem: A rational proof of the validity of the so called homotopy analysis method [J].Applied Mathematics and Mechanics, 2003,24(1): 47―54.(in Chinese)
[21]黄斌, 索建臣, 毛文筠.随机杆系结构几何非线性分析的递推求解方法[J].力学学报, 2007, 39(6): 835―842.Huang Bin, Suo Jianchen, Mao Wenjun.Geometrical nonlinear analysis of truss structures with random parameters utilizing recursive stochastic finite element method [J].Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(6): 835―842.(in Chinese)