世界卫生组织《2015年全球道路安全现状报告》的统计报告显示[1]，每年约有125万人死于道路交通事故，而我国的道路安全状况同样不容乐观。在所有交通事故中，头部在车辆等碰撞载荷作用下发生的创伤性脑损伤(Traumatic Brain Injury, TBI)，成为乘员致死、致伤的主要因素。TBI基于三种不同的分类标准可以分为多种损伤类型：1)基于损伤发生时间的不同，可以分为原发性损伤(Primary Injuries)与继发性损伤(Secondary Injuries)；2)基于损伤发生部位的不同，可以分为弥散性损伤(Diffuse Injuries)与局部损伤(Focal Injuries)；3)基于损伤严重程度的不同，可以分为穿透性损伤(Open Penetrating Injuries)与闭合性损伤(Closed Non-penetrating Injuries)。TBI的具体分类与典型损伤形式如图1所示。基于上述颅脑损伤的分类方法可知，碰撞条件下的闭合性颅脑损伤类型主要包括两大类：集中性脑损伤与弥散性脑损伤。硬脑膜下出血、脑室内血肿与脑组织挫裂伤等是常见的集中性脑损伤，这类损伤易于检测，可形成相关的医学统计数据；而脑震荡、弥散性轴突损伤则是弥散性 脑损伤，对检测设备要求较高。其中，脑组织挫裂伤是一种常见的脑组织器质性损伤，属于原发性的局部脑组织损伤，具有高致死率与高致残率特性。因此，对脑组织挫裂伤开展相关研究，揭示其致伤机理尤为重要。
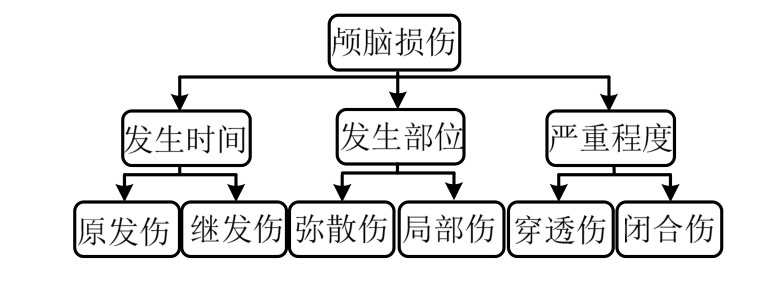
图1 颅脑损伤分类[2]
Fig.1 Traumatic brain injury classification[2]
颅脑损伤的研究方法主要包括尸体实验[3—6]、动物实验[7—8]、生物组织实验[9—10]、物理模型[11—12]与有限元模型[13—18]。尸体实验是最具有说服力的研究方法，为颅脑损伤研究提供了重要实验数据，其中包括Nahum头部碰撞实验[3]、Trosseille尸体撞击试验[4]和Yoganandan 的颅骨断裂试验[5]等。但是，尸体实验的开展受到伦理道德与实验成本等条件的约束，且不能全面反应活体组织在冲击载荷作用下的病理反应。动物实验能够获得脑组织损伤的病理反应，而对应的力学指标通常难以确定和测量，建立两者之间的关系则较为困难。生物组织实验能够直接建立起组织/细胞损伤与力学响应之间的关系，为颅脑损伤研究提供了新的思路。当前，只能进行单一载荷条件下的损伤研究，与实际碰撞损伤情况存在较大差别。物理模型通常对真实头部结构进行合理简化，利于揭示颅脑的动态响应规律，但是不能全面反映颅脑的损伤过程。具有详细解剖学结构的三维头部数值模型可对颅脑损伤过程进行重建，结合动物实验或医学诊断数据，建立损伤与力学响应之间的关系，目前已经成为颅脑损伤机理研究的重要方法。
在大量研究的基础之上，相关学者[19—21]建立了颅脑损伤与头部加速度之间的联系，并确定了相应的损伤准则。但是，这种基于头部加速度的损伤准则不能反映脑组织力学特性(应力、应变与应变率等)的动态演化过程，不能从组织层次上揭示脑组织挫裂伤的致伤机理，具有明显的局限性。Ward等[22]利用头部碰撞实验与有限元数值方法对脑组织挫裂伤的致伤机理进行研究，研究结果表明，挫裂伤与脑组织(拉)压力具有较好的相关性，并提出相应的损伤准则。同时，Takhounts等[23]提出基于脑组织拉力的损伤评价指标Dilatation Damage Measure (DDM)，该指标代表脑组织中低于负压力阈值(-100 kPa)的体积与总体积的比值；并结合动物碰撞试验[24—25]与物理模型[26]研究，确定了脑组织挫裂伤50%发生概率的损伤阈值(7%)。但是，Huang等[27—28]基于简化头部模型对脑组织挫裂伤的研究结果表明，医学上挫裂伤的易发区域与脑组织剪切应力的分布区域是基本一致的，而与脑组织压力的分布则没有明显的相关性。Mao等[29]进一步开展了老鼠头部撞击实验，并建立三维数值模型对碰撞实验进行数值模拟，分析对比脑组织挫裂伤病理区域与对应的力学损伤指标来揭示脑组织挫裂伤的致伤机理。研究结果表明，脑组织三个损伤指标(最大主应变、最大剪切应变与应变能密度)的分布趋势，与脑组织挫裂伤的发生区域具有较好的吻合性，并确定了相应的损伤准则；而冠状面内的切应变、颅内压力等损伤指标的吻合性则相对较差。
由上述分析可知，脑组织挫裂伤的损伤机理依然没有明确，有待于进一步研究。本文基于高仿真头部数值模型与脑组织挫裂伤医学统计数据对这一问题进行数值模拟研究。本文首先建立充分反映颅脑生理结构的三维头部数值模型，利用Nahum死尸头部碰撞试验对头部碰撞模型的有效性进行验证。同时，基于验证的头部模型对枕部碰撞过程进行数值模拟，并对比前额碰撞的模拟结果，分析脑组织压力与Mises应力的动态响应规律；进一步结合脑组织挫裂伤的医学统计数据，揭示其损伤机理，建立相应的损伤准则。
1 三维头部数值模型
1.1 三维头部有限元模型
图2显示了人体头部的生理解剖结构。在颅脑结构中，脑组织包括大脑、小脑与脑干三部分，其表面有3层被膜包裹，由里向外依次为软脑膜、蛛网膜和硬脑膜。软脑膜薄而富含血管，紧贴脑表面并深入脑的沟裂中。蛛网膜是半透明结缔组织薄膜，其与软脑膜之间存在由蛛网膜小梁支撑的蛛网膜下腔，脑脊液(Cerebral Spinal Fluid，CSF)在该腔内循环流动，并且有较大血管分布其中。硬脑膜为双层膜结构，外层膜与颅骨紧密结合；内层膜呈套状包被脑，在颅腔内分化为大脑镰与小脑幕，两者将颅腔分为左、右与下三个腔体。与硬脑膜外侧紧密结合的颅骨，具有典型的类三明治结构，其内、外为刚度与密度较大的骨密质，中间为骨松质。
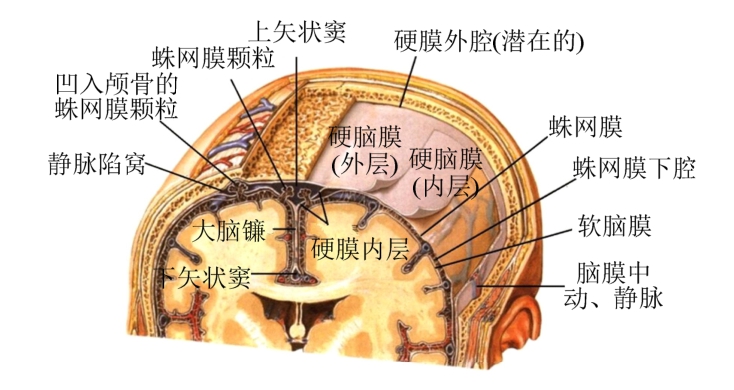
图2 头部解剖结构示意图[30]
Fig.2 Schematic diagram for anatomical structures of head [30]
本文基于颅脑核磁共振切片建立了三维头部有限元模型，单元尺寸约为2 mm～3 mm，共有303588个单元与530954个节点，充分考虑了人体头部的生理结构与相关细节，如图3所示。该模型包括脑组织(大脑、小脑与脑干)，膜结构(软脑膜、蛛网膜、硬脑膜、大脑镰与小脑幕)，脑脊液，颅骨，皮肤与颈部。其中，颅骨采用类三明治结构进行表征，里外两层为骨密质，中间层为骨松质，充分考虑颅骨结构对颅脑动态响应的影响。
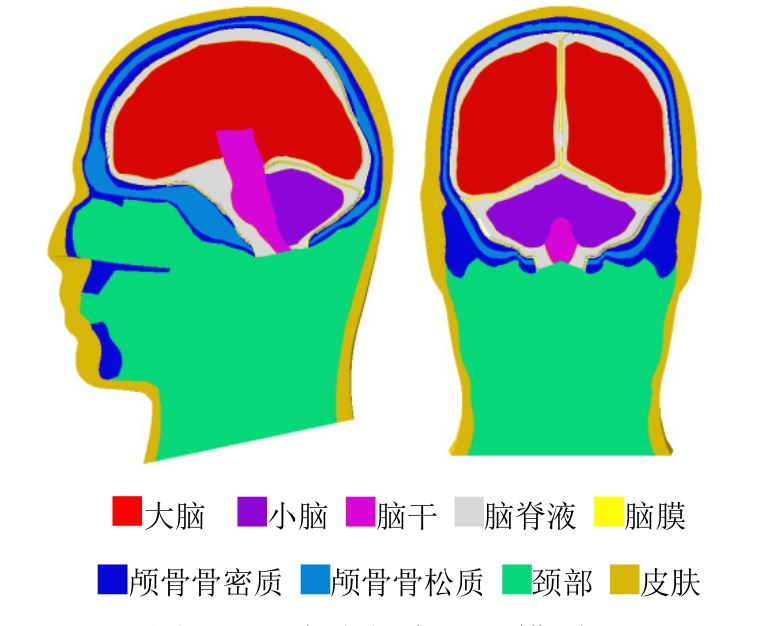
图3 三维头部有限元模型
Fig.3 3-D finite element model of human head
1.2 本构模型与材料参数
本文采用粘超弹性本构模型来表征脑组织在碰撞载荷下的动态响应特性[31]。利用Mooney-Rivlin模型表征其超弹特性，对应的应变能函数定义为：
式中：U为应变势能；C10、C01与D1为温度相关的材料参数(2/D1为体积模量K)；Jel为弹性体积比；I1和I2分别为第一与第二偏应变不变量。
对于脑组织的粘弹部分，第二Kirchhoff 应力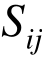
通过卷积形式可表示为：
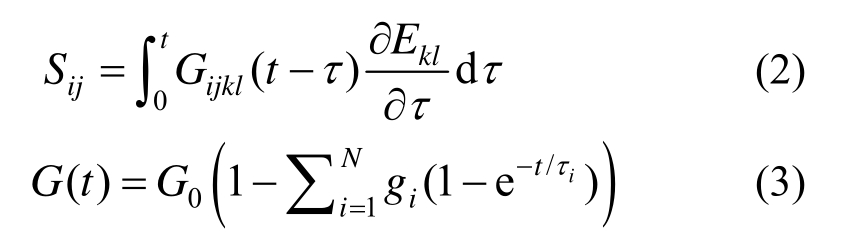
式中：Ekl为Green应变张量；G(t)为t时刻的剪切松弛模量，采用Prony级数进行展开；G0为瞬态剪切模量；gi和τi分别为无量纲剪切松弛模量参数与松弛时间。对应的Cauchy应力σij可表示为：
式中：F为变形梯度矢量；J为变换矩阵的雅克比行列式。由于脑组织接近不可压缩，不考虑体积变形的粘弹特性，相应的无量纲体积模量松弛参数ki均设置为0。
脑脊液与水的性质较为接近，在蛛网膜下腔内流动；该腔是由蛛网膜小梁支撑的腔体，能够传递剪切变形，如图2所示。为了便于建模，头部模型中的脑脊液是物理脑脊液、蛛网膜小梁与较大血管的综合体。对于脑脊液(CSF)的本构模型，相关文献[14—15]直接采用剪切模量相对很小的线弹性模型来进行表征。为了真实反映脑脊液与蛛网膜小梁的力学特性，本模型中采用Mie-Gruneisen状态方程表征脑脊液的不可压缩特性，同时采用较小的剪切模量表征蛛网膜小梁的剪切传递特性[16-18]。Mie-Gruneisen状态方程表示为：
式中：P为压力；C0为声速；ρ0和ρ分别为初始密度与当前密度；s为无量纲材料参数，建立应力波速 Us与粒子速度 UP之间的关系，取为1.921[17]。
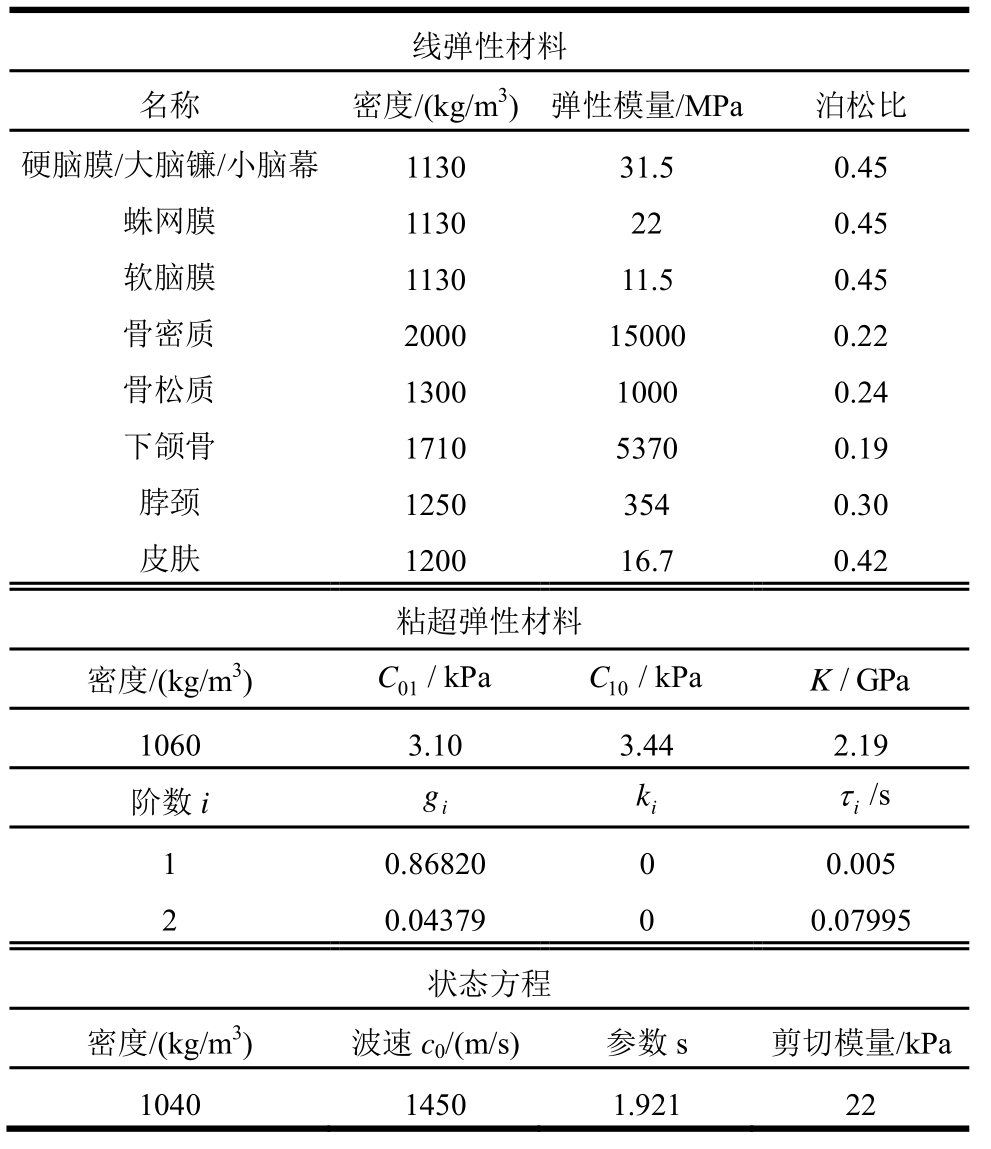
头部模型中的软脑膜、蛛网膜、硬脑膜、大脑镰、小脑幕、头骨、颈部与皮肤，均采用线弹性本构模型进行表征。基于头部模型中各组织所采用的本构模型，并参考相关文献[15—18,31]，确定相应的材料参数，汇总于表1。
表1 头部模型材料参数
Table 1 Material properties for the head model
线弹性材料 名称 密度/(kg/m3)弹性模量/MPa 泊松比 硬脑膜/大脑镰/小脑幕 1130 31.5 0.45 蛛网膜 1130 22 0.45 软脑膜 1130 11.5 0.45 骨密质 2000 15000 0.22 骨松质 1300 1000 0.24 下颌骨 1710 5370 0.19 脖颈 1250 354 0.30 皮肤 1200 16.7 0.42 粘超弹性材料 密度/(kg/m3)01a/kPC 10a/kPC a/GPK 1060 3.10 3.44 2.19 阶数iigikiτ/s 1 0.86820 0 0.005 2 0.04379 0 0.07995 状态方程 密度/(kg/m3) 波速c0/(m/s) 参数s 剪切模量/kPa 1040 1450 1.921 22
1.3 接触关系与边界条件
基于颅脑的生理结构并参考相关文 献[15—18, 31]，三维头部数值模型中的各部分组织之间的接触关系定义为TIE连结。同时，采用状态方程的脑脊液实现了脑组织与颅骨之间的有限滑动，符合颅脑的生理结构。至于数值模型的边界条件，将在下一节对死尸头部碰撞实验模拟时进行讨论。
2 头部碰撞模型验证与仿真
基于上述三维头部数值模型开展颅脑碰撞损伤机理研究，仍需对相应的头部碰撞模型进行有效性验证。Nahum等[3]在1976年进行了人体死尸头部碰撞实验，已成为头部数值模型有效性验证的经典实验。该实验利用运动块体撞击前额部位，利用传感器记录特征部位(前额、颅顶、枕部与颅后窝处)的颅内压力变化过程。由于该头部碰撞实验没有提供与头部发生碰撞块体的材料力学参数，参考Ganpule等[15]进行头部数值模型验证时所使用的方法：将实验中测量所得到的碰撞接触力转化为平均压力作用于前额部位，作用面积为1470 mm2。对应的压力时程曲线如图4所示。
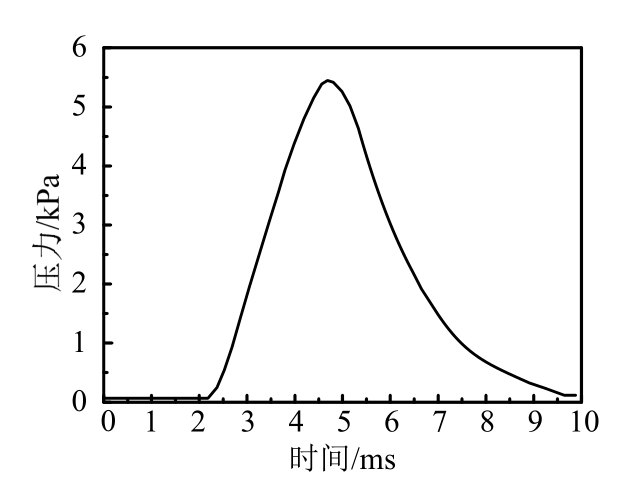
图4 碰撞压力-时间历程曲线
Fig.4 Temporal evolution of the impact pressure
在进行死尸头部碰撞试验时，身体部分为头颈部提供支撑与约束，从而影响头颈部的动态响应过程。但是，对死尸头部碰撞实验进行数值模拟时，出于计算成本的考虑，通常采用头部数值模型。因此，颈部边界条件的合理选择对于获取颅脑动态响应规律就显得尤为重要。为了分析边界条件对撞击载荷下颅内压力变化规律的影响，基于ABAQUS与三维头部数值模型建立了头部碰撞模型，采用三种不同的边界条件对头部碰撞实验进行数值模拟。这三种边界条件分别为自由边界条件，竖向约束边界条件与固定边界条件，对应的头部碰撞模型如图5所示。其中，自由边界条件是不对颈部端面进行约束，颈部端面可以进行旋转运动；竖向约束边界条件仅对颈部端面竖向位移进行约束，颈部端面只能在水平面上进行运动；而固定边界条件则完全限制颈部端面的运动。
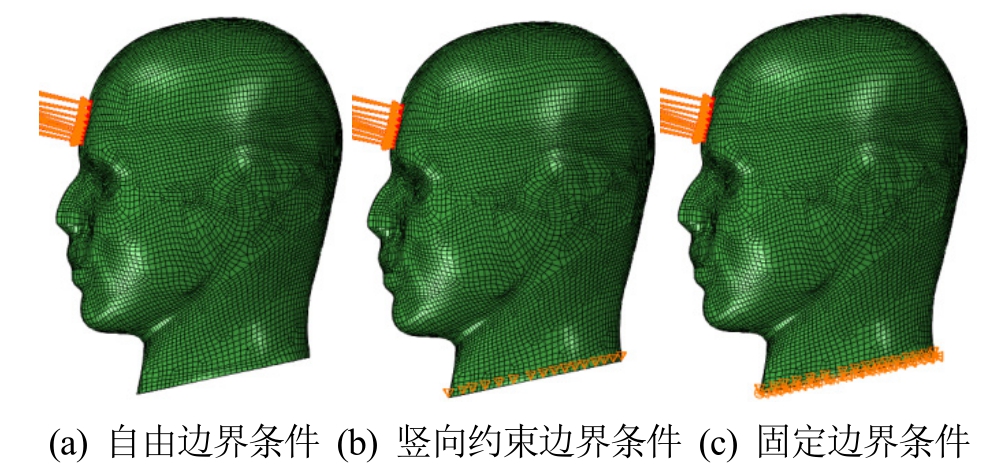
图5 三种不同边界条件的头部碰撞模型
Fig.5 3-D head model with three different boundary conditions
基于上述头部碰撞模型，可获取颅内压力在不同边界条件下的动态响应过程，与头部碰撞实验结果进行对比分析。为减小采样位置对模拟结果与实验结果对比分析的影响，在前额、颅顶、枕部与颅后窝处各取三个特征点的颅内压力时程曲线，特征点位置如图6所示。
首先，提取在自由边界条件下特征点处颅内压力的模拟结果，与头部碰撞实验结果进行对比，两 者具有较好的吻合性，如图7所示。前额与颅顶处的颅内压力在整个碰撞过程中基本上均为正压，表征这两处脑组织处于受压缩状态。同时，前额处的颅内压力要明显高于颅顶处的相应值，这与头部简化模型的理论解相吻合[32]。相比而言，枕部与颅后窝处的颅内压力在碰撞前期阶段为负压，表征脑组织处于拉伸状态，相应的压力幅值较为接近。但是，这两处的颅内压力在后期阶段会发生“反转”，由负压转变为正压，正压幅值相比于负压幅值则相对较小。
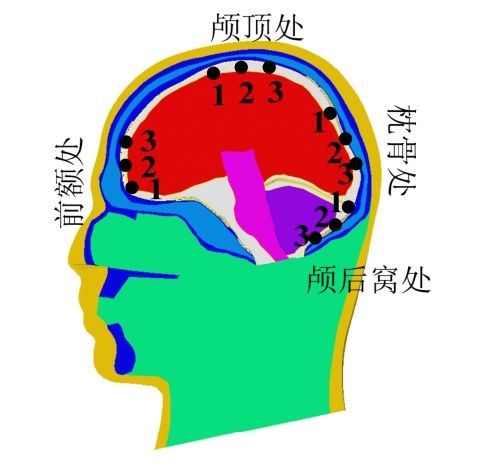
图6 颅内压力测点位置
Fig.6 Locations of measure points for the intracranial pressure
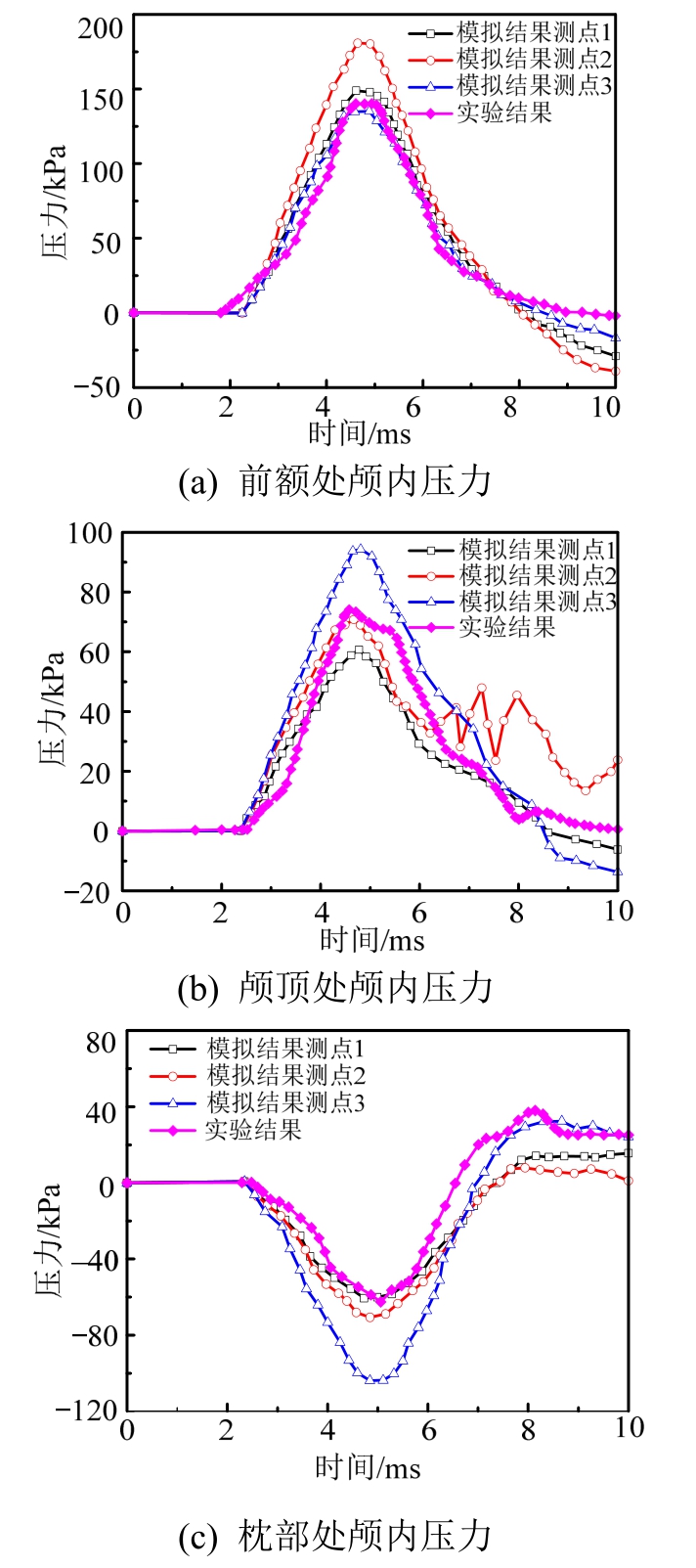
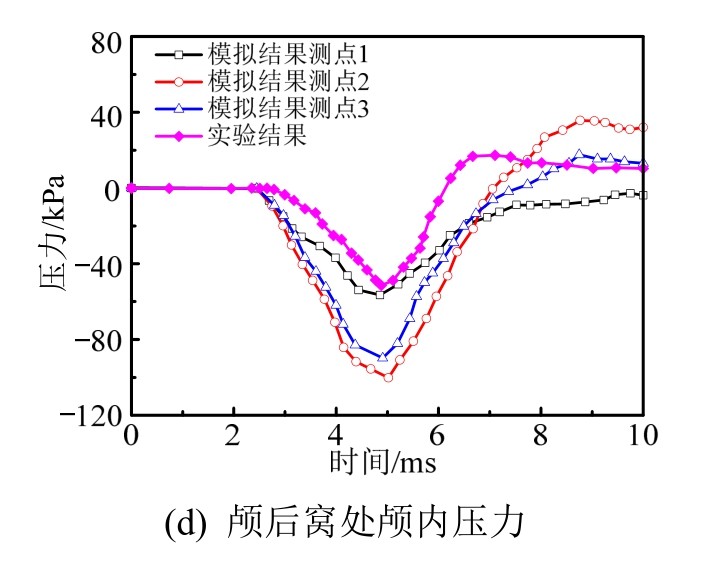
图7 自由边界条件下模拟结果与实验结果对比
Fig.7 Intracranial pressure of numerical results with free boundary condition compared to experimental results
对于竖向约束与固定边界条件，模拟结果与实验结果则存在较大的偏差，如图8所示。约束边界条件的引入，使得前额与枕部处的颅内压力均出现 “反转”现象。竖向约束边界条件下的“反转”拉(压)力的幅值与之前的压(拉)力幅值较为接近；而固定边界条件下前者幅值则远远大于后者。上述模拟结果与实验结果是完全背离的。但是，在头部碰撞的前期阶段(t＜4.5 ms)，两种边界条件对应的模拟结 果与实验结果是基本吻合的，这表明前期阶段的颅内压力演化过程与颈部约束条件是基本无关的。
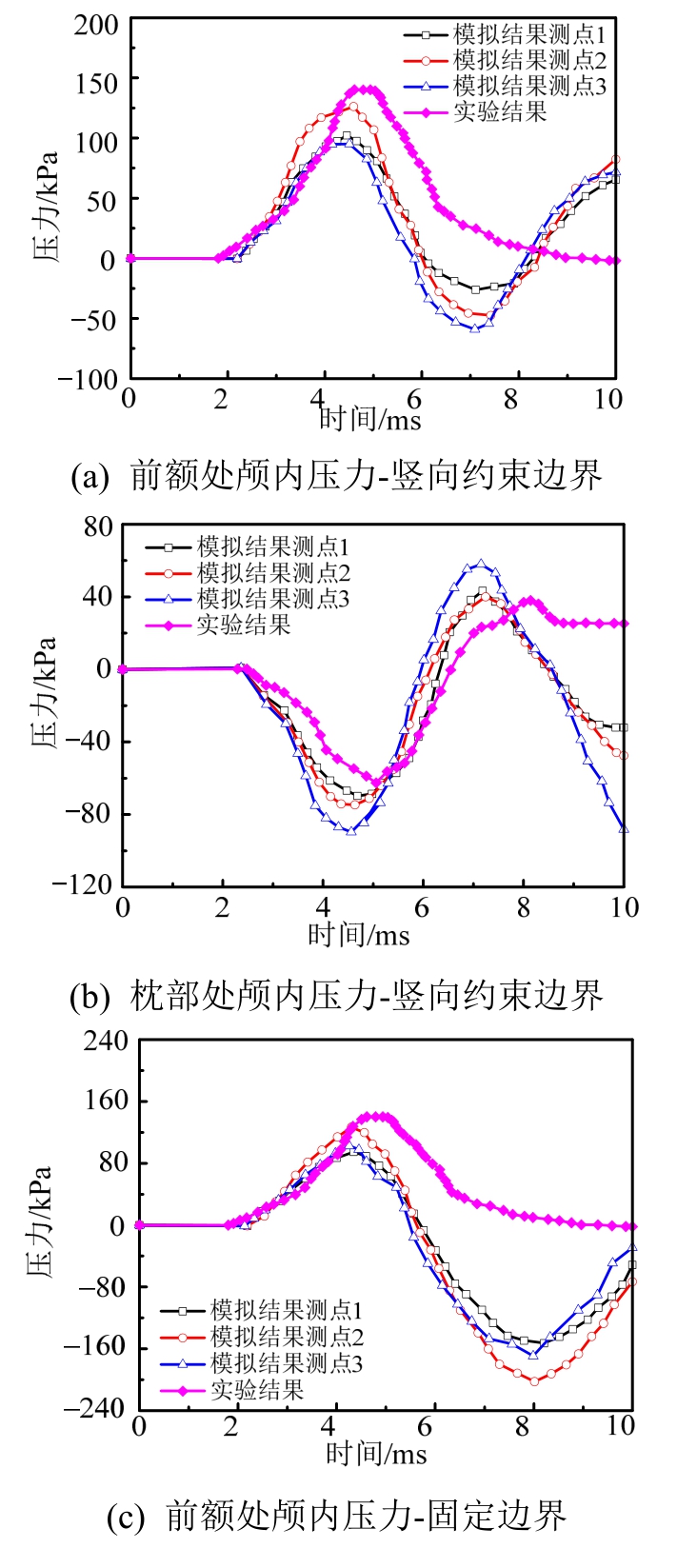
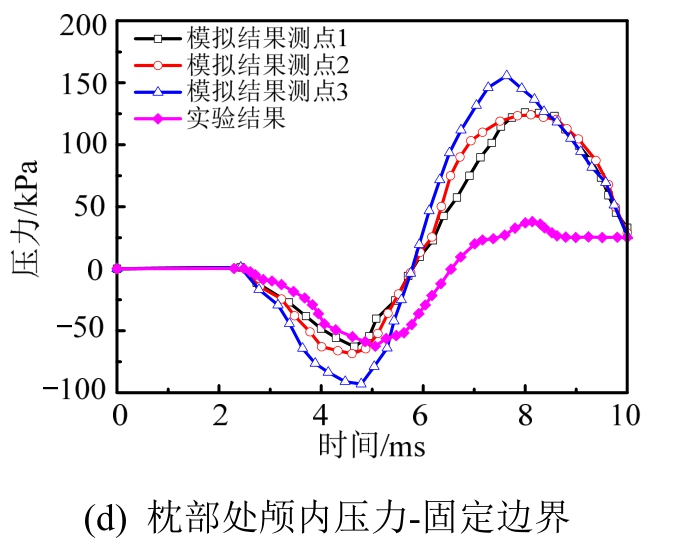
图8 竖向约束和固定边界条件下模拟结果与实验结果对比
Fig.8 Intracranial pressure from experiments compared to numerical results with vertical and fixed boundary condition
基于自由边界条件下的模拟结果与实验结果具有较好的吻合性，而其它两种边界条件的模拟结果在前期阶段吻合性良好，后期阶段则出现较大的偏差。在碰撞的前期阶段，颅内压力的动态演化过程是应力波主导的物理过程，头部的整体位移则相对很小，与颈部的约束条件基本上是无关的。因此，三种边界条件对应的模拟结果在前期阶段与实验数据都具有较好吻合性。随着载荷的持续作用，头部的整体位移会逐步增大，颈部约束条件会对颅内压力产生显著影响。在碰撞实验过程中，头颈部会发生旋转运动，而通常情况颈部肌肉又处于“松弛”状态。在头部整体位移相对较小的条件下，躯体对头颈部的约束作用基本上是可以忽略的。自由边界条件的头颈部模型在碰撞载荷下发生旋转运动，头部与颈部的相对位移在整个碰撞过程中都是较小的，与碰撞实验的物理过程较为吻合。因此，可以基于自由边界条件的头部模型对这一阶段的动态过程进行数值模拟。而对于竖向约束与固定边界条件，由于颈部边界上存在的外界约束会阻碍头颈部的旋转运动，作用于头部的撞击载荷使其与颈部产生相对位移，该位移对头部产生弹性回复力，并会随着碰撞载荷的持续作用而不断增大。当回复力达到某一阈值时，头部加速度会出现转向，颅骨与脑组织的惯性差异使得两者之间的相对位移由压缩转变为拉伸，反之亦然。因此，颅内压力会出现“反转”波动现象，并随着约束条件的增强而愈加显著。但是，随着头部整体位移的进一步增大，躯体对头颈部的约束作用也会逐渐增强，自由边界条件头部模型也将不再适用。
通过上述分析可知，自由边界条件下头部碰撞模型对应的模拟结果与实验结果具有较好的吻合性，能够较好地反映头部在前期阶段(应力波主导阶段)与中期阶段(头部整体位移较小阶段)的动态响应过程，也初步证实了该头部模型的有效性。
为了进一步验证该模型的有效性，基于上述头部模型对Trosseille等[4]在1992年开展的人体死尸头部碰撞实验进行数值模拟。在该实验中，利用质量为23.4 kg的方向盘以7 m/s的速度撞击面部，并记录撞击过程中额叶、顶叶、枕叶、侧脑室与第三脑室处压力的演化过程。由于方向盘材料、形状以及其与头部的碰撞状况都不明确，本文根据参考文献[33]的载荷加载方法，将实验中测试得到的头部中心加速度施加在头部模型(颅骨设为刚性体)的中心点处。关于额叶、顶叶与枕叶处的压力峰值，模拟结果与实验结果如表2所示，两者具有较好的吻合性，验证了该头部模型的有效性。
表2 模拟结果与实验结果对比
Table 2 Comparisons on the simulation and experimental results
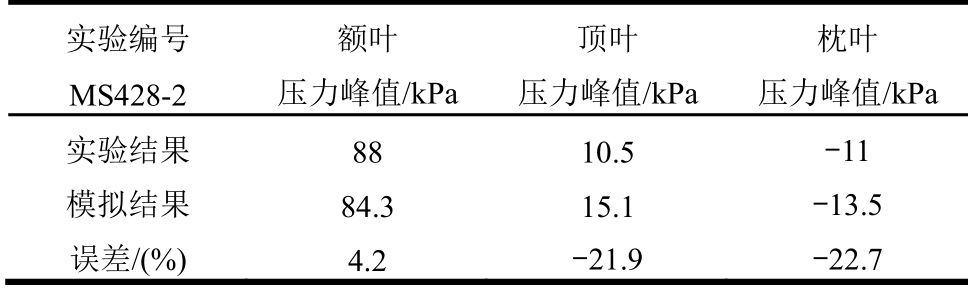
实验编号 MS428-2 额叶 压力峰值/kPa 顶叶 压力峰值/kPa 枕叶 压力峰值/kPa实验结果 88 10.5 -11 模拟结果 84.3 15.1 -13.5 误差/(%) 4.2 -21.9 -22.7
同时，为了分析碰撞位置对颅脑动态响应规律的影响，并为碰撞条件下颅脑损伤机理分析提供数据与理论支撑，基于验证的头部碰撞模型对枕部碰撞过程进行数值模拟。采用与前额碰撞相同的碰撞载荷，且载荷作用面积基本相同，作用位置如图9所示。
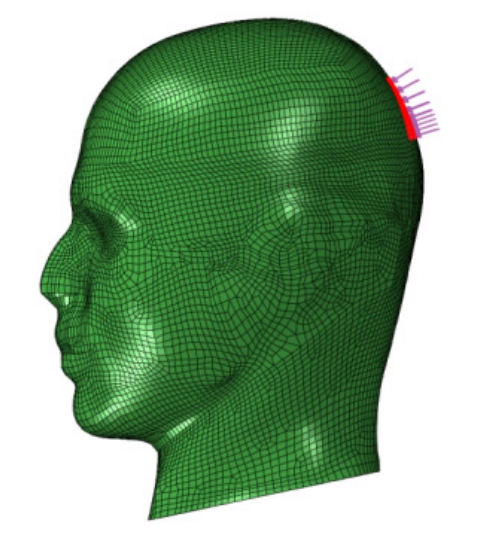
图9 枕部撞击时的头部碰撞模型
Fig.9 3-D numerical head model for the occiput collision
基于上述模拟结果，可提取前额、颅顶、枕部与颅后窝处的颅内压力时程曲线，如图10所示。对比枕部与前额碰撞结果(图7)可知，颅内压力在两种碰撞条件下具有基本相同的动态响应规律。
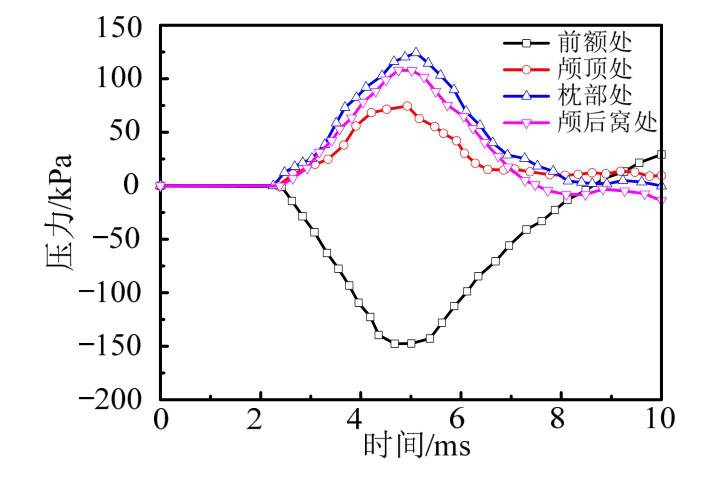
图10 枕部碰撞时颅内压力时程曲线
Fig.10 Temporal evolution of intracranial pressure caused by the occiput collision
3 颅脑损伤机理分析
本节将基于前额与枕部碰撞的数值模拟结果，并结合医学上脑组织挫裂伤的统计数据，对其致伤机理进行分析。
4.1 脑组织压力
为了对脑组织压力的演化过程进行分析，首先提取前额碰撞时的模拟结果，如图11所示。由于颅骨与脑组织的惯性差异，在碰撞载荷作用下，颅骨加速度明显大于脑组织加速度。因此，前额处(撞击处)颅骨与脑组织之间产生相对径向压缩位移，使得脑组织处于压缩状态，对应的压力为正；而枕部处(对撞处)两者之间产生相对径向拉伸位移，脑组织处于拉伸状态，对应的压力为负。随着撞击载荷的持续作用，颅内正、负压的作用范围持续扩大，最终发展成为靠近前额的前半部分脑组织受压而靠近枕部的后半部分脑组织受拉的受力状态。同时，从图中可以看出，颅骨的类三明治结构能够分散冲击处的能量，从而为颅内脑组织提供防护。
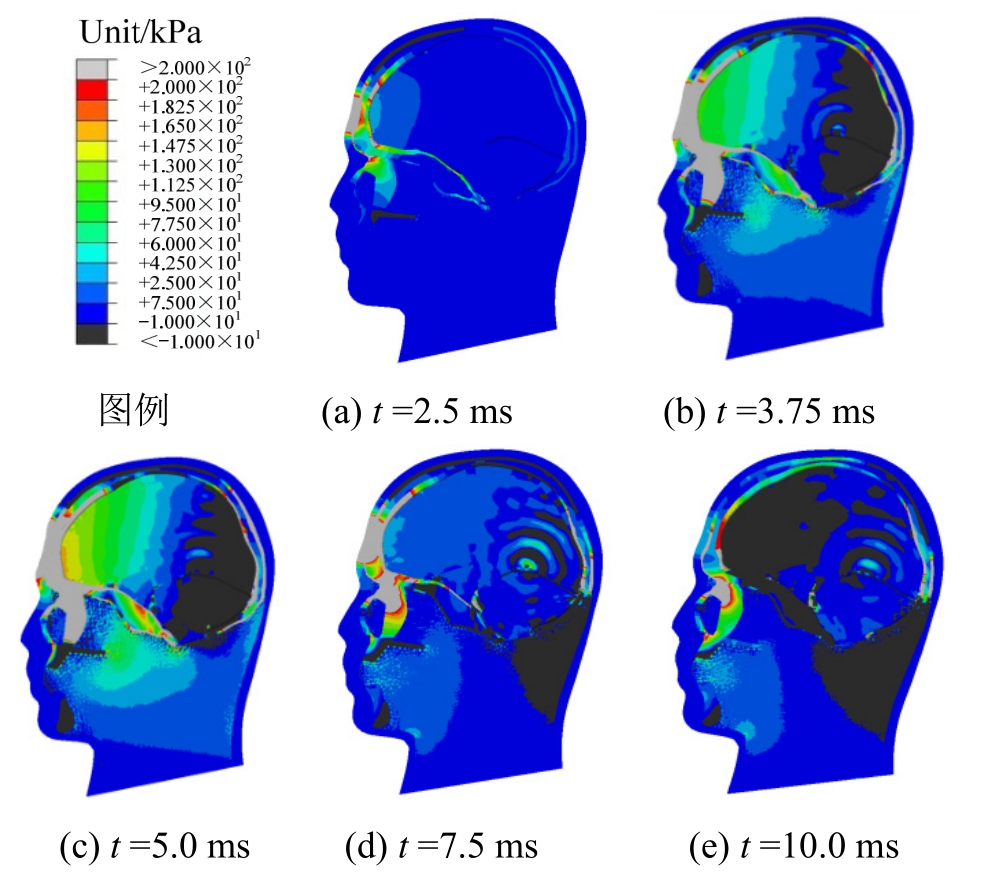
图11 前额撞击时脑组织压力云图
Fig.11 Nephogram of brain pressure for the forehead collision
图12显示了枕部受到碰撞载荷作用时脑组织在特征时刻的压力云图。由于颅骨与脑组织的惯性差异，靠近枕部(撞击处)的后半部分脑组织与颅骨之间存在相对径向压缩位移，该处脑组织处于受压缩状态；而靠近前额部位(对撞处)前半部分脑组织与颅骨之间则存在相对径向拉伸位移，该处脑组织处于拉伸状态。这与前额碰撞时脑组织的压力分布规律是一致性。基于上述分析可知，颅骨与脑组织之间的相对径向位移决定脑组织压力，这与相关文献[22—23]中的结论基本上是一致的。
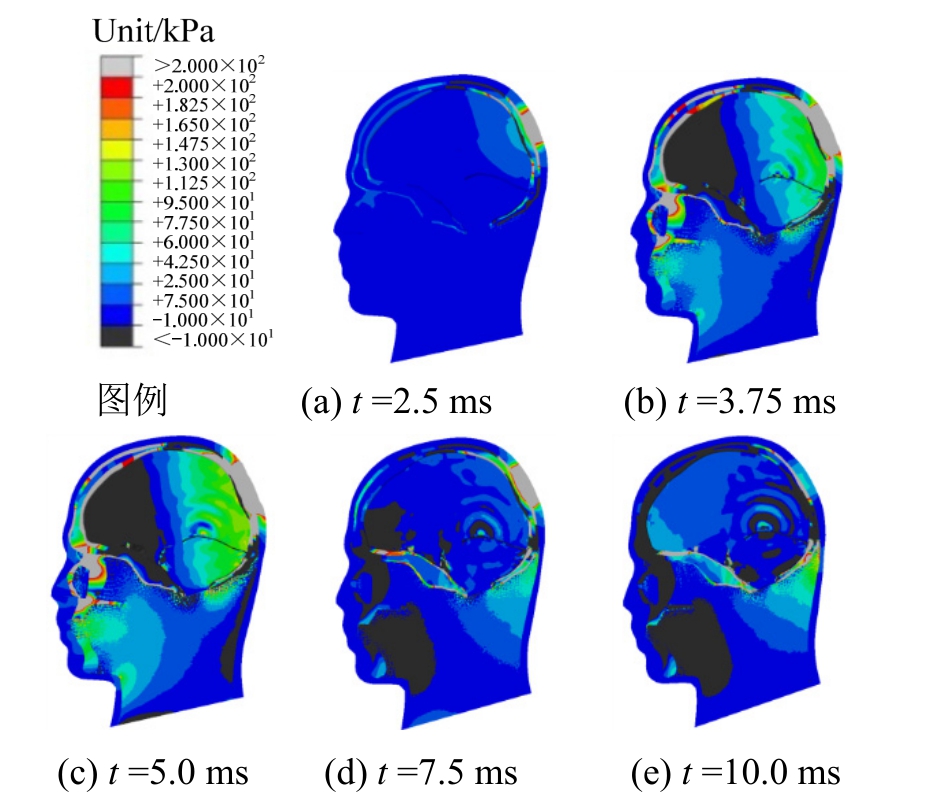
图12 枕部撞击时脑组织压力云图
Fig.12 Nephogram of brain pressure for the occiput collision
3.2 脑组织Mises应力
对于几乎不可压缩的脑组织而言，其体积模量要远大于剪切模量，相应的Mises应力可近似表征脑组织的剪切变形，并用来作为颅脑损伤的评价指标[20,34]。图13显示了前额碰撞条件下颅内脑组织在特征时刻的Mises应力云图。
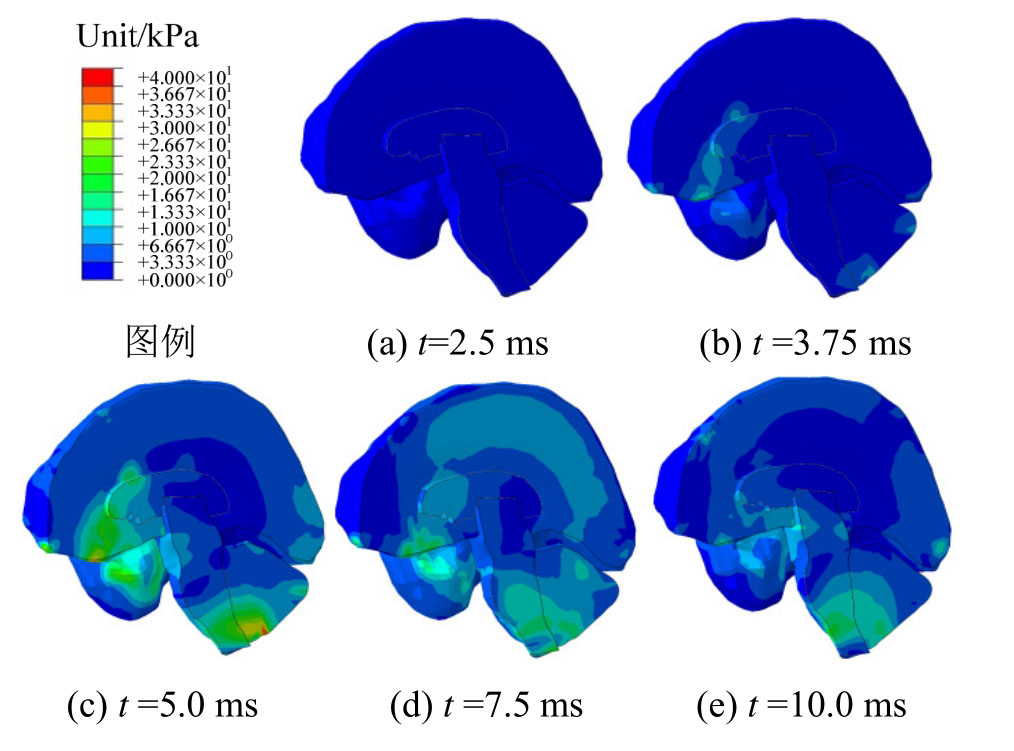
图13 前额撞击时脑组织Mises应力云图
Fig.13 Nephogram of Mises stress for the forehead collision
由图13可以看出，前额处的Mises应力在整个撞击过程中都是很小的，而该处的压力梯度却是最大的。因此，脑组织的Mises应力与压力梯度基本上没有必然的联系，这与相关文献[27—29]中的结论是一致的。同时，颅顶与枕部处的脑组织Mises应力也是相对较小的，而Mises应力较大的位置主要为额颞叶处的大脑部分与靠近枕骨大孔处的小脑脑干部分。在前额撞击时，由于颅骨与脑组织之间存在惯性差异，两者在撞击处产生相对径向位移，而相对切向位移则很小，因此该处压力梯度最大但是Mises应力却很小。在颅顶与枕部处，虽然颅骨与脑组织之间存在较大的相对切向位移，然而这两处颅骨曲率较小且较为光滑，脑脊液(蛛网膜小梁)的低剪切传递特性使得脑组织的剪切变形相对较小。而额颞叶处是左右半球颅骨的交汇处，该处颅骨内表面凹凸不平，曲率变化较大；接近枕骨大孔的颅底曲率较大，且存在枕内隆突。同时，这两处颅骨与脑组织的相对切向位移较大，从而使脑组织易于出现较大的剪切变形。
图14显示了枕部碰撞条件下颅内脑组织在不同时刻的Mises应力云图，与前额碰撞条件下Mises应力的分布规律基本一致：额颞叶处大脑部分与枕骨大孔处小脑脑干部分的Mises应力明显高于其它部位的相应值。
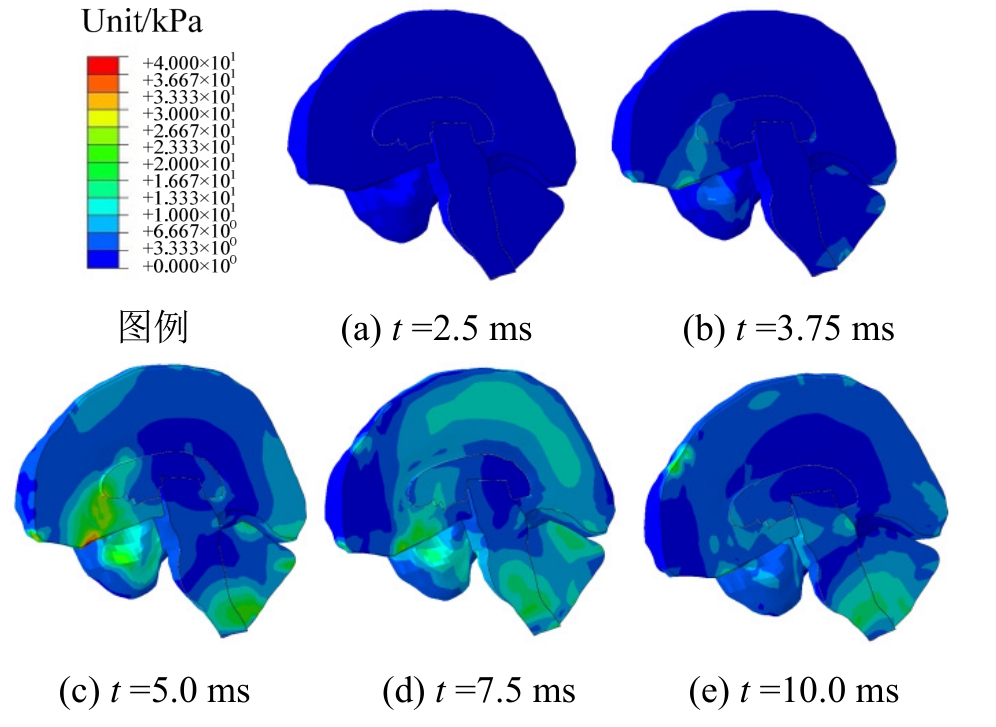
图14 枕部撞击时脑组织Mises应力云图
Fig.14 Nephogram of Mises stress for the occiput collision
图15显示了脑组织在前额与枕部撞击条件下特征点处(1-8特征点)的Mises应力时程曲线。由图可知，两种碰撞条件下脑组织剪切变形的规律基本一致：颅底枕骨大孔处(1、2特征点)与额颞叶处(3、4特征点)脑组织的Mises应力明显高于前额(5特征点)、颅顶(6特征点)、枕部(7特征点)与颅后窝(8特征点)等部位，表征这两处脑组织容易发生严重剪切变形。
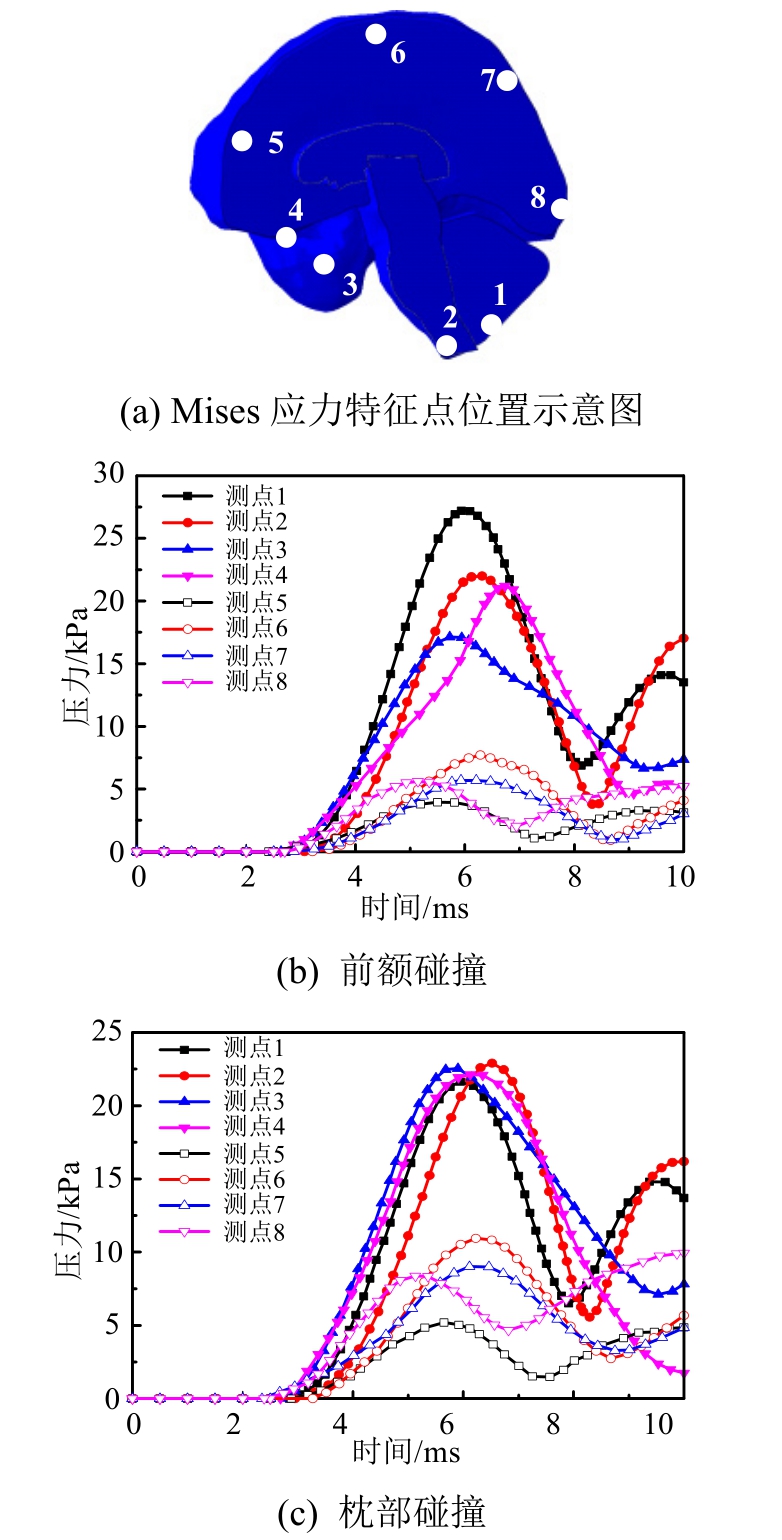
图15 前额与枕部撞击时脑组织Mises应力时程曲线
Fig.15 Temporal evolution of brain Mises stress caused by the forehead and occiput collision
基于上述分析可知，脑组织剪切变形是由颅骨与脑组织之间的相对切向位移与颅骨内表面状况共同决定的。
4.3 脑组织挫裂伤的损伤机理
基于医学统计数据，头部前额与枕部的碰撞均容易在额颞叶部引发脑组织挫裂伤等病变，如图16所示。相关学者[22—23]提出脑组织拉压造成了脑组织挫裂伤的观点，并提出基于脑组织压力的损伤指标；而另一些学者[27—28]则提出剪切致伤机理，脑组织剪切变形造成挫裂伤。上述两种观点都是基于脑组织体积变形或剪切变形单一致伤因素来揭示挫裂伤的致伤机理。由本文的模拟结果可知，脑组织压力在撞击处为压应力，而在对撞处则为拉应力，单独采用脑组织拉(压)应力作为挫裂伤的评价标准，额颞叶处与枕部脑组织均容易出现损伤。而基于脑组织Mises应力(剪切变形)对脑组织挫裂伤进行评价，损伤区域则包括两个，分别为额颞叶处大脑部分与枕骨大孔处小脑脑干部分。因此，基于脑组织压力(体积变形)或Mises应力(剪切变形)等单一力学指标的损伤准则是无法解释上述病理现 象的。
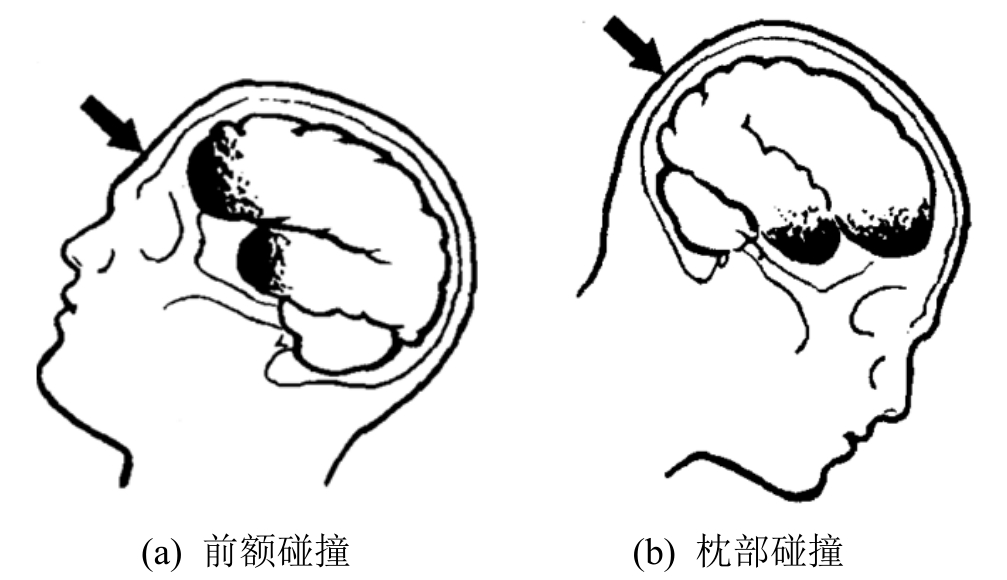
图16 前额与枕部碰撞下脑组织挫裂伤的损伤区域[35]
Fig.16 Injury region of brain contusion under the forehead and occiput collision [35]
额颞叶处是脑组织挫裂损伤的易发区域。该处在前额碰撞时为压缩高压区，而在脑后部碰撞时为拉伸高压区；同时，该处是脑组织剪切变形潜在损伤区。额颞叶处的脑组织挫裂伤应当是脑组织压力(体积变形)或Mises应力(剪切变形)共同作用的 结果。
基于上述分析，可以建立碰撞条件下脑组织挫裂伤的理论损伤准则，定义相应的损伤因子D，具体表达式为：
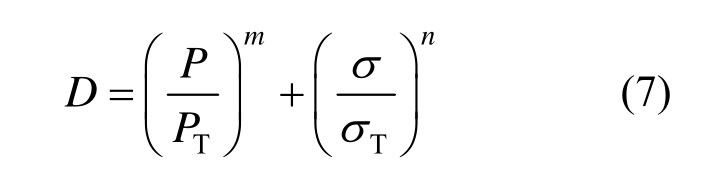
式中：P和σ分别为脑组织当前的压力值与Mises应力值；PT和σT分别为压力损伤阈值与Mises应力损伤阈值；m和n分别为压力与Mises应力的损伤权重系数。当损伤因子D小于1时，表征脑组织不会发生挫裂伤；反之，脑组织出现挫裂伤，且D值越大表征损伤越严重。
基于上述损伤准则，损伤权重系数m和n均取为1，压力损伤阈值PT和Mises应力损伤阈值σT分别取为173 kPa[22]与70 kPa[20]，利用Python语言编写程序脚本对前额与枕部碰撞模拟结果进行处理，可以得到脑组织挫裂伤的损伤因子，如图17所示。
由图17可知，前额与枕部碰撞均易导致额颞叶处脑组织发生挫裂损伤，与医学统计数据相吻合，验证了上述损伤准则的有效性。该损伤准则考虑脑组织压力(体积变形)与Mises应力(剪切变形)的共同作用，这和基于单一力学指标建立的损伤准则[22-23, 27-28]存在显著不同。同时，该损伤准则的相关参数的确定与适用范围还有待于进一步研究。
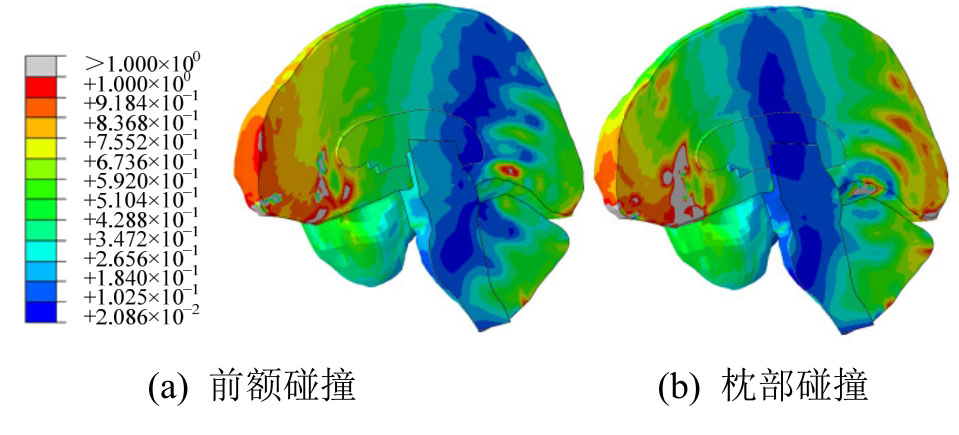
图17 碰撞时脑组织挫裂伤的损伤因子
Fig.17 Damage factors of brain contusion caused by head collisions
4 结论
本文建立了具有详细解剖学结构和较高生物仿真度的三维头部数值模型，并基于Nahum死尸头部碰撞实验验证了头部碰撞模型的有效性。利用该模型对头部前额与枕部碰撞过程进行数值模拟，分析了脑组织的动态响应规律，并结合医学上脑组织挫裂伤的统计数据，揭示了其损伤机理，建立了相应的损伤准则。现将主要结论总结如下：
(1)采用自由边界条件的头部碰撞模型，其模拟结果与死尸头部碰撞实验结果较为吻合；而竖向约束与固定边界条件则引起颅内压力的正负交替变化，严重偏离实际情况。
(2)颅骨与脑组织间的相对径向位移决定脑组织压力，撞击处前半部分脑组织处于压缩状态，而对撞处后半部分脑组织则处于拉伸状态。
(3)脑组织的剪切变形是由颅骨脑组织相对切向位移与颅骨内表面状况共同决定，变形严重区域主要分布在额颞叶处大脑部分与枕骨大孔处小脑脑干部分。
(4)脑组织挫裂伤是由脑组织压力(体积变形)与Mises应力(剪切变形)共同作用产生的，基于这一机理建立了相应的损伤准则。
[1]World Health Organization.Global status report on road safety 2015 [M].World Health Organization, 2015.
[2]Dixit P, Liu G R.A review on recent development of finite element models for head injury simulations[J].Archives of Computational Methods in Engineering, 2017, 24(4): 979—1031.
[3]Nahum A M, Smith R, Ard C C.Intracranial pressure dynamics during head impact [R].Proceedings of 21st Stapp Car Crash Conference.Pennsylvania: Society of Automotive Engineers, 1977: 339—366.
[4]Trosseille X, Tarriere C, Lavaste F, et al.Development of a FEM of the human head according to a specific test protocol [R].Proceedings the 36th Car Crash Conference.Seattle: Society of Automotive Engineers, 1992: 235—253.
[5]Yoganandan N, Pintar F A, Sances A, et al.Biomechanics of skull fracture [J].Journal of neurotrauma, 1995, 12(4): 659—668.
[6]Hardy W N, Foster C D, Mason M J, et al.Investigation of head injury mechanisms using neutral density technology and high-speed biplanar X-ray [J].Stapp Car Crash Journal, 2001, 45: 337—368.
[7]Kilbourne M, Kuehn R, Tosun C, et al.Novel model of frontal impact closed head injury in the rat [J].Journal of Neurotrauma, 2009, 26(12): 2233—2243.
[8]Feng Y, Gao Y, Wang T, et al.A longitudinal study of the mechanical properties of injured brain tissue in a mouse model [J].Journal of the Mechanical Behavior of Biomedical Materials, 2017, 71: 407—415.
[9]Elkin B S, Morrison B.Region-specific tolerance criteria for the living brain [J].Stapp Car Crash J, 2007, 51(10): 127—138.
[10]Dollé J P, Morrison B, Schloss R S, et al.Brain-on-a-chip microsystem for investigating traumatic brain injury: Axon diameter and mitochondrial membrane changes play a significant role in axonal response to strain injuries [J].Technology, 2014, 2(2): 106—117.
[11]Miyazaki Y, Tachiya H, Anata K, et al.Measurement of pressure responses in a physical model of a human head with high shape fidelity based on CT/MRI data [J].International Journal of Modern Physics B, 2008, 22(9): 1718—1723.
[12]Salzar R S, Treichler D, Wardlaw A, et al.Experimental investigation of cavitation as a possible damage mechanism in blast-induced traumatic brain injury in post-mortem human subject heads [J].Journal of Neurotrauma, 2017, 34(8): 1589—1602.
[13]张建国, 王芳, 薛强.后碰撞中人体颈部动力学响应的有限元分析[J].工程力学, 2010, 27(4): 208—211.Zhang Jianguo, Wang Fang, Xue Qiang.Fe anlysis of human neck dynamic responses under rear-end impact [J].Engineering Mechanics, 2010, 27(4): 208—211.(in Chinese)
[14]Kleiven S.Predictors for traumatic brain injuries evaluated through accident reconstructions [R].Stapp Car Crash Journal, 2007, 51: 81—114.
[15]Ganpule S, Alai A, Plougonven E, et al.Mechanics of blast loading on the head models in the study of traumatic brain injury using experimental and computational approaches [J].Biomechanics and Modeling in Mechanobiology, 2013, 12(3): 511—531.
[16]Chafi M S, Ganpule S, Gu L, et al.Dynamic response of brain subjected to blast loadings: influence of frequency ranges [J].International Journal of Applied Mechanics, 2011, 3(4): 803—823.
[17]Wang C, Pahk J B, Balaban C D, et al.Biomechanical Assessment of The Bridging Vein Rupture of Blast-Induced Traumatic Brain Injury Using The Finite Element Human Head Model [C].ASME 2012 International Mechanical Engineering Congress and Exposition.American Society of Mechanical Engineers, 2012: 795—805.
[18]Moore D F, Jérusalem A, Nyein M, et al.Computational biology—modeling of primary blast effects on the central nervous system [J].Neuroimage, 2009, 47: T10—T20.
[19]Versace J.A review of severity index [C].Proc of 15th Stapp Car Crash Conference.San Diego: Society of Automotive Engineers, 1971: 771—796.
[20]Newman J A.A generalized acceleration model for brain injury threshold (GAMBIT)[C]// Proceedings of International IRCOBI Conference, 1986.
[21]Newman J A, Shewchenko N.A proposed new biomechanical head injury assessment function-the maximum power index [R].SAE Technical Paper, 2000.
[22]Ward C, Chan M, Nahum A.Intracranial pressure–a brain injury criterion [R].SAE Technical Paper, 1980.
[23]Takhounts E G, Eppinger R H, Campbell J Q, et al.On the development of the SIMon finite element head model [C]// Sae Conference ProceedingS P.Sae; 1999, 2003: 107—134.
[24]Stalnaker R L, Alem N M, Benson J B.Validation studies for head impact injury model [M].US Department of Transportation, National Highway Traffic Safety Administration, 1978.
[25]Nusholtz G S, Lux P, Kaiker P, et al.Head impact response-Skull deformation and angular accelerations [J].SAE transactions, 1984: 800—833.
[26]Nusholtz G S, Wylie B, Glascoe L G.Cavitation/ boundary effects in a simple head impact model [J].Aviation Space & Environmental Medicine,1995, 66(7): 661—667.
[27]Chu C S, Lin M S, Huang H M, et al.Finite element analysis of cerebral contusion [J].Journal of Biomechanics, 1994, 27(2): 187—194.
[28]Huang H M, Lee M C, Lee S Y, et al.Finite element analysis of brain contusion: an indirect impact study [J].Medical and Biological Engineering and Computing, 2000, 38(3): 253—259.
[29]Mao H, Yang K H.Investigation of brain contusion mechanism and threshold by combining finite element analysis with in vivo histology data [J].International Journal for Numerical Methods in Biomedical Engineering, 2011, 27(3): 357—366.
[30]David L.Felten, Ralph F.Józefowicz 著.奈特人体神经解剖彩色图谱[M].崔益群译.北京: 人民卫生出版社, 2006: 42.David L.Felten, Ralph F.Józefowicz.Netter’s atlas of human neuroscience [M].Translated by Cui Yiqun.Beijing: People’s Medical Publishing House, 2006: 42.(in Chinese)
[31]Chafi M S, Karami G, Ziejewski M.Biomechanical assessment of brain dynamic responses due to blast pressure waves [J].Annals of biomedical engineering, 2010, 38(2): 490—504.
[32]Benedict J V, Harris E H, Von Rosenberg D U.An analytical investigation of the cavitation hypothesis of brain damage [J].Journal of Basic Engineering, 1970, 92(3): 597—603.
[33]Zhang L, Yang K H, Dwarampudi R, et al.Recent advances in brain injury research: a new human head model development and validation [J].Stapp Car Crash J, 2001, 45(11): 369—394.
[34]Willinger R, Baumgartner D, Chinn B, et al.Head tolerance limits derived from numerical replication of real world accidents [C].Proceedings of the International Research Council on the Biomechanics of Injury conference. International Research Council on Biomechanics of Injury, 2000, 28: 209—221.
[35]吴在德.外科学[M].第7版.北京: 人民卫生出版社, 2012: 245.Wu Zaide.Surgery [M].7th ed.Beijing: People’s Medical Publishing House, 2012: 245.(in Chinese)