随着我国核电事业的发展，核电厂选址将不只局限于沿海地区，内陆核电厂的建设也已提上日程。其中，重庆涪陵核电站和四川三坝核电站拟建于我国西南地区。相比东南沿海，我国内陆地区地质条件复杂，发生地震灾害的危险性较大。虽然核电厂选址过程中需要对场地周围较大范围内的地震地质条件进行详细的勘测，但是受到目前勘测技术的限制，核电厂厂址周围可能隐藏有未探明的断层，一旦发生地震，其对核电厂的破坏将远大于远场地震，造成不可估量的损失。这种可能性不止存在于理论中，在工程实际中已经发生了核电厂厂址临近活动断层的事件。有报道表明[1]，日本敦贺核电站反应堆正下方发现可能为活断层的破裂带，导致该核电站很可能做废堆处理。除此之外，台湾第一、第二核能发电厂被指距离活动断层仅5 km～ 7 km，废弃该核电厂的争议持续多年[2]。
不同于远场地震动，近断层地震动主要受到断层的破裂过程、断层面上位错的发展过程、滑动的方向、滑动的速度、以及观测点与断层的相对位置等因素控制和影响，破坏力巨大，可能对结构产生严重的影响[3]。因此，在核电厂的抗震设计和试验研究[4—6]中，近断层地震动是应该纳入考虑的因素。近断层脉冲地震动包括方向性效应引起的速度脉冲和滑冲效应引起的永久位移和单向速度脉冲[7—9]。由于滑冲效应现阶段难以建立合理的数学模型且包含有滑冲效应的地震动记录过少，因此当前研究中主要针对近断层效应中的速度脉冲对核电厂抗震设计谱的影响开展。
国内外在核电厂的抗震设计过程中考虑近断层地震动的影响可归纳为两种思路，一种是在输入地震动时选择近断层地震(NFE)记录，另一种是在设计谱中考虑近断层地震动的影响。Kitada等[10]研究了日本的62条实际NFE，并推荐了其中的16条用于核电厂结构地震反应分析。Galal和 Ghobarah[11]统计了包含美国、日本、土耳其等地区的54条NFE的平均反应谱，并与美国规范NUREG/RC-6728和加拿大规范CSA-N 289.3中规定的设计谱进行了比较，结果表明，核电厂抗震设计谱与真实的近断层记录计算得到的反应谱具有一定的差距，如果要考虑在近断层条件下设计地震动，则仍需对规范谱进行调整。Bray等[12]研究了近断层地区受向前方向性效应的影响，指出方向性效应主要由大振幅、长周期的速度脉冲来确定。徐龙军等[13]按照Bary和Rodriguez-Marek选取NFE的规则，选取了15条基岩场地NFE，采用双规准化的方法得出不同震级和震中距的核电厂设计谱，并与我国规范(GB 50267—97)中规定的 设计谱进行了比较，研究结果表明，具有方向性效应的近断层记录的峰值加速度(PGA)与峰值速度(PGV)之比小于我国核电厂设计地震动中的比值，并且设计谱谱值的平均值加上标准差之和与近断层记录的平均值加上标准差之和在大部分周期范围内均吻合的不好，这说明我国现有核电厂抗震设计谱并不适用于近断层状况[13]。
随着地震危险性分析(PSHA)方法的发展，近断层地震动也被引入到了PHSA中。Shahi和Baker[14—15]选取了美国NGA数据库中179条NFE，建立了脉冲发生概率模型，并将该模型引入到PSHA计算框架中，从而把近断层方向性效应的影响纳入PHSA，该研究同时比较了近断层PSHA方法与Somerville等[16]近断层模型得到的反应谱的差异，结果认为提出的近断层修正更加符合实际地震记录。Tothong和Cornell[17]分析了脉冲型NFE对PHSA的影响，将近断层记录的脉冲周期Tp的分布特征引入到PSHA框架中，进一步完善了近断层条件下的PSHA分析方法。Chioccarelli和Iervolino[18]结合前人的研究成果，继续完善了近断层地震概率危险性分析(NS-PSHA)，考虑了走滑断层和倾滑断层的差异，采用修正的衰减关系，引入脉冲发生概率和脉冲周期模型，提出了利用地震危险性分解结果计算得出核电厂设计谱的方法，并针对意大利Anguilla地震进行了讨论。
针对于上述现状和存在的问题，基于目前全球积累的大量实际脉冲型NFE记录，采用PSHA方法构建设定地震下的我国的核电厂抗震设计谱，对于内陆地区核电厂的抗震设计势在必行。
1 近断层脉冲放大系数的修正
1.1 Baker近断层脉冲放大系数
近断层方向性效应对地震动反应谱的影响最早由Somerville等[16]进行了研究，其提出了一个宽频带的放大系数，该系数根据场地和震源的位置参数单调地放大反应谱的谱值。最新的研究表明[17,19—21]，在脉冲周期处较小的频谱范围内对反应谱进行放大更加准确，更符合实际情况。根据这一结果，Baker[14]等提出了新型的窄频带放大系数，该系数基于近断层地震动记录，属于经验放大系数。其首先通过小波分析来提取近断层脉冲记录中的脉冲，得到提取出的脉冲记录和残余记录，再通过脉冲记录反应谱与残余记录反应谱的比值，得到放大系数。
文献[14]给出了近断层脉冲放大系数模型，其在放大系数中引入了脉冲周期Tp，可以被应用到地震危险性分析(PSHA)中。Chioccarelli等[18]、Shahi等[15]等针对近断层地震危险性分析(NS-PSHA)的研究中均采用了这一形式的放大系数。然而，Baker近断层脉冲放大系数仍有一定的局限性：
1)计算脉冲放大系数的地震动并不完全是实际地震动。取得比值的两组地震动数据，一组是通过小波分析提取的脉冲记录，另一组是提取后剩余的残余记录，两组地震动都是处理后得到的，其比值与实际地震动的特征可能存在差异。
2)采用的衰减关系是基于包含近断层无脉冲记录和脉冲记录取得的，而在研究脉冲造成的谱值放大时，这种无脉冲和脉冲记录的混合并不能作为一个准确的参考。
3)Baker近断层脉冲放大系数选择在T/Tp=1处达到放大系数的最大值。但是根据多条实际地震动记录的分析结果，放大系数峰值出现的位置一般并不在T=Tp处，而是发生在T略小于Tp的位置，这一点在本文接下来的研究中将会详细说明。
1.2 近断层地震动数据库的选取
为了改进上述问题，本文从Baker课题组收集的全球近断层脉冲数据库中选取了115条记录，选取规则如下：
1)震级MW5.0～MW8.0。震级的选取规则主要考虑到5级以下的地震产生脉冲的概率很低，为了包含较多的数据用以分析，震级上限选取到8.0级。
2)断层距Rjb<30 km。研究表明在距离断层30 km的范围内，地震动记录出现脉冲的概率较大，而且能较好地体现近断层地震动对加速度反应谱的放大作用。
3)脉冲周期Tp<5.0 s。Chioccarelli和Iervolino的研究表明[18]，近断层地震动的脉冲周期大小主要跟震级MW相关，震级MW5.0～MW8.0时，脉冲周期大于5.0 s的概率很低，因此在选取过程中我们只选取脉冲周期小于5.0 s的地震动记录。
4)由于目前近断层地震动数据较少，其中基岩场地上的地震动记录更是稀少，因此并没有针对核电厂厂址特点只选取基岩场地记录，根据前三条规则选取的地震动记录的场地VS30分布在200 m/s～ 700 m/s。
1.3 修正近断层脉冲放大系数
由于建立的脉冲放大系数的作用是对地震动衰减关系进行修正得到适用于近断层脉冲条件下的反应谱谱值，因此，本文在Baker定义的脉冲放大系数模型基础之上，考虑到前文对放大系数性质的统计分析结果，建立了修正的放大系数模型，具体形式如式(1)所示：
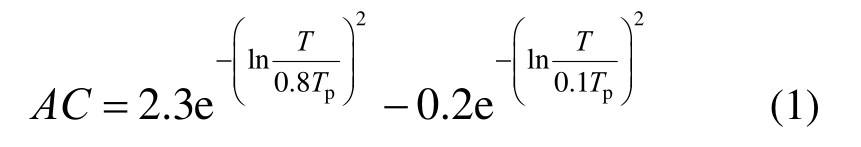
式中：第一项底数2.3表示脉冲放大系数的峰值，达到最大值的位置在T/Tp=0.8处；式中第二项代表了在高频段加速度反应谱谱值在发生脉冲的情况下减小的现象，其系数0.2表示减小后的谱值约为原谱值的0.8倍，达到最小值的位置在T/Tp=0.1处。需要说明的是，式(1)中各项系数的选择并没有针对不同的震级、震中距和场地条件等参数进行回归，是因为由于现有近断层脉冲型地震动记录的数据非常有限，难以如衰减关系那样进行有效的回归得到随地震动参数变化的系数，所以各项系数选取了各组平均值中的最大值，这样能在体现脉冲放大系数特征的情况下最大限度地满足安全性的要求。最后，通过不同震级范围、不同距离和不同场地条件的地震动数据拟合，可得到采用修正公式的脉冲放大系数模型。
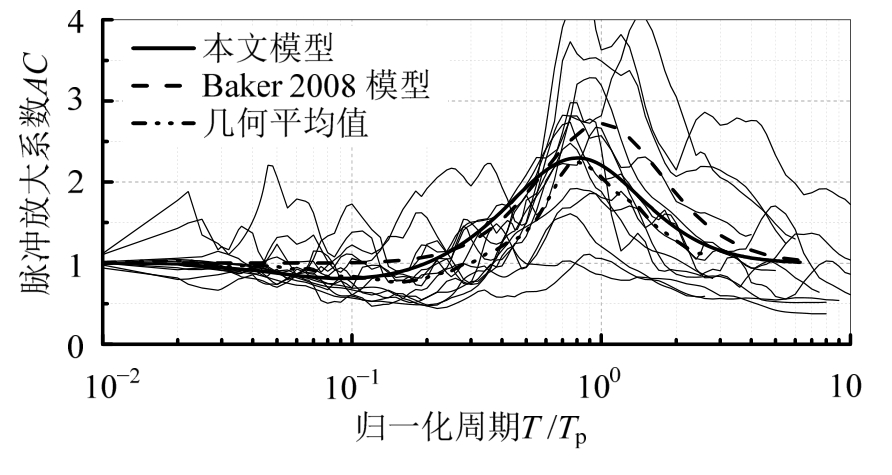
图1 修正的近断层脉冲放大系数
Fig.1 Modified near fault pulse amplification factor
图1给出了MW=6级～7级、Rjb=0 km～30 km、VS30=500 m/s～800 m/s时，Baker脉冲放大系数及本文修正的脉冲放大系数AC与实际放大系数的比较。可看出，与Baker在所提出的脉冲放大系数相比，本文建立的修正放大系数主要有以下特征：① 基本形式与Baker的脉冲放大系数相同，均采用了驼峰型的函数图形；② Baker脉冲放大系数的最大值位于T/Tp=1处，本文的脉冲放大系数的最大值位于T/Tp=0.8处；③ Baker脉冲放大系数的最大值为自然对数e=2.7，本文的脉冲放大系数的最大值为2.3，在数值上比Baker 脉冲放大系数要小；④ Baker脉冲放大系数在偏离T/Tp=1的位置不断减小，最后均趋近于1，整体的放大系数值都大于1，本文的脉冲放大系数在短周期处部分范围内的值小于1，体现了脉冲不仅使反应谱谱值变大，在某些范围内还会使谱值变小的现象。因此，修正的脉冲放大系数更加接近实际的放大系数，最大值、最大值位置以及短周期处比值都比Baker脉冲放大系数更加合理。
2 近断层场地的地震危险性分析
2.1 近断层地震危险性分析
为了将近断层地震动的脉冲影响引入PSHA，一些研究者提出了NS-PSHA的框架。Iervolino和Cornell[22]以73条近断层地震动记录为基础，通过逻辑回归得出了近断层地震动发生脉冲的概率模型，脉冲发生的概率与图2中所示的R、s、θ参数有关[16]，具体形式如式(2)：
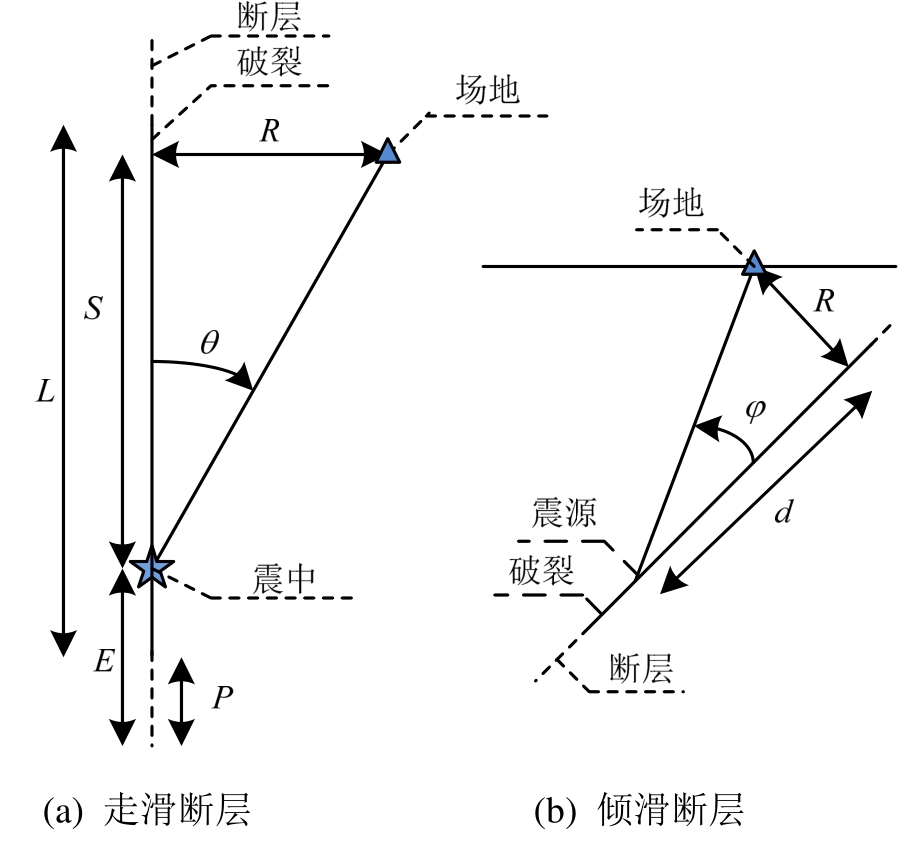
图2 近断层场地与震中、断层的相对位置参数[16]
Fig.2 Relative location of near fault site with epicenter and fault[16]
除了脉冲发生概率外，还需确定脉冲周期TP的分布，即脉冲周期Tp的概率密度函数，其服从正态分布[18]。Chioccarelli和Iervolino[18]的分析表明，TP跟震级具有显著的关系，并给出相应方程式：
由于方向性效应带来的脉冲会使反应谱在周期接近Tp的位置处的谱值变大，所以在NS-PSHA中，需要考虑将地震动衰减关系进行修正，使其符合近断层地震动的特性。常用的修正方法是将谱值在Tp附近处乘以一个放大系数，越偏离Tp处的周期，谱值的放大系数越小。
根据前述各模型，我们就可以将脉冲的影响引入PSHA中。首先，考虑将近断层场地危险性分成两部分，一部分是由脉冲型地震动引起的，另一部分是由非脉冲型地震动引起的，如式(4)所示：
式中：
的计算公式分别如下：
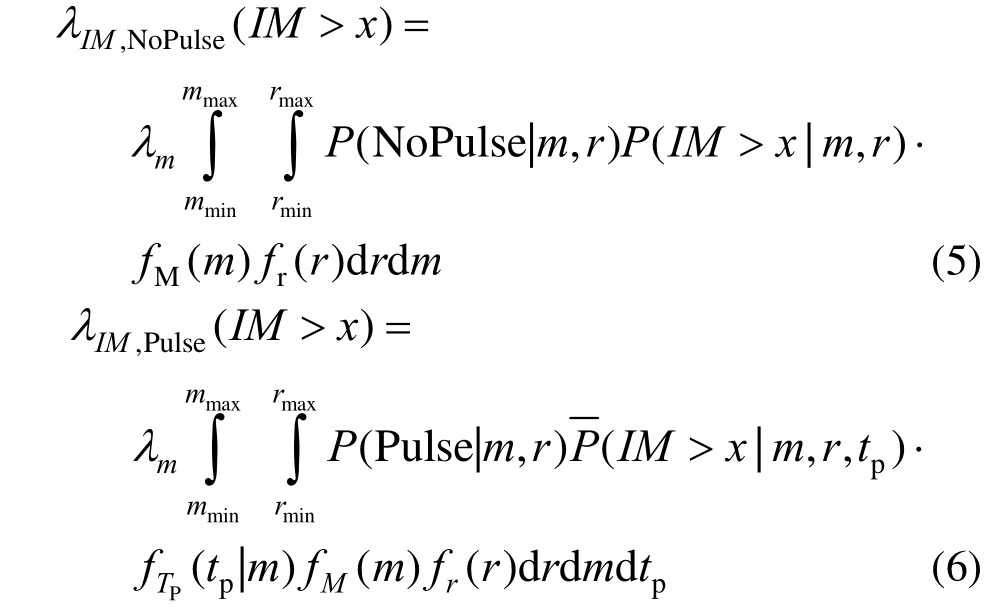
将式(5)和式(6)代入式(4)，即可以得到近断层条件下的地震动参数的超越概率。与PSHA中的分析相同，可以把式(5)和式(6)中的连续积分进行离散化得到可以进行数值计算的近断层地震危险性分析结果。这样我们就将近断层方向性效应引入到PSHA中得到NS-PSHA的计算方法。
2.2 模型算例
为了研究近断层地震在脉冲发生的情况下场地反应谱的变化情况，本文建立了一个典型断层模型，对位于断层周围不同位置的场地进行了NS-PSHA计算。
如图3所示，假设一走滑断层，断层破裂长度与地表破裂长度相同，其中虚线为断层，总长度为100 km，根据Wells和Coppersmith[23]的研究，断层破裂长度主要跟震级相关，长度为100 km的断层大约能够产生震级为7.5级的地震，本文研究的震级为4.5级～7.0级，因此断层长度选为100 km不会对破裂面产生物理上的限制。图3中粗实线为断层破裂面，即地震发生时断层上产生破裂的部分。图中三角标志为近断层场地，共有4个，分别编号为1号～4号，其中1号场地位于断层中部左方，距离断层的距离为5.0 km。
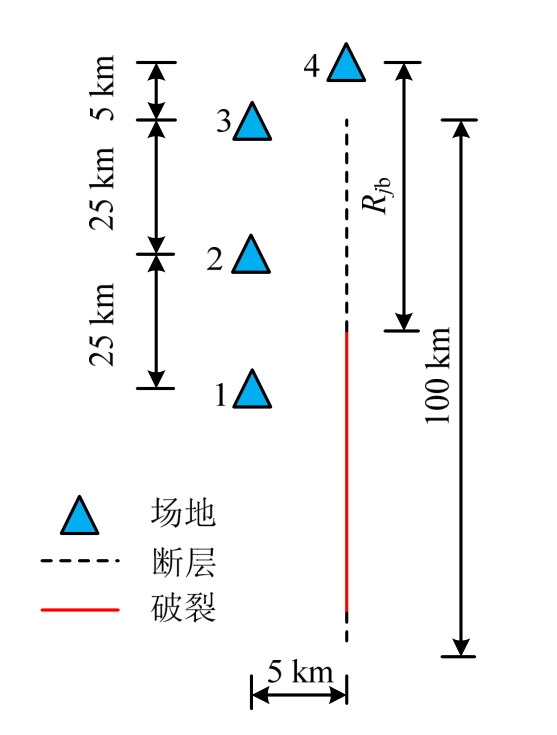
图3 近断层场地与震源模型
Fig.3 Near fault sites and source model
在该模型中，假设震源符合Gutenberg-Richter定律，震级为4.5级～7.0级，b值为1，断层每年发生4.5级以上地震的频率为0.05，每年发生5.0级以上地震的频率为0.01。震级与断层破裂长度RL的关系如式(7)，脉冲发生概率按照式(2)进行计算，脉冲周期与震级的关系按式(3)进行计算。
地震动衰减关系选择NGA-West2计划中Boore等建立的模型[24]。采用前文所建立的修正的脉冲放大系数，乘以通过衰减关系得到的反应谱谱值得到脉冲发生条件下的反应谱，如式(8)所示：
式中：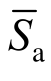
为经脉冲放大系数AC修正后的谱值，为由衰减关系计算得到的谱值，当PSHA计算过程中遇到发生脉冲的情况时，就按式(8)及式(1)对由衰减关系得到的反应谱谱值进行修正。
2.3 一致性危险反应谱
按照前述步骤，计算得到1号～4号场地在起算震级M0为5.0级、场地VS30为1000 m/s时的一致危险性反应谱，其年超越概率为10-4。
从图4可以看出，各个场地谱型基本相似，均在周期为0.1 s～0.2 s达到最大谱值。通过对比不同场地的谱值可以发现，场地与断层相对位置对一致危险性反应谱的谱值具有显著的影响：位于断层中部的场地的谱值明显大于位于断层端部的场地，并随着场地由中部向端部移动逐渐减小。
3 地震危险性的分解
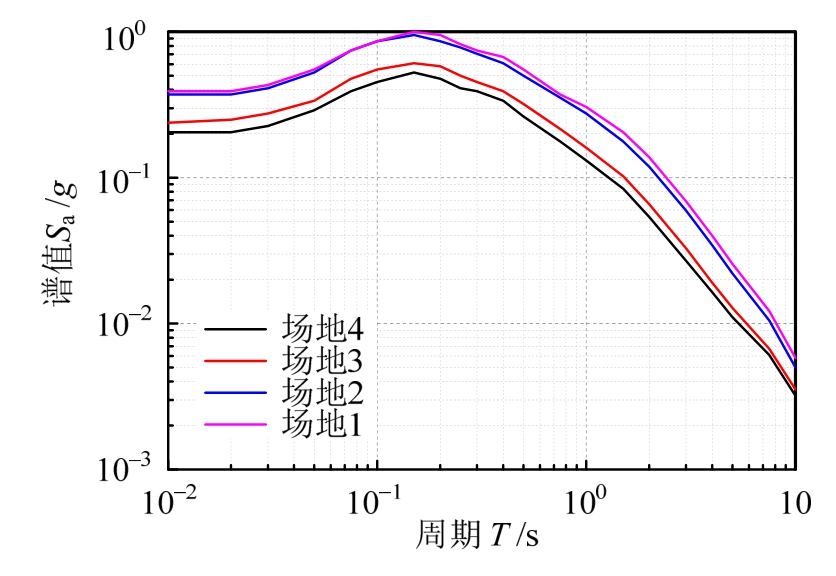
图4 目标场地年超越概率为10-4的一致危险性反应谱
Fig.4 Uniform hazard response spectra for 10-4 exceedance probability of target sites
在PSHA计算中，将场地可能遭受的地震事件分成多个独立的地震，然后计算不同的震级、 震中距、脉冲周期等条件下的概率超越曲线，最后将这些独立的地震事件合并为一致危险性反应谱。而在地震危险性分解中，利用PSHA计算中得到的结果，可以计算每一个独立事件的危险性，从而可以得到具体地震动参数对总的超越概率的贡献程度[25]。
以震级的危险性分解为例，如果已知地震动强度IM>x，那么我们想知道此时震级是m的概率为多大，如果震级M=m的概率越大，说明震级为m的地震对IM>x的情况贡献越大。其计算公式为：
式中：是当震级为m时，IM>x的频率，计算公式如下：
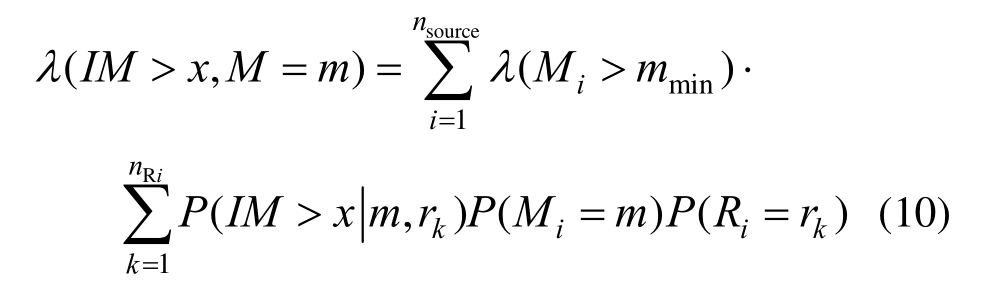
根据地震危险性分解方法[19]，将本文模型的1号场地在0.1 s周期处的地震危险性进行分解。图5和图6分别为对震级和断层距的危险性分解结果。
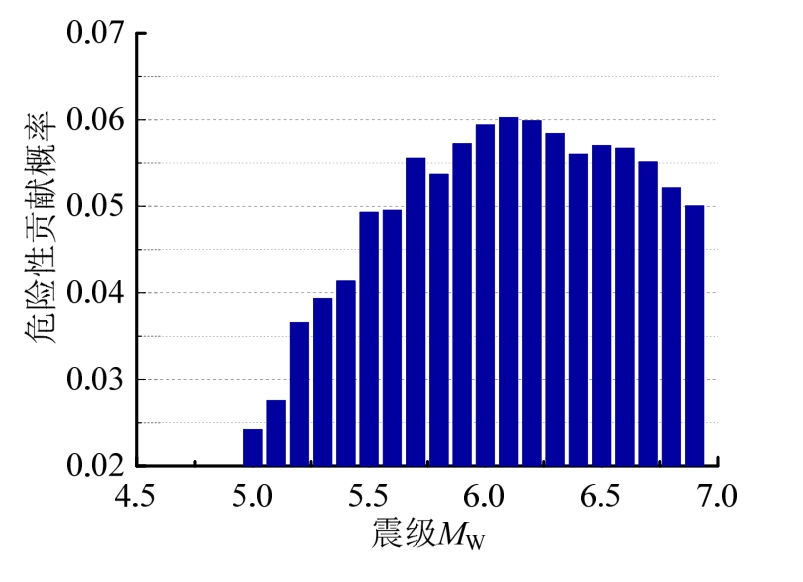
图5 震级的地震危险性分解
Fig.5 Degradation of seismic hazard for magnitude
从图5可以看出，地震危险性主要由中等偏大震级的地震控制；图6的分解结果表明，距离断层破裂面场地10 km以内时，最容易产生超过设计强度的地震动。
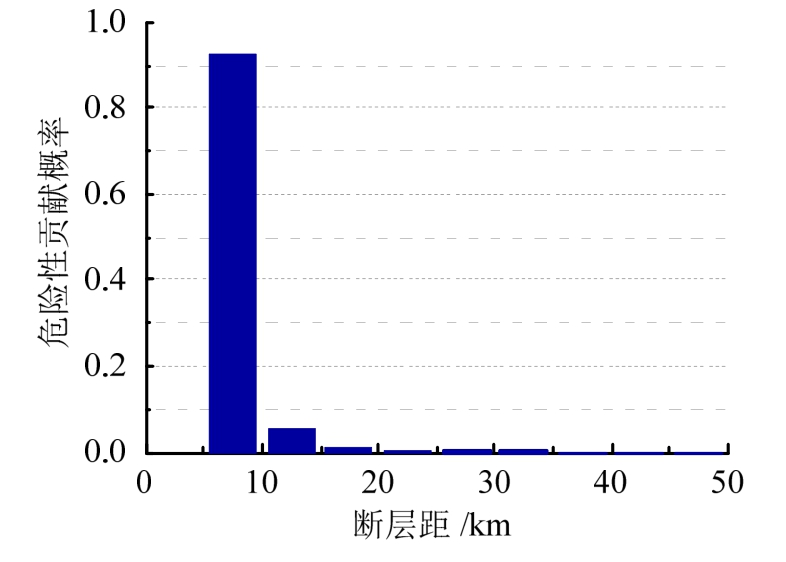
图6 断层距的地震危险性分解
Fig.6 Degradation of seismic hazard for rupture distance
在近断层地震中，速度脉冲对PSHA的结果起了非常大的作用，通过PSHA分解，可以具体了解到速度脉冲对场地地震危险性的贡献程度。图7和图8分别给出了该场地由脉冲造成的危险性占震级和断层距总危险性的比例。通过将脉冲产生的危险性除以震级总的危险性得到，该比例越高，说明场地在该震级情况下越容易遭受脉冲的影响。从图7和图8可以看出，该场地在遭遇中小地震时脉冲产生的危险性很低，在总危险性的20%以下，在遭遇较大地震时脉冲产生的危险性较高，说明该模型发生较大地震时，场地经受的地震动容易产生脉冲。从图8可以看出，场地在最小断层距为10 km～ 15 km时脉冲产生的地震危险性的比例最大，并向两边降低。
图9给出了场地对脉冲周期的危险性分解结果，由于是对周期T=0.1 s的PSHA结果进行分解，所以脉冲周期范围内最靠近0.1 s的周期(0.6 s)产生的危险性最大。
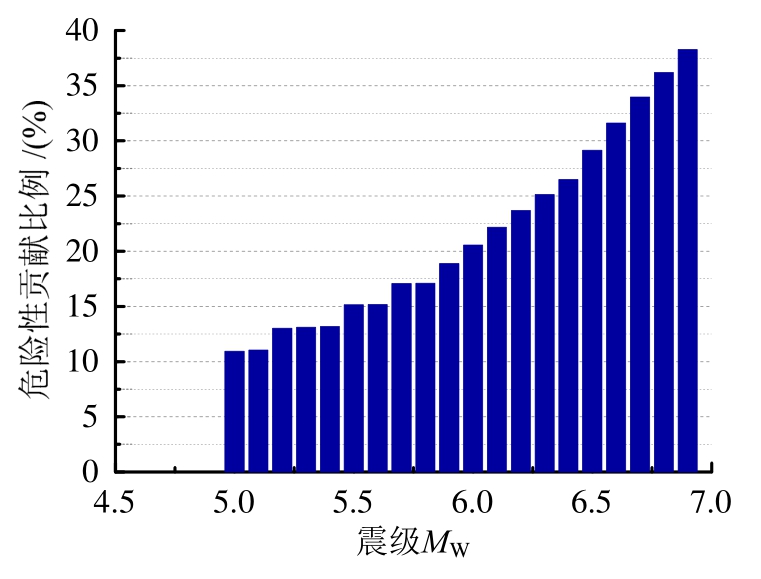
图7 脉冲造成的危险性占震级总危险性的比例
Fig.7 Proportion of risk for pulses to total risk of magnitude
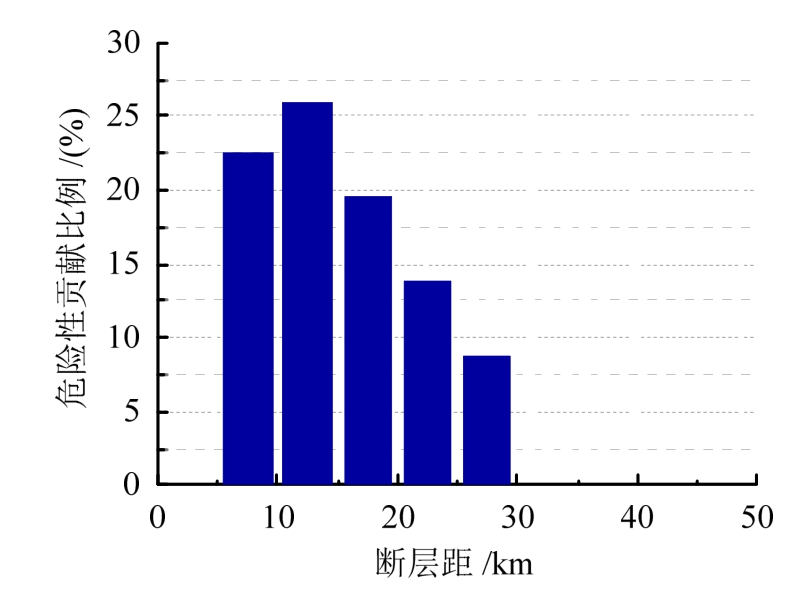
图8 脉冲造成的危险性占断层距总危险性的比例
Fig.8 Proportion of risk for pulses to total risk of rupture distance
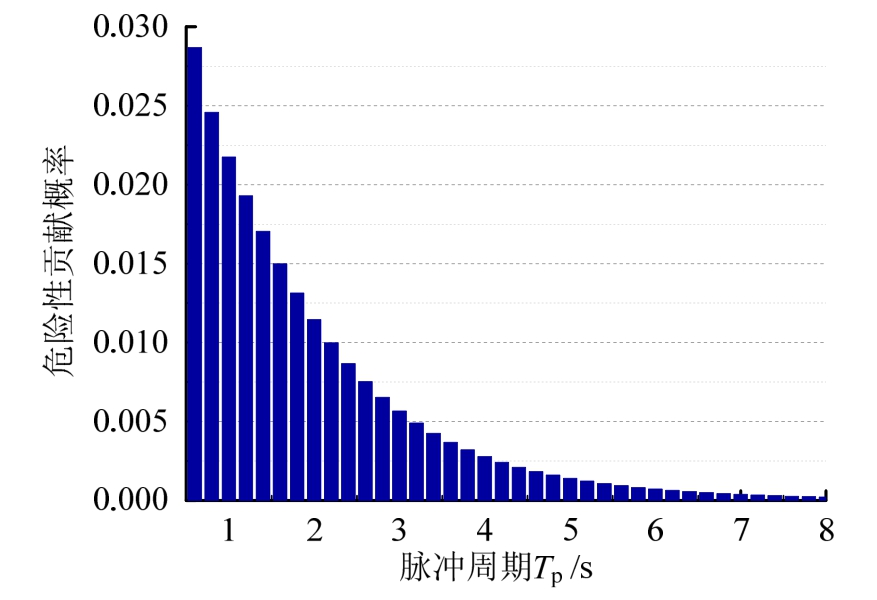
图9 场地对脉冲周期的危险性分解结果
Fig.9 Degradation of seismic hazard for site on pulse period
4 核电厂近断层设计地震动的确定
通过PSHA可以得到场地的一致危险性反应谱，该反应谱综合考虑了场地可能发生的地震事件，代表了场地总的危险性。但是一致危险性反应谱由于考虑了所有的地震事件，各个周期的谱值都普遍偏大，且很难提出一个设计地震的概念。因此，本文利用PSHA分解的结果，给出了近断层条件下的抗震设计谱。以前述算例模型为例，选取目标场地在M0=5.0、VS30=1000 m/s时，0.1 s处的分解结果进行分析。
首先由前述的PSHA分解结果确定最危险地震动参数，其中震级为6.1级，断层距为7.5 km，脉冲周期为0.6 s。将震级和最小断层距带入至衰减关系中，得到未修正的设计谱。将未修正设计谱乘以脉冲放大系数得到修正后的设计谱。为了比较得到的设计谱与一致危险性反应谱的区别，将场地的一致危险性反应谱也做于图10中。从图10可以看出，相比于未修正反应谱，修正的反应谱主要在0.6 s周期附近进行了放大，在0.03 s～0.15 s有少许降低，3.0 s之后的谱值与未修正反应谱的谱值基本相同。
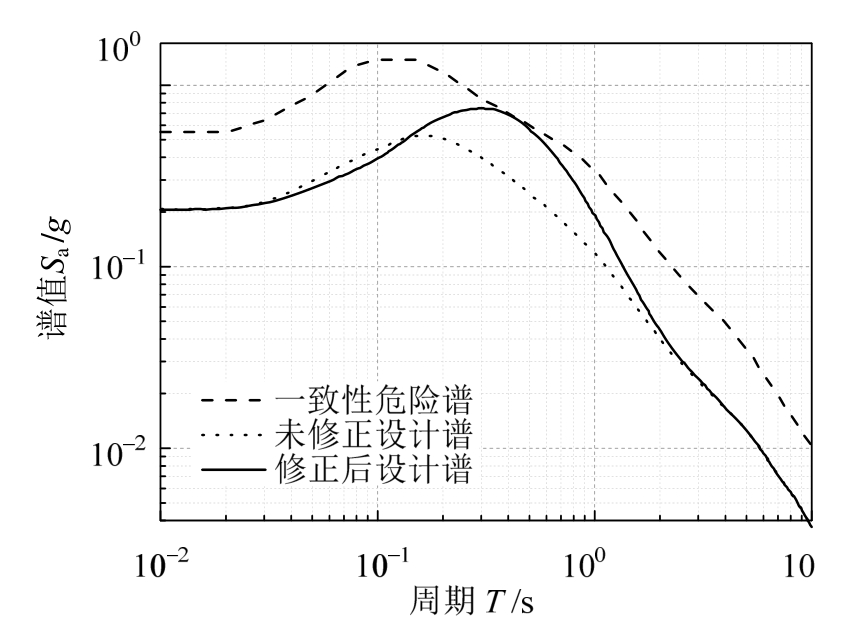
图10 设计谱与一致危险性反应谱的比较
Fig.10 Comparison of design spectrum and uniform hazard response spectra
与一致危险性反应谱相比，设计谱的谱值在各个周期都明显偏小，谱型也有显著区别，设计谱在0.1 s～2.0 s的谱型较为突出，呈明显的驼峰型，并且在0.3 s处达到峰值，而一致危险性反应谱的谱型比较平缓，在0.15 s处达到峰值。在0.4 s处，设计谱的谱值与一致危险性反应谱的谱值相同，说明设计谱在0.4 s处的年超越概率为10-4，因此从概率角度来看，该设计谱在危险周期段符合核电厂抗震设计要求达到的安全水平，同时，该设计谱克服了一致危险性反应谱带来的各周期谱值普遍偏大的缺点，具有明确的设计地震的概念。
5 结论
通过选取大量实际近断层地震动记录，研究了近断层速度脉冲对地震动反应谱的放大作用，建立修正的近断层脉冲放大系数模型，基于一个典型的断层模型，以PSHA方法为核心构建了近断层条件下核电厂的抗震设计谱，主要得到以下几点结论：
(1)通过与Baker脉冲放大系数比较发现，本文建立的脉冲放大系数在短周期处(T/TP = 0.01～0.03)会出现小于1的情况，即脉冲的发生会使一部分周期的谱值减小；本文建立的脉冲放大系数峰值约为2.3，小于Baker 脉冲放大系数的2.7；本文建立的脉冲放大系数峰值位置在T/TP=0.8处，而Baker脉冲放大系数的峰值位置在T/TP=1处。通过对比实际数据，本文的脉冲放大系数更加合理，与真实地震动特征更加吻合。
(2)基于NS-PSHA方法，采用典型断层模型，分析了模型中各个场地年超越概率为10-4的一致危险性反应谱，通过比较发现，场地与断层相对位置对一致危险性反应谱的谱值具有显著的影响：位于断层中部的场地的谱值明显大于位于断层端部的场地，并随着场地由中部向端部移动逐渐减小。
(3)通过对PSHA结果的分解，分析了场地对震级和断层距等参数的危险性分解结果，依据该结果，可以了解各个场地在遭受何等地震时会容易产生超越设计强度的地震动。
通过上述分析，最终通过选取场地最危险震级和断层距等参数带入至衰减关系中得到设计谱，并由本文建立的近断层脉冲放大系数进行修正后，便可得到近断层设计谱。本研究可为考虑近断层地震动的核电厂抗震设计谱的构建提供参考。
[1]环球网.日本敦贺核电站下方系活断层2号机或成废炉[N].http://world.huanqiu.com/exclusive/2013-05/ 3939681.html Huanqiu Network.The Japanese Tsuruga nuclear power station is on an active fault, machine No.2 may be abandoned [N].http://world.huanqiu.com/exclusive/2013- 05/3939681.html.(in Chinese)
[2]中新网.台湾核电厂邻近地壳断层废核争议持续多年[N].http://www.chinanews.com/tw/2011/03-25/2930405.shtml.Chinanews Network.The Taiwan nuclear power plant is close to the fault, and the dispute over the abandon of nuclear power plant continues for many years [N].http://www.chinanews.com/tw/2011/03-25/2930405.shtm l.(in Chinese)
[3]胡进军, 谢礼立.地震破裂的方向性效应相关概念综述[J].地震工程与工程振动, 2011, 31(4): 1—8.Hu Jinjun, Xie Lili.Review of rupture directivity related concepts in seismology [J].Earthquake Engineering and Engineering Vibration, 2011, 31(4): 1—8.(in Chinese)
[4]段安, 钱稼茹.CNP1000核电厂安全壳模型结构抗震安全分析[J].工程力学, 2009, 26(4): 153—157. Duan An, Qian Jiaru.Aseismic safety analysis of a containment vessel model for CNP1000 nuclear power plant [J].Engineering Mechanics, 2009, 26(4): 153—157.(in Chinese)
[5]王涛, 王飞, 侯钢领, 等.核电厂隔震结构的振动台试验研究[J].工程力学,2014, 31(10): 62—68, 84. Wang Tao, Wang Fei, Hou Gangling, et al.Shaking table tests on base-isolated nuclear power plant [J].Engineering Mechanics, 2014, 31(10): 62—68, 84.(in Chinese)
[6]阳涛, 杨哲飚, 陆新征, 等.核电厂安全壳结构模型碳纤维布加固试验研究[J].工程力学, 2017, 34(8): 144—153. Yang Tao, Yang Zhebiao, Lu Xinzheng, et al. Experimental study of nuclear power plant concrete containment strengthened with externally wrapped carbon fiber reinforced polymer sheets [J].Engineering Mechanics, 2017, 34(8): 144—153.(in Chinese)
[7]Ehsan Y D, Azad Y, Ahmad N, et al．Incorporating source rupture characteristics into the near-fault pulse prediction model [J].Bulletin of the Seismological Society of America, 2018, 108(1): 200—209.
[8]Sinan A, Saed M, Yalin A.A study on major seismological and fault-site parameters affecting near-fault directivity ground-motion demands for strike-slip faulting for their possible inclusion in seismic design codes [J].Soil Dynamics and Earthquake Engineering, 2018, 104(1): 88—105.
[9]Mayssa D, Armen D K.Simulation of orthogonal horizontal components of near-fault ground motion for specified earthquake source and site characteristics [J].Earthquake Engineering and Structural Dynamics, 2018, 47(6): 1369—1393.
[10]Kitada Y, Umeki Y.Near-f ield earthquakes observed recently in Japan [R].Proceedings of IAEA Workshop on Safety Signif icance of Near-f ield Earthquakes, Trieste, Italy, 2004: 28—40.
[11]Galal K, Ghobarah A.Effect of near-fault earthquakes on North American nuclear design spectra [J].Nuclear Engineering and Design, 2006, 236(18): 1928—1936.
[12]Bray J D, Rodriguez-Marek A.Characterization of forward-directivity ground motions in the near-fault region [J].Soil Dynamics and Earthquake Engineering, 2004, 24(11): 815—828.
[13]Xu Longjun, Yang Shengchao, Xie Lili.Response spectra for nuclear structures on rock sites considering the near-fault directivity effect [J].Earthquake Engineering and Engineering Vibration, 2010, 9(3): 357—365.
[14]Baker J W.Identification of near-fault velocity pulses and prediction of resulting response spectra [C].Proceedings of Geotechnical Earthquake Engineering and Soil Dynamics, Sacramento, United States, 2008.
[15]Shahi S K, Baker J W.An empirically calibrated framework for including the effects of near-fault directivity in probabilistic seismic hazard analysis [J].Bulletin of the Seismological Society of America, 2011, 101(2): 742—755.
[16]Somerville P G, Smith N F, Graves R W, et al.Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity [J].Seismological Research Letters, 1997, 68(1): 199—222.
[17]Tothong P, Cornell C A.Probabilistic seismic demand analysis using advanced ground motion intensity measures, attenuation relationships, and near-fault effects [R].PEER 2006-10, Pacific Earthquake Engineering Research Center, University of California at Berkeley, Berkeley, California, 2006: 1—205.
[18]Chioccarelli E, Iervolino I.Near-source seismic demand and pulse-like records: a discussion for L’Aquila earthquake [J].Earthquake Engineering and Structural Dynamics, 2010, 39(9): 1039—1062.
[19]Alavi B, Krawinkler H.Consideration of near-fault ground motion effects in seismic design [C]//Proceedings of the 12th World Conference on Earthquake Engineering, New Zealand, 2000: 1—8.
[20]Fu Q, Menun C.Seismic-environment-based simulation of near-fault ground motions [C]// Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, 2004: 15—25.
[21]Somerville P G.Magnitude scaling of the near fault rupture directivity pulse [J].Physics of the Earth and Planetary Interiors, 2003, 137(1): 201—212.
[22]Iervolino I, Cornell C A.Probability of occurrence of velocity pulses in near-source ground motions [J].Bulletin of the Seismological Society of America, 2008, 98(5): 2262—2277.
[23]Wells D L, Coppersmith K J.New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement [J].Bulletin of the Seismological Society of America, 1994, 84(4): 974—1002.
[24]Boore D M, Atkinson G M.Boore-atkinson nga-west2 equations for predicting response spectral accelerations for shallow crustal earthquakes [R].PEER, Pacific Earthquake Engineering Research Center, Berkeley, California, 2013: 142—150.
[25]Robin K, McGuire.Probablistic seismic hazard analysis and design earthquake: closing the loop [J].Bulletin of the Seismological Society of America, 1995, 85(5): 1275—1284.