土的固结与沉降变形计算是地基处理与设计中的重要组成部分。20世纪20年代Terzaghi[1]提出的饱和黏土一维固结理论，至今仍然在工程实践中广泛使用，但理论计算值与实测值之间的误差也不可忽视。Mikasa[2]和Gibson等[3]通过大量的黏土固结试验和非线性应变固结理论研究表明，当土层厚度较大时，自重应力对固结有较大的影响，且考虑土层自重应力时，土体的固结速率比Terzaghi理论值快；窦宜等[4]通过离心试验研究结果也表明了实际土层的固结速率快于Terzaghi理论值。理论计算分析方面，Mesri和Choi[5]、纠永志等[6]、胡安峰等[7]、马崇武和刘忠玉[8]、李冰河等[9]、Chen[10]通过有限单元法、有限差分法、有限体积法、半数值半解析法、Differential Quadrature Method (DQM)法等数值手段分析了考虑自重的固结特性，取得了丰富的研究成果。然而，以上研究基本上都将边界视为完全排水或完全不排水。
在工程实际中，土体边界的实际排水能力介于完全透水与完全不透水之间。基于此，Gray[11]提出完全排水边界和完全不排水边界线性组合的半透水边界，但其在方程求解中较复杂且一般难以得到显式解析解答。针对上述不足，梅国雄等[12]对边界做了修正，提出了考虑边界孔压随时间呈指数衰减的连续排水边界条件。随后，Mei和Chen[13]对文献[12]的解答结果进行了修正。何利军等[14]研究了土层厚度随时间变化的平均固结度。Liu和Lei[15]给出了成层地基一维固结问题半数值半解析解答，Wu等[16]研究了双层黏弹性固结问题。但是上述研究都没有考虑土体自重对固结的影响。蔡烽等[17-18]利用有限元分析了考虑自重的地基一维固结问题和不排水对称面问题，然而，文中只分析了不同位置铺设砂垫层时的土体固结度，并没有给出水平排水砂垫层的最优铺设位置。
本文基于连续排水边界，建立考虑自重的地基一维固结方程，利用有限正弦Fourier变换方法，求解出解析解，然后分析不排水对称面的影响因素。同时，为获得水平排水砂垫层的最优铺设位置，通过建立铺设有水平排水砂垫层时的土体一维固结方程，结合有限正弦Fourier变换的解析方法和数值手段，得到水平排水砂垫层的最优铺设位置，最后讨论分析设置水平排水砂垫层对固结速率的影响。研究结果为地基处理提供理论依据。
1 连续排水边界条件
固结是土体在外荷载作用下，水从孔隙中排出，土体收缩变形的过程。土体排水是从边界逐渐内推的过程，排水边界处孔压的变化应该是一个随时间连续变化的过程。然而，对Terzaghi一维固结理论研究发现，
但
即排水边界处孔压在具有不连续性，孔压由q跳跃到0；Gray提出的半透水边界条件下的孔压解答求解复杂，且不易得到显式解析解。
对比Terzaghi[1]和Gray[11]的解答，其解答分别如下：
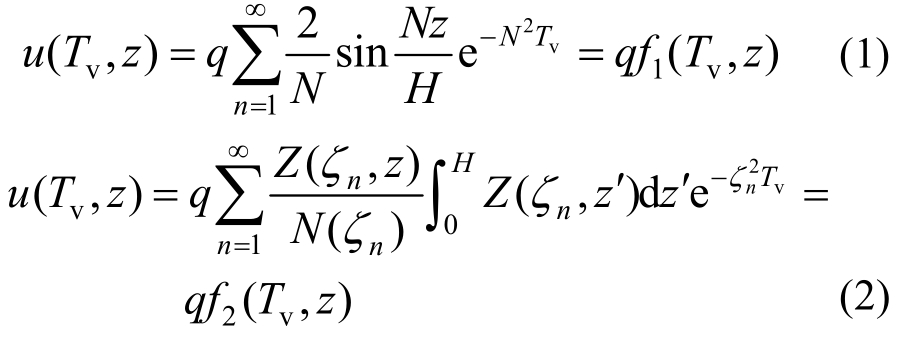
式中：
为时间因数；
为范数；
为特征函数；
为特征值。可以发现二者孔压解答结果都是由外荷载项和包含时间因数的函数项
组成。初始状态时，
中间状态时，
单调递减函数，最终状态时，
Mei和Chen[13]考虑到Terzaghi和Gray的解答都以指数e为底的指数形式，故而选取e的负指数函数作为连续排水边界条件：
式中：q表示外加瞬时荷载；b为界面参数，且b＞0，b越大，表示土体界面透水性能越好。
2 固结模型与基本方程
本文研究的地基模型如图1所示，地基土层的厚度、渗透系数、固结系数和体积压缩系数分别为H、kv、mv和Cv，土体顶面和底面均铺设砂垫层，地基表面荷载为q，土体浮重度为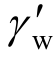
，土体自重应力分布为σ(z)。控制方程和定解条件如下。
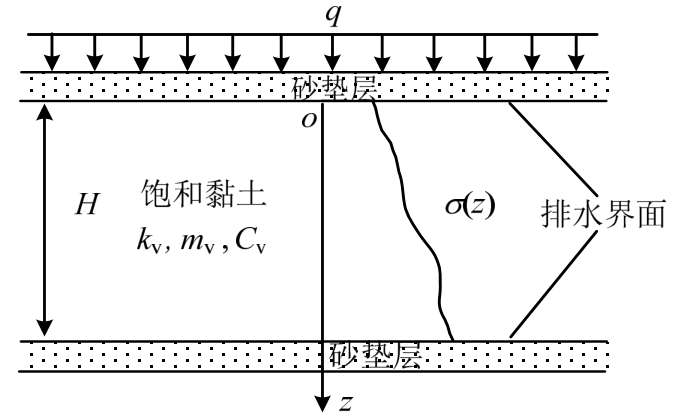
图1 一维固结模型示意图
Fig.1 Sketch of one-dimensional consolidation of saturated soils
控制方程：
初始条件：
边界条件：
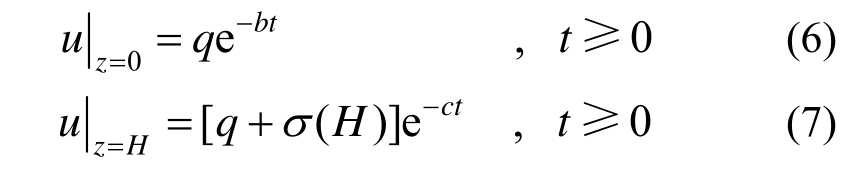
为便于方程求解，定义如下无量纲化参数：
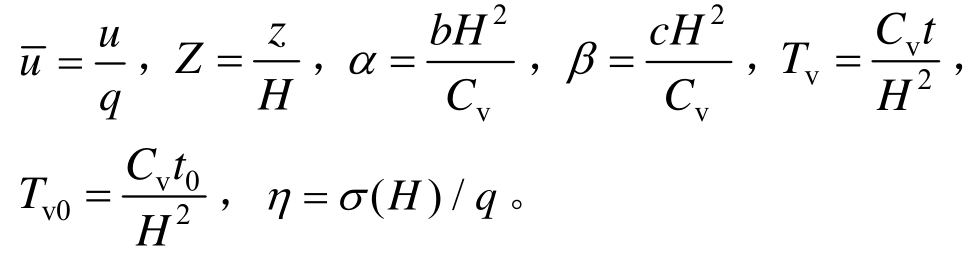
式中：α和β为无量纲化的界面参数，且均大于0，数值越大，表示土体界面的透水性能越好。需要指出的是，本文中的H是指土体的厚度，不是传统固结理论中的排水路径；同时，时间因数Tv只是一个与时间相关的无量纲参数，假设初始的自重应力为线性分布，即
η为自重应力系数。
相应的无量纲参数代入控制方程与初始条件可得连续排水边界条件下考虑自重的无量纲化的一维固结控制方程与定解条件，如下：
控制方程：
初始条件：
边界条件：
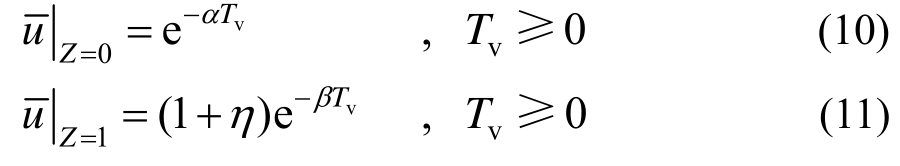
3 方程求解
3.1 超静孔隙水压力解答
由于边界条件式(8)、式(9)为非齐次边界，故作非齐次边界齐次化，令：
将式(12)代入方程及定解条件，得：
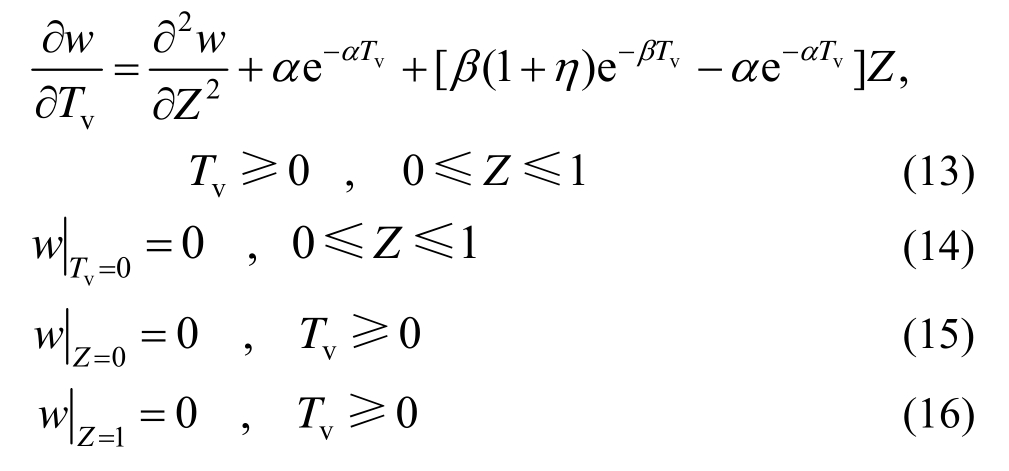
基于齐次边界条件式(15)和式(16)，对方程式(13)及初始条件式(14)作有限正弦Fourier正弦变换，得：
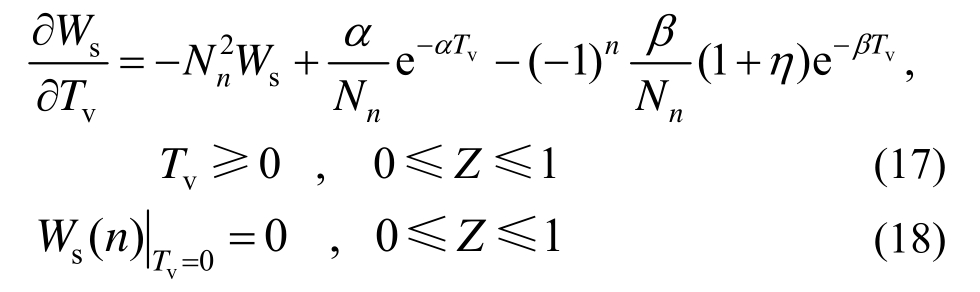
式中：
联立式(18)与常微分方程式(17)，求解得：
式中：
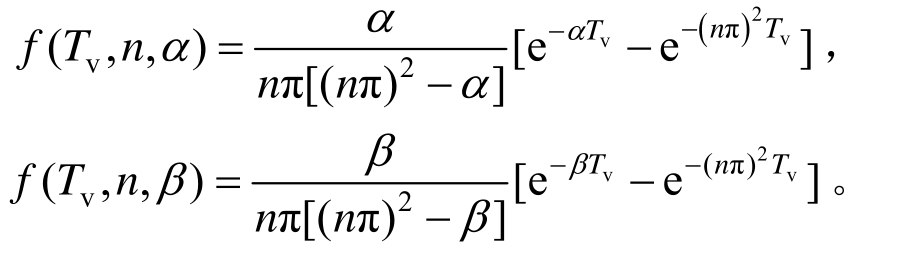
基于有限正弦Fourier逆变换，有：
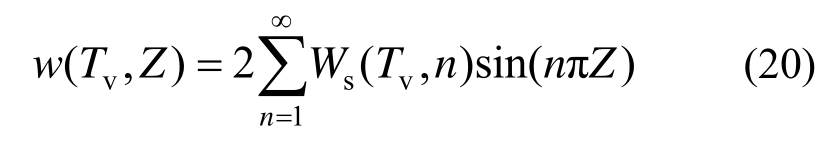
将式(19)代入式(20)进行有限正弦Fourier逆变换，得：
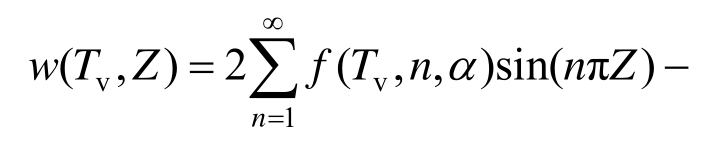
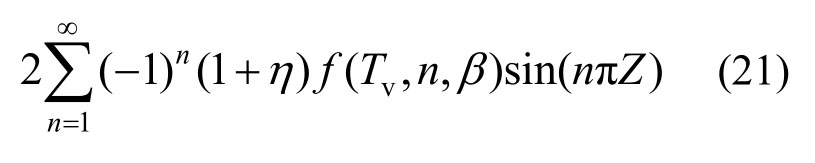
将式(21)代入式(12)，求得无量纲的超静孔隙水压力为：
3.2 地基平均固结度解答
根据超静孔隙水压力定义的地基平均固结度为：
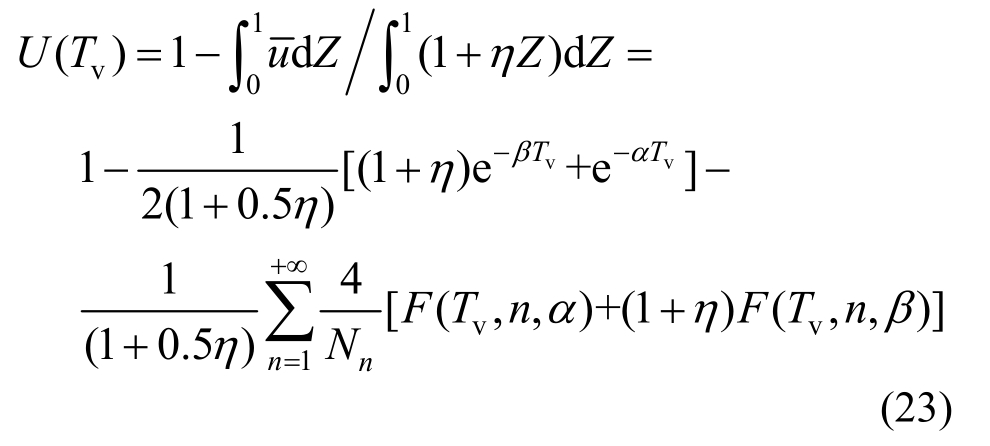
式中：
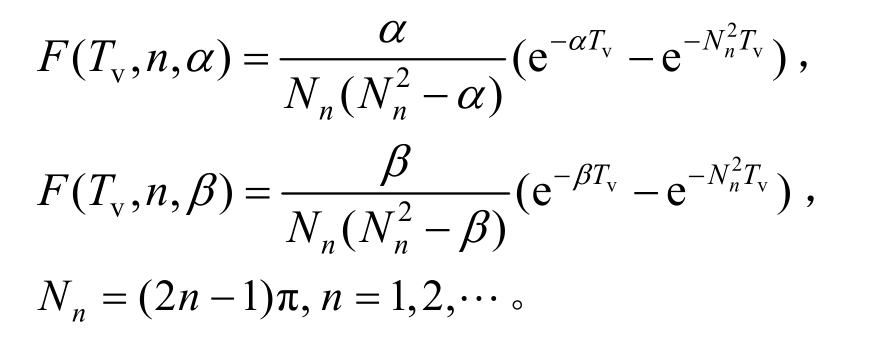
3.3 解的退化验证
令α、β→∞，即边界条件退化为完全排水边界条件，则式(21)退化为：
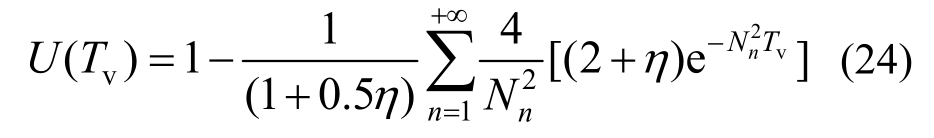
即式(22)为Terzaghi完全排水边界条件下考虑自重的固结度解答。
令η =0，即初始条件退化为不考虑自重的瞬时加载，则式(21)退化为：
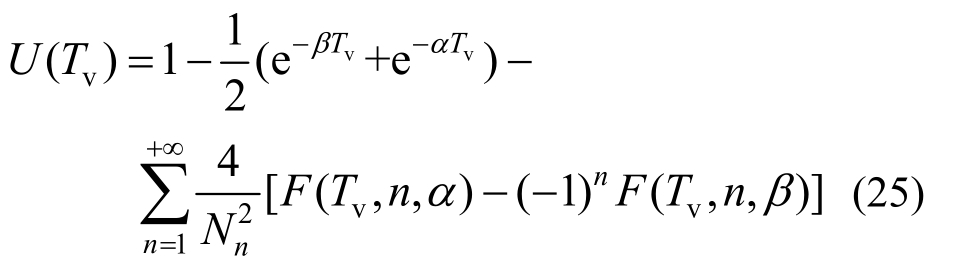
即式(23)为Mei和Chen[13]基于瞬时荷载下连续排水边界条件的固结度解答。
从界面参数α、β和自重应力系数η两个方面进行解答退化后的结果来看，可以初步发现，Terzaghi完全排水边界条件下的一维固结理论解答和Mei基于瞬时荷载下连续排水边界条件下的一维固结解答均是本文解答的特例。
4 不排水对称面的影响因素分析
黄文熙[19]定义土体中间排水通量等于零的平面为不排水对称面，即
由于
所以不排水对称面为孔压峰值点。从不排水对称面的概念可知，只有当荷载和上、下边界同时对称时，孔压才关于土体厚度中间对称。对于Terzaghi双面完全透水条件来说，不排水对称面恒定在土体厚度中间位置不变。但实际工程中，土体顶面和底面边界的排水性能是介于完全透水和不完全透水之间，且透水能力也不完全相同。此外，考虑自重对固结过程的影响时，初始应力沿土体垂直方向呈非对称分布，不排水对称面随时间变化，因此在分析不排水对称面时需要综合考虑自重应力和界面的影响。不排水对称面的解答是一个无穷级数求和项组成的隐式解析解答，本文通过计算机编程计算，然后进行不排水对称面的参数敏感性分析。
4.1 不同界面参数α/β 比值的影响
为研究界面参数对不排水对称面的影响，分别选取上、下界面参数为η = 1, α = 1, β = 2和η = 1, α = 1, β = 3作对比分析，如图2所示。从图中可以发现，不排水对称面位置随时间因数不断往上移动。这是由于底部边界参数大，排水能力强，为了达到排水能力和排水量的平衡，在固结排水过程中，不排水对称面将往排水能力差的一侧移动。同时看到，界面参数越大时，排水能力越强，不排水对称面移动越快。
图2 界面参数对孔压的影响
Fig.2 Influence of interface parameters on excess pore-water pressure
4.2 自重系数η 的影响
自重应力对固结影响主要体现在初始孔压在垂直方向的分布形式，h越大，初始孔压随着深度增大。从图3可以看出，随着h的增大，不排水对称面的位置逐渐下移，且都存在相同现象，即不排水对称面的位置都随着时间不断向界面参数小的边界处移动。
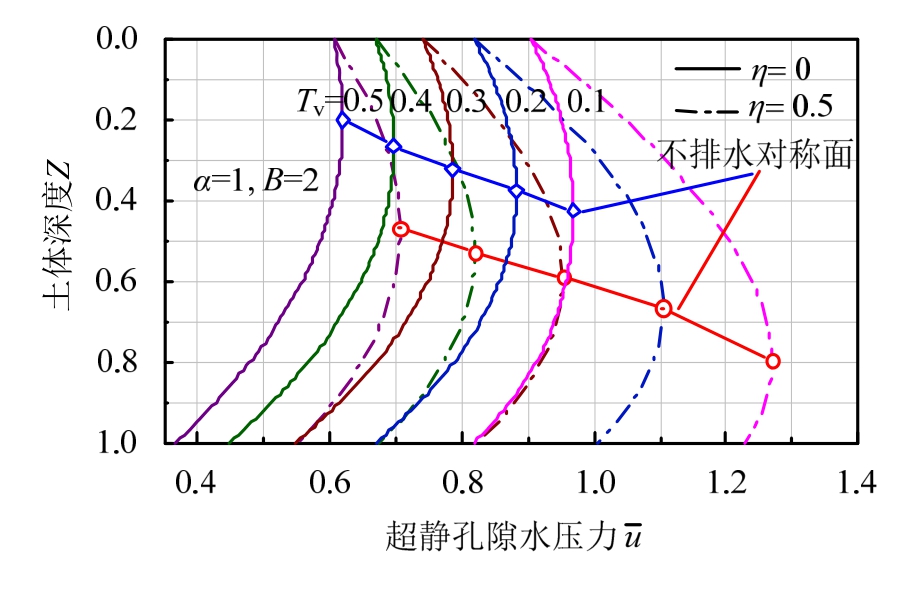
图3 η 对孔压的影响
Fig.3 Influence of η on excess pore-water pressure
5 排水砂垫层铺设位置优化
在吹填土围海造地的工程实际中，为加快排水固结，往往会在土层某一深度设置水平排水砂垫 层[20—23]。许多学者[24—25]对砂垫层位置一定时土体的固结性状进行了研究。但从前面对不排水对称面的分析可以发现，对于某一时刻土体的排水来讲，将水平排水砂垫层设置在不排水对称面位置，土体固结最快，如图4所示。蔡烽等[18]利用有限元分析了不同位置砂垫层的固结度，然而，不排水对称面随时间不断变化，利用有限元分析方法却不能对砂垫层铺设位置进行优化。在工程实际中，往往关心在一定工期条件下，设置排水砂垫层获得土体的最大固结度，因而有必要研究固结度与水平排水砂垫层铺设位置的优化关系。
5.1 模型的建立
为如何优化排水砂垫层铺设位置，从而提高土体排水固结速率，一维固结模型如图4所示。假设排水砂垫层的边界为完全排水，离土体表面的位置为ξH，其他参数及意见与前面相同。
下面对设有水平排水砂垫层的土体建立固结模型。
控制方程：
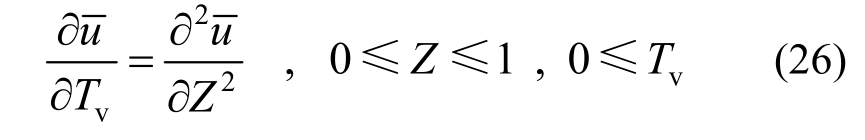
初始条件：
边界条件：
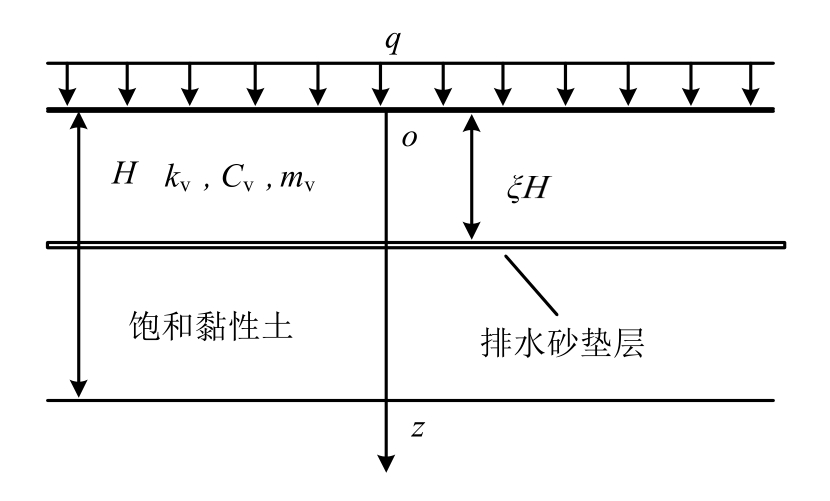
图4 一维固结模型示意图
Fig.4 Sketch of one-dimensional consolidation of saturated soils
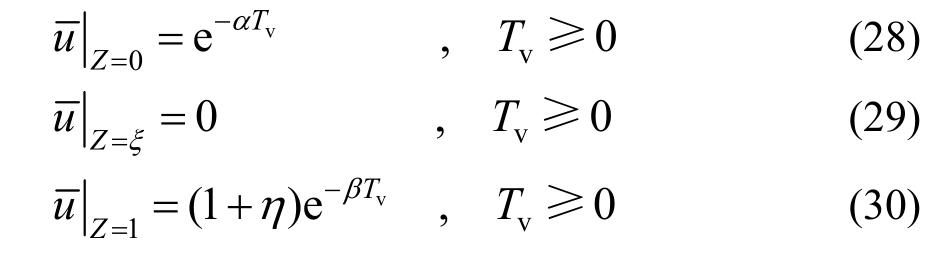
式(26)～式(30)即为土体的固结控制方程与定解条件。
5.2 方程的解答
由于水平排水砂垫层边界被视为完全排水，因此可以将饱和黏土层看作相互独立的顶部和底部两层土。顶部土层的孔压用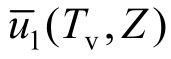
表示，底部土层的孔压用
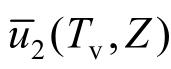表示，采用前面方程求解方法，首先对非齐次边界齐次化，然后利用有限Fourier变换可以求解出相应孔压和固结度。
上部土体的无量纲超静孔隙水压力为：
其中：
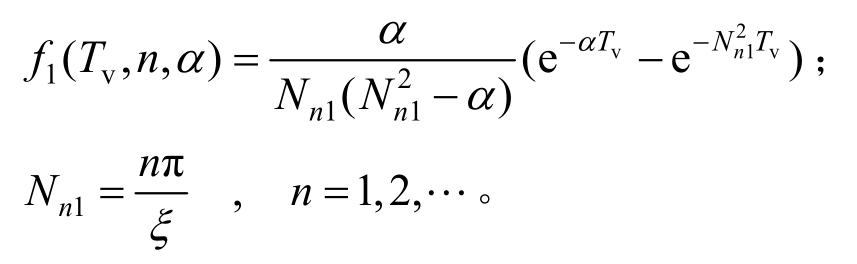
底部土体的无量纲超静孔隙水压力为：
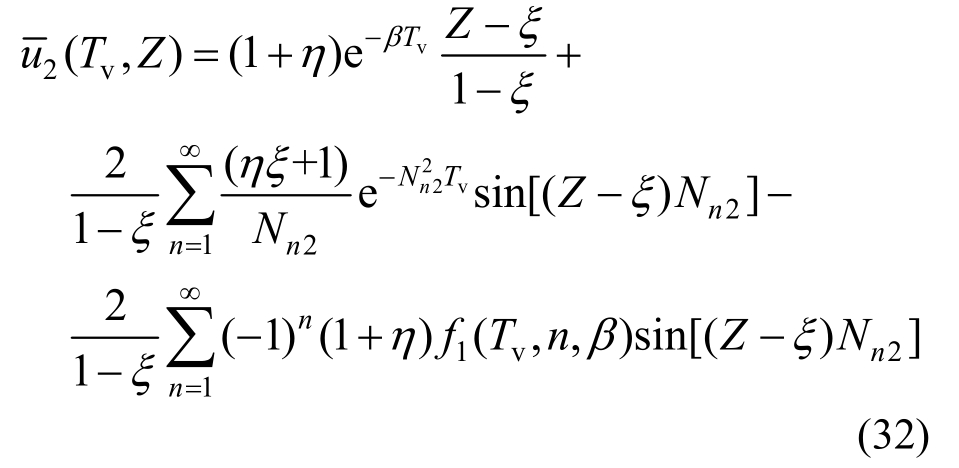
其中：
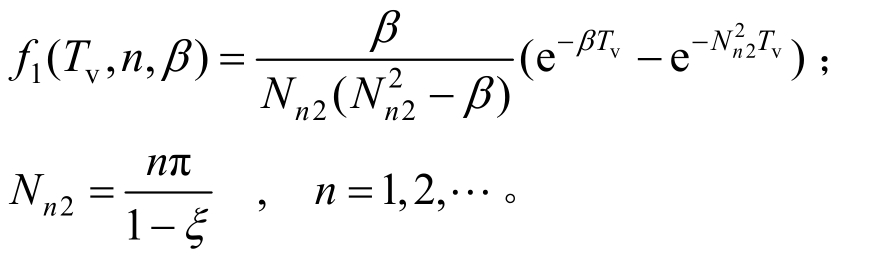
根据孔隙水压力的固结度定义有：
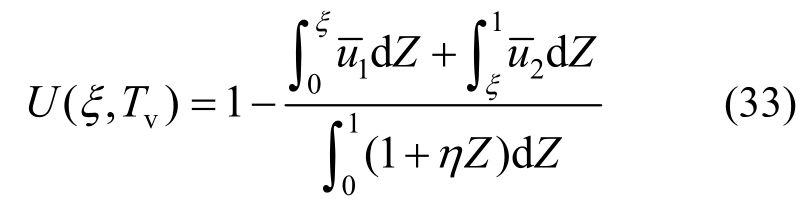
5.3 排水砂垫层最优铺设位置分析
工程建设中，工期是一个重要因素，工期长短关系到工程建设的经济效益。在排水固结的地基处理中，在工期确定的情况下，如何设置排水砂垫层的位置，使得固结度达到最大，是工程中关心的问题，蔡烽等[17]的有限元方法只能求出固定砂垫层位置的固结度，但无法获得砂垫层最优位置使固结度达到最大。从式(33)可以得到，对于确定工期，其时间因数为定值。当
取得最大值，相应的ξ即是确定工期时的水平排水砂垫层的最优铺设位置，这也是本文亟需解决的问题。本文通过计算机编制优化程序计算，得到不同时间因数下的排水砂垫层最优铺设位置。
图5为在不同的时间因数下土体平均固结度与水平砂垫层铺设位置的关系曲线。可以看到，在每一个固定的时间因数下，都存在一个砂垫层的最优铺设位置，使得平均固结度达到最大。同时发现，水平砂垫层的最优铺设位置随时间因数不断变化，与不排水对称面相类似，随时间因数的变化逐渐向排水能力差(界面参数小)的一侧移动。
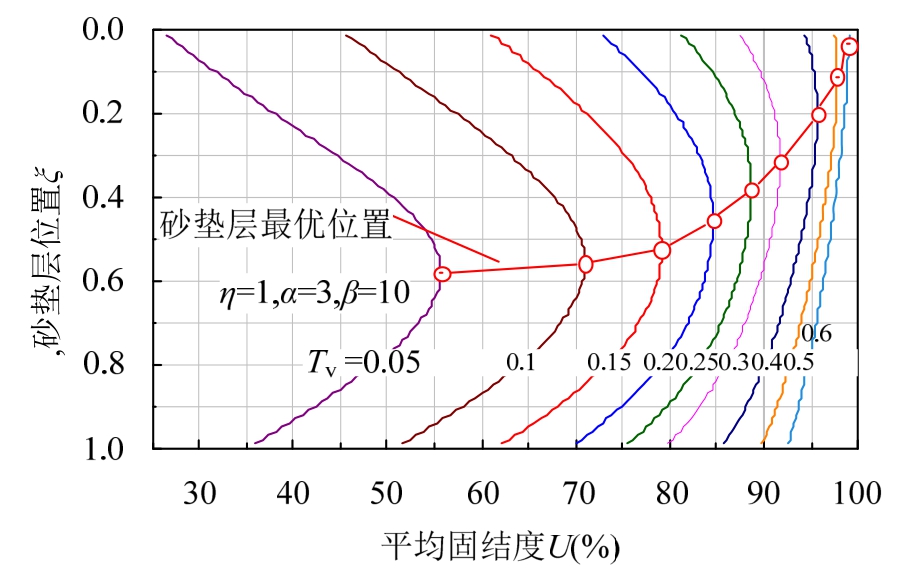
图5 砂垫层铺设位置与平均固结度的关系
Fig.5 Relationship between laying position and average consolidation degree of sand blanket
图6为在时间因数Tv=0.2、0.3、0.4、0.5时的砂垫层最优位置铺设了砂垫层的土体固结度与不铺设砂垫层的土体固结度的对比图。从图中可以看出，铺设了砂垫层的土体的平均固结度都高于不铺设砂垫层的土体平均固结度。进一步对比分析发现，在时间因数Tv=0.2、0.3、0.4、0.5时，在相应的最优铺设砂垫层位置铺设砂垫层的土体的平均固结度是最大的。
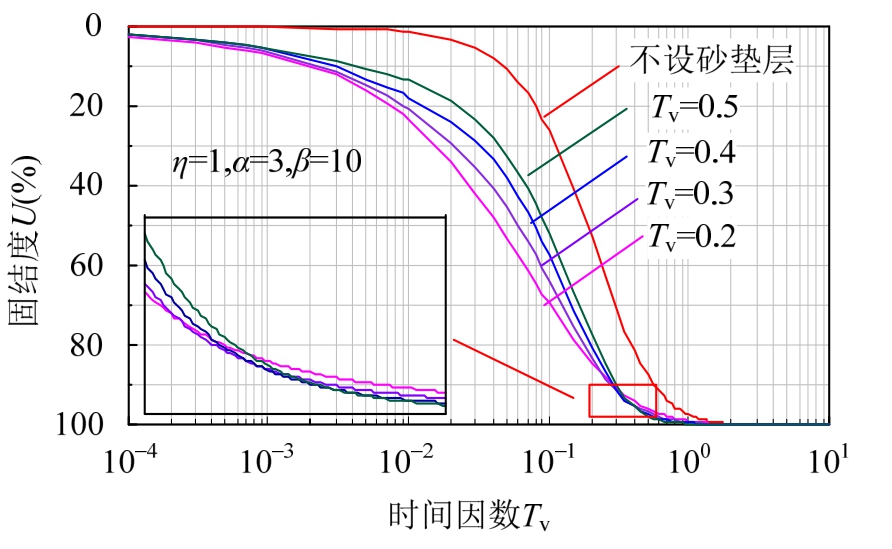
图6 不同砂垫层铺设位置的平均固结度对比图
Fig.6 Comparison of average consolidation under different sand blanket positions
为了进一步给工程实际中提供更为方便的排水砂垫层最优位置的查找，图7给出了η=1、α=3时，不同底部界面参数下水平排水砂垫层最优位置与时间因数的关系。在实际工程设计和计算中，可以根据工程的实际工期，通过查表的方式查出相应的排水砂垫层的最优铺设位置，合理铺设水平排水砂垫层，从而达到土体平均固结度最大的目的。值得注意的是，由于界面参数越大，排水速率越快，因此当工期较长时(时间因数大)，土体基本完成固结，设置水平排水砂垫层与否对于工程实际来说意义不大。
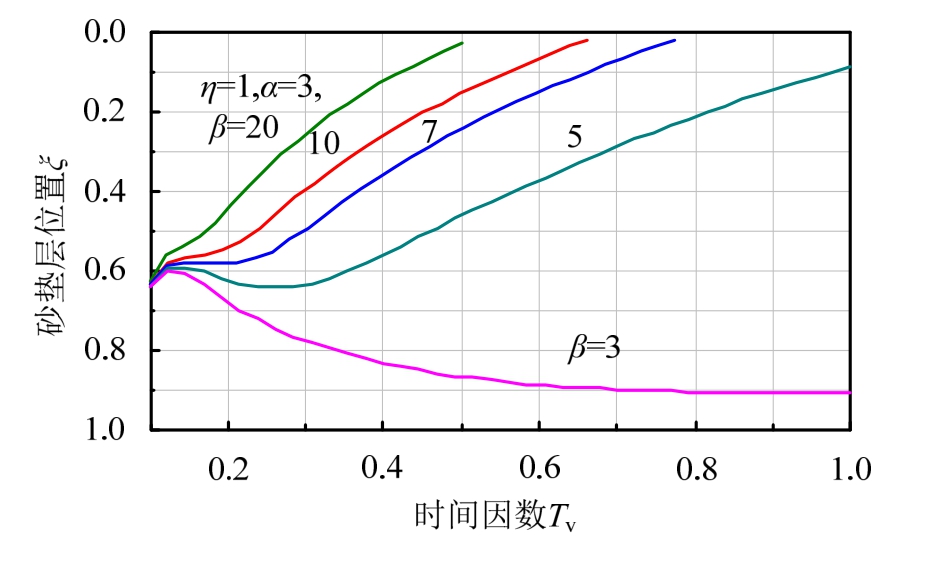
图7 不同界面参数下砂垫层最优铺设位置与时间因素的 关系
Fig.7 Relationship between optimal sand blanket laying position and time factor under different interface parameters
5.4 算例分析
以某填海造陆工程为例，施工方式为堆载预压，相应的土体参数如表1所示，上下界面参数均取3。为了分析优化水平排水砂垫层对固结度的提高，定义与未考虑水平排水砂垫层优化的固结度相对比的固结时间提高率如下式：
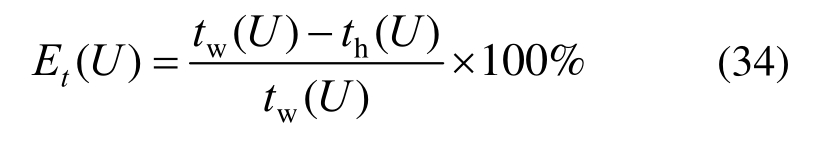
式中：tw(U)表示没有考虑砂垫层优化时，土体达到某固结度时的时间；th(U )表示考虑砂垫层优化时，土体达到某固结度时的时间。
表1 土体参数
Table 1 Parameters of soil
土层厚度/m 竖向固结/(cm2·s-1)重度/(kN·m-3)预压应力/kPa 10.05 4.5×10-4 19.3 100
在堆载预压固结排水法施工中，卸载时固结度一般需要达到90%以上，因此以固结度达到90%作为砂垫层优化的确定固结度，其固结曲线如图8所示。从图中可以看出：未考虑优化砂垫层在中期(固结度20%～60%)的固速率高于考虑优化砂垫层的固结速率，但是在后期的固结速率低于考虑优化砂垫层的固结速率。固结度达到90%时，考虑优砂垫层的时间因数取0.5，未考虑优化砂垫层的时间因数= 0.56, 即相应的固结时间提高率Et=12%，这表明考虑优化砂垫层对于固结时间效率的提高具有明显的效果。
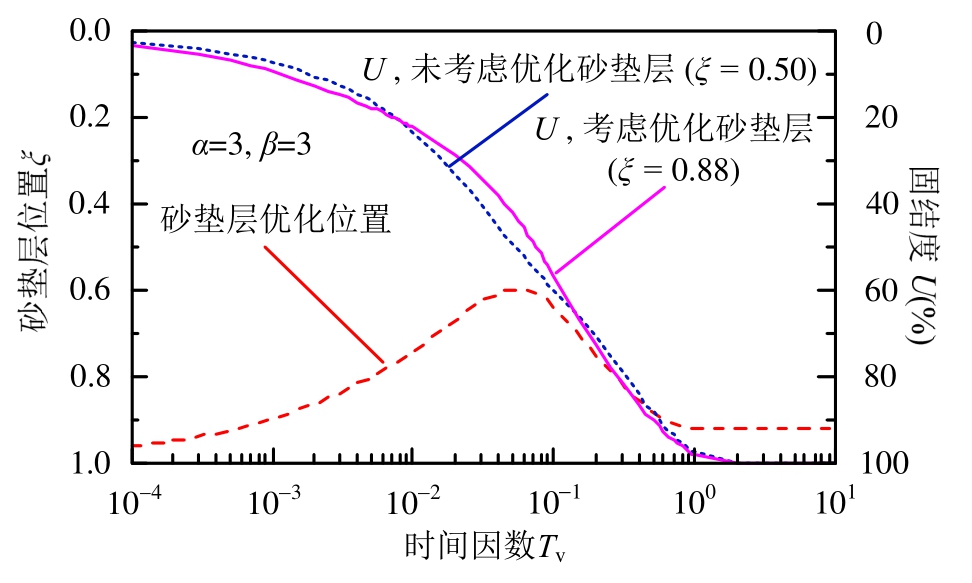
图8 水平排水砂垫层对固结度曲线的影响
Fig.8 Influence of horizontal drainage blanket on consolidation curves.
6 结论
本文基于连续排水边界条件和考虑土体自重作用，利用有限正弦Fourier变换获得了解析解答，并分析了不排水对称面的影响因素。针对水平排水砂垫层位置的优化问题，结合有限正弦Fourier变换的解析方法和数值手段，获得了水平排水砂垫层的最优铺设位置，最后分析了考虑优化的水平排水砂垫层对固结速率的影响。主要研究结论如下：
(1)土体自重应力影响固结的初始应力在垂直方向上呈不均匀分布，势必影响土体固结中不排水对称面的变化。推导出连续排水边界条件下考虑自重应力的一维固结孔压解析解，运用数值分析手段研究不排水对称面得到：自重系数越大，不排水对称面位置越靠近土层底部，且随时间逐渐变化，并向界面参数小的一侧移动。
(2)在确定工期的条件下，土层内部存在排水砂垫层最优铺设位置，且随时间因数不断变化，界面参越大，排水砂垫层最优铺设位置偏离该界面越远。
(3)本文给出的不同界参数下最优砂垫层铺设位置与时间的关系图，可用于实际工程中水平排水砂垫层铺设位置的设计计算。
(4)通过算例可以表明：考虑砂垫层优化的土体固结速率高于未考虑砂垫层优化的土体固结速率，在确定固结度的条件下，相应的固结时间效率的提高具有明显效果，达到12%。
[1]Terzaghi K.Erdbaumechanik auf bodenphysikalischer grundlage [M].Wien: Fanz Deuticke, 1925.
[2]Mikasa M.The consolidation of soft clay-a new consolidation theory and its application [J].Equations, 1965, 1(1): 21—26.
[3]Gibson R E, Schiffman R L, Cargill K W.The theory of one-dimensional consolidation of saturated clays.II.Finite nonlinear consolidation of thick homogeneous layers [J].Canadian Geotechnical Journal, 1981, 18(2): 280—293.
[4]窦宜, 蔡正银, 盛树馨.自重应力作用下饱和粘土的固结变形特性[J].岩土工程学报, 1992, 14(6): 29—37.Dou Yi, Cai Zhengyin, Sheng Shuxin.Consolidation characteristics of saturated clays under self-weight stress [J].Chinese Journal of Geotechnical Engineering, 1992, 14(6): 29—37.(in Chinese)
[5]Mesri G, Choi Y K.Settlement analysis of embankments on soft clays [J].Journal of Geotechnical Engineering, 1985, 111(4): 441—464.
[6]纠永志, 刘忠玉, 乐金朝, 等.考虑非Darcy渗流和自重应力的一维固结分析[J].同济大学学报(自然科学版), 2012, 40(4): 541—548.Jiu Yongzhi, Liu Zhongyu, Yue Jinchao, et al.One-dimensional consolidation with a consideration of non-Darcy flow and self-gravity stress [J].Journal of Tongji University (Natural Science), 2012, 40(4): 541—548.(in Chinese)
[7]胡安峰, 黄杰卿, 谢新宇, 等.考虑自重影响的饱和土体一维复杂非线性固结研究[J].浙江大学学报(工学版), 2012, 46(3): 441—447. Hu Anfeng, Huang Jieqing, Xie Xinyu, et al.Study on properties of one-dimensional complex nonlinear consolidation considering self-weight of saturated soils[J].Journal of Zhejiang University (Natural Science), 2012, 46(3): 441—447.(in Chinese)
[8]马崇武, 刘忠玉.考虑饱和黏土埋深影响的一维非线性固结[J].岩石力学与工程学报, 2007, 26(增刊2): 4372—4377.Ma Chongwu, Liu Zhongyu.One-dimensional nonlinear consolidation considering buried depth of saturated clay layer [J].Chinese Journal of Rock Mechanics and Engineering，2007, 26(Suppl 2): 4372—4377.(in Chinese)
[9]李冰河, 谢康和, 应宏伟, 等.初始有效应力沿深度变化的非线性一维固结半解析解[J].土木工程学报, 1999, 32(6): 47—52.Li Binghe, Xie Kanghe, Ying Hongwei, et al.Semi-analytical solution of 1-D nonlinear considering the initial effective stress distribution [J].China Civil Engineering Journal, 1999, 32(6): 47—52.(in Chinese)
[10]Chen R P, Zhou W H, Wang H Z, et al.One-dimensional nonlinear consolidation of multi-layered soil by differential quadrature method [J].Computers & Geotechnics, 2005, 32(5): 358—369.
[11]Gray H.Simultaneous consolidation of contiguous layers of unlike compressive soils [J].American Society of Civil Engineers, 1945, 110(1): 1327—1356.
[12]梅国雄, 夏君, 梅岭.基于不对称连续排水边界的太沙基一维固结方程及其解答[J].岩土工程学报, 2011, 33(1): 28—31. Mei Guoxiong, Xia Jun, Mei Ling.Terzaghi's one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary [J].Chinese Journal of Geotechnical Engineering, 2011, 33(1): 28—31.(in Chinese)
[13]Mei G X, Chen Q M.Solution of Terzaghi one-dimensional consolidation equation with general boundary conditions [J].Journal of Central South University (Science and Technology), 2013, 20(8): 2239—2244.
[14]何利军, 吴立松, 张涛, 等.基于连续边界条件的土层厚度随时间变化的平均固结度研究[J].工程力学, 2016, 33(S1): 11—17. He Lijun, Wu Lisong, Zhang Tao, et al.The average degree of consolidation of soil layer thickness changing with time based on continuous drainage [J].Engineering Mechanics, 2016, 33(S1): 11—17.(in Chinese)
[15]Liu J C, Lei G H.One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries [J].Computers & Geotechnics, 2013, 54(10): 202—209.
[16]Wu W, Zong M, El Naggar M H, et al.Analytical solution for one-dimensional consolidation of double-layered soil with exponentially time-growing drainage boundary [J].International Journal of Distributed Sensor Networks, 2018, 14(10): 1—11.
[17]蔡烽, 何利军, 张青青, 等.考虑土体自重的不排水对称面有限元分析[J].浙江大学学报(工学版), 2013, 47(12): 2132—2140. Cai Feng, He Lijun, Zhang Qingqing, et al.Finite element analysis of undrained symmetry plane with self-weight [J].Journal of Zhejiang University (Natural Science), 2013, 47(12): 2132—2140.(in Chinese)
[18]蔡烽, 何利军, 周小鹏, 等.连续排水边界下一维固结不排水对称面的有限元分析[J].岩土工程学报, 2012, 34(11): 2141—2147. Cai Feng, He Lijun, Zhou Xiaopeng, et al.Finite element analysis of one-dimensional consolidation of undrained symmetric plane under continuous drainage boundary [J].Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2141—2147.(in Chinese)
[19]黄文熙.土的工程性质[M].北京: 水利电力出版社, 1983. Huang Wenxi.Engineering properties of soil [M].Beijing: Hydraulic and Hydroelectricity Press, 1983.(in Chinese)
[20]Tan S A, Liang K M, Yong K Y, et al.Drainage efficiency of sand layer in layered clay-sand reclamation [J].Journal of Geotechnical Engineering, 1992, 118(2): 209—228.
[21]Nogami T, Li M.Consolidation of system of clay and thin sand layers [J].Soils & Foundations, 2002, 42(4): 1—11.
[22]Rujikiatkamjorn C, Indraratna B.Analytical solutions and design curves for vacuum-assisted consolidation with both vertical and horizontal drainage [J].Canadian Geotechnical Journal, 2007, 44(2): 188—200.
[23]Fukuda M, Ito Y, Suwa S, et al.Presentation of two layers horizontal drain model and design method for reduction of consolidation delay, [J].Jioshinsetikkusu Rombunshu/Geosynthetics Engineering Journal, 2011, 26: 13—18.
[24]Walker R, Indraratna B.Consolidation analysis of a stratified soil with vertical and horizontal drainage using the spectral method [J].Geotechnique, 2009, 59(5): 439—449.
[25]Chai J, Horpibulsuk S, Shen S, et al.Consolidation analysis of clayey deposits under vacuum pressure with horizontal drains [J].Geotextiles and Geomembranes, 2014, 42(5): 437—444.