型钢混凝土(SRC)柱具有良好的延性性能、变形和耗能能力等特点;而钢梁具有自重轻、强度高、工期短等优势,因此,二者结合的型钢混凝土柱-钢梁组合结构作为一种新型结构体系具有广阔的应用前景[1]。然而,根据建筑使用和受力要求,内置型钢截面形式多样,其中配置T形截面型钢不仅可以实现柱肢和填充墙等宽,满足平面布置的灵活性,同时克服了普通钢筋混凝土异形柱轴压比限值难以满足要求、承载力不高、抗震性能差等缺陷[2—3]。
目前,国内外学者采用试验或者有限元手段,对对称配钢型钢混凝土结构和构件的抗震性能研究较多[4—17],而对于配置T形、L形非对称型钢骨架的型钢混凝土结构的研究落后于工程实践,从结构层次对型钢混凝土框架的受力性能所做的研究甚少,同时,我国现行组合结构规程也未涉及任何配置非对称型钢骨架情况的条文,因此限制了该类结构在工程中的应用。
鉴于此,为了研究T形配钢型钢混凝土柱-钢梁框架结构的抗震性能,本文基于3层2跨、缩尺比为1∶3框架模型的拟静力试验研究和有限元数值模拟,揭示该类结构在水平低周往复荷载作用下的破坏形态及破坏机理,通过对滞回曲线和骨架曲线、延性性能、耗能能力、刚度和强度退化规律等分析,充分了解该类结构的抗震性能;同时采用Perform-3D有限元分析软件,分析不同轴压比、配钢率和混凝土强度等设计参数对框架结构抗震性能的影响,研究结果可为该类结构的工程应用以及相应规范的制定提供理论支撑。
1 试验概况
1.1 试件设计
参照现行相关规范,以8度抗震设防、二类场地土为条件,设计制作了3层2跨、缩尺比为1∶3的T形配钢型钢混凝土柱-钢梁框架结构模型试件[18—21],经计算柱、梁实际抗弯强度比为1.26。试件单跨跨度为1500 mm,底层高1260 mm,第2层和顶层高均为1000 mm。框架边柱采用T形配钢型钢混凝土柱,中柱采用十字形配钢型钢混凝土柱,内置型钢骨架均由3 mm厚钢板焊接而成;试件中的所采用的箍筋和纵筋分别为直径4 mm的冷拔钢丝和直径8 mm的HRB335级钢筋,将箍筋加工成U形或矩形焊接在型钢上,并绑扎纵筋与箍筋。框架梁采用工字形钢梁,由3 mm厚钢板焊接而成,沿长度方向等距设置6个加劲肋。试件立面布置及尺寸、梁柱截面尺寸及配钢、节点构造分别如图1、图2和图3所示。
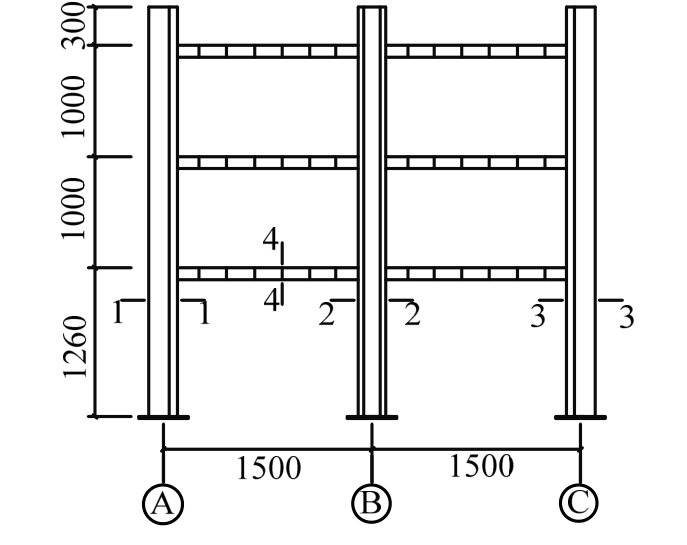
图1 试件立面图
Fig.1 Specimen elevation
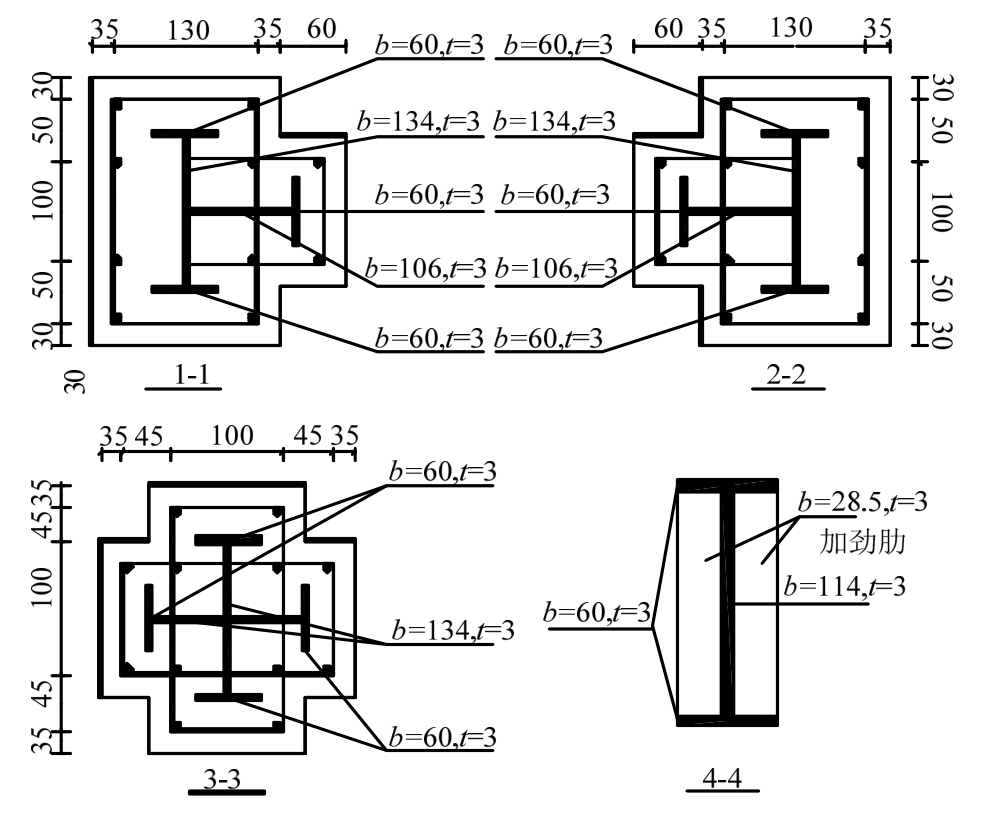
图2 梁柱截面及配钢形式
Fig.2 Sectional dimensions and steel layout of specimen

图3 节点构造示意图
Fig.3 Details of joints
试件采用C30混凝土一次浇筑完成,混凝土配合比如表1所示。实测混凝土立方体抗压强度平均值为35.02 MPa,弹性模量Ec=3.0×104 MPa。钢筋与钢板的实测力学性能指标如表2所示。
表1 混凝土配合比
Table 1 Mixing proportion of concrete
混凝土强度等级 水/(kg/m3)水泥/(kg/m3)砂/(kg/m3)石子/(kg/m3)C30 243 494 914 1490
表2 钢材的力学性能指标
Table 2 Mechanical properties of steel
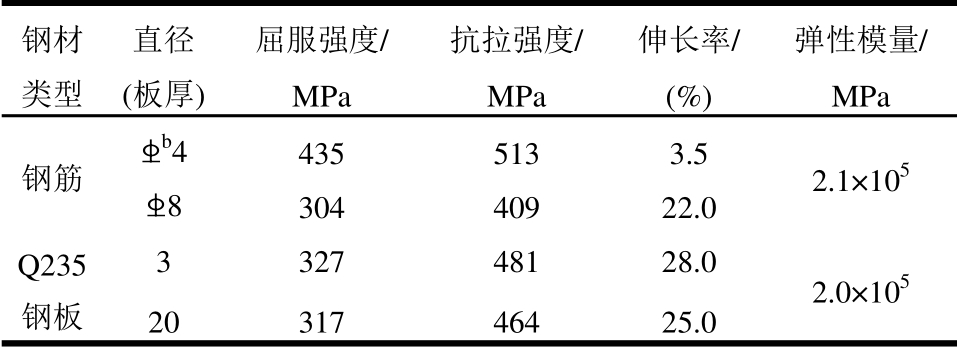
钢材 类型 直径 (板厚)屈服强度/ MPa 抗拉强度/ MPa 伸长率/ (%)弹性模量/MPa 钢筋 ■b4 435 513 3.5 2.1×105 ■8 304 409 22.0 Q235 钢板 3 327 481 28.0 2.0×105 20 317 464 25.0
1.2 加载方案
如图4所示,加载分竖向加载和水平加载两阶段。竖向加载在顶层框架柱顶进行,首先由高精度静态液压伺服千斤顶加载至500 kN并维持2 min,然后分3级加载至800 kN,保持恒定,紧固柱脚及作动器端板处的连接。柱试验轴压比由式(1)计算,本次试验边柱和中柱轴压比分别为0.61和0.59。
式中:n为试验轴压比;N为框架柱试验轴压力;fc、fy、fss分别为实测混凝土轴心抗压强度、纵向钢筋抗压强度和配钢抗压强度;Ac、As、Ass分别为混凝土截面面积、纵向受压钢筋截面面积、配钢截面面积。
根据《建筑抗震试验方法规程》(JGJ 101—96)[22],水平低周往复荷载由电液伺服作动器采用位移控制施加,在试件接近开裂和屈服前以较小级差进行控制加载,循环1次;试件屈服后取屈服时的最大变形值的倍数为级差进行控制加载,循环3次,加载制度见表3。实时量测试件的应变和位移,并记录试验现象。当试件承载力下降到极限荷载的85%时,停止加载,试验结束。
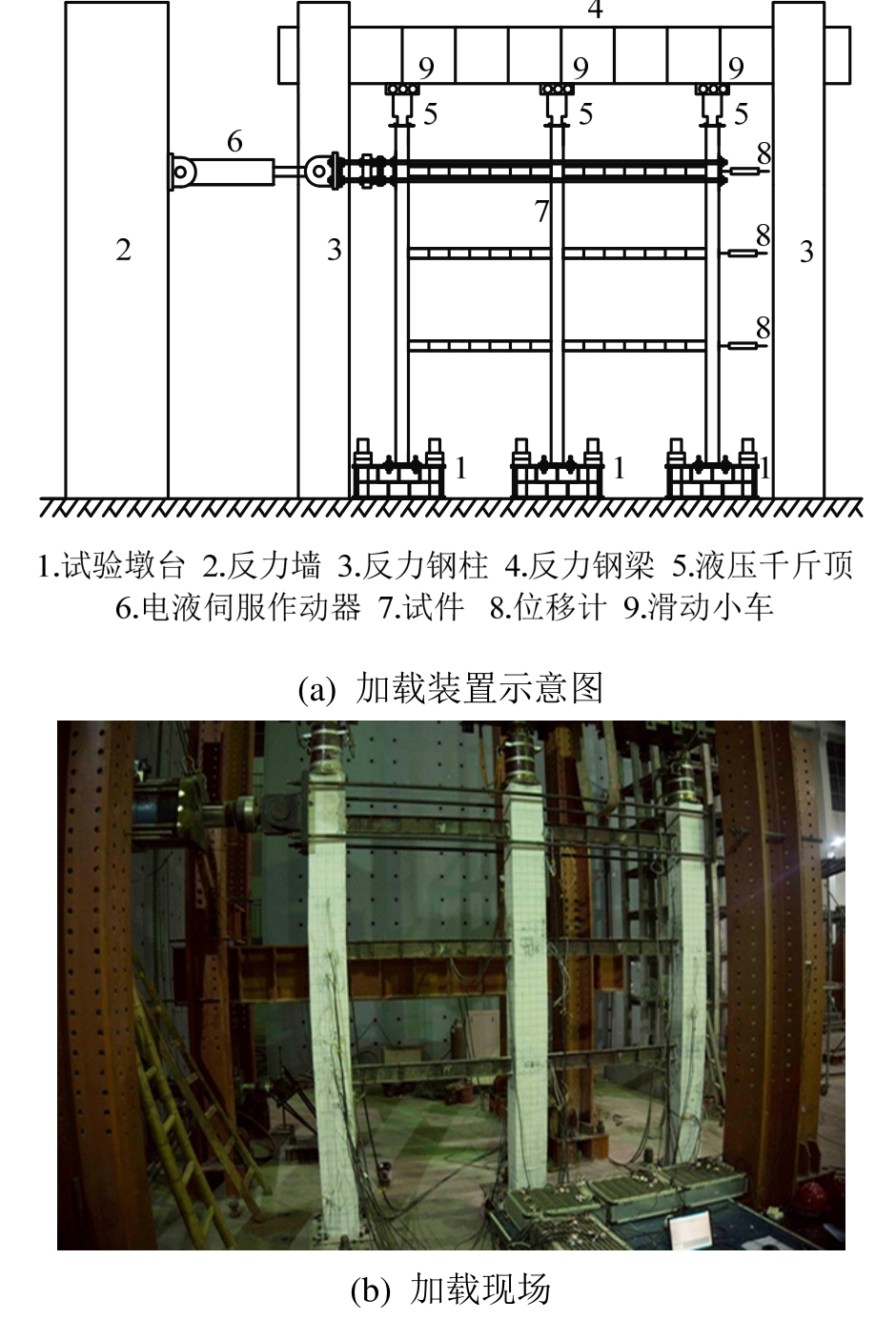
图4 加载装置
Fig.4 Test setup
表3 加载制度
Table 3 Loading protocol
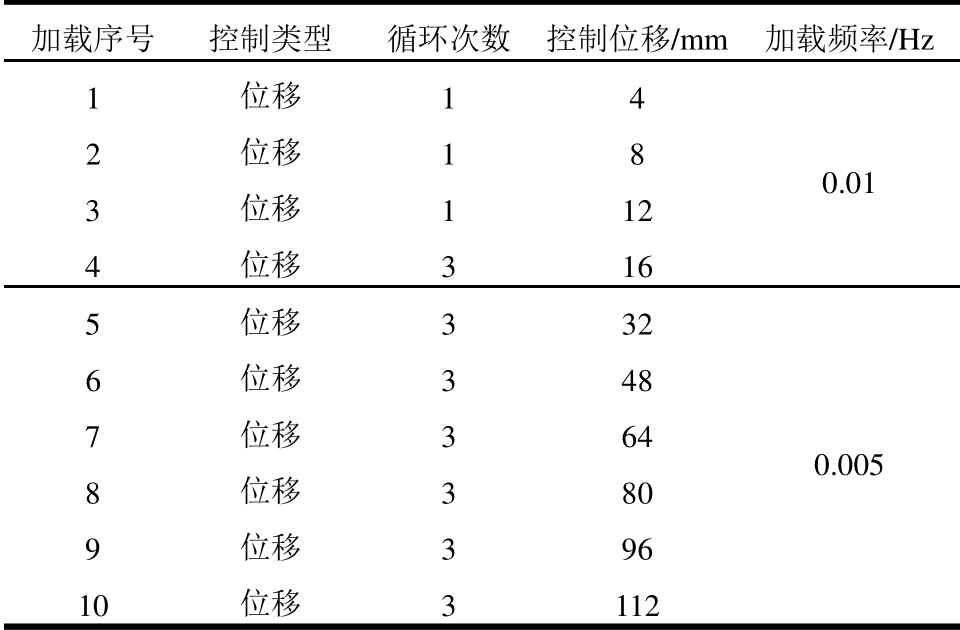
加载序号 控制类型 循环次数 控制位移/mm 加载频率/Hz 1 位移 1 4 0.01 2 位移 1 8 3 位移 1 12 4 位移 3 16 5 位移 3 32 0.005 6 位移 3 48 7 位移 3 64 8 位移 3 80 9 位移 3 96 10 位移 3 112
1.3 量测方案
试件侧面布有位移计,实时测量框架各层侧移(见图4)。为测量试件受力较复杂部位的应变,在梁端上下翼缘布有大标距应变片,梁端腹板和节点核心区钢骨上分别布有三向应变花。
2 试验结果及分析
2.1 试验现象
加载初期,试件处于弹性阶段,框架梁柱均未出现明显的损伤,卸载后也无明显的残余变形;当加载位移达到32 mm时,框架左柱底部、底层和第二层梁柱节点处以及顶层梁柱节点核心区混凝土均有轻微开裂;当水平位移达到48 mm时,第二层梁端出现塑性铰,框架柱底混凝土均出现裂缝,且梁柱节点核心区相继出现“X”形剪切裂缝,试件开始进入屈服阶段;继续增大水平位移,试件塑性变形不断发展,梁端翼缘总体上按照从底层到第二层直至顶层的顺序出现大量波形屈曲,且第二层梁端腹板向平面外发生轻微凸出,柱底和梁柱节点核心区裂缝不断延伸,中柱柱脚两侧出现明显的纵向劈裂裂缝;当水平位移达到96 mm时,左柱和右柱形成了大量水平裂缝,各层梁柱节点核心区的“X”形裂缝发展延伸并贯通,形成较大较深的主斜裂缝;当水平位移达到112 mm时,节点核心区混凝土发生大面积脱落,节点处钢筋以及钢骨外露,试件承载力下降到极限荷载的85%,此时认为试件破坏,试验停止。总体而言,在低周往复荷载作用下,试件的破坏模式属于“梁铰破坏机制”,试件满足“强柱弱梁,强剪弱弯,强节点弱构件”的抗震设计要求,各部分的破坏现象如图5所示。

图5 试件破坏现象
Fig.5 Failure phenomena of specimen
2.2 滞回曲线
通过试验实测数据获得的底层柱底水平剪力和框架顶点水平位移滞回曲线如图6所示,结果表明,试件在加载过程中主要经历了弹性、弹塑性和破坏3个阶段。加载初期,试件处于弹性工作阶段,荷载随位移的增长近似线性关系,加卸载路径基本重合,说明残余变形很小;随着水平位移荷载增大,型钢混凝土框架柱底部,节点处混凝土开始出现细微裂缝,滞回曲线向横轴倾斜,框架进入弹塑性阶段,此时,残余变形开始变大,滞回环的面积也增大,各级循环的峰值荷载增大,但是同级循环的后两次峰值荷载逐渐降低,说明框架的承载力和刚度有所降低,损伤不累积;试验中后期,滞回曲线向横轴倾斜的程度加大,梁端翼缘出现波形屈曲,钢梁腹板向平面外凸出甚至开裂,柱脚混凝土碎裂剥落,节点核心区混凝土大面积剥落,但滞回曲线仍然饱满。总体而言,滞回曲线比较饱满,无明显的“捏拢”效应,说明试件在低周往复荷载下滞回性能良好,耗能能力较强。
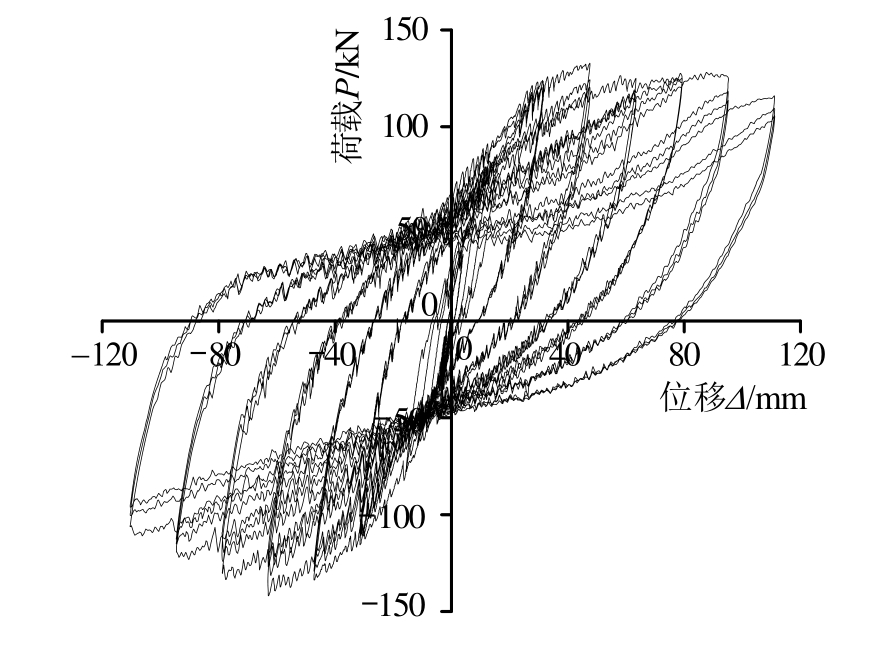
图6 试件的滞回曲线
Fig.6 Hysteretic loops of specimen
2.3 骨架曲线
如图7所示,骨架曲线的形状近似抛物线,在正、负2个加载方向上都有直线上升、水平和下降3个阶段,且在达到峰值荷载后缓慢下降,说明试件的变形性能良好。采用等效能量法确定屈服点,取极限荷载下降15%所对应的荷载作为破坏荷载,得到试件在各个阶段的荷载与位移,见表4,其中Py、Pmax、Pu分别为屈服荷载、极限荷载和破坏荷载,Δy、Δmax、Δu分别为屈服位移、极限位移和破坏位移。
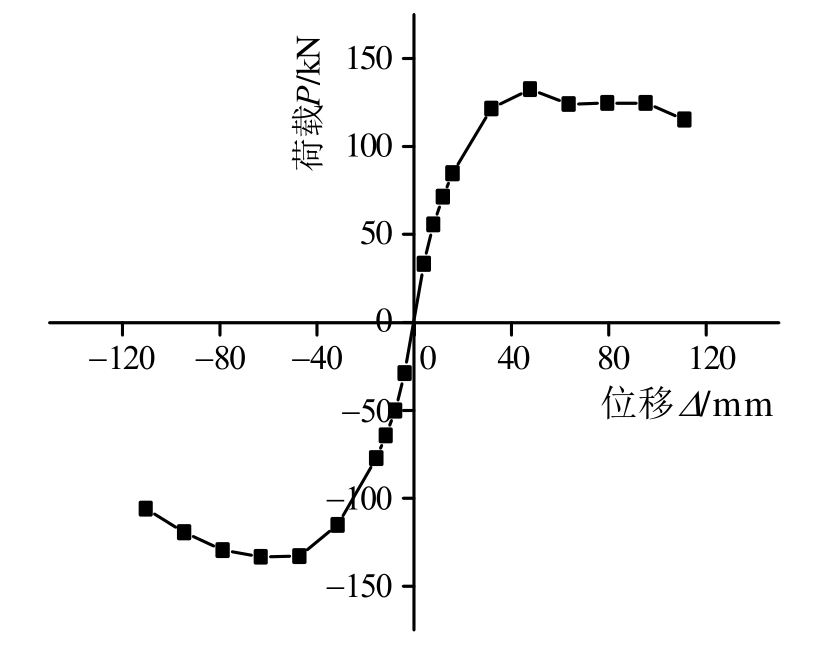
图7 试件的骨架曲线
Fig.7 Skeleton curve of specimen
表4 试件各阶段的荷载与位移
Table 4 Load and displacement of specimen at different
stages

加载方向 Py/kN Δy/mm Pmax/kN Δmax/mm Pu/kN Δu/mm正向 112.60 27.82 132.58 47.61 112.69 104.88负向 109.86 31.67 133.29 45.09 113.29 101.98
2.4 延性与耗能
采用位移延性系数(μ=Δu/Δy)和 位 移 角(θ=Δ/ΔH(或H))来表征试件在水平低周往复荷载作用下的延性特点。其中:Δu为Pu对应的顶点位移或者层间位移;Δy为Py对应的顶点位移或者层间位移;Δ为Py、Pmax或Pu对应的层间位移;ΔH、H为框架的层高或总高度。采用等效黏滞阻尼系数he 来反映试件的耗能能力。
表5列出了试件的延性系数和层间位移角。由表可知,试件正负向的延性系数均大于3,且试件破坏时的层间位移角为1/31和1/32,均超过1/50,这表明试件在地震作用下具有较好的变形能力和抗倒塌能力。
表5 试件的延性系数和层间位移角
Table 5 Ductility coefficient and inter-story drift of specimen
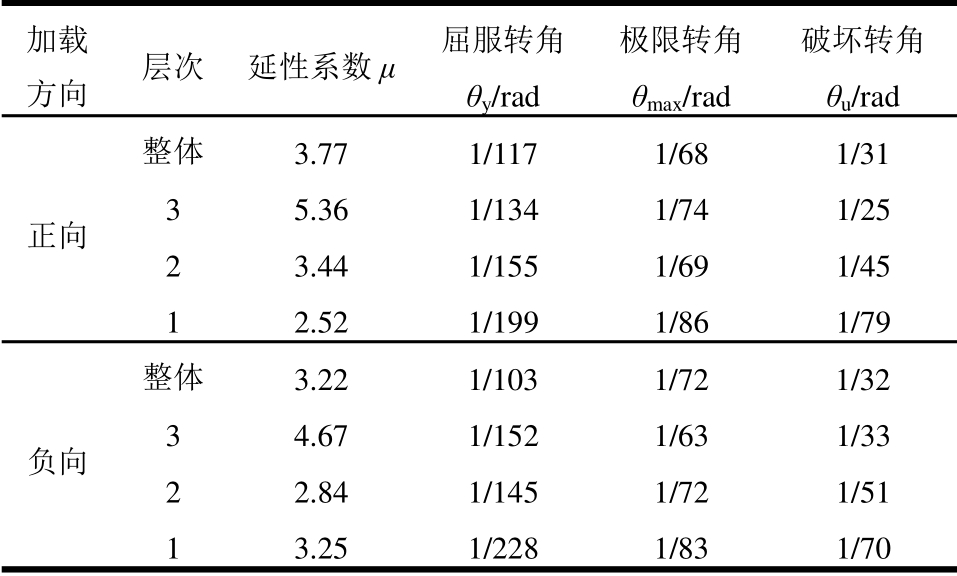
加载 方向 层次 延性系数μ 屈服转角θy/rad 极限转角θmax/rad 破坏转角θu/rad 正向 整体 3.77 1/117 1/68 1/31 3 5.36 1/134 1/74 1/25 2 3.44 1/155 1/69 1/45 1 2.52 1/199 1/86 1/79 负向 整体 3.22 1/103 1/72 1/32 3 4.67 1/152 1/63 1/33 2 2.84 1/145 1/72 1/51 1 3.25 1/228 1/83 1/70
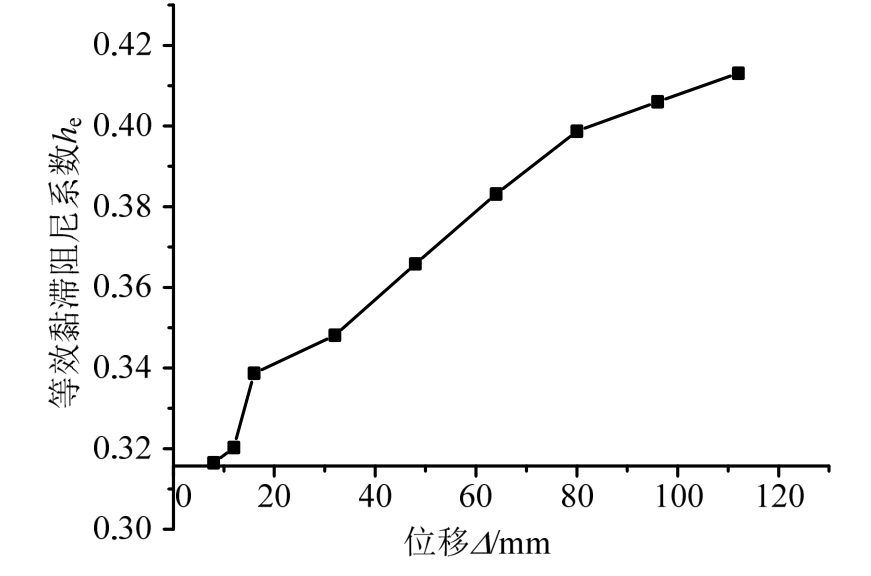
图8 试件的等效黏滞阻尼系数
Fig.8 Equivalent viscous damping coefficients of specimen
图8给出了试件在不同位移幅值下第一次循环的等效黏滞阻尼系数he与位移的关系曲线。整个加载过程中,he均大于0.3,试件破坏时,he达到最大值0.41。当水平位移为48 mm时,试件梁端屈服, 并产生塑性转动;进入破坏阶段后,梁端充分发挥了塑性转动能力,耗散了较多能量,梁端翼缘出现波形鼓曲、腹板向外凸出甚至开裂;同时,部分能量为柱脚与节点核心区型钢屈服、混凝土骨料之间的机械咬合与摩擦所耗散,体现为等效黏滞阻尼系数的快速上升,这说明试件内部的材料性能得到充分利用,试件具有良好的耗能能力。
2.5 强度与刚度退化
采用强度退化系数(λi=Pi/Pmax)来分析试件在整个试验过程中的强度退化规律,其中Pi为第i级位移幅值所对应的峰值荷载,Pmax为加载全过程的极限荷载。通过割线刚度(Ki=±|Pi|/|Δi|)随加载位移的变化曲线了解试件抗侧刚度的退化规律,其中Pi与Δi分别为第i级位移幅值所对应的峰值荷载与位移。
图9为λi随位移荷载增大时的变化曲线。随着位移荷载增大,正、负加载方向的λi都先增大后减小,并呈现一定的对称性。试件屈服后λi仍有明显的上升趋势,说明试件的安全储备较高,屈服后仍具有一定的抗倒塌能力。破坏阶段试件仍能承受较高荷载,且试件强度不会迅速退化,表明试件发生破坏后的残余承载力较高。
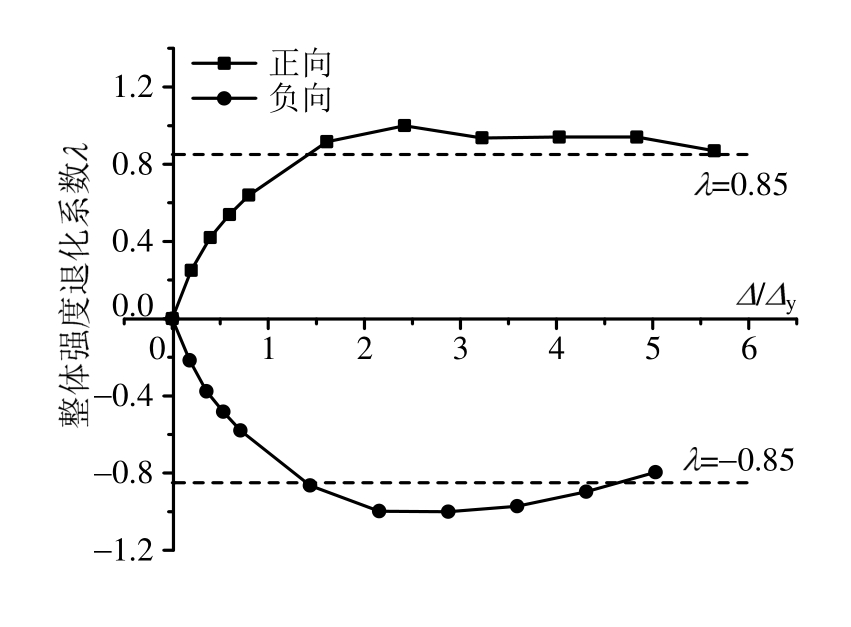
图9 整体强度退化曲线
Fig.9 Degradation curve of integral strength
图10为割线刚度随加载位移的变化曲线。试件在正、负加载方向的抗侧刚度退化都是先快后慢,在加载初期的退化速度基本一致。较短的弹性阶段之后,柱脚和节点处混凝土开裂,框架的刚度退化速度加快,随着水平荷载增加,塑性铰相继出现在各个梁端,试件充分发挥其耗能能力,混凝土随塑性发展而不断退出工作,使得试件抗侧刚度的退化速度减缓。这表明在往复荷载作用下,试件的延性可以得到较好地发挥,其具有良好的抗震性能。
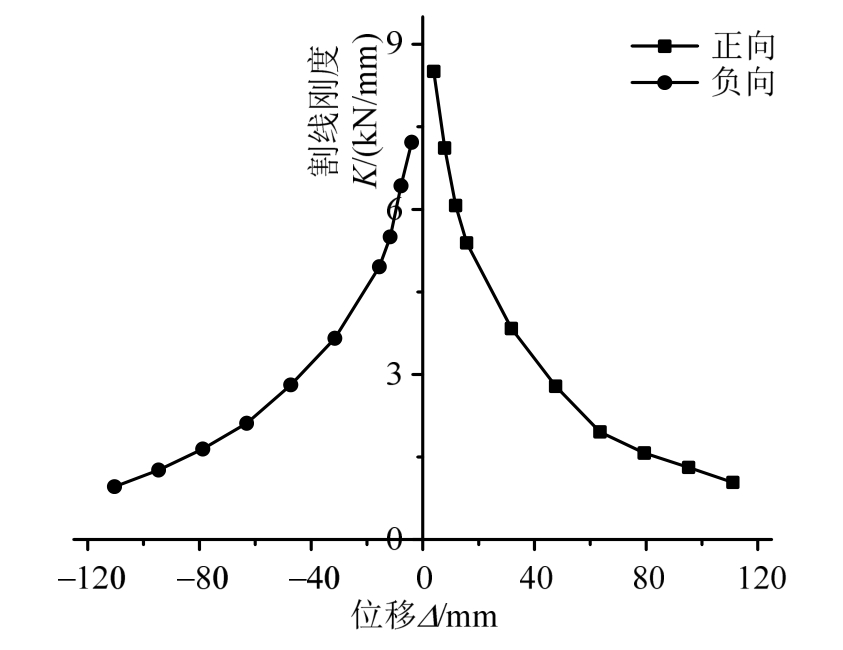
图10 割线刚度退化曲线
Fig.10 Degradation curve of secant stiffness
3 有限元分析
为了充分地了解不同设计参数对型钢混凝土柱-钢梁的抗震性能的影响,基于试验结果,本文采用三维结构非线性分析和抗震性能评估有限元软件Perform-3D对试验模型进行数值模拟,并进行相关参数分析。
3.1 材料和单元
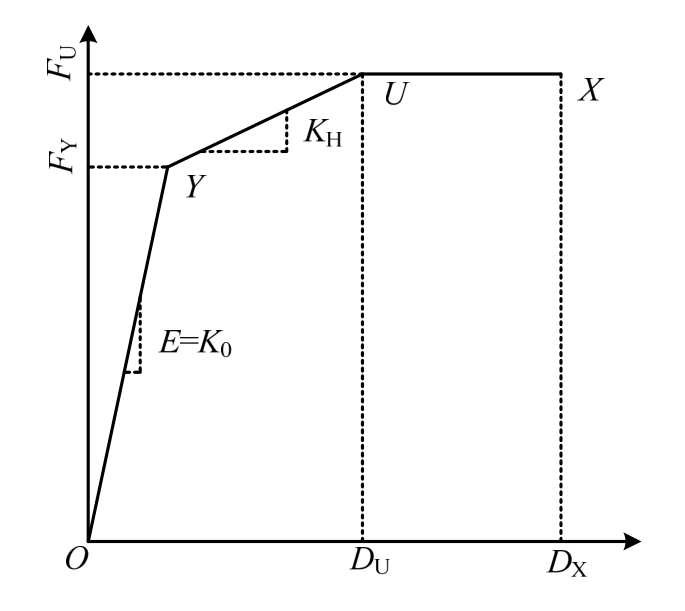
图11 钢材骨架曲线
Fig.11 Skeleton curve of steel
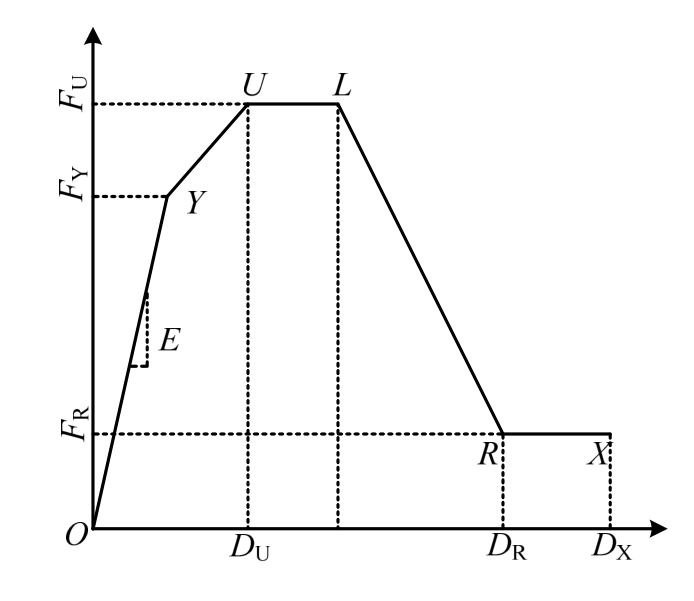
图12 混凝土骨架曲线
Fig.12 Skeleton curve of concrete
钢筋和型钢均采用非屈曲型非线性本构,骨架曲线采用三折线形式,如图11所示。混凝土材料 分为约束混凝土和非约束混凝土两部分,约束混凝土采用基于Mander模型的本构关系[23],非约束混凝土采用《混凝土结构设计规范》本构关系,均用五折线型骨架曲线描述,如图12所示,不考虑混凝土的抗拉强度。钢材骨架曲线包含屈服点Y、峰值广义力开始点U、退出工作点X三个关键点和弹性段OY、强化段YU;混凝土骨架曲线中Y、X、OY和YU的含义与前述相同,另有塑性平台段UL、塑性平台段的结束L,广义力点显著退化段LR、剩余承载力起点R。
梁柱单元采用由纤维截面段和弹性段组成纤维模型,如图13所示,纤维截面段的长度取截面最大尺寸的一半,上述单元形式可增加单元延长度方向的积分点数而不增加自由度,因此提高了计算精度与效率。采用平面纤维方式划分梁单元纤维截面,忽略了加劲肋,最多划分12个纤维,如图14所示;采用空间纤维划分柱单元,最多划分为60个,如图15所示,其中,框架柱内置型钢的纤维截面是基于 面积等效的原则将其划分成钢筋纤维,如图16所示。本文采用基于纤维截面的梁柱宏观单元,能够解决材料、大变形等产生的强非线性问题,且计算效率高,但不能模拟混凝土开裂及破碎等细观特征。
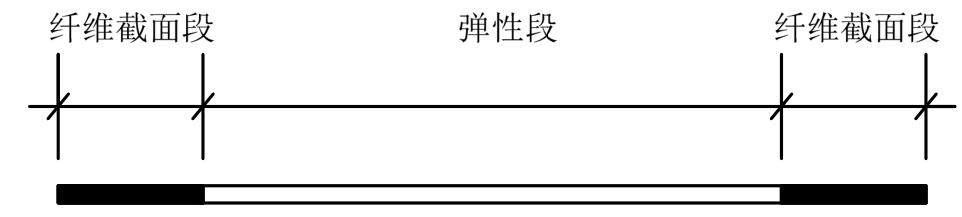
图13 梁、柱单元模型
Fig.13 Element model of beam and column
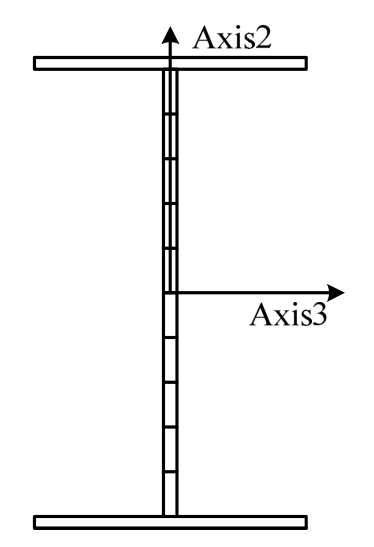
图14 梁纤维截面划分
Fig.14 Fiber section division of beam
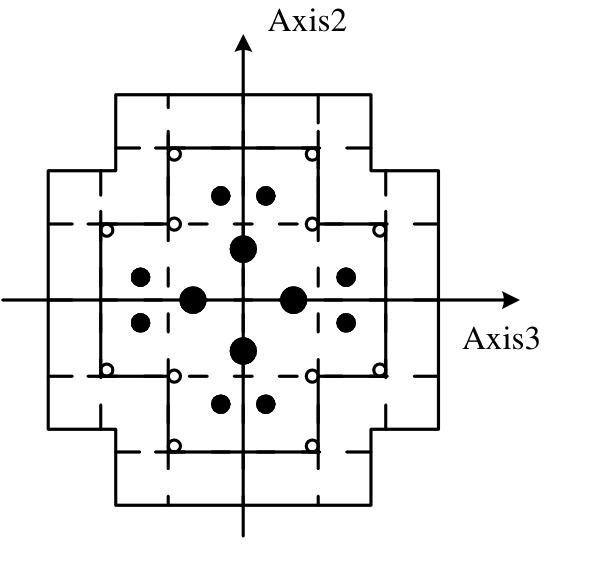
图15 柱纤维截面划分
Fig.15 Fiber section division of column
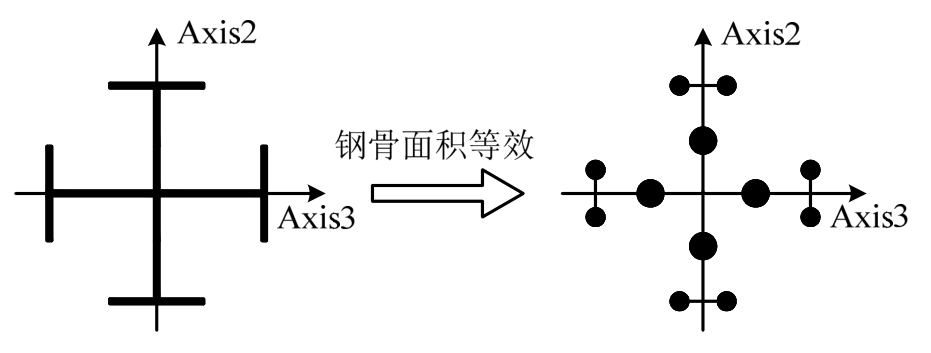
图16 柱钢骨等效
Fig.16 Steel equivalent of column
参考试验工况,将模型底层节点设为固定约束,于顶部节点施加集中力来模拟竖向轴力,通过大刚度弹簧施加于模型顶层施加水平低周往复荷载,加载制度与试验一致。通过输出,可得到模型的基底剪力-顶点位移滞回曲线。
3.2 计算结果与试验结果对比
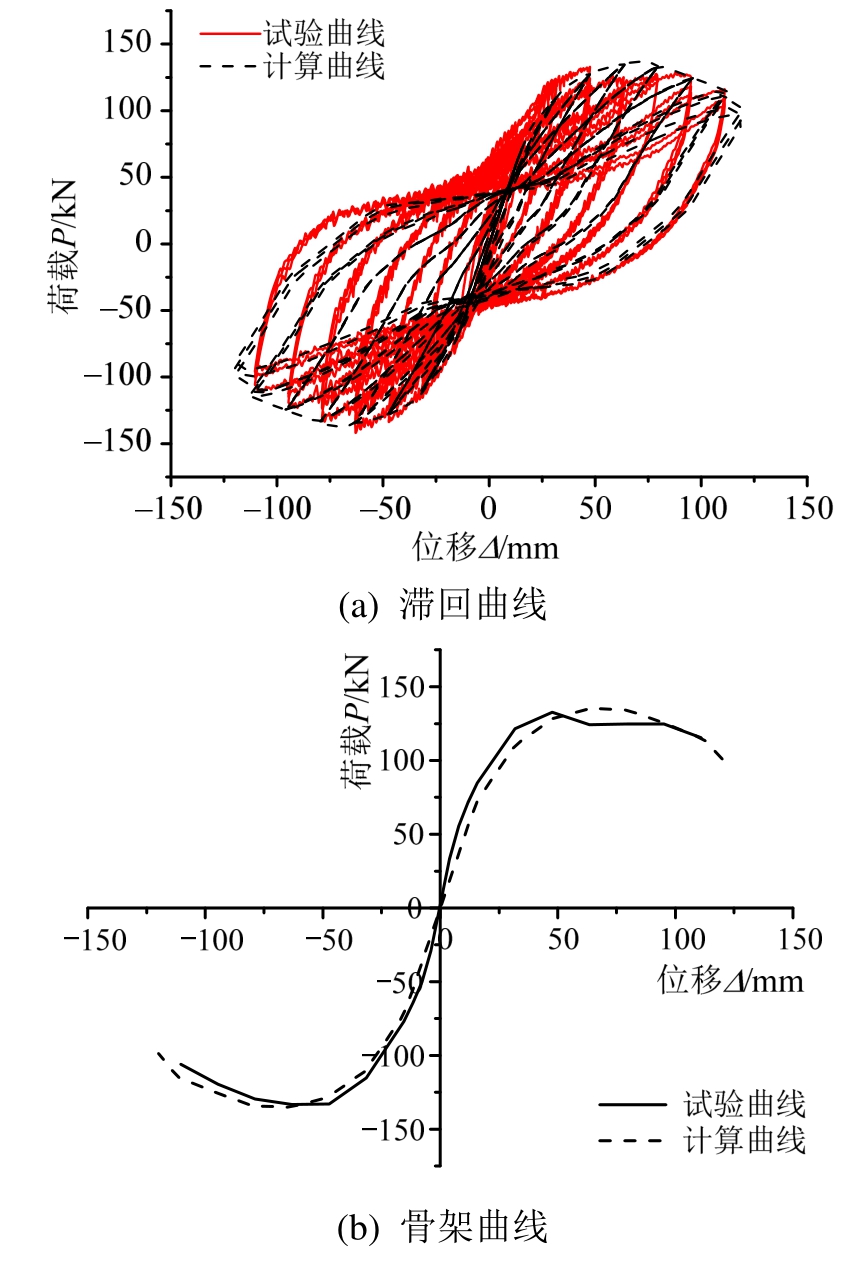
图17 计算结果与试验结果对比
Fig.17 Comparison between calculated and experimental results
图17给出了数值模拟与试验结果的对比。结果表明,数值模拟与试验所得的滞回曲线基本一致,滞回环饱满,有明显的屈服、极限和破坏3个阶段。从骨架曲线来看,屈服点、峰值点和破坏点的位移、荷载以及初始刚度等也与试验结果吻合较 好,且弹塑性上升阶段和峰值点后的下降阶段的变化规律也吻合良好。表6列出了屈服、极限和破坏荷载的对比结果,由表可知,试验和计算得到试件的屈服、极限和破坏荷载比较接近,误差在5%左右,而且计算值往往超过相应的试验值,这是由于计算时没有考虑混凝土与钢材之间的粘结滑移造成的。总的来说,有限元结果与试验结果吻合良好。
表6 计算承载力与试验承载力对比
Table 6 Comparison between calculated and experimental strength
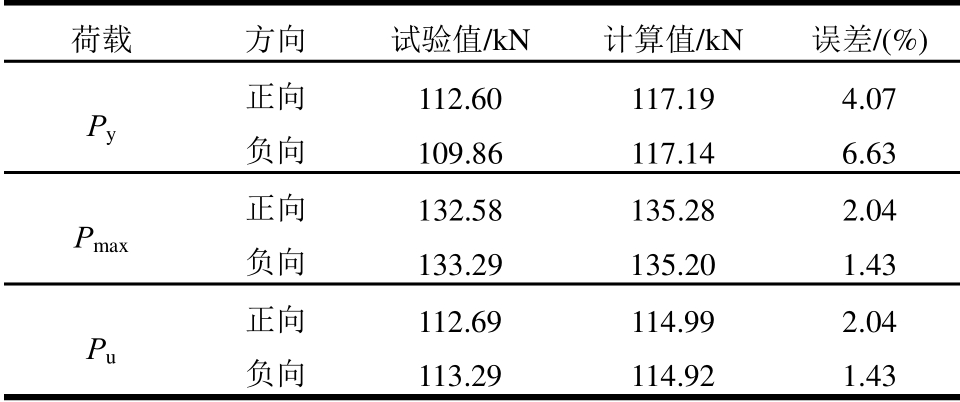
荷载 方向 试验值/kN 计算值/kN 误差/(%)Py正向 112.60 117.19 4.07 负向 109.86 117.14 6.63 Pmax正向 132.58 135.28 2.04 负向 133.29 135.20 1.43 Pu正向 112.69 114.99 2.04 负向 113.29 114.92 1.43
3.3 参数分析
基于前述的有限元模型,研究了T形配钢型钢混凝土柱-钢梁框架抗震性能在不同轴压比n、配钢率ρss和混凝土强度影响下的变化规律。
1)轴压比
保持其他影响因素一致,取框架柱轴压比n为0.4、0.5、0.6、0.7和0.8分别计算,骨架曲线如图18所示。结果表明,不同轴压比下,试件屈服前的受力性能变化较小,但屈服后阶段的变化较大。当n<0.6时,试件的Pmax变化不大,但n>0.6时,由于存在P-Δ效应,导致Pmax及对应的位移随着n的增大显著降低,且下降段更陡,延性变差。轴压比过大会导致该类结构的承载力和延性降低,对结构有不利。
2)配钢率
保持其他影响因素一致,取框架柱配钢率ρss为5%、6%、7%、8%和9%分别计算,骨架曲线如图19所示。结果表明受配钢率影响的主要是初始刚度和极限承载力。当ρss较小时,其初始刚度较小,下降段较平缓。增大配钢率,初始刚度随之有所增大,极限承载力明显提高,下降段更加平缓,延性更好。适当增大配钢率可以有效改善该类结构的抗震性能。
3)混凝土强度
保持其他影响因素一致,取混凝土强度为C25、C30、C35、C40和C45分别计算,骨架曲线如图20所示。结果表明受混凝土强度影响的主要是试件屈服后的受力性能,弹性阶段和初始刚度变化不大。增大混凝土强度,极限承载力略有提高。在整个加载阶段,骨架曲线的形状没有明显的变化,由于混凝土强度等级的提高,框架的延性略微变差。这说明,增大混凝土强度可以提高结构的极限承载力,但略微降低了框架的延性,这是因为框架柱内置钢骨架对混凝土有较强的约束作用,降低了混凝土强度对整体延性的影响。
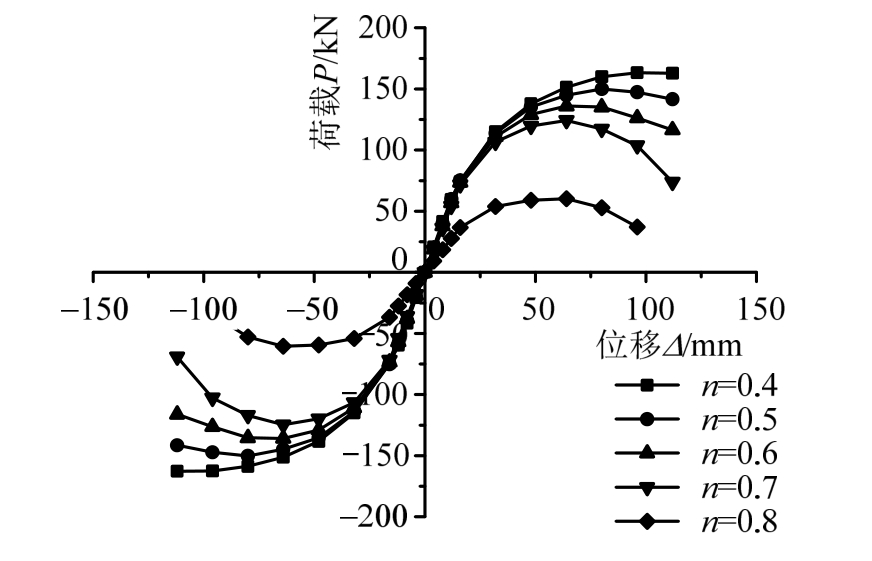
图18 轴压比对骨架曲线的影响
Fig.18 Skeleton curves with different axial compression ratios
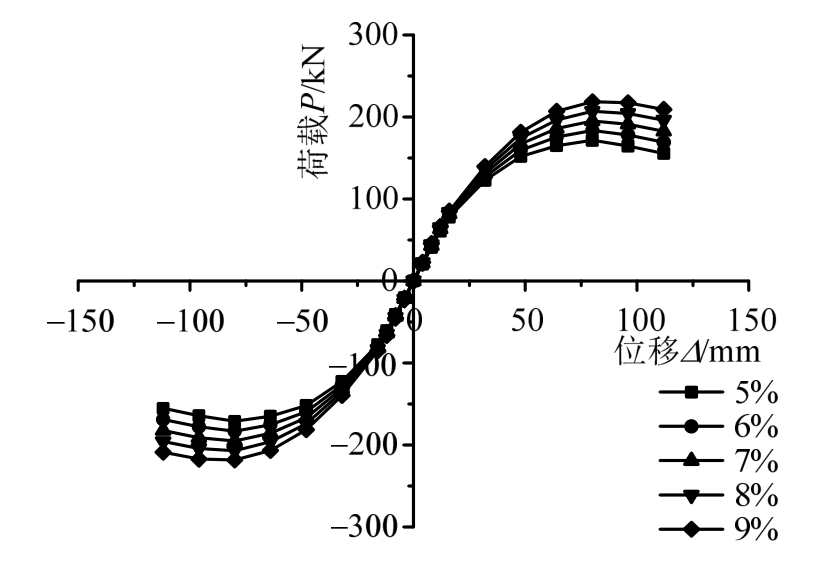
图19 配钢率对骨架曲线的影响
Fig.19 Skeleton curves with different steel ratios
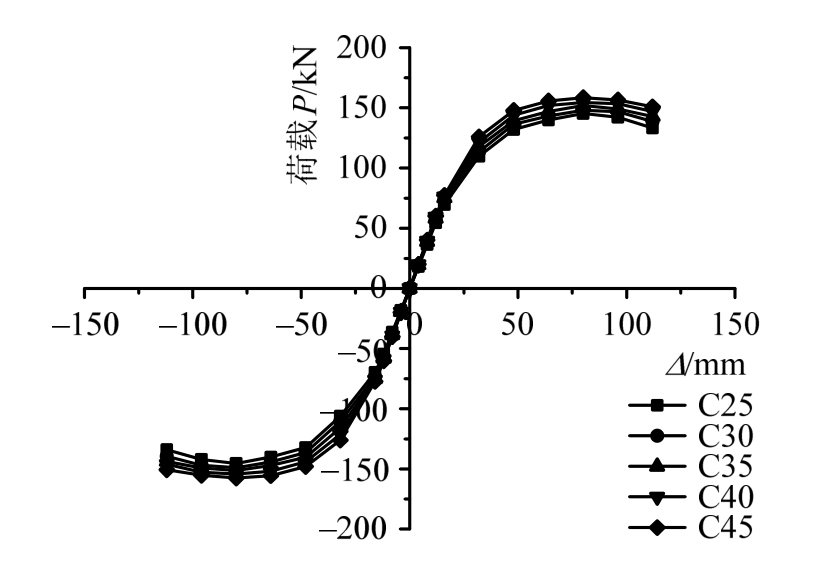
图20 混凝土强度对骨架曲线的影响
Fig.20 Skeleton curves with different concrete strengths
4 结论
基于T形配钢型钢混凝土柱-钢梁框架的拟静力试验和有限元分析,对破坏形态、滞回特性、承载力、耗能能力、刚度与强度退化等进行了分析比较,探讨了轴压比、配钢率和混凝土强度对该类结构抗震性能的影响,得出以下结论:
(1)在水平低周往复荷载作用下,T形配钢型钢混凝土柱-钢梁框架结构满足“强柱弱梁,强剪弱弯,强节点弱构件”的抗震设计要求,破坏模式属于“梁铰破坏机制”。
(2)T形配钢型钢混凝土柱-钢梁框架结构具有良好的滞回性能。在往复荷载作用下主要经历了弹性、弹塑性和破坏3个阶段,滞回曲线比较饱满,无明显的“捏拢”效应。骨架曲线大致呈抛物线形,在正、负加载方向上均经历了直线上升、水平和下降3个阶段,在达到峰值荷载后缓慢下降。
(3)T形配钢型钢混凝土柱-钢梁框架结构具有一定的安全储备,屈服后不会迅速丧失承载力。加载过程中,强度退化系数先增大后减小,强度退化曲线在正、负加载方向上近似对称,试件屈服后仍然有明显的上升。试件在正、负方向上抗侧刚度的退化规律相似,加载初期试件水平抗侧刚度退化较快,但随着水平位移的增加,试件的塑性得以发展,抗侧刚度的退化速度明显减缓,体现出良好的抗震性能。
(4)T形配钢型钢混凝土柱-钢梁框架结构的有限元分析结果与试验结果吻合良好。增大轴压比会降低结构的承载力和延性,设计时需要将其控制在合理范围内;随着型钢混凝土框架柱配钢率的提高,结构的承载力和延性明显提高,初始刚度有所增大;随着混凝土强度等级的提高,结构的极限承载力略有提高,但延性略有下降,设计时要综合考虑;同时框架柱内置钢骨架能为混凝土提供较好的约束。
[1]Ataei A, Bradford M A, Valipour H.Sustainable design of deconstructable steel-concrete composite structures [J].Procedia Engineering, 2016, 145(4): 1153—1160.
[2]Luo Y, Wang M Y, Zhou M, et al.Optimal topology design of steel–concrete composite structures under stiffness and strength constraints [J].Computers & Structures, 2012, 112(4): 433—444.
[3]Papavasileiou G S, Charmpis D C.Seismic design optimization of multi-storey steel-concrete composite buildings [J].Computers & Structures, 2016, 170: 49—61.
[4]张超, 薛素铎, 王广勇, 等.火灾后型钢混凝土框架结构力学性能试验研究及分析[J].工程力学, 2018, 35(5): 152—161.Zhang chao, Xue suduo, Wang guangyong, et al.Experimental research and analysis on the post-fire performance of steel reinforced concrete frame structures [J].Engineering Mechanics, 2018, 35(5): 152—161.(in Chinese)
[5]邓明科, 马福栋, 李勃志, 等.基于修正拉-压杆模型的型钢混凝土深梁受剪承载力分析[J].工程力学, 2017, 34(12): 95—103.Deng Mingke , Ma Fudong , Li Bozhi , et al.Analysis on shear capacity of SRC deep beams based on modified strut-and-tie model [J].Engineering Mechanics, 2017, 34(12): 95—103.(in Chinese)
[6]曾磊, 涂祥, 许成祥, 等.非对称配钢钢骨混凝土柱抗震性能试验研究[J].建筑结构学报, 2013, 34(3): 141—151. Zeng Lei, Tu Xiang, Xu Chengxiang, et al.Experimental study on seismic behavior of steel reinforced concrete column with unsymmetrical steel cross-sections [J].Journal of Building Structures, 2013, 34(3): 141—151.(in Chinese)
[7]Xue B, Gong J.Study on steel reinforced concrete-filled GFRP tubular column under compression [J].Thin-Walled Structures, 2016, 106(4): 1—8.
[8]曾磊, 涂祥, 吴园园.T形配钢型钢混凝土构件正截面承载力计算方法[J].工程力学, 2013, 30(10): 115—121. Zeng Lei, Tu Xiang, Wu Yuanyuan.Normal section bearing capacity calculation of steel reinforced concrete members with T-shaped steel [J].Engineering Mechanics, 2013, 30(10): 115—121.(in Chinese)
[9]Chen S, Wu P.Analytical model for predicting axial compressive behavior of steel reinforced concrete column [J].Journal of Constructional Steel Research, 2017, 128(1): 649—660.
[10]曾磊, 吴园园, 张地, 等.钢骨混凝土异形柱-钢梁节点抗震性能试验研究[J].振动与冲击, 2016, 35(4): 224—229, 240.Zeng Lei, Wu Yuanyuan, Zhang Di, et al.Tests for aseismic behavior of frame joints between a steel reinforced concrete special column and a steel beam [J].Journal of Vibration and Shock, 2016, 35(4): 224—229, 240.(in Chinese)
[11]布欣, 谷倩, 王新武.剖分T型钢梁柱连接框架中柱空间节点抗震试验研究[J].工程力学, 2017, 34(8): 105—116. Bu Xin, Gu Qian, Wang Xinwu.Experimental study on the seismic performance of three-dimensional beam to middle column connection with T-stub [J].Engineering Mechanics, 2017, 34(8): 105—116.(in Chinese)
[12]Braconi A, Elamary A, Salvatore W.Seismic behaviour of beam-to-column partial-strength joints for steel–concrete composite frames [J].Journal of Constructional Steel Research, 2010, 66(12): 1431—1444.
[13]刘祖强, 薛建阳, 韩琛, 等.实腹式型钢混凝土T形柱抗震性能试验研究[J].工程力学, 2018, 35(5): 17—26. Liu Zuqiang, Xue Jianyang, Han Chen, et al.Experimental study on aseismic performance of solid steel reinforced concrete T-shaped column [J].Engineering Mechanics, 2018, 35(5): 17—26.(in Chinese)
[14]杨涛, 张喜德, 钟海牛, 等.T形截面钢骨混凝土异形柱框架抗震性能拟动力试验[J].中南大学学报: 自然科学版, 2015, 46(6): 2171—2177. Yang Tao, Zhang Xide, Zhong Hainiu, et al.Pseudo-dynamic test on seismic behavior of frame with T-shaped SRC columns [J].Journal of Central South University (Science and Technology), 2015, 46(6): 2171—2177.(in Chinese)
[15]薛建阳, 张昭祥, 刘祖强, 等.实腹式型钢混凝土异形柱中框架拟静力试验及静力弹塑性分析[J].工程力学, 2014, 31(5): 137—144. Xue Jianyang, Zhang Zhaoxiang, Liu Zuqiang, et al.Pseudo-static test and static elasto-plastic analysis of middle frame with solid steel reinforced concrete special-shaped columns [J].Engineering Mechanics, 2014, 31(5): 137—144.(in Chinese)
[16]刘祖强, 薛建阳, 赵鸿铁.型钢混凝土异形柱框架滞回性能分析[J].工程力学, 2016, 33(7): 73—83. Liu Zuqiang, Xue Jianyang, Zhao Hongtie.Analysis on hysteretic behavior of steel reinforced concrete frame with special-shaped columns [J].Engineering Mechanics, 2016, 33(7): 73—83.(in Chinese)
[17]Wang G Y, Shi Y, Zhang D M, et al.Experimental research on post-fire seismic performance of steel reinforced concrete columns [J].Procedia Engineering, 2017, 210(11): 456—463.
[18]GB 50010—2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010. GB 50010—2010, Code for design of concrete structures [S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[19]GB 50011—2010, 建筑抗震设计规范[S].北京: 中国建筑工业出版社, 2010. GB 50011—2010, Code for seismic design of buildings [S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[20]JGJ 138—2001, 型钢混凝土组合结构技术规程[S].北京: 中国建筑工业出版社, 2001. JGJ138-2001, Technical specification for steel reinforced concrete composnte structures [S].Beijing: China Architecture & Building Press, 2001.(in Chinese)
[21]任雯婷.非对称配钢型钢混凝土柱-钢梁框架结构抗震性能试验研究及有限元分析[D].荆州: 长江大学, 2018: 33—46. Ren Wenting, Experimental study and finite element analysis on seismic behavior of frame structures composed of concrete encased columns with special section and steel beams [D].Jingzhou: Yangtze University, 2018: 33—46.(in Chinese)
[22]JGJ 101—96, 建筑抗震试验方法规程[S].北京: 中国建筑工业出版社, 1997. JGJ 101—96, Specificating of testing methods for earthquake resistant building [S].Beijing: China Architecture & Building Press, 1997.(in Chinese)
[23]Kent D C, Park R.Flexural members with confined concrete [J].Journal of the Structural Division, 1971, 97(1): 1969—1990.