钢筋混凝土构件按截面受力特性可分为应力连续区(Bernoulli region，简称B区)和应力紊乱的不连续区(Discontinuity region，简称D区)。B区受力问题在平截面假定的基础上已得到较好解决，但因影响因素众多和剪切机理的复杂性，D区的剪切问题一直存在争议，始终是混凝土结构基本理论研究的难点。
深受弯构件斜截面受剪属典型的D区受力，合理的剪切设计是其工程应用的先决条件。拉压杆模型(Strut-and-tie model，简称STM)在桁架模型基础上将实体结构弹性主应力迹线理想化，结合拉拱机制，通过压杆、拉杆和节点进行传力，且通过保证各个机构具有足够的强度进行设计，传力路径与实体结构吻合良好，且力学概念清晰。目前，美国ACI 318-14、加拿大CSA A23.3-04和欧洲EC2等规范[1—3]已将拉压杆模型引入对D区构件进行抗剪设计。但深受弯构件跨高比较小，截面尺寸较大，高度较高，引起的尺寸效应问题显著。然而，拉压杆模型中未考虑尺寸效应的影响，对于大尺寸深受弯构件易造成设计不安全，存在隐患。
Kani[4]通过大量试验证明了“尺寸效应”的存在，即钢筋混凝土无腹筋梁的名义抗剪强度随构件有效截面高度的增加而降低。随后，Bazant等[5]结合断裂力学从裂缝处的能量释放角度解释尺寸效应，从概率和骨料咬合力等方面提出计算模型。Collins等[6]基于压力场理论提出修正压力场模型考虑尺寸效应影响。同时Tan等[7]、Matsuo等[8]、Birrcher等[9]均进行了大尺寸的深受弯构件受剪性能试验研究，分析了尺寸效应的影响因素，并将其与拉压杆模型结合提出计算与设计方法。但各类模型计算过程仍过于复杂，且区别较大，即考虑尺寸效应后的深受弯构件受剪机理更为复杂，仍需进行深入研究。基于此，本文在已有Tan-Cheng模型的基础上，综合考虑斜压杆倾角α和构件复合抗拉强度ft对深受弯构件受剪承载力的影响，并进行修正简化，在保证精度的前提下，给出较为简单的计算模型。
1 Tan-Cheng模型简介
1.1 拉压杆模型
对于深受弯构件而言，斜向开裂前的剪力主要由压区未开裂混凝土、界面骨料咬合力、销栓作用和抗剪钢筋共同承担，但剪跨区斜裂缝出现后，剪力主要通过“拉杆-拱”机制传递，不满足传统平截面假定。基于摩尔-库仑双向应力准则，考虑混凝土压杆底部节点区处于双向拉压应力状态且软化作用显著，建立了深受弯构件底部节点区的拉压杆模型(如图1)。混凝土压杆底部节点区主拉、主压应力的相互作用关系可用如下线性破坏准则表示[10]：
式中：f1和f2分别为混凝土压杆底部节点区所受到的主拉应力和主压应力；f′c为混凝土圆柱体抗压强度；ft为综合考虑混凝土、腹筋和底部纵筋贡献的复合抗拉强度。
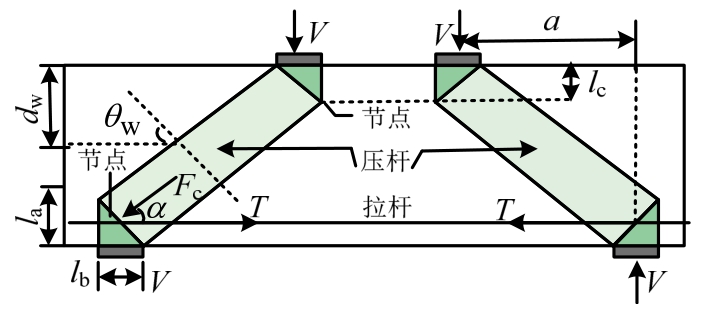
图1 深受弯构件拉压杆模型计算简图
Fig.1 Strut-and-tie model for deep flexural members
1.1.1 主压应力f2的计算
根据图2中混凝土斜压杆底部节点区受力状态建立平衡方程：1)沿支撑板与加载板连线形成的混凝土斜压杆承担的压力式(2)；2)由底部纵筋构成的拉杆承担的拉力式(3)；3)底部节点区的主压应力式(4)：
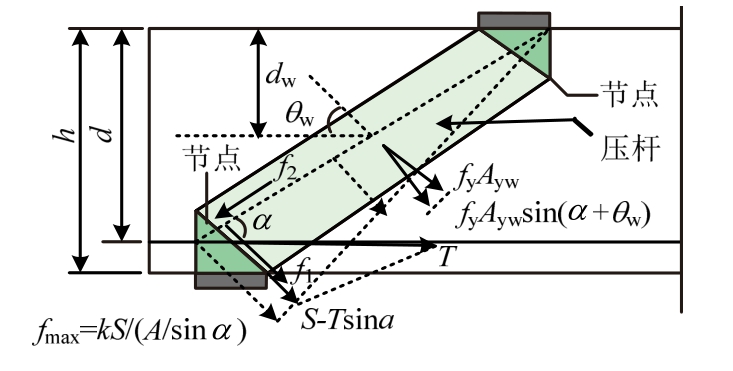
图2 底部节点区主应力状态
Fig.2 Principal stress state at bottom nodal zone
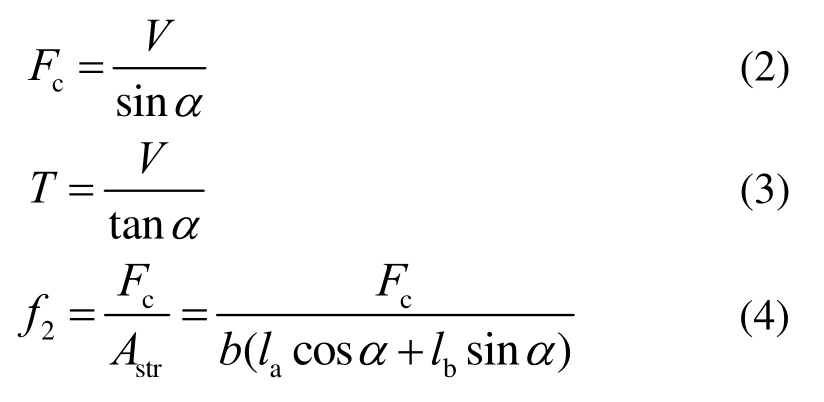
式中：Astr为混凝土斜压杆截面面积；la为压杆底部节点区高度；lb为支座处垫板宽度；α为斜压杆与底部纵筋的夹角，按下式计算：
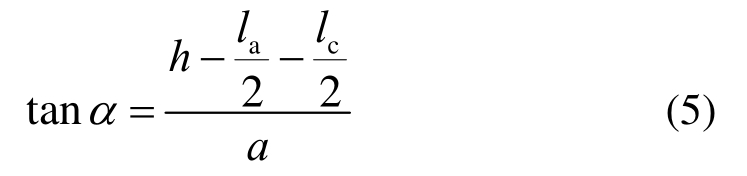
式中：a为剪跨；lc为压杆顶部节点区高度，见式(6)：
1.1.2 主拉应力f1的计算
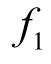为垂直于混凝土斜压杆的主拉应力，由几何关系可得：
式中，k为主拉应力沿垂直于压杆方向的不均匀分布系数，假定该分布沿压杆方向呈三角形[10]，则由式(8)的平衡关系可得k=2。
1.1.3 复合抗拉强度ft的计算
综合考虑深受弯构件中底部纵筋、分布腹筋和混凝土的抗拉贡献[10]，复合抗拉强度ft可计算如下：
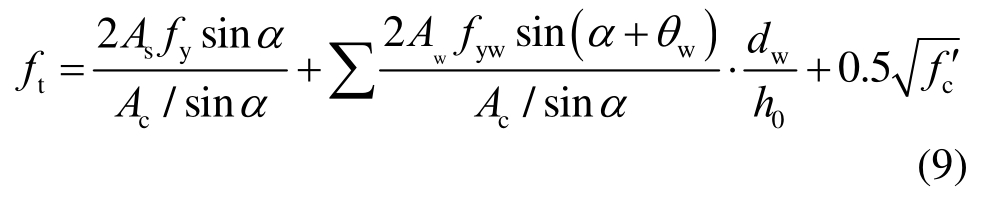
式中：As为底部纵筋截面面积；Ac为深受弯构件截面面积；Aw为腹筋面积；fy和fyw分别为纵筋和腹筋的屈服强度；h0为构件有效截面高度；dw为梁顶至腹筋与斜压杆中心线交点的垂直距离；θw为腹筋与水平轴间的夹角(见图2)。
1.1.4 深受弯构件受剪承载力计算
将式(4)、式(7)和式(9)代入式(1)可得如下方程：
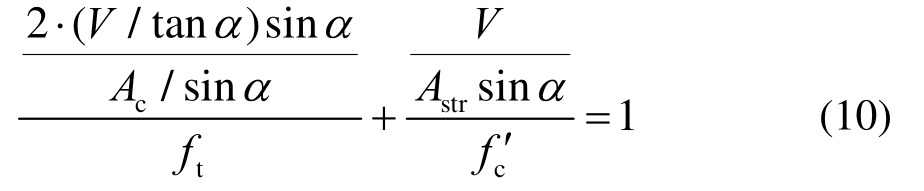
推导式(10)可得深受弯构件的受剪承载力V为：
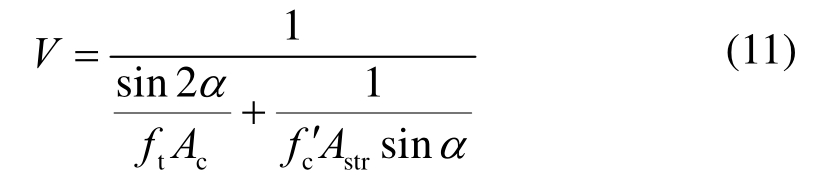
1.2 考虑尺寸效应的修正
尺寸效应是指以名义强度为代表的材料或构件力学性能指标随结构尺寸的增大呈减小趋势。Tan和Cheng[11]研究表明，深受弯构件尺寸效应的主控因素包括两方面：1)混凝土压杆的长度和宽度；2)构件的边界条件，主要考虑分布腹筋的有效性(如图3)。对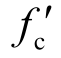
进行以下修正：
1.2.1 压杆几何尺寸修正系数ξ
将STM中混凝土压杆等效为承受轴向荷载的棱柱体压杆，忽略压杆与周围混凝土间的相互作用，引入Kim等[12]提出的圆柱体混凝土试件单轴受压强度尺寸效应公式，即混凝土压杆强度修正系 数ξ：
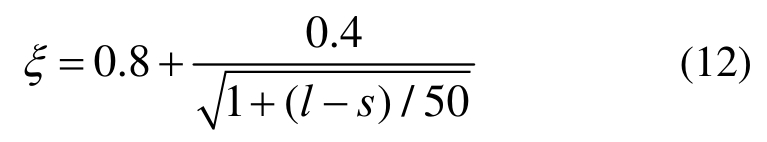
式中：l为压杆长度；s为压杆宽度(见图3)。
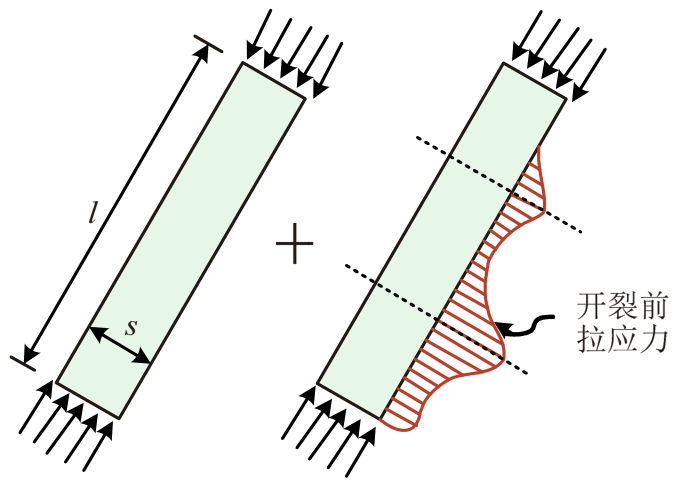
图3 几何尺寸和边界条件
Fig.3 Strut geometry and boundary conditions
1.2.2 压杆边界条件修正系数ζ
为合理量化分析腹筋间距和直径的影响，提出了考虑腹筋与混凝土相互作用关系的修正系数ζ [11]：
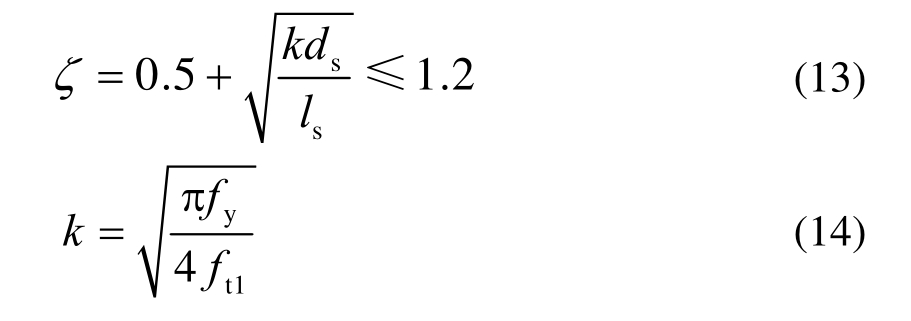
式中：ds为最小腹筋直径；ls为最大腹筋间距；ft1为混凝土抗拉强度。因此，考虑尺寸效应的拉压杆模型对深受弯构件受剪承载力V的计算见下式，即Tan-Cheng模型：
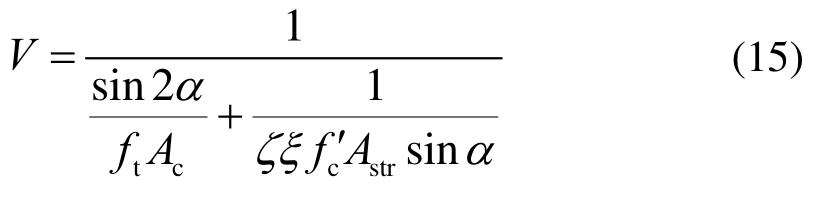
2 模型修正
2.1 压杆倾角α的简化
上述模型对压杆倾角α的计算是基于压杆顶部节点区高度lc等于压杆底部节点区高度la的假定提出的，且需经反复迭代，计算过程复杂。研究表明：当深受弯构件截面高度h≥1000 mm时，压杆顶部节点区高度lc对压杆倾角α的影响可忽略不计；而当h较小时，lc的取值对α的计算结果影响显著。因此，可对不同尺寸深受弯构件压杆倾角α的计算进行简化。根据美国ACI 318-14规范，在考虑CCT和CCC型节点区的受力状态后，建议取lc=0.8la，与迭代过程计算所得lc吻合较好，故本文将压杆倾角α简化如下：
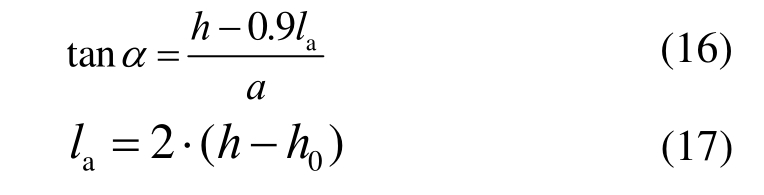
2.2 复合抗拉强度ft的简化
复合抗拉强度ft的计算综合考虑了混凝土、纵筋和腹筋的贡献。对于底部纵筋而言，混凝土开裂退出工作使得纵筋应力突然增大，故本文根据纵筋沿垂直于压杆方向的拉应力分布情况，假定其在试件1/2高度以下部分发挥主要作用，而忽略纵筋在试件1/2高度以上部分的作用；对于腹筋而言，因需明确其在剪跨内的具体分布位置，计算过程较为复杂。然而，Matamoros和Wong[13]指出，深受弯构件斜向开裂后，支座处和加载点附近腹筋应变较小，而穿过斜裂缝中部的腹筋应变较大，因此，为考虑腹筋对抗剪的影响，提出腹筋有效作用区域的概念(见图4)，同时忽略此区域外腹筋的作用。基于上述两点假设，且不考虑腹筋沿试件有效截面高度的分布水平dw/h0，可建议采用下式对ft进行计算：
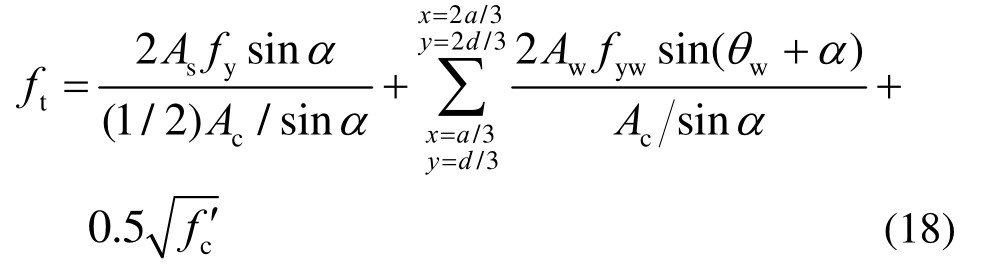
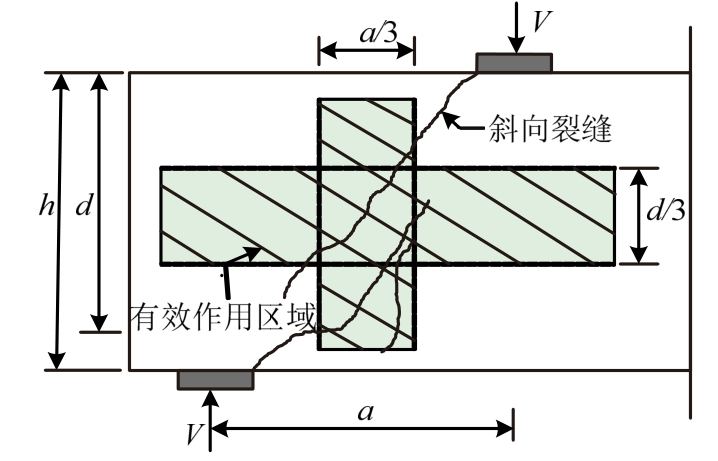
图4 腹筋有效作用区域示意图
Fig.4 Effective area for web reinforcement
2.3 简化STM模型计算步骤
1)通过式(16)得到压杆倾角α；
2)通过式(18)计算得复合抗拉强度ft；
3)通过式(12)、式(13)得到的修正系数ζ和ξ；
4)通过式(15)计算深受弯构件的受剪承载力V。
3 试验验证
3.1 模型验证
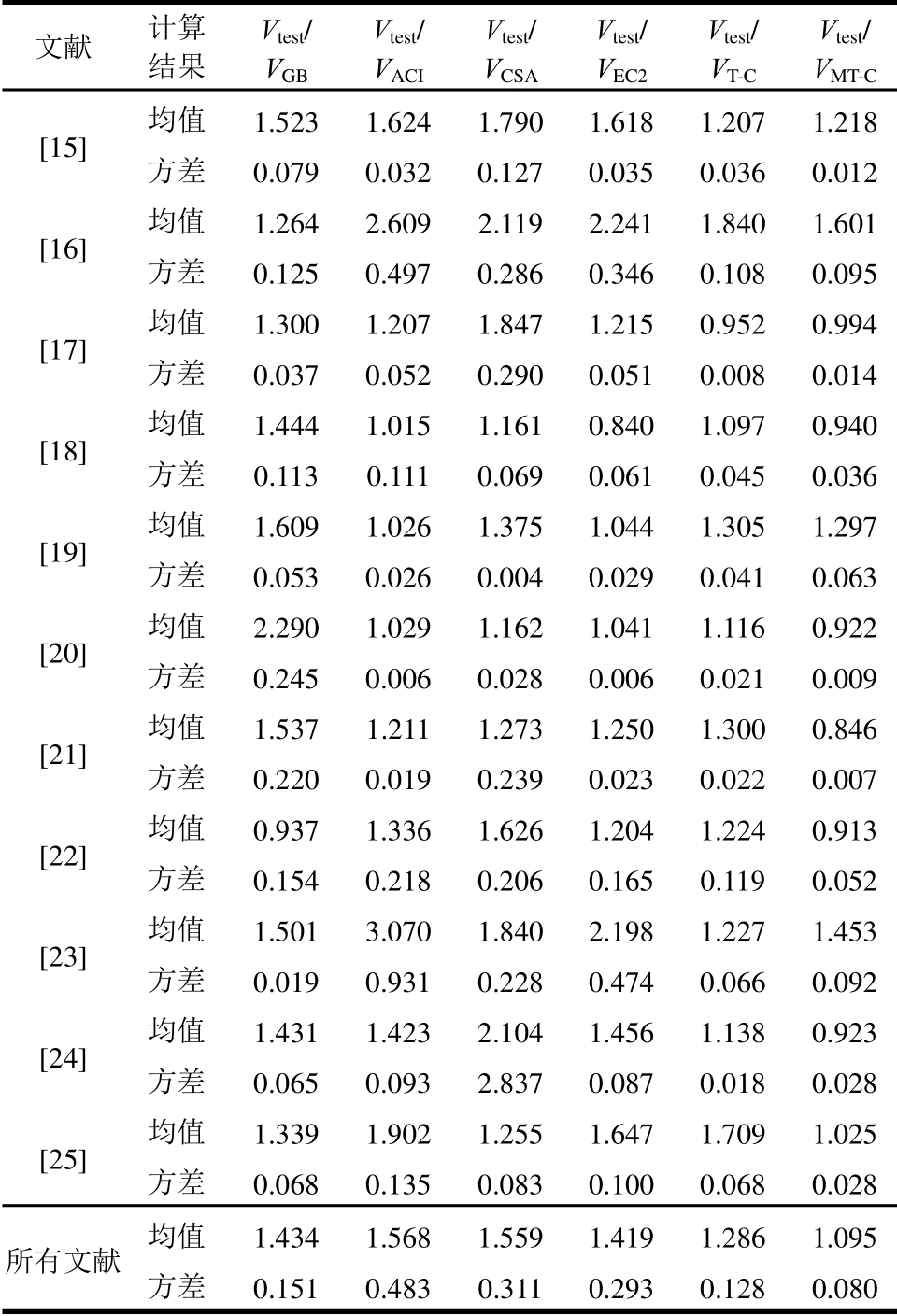
收集了国内外308组深受弯构件受剪试验数据，选取依据：1)简支试件的加载板与支撑板尺寸已知；2)试件剪跨比小于2且跨高比小于5；3)试件均发生剪切破坏。分别采用我国《混凝土结构设计规范》(GB50010—2010)[14]、加拿大CSA A23.3-04规范、美国ACI 318-14规范、欧洲EC2规范、Tan-Cheng模型等相关计算模型和本文建议模型对308组深受弯构件的受剪承载力进行计算，并与试验结果对比，具体结果见表1和图5。由表1可知：1)各国规范对深受弯构件受剪承载力的计算结果偏于安全。美国ACI 318-14、加拿大CSA A23.3-04、欧洲EC2等规范均基于拉压杆模型建立，仅混凝土压杆有效抗压强度和压杆倾角α的计算存在差异，属下限设计方法。而我国规范基于半理论半经验模型建立，因此，计算结果较其余三国规范更接近试验结果，吻合较好；2)试验值与本文建议模型计算值比值的均值为1.095，方差为0.08，模型预测结果与试验结果吻合良好，且离散程度较小，较各国规范计算结果更接近试验值；3)由图5(f)可见，修正后Tan-Cheng模型与Tan-Cheng模型计算精度相近，表明在Tan-Cheng模型基础上本文修正方法是合理的。
表1 各国规范和建议模型预测值与试验值的对比
Table 1 Comparisons between predictions and test results
文献 计算结果Vtest/ VGB Vtest/ VACI Vtest/ VCSA Vtest/ VEC2 Vtest/ VT-C Vtest/VMT-C[15]均值 1.523 1.624 1.790 1.618 1.207 1.218方差 0.079 0.032 0.127 0.035 0.036 0.012[16]均值 1.264 2.609 2.119 2.241 1.840 1.601方差 0.125 0.497 0.286 0.346 0.108 0.095[17]均值 1.300 1.207 1.847 1.215 0.952 0.994方差 0.037 0.052 0.290 0.051 0.008 0.014[18]均值 1.444 1.015 1.161 0.840 1.097 0.940方差 0.113 0.111 0.069 0.061 0.045 0.036[19]均值 1.609 1.026 1.375 1.044 1.305 1.297方差 0.053 0.026 0.004 0.029 0.041 0.063[20]均值 2.290 1.029 1.162 1.041 1.116 0.922方差 0.245 0.006 0.028 0.006 0.021 0.009[21]均值 1.537 1.211 1.273 1.250 1.300 0.846方差 0.220 0.019 0.239 0.023 0.022 0.007[22]均值 0.937 1.336 1.626 1.204 1.224 0.913方差 0.154 0.218 0.206 0.165 0.119 0.052[23]均值 1.501 3.070 1.840 2.198 1.227 1.453方差 0.019 0.931 0.228 0.474 0.066 0.092[24]均值 1.431 1.423 2.104 1.456 1.138 0.923方差 0.065 0.093 2.837 0.087 0.018 0.028[25]均值 1.339 1.902 1.255 1.647 1.709 1.025方差 0.068 0.135 0.083 0.100 0.068 0.028所有文献 均值 1.434 1.568 1.559 1.419 1.286 1.095方差 0.151 0.483 0.311 0.293 0.128 0.080
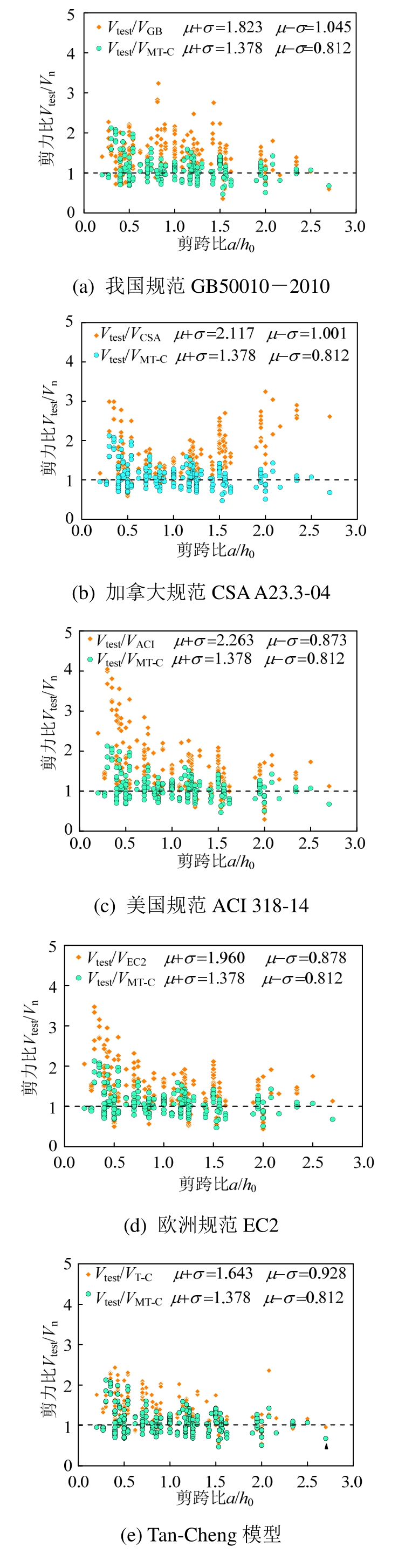
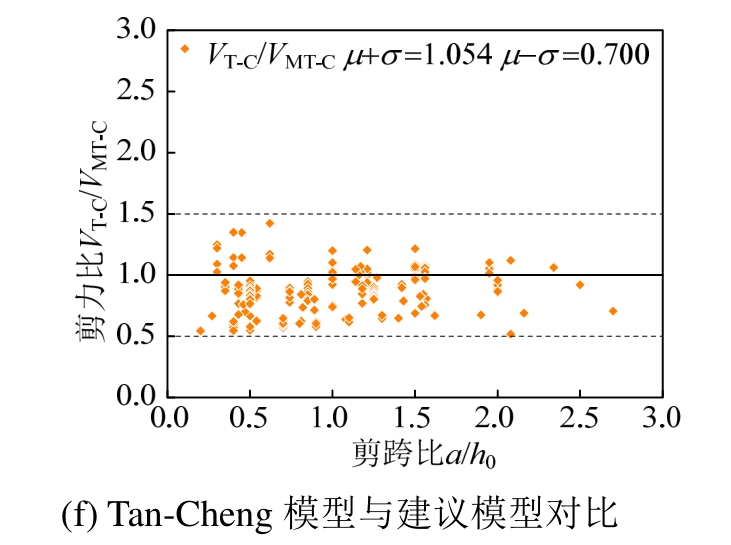
图5 典型模型与本文建议模型对比分析
Fig.5 Comparisons between proposed model and typical provisions
3.2 尺寸效应验证
为验证建议模型是否能够合理考虑尺寸效应对深受弯构件受剪承载力的影响，文中收集了37组不同尺寸的深受弯构件受剪试验数据[26,7,9]，试件主要参数包括截面尺寸、剪跨比、纵筋及腹筋配筋率、混凝土强度等详见表2。
表中，Walravena和Lehwalter[26]为验证深受弯构件受剪尺寸效应影响，于1994年进行了13组剪跨比为1.0的不同尺寸简支深受弯构件受剪性能试验，试件有效截面高度h0为160 mm～930 mm，加载板与支撑板宽度为0.25h0。研究表明：深受弯构件的名义极限抗剪强度随试件截面高度增加呈逐渐降低趋势，其受剪性能受尺寸效应影响显著，但与是否配置竖向腹筋无关。尺寸效应存在的主要原因是梁高不同导致试件在受荷过程中的裂缝发展速率存在差异。应力水平相同时，大尺寸试件的斜裂缝宽度较大，明显降低了裂缝间拉应力的传递效率。
此后，Tan和Lu[7]完成了12根梁宽相同的简支深受弯构件受剪性能试验，试件有效截面高度h0为444 mm～1559 mm，剪跨比为0.56～1.13，而加载板宽度保持不变。研究表明：在不同剪跨比下，腹筋的配置对试件受剪承载力无显著影响，但截面高度的变化对试件名义极限抗剪强度的影响不可忽视，与Walraven和Lehwalter的结论基本一致。近来，Birrcher等[9]对12根有效截面高度h0为495 mm～1750 mm的深受弯构件进行受剪性能试验研究，发现尺寸效应影响尤为显著，且随剪跨比的减小，尺寸效应影响显著性大大增加。
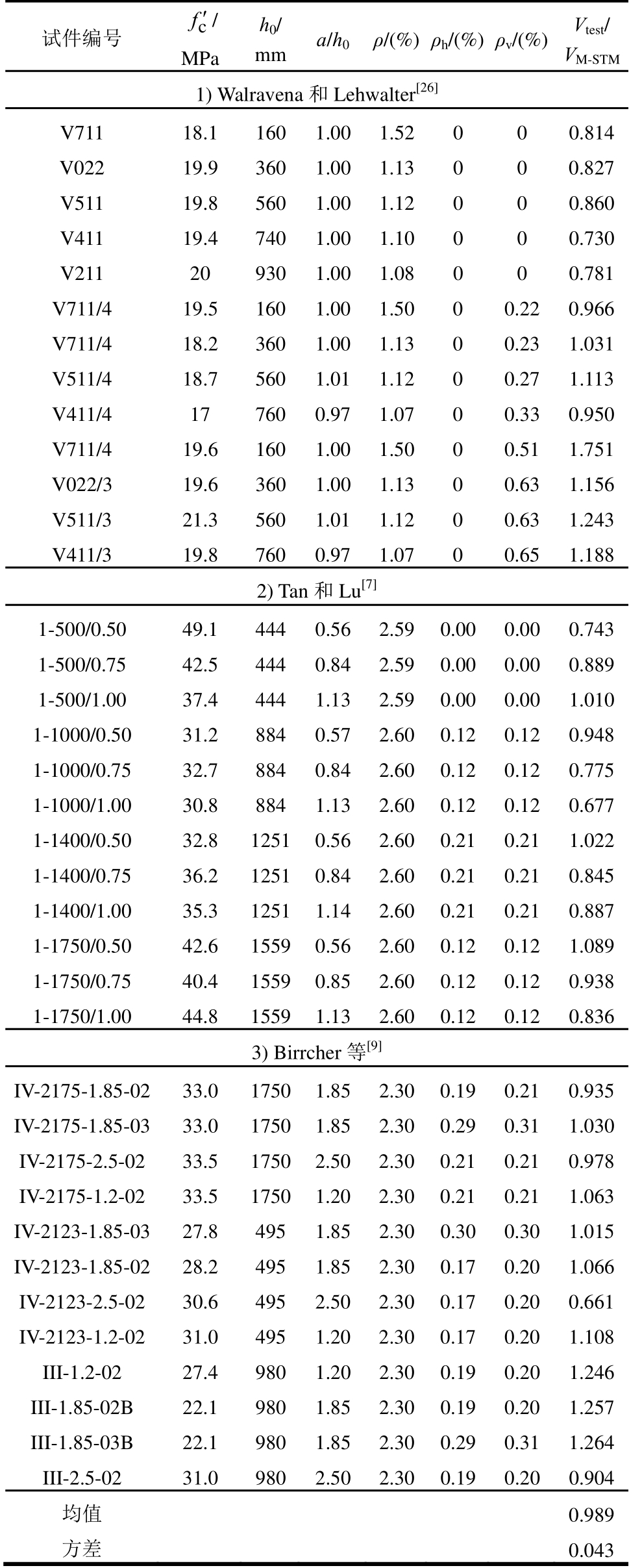
采用本文建议模型对37组不同尺寸深受弯构件的受剪承载力进行预测，重点分析建议模型能否准确考虑尺寸效应的影响，并与试验结果进行对比。具体对比情况见表2和图6。
表2 不同尺寸深受弯构件试验结果与计算结果对比
Table 2 Comparisons between test results and predictions of
specimens with different sizes
试件编号 cf′/ MPa h0/ mm a/h0ρ/(%)ρh/(%)ρv/(%) Vtest/ VM-STM 1)Walravena和Lehwalter[26] V711 18.1 160 1.00 1.52 0 0 0.814 V022 19.9 360 1.00 1.13 0 0 0.827 V511 19.8 560 1.00 1.12 0 0 0.860 V411 19.4 740 1.00 1.10 0 0 0.730 V211 20 930 1.00 1.08 0 0 0.781 V711/4 19.5 160 1.00 1.50 0 0.22 0.966 V711/4 18.2 360 1.00 1.13 0 0.23 1.031 V511/4 18.7 560 1.01 1.12 0 0.27 1.113 V411/4 17 760 0.97 1.07 0 0.33 0.950 V711/4 19.6 160 1.00 1.50 0 0.51 1.751 V022/3 19.6 360 1.00 1.13 0 0.63 1.156 V511/3 21.3 560 1.01 1.12 0 0.63 1.243 V411/3 19.8 760 0.97 1.07 0 0.65 1.188 2)Tan和Lu[7] 1-500/0.50 49.1 444 0.56 2.59 0.00 0.00 0.743 1-500/0.75 42.5 444 0.84 2.59 0.00 0.00 0.889 1-500/1.00 37.4 444 1.13 2.59 0.00 0.00 1.010 1-1000/0.50 31.2 884 0.57 2.60 0.12 0.12 0.948 1-1000/0.75 32.7 884 0.84 2.60 0.12 0.12 0.775 1-1000/1.00 30.8 884 1.13 2.60 0.12 0.12 0.677 1-1400/0.50 32.8 1251 0.56 2.60 0.21 0.21 1.022 1-1400/0.75 36.2 1251 0.84 2.60 0.21 0.21 0.845 1-1400/1.00 35.3 1251 1.14 2.60 0.21 0.21 0.887 1-1750/0.50 42.6 1559 0.56 2.60 0.12 0.12 1.089 1-1750/0.75 40.4 1559 0.85 2.60 0.12 0.12 0.938 1-1750/1.00 44.8 1559 1.13 2.60 0.12 0.12 0.836 3)Birrcher等[9] IV-2175-1.85-02 33.0 1750 1.85 2.30 0.19 0.21 0.935 IV-2175-1.85-03 33.0 1750 1.85 2.30 0.29 0.31 1.030 IV-2175-2.5-02 33.5 1750 2.50 2.30 0.21 0.21 0.978 IV-2175-1.2-02 33.5 1750 1.20 2.30 0.21 0.21 1.063 IV-2123-1.85-03 27.8 495 1.85 2.30 0.30 0.30 1.015 IV-2123-1.85-02 28.2 495 1.85 2.30 0.17 0.20 1.066 IV-2123-2.5-02 30.6 495 2.50 2.30 0.17 0.20 0.661 IV-2123-1.2-02 31.0 495 1.20 2.30 0.17 0.20 1.108 III-1.2-02 27.4 980 1.20 2.30 0.19 0.20 1.246 III-1.85-02B 22.1 980 1.85 2.30 0.19 0.20 1.257 III-1.85-03B 22.1 980 1.85 2.30 0.29 0.31 1.264 III-2.5-02 31.0 980 2.50 2.30 0.19 0.20 0.904均值 0.989方差 0.043
图6给出了建议模型预测结果随试件有效截面高度h0的变化情况。由表2、图6可知，本文建议的简化拉压杆模型计算值与试验值比值的均值为0.989，方差为0.043，表明该建议模型计算结果与试验结果吻合良好，且离散程度较小，合理考虑了深受弯构件受剪承载力受尺寸效应的影响。
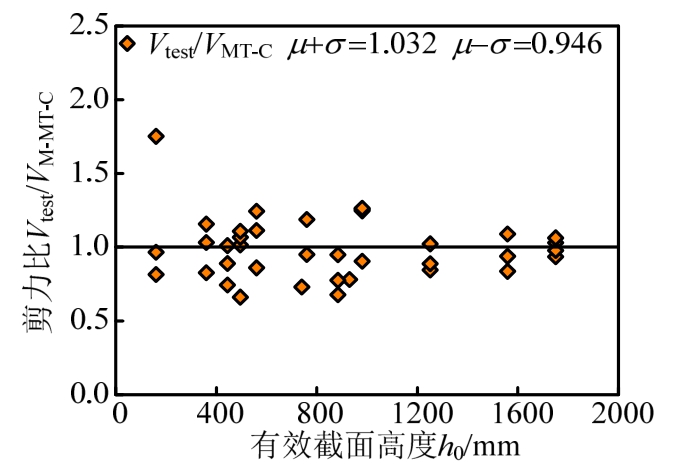
图6 简化STM模型计算结果
Fig.6 Predictions of simplified STM model
图7为名义抗剪强度
预测值随试件有效截面高度h0的变化情况。由图7可见，深受弯构件的名义抗剪强度随构件尺寸增加而逐渐降低，受尺寸效应影响显著；本文建议模型也能够很好的考虑尺寸效应的影响，其计算计算结果与试验结果变化趋势基本吻合，表明该建议模型能够准确预测深受弯构件的名义抗剪强度。
图7 名义抗剪强度计算值与试验值对比情况
Fig.7 Comparisons between test results and predictions of normalized shear strength
4 结论
本文结合Tan-Cheng模型，建立了考虑尺寸效应的深受弯构件拉压杆抗剪模型，并对混凝土斜压杆倾角α和构件复合抗拉强度ft的计算做出简化修正，通过国内外收集的308组深受弯构件受剪试验数据验证了模型的准确性，同时合理的考虑了尺寸效应的影响，主要结论如下：
(1)在保证精度基础上，提出修正后的Tan-Cheng模型。建议计算结果与试验结果吻合良好，与中国GB50010—2010、美国ACI 318-14、加拿大CSA A23.3-04和欧洲EC2等规范计算结果相当，且离散程度较小，能够准确、合理地预测深受弯构件受剪承载力；
(2)通过试验验证表明：建议模型有效考虑了尺寸效应的影响，可用于大尺寸深受弯构件的受剪承载力计算。
[1]ACI Committee 318: Building code requirement for structural concrete (ACI 318-14)and commentary [S].American Concrete Institute, 2014.
[2]CSA A23.3-04, Design of concrete structures[S].Canadian Standards Association, 2004.
[3]The European Standard EN 1992-1-1:2004, Eurocode 2.Design of concrete structures [S].British Standards Institution, 2004.
[4]Kani G N J.How safe are our large reinforced concrete beams? [C]// ACI Journal Proceedings, 1967, 64(3): 128—141.
[5]Bazant Z P, Kazemi M T.Size effect on diagonal shear failure of beams without stirrups [J].ACI Structural Journal, 1991, 88(3): 268—276.
[6]Collins M, Kuchma D.How safe are our large, lightly reinforced concrete beams, slabs, and footings? [J].ACI Structural Journal, 1999, 96(4): 482—490.
[7]Tan K H, Lu H Y.Shear behavior of large reinforced concrete deep beams and code comparisons [J].ACI Structural Journal, 1999, 96(5): 836—845.
[8]Matsuo M, Lertsrisakulrat T, Yanagawa A, et al.Shear behavior in RC deep beams with stirrups [J].Transactions of the Japan Concrete Institute, 2002, 23(5): 385—390.
[9]Birrcher D B, Tuchscherer R G, Huizinga M, et al.Depth effect in deep beams [J].ACI Structural Journal, 2014, 111(4): 731—740.
[10]Tan K H, Tong K, Tang C Y.Direct strut-and-tie model for prestressed deep beams [J].Journal of Structural Engineering, ASCE, 2001, 127(9): 1076—1084.
[11]Tan K H, Cheng G H.Size effect on shear strength of deep beams: Investigating with strut-and-tie model [J].Journal of Structural Engineering, ASCE, 2006, 132(5): 673—685.
[12]Kim J K, Yi S T, Park C K, Eo S H.Size effect on compressive strength of plain and spirally reinforced concrete cylinders [J].ACI Structural Journal, 1999, 96(1): 88—94.
[13]Matamoros A B, Wong K H.Design of simply supported deep beams using strut-and-tie models [J].ACI Structural Journal, 2003, 100(6): 704—712.
[14]GB50010—2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB50010—2010, Code for design of concrete structures [S].Beijing: China Architectural & Building Press, 2010.(in Chinese)
[15]Smith K N, Vantsiotis A S.Shear strength of deep beams [J].ACI Structural Journal, 1982, 79(3): 201—213.
[16]Kong F K, Robins P J, Cole D F.Web reinforcement effects on deep beams [C]// ACI Journal Proceedings.1970, 67(12): 1010—1018.
[17]Clark A P.Diagonal tension in reinforced concrete beams [C]// ACI Journal Proceedings, 1951, 48(10): 145—156.
[18]Gardoni P, Der Kiureghian A, Mosalam K M.Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations [J].Journal of Engineering Mechanics, ASCE, 2002, 128(10): 1024—1038.
[19]Aguilar G, Matamoros A B, Parra-Montesinos G J, et al.Experimental evaluation of design procedures for shear strength of deep reinforced concrete beams [J].ACI Structural Journal, 2002, 99(4): 539—548.
[20]Quintero-Febres C G, Parra-Montesinos G, Wight J K.Strength of struts in deep concrete members designed using strut-and-tie method [J].ACI Structural Journal, 2006, 103(4): 577—586.
[21]Tan K H, Tang C Y, Tong K.Shear strength predictions of pierced deep beams with inclined web reinforcement [J].Magazine of Concrete Research, 2004, 56(8): 443—452.
[22]Subedi N K, Vardy A E, Kubotat N.Reinforced concrete deep beams some test results [J].Magazine of Concrete Research, 1986, 38(137): 206—219.
[23]Ramakrishnan V, Ananthanarayana Y.Ultimate strength of deep beams in shear [C]// ACI Journal Proceedings, 1968, 65(2): 87—98.
[24]刘立新, 谢丽丽, 陈萌.钢筋混凝土深受弯构件受剪性能的研究[J].建筑结构, 2000, 30(10): 19—22.Liu Lixin, Xie Lili, Chen Meng.The shear strength capability of reinforced concrete deep flexural members [J].Building Structure, 2000, 30(10): 19—22.(in Chinese)
[25]龚绍熙.钢筋混凝土深梁在对称集中荷载下抗剪强度的研究[J].郑州工学院学报, 1982, 1: 52—68.Gong Shaoxi.The shear strength capability of reinforced concrete deep beam under symmetric concentrated loads [J].Journal of Zhengzhou Technology Institute, 1982, 1: 52—68.(in Chinese)
[26]Walravena J, Lehwalter N.Size effects in short beams loaded in shear [J].ACI Structural Journal, 1994, 91(5): 585—593.