钢桁腹-混凝土组合结构桥梁最早出现在法国,后来在国内外得到逐步应用[1],我国在西安-平凉货运专线以及广佛环线铁路的建设中成功运用了此结构[2]。该结构桥梁将钢与混凝土两种不同的材料有机结合起来,一方面,对以受压为主的弦杆采用混凝土结构可大幅降低钢材用量;另一方面,采用组合桁架的形式,可有效降低截面高度,使适用范围更广。
外接式组合桁架节点为半刚性节点的一种,对于半刚性节点的研究国内外已有很多研究成果,根据研究方法的不同可分为试验研究、有限元研究以及理论研究。
1)试验研究
对于半刚性节点性能的研究起源于上世纪初,最早的研究对象是钢结构中的半刚性节点。1917年,Wilson和Moore在搜集了数百次试验结果后,首次对铆钉连接的柔度进行了相关研究。2005年,Fukumot[2]为了研究梁柱节点的弹塑性行为,对节点进行了试验研究,提出了计算节点弹塑性行为的非线性剪切力-变形叠加模型。2002年~2007年,陈志华等[3]对方钢管混凝土柱-H型钢梁节点进行了静力拉伸试验,将节点承载力实测值与理论解进行了对比。2005、2006年同济大学李国强等[4—5]通过对组合框架梁节点的足尺试验,获得了节点的初始转动刚度和极限承载力,并对影响节点性能的各因素进行了分析,提出了相应的计算公式。2012年中南大学周凌宇和贺桂超[6]对铁路桥梁中采用的外接式和耳板式两种节点的极限承载力进行了缩尺试验研究,并进行了对比分析。2013年重庆大学李正良等[7]为研究特高压输电塔K形节点的弯矩-转角关系,进行了5个足尺节点试验,并拟合出了弯 矩-转角全曲线公式。2017年北京工业大学张爱林等[8]对钢梁螺栓连接节点的静力性能进行了试验研究,探究了节点的初始转动刚度、极限承载能力。2018年赵根田等[9]通过端板连接框架结构的试验研究,发现增加端板厚度可以明显改善框架节点的转角延性,增加柱翼缘厚度会降低框架的转角延性。
2)有限元研究
20世纪50年代,随着计算机技术的不断成熟,为半刚性节点的研究提供了有限元分析的基础,促进了半刚性节点的研究。1963年,Monforton和Wu[10]在节点弹性分析中采用了矩阵位移法,也取得了较好的效果。1990年Barakat和Chen[11]提出了一种计算程序来分析钢框架结构。2014年刘军[12]针对外接式钢-混凝土组合桁架节点,通过有限元分析,提出了节点初始转动刚度的拟合公式,并将其引入到简支梁桥分析中。2016年王海波和杜元涛[13]采用有限元分析软件ABAQUS建立了3种钢-混组合桁架节点的简化模型,根据单根PBL剪力键的荷载-滑移关系反推PBL剪力键的荷载,研究了PBL剪力键群的负载分布规律及其受力性能。
3)理论研究
1936年,Rathbum[14]首次提出了倾角-挠度法,并应用到节点的弹性分析中,此时将节点的弯矩-转角曲线假定为直线。20世纪70年代,钢结构半刚性节点的研究进入了一个新阶段,学者们摒弃之前的线性假定,开始了对钢框架节点的非线性研究。1970年,Ronstad和Sunramanian[15]首次提出节点弯矩-转角关系的双线性模型,Frye和Morris[16]在1975年进一步提出了多项式模型,促进了对节点弯矩-转角关系的准确表达。20世纪90年代以后,学者们不再局限于对节点本身力学特性的研究,开始致力于探索半刚性节点对整个结构(如钢框架)的影响。Kish和Chen[17]提出了针对钢框架的二阶非线性分析方法。随着半刚性节点研究的逐步成熟,1993年欧洲钢结构设计规范EC3、EC4以及2000年英国规范BS5950,基于节点性能给出了判断节点铰接、半刚接和刚接的计算公式。
2005年上海大学侯娟等[18]综合考虑了端板变形、柱翼缘以及螺栓对初始转动刚度的贡献,利用分解法建立了梁柱螺栓端板连接节点的力学模型,然后基于梁板理论给出了节点初始转动刚度的解析公式。2009年福州大学吴兆旗等[19]考虑了端板受弯、柱翼缘受弯、螺栓受拉、柱子腹板受剪、柱子腹板受压和柱子腹板受拉变形对连接节点转动刚度的影响,应用组件法建立了端板连接节点初始转动刚度的计算模型。2011年厦门大学高婧等[20]考虑了钢梁与混凝土楼板之间的相对滑移,利用组件法推导了组合节点在正、负弯矩作用下初始转动刚度的计算公式,并与试验结果吻合较好。2017年合肥工业大学王冬花和王静峰[21]基于组件法提出了负弯矩作用下端板连接半刚性钢管混凝土组合节点初始刚度计算公式。
经过了对于节点初始转动刚度的研究之后,学者开始对节点的弯矩-转角全曲线展开探索。清华大学石永久和施刚教授等[22—25]对端板连接节点进行了较为系统的研究。石永久于2006年提出了一种计算钢结构梁柱端板连接转动变形的方法,该方法能够提供弯矩-剪切转角和弯矩-缝隙转角曲线,为我国钢结构设计规范中关于节点转动变形的具体计算方法提供了有益补充,并结合已有研究成果及国外规范的建议,对应用于多层钢框架中的端板连接梁柱节点提出了标准构造建议,针对此类端板连接节点提出了相应的弯矩-转角曲线形式及简化计算方法。2012年施刚发现现有测量方法得到的节点转角中大多包括梁与柱变形的影响,针对这种不足,对全焊接节点及栓焊混接节点提出了改进的节点转角测量计算方法,并验证了其精确性和可行性。2017年施刚针对超大承载力端板连接节点,提出新的组件形式,并基于组件法提出了该类节点的抗弯承载力和转动刚度的计算方法,提出了更为合理的节点弯矩-转角曲线模型。
综上可知,对于半刚性节点转动刚度研究在理论和试验方面都取得了较为突出的成果,但现有研究多是针对钢框架和钢桁架中的半刚性节点[26—27],对于组合结构中的半刚性节点转动刚度的研究较少。组合结构中的节点无论是材料还是节点构造形式都与普通钢节点存在较大差异,因此不能直接采用钢节点的研究成果,但可以借鉴其研究思想,为组合结构中半刚性节点的研究提供思路。
本文以银西铁路线渭河特大桥为工程背景,该桥为4×60 m钢桁腹-混凝土连续箱梁桥,对外接式组合桁架节点初始转动刚度展开研究,该研究具有明确的理论价值和实际工程意义。
1 工程背景
新建银川至西安铁路线渭河特大桥主桥与福银高速公路并行,为减轻结构自重,同时为更好地增加铁路桥的通透性,减小对公路通车的压抑感,选择通透性良好的钢桁腹组合箱梁,跨度为4×60 m。主桥立面如图1所示。

图1 银西线渭河主桥立面图
Fig.1 The main Bridge elevation crossing weihe in Yinchuan-Xi’an railway
该桥设计等级为铁路I级,双线上承式,结构形式采用钢桁腹-混凝土连续梁,主要由混凝土弦杆、方钢管腹杆、混凝土顶底板以及混凝土墩顶块组成,图1中所示节点详图如图2所示。
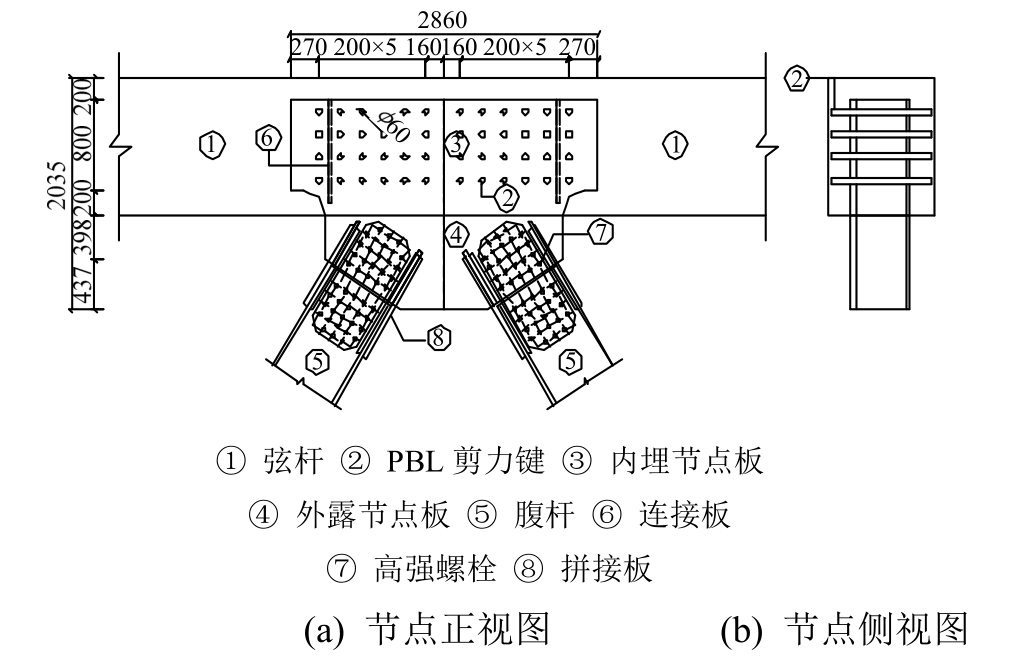
图2 节点构造图 /mm
Fig.2 The structure diagram of joint
在传统桁架结构设计中,对节点的处理方式是将节点看作理想铰接,采用如下假定:1)各节点都是理想的无摩擦铰;2)各杆轴线均为直线,并在同一平面内通过铰的中心;3)荷载为节点平面内荷载。采用此种假设可以简化计算,实现对复杂问题的简化处理,提高设计效率,但对于铁路桥梁,一方面实际施工无法满足上述三个假设,另一方面为了保证行车的平稳性,桥梁对节点刚度要求高,采用节点铰接的简化方式会大幅增加建设成本,如果采用节点全刚接简化方式,又担心结构安全问题。
图2所示节点形式在国内铁路桥梁中首次运用,其力学性能尚未研究清楚,而节点作为该桥梁中关键的传力部件,对结构整体工作性能的影响较大,设计中如何准确地考虑节点的转动性能,成为亟待解决的问题。为了解决设计中遇到的问题,本文对该类型节点的转动刚度从理论推导和数值模拟两个角度进行了研究。
2 理论研究
2.1 节点域的定义
在对节点转动性能开展研究前,首先对节点域进行定义,以明确研究对象,方便后文叙述。本文所讲的节点域是指节点在受弯矩作用时,混凝土弦杆与钢腹杆连接处对抗弯承载力以及转动变形做出贡献的连接部件所围成的区域,如图3虚线内区域所示。
结合图2可知,对节点域转动变形有贡献的部件包括七个,分别为:混凝土弦杆、内埋节点板、外露节点板、PBL剪力键群、连接板、高强螺栓、拼接板。
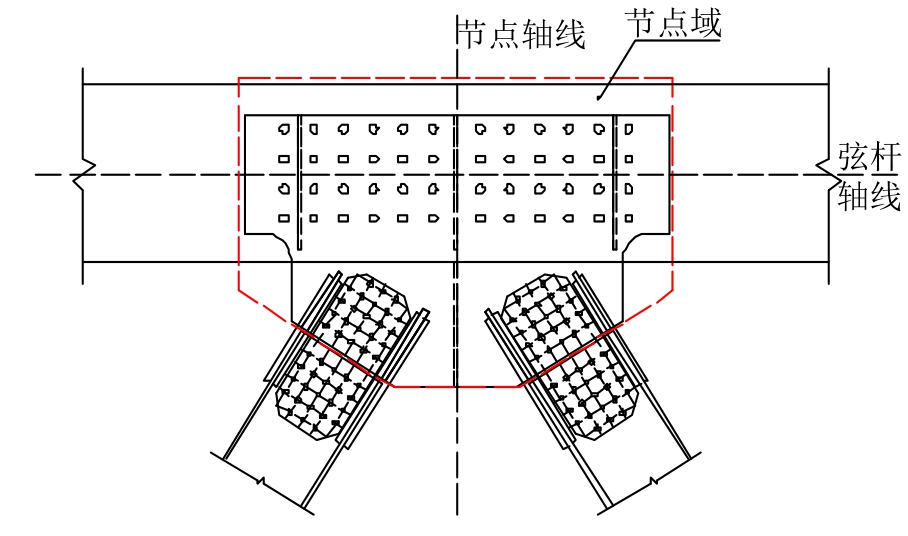
图3 节点域详图
Fig.3 The detailed drawing of the joint zone
2.2 传力路径
研究节点的初始转动刚度,首先需要明确节点的转动位移,由图3可知在外界弯矩作用下,节点域范围内的转动变形由弦杆、内埋节点板等七个部件构成,为了明确节点域的转动位移,我们必须对各组成部件的受力以及变形展开研究,这样研究的对象就从复杂的节点域,变成了各个材料明确、结构简单、受力清晰的部件。
由于节点域构造复杂,当节点域受到弯矩作用时,力在节点域内的传递不便于从上往下分析,所以采取从下往上的分析方法。
外界弯矩最终由支座或者具有支座功能的结构承担,对于节点域来说,与之相连的钢腹杆起到了支座的作用。腹杆的内力有弯矩、剪力和轴力,由于腹杆为轴拉(压)构件,为了方便分析,这里忽略弯矩和剪力的影响,仅考虑腹杆轴力的作用;根据节点域的构造,钢腹杆的拉力、压力会通过高强螺栓以及拼接板传递给与之相连的外露节点板,当弯矩较小时,摩擦型高强螺栓与拼接板几乎无相对位移,故忽略其对节点域变形的贡献,外露节点板在钢腹杆拉力和压力作用下承受双向剪切作用;外露节点板与内埋节点板相连,剪力传递到内埋节点板时,内埋节点板也承受双向剪切作用,由于内埋节点板与混凝土弦杆粘结,所以长边方向的剪力会转化成为弦杆的轴力,主要引起节点的平动,不在讨论范围,予以忽略,认为内埋节点板承受单向剪切作用;内埋节点板的剪力会继续传递到与之接触的混凝土弦杆以及PBL剪力键群上,由于PBL剪力键群内置于混凝土中,故这部分剪力最终传递给混凝土弦杆。通过以上分析可知在弯矩作用下,连接板并不直接参与力的传递,其主要起到协调前后节点板变形的作用,故忽略连接板对节点域变形的贡献。
综合以上分析可以得出,对节点域转动变形有贡献的部件可以简化为以下四个:混凝土弦杆、内埋节点板、外露节点板、PBL剪力键群,力在节点域内的传递路径以及每个组件的受力状态如图4所示。
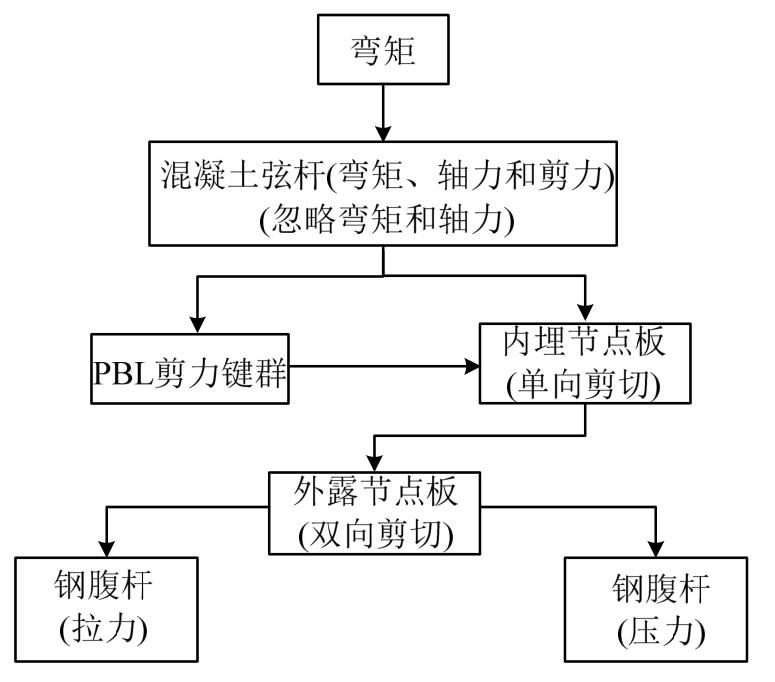
图4 力的传递路径
Fig.4 The transfer path of force
2.3 计算理论
由于节点构造复杂,无法采用单一公式确定节点初始转动刚度,基于此种情况,本文采用组件法计算节点初始转动刚度。
组件法的基本思路可以分为以下三个步骤:1)节点域拆分,确定节点域中的有效力学组件; 2)分析各组件的力学性能,通过经典力学理论确定每个组件的力学参数,给出每个组件的弹簧模型表达式;3)进行弹簧组合,通过组合的弹簧体系计算出节点域的初始转动刚度。
根据已有研究可知内埋节点板的变形主要由PBL剪力键变形引起[13],两者不相互独立,故内埋节点板不作为一个独立力学组件进行讨论,但在分析PBL剪力键群的受力时,会引入内埋节点板的力学参数。
经过以上分析,将节点域拆分为以下三个有效力学组件:弦杆、PBL剪力键群、外露节点板。
为了方便推导运算,本章节采用如下基本假定:
1)材料处于弹性阶段,符合小变形假定。
2)摩擦性高强螺栓不会发生相对滑移。
3)节点域绕腹杆延伸交点转动。
4)忽略弦杆中钢筋贡献。
2.4 弹簧组件组合
根据前文分析,可以将节点域简化为弹簧模型,如图5(b)所示。其中KXG为混凝土弦杆的抗剪刚度,KPBL为PBL剪力键群的抗剪刚度,KJDBW为外露节点板的抗剪刚度,视前后两侧PBL剪力键群、外露节点板的抗剪刚度一致。
根据节点构造以及力在节点域内的传递路径可知节点域的初始转动刚度可表达如下:
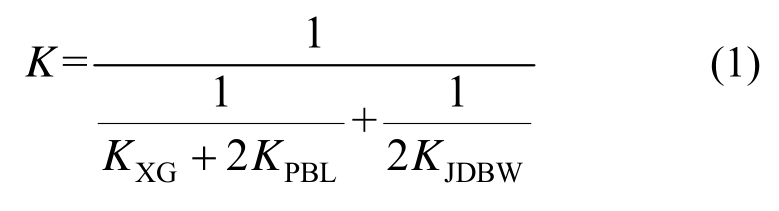
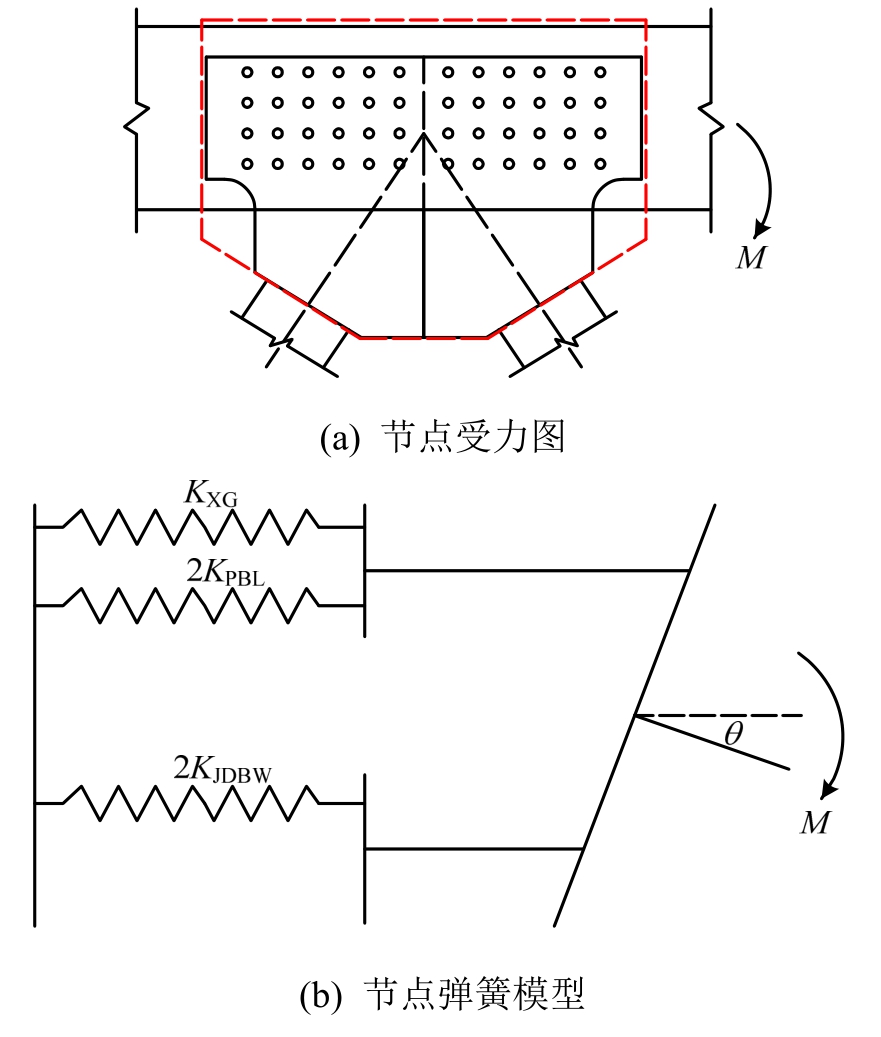
图5 弹簧简化模型
Fig.5 The simplified spring model
2.5 弦杆在节点域的抗剪刚度
通过2.2节的分析可知,在外界弯矩作用下,弦杆为受弯、受剪和受压的复合受力构件,由于受压主要引起节点域的平动,对节点转动没有影响,故忽略压力作用,另外节点域弦杆较短,弯矩引起的变形较小,故此处仅讨论弦杆的剪切变形。
为了便于分析,将内埋节点板传递给混凝土的均布剪力简化为多个集中力,作用点为PBL剪力键所处的位置,则节点域弦杆就变成了受多个集中力作用的剪切构件,集中力的个数与PBL剪力键的列数相同,其受力变形如图6所示(以四列剪力键为例)。
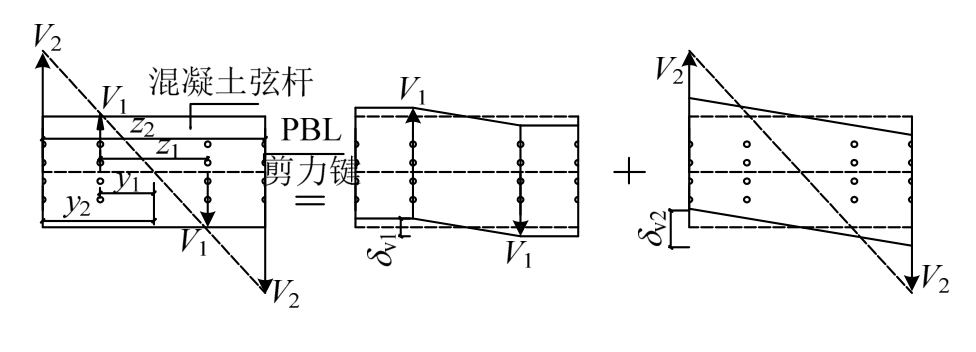
图6 弦杆变形图
Fig.6 The chord deformation diagram
当有2n排剪力键时,根据材料力学相关理论以及叠加原理,弦杆在每对Vi作用下的变形分 别为:
弦杆总的剪切变形为δXG,转角为θ,则有:
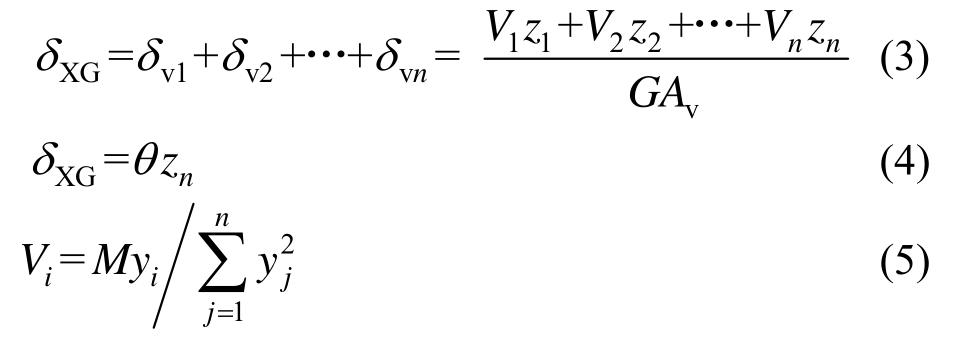
式中:G、E为混凝土的剪切模量和弹性模量;Vi为第i排剪力键传递给弦杆的剪力;yi为Vi到转动中心的距离;Zi为上部和下部第i排剪力键的距离,即受剪切域高度,当对称布置时Zi=2yi;M为弦杆受剪域承受的弯矩;Av为弦杆的受剪切面积,取弦杆截面面积。
将式(4)和式(5)代入式(3),其中![]() 并取ν=0.2,得到弦杆初始转动刚度:
并取ν=0.2,得到弦杆初始转动刚度:
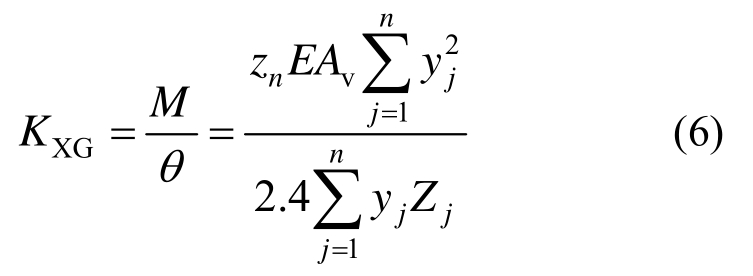
2.6 PBL剪力键群的抗剪刚度
节点域内PBL剪力键横穿内埋节点板,并与内埋节点板协同受力,根据已有的实验可知,内埋节点板相对于弦杆的转动变形,主要由PBL剪力键群的变形引起,两者不相互独立,故此处将内埋节点板与PBL建立键合成一个组件分析。假定内埋节点板在PBL剪力键群作用下,转动中心在剪力键群形心处,对于受力相同而位于不同高度处的剪力键(例如各列剪力键受力相同但到形心的距离不同),可以用一个等效力臂Zeq来代替原来的力臂Zi,从而得到不同高度剪力键的等效刚度Keq,转换模型如图7所示(以四排剪力键为例)。
学者王振海[28]以南京三桥和南京四桥埋入式PBL剪力键的试验为基础得到了剪力键加载过程中的荷载-滑移关系,其中弹性阶段的计算公式为:
式中:P为PBL剪力键受到的荷载;fc为混凝土的抗压强度设计值;Ac为混凝土隼的面积Ac=πd2/4,d为混凝土隼直径;u为PBL剪力键的滑移量。
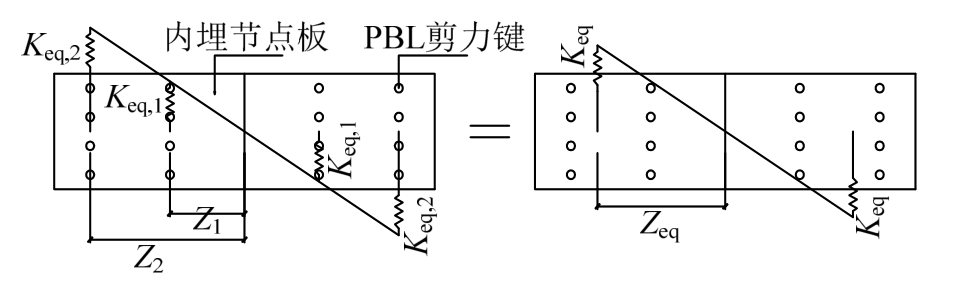
图7 PBL剪力键群等效刚度示意图
Fig.7 The equivalent stiffness diagram of the PBL shear key group
根据式(7)可得单根PBL剪力键的剪切刚度为:
式(7)和式(8)中力的单位为kN,应力的单位为MPa,长度的单位为mm。假设每一排中的n个剪力键受力均衡,可以协同发挥作用,则每一排的抗剪刚度为:
对图3中的结构进行分析,根据合力等效以及弯矩等效可得:
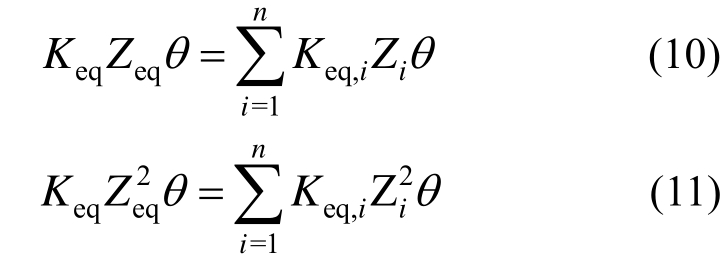
由式(9)、式(10)和式(11)可得:
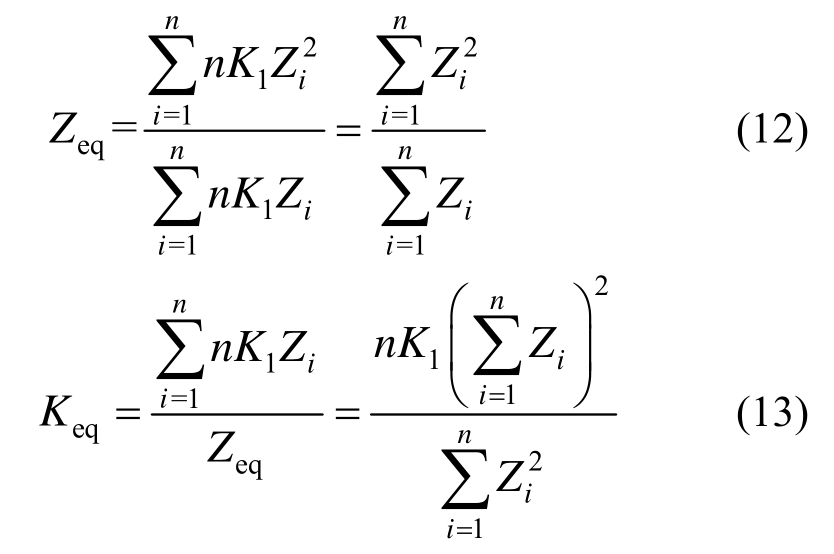
在等效力臂Zeq处由于PBL剪力键的剪切变形造成的内埋节点板位移为:
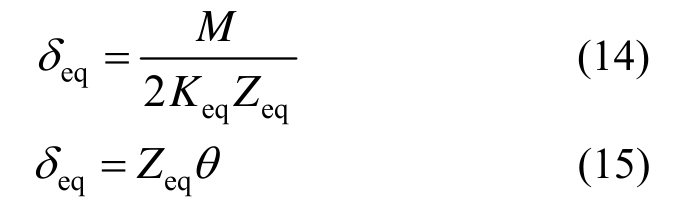
由式(14)和式(15)可得PBL剪力键群的抗剪刚度为:
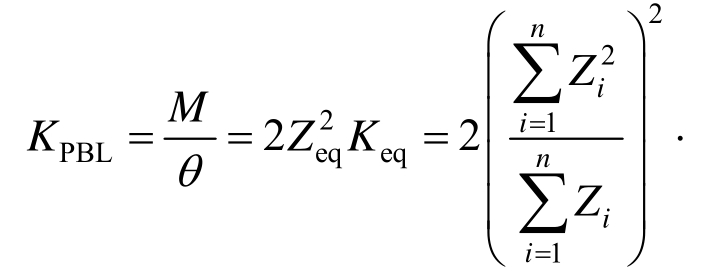
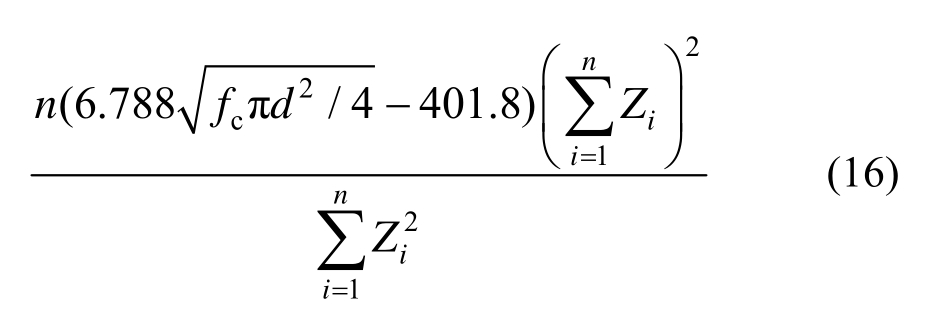
2.7 外露节点板的抗剪刚度
外露节点板在节点弯矩作用下,通过高强螺栓与钢腹杆可靠连接,承受钢腹杆传递的拉力和压力作用,如图8所示,Vx方向的剪力与内埋节点板传来的剪力Vn相平衡。根据面积相等以及对形心轴的惯性矩相等的原则,将外露节点板简化为长为L,高为H的矩形,变形如图9所示。
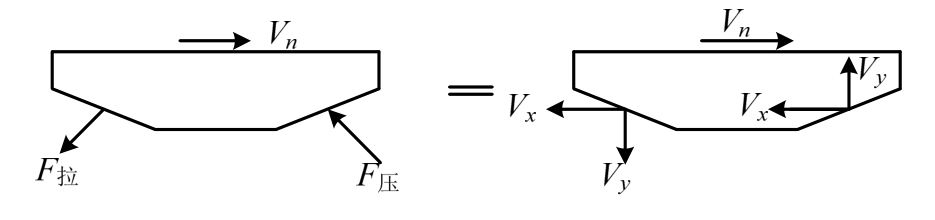
图8 外露节点板受力分析图
Fig.8 The stress analysis diagram of exposed nodal plate
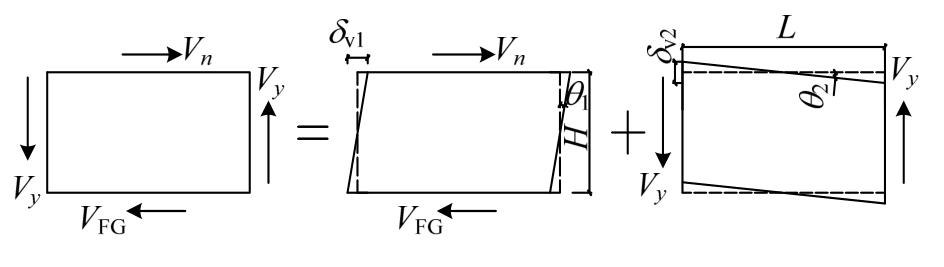
图9 外漏节点板变形图
Fig.9 The deformation figure of exposed nodal plate
在Vn和VFG(Vn=VFG)作用下,节点板的剪切变形为:
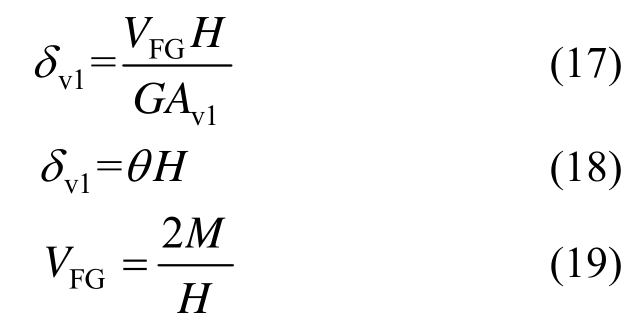
式中:G、E为钢板的剪切模量和弹性模量;VFG为腹杆传递给节点板的剪力;H为等效节点板的高度;M为节点域节点板承受的弯矩;Av1为节点板的受剪切面积,取Av1=t×H,t为节点板厚度。
由式(17)~式(19),其中![]() 并取ν=0.3,得到外露节点板的单向抗剪刚度:
并取ν=0.3,得到外露节点板的单向抗剪刚度:
同理可得:
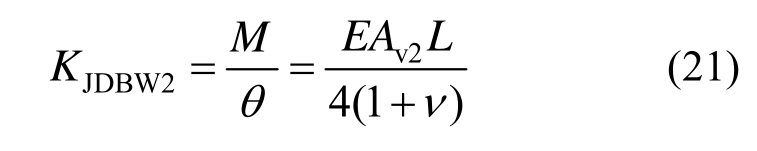
由式(20)和式(21)可得外露节点板的抗剪刚度为:
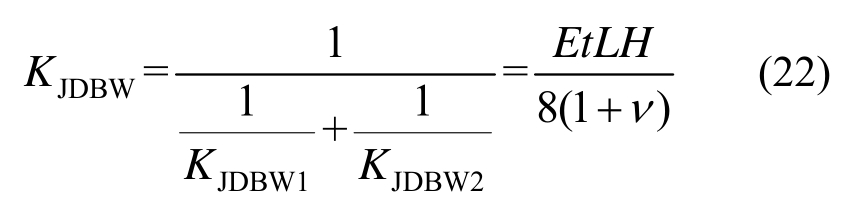
2.8 节点的初始转动刚度
前文(2.5~2.7节)分析了外接式组合桁架节点三个有效力学组件的刚度,根据组件法的思想,结合式(1)可得:
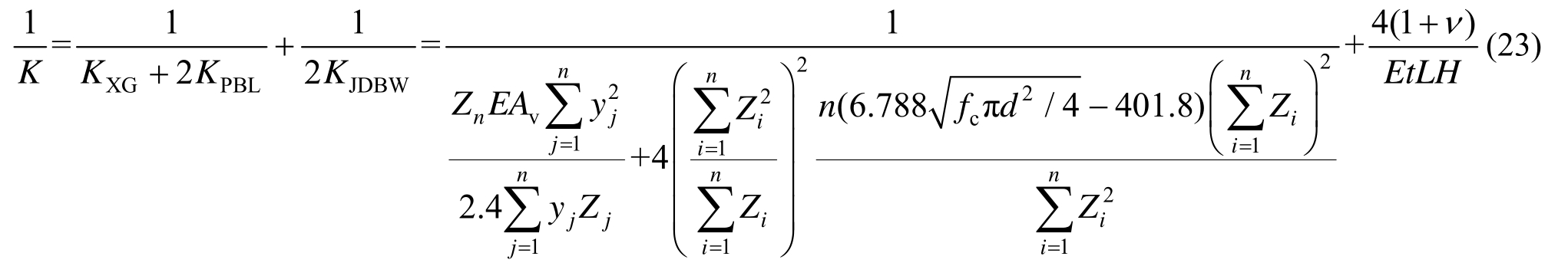
式中:各项参数意义同前。
由于未讨论其他节点形式,式(23)对于本文研究的对称K形外接式组合桁架节点形式是适用的,对于其他节点形式的适用性尚待探讨。
3 数值分析
3.1 模型建立
基于有限元程序A NSYS建立了节点三维非线性有限元模型,节点模型主要包括弦杆、节点板、横隔板、连接板、PBL剪力键、腹杆、支座七大部分。需要说明的是,为了较为准确地模拟节点域的边界条件,建模时考虑了钢腹杆以及节点域外弦杆。混凝土弦杆采用SOLID65单元模拟,节点板、连接板、横隔板与腹杆均采用SHELL181单元模拟,PBL剪力键采用BEAM188单元模拟,混凝土弦杆与PBL剪力键、节点板、横隔板的连接以及高强螺栓均采用节点自由度耦合模拟。模型采用映射网格划分,实体单元、板单元以及梁单元的划分尺寸约为50 mm,模型如图10所示。
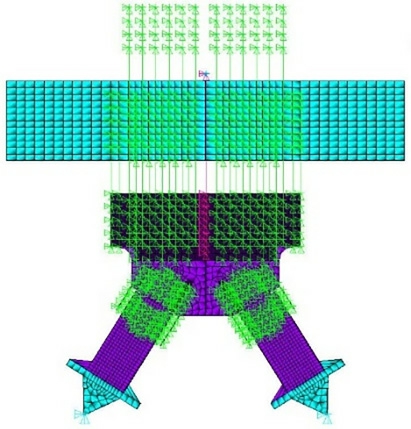
图10 节点有限元模型
Fig.10 The finite element model of joint
弦杆采用solid65单元模拟,solid65单元可用于模拟加筋的3D实体结构,具有受拉开裂的性能。模型中考虑材料非线性的影响,混凝土采用多线性随动强化准则,根据《混凝土结构设计规范》(GB50010—2010)附录C中定义的本构关系,如图11(a)所示。混凝土弹性模量Ec=35500 MPa,泊松比为0.2,破环准则采用Willam-Warnke五参数破环准则。
钢材本构关系采用有屈服点模型,屈服强度为390 MPa,极限强度为500 MPa,弹性模量为2.06×105 MPa,泊松比为0.3,应力-应变曲线如图11(b)所示。
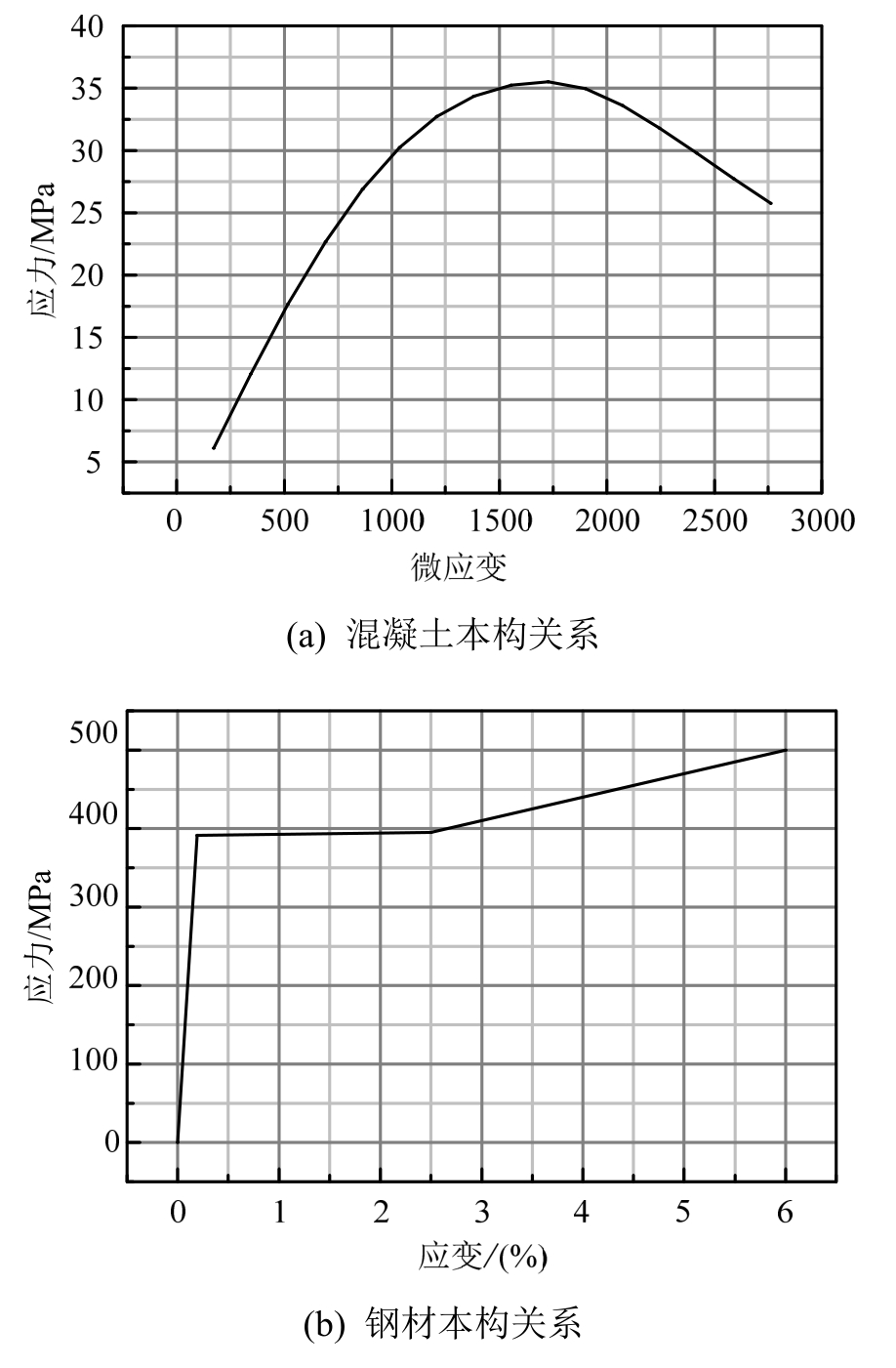
图11 材料本构关系
Fig.11 Constitutive law for materials
支座采用实体单元模拟,按照实际受力情况约束支座端部UX、UY、UZ平动自由度,为保证弦杆平面外稳定,选取弦杆两端部分节点约束UY平动自由度。
假设材料服从Mises屈服准则,采用Newton- Raphson迭代法与弧长法相结合求解。
3.2 节点弯矩-转角曲线
图12为节点弯矩-转角曲线,从图中可以看出曲线大致分为弹性阶段和屈服阶段,节点呈现出典型的弹塑性特征,节点的极限弯矩约为17481 kN·m,屈服弯矩约为11700 kN·m,为极限弯矩的67%,节点转动刚度大,节点的弹性段较长,转角变形小,说明2.3节中关于材料处于弹性阶段的小变形假定符合实际情况。
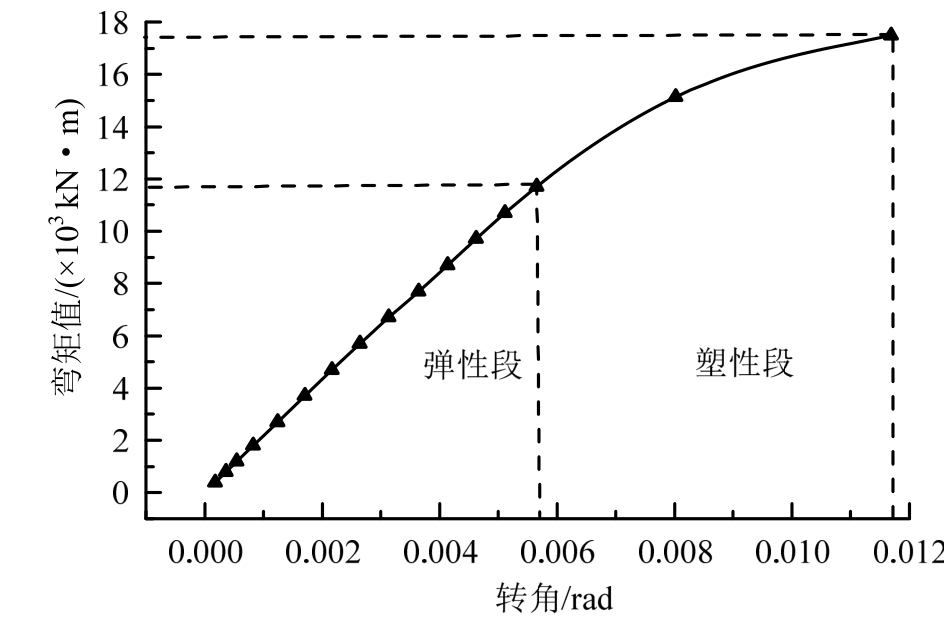
图12 节点弯矩-转角曲线
Fig.12 Moment - rotation curve of joint
3.3 模型验证
为了验证有限元模型的有效性以及前文理论推导的正确性,在保持其他参数不变的情况下,本文选取五个参数作为变化对象,建立表1中的六个模型,并将有限元解与理论解进行对比,对比结果记录在表2中。
表1 模型参数表
Table 1 Model parameter table
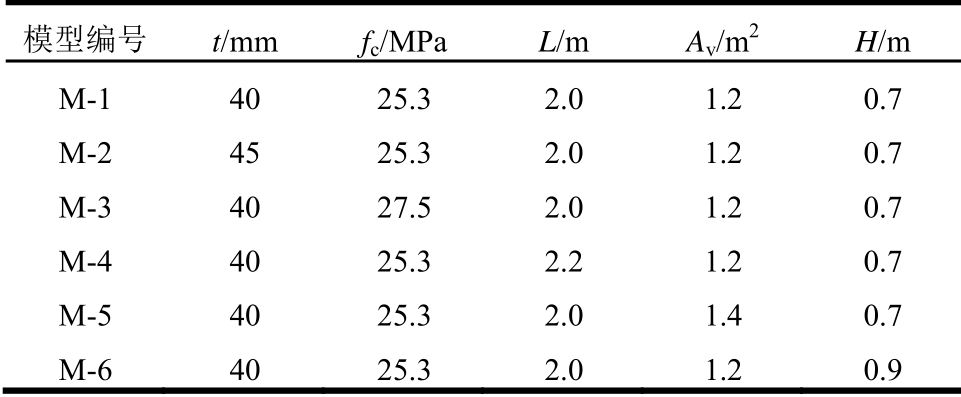
模型编号 t/mm fc/MPa L/m Av/m2 H/m M-1 40 25.3 2.0 1.2 0.7 M-2 45 25.3 2.0 1.2 0.7 M-3 40 27.5 2.0 1.2 0.7 M-4 40 25.3 2.2 1.2 0.7 M-5 40 25.3 2.0 1.4 0.7 M-6 40 25.3 2.0 1.2 0.9
下面作者从两层次验证模型的有效性,一是相同参数下,理论解与有限元解的相对误差;二是有限元解的参数敏感性是否同理论分析一致。
对比M-1和M-2可知,当改变外露节点板厚度t时,理论解的节点初始转动刚度增加了2.7×108 N·m/rad,相对增长率为12.56%,有限元解的节点初始转动刚度增加了2.6×108 N·m/rad,相对增长率为11.67%,故认为有限元解和理论解在参数t方面具有一致的敏感性;对比M-1和M-3可知,当改变混凝土型号时,理论解的节点初始转动刚度基本不变,都是2.09×109 N·m/rad,有限元解都为2.23×109 N·m/rad,故认为有限元解和理论解在参数fc方面具有一致的敏感性;对比M-1和M-4可知,当改变外露节点板长度L时,理论解的节点初始转动刚度增加了2.1×108 N·m/rad,相对增长率为9.77%,有限元解的节点初始转动刚度增加了2.1×108 N·m/rad,相对增长率为9.42%,故认为有限元解和理论解在参数L方面具有一致的敏感性;对比M-1和M-5可知,当改变弦杆截面积AV时,理论解和有限元解的节点转动刚度都基本保持不变,故认为有限元解和理论解在参数AV方面具有一致的敏感性;对比M-1和M-6可知,当改变外露节点板高度H时,理论解的节点初始转动刚度增加了6.1×108 N·m/rad,相对增长率为28.37%,有限元解的节点初始转动刚度增加了5.4×108 N·m/rad,相对增长率为25.12%,故认为有限元解和理论解在参数H方面具有一致的敏感性。
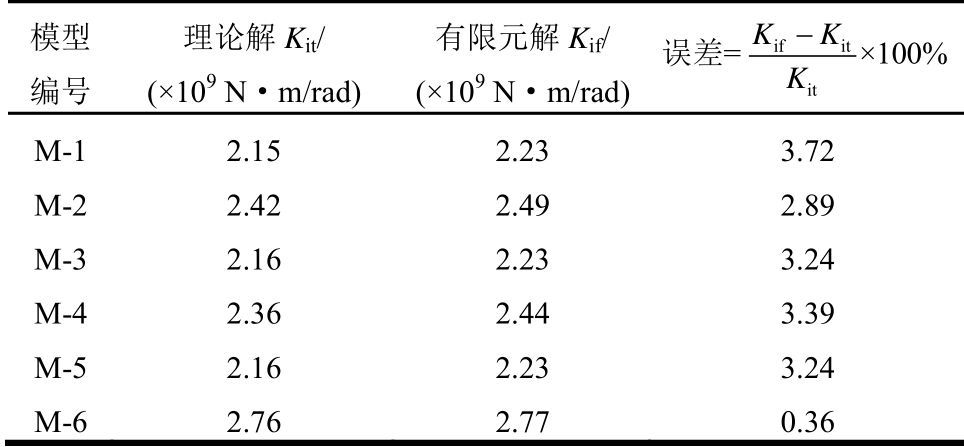
表2 理论值与有限元值对比
Table 2 The theoretical value and the finite element value
模型编号理论解Kit/ (×109 N·m/rad)有限元解Kif/ (×109 N·m/rad)误差=if it it×100%K K K-M-1 2.15 2.23 3.72 M-2 2.42 2.49 2.89 M-3 2.16 2.23 3.24 M-4 2.36 2.44 3.39 M-5 2.16 2.23 3.24 M-6 2.76 2.77 0.36
综上所述,有限元模型在相对误差以及参数敏感性两方面都与理论分析结果保持一致,可以较准确地反映节点受力性能。
4 结论
(1)定义节点域明确了本文研究对象,通过对节点域在外界弯矩作用下力的传力路径进行分析,详细阐述了组成节点域各组件的受力状态。弦杆承受弯矩、轴力和剪力的作用,但由于节点域内弦杆较短,主要发生轴向和剪切变形;PBL剪力键横穿内埋节点板,与内埋节点板协同受力,内埋节点板相对于弦杆的转动变形,主要由PBL剪力键群的变形引起;外露节点板为双向受剪部件,主要发生剪切变形。
(2)采用组件法原理将节点域分成弦杆、PBL剪力键群和外露节点板三个有效力学组件,并提出了弹簧简化模型。
(3)根据经典力学原理,采用合理假设,分别推导出了三个有效力学组件的弹簧刚度表达式,进而组合得出了外接式组合桁架节点的初始转动刚度函数表达式。
(4)建立了节点有限元模型,通过对比不同参数下理论解与有限元解,从以下两个层次验证了模型的有效性以及理论推导的正确性,一是相同参数下,理论值与有限元值的相对误差,二是有限元值的参数敏感性是否同理论分析一致。
(5)该类型节点的初始转动刚度约为2×109 N·m/rad ~ 3×109 N·m/rad,为工程设计提供了具体数值参照。
(6)本论文中对节点初始动刚度的理论推导以及节点有限元模型的建立,为后续此类节点的弯 矩-转角曲线研究奠定了基础。
[1]聂建国.钢-混凝土组合结构桥梁[M].北京: 人民交通出版社, 2011. NIE Jianguo.Steel and concrete composite bridge [M].Beijing: China Communication Press, 2011.(in Chinese)
[2]Fukumoto T.Morita K.Elastoplastic behavior of panel zone in steel beam-to concrete filled tube column moment connection [J]. Journal of Structural Engineering, 2005, 13(7): 1841—1853.
[3]陈志华, 苗纪奎, 赵莉华, 等.方钢管混凝土柱-H钢梁节点研究[J].建筑结构, 2007, 37(1): 50—56.Chen Zhihua, Miao Jikui, Zhao Lihua, et al.Study on joint of concrete-filled rectangular tubular column and h-shaped steel beam [J].Building Structure, 2007, 37(1): 50—56.(in Chinese)
[4]王静峰.竖向荷载作用下半刚性连接组合框架的使用设计方法[D].上海: 同济大学, 2005.Wang Jingfeng.The practical design approach of semi-rigidly connected composite frames under vertical loads [D].Shanghai: Tongji University, 2005.(in Chinese)
[5]刘清平.水平荷载作用下半刚性连接组合框架的使用设计方法[D].上海: 同济大学, 2006.Liu Qingping.The practical design approach of semi-rigidly connected composite frames under lateral loads [D].Shanghai: Tongji University, 2006.(in Chinese)
[6]周凌宇, 贺桂超.2种不同构造形式的钢-混组合桁架节点试验研究[J].铁道科学与工程, 2012, 9(6): 7—12.Zhou Lingyu, He Guichao.Experimental study on steel- concrete composite joints with two kinds of fabrication [J].Journal of Railway Science and Engineering, 2012, 9(6): 7—12.(in Chinese)
[7]李正良, 赵楠, 尤军, 等.角钢塔K形节点弯矩-转角曲线研究[J].四川大学学报, 2013, 45(4): 46—54.Li Zhengliang, Zhao Nan, You Jun, et al.Development of moment-rotation curves of angle steel tower K-joints [J].ournal of Sichuan University (Engineering Science Edition), 2013, 45(4): 46—54.(in Chinese)
[8]张爱林, 孙勇, 刘学春, 等.方钢管混凝土柱-H形钢梁螺栓连接节点受力性能试验研究[J].建筑结构学报, 2017, 38(11): 64—73. Zhang Ailin, Sun Yong, Liu Xuechun, et al.Experimental study on mechanical performance of concrete-filled square steel tubular columns to H-section steel beam bolted connection [J].Journal of Building Structures, 2017, 38(11): 64—73.(in Chinese)
[9]赵根田, 王丽娜, 狄昊.部分包裹混凝土组合柱-钢梁端板连接框架结构抗震性能试验研究[J].建筑结构, 2018, 48(6): 68—75.Zhao Gentian, Wang Lina, Di Hao.Experimental research on frame seismic behavior of the PEC column-steel beam connected by end plate [J].Building Structure, 2018, 48(6): 68—75.(in Chinese)
[10]Monforton G R, Wu T S.Matrix analysis of semi-rigidly connected frames [J].Journal of the Structural Division, 1963, 89(6): 13—24.
[11]Barakat M, Chen W F.Practical analysis of semi-rigid frames [J].Engineering Journal, 1990, 27(2): 54—68.
[12]刘军.外接式钢-混凝土组合桁架节点转动刚度研究[D].长沙: 中南大学, 2014.Liu Jun.The research on rotational stiffness of external steel-concrete composite truss joint [D]Changsha: Central South University, 2014.(in Chinese)
[13]王海波, 杜元涛.钢-混组合桁架节点处PBL剪力键群受力性能研究[J].中国铁道科学, 2016, 37(2): 33—40.Wang Haibo, Du Yuantao.Mechanical behaviors of PBL shear connector group at steel concrete composite truss joints [J].China Railway Science, 2016, 37(2): 33—40.(in Chinese)
[14]Rathbum J C.Elastic properties of riveted connections [J].Transactions of American Society of Civil Engineers, 1936, 101(2): 524—563.
[15]Ronstad K M, Sunramanian C V.Analysis of frames with partial connection rigidity [J].Journal of the Structural Division, 1970, 96(11): 2283—2300.
[16]Frye M J, Morris G A.Analysis of flexibly connected steel frames [J].Canadian Journal of Civil Engineering, 1975, 2(3): 280—291.
[17]Kishi N, Chen W F.Moment-rotation relations of semi-rigid connections with angles [J].Journal of Structural Engineering, 1990, 116(7): 1813—1834.
[18]侯娟, 叶志明, 邹立华.梁柱端板连接节点的初始转动刚度计算模型[J].建筑结构, 2005, 35(2): 37—39.Hou Juan, Ye Zhiming, Zhou lihua.Calculation model of the initial stiffness of beam to column end-plate connections [J].Building Structure, 2005, 35(2): 37—39.(in Chinese)
[19]吴兆旗, 张素梅, 姜绍飞.梁柱端板连接节点初始转动刚度计算模型[J].工程力学, 2009, 26(6): 226—233. Wu Zhaoqi, Zhang Sumei, Jiang Shaofei.Calculation model of initial rotational stiffness of steel beam-to-column bolted end-plate connections [J].Engineering Mechanics, 2009, 26(6): 226—233.(in Chinese)
[20]高婧, 石文龙, 李国强, 等.平端板连接半刚性梁柱组合节点的初始转动刚度[J].工程力学, 2011, 28(3): 55—61.Gao Jing, Shi Wenlong, Li Guoqiang, et al.Initial rotational stiffness of semi-rigid composite beam-to-column joints with flush end plate connections [J].Engineering Mechanics, 2011, 28(3): 55—61.(in Chinese)
[21]王冬花, 王静峰.负弯矩作用下半刚性钢管混凝土组合节点初始刚度计算[J].合肥工业大学学报, 2017, 40(9): 1231—1236.Wang Donghua, Wang Jingfeng.Calculation of initial stiffness of semi-rigid CFST composite joints subjected to negative moment [J].Journal of Hefei University of Technology, 2017, 40(9): 1231—1236.(in Chinese)
[22]施刚, 石永久, 王元清.钢结构梁柱半刚性端板连接弯矩-转角全曲线计算方法[J].工程力学, 2006, 23(5): 67—74.Shi Gang, Shi Yongjiu, Wang Yuanqing.Calculation method on moment-rotation curves of beam-to-column semirigid end-plate connections [J].Engineering Mechanics, 2006, 23(5): 67—74.(in Chinese)
[23]石永久, 施刚, 王元清.钢结构半刚性端板连接弯矩-转角曲线简化计算方法[J].工木工程学报, 2006, 39(3): 19—23.Shi Yongjiu, Shi Gang, Wang Yuanqing.A simplified calculation method for moment-rotation curves of semi-rigid end-plate connections [J].China Civil Engineering Journal, 2006, 39(3): 19—23.(in Chinese)
[24]施刚, 袁峰, 霍达, 等.钢框架梁柱节点转角理论模型和测量计算方法[J].工程力学, 2012, 29(2): 52—60.Shi Gang, Yuan Feng, Huo Da, et al.The theoretical model and measuring calculation method of the beam-to-column joint rotation in steel frames [J].Engineering Mechanics, 2012, 29(2): 52—60.(in Chinese)
[25]陈学森, 施刚, 赵俊林, 等.基于组件法的超大承载力端板连接节点弯矩-转角曲线计算方法[J].工程力学, 2017, 34(5): 30—41. Chen Xueshen, Shi Gang, Zhao Junlin, et al.Calculation of moment-rotation curves of ultra-large capacity end-plate connections based on component method [J].Engineering Mechanics, 2017, 34(5): 30—41.(in Chinese)
[26]赵楠, 李正良, 刘红军.角钢塔K形节点初始转动刚度计算模型[J].工程力学, 2014, 31(4): 93—101.Zhao Nan, Li Zhengliang, Liu Hongjun.Calculation model of initial stiffness of angle steel tower K-joints [J].Engineering Mechanics, 2014, 31(4): 93—101.(in Chinese)
[27]潘伶俐, 陈以一.H形梁柱节点域弹性刚度的修正计算公式[J].工程力学, 2016, 33(11): 68—74, 94. Pan Lingli, Chen Yiyi.Modified formula for calculating elastic stiffness of panel zone in H-shaped beam-column connections [J].Engineering Mechanics, 2016, 33(11): 68—74, 94.(in Chinese)
[28]王振海.埋入式PBL剪力连接件力学特性及承载机理研究[D].成都: 西南交通大学, 2011.Wang Zhenhai.Study on mechanical property and load- bearing mechanism of embedded PBL shear connectors [D].Chengdu: Southwest Jiaotong University, 2011.(in Chinese)