混凝土属于准脆性材料的范畴,以名义强度为代表的宏观力学性能参数的尺寸效应十分明显[1—4]。实际上,混凝土宏观力学性能与其内部细观结构构造密切相关,其中骨料级配和界面特性对其影响尤为显著[5—9]。
骨料级配与配制混凝土采用的最大骨料粒径有关[5—7]。根据我国《水工混凝土配合比设计规程DLT 5330—2015》[10]的相关规定,水工大体积混凝土依据采用的粗骨料粒径范围可分为四个级配,最大粒径可达约150 mm。根据相关文献研究,随着骨料粒径的增加,混凝土宏观力学性能有劣化的趋势[11—20],如:当最大骨料粒径在10 mm~64 mm范围内变化时,抗压强度可减小约10%[11];当最大骨料粒径在20 mm~160 mm范围内变化时,抗拉强度下降可达30%~50%[12]。然而,也有研究表明:混凝土抗压强度随骨料粒径增加亦增大(约12%)[21]。Su和Cheng[22]通过试验总结到:对于抗压强度小于60 MPa的普通混凝土,其抗压强度随最大骨料粒径的增大而减小;对于抗压强度大于80 MPa的高强混凝土,这种骨料效应则几乎消失。对于抗拉强度,Zhang等[23]的试验分析也表明其与混凝土强度等级有关。此外,由于混凝土断裂参数均与最大骨料粒径相关,通过试验方法测得小尺寸试件的断裂参数能否用于大体积混凝土的设计值得商榷[23—31]。因此,混凝土宏观力学性能的尺寸效应行为不仅与其构件截面的尺度相关,与其材料内部细观结构构造(如骨料粒径等)的尺度亦相关[32—34]。即,存在材料层次的尺寸效应行为。文献[35]结合混凝土细观结构形式,将混凝土看作由骨料颗粒、砂浆基质以及界面过渡区组成的三相复合材料,从细观力学的基本理论出发,推导建立了单轴拉伸条件下不同骨料颗粒级配混凝土断裂裂缝扩展路径长度及其单轴抗拉强度的理论表达式,并通过与细观数值模拟结果的对比初步验证了该方法的合理性。
骨料颗粒与砂浆基质之间的界面过渡区对混凝土宏观力学性能亦存在显著影响[8—9,16]。通常认为,界面过渡区是混凝土中相对薄弱的区域,有低密度、高孔隙率的结构特征,对混凝土的强度、变形能力以及耐久性等有重要影响。因此,混凝土宏观力学性能的强弱从很大程度上取决于其界面的力学特性。实际上,骨料的种类、含量、粒径、表面积及其粗糙程度等均对界面特性存在影响。因此,有必要将骨料与界面对混凝土宏观力学性能的影响结合起来,建立一类能够同时考虑骨料级配和界面特性影响的理论预测模型。Elices等[36—38]设计了一组简单混凝土断裂模型,通过细观试验方法探讨了骨料粒径和界面特性对混凝土断裂力学参数影响的一般规律。该模型试验为建立理论预测模型提供了细观参数,并适合通过细观数值试验方法对理论模型中的各项参数进行标定。
鉴于以上分析,本文拟建立一类能够考虑细观组分(以骨料级配和界面特性为例)影响的混凝土宏观力学性能理论预测模型,并就该模型的适用性及合理性展开分析与讨论,为后续基于该理论方法的研究奠定基础。
1 理论预测模型建立
1.1 解析分析
采用与文献[35]相同的理论分析模型及细观组分本构模型,如图1所示。假设骨料颗粒强度较高,在混凝土断裂过程中不发生破裂(这里暂不考虑软骨料夹杂情况),细观裂缝仅在砂浆及界面中扩展。根据文献[35]的推导,对于边长为的二维模型混凝土试件,单轴受拉加载条件下,细观裂缝长度lmeso为:
式中,λ定义为混凝土细观裂缝曲折度指数,并有:
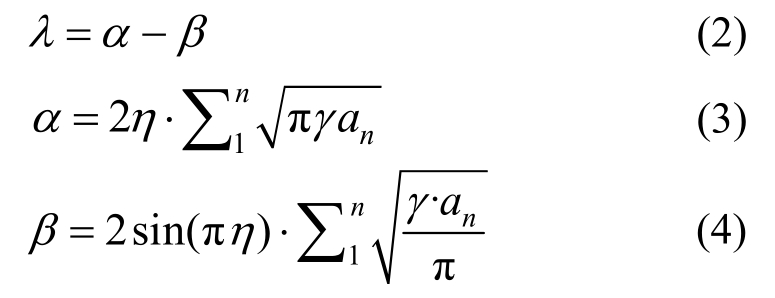
式中:α和β分别为界面裂缝和砂浆裂缝的长度分配系数;γ、n和an为根据我国《水工混凝土配合比设计规程DLT 5330—2015》[10]确定的粗骨料含量、级配和相应级配骨料含量的组合比;η为界面裂缝指数,用于确定界面过渡区中裂缝的长度,根据裂缝扩展路径遵循“最低能量原理”,文献[35]推导得到:
式中: 分别为砂浆基质和界面过渡区的应变能密度;σmo/εu,mo和σITZ/εu,ITZ分别为砂浆基质和界面过渡区的极限应力/极限应变。式(5)表明,通过界面过渡区和砂浆基质二者力学性能的比值就能够确定界面裂缝指数。
分别为砂浆基质和界面过渡区的应变能密度;σmo/εu,mo和σITZ/εu,ITZ分别为砂浆基质和界面过渡区的极限应力/极限应变。式(5)表明,通过界面过渡区和砂浆基质二者力学性能的比值就能够确定界面裂缝指数。
混凝土宏观断裂行为实际上是由其细观组分的断裂引起的,故混凝土宏观断裂能Gf可以表达为:
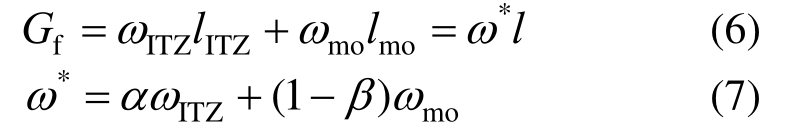
式(7)即为考虑细观组分影响的混凝土应变能密度ω*。这里,混凝土应变能密度由界面过渡区和砂浆基质两部分的贡献组成,并应同时满足条件α>0以及(1-β )>0。则混凝土单轴抗拉强度ft表达式为:

式中,εu为混凝土极限应变。基于本文建立的混凝土单轴受拉细观断裂理论分析模型及其基本假定,从混凝土材料细观断裂过程角度分析,这里认为εu=εu,mo,即当砂浆基质达到其极限应变时认为宏观混凝土完全断裂[35]。
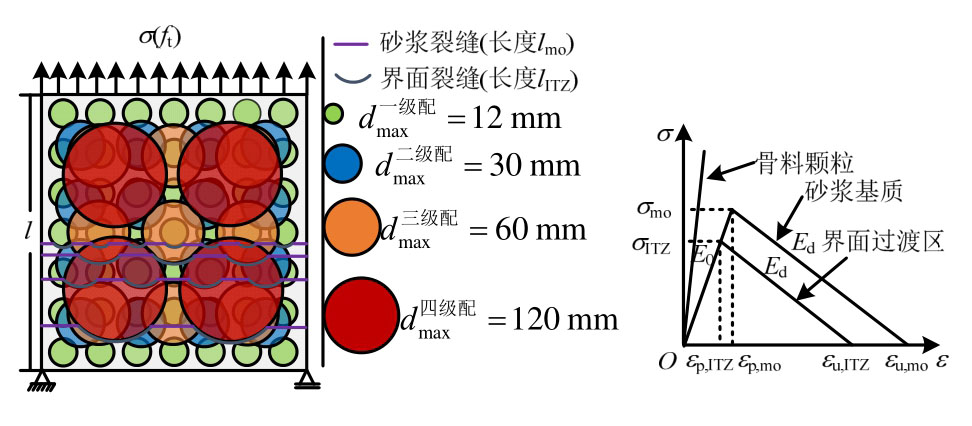
图1 理论分析模型
Fig.1 Theoretical analysis model
1.2 验证及讨论
Elices等[36—38]设计了一组简单的混凝土细观断裂模型,通过试验方法分析了骨料粒径和界面特性对混凝土断裂力学参数的影响。采用文献[36—37]中的试验参数对本文理论模型进行验证,令l=40 mm、γ =0.258、n=1、Gf,mo=52 J/m2、Gf,ITZ-1= 50 J/m2、Gf,ITZ-2=30 J/m2、Gf,ITZ-3=10 J/m2,根据式(5)可以得到,三种不同力学性能的界面过渡区对应的界面裂缝指数分别为:η1=0.088、η2=0.304、η3=0.439。进而,根据式(6)计算得到三种不同界面特性的混凝土宏观断裂能为:Gf,1=51.79 J/m2、Gf,2=44.09 J/m2、Gf,3=30.64 J/m2。图2给出了本文理论解析结果与Elices等[36—37]试验测得的混凝土断裂能Gf随界面裂缝指数η变化趋势的对比,可以发现,建立的理论预测模型能够较好地预测混凝土宏观力学参数随界面特性变化的趋势。
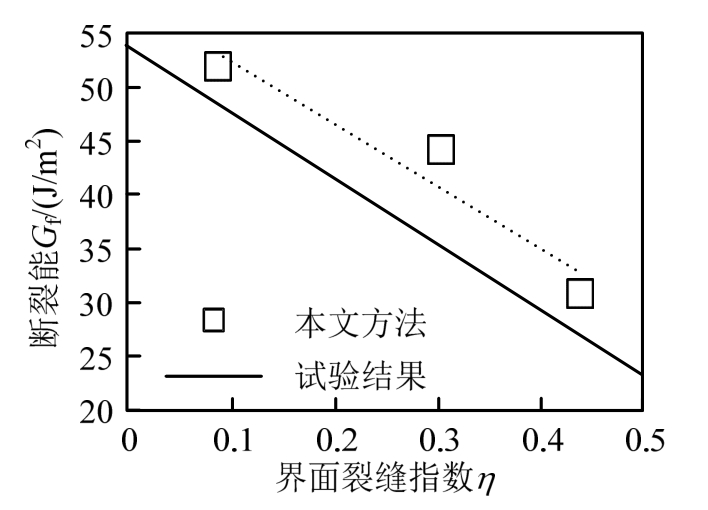
图2 本文理论解析结果与试验结果对比
Fig.2 Comparison of theoretical and experimental results
通过以上分析可以发现,本文理论分析模型能够较好地预测单一级配混凝土材料的宏观力学性能,这是由于基于本文模型的基本假定,对于单一级配混凝土,能够保证式(7)中(1-β )均为正值,如图3中左侧方框区域所示。然而,对于二、三和四级配混凝土,由于在理论解析过程中为方便推导细观裂缝长度进行了相应的假设,即,令不同粒径骨料在二维模型混凝土试件内部规则排列(图1),故而在求解细观裂缝总长度时将使得理论解析值大于实际混凝土中的裂缝长度,并且随着骨料含量和骨料粒径的增大,该问题更加严重。如图3中右侧方框区域所示,对于粗骨料体积分数约为45%的混凝土材料,随着骨料级配n(即最大骨料粒径)以及界面裂缝指数η增加,(1-β )的值逐渐出现在横坐标轴下方(即出现负值),这显然与真实情况不符。
实际上,式(7)中α和(1-β )是具有实际物理含义的参数,均应大于0值。因此,应对长度分配系数α和β进行修正,使其符合真实情况。

图3 本文理论解析方法的固有缺陷
Fig.3 Inherent drawback hidden inside theoretical model
2 细观数值试验及理论模型修正
对理论模型进行修正,最好的方式是通过大量的细观尺度物理试验找出真实的修正系数。但由于物理试验离散性大且细观组分各项力学参数难以准确测量,故而难以开展。随着有限元方法以及高速电子计算平台的发展和普及,使用细观力学数值试验方法研究混凝土内部细观组分对其宏观力学性能的影响已成为当今热点。本文即采用混凝土细观力学数值试验模拟真实的细观尺度物理试验,对建立的考虑细观组分影响的混凝土宏观力学性能理论预测模型进行修正。
2.1 细观力学模型及其验证
图4以二级配混凝土为例给出了本文建立的细观力学模型。将混凝土看作三相复合材料,深灰色区域表示骨料颗粒,灰色区域表示砂浆基质,浅灰色区域表示界面过渡区。根据Walraven公式,基于Monte-Carlo方法对骨料颗粒进行随机投放。考虑到计算量限制,参考文献[39—40],界面厚度设为1.5 mm。采用四节点等参线性单元对混凝土各细观组分进行网格划分,网格平均尺寸1 mm。
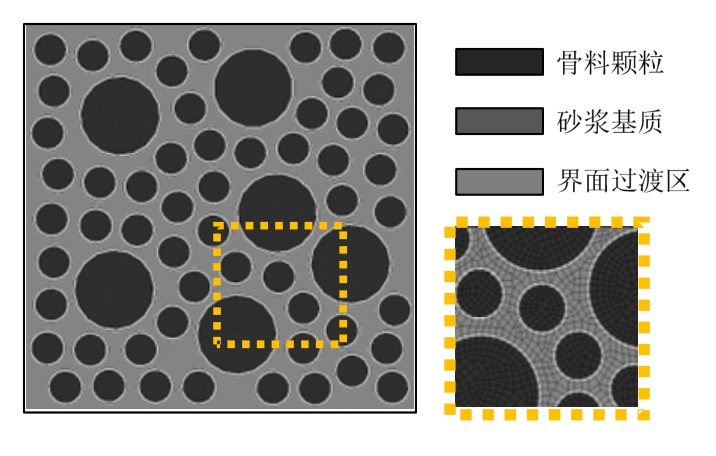
图4 混凝土细观力学模型
Fig.4 Meso-scale mechanical model of concrete
表1给出了建立的不同级配混凝土试件中的骨料数量。尺寸为100 mm×100 mm的三组混凝土试件与文献[38]中使用的试件相同,均为一级配,粗骨料含量为25.8%,骨料平均粒径分别为3 mm、9 mm和14 mm,用以验证本文建立的细观力学模型的合理性。尺寸为450 mm×450 mm的混凝土试件按照我国《水工混凝土配合比设计规程DLT 5330—2015》[10]相关规定,设置粗骨料含量约45%,按照不同骨料粒径配置不同级配混凝土试件,用以模拟真实物理试验,进而对理论模型进行修正。
将骨料颗粒设为弹性体(暂不考虑软骨料夹杂情况),在受力过程中不破坏。需要说明的是,为了使细观试验结果更符合实际混凝土的断裂破坏行为,数值模拟中并未采用与理论模型中相同的双线性本构模型来表征砂浆基质与界面过渡区的力学性能,而是采用塑性损伤本构模型[41],从而模拟真实的物理试验,进而对理论模型中的参数进行修正。此外,由于界面力学性能难以通过试验量测,而界面过渡区实际上是含有较多孔洞或初始缺陷的砂浆基质,因此采用削弱文献[36—38]给定的实测砂浆的力学性能的方式赋予界面相参数。表2给出了混凝土材料中各细观组分的物理/力学参数,其中定义一个控制参数κ,对界面过渡区的力学性能进行调整。根据本文模型的基本假定,容易得到:
表1 不同级配混凝土中骨料数量
Table 1 Numbers of aggregates in multi-graded concrete
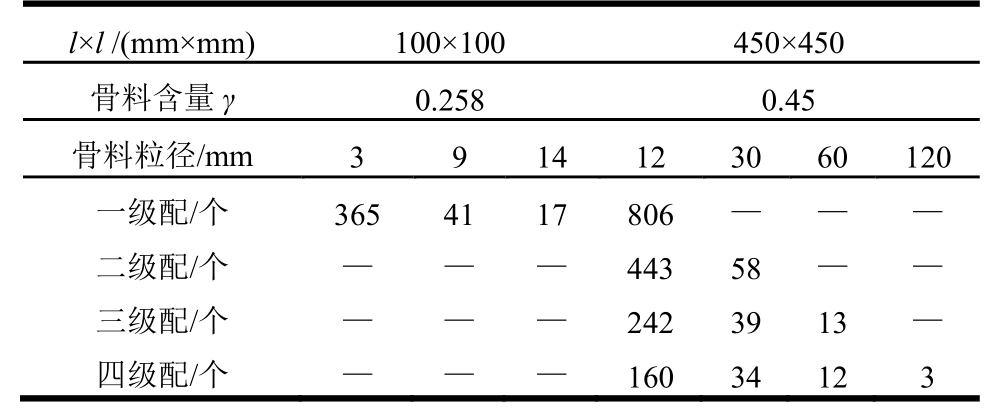
l×l /(mm×mm) 100×100 450×450 骨料含量γ 0.258 0.45 骨料粒径/mm 3 9 14 12 30 60 120一级配/个 365 41 17 806 — —— 二级配/个 — —— 443 58 —— 三级配/个 — —— 242 39 13— 四级配/个 — —— 160 34 12 3
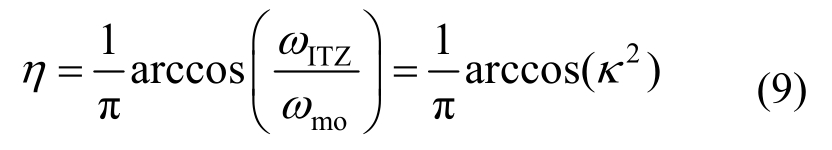
则
表2 细观组分力学参数[36-38]
Table 2 Mechanical parameters of meso-scale components[36-38]
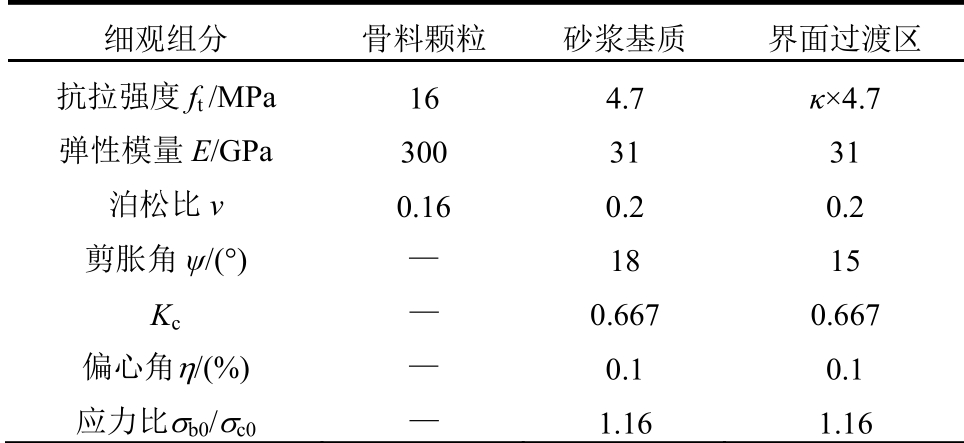
细观组分 骨料颗粒 砂浆基质 界面过渡区 抗拉强度ft /MPa 16 4.7 κ×4.7 弹性模量E/GPa 300 31 31 泊松比ν 0.16 0.2 0.2 剪胀角ψ/(°) — 18 15 Kc— 0.667 0.667 偏心角η/(%) — 0.1 0.1 应力比σb0/σc0— 1.16 1.16
图5给出了尺寸为100 mm×100 mm的三组混凝土试件的数值模拟结果(κ=0.76,η=0.304[38])。从图中可以看到,骨料粒径越大,细观裂缝越曲折,并且其峰值强度(均值)有减小的趋势。
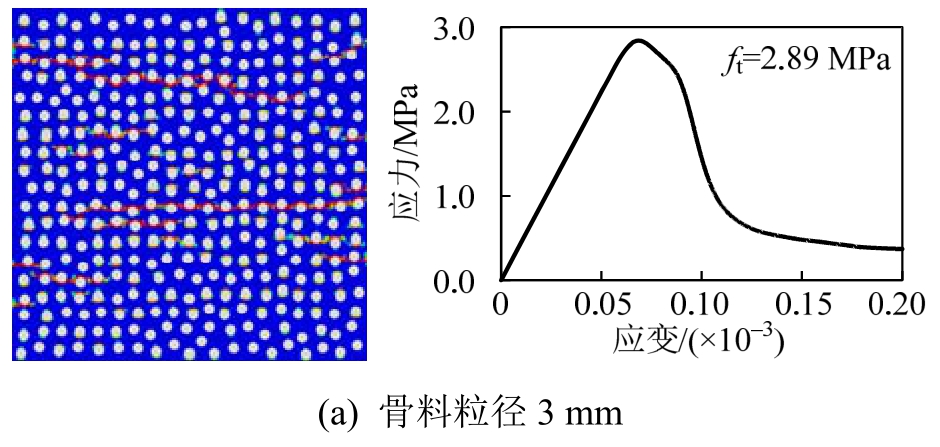
图5 100 mm×100 mm混凝土试件数值模拟结果
Fig.5 Numerical test results of concrete specimens of 100 mm×100 mm
图6给出了试验结果与数值结果的对比。需要说明的是,由于本文数值模型采用的是2D平面模型进行单轴受拉加载,而文献[38]则是对立方体试件(3D)进行劈裂抗拉试验,因此结果存在一定差异,但试验结果与数值结果的对比曲线处于两条平行线上,其变化趋势一致,因此表明本文建立的细观数值模型是合理的。
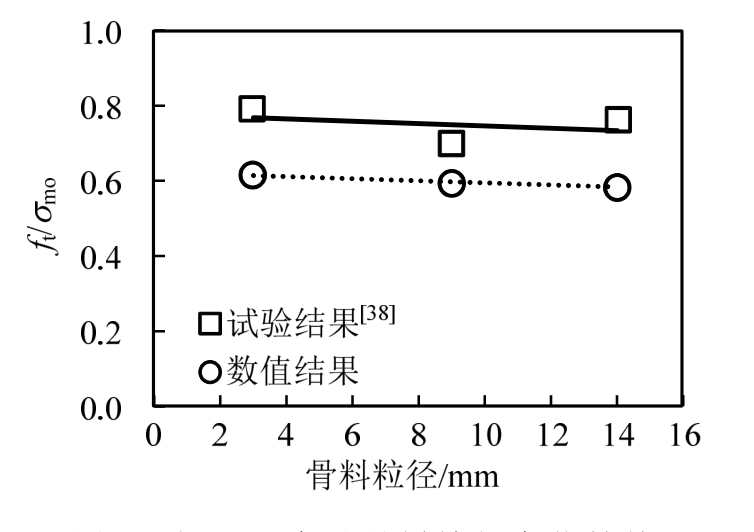
图6 相对强度随骨料粒径变化趋势
Fig.6 Variation of relative strength with aggregate size
2.2 不同级配混凝土单轴抗拉数值试验
使用尺寸为450 mm×450 mm的不同级配混凝土试件,进行单轴抗拉数值试验,并且令控制参数κ =0.2、0.4、0.6和0.8,对应界面裂缝指数η =0.488、0.449、0.383和0.279。以二、四级配为例,图7给出了二维模型混凝土试件的最终破坏模式,可以看到,随着骨料级配n(即最大骨料粒径)的增加和界面裂缝指数η的增大,细观裂缝更加曲折。此外,当界面过渡区较强时(κ =0.8),细观裂缝集中在较窄的带中发展,当界面过渡区较弱时(κ =0.4),细观裂缝则在较大范围内发展。

图7 单轴拉伸条件下不同级配混凝土破坏模式
Fig.7 Failure patterns of multi-graded concrete in direct tension
图8给出了二维模型混凝土试件的单轴抗拉强度随骨料级配和界面特性的变化趋势,从数值解和理论解的对比可以发现:对于一级配混凝土,理论模型预测值较为符合实际,如左侧方框区域所示;对于二、三和四级配混凝土,理论模型的预测值则出现了不真实的负值,如右侧方框区域所示。因此,需要根据数值试验结果对理论模型进行修正。

图8 单轴抗拉强度随骨料级配和界面特性变化趋势
Fig.8 Trends of uniaxial tensile strength with aggregate gradation and aggregate-matrix interface
2.3 理论模型修正
基于以上分析可知,应分别对各个级配混凝土理论计算公式中的长度分配系数α和β进行修正。图9给出了数值试验得到的不同级配混凝土单轴抗拉强度随界面裂缝指数的变化关系,并描绘出了界面裂缝指数η在0~0.5之间变化时的拟合曲线。根据拟合公式,计算出分别对应η =0(即ωITZ=ωmo,界面过渡区性能与砂浆性能相同)和η =0.5(即ωITZ=0,在加载之前界面过渡区与骨料已分离)时的混凝土单轴抗拉强度值,如图9中拟合曲线两端数值所示。使用本文式(7)和式(8)进行修正系数的标定,则有:
式中:根据文献[36—38]以及本文模型的基本假定取εu=0.0006,ωmo=1410 N/m2,η =0时,ω ITZ=1410 N/m2,η =0.5时,ωITZ=0。根据式(3)和式(4),可以得到不同级配混凝土长度分配系数α和β在η =0.5时的取值(η =0时,α=β=0),如表3所示。
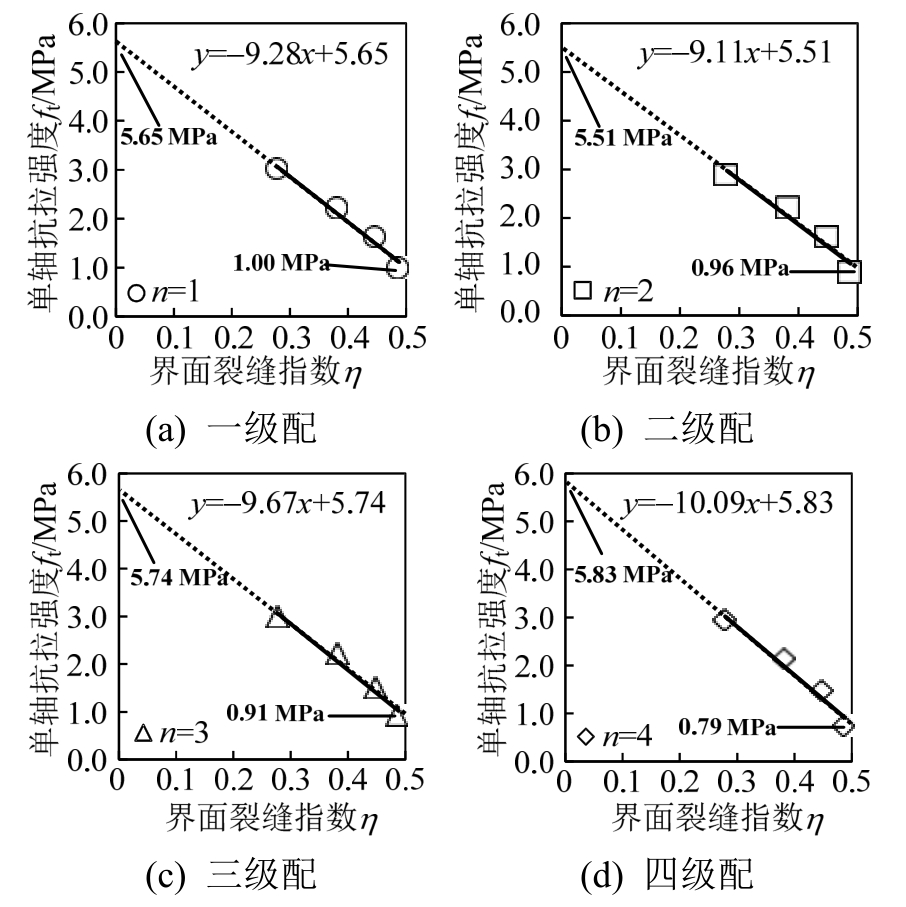
图9 单轴抗拉强度随界面裂缝指数变化趋势
Fig.9 Trend of uniaxial tensile strength with aggregate-matrix interface
表3 不同级配混凝土长度分配系数(η=0.5)
Table 3 Partition coefficients for differently-graded concrete(η=0.5)

骨料级配n 1 2 3 4 α 1.19 1.68 2.05 2.37 β 0.76 1.07 1.31 1.51
基于上述线性拟合分析,可以给出各个级配混凝土在η=0和η=0.5时的理论计算公式如下:
一级配混凝土:
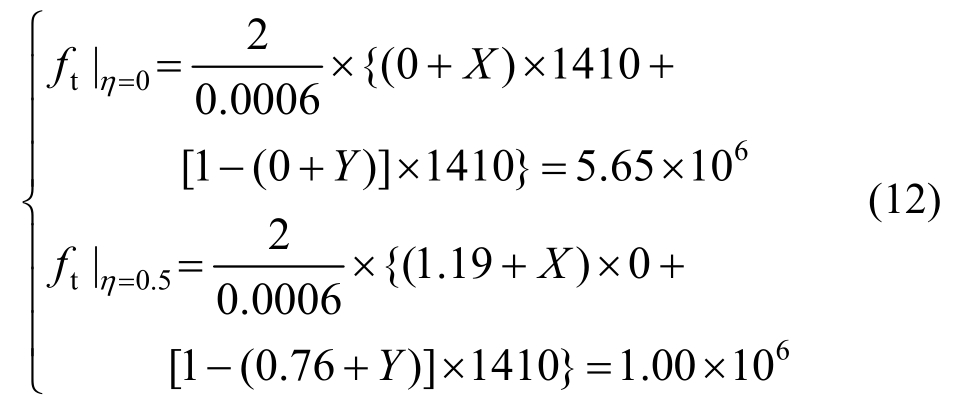
二级配混凝土:
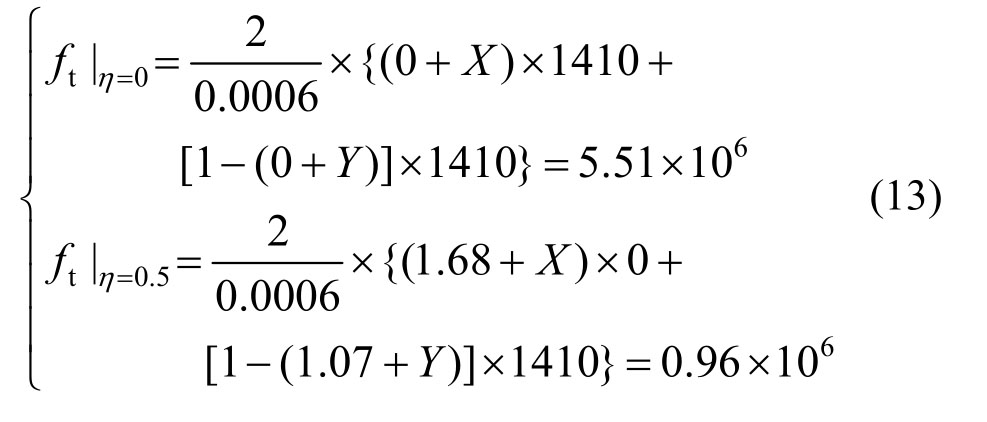
三级配混凝土:
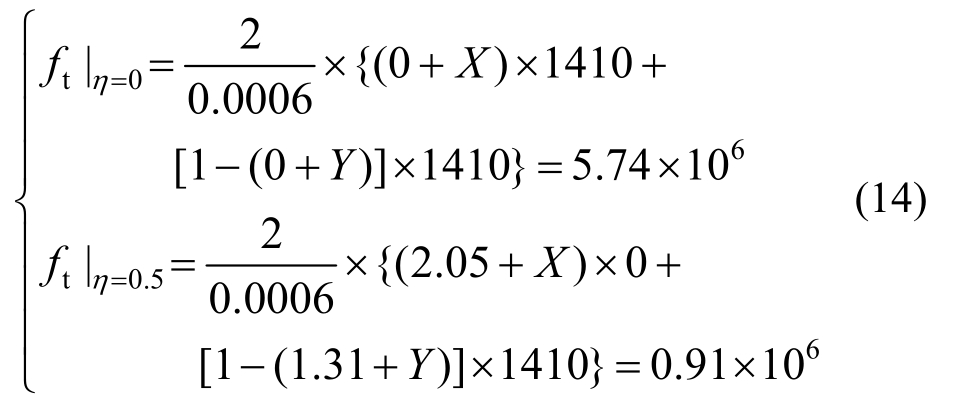
四级配混凝土:
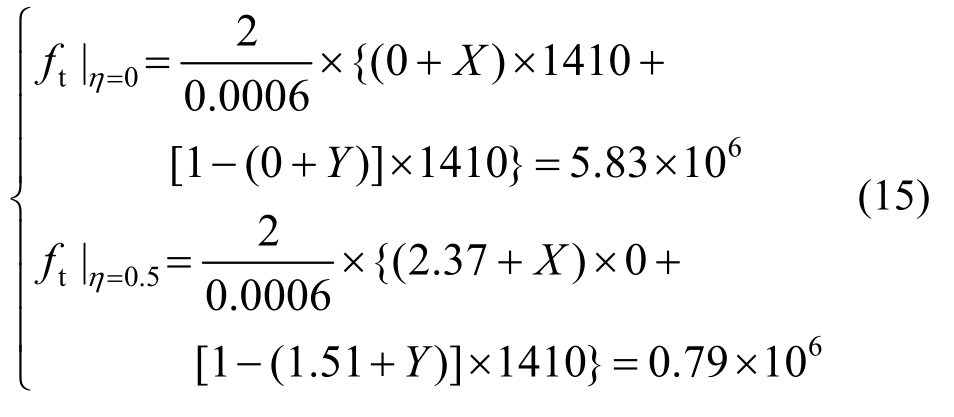
表4给出了基于式(12)~式(15)计算得到的长度分配系数α和β的修正系数,从表中可以看到,随着骨料级配的增大,修正幅度亦增大,与上文分析一致。
表4 不同级配混凝土修正系数
Table 4 Correction factors for differently-graded concrete

骨料级配n 1 2 3 4 X 0.229 -0.102 -0.283 -0.438 Y 0.027 -0.274 -0.504 -0.678
3 材料层次尺寸效应分析
基于修正的考虑细观组分影响的混凝土宏观力学性能理论预测模型,图10给出了单轴拉伸加载条件下混凝土断裂能和单轴抗拉强度随骨料级配的变化趋势。从图中可以看到,混凝土断裂能和单轴抗拉强度均随骨料级配(即最大骨料粒径)发生变化,并且受到界面特性的影响。
当界面过渡区力学性能相对薄弱时(0<κ<0.4),混凝土单轴抗拉强度约1 MPa~3 MPa,混凝土强度较低(普通混凝土),断裂能和单轴抗拉强度随骨料级配增大而呈现减小的趋势,这与石建光等[5]、杜敏等[6—7]、Akçaoğlu等[16]、Uddin等[20]、Zhang等[23]的试验结果一致。
当界面过渡区力学性能较强时(0.4<κ<1),混凝土单轴抗拉强度约3 MPa~6 MPa,混凝土强度较高(高强混凝土),断裂能和单轴抗拉强度随骨料级配增大亦呈现增大的趋势,这与Zhang等[23]、Tasdemir等[25]、Wu等[26]、Rao和Prasad [27]、Chen和Liu [29]、Ohno等[30]的试验结果一致。
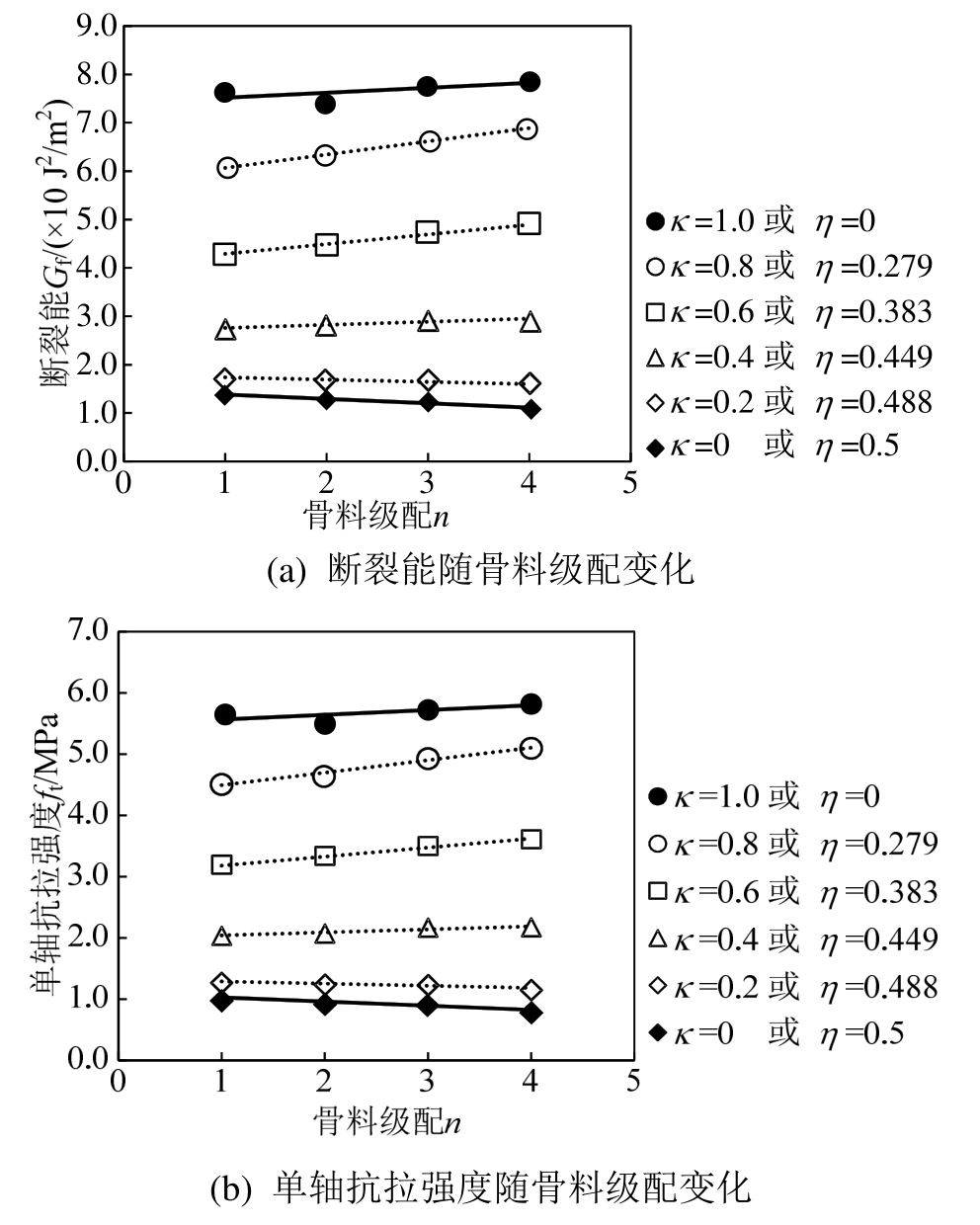
图10 混凝土宏观力学性能随骨料级配的变化趋势
Fig.10 Trend of macroscopic mechanical properties of concrete with aggregate gradation
根据阮征等[18]对混凝土强度的细观机理分析,对于混凝土材料而言,骨料的加入会降低水泥基材料的强度,并且混凝土的强度小于相同配比条件下的砂浆。此外,骨料对界面过渡区的粘结性能也存在影响[8—9,19,42]。实际上,骨料的加入会显著影响混凝土材料的均匀性,并且随着骨料含量、粒径等增加,其非均质性亦显著提高,从而造成混凝土力学性能的劣化。然而,界面的特性对于混凝土宏观力学性能的影响也非常显著。界面过渡区的力学性能越强,混凝土材料均匀性越好,混凝土强度也越高,即界面特性的提高又可使得混凝土材料的非均质性降低。因此,骨料粒径(级配)和界面特性对混凝土材料宏观力学性能的影响是相对的,在不同骨料级配和不同界面力学性能组合情况下混凝土宏观力学参数也呈现出不同的变化趋势。
基于上述分析可知,针对混凝土材料层次的尺寸效应行为,应根据不同强度等级分开考虑,本文建立的考虑细观组分影响的混凝土宏观力学性能理论预测模型以及大量试验研究[5—7,11—31]均证实了这一点。
4 结论
本文建立了一类能够考虑细观组分(以骨料级配和界面特性为例)影响的混凝土宏观力学性能理论预测模型。首先,采用细观力学数值试验法对理论模型中的参数进行了标定;进而,基于该模型对混凝土断裂能和单轴抗拉强度在材料层次的尺寸效应行为进行了分析。结果表明:
混凝土断裂能和单轴抗拉强度均随骨料级配(即最大骨料粒径)发生变化,且受到界面特性的影响。当界面过渡区力学性能相对薄弱时,混凝土强度较低,断裂能和单轴抗拉强度随骨料级配增大而呈现减小的趋势;当界面过渡区力学性能较强时,混凝土强度较高,断裂能和单轴抗拉强度随骨料级配增大亦呈现增大的趋势。因此,对于混凝土材料层次的尺寸效应行为分析,应根据不同强度等级分开考虑。
本文建立的考虑细观组分影响的混凝土宏观力学性能理论预测模型,为后续基于该理论方法的研究奠定了基础,如对于构件层次尺寸效应行为的研究,均应在明确材料层次尺寸效应行为基础上进行。此外,针对软骨料夹杂的情况,即在加载过程中出现的骨料破裂等现象,作者将另文探讨。
[1]Bažant Z P, Planas J.Fracture and size effect in concrete and other quasibrittle materials [M].New York: CRC press, 1998, 7—15.
[2]刘兴阳, 邹德高, 李占超.混凝土名义强度的尺寸效应研究[J].建筑材料学报, 2017, 20(5): 680—684.Liu Xingyang, Zou Degao, Li Zhanchao.Study on size effect of concrete nominal strength [J].Journal of Building Materials, 2017, 20(5): 680—684.(in Chinese)
[3]杜修力, 金浏, 李冬.混凝土与混凝土结构尺寸效应述评(Ⅰ):材料层次[J].土木工程学报, 2017, 50(9): 28—45.Du Xiuli, Jin Liu, Li Dong.A state-of-the-art review on the size effect of concretes and concrete structures (Ⅰ): Concrete materials [J].China Civil Engineering Journal, 2017, 50(9): 28—45.(in Chinese)
[4]杜修力, 金浏, 李冬.混凝土与混凝土结构尺寸效应述评(Ⅱ):构件层次[J].土木工程学报, 2017, 50(11): 24—44.Du Xiuli, Jin Liu, Li Dong.A state-of-the-art review on the size effect of concretes and concrete structures (Ⅱ): RC members [J].China Civil Engineering Journal, 2017, 50(11): 24—44.(in Chinese)
[5]石建光, 许岳周, 叶志明.骨料级配对混凝土性能影响的细观分析[J].工程力学, 2009, 26(4): 134—138.Shi Jianguang, Xu Yuezhou, Ye Zhiming.Mesoanalysis of concrete behavior due to effect of aggregate gradation [J].Engineering Mechanics, 2009, 26(4): 134—138.(in Chinese)
[6]杜敏, 金浏, 李冬, 等.粗骨料粒径对混凝土弯拉强度尺寸效应影响的试验研究[J].北京工业大学学报, 2016, 42(6): 912—918.Du Min, Jin Liu, Li Dong, et al.Experimental study of the influence of coarse aggregate size on the size effect of concrete flexural strength [J].Journal of Beijing University of Technology, 2016, 42(6): 912—918.(in Chinese)
[7]杜敏, 金浏, 李冬, 等.骨料粒径对混凝土劈拉性能及尺寸效应影响的细观数值研究[J].工程力学, 2017, 34(9): 54—63.Du Min, Jin Liu, Li Dong, et al.Mesoscopic simulation study of the influence of aggregate size on mechanical properties and specimen size effect of concrete subjected to splitting tensile loading [J].Engineering Mechanics, 2017, 34(9): 54—63.(in Chinese)
[8]Scrivener K L, Crumbie A K, Laugesen P.The interfacial transition zone (ITZ)between cement paste and aggregate in concrete [J].Interface Science, 2004, 12(4): 411—421.
[9]董芸, 杨华全, 张亮, 等.骨料界面特性对混凝土力学性能的影响[J].建筑材料学报, 2014, 17(4): 598—605.Dong Yun, Yang Quanhua, Zhang Liang, et al.Effects of aggregate interface characteristics on the mechanical property of concrete [J].Journal of Building Materials, 2014, 17(4): 598—605.
[10]DL/T 5330—2015, 水工混凝土配合比设计规程[S].北京: 中国电力出版社, 2015.DL/T 5330—2015, Code for mix design of hydraulic concrete [S].Beijing: China Electric Power Press, 2015.(in Chinese)
[11]Hughes B P, Chapman G P.The deformation of concrete and micro-concrete in compression and tension with particular reference to aggregate size [J].Magazine Concrete Research, 1966, 18(54): 19—24.
[12]Thomas T C, Slate F O.Tensile bond strength between aggregate and cement paste or mortar [C].ACI Journal Proceedings, 1963, 60(4): 465—486.
[13]Tsiskreli G D, Dzhavakhidze A N.The effect of aggregate size on strength and deformation of concrete [J].Hydrotechnical Construction, 1970, 4(5): 448—453.
[14]Saouma V E, Broz J J, Brühwiler E, et al.Effect of aggregate and specimen size on fracture properties of dam concrete [J].Journal of Materials in Civil Engineering, 1991, 3(3): 204—218.
[15]Deng Z, Li Q.Effect of aggregate type on mechanical behavior of dam concrete [J].ACI Materials Journal, 2004, 101(6): 483—492.
[16]Akçaoğlu T, Tokyay M, Çelik T.Effect of coarse aggregate size and matrix quality on ITZ and failure behavior of concrete under uniaxial compression [J].Cement and Concrete Composites, 2004, 26(6): 633—638.
[17]苏捷, 方志.不同骨料组分混凝土立方体抗压强度尺寸效应试验研究[J].建筑结构学报, 2014, 35(2): 152—157.Su Jie, Fang Zhi.Experimental study on impact of aggregate mixture on dimensional effect of concrete cubic compressive strength [J].Journal of Building Structures, 2014, 35(2): 152—157.(in Chinese)
[18]阮征, 陈力, 洪建, 等.骨料和砂浆等影响混凝土强度的细观层次机理分析[J].建筑材料学报, 2014, 17(6): 952—958.Ruan Zheng, Chen Li, Hong Jian, et al.Mesoscopic analysis on the mechanism of effects of aggregate and mortar on concrete strength [J].Journal of Building Materials, 2014, 17(6): 952—958.(in Chinese)
[19]周尚志, 谌林, 刘明群.骨料对混凝土力学性能的影响分析[J].建筑材料学报, 2016, 19(1): 143—148.Zhou Shangzhi, Zhan Lin, Liu Mingqun.Analysis on effect of aggragate on mechanical property of concrete [J]Journal of Building Materials, 2016, 19(1): 143—148.(in Chinese)
[20]Uddin M T, Mahmood A H, Kamal M R I, et al.Effects of maximum size of brick aggregate on properties of concrete [J].Construction and Building Materials, 2017, 134: 713—726.
[21]Meddah M S, Zitouni S, Belâabes S.Effect of content and particle size distribution of coarse aggregate on the compressive strength of concrete [J].Construction and Building Materials, 2010, 24(4): 505—512.
[22]Su R K L, Cheng B.The effect of coarse aggregate size on the stress-strain curves of concrete under uniaxial compression [J].Hkie Transactions, 2008, 15(3): 33—39.
[23]Zhang J, Liu Q, Wang L.Effect of coarse aggregate size on stress crack opening relationship in normal and high strength concrete [J].Journal of Materials Science and Technology, 2005, 21(5): 691—700.
[24]Petersson P E.Fracture energy of concrete: Practical performance and experimental results [J].Cement and Concrete Research, 1980, 10(1): 91—101.
[25]Tasdemir C, Tasdemir M A, Lydon F D, et al.Effects of silica fume and aggregate size on the brittleness of concrete [J].Cement and Concrete Research, 1996, 26(1): 63—68.
[26]Wu K, Chen B, Yao W.Study of the influence of aggregate size distribution on mechanical properties of concrete by acoustic emission technique [J].Cement and Concrete Research, 2001, 31(6): 919—923.
[27]Rao G A, Prasad B K.Fracture energy and softening behavior of high-strength concrete [J].Cement and Concrete Research, 2002, 32(2): 247—252.
[28]Wu K R, Yan A, Yao W, et al.The influence of RPCA on the strength and fracture toughness of HPC [J].Cement and Concrete Research, 2002, 32(3): 351—355.
[29]Chen B, Liu J.Effect of aggregate on the fracture behavior of high strength concrete [J].Construction and Building Materials, 2004, 18(8): 585—590.
[30]Ohno K, Uji K, Ueno A, et al.Fracture process zone in notched concrete beam under three-point bending by acoustic emission [J].Construction and Building Materials, 2014, 67(6): 139—145.
[31]管俊峰, 李庆斌, 吴智敏, 等.确定现场浇筑全级配水工混凝土双K断裂参数的最小试件尺寸[J].应用基础与工程科学学报, 2016, 24(6): 1219—1231.Guan Junfeng, Li Qingbin, Wu Zhimin, et al.Determination of minimum size for double K fracture parameters of site-casting fully-graded hydraulic concrete [J].Journal of Basic Science and Engineering, 2016, 24(6): 1219—1231.(in Chinese)
[32]Bažant Z P.Size effect in blunt fracture: concrete, rock, metal [J].ASCE Journal of Engineering Mechanics, 1984, 110(4): 518—535.
[33]Carpinteri A, Cornetti P, Puzzi S.A stereological analysis of aggregate grading and size effect on concrete tensile strength [J].International Journal of Fracture, 2004, 128(1-4): 233—242.
[34]管俊峰, 王强, Hu Xiaozhi, 等.考虑骨料尺寸的混凝土岩石边界效应断裂模型[J].工程力学, 2017, 34(12): 22—30.Guan Junfeng, Wang Qiang, Hu Xiaozhi, et al.Boundary effect fracture model for concrete and granite considering aggregate size [J].Engineering Mechanics, 2017, 34(12): 22—30.(in Chinese)
[35]李冬, 金浏, 杜修力, 等.骨料级配对二维模型混凝土单轴抗拉强度影响的理论研究[J].工程力学, 2017, 34(6): 64—72.Li Dong, Jin Liu, Du Xiuli, et al.A theoretical study on the influence of aggregate gradation on the tensile strength of 2-dimensional model concrete [J].Engineering Mechanics, 2017, 34(6): 64—72.(in Chinese)
[36]Rosselló C, Elices M.Fracture of model concrete: 1.Types of fracture and crack path [J].Cement and Concrete Research, 2004, 34(8): 1441—1450.
[37]Rosselló C, Elices M, Guinea G V.Fracture of model concrete: 2.Fracture energy and characteristic length [J].Cement and Concrete Research, 2006, 36(7): 1345—1353.
[38]Elices M, Rocco C G.Effect of aggregate size on the fracture and mechanical properties of a simple concrete [J].Engineering Fracture Mechanics, 2008, 75(13): 3839—3851.
[39]Unger J F, Eckardt S.Multiscale modeling of concrete [J].Archives of Computational Methods in Engineering, 2011, 18(3): 341.
[40]Song Z, Lu Y.Mesoscopic analysis of concrete under excessively high strain rate compression and implications on interpretation of test data [J].International Journal of Impact Engineering, 2008, 35(6): 41—55.
[41]Lee J, Fenves G L.Plastic-damage model for cyclic loading of concrete structures [J].Journal of Engineering Mechanics, 1998, 124(8): 892—900.
[42]周甲佳, 潘金龙, 梁坚凝, 等.尺寸效应对水泥净浆与粗骨料界面黏结性能的影响[J].建筑材料学报, 2012, 15(5): 712—716.Zhou Jiajia, Pan Jinlong, Liang Jianning, et al.Influence of size effect on bonding performance between coarse aggregate and cement paste [J].Journal of Building Materials, 2012, 15(5): 712—716.(in Chinese)