隧道穿越复杂地层施工时，为了维持隧道围岩稳定，锚杆、锚索支护得到了广泛应用。现有研究表明，锚杆、锚索支护可有效改善隧道围岩的受力状态，控制围岩变形能力较强，且适用于多种工程地质条件，其应用前景十分可观[1]，而正确地设计和应用锚杆、锚索支护，必须对其作用机理有清楚的认识。
基于支护-围岩相互作用的理念，国内外学者对于锚杆支护作用机理进行了诸多研究。Stille等[2]提出了全长粘结锚杆的解析模型，并分析了锚杆对理想弹塑性围岩应力和位移的影响；Fahimifar等[3]假定锚杆为理想弹塑性材料，对无限长锚杆与围岩的相互作用进行了解析；李大伟和侯朝炯[4]将锚杆对围岩的支护作用描述为锚杆两端对围岩施加的两组夹紧力，对应变软化围岩锚杆支护作用进行了弹塑性解析。
上述研究成果对于理解锚杆与岩体的相互作用关系具有重要意义，然而这些研究主要侧重于锚杆对围岩的力学作用，而忽略了隧道围岩本身的结构性，且未考虑锚杆与围岩结构的相对位置关系，具有一定局限性。大量研究表明[5—7]，隧道围岩变形破坏具有明显的渐进性和阶段性，围岩内部结构的存在已被人们广泛接受，因此，上述研究不能很好地体现隧道围岩的渐进破坏行为对锚杆支护作用及受力特性的影响，对于锚杆的支护效果和支护机理仍不能定量解释和正确评价。
随着预应力锚固技术的发展，锚杆-锚索组合支护理论和技术也得到极大地推广应用，但对其协同作用原理和评价方法尚处于探索阶段，缺乏系统完整的认识，因此也给隧道支护设计带来困难。
本文基于隧道围岩的结构性特点，阐明了锚杆支护的作用机理及其作用本质，分析了锚杆与隧道围岩结构可能的相对位置关系，由此建立了锚杆-围岩相互作用模型，对其全过程进行了解析，在此基础上建立了锚固体系协同作用模型，提出了隧道锚固体系设计方法及评价体系，并对隧道锚固体系的参数匹配效应进行了分析，对于锚固体系协同作用机制给出了全面、深入的研究与最新的认识。
1 锚固体系对隧道围岩的作用机理
在现行的隧道设计规范中，主要依靠工程经验确定锚固体系支护参数，以致其应用效果较差，究其原因就是对围岩的结构性认识不足，对于锚固体系与围岩的作用机理缺乏系统的认识。因此，要明确锚固体系作用机理，首先必须对围岩结构性有清楚的认识。
1.1 隧道围岩复合结构特性
天然岩体受开挖扰动后，伴随着应力释放，围岩变形破坏呈现出显著的结构性特点。靠近隧道临空面一定范围内的围岩应力集中程度较高，稳定性较差，无法实现长期自稳，这部分围岩可划分为浅层围岩；在此范围以外的围岩整体稳定性较好，承载能力较强，称为深层围岩，如图1所示。
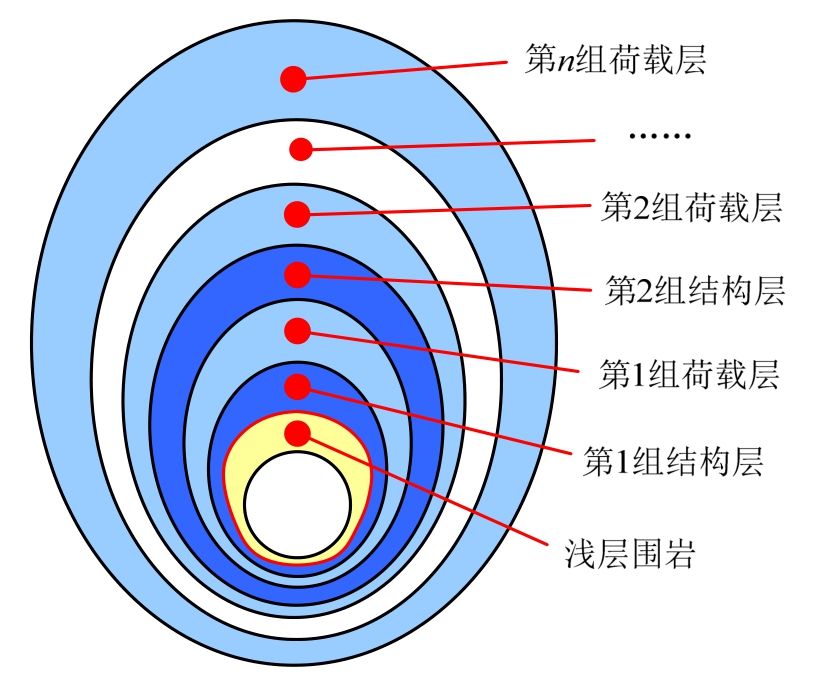
图1 围岩复合结构示意图
Fig.1 Schematic of surrounding rock compound structure
隧道围岩渐进破坏的阶段性特征和压力拱动态发展现象表明了围岩变形和破坏的分组性特点，作为天然地质材料，围岩应力传递和位移释放的时效性及地层材料的结构性决定了深层围岩的分组特性，每组深层围岩近乎同时失稳。而长期地质作用下每组岩层中靠近隧道内侧的岩层力学性能和稳定性一般优于外侧，因此可将内侧具有一定承载能力的围岩划分为“结构层”，外层则作为载荷体而存在，称之为“荷载层”，可见，每组深层围岩均由“荷载层”和“结构层”组成[8]。
1.2 锚固体系与围岩作用力学机理
隧道施工打破了岩体的原有平衡状态，受扰动岩体为寻求新的平衡而向开挖临空面内发生变形，当其无法自行平衡时则需要施作隧道支护[9]。隧道支护作用的本质是“调动”和“协助”围岩承载[10]，即承担施工引起的围岩附加荷载。
与喷射混凝土、钢架等作用于隧道表面的支护形式不同，锚杆、锚索深入围岩内部，既可约束深层围岩变形的发展，又可加固浅层围岩，控制浅层围岩的扩展，其作用原理具体如下：
1)锚固体系通过在浅层围岩中形成“组合梁”或“压缩拱”作用，提高围岩力学参数，从而改善围岩整体力学性能，延长其自稳时间，此即为调动围岩承载的第1层内涵。
2)锚固体系将浅层围岩与深层围岩有机结合，通过调动深层围岩承载进一步改善浅层围岩的应力状态，充分发挥围岩内在抗力，此即为调动围岩承载的第2层内涵。
3)锚固体系与围岩相互作用使得浅层围岩挤密压实，在隧道洞周形成压力拱效应，从而降低了浅层围岩所受荷载，防止浅层围岩承担过大荷载而失稳，由此实现了锚固体系协助围岩承载功能。
综上可见，锚固体系兼有“调动”和“协助”围岩承载的双重作用，既充分调动了围岩的自承能力，又协助围岩承担其自身无法承担的部分荷载，与围岩实现共同承载，从而增强了围岩稳定性。
2 锚杆-围岩相互作用全过程解析
传统的支护-围岩相互作用分析只能对支护结构与围岩力学行为独立时进行解答，而锚杆深入岩体内部，其与围岩接触面上每一点的应力状态均不相同，而是取决于该点的围岩变形，因此以往的支护-围岩相互作用模型仅适用于表面支护形式，而无法适用于锚杆设计[11]。锚固体系与围岩的相互作用是研究其协同作用的前提，因此，需要对锚杆-围岩相互作用全过程进行准确描述并对其解析，为确定锚杆支护的优化方案提供理论依据。
2.1 隧道围岩分析模型
研究表明，作为隧道围岩的大部分岩土材料通常表现为应变软化行为[12]，可运用弹性-塑性软化-塑性残余三线性应力-应变模型进行描述，如图2所示[13]。图2中，h、f分别为软化区和破碎区的扩容系数；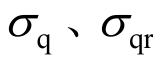
分别为岩体峰值强度和残余强度；
分别为峰值强度和开始进入残余强度时对应的应变值。
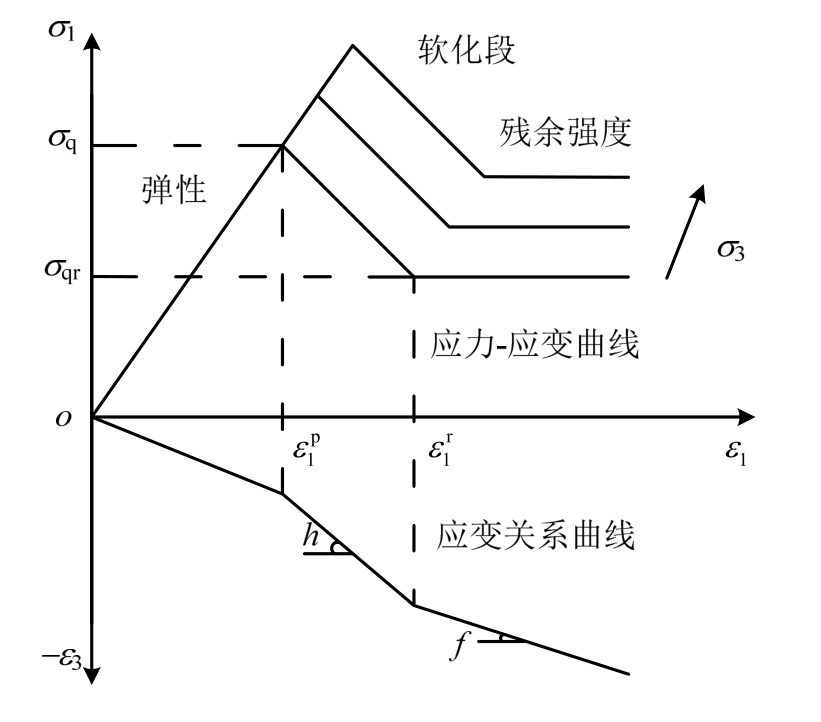
图2 隧道围岩本构模型
Fig.2 Tunnel surrounding rock constitutive model
由图2可知，岩土在弹性阶段服从胡克定律，在塑性软化阶段围岩强度随着应变增加而降低直至达到残余强度，对于此三线性应力-应变模型，本构关系表达式为：
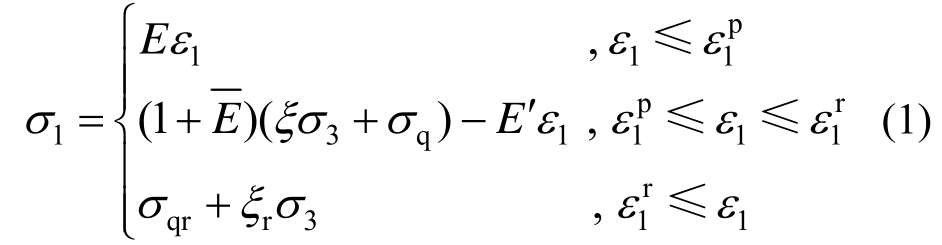
式中：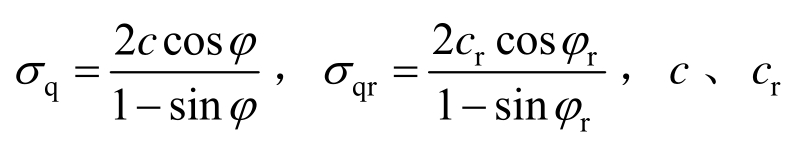
分别为岩体软化阶段和残余阶段的统一黏聚力，φ、φr分别为岩体软化阶段和残余阶段的统一内摩擦角；ξ、ξr为与岩体力学参数有关的常数，且有
为岩体软化模量E′与弹性模量E的比值。
由前述深浅层围岩物理概念可知，围岩破碎区稳定性较差，可划分为浅层围岩，破碎区以外的岩体稳定性较好，属于深层围岩的范畴，因此可将围岩力学特性具有明显差异性的塑性软化区和弹性区分别划分为第1组和第2组深层围岩，需要指出的是，本文基于连续介质理论求解，因此同一组深层围岩力学行为完全相同，作为承担荷载的主体结构，均表现出“结构层”的性能，且本文研究对象为深埋隧道受静水应力场作用，因此围岩结构均表现为圆形，如图3所示。
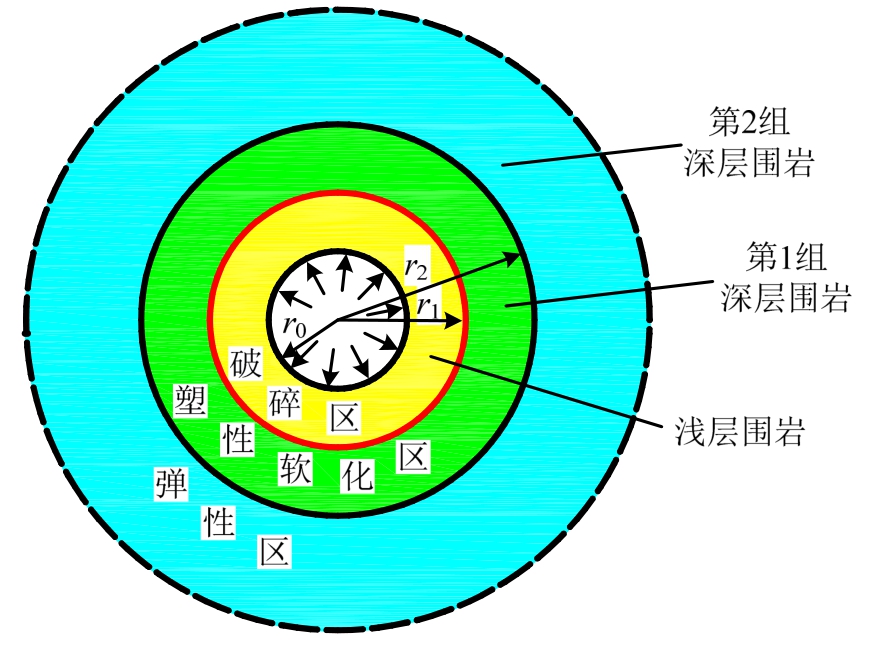
图3 深浅层围岩分布范围
Fig.3 Distribution of internal and external surrounding rock
2.2 锚杆-围岩相互作用力学模型
随着隧道纵向推进，在隧道开挖显著影响范围内，隧道纵向上随着应力释放会依次出现软化区和破碎区，根据隧道纵向上围岩所处应力状态以及和锚杆长度相对位置的不同，可将围岩分析模型分为6种工况，如图4所示。
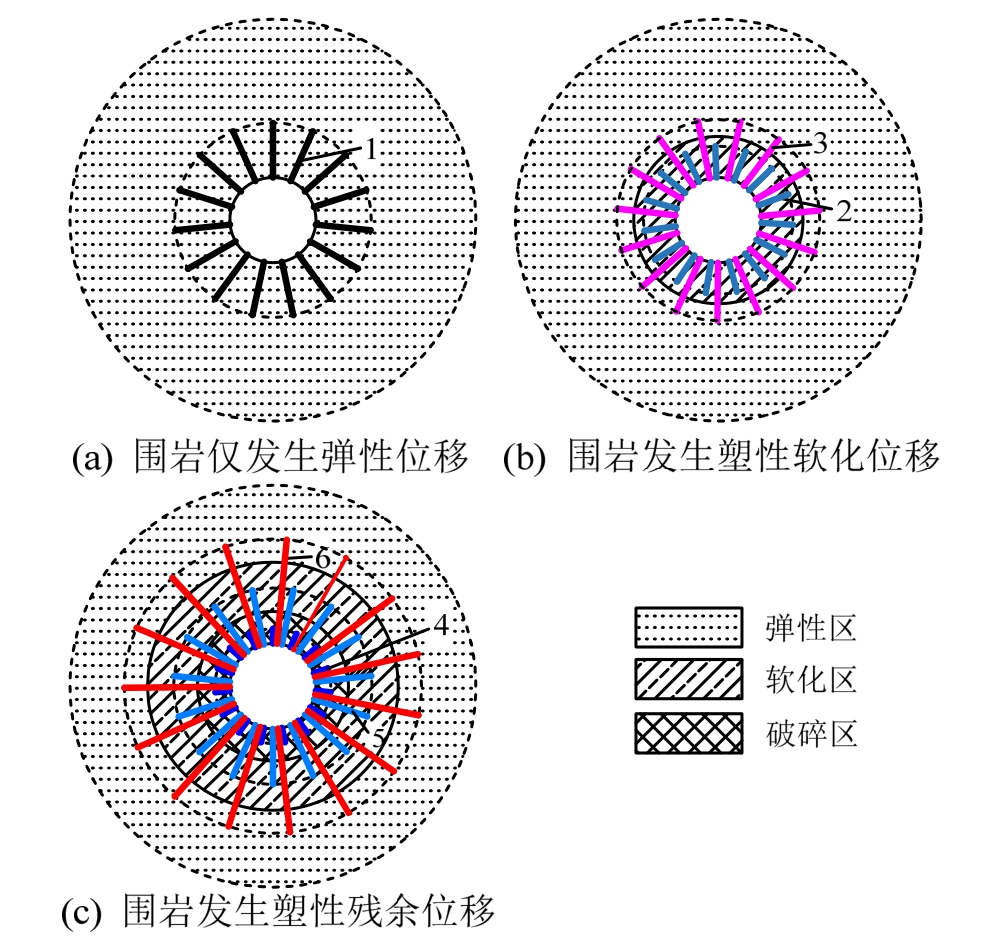
图4 锚杆-围岩相互作用力学模型
Fig.4 Mechanical model for the interaction between rockbolt and surrounding rock
2.3 锚杆-围岩相互作用全过程解析
2.3.1 弹性阶段围岩
弹性区内应力表达式为[14]：
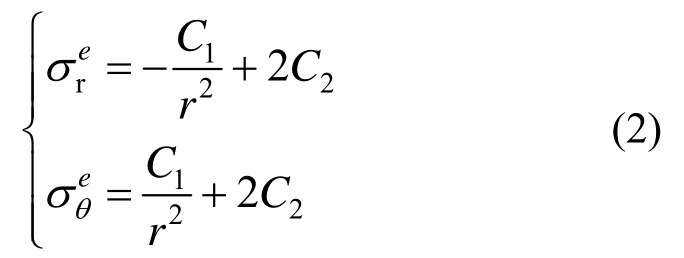
当隧道周围岩体处于弹性状态时，对于锚固区和原岩区，隧道径向位移均可表达为如下形式[15]：
式中：Ei为围岩弹性模量；μi为泊松比；下标i分别表示原岩区和锚固区；C1和C2为待定系数，分别由锚固区和原岩区的边界条件确定。
对于径向均布锚杆，当围岩处于弹性状态时，锚杆对于围岩的作用可等效为围岩弹性模量的提高[3]，锚固围岩的弹性模量为：
式中：C为锚杆布置密度，有
分别为锚杆间、排距；Ab为锚杆横截面积；Es为锚杆弹性模量。
由于锚杆的施作使得隧道周围岩体不再是单一均质围岩，因此求解需要用到的边界条件为：
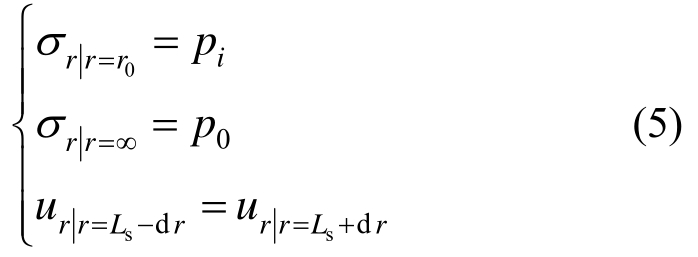
式中：r0为隧道半径；Ls为锚杆长度；pi为支护力；p0为原岩应力。
联立式(2)～式(5)可得锚固区隧道洞壁位移值为：
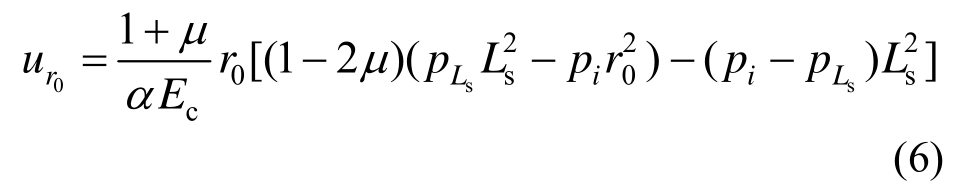
式中，pLs为锚固区与原岩区径向接触力，有：
式中，
2.3.2 软化阶段围岩，锚杆伸入软化区
Huang等[16]指出，锚杆对于围岩的作用可通过在岩体中施加径向约束力来描述。因此，本文参考文献[17]的思想，将锚杆对塑性围岩的控制作用描述为岩体径向应力的增加，即由于锚杆对围岩的约束作用，围岩对锚杆产生轴向反力作用。考虑到锚杆的作用，调整后的围岩径向应力可表示为[3]：
式中，εb为锚杆轴向应变。
对于预应力锚杆，锚杆轴向力不仅包括与围岩相互作用产生的剪应力，还应包括施加于锚杆本身的预紧力Fs(以压应力为正，则此为负值)，其中由Fs导致的锚杆轴向应变为常量，可表示为：
由锚杆与围岩变形协调可得[17]：
式中，εr为围岩塑性区径向应变，此处εt为负值。
联立式(9)～式(10)可得：
求解需要用到的边界条件除式(5)外，还需满足锚固区与原岩区边界上的应力连续条件：
塑性软化区径向应变表达式为[12]：
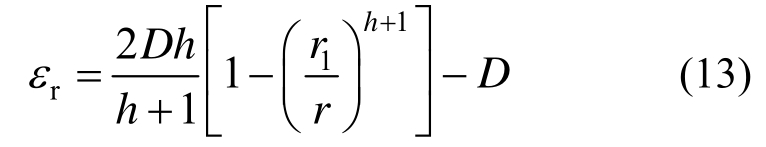
式中：r1为塑性软化区半径；D为中间参数，有：
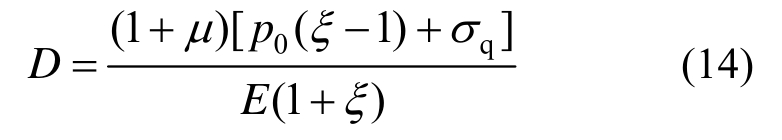
将式(11)中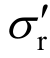
代替式(1)中第二式
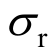可得：
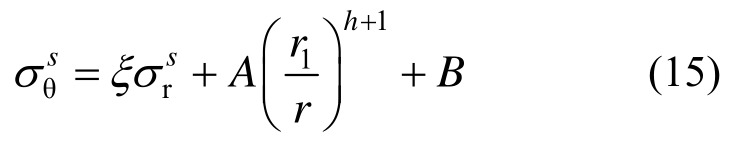
式中：
将式(15)与平衡方程：
联立可得：
对式(17)求解并代入式(5)中第一式可得软化区应力表达式为：
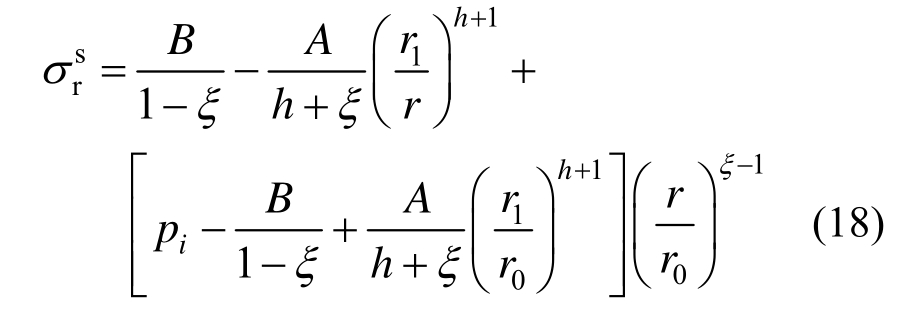
从而可得锚固区与原岩区径向接触力为：
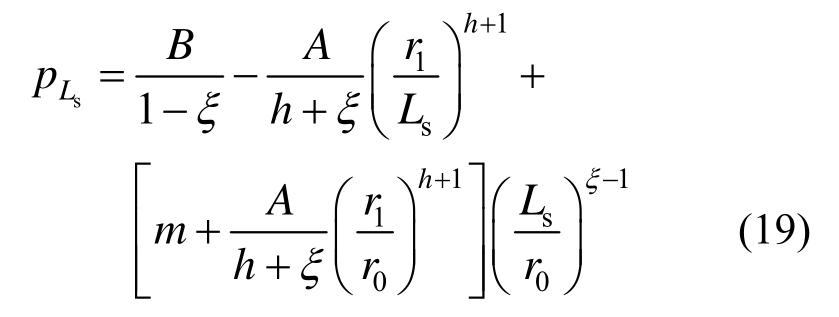
式中，
而原岩软化区径向应力表达式为：
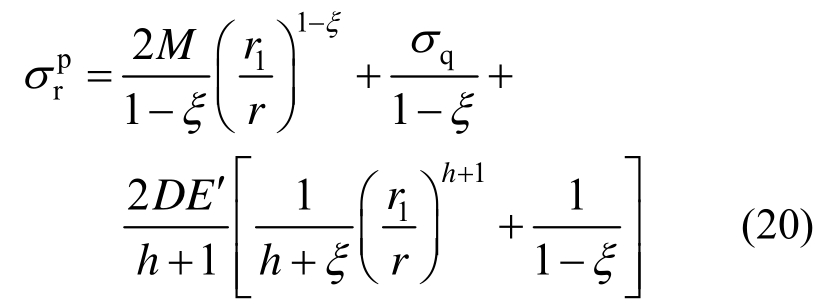
式中，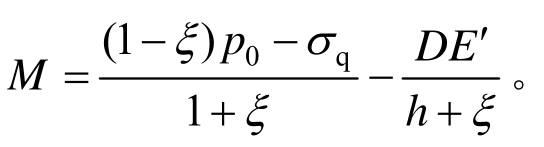
将r=Ls 代入式(20)与式(1)和式(19)联立并考虑式(12)得软化区半径r1满足：
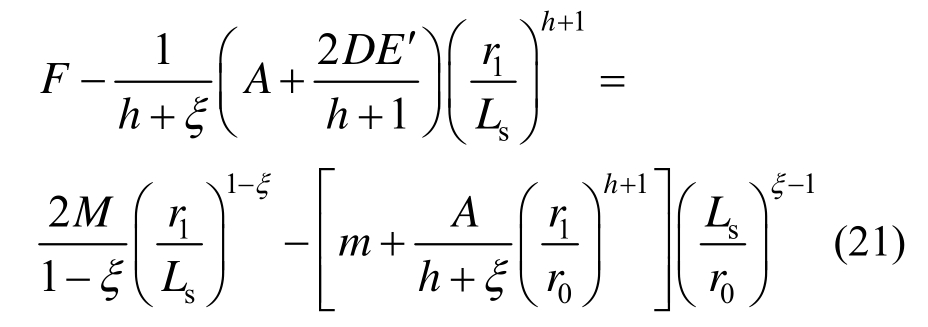
式中，
隧道围岩软化区径向位移可由下式确定：
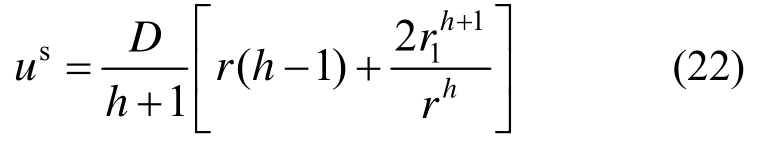
由式(21)中求得软化区半径r1后，将r=r0代入式(22)即可求得隧道洞周位移为：
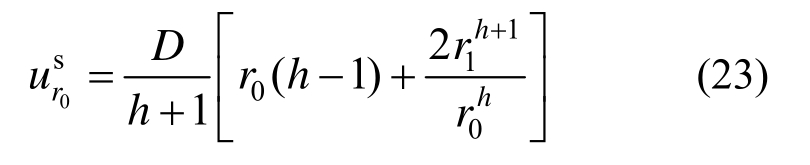
2.3.3 软化阶段围岩，锚杆仅作用于弹性区
当锚杆伸入弹性区时，求解需要用到的边界条件除满足式(5)和式(12)外，还需满足锚固软化区与弹性区边界上的应力和位移连续条件。
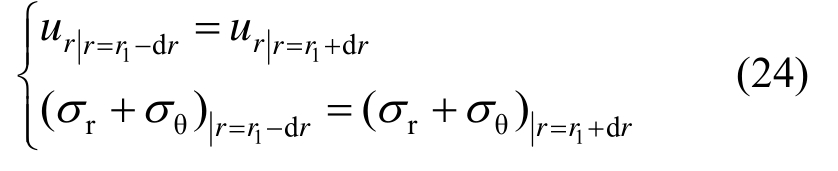
围岩锚固弹性区径向位移表达式为：
将
代入式(2)可得：
式中，
从而可得r=r1时弹性应变表达式为：
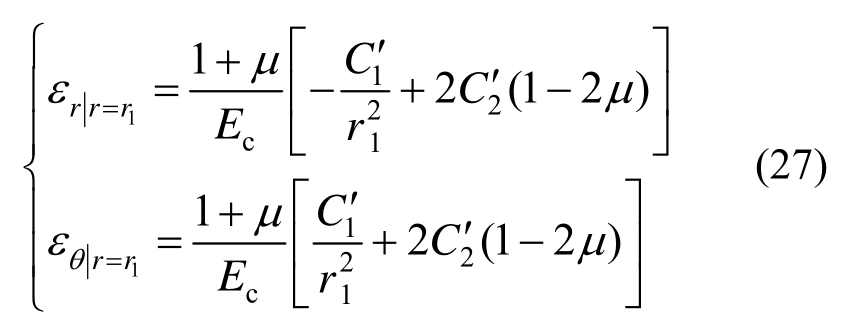
塑性软化区非关联流动法则为[16]：
从而可得软化区位移微分方程为：
式中，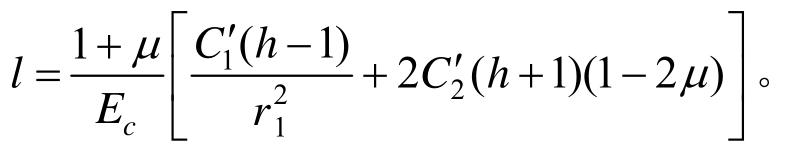
将式(6)中pi以pr1代替，r1代替r0可得软化区与弹性区界面位移为：
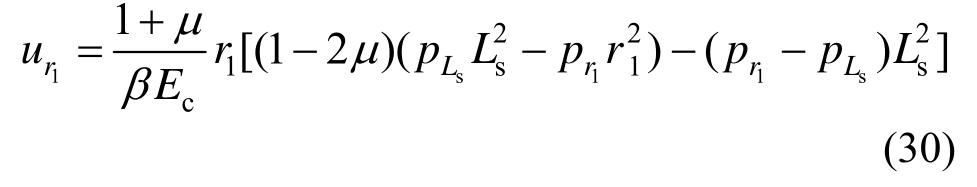
对式(29)积分并考虑式(30)可得软化区位移解：
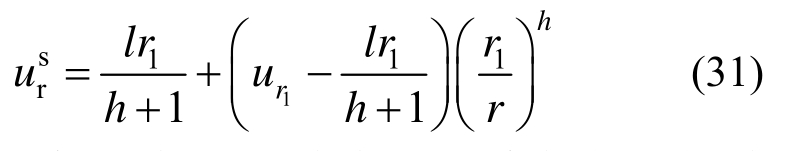
将r=r1代入式(18)可得锚固区内软化区与弹性区径向接触力pr1表达式为：
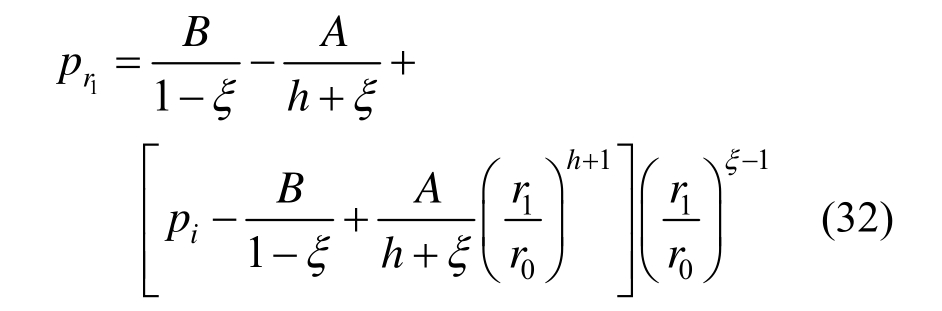
由式(7)可得锚固区与原岩区径向接触力pLs为：
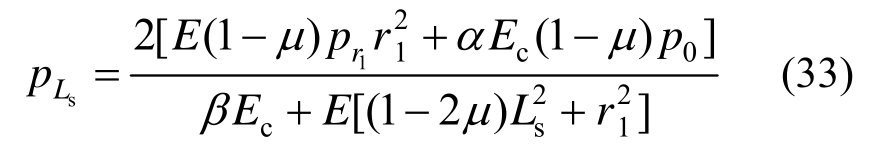
由式(24)中第二式联立式(2)和式(32)并考虑式(15)可得：
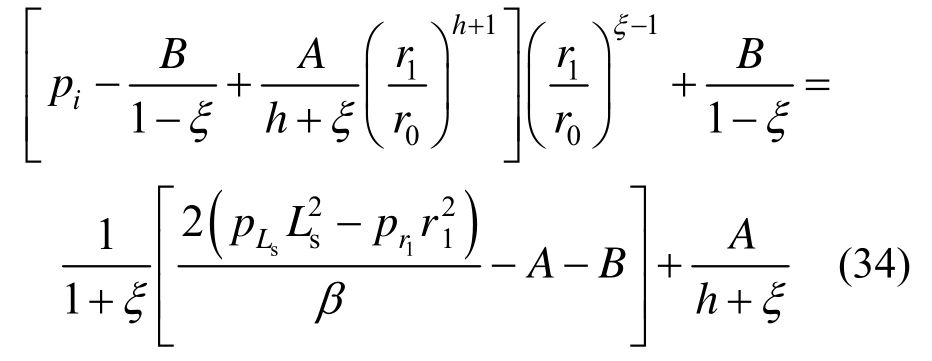
联立式(32)～式(34)即可求得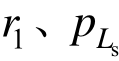
和
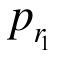解答，将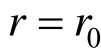
代入式(31)即可求得隧道洞周位移为：
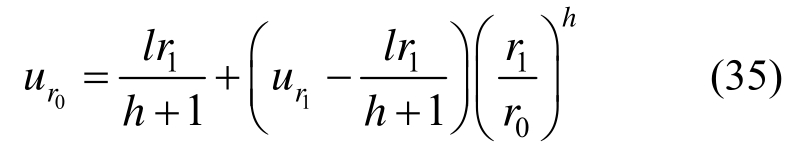
2.3.4 残余阶段围岩，锚杆伸入破碎区
塑性软化区径向应变可由下式求得：
式中：
为破碎区半径，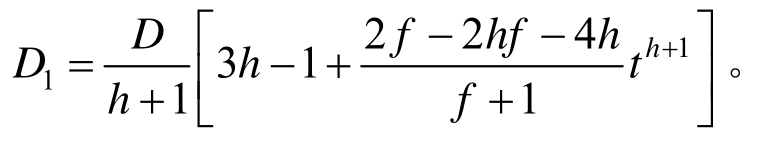
将式(11)中
代替式(1)中第三式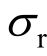
并考虑式(36)可得：
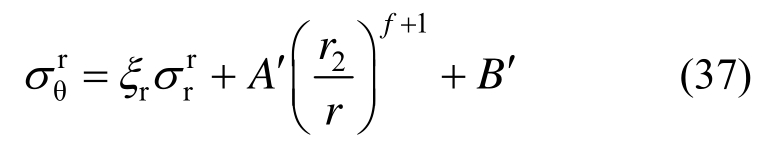
式中：
将式(37)与式(16)联立并代入式(5)第一式可得：
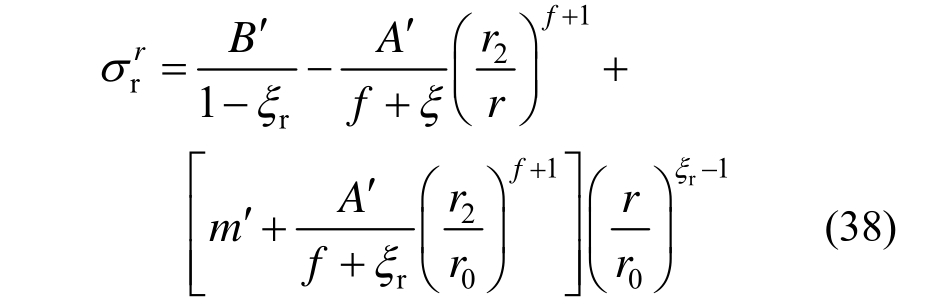
式中：
从而可得当
时，锚固区与原岩区径向接触力为：
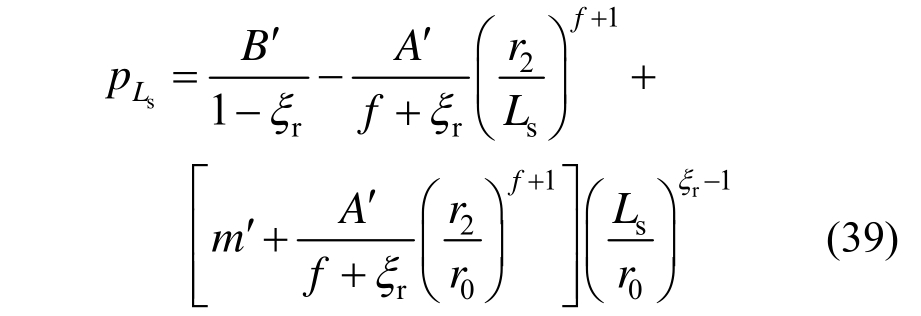
而围岩破碎区径向应力表达式为：
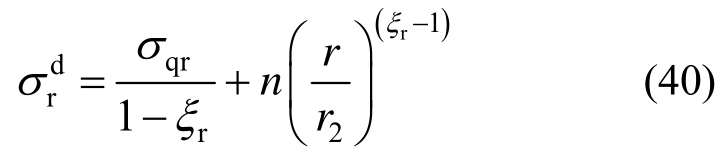
式中：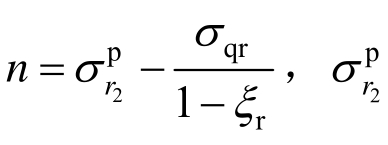
为塑性软化区与破碎区接触面径向应力，由式(21)中令r=r2得到。
将r=Ls代入式(40)并与式(39)联立并考虑式(12)得破碎区半径r2满足：
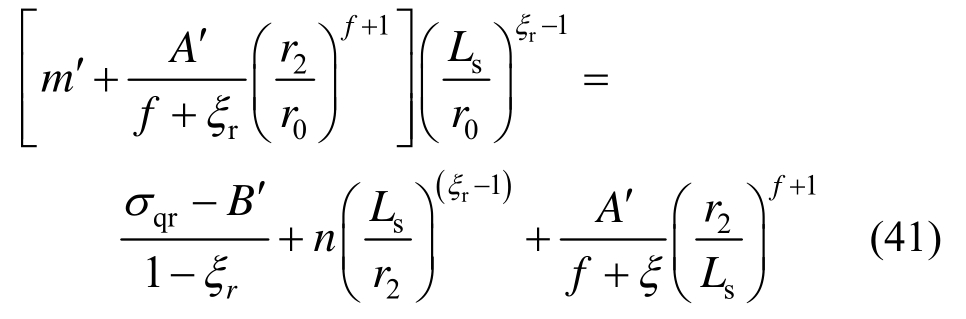
塑性软化区环向塑性应变为：
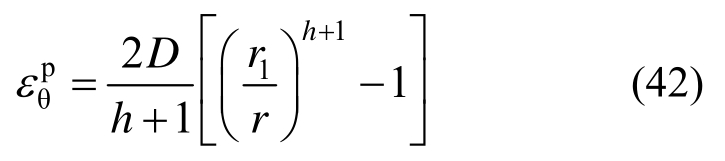
代入式(1)中第二式并令r=r2可得：
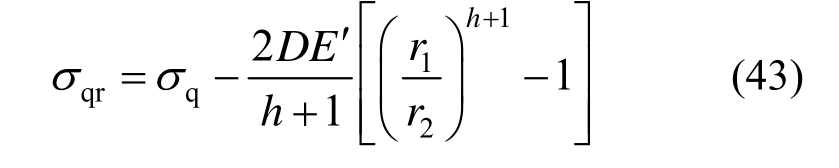
从而可得软化区半径与破碎区半径关系式：
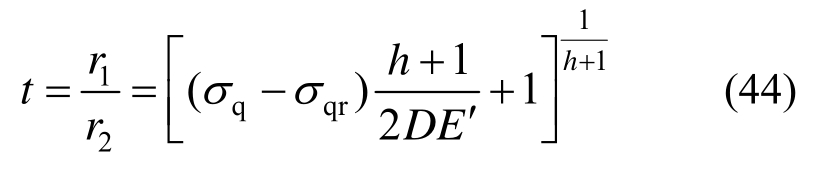
隧道围岩破碎区径向位移可由下式确定：
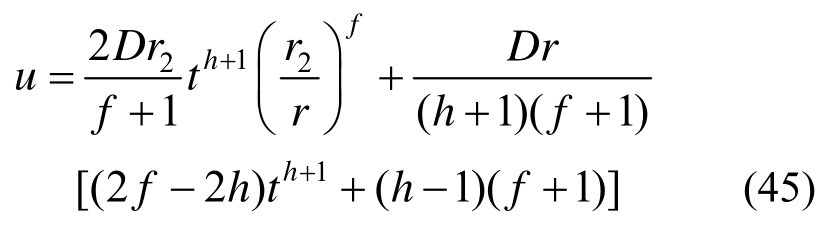
由式(41)中求得破碎区半径r2后，将 r=r0代入式(45)即可求得隧道洞周位移为：
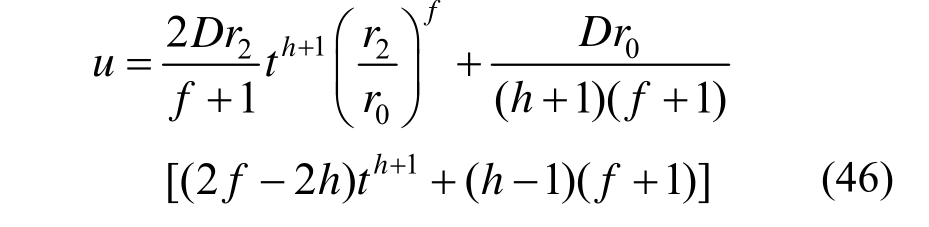
2.3.5 残余阶段围岩，锚杆伸入软化区
当锚杆伸入软化区时，求解需要用到的边界条件除满足式(5)和式(12)外，还需满足锚固破碎区与软化区边界上的应力和位移连续条件。
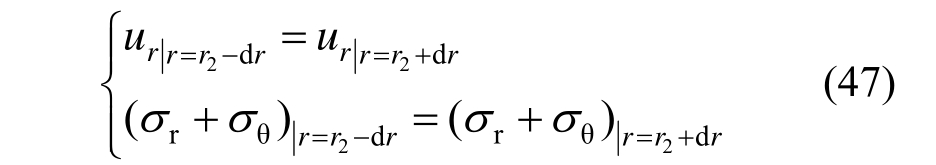
对式(17)求解并代入
可得锚固软化区径向应力表达式为：
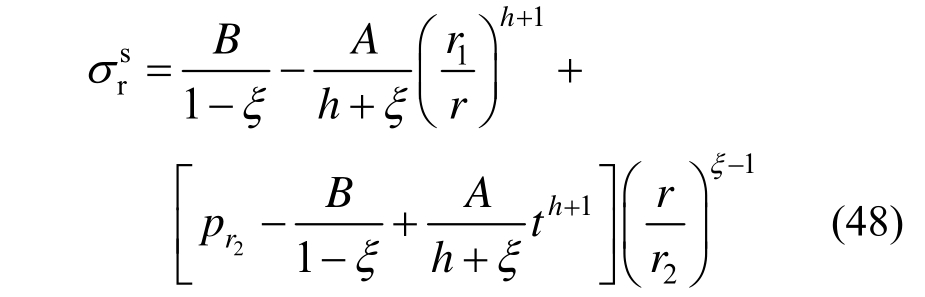
将r=r2代入式(38)可得锚固区内破碎区与软化区径向接触力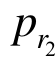
表达式为：
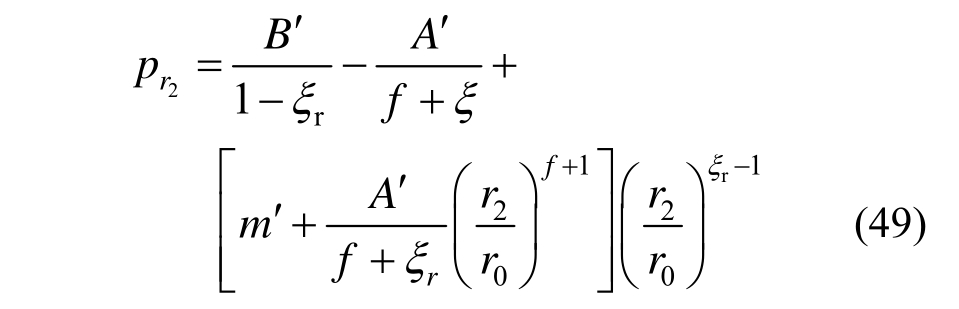
由式(47)中第二式联立式(49)和式(48)并考虑式(37)和式(15)可得：
由式(48)得锚固区与原岩区径向接触力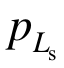
为：
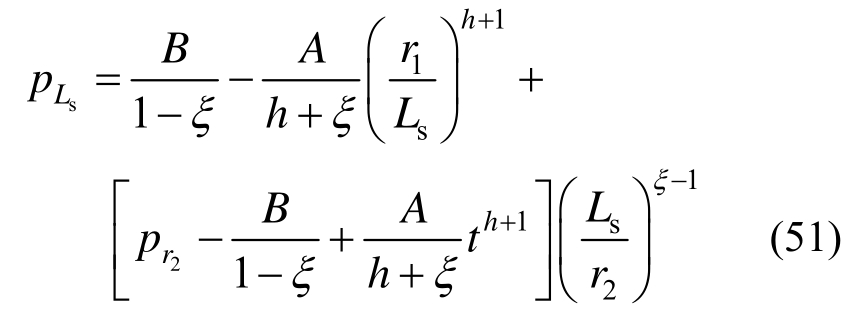
将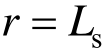
代入式(20)并与式(51)联立并考虑式(12)得软化区半径r1满足：
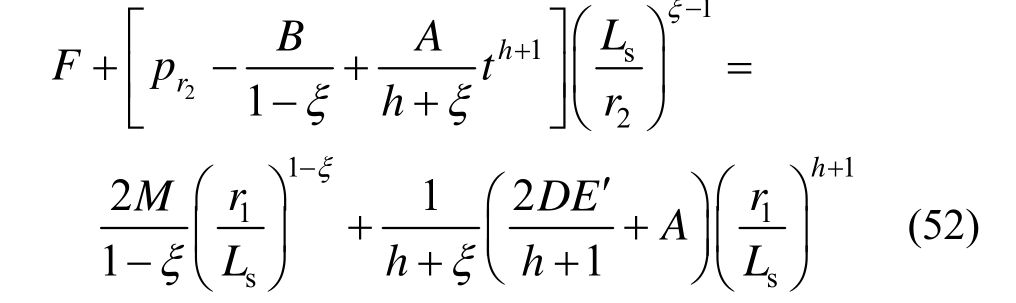
联立式(49)～式(52)可求得r1、r2、pLs和pr2解答，而后代入式(46)即得到隧道洞周位移。
2.3.6 残余阶段围岩，锚杆仅作用于弹性区
当锚杆伸入弹性区时，求解需要用到的边界条件应同时满足式(5)、式(12)、式(24)和式(47)。破碎区非关联流动法则为[18]。
由式(31)得软化区与破碎区边界应变表达式为：
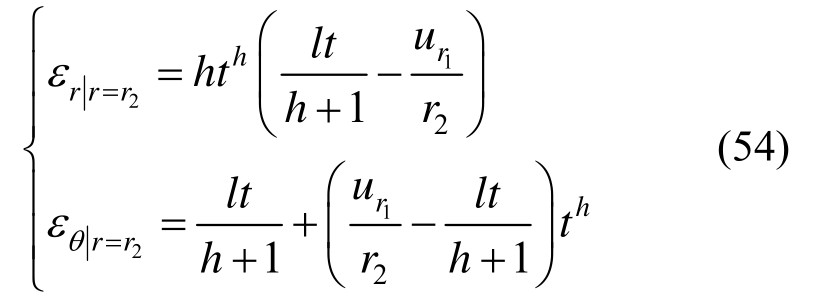
从而可得破碎区位移微分方程为：
式中：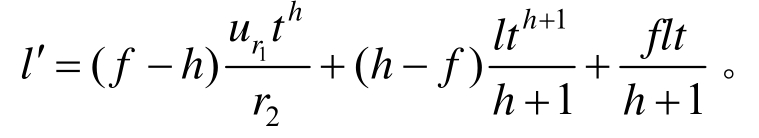
将r=r2代入式(31)可得软化区与破碎区界面位移表达式为：
对式(55)求解并代入式(56)可得破碎区位移解：
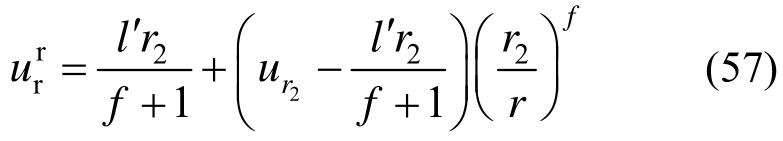
将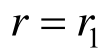
代入式(48)可得锚固区内软化区与弹性区径向接触力
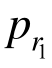表达式为：
由式(24)中第二式联立式(2)和式(58)并考虑式(15)可得：
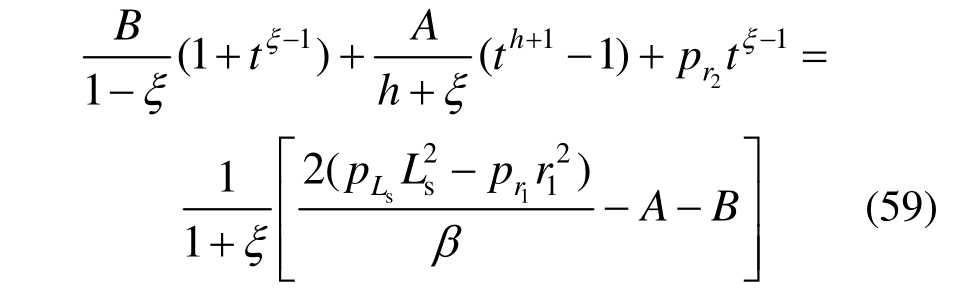
联立式(33)、式(49)、式(50)、式(58)和式(59)可求得r1、r2、pLs和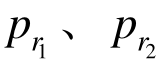
解答，而后将r=r0代入式(57)即得到隧道洞周位移为：
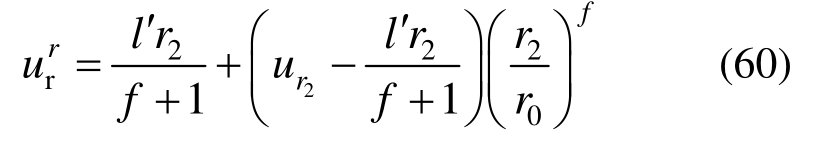
3 锚固系统协同作用及全过程解析
由于隧道中常用的锚杆长度有限，规范[19]建议岩石隧道中锚杆长度一般不大于8 m，土层隧道一般小于12 m，然而对于不良地质条件下修建的大断面隧道，浅层围岩范围过大[20]，此时锚杆支护不能伸入深层围岩，无法有效控制围岩变形，在与围岩相互作用的过程中甚至可能导致支护失效而引发系统失稳，威胁施工安全，例如十堰至房县高速公路通省隧道就曾因锚杆长度不足而导致锚杆失效致使施工期间发生多次大变形和破坏[21]。此外，由于大跨隧道的整体稳定性和高可靠性要求，锚固支护应具有一定的富余度，此时仅依靠锚杆支护无法满足隧道围岩稳定性的需求，因此常需配合锚索组合支护，二者协同作用维护隧道稳定。
3.1 锚固系统协同作用原理
隧道锚固系统是由围岩与锚杆、锚索等组成的锚固机构按照一定工作方式组成的复杂系统，通过与外部地层和工程环境之间的有机联系而处于动态平衡状态。锚固系统的稳定性是其子系统间相互作用的结果，主要受到锚固材料性能、围岩质量及锚固岩体性能的综合影响。锚固系统的协同作用内涵包括3个方面，即锚固体系与复合围岩结构的相互作用、锚杆、锚索单一支护型式各参数之间的匹配效应以及锚杆、锚索之间的协同作用，前1个方面已在前文进行阐述，下文研究主要涉及后2个方面。
根据前文分析，锚杆支护作用的核心是通过“组合梁”或“压缩拱”效应形成围岩整体结构，锚索则将该结构悬吊至稳定岩层，承担其自重荷载和由于围岩进一步变形而传递给锚索的形变荷载，二者协同作用从而调动深层围岩承载，如图5所示。通过锚固体系与围岩之间的协同作用，可使锚固体系变形相协调，围岩荷载分配与支护性能相匹配，从而达到科学合理地控制围岩变形的目的。
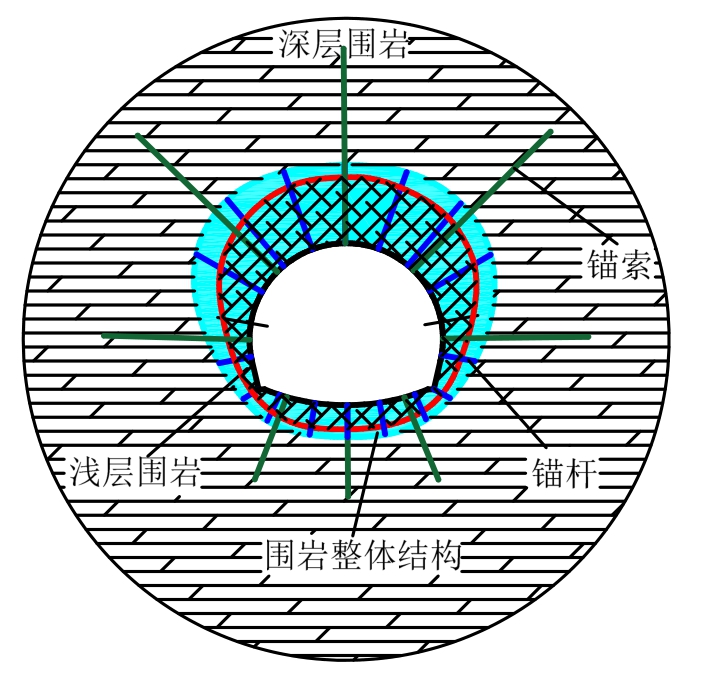
图5 锚固体系协同作用机理
Fig.5 Synergistic mechanism of anchoring system
3.2 隧道围岩锚固系统协同作用模型
为了使计算分析具有普适性，对锚固体系以及围岩结构之间可能出现的所有工况进行解析。
当锚杆与锚索伸入同一围岩结构中时，可采用图4中力学分析模型进行计算，只需将式(8)～式(11)中叠加上锚索的作用即可，如式(11)中只需将 EsAb替换为锚杆与锚索之和
而Fs视为二者预应力之和，结合前文计算原理，后续推导过程基本相同，此处不再赘述。因此，只需对锚杆与锚索位于隧道围岩的不同结构中时二者的协同作用进行解析，共有4种分析工况，如图6所示。
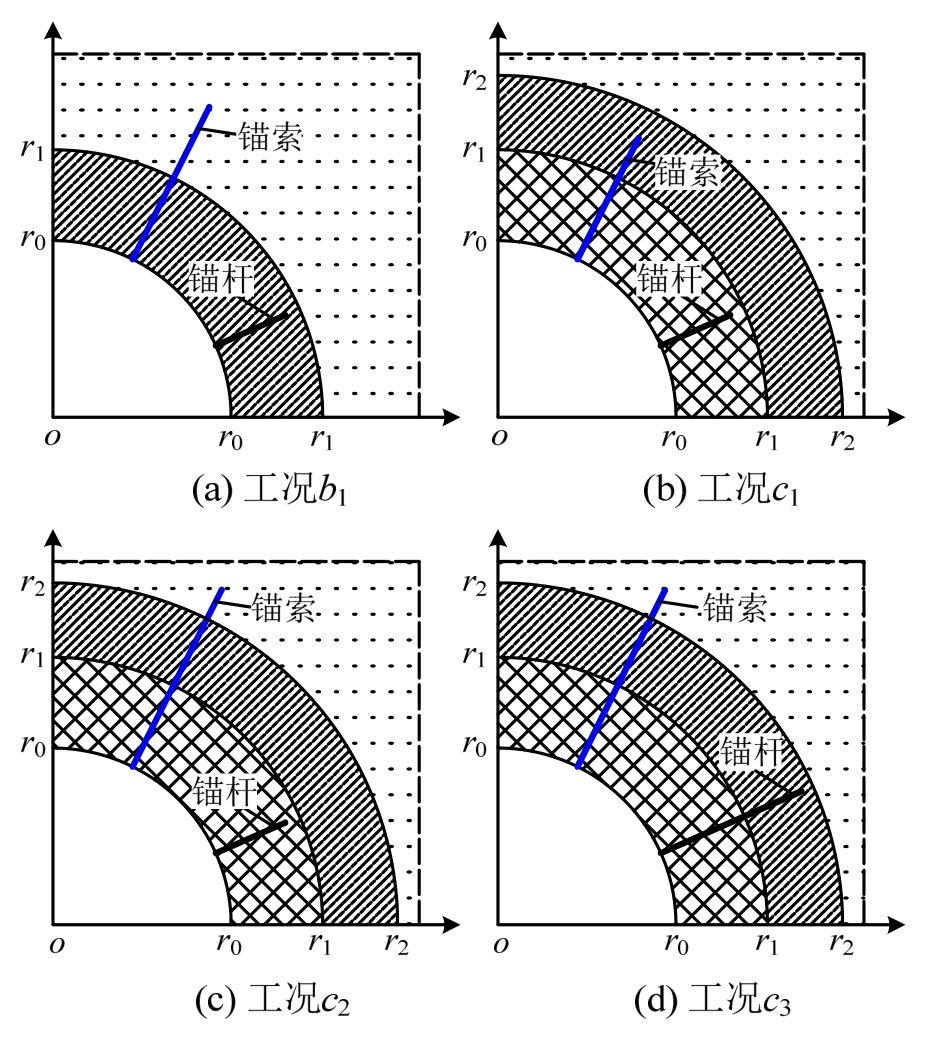
图6 锚固系统协同作用力学模型
Fig.6 Mechanical model for synergy of anchoring system
3.3 协同锚固全过程解析
为便于描述，将锚杆与锚索共同作用的区域定义为双重锚固区，而锚索单独作用区则称为单一锚固区，对图6中4种工况模型进行解答。
3.3.1 工况b1解答
图6中工况b1表示破碎区范围为零，锚杆伸入软化区，锚索则伸入弹性区，求解需用到的边界条件形式与3.3节第3种工况基本相同，只需将式(12)中考虑单一锚固区与双重锚固区的应力边界条件即可，即：
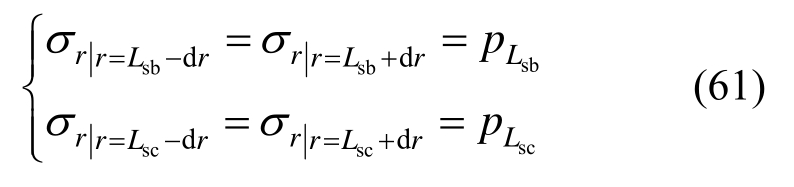
式中：下标b和c分别代表锚杆和锚索，下文亦然。
由式(33)可得锚固区与原岩区径向接触力pLsc：
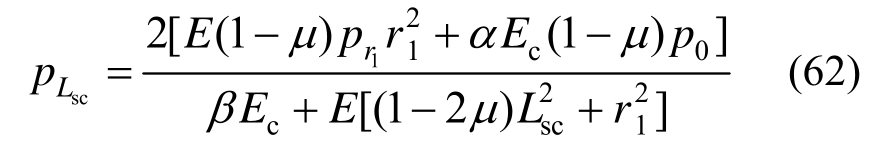
将式(32)中r0、pi分别用Lsb、pLsb代替可得：
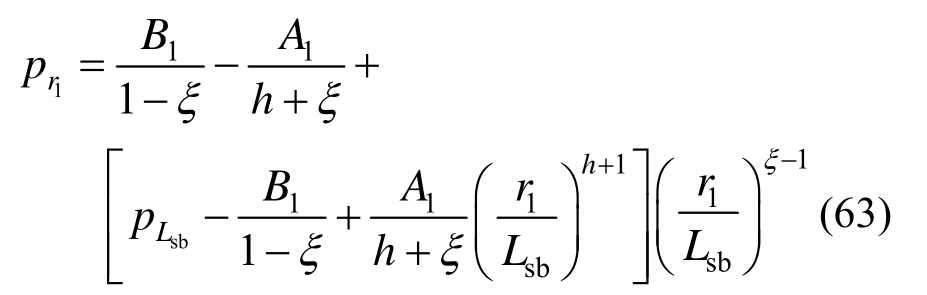
式中：
由式(18)可得双重锚固区内径向应力表达式为：
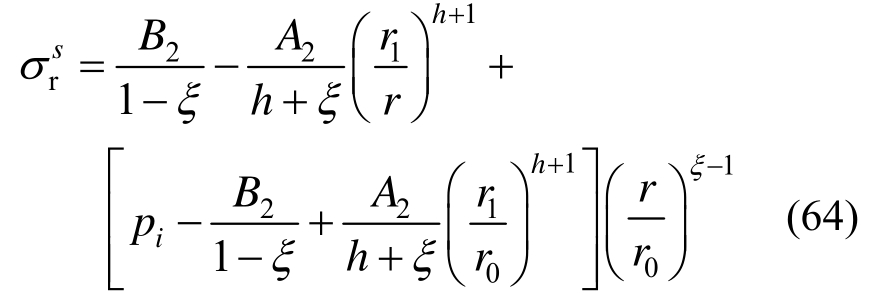
式中：
将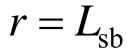
代入式(64)可得双重锚固区与单一锚固区界面处接触应力为：
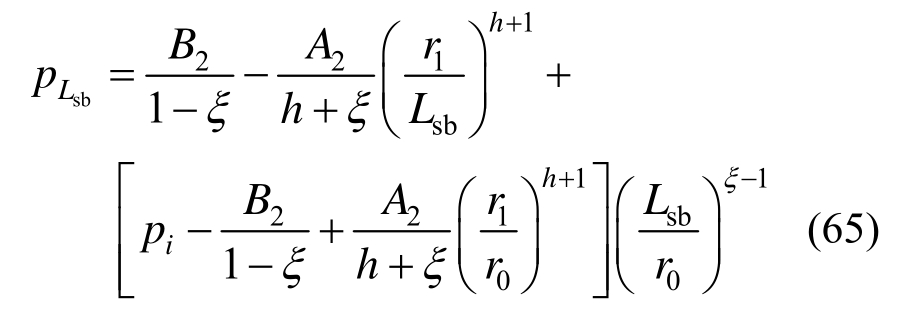
由软化区与弹性区应力连续条件可得：
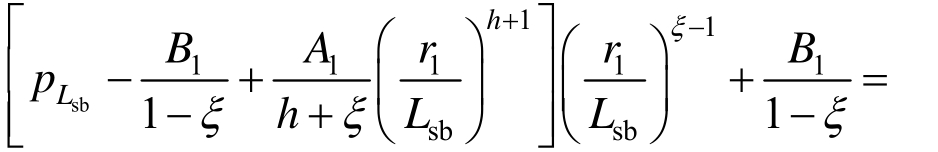
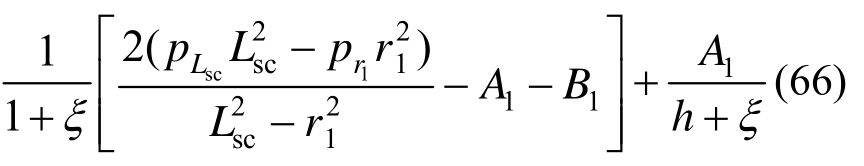
将式(62)、式(63)、式(65)、式(66)联立可求得
的值，代入式(35)即可得到隧道周边位移解答。
3.3.2 工况c1解答
图6中工况c1表示破碎区产生时，锚杆伸入破碎区，锚索伸入软化区，此时求解需要满足的边界条件除与3.3节第5种工况基本相同外，还需满足式(61)。
由式(49)可得单一锚固区内破碎区与软化区径向接触力pr2表达式为：
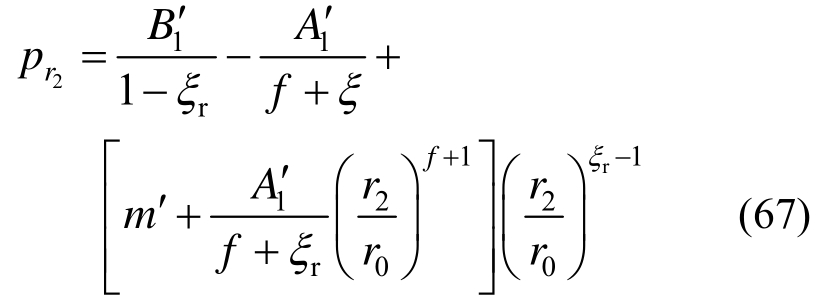
式中：
将
代入式(48)得单一锚固区与原岩区径向接触力
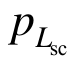为：
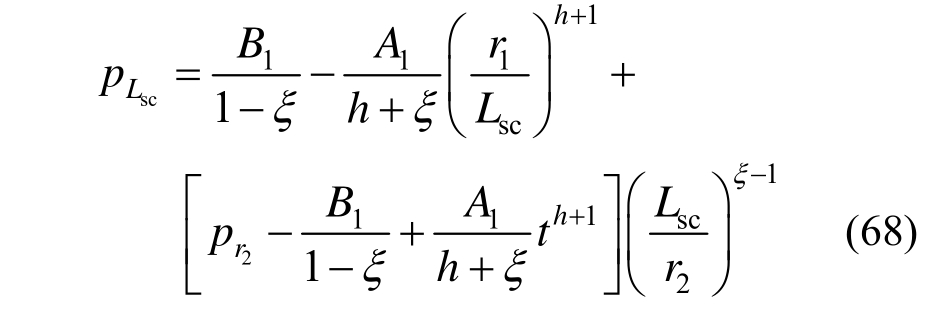
由单一锚固区与原岩区应力连续条件可得软化区半径r1满足：
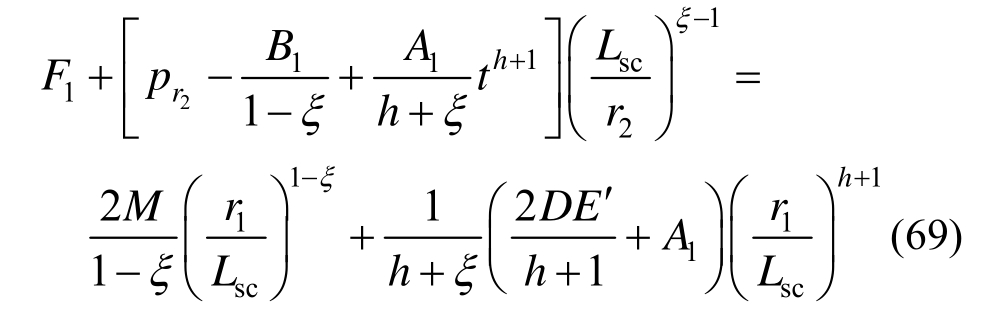
式中：
由软化区与破碎区应力连续条件可得破碎区半径r2满足：
由式(39)可得双重锚固区与单一锚固区径向接触力表达式为：
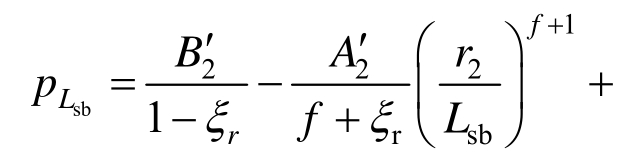
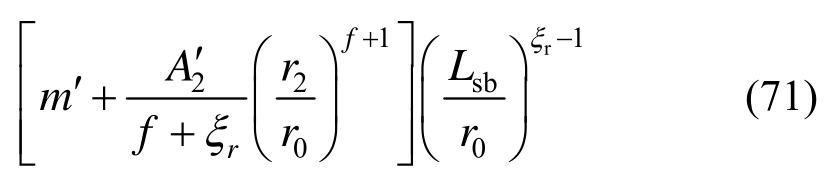
式中：
将式(67)～式(71)联立可求得pLsb、pLsc、pr1、r1、r2的值，代入式(46)即可得到隧道周边位移解答。
3.3.3 工况c2解答
图6中工况c2表示破碎区产生时，锚杆伸入破碎区，锚索伸入弹性区，此时求解需要满足的边界条件形式与3.3节第6种工况基本相同，此外还需满足式(61)。
将r=r1代入式(48)可得单一锚固区内软化区与弹性区径向接触力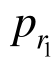
表达式为：
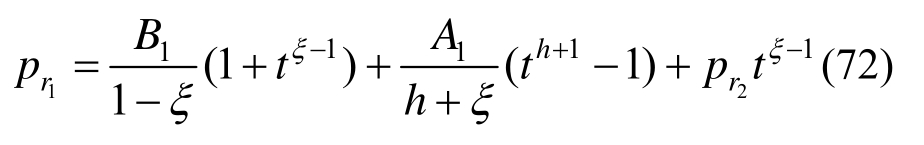
由软化区与弹性区应力连续条件可得：
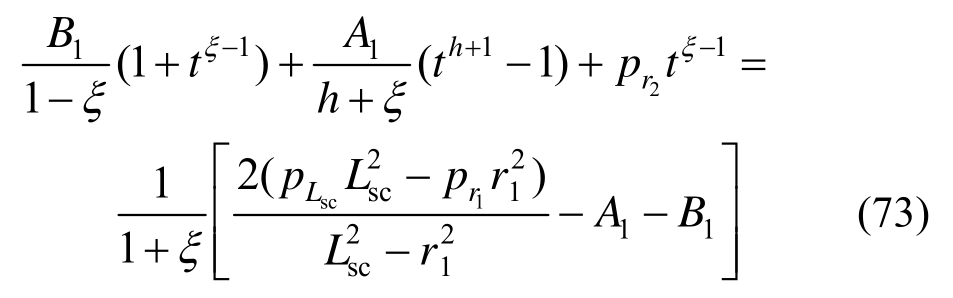
联立式(62)、式(67)、式(68)、式(71)～式(73)可求得r1、r2、pLsb、pLsc和pr1、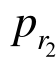
解答，而后代入式(60)即得到隧道洞周位移。
3.3.4 工况c3解答
图6工况c3表示破碎区产生时，锚杆伸入软化区，锚索则伸入弹性区，此时求解需要满足的边界条件包括与3.3节第5种、第6种工况相同部分和式(61)。
由式(51)得单一锚固区与双重锚固区径向接触力pLsb为：
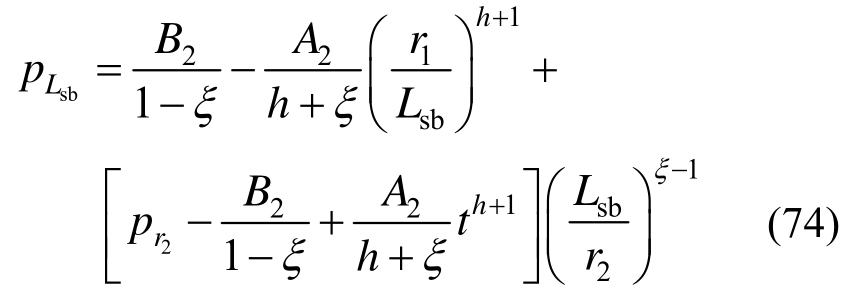
由式(49)可得双重锚固区内破碎区与软化区径向接触力2rp表达式为：
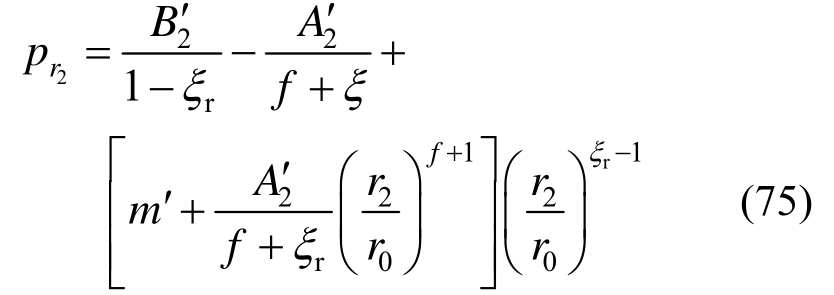
联立式(62)～式(63)、式(72)～式(75)可求得r1、r2、pLsb、pLsc和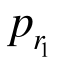
、pr2解答，而后代入式(60)即可得到隧道洞周位移。
3.4 协同作用效果评价方法
由本文假设可知，隧道锚固体系受力最大点位于洞壁处，因此只需通过前述公式求得洞壁处围岩应变值，从而可得锚杆(索)最大轴力为：
基于前述分析，锚固体系失效本质为锚杆-围岩整体结构变形过大而导致锚索受力过大而拉断。可见，锚固系统失稳的必要条件为锚索失效，结合锚固体系作用机理可知，在锚固体系中锚杆支护性能应充分利用，锚索承载能力较大应具有足够冗余度。为了定量描述锚固体系协同效应的范围、条件及其影响因素，定义锚固体系协同度为η如下：
式中：wb、wc分别为锚杆和锚索的权重，可通过工程类比法或层次分析法等手段得到，借鉴前人研究成果[22—23]；wb和wc可分别取为0.6和0.4；ξb、ξc分别为锚杆和锚索的平均利用率，本文定义为材料的最大轴力与其极限强度的比值，即：
式中，Ftb,c为锚杆(索)极限抗拉强度。
当采用式(78)所得ξi≥1时表明锚杆(索)已屈服失效，此类支护方案应剔除。此外，由于隧道锚固体系协同作用的目标为控制围岩稳定性，而隧道围岩变形量不仅可反映复合围岩结构的发展状况，又与荷载效应存在一定相关关系，可作为围岩稳定性的判断依据，因此也将其作为协同作用效果的评价指标。
4 隧道锚固体系设计方法
4.1 隧道锚固体系协同设计程序
实际工程中，由于地层条件的复杂性，隧道围岩结构也呈现出多样性，给隧道设计和施工带来极大挑战。在复杂围岩条件下，如何合理确定锚固体系参数是隧道施工所面临的难点及重点问题。因此，本文提出一种基于锚固体系协同作用的隧道锚固参数的确定方法，具体如图7所示。
1)围岩稳定性判别与结构性预测：首先采用理论分析或对实测数据进行反分析等手段对围岩最大变形量umax进行预测；然后基于隧道围岩的变形破坏过程，通过理论分析、现场调查和室内试验等手段，并结合相关规范确定隧道变形控制标准[u]；最后将两者进行对比，若umax＞[u]，则表明隧道施工过程中围岩将发生失稳，可通过锚固措施对其进行控制，若umax<[u]，则表明隧道围岩能保证其安全施工，无须另行锚固设计。当确定采用锚固手段后，可通过本文公式对围岩结构性进行预测，若浅层围岩范围超过锚杆支护范围，则需采用锚固体系协同支护，否则可仅采用锚杆支护。
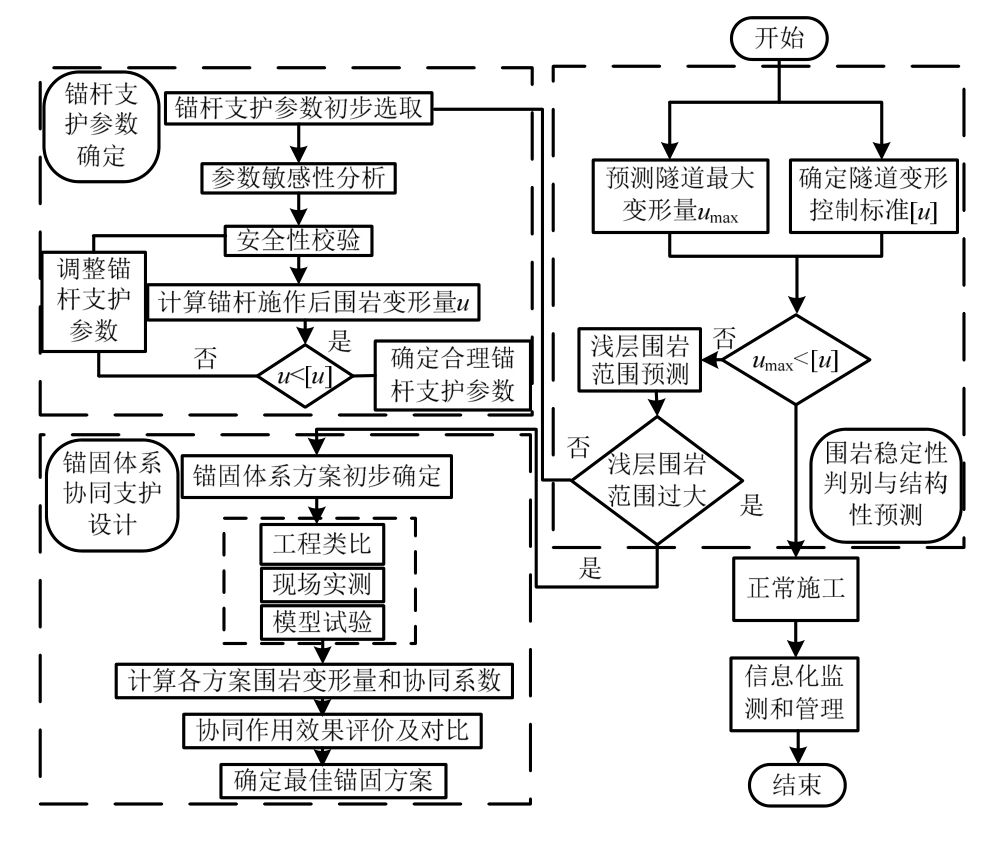
图7 隧道锚固体系设计程序
Fig.7 Design program of tunnel anchorage system
2)锚杆支护参数确定：当确定采用锚杆支护时，借助工程类比方法并结合相关规范，初步选取隧道锚杆支护参数的变化范围，并代入本文对应工况中对各参数的敏感性进行计算分析，可得到锚杆支护参数的最优解集，将其代入本文公式中进行计算可得锚杆作用下隧道围岩变形量u，若u>[u]，则表明选取的锚杆支护参数范围不合理，因此需对参数进行调整后再次进行安全性校验，直到所得到的最优解集满足u<[u]，则此时最优解集即为锚杆支护的合理参数。
3)锚固体系协同支护设计：当采用锚杆与锚索组合支护时，以围岩变形量和支护协同度作为协同作用效果的评价指标，首先通过工程类比、现场实测与模型试验等方法初步拟定组合方案，并代入相应工况计算各支护方案围岩变形量，根据式(78)剔除结构失效的支护方案，对比有效方案的支护协同度，选择围岩变形控制效果最优且支护协同度最大的支护方案。
4.2 工程实例分析
4.2.1 算例1(锚杆支护设计)
某深埋圆形隧道半径r0=6 m，受静水压力p0=6 MPa 。隧道处于软岩中，围岩弹性阶段力学参数为E=1.5 GPa ，μ=0.3；软化阶段参数为
残余阶段参数为
采用本文公式计算可得隧道开挖后围岩位移最大值为umax=127 mm。根据Hoek[24]的研究成果，结合规范[25]中对初期支护极限相对位移的规定，取隧道围岩变形控制标准为[u]=60 mm，显然umax>[u]可知隧道开挖后，若不对围岩进行提前处理，则初期支护将会严重侵限，影响施工安全。进一步对浅层围岩范围进行预测，计算可得浅层围岩厚度为2.36 m，因此可仅采用锚杆支护对围岩进行控制。为了研究锚杆参数对隧道围岩特性曲线的影响，参考文献[1]提出的预应力锚杆支护的建议参数范围，锚杆直径(d)、布置密度(C)、锚杆长度(Ls)以及预紧力(Fs)分别取7种工况进行分析，计算工况如表1所示。
表1 锚杆参数波动范围
Table 1 The range of rockbolt parameters
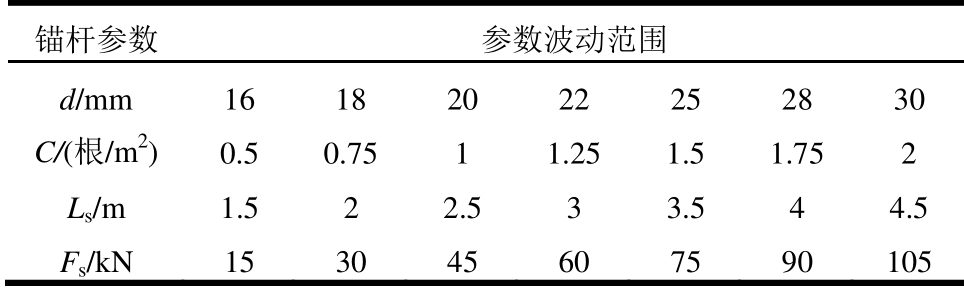
锚杆参数 参数波动范围 d/mm 16 18 20 22 25 28 30 C/(根/m2) 0.5 0.75 1 1.25 1.5 1.75 2 Ls/m 1.5 2 2.5 3 3.5 4 4.5 Fs/kN 15 30 45 60 75 90 105
在研究某一个参数变化(sE除外)对围岩特性曲线影响时，锚杆弹性模量sE=200 GPa，其他参数取7种情况中的最小值。特别地，为了验证本文计算方法的正确性，令本文公式中锚杆直径 0d= 进行计算模拟无锚杆情况，并将计算结果与Panet[26]得到的经典位移解进行对比研究，同时将Ls=2.5 m时本文计算结果与文献[4]进行对比，结果如图8 所示。
由图8分析可知：
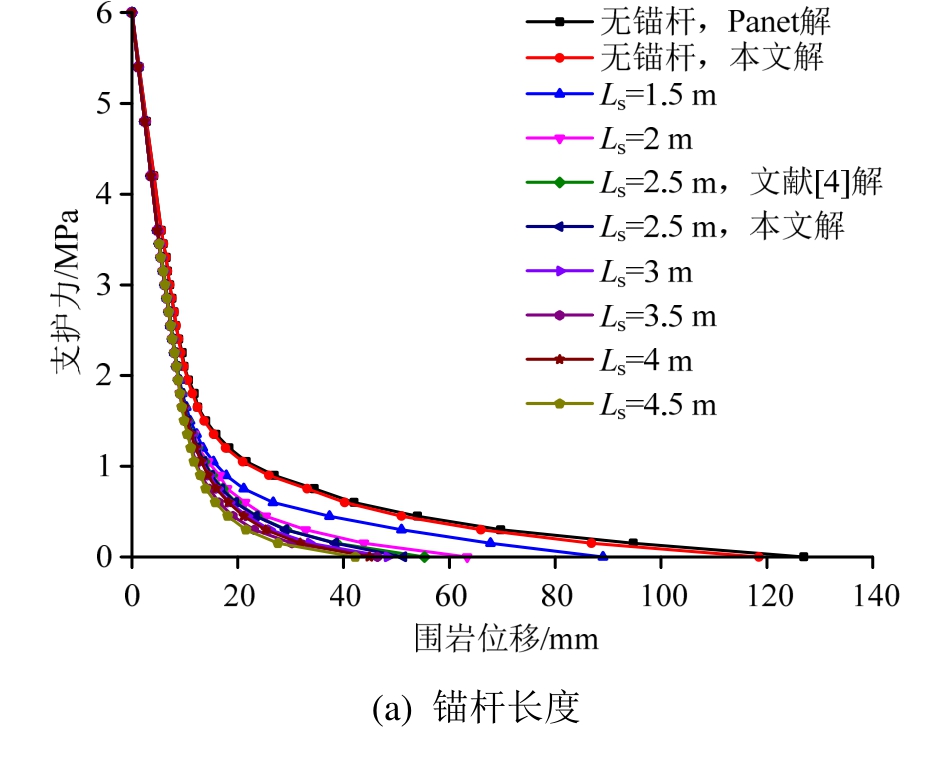
图8 锚杆参数对围岩特性曲线的影响
Fig.8 The influence of rockbolt parameters on ground reaction curve
1)本文计算方法与Panet法计算的围岩特性曲线几乎重合，随着应力释放率的增大差值越大，但总体相差仍很小，说明本文计算方法是有效的。由于本文基于三线性应变软化本构模型推导，而Panet法未考虑破碎区粘聚力，因此本文计算结果比Panet法偏小。此外，本文解相对于文献[4]也较小，这是由于文献[4]将锚杆作用简化为端部力，而本文考虑了锚杆沿长度方向各点与围岩的相互作用，更符合工程实际。
2)当锚杆长度为1.5 m时，围岩发生残余位移，此时锚杆仅伸入破碎区内，即前述工况4，围岩最大位移为89 mm，仍大于变形控制标准，无法满足施工要求；当锚杆长度增加至2.5 m时，围岩发生软化位移，此时锚杆伸入软化区内，对应前述工况2，围岩最大位移为49 mm，满足施工要求。即由于锚杆将浅层围岩附加荷载传递至深层围岩，围岩稳定性显著提高；随着锚杆逐渐深入深层围岩直至达到第2组结构层，锚杆对围岩变形控制的作用效果随着锚杆长度的增加而越不明显。可见，锚杆的核心作用是调动深层围岩承载，从而提高浅层围岩的稳定性，且并非锚杆越长对围岩位移的控制效果越好。因此，合理的锚杆长度应伸入深层围岩第1组结构层，从而达到经济合理的施工效果。
3)随着锚杆直径增大，围岩位移有所减小，但并不十分明显。因此，对于锚杆直径的选取，只需满足工程需求即可，盲目加大锚杆直径对于隧道围岩控制作用并不大，反而会大大增加工程成本。
4)增大锚杆布置密度和预应力时隧道围岩位移明显减小。而当二者超过一定程度时，继续增大锚杆布置密度或预应力对减小围岩位移的作用效果已不明显。可见，锚杆设计参数存在相对经济合理的取值。
由以上分析可见，合理的锚杆设计参数之间具有明显的匹配效应，只有当锚杆各参数之间相互匹配时，方能使得锚杆-围岩作用体系以最小的外部干预能量达到最优的平衡状态。由前述敏感性分析可知锚杆参数最优解集如表2所示。
表2 隧道锚杆参数最优解集
Table 2 Optimal solution set of tunnel rockbolt parameters
长度l/m 直径d/mm 布置密度C/(根/m2) 预紧力F/kN 2.5 22 1.25 60
代入本文公式中计算可得隧道围岩变形量为38 mm，小于围岩变形量控制标准[u]=60 mm，满足施工要求。需要指出的是，上述参数为理论计算值，在现场应用时应根据具体地质条件和施工方法作适当调整。
4.2.2 算例2(锚固体系协同优化设计)
计算选取的围岩参数与4.2.1节相同，为了验证锚杆与锚索的协同作用，隧道半径r0取为10 m，受静水压力p0=8 MPa ，计算可得围岩最大变形为umax=216 mm，由文献[24]可得隧道围岩变形控制标准为[u]=100 mm，显然umax＞[u]。而浅层围岩厚度为8.35 m，超出了岩石隧道中锚杆支护的锚固范围，因此需采用锚杆与锚索组合支护，参考相关工程案例，选择6组支护方案如表3所示。
表3 计算支护方案
Table 3 Calculation support schemes
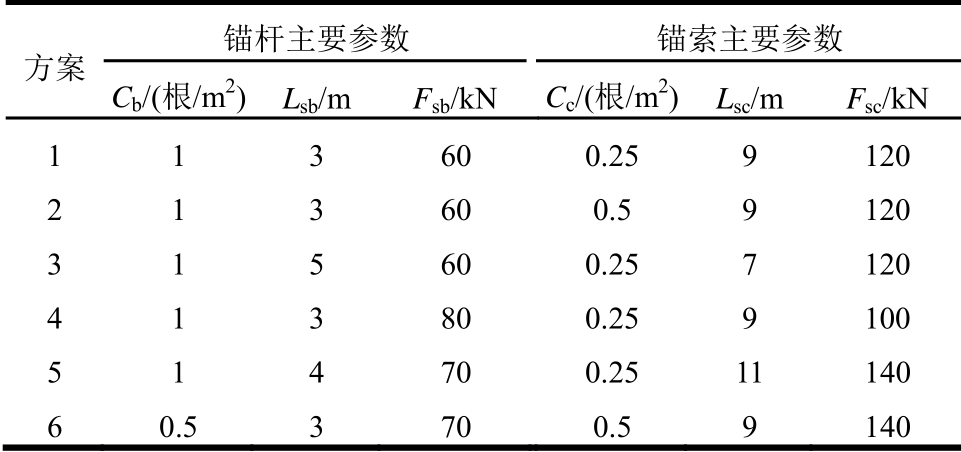
方案 锚杆主要参数 锚索主要参数 Cb/(根/m2) Lsb/m Fsb/kN Cc/(根/m2) Lsc/m Fsc/kN 1 1 3 60 0.25 9 120 2 1 3 60 0.5 9 120 3 1 5 60 0.25 7 120 4 1 3 80 0.25 9 100 5 1 4 70 0.25 11 140 6 0.5 3 70 0.5 9 140
需要指出，由于锚杆(索)支护的直径对其作用效果影响并不明显，因此本文主要对二者的布置密度、长度以及预应力的协同作用进行分析，计算时锚杆直径取为
锚索体截面积取为
锚杆弹性模量
锚索弹性模量
1)围岩变形控制效果分析
将上述各方案参数代入本文公式中计算可得到隧道洞壁最大位移如图9所示。
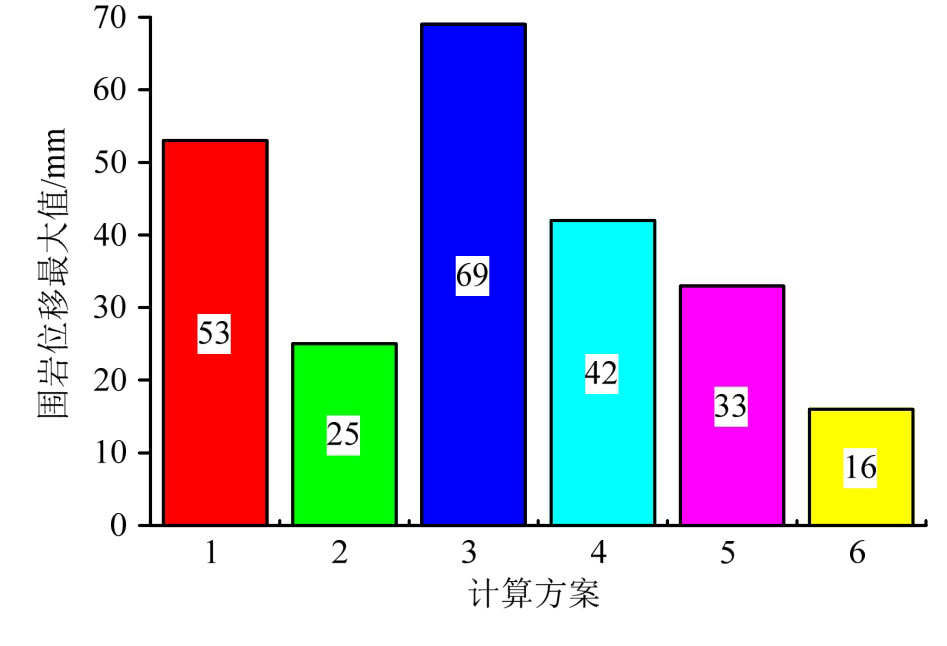
图9 各方案隧道围岩变形量
Fig.9 Tunnel surrounding rock deformation for each scheme
对比图9中各方案计算结果可知：
① 当锚索伸入深层围岩第一组结构层时的组合方案(如方案1)对围岩变形控制效果明显优于锚索仅作用于浅层围岩的方案(如方案3)，这说明在锚杆与锚索组合使用时，锚索的主要作用为将内侧锚杆-围岩整体结构与外侧深层围岩锚固在一起形成一个有机整体，从而增强浅层围岩完整性。
② 当锚杆密度适当时，较小的锚索密度即可有效控制围岩变形，这是由于浅层围岩的处置是围岩稳定性控制的核心，当锚杆-围岩整体结构具有足够的强度和完整性时即可保证隧道整体稳定性，因此锚杆布设密度应相对大一些，尽可能提高该整体结构的自承载能力，从而达到较为理想的锚固效果。
2)锚固体系协同作用分析
经式(78)检验表明，本文初步选取的各计算方案锚杆(索)均处于弹性状态。利用式(77)对各计算方案的协同度进行计算，结果如图10所示。
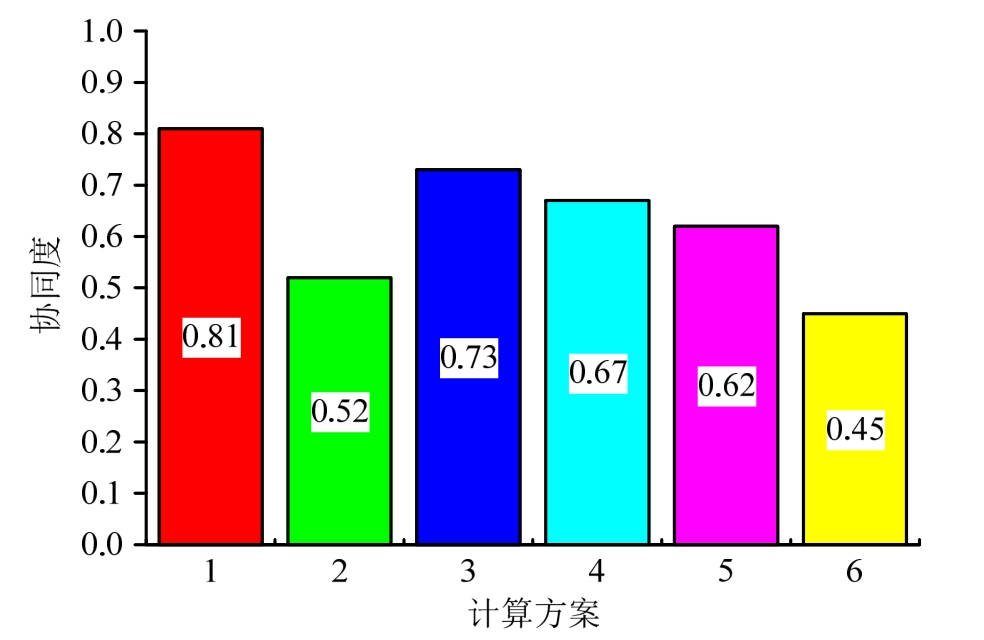
图10 各方案锚固协同度
Fig.10 The anchorage synergistic degree for each scheme
由图10分析可知：
① 协同效果最好的计算方案为方案1，协同效果较差的为方案6，这说明围岩变形控制效果好时锚固体系协同度并不一定大，需要通过协同优化设计寻求最优方案。综合以上分析可知，本算例中最优组合方案为方案1，围岩变形量为53 mm，满足施工要求。
② 锚杆与锚索的预应力大小对锚固体系协同度具有较为显著的影响。低预应力锚索与高预应力锚杆的组合或高预应力锚索与低预应力锚杆的组合均可能使得体系的协同程度降低，二者的预应力存在相对合理的取值区间。
③ 锚索密度过大时锚固体系协同程度降低，这是由于锚索分担的围岩荷载过多，锚索利用率较大，而锚杆力学性能未得到充分发挥，其利用率很低，在工程中应尽量避免此类设计。
④ 当锚索伸入深层围岩范围较大时，锚杆与锚索的平均利用率均较低，未形成协同支护，因此组合支护时锚索伸入深层围岩第1组结构层为宜。
5 结论
本文基于隧道围岩的复合结构特性，阐明了锚固体系协同作用原理，根据锚固体系与隧道复合围岩结构的相对位置关系，提出了锚固体系与隧道复合围岩结构协同作用的力学和数学模型，并对其全过程进行了解析，据此提出了锚固体系协同优化设计方法及评价体系，得到了以下主要结论：
(1)隧道围岩由内部稳定性较差的浅层围岩和外层承载能力较强的深层围岩复合而成，锚固体系一方面为浅层围岩提供径向约束力，并将浅层围岩的附加荷载传递到深层围岩中，调动围岩承载；另一方面在隧道周边形成一定拱效应，协助围岩荷载。
(2)通过对隧道锚杆支护参数的影响分析可知，增大锚杆长度、预应力以及布置密度对控制围岩变形作用影响显著，而锚杆直径对围岩变形影响较小。计算表明，锚杆端部伸入深层围岩第一组结构层时对围岩位移控制效果良好，各参数存在相对经济合理的取值。
(3)锚固体系协同作用核心为通过锚杆与围岩形成整体结构，同时作为锚索悬吊作用的基础，调动深层围岩承载，其内涵包括锚固体系与复合围岩结构的相互作用、锚杆(索)单一支护型式的参数匹配以及锚杆、锚索之间的协同作用等3个方面，其本质为变形协调和围岩荷载的合理分配。
(4)通过对锚固体系的协同效应3个方面进行定量研究，提出了采用围岩变形量和协同度2个指标来衡量锚杆与锚索的协同作用效果，建立了锚固体系协同作用评价体系，据此提出了基于锚固体系协同作用的隧道锚固参数确定方法，为定量化设计隧道锚固支护体系提供一种思路。
[1]康红普, 王金华, 林健.煤矿巷道支护技术的研究与应用[J].煤炭学报, 2010, 35(11): 1809—1814. Kang Hongpu, Wang Jinhua, Lin Jian.Study and application of roadway support techniques for coal mines [J].Journal of China Coal Society, 2010, 35(11): 1809—1814.(in Chinese)
[2]Stille H, Holmberg M, Nord G.Support of weak rock with grouted bolts and shotcrete [J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1989, 26(1): 99—113.
[3]Fahimifar A, Soroush H.A theoretical approach for analysis of the interaction between grouted rockbolts and rock masses [J].Tunnelling and Underground Space Technology, 2005, 20(4): 333—343.
[4]李大伟, 侯朝炯.围岩应变软化巷道锚杆支护作用的计算[J].采矿与安全工程学报, 2008, 25(1): 123—126.Li Dawei, Hou Chaojiong.Calculation of bolt support in surrounding rock strain softening roadway [J].Journal of Mining & Safety Engineering, 2008, 25(1): 123—126.(in Chinese)
[5]余伟健, 高谦, 朱川曲.深部软弱围岩叠加拱承载体强度理论及应用研究[J].岩石力学与工程学报, 2010, 29(10): 2135—2142. Yu Weijian, Gao Qian, Zhu Chuanqu.Study of strength theory and application of overlap arch bearing body for deep soft surrounding rock [J].Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2135—2142.(in Chinese)
[6]Fengyun Wang, Deling Qian.Difference solution for a circular tunnel excavated in strain-softening rock mass considering decayed confinement [J].Tunnelling and Underground Space Technology, 2018(82): 66—81.
[7]Ghorbani A, Hasanzadehshooiili H.A novel solution for ground reaction curve of tunnels in elastoplastic strain softening rock masses [J].Journal of Civil Engineering and Management, 2017, 23(6): 773—786.
[8]张顶立, 陈立平.隧道围岩的复合结构特性及其荷载效应[J].岩石力学与工程学报, 2016, 35(3): 456-469. Zhang Dingli, Chen Liping.Compound structural characteristics and load effect of tunnel surrounding rock [J].Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 456—469.(in Chinese)
[9]孙毅, 张顶立.隧道复杂支护结构体系的协同作用原理[J].工程力学, 2016, 33(12): 52—62. Sun Yi, Zhang Dingli.Synergy principle of complex supporting structural systems in tunnels [J].Engineering Mechanics, 2016, 33(12): 52—62.(in Chinese)
[10]张顶立.隧道围岩稳定性及其支护作用分析[J].北京交通大学学报, 2016, 40(4): 9—18. Zhang Dingli.Analysis of surrounding rock stability and support action in tunnels [J].Journal of Beijing Jiaotong University, 2016, 40(4): 9—18.(in Chinese)
[11]Bobet A, Einstein H H.Tunnel Reinforcement with Rockbolts [J].Tunnelling and Underground Space Technology, 2011, 26(1): 100—123.
[12]沈华章, 王水林, 刘泉声.模拟应变软化岩石三轴试验过程曲线[J].岩土力学, 2014, 35(6): 1647—1654. Shen Huazhang, Wang Shuilin, Liu Quansheng.Simulation of constitutive curves for strain-softening rock in triaxial compression [J].Rock and Soil Mechanics, 2014, 35(6): 1647—1654.(in Chinese)
[13]孙振宇, 张顶立, 房倩, 等.隧道初期支护与围岩相互作用的时空演化特性[J].岩石力学与工程学报, 2017, 36(增2): 3943—3956. Sun Zhenyu, Zhang Dingli, Fang Qian, et al.Spatial and temporal evolution characteristics of interaction between primary support and tunnel surrounding rock [J].Chinese Journal of Rock Mechanics and Engineering, 2017, 36 (Suppl 2): 3943—3956.
[14]蔡美峰, 何满潮, 刘东燕.岩石力学与工程[M].北京: 科学出版社, 2002: 327—328. Cai Meifeng, He Manchao, Liu Dongyan.Rock mechanics and engineering [M].Beijing: Science Press, 2002: 327—328.(in Chinese)
[15]孙振宇, 张顶立, 房倩, 等.基于超前加固的深埋隧道围岩力学特性研究[J].工程力学, 2018, 35(2): 92—104. Sun Zhenyu, Zhang Dingli, Fang Qian, et al.Research on the mechanical property of the surrounding rock of deep-buried tunnel based on the advanced reinforcement [J].Engineering Mechanics, 2018, 35(2): 92—104.(in Chinese)
[16]Huang Z, Broch E, Lu M.Cavern roof stability- mechanism of arching and stabilization by rockbolting [J].Tunnelling and Underground Space Technology, 2002, 10(17): 249—261.
[17]Fahimifar A, Ranjbarnia M.Analytical approach for the design of active grouted rockbolts in tunnel stability based on convergence-confinement method [J].Tunnelling and Underground Space Technology, 2009, 24(4): 363—375.
[18]Brown E T, Bray J W, Ladanyi B, et al.Ground response curves for rock tunnels [J].Journal of Geotechnical Engineering, ASCE, 1983, 109(1): 15—39．
[19]CECS22: 2005, 岩土锚杆(索)技术规程[S].北京: 计划出版社, 2005. CECS22: 2005, The technical specifications for ground anchor [S].Beijing: China Planning Press, 2005.(in Chinese)
[20]Wang S L, Yin S D, Wu Z J.Strain-softening analysis of a spherical cavity [J].International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36: 182—202.
[21]左昌群, 丁少林, 刘代国, 等.加锚云母片岩隧道围岩失效特征及力学效应[J].现代隧道技术, 2014, 51(4): 39—45. Zuo Changqun, Ding Shaolin, Liu Daiguo, et al.Failure characteristics and the mechanical effect of mica schist in an anchored tunnel [J].Modern Tunnelling Technology, 2014, 51(4): 39—45.(in Chinese)
[22]龙景奎, 蒋斌松, 刘刚, 等.巷道围岩协同锚固系统及其作用机理研究与应用[J].煤炭学报, 2012, 37(3): 372—378. Long Jingkui, Jiang Binsong, Liu Gang, et al.Study on the mechanism and application of synergistic anchoring systems in roadway surrounding rocks [J].Journal of China Coal Society, 2012, 37(3): 372—378.(in Chinese)
[23]王琦, 李术才, 李为腾, 等.让压型锚索箱梁支护系统组合构件耦合性能分析及应用[J].岩土力学, 2012, 33(11): 3374—3384. Wang Qi, Li Shucai, Li Weiteng, et al.Analysis and application on combination components coupling of pressure relief anchor box beam support system [J].Rock and Soil Mechanics, 2012, 33(11): 3374—3384.(in Chinese)
[24]Hoek E.Tunnel support in weak rock [C]// Symposium of Sedimentary Rock Engineering, Taipei, 1998: 1—12.
[25]TB 10003—2005, 铁路隧道设计规范[S].北京：中国铁道出版社, 2005. TB 10003—2005, Code for Design of Railway Tunnel [S].Beijing: China Railway Publishing House, 2005.(in Chinese)
[26]Panet M.Analyse de la Stabilité d'un Tunnel Creusé dans un Massif Rocheux en Tenant Compte du Comportement aprés la Rupture [J].Rock Mechanics, 1976, 4(8): 209—223.