建筑结构的连续倒塌是指偶然荷载造成局部结构的小范围初始破坏，此后破坏在结构系统内传播导致整体结构或者大范围结构的倒塌[1]。连续倒塌是一个非线性动力过程，涉及材料的大变形、构件受力模式的变化和结构系统的内力重分布等[2—10]。准确评估和设计结构的抗连续倒塌能力需要采用非线性动力计算方法，以考虑非线性动力效应对变形和内力的影响，但非线性动力计算方法建模复杂且计算耗时，适用于安全等级高或结构体系复杂的建筑物。一般工程可采用建模和计算更为简便的线性或非线性的静力计算方法，利用动力放大系数对计算结果进行修正来近似考虑非线性动力效应的影响[11—12]。
目前国际上主要规范DOD2013[11]和GSA2013[12]在钢和混凝土框架结构连续倒塌抗力计算时所采用的动力放大系数如下：1)脆性结构仅采用基于力控制的线性静力方法，基于力的方法要求静力计算考虑的荷载和导致实际结构发生非线性动力倒塌的荷载相同，因此规范取动力放大系数为2，该条文要求结构在动力倒塌过程中处于弹性变形范围内；2)延性结构还可采用基于位移控制的线性或非线性静力方法，基于位移的方法要求静力计算考虑的变形和实际结构发生非线性动力倒塌的极限变形相同，其动力放大系数采用与延性相关的经验公式进行计算(其中线性分析采用延性有关的m系数、非线性分析直接采用延性系数)，该公式是通过拟合有限数量的3层和10层框架数值算例的计算结果得到的[13]。考虑我国规范对框架结构的延性要求以及计算准确性，非线性静力方法是最为合适的计算方法。但现有规范给出的经验公式可靠性不足且仅适用于小变形下的梁机制。本文前期工作中将混凝土框架的抗连续倒塌子结构简化为单自由度系统，基于等能量原理得到了混凝土框架在小变形梁机制下动力放大系数的理论解[14]，证明了现有规范给出的动力放大经验系数偏低不安全，并给出了大变形下悬链线机制的动力放大系数[15]。
现有数值和理论研究采用了理想化的假设前提，在反映实际动力效应规律时可能存在偏差，比如假设静力和动力条件下材料和构件的受力行为相同并且变形和损伤在塑性区均匀对称发展，因此有必要采用试验手段研究验证结构连续倒塌的动力效应。为节省试件数量开展更多的参数对比，目前的连续倒塌动力试验主要采用等力准则，采用静动力试验的对比结果分析动力放大系数。Tian等[16]研究了中柱拆除工况的梁柱子结构在等力准则下的内力放大系数，表明延性使得结构的动力放大系数小于2，在1.36～1.7之间分布。Qian等[17—18]研究了角柱拆除工况的梁柱子结构的动力响应，通过静动力试验对比推测该系列试件的动力放大系数在1.12和2.16之间。Pham等[19]对中柱拆除工况的梁柱子结构开展了动力及静力对比试验，发现动力放大系数在1.22～2.22之间，其中悬链线机制下的动力放大系数在2左右。这些试验受条件限制，有的静动力试验加载方式不同，有的仅简单对比单个动力工况和静力工况的结果，并且大部分试件批次不同混凝土强度差别较大、不同试件间考虑多种钢筋构造来考虑配筋率、钢筋构造、边界约束条件等对动力效应的影响，因此难以深入理解结构动力效应的变化规律。
本文设计制作了6个尺寸、配筋和边界条件完全相同的混凝土梁柱子结构试件，这些试件采用同一批混凝土进行浇筑，对试件分别进行了拆除中柱工况下的静力和动力连续倒塌试验。静力试验通过千斤顶对试件施加从零到倒塌极限的连续变形，获得了试件的静力抗力-变形全曲线。动力试验成功进行了4次，在试件上施加了4个不同等级的配重，然后通过瞬脱钩突然释放配重，使得试件进入动力倒塌过程并产生不同程度的动力破坏和变形。通过结构变形和材料应变响应分析了试件的动力倒塌破坏机理，并基于能量平衡原理分析了动力效应对结构连续倒塌抗力的影响。
1 试验概况
1.1 试件设计
参考了文献[20]的试验，设计了6根尺寸和配筋相同的试验梁，如图1所示。试验梁与原型结构按照1∶3的尺寸进行缩尺，由于本文研究侧重于动力效应，即结构静力和动力状态下抗力的相对值而非抗力绝对值，因此尺寸效应影响降低，文中不考虑该因素。为实现良好的固结边界条件，每3根试验梁和尺寸较大的边界梁整体浇筑，边界梁具有足够的刚度并通过焊接钢板与支座固定，边界梁上整体浇筑了两个吊梁保证试件吊装安全。试验梁有两跨，每跨2000 mm(含柱头)，截面尺寸170 mm× 85 mm，在顶底各配置两根直径8 mm的通长钢筋，并在每跨梁端480 mm内配置直径6 mm的顶部负弯矩筋，保护层厚度为6 mm。跨中和加密区箍筋配置见图2。6根试验梁均采用同批次的钢筋和混凝土进行制作，其材性试验结果见表1。
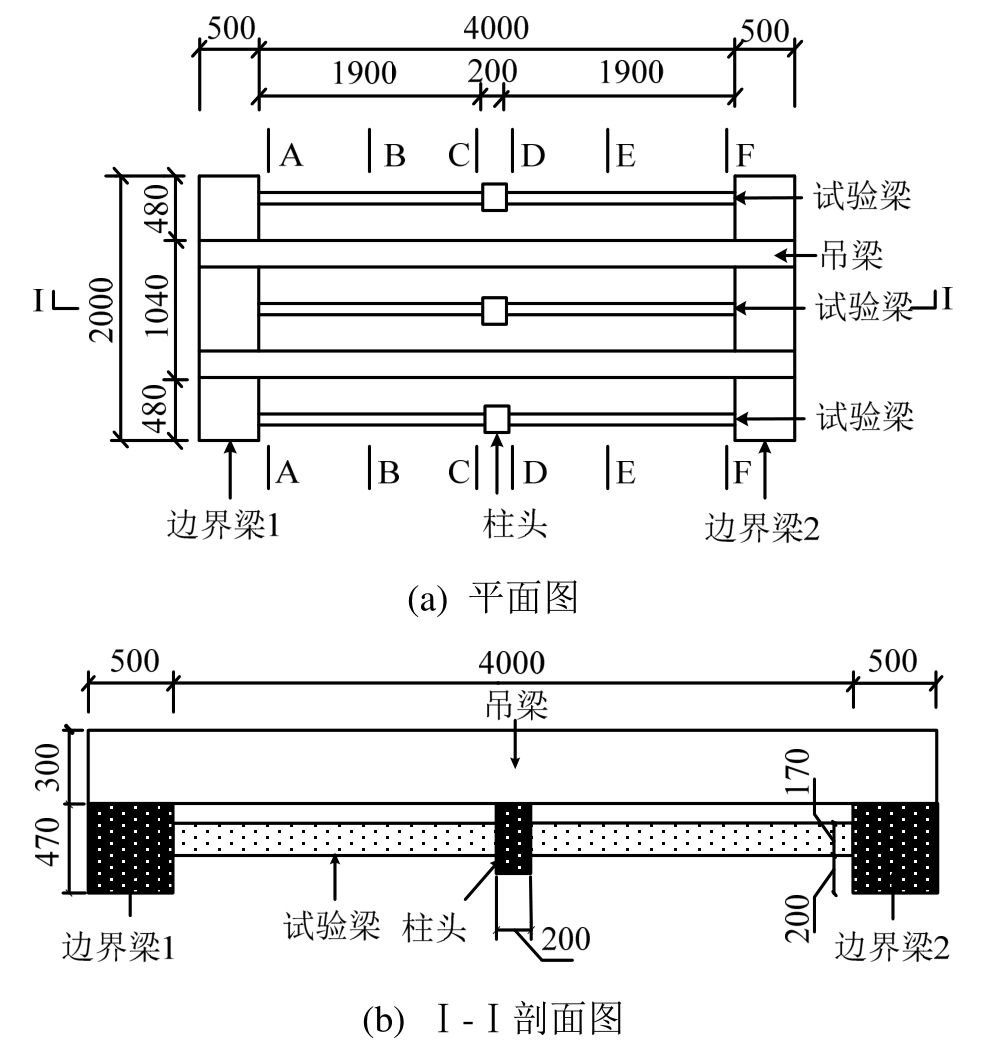
图1 试件尺寸
Fig.1 Dimensions of specimens
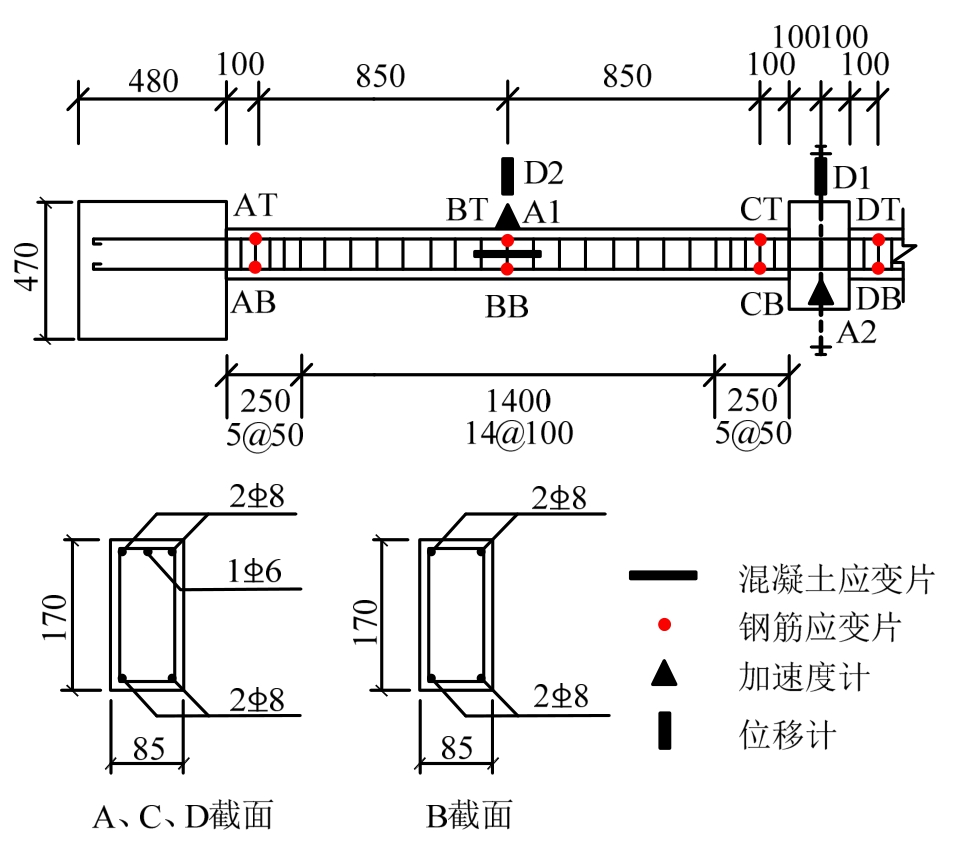
图2 试件配筋
Fig.2 Reinforcement of specimens
表1 试件材料性质
Table 1 Material properties for specimens
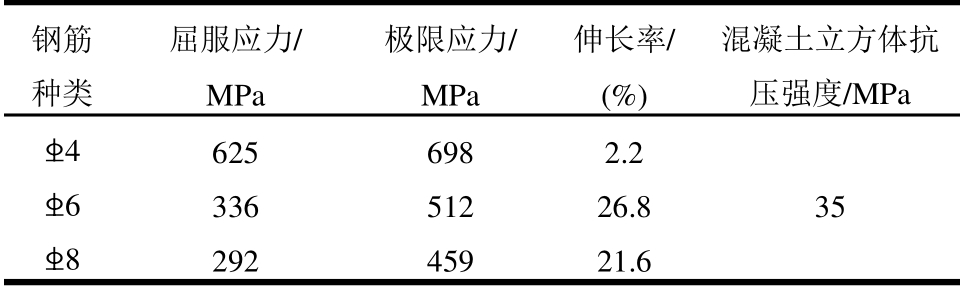
钢筋种类屈服应力/ MPa 极限应力/ MPa 伸长率/ (%)混凝土立方体抗压强度/MPa ■4 625 698 2.2 35 ■6 336 512 26.8 ■8 292 459 21.6
1.2 试验加载及测量方案
首先对1根梁(ST)采用静力进行加载，试验中在柱头处通过液压千斤顶对其施加持续向下的位移，使试件经历不同变形至完全倒塌破坏，测量了材料应变和承载力随变形增大的连续发展。动力试验方案如图3所示，试验中试件边界条件与静力试验相同。试验设计了专用的配重箱，其内可以放置不同数量的铅块，从而达到分级加载的目的。配重箱用夹板和螺杆与柱头固定，箱内用螺杆和螺栓固定铅块，防止配重系统的自振动。试验时先将柱头与瞬脱钩连接，然后将配重系统和柱头固定连接，然后突然释放瞬脱钩使得试件进入动力倒塌过程。成功对剩余的5个试件中的3个开展了4次动力倒塌试验，加载的总重力(包括铅块、配重箱及连接件)分别为：14.11 kN(DT-1)，19.21 kN(DT-2)，21.17 kN (DT-3)，28.03 kN(DT-4)，其中DT-1试验中试件变形很小，挠度仅31 mm，对应结构耗能也较小，增加荷载进行了DT-2试验。
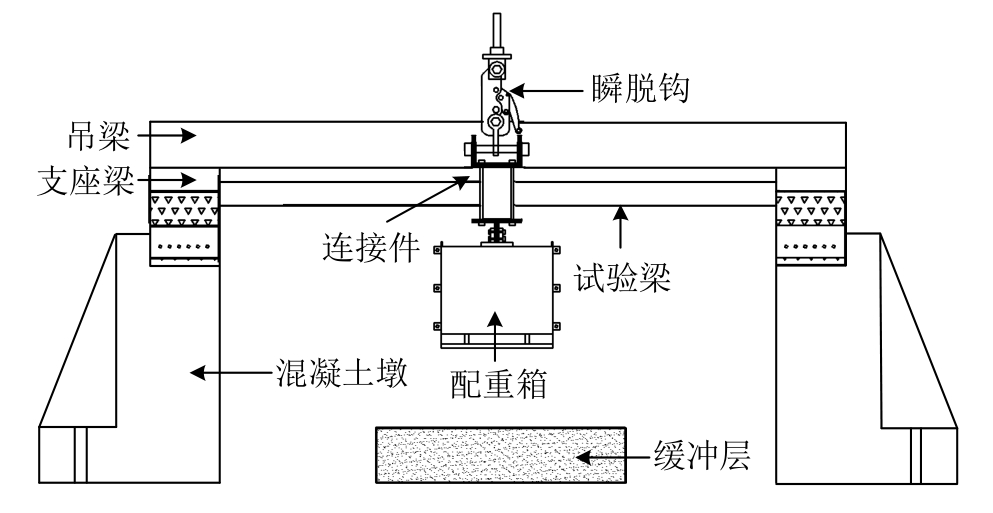
图3 动力试验示意图
Fig.3 Test set-up of dynamic tests
采用2000 Hz的频率采集位移、应变数据。每个试验的重力释放时间见表2，均小于连续梁自振周期的1/10，表明释放装置释放时间足够短不会引起附加振动。表中释放时间指从开始释放到瞬脱钩完全不受力的时间，实测振动周期为重物到达极限位移后在极限位移附近做的类似简谐运动的振动周期，振幅指该振动的第1个周期往返最大位移差值。试验测量了支座梁端、跨中和柱头梁端截面处的钢筋应变以及跨中混凝土应变；在柱头和跨中位置分别布置了激光位移计和加速度计(图2)。
表2 动力试验试件动力响应
Table 2 Dynamic responses of specimens in dynamic tests
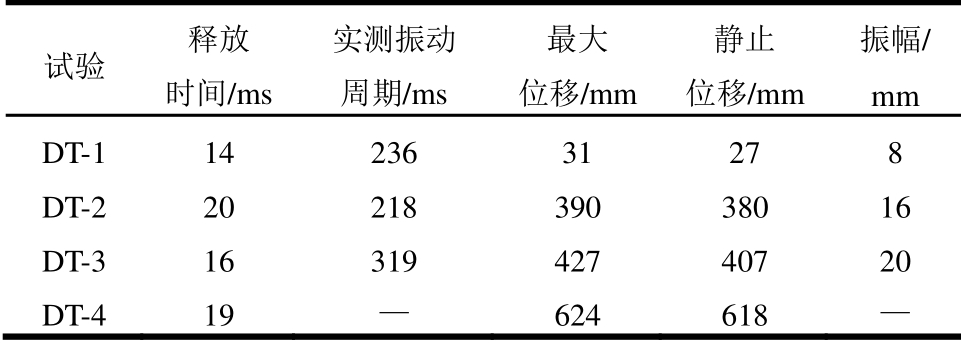
试验 释放 时间/ms 实测振动 周期/ms 最大 位移/mm 静止 位移/mm振幅/ mm DT-1 14 236 31 27 8 DT-2 20 218 390 380 16 DT-3 16 319 427 407 20 DT-4 19 — 624 618 —
2 试验结果
2.1 试验现象
静力试验中，在小变形下试件先后在支座梁端(A/F截面)顶部和柱头梁端(C/D截面)底部出现多条受拉裂缝，在相应的受压区出现混凝土压酥现象。当中柱位移达到31 mm时试件承载力达到压拱机制峰值承载力28.21 kN。此后承载力迅速下降，混凝土不断剥落。当中柱位移到达到159 mm时，承载力下降开始回升，试件进入悬链线机制受力阶段。在此阶段，沿梁长度方向出现数条垂直于梁轴线、沿梁高通长的受拉裂缝。当位移达到405 mm和437 mm时D截面底部的两根钢筋依次断裂，导致承载力出现两次波动，试验终止，最终悬链线机制的最大承载力为34.93 kN。静力试验中试件的 变形受力相对充分，梁端受拉裂缝开展较多，最终达到极限破坏状态前其中两条裂缝处张开较大，而在受压区混凝土压碎剥落区域较大，如图4所示。
在DT-1的动力试验中，瞬间释放结构后试件发生向下的变形，其中在第1次振动中达到最大位移31 mm，此后在阻尼作用下振动逐渐停止，位移稳定在27 mm，梁端仅产生轻微的受拉裂缝。由于试件变形很小，在此试件上将配重增加至19.21 kN重新进行试验，最终试件的最大位移为390 mm。相比静力试验，试件局部变形集中，梁端仅在梁和中柱柱头/边界梁的界面和梁端截面发展出两条大的受拉裂缝，没有其他细微裂缝开展，混凝土压碎区的长度减小。随着配重增大这种现象更加明显，在荷载最大的DT-4试验(配重28.03 kN)中，中柱梁端裂缝仅出现在梁柱界面处且最终裂缝宽度为58 mm，远大于其他试件，这导致梁端钢筋变形在该裂缝处的集中。另外，该试件中柱梁端的受压区没有压酥破坏的迹象，很小的局部混凝土压碎是梁发生大转动变形时梁和中柱柱头/边界梁挤压所致，没有静力试验中试件充分弯曲变形所产生的受压区范围大(图4)，动力条件下试件的应力集中以及钢筋滑移导致的截面转动变形增大导致了该现象的出现。
图4 试验裂缝
Fig.4 Cracks of specimens
2.2 位移时程曲线
采用激光位移计测量得到了柱头位移随时间的变化，如图5所示。可以看到，随着配重增大，试件的挠度和变形发展速度(位移曲线斜率)增大，表明试件倒塌的速度和加速度更大，结构需要提供更大的抗力和变形来消耗结构势能转化的动能。其中DT-1试验中梁发生轻微塑性变形，钢筋进入强化阶段，导致随后进行的DT-2试验的初始位移和DT-3重叠，但由于试验荷载大，最终DT-3最大位移比DT-2大。对于DT-4试验，荷载已经接近极限承载力，试件后期没有明显的振动。但是值得注意的是，极限荷载下的动力试验中试件发生的变形远大于静力试验(从463 mm增大到624 mm)，并且钢筋并没有发生断裂。根据上节描述的实验现象可知，动力条件下梁的转动变形发展迅速，梁顶钢筋较早参与受拉分担了底部钢筋受力，避免底部钢筋断裂。另外，动力条件下材料的强度和极限应变提高[21—22]对此也有帮助。
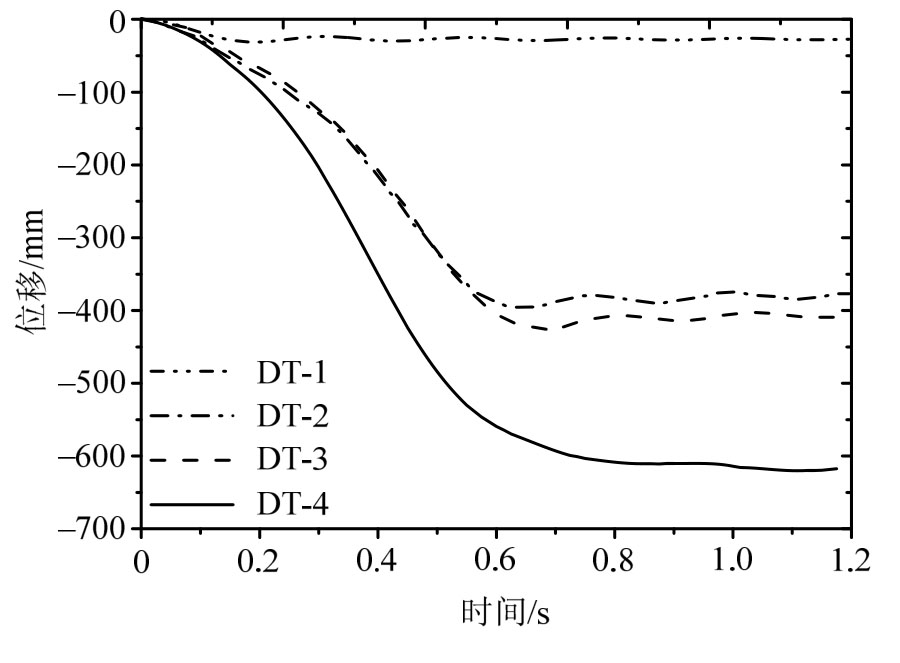
图5 位移-时间曲线
Fig.5 Displacement-time curves
2.3 钢筋应变分析
关键截面的钢筋应变如图6所示，为了方便与静力试验比较，横坐标取中柱位移。倒塌是结构的极限动力破坏行为，本文动力试验中实测最大钢筋应变率达到1.4 s-1，其他动力连续倒塌试验实测应变率也在10-2～10-1量级[23]，远高于地震研究中常见的应变率范围(10-4～10-2)[21—22]。由于应变值大且应变率高，在试验中部分应变片破坏，导致应变数据失效而被剔除。从应变数据发现了两个现象：
1)材料应变率效应
大部分动力试验的材料应变比静力试验小，如A、C、D截面受压区钢筋应变。这印证了试验现象的发现：加载速度对材料的变形产生影响，导致受压区压酥现象轻、材料破坏范围小，受拉区裂缝集中开展。动力试验的材料应变率效应(强度和刚度的提高)是造成该现象的原因。
2)非对称受力
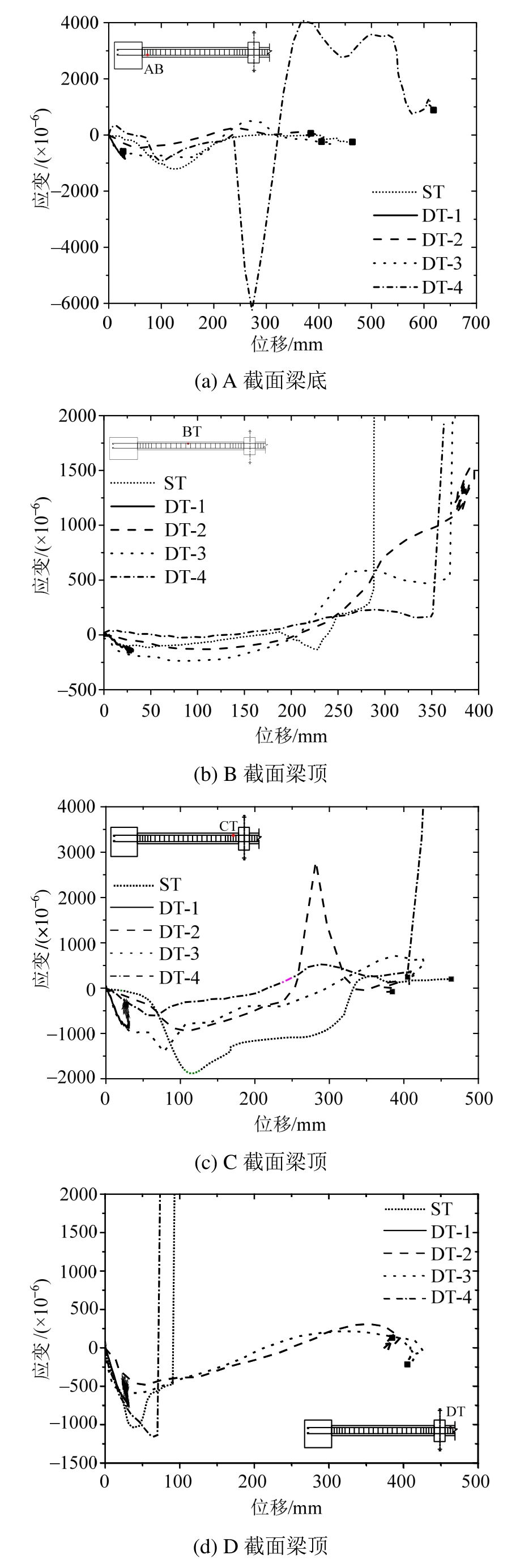
图6 各截面梁顶钢筋应变
Fig.6 Steel strains at different sections
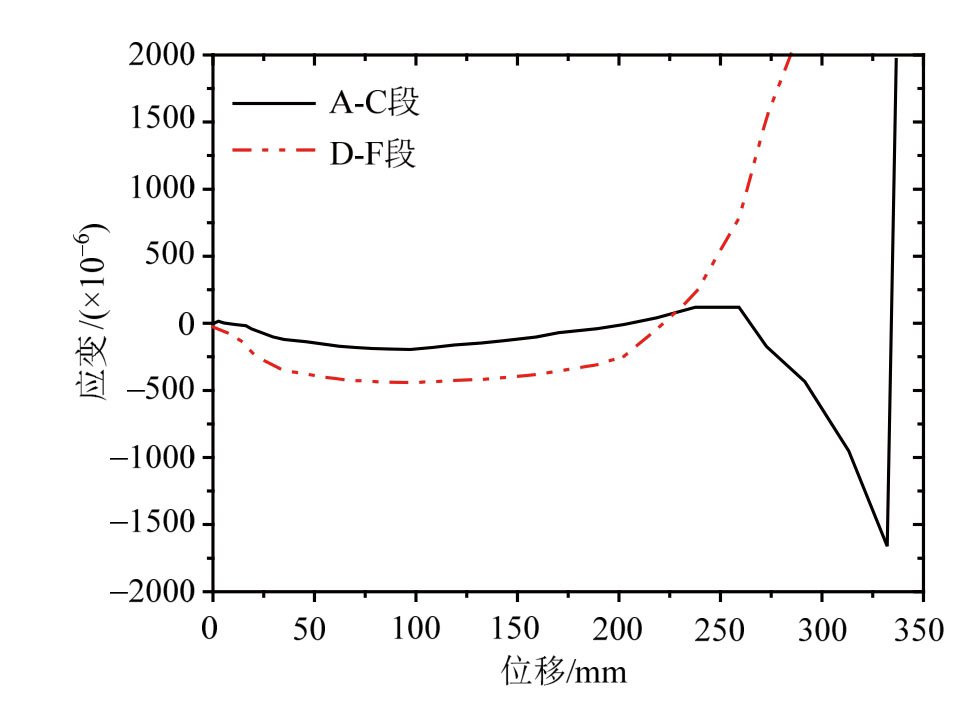
图7 DT-4试件跨中混凝土应变-位移曲线
Fig.7 Concrete strain at mid-span of DT-4
实际结构存在初始缺陷，加载力存在偏心，因此实际结构受力往往是不对称的，动力场景下该现象变得突出。图7给出了DT-4试验的两侧梁跨中混凝土应变，可以看到加载初期随着变形加大，不 均匀受力导致应变差不断增大。在构件层次上，将会导致积累的梁轴向出现变形差，当变形差足够大时，构件约束使得两侧梁的变形重新调整、应变重新同步发展，这导致材料应变出现一个波动(图6(a)和图7中250 mm～325 mm之间)。试件的这种不对称受力还会进一步减弱结构的实际承载力。
3 连续倒塌动力抗力评估
3.1 狭义和广义的动力效应
结构的静力和动力倒塌抗力不同[14—15]：1)静力抗力是结构承受准静态倒塌荷载时的承载力，结构的静力抗力和倒塌重力荷载间满足静力平衡条件，结构的完整静力抗力-变形曲线可通过一次静力Pushdown试验获得；2)动力抗力是结构承受动态倒塌荷载时的承载力，结构的动力抗力和倒塌重力荷载满足动力平衡条件和能量平衡条件，一次动力倒塌试验仅能获得动力倒塌荷载-抗力曲线上的一个性能点，因此需要一系列动力试验才能获得结构的完整动力倒塌荷载-变形曲线。目前的理论研究中，通常采用能量方法将静力-变形能力曲线转换为动力倒塌荷载-变形能力曲线[14—15]。两个曲线的比值就是结构系统抗连续倒塌的动力放大系数，动力放大系数是位移的函数，而位移和结构变形(延性)相关。因此，目前规范[11—12]和研究[14—15]给出了目标位移下动力放大系数和延性系数的关系，为工程设计参考。在本文研究中，称这种仅考虑结构连续倒塌动力平衡条件对抗力和变形需求的影响为狭义的动力效应，相应的结构静力倒塌抗力和动力倒塌抗力为结构狭义静力抗力和狭义动力抗力。
本文试验表明动力条件下材料应变率效应、结构应力集中和非对称受力，导致结构自身抗力发生改变，进一步对结构的内力和变形产生影响。这一影响包含结构动力平衡条件对结构的影响，因此称之为广义的动力效应，相应的结构静力倒塌抗力和动力倒塌抗力为结构广义静力抗力和广义动力抗力。需要说明的是广义静力抗力是指考虑动力受力条件、与倒塌荷载满足静力平衡的结构抗力，该概念有助于动力效应的分析。
3.2 广义静力抗力曲线
静力试验获得的试件狭义静力抗力(荷载-中柱位移曲线)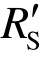
如图8(a)红色虚线所示，广义静力抗力
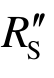的曲线按本节方法近似获得。考虑动力试验中配重系统时刻满足动力平衡方程：
其中：P为配重箱及结构自身重力，试验中已知；Δ为中柱位移；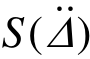
为配重箱及结构自身的惯性力，可由动力试验的加速度记录计算获得；
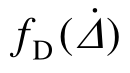和结构的广义静力抗力
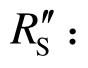fS(Δ)为结构的阻尼力和恢复力，这两项之和即为
根据式(2)和实测数据可以直接计算获得结构的广义静力抗力。由于转动惯量引起的抗力误差在3%之内，故该方法忽略转动惯量产生的误差。需要注意的是，计算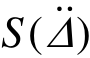
时结构自重取试件总质量，
取柱头处实测加速度值。由于DT-4试验中试件绝对变形和变形速度最大、能够激励出结构的最大动力效应影响，并且结构自重仅为附加质量的5.4%，近似计算误差最小，因此采用该试验结果进行分析。由于实际试验中的非理想受力状态，根据实测加速度数据直接得到的广义静力抗力是振荡的(图8(b))，因此采用9次多项式方程对该曲线拟合，获得了光滑连续的广义静力抗力曲线。
广义静力抗力曲线具有3个特点：1)梁机制下，试件位移速度相对较小，因此材料应变率效应影响不大，结构应力集中和非对称受力导致广义静力抗力峰值比狭义静力抗力小22%，意味着不同于传统的观点，即认为动力作用下由于应变率效应等因素使得承载力增大。实际试验数据表明梁机制阶段的承载力比静力试验获得的数据更小。表明相比于应变率效应对材料强度的增加，不均匀的受力以及偏心等作用更显著，导致该阶段的承载力下降；2)悬链线机制下，虽然应力集中和非对称受力的影响存在，但是材料应变率效应影响增大，试件在经历非对称受力的再平衡后(325 mm)，广义静力抗力大于狭义静力抗力，同时极限变形也被推迟；3)虽然没有发生钢筋断裂，但是广义静力抗力在后期(550 mm后)下降，这一方面是因为试件趋于静止状态，应变率降低使得材料增强效应减小，另一方面是因为钢筋接近极限应变，强度也开始下降所致。
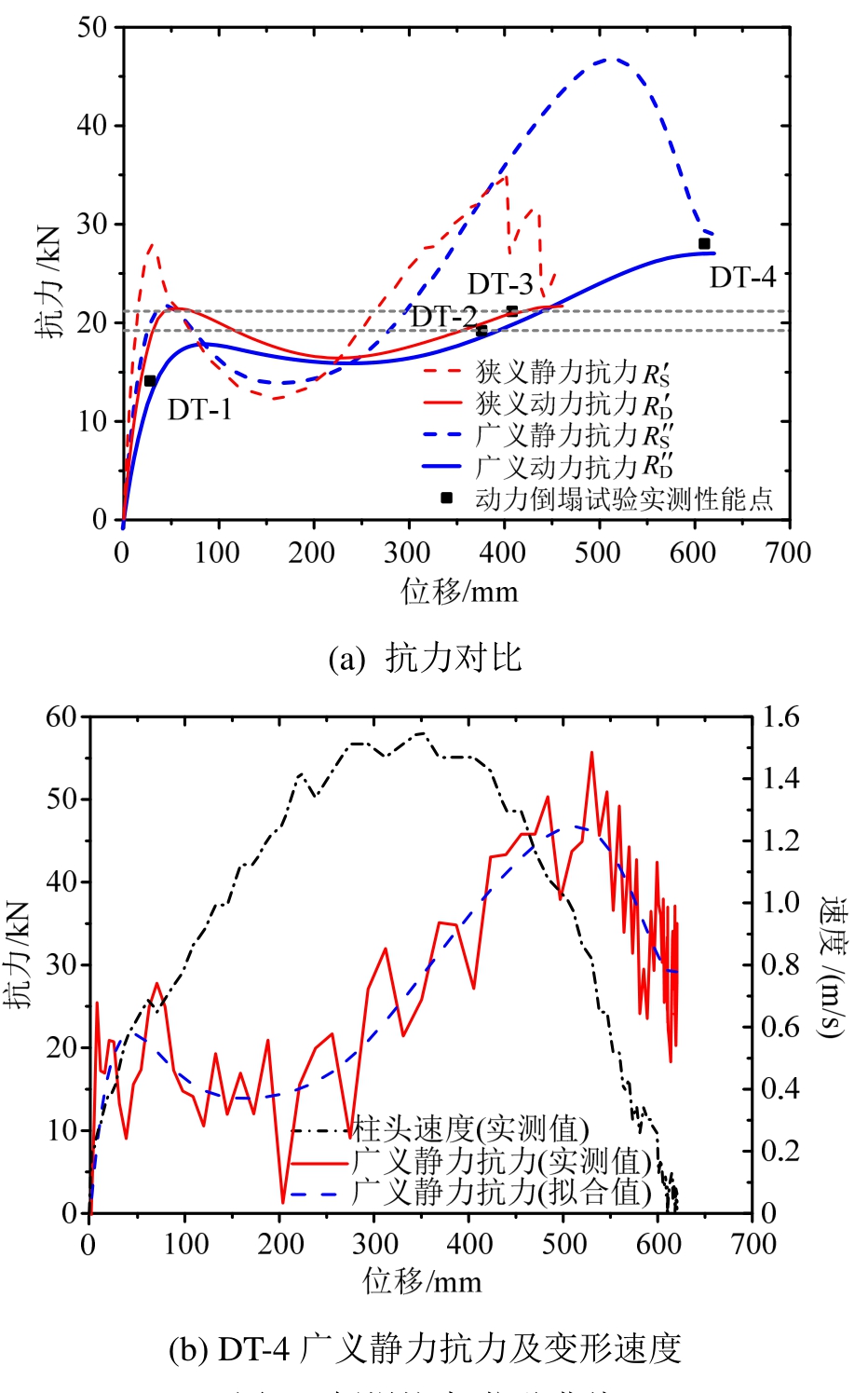
图8 倒塌抗力-位移曲线
Fig.8 Collapse resistance-displacement curves
3.3 动力抗力曲线
基于等能量原理可以将静力抗力曲线转换为动力抗力曲线，所采用的计算原理如下：
试件的静力抗力RS可以描述为柱头位移 Δ的函数：
倒塌过程中结构的弹塑性耗能U满足：
倒塌过程中结构重力荷载G的势能W可转化为结构动能：
当倒塌被结构有效抵抗时，势能转化的动能要被结构有效耗散，即满足：
此时重力荷载G即为结构抵抗倒塌的最低抗力，因为能量平衡原理描述的是结构的动态平衡状态，所以该抗力即为结构的动力抗力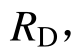
满足：
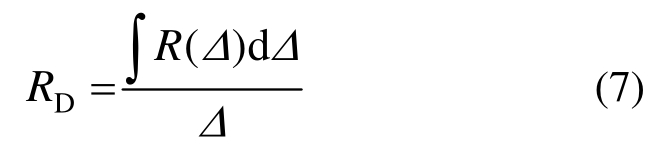
通过该方法得到的狭义动力抗力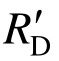
和广义动力抗力
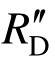如图8(a)细实线和粗实线所示。
3.4 实验数据检验
4次动力试验的性能点如图8(a)中4个方形点所示，其中每个点的横坐标为动力倒塌试验中结构的最大位移，纵坐标为试验中结构自重和配重的总重力。从曲线对比，可以发现：广义动力抗力曲线能够更好地描述结构的实际性能，4个性能点均穿过了该曲线。特别是DT-2和DT-3，如按照狭义动力抗力曲线进行分析，小变形下结构具有两个抗力相同的性能点，试件应该在该变形下达到新的平衡状态，结构的倒塌变形分别为29 mm或69 mm (DT-2)、39 mm或55 mm (DT-3)。但根据广义动力抗力曲线，小变形下结构抗力低，因此试件不可能在该变形下平衡，只能在实测位移376 mm或408 mm时达到平衡。这进一步证明了上述试验和理论分析的正确性。
3.5 动力效应分析
根据动力效应的定义[14—15]，取等位移条件下的结构静力抗力和动力抗力之比为动力放大系数，其中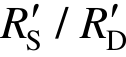
是不考虑动力损伤的现有理论动力放大系数，
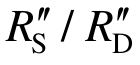是考虑动力损伤的实际动力放大系数。本试验获得的2类动力放大系数如图9所示，其中考虑到线弹性阶段的动力放大系数为2，故各动力放大系数曲线取第1根钢筋屈服后的部分。可以发现有以下3个规律：
1)抗连续倒塌设计目标机制(小变形的梁机制和大变形的悬链线机制)下动力放大效应较大，而两个机制转换区间的动力放大效应较小，动力放大系数甚至小于1.0。这是因为RS是当前状态指标而RD是累积耗能指标，两者的发展不一致所致。在机制转换阶段：结构在静平衡中处于“失稳”状态、静力抗力RS最低；在动平衡中结构刚经历梁机制下的承载力峰值，消耗了大量的动能，此时动力抗力RD下降平缓。这导致机制转换阶段结构动力放大系数小于1。
2)梁机制下：动力损伤对该阶段动力效应的影响比材料应变率效应大，此时结构累积耗能不大，动力损伤能够同时降低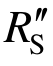
和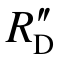
，导致实际动力放大系数
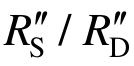大于理论动力放大系数
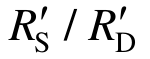。在极限位移处(85%
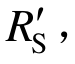位移为42 mm)，理论和实际的动力放大系数分别为1.12和1.41。这表明传统的抗连续倒塌动力效应理论低估了结构的动力效应。
3)悬链线机制下：材料应变率效应对该阶段的影响增强，但是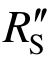
增大快于累积耗能指标
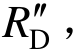使得后期实际动力放大系数
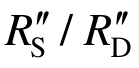大于理论动力放大系数
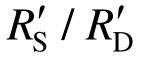。在设计最关注的位移为 L/5 (400 mm)处，理论和实际动力放大系数分别为1.64和1.74。这表明传统理论同样低估了结构的动力效应，但是原因和梁机制不同。
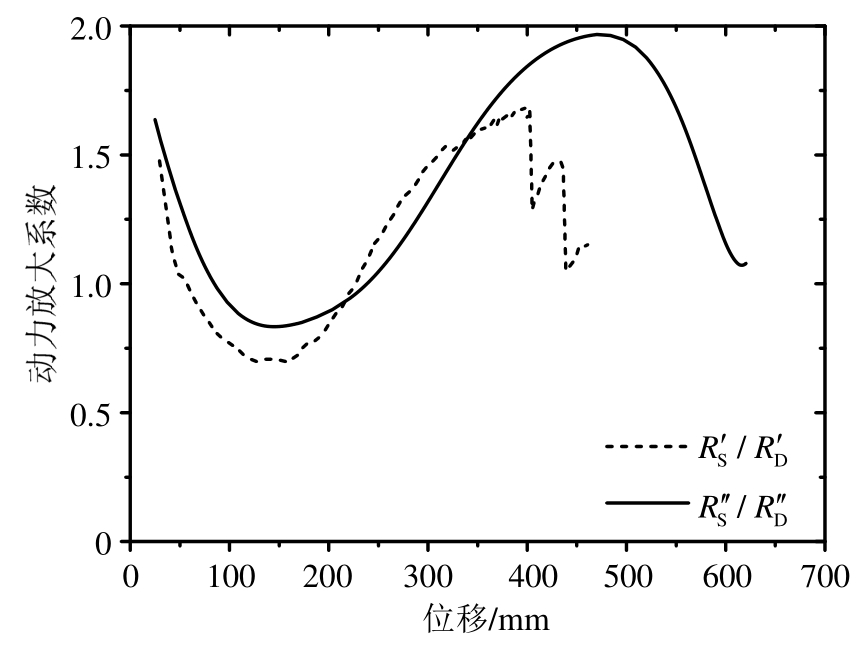
图9 动力放大系数对比
Fig.9 Comparison of DAFs
4 结论
本文对4个尺寸和配筋完全相同的混凝土试验梁柱子结构分别进行1次静力和4次动力连续倒塌试验，对比分析了结构的动力效应，主要结论如下：
(1)动力试验中材料应变速度达到1.4×100量级，受动力损伤集中和材料应变率效应影响，梁端受拉裂缝集中开展，受压区混凝土压碎剥落区域较小；
(2)因为考虑动力损伤和材料应变率对结构自身抗力特征的影响，广义动力抗力能够更加准确地描述结构在实际动力连续倒塌过程中的抗力需求；
(3)动力损伤(包括集中和非对称受力)对梁机制动力效应的影响大，材料应变率效应对悬链线机制动力效应的影响大，在工程感兴趣的目标位移处，结构的实际动力放大系数均大于不考虑动力损伤和材料应变率效应的传统理论预测值。
[1]ASCE/SEI 7-10, Minimum design loads for buildings and other structures [S].Reston, Virginia: American Society of Civil Engineers, 2010.
[2]郭义庆, 喻军.单柱失效下结构连续倒塌的动力响应分析[J].工程力学, 2017, 34(4): 72—77.Guo Yiqing, Yu Jun.Dynamic structural response of progressive collapse under a single-column-removal scenario [J].Engineering Mechanics, 2017, 34(4): 72—77.(in Chinese)
[3]喻莹, 谭长波, 金林, 等.基于有限质点法的单层球面网壳强震作用下连续倒塌破坏研究[J].工程力学, 2016, 33(5): 134—141.Yu Ying, Tan Changbo, Jin Lin, et al.Research on seismic progressive collapse of single-layer reticulated dome using the finite particle method [J].Engineering Mechanics, 2016, 33(5): 134—141.(in Chinese)
[4]孟宝, 钟炜辉, 郝际平.不同跨度比下栓焊刚性连接梁柱子结构抗倒塌性能试验研究[J].工程力学, 2018, 35(1): 79—87.Meng bao, Zhong Weihui, Hao Jiping.Experimental study on anti-collapse performance for beam-column assemblies with bolt and weld rigid connection based on different span ratio [J].Engineering Mechanics, 2018, 35(1): 79—87.(in Chinese)
[5]潘毅, 陈侠辉, 姚蕴艺, 等.基于抽柱法的无粘结预应力装配式框架结构连续倒塌分析[J].工程力学, 2017, 34(12): 162—170.Pan Yi, Chen Xiahui, Yao Yunyi, et al.Progressive collapse analysis of unbonded post-tensioned precast RC frame structures using column removal method [J].Engineering Mechanics, 2017, 34(12): 162—170.(in Chinese)
[6]Peng Z, Orton L S, Liu J, et al.Experimental study of dynamic progressive collapse in flat-plate buildings subjected to an interior column removal [J].Journal of Structural Engineering, ASCE, 2018, 144(8): 04018094.
[7]Gao S, Xu M, Zhang S.Dynamic analysis of concrete-filled steel tube composite frame against progressive collapse based on benchmark model [J].Advances in Structural Engineering, 2018, 21(7): 1021—1035.
[8]Ma K, Xu Y, Li W.Dynamic response analysis of steel frame with a sudden removal first floor column [J].Journal of Intelligent and Fuzzy Systems, 2018, 34(2): 1133—1140.
[9]高佳明, 刘伯权, 黄华, 等.带板钢筋混凝土框架连续倒塌理论分析[J].工程力学, 2018, 35(7): 117—126.Gao Jiaming, Liu Boquan, Huang Hua, et al.Theoretical analysis on the progressive collapse of RC frame structures with slabs [J].Engineering Mechanics, 2018, 35(7): 117—126.(in Chinese)
[10]周云, 陈太平, 胡翔, 等.考虑周边结构约束影响的RC框架结构防连续倒塌性能研究[J].工程力学, 2018, 36(1): 216—226.Zhou Yun, Chen Taiping, Hu Xiang, et al.Progressive collapse resistance of RC frame structures considering surrounding structural constraints [J].Engineering Mechanics, 2018, 36(1): 216—226.(in Chinese)
[11]DOD2013, Design of buildings to resist progressive collapse [S].Washington D.C.: Department of Defense, 2013.
[12]GSA2013, Alternate path analysis and design guidelines for progressive collapse resistance [S].Washington D.C.: the U.S.General Services Administration, 2013.
[13]Marchand K, McKay A, Stevens D.Development and application of linear and non-linear static approaches in UFC 4-023-03 [C]// Lawrence G, Todd H, Mark W, Marc H.Proceedings of the 2009 Structures Congress.Texus: American Society of Civil Engineers, 2009: 1729—1738.
[14]李易, 叶列平, 陆新征.基于能量方法的RC框架结构连续倒塌抗力需求分析I：梁机制[J].建筑结构学报, 2011, 32(11): 1—8. Li Yi, Ye Lieping, Lu Xinzheng.Progressive collapse resistance demand of RC frame structures based on energy method I: Beam mechanism [J].Journal of Building Structures, 2011, 32(11): 1—8.(in Chinese)
[15]李易, 陆新征, 叶列平.框架结构连续倒塌抗力需求分析II：悬链线机制[J].建筑结构学报, 2011, 32(11): 9—16. Li Yi, Lu Xinzheng, Ye Lieping.Progressive collapse resistance demand of RC frame structures based on energy method II: Catenary mechanism [J].Journal of Building Structures, 2011, 32(11): 9—16.(in Chinese)
[16]Tian Y, Su Y.Dynamic response of reinforced concrete beams following instantaneous removal of a bearing column [J].International Journal of Concrete Structures and Materials, 2011, 5(1): 19—28.
[17]Qian K, Li B.Performance of three-dimensional reinforced concrete beam-column substructures under loss of a corner column scenario [J].Journal of Structural Engineering, ASCE, 2013, 139(4): 584—594.
[18]Qian K, Li B.Dynamic performance of RC beam-column substructures under the scenario of the loss of a corner column-Experimental results [J].Engineering Structures, 2012, 42: 154—167.
[19]Pham A T, Tan K H.Experimental study on dynamic responses of reinforced concrete frames under sudden column removal applying concentrated loading [J].Engineering Structures, 2017, 139: 31—45.
[20]初明进, 周育泷, 陆新征, 等.钢筋混凝土单向梁板子结构抗连续倒塌试验研究[J].土木工程学报, 2016, 49(2): 31—40.Chu Mingjin, Zhou Yulong, Lu Xinzheng, et al.An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse [J].China Civil Engineering Journal, 2016, 49(2): 31—40.(in Chinese)
[21]Bischoff P H, Perry S H.Compressive behavior of concrete at high-strain rates [J].Materials and Structures, 1991, 24(144): 425—450.
[22]Majzoobi G H, Mahmoudi A H, Moradi S.Ductile to brittle failure transition of HSLA-100 Steel at high strain rates and subzero temperatures [J].Engineering Fracture Mechanics, 2016, 158: 179—193.
[23]Peng Z, Orton L S, Liu J, et al.Experimental study of dynamic progressive collapse in flat-plate buildings subjected to exterior column removal [J].Journal of Structural Engineering, ASCE, 2017, 143(9): 04017125.