经典的金属塑性理论认为剪切是导致材料屈服的主要原因，例如最常用的von Mises屈服准则(J2屈服准则)就是由剪切应变能推导得到，即认为金属屈服与应力三轴度η和罗德角θ无关[1]。但当研究金属材料的延性断裂时，应力三轴度η对金属断裂性能的影响首先被发现。McClintock[2]，Rice和Tracey[3]通过分析空穴在静水压力下的增长，分别独立提出随着应力三轴度η的增大，钢材的断裂应变εf会减小，并指出了断裂应变与应力三轴度之间有单调的指数关系
之后，Johnson和Cook[4]通过一系列光滑圆棒和缺口圆棒试验，建立了可以同时考虑应力三轴度、温度和应变率影响的断裂模型，具体的表达式与Rice和Tracey模型相似，都假定断裂应变与应力三轴度为单调的指数关系。但是，由于此模型是基于高应力三轴度状态下的空穴生长理论推导得出，直接将其推广到低应力三轴度状态缺乏相应的理论依据。通过一系列钢材剪切平板和受压圆柱的断裂试验，Bao[5]发现钢材的断裂应变和应力三轴度之间并非单调的指数关系，而是有三个明显的分段。在高应力三轴度区，断裂应变和应力三轴度之间表现出如Rice和Tracey模型表征的单调指数关系；在低应力三轴度区(η＜-1/3)，钢材不再发生断裂；而在二者之间的区域，断裂应变和应力三轴度之间的关系由剪切断裂模式控制。以上这些研究均只考虑了应力三轴度的影响。Wilkins等[6]由铝试件的扭转和拉伸试验结果，提出了一种可以考虑偏应力对断裂应变影响的损伤模型，而偏应力与罗德角参数有关。在Wilkins模型中，应力三轴度和罗德角参数相互独立。Xue[7]在Wilkins模型基础上提出了一个应力三轴度和罗德角参数耦合作用于断裂应变的模型，并且此断裂模型的断裂面相对于罗德角参数对称，亦即假定钢材在受拉和受压状态下的断裂行为相同，但目前缺乏试验验证。Bai[8]基于Wierzbicki等[9]蝴蝶形铝合金试件的试验结果，在Rice和Tracey模型的基础上提出了一个相对于罗德角参数不对称的断裂模型。Bai模型中有6个待定参数，因此需要设计至少6种能够反映不同应力状态的材性试件进行标定，这对于工程应用来说过于复杂。通过模拟A710钢的材性试验，Bai和Wierzbicki[10]发现其模型当引入断裂面相对于罗德角参数对称假定后的预测结果与原模型相近，两者的误差分别为3.0%和4.5%，但后者待定参数仅为4个，从而简化了工程应用。但是，Bai[8]标定断裂模型参数时采用圆棒单调拉伸试验进行。在实际钢结构工程中，经常会遇到比较薄的钢梁腹板，其断裂行为明显受到与剪切断裂相关的罗德角参数的影响。但是，由于加工圆棒过程中的磨损，这种薄板很难加工成适于标定上述断裂模型的光滑圆棒，更难做成开槽口圆棒，即便做成其有效截面也极小，难以进行精确测量。目前尚未有标定薄板断裂的相应方法。因此，本文基于引入断裂面相对于罗德角参数对称假定后的简化Bai模型，利用平板和开孔平板替代光滑圆棒和开槽口圆棒，并结合相应的有限元反演，提出一种适用于钢材薄板延性断裂预测的标定方法。
1 断裂模型
如图1所示，由三个主应力
组成的空间直角坐标系，可以转换为由
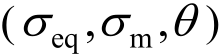表示的圆柱坐标系，其中，等效应力σeq表示圆柱坐标系的半径，平均应力σm表示圆柱坐标系的高，θ表示方位角，也叫作罗德角(lode angle)，为当前应力状态在π平面上与主应力的夹角，变化范围为
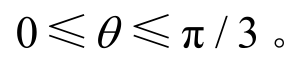钢材的屈服行为会同时受到等效应力σeq和平均应力σm的影响[11]，但为了便于工程应用和有限元计算，此处采用表达式最简单也比较符合试验数据的von Mises屈服准则来描述钢材的屈服行为，亦即忽略了平均应力σm对屈服面形状的影响[12]。对于钢材这种各向同性材料来说，其应力状态可以由三个应力不变量表示。σeq与第二应力不变量有关，由式(1)、式(2)和式(4)可知，应力三轴度η为利用第二应力不变量无量纲化后的第一应力不变量，ξ为归一化的第三应力张量不变量，通过式(5)可知，罗德角参数与ξ有一一对应关系，因此，钢材的应力状态可以由一组
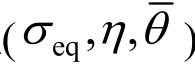确定[13]。应力三轴度η表征相应位置处的应力集中程度。罗德角参数
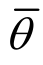表征当前应力状态与轴向应力状态的偏移，其变化范围为
时为轴对称拉伸状态，
时为轴对称压缩，θ=0时为纯剪状态或平面应变状态。此外，图1中的s1、s2和s3代表3个主偏应力。
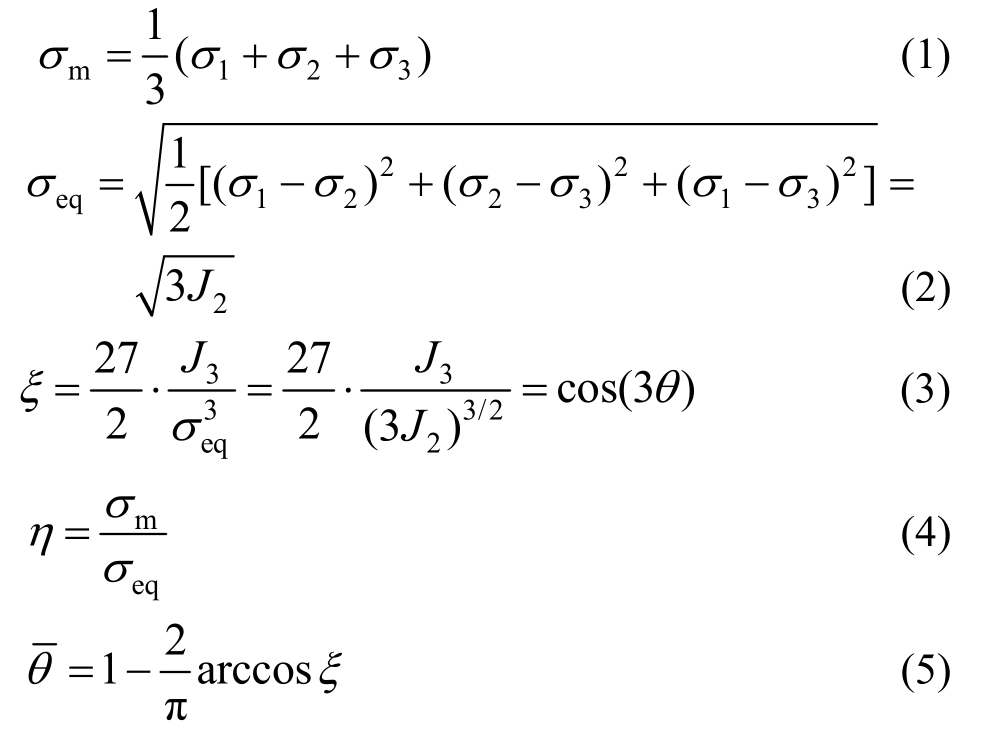
Bai和Wierzbicki[10]提出的相对于罗德角参数不对称的断裂模型表达式如式(6)，断裂面如图2所示。此断裂模型共有6个待定参数：D1，D2，D3，
式(6)里的
分别为罗德角参数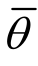
为1，-1和0的平面与断裂面的交线。
图1 主应力空间
Fig.1 Principal stress space
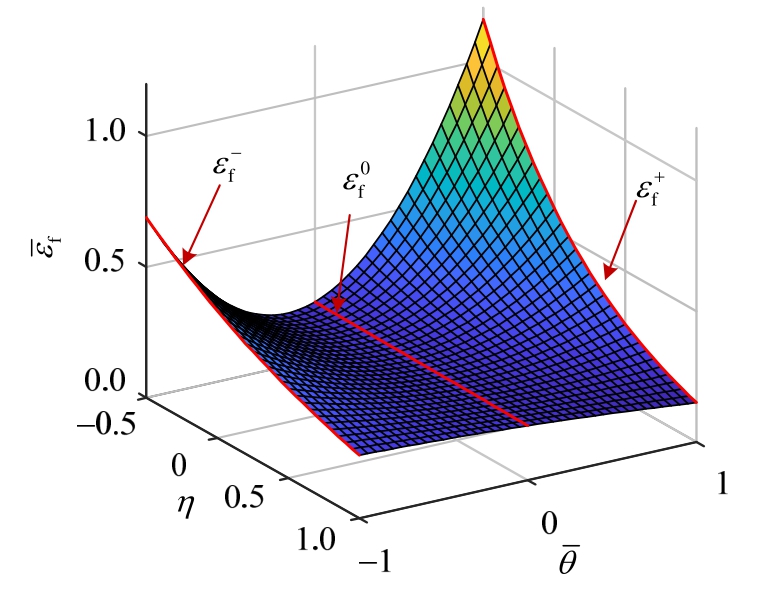
图2 Bai[10]断裂模型的3D断裂面
Fig.2 3D fracture locus of Bai fracture model[10]
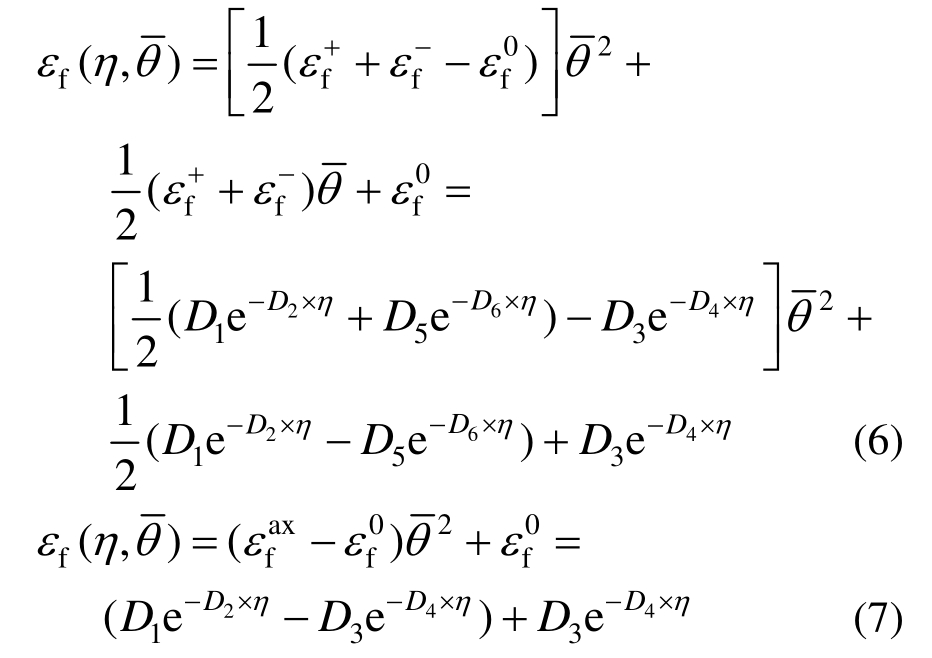
当引入断裂面相对于罗德角参数对称假定后，对于钢材来说，
则式(6)可简化为式(7)。同时，模型的待定参数减少为4个，即D1，D2，D3，D4。因此，若要标定上述模型，只需要提供4组不同应力状态下的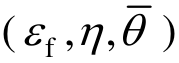
即可，其中εf为等效塑性断裂应变。此断裂模型主要适用于低碳钢。
2 试验设计
此试验研究是一个钢-混凝土组合楼盖试验的组成部分，目的是为之后的有限元模拟提供必要的材料参数。此组合楼盖中钢梁采用HW150×150型钢，在梁柱节点处，钢梁腹板会发生剪切断裂。本文中的试件均取自HW150×150型钢腹板，钢板厚度约为6.5 mm，钢材为Q345钢。如表1和图3所示，共设计了5组试件，各组试件所对应的应力三轴度η和罗德角参数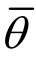
状态列于表1中。同时，图3给出了各试件的加工详图，每个试件的厚度都是原始厚度，约为6.5 mm。
表1 材性试件
Table 1 Coupon test specimens
材性试件 数量 η θ 平板试件 4 0.33≈ 1≈ 开孔平板 2 >0.33 1≈ 开槽平板 2 >1/3 0≈ 90°剪切试件 2 0≈ 0≈ 45°剪切试件 2 >0 1 1θ-＜ ＜
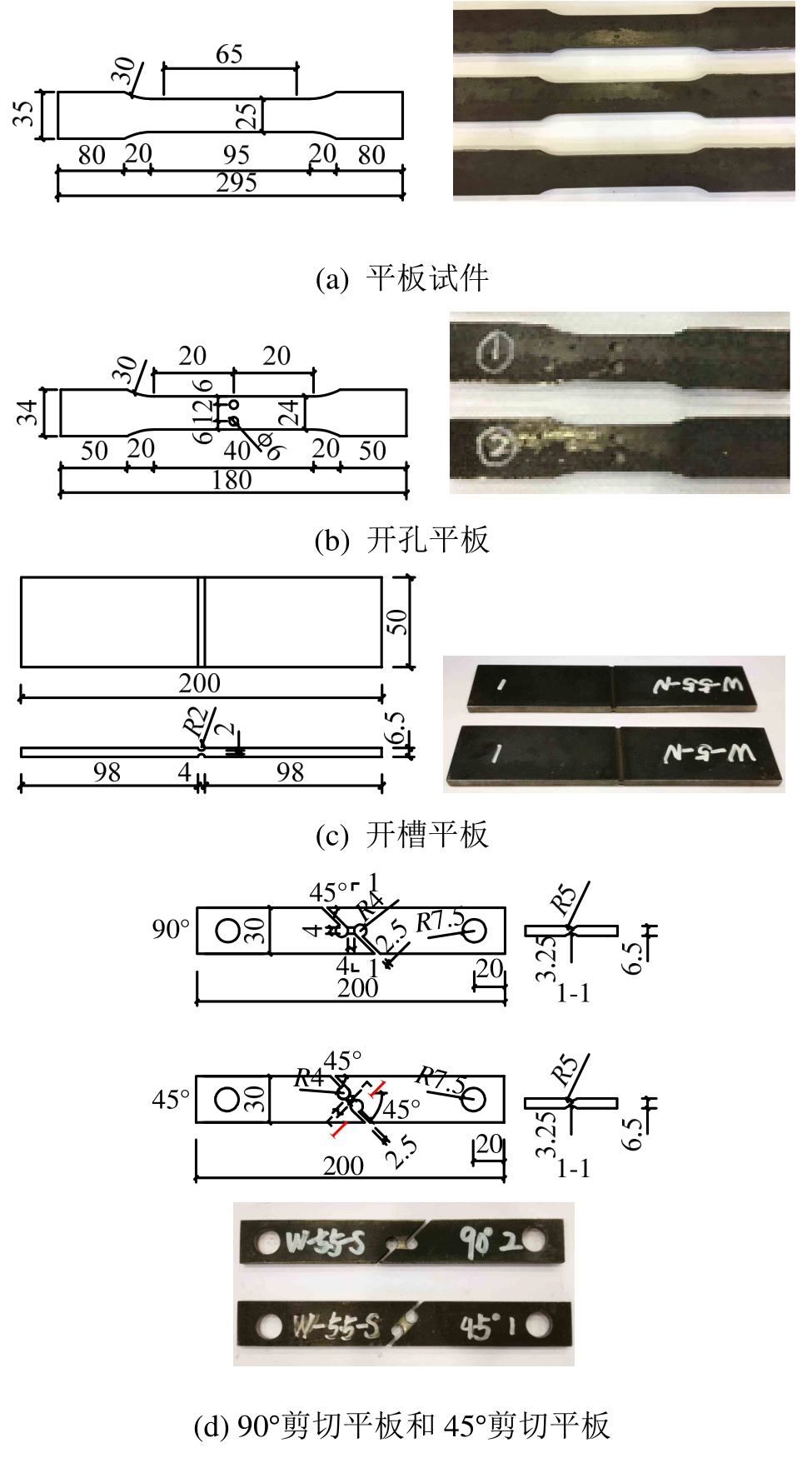
图3 材性试件
Fig.3 Details of coupon test specimens
试验采用50 mm引伸计测量试件标距段的变形，测量过程中的加载速率为0.002 s -1。
3 标定方法与步骤
1)进行3根平板试件单向拉伸试验，得到荷 载-位移曲线，计算确定断裂点处的平均位移。
2)进行1根平板停机试件单向拉伸试验，在达到平均断裂位移的90%时停机。
3)利用断裂点和停机点的荷载和截面面积，计算得到各自对应的(σ,ε)，并考虑颈缩起始点的(σ,ε)，用二次多项式拟合此三点得到颈缩后的真实应力-应变曲线。将此代入到有限元模型中进行计算后与试验结果对比，若有偏差，则微调断裂点对应的断裂应力后再次计算，直至与试验结果吻合，则可认为此时得到了真实的σ-ε关系。然后，计算得到此种情况下的等效应力三轴度η～和等效罗德角参数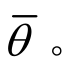
4)将此σ-ε关系分别代入到开孔平板、开槽平板和剪切平板的有限元模型中，将各个试件的起裂点对应的有限元中的等效塑性应变定为对应工况下的等效断裂应变εf。然后，计算得到各自情况下的等效应力三轴度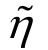
和等效罗德角参数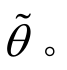
5)用Matlab中的优化工具箱将得到的至少4组
对式(7)进行优化，获得最优参数值从而确定相应的断裂面方程。
4 断裂参数标定
4.1 确定全过程真实应力-真实应变曲线
应变的计算可以以材性试件标距段初始长度L0为基准计算，通过式(8)，得到名义应变εnom。本试验的标距段选取的为引伸计的初始测量长度，即50 mm。同样，应力的计算可以以材性试棒初始截面面积A0为基准，通过式(9)，得到名义应力σnom。
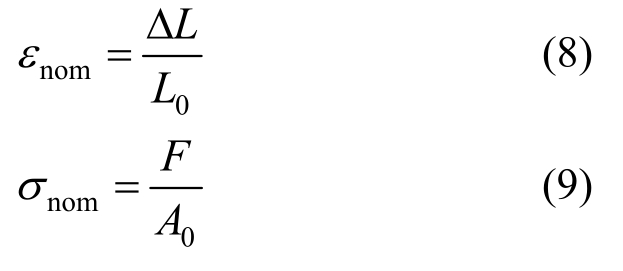
然后，利用式(10)和式(11)可以将名义应力σnom 和名义应变εnom转化为材料的真实应力σ和真实应变ε。
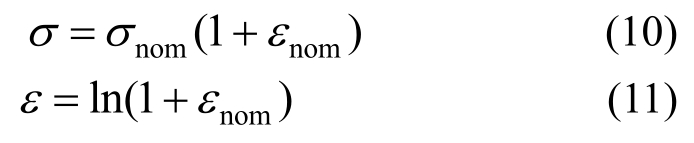
然而，当材料发生颈缩后，由于变形局部化，通过测量标距段得到的平均值不能真实反映颈缩区的真实应力和真实应变。通常，将试棒力-位移曲线或者工程应力-工程应变曲线斜率为零的点看作颈缩的起始点。
颈缩出现后，颈缩区的真实应力和真实应变可以通过式(12)和式(13)求得，其中F和A为同一时刻测得的加载力和真实截面面积。由于试验进行时不方便实时测量试件颈缩区的截面面积，可以通过设置停机试件来得到试件颈缩后的几个离散点(σ,ε)，而后用多项式拟合的方式得到颈缩后的真实应力-应变曲线。本试验设置了一个90%停机试件，如图4所示，即先做3个单轴拉伸平板试件，测量三根试件的平均断裂变形，而后将停机试件拉伸到之前3根试件的标距段平均断裂位移的90%时停机。因此，在颈缩后的区域可以得到两组(σ,ε)，分别对应停机点和最后的断裂点。试件发生颈缩之后，其截面面积不能通过游标卡尺测量求得，本试验采用双尖头螺旋测微器在颈缩截面上测量多个点的截面厚度，然后将截面面积等效为多个梯形的面积之和。
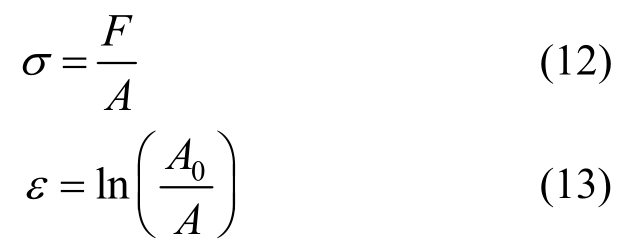
图4 平板停机试件
Fig.4 Halted flat plate specimen
直接将此应力-应变关系代入到图5中的有限元模型计算，得到的有限元结果与试验结果差别较大。这是由于断裂后的断口截面出现严重颈缩，此时的截面面积比截面核心点刚开始起裂时的面积要小，则直接用断裂后的截面面积A代入式(12)和式(13)会得到偏大的真实应力和真实应变。为了控制此误差且操作方便，此处仅对由式(12)得到的断裂时的真实应力进行折减，经过多次试探，发现折减系数选为0.9时得到的模拟结果和试验较为吻合。将颈缩起始点考虑进来，如图6中的3个三角标志所示，可以得到3组(σ,ε)，分别对应颈缩起始点、停机点和断裂点，将断裂点处的真实应力折减以后，用二次多项式拟合颈缩后的真实应力-应变曲线，然后把此σ-ε关系代入到有限元模型中。若是有限元计算结果仍与试验结果有差别，可以将断裂点的真实应力的折减系数在0.9附近微调，直至有限元结果和试验结果吻合(如图7所示)，此时可认为该σ-ε曲线是正确的真实应力-应变曲线(如图8所示)。值得注意的是，断裂点处的折减系数对于不同标号的钢材可能会有变化，需要跟据迭代结果来确定每种钢材合理的折减系数。
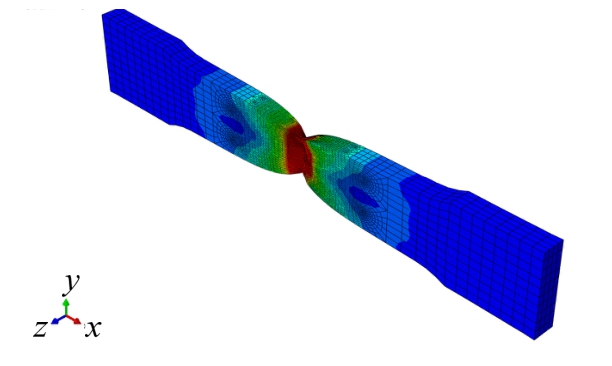
图5 平板试件有限元模型
Fig.5 Finite element model of flat plate specimen
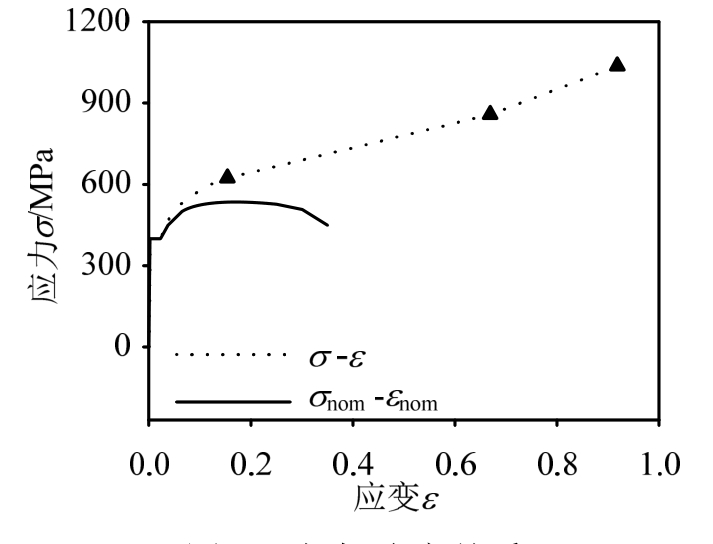
图6 应力-应变关系
Fig.6 Stress-strain relationship
4.2 材性试件断裂参数校核
各试件有限元模型的几何尺寸根据其实际测量尺寸建立，单元选用C3D8R一阶减缩积分单元，核心区单元尺寸为0.2 mm，通过Abaqus/Standard求解器计算。各试件的有限元模型如图6和图9所示。将之前得到的真实应力-应变关系代入到各试件的有限元模型中，并与试验结果对比，对比结果如图7和图10所示。将与试验起裂点对应的有限元模型核心点的等效塑性应变定为此种试件的等效断裂应变εf。如图7和图10所示，各试件虚线对应的位移处承载力突然开始降低，那么此处就可看作各试件的起裂点。图10中，各试件的有限元模拟结果与试验结果的差异主要由以下两个原因导致：1)有限元模型根据设计尺寸建立，而各试件的实际尺寸与设计尺寸存在大小不一的误差。其中，90°剪切平板试件中心点的实际厚度应为3.1 mm，而不是最初设计的3.25 mm。图10(c)为依照实际尺寸建模后的有限元模拟结果，其他试件没有考虑加工误差。2)图10所示的有限元模型都没有加入断裂参数，这会导致模拟结果与试验在下降段误差较大。各试件的等效断裂应变εf列于表2中。
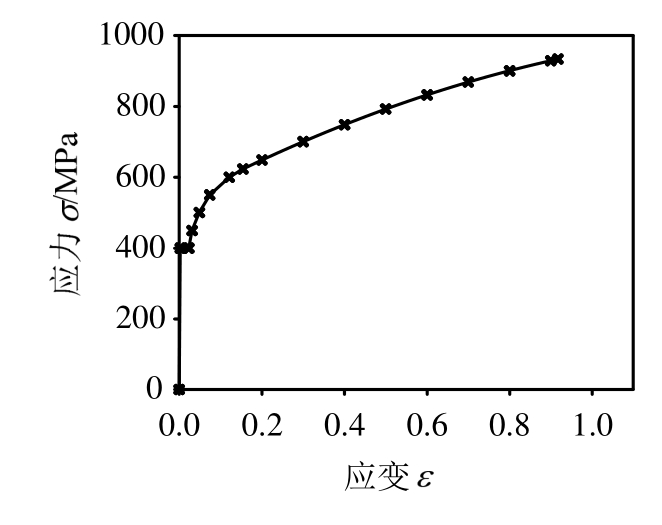
图8 多次迭代后得到的真实应力-应变关系
Fig.8 Ture stress-ture strain relationship
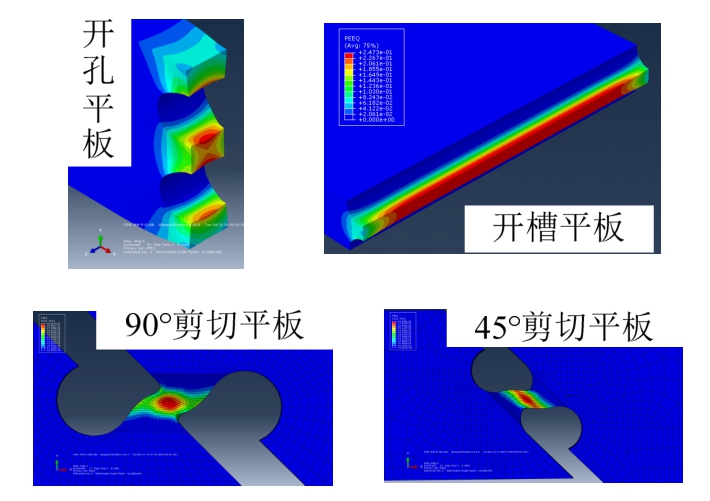
图9 试件有限元模型
Fig.9 Finite element models of specimens
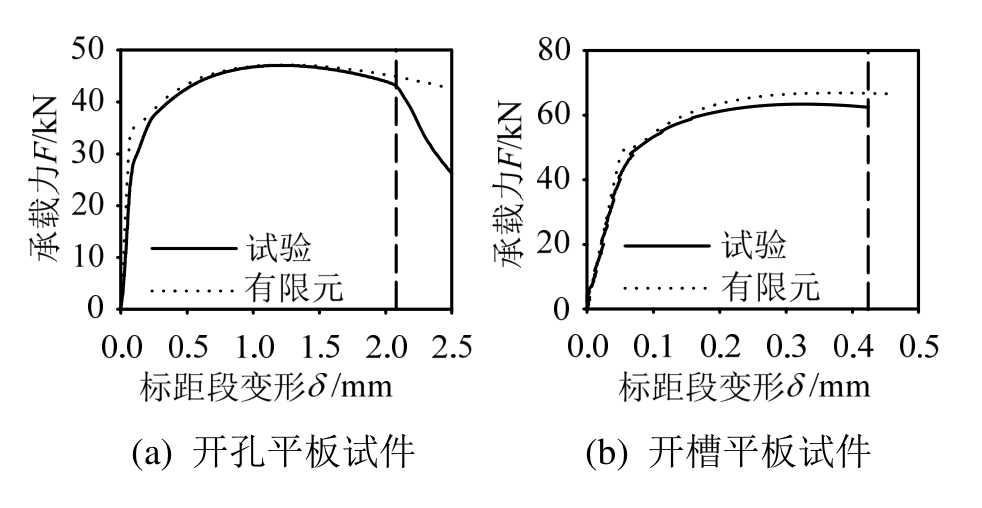
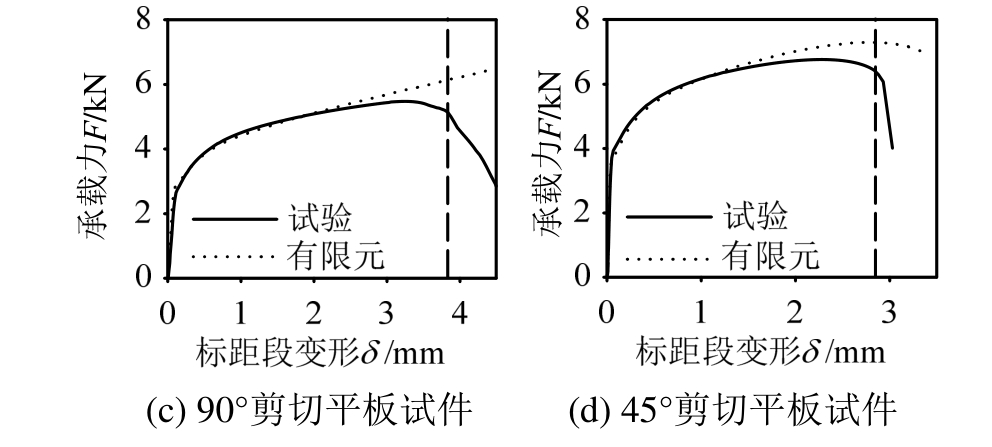
图10 试件力-位移曲线
Fig.10 Force-displacement curves of specimens
提取各试件有限元模型核心点处起裂前的静水压力、Mises应力、第三应力不变量J3和等效塑性应变，并计算出相应的应力三轴度η和罗德角参数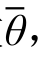
如图11所示。从图11可以看出，随着等效塑性应变的增加，各试件的应力三轴度和罗德角参数会不断变化，为了能够反映加载全过程的状态变化，故将应力三轴度η和罗德角参数
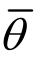在断裂应变上积分得到各试件的等效应力三轴度
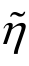和等效罗德角参数
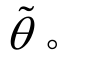等效应力三轴度和等效罗德角参数的计算方法可参照式(14)和式(15)。各试件的等效应力三轴度
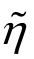和等效罗德角参数
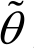列于表2中。
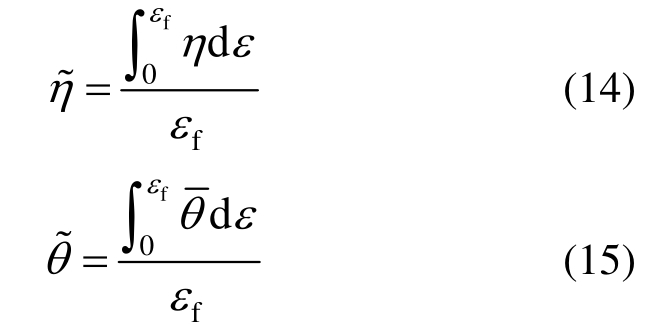
表2 材性试验结果
Table 2 Results of coupon tests
材性试件 εfη～ θ～ 平板试件 1.1581 0.4762 0.6994 开孔平板 0.6449 0.7377 0.8718 开槽平板 0.2746 0.9095 0.0158 90°剪切试件 0.6907 0.0856 0.1404 45°剪切试件 0.7139 0.2958 0.5093
4.3 断裂模型的优化拟合
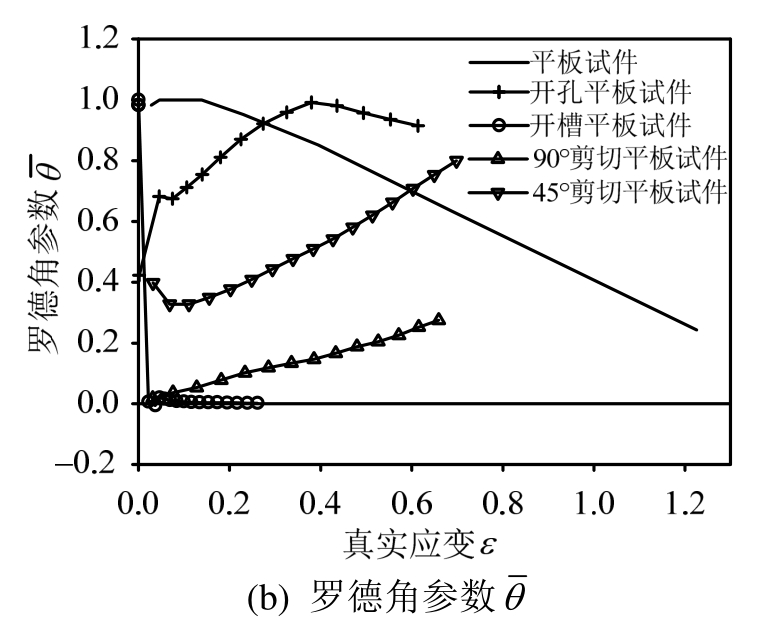
图11 应力三轴度与罗德角参数
Fig.11 Stress triaxiality and lode angle parameter
利用表2中的5组数据，可以优化得到最优的 断裂面。在优化过程中，当式(16)的平均误差(Error)最小时，即可认为此时的断裂面为最优断裂面。在式(16)中，N表示表2中的5组数据，i表示5组数据中的1组。
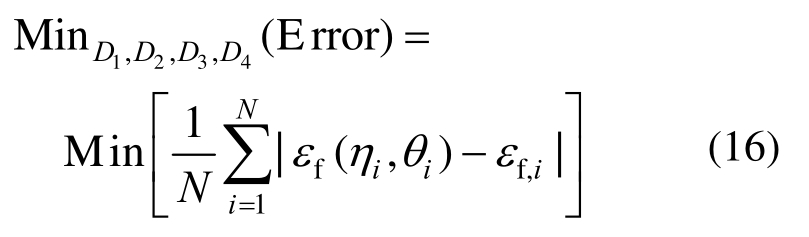
借助MATLAB 2016b的优化工具箱，利用式(16)将表2中5组不同的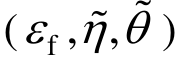
代入式(7)进行优化。
优化得到(D1，D2，D3，D4)=(3.732, 1.962, 0.644, 0.944)。此时，式(7)可以表示为式(17)：
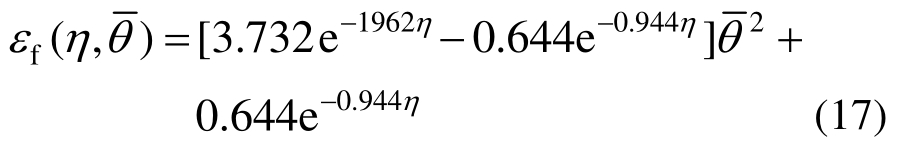
式(17)代表的断裂面如图12所示。由此断裂面就可得知试验中所采用钢材在不同应力三轴度和罗德角参数组合下的等效断裂应变εf。将此断裂模型代入到各试件的有限元模型中，计算得到的结果如图13所示，与试验结果吻合较好，从而证明了上述方法的可行性。不过，加工开槽平板的槽口需要板件满足一定的厚度要求，因此本文的标定方法可能不适用于过薄的板件。
图12 三维断裂面示意图
Fig.12 3D fracture locus
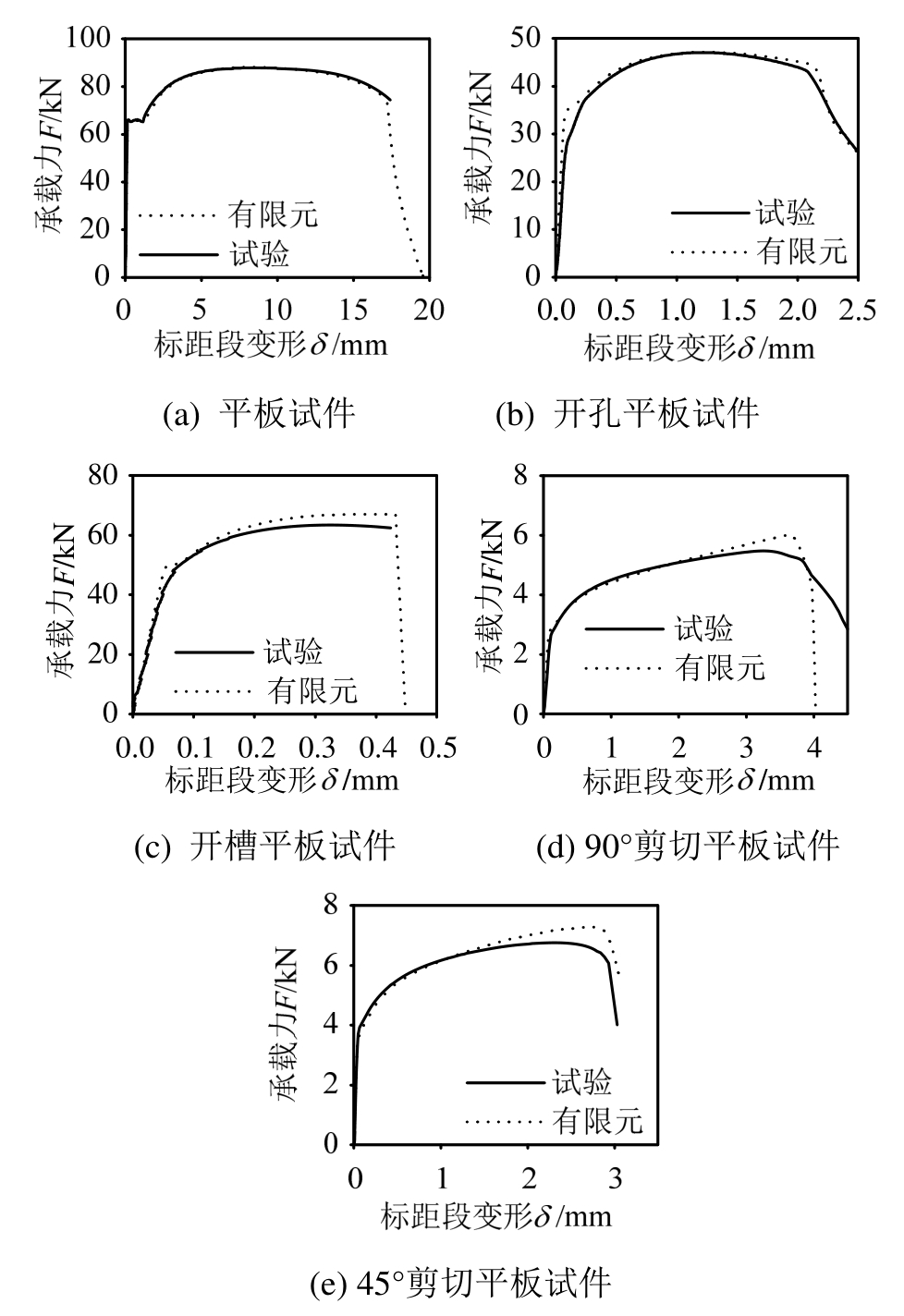
图13 有限元与试验对比
Fig.13 Comparison of FE method and test results
5 结论
本文介绍了可以同时考虑应力三轴度和罗德角参数影响的钢材延性断裂模型，并提出了将其应用于钢材薄板延性断裂预测的标定方法，得到以下结论：
(1)钢结构中腹板的断裂表现出明显的剪切断裂模式，因此进行相关的有限元模拟时必须要考虑与剪切断裂有关的罗德角参数的影响。
(2)本文给出的标定方法可以用较简单的方式精确考虑钢材薄板的剪切断裂行为，通过平板试件、开孔平板试件、开槽平板试件和剪切平板试件来标定相应的模型参数。
(3)本文给出的标定方法适用于低碳钢单调加载断裂时的模拟。
[1]许金泉.材料强度学[M].上海：上海交通大学出版社, 2009.Xu Jinquan.Strength of materials [M].Shanghai: Shanghai Jiao Tong University Press, 2009.(in Chinese)
[2]McClintock F A.A criterion for ductile fracture by the growth of holes [J].Journal of applied mechanics, 1968, 35(2): 363—371.
[3]Rice J R, Tracey D M.On the ductile enlargement of voids in triaxial stress fields[J].Journal of the Mechanics and Physics of Solids, 1969, 17(3): 201—217.
[4]Johnson G R, Cook W H.Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J].Engineering Fracture Mechanics, 1985, 21(1): 31—48.
[5]Bao Y.Prediction of ductile crack formation in uncracked bodies [D].Boston: Massachusetts Institute of Technology, 2003.
[6]Wilkins M L, Streit R D, Reaugh J E.Cumulative-strain-damage model of ductile fracture: simulation and prediction of engineering fracture tests [R].Lawrence Livermore National Lab, California, USA, 1980: 1—65.
[7]Xue L.Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading [J].International Journal of Solids and Structures, 2007, 44(16): 5163—5181.
[8]Bai Y.Effect of loading history on necking and fracture [D].Boston: Massachusetts Institute of Technology, 2007: 1—262.
[9]Wierzbicki T, Bao Y, Bai Y.A new experimental technique for constructing a fracture envelope of metals under multi-axial loading [C]// Proceedings of the 2005 SEM Annual Conference and Exposition on Experimental and Applied Mechanics, Portland, USA: Society for Experimental Mechanics (SEM), 2005, 1: 1295—1303.
[10]Bai Y, Wierzbicki T.A new model of metal plasticity and fracture with pressure and Lode dependence [J].International Journal of Plasticity, 2008, 24(6): 1071—1096.
[11]王万祯.结构钢开裂准则及断裂试验分析[J].工程力学, 2008, 25(5): 27—31.Wang Wanzhen.Crack criterion and fracture tests of structural steel [J].Engineering Mechanics, 2008, 25(5): 27—31.(in Chinese)
[12]王仲仁, 胡卫龙, 胡蓝.屈服准则与塑性应力-应变关系理论及应用[M].北京：高等教育出版社, 2014.Wang Zhongren, Hu Weilong, Hu Lan.Yield criteria and plastic stress-strain relations theory and application [M].Beijing: Higher Education Press, 2014.(in Chinese)
[13]Bai Y, Wierzbicki T.A comparative study of three groups of ductile fracture loci in the 3D space [J].Engineering Fracture Mechanics, 2015, 135: 147—167.