高聚物粘接炸药(Polymer Bonded Explosive, PBX)是一种由晶体颗粒与粘接剂通过一定工艺压制而成的复合材料，其力学特性的准确描述对于武器装备贮存、运输、使用过程的数值仿真分析都有较大的指导意义。PBX在服役期间常密封于金属壳体之中，处于受压状态(装配、热膨胀等)。为了准确仿真其在各种复杂应力环境中的力学响应，研究围压条件下PBX的力学特性以及相应的本构关系非常必要。
对于PBX材料本构模型，国内外均有诸多研究，大多集中在应变率影响下的粘弹性本构模型[1-6]，其中具有代表性的是朱王唐(ZWT)模型和visco- SCRAM模型，朱王唐模型[7-10]是一种率相关的粘弹性材料本构模型，可以综合高应变率和低应变率载荷对材料动态响应的影响。visco-SCRAM模型[11-18]引入了表示内部细观裂纹扩展的损伤变量(微裂纹平均尺寸)，宏观地来描述炸药的黏弹性损伤本构模型。同时，传统粘弹性本构模型的发展也有望应用于PBX材料，如Maxwell模型[19]、Burger模型[20]等。这些率相关本构模型虽能描述不能应变率影响，但对于特定应变率(如准静态)下描述静态仍有待提升。国外在2005年[21-24]便已研究过围压对于复合炸药的影响。对于多晶炸药[22-24](TNT和B炸药，TNT和RDX)，围压仅影响其失效模式，而不影响其弹性模量，且其屈服强度也与围压无关。而对于塑性粘接炸药[21]，通过研究PBS9501在不同高低围压下的力学特性，不同围压下应力-应变曲线变化显著。低围压下，载荷达到破坏应力后材料出现应变软化，而高围压下表现出硬化特性，不存在破坏应力。随着围压的增大，初始斜率(即弹性模量)逐渐增加，屈服强度也一直变化。这表明围压对于PBX的力学特性具有重要影响，而国内关于围压下PBX材料力学性能研究少有报道，因此探索围压下的PBX的本构关系很有必要。围压仅是实验过程中提出的一个概念，无法在本构模型中直接引入，其对于材料的影响，实为静水压力项。
本文通过自主研发的主动围压实验机开展不同围压下TATB基PBX的压缩性能实验，在Boltzmann准静态本构模型基础上，建立考虑静水压力影响的Boltzmann-P准静态非线性本构模型以及对应的数值实现计算方法，最后通过对单位体积单元仿真计算验证该本构模型的准确性。
1 实验
1.1 单轴实验
材料为TATB基PBX，其为TATB炸药晶体、F2314粘结剂以及其他少量添加剂通过等静压压制而成，然后机械加工为Φ20 mm×20 mm的圆柱体压缩样品以及Φ65 mm×15 mm的哑铃型拉伸试样，实验INSTRON5969万能材料试验机上进行，通过载荷传感器、应变引伸计分别记录试样压力与应变，实验温度为20℃，测试方法按照GJB772A-1997 执行。
图1为实验获得的单轴拉伸及单轴压缩应力-应变曲线合并图。由图可知，TATB基PBX拉伸和压缩应力-应变曲线关于0点对称，但不相等，且压缩强度远大于拉伸强度。
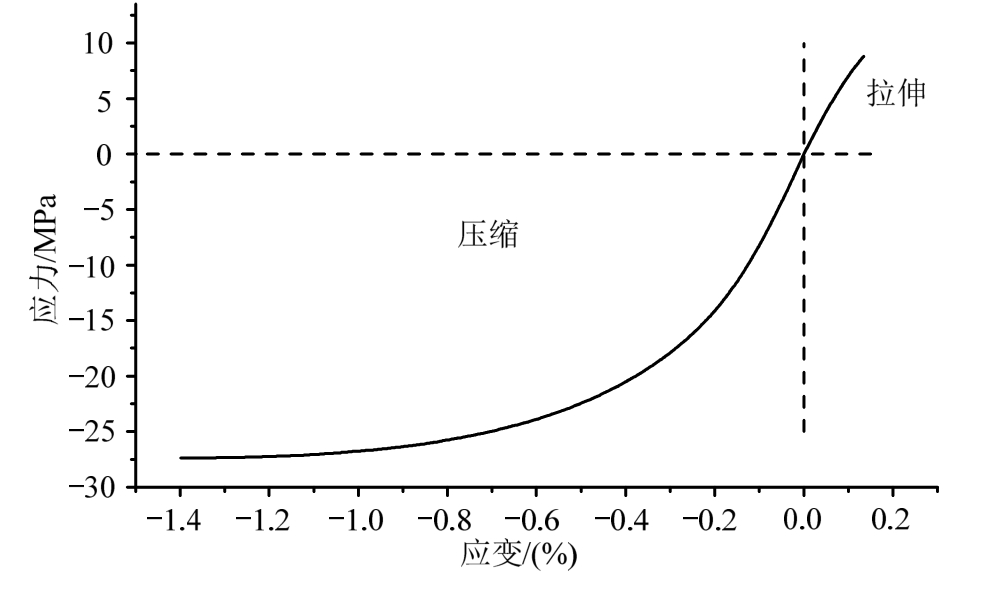
图1 单轴应力-应变曲线(拉伸+压缩)
Fig.1 Uniaxial stress-strain curve (tension+compression)
1.2 围压压缩实验
实验样品同上，实验平台为自主研发的主动围压压缩试验机，其围压加载以及轴向加载均采用独立的液压加载系统，轴向加载过程中通过双缸压力自平衡室保持围压一定。其主动围压范围为 0 MPa～30 MPa，显示分辨率优于0.01 MPa；温度控制范围为环境温度到60 ℃，显示分辨率优于0.1 ℃；轴向最大加载载荷30 kN，分辨率1 N。
通过该主动围压试验机，在20 ℃下对TATB基PBX开展了不同围压(0 MPa、2 MPa、4 MPa、6 MPa、8 MPa、10 MPa)下的准静态压缩实验，加载速率为0.5 mm/min。其实验结果如图2所示。
在压缩过程中，TATB基PBX应力-应变曲线经历了三个阶段，弹性段、过渡段和屈服段。从图中可以看出，PBX在不同围压下的压缩力学特性具有显著差异。随着围压的增加，压缩强度以及破坏应变都逐渐增加，而弹性模量变化不明显，因此在后续研究中不同围压下的初始弹性模量取为定值。在达到压缩强度后，屈服段的斜率(绝对值)也随着围压的增大而减小，规律与文献[8]类似。由于缺少高围压数据，故没有出现屈服段斜率反向的现象。
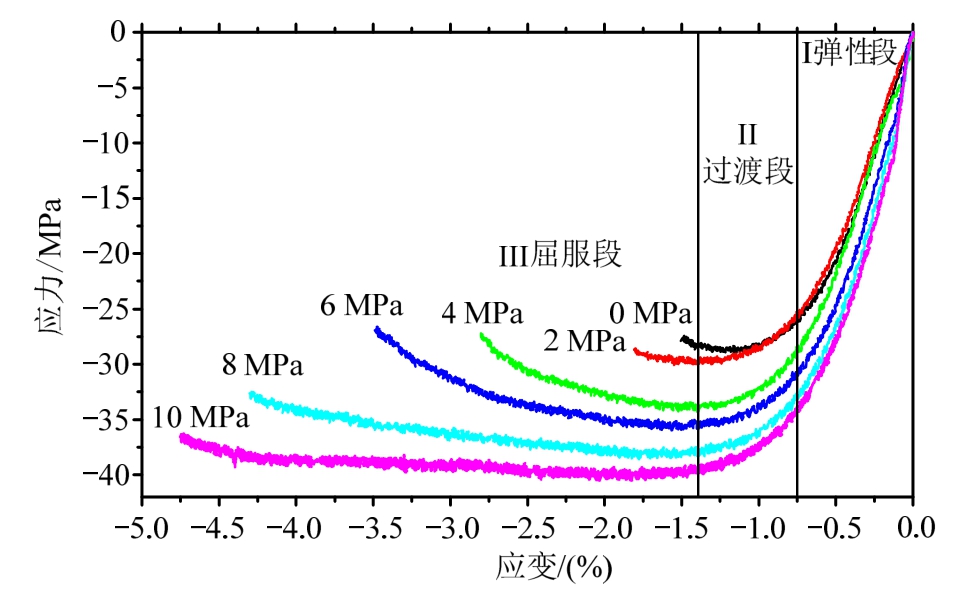
图2 室温下不同围压下压缩应力-应变曲线
Fig.2 Stress-strain curves under different confining pressures
1.3 围压压缩实验数据修正
为了获取能准确描述包含围压的本构关系，本文首先对比了修正后的在主动围压设备中围压为0 MPa时得到的应力-应变曲线与无围压设备即常规方法测得材料的应力-应变曲线，如图3所示。两者总体差异不大，压缩强度近乎一致，而弹性模量有明显差异。理论上围压为0 MPa时压缩曲线与单轴压缩曲线应完全一致，差异导致的原因是由于围压设备难以采用引伸计等直接测量局部应变，而是通过测量上下压头间距离间接进行测试的，如压头与试件之间空隙，以及油摩擦阻尼等因素影响了应变的准确测量。
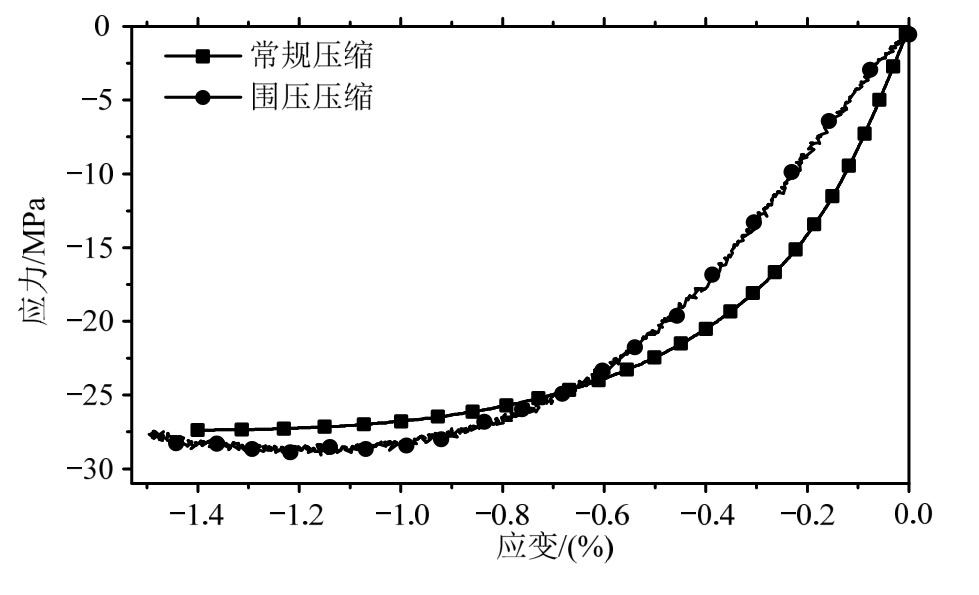
图3 0 MPa围压与无围压装置时压缩应力-应变曲线
Fig.3 Stress-strain curves under zero confining pressure and without confine instrument
本文主在研究围压对于PBX本构关系的影响，故假设不同围压下初始弹性模量一致。为获取不同围压下典型参数，提取了不同围压下PBX压缩强度分析寻找规律，而忽略围压曲线中弹性模量的变化。如图4所示，压缩强度与围压成很好的线性关系。围压下测量得到的应力为轴向应力与围压应力的差值，即
围压的影响，本质上是静水压力的影响，故
与静水压力也成很好的线性关系，这为后面含静水压力本构关系的提出奠定了 基础。
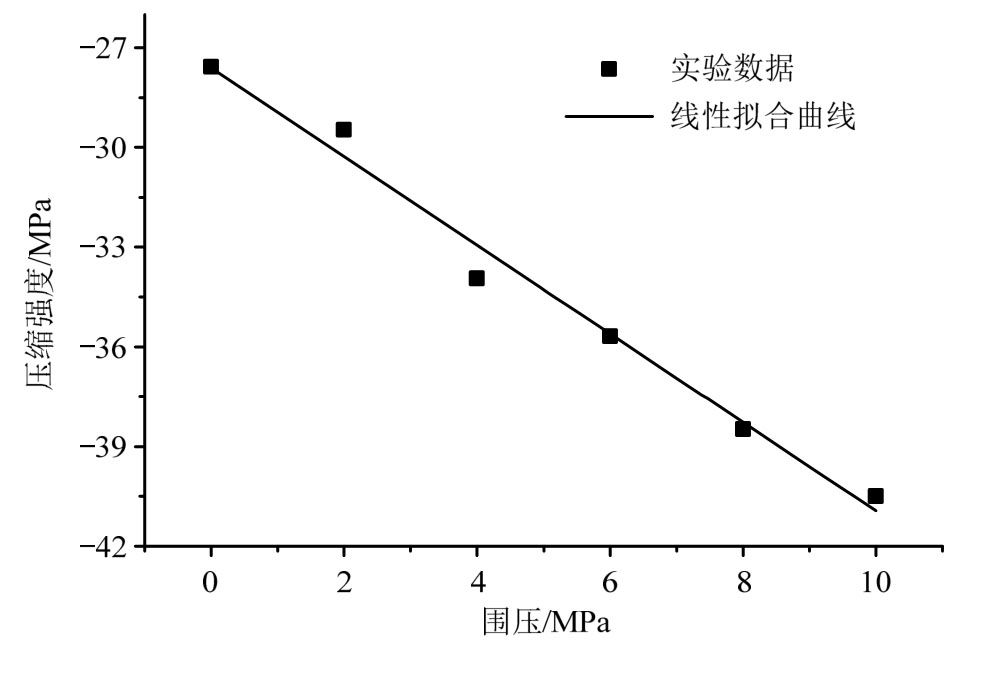
图4 不同围压下PBX压缩强度
Fig.4 Compression strength of PBX under different confining pressures
2 本构模型
2.1 Boltzmann本构模型
现有的PBX准静态本构模型多以单轴实验数据寻找合适的函数进行描述，即应力是应变的 函数。
式中：σ为单轴拉伸或压缩应力；ε为单轴拉伸或压缩应变。
在已有的准静态本构模型中，具体代表性的是唐维等[24-25]提出的基于Boltzmann方程的“S”型非线性弹性本构模型，能精确地描述不同温度下各类PBX材料的单轴实验数据，其表达式为：
式中：σc为压缩强度；α为一常数，其定义为：
式中，E0为初始弹性模量。
以Boltzmann为代表的简单非线性本构模型，由于应力仅仅是应变的关系，不能考虑静水压力对于本构模型的影响。而实验表明，静水压力对于材料性能具有重要影响。
2.2 考虑静水压力的Boltzmann-P本构模型
围压仅为一实验变量，无法直接引入本构模型，围压的影响，其实质为静水压力的影响。在本构模型的建立过程中，为了考虑围压的影响，在Boltzmann非线性本构模型的前提下，引入静水压力，进一步提出了考虑静水压力项的Boltzmann-P本构模型，其广义形式为：
式中：σm为静水压力项，其表达式为
σ1、σ2、σ3分别为第一、第二和第三主应力。
由实验数据分析可知，压缩强度与静水压力关系密切，且成近似线性关系，故将压缩强度修正为：
式中，a1、a2为待确定的常数。
由于静水压力项的引入，对应的，常数项α修正公式为：
式中，b1、b2为待确定的常数。
如此，便建立了考虑静水压力非线性本构模 型—Boltzmann-P模型：
可以看出，考虑静水压力的本构模型是一个隐式方程，在该方程中，静水压力项既是自变量，也是因变量，在给定应变计算应力时，需要特殊的算法来实现。
2.3 不同温度下本构模型参数
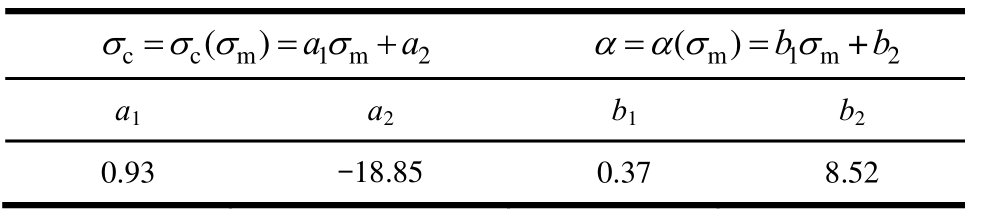
根据实验所得TATB基PBX压缩强度与静水压力的线性关系，进行线性拟合可确定式(7)中σc的参数a1和a2，进而将无围压设备时获得单轴拉压曲线数据以及确定的σc，代入本构模型，得到残留值a与静水压力的关系，再次进行线性拟合，确定了式(7)中a的参数b1和b2，具体取值如表1所示。
表1 Boltzmann-P模型中的参数取值
Table 1 Parameters of Boltzmann-P model
c c m 1m 2( )a a σ σσ σ==+ m1m2( ) +b b αασ σ== a1a2b1b2 0.93 -18.85 0.37 8.52
3 本构模型的数值实现
在本构模型二次开发过程中，需根据应变状态求解当前步应力状态以及雅克比矩阵。2.2中提出的本构模型仍然是根据实验结果拟合得到的一维方程，本节将讨论在实际有限元应用计算中如何将一维本构模型应用于三维计算，以及如何求解Boltzmann-P模型的隐式方程。
3.1 本构模型三维扩展方法
由于等静压成型的PBX是各向同性的材 料[26—27]，且拉伸与压缩应力-应变曲线对称，同时由于体积应力与体积应变实验数据的缺失，故本文预引入泊松比ν并采用Mises等效应力和等效应变将一维本构模型扩展为三维本构模型。Mises等效应力和等效应变定义为：
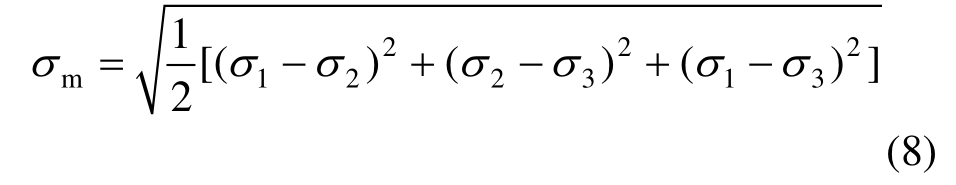
通过式(8)可分析得到对于单轴拉伸与压缩实验，Mises等效应力 σm等于实验所得单轴应力。为了方便数值实现，令单轴实验的Mises等效应变εm等于实验所得应变，因此定义对应的Mises等效应变εm为：
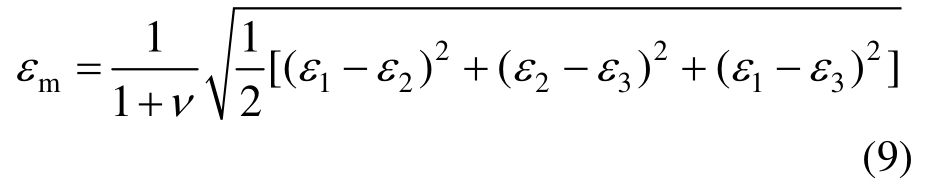
式中，ε1、ε2、ε3分别为第一、第二、第三主应变。
定义了适用于单轴实验的Mises等效应力与应变，需进一步分析其是否适用于围压压缩实验。对于围压压缩，试样应力-应变状态为：
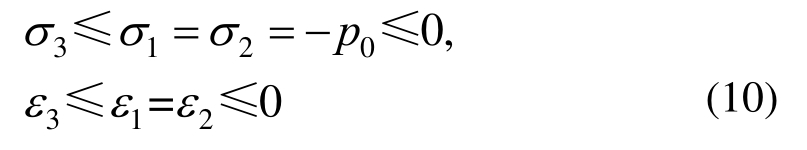
式中，p0为围压压力。
围压压缩直接采集的实验数据为
为围压载荷施加后的初始应变：
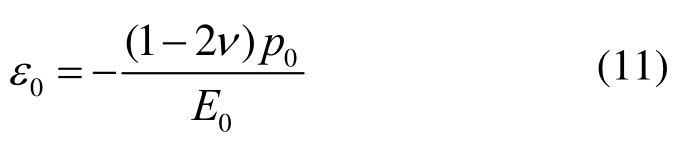
将式(10)代入式(8)和式(9)，可得围压压缩状态下Mises等效应力和应变为：
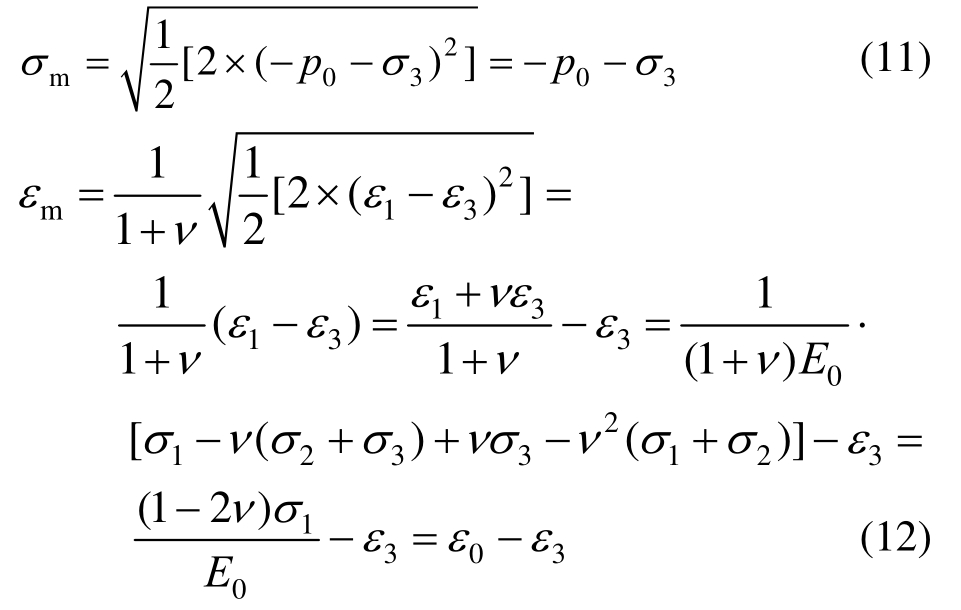
上述推导过程中，E0可为任意应变时刻对应弹性模量，所以上述推导也适用于非线性弹性问题。通过分析可知，对于围压压缩，Mises等效应力和应变也为
即实验直接得到的应 力-应变。因此，已获得的所有实验(单轴拉伸、单轴压缩、围压压缩)应力-应变皆等于Mises等效应力和应变，后续研究不需要对已有的实验数据进行特殊处理，并且 σm与εm之间也满足式(7)所示本构关系，即：
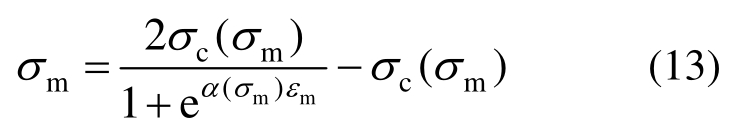
基于以上分析，三维弹性本构模型依然保持以下形式：
式中：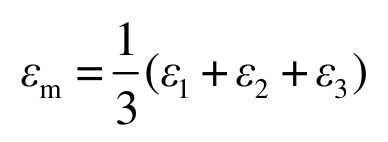
为体积应变；δij为Kronecker函数；弹性模量E定义为：
对于非线性计算中需要使用到的雅克比矩阵，由于缺少真实三维本构，故将雅克比矩阵形式假设等同于弹性矩阵，仅将其中的切线模量 H(εm)其定义为：
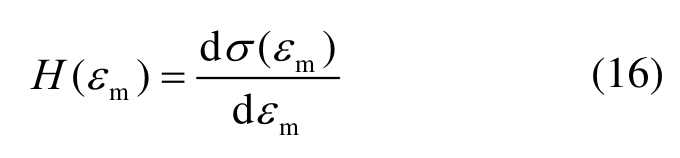
具体的计算流程如下：① 根据应变状态和式计算等效应变εm；② 根据本构关系式(13)和式(15)计算该等效应变下的弹性模量E；③ 根据式(14)计算应力状态；④ 进而根据式(16)计算雅克比矩阵。
3.2 非线性计算方法
由于本构模型是一个隐式方程，静水压力项既是自变量，也是因变量，故在给定应变状态求解应力时需要进行非线性迭代求解。由于Mises等效应力与静水压力没有直接的关系，故无法采用最速下降法，牛顿-拉普逊迭代法等常用有效的非线性计算方法。
针对这种情况，本文提出了一种简单有效的非线性计算方法，具体操作方法如下：
Step 1：给定最大迭代步数N、允许误差r、收敛控制因子β；
Step 2：初始化i=0及应力向量
根据应变向量计算等效应变εm；
Step 3：根据应力向量计算静水压力
代入式(7)计算等效应力σm；
Step 4：计算弹性模量
根据式(10)计算应力向量
并计算绝对误差
Step 5：判断误差是否满足要求或者迭代步数是否达到最大，若是，则跳转到Step 7，否则继续；
Step 6：i=i+1，并更新迭代应力向量
返回Step 3；
Step 7：结束计算。
根据所提出的本构模型以及实现方法，借助于商业软件ANSYS中User Programmable Features (UPFs)二次开发平台，本文开发了对应的材料本构子程序。
4 结果与分析
本节通过采用开发后的材料本构模型，仿真计算了单位体积单元在单轴拉伸、单轴压缩以及围压条件下的应力-应变响应，以验证所提出本构模型以及开发的材料子程序以及对应算法的可行性和有效性。
4.1 计算模型
计算对象为1×1×1 mm单位单元，即仅一个单元，采用Solid45八节点单元。其计算模型如图5所示，底面简支(约束其Z向位移以及转动)，侧面通过压力施加围压载荷，为了便于非线性计算收敛，顶面采用位移载荷来进行静力学计算。通过给定不同位移求解得到支反力，即给定轴向应变求解得到轴向应力，以此求得应力-应变曲线。
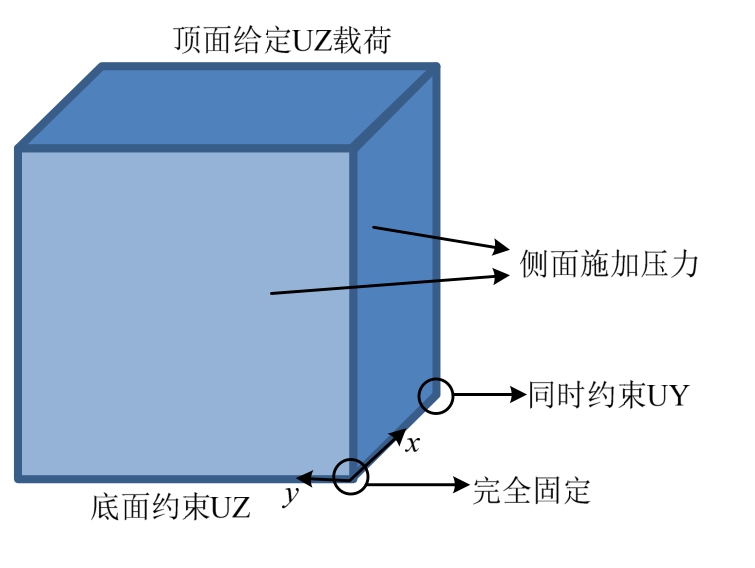
图5 单位单元计算模型
Fig.5 Simulation model of unit element
4.2 单轴拉伸压缩仿真结果分析
本小节计算单轴拉伸压缩(即无围压)下材料的力学响应，并与实验进行了对比。
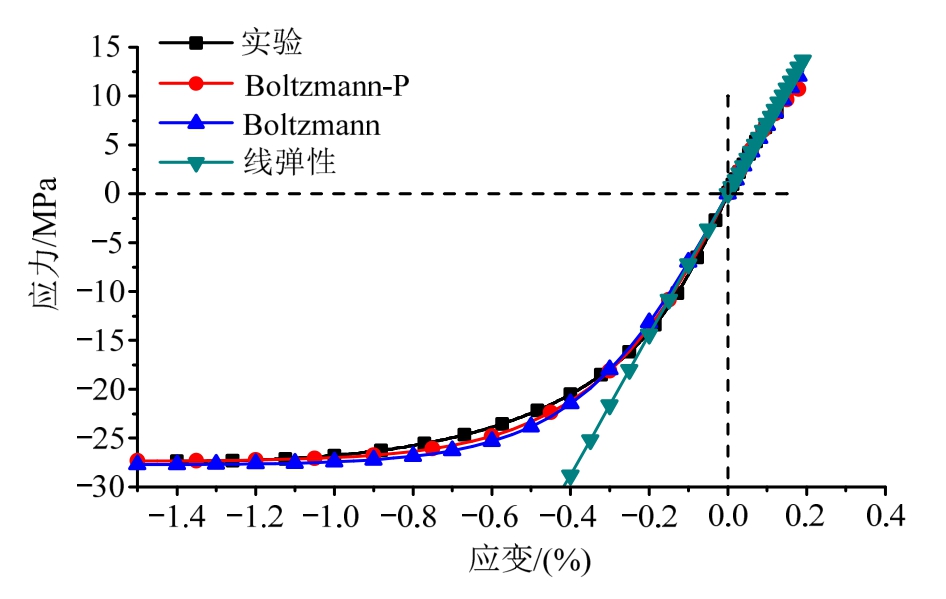
图6 无围压应力-应变曲线(拉伸+压缩)
Fig.6 Stress-strain curves with zero confining pressure (tension and compression)
图6为实验结果、线弹性本构计算结果、Boltzmann以及考虑静水压力项的Boltzmann-P本构模型计算结果的之间对比。通过对比可以发现，线性模型仅在低应力段与实验结果比较吻合(≤7 MPa)，在高应力区域与实验相差较大，已无法使用。而Boltzmann本构模型与考虑静水压力的Boltzmann-P本构模型与实验结果都吻合地较好。
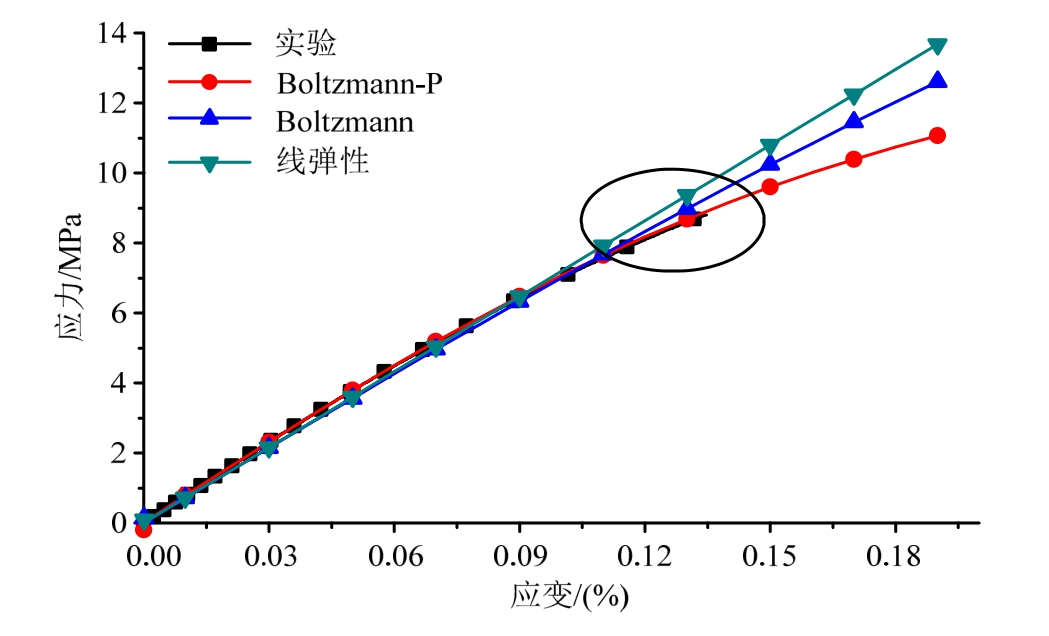
图7 无围压应力-应变曲线(拉伸)
Fig.7 Stress-strain curves with zero confining pressure (only tension)
图7为拉伸段放大图，尽管三种本构仿真结果与实验都吻合得比较好，仔细观察可知，随着应变增大，切线模量逐渐减小，相对于Boltzmann本构模型，考虑静水压力影响的Boltzmann-P本构模型更能考虑这种变化，与实验结果吻合得更好。对比结果表明，描述无围压时TATB基PBX的应力-应变规律，考虑静水压力的Boltzmann-P本构模型的描述精度与Boltzmann模型一致，且在局部细节方面更优于Boltzmann模型。
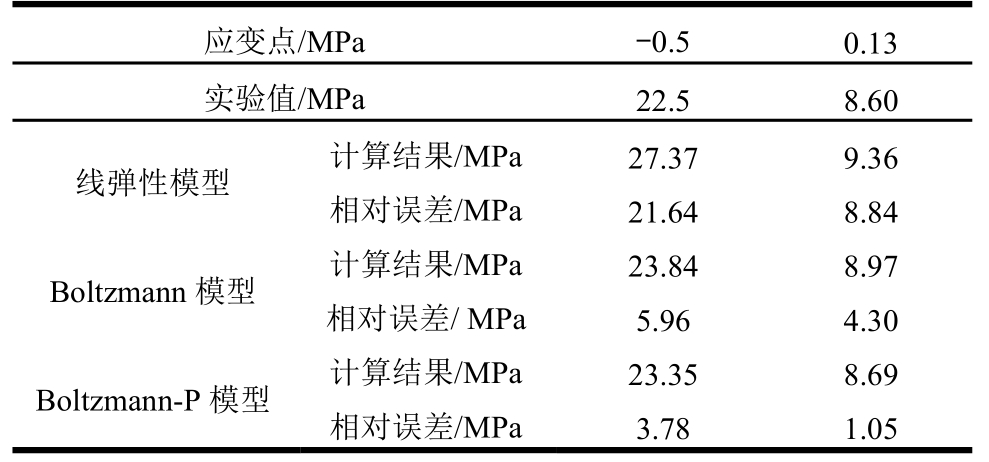
表2提取了描述误差较大的两个应变点(-0.5%与0.13%)下不同本构模型计算得到的应力值。通过对比可以发现，Boltzmann本构模型在压缩段和拉伸段描述误差分别为5.96%和4.30%，而Boltzmann-P描述误差为3.78%和1.05%，Boltzmann-P精度更高。
表2 不同本构模型计算精度对比
Table 2 Result comparison of different constitutive models
应变点/MPa -0.5 0.13 实验值/MPa 22.5 8.60 线弹性模型 计算结果/MPa 27.37 9.36 相对误差/MPa 21.64 8.84 Boltzmann模型 计算结果/MPa 23.84 8.97 相对误差/ MPa 5.96 4.30 Boltzmann-P模型 计算结果/MPa 23.35 8.69 相对误差/MPa 3.78 1.05
4.3 围压压缩仿真结果分析
本小节进行了20 ℃时不同围压条件(0 MPa、2 MPa、4 MPa)下压缩过程的仿真分析，由3.1中分析可知，实验得到的结果是
曲线(考虑正负)，而仿真得到的结果是
曲线，故为了与实验结果进行对应，仿真计算得到的结果进行预处理后再与实验结果进行对比，即应力加上围压载荷p0，应变减去初始应变ε0，得到以下 结果：
图8展示了不同围压下(0 MPa、2 MPa、4 MPa)压缩应力-应变曲线，从曲线可知，考虑静水压力的Boltzmann-P本构模型可以考虑不同围压下的影响，即静水压力的影响，并且随着围压的增大，破坏载荷逐渐增加，符合实验规律。
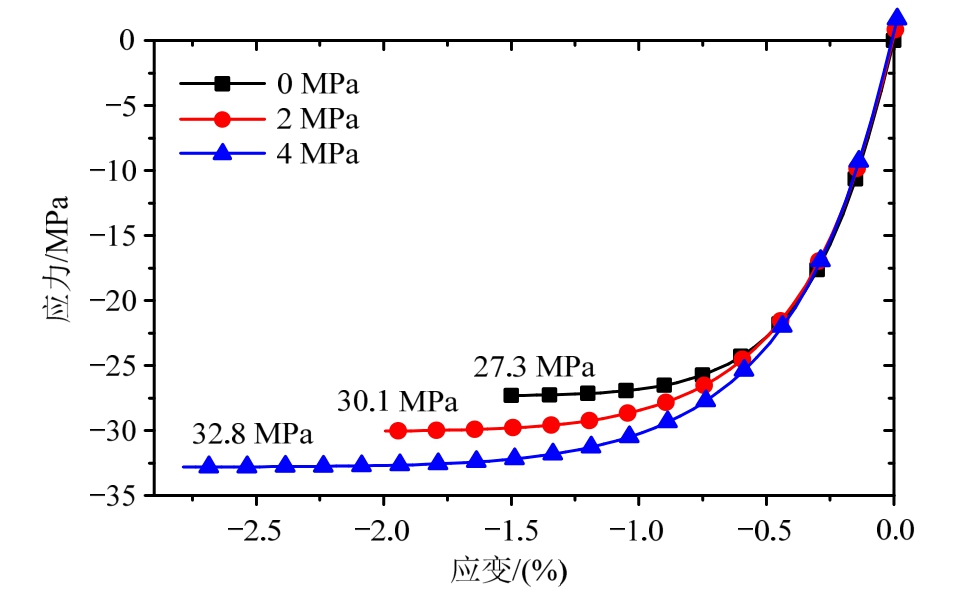
图8 Boltzmann-P模型仿真得到的不同围压下 压缩应力-应变曲线
Fig.8 Stress-strain curves simulated using Boltzmann-P model under different confining pressures
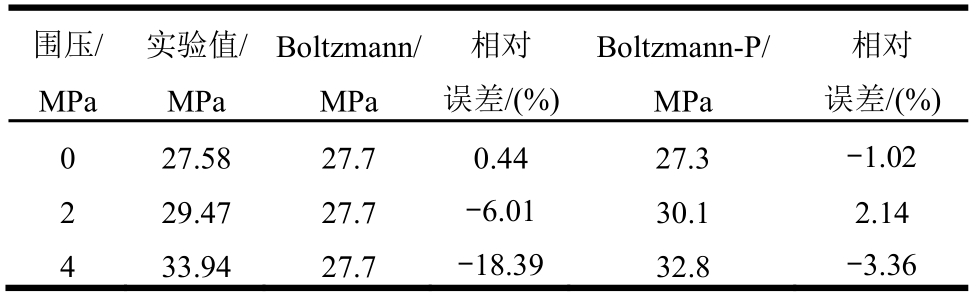
图9～图11为不同围压下仿真结果与实验结果的对比图，通过对比发现，Boltzmann本构模型没有考虑静水压力的影响，仿真得到的不同围压下的应力-应变曲线完全一致，没有区别，不能正确描述材料的本构关系，而考虑了静水压力影响的Boltzmann-P本构模型计算得到的结果与实验结果比较吻合。表3展示了不同围压下实验、Boltzmann模型与Boltzmann-P模型计算得到的破坏时刻σ1-σ3，数据再次表明，考虑了静水压力影响的Boltzmann-P本构模型计算得到的结果与实验差距较小，围压为0 MPa、2 MPa、4 MPa时相对误差分别为-1.02%、2.14%、-3.36%，仿真误差随着围压的增大有增大的趋势。即使如此，在围压小于4 MPa时，Boltzmann最大误差已到18.39%，而Boltzmann最大误差小于4%，且4 MPa以内围压已满足于大多材料的服役场景。通过对比，验证了Boltzmann-P本构模型的有效性以及所开发材料子程序的正确性。
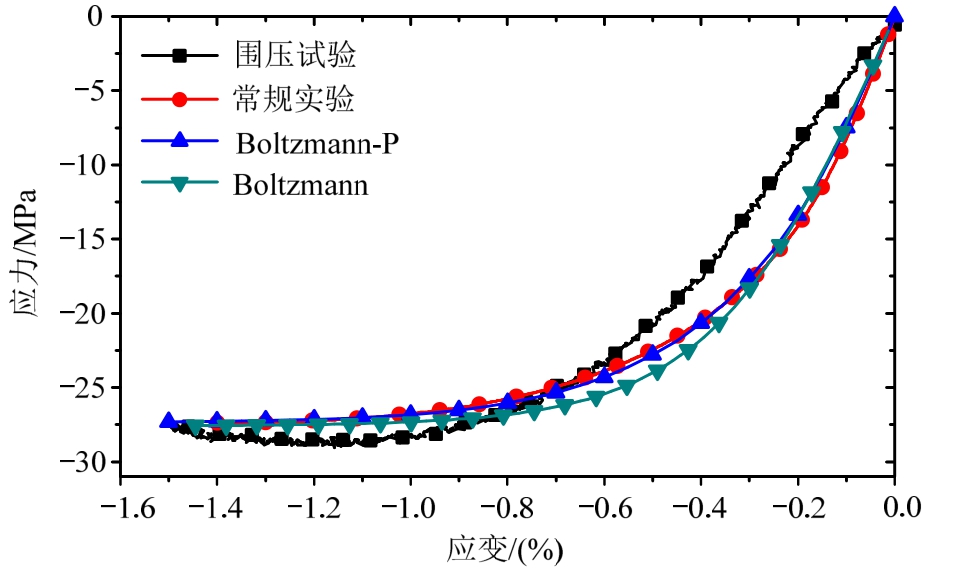
图9 0 MPa围压下压缩应力-应变曲线对比
Fig.9 Comparison of stress-strain curves under zero confining pressure
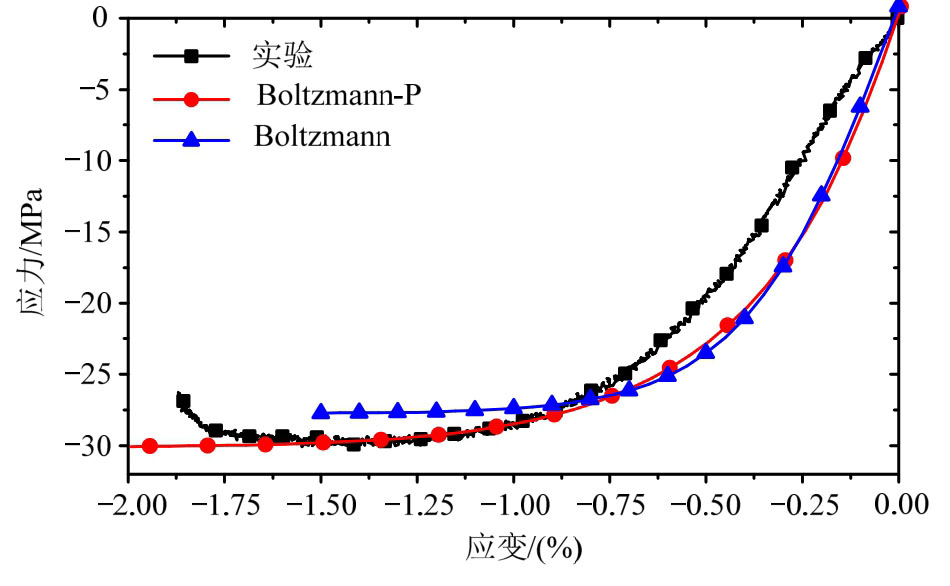
图10 2 MPa围压下压缩应力-应变曲线
Fig.10 Comparison of stress-strain curves under confining pressure of 2 MPa
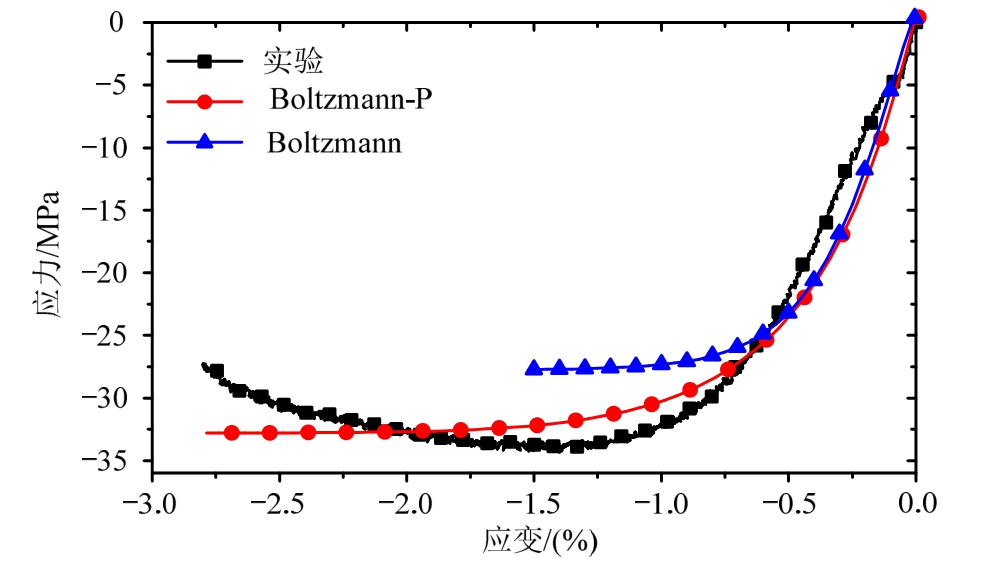
图11 4 MPa围压下压缩应力-应变曲线
Fig.11 Comparison of stress-strain curves under confining pressure of 4 MPa
表3 不同围压下实验与仿真获得的压缩破坏应力
Table 3 Compression failure stress of experiment and simulation under different confining pressures
围压/ MPa实验值/ MPa Boltzmann/MPa 相对 误差/(%)Boltzmann-P/ MPa 相对 误差/(%)0 27.58 27.7 0.44 27.3 -1.02 2 29.47 27.7 -6.01 30.1 2.14 4 33.94 27.7 -18.39 32.8 -3.36
5 结论
(1)不同围压的实验结果表明，静水压力对于PBX材料的力学特性影响显著，随着静水压力的增大，材料的压缩强度呈线性逐渐增大；针对该现象，本文在Boltzmann本构模型的基础上，通过修正相关参数，提出了考虑静水压力的Boltzmann-P本构模型；
(2)针对本构模型的隐式方程特点，建立了对应的非线性迭代算法，并提出了通过Mises等效应力-应变以及泊松比的引入将该一维型本构模型扩展为三维模型，通过对实验过程的分析论证了该方法的合理性；基于ANSYS中UPFs二次开发平台，开发了能考虑静水压力影响的材料子程序，实现了所提出的算法；
(3)通过对单位体积单元进行分析计算，在无围压以及围压条件下Boltzmann-P模型的描述精度均高于Boltzmann本构模型：无围压时压缩段Boltzmann-P的描述误差小于4%，Boltzmann约为8%；围压条件下Boltzmann-P计算得到的压缩强度误差小于4%，Boltzmann误差最大为18%。Boltzmann-P本构模型描述精度满足工程需要。
[1]唐明峰, 庞海燕, 蓝林钢, 等.RDX基PBX的本构行为与应变历史、应变率效应[J].含能材料, 2016, 24 (9): 832—837.Tang Mingfeng, Pang Haiyan, Lan Lingang, et al.Constitutive behavior of RDX-based PBX with loading-history and loading-rate effects [J].Chinese Journal of Energetic Materials (Hanneng Cailiao), 2016, 24(9): 832—837.(in Chinese)
[2]Kakavas P A.Mechanical properties of propellant composite materials reinforced with ammonium perchlorate particles [J].International Journal of Solids & Structures, 2014, 51(10): 2019—2026.
[3]Boddy R L, Gould P J, Jardine A P, et al.Damage in Polymer Bonded Energetic Composites: Effect of Loading Rate [J].Journal of Dynamic Behavior of Materials, 2016, 2(1): 157—165.
[4]Xiao Y C, Sun Y, Wang Z J.Investigating the static and dynamic tensile mechanical behaviour of polymerbonded explosives [J].Strain, 2018, 54(2): e12262.
[5]Xiao Y C, Sun Y, Li X, et al.Dynamic mechanical behavior of PBX [J]. Propellants Explosives Pyrotechnics, 2016, 41(4): 629—636.
[6]陈蓉, 卢芳云, 林玉亮, 等.一种含铝炸药压缩力学性能和本构关系研究[J].含能材料, 2007, 15(5): 460—463.Chen Rong, Lu Fangyun, Lin Yuliang, et al.Mechanical behavior and constitutive model of pressed aluminized explosive [J].Chinese Journal of Energetic Materials (Hanneng Cailiao), 2007, 15(5): 460—463.(in Chinese)
[7]王礼立, 施绍裘.ZWT非线性热粘弹性本构关系的研究与应用[J].宁波大学学报: 理工版, 2000(B12): 141—149.Wang Lili, Shi Shaoqiu.Research and application of ZWT nonlinear thermo-viscoelastic constitutive model [J].Journal of Ningbo University (Natural Science & Engineering Edition), 2000(B12): 141—149.(in Chinese)
[8]卢强, 王占江, 王礼立, 等.基于ZWT方程的线黏弹性球面波分析[J].爆炸与冲击, 2013, 33(5): 463—470.Lu Qiang, Wang Zhanjiang, Wang Lili, et al.Analysis of linear visco-elastic spherical waves based on ZWT constitutive equation [J].Explosion and Shock Waves, 2013, 33(5): 463—470.(in Chinese)
[9]Feng Zhenzhou, Wang Xinjun, Wang Fusheng, et al.Implementation and its application in finite element analysis of constitutive model for ZWT nonlinear viscoelastic material [J].Journal of Materials Science and Engineering, 2007, 25(2): 269—272.
[10]Clements B.ViscoSCRAM: past, present and future [P].LANL, LA-UR-11-1245, 2011.
[11]罗景润.PBX的损伤、断裂及本构关系研究[D].绵阳:中国工程物理研究院, 2001.Luo Jingrun.Study on damage, fracture and constitutive relation of PBX [D].Mianyang: China Academy of Engineering Physics, 2001.(in Chinese)
[12]郭虎.高聚物粘结炸药微裂纹统计本构模型研究[D].绵阳: 中国工程物理研究院, 2012.Guo Hu.Study on the visco statistical crack mechanics for PBXs [D].Mianyang: China Academy of Engineering Physics, 2012.(in Chinese)
[13]张延耿, 楼建锋, 周婷婷, 等.PBX炸药含各向异性损伤的黏弹性统计微裂纹本构模型初步研究[J].高压物理学报, 2016, 30(4): 301—310.Zhang Yangeng, Lou Jianfeng, Zhou Tingting, et al.Initial study on constitutive model of PBXs via viscoelastic statistical crack mechanics including anisotropic damage [J].Chinese Journal of High Pressure Physics, 2016, 30(4): 301—310.(in Chinese)
[14]高军, 黄再兴.PBX炸药粘弹性损伤本构模型参数敏感度分析[J].工程力学, 2015, 32(2): 201—206.Gao Jun, Huang Zaixing.Parameter sensitivity analysis for viscoelastic damage constitutive model for PBX materials [J].Engineering Mechanics, 2015, 32(2): 201—206.(in Chinese)
[15]高军, 黄再兴.PBX 炸药粘弹性损伤本构模型的参数识别[J].工程力学, 2013, 30(7): 299—304.Gao Jun, Huang Zaixing.Parameter identification for viscoelastic damage constitutive of PBX [J].Engineering Mechanics, 2013, 30(7): 299—304.(in Chinese)
[16]成丽蓉, 施惠基.PBX炸药含裂纹扩展损伤的粘塑性本构关系[J].含能材料, 2015, 23(10): 999—1003.Cheng Lirong, Shi Huiji.Elastic-viscoplastic constitutive coupled micro-cracks propagation damage of PBX [J].Chinese Journal of Energetic Materials (Hanneng Cailiao), 2015, 23(10): 999—1003.(in Chinese)
[17]周栋, 黄风雷, 姚惠生.PBX炸药粘弹性损伤本构关系研究[J].北京理工大学学报, 2007, 27(11): 945—947.Zhou Dong, Huang Fenglei, Yao Huisheng.Study on the visco-Elastic constitutive model of PBX [J].Transactions of Beijing Institute of Technology, 2007, 27(11): 945—947.(in Chinese)
[18]冯希金, 危银涛, 李志超, 等.未硫化橡胶非线性粘弹性本构模型研究[J].工程力学, 2016, 33(7): 212—219.Feng Xijin, Wei Yintao, Li Zhichao, et al.Research on nonlinear viscoelastic constitutive model for uncured rubber [J].Engineering Mechanics, 2016, 33(7): 212—219.(in Chinese)
[19]董满生, 鹿婧, 凌天清, 等.考虑温度效应的沥青混合料参数模型[J].工程力学, 2016, 33(6): 180—185.Dong Mansheng, Lu Jin, Ling Tianqing, et al.Parametric model for asphalt mixtures considering temperature effect [J].Engineering Mechanics, 2016, 33(6): 180—185.(in Chinese)
[20]Donald A Wiegand, Brett Reddingius.Mechanical properties of confined explosives [J].Journal of Energetic Materials, 2005, 23(2): 75—98.
[21]Wiegand D A, Pinto J, Nicolaides S.The mechanical response to TNT and a composite, composition B, of TNT and RDX to compressive stress: I.Uniaxial stress and fracture [J].Journal of Energetic Materials, 1991, 9(1/2): 19—80.
[22]Pinto J, Wiegand D A.The mechanical response of TNT and A composite, composition B, of TNT and RDX to compressive stress: II Triaxial stress and yield [J].Journal of Energetic Materials, 1991, 9(3): 205—263.
[23]Wiegand D A, Pinto J.The mechanical response of TNT and A composite, composition B, of TNT and RDX to compressive stress: III Dependence on processing and composition [J].Journal of Energetic Materials, 1991, 9(5): 349—413.
[24]唐维.TATB基PBX炸药的准静态本构模型与强度准则[D].南京: 南京理工大学, 2016.Tang Wei.Constitutive models and strength criterions of a TATB-based PBX under quasi-static loading [D].Nanjing: Nanjing University of Science & Technology, 2016.(in Chinese)
[25]Tang Wei, Yan Xilin, Wen Maoping, et al.Boltzmann function based nonlinear tension-compression constitutive model for typical polymer bonded explosives under quasi-static loading [J].Chinese Journal of Energetic Materials (English Version), 2017, 25(8): 689—693.
[26]温茂萍, 李明, 庞海燕, 等.炸药件力学性能各向同异性试验研究[J].含能材料, 2006, 14(4): 286—289.Wen Maoping, Li Ming, Pang Haiyan, et al.Study on mechanical isotropic of PBX [J].Chinese Journal of Energetic Materials (Hanneng Cailiao), 2006, 14(4): 286—289.(in Chinese)
[27]温茂萍, 庞海燕, 敬仕明, 等.等静压与模压JOB-9003炸药力学性能比较研究[J].含能材料, 2004, 12(6): 338—341.Wen Maoping, Pang Haiyan, Jing Shiming, et al.Comparative study on mechanical properties of two kinds of JOB-9003 shaped separately by isostatic liquid pressing and mould pressing [J].Chinese Journal of Energetic Materials (Hanneng Cailiao), 2004, 12(6): 338—341.(in Chinese)