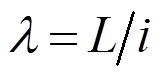 ,L为构件的计算长度,i为截面的回转半径,参考《钢管混凝土结构技术规范》(GB 50936―2014)[11],
,L为构件的计算长度,i为截面的回转半径,参考《钢管混凝土结构技术规范》(GB 50936―2014)[11],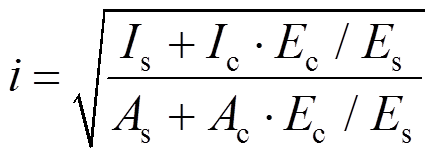 ,经计算,试件绕弱轴的截面回转半径i约为75 mm)。试件的截面尺寸及钢筋笼的布置如图1所示,其中截面的钢板(Q235)厚度设计为3 mm和4 mm,腔内钢筋笼的钢筋(HPB300)直径为6 mm。
,经计算,试件绕弱轴的截面回转半径i约为75 mm)。试件的截面尺寸及钢筋笼的布置如图1所示,其中截面的钢板(Q235)厚度设计为3 mm和4 mm,腔内钢筋笼的钢筋(HPB300)直径为6 mm。摘 要:以天津高银117大厦巨型柱为原型,按1/20缩尺设计制作11根多腔式多边形钢管混凝土柱偏压试件,通过静力试验研究其偏心受压性能,包括破坏形态、荷载-侧向挠度关系曲线和荷载-应变关系曲线,采用ABAQUS软件拓展分析钢管壁厚、长细比、偏心率和混凝土强度等参数对试件极限承载力的影响规律。研究结果表明:多腔式多边形钢管混凝土柱偏心受压试件主要发生弯曲型失稳破坏;提高混凝土强度或钢管壁厚,可提高试件的极限承载力;腔内钢筋笼可显著提高其延性及后期承载力;当长细比从24增加到70,其极限承载力下降38.6%;当偏心率从0.2增加到1,其极限承载力下降54.1%;基于有限元结果,参考相关的承载力计算方法,建立适用于六边形六腔及五边形四腔的钢管混凝土柱偏心受压承载力计算公式,可为实际工程应用提供参考。
关键词:多腔式多边形;钢管混凝土;偏心受压;有限元;极限承载力
传统钢管混凝土柱截面形式主要采用圆形、方形和矩形,若在建筑中采用此类截面,柱角往往会凸出墙面,特别是在高层和超高层建筑,影响建筑美观,而采用异形截面钢管混凝土柱可以达到内墙不出棱的效果,目前异形截面钢管混凝土柱已在广州名励大厦、大连国贸中心大厦和天津高银117大厦建筑中相继得到应用。在实际工程中,由于在外荷载(如侧向水平风荷载或竖向荷载)的作用下,构件不仅处于轴压状态,常常处于偏压或压弯状态,因此对异形截面钢管混凝土偏心受压柱力学性能的研究,显得尤为重要。
国内外许多专家学者对异形截面钢管混凝土柱受力性能进行了广泛研究,徐礼华、杜国锋等[1]对18根组合T形钢管混凝土柱进行了偏心受压试验研究,研究结果表明组合T形钢管混凝土柱能很好的协同工作,同时建立了组合T形钢管混凝土柱偏心受压承载力计算方法。左志亮等[2]对8根带约束拉杆L形钢管混凝土偏压短柱进行了试验研究,研究结果表明设置约束拉杆可以延迟钢管局部屈曲的发生,同时可以提高其极限承载力。曹万林等[3−4]对五边形不同腔体钢管混凝土巨型柱进行了轴压及偏压试验研究,同时结合有限元软件进行了参数分析,研究结果表明轴压试件中四腔体截面试件较单腔体试件的承载力及延性有所提高;偏压试件中增加腔内竖向肋板的厚度,试件截面内力分布更均匀,同时可以提高其承载力及刚度。沈祖炎等[5]对6根L形钢管混凝土长柱进行了单向偏压试验研究,研究结果表明构件的破坏均因侧向挠度的增加而发生整体失稳破坏,其截面变形符合平截面变形。张广泰等[6]对由4根方钢管组成的T形压弯构件进行了试验研究,同时采用有限元软件进行了参数分析,研究结果表明试件具有良好的延性和较高的承载力,柱高及钢材强度对其极限承载力影响较大。Yang等[7]对带拉杆的T形钢管混凝土柱进行了轴压及偏压试验研究,研究结果表明增加对拉钢筋的数量可以明显提高试件的延性及抗弯能力。Xu 等[8]对8根由连接板相连的L形钢管混凝土柱进行了轴心受压及双向偏压试验研究,研究结果表明长细比或偏心距越大,试件的极限承载力越低,同时连接板能有效限制柱的侧向变形。Rong等[9]对2根由带孔洞的连接板相连的L形组合钢管混凝土压弯构件进行了试验研究,同时采用有限元软件进行了相关分析,研究结果表明试件最终发生整体失稳破坏且组合柱的承压能力大于单肢柱,提出了适合L形组合钢管混凝土压弯构件承载力计算方法。
综上所述,目前关于T、L形异形截面钢管混凝土柱研究较多,而对于多腔式多边形钢管混凝土的研究尚处于起步阶段,本文以天津117大厦巨型多腔体钢管混凝土柱为原型,对多腔式多边形钢管混凝土偏心受压柱受力性能进行试验研究,采用有限元软件ABAQUS,拓展分析不同参数对多腔式多边形钢管混凝土偏压柱承载力的影响规律,最后基于试验与有限元分析结果,建立多腔式多边形钢管混凝土柱偏心受压承载力计算公式,为工程应用提供依据。
1.1.1 构件设计及制作
本文试验以天津高银117大厦巨型多腔式多边形钢管混凝土柱为原型[10],按1/20缩尺设计11个多腔式多边形钢管混凝土柱试件,考虑5种影响因素,分别为钢管壁厚、混凝土强度等级、试件高度、偏心距和腔内有无钢筋笼,其中钢管壁厚度t设置3 mm、4 mm两个水平,分别用T1和T2表示;混凝土强度等级设置C60、C70、C80三个水平,分别用C1、C2和C3表示;试件高度设置1800 mm和2500 mm两个水平,分别用H5和H6来表示;偏心距e设置30 mm、60 mm、80 mm三个水平,分别用E1、E2和E3来表示;配筋率设置为0.75%(腔内设置钢筋笼)和0%(腔内不设置钢筋笼)两个水平,分别用S1和S0来表示,具体的试件参数见表1(长细比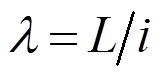 ,L为构件的计算长度,i为截面的回转半径,参考《钢管混凝土结构技术规范》(GB 50936―2014)[11],
,L为构件的计算长度,i为截面的回转半径,参考《钢管混凝土结构技术规范》(GB 50936―2014)[11],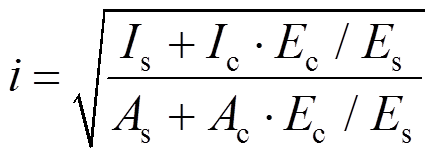 ,经计算,试件绕弱轴的截面回转半径i约为75 mm)。试件的截面尺寸及钢筋笼的布置如图1所示,其中截面的钢板(Q235)厚度设计为3 mm和4 mm,腔内钢筋笼的钢筋(HPB300)直径为6 mm。
,经计算,试件绕弱轴的截面回转半径i约为75 mm)。试件的截面尺寸及钢筋笼的布置如图1所示,其中截面的钢板(Q235)厚度设计为3 mm和4 mm,腔内钢筋笼的钢筋(HPB300)直径为6 mm。
表1 试件参数
Table 1 Parameters of specimens
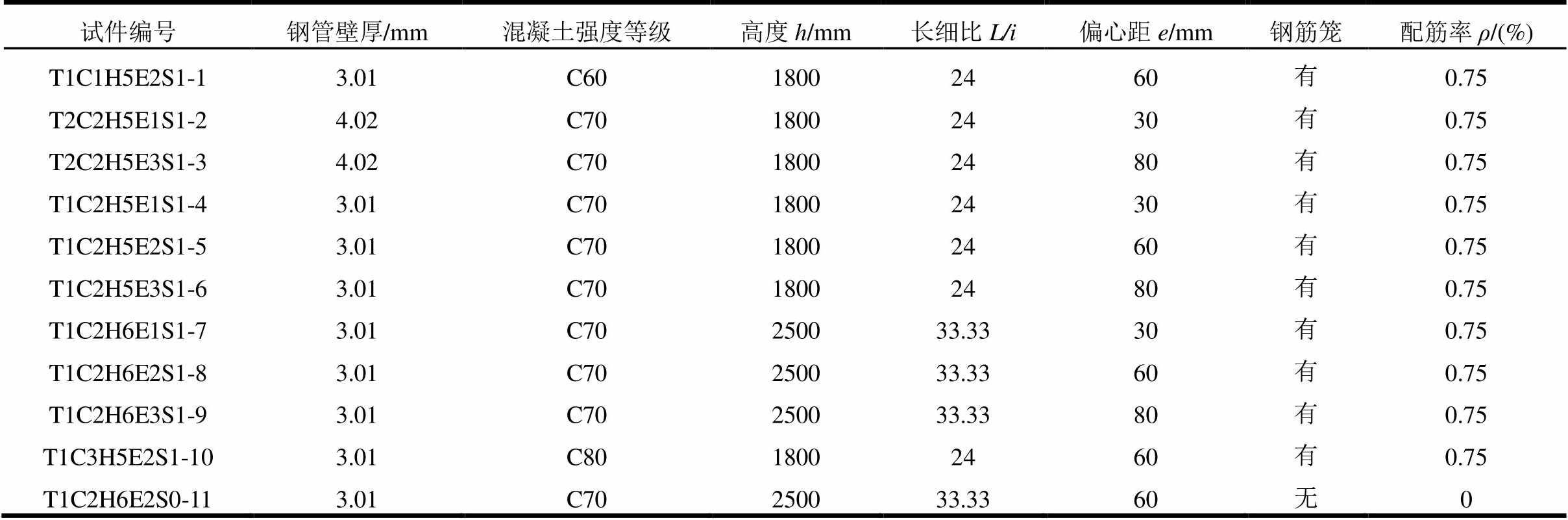
试件编号钢管壁厚/mm混凝土强度等级高度h/mm长细比L/i偏心距e/mm钢筋笼配筋率ρ/(%) T1C1H5E2S1-13.01C6018002460有0.75 T2C2H5E1S1-24.02C7018002430有0.75 T2C2H5E3S1-34.02C7018002480有0.75 T1C2H5E1S1-43.01C7018002430有0.75 T1C2H5E2S1-53.01C7018002460有0.75 T1C2H5E3S1-63.01C7018002480有0.75 T1C2H6E1S1-73.01C70250033.3330有0.75 T1C2H6E2S1-83.01C70250033.3360有0.75 T1C2H6E3S1-93.01C70250033.3380有0.75 T1C3H5E2S1-103.01C8018002460有0.75 T1C2H6E2S0-113.01C70250033.3360无0
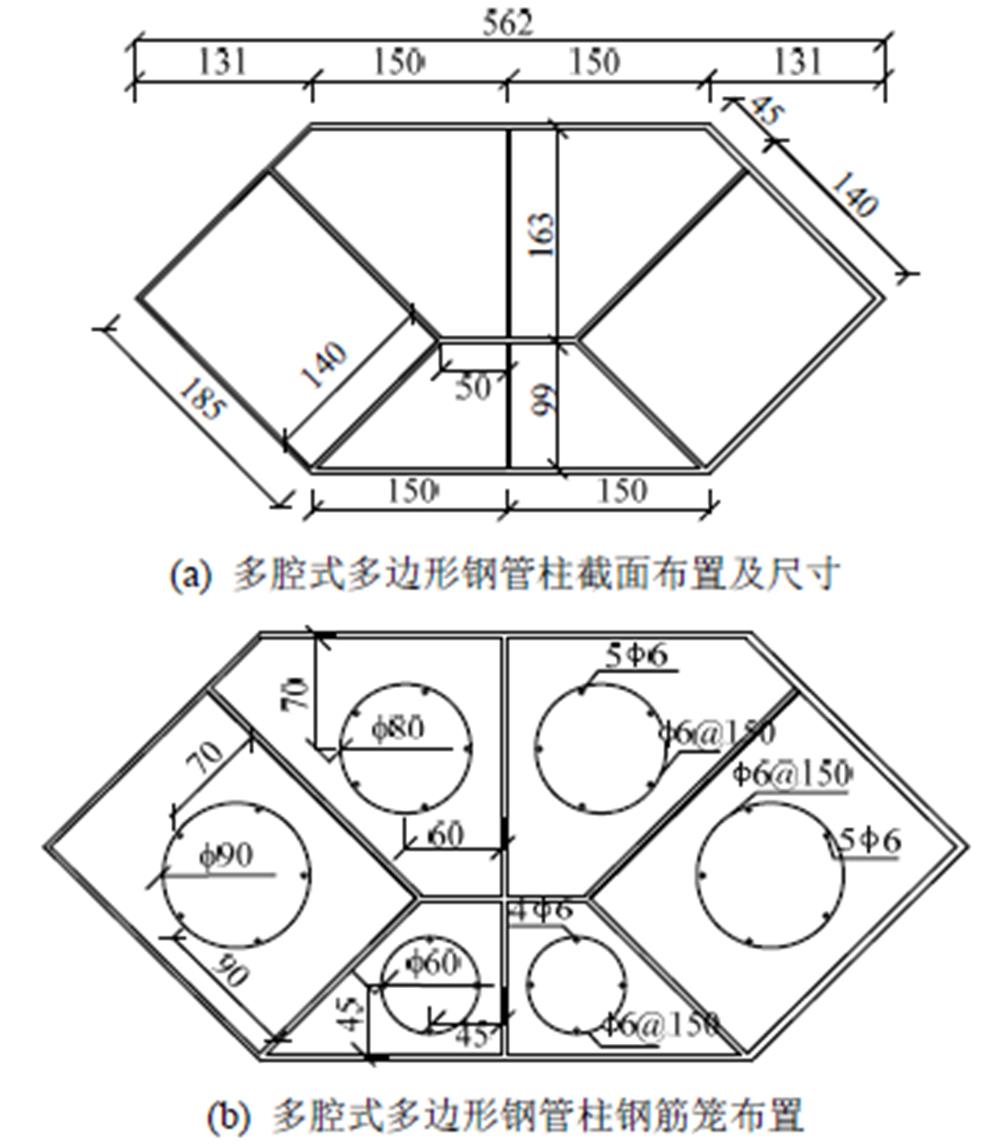
图1 截面尺寸布置图
Fig.1 Section of specimens
1.1.2 材料选择及材性试验
本文试验采用中建商品混凝土公司生产强度等级为C60、C70、C80的混凝土,其抗压强度由与试件同条件下成型养护的150 mm×150 mm× 150 mm立方体测得,测试方法依据《普通混凝土力学性能试验方法标准》(GB/T 50081—2002)[12]进行,数值取每组3个试块实测强度的统计平均值,C60、C70、C80混凝土立方体抗压强度分别为67.8 N/mm2、81.1 N/mm2、84.1 N/mm2;钢材性能由标准拉伸试验确定,按《金属材料室温拉伸试验方法》(GB/T 228—2002)[13]规定的测试方法,测得钢材力学性能指标见表2。
1.1.3 测点布置及加载方案
在试件柱高1/4、1/2、3/4处各布置1个位移计,以测量试件的侧向变形,同时为测量截面应变,在试件的柱中截面钢管外壁沿周长布置横向和纵向电阻应变片总计16片,数据通过DH3816N静态采集系统进行采集。偏心加载试验在武汉大学土木建筑工程学院土木工程试验中心进行,试验加载方式采取力控制分级加载,试验开始时,预先加载至2000 kN,观察加载装置及测量装置是否正常工作,完全卸载后正式加载,在加载初期,每级为计算极限荷载的1/10,同时持荷2 min;当超过计算极限荷载的75%以后,每级荷载改为计算极限荷载的1/15,持荷2 min;当荷载接近计算极限荷载时,缓慢加载,直到试件轴向荷载下降到最大荷载的60%时,停止加载,测点布置及加载装置如图2所示。
表2 钢材力学性能指标
Table 2 Mechanical properties of steel

材料类别板厚(直径)/mm屈服强度fy/MPa极限抗拉强度fu/MPa弹性模量Es/MPa泊松比延伸率/(%) Q2353.013014031.93×1050.26525.4 钢板4.022893902.01×1050.25824.8 HPB300钢筋63054751.90×105-26.5
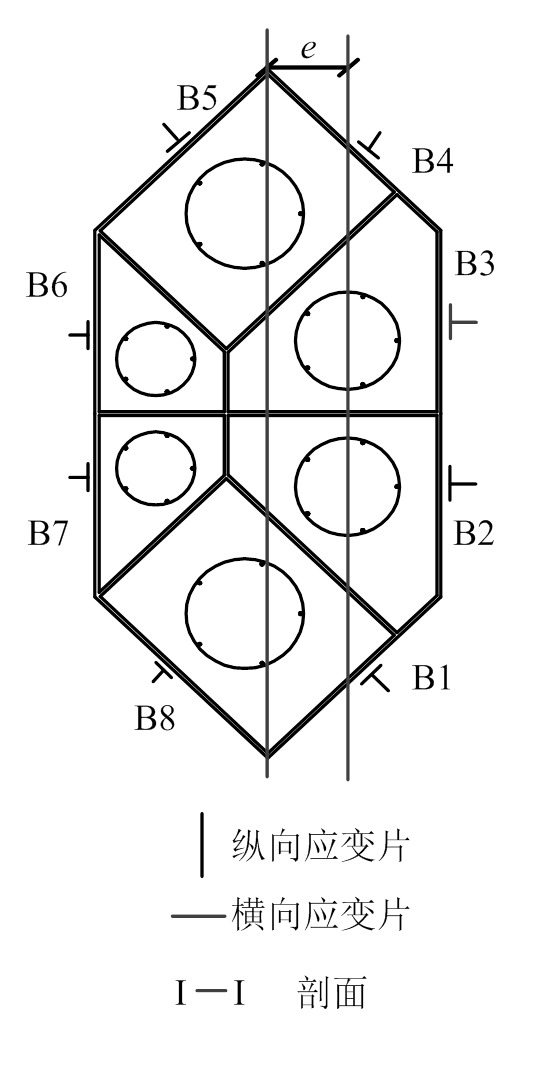
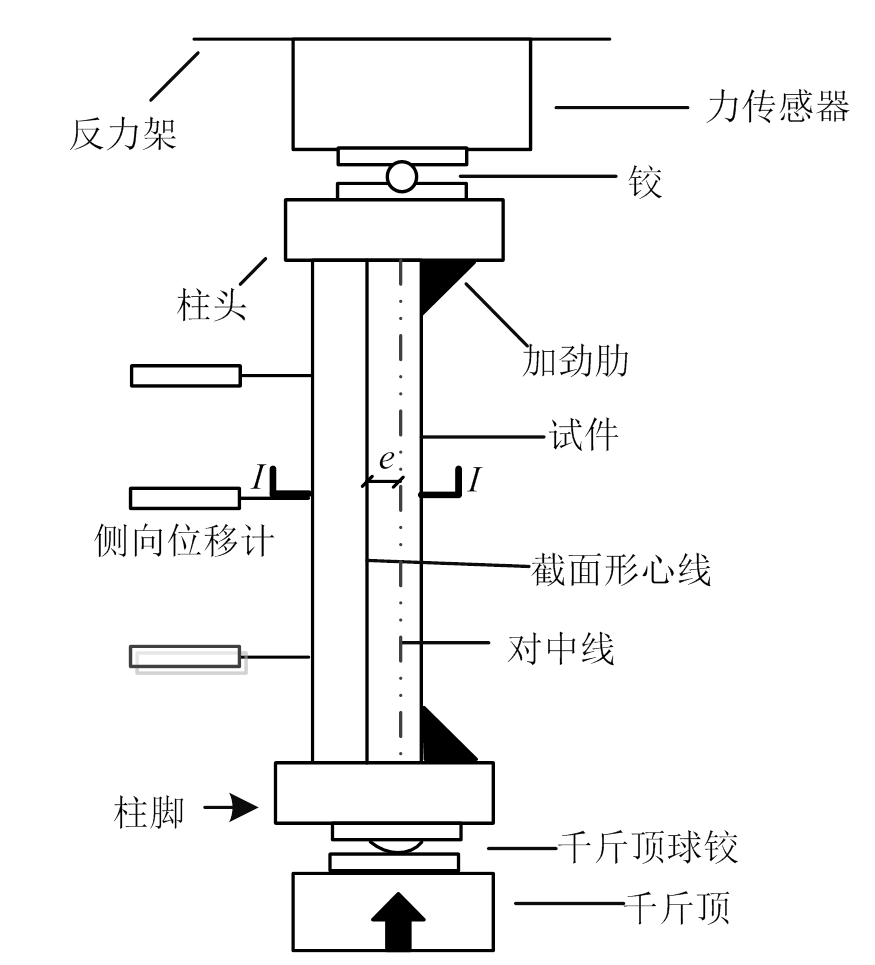
图2 试验布置示意图
Fig.2 Test setup and layout of measuring points
通过对整个试验现象的观察以及结合典型荷载-柱中侧向挠度曲线(图3),试验中所有的多腔式多边形钢管混凝土偏心受压柱在加载时的受力过程可以分为以下四个阶段:
第一阶段(OA):从开始加载到峰值荷载的75%左右的阶段,试件表面没有发生明显变化,钢管的应变也未超过钢材屈服应变,试件处于弹性工作 状态。
第二阶段(AB):从峰值荷载的75%左右到峰值荷载阶段,轴向变形和侧向挠曲变形增长较快,而荷载增长缓慢,受压区钢管的应变超过钢材的屈服应变,试件处于弹塑性工作状态,当加载接近峰值荷载时,试件钢板焊接处的部分漆皮出现裂纹,受压区开始产生鼓包,同时部分试件在钢板焊接处开始开裂。
第三阶段(BC):达到峰值荷载以后承载力较快下降阶段,即荷载-柱中侧向挠度曲线中最高点与下降段拐点之间的阶段,在此阶段荷载下降较快,随各试件影响参数的不同,下降的幅度有所差别(56.5%~77.9%),同时轴向变形和侧向挠曲变形增加明显,原有的裂缝扩大,受压区钢管的鼓包数量增多。
第四阶段(CD):从荷载-柱中侧向挠度曲线的下降段出现拐点至构件破坏阶段。荷载下降缓慢,试件的受压区出现更多的鼓包,并凸出明显,原有裂缝的范围进一步变大,侧向挠度增加较快,最终试件因弯曲失稳而破坏。
其中在第三阶段和第四阶段时荷载出现下降,变形增加较快,试件处于塑性工作状态。
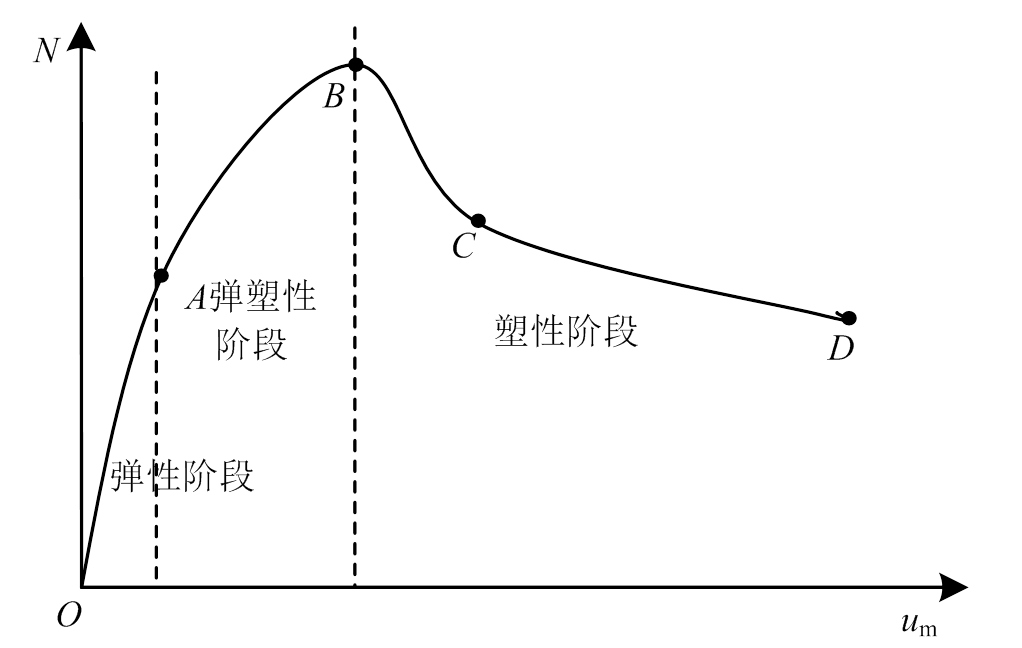
图3 典型受力全过程图
Fig.3 Typical destruction of the whole process
加载过程中试件各阶段对应的典型变化过程如图4所示。加载结束后,全部试件在受压侧均出现不同程度的鼓包(图5(a)),鼓包大多出现在试件的中上部,这是由于加载装置中辊轴的转动能力大于千斤顶,在极限荷载以后,下部的千斤顶转动到极限状态,而上部的辊轴还能随着试件弯曲继续转动,导致鼓包主要集中在试件中上部;部分试件(T2C2H5E1S1-2、T1C2H5E1S1-4、T1C2H6E1S1-7)出现焊缝撕裂现象,撕裂的位置同轴压短柱[14]焊缝撕裂最严重的地方一致(试件两边的尖端处)(图5(b)),说明不管对于轴压还是偏压柱,该交界面都是薄弱处,在实际工程中应采取加强措施。在整个加载过程中,试件的整体性较好,未出现腔体分离现象,所有试件均表现为弯曲失稳破坏,且长细比或偏心距越大,弯曲破坏特征越明显。

图4 试件各阶段试验现象图
Fig.4 Specimen test up chart of the various stages

图5 试件破坏
Fig.5 Failure mode
图6为不同混凝土强度、偏心距、钢管壁厚、长细比和腔内有无钢筋笼条件下荷载-柱中侧向挠度关系曲线(由于所有试件在曲线C点上对应的荷载均小于B点峰值荷载的85%,故可直接将BC段下降的陡缓,作为评判试件延性的标准)。


图6 荷载侧向挠度曲线
Fig.6 N-um curves
1) 混凝土强度
从图6(a)可以看出,混凝土强度从67.8 MPa增加到84.1 MPa,曲线OA段斜率增大,试件初始抗弯刚度增加;试件极限承载力由4153 kN增加到6197 kN,但曲线BC段下降较陡,表明提高混凝土强度可提高试件极限承载力但会降低其延性,究其原因在于,一方面在相同含钢率条件下,混凝土强度的提高降低了套箍系数,减小了钢管对受压区混凝土的约束作用;另一方面混凝土强度越高,其脆性越明显,影响了试件的整体延性。另外,混凝土强度越高,曲线CD段越高,在相同的侧向挠度下,试件后期承载力越大。
2) 偏心距
从图6(b)可以看出,荷载偏心距从30 mm增加大到80 mm,曲线OA段变短,试件越早进入弹塑性工作阶段,极限承载力降低明显,同时曲线CD段也越低,在相同的侧向挠度下,后期承载力低。这是由于随着荷载偏心距的增大,荷载产生的弯矩增加,弯曲变形加剧,进而降低了试件的承载力。
3) 钢管壁厚
从图6(c)可以看出,随着钢管壁厚增加,曲线OA段斜率增大,试件初始抗弯刚度增加,同时弹性工作阶段也变长,构件极限承载力也越大。相比于钢管厚度为3 mm试件,钢管厚度为4 mm试件极限承载力提高了13.2%,且曲线CD段高,在相同的侧向挠度下,后期承载力大,这是由于在峰值荷载以后,虽然钢材已进入塑性,承担荷载的能力下降,但对核心混凝土的约束作用仍然存在,且钢管壁厚越厚,约束作用越强,从而提高了试件的后期承载力。
4) 腔内钢筋笼
从图6(d)可以看出,腔内有无钢筋笼对试件的弹性和弹塑性工作阶段,影响不明显,但对塑性工作阶段影响较大,相比无钢筋笼试件,腔内有钢筋笼试件极限承载力仅提高3.4%,试件延性及后期承载力明显提高,其原因在于峰值荷载以前,侧向变形较小,混凝土受拉开裂较少,钢筋笼提供的抗弯能力所占比重较钢材和混凝土提供的小;峰值荷载以后,侧向变形增加较快,二阶效应增加明显,附加弯矩增加显著,受拉区大部分混凝土受拉开裂,退出工作,钢筋笼提供的抗弯能力所占比重增加,其优势逐渐凸显。
5) 长细比
从图6(e)可以看出,相比长度为1800 mm的试件,长度为2500 mm的试件,曲线OA段短,其弹性工作阶段也变短,极限承载力降低了11.2%,这是由于柱试件长度的增加,抗弯线刚度减小,随着荷载的增加,受二阶效应的影响,弯曲变形加快,导致试件较快达到极限承载力。同时长度为2500 mm的试件较长度为1800 mm的试件,曲线BC段下降段缓,其延性较好。
图7绘制了代表性试件T2C2H5E1S1-2和T1C2H6E2S1-8,在不同荷载阶段时相对高度-侧向挠度关系曲线,其中H/L为试件的相对高度,H为测点距柱底的高度,L为柱高,n为施加荷载与极限荷载之比,从图中可以看出试件在极限荷载以前,水平挠度曲线上下对称,基本符合正弦半波曲线;在极限荷载以后,由于加载装置中上部锟轴的转动能力较大,导致柱的侧向挠度越靠近上侧数值越大。
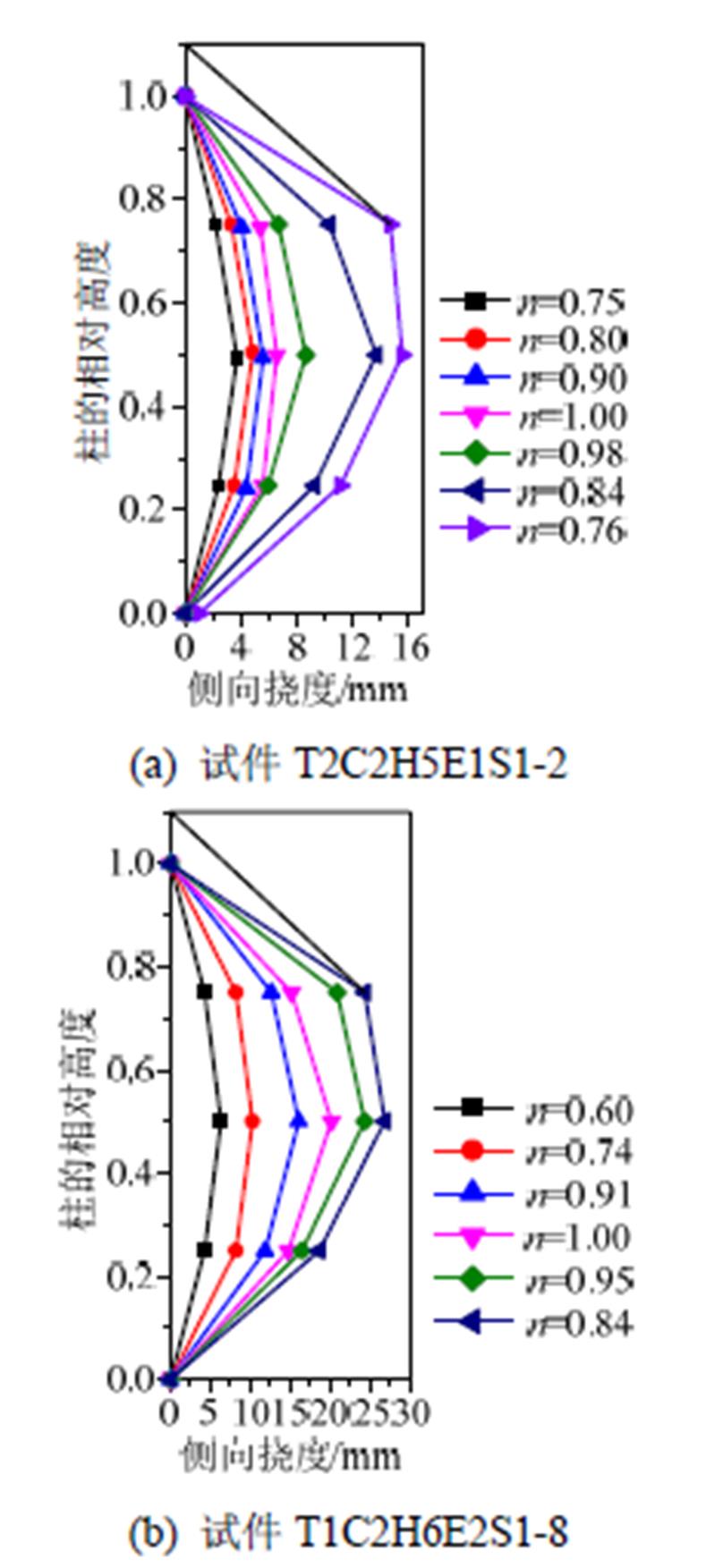
图7 代表性试件在不同荷载阶段水平挠度曲线
Fig.7 Horizontal deflection curves of specimens
图8绘制了不同偏心距和有无钢筋笼的试件柱高中点处受压侧截面的荷载-纵(横)向应变关系曲线,从图中可以看出在加载初期,外部钢管的纵向应变和横向应变随着荷载的增大而线性增加;接近极限荷载时,试件纵向和横向应变增速均变快;在达到极限荷载时,试件的纵向应变大部分位于 2000 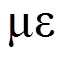 ~2500
~2500 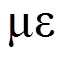 且都超过了实测的钢材屈服应变1560
且都超过了实测的钢材屈服应变1560 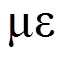 ,表明受压侧钢板屈服,同时横向与纵向应变的比值在0.41~0.505,大于钢材的泊松比0.265,表明受压侧钢管对腔内核心混凝土产生了较明显的约束作用,这也说明了,虽然多腔式多边形钢管混凝土柱处于偏心受压状态,但钢管对核心混凝土仍然可产生明显的约束套箍作用,由于多腔式多边形钢管混凝土柱由多个腔体组成,可对其内部受压区的混凝土产生复合约束,使得约束作用更强,承载力提高明显。
,表明受压侧钢板屈服,同时横向与纵向应变的比值在0.41~0.505,大于钢材的泊松比0.265,表明受压侧钢管对腔内核心混凝土产生了较明显的约束作用,这也说明了,虽然多腔式多边形钢管混凝土柱处于偏心受压状态,但钢管对核心混凝土仍然可产生明显的约束套箍作用,由于多腔式多边形钢管混凝土柱由多个腔体组成,可对其内部受压区的混凝土产生复合约束,使得约束作用更强,承载力提高明显。
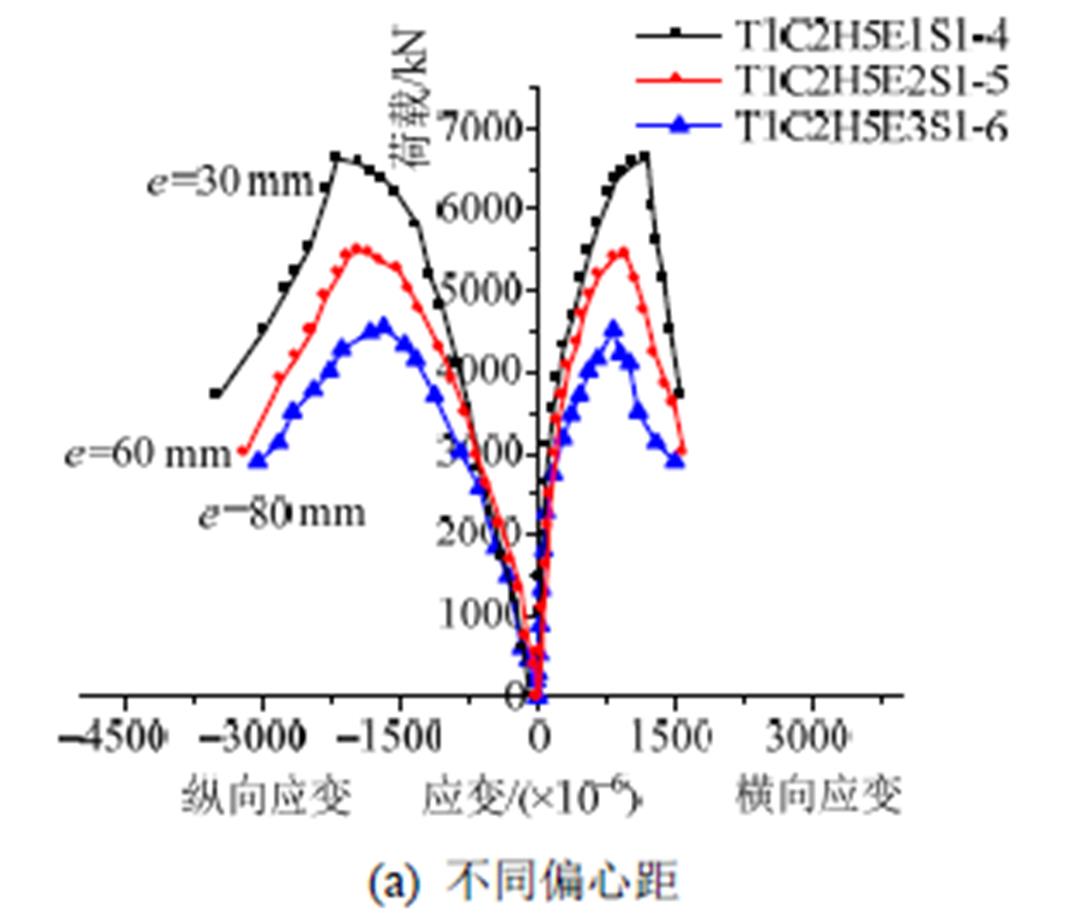
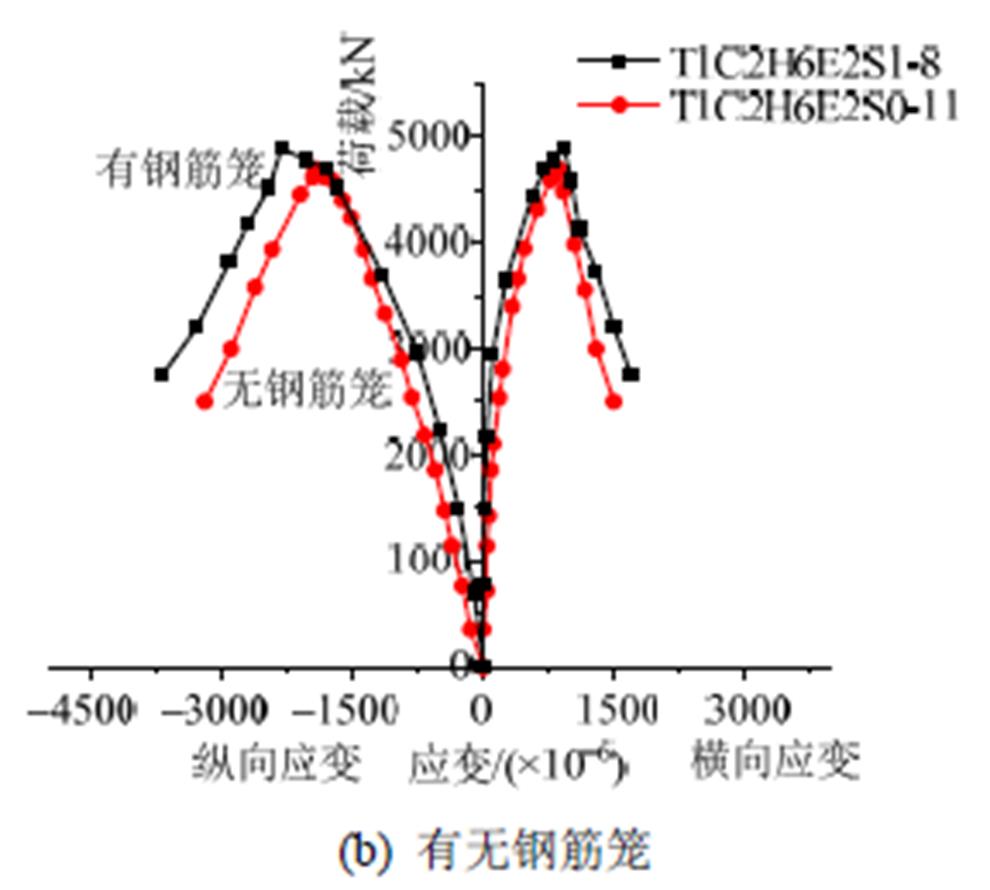
图8 荷载-应变曲线
Fig.8 N-e curves
2.1.1 钢材的本构模型
钢材的本构关系模型选用ABAQUS软件提供的等向弹塑性模型,满足Von Mises屈服准则,其应力-应变关系采用多折线形式,如式(1)所示,钢材的屈服强度、弹性模量和泊松比按实测材性试验取值。
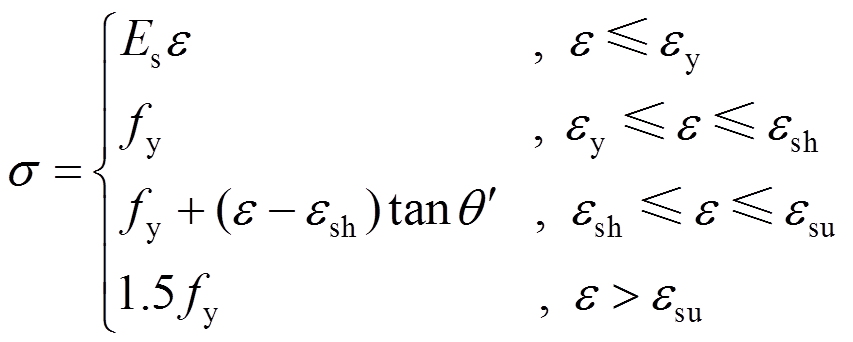 (1)
(1)式中: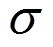 为钢材等效应力;
为钢材等效应力;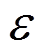 为钢材等效应变;fy为钢材屈服强度;Es为弹性模量;
为钢材等效应变;fy为钢材屈服强度;Es为弹性模量;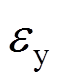 为屈服应变;
为屈服应变;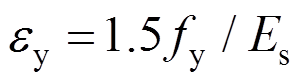 ;
;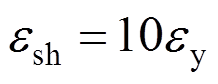 ;
;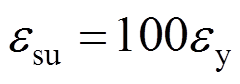 ;
;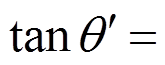
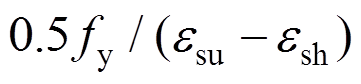 。
。
2.1.2 混凝土的本构模型
混凝土本构关系模型采用ABAQUS软件自有的混凝土损伤塑性模型,应力-应变关系采用《混凝土结构设计规范》(GB 50010―2010)[15]中所给出的本构关系,如式(2)所示,混凝土的泊松比取0.2,弹性模量按文献[15]取值。
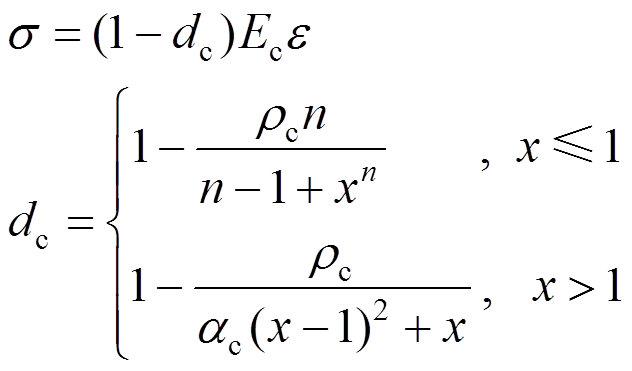 (2)
(2)式中: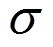 为混凝土应力;
为混凝土应力;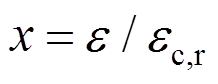 ;
;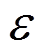 为混凝土应变;
为混凝土应变;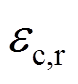 为相应的混凝土峰值压应变;其他参数的具体含义及取值参照文献[15]。
为相应的混凝土峰值压应变;其他参数的具体含义及取值参照文献[15]。
2.2.1 单元选取及网格划分
混凝土与钢管采用八节点减缩积分格式的三维实体单元(C3D8R)来模拟,腔内钢筋笼采用三维桁架单元(T3D2),试件的柱头与柱脚采用解析刚体(analytical rigid)来模拟。混凝土在接触分析中为从属表面,其网格密度不应低于钢管,同时为保证精度,网格三向尺寸不应相差过大[16]。
2.2.2 边界条件及加载方式
为了更好的收敛,同时方便计算,各实体与实体、实体与刚体之间采用绑定(tie)约束,钢筋笼嵌入(embed)混凝土中。模型采用位移加载,在其加载顶板的参考点上施加竖向位移来进行加载,同时将加载底板的参考点设为铰接。
图9为试件T1C2H5E3S1-6和对应有限元模型破坏对比图,从图中可以看出,试件和模型都是柱中发生较大的侧向挠度,最后发生弯曲失稳破坏,且发生破坏时两者的弯曲程度相当。

图9 试验构件与有限元模型破坏对比图
Fig.9 Comparison failure model
将试验实测的各试件极限承载力值(Nu)与有限元模拟计算值(N1)进行比较(表3),从表中可以看出有限元分析结果与试验数据的平均值为0.97,标准差为0.058,极限承载力整体上吻合良好;图10为有限元计算的荷载-侧向挠度曲线与部分试验实测的荷载-侧向挠度曲线对比图,从对比图中可以看出,两者的荷载-侧向挠度曲线在达到极限荷载之前基本保持一致,在曲线下降段,由于试验偏心加载的支座和有限元模拟的铰支座边界条件有所不同,同时在模拟时,没有设置多腔钢管的焊缝开裂情况,如试件T2C2H5E1S1-2,故曲线在下降段有一定的误差。
表3 试验承载力与有限元结果及公式计算值对比
Table 3 Comparison of test bearing capacity with finite element results and formula calculation value
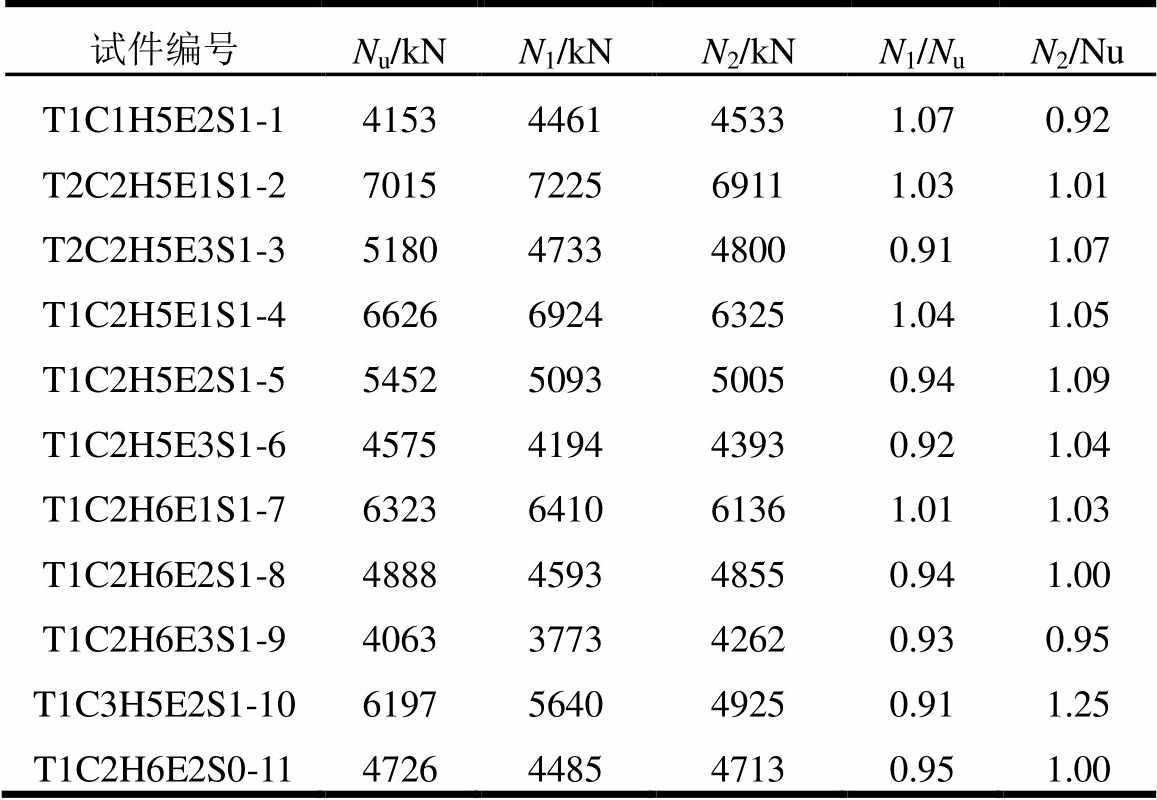
试件编号Nu/kNN1/kNN2/kNN1/NuN2/Nu T1C1H5E2S1-14153446145331.070.92 T2C2H5E1S1-27015722569111.031.01 T2C2H5E3S1-35180473348000.911.07 T1C2H5E1S1-46626692463251.041.05 T1C2H5E2S1-55452509350050.941.09 T1C2H5E3S1-64575419443930.921.04 T1C2H6E1S1-76323641061361.011.03 T1C2H6E2S1-84888459348550.941.00 T1C2H6E3S1-94063377342620.930.95 T1C3H5E2S1-106197564049250.911.25 T1C2H6E2S0-114726448547130.951.00
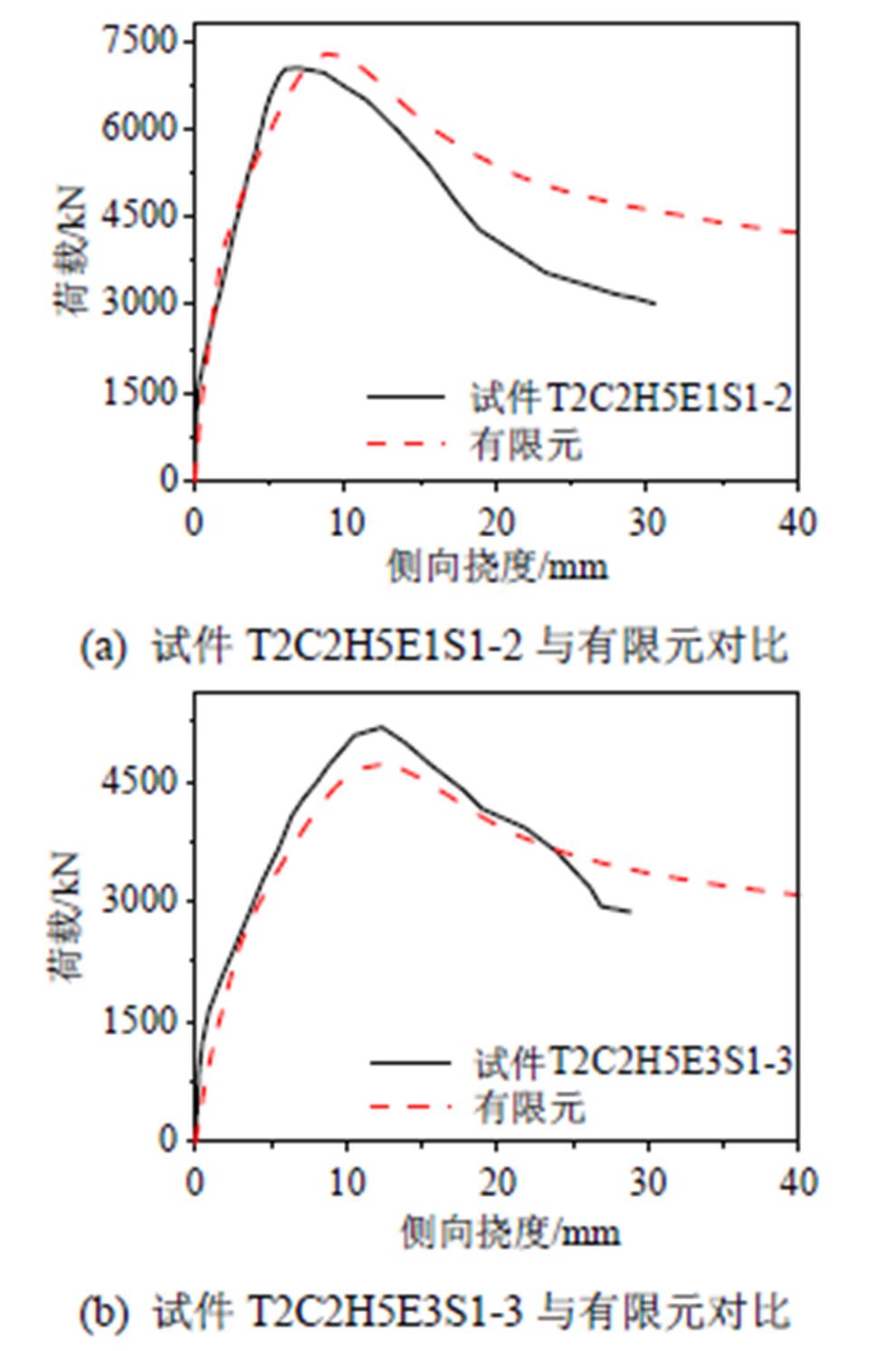
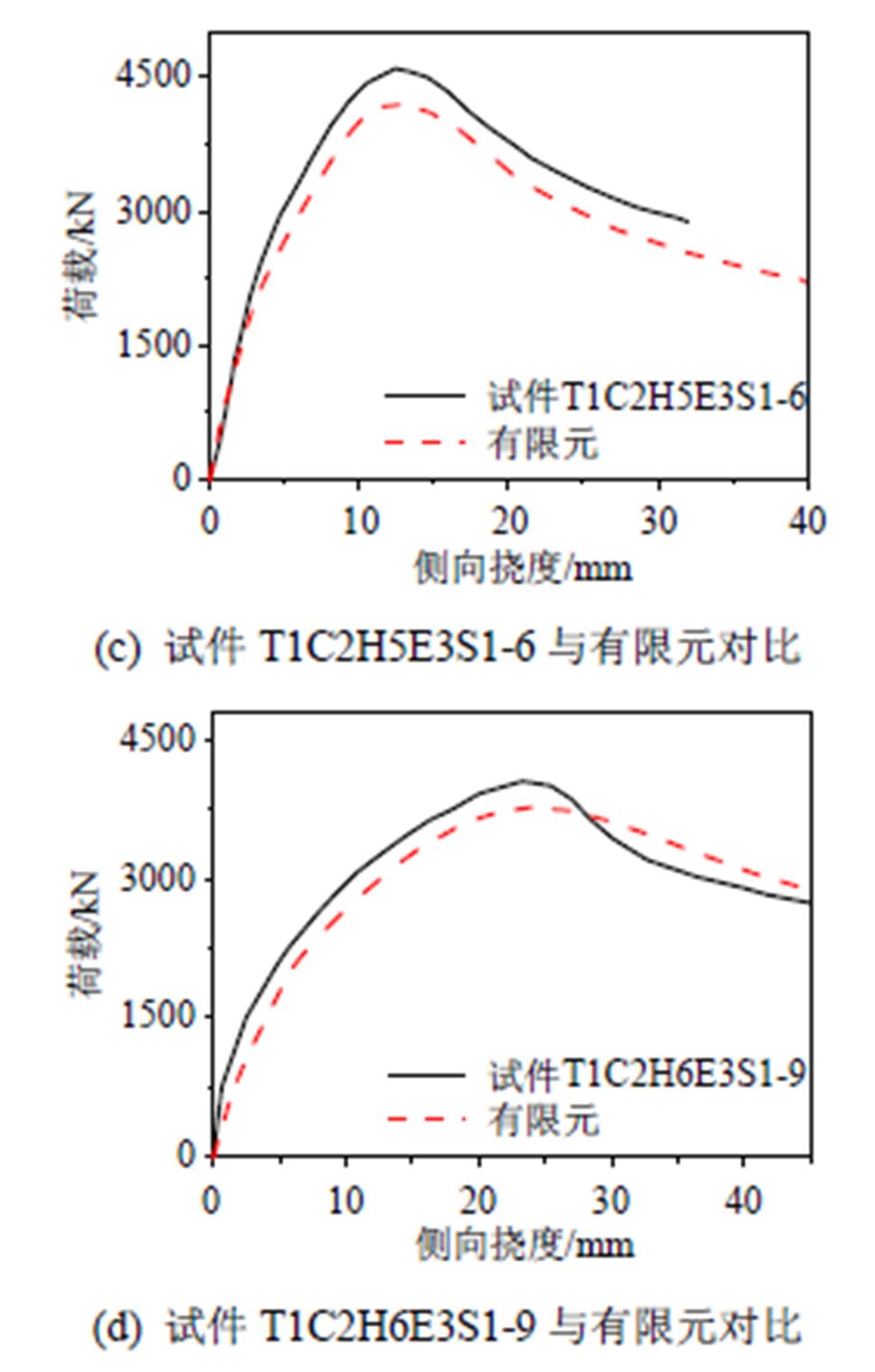
图10 有限元与部分试验荷载变形曲线对比
Fig.10 Comparison between calculated and measured N-um curves
总体来看,有限元模拟结果与试验结果吻合较好,说明有限元模型设置合理,计算精度满足要求,结果可以信任。
在有限的试验数据基础上,通过有限元模拟,深入拓展分析混凝土强度、偏心率、钢管壁厚和长细比对多腔式多边形钢管混凝土柱偏心受压极限承载力的影响规律。
1) 混凝土强度
以试件T1C2H6E2S1-8为基准模型,建立足尺模型,同时考虑了5种不同混凝土强度等级的柱模型,混凝土强度等级分别为C40、C50、C60、C70和C80,有限元计算的长细比与极限承载力关系如图11所示, 从图中可以看出混凝土强度等级为C40~C80的模型对应的极限承载力分别为1.32×106 kN、1.44×106 kN、1.53×106 kN、1.68×106 kN和1.71×106 kN,同强度等级为C40的构件相比,极限承载力分别提高了9.2%、16.4%、27.7%和30.0%,提高混凝土强度可提高构件的极限承载力,但同时会降低套箍系数,钢管对受压区的混凝土约束作用减弱,且混凝土强度越高脆性越大,对柱的综合受力性能产生不利影响。
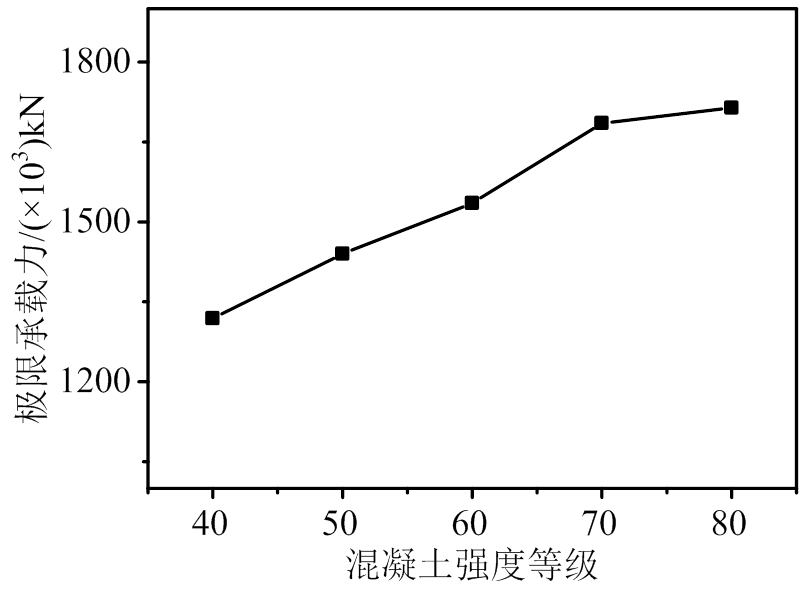
图11 不同混凝土强度等级与极限承载力的关系
Fig.11 Ultimate bearing capacity with different concrete strength
2) 偏心率
以试件T1C2H5E2S1-5为基准模型,建立足尺模型,同时考虑了5种不同偏心率的柱模型,偏心率分别为0.2、0.4、0.6、0.8和1,有限元计算偏心率与极限承载力关系如图12所示,从图中可以看出,偏心率为0.2~1的模型对应的极限承载力分别为3.08×106 kN、2.67×106 kN、2.28×106 kN、1.95×106 kN和1.67×106 kN,随着偏心率的增大,极限承载力降低明显,与偏心率为0.2的构件相比,极限承载力分别降低了13.5%、26.0%、36.7%和54.1%,这是由于偏心率的增加,构件越容易发生弯曲,随着荷载的增加弯曲增大,进而使得附加偏心距增加,偏心距和弯曲作用相互影响,最终结果导致构件承载力降低。
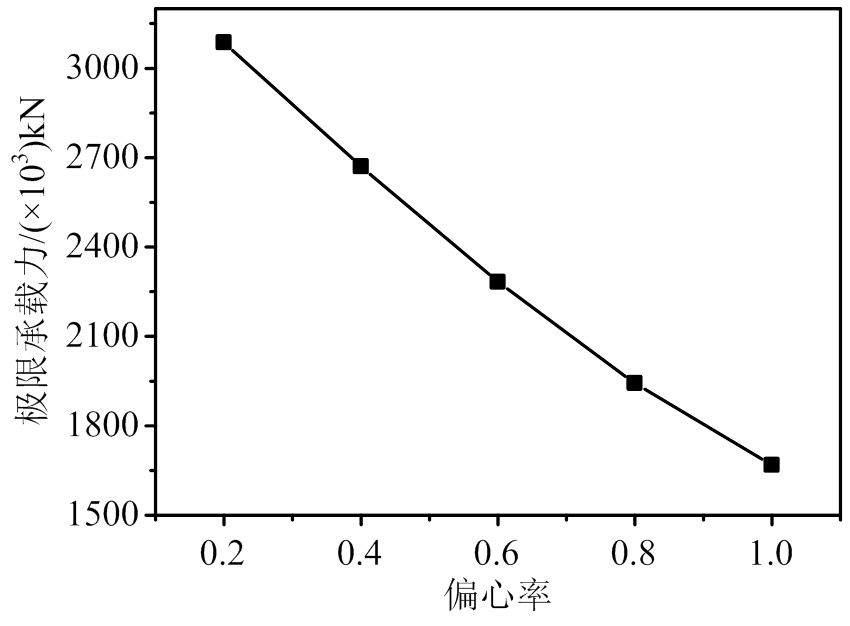
图12 不同偏心率与极限承载力的关系
Fig.12 Ultimate bearing capacity with different e/i
3) 钢管壁厚
以试件T1C2H6E2S1-8为基准模型,建立足尺模型,同时考虑了5种不同钢管壁厚的柱模型,钢管壁厚分别为60 mm、80 mm、100 mm、120 mm和140 mm,有限元计算钢管壁厚与极限承载力关系如图13所示。从图中可以看出,钢管壁厚为60 mm~140 mm的模型对应的极限承载力分别为1.68×106 kN、1.96×106 kN、2.21×106 kN、2.43×106 kN和2.64×106 kN,与钢管壁厚为60 mm的构件相比,极限承载力分别提高了16.1%、31.3%、44.3%和56.6%,这主要是由于多腔式多边形钢管混凝土柱内部由多个腔体组成,增加钢管壁厚也即增加腔内钢板及外钢管的壁厚,一方面提高了构件的含钢率,另一方面增强了其抗弯能力,从而提高其极限承载力。
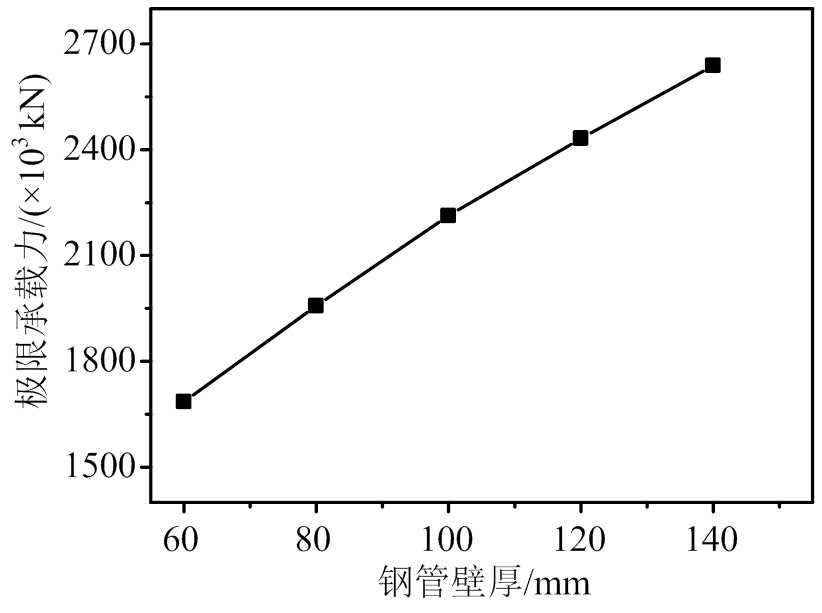
图13 不同钢材壁厚与极限承载力的关系
Fig.13 Ultimate bearing capacity with different steel wall thickness
4) 长细比
以试件T1C2H5E2S1-5为基准模型,建立足尺模型,同时考虑了5个不同长细比的柱模型,模型的长细比分别为24、40、50、60和70,有限元计算极限承载力与长细比关系如图14所示,从图中可以看出,长细比为24~70的模型对应的极限承载力分别为1.95×106 kN、1.70×106 kN、1.53×106 kN、1.36×106 kN和1.20×106 kN,随着长细比的增加,构件越容易发生弯曲和失稳,对承载力的影响同偏心率相似,与长细比为24的构件相比,极限承载力分别降低了13.2%、21.6%、31.0%和38.6%,随长细比的增加,极限承载力显著降低。
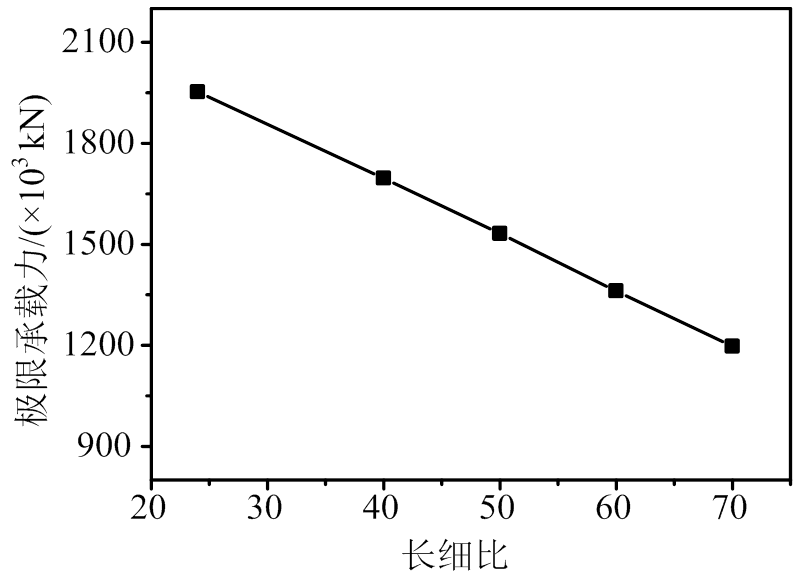
图14 不同长细比与极限承载力的关系
Fig.14 Ultimate bearing capacity with different slenderness ratio
目前关于钢管混凝土压弯构件承载力的计算方法主要有最大荷载理论、轴力与弯矩相关方程、偏心距增大系数法和经验系数法四种方法[17],前三种方法涉及的参数众多,若用来计算多腔式多边形钢管混凝土柱的承载力,方法中相关参数的取值确定较为困难,且计算过程繁琐,不利于在实际工程中的应用,同时从承载力影响因素分析中可以得出长细比和偏心率依然为多腔式多边形钢管混凝土偏心受压构件极限承载力主要影响因素,故本文参考经验系数法[18]及现有的组合T形钢管混凝土柱偏心受压承载力计算方法[1],建立多腔式多边形钢管混凝土柱偏心受压承载力计算公式,公式的形式如式(3)所示。
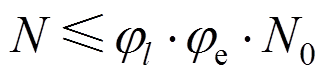 (3)
(3)式中:N0为轴压短柱承载力计算公式;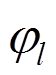 为与长细比有关的稳定系数;
为与长细比有关的稳定系数;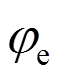 为偏心率影响因子。
为偏心率影响因子。
由于多腔式多边形钢管混凝土柱由多个腔体构成,比单腔体钢管混凝土柱对混凝土的约束能力强,文献[14]以钢管混凝土极限平衡理论为基础,考虑每个腔体对腔内混凝土的约束作用,建立了多腔式多边形钢管混凝土短柱承载力计算公式,公式具体形式如式(4)所示。
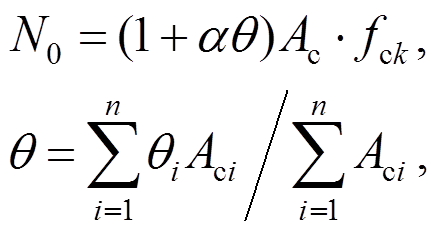
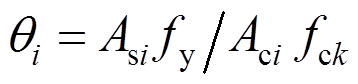 。 (4)
。 (4)
式中: 为提高系数,在文献[19]中经过大量有限元算例分析,认为取1.1;其余参数取值及含义见文献[14]。
为提高系数,在文献[19]中经过大量有限元算例分析,认为取1.1;其余参数取值及含义见文献[14]。
各国规范中将稳定系数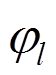 和强度承载力的计算公式相乘,作为轴压长柱承载力计算公式,本文参考GB 50936[11]中多边形钢管混凝土稳定系数
和强度承载力的计算公式相乘,作为轴压长柱承载力计算公式,本文参考GB 50936[11]中多边形钢管混凝土稳定系数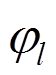 的计算公式,如式(5)所示,针对大量有限元结果,对
的计算公式,如式(5)所示,针对大量有限元结果,对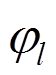 和
和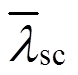 进行拟合,以稳定系数
进行拟合,以稳定系数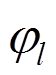 为纵坐标,正则长细比
为纵坐标,正则长细比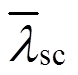 为横坐标,拟合关系曲线如图15所示,得到k=0.246,这和规范中的0.25很接近,为方便使用,直接采用规范数值。
为横坐标,拟合关系曲线如图15所示,得到k=0.246,这和规范中的0.25很接近,为方便使用,直接采用规范数值。
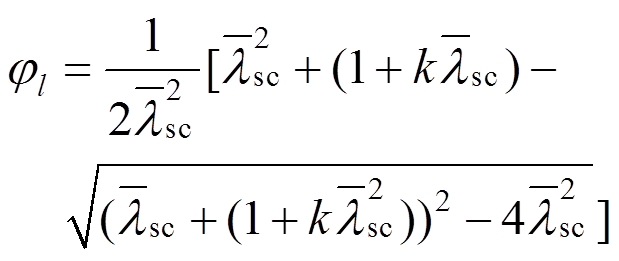 (5)
(5)式中: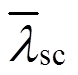 为构件正则长细比;
为构件正则长细比;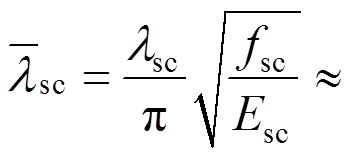
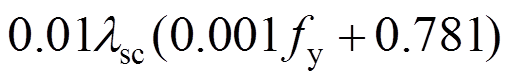 ,其中
,其中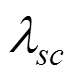 为构件的长细比,fy为钢材的强度。
为构件的长细比,fy为钢材的强度。
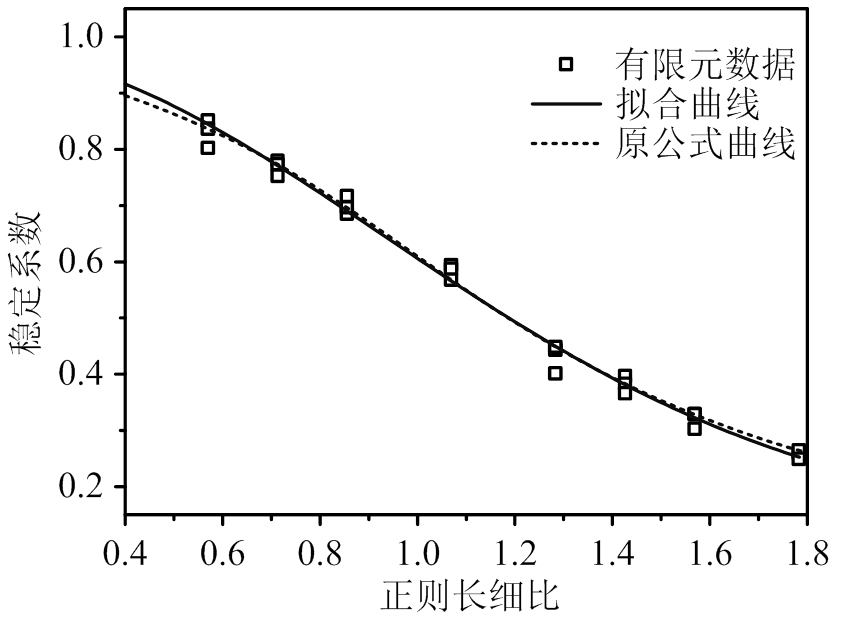
图15 稳定系数与正则长细比关系
Fig.15 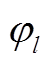 -
-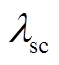 curve
curve
为进一步验证稳定系数的正确性,将轴压中长柱承载力公式计算值与课题组前期关于多腔式多边形钢管混凝土轴压中长柱试验得到的稳定承载力数据进行对比(表4),从表中的对比可以看出,试验值与计算值之比平均值为1.02,标准差为0.04。
经验公式中的另一个系数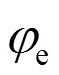 ,为偏心率影响因子,由极限平衡理论[18]可知,当偏心率较小时,钢管混凝土柱的轴力N和端弯矩M在直角坐标系中可足够精确的简化为一条直线,计算式为:
,为偏心率影响因子,由极限平衡理论[18]可知,当偏心率较小时,钢管混凝土柱的轴力N和端弯矩M在直角坐标系中可足够精确的简化为一条直线,计算式为:
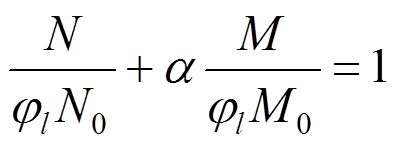 (6)
(6)表4 长柱轴心受压试验数据
Fig.4 Test results of long slenderness ratio specimens

试件编号钢材壁厚/mm混凝土强度等级长细比L/i钢筋笼钢材强度等级钢筋强度等级长度/mm试验值Nu/kN计算值Nc/kNNu/Nc T1C1H5S1-13C6024有Q235HPB3001800750177820.96 T2C2H5S1-24C7024有Q235HPB3001800945893881.01 T1C2H4S1-33C7020有Q235HPB3001500922186951.06 T1C2H5S1-43C7024有Q235HPB3001800898085921.05 T1C2H6S1-53C7033.33有Q235HPB3002500835083351.00 T1C2H6S0-63C7033.33无Q235—2500853380921.05
式中: 为待定系数;M0为钢管混凝土柱纯弯时的承载力。
为待定系数;M0为钢管混凝土柱纯弯时的承载力。
由文献[18]可知,钢管混凝土纯弯时的极限弯矩为:
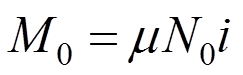 (7)
(7)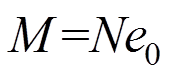 (8)
(8)
式中: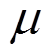 为小于1的系数;
为小于1的系数;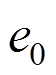 为荷载初始偏心距;i为截面回转半径。
为荷载初始偏心距;i为截面回转半径。
于是式(6)为:
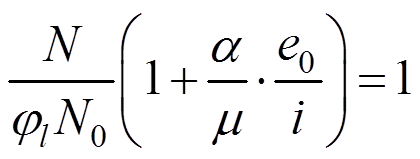 (9)
(9)同时由式(3)可知,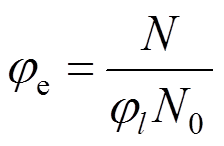 ,令
,令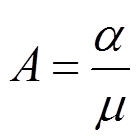 ,于是式(9)为:
,于是式(9)为:
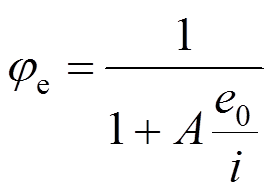 (10)
(10)
根据大量有限元结果,在图16中绘制出折减系数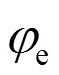 和偏心率e0/i的相关曲线,通过回归分析得到A=0.896,于是式(10)为:
和偏心率e0/i的相关曲线,通过回归分析得到A=0.896,于是式(10)为:
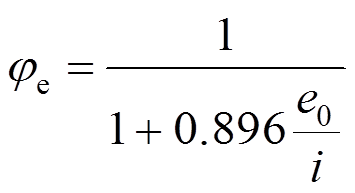
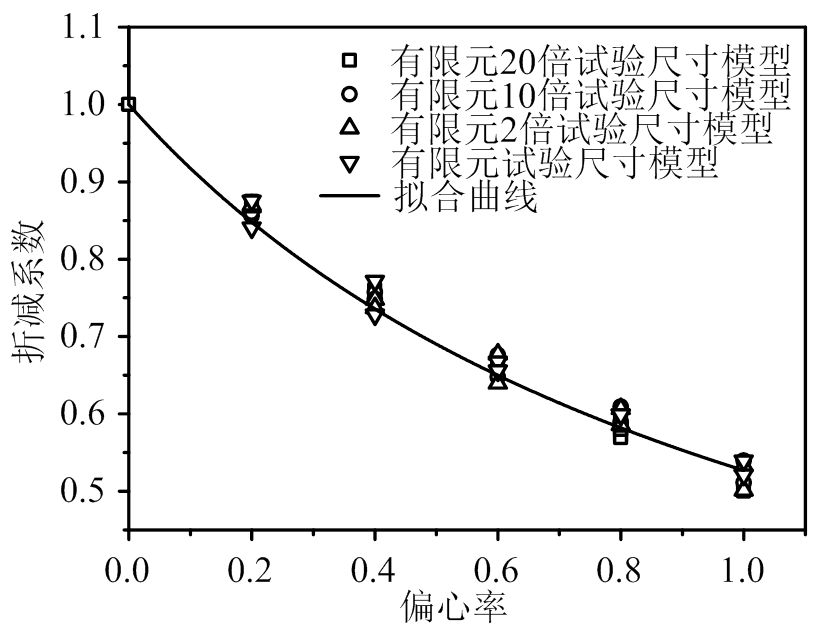
图16 折减系数与偏心率的关系
Fig.16 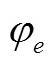 -e0/i curve
-e0/i curve
为验证本文提出的多腔式多边形钢管混凝土偏心受压柱承载力计算公式的可靠性,将承载力公式的计算值N2列于表3,从表中的对比可以看出,公式计算结果与本文试验结果比值的平均值为1.04,标准差为0.08;将公式计算值与文献[20]中试验数据进行对比,计算结果列于表5,从表5的对比中可以看出,公式计算值与试验值的比值为1.01,标准差为0.03,从上述的对比可知,承载力公式的计算值与六边形六腔及五边形四腔的钢管混凝土偏压柱试验值吻合较好,可为实际工程应用提供参考。
表5 文献[20]中极限承载力与公式计算值对比
Table 5 Comparison between literary and the calculation results of the formula

钢管形式截面积/m2混凝土等级钢板强度钢管壁厚/mm试件高度/mm钢筋笼偏心距/mm试验值N5/kN计算值N6/kNN6/N5 五边四腔0.354C50Q345b122500无20017037175691.03 0.354C50Q345b122500有20017248177031.02 0.354C50Q345b122500有20018140177030.98
注:截面回转半径i的计算按照本文采用的计算方法,经计算i约为236 mm。
通过静力试验对多腔式多边形钢管混凝土柱进行了偏心受压性能研究,包括破坏形态、荷载-侧向挠度关系曲线和荷载-应变关系曲线,采用ABAQUS软件拓展分析钢管壁厚、长细比、偏心距和混凝土强度等参数影响规律,最后基于大量有限元结果,建立了偏心受压承载力计算公式,得到以下主要结论:
(1) 多腔式多边形钢管混凝土柱偏心受压全过程分为以下四个阶段:第一阶段从开始加载到峰值荷载的75%左右;第二阶段为从峰值荷载的75%到峰值荷载;第三阶段为即荷载-柱中侧向挠度曲线中最高点与下降段拐点之间;第四阶段为从荷载-柱中侧向挠度曲线中下降段出现拐点至构件破坏。试件破坏形态主要为弯曲型失稳破坏,侧向挠曲变形大致呈正弦半波曲线形态。
(2) 多腔式多边形钢管混凝土偏心受压柱的后期承载力,随着混凝土强度或钢材壁厚的增加而增加,随着偏心距的增加而降低;多腔式多边形钢管混凝土偏心受压柱的延性,随着长细比的增加而提高,随着混凝土强度的增加而降低。
(3) 腔内钢筋笼可显著提高多腔式多边形钢管混凝土偏心受压柱的延性及后期承载力,但对其极限承载力影响不明显。
(4) 在试验数据基础上,通过有限元模拟,发现多腔式多边形钢管混凝土偏心受压柱的极限承载力,随钢管壁厚或混凝土强度等级的增加而提高,随长细比或偏心率的增加而降低,当钢管壁厚从60mm增加到140mm,极限承载力增大56.6%;混凝土强度从C30增加到C80,极限承载力增大30.0%;长细比从24增加到70,极限承载力下降38.6%;偏心率从0.2增加到1,极限承载力下降54.1%。
(5) 建立了适用于六边形六腔及五边形四腔的钢管混凝土柱偏心受压承载力计算公式,对于更多的截面形式有待进一步验证。
参考文献:
[1] 杜国锋, 徐礼华, 徐浩然. 组合T形截面钢管混凝土柱偏心受压试验研究[J]. 建筑结构学报, 2010, 31(7): 72―77.
Du Guofeng, Xu Lihua, Xu Haoran. Study on composite T-shaped concrete filled steel tubular columns under eccentric compression [J]. Journal of Building Structures. 2010. 31(7): 72―77. (in Chinese)
[2] 左志亮, 蔡健, 朱昌宏. 带约束拉杆L形钢管混凝土短柱的偏压承载力[J]. 工程力学, 2010, 27(7): 161―167.
Zuo Zhiliang, Cai Jian, Zhu Changhong. Bearing capacity of L-shape CFT stub columns with binding bars subjected to eccentric compression load [J]. Engineering Machanics, 2010, 27(7): 161―167. (in Chinese)
[3] 曹万林, 徐萌萌, 董宏英, 等. 不同构造五边形钢管混凝土巨型柱轴压性能计算分析[J]. 工程力学, 2015, 32(6): 99―108.
Cao Wanlin, Xu Mengmeng, Dong Hongying, et al. Analysis on axial compression behavior of pentagonal CFST mega columns [J]. Engineering Machanics, 2015, 32(6): 99―108. (in Chinese)
[4] 曹万林, 徐萌萌, 武海鹏, 等. 五边形钢管混凝土巨型柱偏压性能计算分析[J]. 自然灾害学报, 2015, 24(1): 114―122.
Cao Wanlin, Xu Mengmeng, Wu Haipeng, et al. Calculation analysis of eccentric compression behavior of pentagonal CFST mega columns [J]. Journal of Natural disasters, 2015, 24(1): 114―122. (in Chinese)
[5] 沈祖炎, 林震宇. L形钢管混凝土柱钢框架滞回性能研究[C]. 结构工程新进展国际论坛, 2009, 65―99.
Shen Zuyan, Lin Zhenyu. Hysteretic behaviors of steel frames with concrete-filled l-shaped steel tubular columns [C]. International Forum on New Progress In Structural Engineering, 2009, 65―99. (in Chinese)
[6] 张广泰, 姚亚楠, 荣彬, 等. T形截面方钢管混凝土组合异形柱压弯性能研究[J]. 建筑结构, 2014, 44(21): 27―31.
Zhang Guangtai, Yao Yanan, Rong Bin, et al. Study on mechanical properties of T-shaped column composed of concrete-filled square steel tubes under eccentric compression [J]. Building Structure, 2014, 44(21): 27―31. (in Chinese)
[7] Yang Y, Wang Y, Fu F, et al. Static behavior of T-shaped concrete-filled steel tubular columns subjected to concentric and eccentric compressive loads [J]. Thin-Walled Structures, 2015, 95: 374―388.
[8] Xu M, Zhou T, Chen Z, et al. Experimental study of slender LCFST columns connected by steel linking plates [J]. Journal of Constructional Steel Research, 2016, 127: 231―241.
[9] Rong B, Feng C, Zhang R, et al. Compression-bending performance of L-shaped column composed of concrete filled square steel tubes under eccentric compression [J]. International Journal of Steel Structures, 2017, 17(1): 325―337.
[10] 刘鹏, 殷超, 李旭宇, 等. 天津高银117大厦结构体系设计研究[J]. 建筑结构, 2012, 42(3): 1-9.
Liu Peng, Yin Chao, Li Xuyu, et al. Structural system design and study of Tianjin Goldin 117 mega tower [J]. Building Structure, 2012, 42(3): 1―9. (in Chinese)
[11] GB 50936—2014 钢管混凝土结构技术规范[S]. 北京: 中国建筑工业出版社, 2014.
GB 50936—2014, Technical standard of concrete filled steel tubular structures [S]. Beijing: China Building Industry Press, 2014. (in Chinese)
[12] GB/T 50081—2002, 普通混凝土力学性能试验方法标准[S]. 北京: 中国计划出版社, 2002.
GB/T 50081—2002, Ordinary concrete mechanical properties of the standard test method [S]. Beijing: China Plan Press, 2002. (in Chinese)
[13] GB/T 228—2002, 金属材料室温拉伸试验方法[S]. 北京: 中华人民共和国国家质量监督检验检疫总局, 2002.
GB/T 228—2002, Metallic material room temperature pulling test method [S]. Beijing: General Administration of Quality supervision, Inspection and Quarantine of the People’s Republic of China, 2002. (in Chinese)
[14] 徐礼华, 徐鹏, 侯玉杰, 等. 多腔式多边形钢管自密实高强混凝土短柱轴心受压性能试验研究[J]. 土木工程学报, 2017, 50(1): 37―45.
Xu Lihua , Xu Peng, Hou Yujie, et al. Experimental study in axial compression behavior of short polygonal multi-cell self-compacting high-strength CFST columns [J]. China Civil engineering journal, 2017, 50(1): 37―45. (in Chinese)
[15] GB 50010—2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011.
GB 50010—2010, Code for design of concrete structures [S]. Beijing: China Plan Press, 2011. (in Chinese)
[16] 韩林海. 钢管混凝土结构: 理论与实践[M]. 北京: 科学出版社, 2007: 107―108.
Han Linhai. Concrete filled steel tubular structures-theroy and practice [M]. Beijing: Science Press, 2007: 107―108. (in Chinese)
[17] 侯晓英, 王华. 钢管混凝土柱偏心受压承载力计算方法探讨[J]. 郑州大学学报(理学版), 2002, 34(3): 91―94.
Hou Xiaoying, Wang Hua. Comparison of calculation methods for bearing capacity of CFST under eccentrically loading [J]. Journal of Zhengzhou University: Natural Science Press, 2002, 34(3): 91―94. (in Chinese)
[18] 蔡绍怀. 现代钢管混凝土结构(修订版)[M]. 北京: 人民交通出版社, 2007: 81―83.
Cai Shaohuai. Modern steel tube confined concrete structures (Revised Edition) [M]. Beijing: China Communication Press, 2007: 81―83. (in Chinese)
[19] 徐鹏. 多腔钢管高强混凝土柱轴心受压工作机理与承载力研究[D]. 武汉: 武汉大学, 2017: 50―55.
Xu Peng. Study on working mechanism and bearing capacity of high-strength concrete filled multi-cell steel tube columns [D]. Wuhan: Wuhan University, 2017: 50―55. (in Chinese)
[20] 王立长, 曹万林, 徐萌萌, 等. 五边形截面钢管混凝土巨型柱受压性能试验研究[J]. 建筑结构学报, 2014, 35(1): 77―84.
Wang Lichang, Cao Wanlin, Xu Mengmeng, et al. Experimental research on compression behavior of pentagonal cross-section CFST mega-columns [J]. Journal of Building Structures, 2014, 35(1): 77―84. (in Chinese)
STUDY ON THE ECCENTRIC COMPRESSIVE BEARING CAPACITY OF POLYGONAL MULTI-CELL CONCRETE FILLED STEEL TUBULAR COLUMNS
Abstract: Based on the giant columns of Goldin Finance 117 tower in Tianjin, 11 eccentric compressive test specimens of polygonal multi-cell concrete filled steel tubular columns were designed and fabricated at a scale of 1/20. Mechanical behavior of the specimens was studied through the eccentric compression test. The failure mode, the load-lateral deformation curve and the load-strain curve were investigated. The influence of the steel wall’s thickness, slenderness ratio, eccentricity and concrete strength on the ultimate bearing capacity of the specimens were analyzed by using the software package ABAQUS. The results show that the eccentric compression specimens mainly demonstrated a flexible buckling failure; the ultimate bearing capacity of the specimen increased with the increase in the strength of concrete or steel wall’s thickness; the late bearing capacity and ductility of the specimen could be increased notably by the reinforced cage in the specimens. When the slenderness ratio increased from 24 to 70, the ultimate bearing capacity decreased by 38.6%. When the eccentricity ratio increased from 0.2 to 1, the ultimate bearing capacity decreased by 54.1%. Based on the results from the finite element analysis and the subsequent calculations about the bearing capacity of the columns, a calculation formula of the bearing capacity for hexagonal six-cell and pentagon four-cell concrete filled steel tubular columns was developed which can be used as a reference for practical engineering implementation.
Key words: polygonal multi-cell; concrete filled steel tube; eccentric compression; finite element; ultimate bearing capacity
文章编号:1000-4750(2019)04-0135-12
中图分类号:TU398+.9
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.02.0090
收稿日期:2018-02-07;
修改日期:2018-06-27
基金项目:国家自然科学基金重点项目(51738011)
刘素梅(1978―),女,湖北人,副教授,博士,硕导,主要从事钢管混凝土和纤维混凝土研究(E-mail: 1225101791@qq.com);
李 彪(1991―),男,河南人,博士生,主要从事钢管混凝土和纤维混凝土研究(E-mail: 752919556@qq.com);
余 敏(1982―),男,湖北人,副教授,博士,硕导,主要从事钢管混凝土研究(E-mail: ceyumin@whu.edu.cn);
周凯凯(1991―),男,河南人,硕士生,主要从事钢管混凝土研究(E-mail: 1597545219@qq.com).