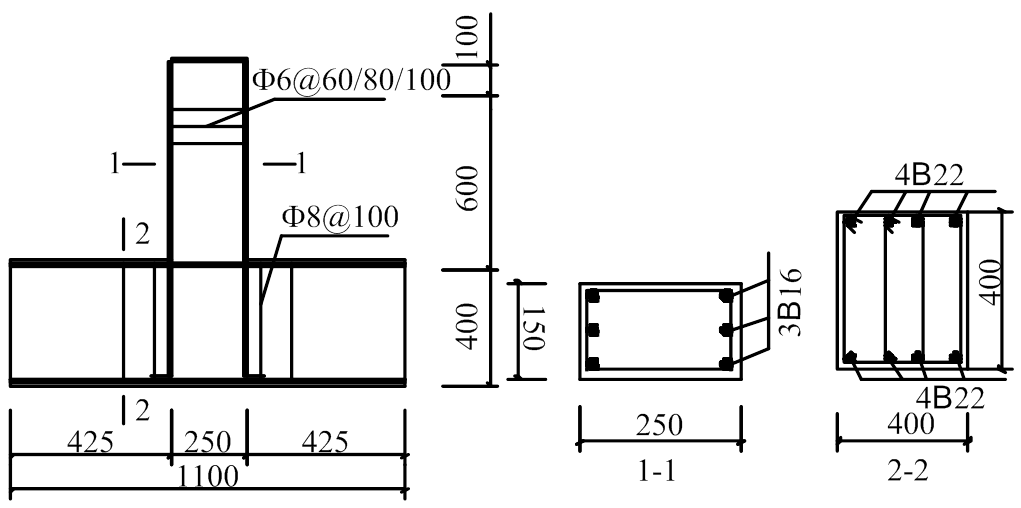
图1 试件截面尺寸及配筋图
Fig.1 Cross section and distributed steel of specimens
摘 要:为了研究近海大气环境下锈蚀RC框架梁的抗震性能,对8榀经受不同盐雾腐蚀循环作用的RC框架梁进行了低周反复加载试验,分析RC框架梁的滞回特性。基于试验结果,得到了带有负刚度段的三折线骨架曲线,并根据完好构件恢复力模型特征参数,得到了考虑钢筋锈蚀率和配箍率的锈蚀RC框架梁骨架曲线特征点计算公式。采用回归分析法,得到基于滞回耗能的循环退化指数,通过循环退化指数建立可综合考虑构件的捏拢效应、强度退化、卸载刚度退化、硬化刚度退化和再加载刚度加速退化的锈蚀RC框架梁恢复力模型。研究表明:随着钢筋锈蚀程度的增加,锈蚀RC框架梁的抗震性能劣化较明显,滞回耗能逐渐降低;配箍率对锈蚀RC框架梁恢复力特性的影响与未锈蚀RC框架梁相似;所建立的恢复力模型能够较好的描述锈蚀RC框架梁的滞回特性,可为该类结构的弹塑性时程分析提供理论参考。
关键词:近海大气环境;RC框架梁;锈蚀;滞回特性;恢复力模型
我国海域辽阔,沿海建筑物由于长期遭受盐雾腐蚀,其耐久性受到严重破坏,进而导致其承力、变形、耗能等力学性能退化[1]。RC (reinforced concrete)框架结构是我国最主要的结构形式之一,目前关于氯盐腐蚀混凝土结构的研究较多,但大多数研究主要基于材料层面[2―4],对于钢筋混凝土结构在近海大气环境下的抗震性能研究较少[5]。恢复力模型是结构或构件的抗震性能在结构弹塑性地震反应分析中的具体体现,理想的恢复力模型可较好地反映结构在地震作用下的受力情况,因此锈蚀构件恢复力模型的合理选取十分重要。目前,国内外关于结构或构件的恢复力模型已做了大量研究,建立的典型恢复力模型主要有[6―8]:Clough退化双线性模型[6]、Ramberg-Osgood恢复力模型[7]、武田退化三线型模型[8]、Bouc-Wen恢复力模型[9―10]等,但这些研究均是基于完好试件进行的,并未考虑环境因素对结构耐久性的影响,例如近海大气环境下盐雾腐蚀等不利因素对RC框架结构抗震性能影响的研究较少,而对其恢复力模型的研究几乎为零。
鉴于此,基于8榀经受不同盐雾腐蚀循环作用和配箍率的RC框架梁低周反复加载试验研究结果,得到RC框架梁的骨架曲线模型和基于盐雾损伤的循环退化指数,在此基础上获得考虑钢筋锈蚀损伤的RC框架梁的恢复力模型。结合试验结果,对提出的恢复力模型进行验证,从而为近海大气环境下在役混凝土结构的抗震性能评估提供依据。
本试验试件根据《建筑抗震设计规范》(GB 50011—2010)[11]中的“强柱弱梁”的设计原则进行设计,以钢筋锈蚀率和箍筋体积配箍率为影响RC框架梁抗震性能的参数,共设计了8榀RC框架梁,试件高度为700 mm,混凝土强度等级均为C30,采用P.O32.5R水泥配制,配合比为水泥∶砂∶石∶水=320∶870∶870∶135,实测混凝土28 d立方体抗压强度为27.05 MPa。柱的混凝土强度等级均为C40,截面尺寸均为400 mm×400 mm,试件截面尺寸和配筋如图1所示,各设计参数如表1所示。

图1 试件截面尺寸及配筋图
Fig.1 Cross section and distributed steel of specimens
表1 锈蚀RC框架梁试件设计参数
Table 1 Design parameters of corroded RC frame beams
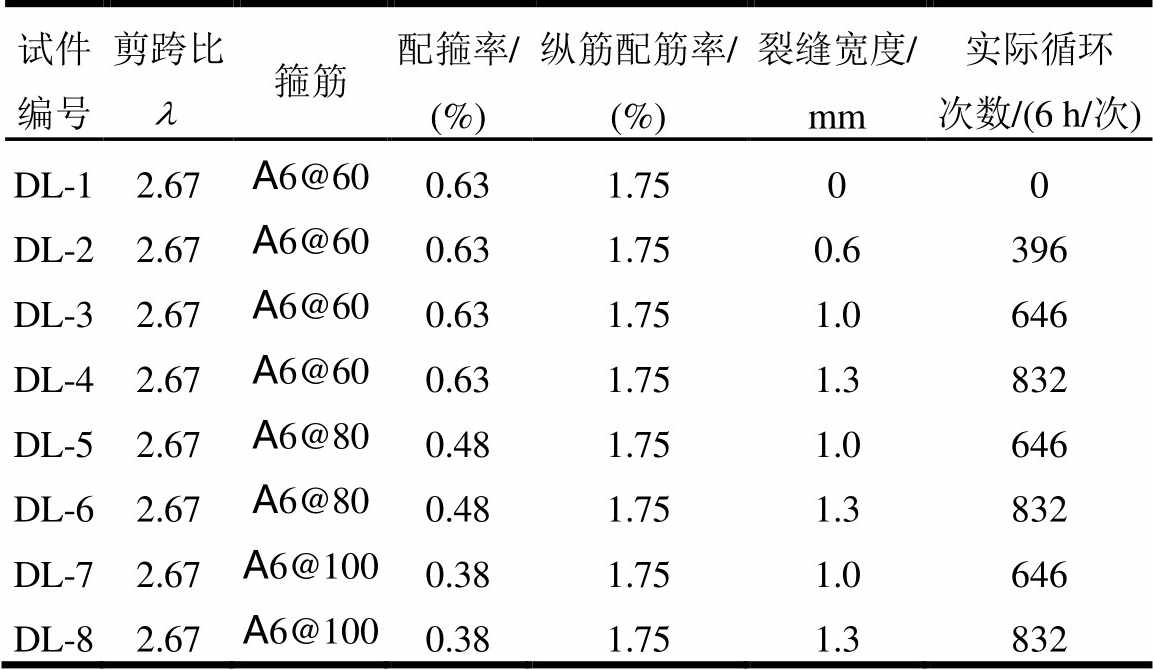
试件编号剪跨比箍筋配箍率/ (%)纵筋配筋率/ (%)裂缝宽度/ mm实际循环次数/(6 h/次) DL-12.67A6@600.631.7500 DL-22.67A6@600.631.750.6396 DL-32.67A6@600.631.751.0646 DL-42.67A6@600.631.751.3832 DL-52.67A6@800.481.751.0646 DL-62.67A6@800.481.751.3832 DL-72.67A6@1000.381.751.0646 DL-82.67A6@1000.381.751.3832
注:由于钢筋锈蚀程度差别较大,各试件中纵筋和箍筋的锈蚀率均取其平均值。
盐雾腐蚀试验在西安建筑科技大学气候模拟试验室进行,如图2(a)所示,为了加快钢筋锈蚀,此次试验浇筑构件时在混凝土中加入水泥质量5%的NaCl,并采用间断喷雾的方式模拟干湿循环的实际环境,盐雾腐蚀试验室的盐雾氯离子浓度取为5%,温度控制在45℃,以1 h为周期,喷雾20 min间歇40 min,以保持气候模拟试验室内的盐雾浓度恒定,并持时3 h,然后将气候箱内温度升至60℃±2℃进行烘干,持续2 h;室内湿度控制在90%左右,温差15℃,温度升降按照0.5℃/min,则盐雾烘干转化时间设定为30 min。因此,一次盐雾腐蚀循环需要6 h,每天可进行4个循环,本试验干湿循环过程示意图如图2(b)所示。
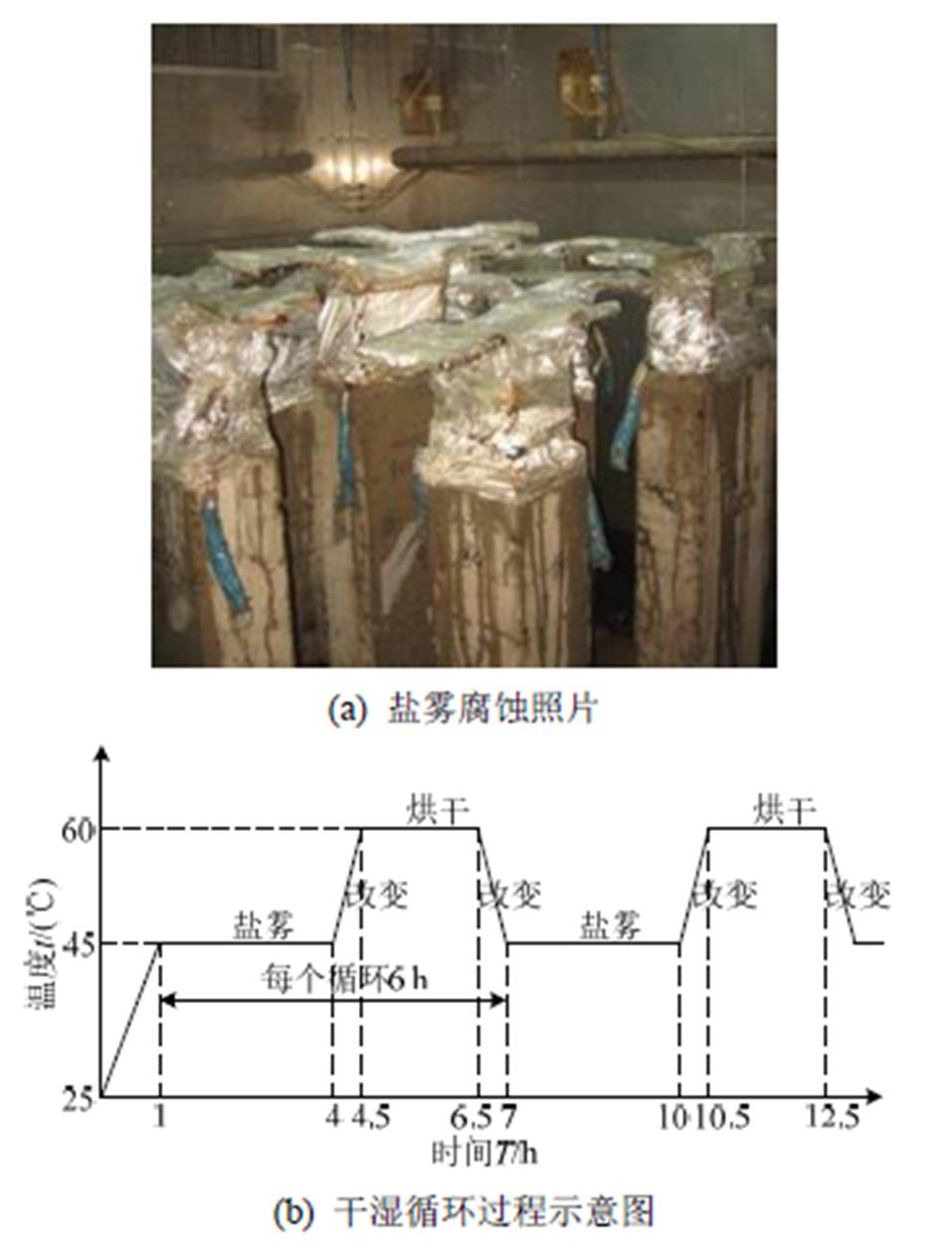
图2 盐雾模拟实验室及干湿循环过程
Fig.2 Salt spray simulation laboratory and wet-dry cycle
试件腐蚀完成后对试件进行低周反复循环加载,采用悬臂梁式加载方法[12],加载装置如图3所示。此试验加载制度采用位移控制加载,在试件屈服以前,控制位移幅值为采用有限元软件分析所得屈服位移的0.2倍,每级控制位移往复循环1次;在接近开裂和屈服荷载前控制位移减小级差加载;构件加载至屈服位移后,以该屈服位移的倍数为级差进行控制加载,每级控制位移循环3次。试验中各试件测试内容及测点布置见文献[13]。
低周反复加载试验完成后,对试件的锈蚀率进行测定,具体测定方法见文献[13]。本文用钢筋质量损失率来定量地描述钢筋锈蚀程度,按下式计算:
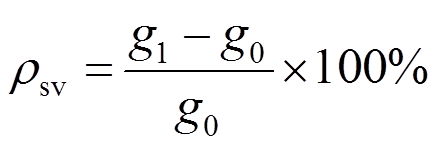 (1)
(1)
式中: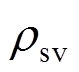 为钢筋实际锈蚀率;
为钢筋实际锈蚀率; 为预留完好钢筋单位长度的重量;
为预留完好钢筋单位长度的重量;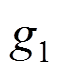 为除锈后钢筋单位长度的重量。由于各试件中钢筋的锈蚀程度差别较大,故采用各试件所有同类钢筋锈蚀率的平均值作为锈蚀钢筋的质量损失率,各试件钢筋锈蚀质量损失率如表2所示。
为除锈后钢筋单位长度的重量。由于各试件中钢筋的锈蚀程度差别较大,故采用各试件所有同类钢筋锈蚀率的平均值作为锈蚀钢筋的质量损失率,各试件钢筋锈蚀质量损失率如表2所示。
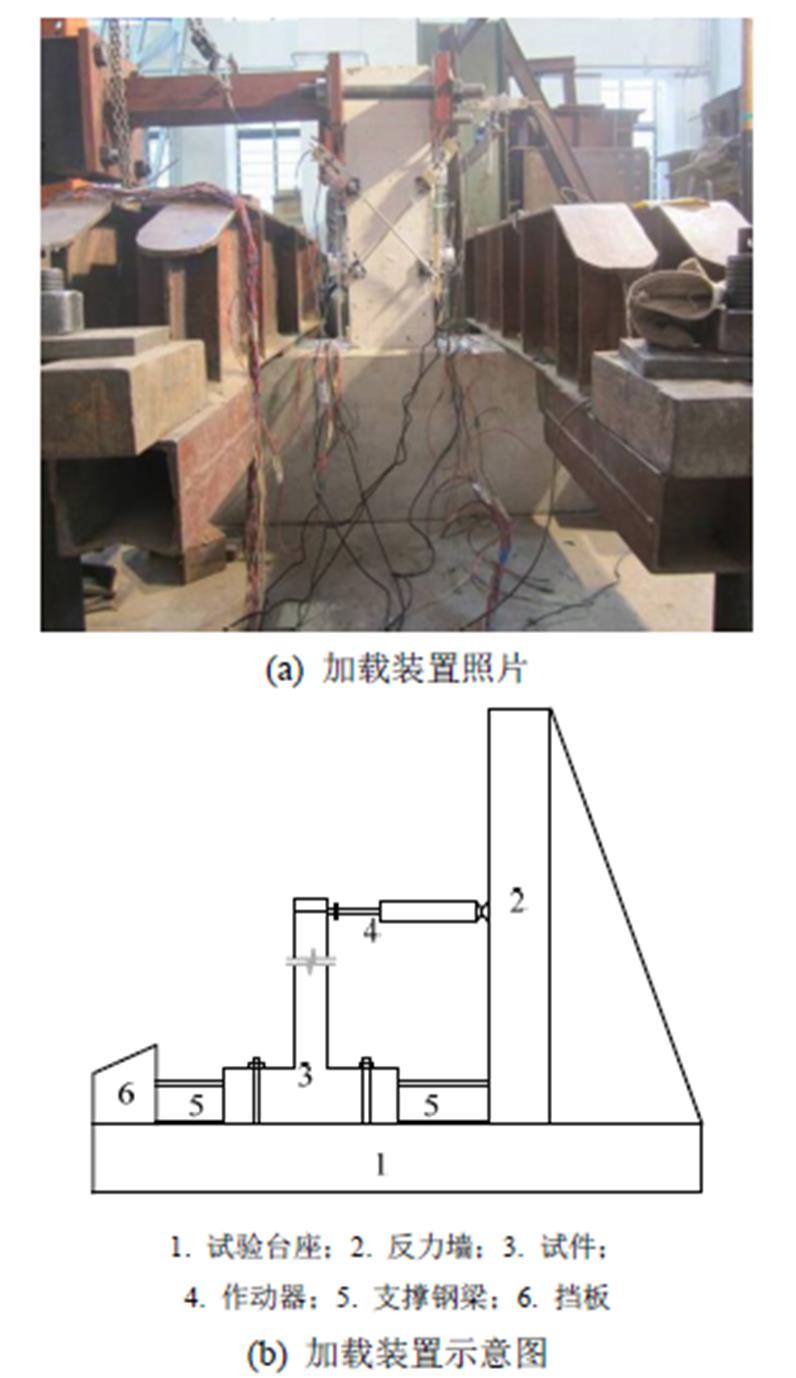
图3 加载装置
Fig.3 Test set-up
表2 钢筋锈蚀质量损失率
Table 2 Weight-loss rate of corroded reinforcement

试件DL1DL2DL3DL4DL5DL6DL7DL8 纵筋/(%)03.33.46.53.74.54.66.8 箍筋/(%)06.36.511.37.18.99.311.4
为便于分析钢筋锈蚀对RC框架梁抗震性能的影响,将DL-1定义为未锈蚀试件,DL-2、DL-3定义为轻微锈蚀试件,DL-5、DL-7定义为中度锈蚀试件,DL-4、DL-6、DL-8定义为重度锈蚀试件。图4为锈蚀RC框架梁荷载-位移滞回曲线。从图中可以看出,各试件的滞回特性基本相同,滞回曲线形状相似,基本都呈“捏拢”型,但是由于各试件配箍率及裂缝宽度的不同,各试件的滞回特性又有以下不同。
比较图4(a)~图4(h)发现,随着试件腐蚀程度的增加,试件的峰值荷载逐渐减小,加卸载曲线斜率逐渐降低,表明试件刚度逐渐退化;试件滞回曲线的“捏拢”效应更为明显,说明试件滞回耗能能力不断降低,试件破坏形式由延性破坏转为脆性破坏;随着试件配箍率的减小,试件的峰值荷载减小,滞回耗能能力、累计耗能能力逐渐降低,延性变差。
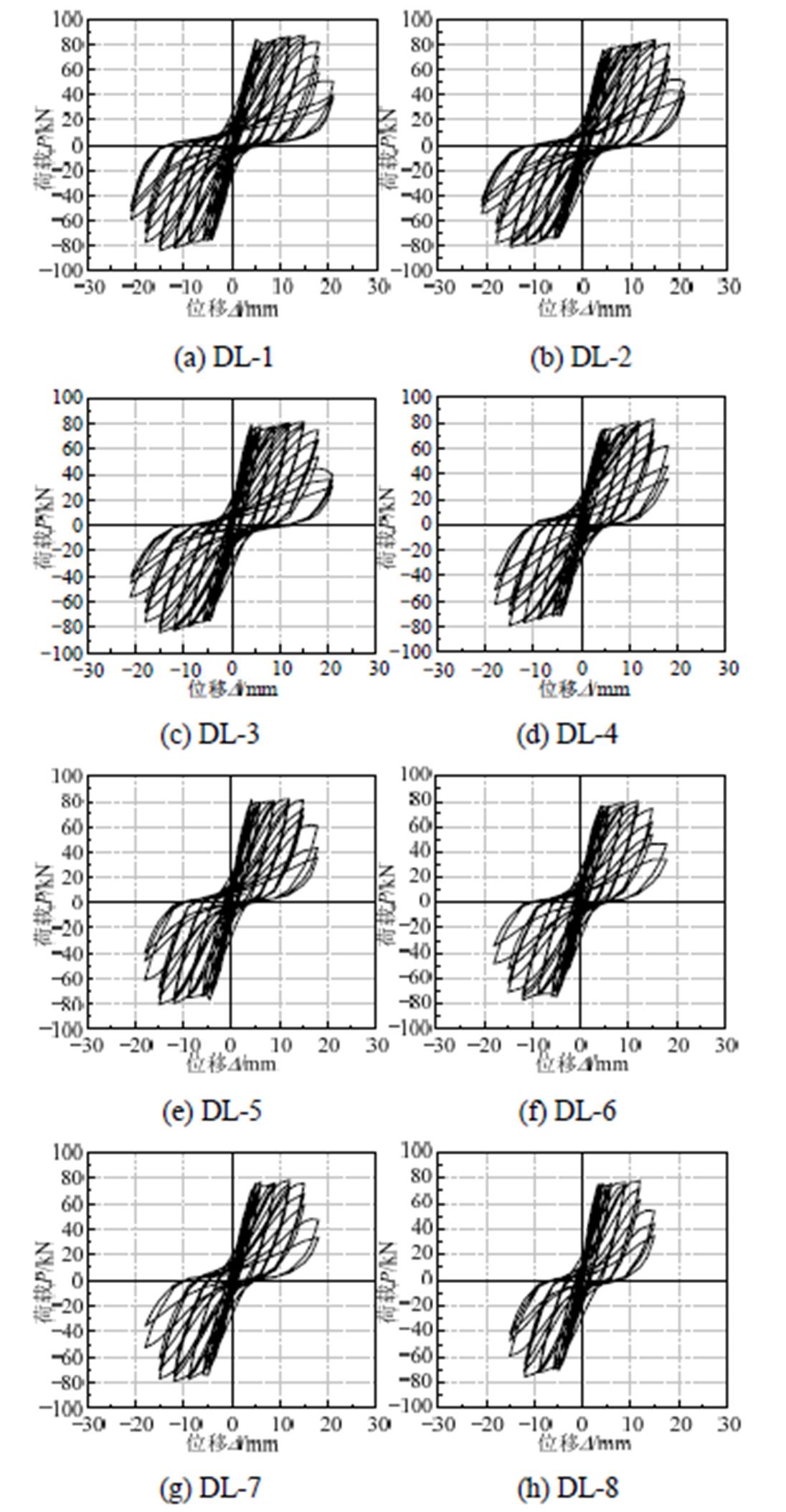
图4 试件滞回曲线
Fig.4 Hysteric curves of specimens
由图4(a)可知,在试件屈服之前,其基本处于弹性阶段,水平荷载与位移基本满足线性关系,试件滞回耗能较少;当试件屈服后,滞回曲线逐渐向右倾斜呈弯曲型,试件滞回耗能增大,随着循环周数和加载位移的增大,试件出现较为明显的强度、刚度退化现象,滞回曲线由于弯剪斜裂缝的张合而呈现较明显的捏拢现象。比较图4(a)和图4(b)、图4(c),其滞回曲线基本相同,这说明钢筋轻微锈蚀对RC框架梁耗能能力、滞回特性、延性、刚度及强度退化规律几乎没有影响。但图4(e)、图4(g)与图(a)、图4(b)、图4(c)相比,试件加卸载曲线更为平缓,极限承载力和加卸载刚度均有明显降低,如试件DL-5的极限承载力比DL-1降低约5.82%,DL-7比DL-1降低约8.42%;滞回曲线的捏拢现象更为明显,这是由于钢筋锈蚀程度增加,箍筋对核心混凝土的约束作用逐渐削弱,斜裂缝沿框架梁截面不断延伸且宽度增大,剪切变形越大,斜裂缝张合引起的捏拢现象越明显。随着腐蚀程度的进一步加大,如图4(d)、图4(f)、图4(h)所示,试件滞回性能各项力学指标则下降更严重。
通过对试件Ρ-D滞回曲线进行分析,得到各试件骨架曲线如图5所示。
从图5可以看出,当试件水平位移较小时,锈蚀RC框架梁的刚度较完好RC框架梁略有降低;屈服位移之后,锈蚀RC框架梁承载力和刚度有较为明显的降低,且随着锈蚀程度的增加,其承载力降低更严重。试件DL-1屈服后,其骨架曲线有较长的平直段,说明试件具有很好的延性,各锈蚀试件骨架曲线的平直段则变短,且钢筋锈蚀越严重,平直段越短,延性变形能力退化越明显。试件配箍率相同时,随着钢筋锈蚀程度的增大,试件极限位移和延性变形能力不断降低,RC框架梁由延性破坏发展为脆性破坏,降低了结构的抗震性能。钢筋锈蚀程度相近时,随着配箍率的减小,锈蚀RC框架梁的延性变形能力和极限位移不断降低,对结构抗震不利。由图5可知,随着钢筋锈蚀率的增大,配箍率较小的试件延性和极限位移降低更多,这说明钢筋锈蚀对配箍率较小的RC框架梁影响更大。
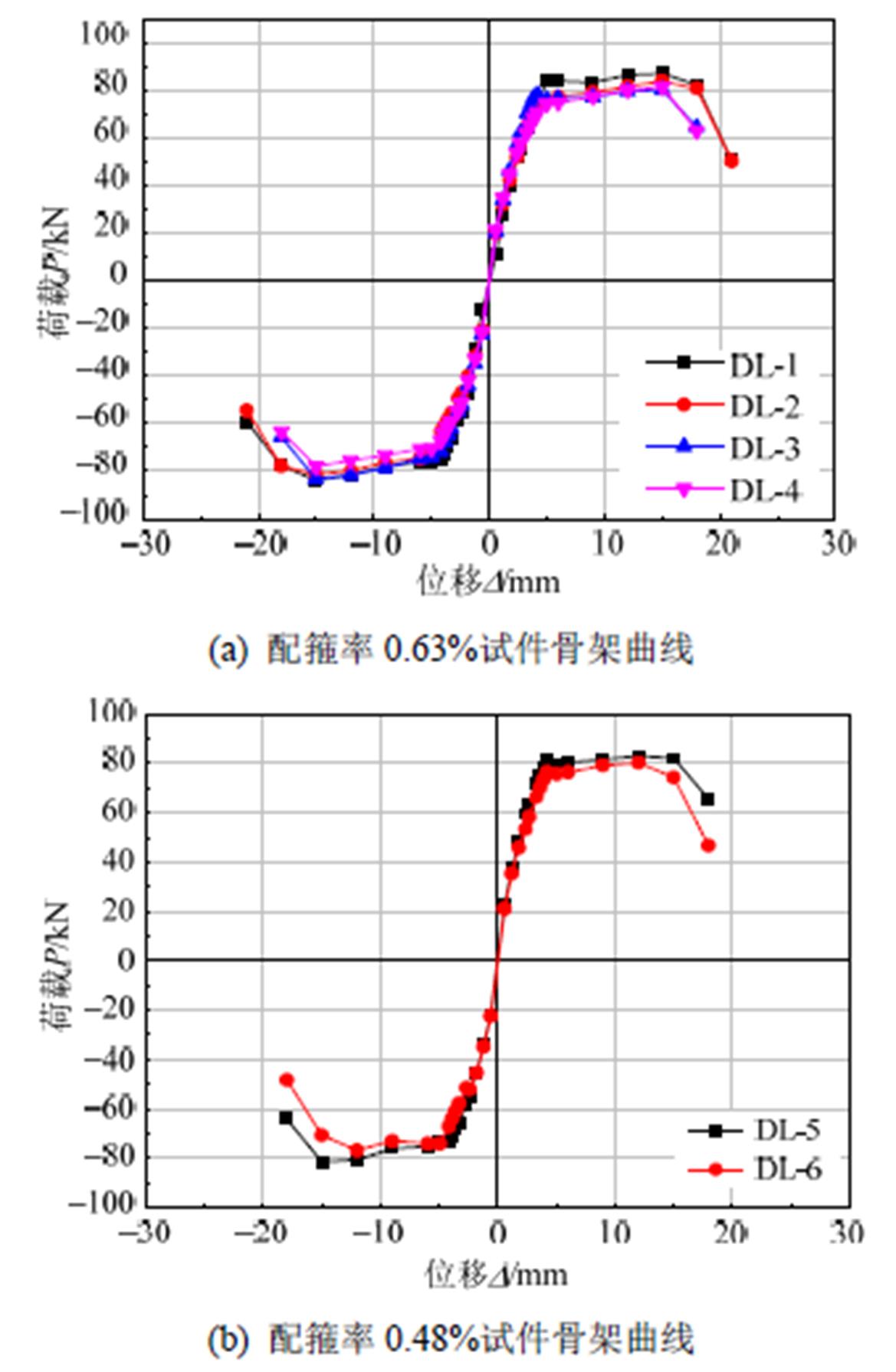
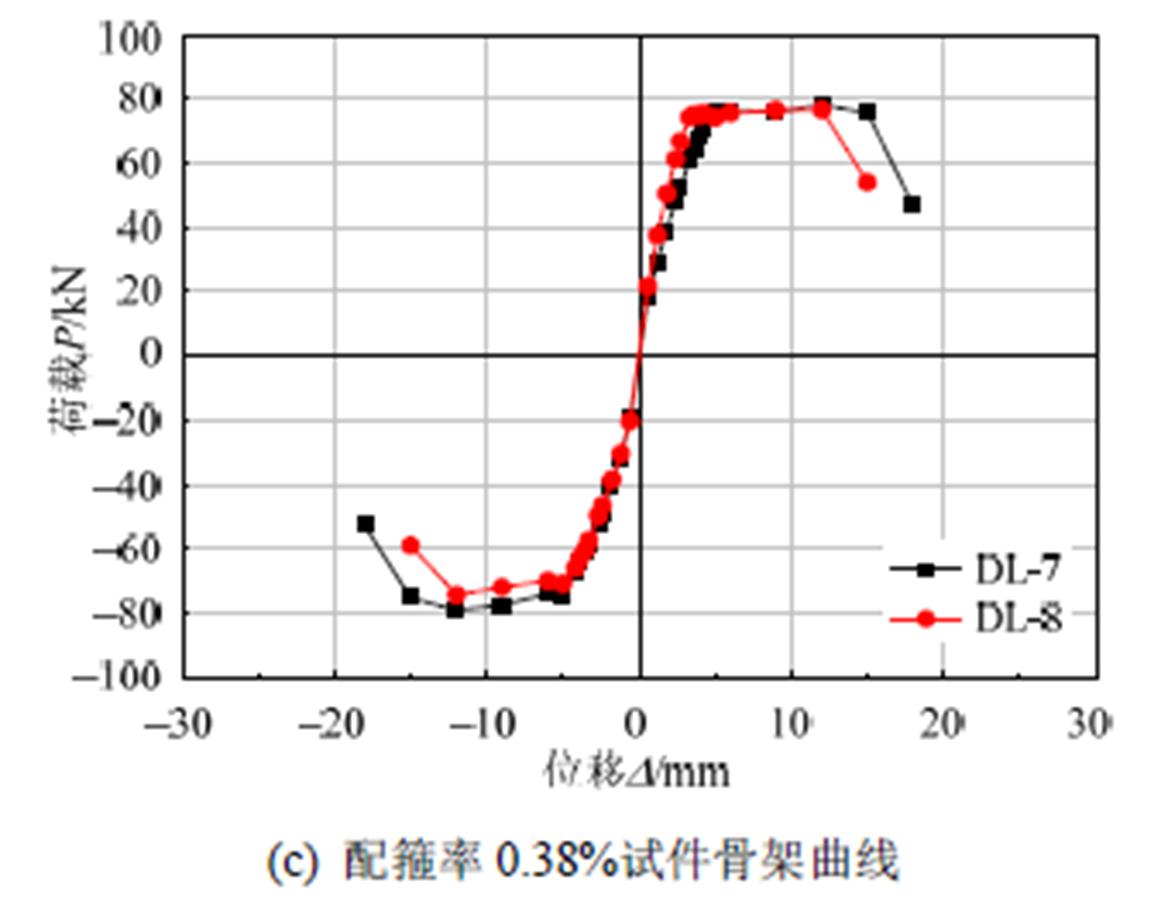
图5 试件骨架曲线
Fig.5 Specimen skeleton curves
综上所述,为了研究近海大气环境下锈蚀对RC框架梁承载力和变形性能之间关系的影响,本文基于试验结果,发现在往复循环加载中,钢筋锈蚀会导致试件恢复力特性退化,但并不影响试件滞回曲线形状,仅影响模型参数的取值。故笔者基于试验结果分析恢复力模型特征参数与钢筋锈蚀率的关系,以此体现钢筋锈蚀引起RC框架梁恢复力性能退化。此外,由文献[14]的分析结果可知,考虑滞回模型中的负刚度段可准确地分析RC结构地震损伤破坏乃至倒塌的全过程,同时前文锈蚀RC 框架梁滞回特性分析结果亦表明,钢筋锈蚀对滞回曲线负刚度段力学特性有显著影响。
因此,本文建立恢复力模型时,采用基于滞回耗能的退化指数来描述滞回模型的诸循环退化特性,骨架曲线选用考虑负刚度段的三折线型曲线,如图6所示。该骨架曲线共有6个特征点参数:屈服荷载、屈服位移、峰值荷载、峰值位移、极限荷载和极限位移。其中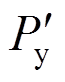 、
、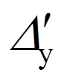 、
、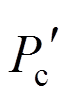 、
、 、
、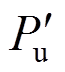 、
、 为未锈蚀构件骨架曲线特征点参数,具体计算方法参见文献[13]。对应的
为未锈蚀构件骨架曲线特征点参数,具体计算方法参见文献[13]。对应的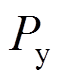 、
、 、
、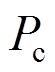 、
、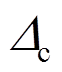 、
、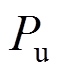 、
、 为锈蚀构件骨架曲线特征点参数,锈蚀试件骨架曲线特征点参数是在未锈蚀试件的基础上进行修正获得的。
为锈蚀构件骨架曲线特征点参数,锈蚀试件骨架曲线特征点参数是在未锈蚀试件的基础上进行修正获得的。
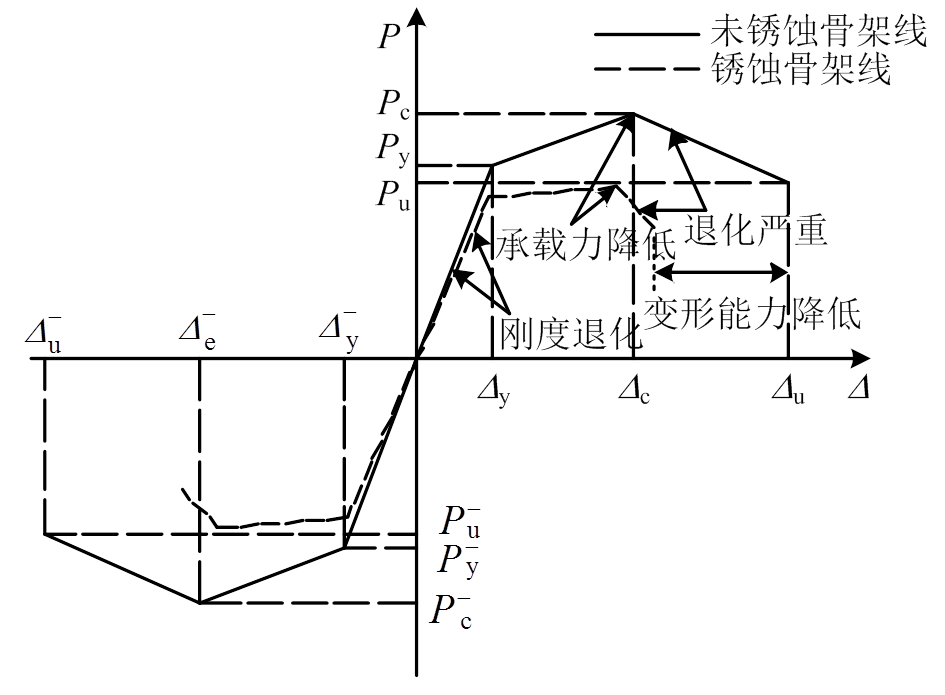
图6 三折线骨架曲线
Fig.6 Triangle line skeleton curve
本文对试验数据进行回归分析,得到锈蚀RC框架梁滞回模型特征点参数与钢筋锈蚀率、配箍率以及未锈蚀梁特征点参数间的关系式,其中钢筋锈蚀率的确定见文献[13]。不同钢筋锈蚀率和配箍率下锈蚀RC框架梁位移特征值和荷载特征值的表达式分别如下。
1) 屈服荷载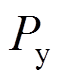 和屈服位移
和屈服位移
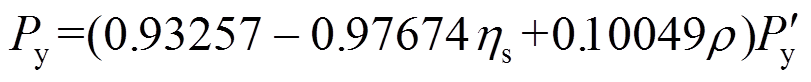 (2)
(2) (3)
(3)
式中: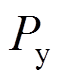 和
和 分别为锈蚀试件屈服荷载、屈服位移;
分别为锈蚀试件屈服荷载、屈服位移;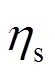 为钢筋锈蚀率;
为钢筋锈蚀率; 为配箍率。
为配箍率。
2) 峰值荷载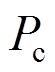 和峰值位移
和峰值位移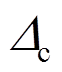
 (4)
(4)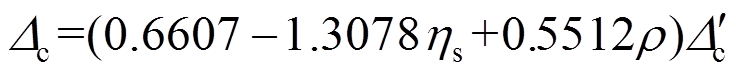 (5)
(5)
式中: 和
和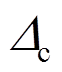 分别为锈蚀试件峰值荷载、峰值位移;
分别为锈蚀试件峰值荷载、峰值位移;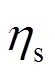 为钢筋锈蚀率;
为钢筋锈蚀率; 为配箍率。
为配箍率。
3) 极限荷载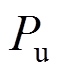 和极限位移
和极限位移
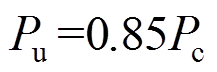 (6)
(6) (7)
(7)
式中: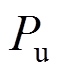 和
和 分别为锈蚀试件极限荷载、极限位移;
分别为锈蚀试件极限荷载、极限位移;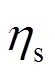 为钢筋锈蚀率;
为钢筋锈蚀率; 为配箍率。
为配箍率。
4) 恢复力模型骨架曲线各折线段刚度。
弹性段刚度:
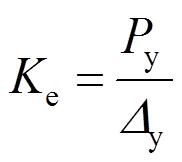 (8)
(8)硬化段刚度:
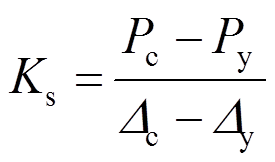 (9)
(9)
下降段刚度: (10)
(10)
利用式(2)~式(7),可计算锈蚀后骨架曲线的特征点,并与本试验所得的数据进行对比,试件特征点所对应的理论计算值和试验值分别见表3和表4。可以看出:荷载特征点的误差最大为8%,位移特征点的误差最大为15%,误差总体较小,预测精度位移的影响分析是正确的,提出的锈蚀RC框架梁滞回模型是合理的。
将恢复力模型骨架曲线计算结果与试验结果进行比较,如图7所示。可以看出,两者吻合较好,表明本文提出的锈蚀RC框架梁恢复力模型骨架曲线特征点简化计算方法是可行的,且此方法有一定适用性。
表3 特征点荷载计算值与试验值对比
Table 3 The comparison of the load between computation and test at feature points
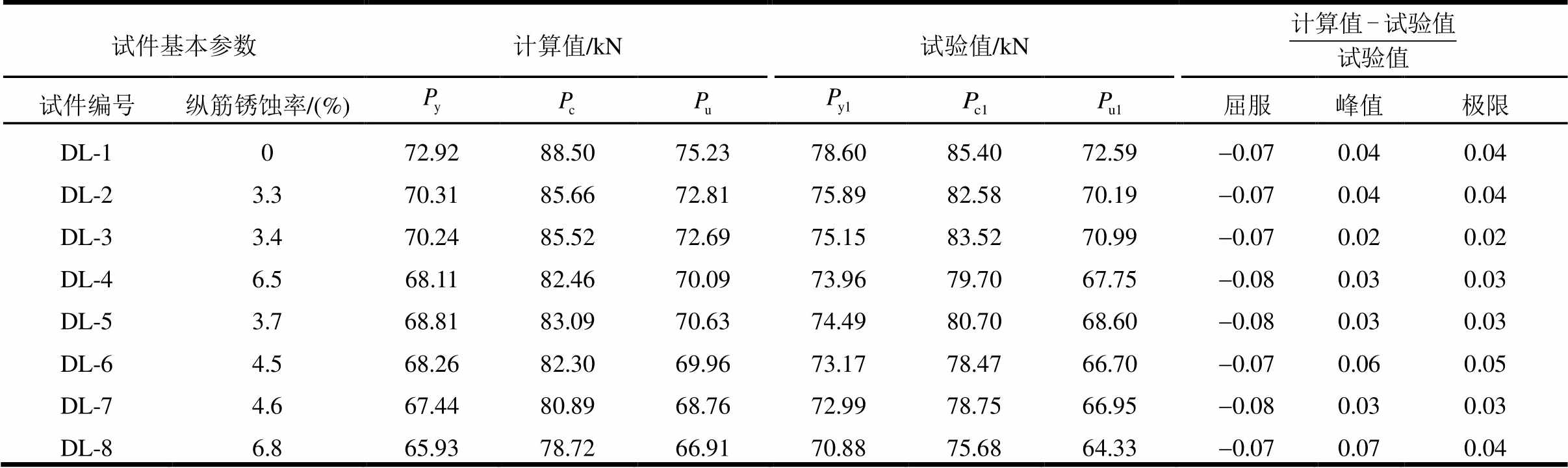
试件基本参数计算值/kN试验值/kN 试件编号纵筋锈蚀率/(%)屈服峰值极限 DL-1072.9288.5075.2378.6085.4072.59-0.070.040.04 DL-23.370.3185.6672.8175.8982.5870.19-0.070.040.04 DL-33.470.2485.5272.6975.1583.5270.99-0.070.020.02 DL-46.568.1182.4670.0973.9679.7067.75-0.080.030.03 DL-53.768.8183.0970.6374.4980.7068.60-0.080.030.03 DL-64.568.2682.3069.9673.1778.4766.70-0.070.060.05 DL-74.667.4480.8968.7672.9978.7566.95-0.080.030.03 DL-86.865.9378.7266.9170.8875.6864.33-0.070.070.04
表4 特征点位移计算值与试验值对比
Table 4 The comparison of displacement between computation and test at feature points

试件基本参数计算值/mm试验值/mm 试件编号纵筋锈蚀率/(%)屈服峰值极限 DL-104.2014.3020.784.8015.0218.89-0.13-0.050.11 DL-23.34.0913.7819.904.8014.8818.32-0.15-0.070.09 DL-33.44.0913.7719.864.6514.0018.40-0.12-0.020.08 DL-46.53.9413.2318.624.5614.0217.04-0.14-0.060.09 DL-53.73.9612.4818.154.4514.5816.83-0.11-0.140.08 DL-64.53.9212.3317.824.5012.0115.70-0.130.030.14 DL-74.63.8411.5516.804.5012.0015.97-0.15-0.040.05 DL-86.83.7411.1715.924.2012.0013.88-0.11-0.070.15

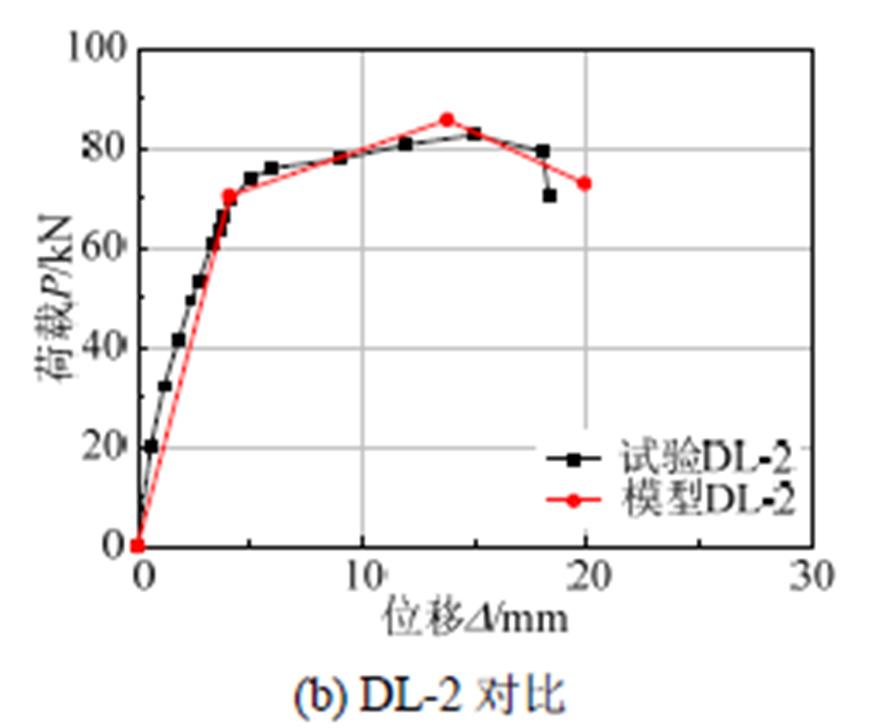
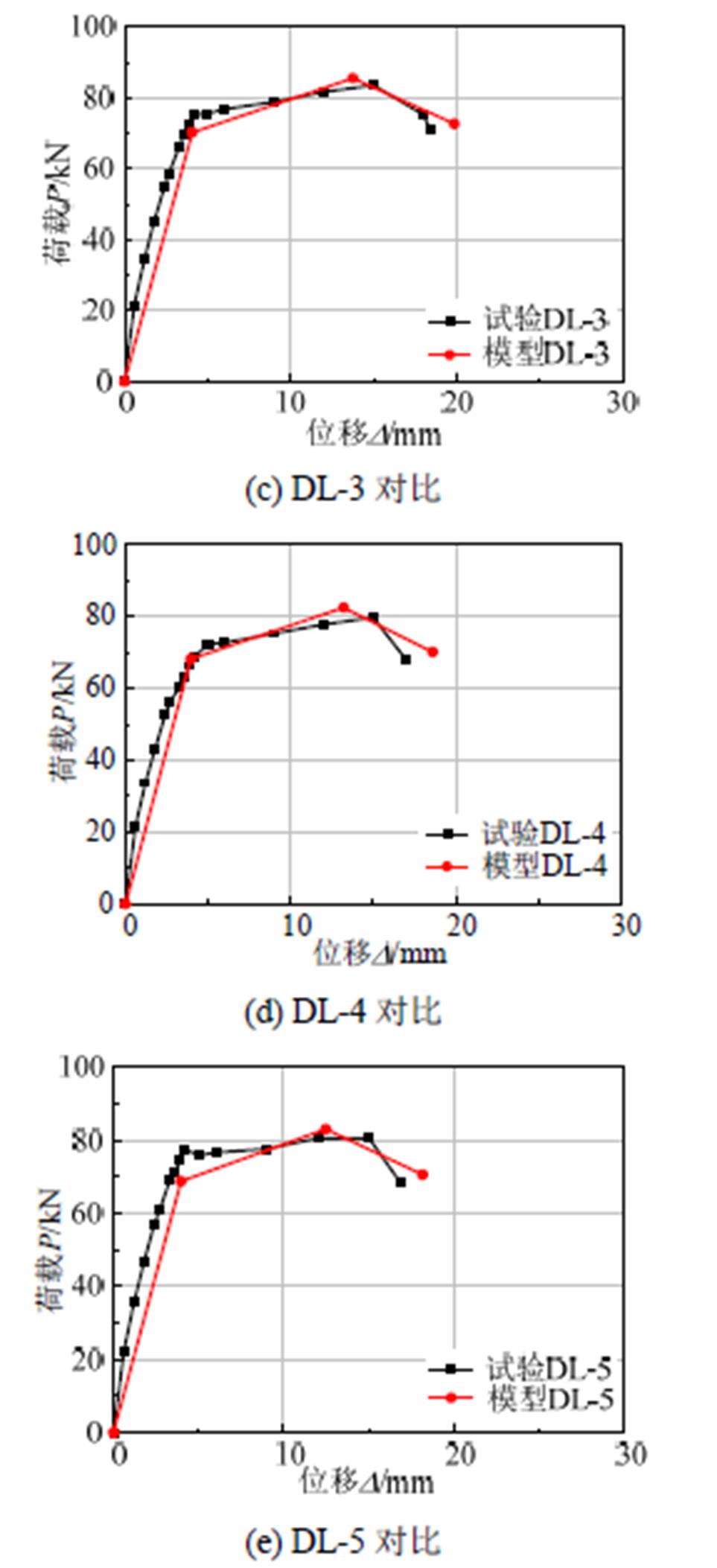
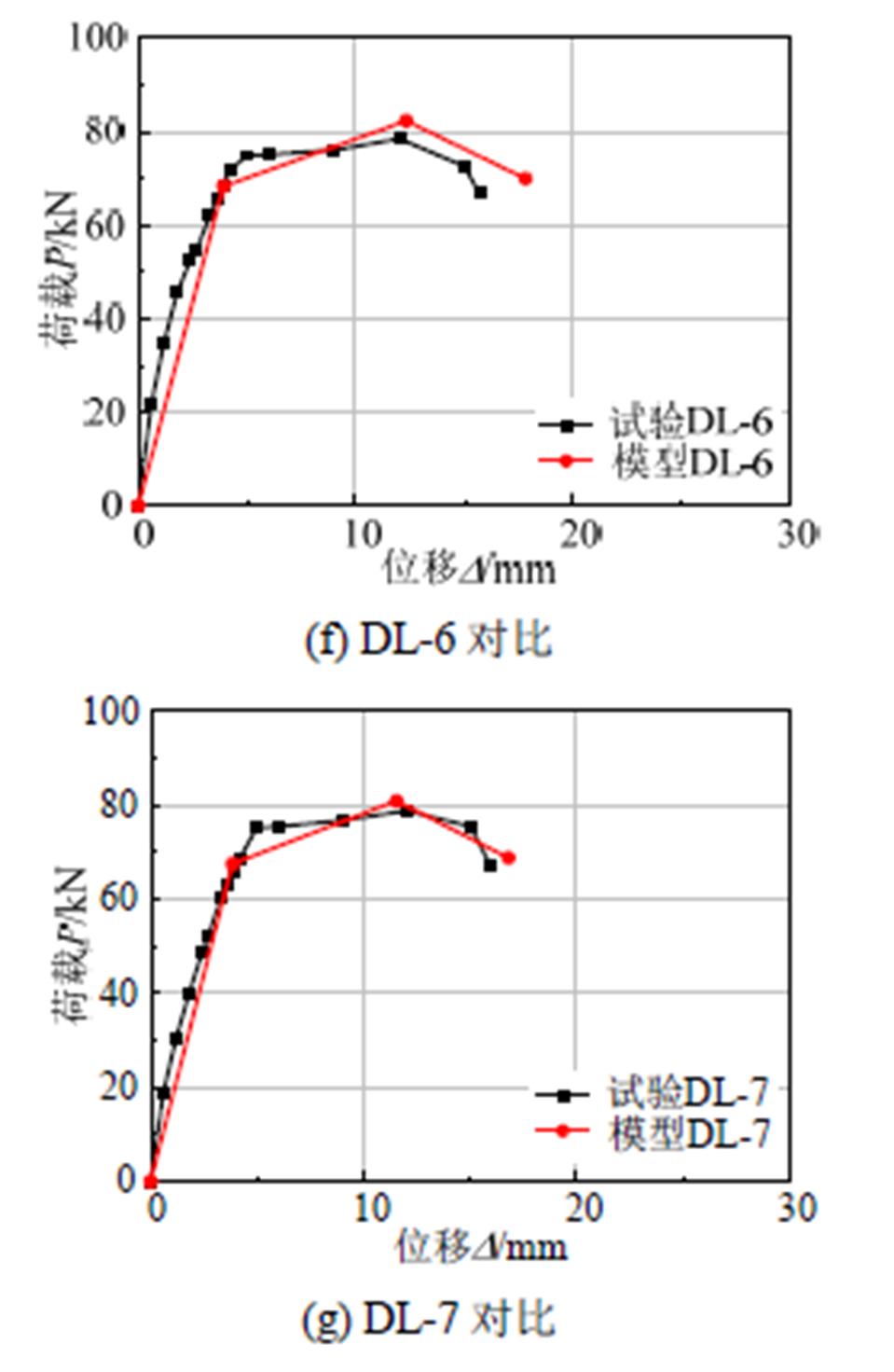

图7 恢复力模型骨架曲线计算结果与试验结果比较
Fig.7 Comparison of calculation and test results of the restoring force model skeleton curve
为了建立锈蚀RC框架梁的恢复力模型,则需要考虑不同锈蚀损伤程度下RC框架梁的滞回规则。锈蚀RC框架梁恢复力模型滞回规则包含两个方面:一般滞回规则和循环退化规则。考虑本试验捏拢效应较明显,故一般滞回规则采用捏拢型规则;循环退化规则包含:上升段强度退化、软化段强度退化、卸载刚度退化和再加载刚度加速退化(各退化示意如图8~图10所示)。本文建立锈蚀RC框架梁恢复力模型滞回规则的基本思路:根据试验得到基于滞回耗能的循环退化指数,通过循环退化指数来反映锈蚀RC框架梁滞回性能的退化;荷载超过构件屈服荷载后,卸载时根据循环退化指数来计算卸载刚度退化;再加载时根据循环退化指数计算强度退化和再加载刚度退化等,并通过强度退化和再加载刚度退化修改指向点,本文所建立的恢复力模型如图11所示。循环退化指数的表达式为[15]:
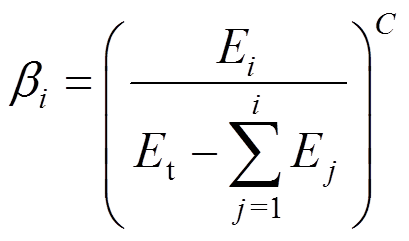 (11)
(11)式中: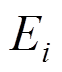 为锈蚀构件在第
为锈蚀构件在第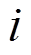 次正向或负向循环时的滞回耗能,如图12所示;
次正向或负向循环时的滞回耗能,如图12所示;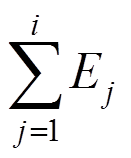 为锈蚀构件在第j次正向和负向循环时的累积滞回耗能;C为用于控制循环退化速率的参数,按照文献[16]建议的方法,本文取C为3/2;
为锈蚀构件在第j次正向和负向循环时的累积滞回耗能;C为用于控制循环退化速率的参数,按照文献[16]建议的方法,本文取C为3/2; 为锈蚀构件自身滞回耗能能力,由下式计算[17]:
为锈蚀构件自身滞回耗能能力,由下式计算[17]:
 (12)
(12)
式中: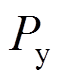 为锈蚀构件屈服荷载;
为锈蚀构件屈服荷载; 为锈蚀构件屈服位移;
为锈蚀构件屈服位移; 为锈蚀构件达到极限状态时的功比系数,其值由试验确定。
为锈蚀构件达到极限状态时的功比系数,其值由试验确定。
在循环加载全过程,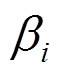 的取值范围为
的取值范围为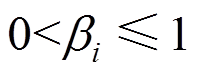 ,
,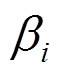 取值越大,说明锈蚀构件循环退化越严重。如果
取值越大,说明锈蚀构件循环退化越严重。如果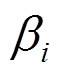 取值超出了有效范围(
取值超出了有效范围( 或
或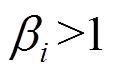 ),则认为结构滞回耗能能力全部耗散,结构发生倒塌。锈蚀试件失效准则如下:
),则认为结构滞回耗能能力全部耗散,结构发生倒塌。锈蚀试件失效准则如下:
 (13)
(13)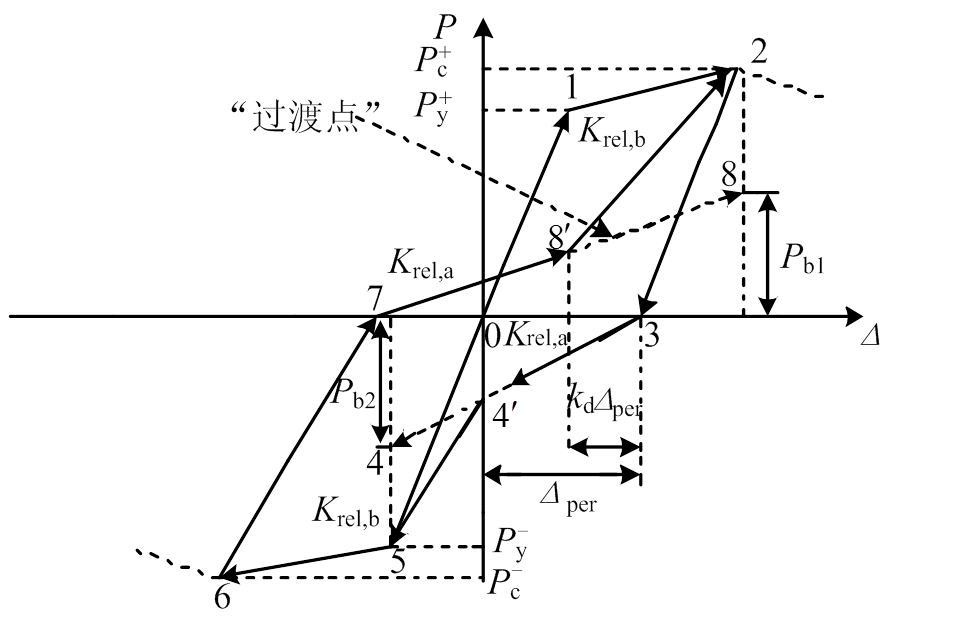
图8 捏拢规则示意图[15]
Fig.8 Pinch rule diagram
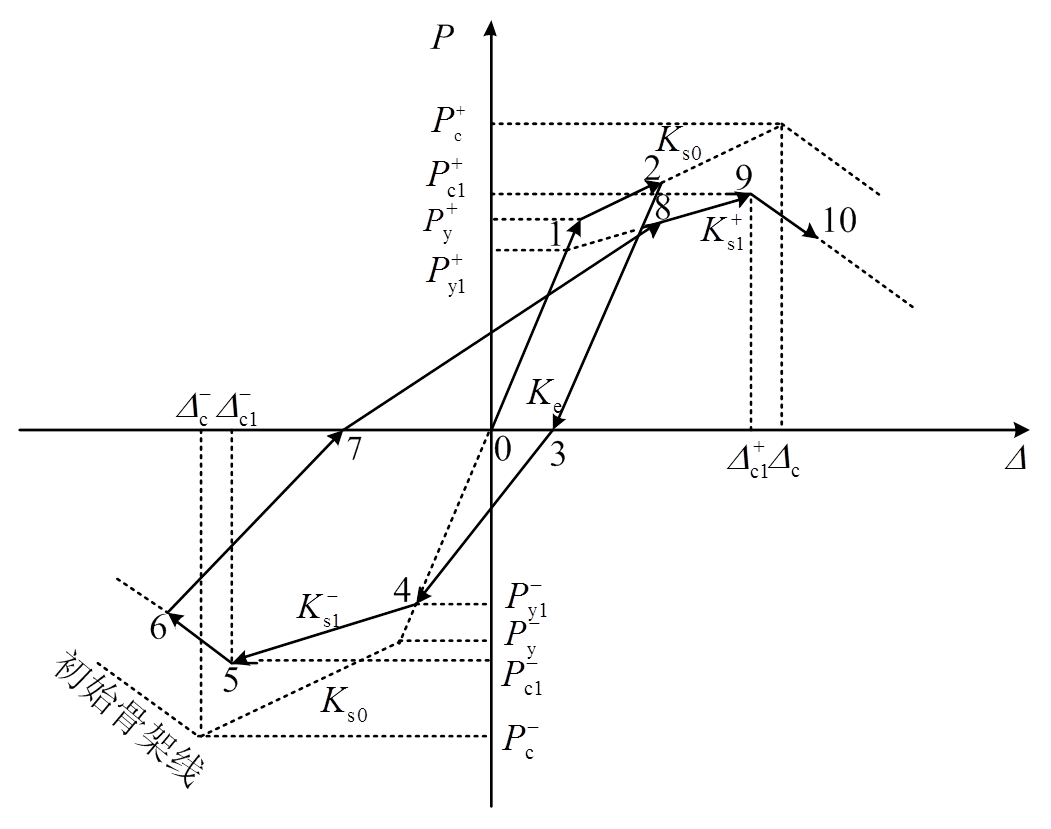
图9 上升和下降段强度退化示意图
Fig.9 The strength degradation of ascending and descending phase
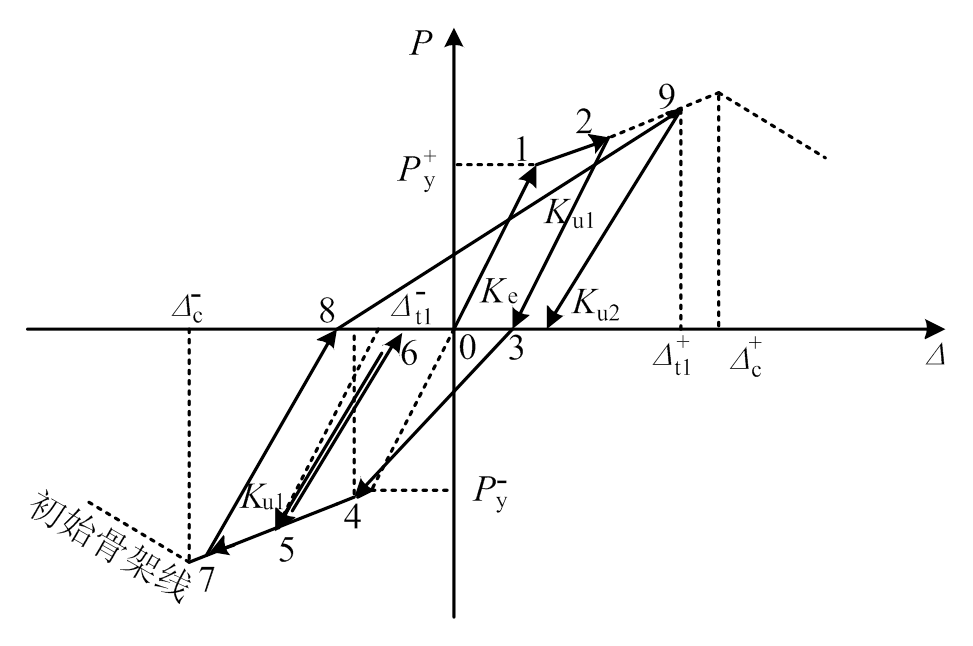
图10 卸载和再加载刚度退化示意图
Fig.10 The stiffness degradation of unloading and reloading phase
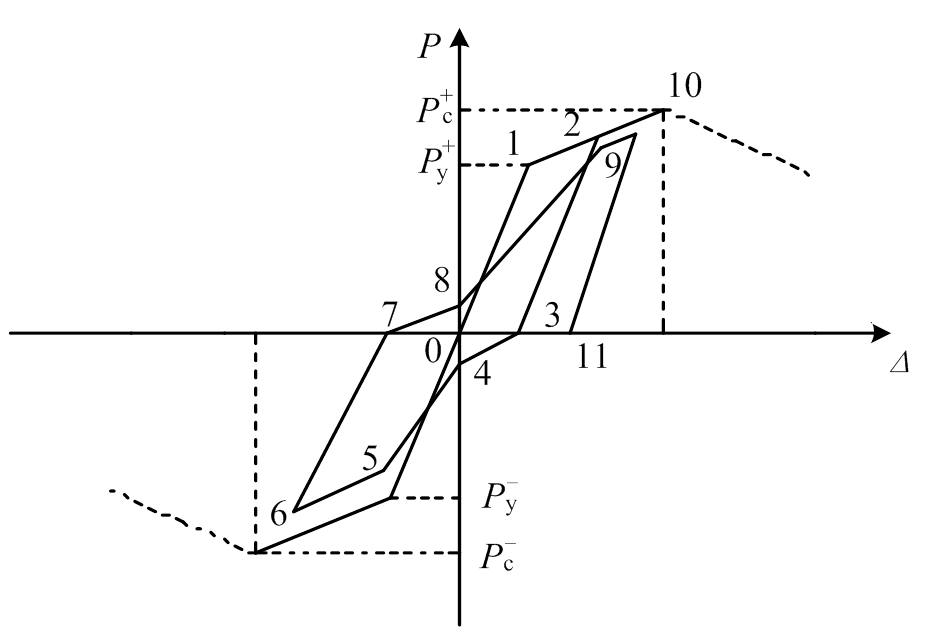
图11 恢复力模型简图
Fig.11 The restoring force model diagram
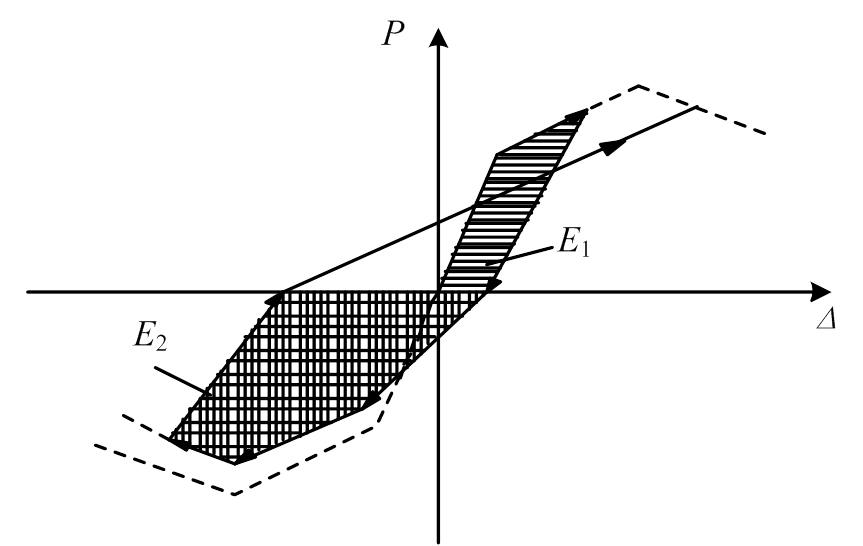
图12 滞回耗能简图
Fig.12 Hysteresis energy consumption diagram
将本文提出的恢复力模型计算滞回曲线与试验滞回曲线进行对比,如图13所示。可以看出,两者基本吻合,但仍有一定误差,主要因为钢筋锈蚀不均匀引起试验实测滞回曲线不对称,而本文建立恢复力模型时,原始骨架曲线正反向承载力特征值是相同的,因此两者存在一定误差,但是误差在允许范围内。同时,本文建立的恢复力模型在下降段时误差相对较大,这是因为再加载刚度加速退化由目标位移控制,随着锈蚀试件损伤逐渐累积,加载后期循环退化显著,循环退化指数增大,模型中目标位移较实际滞回曲线的控制位移有一定增加,但亦在允许范围内。综上,本文建立的锈蚀RC框架梁恢复力模型可用于实际结构中。
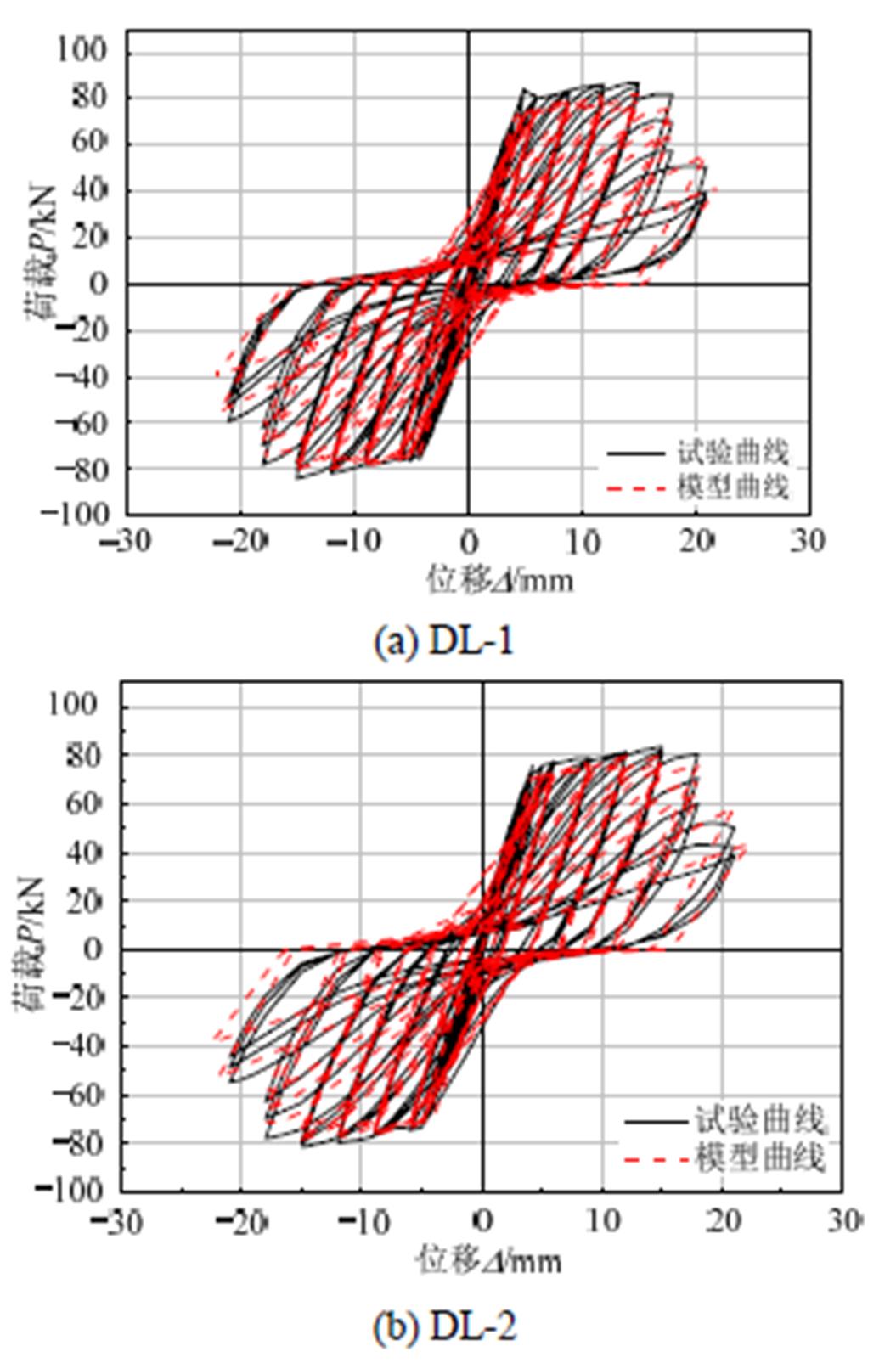
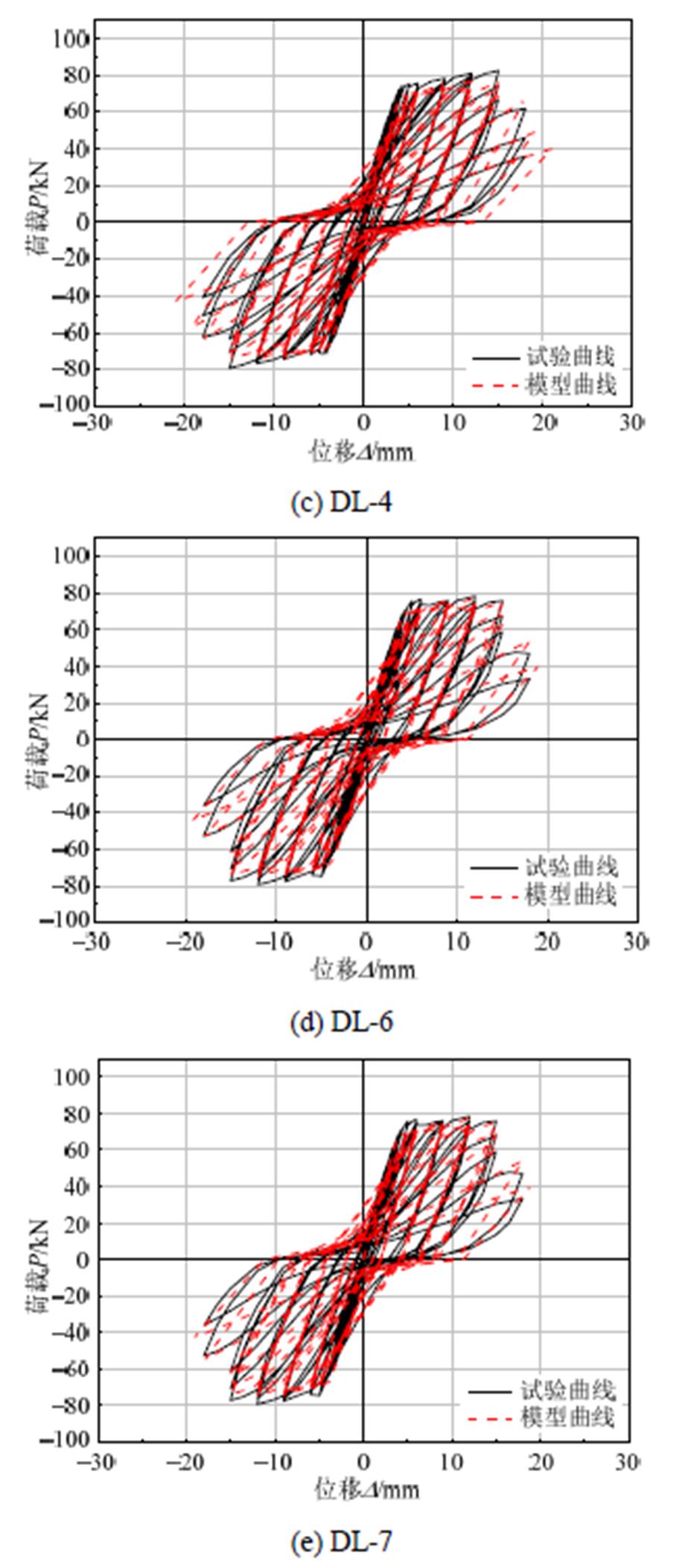
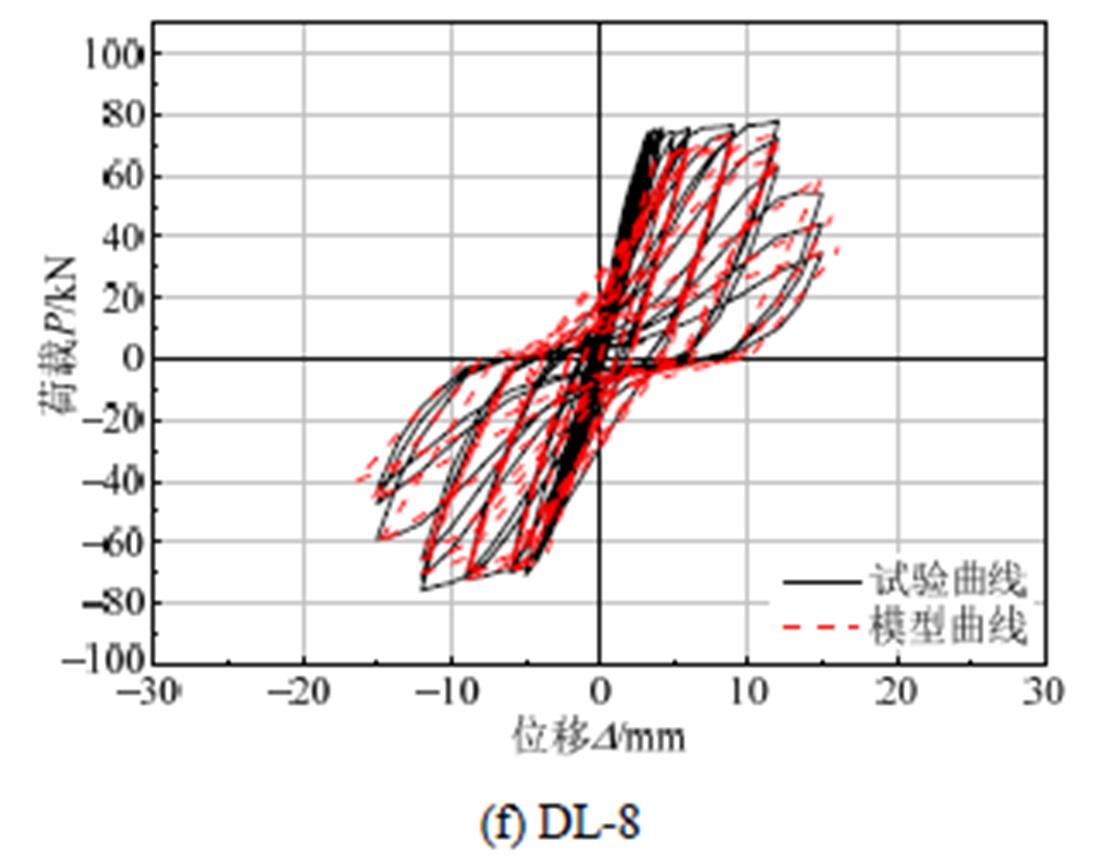
图13 计算滞回曲线与试验滞回曲线对比
Fig.13 Comparison of testing and calculating hysteretic curves
耗能能力是反映结构或构件滞回性能的重要指标,本文以名义滞回耗能表示模型计算曲线和试验曲线的滞回耗能,名义滞回耗能按下式计算:
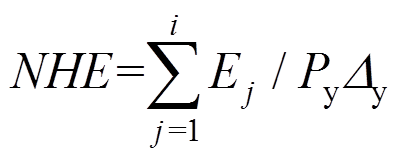 (14)
(14)式中: 为名义滞回耗能;
为名义滞回耗能;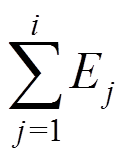 为荷载循环到第j次时构件的累积耗能;
为荷载循环到第j次时构件的累积耗能;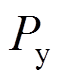 、
、 分别为锈蚀RC框架梁的屈服荷载和屈服位移。
分别为锈蚀RC框架梁的屈服荷载和屈服位移。
各试件名义滞回耗能和循环次数的关系曲线如图14所示。由图14可知,与试验滞回曲线的名义滞回耗能相比,模型计算曲线的耗能偏小。这是因为,本文提出的恢复力模型在屈服之前按理想弹性考虑,即屈服之前不考虑滞回耗能,但试验滞回曲线在屈服之前是有一定能量耗散的,因此,两者有较小差别。总体而言,本文提出的锈蚀RC框架梁恢复力模型能够较好的反映锈蚀构件恢复力特性,对实际结构具有较好的适用性。
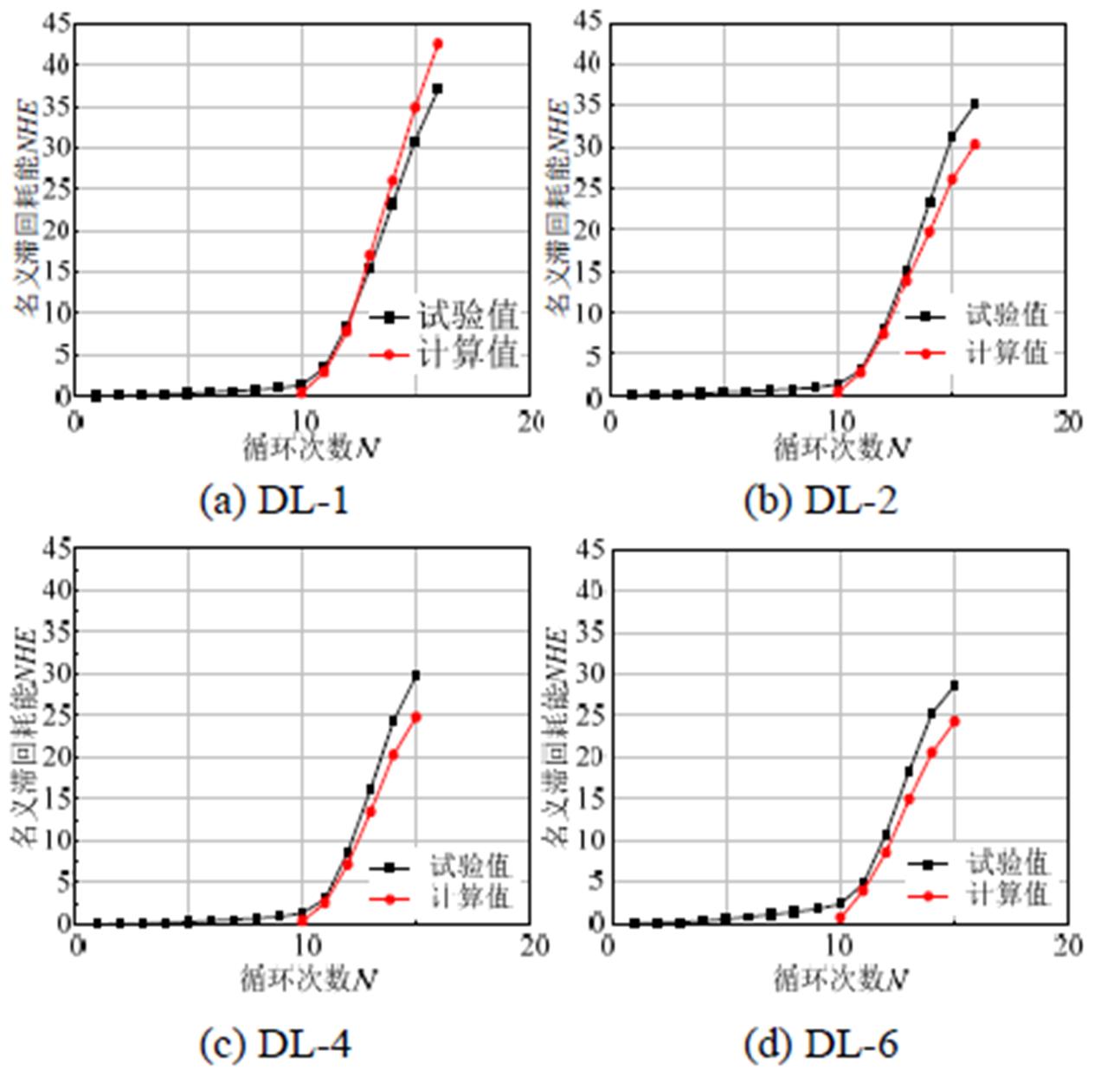

图14 各试件耗能对比
Fig.14 The energy consumption comparison of the specimens
(1) 在配箍率相同条件下,随着盐雾腐蚀循环次数的增加,RC框架梁的承载力、刚度、耗能能力等呈降低的趋势;在钢筋锈蚀率相同时,随着配箍率的减小,RC框架梁对钢筋锈蚀程度更加敏感。
(2) 基于三折线骨架曲线模型并考虑近海大气环境盐雾腐蚀的RC框架梁恢复力模型较为准确地描述了循环加载和腐蚀损伤共同引起的强度、刚度的循环退化以及捏缩效应。
(3) 建立的锈蚀RC框架梁恢复力模型计算结果与试验结果吻合较好,且模型计算的滞回耗能与试验实测的滞回耗能相近,说明该恢复力模型能够较好地反映近海环境下RC框架梁的滞回特征,可为近海环境下RC框架结构的弹塑性地震反应分析提供理论参考。
参考文献:
[1] 史庆轩, 牛荻涛, 颜桂云. 反复荷载作用下锈蚀混凝土压弯构件恢复力性能的试验研究[J]. 地震工程与工程振动, 2000, 20(4): 45―50.
Shi Qingxuan, Niu Ditao, Yan Guiyun. Experimental research on hysteretic characteristics of corroded RC members with flexural and compressive axial loads under repeated horizontal loading [J]. Earthquake Engineering And Engineering Vibration, 2000, 20(4): 45―50. (in Chinese)
[2] 闫西康, 魏志敏, 丁其元. 盐雾腐蚀混凝土后对其抗剪性能的影响分析[J]. 混凝土, 2011(3): 21―24.
Yan Xikang, Wei Zhimin, Ding Qiyuan. Analysis of the influence of salt fog corrosion concrete shear performance [J]. Concrete, 2011(3): 21―24. (in Chinese)
[3] 金伟良, 赵羽习. 锈蚀钢筋混凝土梁抗弯强度的试验研究[J]. 工业建筑. 2001, 31(5): 9―11.
Jin Weiliang, Zhao Yuxi. Test study on bending strength of corroded reinforced concrete beams [J]. Industrial Construction, 2001, 31(5): 9―11. (in Chinese)
[4] 李士彬, 张鑫, 贾留东, 等. 箍筋锈蚀钢筋混凝土梁的抗剪承载力分析[J]. 工程力学, 2011, 28: 60―63.
Li Shibin, Zhang Xin, Jia Liudong, et al. Analysis for shear capacity of reinforced concrete beams with corrosion stirrups [J]. Engineering Mechanics, 2011, 28: 60―63. (in Chinese)
[5] 郑山锁, 秦卿, 杨威, 等. 近海大气环境下低矮RC剪力墙抗震性能试验[J]. 哈尔滨工业大学学报, 2015, 47(12): 64―69
Zheng Shansuo, Qin Qing, Yang Wei, et al. Experimental research on theseismic behaviors of squat RC shear walls under offshore atmospheric environment [J]. Journal of Harbin Institute of Technology, 2015, 47(12): 64―69. (in Chinese)
[6] Clough RW. Effect of stiffness degradation on earthquake ductility requirements [D]. California: University of California, 1966.
[7] Ramberg W, Osgood WR. Description of steel strain curve by three parameters [R].Technical Note 902, National Advisory Committee for Aeronautics, July, 1943.
[8] 闫长旺, 杨勇, 贾金青, 等. 钢骨超高强混凝土框架节点恢复力模型 [J]. 工程力学, 2015, 32(12): 154―160.
Yan Changwang, Yang Yong, Jia Jinqing, et al. Study on restoring force model of steel reinforced ultra high strength concrete frame joints [J]. Engineering Mechanics, 2015, 32(12): 154―160. (in Chinese)
[9] Bouc R. Forced vibration of mechanical systems with hysteresis [C]// Proceedings of the 4th International Conference on Nonlinear Oscillations , Prague, Czecho-slovakia, 1967.
[10] Wen YK. Method for random vibration of hysteretic systems [J]. ASCE Journal of Engineering Mechanics 1976, 102(2): 249―263.
[11] GB 50011―2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.
GB 50011―2010, Code for seismic design of building [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[12] JGJ 101―1996, 建筑抗震试验方法规程[S]. 北京: 中国建筑工业出版社, 1996.
JGJ 101―1996, Specificating of testing methods for earthquake resistant building [S]. Beijing: China Architecture & Building Press, 1996. (in Chinese)
[13] 赵彦堂. 人工气候环境下锈蚀 RC框架梁抗震性能试验研究[D]. 西安: 西安建筑科技大学, 2014.
Zhao Yantang. Experimental study on seismic performance of corroded RC frame beam under artificial climate [D]. Xi’an: Xi’an University of Architecture and Technology, 2014. (in Chinese)
[14] 潘士劼, 许哲明. 框架结构的非线性地震反应分析[J]. 同济大学学报, 1980(2): 43―63.
Pan Shijie, Xu Zheming. Nonlinear earthquake response analysis of rigid frames [J]. Journal of Tongji University, 1980(2): 43―63. (in Chinese)
[15] Rahnama M, Krawinkler H. Effects of soft soil and hysteresis model on seismic demands [D]. John A. Blume Earthquake Engineering Center Report No. 108. Department of CEE, Stanford University, 1993.
[16] Medina R A, Krawinkler H. Hysteretic models that incorporate strength and stiffness deterioration [J]. Earthquake Engineering & Structural Dynamics, 2005, 34(12): 1489―1511.
[17] 李磊, 郑山锁, 王斌, 等. 型钢高强混凝土框架的循环退化效应[J]. 工程力学, 2010, 27(11): 81―88.
Li Lei, Zheng Shansuo, Wang Bin, et al. Cyclic deterioration effect of the steel reinforced high performance concrete frames [J]. Engineering Mechanics, 2010, 27(11): 81―88. (in Chinese)
A RESTORING FORCE MODEL OF CORRODED REINFORCED CONCRETE FRAME BEAMS IN OFFSHORE ATMOSPHERIC ENVIRONMENT
Abstract: To study the seismic behavior of corroded Reinforced Concrete (RC) frame beams in offshore atmosphere, the hysteretic behavior of 8 RC frame beams were investigated experimentally, which have been damaged by the salt spray corrosion cycles under low cyclic reversed loading. Based on the test results, a trilinear skeleton curve model with negative stiffness of frame beams was established. According to the characteristic parameters of the intact member's restoring force model, the formula of the characteristic points of the skeleton curve of RC frame beams with corrosion was obtained, which considered the corrosion rate and stirrup ratio. The cyclic degradation indexes of RC frame beams based on hysteresis energy dissipation was obtained through regressive analysis. Subsequently, the restoring force model of corroded RC frame beams was established, which considered the pinch-in effect, strength degradation, unloading stiffness degradation, hardening stiffness degradation and reloading stiffness accelerates degradation. The results show that the seismic performance of RC frame beams deteriorates obviously with the increase of corrosion degree, and the hysteretic energy consumption decreases gradually. The influence of stirrup ratio on the restoring force of RC frame beams is similar to the un-corroded frame beams. The restoring force model can describe the hysteretic behavior of corroded RC frame beams well. The study results will shed light on the theoretical research about the elastic-plastic dynamic analysis of RC structures.
Key words: coastal atmosphere; RC frame beam; corrosion; hysteretic behavior; restoring force model
文章编号:1000-4750(2019)04-0125-10
中图分类号:TU375;TU317+.1
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.01.0085
收稿日期:2018-01-29;
修改日期:2018-05-23
基金项目:国家科技支撑计划项目(2013BAJ08B03);国家自然科学基金项目(51678475);陕西省重点研发计划项目(2017ZDXM-SF-093);陕西省教育厅产业化项目(18JC020)
郑山锁(1960―),男,陕西渭南人,教授,博士后,博导,主要从事结构工程与工程抗震研究(E-mail: zhengshansuo@263.net);
赵彦堂(1988―),男,山东人,硕士,主要从事结构工程抗震研究(E-mail: sdlszyt@126.com);
郑 捷(1988―),女,陕西渭南人,硕士,主要从事建筑结构优化设计研究(E-mail: julie1314fl@126.com);
周 炎(1993―),男,湖北人,博士生,主要从事结构工程与工程抗震研究(E-mail: 770572016@qq.com).