电磁调谐双质阻尼器的H2参数优化及对结构减震分析
罗一帆1,2,孙洪鑫2,王修勇2
(1.湖南科技大学机电工程学院,湖南,湘潭 411201;2.湖南科技大学结构抗风与振动控制湖南省重点实验室,湖南,湘潭 411201)
摘 要:该文在利用电磁阻尼单元代替经典型调谐质量阻尼器中的粘性阻尼单元的基础上,引入惯质单元,形成一种新型的具有结构减振和能量收集双重功能的电磁调谐双质阻尼器(electromagnetic tuned mass-inerter damper,EM-TMID)。依据达朗伯定理,建立EM-TMID与单自由度结构耦合结构受地震作用时的动力学模型。然后基于H2优化理论,即以主结构位移均方根值最小为目标函数,对EM-TMID进行参数优化,得到EM-TMID的结构频率比、电磁阻尼比和机电耦合系数的最优解析式。最后通过频域和时域两种仿真方法数值仿真分析了EM-TMID对结构的减震和能量收集的双重性能。结果表明,在频域分析中,EM-TMID的主结构位移峰值和频响面积均优于经典TMD、EM-TMD和TMDI。在时域分析中,EM-TMID对结构位移、加速度的峰值和均方根值的减震性能均优于经典TMD,同时能够进行能量收集。
关键词:防灾减灾工程;结构振动控制;调谐质量阻尼器;电磁阻尼器;惯质;能量回收
地震是最具破坏性的自然灾害之一,它能对民用基础设施产生大规模的破坏,进而威胁人类的生命。为了降低或消除结构的动力荷载响应,众多结构振动控制技术被研究和提出。随着结构振动控制理论体系的不断丰富与完善,越来越多的振动控制技术应用到工程中。在众多应用中,调谐质量阻尼器(tuned mass damper,TMD)是应用最为广泛的。
针对TMD在外界激励下的减振鲁棒性和性能的优化问题,国内外学者开展了一系列研究。Hartog[1]利用fixed-points法推导了TMD在主结构无阻尼情况下、简谐荷载作用下的最优参数解析式。之后,Rana和Soong[2]发现固定点法理论推导的最优参数表达式在对主结构有阻尼TMD设计时,会对TMD的减振效果造成偏差,同时他们通过数值方法研究了主结构有阻尼的TMD最优参数,最后归纳了频率比是影响减振性能的重要指标。林均岐等[3]基于双自由度系统的随机反应,推导了TMD与单自由度耦合系统在白噪声基底激励下的运动方程,利用模式搜索法对TMD优化并对验证了减振效果。李宏男等[4]基于振型叠加法,探讨了不同TMD布置方式对高层建筑减震效果的影响。李春祥[5]提出了双层多重调谐质量阻尼器控制策略,并通过数值仿真验证了其减振性能。王文熙[6]基于蒙特卡洛-模式搜索法,分别对STMD和MTMD的调谐参数进行优化,并以一座城市人行桥为例进行了参数优化设计。喻梅等[7]研究了TMD对桥梁涡激振动的控制,给出了TMD参数优化设计方法,最后以悬索桥为实例进行了分析。刘良坤等[8]提出了一种将TMD与非线性能量阱混合控制结构振动的方案,数值仿真结果表明混合系统不仅拓宽了频带,而且降低了对初始能量的敏感性。
2002年,Smith[9]基于机电系统的相似性,首次提出“惯质”的概念,理想状态下,惯质是指包含两个相对自由终端的机械装置,其中两端相向或相对作用力与其相对加速度成比例,并且该比值为常数,称为惯质系数[10]。目前针对惯质的研究主要在车辆悬架和土木建筑物减隔振方面。例如,陈龙等[11―12]基于齿轮齿条和滚珠丝杆式的“惯质-弹簧-阻尼”,构筑了二元车辆悬架减振系统,与传统悬架相比,减振效果有了较大的提升,并同时改善了车辆的乘坐舒适性。基于经典TMD,Giaralis等[13―14]引入惯质单元,形成了TMDI (tuned mass-damper-inerter),并分析了TMDI对单层结构和多层结构的减震效果。Nakamura等[15]基于滚珠丝杆和旋转电机,提出了EIMD (electromagnetic inertial mass dampers)。然后通过小尺寸和全尺寸的力学实验研究了阻尼器的力学性能,最后通过3层框架结构的振动台实验验证了阻尼器的减振效果。Wen等[16]基于表观质量,开展了TIBD (tuned inerter-based damper)对多自由度结构的减震研究,并通过10层框架数值仿真验证了基于惯质的TID和TVMD的减震性能。汪志昊等[17]结合理论分析和模型试验两种方法建立了基于以惯性飞轮和滚珠丝杆结构的表观质量的负刚度效应模型,分析了将其应用到TMD频率调整的可行性。
近年,研究人员开展了TMD结构控制与减振耗能中能量转换回收的相关研究。Inoue等[18]提出了电磁谐振阻尼器的概念,建立了电磁谐振阻尼器与单自由度结构的耦合系统的动力学模型,并通过fixed-points理论对耦合系统的调谐参数进行优化,得出最优频率比和阻尼比的理论解析解。Zuo等[19]以台北101为例验证了电磁谐振阻尼器替代经典TMD中的粘性阻尼单元的可能性。Liu等[20]提出了一种具有结构振动控制和能量收集双重功能的EMTMD (electromagnetic tuned mass dampers),并基于主结构位移均方根值最优理论,得到EMTMD在主结构激励下的最优参数解析解,最后通过实验验证了EMTMD的双重功能。
本文基于经典TMD,将电磁阻尼元件置换经典TMD中的粘性阻尼元件,又引入惯质单元,形成具有电磁耗能、惯质和调谐三重复合减振阻尼器,即电磁调谐双质阻尼器(electromagnetic tuned mass-inerter damper,EM-TMID) [10]。它不仅可对被控结构进行减振,同时还能回收被控结构的振动能量;此外,还可以调节发电机的终端电阻值实现对EM-TMID的阻尼调整。从回收的能量供应功率分析,回收的能量足够解决小型无线传感器(能耗几十毫瓦)的供电需求,也为进一步实现对于结构半主动振动控制系统供能提供了可能性[21―23]。
本文首先建立EM-TMID—单自由度结构耦合系统在地震激励下的动力学模型,然后利用H2优化理论,即主结构位移均方根值最小优化理论,和残值定理,对耦合系统进行参数优化,得到耦合系统的3个调谐参数的最优解析解,即最优结构频率比fT、电磁阻尼比ze和机电耦合系数mk[10, 21]。最后,基于频域和时域两种数值仿真方法,分析了EM-TMID减振与能量收集的双重性能[21]。
1 电磁调谐双质阻尼器(EM-TMID)与单自由度结构耦合减震系统的力学模型
在地震加速度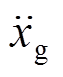 下,EM-TMID与被控结构的耦合减震模型如图1所示,为了更好地分析阻尼器对主结构的减震效果,主结构被简化为一个单自由度结构,其质量为ms,刚度为ks,阻尼为cs,其数值分别对应于结构主要模态[10, 21]。在EM-TMID中,将经典TMD中的粘性阻尼单元替换成基于直线发电机的能量收集单元,从而产生电磁阻尼力,然后基于滚珠丝杆元件的惯质单元被连接在TMD与下一层主结构之间,系统构造图如图1(b)所示。基于直线发电机原理,能量收集单元可以简化为一个电感L,和一个内阻Ri,与此同时,能量储存单元的外阻等为Re,两者串联后,等效为RL电路[10, 21]。因此,EM-TMID基本结构主要包括弹簧—质量单元、惯质单元以及基于直线发电机的能量收集单元[21]。
下,EM-TMID与被控结构的耦合减震模型如图1所示,为了更好地分析阻尼器对主结构的减震效果,主结构被简化为一个单自由度结构,其质量为ms,刚度为ks,阻尼为cs,其数值分别对应于结构主要模态[10, 21]。在EM-TMID中,将经典TMD中的粘性阻尼单元替换成基于直线发电机的能量收集单元,从而产生电磁阻尼力,然后基于滚珠丝杆元件的惯质单元被连接在TMD与下一层主结构之间,系统构造图如图1(b)所示。基于直线发电机原理,能量收集单元可以简化为一个电感L,和一个内阻Ri,与此同时,能量储存单元的外阻等为Re,两者串联后,等效为RL电路[10, 21]。因此,EM-TMID基本结构主要包括弹簧—质量单元、惯质单元以及基于直线发电机的能量收集单元[21]。
EM-TMID工作原理可以简单地概括为:当EM-TMID安装在被控结构中时,在外部激励作用下,TMD质量块在被控结构上产生相对运动,从而引起直线发电机的动子相对于定子产生移动,随着动子的移动,发电机线圈中的磁通量将发生改变,从而在线圈中产生感生电动势;在产生电动势的同时,获得电磁阻尼力,将被控结构的振动能转换为电能,从而对被控结构进行振动控制和能量回收[10, 21]。
基于达朗伯原理,可以建立EM-TMID—单自由度结构耦合系统的力学模型如下[20]:
为了方便进行后续耦合系统的参数优化,忽略主结构阻尼的影响,式(1)经拉普拉斯变换可得[21]:
 (2)
(2)
令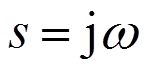 ,
,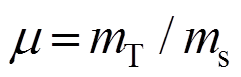 ,
,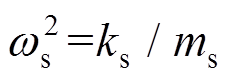 ,
,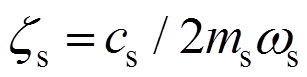 ,
,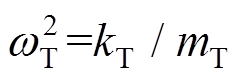 ,
,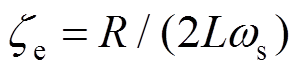 ,
,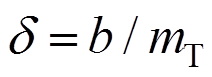 ,对式(2)进行无量纲化,可有:
,对式(2)进行无量纲化,可有:
令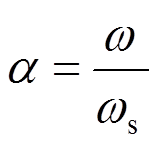 ,
,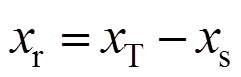 ,
,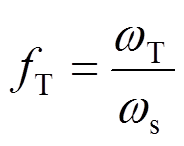 ,
,
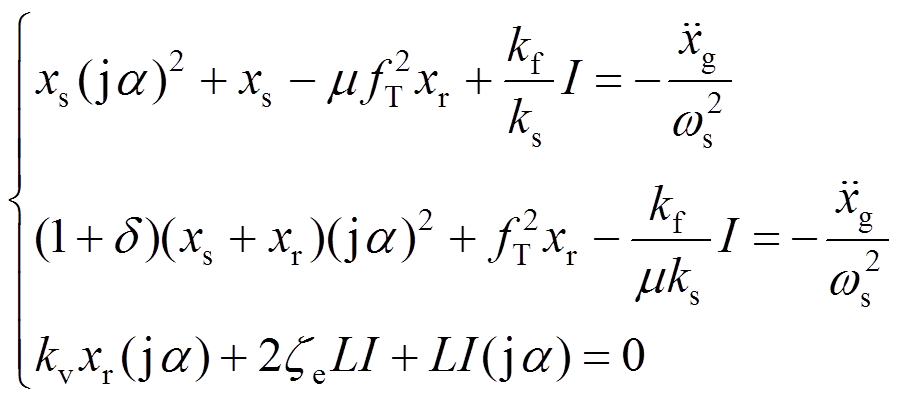 (4)
(4)
式中[20]:mT为TMD的质量;kT为TMD的刚度;I为电流;b为惯质;R为电阻,R=Ri+Re;kv、kf为电磁传感器常数,理想状态下kv=kf;w为外激频率;m为TMD与主结构的质量比;ws为主结构的频率;wT为EM-TMID的频率; zs为主结构的阻尼比;d为惯质与TMD质量的比值,惯质比;a为外激励频率比;xs为主结构的位移;xT为TMD的位移;xr为相对位移;ze为EM-TMID的电磁阻尼比;fT为EM-TMID的结构频率比;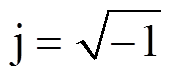 为虚数单位。
为虚数单位。
2 耦合系统的参数优化
2.1 耦合减震模型的频响函数
在地震波加速度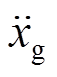 的作用下,从
的作用下,从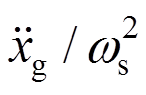 到xs的频响函数为[20]:
到xs的频响函数为[20]:
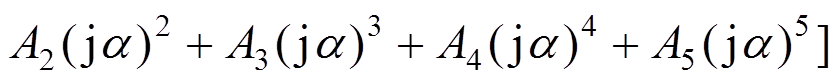 (5)
(5)
式中: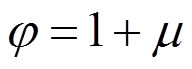 ,
,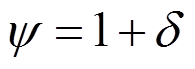 ;机电耦合系数为
;机电耦合系数为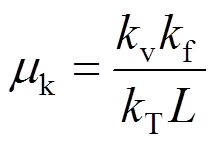 ,且分母相关系数为:
,且分母相关系数为:
从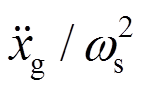 到xr的频响函数为:
到xr的频响函数为:
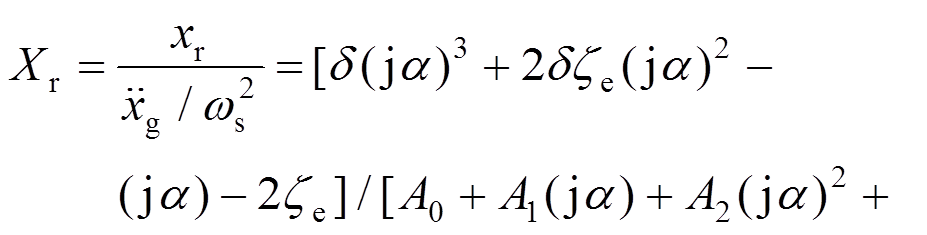
从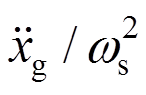 到I的频响函数为:
到I的频响函数为:
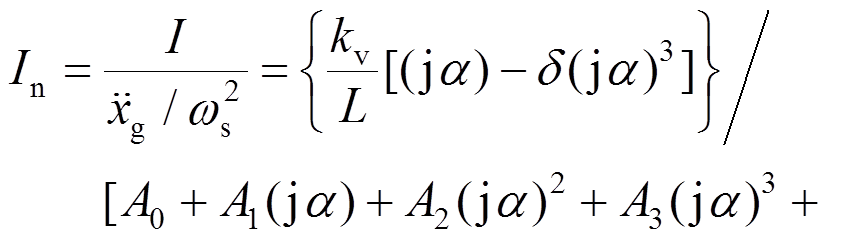
2.2 基于H2理论的参数优化
由于地震激励所包含的频带较为广泛,故采用H2范数评估阻尼器对主结构的减震效果是较为恰当的;且在白噪声激励下,H2范数能够表示主结构响应的均方根值(root mean square,RMS) [21, 24]。本文基于主结构位移的H2范数性能评价指标最优来开展EM-TMID耦合系统的参数优化,获得其调谐参数最优解析式[21]。因此,可以定义地震波加速度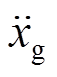 下被控结构位移xs的减震性能评价指标PIv为:
下被控结构位移xs的减震性能评价指标PIv为:
式中:E[×]代表RMS值; 代表瞬时平均值;S0代表外激励的能量强度,单位是
代表瞬时平均值;S0代表外激励的能量强度,单位是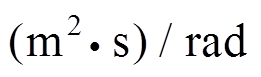 [21]。
[21]。
因此,引入主结构位移xs的RMS值[21]:
将式(10)代入式(9),评价指数PIv表示为:
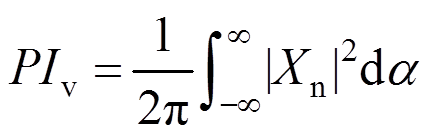 (11)
(11)
式(11)中的积分可以通过残数定理[25]求得。在无主结构阻尼的情况下,结合式(9),评价指标PIv可以表示为3个调谐参数结构频率比fT,机电耦合系数mk,电磁阻尼比ze的函数形式[21]:
为了获得性能评价指标PIv最小时对应的最优调谐参数,即PIv对每个调谐参数的偏导数为零,则有[21]:
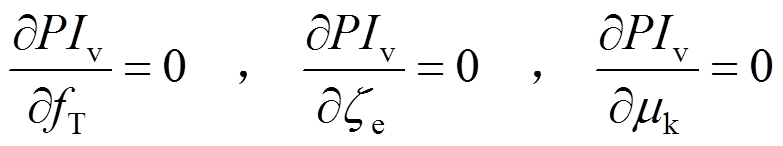 (13)
(13)
通过求解方程组式(13),可以得到3个参数的最优理论解析式:
其中,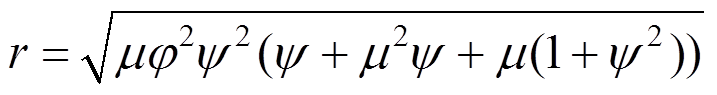 。
。
因此,相对的基本物理参数kT、R、L可以通过上述参数表示为[21]:
需要说明的是,经典TMD在地震激励下的H2理论优化参数表示为[21, 26]:
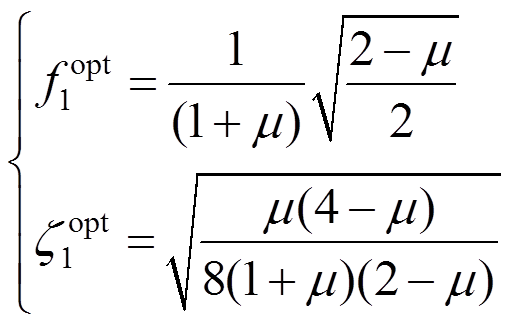 (16)
(16)
TMDI在地震波下的H2理论优化参数为[12]:
其中,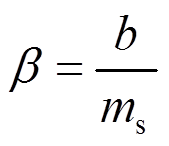 。
。
另外,EM-TMD在地震波激励下的H2理论优化参数为[21]:
3 频域数值分析
3.1 减震性能分析
1) EM-TMID的H2最优调谐参数分析[21]:
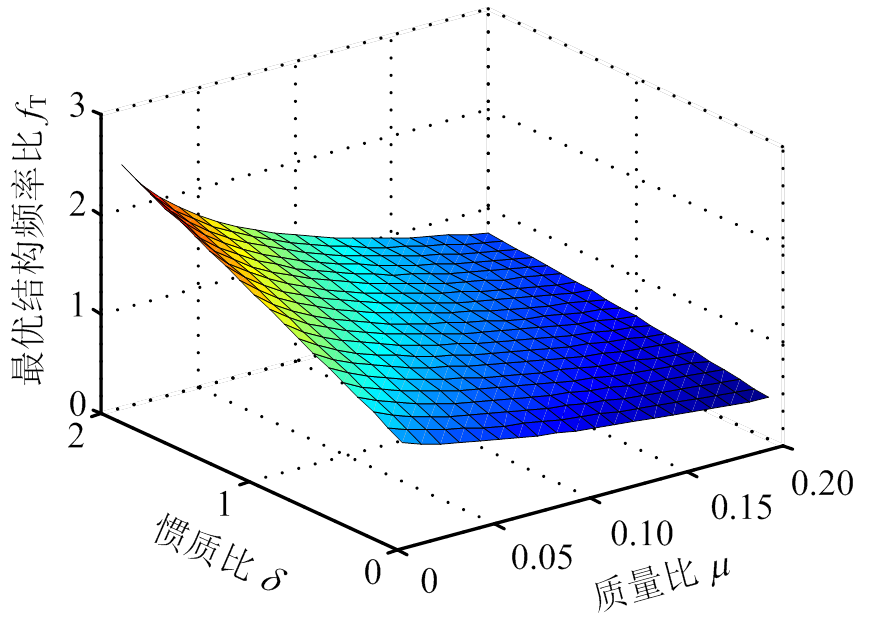
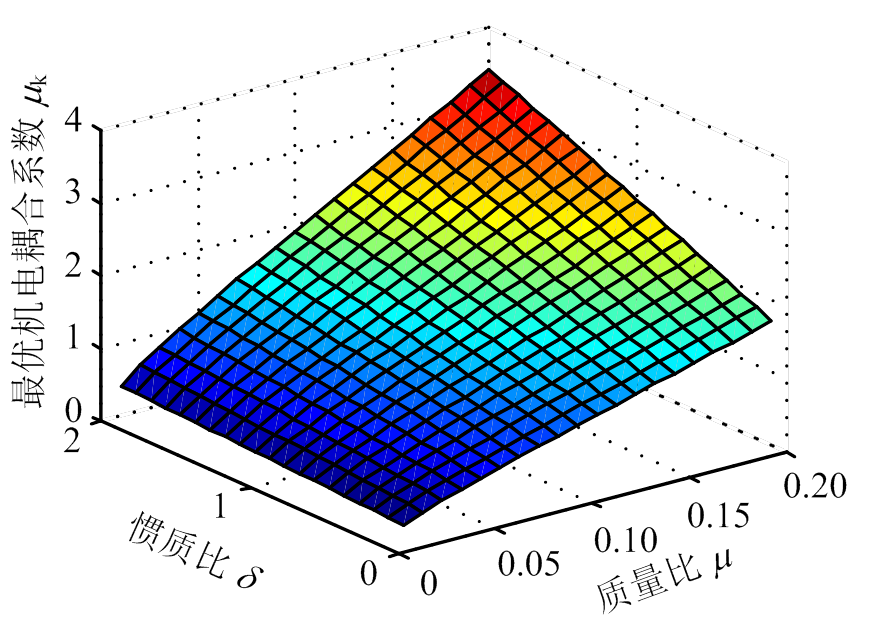
如图2所示,分别对地震波作用下的EM-TMID的3个H2调谐参数的变化趋势进行三维分析。从图2可以看出,当惯质比一定时,随着质量比的增加,电磁阻尼比和机电耦合系数将会增加,而结构频率比则会降低。在质量比一定时,随着惯质比的增大,3个系数都会增大。当质量比和惯质比同时增大时,电磁阻尼比和机电耦合系数会增大,而结构频率比则会减小。
(a) 结构频率比
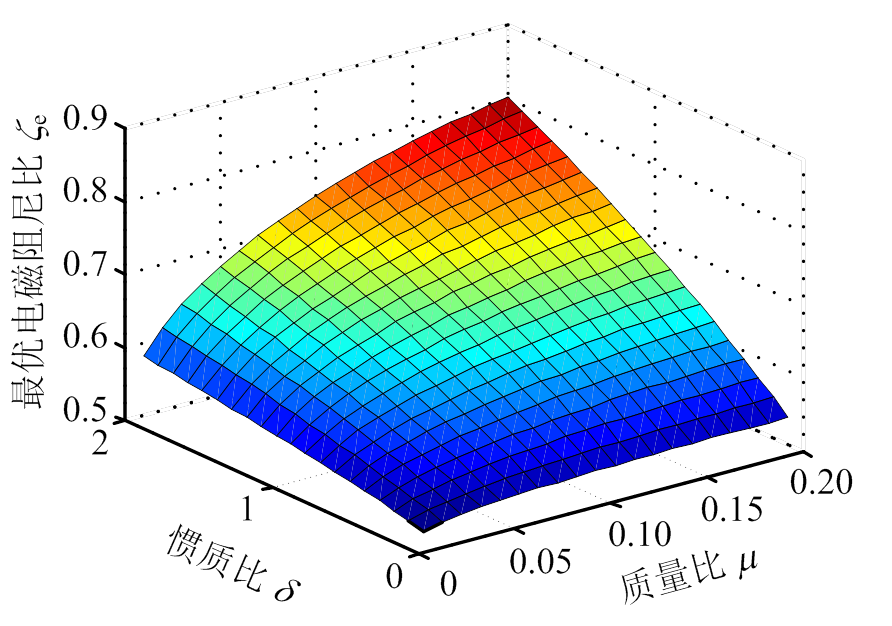
(b) 电磁阻尼比
2) 不同系统的减振性能对比
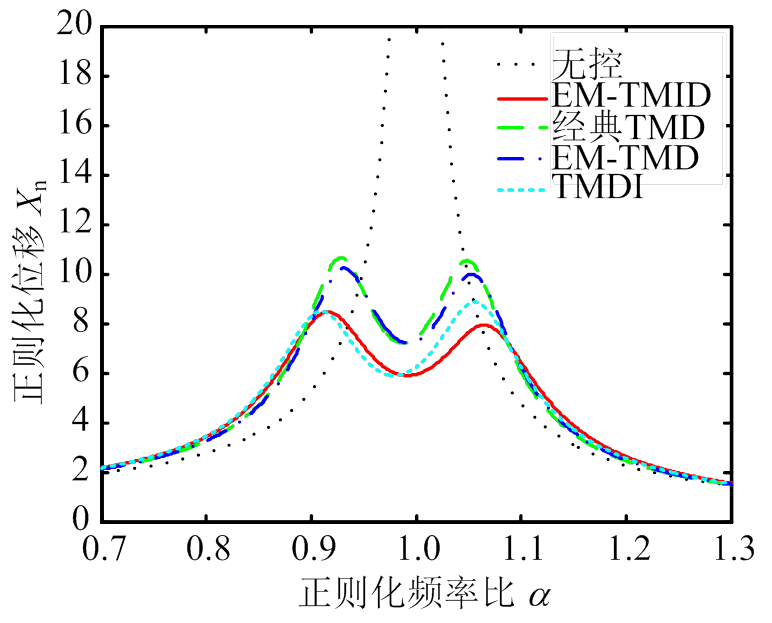
如图3所示,对主结构位移和相对位移频响的传递函数进行描述。通过图3可知,当EM-TMID与TMDI惯质比为0.5时,当所有系统的质量比m=0.02时,EM-TMID的H2范数减振性能要比其他系统更加出色,其次减振频带宽度也增宽了。更确切地,EM-TMID主结构位移频响函数的峰值比经典TMD降低了20.57%,比EM-TMD降低了17.27%,比TMDI降低了4.43%。除此之外,当a范围为0.7~1.3,EM-TMID的Xn的积分面积比经典TMD降低了8.43%,比EM-TMD降低了7.40%,比TMDI降低了1.41%。
(a) 主结构位移的频响函数
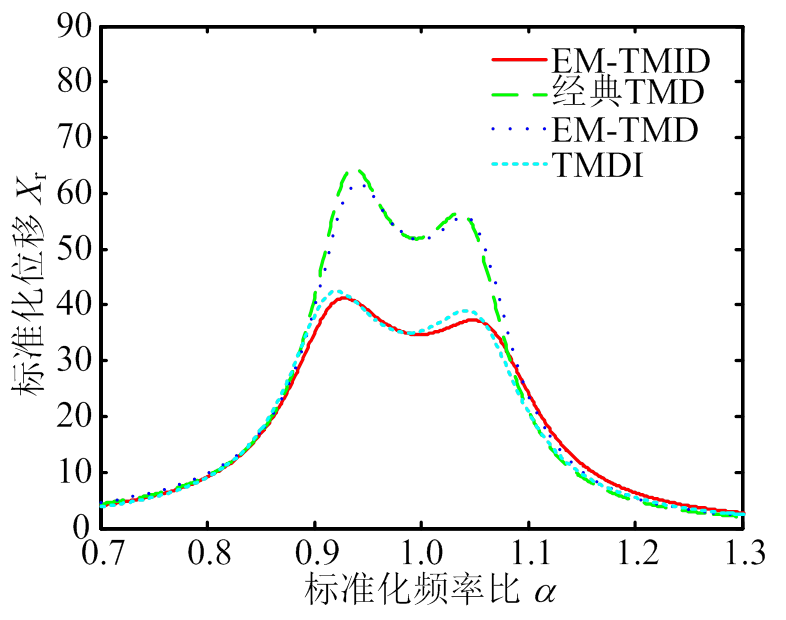
(b) 相对位移的频响函数
图3 不同系统下的频响函数
Fig.3 Frequency response functions of different systems
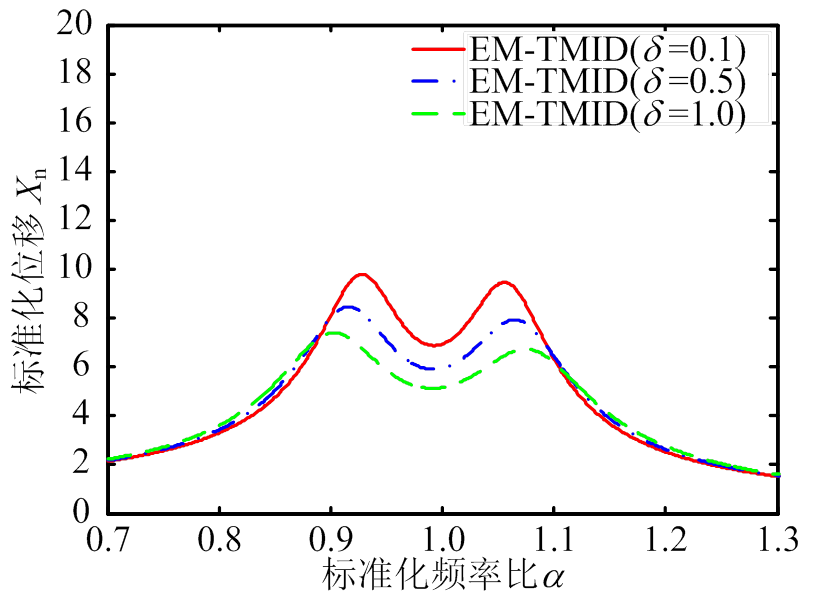
3) 不同惯质比下EM-TMID的减振性能对比
由图4可知,在质量比一定的情况下,惯质比越大,EM-TMID对主结构位移的减震性能越好。
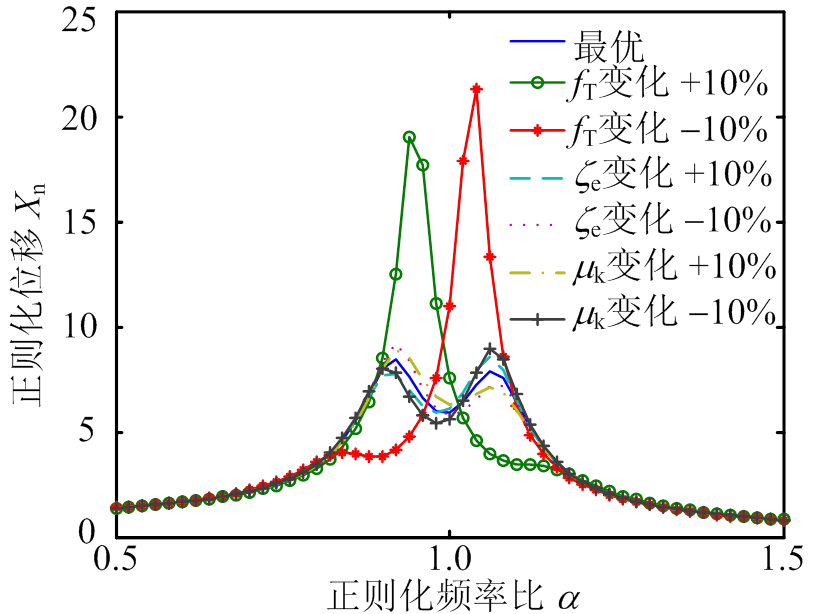
4) 调谐参数的鲁棒性分析
然而,在实际过程中,受到外界因素的干扰,EM-TMID的参数很难调谐到最优状态,一些调谐参数的数值可能会发生变化,从而对减震性能造成影响[21]。调谐参数的变化对EM-TMID减振鲁棒性的影响如图5所示。从图5可得,结构频率比的改变对EM-TMID的主结构位移频响的鲁棒性影响较大,而电磁阻尼比和机电耦合系数的影响较小。
3.2 能量收集分析
另一方面,为了提高EM-TMID的能量收集效率,可以通过提高作用在外接电阻Re上的功率来实现。其中,作用在外接电阻Re的瞬时功率为[21]:
为进一步评估能量收集效果,引入能量回收评价指标[21]:
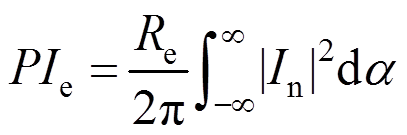 (20)
(20)
将式(8)代入式(20)中可得:
4 时域数值分析
EM-TMID的H2最优参数是在假设激励是白噪声激励下获得的。然而,地震激励并不是理想中的白噪声激励。因此,本节中将通过使用真实地震波激励来仿真时域中EM-TMID的减震和能量收集双重性能[21]。
4.1 数学模型
由于在实际结构中,主结构存在阻尼,故在时程分析中建立数学模型时考虑主结构阻尼。式(1)可以表述成另一种形式:
引入相对位移xr,式(22)可进一步化简:
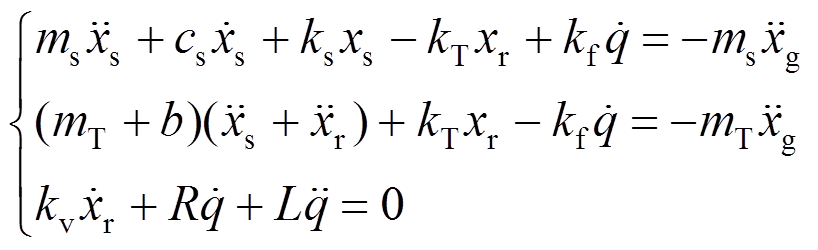 (23)
(23)
式(23)可以用矩阵形式表示为:
其中:
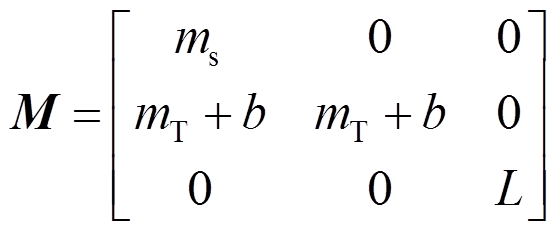 ,
,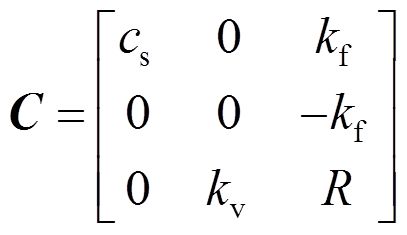 ,
,
定义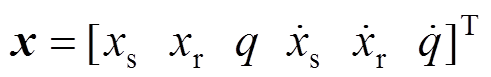 ,则状态方程为:
,则状态方程为:
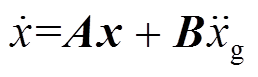 (25)
(25)
其中: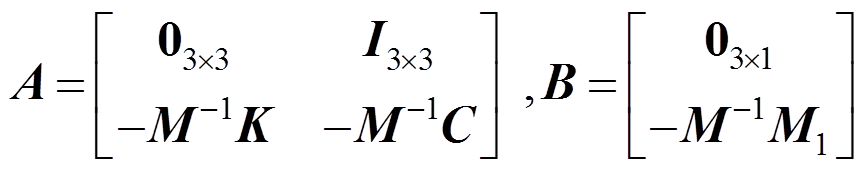 。
。
4.2 减震指标
1) 峰值减震评价指标
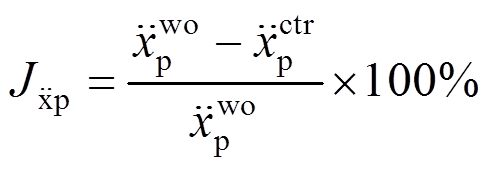 (27)
(27)
式中: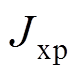 、
、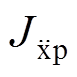 为地震作用下主结构相对位移和相对加速度峰值减震效果指标;
为地震作用下主结构相对位移和相对加速度峰值减震效果指标;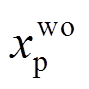 、
、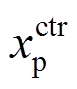 、
、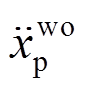 和
和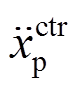 为结构无控与有控时的峰值位移,结构无控与有控时的峰值加速度[10, 21]。
为结构无控与有控时的峰值位移,结构无控与有控时的峰值加速度[10, 21]。
2) 均方根值减震评价指标
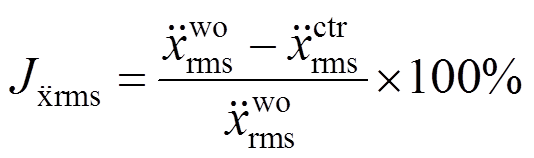 (29)
(29)
式中: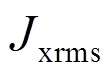 、
、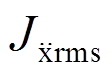 为地震作用下主结构相对位移和相对加速度均方根值减震效果指标;
为地震作用下主结构相对位移和相对加速度均方根值减震效果指标;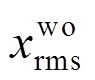 、
、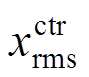 、
、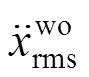 和
和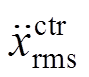 为结构无控与有控时的位移均方根值,结构无控与有控时的结构加速度均方根值[10, 21]。
为结构无控与有控时的位移均方根值,结构无控与有控时的结构加速度均方根值[10, 21]。
4.3 仿真参数
为更好地研究EM-TMID两重功能,时域仿真结果将与H2理论最优下经典TMD进行对比[21]。此次仿真主结构参数来源于一10层框架结构的首阶模态参数,相关阻尼器参数根据第2节的H2最优解析解确定,具体如表1所示[21]。
表1 仿真参数
Table 1 Parameters of the simulation

参数名称符号数值 主结构质量ms58970 kg 主结构刚度ks4.81×104 kN/m 主结构阻尼cs67.4 kN·s/m 主结构振动周期T0.22 s TMD质量mT1179 kg TMD刚度kT1.15×103 kN/m 惯质b589.7 kg 电感L5.2 mH 内阻Ri0.08Ω 外阻Re0.08Ω 电磁传感器常数kv,kf50
4.4 减震仿真
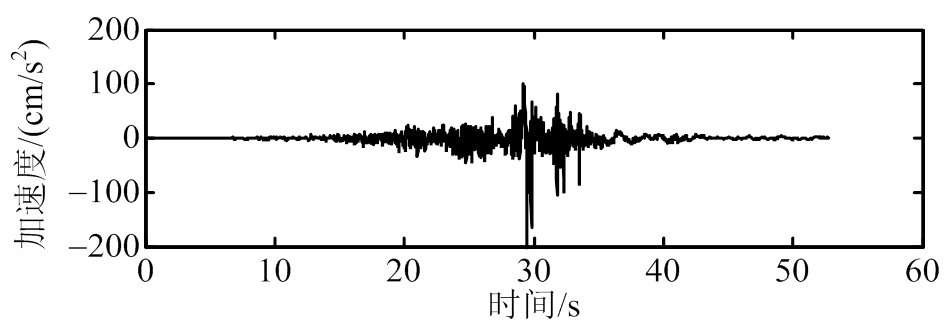
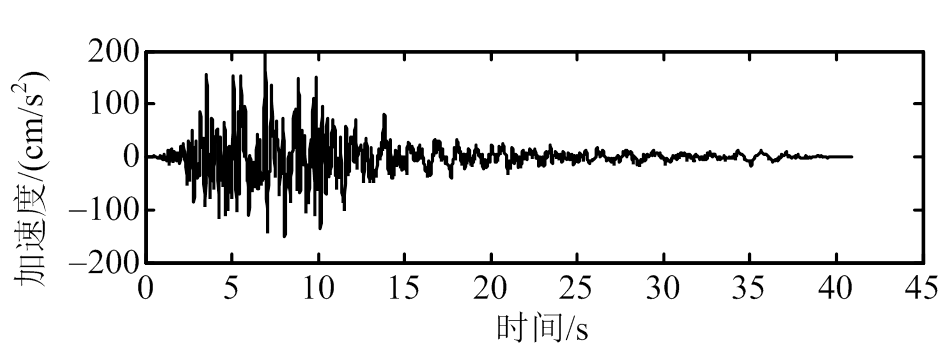
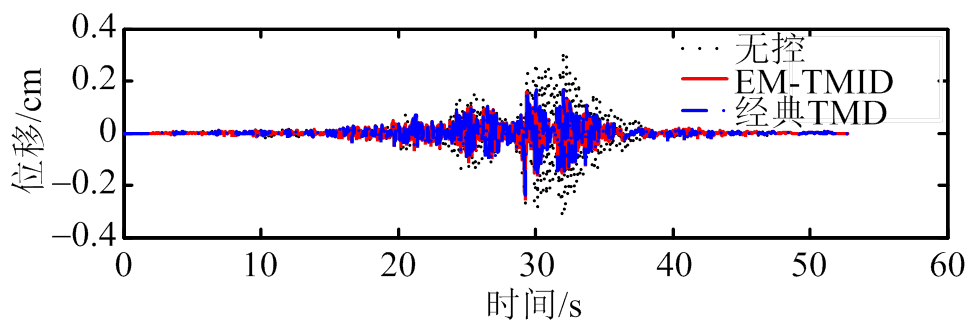
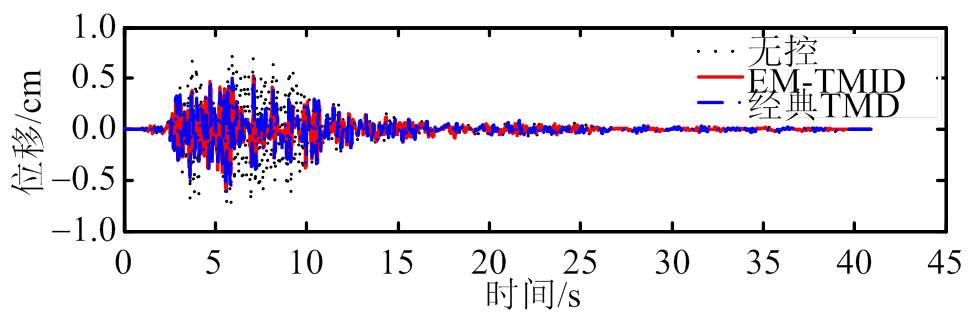
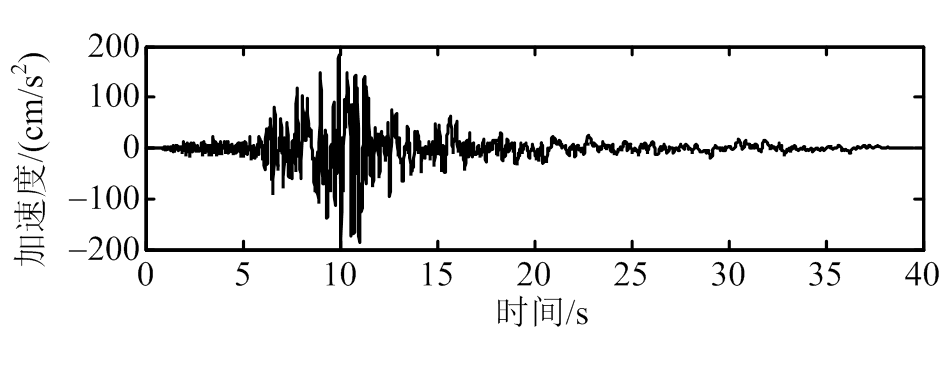
本时程分析中,将选取典型的4种地震波对耦合系统激励[21]。为了更好地分析峰值减震效果,统一将4种地震波的加速度振幅调到200 伽,4种地震波分别为:1) ChiChi;2) El Centro;3) Kobe;4) Northridge,地震波加速度时程图如图6所示[21]。主结构位移减震时程图如7所示;主结构加速度减震时程图如8所示;主结构位移和加速度峰值和均方值减震率图如图9、图10所示(见表2所示) [21]。
(a) ChiChi
(b) El Centro
(c) Kobe
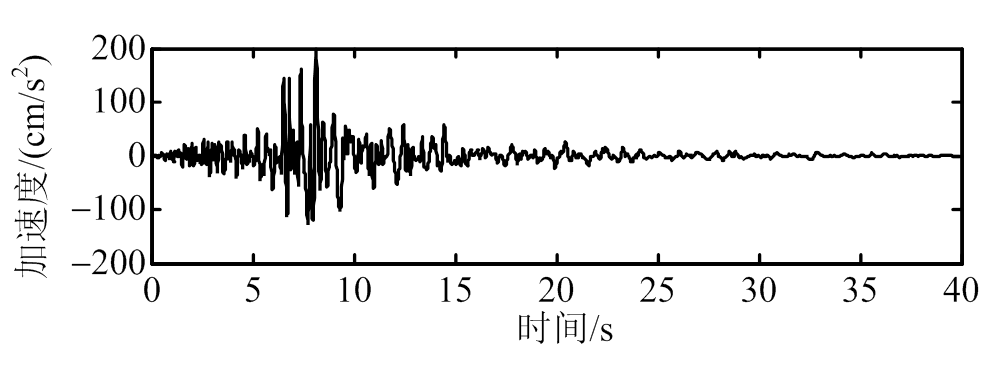
(d) Northridge
图6 地震波时程图
Fig.6 Time-history responses of observed earthquake records
(a) ChiChi
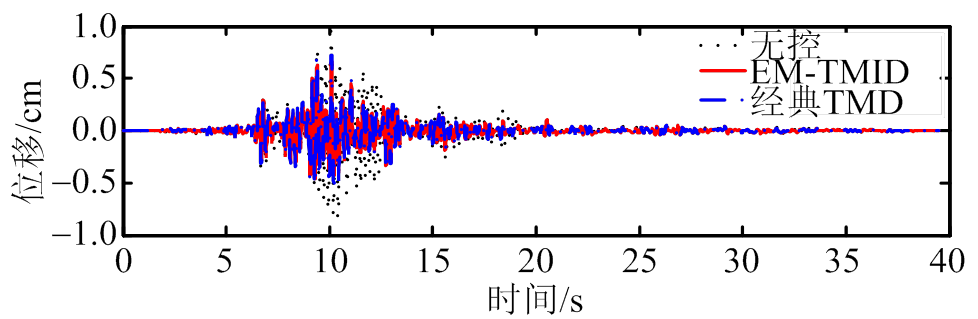
(b) El Centro
(c) Kobe
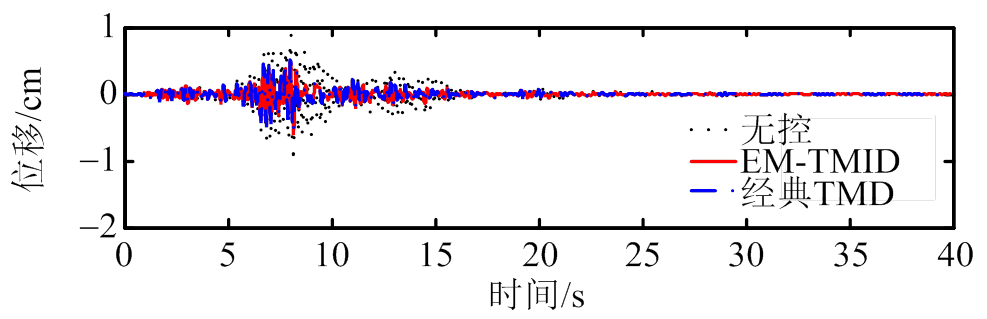
(d) Northridge
图7 位移减震时程图
Fig.7 Time-history displacement responses
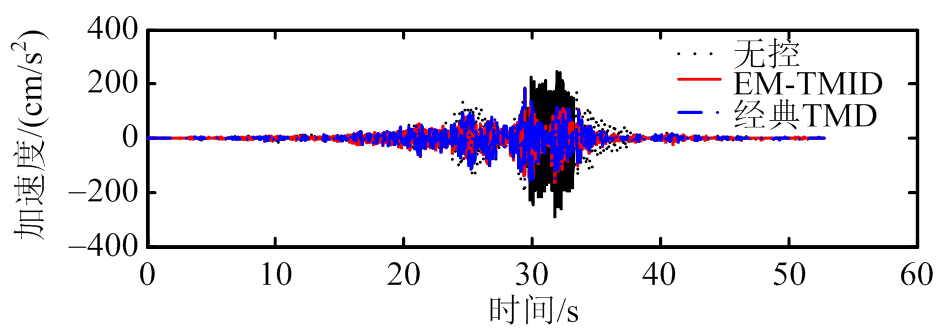
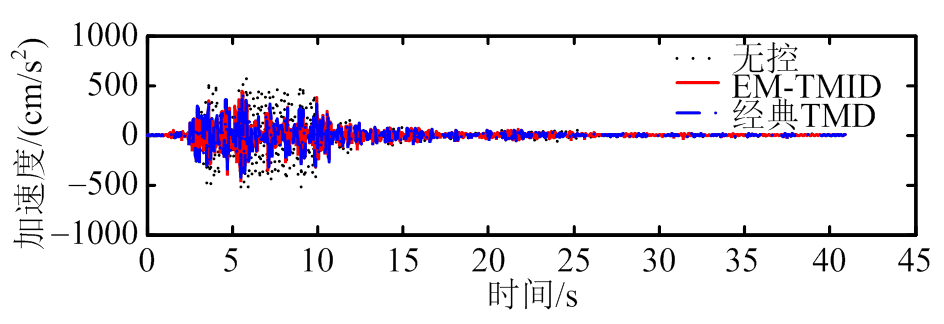
(a) ChiChi
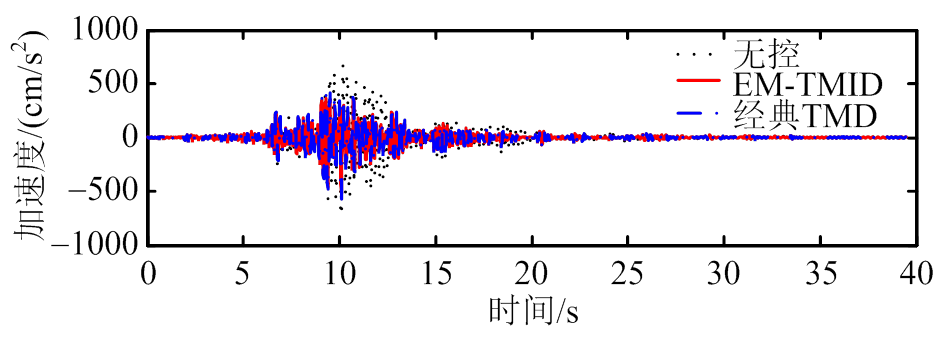
(b) El Centro
(c) Kobe
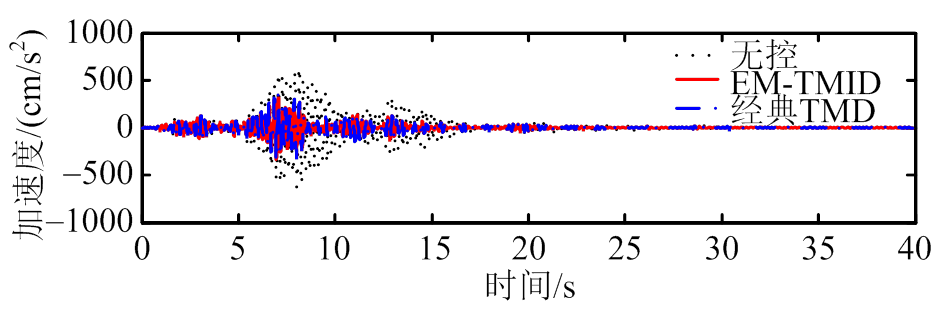
(d) Northridge
图8 加速度减震时程图
Fig.8 Time-history acceleration responses
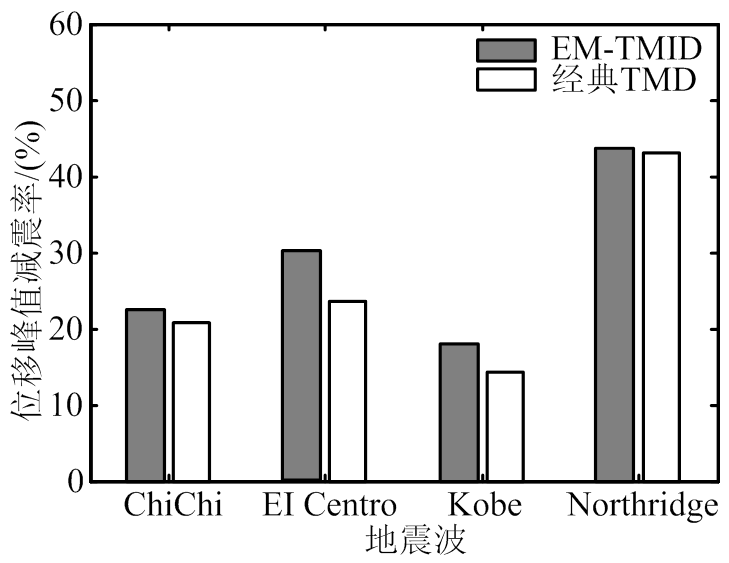
(a) 位移
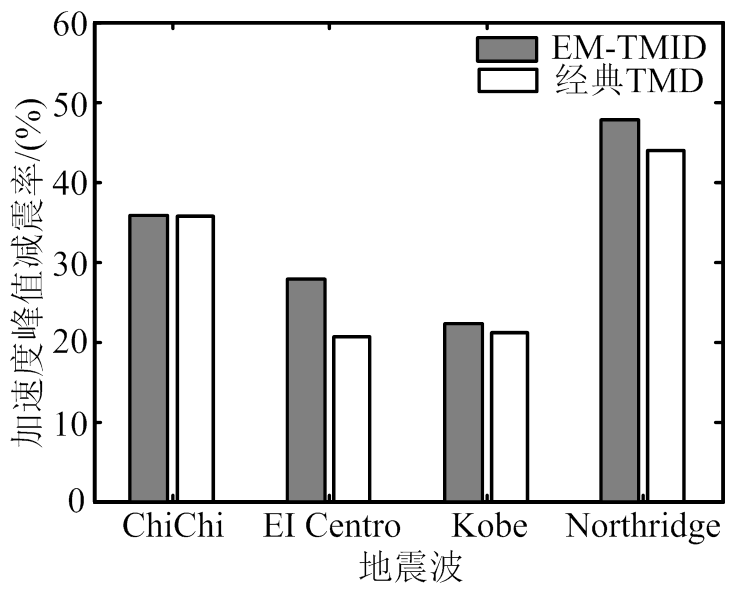
(b) 加速度
图9 峰值减震率
Fig.9 Reduction ratio related to response peak
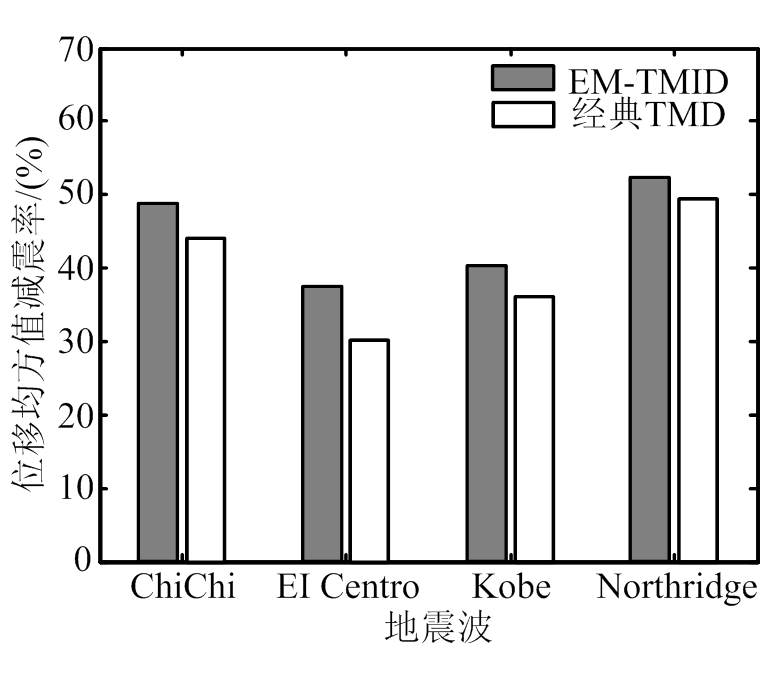
(a) 位移
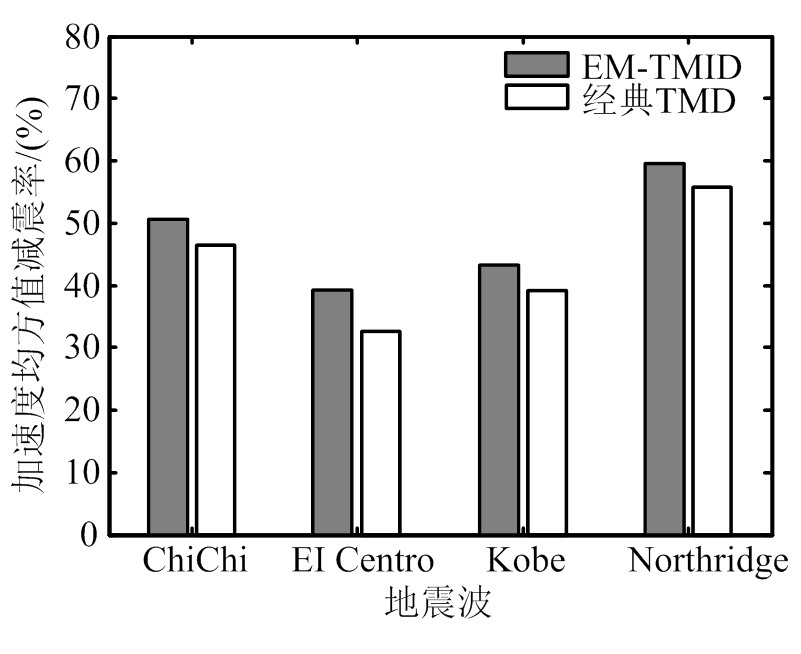
(b) 加速度
图10 均方值减震率
Fig.10 Reduction ratio related to response RMS value
表2 EM-TMID与经典TMD的减震指标
Table 2 Vibration reduction indexes of EM-TMID and classical TMD
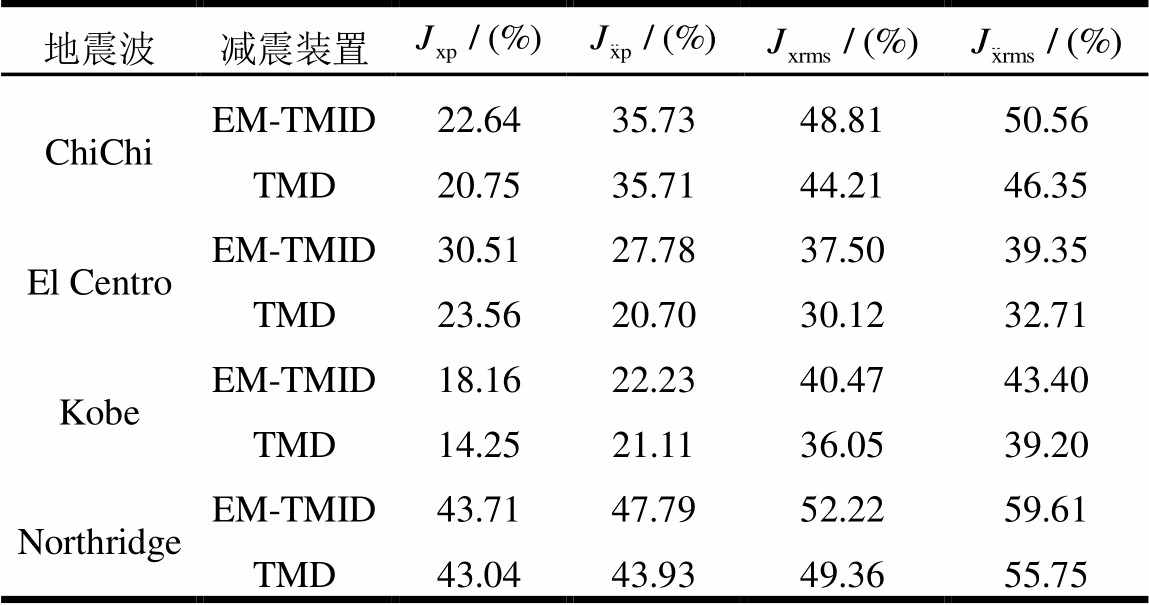
地震波减震装置 ChiChiEM-TMID22.6435.7348.8150.56 TMD20.7535.7144.2146.35 El CentroEM-TMID30.5127.7837.5039.35 TMD23.5620.7030.1232.71 KobeEM-TMID18.1622.2340.4743.40 TMD14.2521.1136.0539.20 NorthridgeEM-TMID43.7147.7952.2259.61 TMD43.0443.9349.3655.75
由图9、图10及表2可知,相对于经典TMD,EM-TMID对于主结构位移峰值和均方值、加速度峰值和均方值减震效果比经典TMD均有所提升。
4.5 能量收集仿真
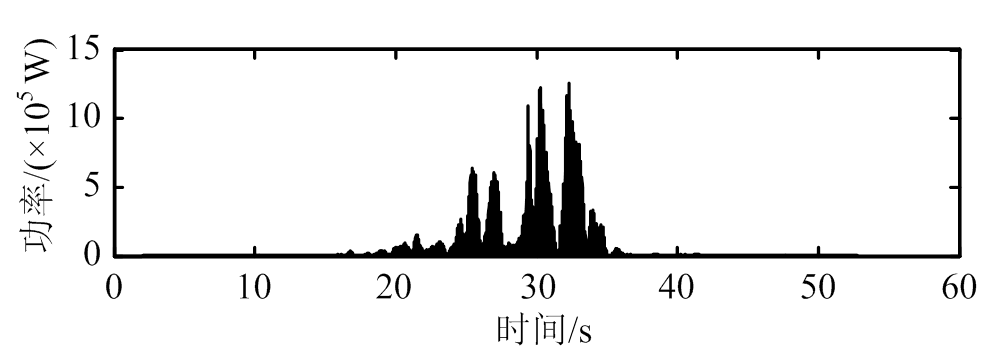
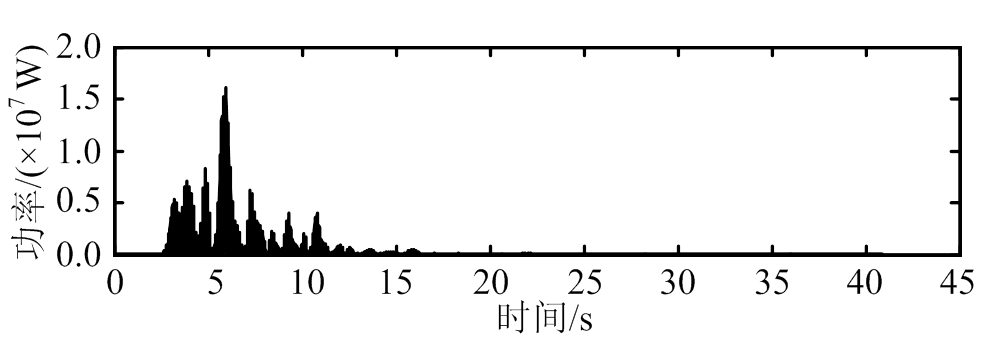
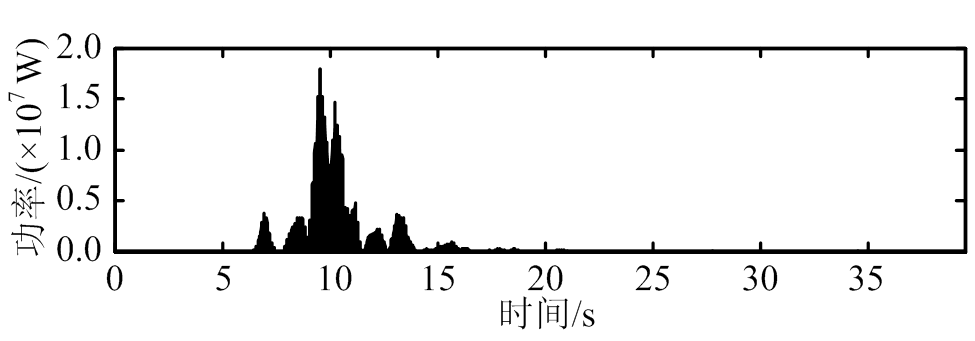
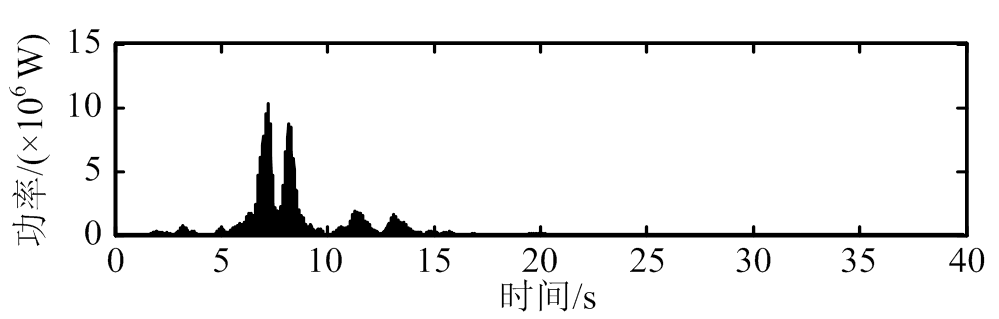
通过式(25),可以求解电流时程。根据电流时程和式(19),画出EM-TMID的功率时程,如图11所示;相关能量收集指标如表3所示[21]。
由图11和表3可知,与经典TMD相比,EM-TMID在其减震性能更加优越的同时,还具备一定的能量收集效果。其中,EM-TMID在Kobe地震波下的平均功率最高,达到4.11×102 kW。
(a) ChiChi
(b) El Centro
(c) Kobe
(d) Northridge
图11 能量收集功率时程图
Fig.11 Time histories of energy harvesting power
表3 能量收集指标
Table 3 Indexes of energy harvesting
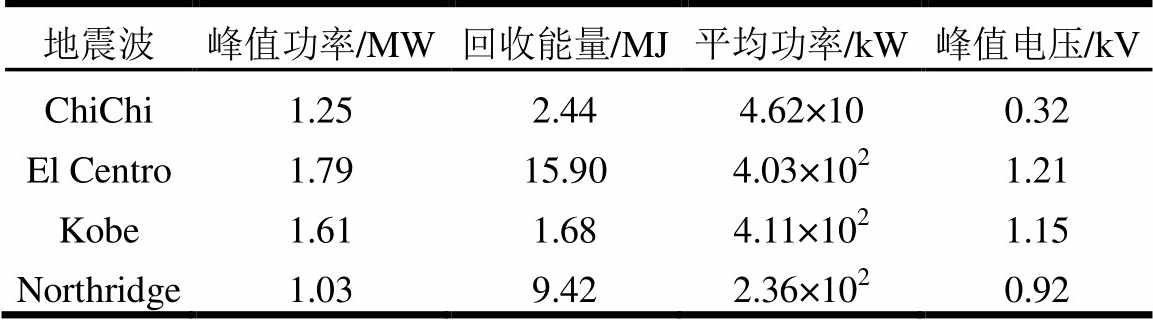
地震波峰值功率/MW回收能量/MJ平均功率/kW峰值电压/kV ChiChi1.252.444.62×100.32 El Centro1.7915.904.03×1021.21 Kobe1.611.684.11×1021.15 Northridge1.039.422.36×1020.92
5 结论
本文基于经典TMD,将电磁阻尼单元代替粘性阻尼单元,引入惯质单元,形成新型的电磁调谐双质阻尼器(EM-TMID)。并且建立了EM-TMID与单自由度结构耦合减震模型的动力学模型。然后基于H2理论和残值定理,获得了主结构位移均方根值最优状况下的EM-TMID的3个最优调谐参数解析式,即最优结构频率比、电磁阻尼比和机电耦合系数。具体结论如下:
(1) 频域分析可知,在质量比和惯质比分别为0.02和0.5时,EM-TMID的主结构位移频响函数的峰值相对于经典TMD降低了20.57%,相对于EM-TMD降低了17.27%,相对于TMDI降低了4.43%;EM-TMID的主结构位移频响函数的积分面积相对于经典TMD降低了8.43%,相对于EM-TMD降低了7.40%,相对于TMDI降低了1.41%。
(2) 时域分析可知,EM-TMID对于主结构位移和加速度的峰值和均方值的减震性能均优于经典TMD,并且增加能量收集装置后的EM-TMID能够进行能量收集,如在Kobe地震波下,平均功率达到4.11×102 kW。
参考文献:
[1] Hartog D J P. Mechanical vibrations [M]. 4th ed. New York: McGraw-Hill Book Company, Inc, 1956.
[2] Rana R, Soong T T. Parametric study and simplified design of tuned mass dampers [J]. Engineering Structures, 1998, 20(3): 193―204.
[3] 林均岐, 王云剑. 调谐质量阻尼器的优化分析[J]. 地震工程与工程振动, 1996,16(1): 116―121.
Lin Junqi, Wang Yunjian. Optimal analysis of tuned mass damper [J]. Earthquake Engineering and Engineering vibration, 1996, 16(1): 116―121. (in Chinese)
[4] 李宏男, 王苏岩. 利用TMD减小高层建筑地震反应的研究[J]. 工程力学, 1997, (a03): 136―140.
Li Hongnan, Wang Suyan. Reducing the seismic response of high-rise buildings with TMD [J]. Engineering Mechanics, 1997, (a03): 136―140. (in Chinese)
[5] 李春祥. 土木工程结构的双层多重调谐质量阻尼器控制策略[J]. 地震工程与工程振动, 2005, 25(1): 113―119.
Li Chunxiang. Dual layer multiple tuned mass damper control strategy of civil engineering structures [J]. Earthquake engineering and engineering vibration, 2005, 25(1): 113―119. (in Chinese)
[6] 王文熙. 桥梁TMD系统的参数优化与设计[D]. 湖南大学, 2014.
Wang Wenxi. Parametric optimization and design of bridge TMD system [D]. Hu’nan: Hunan University, 2014. (in Chinese)
[7] 喻梅, 廖海黎, 李明水, 等. 基于经验线性涡激力的桥梁涡激振动TMD控制[J]. 工程力学, 2013, 30(6): 269―274.
Yu Mei, Liao Haili, Li Mingshui, et al. Suppression of vortex-induced vibration of bridges using TMD based on linear empirical vortex-shedding forces model [J]. Engineering Mechanics, 2013, 30(6): 269―274. (in Chinese)
[8] 刘良坤, 谭平, 闫维明, 等. 一种NES与TMD的混合控制方案研究[J]. 工程力学, 2017, 34(9): 64―72.
Liu Liangkun, Tan Ping, Yan Weiming, et al. Analysis of a hybrid scheme comprised of nonlinear energy sink and tuned mass damper [J]. Engineering Mechanics, 2017, 34(9): 64―72. (in Chinese)
[9] Smith M C. Synthesis of mechanical networks: The inerter [J]. Automatic Control, IEEE Transactions on, 2002, 47(10): 1648―1662.
[10] 孙洪鑫, 罗一帆, 王修勇, 等. 电磁调谐双质阻尼器的参数优化及对结构减震分析[J]. 沈阳建筑大学学报(自然科学版), 2018, 34(3): 410―418.
Sun Hongxin, Luo Yifan, Wang Xiuyong, et al. Parametric optimization and vibration control of electromagnetic tuned mass-inerter dampers for the structures [J]. Journal of Shenyang Jianzhu University (Natural Science), 2018, 34(3): 410―418. (in Chinese)
[11] 陈龙, 张孝良, 聂佳梅, 等. 基于半车模型的两级串联型ISD悬架性能分析[J]. 机械工程学报, 2012, 48(6): 102―108.
Chen Long, Zhang Xiaoliang, Nie Jiamei, et al. Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model [J]. Journal of Mechanical Engineering, 2012, 48(6): 102―108. (in Chinese)
[12] 陈龙, 杨晓峰, 汪若尘, 等. 基于二元件ISD结构隔振机理的车辆被动悬架设计与性能研究[J]. 振动与冲击, 2013, 32(6): 90―95.
Chen Long, Yang Xiaofeng, Wang Ruochen, et al. Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structure vibration isolation mechanism [J]. Journal of Shock and Vibration, 2013, 32(6): 90―95. (in Chinese)
[13] Marian L, Giaralis A. Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems [J]. Probabilistic Engineering Mechanics, 2014, 38: 156―164.
[14] Salvi J, Giaralis A. Concept study of a novel energy harvesting-enabled tuned mass-damper-inerter (EH-TMDI) device for vibration control of harmonically- excited structures [C]. Journal of Physics: Conference Series, 2016, 744(1): 012082.
[15] Nakamura Y, Fukukita A, Tamura K, et al. Seismic response control using electromagnetic inertial mass dampers [J]. Earthquake Engineering & Structural Dynamics, 2014, 43(4): 507―527.
[16] Wen Y, Chen Z, Hua X. Design and evaluation of tuned inerter-based dampers for the seismic control of MDOF structures [J]. Journal of Structural Engineering, 2016, 143(4): 04016207.
[17] 汪志昊, 许艳伟, 赵顺波, 等. 基于表观质量负刚度效应的调谐质量阻尼器频率调节[J]. 科学技术与工程, 2016, 16(27): 246―250.
Wang Zhihao, Xu Yanwei, Zhao Shunbo, et al. Frequency tuning of tuned mass dampers based on negative stiffness generated by apparent mass [J]. Science Technology and Engineering, 2016, 16(27): 246―250. (in Chinese)
[18] Inoue T, Ishida Y, Sumi M. Vibration suppression using electromagnetic resonant shunt damper [J]. Journal of Vibration & Acoustics, 2008, 130(4): 2727―2747.
[19] Zuo L, Cui W. Dual-functional energy-harvesting and vibration control: electromagnetic resonant shunt series tuned mass dampers [J]. Journal of Vibration & Acoustics, 2013, 135(5): 510181―510189.
[20] Liu Y, Lin C-C, Parker J, et al. Exact H2 optimal tuning and experimental verification of energy-harvesting series electromagnetic tuned-mass dampers [J]. Journal of Vibration and Acoustics, 2016, 138(6): 061003.
[21] 罗一帆, 孙洪鑫, 王修勇. 电磁调谐质量阻尼器的H2参数优化及对结构减震分析[J]. 振动工程学报, 2018, 31(3): 529―538.
Luo Yifan, Sun Hongxin, Wang Xiuyong. H2 paramenters optimization and vibration reduction analysis of electromagnetic tuned mass damper [J]. Journal of Vibration Engineering, 2018, 31(3): 529―538. (in Chinese)
[22] Zuo L, Tang X. Large-scale vibration energy harvesting [J]. Journal of Intelligent Material Systems and Structures, 2013, 24(11): 1405―1430.
[23] Shen W, Zhu S, Zhu H. Experimental study on using electromagnetic devices on bridge stay cables for simultaneous energy harvesting and vibration damping [J]. Smart Material and Structures, 2016, 25(6): 065011.
[24] Doyle J. Robust and optimal control [C]. Proceedings of the IEEE Conference on the Decision and Control, 2002, 2(97): 1595―1598.
[25] Nishihara O, Asami T. Closed-form solutions to the exact optimizations of dynamic vibration absorbers (minimizations of the maximum amplitude magnification factors) [J]. Journal of Vibration & Acoustics, 2002, 124(4): 576―582.
[26] Asami T, Nishihara O, Baz A M. Analytical solutions to H∞and H2 optimization of dynamic vibration absorbers attached to damped linear systems [J]. Journal of Vibration & Acoustics, 2002, 124(2): 284―295.
THE H2 PARAMETRIC OPTIMIZATION AND STRUCTURAI VIBRATION SUPPRESSION OF ELECTROMAGNETIC TUNED MASS-INERTER DAMPERS
LUO Yi-fan1,2 , SUN Hong-xin2 , WANG Xiu-yong2
(1. School of Mechanical Engineering, Hunan University of Science and Technology, Xiangtan, Hu’nan 411201, China; 2. Hunan Provincial Key Laboratory of Structural Engineering for Wind Resistant and Vibration Control, Hunan University of Science and Technology, Xiangtan, Hu’nan 411201, China)
Abstract: A novel electromagnetic shunt tuned mass-inerter damper (EM-TMID) is proposed, which can realize dual functions of both vibration suppression and energy harvesting. A novel feature of the damper is that the viscous damping of traditional tuned mass dampers is replaced by that of electromagnetic transducers with inertance. According to the Alembert’s theorem, the dynamic model of a coupled EM-TMID and a single degree of freedom structural system under seismic excitation is established. Based on the H2 norm method with the aim of minimizing the root mean square value of the damage to the main structure, solutions of the three parameters, that is, the mechanical tuning ratio, electrical damping ratio and electromagnetic mechanical coupling coefficient, are obtained. With the optimal parameters, the frequency-domain and time-domain numerical simulations of the EM-TMID are conducted to analyze the dual functions of the vibration suppression and energy harvesting. The results show that in the frequency domain, the EM-TMID is superior to the classical TMD, EM-TMD and TMDI in terms of the reduction of the peak and area of the frequency response of the displacement of the main structure.In the time domain, the EM-TMID is superior to classical TMDs in terms of the reduction of the peak and root mean square value of displacement and acceleration. Meanwhile, the EM-TMID can also harvest energy.
Key words: disaster prevention and reduction; structural vibration control; tuned mass damper; electromagnetic damper; inertance; energy harvesting
文章编号:1000-4750(2019)04-0089-11
中图分类号:TU352.1
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.01.0027
收稿日期:2018-01-10;
修改日期:2018-11-02
基金项目:国家自然科学基金项目(51508185,51778228);973计划项目(2015CB057702)
通讯作者:孙洪鑫(1980―),男,河南人,教授,博士,博导,从事结构振动控制和结构抗风研究(E-mail: cehxsun@hnust.edu.cn).
作者简介:罗一帆(1992―),男,湖南人,博士生,从事结构振动控制和结构抗风研究(E-mail: 984512203@qq.com);
王修勇(1962―),男,湖南人,教授,博士,博导,从事结构振动控制和结构抗风研究(E-mail: cexywang@hnust.edu.cn).
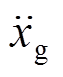 下,EM-TMID与被控结构的耦合减震模型如图1所示,为了更好地分析阻尼器对主结构的减震效果,主结构被简化为一个单自由度结构,其质量为ms,刚度为ks,阻尼为cs,其数值分别对应于结构主要模态[10, 21]。在EM-TMID中,将经典TMD中的粘性阻尼单元替换成基于直线发电机的能量收集单元,从而产生电磁阻尼力,然后基于滚珠丝杆元件的惯质单元被连接在TMD与下一层主结构之间,系统构造图如图1(b)所示。基于直线发电机原理,能量收集单元可以简化为一个电感L,和一个内阻Ri,与此同时,能量储存单元的外阻等为Re,两者串联后,等效为RL电路[10, 21]。因此,EM-TMID基本结构主要包括弹簧—质量单元、惯质单元以及基于直线发电机的能量收集单元[21]。
下,EM-TMID与被控结构的耦合减震模型如图1所示,为了更好地分析阻尼器对主结构的减震效果,主结构被简化为一个单自由度结构,其质量为ms,刚度为ks,阻尼为cs,其数值分别对应于结构主要模态[10, 21]。在EM-TMID中,将经典TMD中的粘性阻尼单元替换成基于直线发电机的能量收集单元,从而产生电磁阻尼力,然后基于滚珠丝杆元件的惯质单元被连接在TMD与下一层主结构之间,系统构造图如图1(b)所示。基于直线发电机原理,能量收集单元可以简化为一个电感L,和一个内阻Ri,与此同时,能量储存单元的外阻等为Re,两者串联后,等效为RL电路[10, 21]。因此,EM-TMID基本结构主要包括弹簧—质量单元、惯质单元以及基于直线发电机的能量收集单元[21]。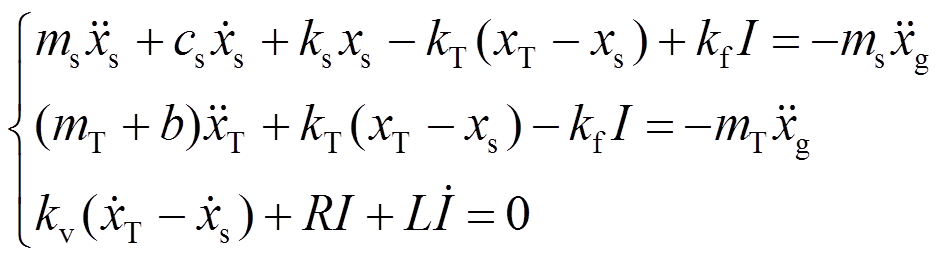 (1)
(1) (2)
(2)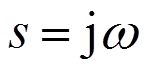 ,
,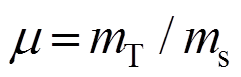 ,
,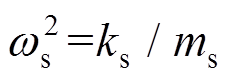 ,
,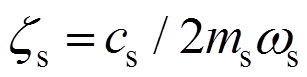 ,
,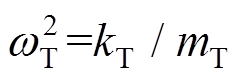 ,
,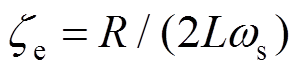 ,
,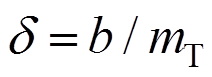 ,对式(2)进行无量纲化,可有:
,对式(2)进行无量纲化,可有: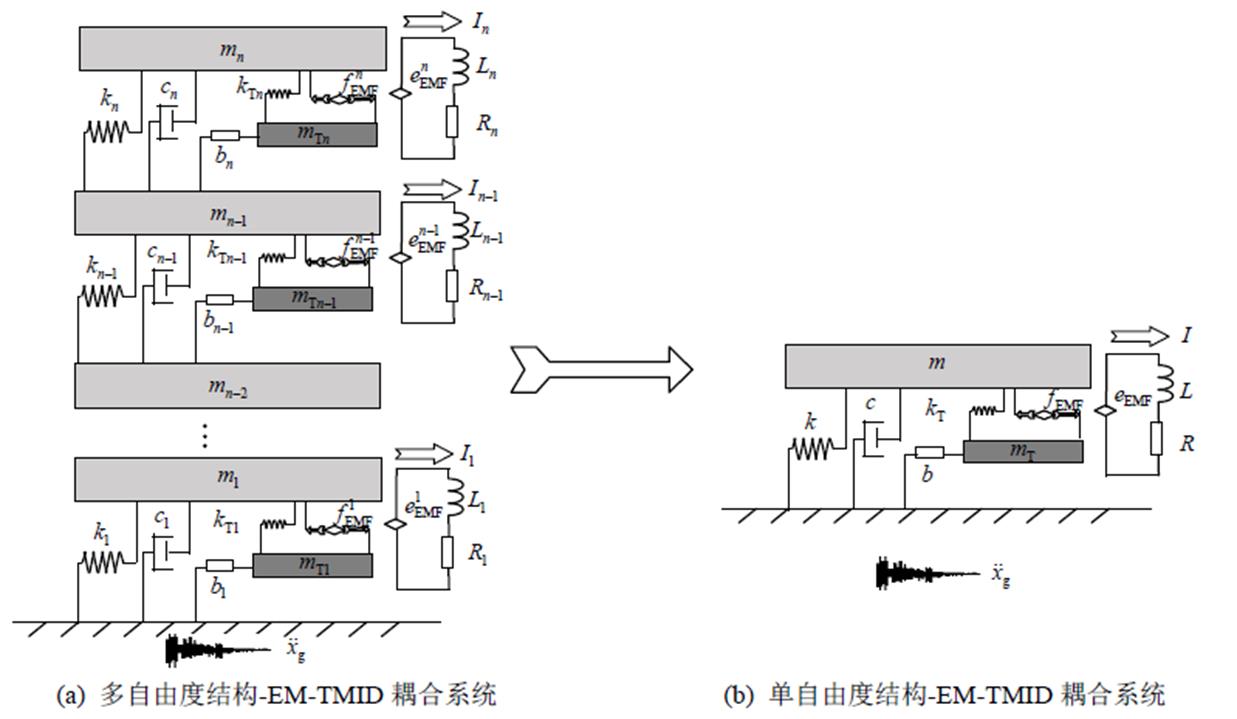
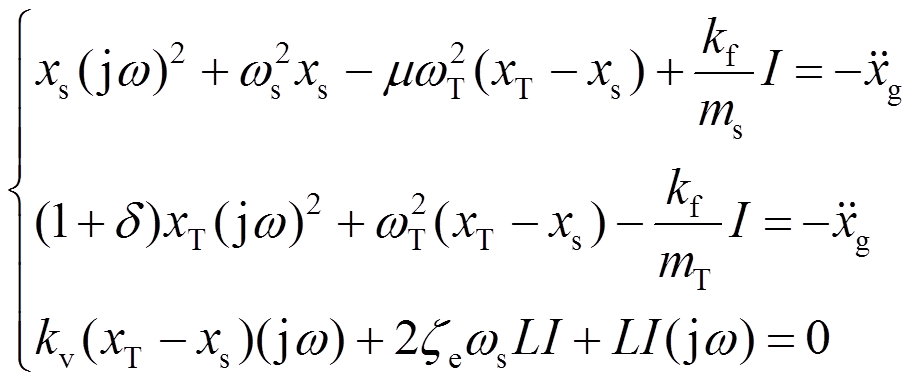 (3)
(3)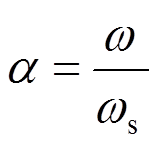 ,
,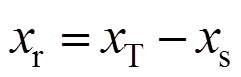 ,
,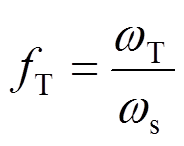 ,
,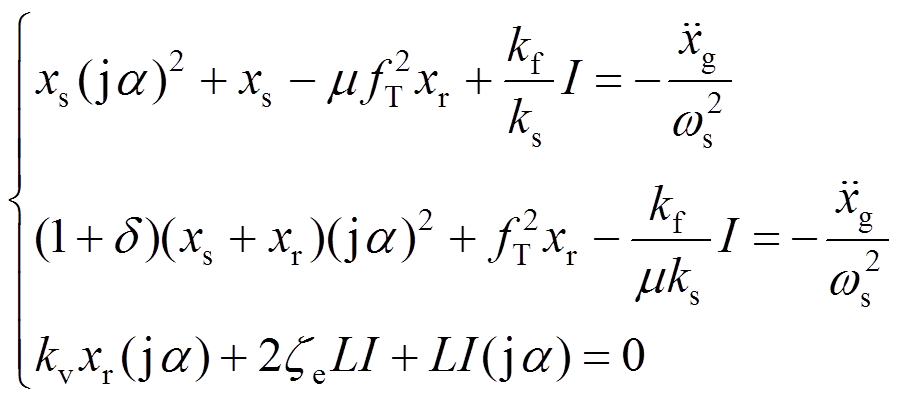 (4)
(4)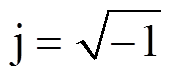 为虚数单位。
为虚数单位。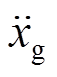 的作用下,从
的作用下,从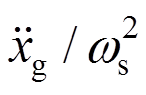 到x
到x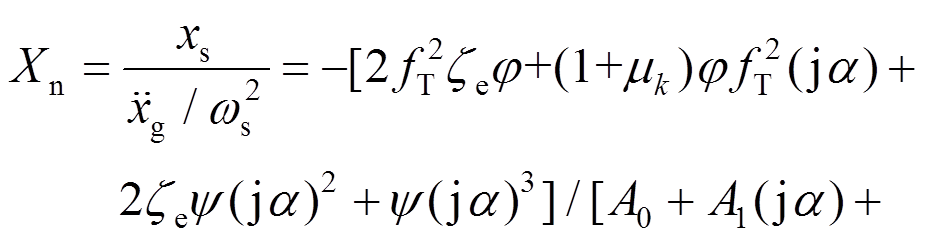
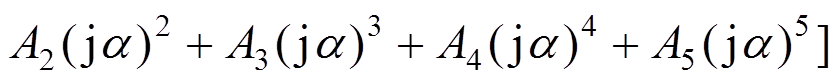 (5)
(5)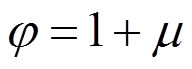 ,
,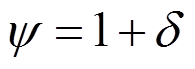 ;机电耦合系数为
;机电耦合系数为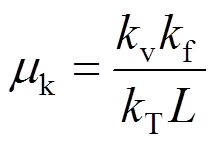 ,且分母相关系数为:
,且分母相关系数为: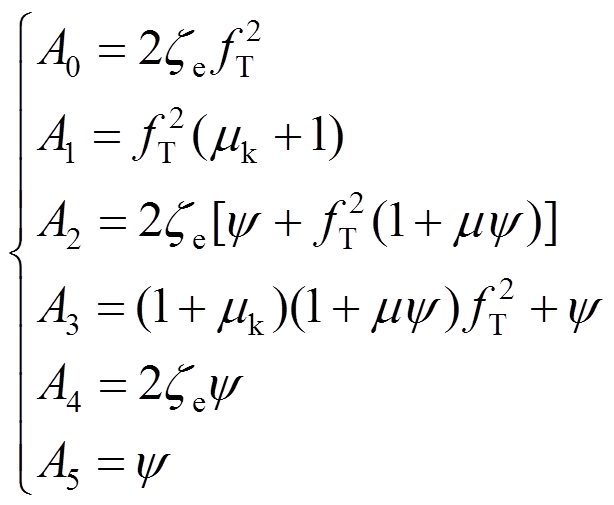 (6)
(6)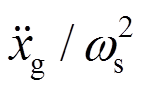 到x
到x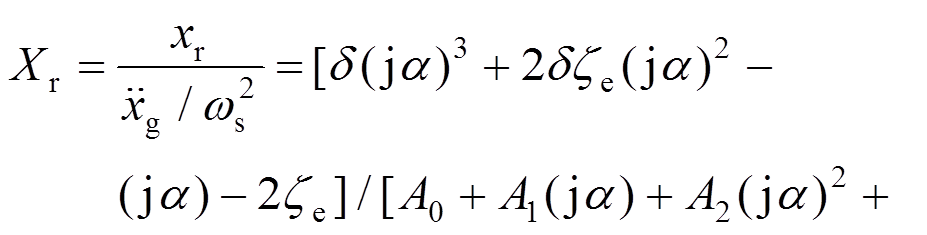
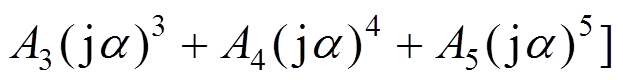 (7)
(7)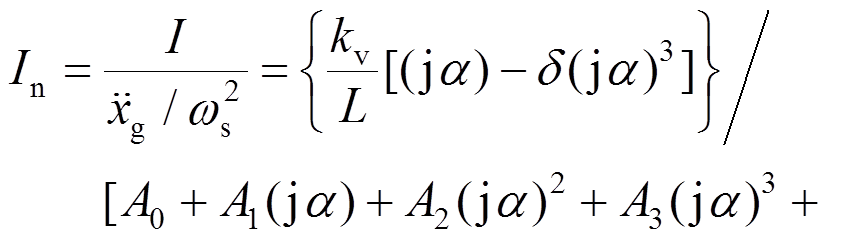
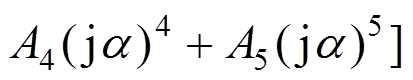 (8)
(8)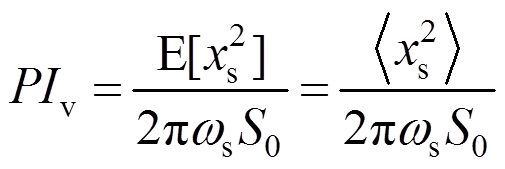 (9)
(9) 代表瞬时平均值;S
代表瞬时平均值;S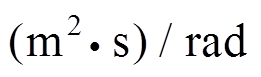
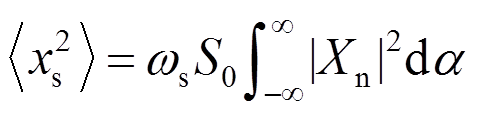 (10)
(10)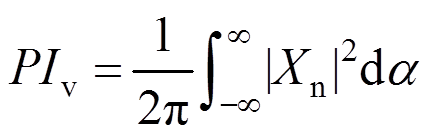 (11)
(11)
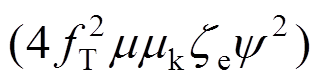 (12)
(12)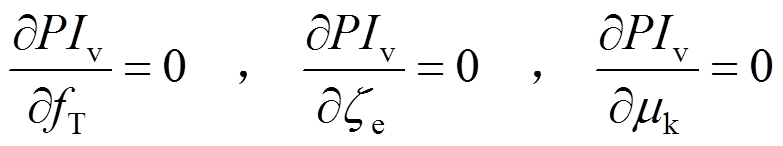 (13)
(13)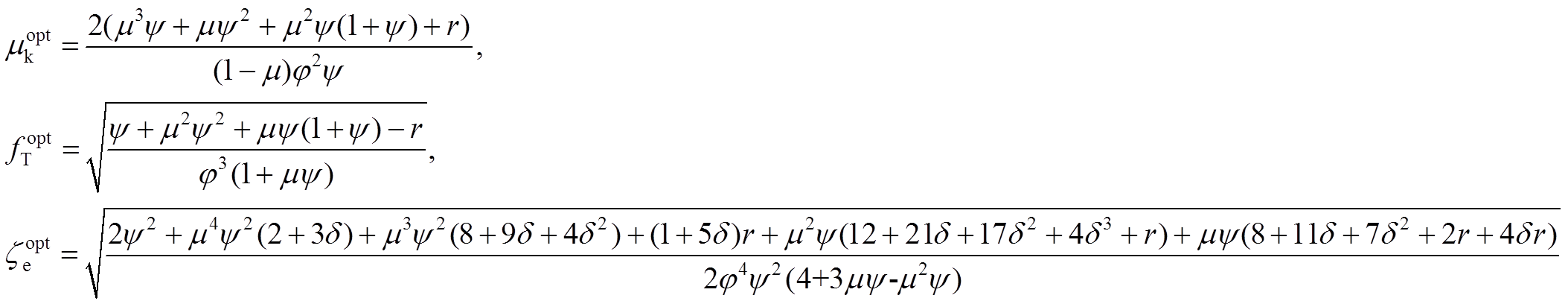 (14)
(14)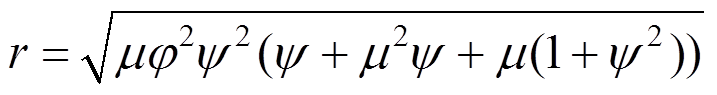 。
。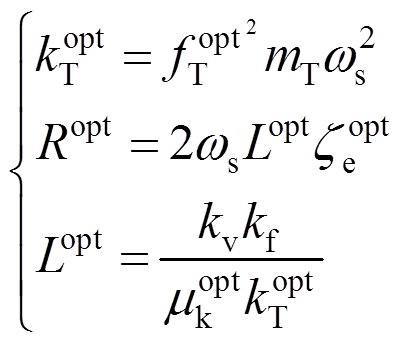 (15)
(15)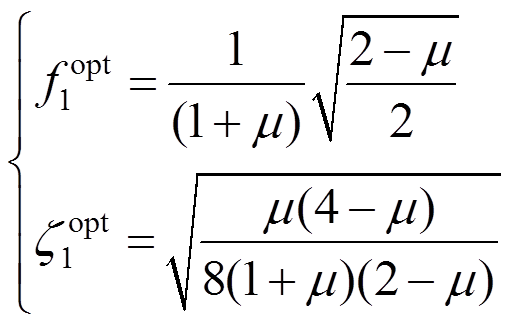 (16)
(16)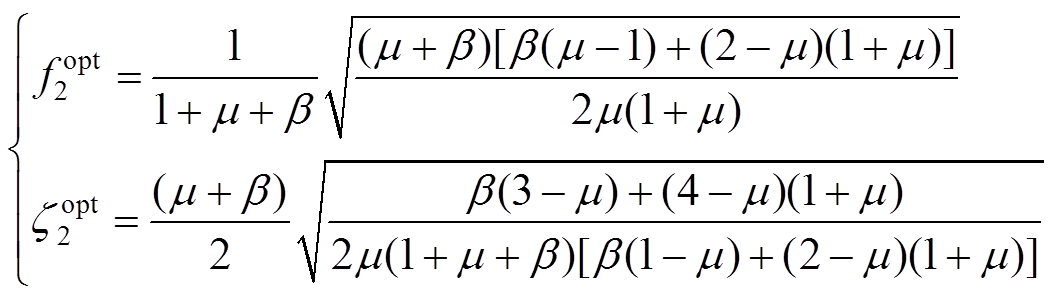 (17)
(17)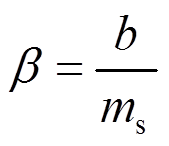 。
。 (18)
(18)


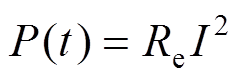 (19)
(19)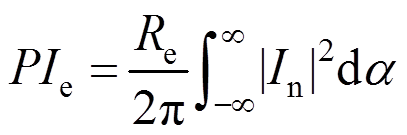 (20)
(20)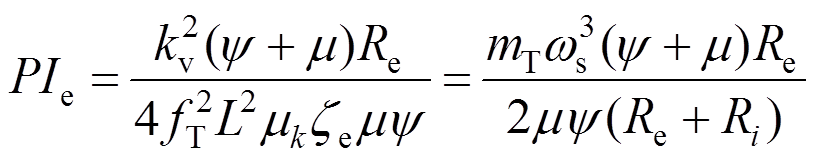 (21)
(21)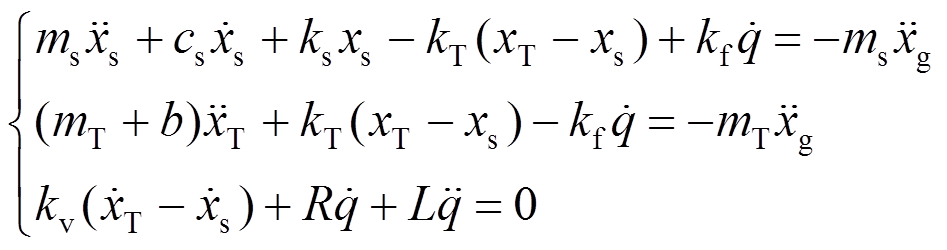 (22)
(22)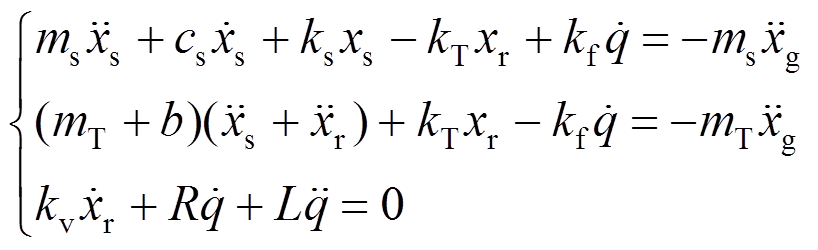 (23)
(23)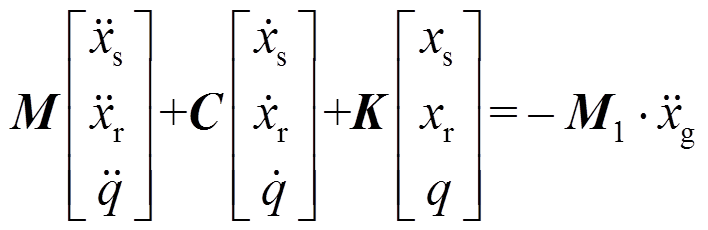 (24)
(24)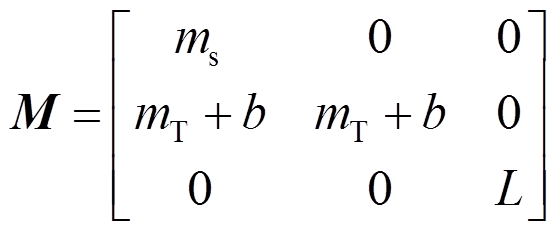 ,
,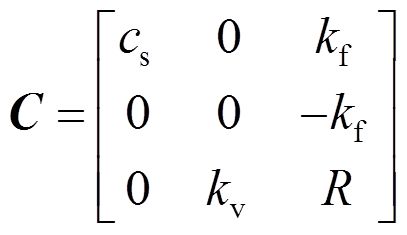 ,
,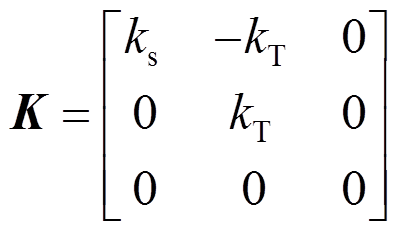 ,
,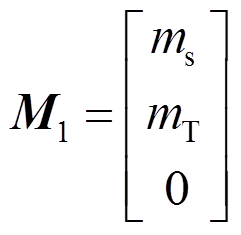 。
。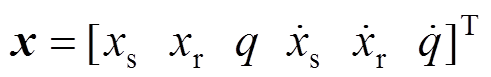 ,则状态方程为:
,则状态方程为: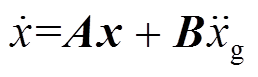 (25)
(25)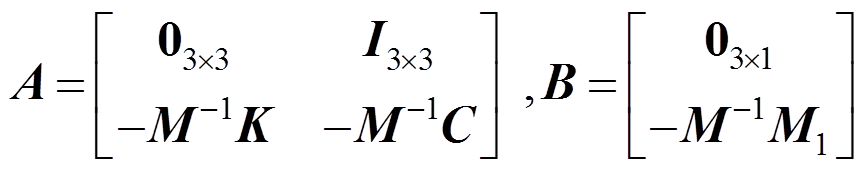 。
。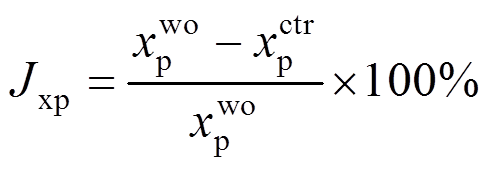 (26)
(26)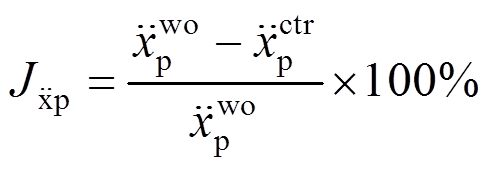 (27)
(27)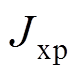 、
、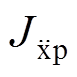 为地震作用下主结构相对位移和相对加速度峰值减震效果指标;
为地震作用下主结构相对位移和相对加速度峰值减震效果指标;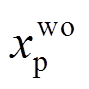 、
、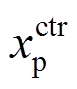 、
、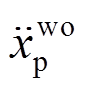 和
和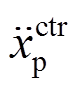 为结构无控与有控时的峰值位移,结构无控与有控时的峰值加速度
为结构无控与有控时的峰值位移,结构无控与有控时的峰值加速度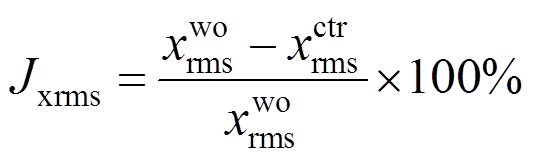 (28)
(28)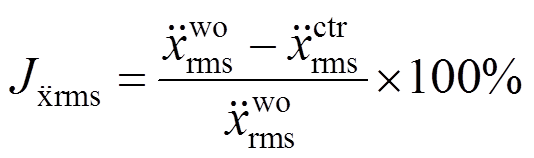 (29)
(29)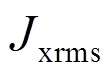 、
、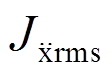 为地震作用下主结构相对位移和相对加速度均方根值减震效果指标;
为地震作用下主结构相对位移和相对加速度均方根值减震效果指标;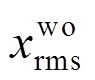 、
、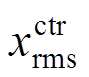 、
、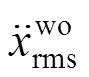 和
和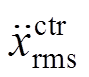 为结构无控与有控时的位移均方根值,结构无控与有控时的结构加速度均方根值
为结构无控与有控时的位移均方根值,结构无控与有控时的结构加速度均方根值