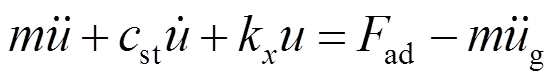 (1)
(1)摘 要:风力发电机受到的气动力作用表现为气动阻尼和空气动力荷载,对结构地震响应分别具有阻尼效应和动力效应。该文建立理论分析模型,考虑运行和停机两种工况,分析工作状态影响风力发电机地震响应的规律和机理;针对NREL 5 MW基准风机,采用FAST软件分析不同风-地震组合作用下风力发电机结构动力响应,验证理论分析结果的正确性;同时,分析输入地震动方向对风力发电机地震响应的影响。结果表明:工作状态对风力发电机地震响应的影响与地震动幅值和风速有关;强震作用下,停机状态地震单独作用为最不利工况;弱震作用下,额定风速-设计地震动组合是最不利荷载组合;输入地震动方向影响风力发电机动力响应。
关键词:地震响应;阻尼效应;动力效应;工作状态;风-地震组合
随着能源危机和人们环保意识的兴起,风能作为一种清洁可再生能源,在现代能源结构中的比例不断扩大[1-2]。20世纪90年代,风力发电在欧洲兴起;21世纪以来,随着兆瓦级风力发电机的出现,风力发电从北欧扩展至世界各地[3-4]。随着风力发电场在中国、美国等高地震危险性区域的建设,风电抗震受到研究者的关注[5-6]。
Zhao和Maißer[7]采用多体动力学方法分析运行状态风力发电机地震响应,发现PGA=0.056 g的地震动对塔架弯矩有显著影响。金鑫等[8]分析了风-地震作用下3.6 MW风力发电机的动力响应,发现地震作用效应超过风荷载。何玉林等[9]分析了风-地震共同作用下风力发电机地震响应,认为地震作用显著改变塔架响应。不同工作状态,风力发电机受到的气动力存在显著差异,因此,需考虑工作状态对其地震响应的影响。Witcher[10]采用一条人造波作为输入地震动,发现运行状态风-地震共同作用时塔顶位移幅值最大,停机时塔顶位移幅值最小。彭超[11]发现风-地震共同作用下风力发电机的地震响应大于应急停机状态,但也仅采用一条人造波。少量地震波无法考虑地震动特性影响,因此,所得结论不具有普遍性。
为考虑地震动随机性,研究者选取足够数量的地震波,分析不同工作状态风力发电机的地震响应。Asareh等[12]发现运行状态风-地震共同作用下,塔架地震响应超过停机状态,认为气动力作用增大结构响应。Yuan等[13]认为运行状态风-地震共同激励下,气动力作用减小结构响应,停机状态结构最危险。研究者[12-13]采用同一软件,分析NREL 5 MW风力发电机的地震响应,但在工作状态对风力发电机地震响应的影响规律方面得出不同结论。Prowell 等[14]通过室外振动台试验,发现气动力作用使得风力发电机的地震响应小于停机状态,试验采用的最高风速仅为5.1 m/s,只能反映低风速时的规律。
研究者分析工作状态影响风力发电机地震响应时,主要采用数值模拟方法,未进行理论分析,试验研究只考虑了低风速的影响,结论也不一致。为研究工作状态影响风力发电机地震响应的规律和机理,确定最不利风-地震组合。本文建立理论模型,揭示工作状态影响风力发电机结构地震响应的规律,通过数值模拟方法验证其正确性;分析风荷载作用下风力发电机动力响应,初步探讨了输入地震动方向对风力发电机地震响应的影响。根据现有研究方法、结论及本文研究目的,建立分析模型,暂不考虑结构几何非线性的影响。
地震作用下,风力发电机发生往复运动。IEC 61400-1[15]提出一种等效单自由度(SDOF)模型,用于分析风力发电机地震响应。该模型假定叶轮为刚体,不考虑塔顶转动影响,将支撑结构作为弹性构件,系统简化为质量集中于塔顶的SDOF体系,如图1所示。运动方程为:
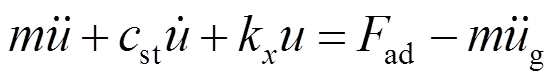 (1)
(1)式中:m为质量;u为塔顶相对塔底沿x方向(前后向)位移;cst为系统的结构阻尼系数;kx为刚度;SDOF体系参数根据IEC 61400-1[15]确定;Fad为气动力;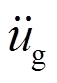 为x方向地震动加速度。
为x方向地震动加速度。
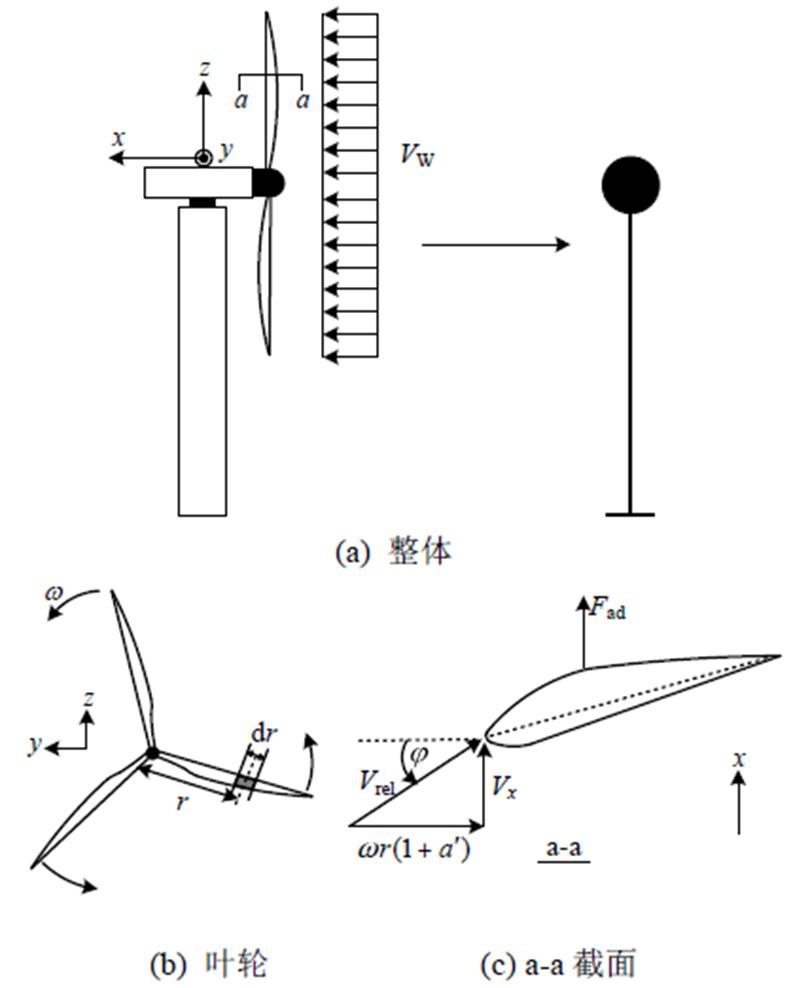
图1 分析模型
Fig.1 Analysis model
假设叶轮受水平均匀风作用,采用叶素动量理论[16],Fad为:
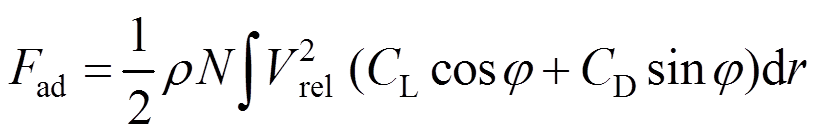 (2)
(2)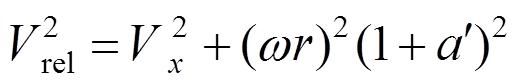 (3)
(3)
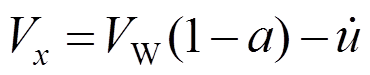 (4)
(4)
式中:ρ为空气密度;N为叶片数量;CL为升力系数;CD为阻力系数;φ为攻角;r为半径;ω为叶轮转动角速度;![]() 、
、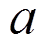 分别为切向、轴向速度诱导因子;VW为风速;
分别为切向、轴向速度诱导因子;VW为风速;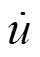 为叶轮前后向运动速度。
为叶轮前后向运动速度。
对于式(4),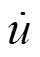 相对Vx为小量,将其作为Vx的增量。令
相对Vx为小量,将其作为Vx的增量。令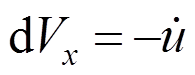 ,气动力Fad可分解为:
,气动力Fad可分解为:
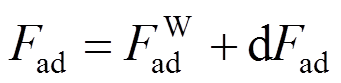 (5)
(5)式中: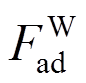 是风作用下,不考虑叶片前后向运动的气动力荷载;dFad是叶片前后向振动引起的气动力增量。
是风作用下,不考虑叶片前后向运动的气动力荷载;dFad是叶片前后向振动引起的气动力增量。
首先,考虑风作用产生的气动力荷载,令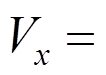
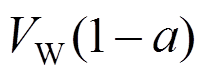 ,代入式(3),根据式(2)得:
,代入式(3),根据式(2)得:
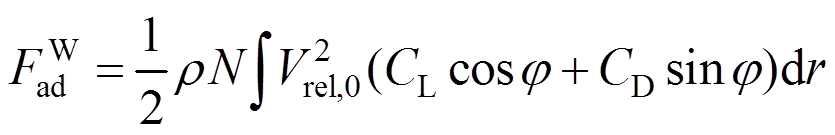 (6)
(6)式中: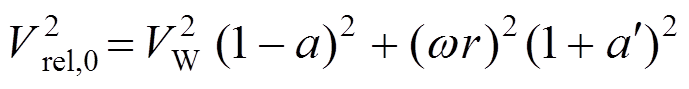 。
。
然后,考虑叶片振动引起的气动力增量,根据Valamanesh和Myers[17]提出的气动阻尼模型,气动力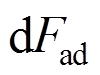 为:
为:
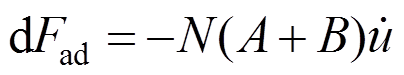 (7)
(7)式中: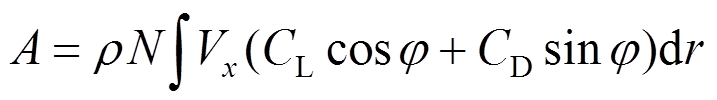 ;
;
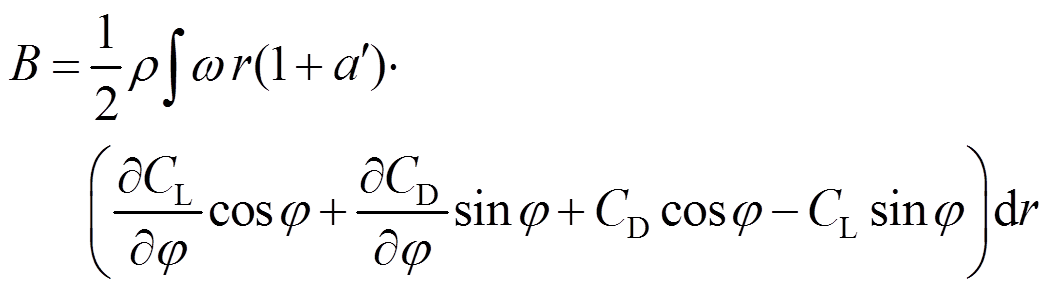
将式(6)和式(7)代入式(5),可得气动荷载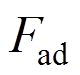 为:
为:
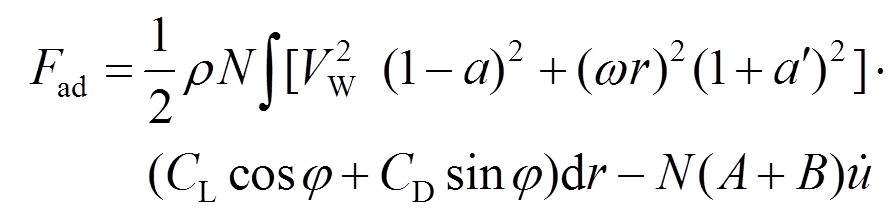 (8)
(8)由式(8)可知,叶轮受到的气动力可分解为气动荷载和气动阻尼两部分。
停机状态,气动力作用可忽略,系统运动方程式(1)简化为:
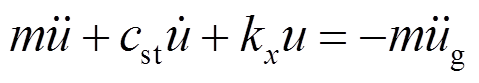 (9)
(9)运行状态,将式(8)代入式(1),可得风-地震共同作用下风力发电机运动方程。将其分解为:
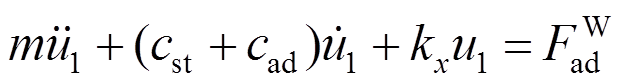 (10)
(10)
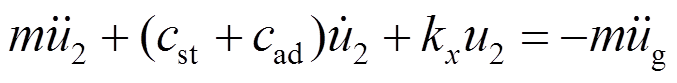 (11)
(11)式中: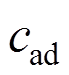 =N(A+B),是气动阻尼系数。运行状态,风-地震共同作用下风力发电机动力响应为式(10)、式(11)之和。
=N(A+B),是气动阻尼系数。运行状态,风-地震共同作用下风力发电机动力响应为式(10)、式(11)之和。
式(9)和式(11)为地震动激励下SDOF系统运动方程,式(9)对应停机状态,只有结构阻尼;式(11)对应运行状态,阻尼包含结构阻尼和气动阻尼。根据Valamanesh和Myers[17]的研究,cst取临界阻尼的1%,cad取临界阻尼的4%。阻尼差异使得式(11)的解小于式(9),即为气动力作用的阻尼效应。
给定参数,解式(9)~式(11),位移幅值记为:
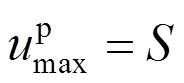 (12)
(12)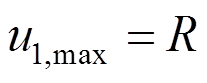 (13)
(13)
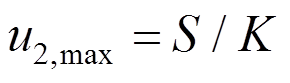 (14)
(14)
式中: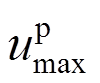 、
、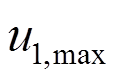 、
、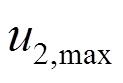 分别为式(9)、式(10)和式(11)的位移幅值。系统阻尼不同造成
分别为式(9)、式(10)和式(11)的位移幅值。系统阻尼不同造成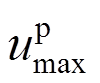 和
和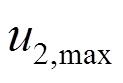 的差异,K为两者的比例系数,与地震动、结构特性等有关,取值大于1[18]。为获得风-地震共同作用时结构最大响应
的差异,K为两者的比例系数,与地震动、结构特性等有关,取值大于1[18]。为获得风-地震共同作用时结构最大响应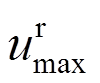 ,需要将
,需要将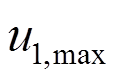 、
、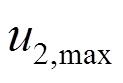 组合。Asareh 等[19]推荐了一种线性组合方法:
组合。Asareh 等[19]推荐了一种线性组合方法:
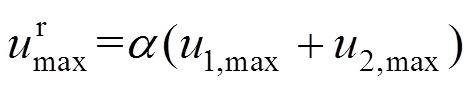 (15)
(15)式中: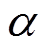 为荷载组合系数,取0.75。
为荷载组合系数,取0.75。
为判断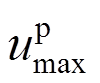 、
、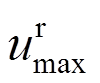 的大小,计算:
的大小,计算:
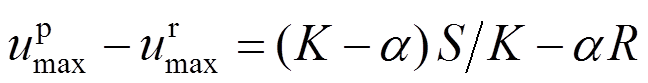 (16)
(16)式中: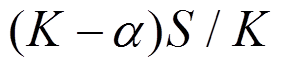 为气动阻尼减小的结构位移;
为气动阻尼减小的结构位移;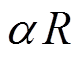 是风荷载做功引起的结构位移。
是风荷载做功引起的结构位移。
强震作用下,当地震动幅值较大,作用效应满足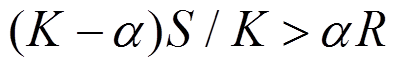 时,气动阻尼耗散的能量超过风荷载对风力发电机所做功,使得
时,气动阻尼耗散的能量超过风荷载对风力发电机所做功,使得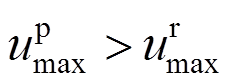 。相应的,停机状态风力发电机的其他响应也超过运行状态的取值。因此,停机状态为最不利工况,与Yuan 等[13]所得结论一致。
。相应的,停机状态风力发电机的其他响应也超过运行状态的取值。因此,停机状态为最不利工况,与Yuan 等[13]所得结论一致。
弱震作用下,当地震动幅值较小,作用效应满足 时,气动阻尼耗散的能量小于风荷载对风力发电机所做功,使得
时,气动阻尼耗散的能量小于风荷载对风力发电机所做功,使得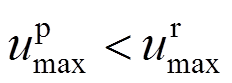 。对应的,运行状态风力发电机的其它响应也超过停机状态的数值。因此,风-地震共同作用的运行状态为最不利工况,与Asareh等[12]所得结论相同。
。对应的,运行状态风力发电机的其它响应也超过停机状态的数值。因此,风-地震共同作用的运行状态为最不利工况,与Asareh等[12]所得结论相同。
本节采用等效SDOF体系,发现工作状态对风力发电机地震响应的影响与地震幅值有关,为Asareh等[12]和Yuan等[13]的研究结论提出统一解释。同时,季亮等[20]比较了IEC 61400-1[15]等效SDOF模型与有限单元法分析风力发电机地震响应的差异,认为等效SDOF模型误差约为10%,满足初步设计需要。因此,上述模型及结论具有可靠性。但该模型未考虑叶轮变形、传动及控制系统的影响。为验证结论,给出强、弱震界限,下节采用FAST软件[21],通过多体动力学方法分析风力发电机地震响应。
美国可再生能源实验室(National Renewable Energy Laboratory, NREL)开发了额定功率为5 MW的风力发电机[22],如图2(a)所示,采用可变速发电机、变桨距控制技术,部分参数见表1。以塔架材料屈服作为承载力极限状态,根据结构几何、物理参数,可得塔顶极限位移为2.42 m,塔底极限弯矩为307 MN·m[13]。
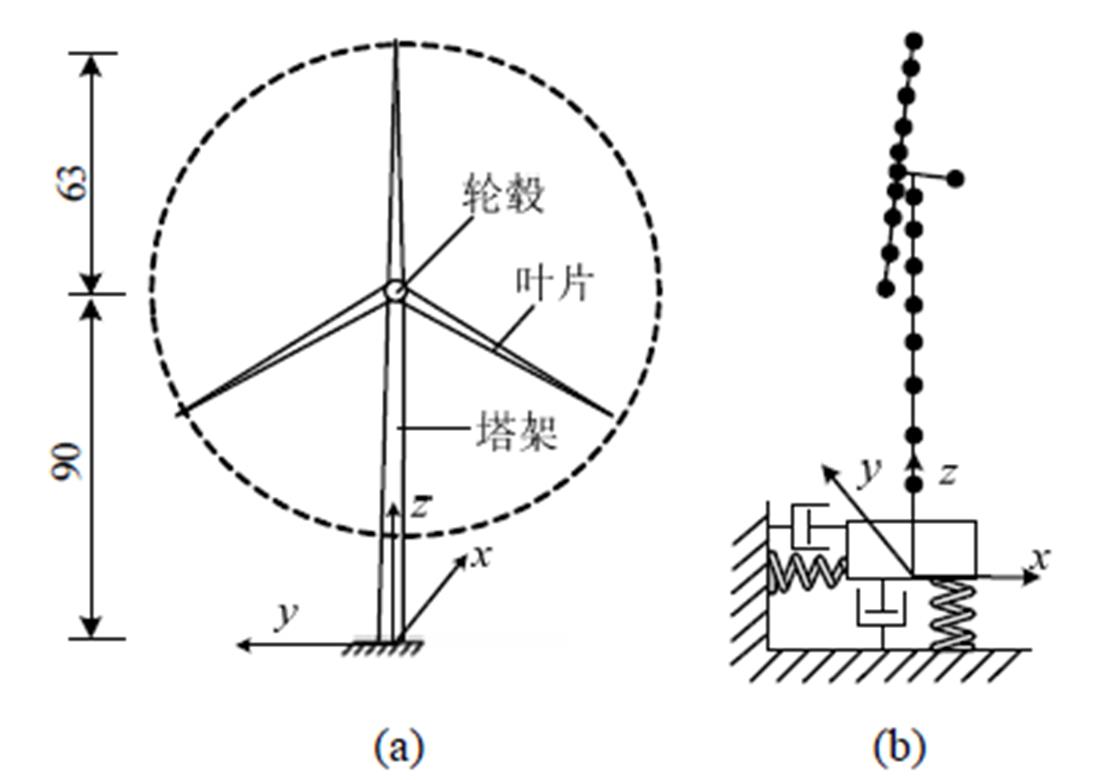
图2 NREL 5 MW基准风力发电机
Fig.2 NREL 5 MW baseline wind turbine
表1 NREL 5 MW基准风机特性
Table 1 Specifications of NREL 5 MW wind turbine
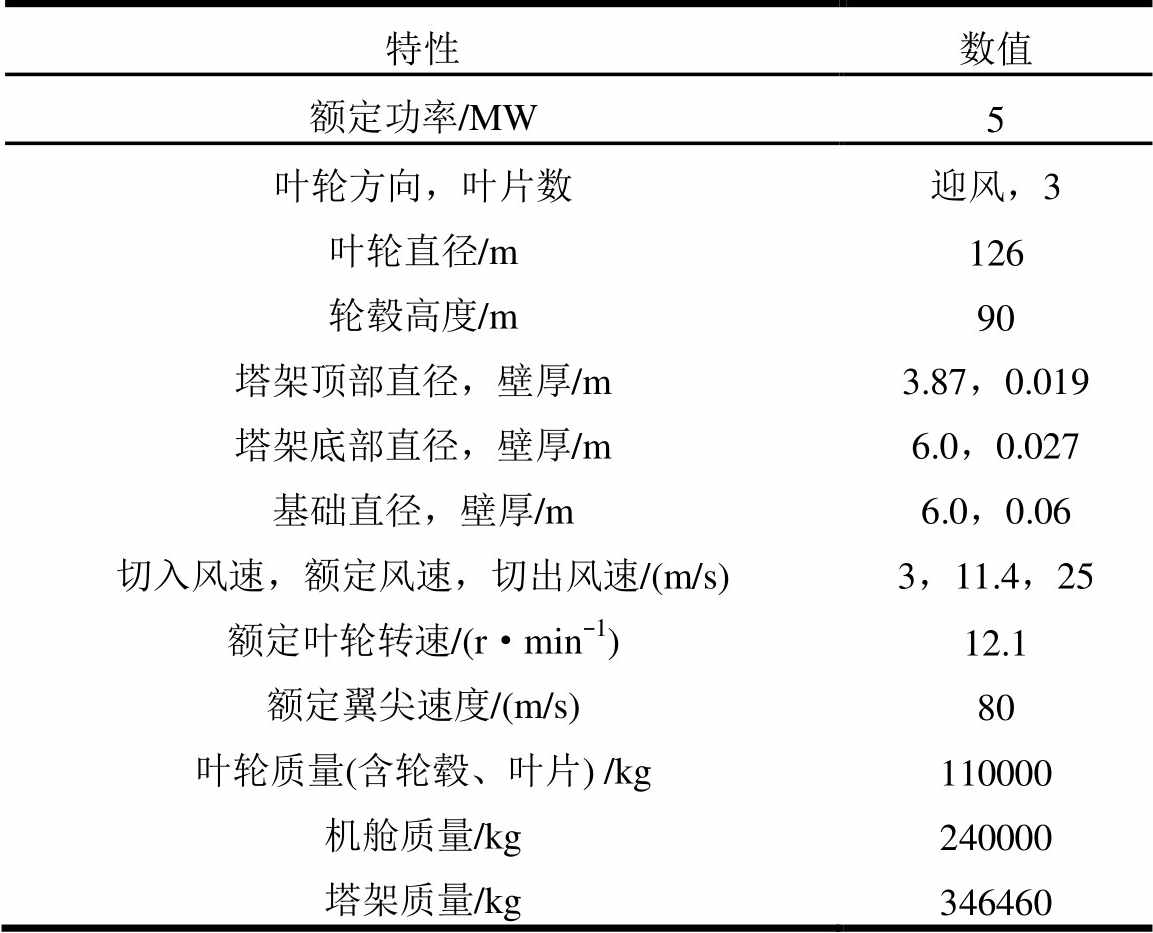
特性数值 额定功率/MW5 叶轮方向,叶片数迎风,3 叶轮直径/m126 轮毂高度/m90 塔架顶部直径,壁厚/m3.87,0.019 塔架底部直径,壁厚/m6.0,0.027 基础直径,壁厚/m6.0,0.06 切入风速,额定风速,切出风速/(m/s)3,11.4,25 额定叶轮转速/(r·min−1)12.1 额定翼尖速度/(m/s)80 叶轮质量(含轮毂、叶片) /kg110000 机舱质量/kg240000 塔架质量/kg346460
Asareh等[12]利用FAST软件,在塔底添加弹簧和阻尼器,通过地震动激励下弹簧、阻尼器作用于塔底的荷载实现地震动输入,如图2(b)所示。弹簧刚度k=m(2πf )2,阻尼器粘滞阻尼系数c=2m(2πf )ξ,阻尼比ξ取0.67,频率f取30 Hz,系统质量m取696460 kg。
结构采用梁单元,为计算气动力,塔架分为20个等长度单元;每个叶片沿轴线从翼根至翼尖分为17个单元,长度为:3个长2.73 m、11个长4.1 m和3个长2.73 m。采用振型分解法计算塔架、叶片变形,需提供振型函数。塔架前后向、侧向运动及叶片挥舞运动考虑各自前2阶振型,叶轮摆振运动考虑1阶振型。分别沿塔架、叶片轴线建立局部坐标轴r,将长度单位化,塔底、翼根坐标为0,塔顶、翼尖坐标为1。振型函数表示为位置r的6阶多项式,系数见表2和表3。
表2 塔架振型
Table 2 Tower mode shape
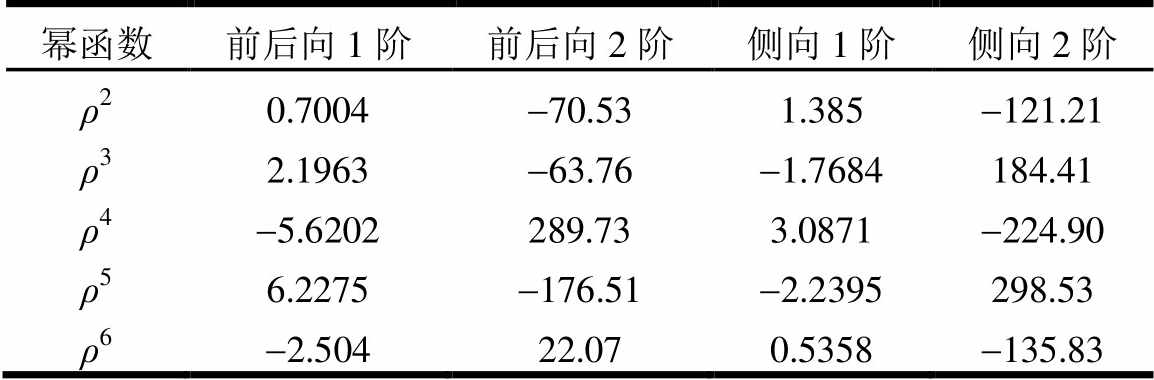
幂函数前后向1阶前后向2阶侧向1阶侧向2阶 ρ20.7004-70.531.385-121.21 ρ32.1963-63.76-1.7684184.41 ρ4-5.6202289.733.0871-224.90 ρ56.2275-176.51-2.2395298.53 ρ6-2.50422.070.5358-135.83
表3 叶轮振型
Table 3 Blade mode shape
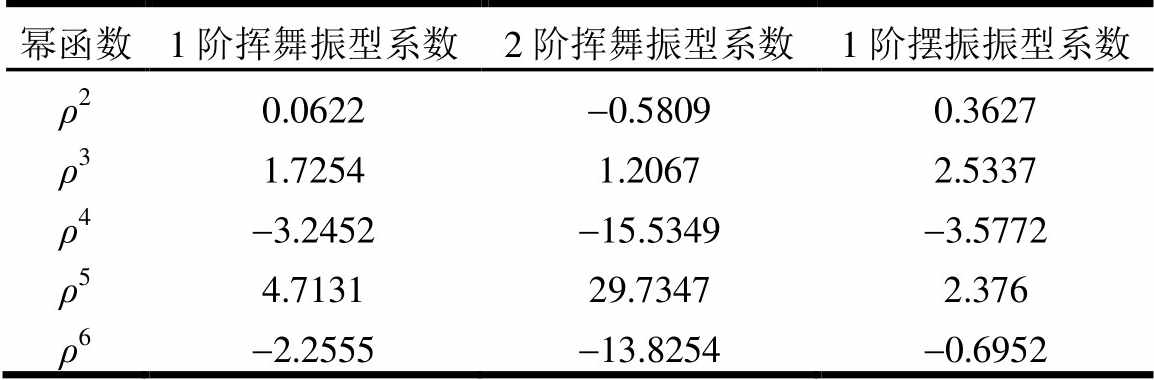
幂函数1阶挥舞振型系数2阶挥舞振型系数1阶摆振振型系数 ρ20.0622-0.58090.3627 ρ31.72541.20672.5337 ρ4-3.2452-15.5349-3.5772 ρ54.713129.73472.376 ρ6-2.2555-13.8254-0.6952
为考虑停机、运行两种工作状态,轮毂高度处10 min平均风速分别取2 m/s,5 m/s,7 m/s,9 m/s,11.4 m/s,13 m/s,15 m/s,18 m/s,21 m/s,24 m/s。根据IEC 61400-1[15]的建议,平均风速沿高度变化采用幂函数,地面粗糙度指数α取0.2,平均风速U(z)为:
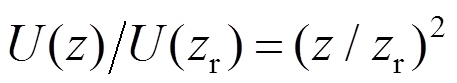 (17)
(17)式中:z为高度,采用图2所示坐标系;zr为参考高度,取轮毂高度,即zr=90 m;U(zr)为参考高度处平均风速。脉动风速功率谱采用Kaimal谱,湍流强度为B类。风速场总时长取为700 s,利用Turbsim软件,采用随机相位,共生成38个三维风速场。
选择两组地震动,第1组地震动为ATC-63的远场地震动[23],见表4。NREL 5 MW风力发电机前后向基准周期达3.1 s,第2组地震动从PEER强震数据库选择,具有较丰富的长周期成分,见表5。
表4、表5中F-x、F-y为x、y方向输入地震动在PEER强震数据库的文件名;Sa为结构基准周期T1对应5%阻尼比加速度反应谱值,可记为Sa(T1, 0.05)。地震动PGA变化区间为[0.1 g, 0.8 g],Sa(T1, 0.05)变化范围为[0.05 g, 0.5 g]。分析NREL 5MW风力发电机地震响应时,计算时长取600 s,时间步长取0.005 s,为避免初始条件影响,地震动在400 s输入。塔底作为固定端,不考虑场地影响。
表4 第1组地震动特性
Table 4 Characteristics of first set ground motions
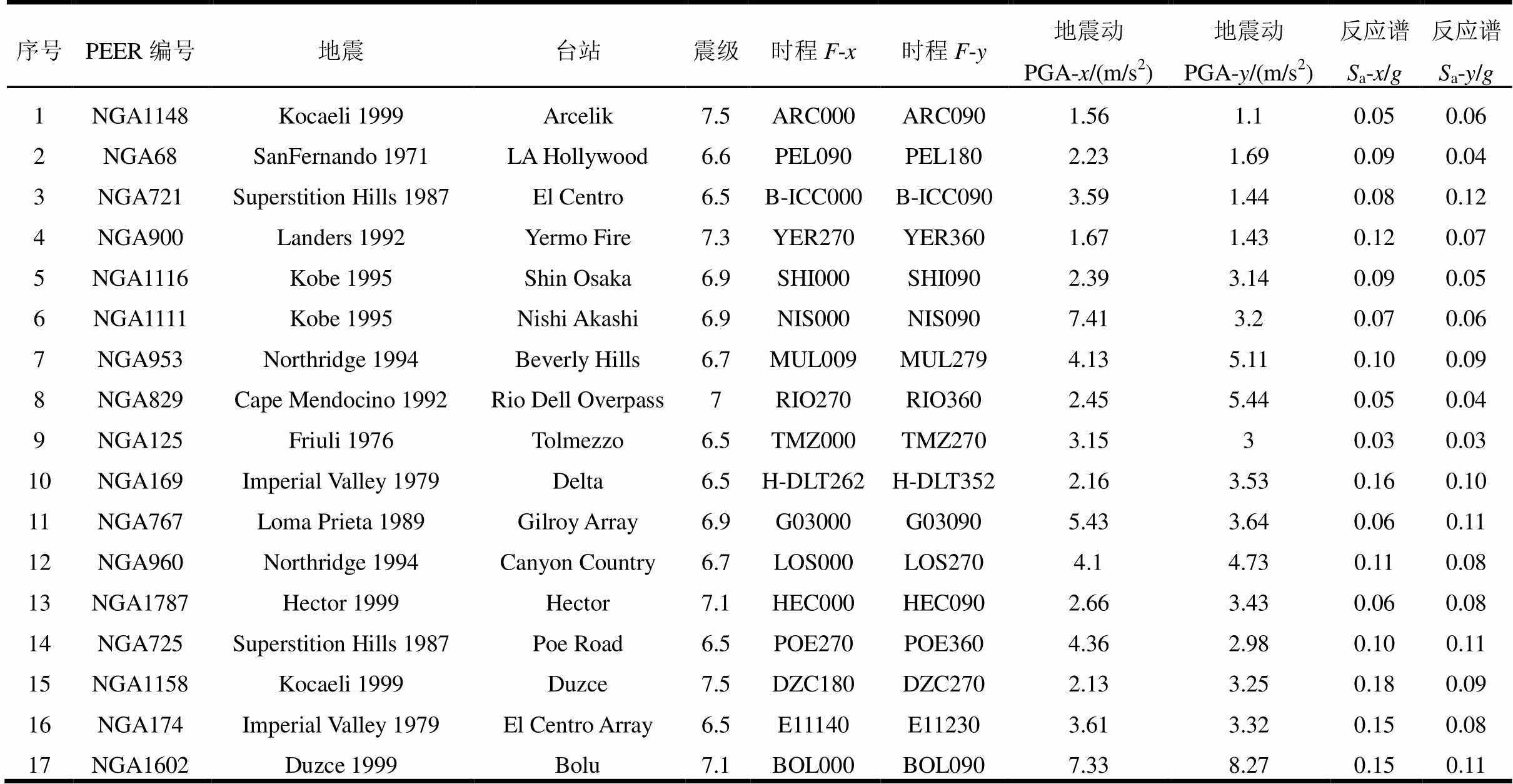
序号PEER编号地震台站震级时程F-x时程F-y地震动 PGA-x/(m/s2)地震动 PGA-y/(m/s2)反应谱Sa-x/g反应谱Sa-y/g 1NGA1148Kocaeli 1999Arcelik7.5ARC000ARC0901.561.10.05 0.06 2NGA68SanFernando 1971LA Hollywood6.6PEL090PEL1802.231.690.09 0.04 3NGA721Superstition Hills 1987El Centro6.5B-ICC000B-ICC0903.591.440.08 0.12 4NGA900Landers 1992Yermo Fire7.3YER270YER3601.671.430.12 0.07 5NGA1116Kobe 1995Shin Osaka6.9SHI000SHI0902.393.140.09 0.05 6NGA1111Kobe 1995Nishi Akashi6.9NIS000NIS0907.413.20.07 0.06 7NGA953Northridge 1994Beverly Hills6.7MUL009MUL2794.135.110.10 0.09 8NGA829Cape Mendocino 1992Rio Dell Overpass7RIO270RIO3602.455.440.05 0.04 9NGA125Friuli 1976Tolmezzo6.5TMZ000TMZ2703.1530.03 0.03 10NGA169Imperial Valley 1979Delta6.5H-DLT262H-DLT3522.163.530.16 0.10 11NGA767Loma Prieta 1989Gilroy Array6.9G03000G030905.433.640.06 0.11 12NGA960Northridge 1994Canyon Country 6.7LOS000LOS2704.14.730.11 0.08 13NGA1787Hector 1999Hector7.1HEC000HEC0902.663.430.06 0.08 14NGA725Superstition Hills 1987Poe Road6.5POE270POE3604.362.980.10 0.11 15NGA1158Kocaeli 1999Duzce7.5DZC180DZC2702.133.250.18 0.09 16NGA174Imperial Valley 1979El Centro Array6.5E11140E112303.613.320.15 0.08 17NGA1602Duzce 1999Bolu7.1BOL000BOL0907.338.270.15 0.11
表5 第2组地震动特性
Table 5 Characteristics of second set ground motions
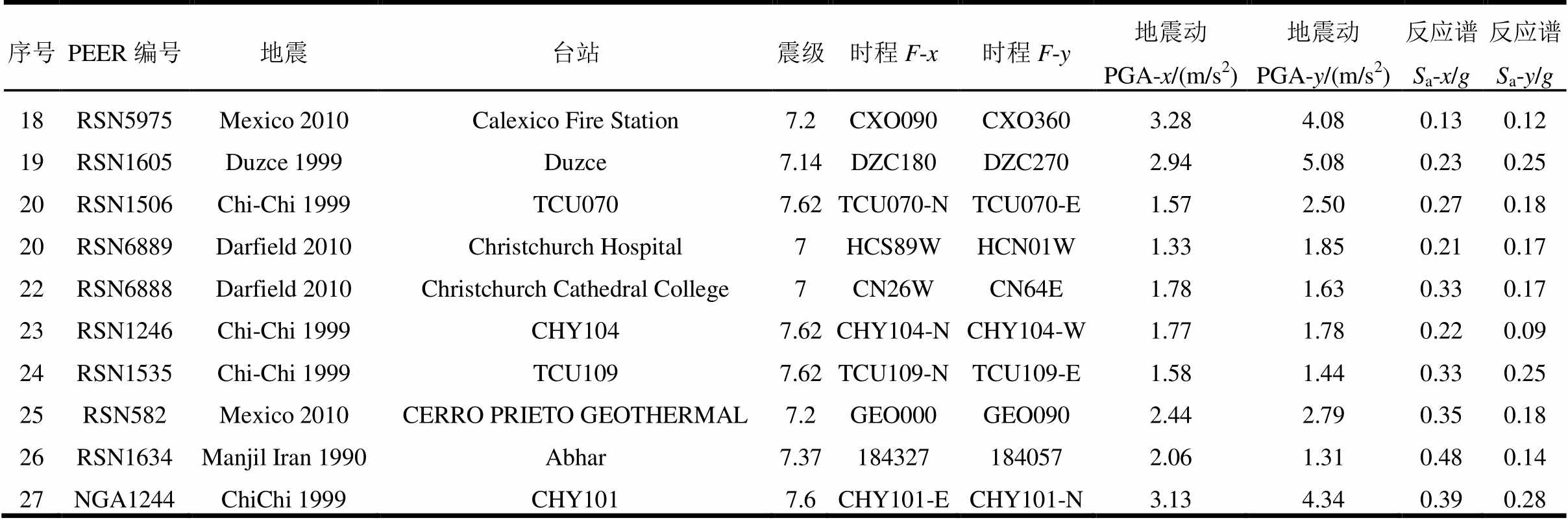
序号PEER编号地震台站震级时程F-x时程F-y地震动 PGA-x/(m/s2)地震动 PGA-y/(m/s2)反应谱Sa-x/g反应谱Sa-y/g 18RSN5975Mexico 2010Calexico Fire Station7.2CXO090CXO3603.284.080.130.12 19RSN1605Duzce 1999Duzce7.14DZC180DZC2702.945.080.230.25 20RSN1506Chi-Chi 1999TCU0707.62TCU070-NTCU070-E1.572.500.270.18 20RSN6889Darfield 2010Christchurch Hospital7HCS89WHCN01W1.331.850.210.17 22RSN6888Darfield 2010Christchurch Cathedral College7CN26WCN64E1.781.630.330.17 23RSN1246Chi-Chi 1999CHY1047.62CHY104-NCHY104-W1.771.780.220.09 24RSN1535Chi-Chi 1999TCU1097.62TCU109-NTCU109-E1.581.440.330.25 25RSN582Mexico 2010CERRO PRIETO GEOTHERMAL7.2GEO000GEO0902.442.790.350.18 26RSN1634Manjil Iran 1990Abhar7.371843271840572.061.310.480.14 27NGA1244ChiChi 1999CHY1017.6CHY101-ECHY101-N3.134.340.390.28
为比较地震和风荷载作用效应,采用2.2节风速场,分析风荷载作用下结构动力响应。塔底剪力幅值如图3所示,Fsx、Fsy分别为x方向(前后向)、y方向(侧向)剪力,风速主方向沿x轴。由图3可知,Fsx远大于Fsy;风速等于11.4 m/s(额定风速)时,Fsx取最大值900 kN。
图4为塔底弯矩幅值,Mtwx为x轴弯矩,由y方向的横向荷载引起;Mtwy为y轴弯矩,由x方向的横向荷载引起。由图4可知,Mtwy远大于Mtwx,风荷载作用下,可只考虑前后向风荷载引起的弯矩。与剪力相同,风速等于额定风速时,Mtwy取最大值80 MN· m。
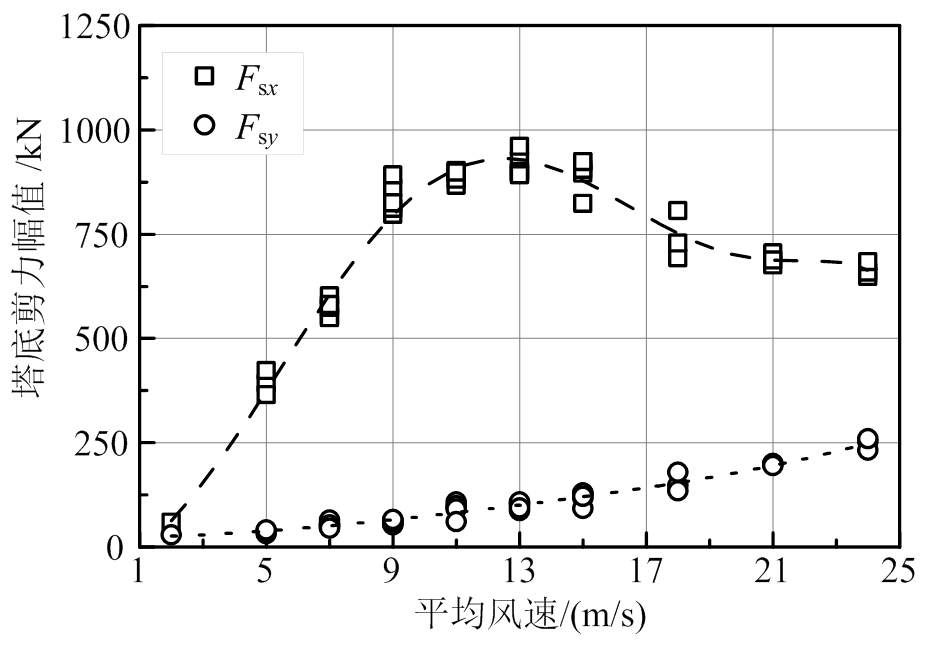
图3 塔底剪力幅值
Fig.3 Maximum base shear
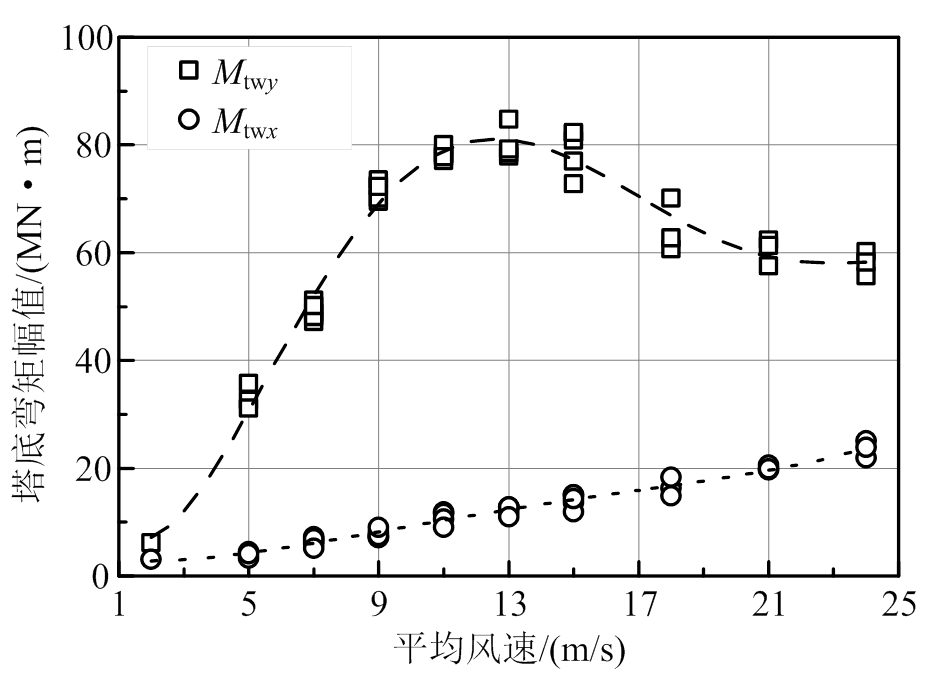
图4 塔底弯矩幅值
Fig.4 Maximum base moment
以NREL 5 MW风力发电机为代表的现代风机普遍采用变桨距控制。轮毂高度处平均风速低于额定风速时,桨距角不变,随风速增大,作用于风力发电机叶轮、塔架上的风荷载递增;风速超过额定风速时,为避免结构损伤,变桨距控制系统通过增大桨距角控制叶轮的气动力,使得作用于叶轮的气动推力随风速递减。因此,变桨距控制造成了塔底剪力、弯矩幅值等随平均风速的非单调变化。
将第1组地震动与风速场组合,分析风力发电机动力响应。图5是塔底剪力幅值,风-地震共同作用下,其最大值为3100 kN,超过风荷载作用效应,因此,地震作用显著增大塔底剪力。同时,风-地震共同作用下,平均风速低于额定风速时,塔底剪力幅值随风速单调递增;平均风速超过额定风速时,塔底剪力幅值随风速单调递减。变桨距操作使得平均风速等于额定风速时气动力最大。因此,运行状态风-地震共同作用下,平均风速等于额定风速时,塔底剪力幅值最大。
由图5可知,额定风速-地震作用下,塔底剪力幅值超过地震单独作用效应。部分风-地震组合,风速较低时,剪力幅值小于地震单独作用时的数值;随风速增大,剪力幅值增大,其最大值超过地震单独作用时的取值,如10号、13号和15号地震动。
图6是塔顶相对位移幅值,运行状态风-地震共同作用下,由于变桨距操作的影响,风速等于额定风速时,其值最大。部分风-地震组合,风速较低时,塔顶相对位移小于地震动单独作用;随风速增大,塔顶相对位移幅值增大,其最大值超过停机状态地震作用效应,如3号、4号和16号地震动。
图7是塔底弯矩幅值,风-地震共同作用下,其最大值为170 MN·m,超过风荷载作用效应。由于采用变桨距控制,平均风速等于额定风速时,塔底弯矩幅值最大,超过停机状态地震作用效应。
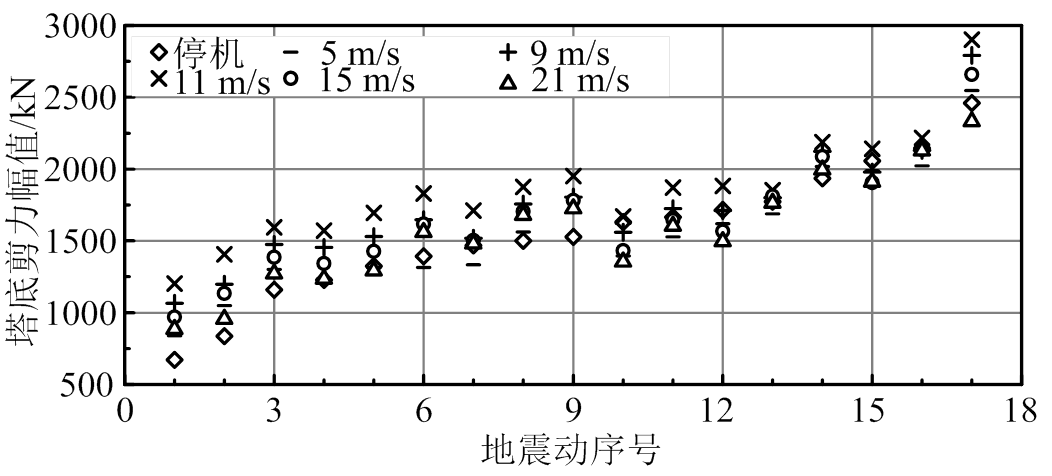
图5 塔底剪力幅值
Fig.5 Maximum base shear
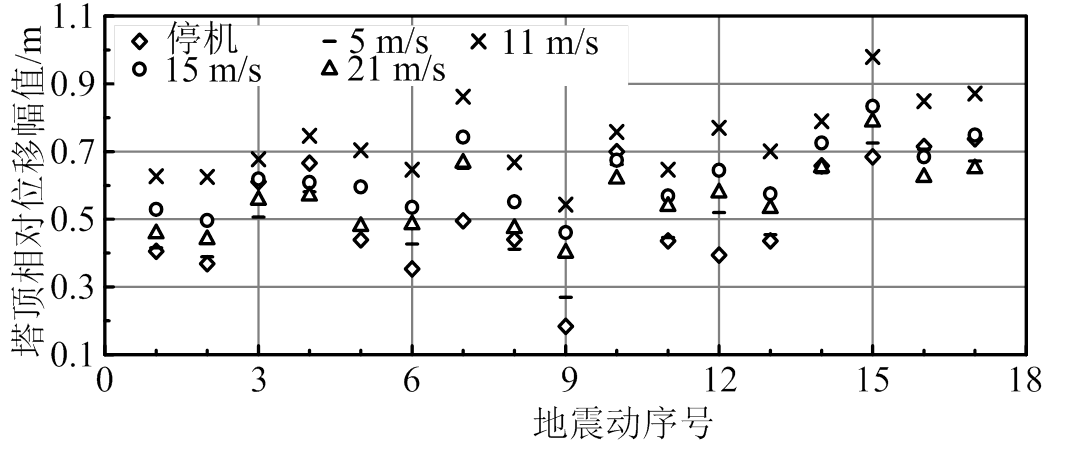
图6 塔顶相对位移幅值
Fig.6 Maximum relative displacement of tower tip
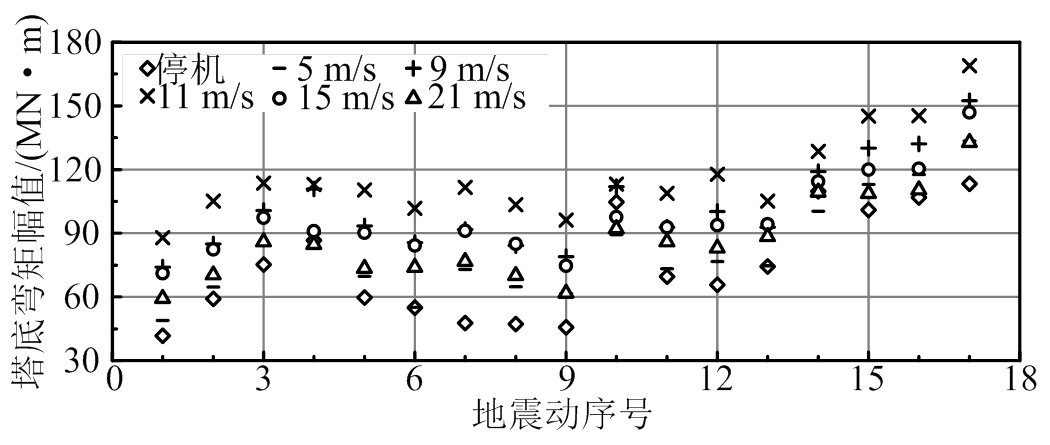
图7 塔底弯矩幅值
Fig.7 Maximum base moment
风速较低时,气动力作用的动力效应小,对风力发电机所做功小于气动阻尼消耗的能量,停机状态风力发电机的地震响应超过运行状态,与Prowell[14]的发现一致。随风速增大,气动力作用的动力效应超过阻尼效应,平均风速等于额定风速时,运行状态结构响应超过停机状态。因此,工作状态对风力发电机地震响应的影响与风速有关。
然后,将第2组地震动与风速场组合,分析风力发电机地震响应。NREL 5 MW风力发电机的基准周期达3.1 s,地震响应取决于输入地震动的长周期分量。图8、图9为塔底弯矩幅值Mtwy与x方向结构基准周期对应地震动加速度反应谱值Sa(T1, 0.05)、峰值加速度PGA的关系。
由图8、图9可知,塔底弯矩幅值与地震动Sa(T1, 0.05)线性相关性好;与地震动PGA相关性差,同一峰值加速度对应塔底弯矩幅值具有显著离散性。PGA取决于地震动的高频分量,不能反映长周期成分,而反应谱值Sa(T1, 0.05)能反映地震动长周期成分,因此,与塔底弯矩相关性好。
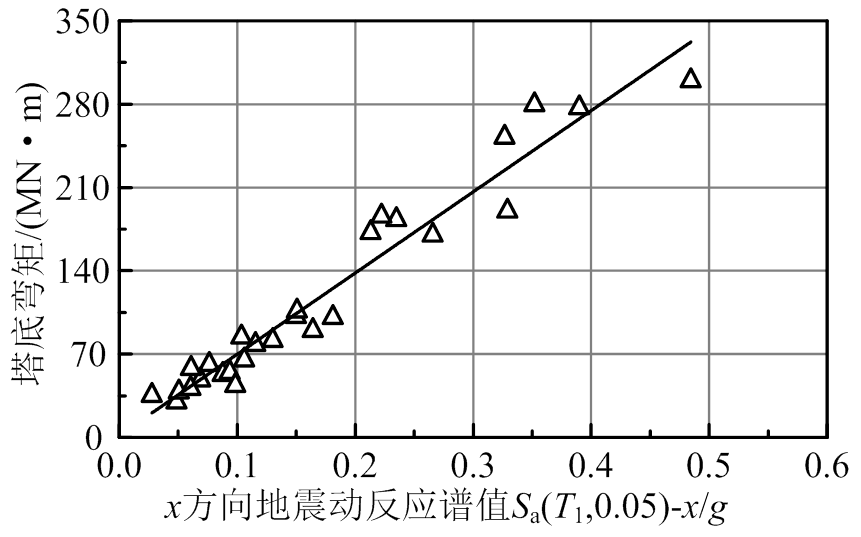
图8 塔底弯矩-加速度反应谱关系
Fig.8 Relationship between base moment and spectral acceleration
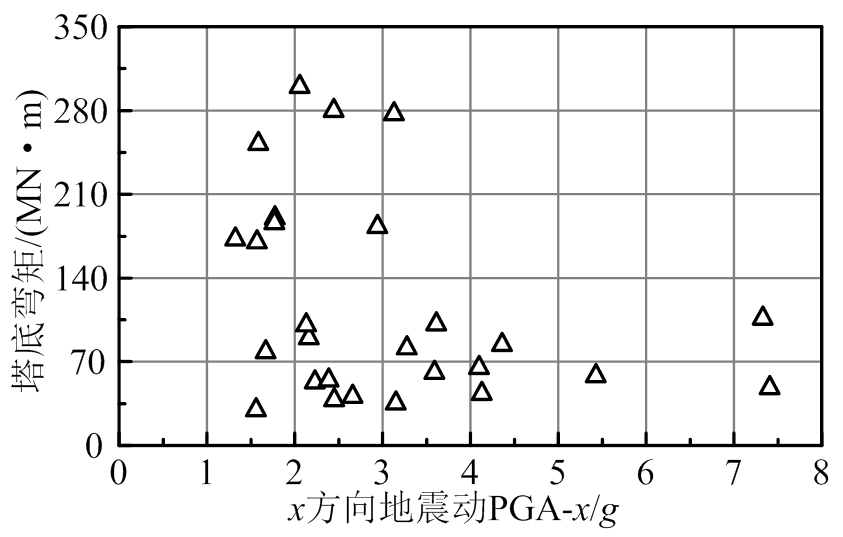
图9 塔底弯矩幅值-峰值加速度关系
Fig.9 Relationship between base moment and peak ground acceleration
图10为第2组地震动与风速场组合的塔顶相对位移幅值,对于19号~27号地震动,塔顶位移幅值较大,停机状态地震单独作用下,塔顶位移幅值超过运行状态。结合图6,弱震作用下,平均风速等于额定风速时,运行状态的塔顶位移幅值大于停机状态;强震作用下,规律相反。图11为第2组地震动与风速场组合的塔底弯矩幅值。对于19号~ 27号地震动,塔底弯矩幅值较大,停机状态地震单独作用下,其值超过运行状态。
根据图7和图11可知,表4、表5所选地震动与风速场组合,塔底弯矩幅值最大为322 MN·m,输入地震动时程为27号强震记录时取得。对于其余地震动,本文所采用的荷载组合作用下,塔底弯矩均小于其屈服值307 MN·m。此外,根据图6和图10,塔顶相对位移幅值均小于Yuan等[13]确定的屈服值。因此,前述计算结果符合弹性假设。
根据表4、表5,第1组地震动的加速度反应谱值Sa(T1, 0.05)总体小于第2组,对于NREL 5 MW风力发电机,第1组地震动为弱震,第2组地震动为强震。风力发电机结构地震响应表明:弱震激励下,运行状态为最不利工况;强震激励下,停机状态为最不利工况,与第2部分理论分析所得结论一致。同时,由于变桨距控制策略的影响,运行状态,风-地震共同作用下,当风速等于额定风速时,结构地震响应最大。
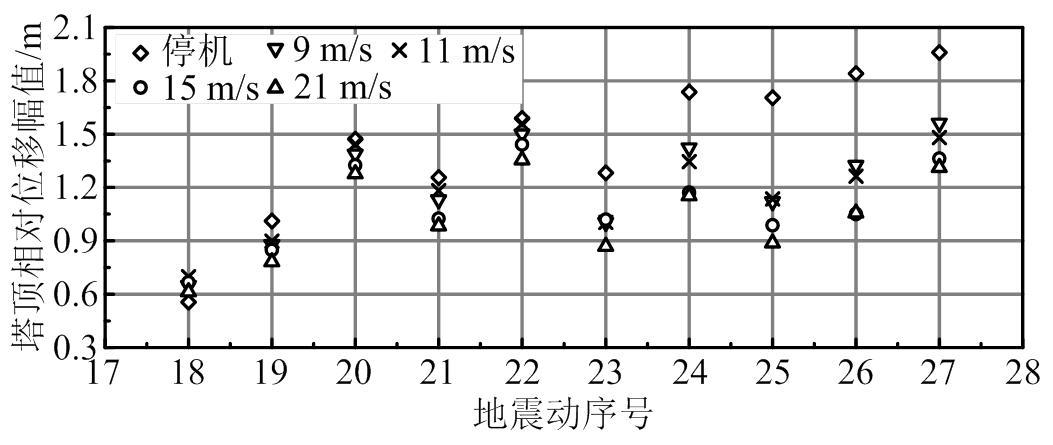
图10 塔顶相对位移幅值
Fig.10 Maximum relative displacement at tower top
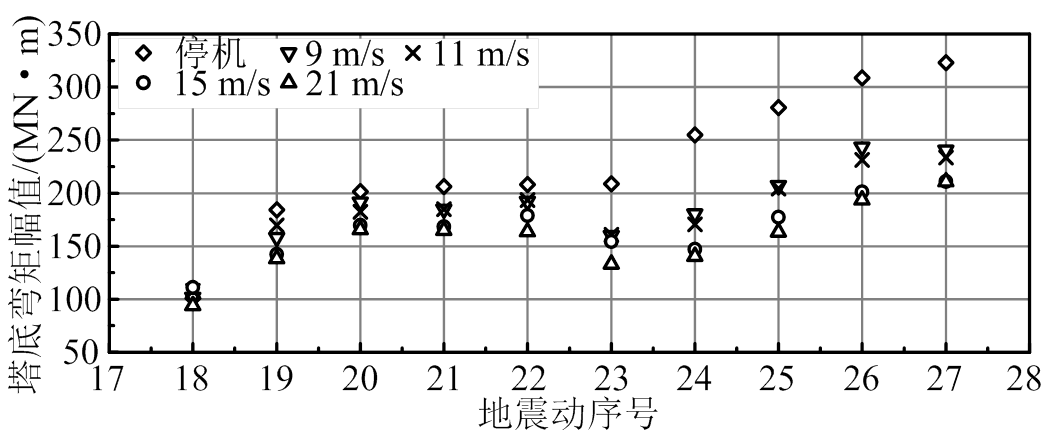
图11 塔底弯矩幅值
Fig.11 Maximum base moment
为进一步验证上述结论,以19号地震动为例,将地震动乘以折减系数,与风速场组合,分析风力发电机地震响应。定义弯矩系数K为:
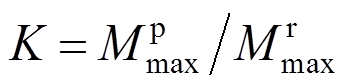 (18)
(18)式中: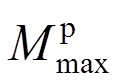 为停机状态塔底弯矩幅值;
为停机状态塔底弯矩幅值;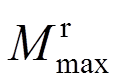 为运行状态,额定风速-地震作用下塔底弯矩幅值。K<1,运行工况为最不利工况;K>1,停机工况为最不利工况。
为运行状态,额定风速-地震作用下塔底弯矩幅值。K<1,运行工况为最不利工况;K>1,停机工况为最不利工况。
图12为弯矩系数与地震动折减系数关系,折减系数为0.3~0.8时,K<1,运行工况为最不利工况;折减系数为0.8~1.0时,弯矩系数K>1,停机状态为最不利工况。因此,地震动幅值小时,运行状态为最不利工况;地震动幅值大时,停机状态为最不利工况。
根据表4、表5地震动特性和NREL 5 MW风力发电机动力响应,以塔底弯矩幅值为指标,强、弱震界限为Sa(T1,0.05)=0.18 g。根据中国建筑抗震设计规范,对III类场地,采用第3组设计地震,该界限值相当于PGA=0.3 g的八度区设防地震[24]。因此,风力发电机地震响应分析需考虑风-地震共同作用。应当注意,由于结构动力特性差异及地震动复杂性,上述界限值仅适用于本文所选风力发电机和输入地震动。
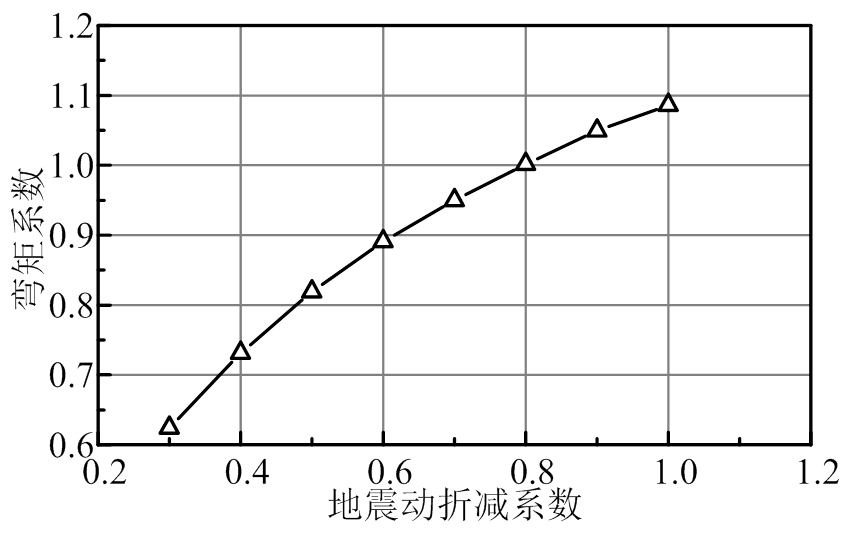
图12 地震动对塔底弯矩的影响
Fig.12 Effect of ground motion on maximum base moment
风力发电机处于运行状态时,气动力作用使得结构阻尼具有方向性[17]。为分析输入地震动方向的影响,交换表4、表5地震动方向。定义方向影响系数K:
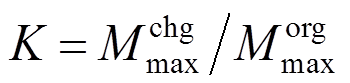 (19)
(19)式中: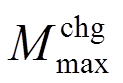 为交换输入地震动方向后塔底弯矩幅值;
为交换输入地震动方向后塔底弯矩幅值;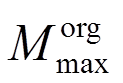 为不改变地震动方向的塔底弯矩幅值。
为不改变地震动方向的塔底弯矩幅值。
对第1组地震动,风速等于额定风速时,塔底弯矩幅值最大,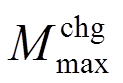 、
、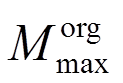 均取额定风速-地震作用时塔底弯矩幅值。图13为第1组地震动的方向影响系数,交换水平向地震动方向后,塔底弯矩幅值变化率最大为15%,是结构阻尼和动力特性方向性效应造成的。
均取额定风速-地震作用时塔底弯矩幅值。图13为第1组地震动的方向影响系数,交换水平向地震动方向后,塔底弯矩幅值变化率最大为15%,是结构阻尼和动力特性方向性效应造成的。
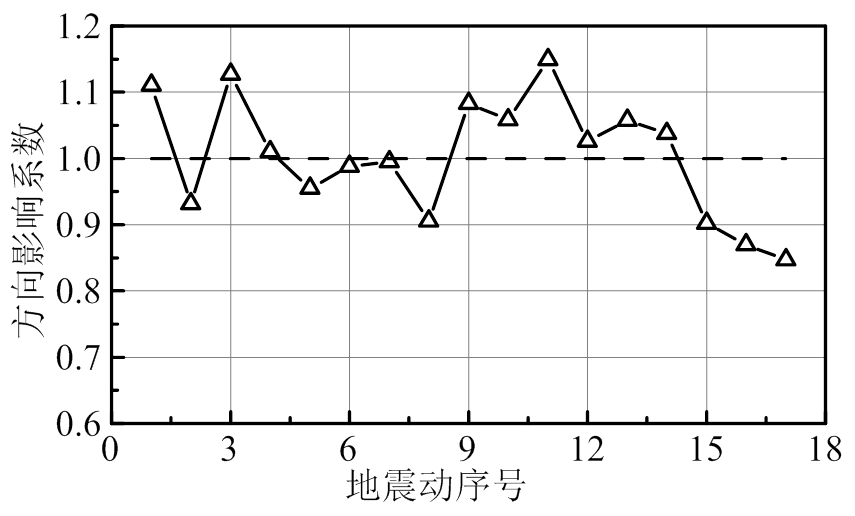
图13 第1组地震动方向影响
Fig.13 Effect of incident angles of first set ground motions
对第2组地震动,停机状态风力发电机塔底弯矩幅值最大,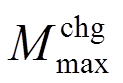 、
、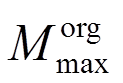 取停机状态塔底弯矩幅值。图14是第2组地震动的方向影响系数,总体小于第1组地震动。停机状态,气动阻尼不存在,输入地震动方向的影响取决于结构自振特性。
取停机状态塔底弯矩幅值。图14是第2组地震动的方向影响系数,总体小于第1组地震动。停机状态,气动阻尼不存在,输入地震动方向的影响取决于结构自振特性。
风和地震动的方向都具有随机性,为保证结构安全,在分析风力发电机地震响应时,应考虑输入地震动方向影响。对于确定性分析,可采用最不利输入地震动方向确定荷载作用效应;对于概率化分析,应考虑输入地震动方向的随机特性。
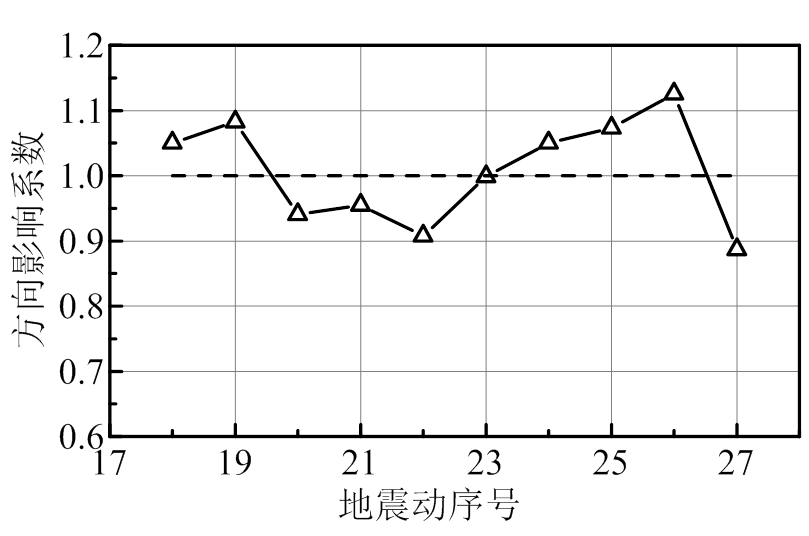
图14 第2组地震动方向影响
Fig.14 Effect of incident angles of second set ground motions
将地震动与风速场组合,采用理论分析和数值模拟方法,研究了工作状态对风力发电机地震响应的影响。通过对塔架剪力、弯矩、相对位移等参数的分析,得出以下结论:
(1) 工作状态对风力发电机地震响应的影响取决于气动力作用的动力效应和阻尼效应,动力效应增大结构反应,阻尼效应耗散能量,减小结构响应。平均风速等于额定风速时,叶轮受到的气动力作用最大。
(2) 风力发电机动力响应特性与风速场、地震动有关。强震作用下,停机状态地震单独作用为最不利工况;弱震作用下,额定风速-设计地震动是最不利荷载组合。算例表明:以塔底弯矩幅值为指标,NREL 5 MW风力发电机的强、弱震界限为Sa(T1, 0.05)=0.18 g。
(3) 弱震作用下,风速较低时,风-地震共同作用下结构响应可能小于停机状态地震作用效应;随风速增大,气动力作用的动力效应增强,平均风速等于额定风速时,结构动力响应最大,超过停机状态的地震作用效应。
(4) 气动力作用产生的阻尼效应使得风力发电机前后向、侧向阻尼具有显著差异,输入地震动方向影响结构动力响应。分析表明:对于第1组地震动,交换水平向输入地震动方向后,塔底弯矩幅值变化率最大为15%。
(5) 现代大型风力发电机基准周期较长,分析其地震响应时,地震动参数应能反映长周期成分,例如:结构基准周期对应加速度反应谱值Sa(T1)等。
本文研究了工作状态对风力发电机地震响应的影响,结论可用于确定风力发电机的最不利荷载。风力发电机抗震设计和地震响应分析,应根据场地地震危险性,考虑工作状态影响,选择合适的荷载组合。在分析输入地震动方向影响时仅交换地震动方向,应考虑更多的方向,以确定其影响规律。同时,本文采用现行规范推荐的地震动-风速场组合具有不同发生概率,从概率角度看,是不同概率荷载作用效应的比较。应建立具有相同发生概率的风-地震组合。此外,风-地震共同作用下,风力发电机叶片变形较大,本文及现有研究尚未考虑几何非线性的影响,在后续工作中,应针对该问题开展深入探讨。
参考文献:
[1] 许斌, 韩继龙. 预应力装配式风机叶片连接段结构模拟分析[J]. 工程力学, 2016, 33(2): 209-215.
Xu Bin, Han Jilong. Numerical simulation on a joint segment of a prestressed prefabricated sectional wind turbine blade model [J]. Engineering Mechanics, 2016, 33(2): 209-215. (in Chinese)
[2] BP. Energy outlook [EB/OL]. http://www. bp.com/, 2015, 2017-08-10.
[3] 李斌, 文昊天, 宫兆宇. 风力发电机塔筒风致响应分析与风振控制研究[J]. 工程力学, 2017, 34(增刊1): 134-138.
Li Bin, Wen Haotian, Gong Zhaoyu. Wind-induced response analysis and wind vibration control of a wind turbine tower drum [J]. Engineering Mechanics, 2017, 34(Suppl1): 134-138. (in Chinese)
[4] Dodge, D. Illustrated history of wind power development [EB/OL]. http://telosnet.com/wind, 2009, 2017-8-10.
[5] Sadowski A J, Camara A, Dai K. Seismic analysis of a tall metal wind turbine support tower with realistic geometric imperfections [J]. Earthquake Engineering & Structural Dynamics, 2017, 46(2): 201-219.
[6] Ghaemmaghami A R, Mercan O, Kianoush R. Seismic soil-structure interaction analysis of wind turbines in frequency domain [J]. Wind Energy, 2017, 20(1): 125-142.
[7] Zhao X, Maißer P. Seismic response analysis of wind turbine towers including soil structure interaction [J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multibody Dynamics, 2006, 220(1): 53-61.
[8] 金鑫, 王磊, 刘桦. 大功率风力发电机地震动力学建模及载荷计算[J]. 工程力学, 2012, 29(5): 224-229.
Jin Xin, Wang Lei, Liu Hua. A large scale wind turbine dynamic model and its load calculation in earthquake [J]. Engineering Mechanics, 2012, 29(5): 224-229. (in Chinese)
[9] 何玉林, 王磊, 杜静, 等. 地震作用下的风电机组振动仿真分析[J]. 太阳能学报, 2012, 33(2): 179-184.
He Yulin, Wang Lei, Du Jing, et al. Vibration simulation analysis of wind turbine under seismic load [J]. Acta Energiae Solaris Sinica, 2012, 33(2): 179-184. (in Chinese)
[10] Witcher D. Seismic analysis of wind turbines in the time domain [J]. Wind Energy, 2005, 8(1): 81-91.
[11] 彭超. 风力发电机组地震动力响应分析[J]. 太阳能学报, 2016, 37(12): 3189-3194.
Peng Chao. Seismic dynamic response analysis of wind turbine [J]. Acta Energiae Solaris Sinica, 2016, 37(12): 3189-3194. (in Chinese)
[12] Asareh M A, Schonberg W, Volz J. Effects of seismic and aerodynamic load interaction on structural dynamic response of multi-megawatt utility scale horizontal axis wind turbines [J]. Renewable Energy, 2016(86): 49-58.
[13] Yuan C, Chen J, Li J, et al. Fragility analysis of large-scale wind turbines under the combination of seismic and aerodynamic loads [J]. Renewable Energy, 2017(113): 1122-1134.
[14] Prowell I, Elgamal A, Uang C M, et al. Shake table testing and numerical simulation of a utility-scale wind turbine including operational effects [J]. Wind Energy, 2014, 17(7): 997-1016.
[15] IEC 61400-1, Wind Turbines Part 1: Design requirements [S]. Geneva: International Electrotechnical Commission, Switzerland, 2005.
[16] Hansen M O L. Aerodynamics of wind turbines [M]. London: Earthscan, 2015: 27-40.
[17] Valamanesh V, Myers A T. Aerodynamic damping and seismic response of horizontal axis wind turbine towers [J]. Journal of Structural Engineering, 2014, 140(11): 04014090-1-04014090-9.
[18] 谢闽生, 麦淑良. 阻尼对加速度反应谱影响的进一步研究[J]. 华侨大学学报自然科学版, 1988, 9(3): 340-345.
Xie Minsheng, Mai Shuliang. A further study of the influence of damping on response spectrum [J]. Journal of HuaQiao University (Natural science), 1988, 9(3): 340-345. (in Chinese)
[19] Asareh M A, Prowell I, Volz J, et al. A computational platform for considering the effects of aerodynamic and seismic load combination for utility scale horizontal axis wind turbines [J]. Earthquake Engineering and Engineering Vibration, 2016, 15(1): 91-102.
[20] 季亮, 祝磊, 姚小芹, 等. 现有风力发电机组地震作用计算方法对5 MW风力发电机组的适用性研究[J]. 太阳能学报, 2014, 35(11): 2300-2305.
Ji Liang, Zhu Lei, Yao Xiaoqin, et al. Applicability of existing seismic calculation methods for wind turbines on a 5 MW of wind turbine [J]. Acta Energiae Solaris Sinica, 2014, 35(11): 2300-2305. (in Chinese)
[21] Jonkman J M, Buhl M L. FAST user’s guide [R]. Colorado: National Renewable Energy Laboratory, 2005.
[22] Jonkman J M, Butterfield S, Musial W, et al. Definition of a 5 MW Reference wind turbine for offshore system development [R]. Colorado: National Renewable Energy Laboratory, 2009.
[23] FEMA P-695. Quantification of building seismic performance factors [R]. Redwood City: Applied Technology Council, 2009.
[24] GB 50011-2011, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.
GB 50011-2011, Code for seismic design of building [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
EFFECTS OF OPERATING CONDITIONS ON THE SEISMIC RESPONSE OF WIND TURBINES
Abstract: Aerodynamic loading of wind turbines can be divided into aerodynamic damping and dynamic loading which have damping effect and dynamic effect on the seismic response of structures, respectively. A theoretical model is set up for analyzing the regularities and mechanism of how operating conditions affect the seismic response of wind turbine considering the running and parked conditions. The dynamic response of wind turbines is analyzed using FAST software under different wind-earthquake combinations for NREL baseline 5 MW wind turbines to validate the findings obtained in the theoretical model. The effects of input earthquake direction on the seismic response of wind turbines are analyzed. The results show that the effect of operating condition on the dynamic response of wind turbines depends on the seismic amplitude and wind speed. The most unfavorable load combination is seismic excitation in parked condition under strong ground motions. When the seismic action is weaker, it is the rated wind speed-design seismic action combination. The incident angle of earthquake waves significantly affects the dynamic response of wind turbines.
Key words: seismic response; damping effect; dynamic effect; operating condition; wind-earthquake combination
文章编号:1000-4750(2019)04-0080-09
中图分类号:TK89
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.12.0939
收稿日期:2017-12-11;
修改日期:2018-05-17
基金项目:国家自然科学基金创新群体项目(51421005);国家自然科学基金优秀青年科学基金项目(51722801);国家自然科学基金青年科学基金项目(51808061)
杜修力(1962―),男,四川人,教授,博士,博导,主要从事地震工程领域研究工作(E-mail: duxiuli@bjut.edu.cn);
许 坤(1988―),男,山东人,讲师,博士,主要从事桥梁与结构抗风研究(E-mail: xukun@bjut.edu.cn).