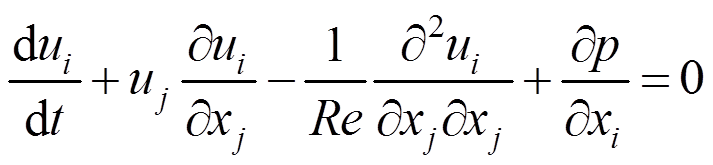 (1)
(1)摘 要:利用谐波合成法生成粗网格的脉动风速时程,通过双线性插值得到入口节点时程数据,考虑时程互相关性对时程进行修正得到大涡模拟湍流入口。采用谱元法对两种不同坡度的三维山丘地形进行大涡数值模拟,将结果与风洞试验及有限体积法数值模拟进行对比。结果表明:大涡模拟能较准确地预测山丘地形的风场及湍流特性;与有限体积法相比,谱元法的计算效率更高,在复杂山地地形的风场预测上有较好的应用前景。
关键词:谐波合成法;湍流入口;谱元法;有限体积法;三维山丘地形;风洞试验
准确预测山地地形的风场风速分布,对于山区建筑物选址、风机选址、风能资源评估和风力发电量预测等均十分重要。湍流大气边界层风场流经山地地形时,由于地面的隆起或下降,通常伴随着非常复杂的流动现象,如撞击、分离、环绕、再附着、漩涡脱落等,使得风速预测变得困难。
目前关于山地地形的研究方法主要包括理论模型[1-4]、风洞试验[5―8]和数值模拟[9―13]。随着计算机能力的提升,数值模拟方法发展迅速,根据湍流模型通常可分为雷诺时均法(reynolds averaged turbulence model, RANS)和大涡模拟法(large eddy simulation, LES)。RANS能高效且较准确地得到平均风场,但无法获得瞬态风场,不适用于动力特性及疲劳特性的研究;LES可以较准确得到风场的时均量和湍流特性,但计算量远大于RANS,且对于入口条件有较高的要求。
LES的湍流入口生成方法主要包括循环站(Recycling-Rescaling Method)、预处理法(Precursor Databases)和人工合成法(Synthetic Turbulence)[14],详细见参考文献[15]。本文采用谐波合成法[16]生成脉动风速时程,通过对谱分解矩阵引入拉格朗日插值近似,减少谱分解的次数,提高计算效 率[17]。首先生成满足目标谱和互相关性的粗网格脉动风速时程,然后双线性插值得到节点时程,基于时程互相关性对脉动风速进行修正,得到数值湍流入口。
根据空间离散方法的不同,数值方法通常分为有限元、有限差分、有限体积和谱方法等[18]。 Patera[19]结合有限元法和谱方法提出了谱元法(spectral element method,SEM),该方法不仅适用任意外形的数值模拟,而且可以通过提高单元内插值阶数达到高阶精度,具有指数收敛特性,因此非常适用于复杂山地地形的风场模拟。
本文基于开源平台Nek5000[20],采用谱元法进行大涡数值模拟,谐波合成法生成湍流入口,模拟两种不同坡度的三维山丘地形风场风速分布,并与风洞试验及有限体积法数值结果进行对比,研究山丘地形的风场特性。
谱元法是Patera和Maday提出的一种高阶数值方法,其基本思想是将计算域划分为若干个单元,单元内的基函数取特殊的正交多项式,在特定的节点上展开,采用Galerkin法求解偏微分方程,得到全域的数值解。谱元法的各个单元内部节点之间不需要信息传递,因此并行效率非常高。
以不可压缩N-S方程为例,控制方程为:
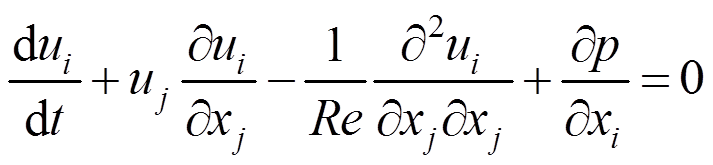 (1)
(1)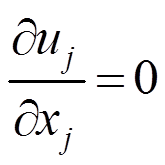 (2)
(2)
式中:下标i=1, 2, 3,分别表示纵向、横向、竖向;j为张量乘积下标;ui表示i方向速度;p表示压强;Re表示雷诺数,Re=1/ν,ν为运动粘度。
对式(1)和式(2)采取Galerkin变分得到:
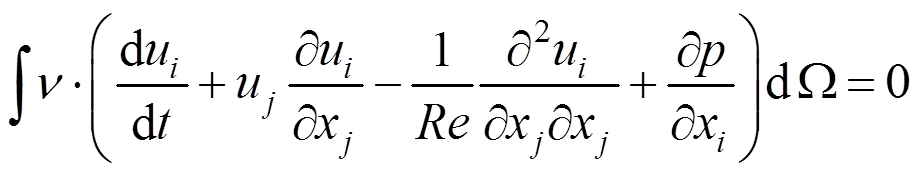 (3)
(3)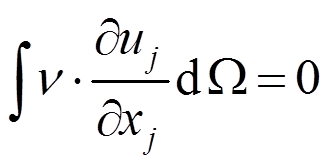 (4)
(4)
原微分方程变为变分问题:求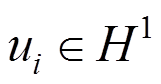 使得
使得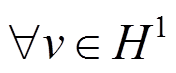 满足式(3)和式(4)。将计算域
满足式(3)和式(4)。将计算域![]() 划分为Nm个互不重叠的单元
划分为Nm个互不重叠的单元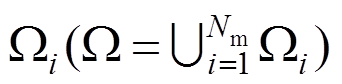 ,每个单元通过坐标变换转换到标准单元
,每个单元通过坐标变换转换到标准单元 =[-1,1]。在标准单元内选取特定的插值多项式和节点,试探函数和检验函数为:
=[-1,1]。在标准单元内选取特定的插值多项式和节点,试探函数和检验函数为:
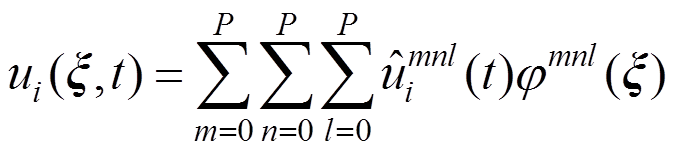 (5)
(5)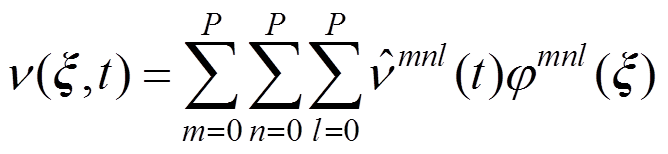 (6)
(6)
 (7)
(7)
式中: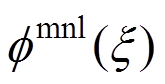 为基函数;
为基函数;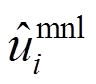 、
、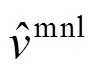 为展开系数;P为基函数最大阶数;B为基函数矩阵;W为权重矩阵;M为质量矩阵。将式(5)~式(7)代入式(3)和式(4),可得:
为展开系数;P为基函数最大阶数;B为基函数矩阵;W为权重矩阵;M为质量矩阵。将式(5)~式(7)代入式(3)和式(4),可得:
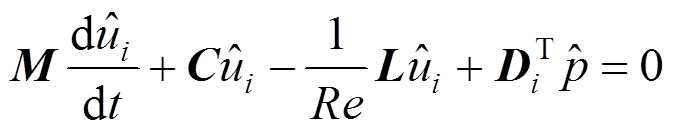 (8)
(8)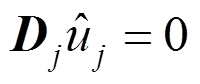 (9)
(9)
式中:C为对流矩阵;L为拉普拉斯矩阵;Di为求导矩阵。
采用高阶分裂法[21-22]进行时间离散,求解式(8)和式(9),依次解得压力、速度的展开系数,代入式(5)即可得到全域的数值解。
基函数取勒让德多项式,一维标准单元表达式:
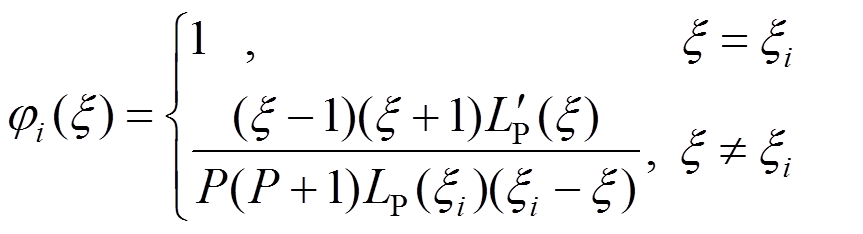 (10)
(10)式中: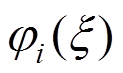 为基函数;i为插值阶数,
为基函数;i为插值阶数,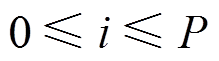 ;
;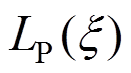 为勒让德多项式;
为勒让德多项式;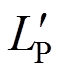 为
为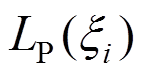 的导数;
的导数; 为节点坐标,在[-1,1]区间。
为节点坐标,在[-1,1]区间。
节点分为GLL点(Gauss-Lobatto-Legendre)和GL点(Gauss-Legendre),其中GLL点为多项式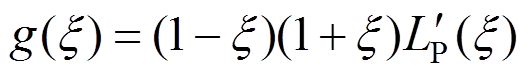 的零点,GL点为多项式
的零点,GL点为多项式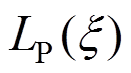 的零点。以P=6为例,二维GLL点和GL点分布如图1,可以明显看出,GLL点包含了边界点而GL点没有。
的零点。以P=6为例,二维GLL点和GL点分布如图1,可以明显看出,GLL点包含了边界点而GL点没有。
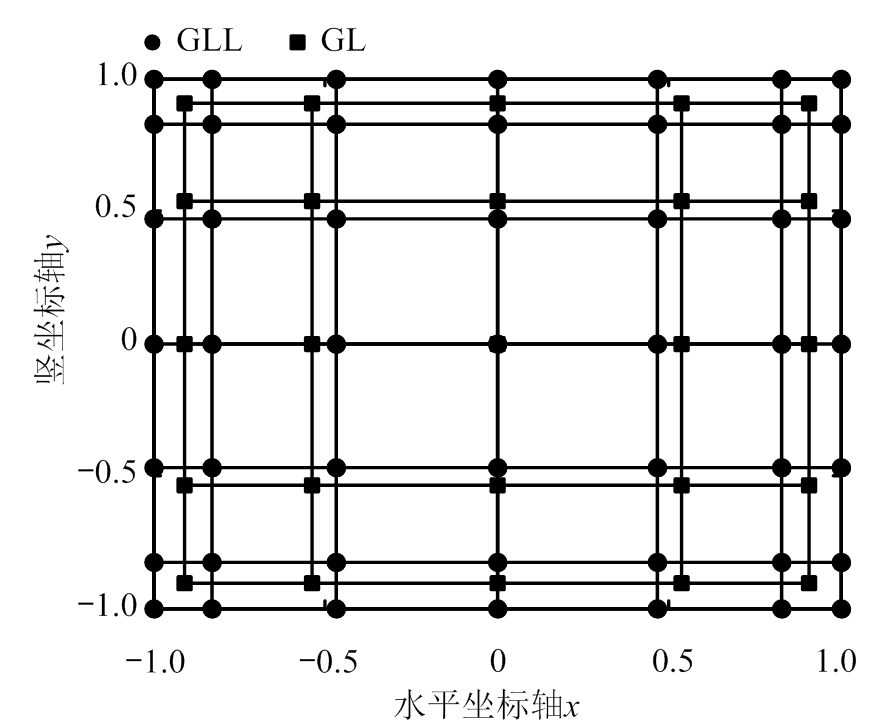
图1 GLL点和GL点分布
Fig.1 Distribution of GLL and Gl points
根据速度场和压力场的网格节点是否同位处理,谱元法可分为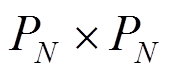 和
和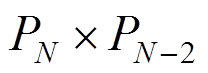 两种网格离散方案,前者表示速度场和压力场均用GLL节点,后者表示速度场用GLL节点而压力场用GL节点。
两种网格离散方案,前者表示速度场和压力场均用GLL节点,后者表示速度场用GLL节点而压力场用GL节点。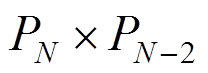 方案的优点是不需要给定压力边界即可求解,
方案的优点是不需要给定压力边界即可求解,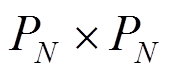 方案的优点是时间迭代时不需要对压力场进行网格变换。本文出口为自由出口,不需要特定的压力边界,因此采用
方案的优点是时间迭代时不需要对压力场进行网格变换。本文出口为自由出口,不需要特定的压力边界,因此采用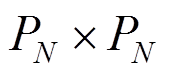 方案。
方案。
大涡模拟是Smagorinsky[23]提出的一种数值方法,其基本思想是利用滤波函数将大尺度涡和小尺度涡分离,大尺度涡直接模拟,小尺度涡用湍流模型封闭。滤波后N-S方程多出来未知量亚格子应力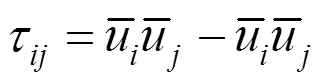 ,需要建立亚格子模型使方程封闭,常用的亚格子模型为动态Smagorinsky亚格子模型[24-25]:
,需要建立亚格子模型使方程封闭,常用的亚格子模型为动态Smagorinsky亚格子模型[24-25]:
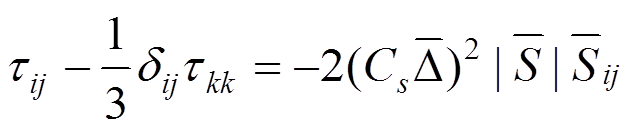 (11)
(11)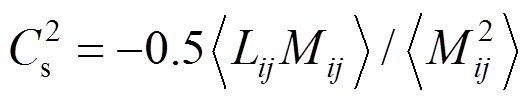 (12)
(12)
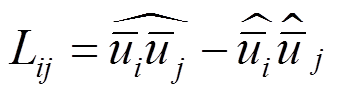 (13)
(13)
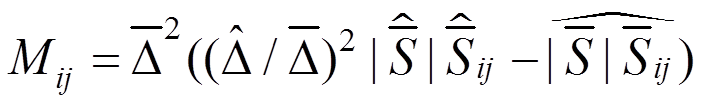 (14)
(14)式中:Cs为Smagorinsky常数;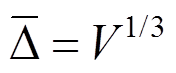 (V为网格体积)为滤波尺度;
(V为网格体积)为滤波尺度;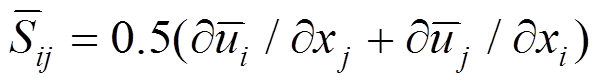 为应力张量的速率,
为应力张量的速率,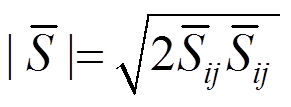 ;上划横线
;上划横线 表示滤波后变量;上划折线
表示滤波后变量;上划折线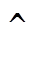 表示二次滤波,采用Boyd-Vandeven滤波[26];符号
表示二次滤波,采用Boyd-Vandeven滤波[26];符号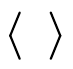 表示取横向平均。
表示取横向平均。
采用文献[27]的滤波函数提高数值稳定性:
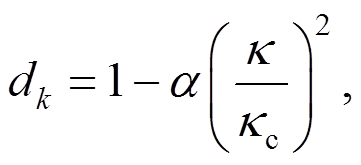
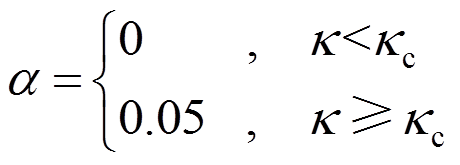 (15)
(15)式中: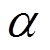 为滤波权重;
为滤波权重;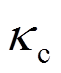 =P-1为截断阶数;
=P-1为截断阶数;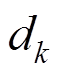 为
为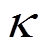 阶转换函数的值。
阶转换函数的值。
脉动风速时程采用Deodatis提出的谐波合成法生成,其基本思想是对一维n变量平稳高斯随机过程{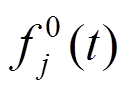 }(j=1,2,…,n)的互谱密度矩阵
}(j=1,2,…,n)的互谱密度矩阵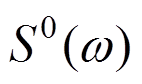 进行Cholesky分解,得到矩阵
进行Cholesky分解,得到矩阵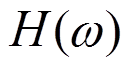 ,对若干个序列点谐波叠加得到满足目标功率谱和互相关性的脉动风速时程。通过对谱分解矩阵引入拉格朗日插值近似,减少谱分解的次数,提高计算效率。
,对若干个序列点谐波叠加得到满足目标功率谱和互相关性的脉动风速时程。通过对谱分解矩阵引入拉格朗日插值近似,减少谱分解的次数,提高计算效率。
相关公式:
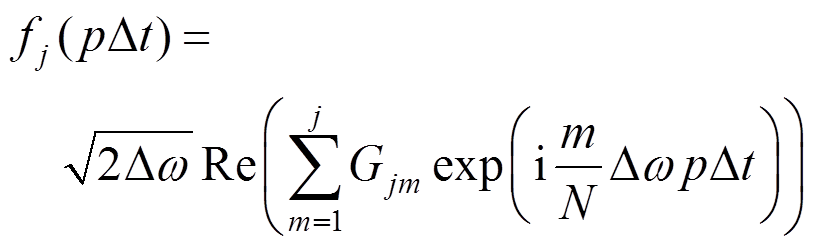 (16)
(16)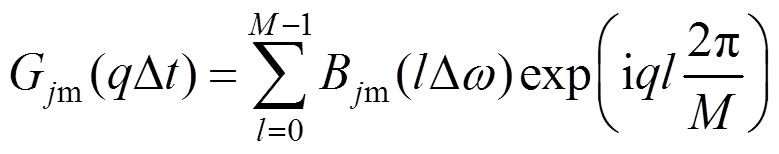 (17)
(17)
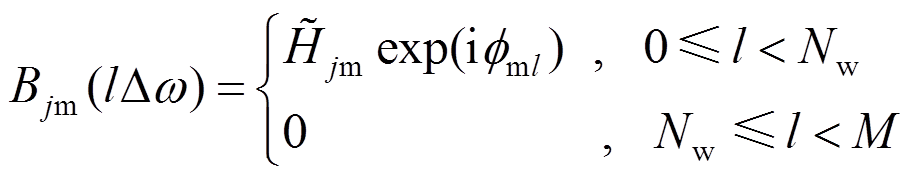 (18)
(18)
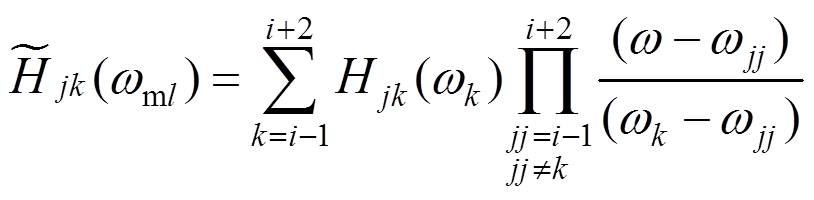 (19)
(19)式中:N为节点数;Nw为频率等分数;M=2Nw;p=0,1,2,…,N×M-1;q=mod(p,M);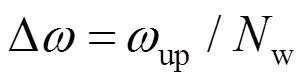 为频率增量;
为频率增量;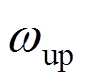 为截止频率,
为截止频率,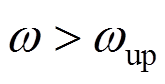 时
时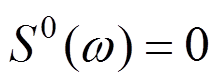 ;
;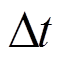 为时间增量;
为时间增量;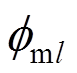 为[0,2p]的随机相位;
为[0,2p]的随机相位;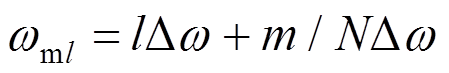 为双索引频率。
为双索引频率。
采用Karman谱,互谱密度矩阵计算公式为:
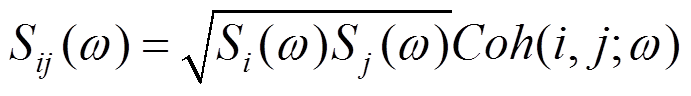 (20)
(20)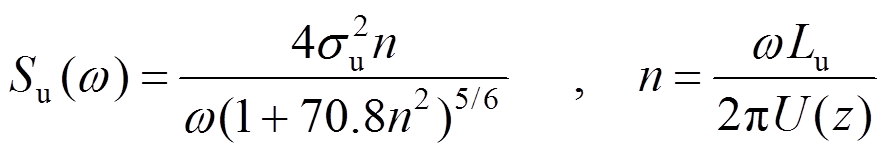 (21)
(21)
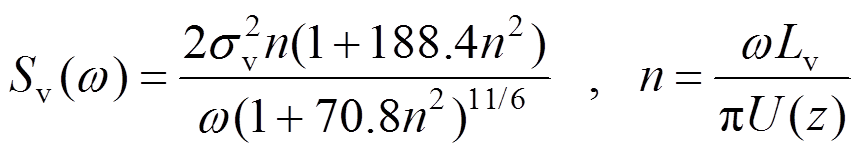 (22)
(22)
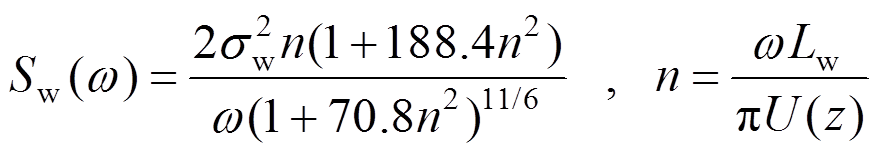 (23)
(23)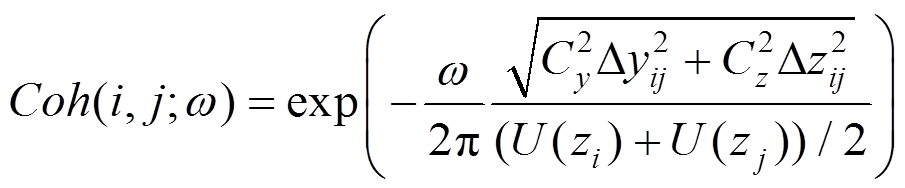 (24)
(24)
式中:Cy=16,Cz=10;Si为i方向脉动风速功率谱;Li为i方向湍流积分尺度,由风洞试验结果给出,基于泰勒冻结假设对自相关函数积分计算得到;U(z)表示z高度平均风速;Dyij、Dzij表示i和j两点的坐标差。
本次风洞试验在北京交通大学BJ-1回流风洞的大试验段中进行,横截面尺寸为5.2 m(宽)× 2.5 m(高)×14 m(长),x表示纵向,y表示横向,z表示竖向。测速装置采用澳大利亚公司生产的Cobra Probe眼镜蛇,采样频率高达2500 Hz,可以同时测量三个方向的脉动风速。风洞中布置粗糙元、地毯等,模拟缩尺比1/1000的GB5009―2012规范中标准B类地貌,边界层高度为350 m,对应风洞为0.35 m,取为参考高度。试验测得平均风速和湍流强度剖面及参考高度处的纵向脉动风速功率谱如图2和图3,均与目标值吻合,其中Uref是参考风速,为3.87 m/s。
两个三维山丘模型形状均采用余弦函数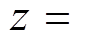
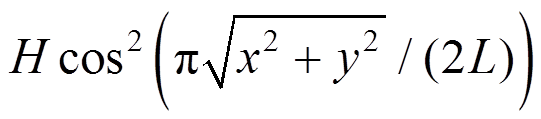 ,模型1高度H1=0.1 m,L1=0.75 m,模型2高度H2=0.08 m,L2=0.25 m,风洞中山丘模型布置如图4所示,阻塞率均小于5%。Finnigan研究发现二维山峰发生稳定流动分离的临界坡度为16° [3],而三维效应会削弱分离再附强度,导致临界坡度更大。本文所取两种山丘模型最大坡度分别为12°和29°,对应不同的分离现象。
,模型1高度H1=0.1 m,L1=0.75 m,模型2高度H2=0.08 m,L2=0.25 m,风洞中山丘模型布置如图4所示,阻塞率均小于5%。Finnigan研究发现二维山峰发生稳定流动分离的临界坡度为16° [3],而三维效应会削弱分离再附强度,导致临界坡度更大。本文所取两种山丘模型最大坡度分别为12°和29°,对应不同的分离现象。
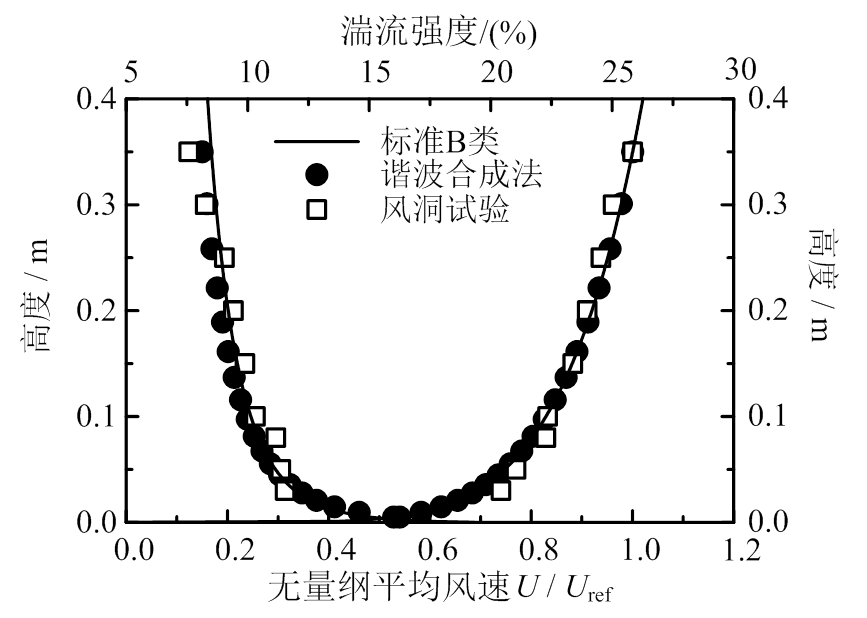
图2 平均风速和湍流强度剖面
Fig.2 Mean wind velocity and turbulent intensity profiles
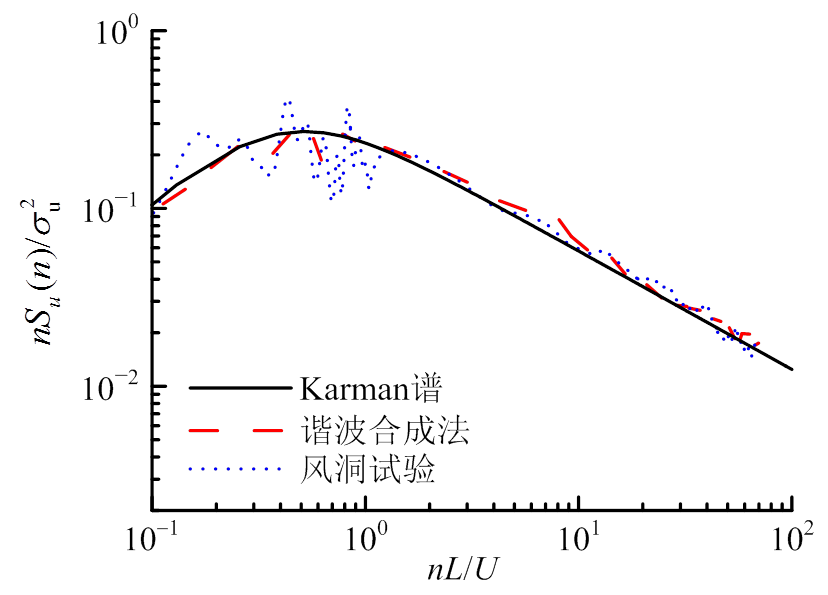
图3 纵向脉动风速功率谱
Fig.3 Wind velocity power spectrum at along-wind direction

图4 山丘模型风洞布置图
Fig.4 Layout of hilly models in wind tunnel
2.2.1 计算域及网格划分
计算域在(x,y,z)方向尺寸为(40H,40H,15H),其中x、y、z分别表示顺风向、横风向、竖向。模型中心为坐标原点,距离入口和出口分别为15H和25H,其中特征高度H=0.1 m。以高度H和风速UH计算的雷诺数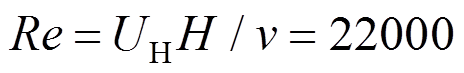 。
。
对于模型1,计算域划分为24×18×14共6048个单元,插值阶数P=5,如图5。x方向,山体划分为12个均匀单元,山体到入口划分为渐变率1.15的5个单元,山体到出口划分为渐变率1.1的7个单元;y方向,山体划分为10个均匀单元,两侧划分为渐变率1.4的4个单元;z方向,地面到5H高度划分为渐变率1.09的12个单元,5H高度以上划分为渐变率3的2个单元。对于模型2,计算域划分为26×20×14共7280个单元,插值阶数P=5。x方向,山体划分为10个均匀单元,山体到入口划分为渐变率1.25的4个单元,山体到出口划分为渐变率1.18的12个单元;y方向,山体划分为8个均匀单元,两侧划分为渐变率1.5的6个单元;z方向划分同模型1。
2.2.2 湍流入口边界条件
计算域边界处理如下:出口为自由出口;地面为无滑移固壁;两侧及顶部为对称边界;湍流入口采用谐波合成法生成。由于入口节点过多,若全部生成时程数据,计算量极大,且占用内存很高;因此首先利用谐波合成法生成粗网格的时程数据,然后通过双线性插值得到入口节点的脉动风速,利用时程互相关性对插值后的时程进行修正。下面推导脉动风速修正的计算公式:
以一维线性插值为例,假设由粗网格的A、B两点,插值得到节点P的脉动风速。A、B两点的脉动风速时程满足条件:1) 零均值;2) 脉动风速标准差均为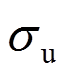 ;3) 满足互相关性:
;3) 满足互相关性: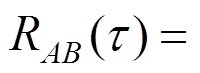
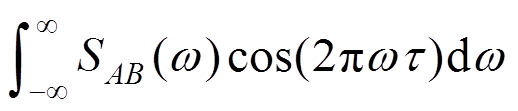 。插值节点P时程为
。插值节点P时程为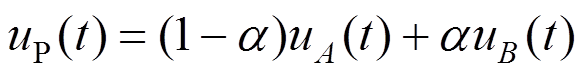 ,其中
,其中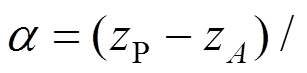
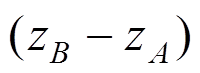 。故将式(26)代入式(25)得到节点P的脉动风速标准值
。故将式(26)代入式(25)得到节点P的脉动风速标准值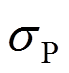 ,引入修正因子
,引入修正因子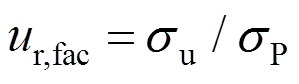 对插值后的脉动风速进行修正,从而保证插值后的脉动风速标准差仍为
对插值后的脉动风速进行修正,从而保证插值后的脉动风速标准差仍为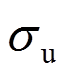 。以上为一维插值,容易推广到二维双线性插值。下面是双线性插值后的脉动风速标准差
。以上为一维插值,容易推广到二维双线性插值。下面是双线性插值后的脉动风速标准差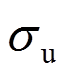 剖面修正前后对比图,可以看出双线性插值导致脉动风速标准值减小了20%,经过互相关修正后的
剖面修正前后对比图,可以看出双线性插值导致脉动风速标准值减小了20%,经过互相关修正后的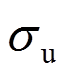 与原始数据一致。
与原始数据一致。
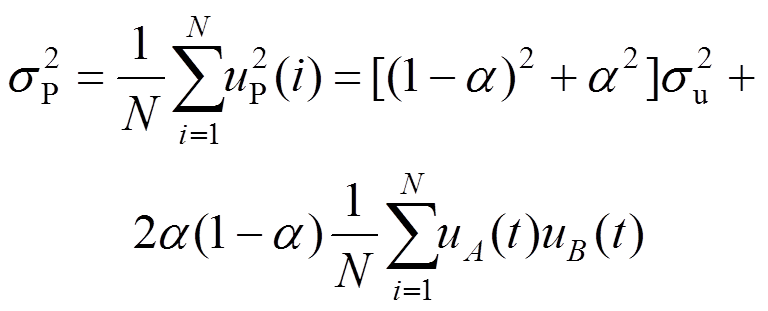 (25)
(25)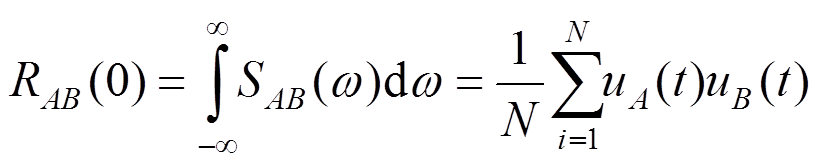 (26)
(26)
综上,大涡模拟湍流入口生成步骤:
1) 将入口梯度风高度以下区域划分为10(y)×20(z)的粗网格,以参考高度处风洞试验值为目标,Dt=0.001 s,Nw=2048,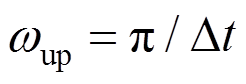 ,利用谐波合成法生成u(t),模拟结果见图2和图3;
,利用谐波合成法生成u(t),模拟结果见图2和图3;
2) 编写数值模拟入口边界条件代码,由粗网格时程双线性插值得到节点的脉动时程;
3) 导出入口节点坐标,基于时程互相关性计算节点修正因子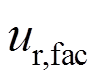 ,对入口脉动风速进行修正;
,对入口脉动风速进行修正;
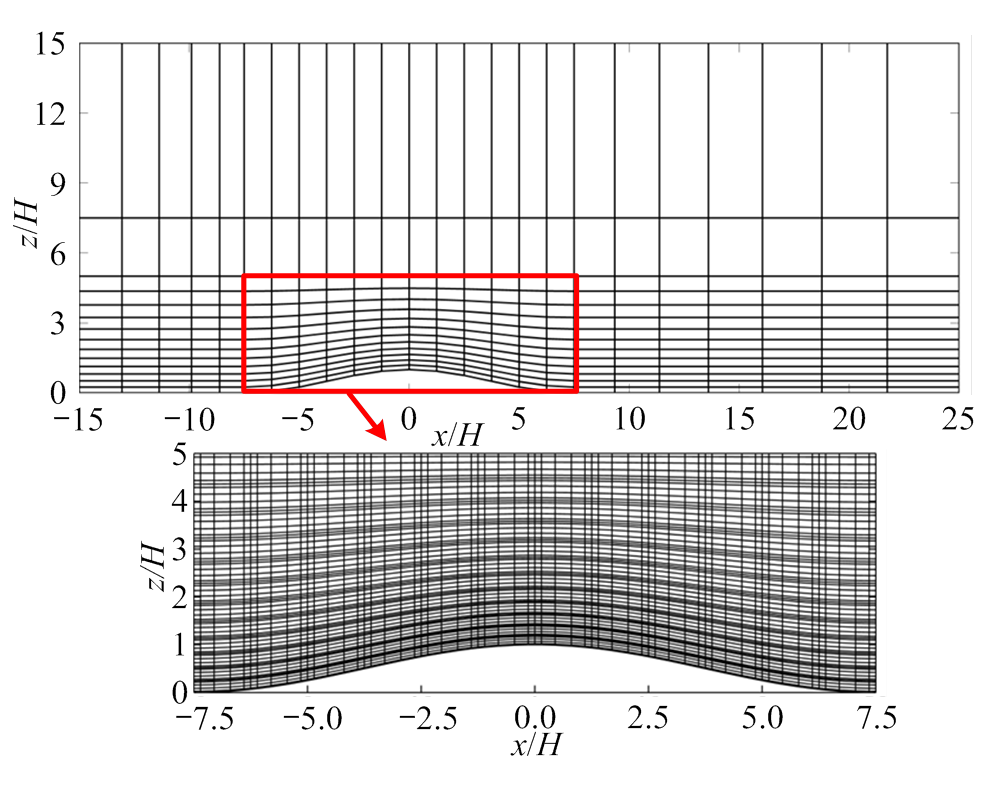
图5 山体中心垂直切面的单元划分及细部节点分布-模型1
Fig.5 Distributions of element and mesh on vertical slice across center of Model 1
4) v(t)和w(t)处理同u(t),由于篇幅限制,这里不赘述。
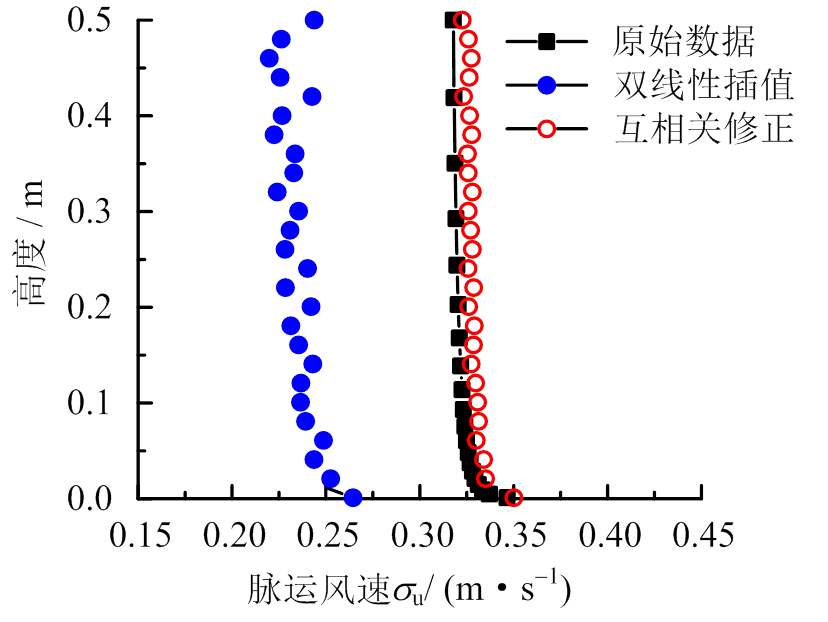
图6 脉动风速剖面修正前后对比图
Fig.6 Wind velocity standard deviation profiles before and after modification
2.2.3 其它参数
基于Nek5000平台,谱元法选用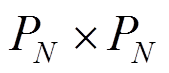 网格方案,GMRES算法解压力场,三阶时间离散方案,对流形式处理对流项,速度场和压力场收敛的精度分别为10-8和10-5,采用非定常求解器,时间步长取0.001 s,保证CFL数在1以内,每40步存储一次结果,流场趋于稳定后(8000个时间步),对12000步的模拟结果进行统计分析。模型1和模型2的网格无关性分别用26×20×14(P=5)和20×14×10(P=7)的单元进行验证。
网格方案,GMRES算法解压力场,三阶时间离散方案,对流形式处理对流项,速度场和压力场收敛的精度分别为10-8和10-5,采用非定常求解器,时间步长取0.001 s,保证CFL数在1以内,每40步存储一次结果,流场趋于稳定后(8000个时间步),对12000步的模拟结果进行统计分析。模型1和模型2的网格无关性分别用26×20×14(P=5)和20×14×10(P=7)的单元进行验证。
为将谱元法与常用的有限体积法对比,利用软件Fluent对两个山丘地形进行大涡数值模拟。模型1和模型2分别采用网格划分126×91×71和127×97×71,划分原则基本同谱元法。LES采用SIMPLE算法解瞬态方程,亚格子模型采用Dynamic Smagorinsky-Lilly,时间离散为二阶隐式,动量方程离散为有界中心差分格式,连续性方程和速度场的收敛精度分别为10-3和10-5。模型1和模型2的网格无关性分别采用164×107×101和179×111×101的网格进行验证。
同时,为对比LES和RANS,Fluent采用相同的网格进行RANS模拟,湍流模型采用Realizable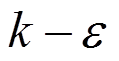 模型,近壁面采用Enhanced Wall Treatment处理,时间离散为一阶隐式,动量方程离散为二阶迎风格式。入口的湍动能k剖面基于风洞试验数据进行插值,耗散率剖面采用经验公式
模型,近壁面采用Enhanced Wall Treatment处理,时间离散为一阶隐式,动量方程离散为二阶迎风格式。入口的湍动能k剖面基于风洞试验数据进行插值,耗散率剖面采用经验公式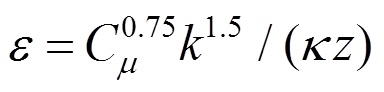 ,其中
,其中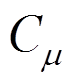 =0.03,
=0.03,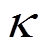 =0.4。连续性方程和速度场的收敛精度分别为10-5和10-6,监控山顶和出口的速度u,设定最大迭代步3000,避免计算结果不收敛。
=0.4。连续性方程和速度场的收敛精度分别为10-5和10-6,监控山顶和出口的速度u,设定最大迭代步3000,避免计算结果不收敛。
本次模拟在配置相同的服务器上进行,对于模型1和模型2,SEM-LES分别耗时16 h和23.2 h,FVM-LES模拟分别耗时34.5 h和40.5 h,FVM- RANS模拟耗时0.5 h左右。从单位时间步单位节点计算耗时来看,SEM-LES分别耗时3.7×10-6s和4.4×10-6s,FVM-LES分别耗时7.6×10-6s和8.3×10-6s。可以发现,有限体积法计算耗时远高于谱元法,几乎是后者的两倍。
图7和图8分别为山丘模型1和山丘模型2在垂直切面y=0的平均风场流线图。可以看出,对于模型1,由于坡度小于临界坡度,背风区不存在稳定的分离再附现象;对于模型2,坡度大于临界坡度,背风区存在稳定的分离再附现象,流动从距离山顶0.8H处开始分离,在背风区山脚发生再附,漩涡中心距离山体表面高度约0.2H。
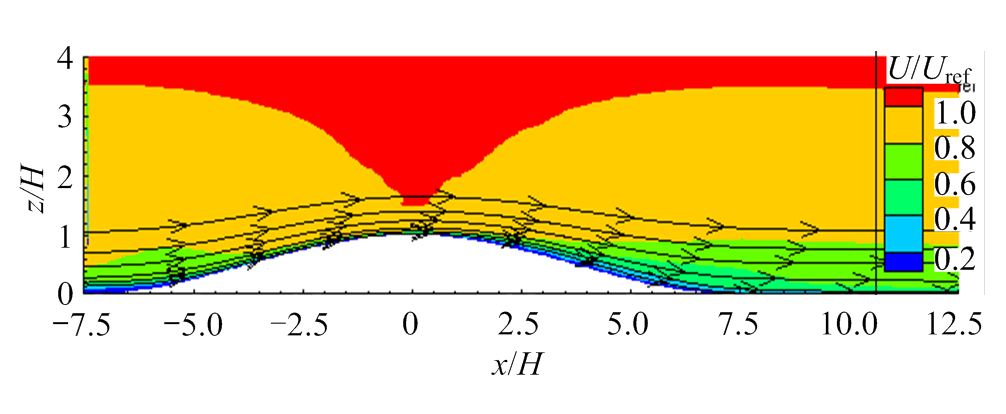
图7 垂直切面y=0的平均流线图-模型1 (FVM-LES)
Fig.7 Streamline of time averaged flow on vertical slice across y=0 - Model 1 (FVM-LES)
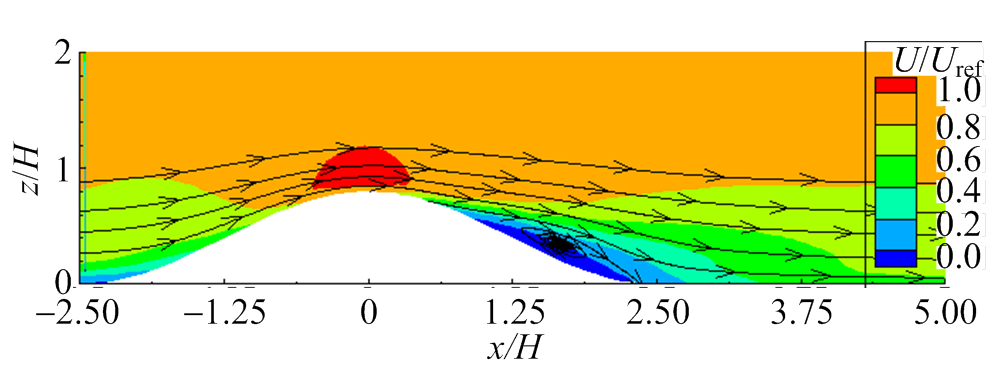
图8 垂直切面y=0的平均流线图-模型2 (FVM-LES)
Fig.8 Streamline of time averaged flow on vertical slice across y=0 - Model 2 (FVM-LES)
图9为山丘模型1的数值模拟与风洞试验剖面对比图。对于平均风速U和W,SEM-LES、FVM-LES和FVM-RANS均与实验结果十分吻合;对于脉动风速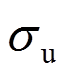 ,SEM-LES和FVM-LES与实验结果十分吻合,前者在背风区近地面有一定高估,FVM-RANS模拟结果仅在迎风山脚与实验较吻合,其余均误差较大;对于脉动风速
,SEM-LES和FVM-LES与实验结果十分吻合,前者在背风区近地面有一定高估,FVM-RANS模拟结果仅在迎风山脚与实验较吻合,其余均误差较大;对于脉动风速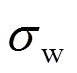 ,SEM-LES与实验较吻合,仅背风区近地面结果偏大,FVM-LES整体稍偏小,特别是迎风区,这主要是因为入口湍流经过边界层发展后发生了耗散导致的。
,SEM-LES与实验较吻合,仅背风区近地面结果偏大,FVM-LES整体稍偏小,特别是迎风区,这主要是因为入口湍流经过边界层发展后发生了耗散导致的。
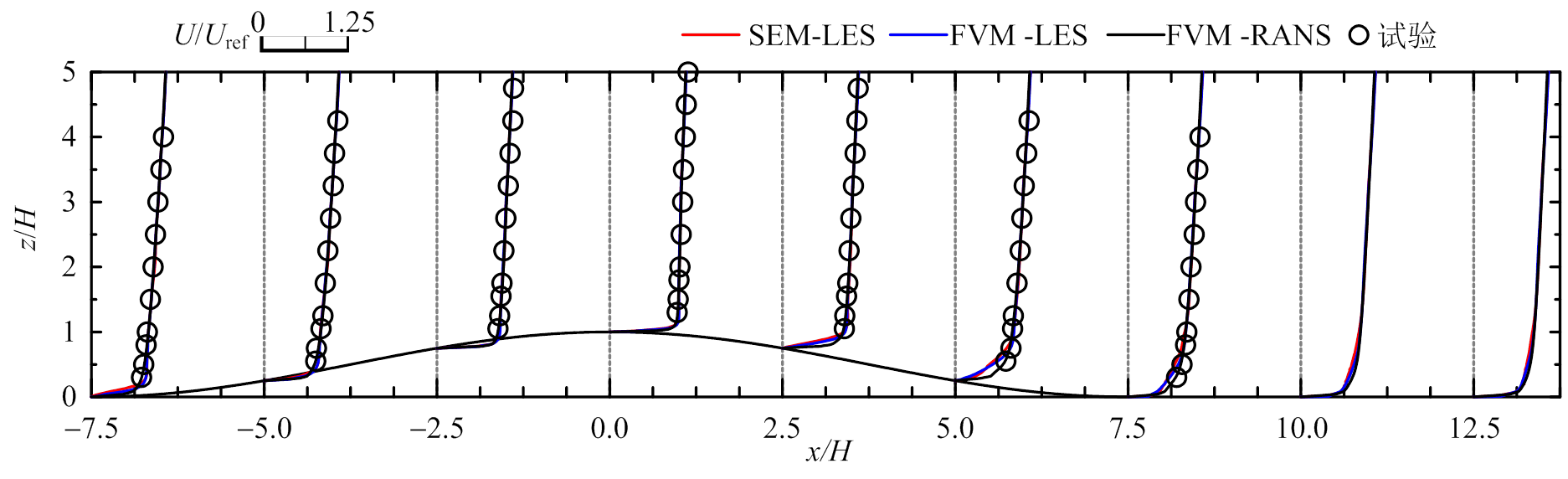
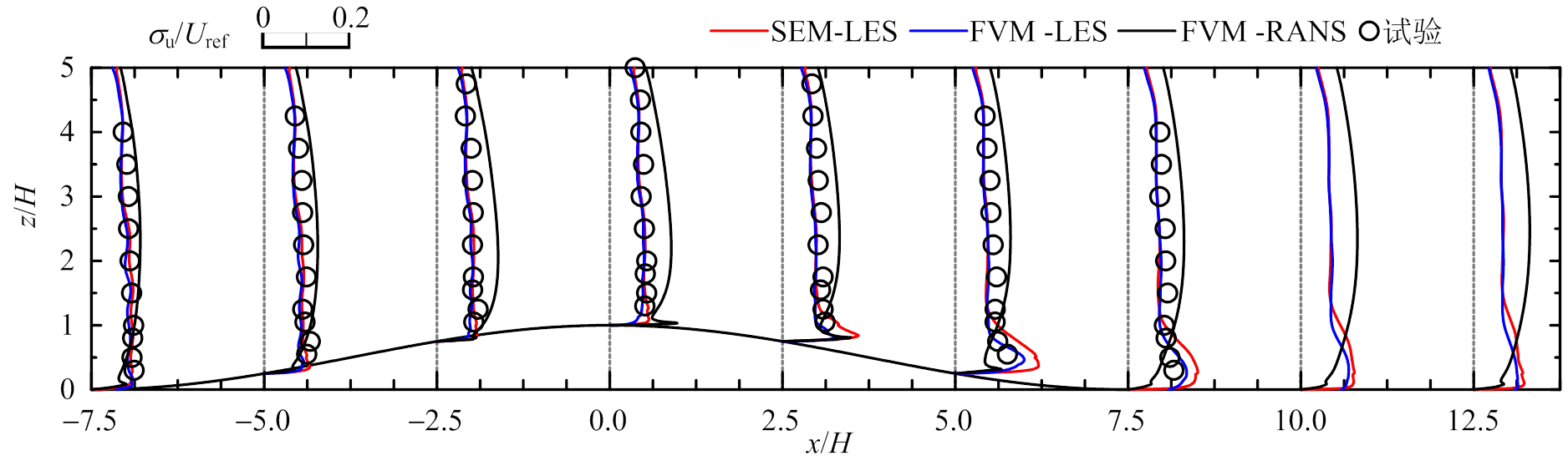
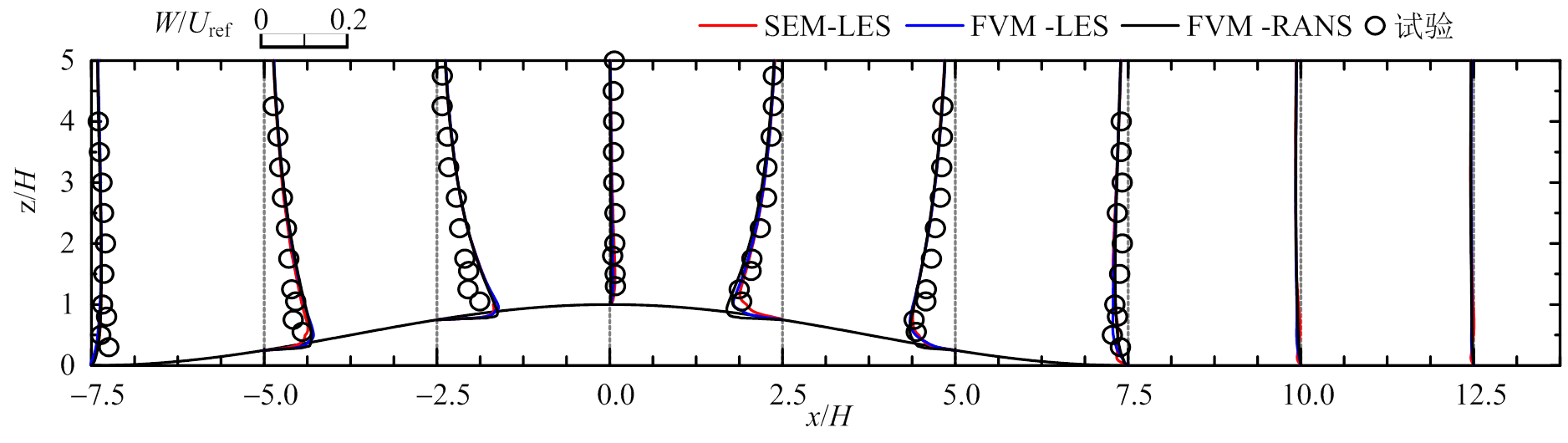
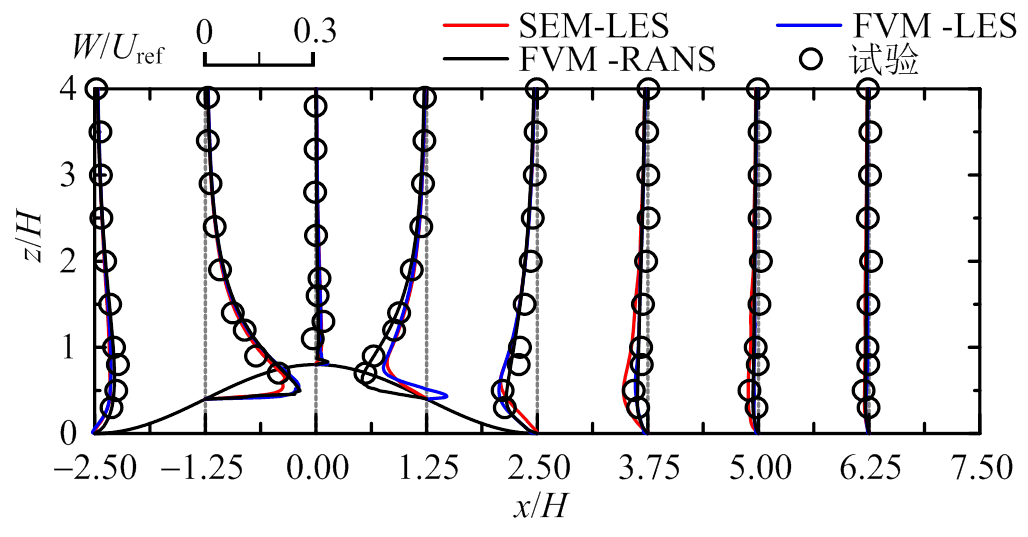
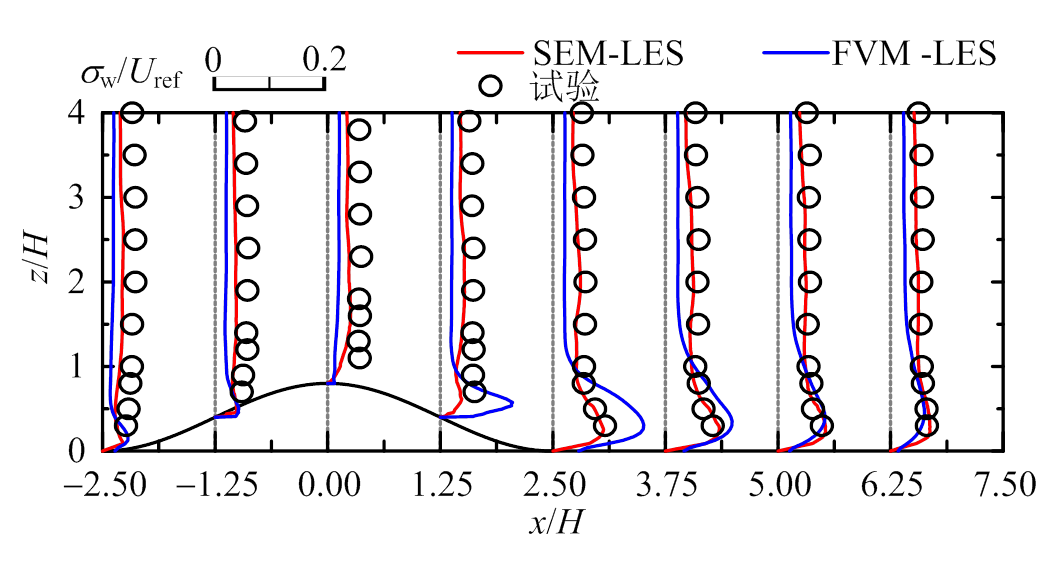
图10为山丘模型2的数值模拟与风洞试验剖面对比图。对于平均风速U和W,SEM-LES、FVM- LES和FVM-RANS均与实验结果吻合;对于脉动风速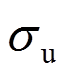 ,SEM-LES和FVM-LES与实验结果十分吻合,后者在背风区近地面有一定高估,FVM-RANS模拟结果仅在迎风山脚与实验较吻合,其余均一定程度偏大;对于脉动风速
,SEM-LES和FVM-LES与实验结果十分吻合,后者在背风区近地面有一定高估,FVM-RANS模拟结果仅在迎风山脚与实验较吻合,其余均一定程度偏大;对于脉动风速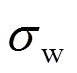 ,SEM-LES与实验较吻合,FVM-LES整体稍偏小,在背风区近地面偏大。
,SEM-LES与实验较吻合,FVM-LES整体稍偏小,在背风区近地面偏大。
(a) U/Uref
(b) σu/Uref
(c) W/Uref
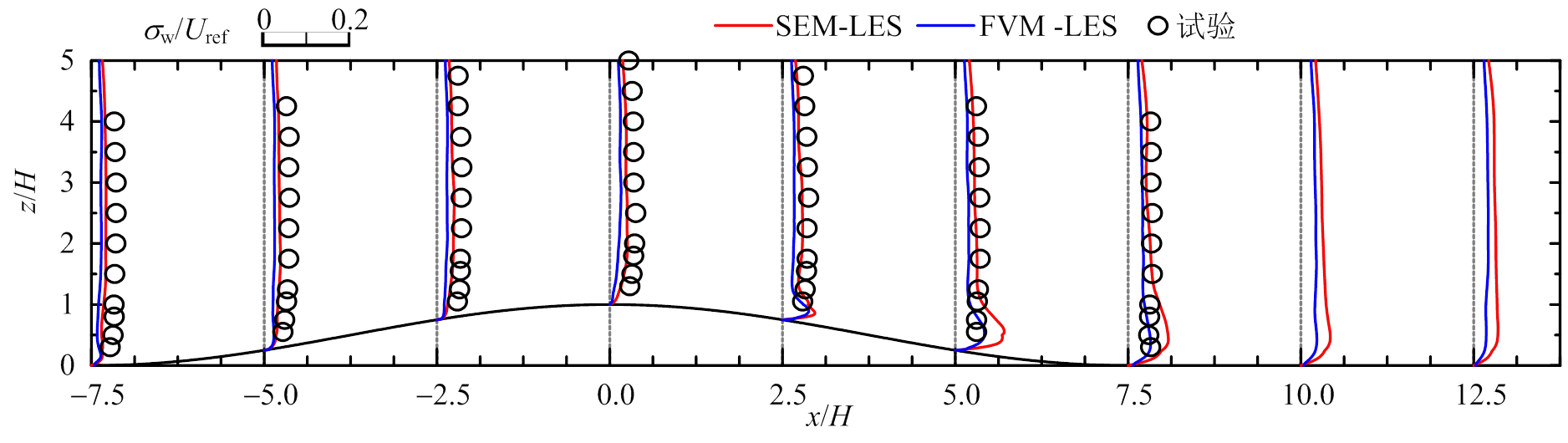
(d) σw/Uref
图9 模型1风剖面对比图(y=0)
Fig.9 Wind profiles for Model 1 (y=0)
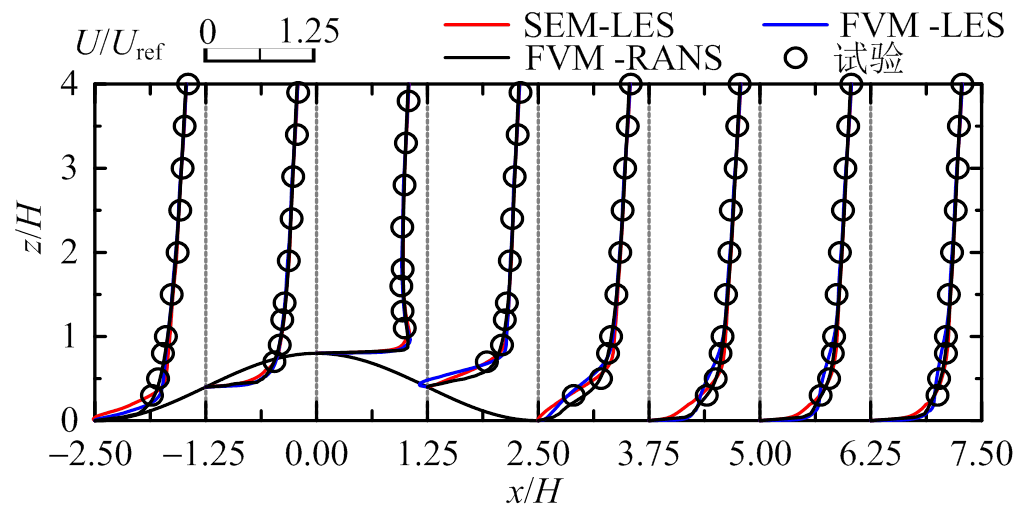
(a) U/ Uref
(b) σu/ Uref
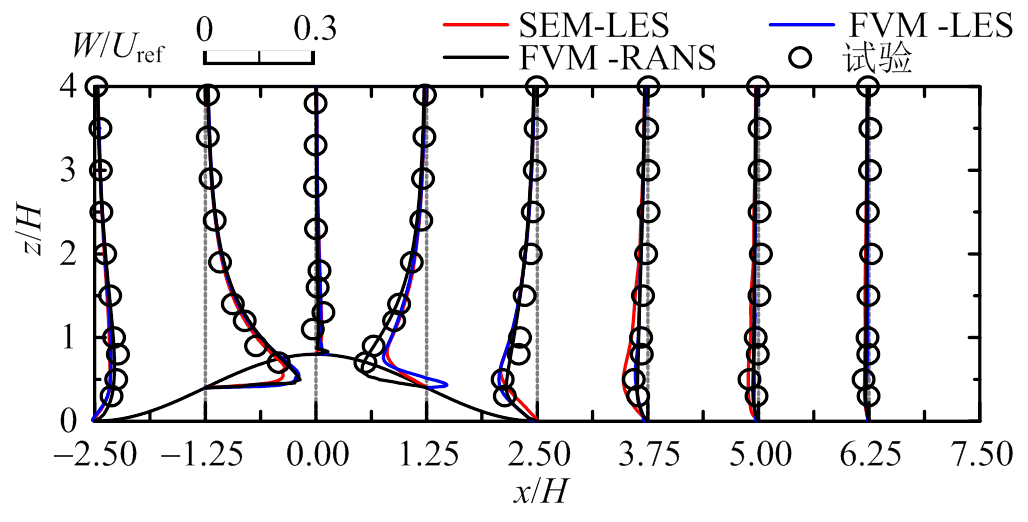
(c) W/ Uref
(d) σw/ Uref
图10 模型2风剖面对比图(y=0)
Fig.10 Wind profiles for Model 2 (y=0)
综上,谱元法和有限体积法的大涡模拟均能较好的预测山丘地形风场的平均风速分布和湍流特性;对于低坡度(12°)和高坡度(29°)山丘地形脉动风场的预测,谱元法和有限体积法分别在背风区近地面有一定高估,这可能是因为湍流入口时程数据经过双线性插值和互相关修正,不满足连续性方程,近地面湍流和背风区产生的特征湍流相互作用导致脉动效应放大,湍流强度偏大。雷诺时均法能较好预测平均风场,但对于脉动风场的预测极差,仅在迎风山脚处与试验吻合,其余均误差较大,这主要是因为RANS通过经验模型考虑湍流效应,不具备广泛性和统一性。
本文利用谐波合成法生成大涡模拟湍流入口时程,采用谱元法和有限体积法对两种不同坡度的三维山丘地形风场进行大涡数值模拟,并与风洞试验及RANS数值结果进行对比,得出以下主要结论:
(1) 采用谐波合成法生成粗网格下脉动风速时程,由双线性插值及互相关修正得到数值模拟湍流入口,满足目标湍流特性指标;
(2) 谱元法和有限体积法的大涡模拟均能较好的预测山丘地形风场的平均风速分布和湍流特性;
(3) 与大涡模拟相比,雷诺时均模拟能高效预测山丘地形平均风场,但对于脉动风场的预测误差较大;
(4) 与有限体积法相比,谱元法的计算效率更高,在复杂山地地形风场预测上有较好的应用前景。
参考文献:
[1] Jackson P S, Hunt J C R. Turbulent wind flow over a low hill [J]. Quarterly Journal of the Royal Meteorological Society, 1975, 101(430): 929―955.
[2] Hunt J C R, Leibovich S, Richards K J. Turbulent shear flows over low hills [J]. Quarterly Journal of the Royal Meteorological Society, 1988, 114(484): 1435―1470.
[3] Finnigan J J. Air Flow Over Complex Terrain [M]// Flow and Transport in the Natural Environment: Advances and Applications. Springer Berlin Heidelberg, 1988: 183―229.
[4] Taylor P A, Lee R J. Simple guidelines for estimating wind speed variations due to small scale topographic features [J]. Climatol Bull, 1984.
[5] Ishihara T, Hibi K, Oikawa S. A wind tunnel study of turbulent flow over a three-dimensional steep hill [J]. Journal of Wind Engineering & Industrial Aerodynamics, 1999, 83(1/2/3): 95―107.
[6] Ishihara T, Fujino Y, Hibi K. A wind tunnel study of separated flow over a two-dimensional ridge and a circular hill [J]. Journal of Wind Engineering & Industrial Aerodynamics, 2001, 89: 573―576.
[7] Cao S, Tamura T. Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill [J]. Journal of Wind Engineering & Industrial Aerodynamics, 2006, 94(1): 1―19.
[8] Cao S, Tamura T. Effects of roughness blocks on atmospheric boundary layer flow over a two-dimensional low hill with/without sudden roughness change [J]. Journal of Wind Engineering & Industrial Aerodynamics, 2007, 95(8): 679―695.
[9] Ishihara T, Hibi K. Numerical study of turbulent wake flow behind a three-dimensional steep hill [J]. Wind & Structures An International Journal, 2002, 5(2/3/4): 317―328.
[10] Liu Z, Ishihara T, He X, et al. LES study on the turbulent flow fields over complex terrain covered by vegetation canopy [J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 155: 60―73.
[11] Cao S, Wang T, Ge Y, et al. Numerical study on turbulent boundary layers over two-dimensional hills — Effects of surface roughness and slope [J]. Journal of Wind Engineering & Industrial Aerodynamics, 2012, 104―106: 342―349.
[12] 遆子龙, 李永乐, 廖海黎. 地表粗糙度对山区峡谷地形桥址区风场影响研究[J]. 工程力学, 2017, 34(6): 73―81. Ti Zilong, Li Yongle, Liao Haili. Effect of ground surface roughness on wind field over bridge site with a gorge in mountainous area [J]. Engineering Mechanics, 2017, 34(6): 73―81. (in Chinese)
[13] Bilal M, Birkelund Y, Homola M, et al. Wind over complex terrain – Microscale modelling with two types of mesoscale winds at Nygårdsfjell [J]. Renewable Energy, 2016, 99: 647―653.
[14] Keating A, Piomelli U, Balaras E, et al. A priori and a posteriori tests of inflow conditions for large-eddy simulation [J]. Physics of Fluids, 2004, 16(12): 4696―4712.
[15] Overview of Turbulent Inflow Boundary Conditions for Large-Eddy Simulations [J]. AIAA Journal, 2017: 1―18.
[16] Deodatis G. Simulation of ergodic multivariate stochastic processes [J]. Journal of Engineering Mechanics, 1996, 122(8): 778―787.
[17] 丁泉顺, 陈艾荣, 项海帆. 大跨度桥梁空间脉动风场的计算机模拟[J]. 力学季刊, 2006(2): 184―189.
Ding Quanshun, Chen Airong, Xiang Haifan. Computer simulation of space fluctuation wind field of long - span bridge [J]. Chinese Quarterly of Mechanics, 2006(2): 184―189. (in Chinese)
[18] 张来平, 贺立新, 刘伟, 等. 基于非结构/混合网格的高阶精度格式研究进展[J]. 力学进展, 2013, 43(2): 202―236.
Zhang Weiping, He Lixin, Liu Wei, et al. High order accuracy scheme research based on unstructure/hybrid grid [J]. Advances In Mechanics, 2013, 43(2): 202―236. (in Chinese)
[19] Patera A T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion [J]. Journal of Computational Physics, 1984, 54(3): 468―488.
[20] Fischer P F, Lottes J W, Kerkemeier S G. Nek5000 Web Page [CP]. http://nek5000.mcs.anl.gov, 2008.
[21] Karniadakisa G E. High-order splitting methods for the incompressible Navier-Stokes equations [J]. Journal of Computational Physics, 1991, 97(2): 414―443.
[22] Karamanos G S, Sherwin S J. A high order splitting scheme for the Navier–Stokes equations with variable viscosity [J]. Applied Numerical Mathematics, 2000, 33(1): 455―462.
[23] Smagorinsky J S. General circulation experiments with the primitive equations [J]. Monthly Weather Review, 1963, 91(3): 99―164.
[24] Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model [J]. Physics of Fluids, 1991, 3(7): 1760―1965.
[25] Lilly D K. A proposed modification of the Germano subgrid-scale closure method [J]. Physics of Fluids A Fluid Dynamics, 1992, 4(4): 633―633.
[26] Levin J G, Iskandarani M, Haidvogel D B. A spectral filtering procedure for Eddy-resolving simulations with a spectral element ocean model [J]. Journal of Computational Physics, 2015, 137(1): 130―154.
[27] Kanchi H, Sengupta K, Mashayek F. Effect of turbulent inflow boundary condition in LES of flow over a backward-facing step using spectral element method [J]. International Journal of Heat & Mass Transfer, 2013, 62(1): 782―793.
LES STUDY OF TURBULENT BOUNDARY LAYERS OVER THREE-DIMENSIONAL HILLS
Abstract: The harmonic synthesis method was applied to generate fluctuating wind velocity for coarse grids. Turbulent inlet for large eddy simulation (LES) was calculated by bilinear interpolation and cross-correlation modification. The spectral element method (SEM) was introduced to simulate two kinds of three-dimensional hills by LES. The results were compared to the wind-tunnel tests and finite volume method (FVM) numerical simulation. It was found that LES can accurately predict the wind speed distribution and turbulence characteristics of hilly terrain. Compared to FVM, SEM is more efficient and its applications in the fields of wind fields prediction for complex terrain is promising.
Key words: Harmonic synthesis method; turbulent inlet; spectral element method; finite volume method; three-dimensional hills; wind-tunnel test
文章编号:1000-4750(2019)04-0072-08
中图分类号:P425;P421.3
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.03.0138
收稿日期:2018-03-13;
修改日期:2018-09-06
基金项目:国家自然科学基金国际(地区)合作与交流项目(51720105005)
张 建(1981―),男,辽宁人,讲师,博士,硕导,主要从事结构风工程和流固耦合等研究(E-mail: zhangjian@bjtu.edu.cn).