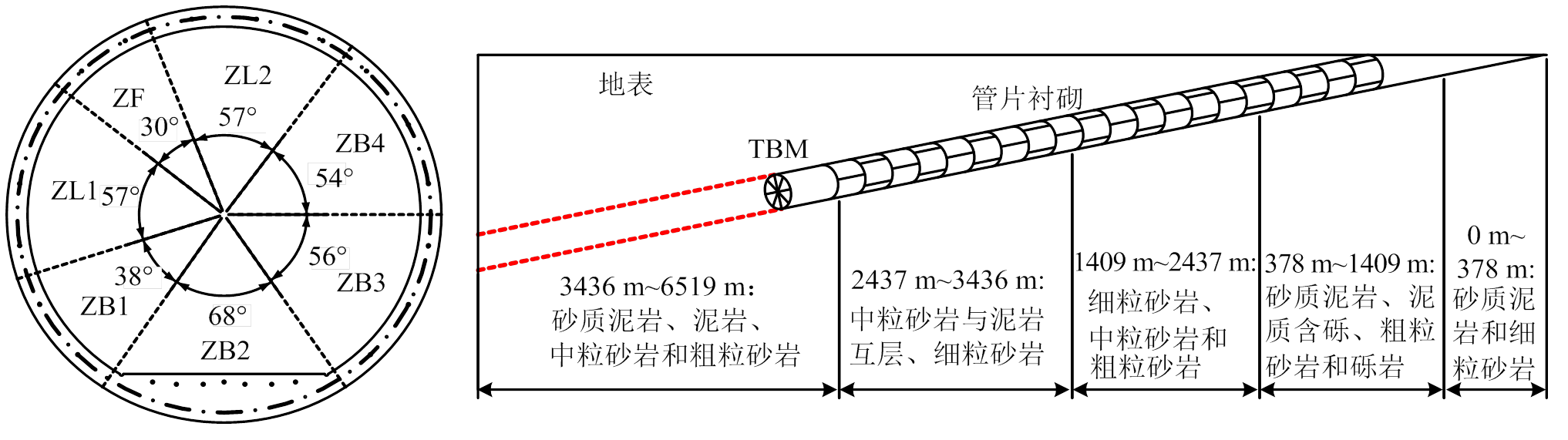
图1 斜井穿越地层示意图
Fig.1 Schematic of strata which inclined shaft passes through
摘 要：深埋盾构隧道所受围岩压力主要为围岩挤压型大变形产生的形变压力，其主要特点是变形持续时间长且具有重复性，支护完成后围岩压力仍将持续增大，企图通过增加支护刚度来抑制围岩变形是不现实的，采用让压支护是解决问题的一个方向。同时，深部围岩赋存条件复杂，岩体结构复杂多变，盾构隧道穿越复合地层不可避免。以国内两座大埋深盾构煤矿斜井为背景，采用相似模型试验和有限元数值计算手段，对比分析不同复合地层条件下管片衬砌+可压缩层联合支护时管片衬砌的力学性能。研究结果表明：在模型正确建立且参数取值合理的前提下，有限元数值计算结果可以和相似模型试验结果很好的吻合。均一地层条件下可压缩层可使管片最大弯矩减小12.5%~19.9%，最大轴力减小14.2%。复合地层使管片弯矩量值和分布均产生明显变化，但对管片轴力的影响则不明显，管片弯矩对复合地层抗力更为敏感，而轴力对复合地层抗力不敏感。有可压缩层情况下，复合地层中管片内力分布更加均匀，轴力的变化不明显。复合地层相对厚度对管片最大正弯矩的影响较为稳定，对管片最大负弯矩影响显著，使其产生位置偏向相对较软一侧的地层，且相对厚度越大偏移越明显。“上硬下软”复合地层中管片弯矩更容易受地层相对刚度的影响。
关键词：盾构(TBM)工法；模型试验；复合地层；管片衬砌；可压缩层；让压支护
近年来，随着我国国民经济的快速发展，迎来了一波基础设施大建设的高潮。高速公路和铁路逐步向西部山区延伸；矿产资源开采逐步向超千米深部大规模发展；一大批大型水电站和跨流域调水工程的建设也如火如荼，而深长隧道(洞)往往是这些生命线工程的关键控制性工程。相比传统的钻爆法，盾构/TBM工法无论从建设周期、安全保障，还是从环境保护、造价控制考虑，都是最佳选择，在技术条件和在经济性上均具有显著的优越 性[1－2]。可以预见，盾构/TBM工法将成为深长隧道(洞)和井巷掘进施工的发展趋势。
与浅埋隧道不同，高地应力背景下的深埋隧道开挖后主要承受围岩挤压型大变形产生的形变压力，其主要特点是变形持续时间长且具有重复性，支护完成后变形仍将持续[3－6]。针对隧道大变形问题，长期以来国内外最普遍的还是采用加强型常规支护来应对，该支护型式属于刚性支护，企图通过增加支护刚度以达到抑制围岩变形的目的，支护参数往往突破现有规范的推荐值。但由于围岩形变和荷载持续增加，支护往往难以抵抗不断增加的形变压力而破坏。因此，国内外学者提出了柔性支护的理念，即治理大变形不能单纯依靠“强支硬顶”的支护方式，而是要适当释放围岩压力。分层初期支护便是柔性支护的一种实现方式，但由于理论基础和工程经验不完善，在实施中陷入了初喷较薄易塌方、初喷较厚又回到常规强支护上来的尴尬境地[6]。
针对深部围岩特点和现有大变形支护型式存在的问题，国内外学者提出了让压支护的理念，其主要思想是隧道(洞)或井巷开挖后，允许围岩发生一定的初期变形实现让压，从而实现围岩应力的部分释放，减小作用在支护结构上的形变压力[7－10]。Ramoni、Cantieni和Anagnostou等[10－11]认为对于高地应力大变形隧道，其支护应当具有可压缩性并辅以扩挖以适应较大的变形量，并基于此提出让压支护的两种实现形式：衬砌与围岩之间设置可压缩层或者允许支护环向压缩变形。Yu等[4]针对深井煤矿巷道大变形和长时间流变问题，提出高阻限制-让压支护原理，并建立了“高预紧力让压锚杆+小孔径预紧力锚索+钢筋梯梁+菱形金属网+滞后注浆”的高阻限制-让压支护技术。胡雄玉等[12]借鉴传统的让压支护思想，提出了一种适用于TBM工法修建高地应力深部斜井的管片衬砌配合碎石可压缩层的让压支护技术，通过在管片衬砌壁后充填孔隙率大、压实性能好的碎石散粒体材料，实现管片衬砌结构的让压，并针对该支护型式采用数值模拟手段开展了初步研究。
深部隧道工程所面临的另一个重要挑战是复合地层。复合地层指的是在隧道工程开挖断面范围内或开挖延伸方向上，由两种或两种以上不同地层组成，且这些地层的岩土力学、工程地质和水文地质等特征相差悬殊[13]。复合地层以“上软下硬”或“上硬下软”的层状复合地层最为典型。复合地层导致地应力场具有明显的空间效应，使赋存于其中的支护结构同时面临高地应力和非均匀应力的挑战。针对复合地层中修建盾构隧道的问题，国内外学者开展了较多研究。何川等[14]采用模型试验手段研究了武汉长江隧道局部穿越上软下硬复合地层对管片衬砌结构力学特征的影响，认为硬岩区域管片局部弯矩会明显减小。徐国文等[15]采用数值计算和模型试验手段对狮子洋隧道复合地层中管片衬砌受力进行了分析，给出了复合地层中管片接头抗弯刚度的取值方法建议。朱宏海[16]对上软下硬复合地层中地铁盾构隧道设计、盾构选型及施工中存在的困难和问题进行了详细地介绍和分析，并结合国内大量工程的实施情况和经验提出相应处理方案和措施。
从已有研究成果来看，国内外学者针对深部围岩中隧道结构面临的高地应力和大变形等问题开展了大量研究，取得了丰硕的成果，但多集中于采用传统钻爆法施工的隧道，相应结合钻爆法支护特点提出的让压支护中的让压构件多为锚杆(索)、钢拱架或其组合，并不能直接应用到采用盾构/TBM工法掘进、管片衬砌支护的隧道(洞)和井巷中。对于复合地层的研究，虽然也取得了较多成果，但仍着眼于浅埋地铁盾构隧道，且关注点多为盾构施工参数控制，对管片衬砌结构力学性能认识尚不足。鉴于此，本文依托神华新街台格庙矿区主斜井和神东补连塔煤矿通道斜井开展研究，采用相似模型试验和数值计算手段研究深部复合地层中不同地层参数下可压缩层对管片衬砌结构的影响，以期为采用盾构/TBM工法修建深部隧道(洞)和井巷的支护型式设计提供参考。
神华新街台格庙矿区位于鄂尔多斯市伊金霍洛旗和乌审旗境内，其1号矿井的主、副斜井由浅至深依次穿越侏罗系中下统延安组(J1-2y)，侏罗系中统直罗组(J2z)、安定组(J2a)，白垩系下统志丹群(K1zh)和第四系(Q4)地层，围岩主要岩性为粗粒砂岩、含砾粗粒砂岩、中粒砂岩、细粒砂岩、泥岩和砂岩与泥岩互层，砂质泥岩。工程主斜井坡度-6°，长度为6553 m，最大埋深685 m。盾构掘进段长6402.691 m。斜井穿越地层如图1所示。
神东补连塔煤矿位于鄂尔多斯市伊金霍洛旗境内，其辅助运输通道斜井总长度为2744.54 m，其中盾构掘进段长2718.224 m，坡度-5.5°，穿越地层情况与新街台格庙矿区斜井类似。
两个依托工程的地质情况和使用目的类似，因此盾构掘进段采用相同的盾构机械、开挖断面和支护型式。斜井开挖直径7.62 m，净空直径6.6 m，采用C40预制钢筋混凝土管片支护，管片衬砌厚350 mm，幅宽1500 mm，采用左右转弯环管片衬砌错缝拼装。管片分块如图1所示。
以依托斜井工程穿越的典型地层为原型，以几何相似比CL=20和容重相似比Cα=1为基础相似比，实现在弹性范围内控制各物理力学参数的相似性。根据相似理论原理推出各物理力学参数原型值与模型值的相似比：泊松比、应变、摩擦角相似比Cμ=Cε=Cφ=1，强度、应力、粘聚力、弹性模量相似比CR=Cσ=Cc=CE=20。
图1 斜井穿越地层示意图
Fig.1 Schematic of strata which inclined shaft passes through
2.1.1 土体
以容重、弹性模量、粘聚力和内摩擦角为主要控制参数进行模型土体的配制。采用粉煤灰和河砂为基材，并掺入一定比例的重晶石粉、粗石英砂、细石英砂、凡士林、松香和机油的热熔混合物拌和均匀并压实后作为土体材料。原型和模型土体材料的物理力学参数见表1，试验模拟地层情况如图2所示。
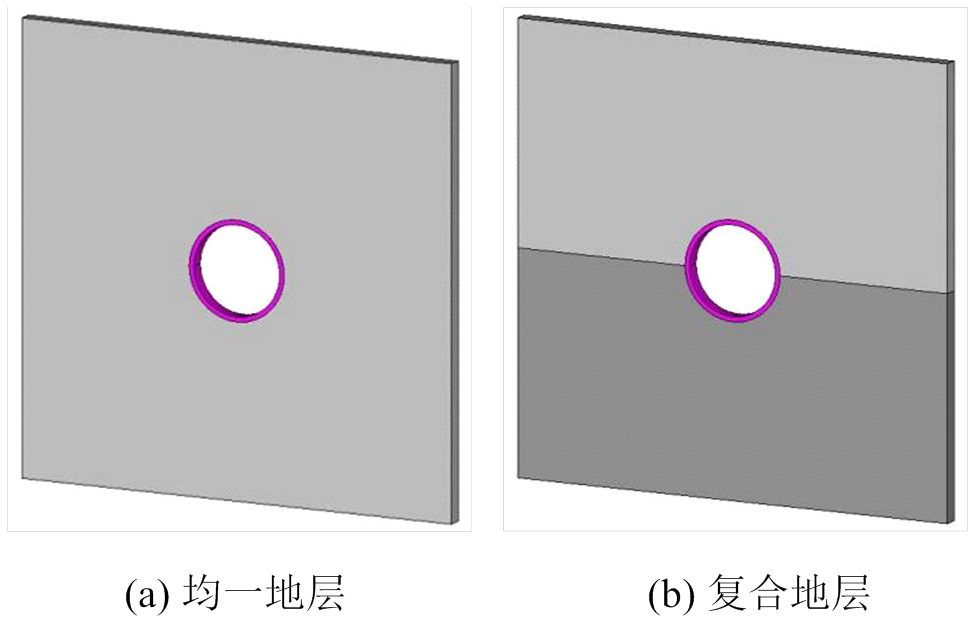
图2 试验模拟地层情况示意图
Fig.2 Schematic of model test strata
表1 材料物理力学参数
Table 1 Mechanical parameters of materials
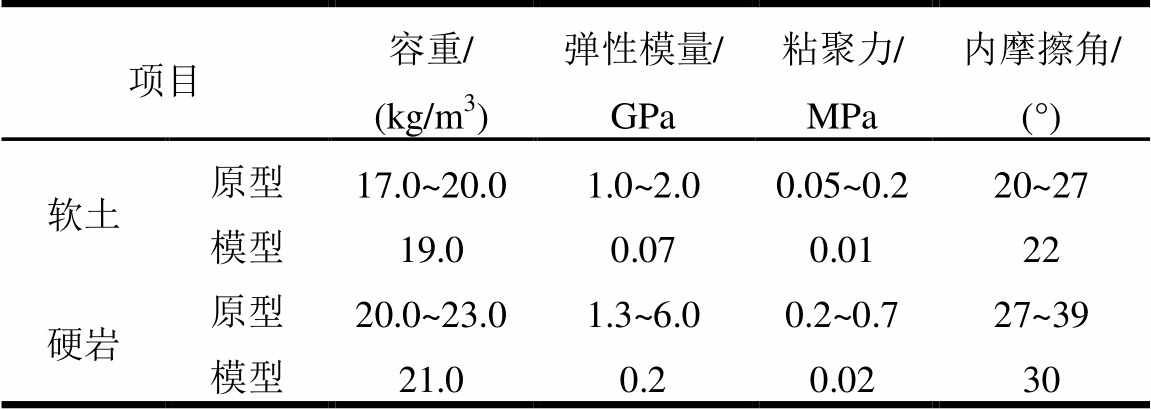
项目容重/(kg/m3)弹性模量/GPa粘聚力/MPa内摩擦角/ (°) 软土原型17.0~20.01.0~2.00.05~0.220~27 模型19.00.070.0122 硬岩原型20.0~23.01.3~6.00.2~0.727~39 模型21.00.20.0230
2.1.2 管片衬砌
管片混凝土采用特定水膏质量比的特种石膏材料通过预制加工的方法模拟。依托斜井工程管片混凝土强度等级为C40，通过试配确定材料配比为水∶石膏∶硅藻土=1.5∶1.0∶0.1，材料参数以石膏终凝的试验值为准。管片环向主筋根据模型与原型抗弯刚度相似确定，采用直径1.0 mm的细铁丝网对称配筋模拟。管片衬砌采用模具预制加工，脱模后在养护箱内养护而成。管片环向接头采用在接头部位切槽的方式模拟，切槽深度根据环向抗弯刚度等效原理计算得出，且考虑了正、负抗弯刚度的不同。根据已有研究成果，盾构隧道相似模型试验管片接头处切槽多位于管片外侧，这种处理方式对于弹性阶段管片及接头变形较小是适用的，但对于本文，当管片承受较大荷载作用时，管片整体可能发生较大的位移，接缝张开、闭合量大幅增加，正弯区的接头张开闭合效应会受到切槽的限制而无法真实模拟，因此本试验采用内外分区切槽的方式，即以±45°线将管片环划分为上下正弯区和左右负弯区，分别在内、外侧切槽。管片环向接头刚度和切槽深度见表2。环间接头刚度偏安全地取为无穷大，采用直径为4 mm，长度为40 mm的钢棒模拟，并用环氧树脂粘固干燥。
表2 环向接头对应槽缝深度
Table 2 Cutting depth of groove for modeling circumferential joints
弯曲刚度/(N·m/rad)原型槽缝深度/m模型槽缝深度/mm 正弯曲3.0×1070.1558 负弯曲2.0×1070.1809
2.1.3 可压缩层
根据文献[14]，可压缩层是通过散粒体材料的流动转移导致的孔隙率减小来实现让压，从而减小作用在衬砌上的围岩压力，而可压缩层材料本身的变形可以忽略，因此，“可压缩层”设计的主要参数便是其孔隙率的可减小程度。基于此，本试验采用小粒径的碎石模拟可压缩层材料，控制参数为碎石的孔隙率。
针对管片壁后不设置可压缩层和设置碎石可压缩层(厚度3 cm，对应原型0.6 m；孔隙率0.6)的工况进行对比，如图3所示。图中尺寸标注为原型值。
图3 可压缩层设置情况
Fig.3 Arrangement of compressible layer
为了保证可压缩层的厚度，先根据可压缩层厚度及管片环外径，将厚铁皮卷成所需直径的护壳，并放置于填土上方，依此将填土中心部位护壳范围内的土体挖出，并居中放入管片环，再填入碎石，缓缓抽出护壳，再将管片壁后碎石层及土体夯实挤密。
试验在“盾构隧道-地层复合体模型试验系统”上开展。“盾构隧道-地层复合体模型试验系统”的装置总体尺寸为3 m×3 m×0.16 m，采用卧式加载方式，可实现竖向(I方向)、水平(II方向)和纵向(III方向)三个方向的荷载施加。每个方向均由4台液压千斤顶通过工字钢或盖板作为荷载分配梁对土体施加均布面荷载。其中I、II方向的千斤顶两两成组，对称布置，I方向施加荷载为结构所受竖向荷载，根据地层条件和埋深等因素计算确定；II方向施加水平荷载，根据侧压力系数和I方向荷载计算确定。III方向为纵向荷载，通过盖板施加，目的是保证加载过程满足平面应变状态。试验装置如图4所示。
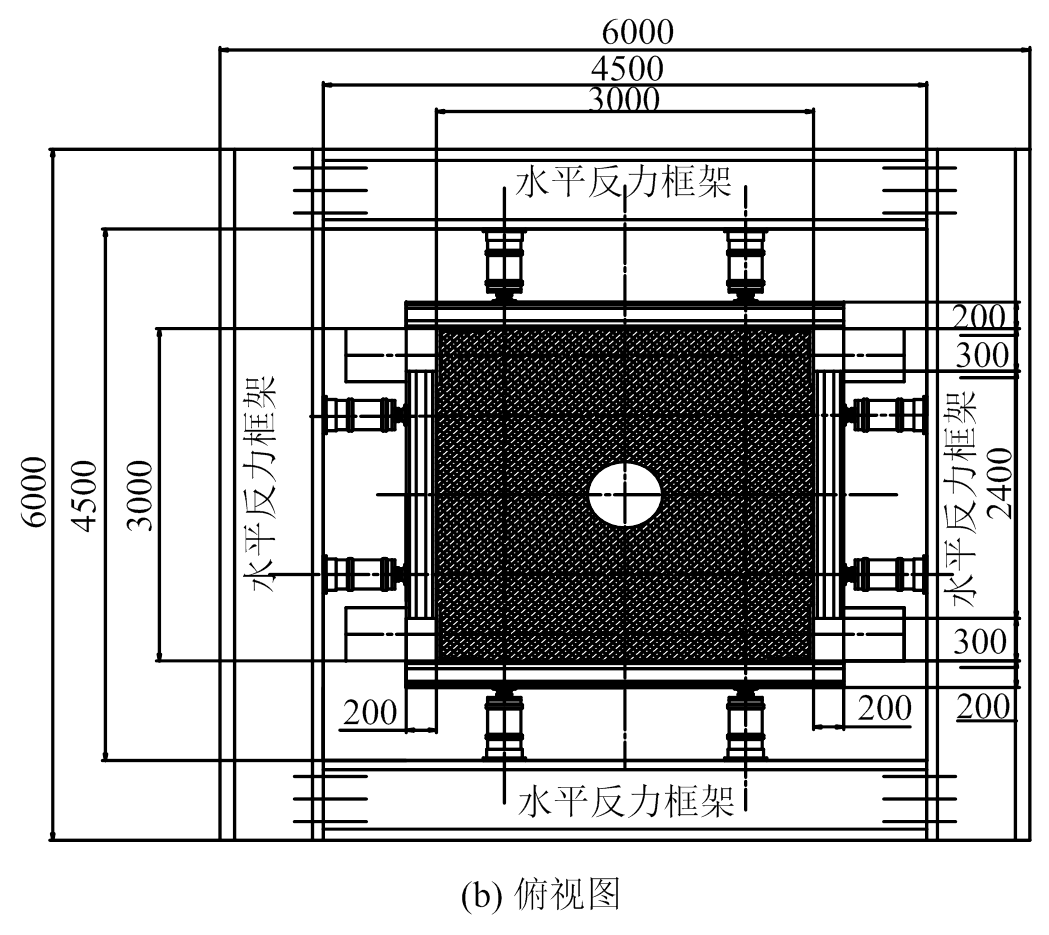
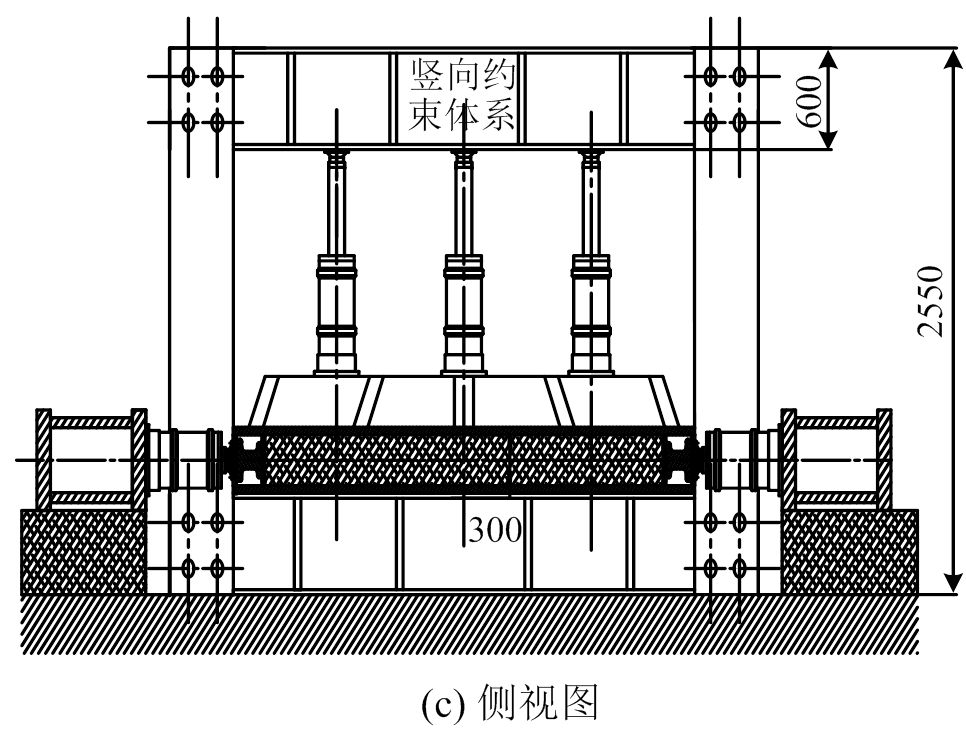
图4 盾构隧道-地层复合体模型试验系统
Fig.4 Schematic of shield tunnel-stratum-complex model test system
试验主要对管片结构内力进行量测。以24°为单位在管片环内、外侧对称布设环向电阻应变片，测试内外侧应变值，根据式(1)计算管片环结构截面内力。应变测点布置如图5所示。
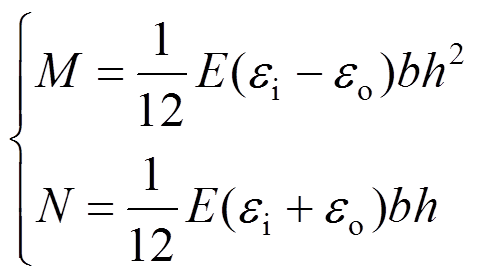(1)式中：M、N分别为管片衬砌弯矩和轴力；b、h分别为管片衬砌的宽度和厚度；E为管片衬砌弹性模量；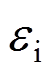
和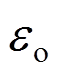
分别为管片衬砌内、外侧应变。
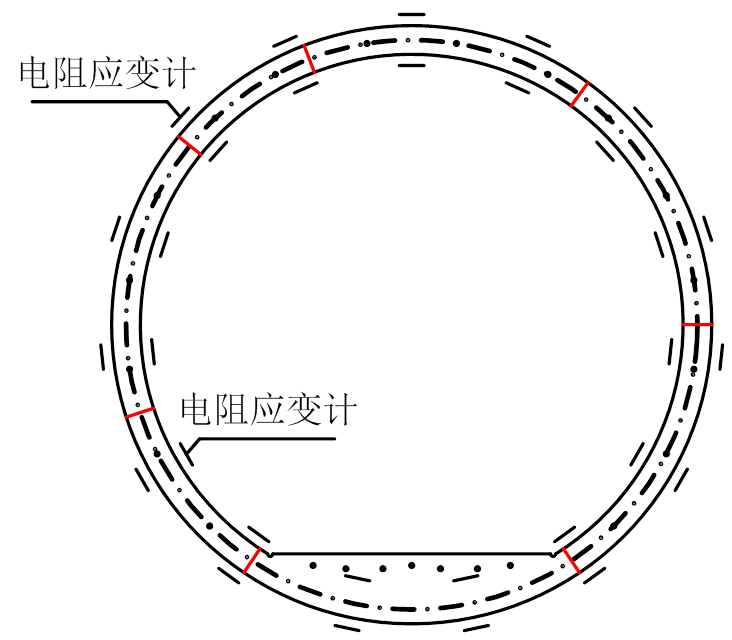
图5 测点布置示意图
Fig.5 Schematic of gauge arrangement
试验按如下分组：
①均一地层，管片衬砌支护；
②均一地层，管片衬砌+可压缩层联合支护；
③上硬下软复合地层，管片衬砌支护；
④上硬下软复合地层，管片衬砌+可压缩层联合支护。
加载过程中保持侧压力系数0.5不变，竖向土压力从0开始，初期按照10 m等效覆土厚度的增量逐级加载，当根据测试数据发现管片内力有增速加快的迹象时，减为5 m每级加载。每级荷载保持10 min左右，待数据稳定后进行下一级加载，直至管片发生失稳破坏。水平土压力由竖向土压力和侧压力系数计算得到。
虽然模型试验结果更加直观，但其试验过程复杂，成本较高，且可重复性较差，因此只能开展有限的组数。为能够更系统地研究复合地层中管片衬砌与可压缩层联合支护的效果，需开展多种工况的对比研究，因此采用ANSYS软件建立数值计算模型，针对不同参数下联合支护体系中管片衬砌的受力情况进行对比分析，探讨联合支护的效果。
计算模型按平面应变问题考虑，各材料的几何参数及物理力学参数取值同模型试验。管片衬砌和可压缩层为线弹性材料，地层材料满足Drucker- Prager屈服准则。管片衬砌采用Beam单元模拟，地层和可压缩层采用Plane单元模拟，可压缩层与管片衬砌和地层之间分别设置接触单元，以模拟其间的相互滑动、分离和闭合等行为，更符合实际情况。为避免管片接头和接触单元同时存在造成的计算难以收敛问题，采用刚度有效系数近似考虑管片接头导致的整环刚度下降，其取值可通过分别建立梁-弹簧模型和考虑刚度折减的匀质圆环模型对比得到，计算可得η=0.62。边界条件与模型试验相同，在上下左右四个边界分别施加法向均布压力，不考虑材料自重。
首先将相同条件下的数值计算结果与模型试验结果对比，以验证数值计算方法的可靠性。在此基础上，增加更多工况，采用数值计算手段进行参数化分析，研究复合地层中软、硬地层相对厚度和相对刚度对支护效果的影响。计算模型如图6所示，其物理力学参数和几何尺寸均根据原型取值。根据对称性，图中仅示出了1/2模型。图中t为管片拱顶至软硬地层分界面范围内的硬岩厚度，D为管片直径。
以竖向土压力为30 m等效土柱时的结果为例进行对比(下同)，此时管片处于弹性工作状态。图7所示为均一地层条件下管片衬砌弯矩和轴力的试验值与计算值对比。图中试验值为根据模型试验结果和相似比例换算成原型后整个幅宽上的结果，计算下同。
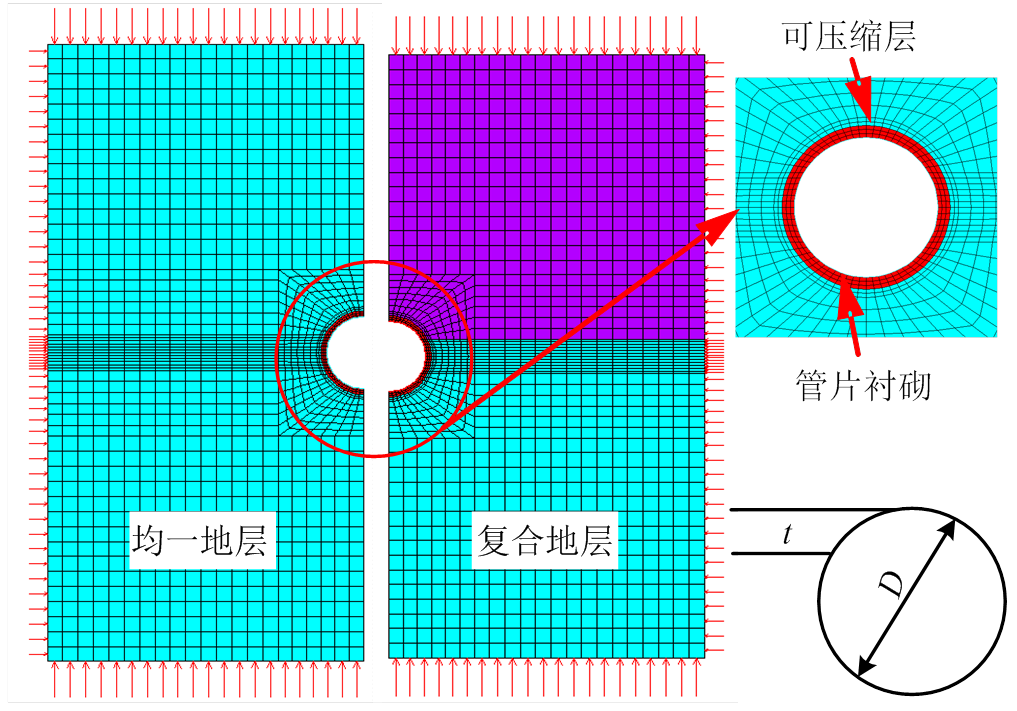
图6 有限元计算模型
Fig.6 Schematic of FEM model
总体上看，对于均一地层，管片内力试验值和计算值的分布规律和量值都很接近。
如图7(a)所示，对于模型试验，无可压缩层情况下，管片最大正弯矩240.31 kN·m，位于拱顶偏左位置，最大负弯矩-206.43 kN·m，位于右侧拱腰附近；有可压缩层情况下，最大正负弯矩分别为192.24 kN·m和-180.7 kN·m，分别位于拱顶偏左位置和右侧拱腰附近。可压缩层的存在不仅降低了弯矩量值，还使得弯矩沿环向的分布更为均匀。相比无可压缩层，管片最大正弯矩减小了19.9%，最大负弯矩减小了12.5%。对于数值计算，无可压缩层情况下，管片最大正弯矩251.62 kN·m，位于拱顶，最大负弯矩-259.96 kN·m，位于左侧拱腰；有可压缩层情况下，最大正负弯矩分别为211.57 kN·m和-207.90 kN·m，分别位于拱顶和左侧拱腰附近，最大正负弯矩分别减小了15.9%和20.0%。模型试验情况下，由于接头的存在改变了管片环局部刚度，故最大正弯矩出现在拱顶左侧，最大负弯矩出现于右侧拱腰；而数值计算中通过刚度有效系数对整环管片进行了刚度折减，管片环整体刚度是均匀的，故最大正负弯矩分别出现在拱顶和左侧拱腰。
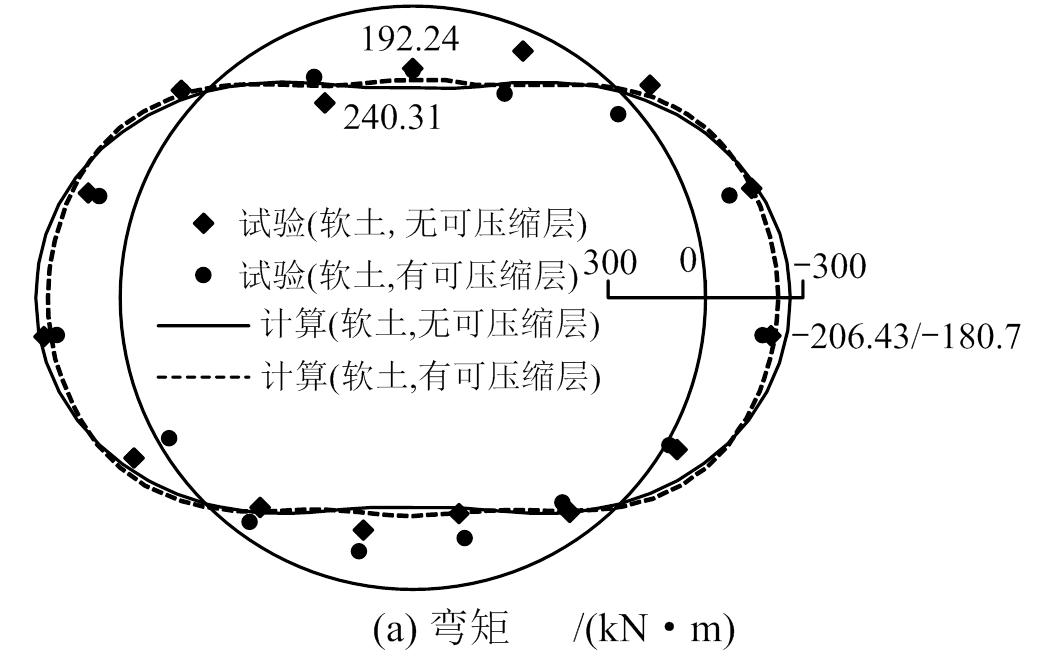
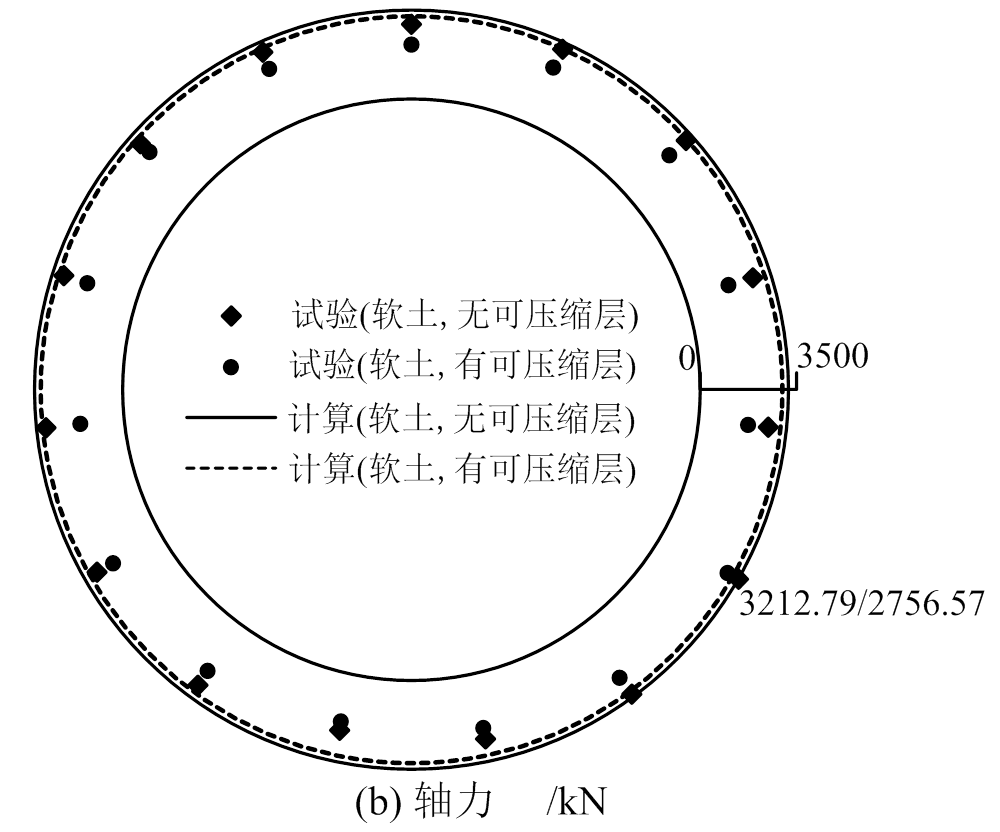
图7 均一地层条件下管片内力环向分布
Fig.7 Circumferential distribution of segment internal forces in uniform stratum
如图7(b)所示，对于模型试验，无可压缩层情况下，管片最大轴力3212.79 kN，位于右侧拱脚附近；有可压缩层情况下，最大轴力2756.57 kN，仍位于右侧拱脚附近。可压缩层的降低了轴力量值。相比无可压缩层，管片最大轴力减小了14.2%。对于数值计算，无可压缩层情况下，管片最大轴力3364.21 kN，位于拱底；有可压缩层情况下，最大轴力2799.01 kN，位于左侧拱腰，比无可压缩层时减小了12.9%。实际上，有无可压缩层情况下轴力的计算结果沿环向分布均很均匀。
4.2.1 复合地层与均一地层
将无可压缩层条件下复合地层与均一地层的试验结果和计算结果进行对比。图8所示为t/D= 0.25时管片衬砌弯矩和轴力试验值与计算值的分布情况。
总体上看，对于复合地层而言，管片内力试验值和计算值的分布规律和量值都很接近。
如图8(a)所示，复合地层条件下，模型试验所得的管片最大正弯矩132.17 kN·m，位于拱顶偏左位置，最大负弯矩-156.27 kN·m，位于左侧拱腰附近；与均一地层相比较，最大正负弯矩出现的位置没有发生变化，但量值分别减小45%和24.3%，圆周上其他各点弯矩均有不同程度的减小，且拱顶附近的减小幅度比拱底附近的大。说明上方硬岩对管片的约束作用强，能够提供更大的地层抗力，从而分担较多的围岩荷载，减小了管片弯矩。对于数值计算，均一地层时管片弯矩分布与量值上下对称，最大正负弯矩分别产生于拱顶和左侧拱腰。复合地层条件下管片弯矩的分布上下不再对称，最大负弯矩出现的位置由拱腰偏移至下伏软土层，因此对管片弯矩的分布和量值均产生了影响。
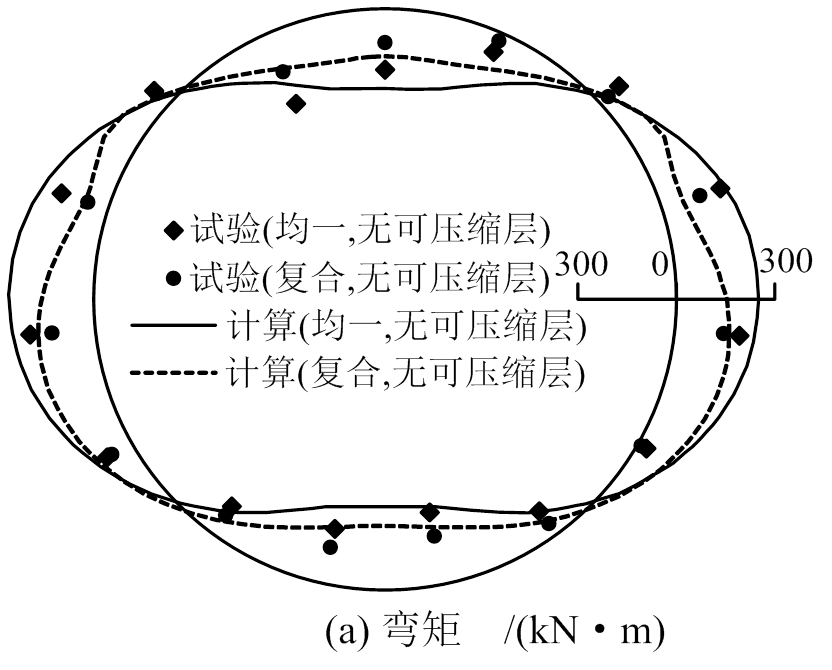
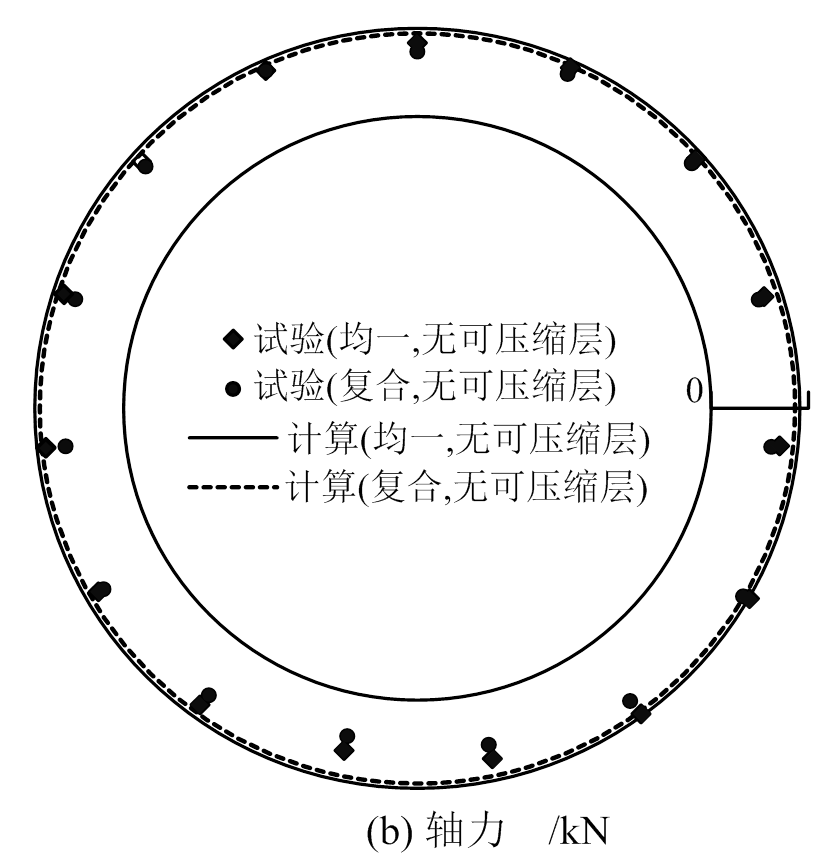
图8 复合地层与均一地层管片内力环向分布
Fig.8 Circumferential distribution of segment internal forces in composite and uniform strata
如图8(b)所示，对于试验结果，相比均一地层而言，复合地层条件下管片轴力的分布情况未产生明显变化，轴力量值有所减小，最大轴力减小9.6%。轴力的计算结果分布更加均匀，最大轴力减小约8%。
管片衬砌需要承担地层主动荷载和以地层抗力形式存在的被动荷载。对于本文而言，无论均一地层还是复合地层，管片拱顶上方地层都是均一的，则作用在管片上的主动荷载可视为常值，因此，上述不同工况管片内力的差异主要由各自产生的不同被动荷载引起。可以看出，管片弯矩对复合地层抗力更为敏感，而轴力对复合地层反力不敏感，说明管片轴力主要由作用在结构上的地层主动荷载决定。
4.2.2 复合地层有无可压缩层
将复合地层条件下有无可压缩层时的试验结果和计算结果进行对比。图9所示为t/D=0.25时管片衬砌弯矩和轴力试验值与计算值的分布情况。
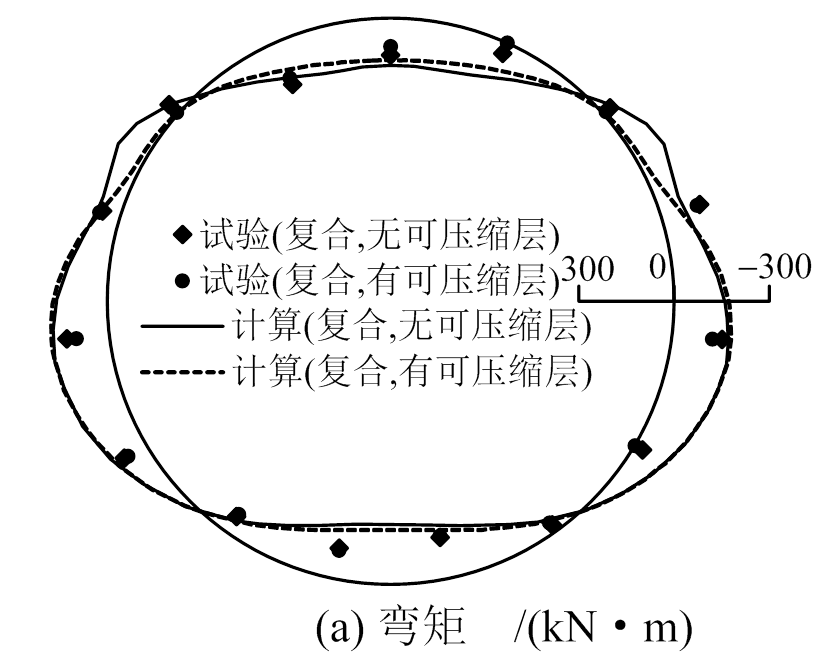
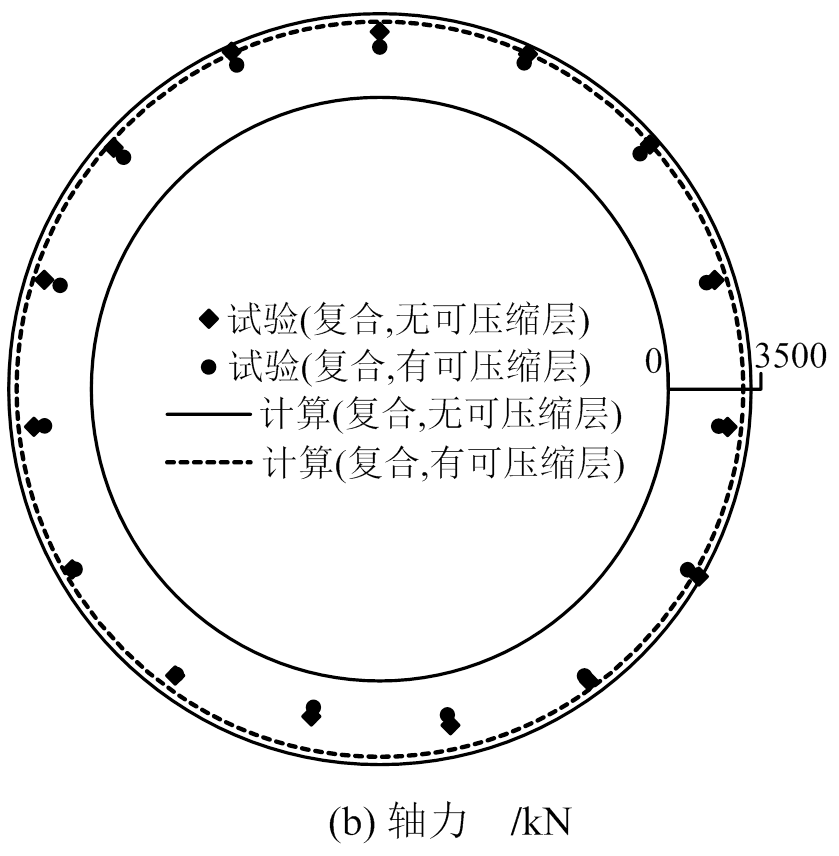
图9 复合地层有无可压缩层时管片内力环向分布
Fig.9 Circumferential distribution of internal forces of segment with or without compressible layer in composite strata
如图9(a)所示，复合地层条件下，模型试验结果表明可压缩层会减小管片弯矩。无可压缩层时管片最大正弯矩132.17 kN·m，位于右侧拱肩，最大负弯矩-156.27 kN·m，位于左侧拱腰附近；设置可压缩层后，管片最大正弯矩减小至113.01 kN·m，减幅14.5%，最大负弯矩减小至-127.67 kN·m，减幅18.3%。可压缩层的存在使得管片弯矩沿环向的分布更加均匀，且关于竖轴的对称性更好。
数值计算结果与试验结果较为吻合，且对有无可压缩层时弯矩分布情况的差异展示的更为清楚。从图9(a)可以看出，无可压缩层时软硬地层分界面位置附近管片弯矩存在明显的起伏变化，而设置可压缩层之后，可根据地层软硬的变化作出相应调整，从而消除分界面附近弯矩的起伏变化。而在模型试验中由于软硬地层分界面正好位于两对应变片之间，分界面附近弯矩起伏变化情况在模型试验中无法观测到。
如图9(b)所示，对于试验结果和计算结果，相比较均一地层而言，复合地层条件下管片轴力的分布情况未产生明显变化，轴力的量值略有减小，但不显著。
定义t/D为上覆硬岩相对厚度(如图6)。分别取t/D=0.000、0.250、0.375、0.500、0.625、0.750、1.000，得到各工况下管片弯矩的分布曲线，如图10所示。以t/D=0.0时的弯矩(M0)为基准对各工况最大正负弯矩进行规范化，可得管片最大弯矩随t/D的变化曲线，如图11所示。
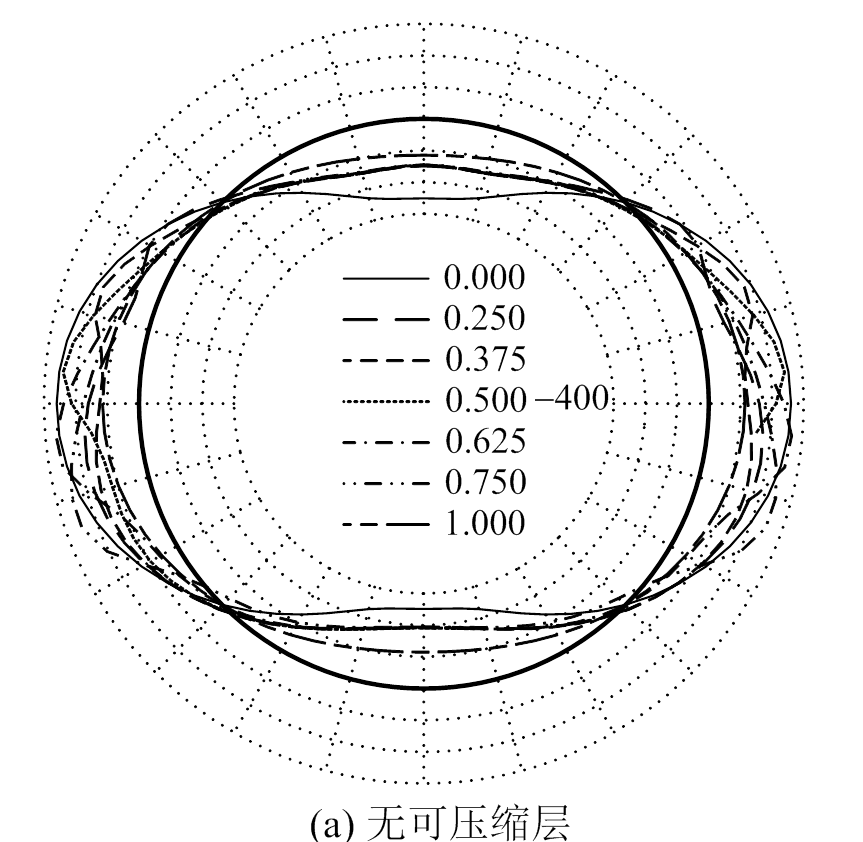
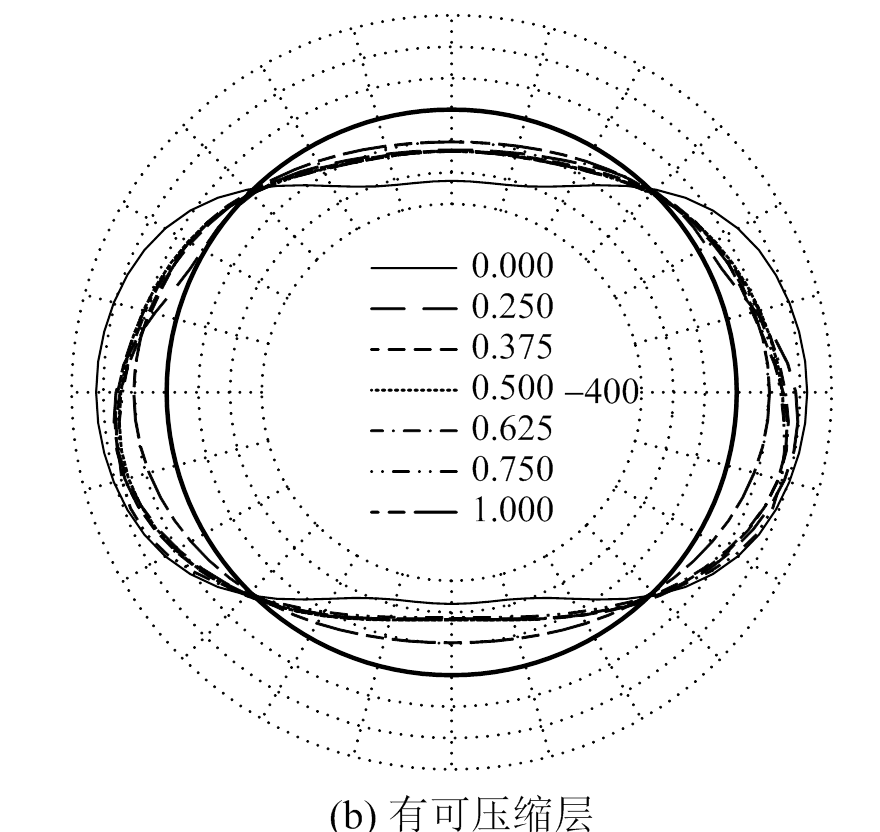
图10 不同地层相对厚度时管片弯矩环向分布 /(kN·m)
Fig.10 Circumferential distribution of segment internal forces with different relative thicknesses of strata
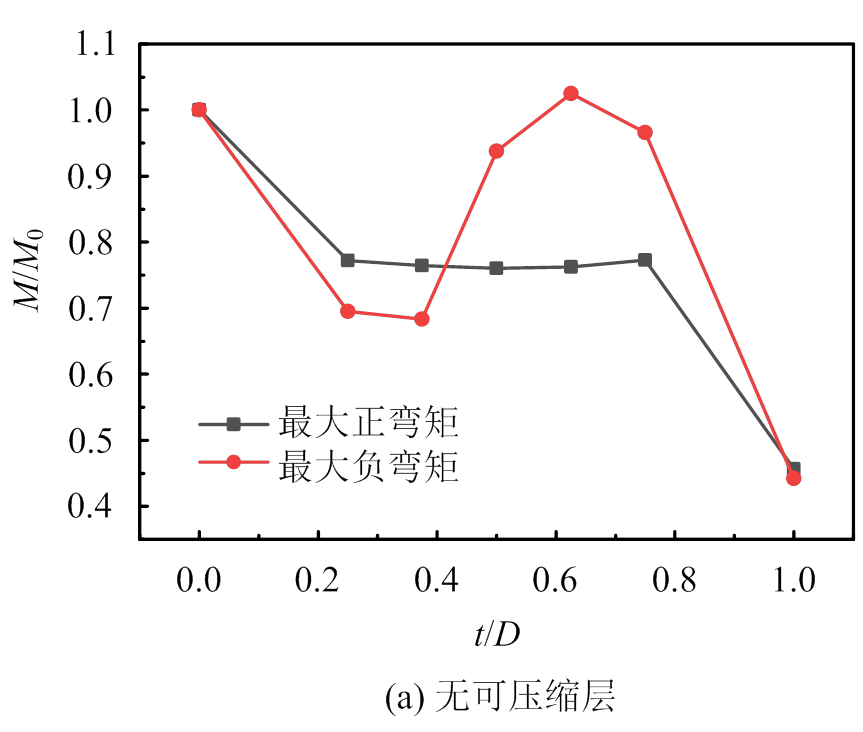
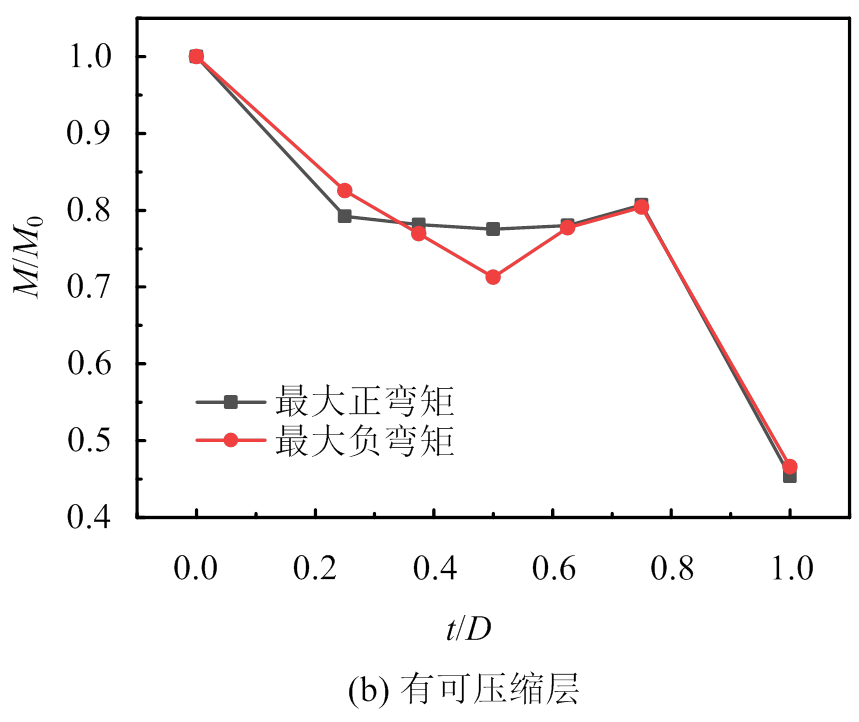
图11 管片最大弯矩随t/D的变化曲线
Fig.11 Variation curves of maximum bending moment with t/D
从图中可以看出，无可压缩层条件下，随着t/D的增大，管片最大正弯矩均产生于拱顶，除去t/D=0.0和t/D=1.0两种极端情况外，量值未发生明显变化，始终保持为均一软土地层弯矩的76%左右；但最大负弯矩变化显著，其产生位置偏向下伏软土一侧，且t/D越大偏移越明显，除去t/D=0.0和t/D=1.0两种极端情况外，量值在均一软土地层弯矩的68%~103%之间变化。究其原因，是因为对于拱顶正弯矩而言，虽然t/D在不断变化，但拱顶始终处于均一硬岩地层中，故变化相对缓和；而对于两侧拱腰的负弯矩，随着t/D的变化，拱腰从处于单一软岩过渡到软硬复合地层，再到单一硬岩，管片与地层的相互作用更为复杂，因此变化更为明显。
有可压缩层条件下，最大正弯矩量值和变化情况与无可压缩层时类似，但最大负弯矩的变化明显缓和，除去t/D=0.0和t/D=1.0两种极端情况外，量值在均一软土地层弯矩的71%~83%之间变化，管片弯矩沿环向的变化明显比无可压缩层时缓和。
随着t/D的增大，管片轴力变化甚微，此处未列出。
定义复合地层相对刚度Et/Eb为上覆地层刚度与下伏地层刚度之比，保持上覆地层刚度不变，通过改变下伏地层刚度，使得Et/Eb依次取0.10、0.25、0.50、1.00、1.50、2.43、5.00、10.00，并保持t/D=0.50得到各工况下管片弯矩的分布曲线，如图12所示。以均一硬岩地层时的弯矩为基准对各工况最大正负弯矩进行规范化，可得管片最大弯矩随Et/Eb的变化曲线，如图13所示。
从图13(a)可以看出，无可压缩层条件下，随着Et/Eb的增大，管片最大正弯矩先产生于拱顶；当Et/Eb大于1.50后，随着Et/Eb的继续增大，最大正弯矩开始出现在拱底，这是由于当Et/Eb较小时，地层为“上软下硬”复合地层，拱顶上方围岩对管片的约束作用弱，能够提供的地层抗力较小，从而分担围岩荷载比重较小，管片弯矩相应要大一些。而当Et/Eb较大时，情况则正好相反，地层成为“上硬下软”复合地层，拱底下方围岩对管片的约束作用弱，能够提供的地层抗力较小，从而分担围岩荷载比重较小，管片弯矩相应要大一些。
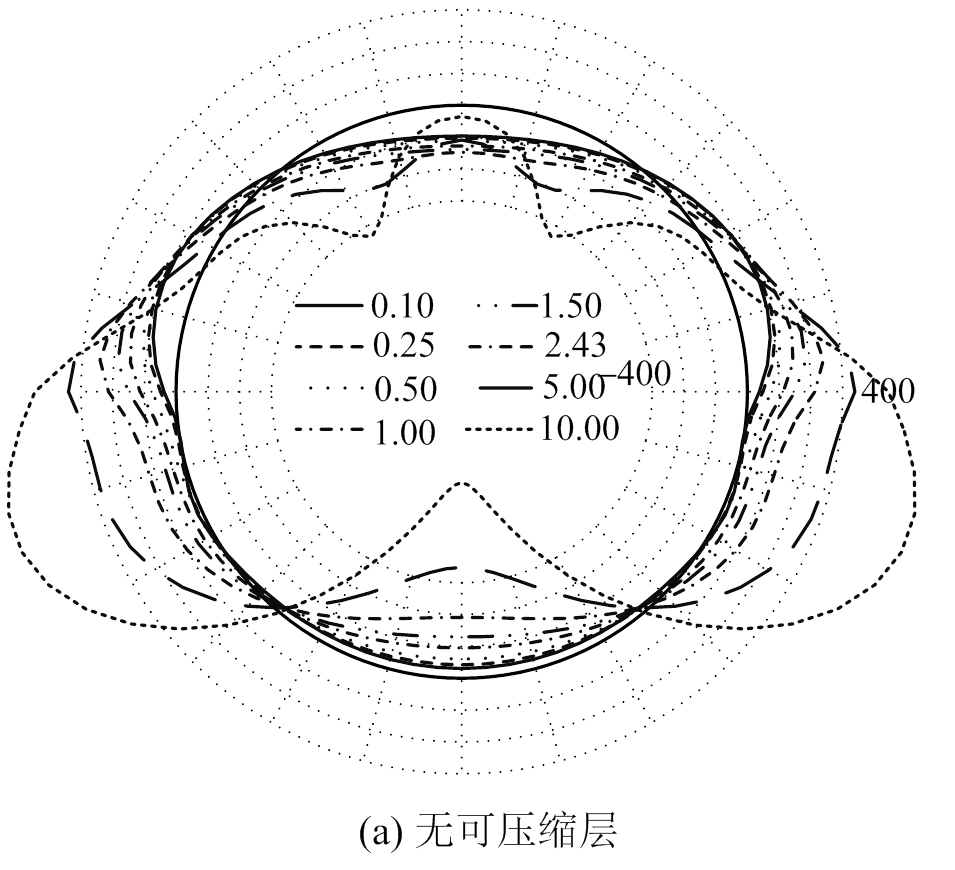
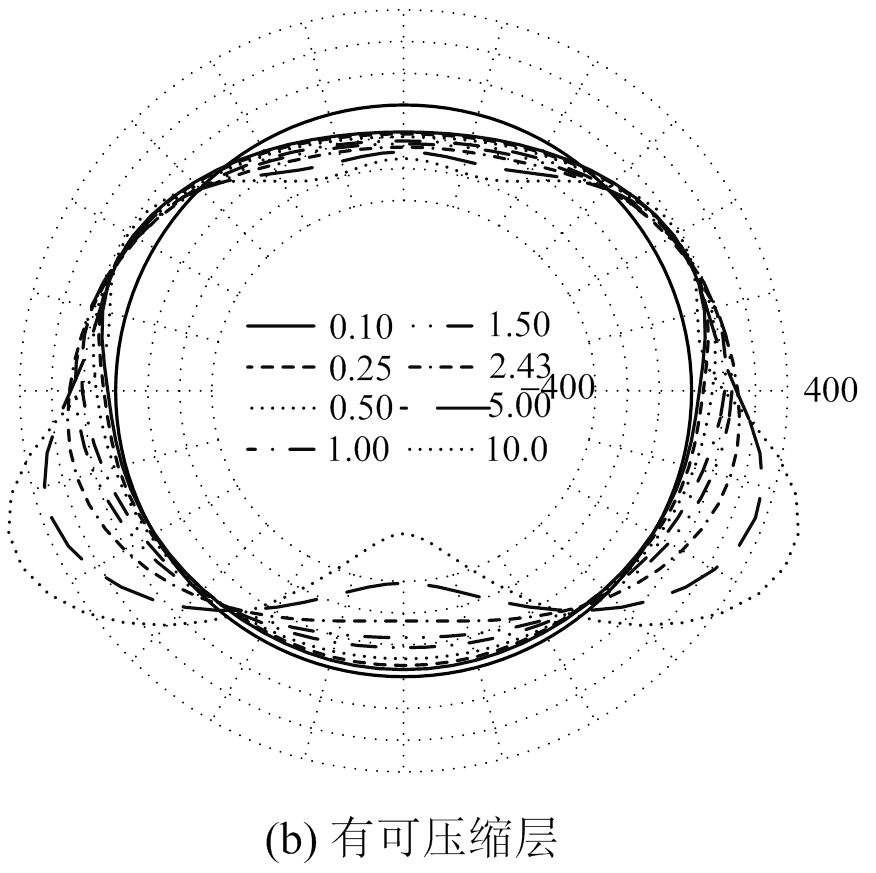
图12 不同相对刚度时管片弯矩环向分布 /(kN·m)
Fig.12 Circumferential distribution of segment internal forces with different relative stiffnesses of strata
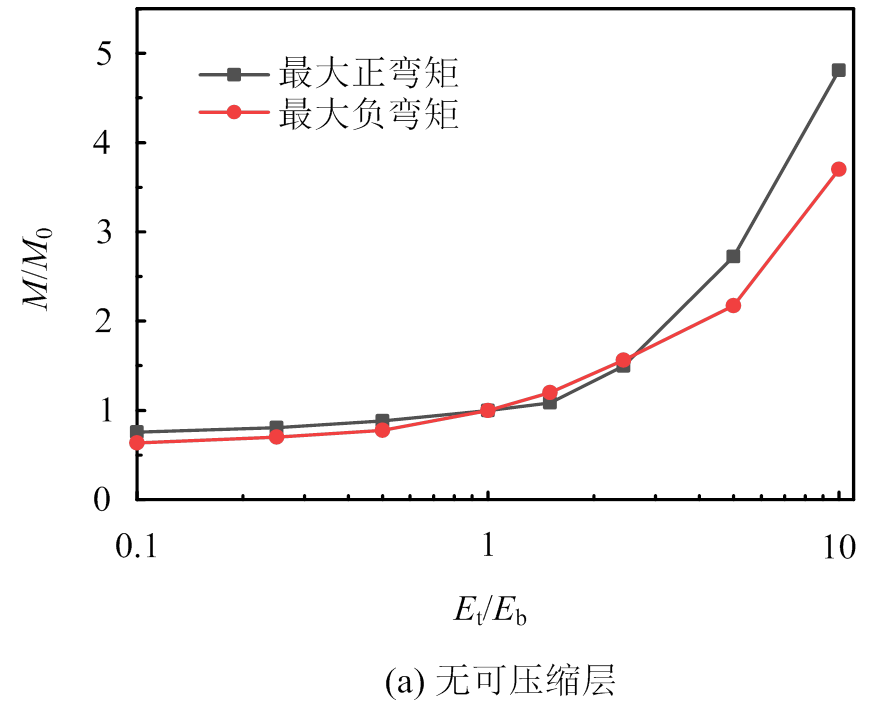
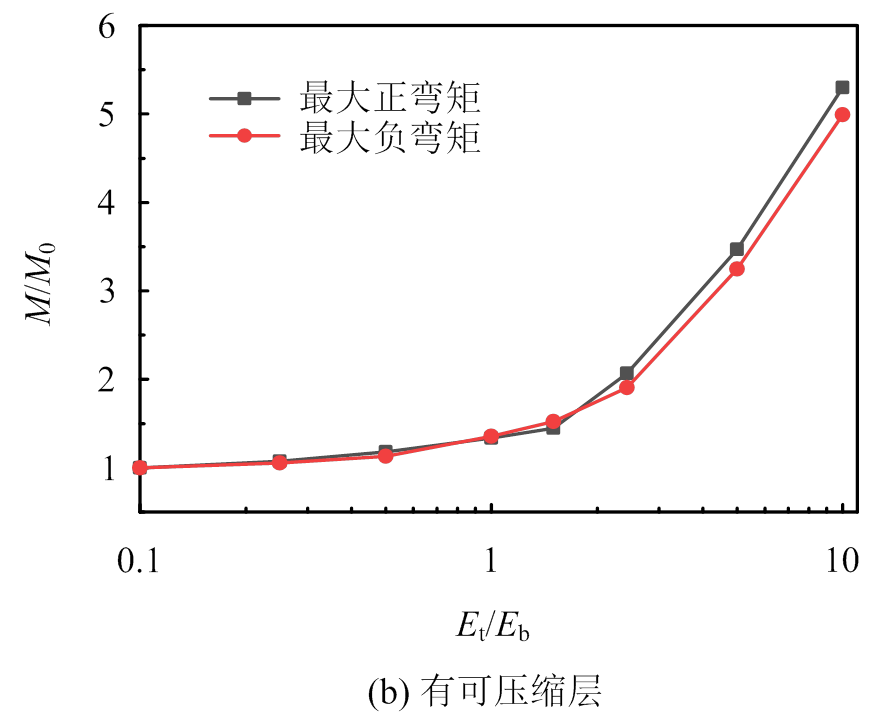
图13 管片最大弯矩随Et/Eb的变化曲线
Fig.13 Variation curves of maximum bending moment with Et/Eb
从图13(b)可以看出，当Et/Eb小于1.0，即地层为“上软下硬”复合地层时，管片弯矩受复合地层相对刚度的影响较小，其变化曲线较平缓；一旦Et/Eb超过1.0，即地层为“上硬下软”复合地层时，管片弯矩随相对刚度急剧变化，说明对于“上硬下软”复合地层，管片弯矩更容易受地层相对刚度的影响。
随着Et/Eb的增大，管片轴力变化甚微，此处未列出。
(1) 在模型正确建立且参数取值合理的前提下，有限元数值计算结果可以和相似模型试验结果很好的吻合，包括管片内力分布规律及其量值。
(2) 对于均一地层，可压缩层的存在可使管片最大弯矩减小12.5%~19.9%，最大轴力减小14.2%；对于复合地层，可压缩层的存在可使管片最大弯矩减小14.5%~18.3%，对轴力的影响不明显。可压缩层的存在使得管片内力分布更加均匀。
(3) 复合地层条件下，管片内力的差异主要由各自产生的不同地层抗力引起。管片弯矩对复合地层抗力更为敏感，而轴力对复合地层反力不敏感。
(4) 复合地层相对厚度对管片最大正弯矩的影响较为恒定，无论有无可压缩层，最大正弯矩始终保持为均一地层的76%左右；但其对管片最大负弯矩影响显著，使其产生位置偏向相对较软一侧的地层，且相对厚度越大偏移越明显。
(5) 复合地层中相对较硬的一方对管片约束作用强，能够提供更大的地层抗力，从而分担较多的围岩荷载，减小管片内力。“上硬下软”复合地层中管片弯矩更容易受地层相对刚度的影响。
参考文献：
[1] 何川. 盾构/TBM施工煤矿长距离斜井的技术挑战与展望[J]. 隧道建设, 2014, 34(4): 287―297.
HE Chuan. Challenges and prospective of construction of long-distance inclined shafts of coal mine by shield/TBM [J]. Tunnel Construction, 2014, 34(4): 287―297. (in Chinese)
[2] 刘泉声, 黄兴, 刘建平, 等. 深部复合地层围岩与TBM的相互作用及安全控制[J]. 煤炭学报, 2015, 40(6): 1213―1224.
Liu Quansheng, Huang Xing, Liu Jianping, et al. Interaction and safety control between TBM and deep mixed ground [J]. Journal of China Coal Society, 2015, 40(6): 1213―1224. (in Chinese)
[3] 王俊奇, 何本国, 张有天, 等. 深埋隧道轴线合理布置与衬砌结构稳定性研究[J]. 工程力学, 2015, 32(12): 188―197.
Wang Junqi, He Benguo, Zhang Youtian, et al. Study on the axis orientation and stability of linings for deep tunnels [J]. Engineering Mechanics, 2015, 32(12): 188―197. (in Chinese)
[4] Yu Yang, Bai Jianbo, Wang Xiangyu, et al. High-resistance controlled yielding supporting technique in deep-well oil shale roadways [J]. International Journal of Mining Science and Technology, 2014, 24(2): 229―236.
[5] 袁亮. 深井巷道围岩控制理论及淮南矿区工程实践[M]. 北京: 煤炭工业出版社, 2006.
Yuan Liang. Control of surrounding strata in deep mine roadways and practice in Huainan area [M]. Beijing: China Coal Industry Publishing House, 2006. (in Chinese)
[6] 赵玉东. 挤压型大变形地下硐室中支护型式的适宜性研究[D]. 成都: 西南交通大学, 2016.
Zhao Yudong. Research on suitability of supporting types for large deformation underground chamber in squeezing ground [D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese)
[7] 孙闯, 张向东, 张建俊. 深部断层破碎带竖井围岩与支护系统稳定性分析[J]. 煤炭学报, 2013, 38(4): 2282―2292.
Sun Chuang, Zhang Xiangdong, Zhang Jianjun. Stability analysis of vertical shaft surrounding rock and supporting system in deep fault fracture [J]. Journal of China Coal Society, 2013, 38(4): 2282―2292. (in Chinese)
[8] 牛双建, 靖洪文, 张忠宇, 等. 深部软岩巷道围岩稳定控制技术研究及应用[J]. 煤炭学报, 2011, 36(4): 914―920.
Niu Shuangjian, Jing Hongwen, Zhang Zhongyu, et al. Study on control technology of surrounding rocks in deep soft roadway and its application [J]. Journal of China Coal Society, 2011, 36(4): 914―920. (in Chinese)
[9] 王卫军, 彭刚, 黄俊. 高应力极软破碎岩层巷道高强度耦合支护技术研究[J]. 煤炭学报, 2011, 22(2): 223―229.
Wang Weijun, Peng Gang, Huang Jun. Research on high-strength coupling support technology of high stress extremely soft rock roadway [J]. Journal of China Coal Society, 2011, 22(2): 223―229. (in Chinese)
[10] Ramoni M, Anagnostou G. Tunnel boring machines under squeezing conditions [J]. Tunneling and Underground Space Technology, 2010, 25(2): 139―157.
[11] Cantieni L, Anagnostou G. The interaction between yielding supports and squeezing ground [J]. Tunneling and Underground Space Technology, 2009, 24(3): 309―322.
[12] 胡雄玉, 晏启祥, 何川, 等. 管片衬砌配合碎石可压缩层的斜井支护结构型式及其应用[J]. 岩石力学与工程学报, 2016, 35(3): 579―591.
Hu Xiongyu, Yan Qixiang, He Chuan, et al. A support structure of segment lining combined with compressible crushed stone and its applications in inclined shaft [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 579―591. (in Chinese)
[13] 竺维彬, 鞠世健. 复合地层中的盾构施工技术[M]. 北京: 中国科学技术出版社, 2006. Zhu Weibin, Ju Shijian. Shield tunneling technology in nixed face ground conditions [M]. Beijing: China Science and Technology Press, 2006. (in Chinese)
[14] 何川, 张建刚, 杨征. 层状复合地层条件下管片衬砌结构力学特征模型试验研究[J]. 岩土工程学报, 2008, 30(10): 1537―1543.
He Chuan, Zhang Jiangang, Yangzheng. Model test on mechanical characteristics of segment lining structure under multi-layered strata [J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1537―1543. (in Chinese)
[15] 徐国文, 王士民, 汪冬兵. 基于接头抗弯刚度非线性的壳-弹簧-接触-地层模型的建立[J]. 工程力学, 2016, 33(12): 158―166.
Xu Guowen, Wang Shimin, Wang Dongbing. Shell- spring-contact-ground model based on segment joint stiffness nolinearity [J]. Engineering Mechanics, 2016, 33(12): 158―166. (in Chinese)
[16] 朱宏海. 上软下硬复合地层地铁盾构隧道设计及施工探析[J]. 隧道建设, 2015, 35(2): 144―148.
Zhu Honghai. Design and construction of shield-bored metro tunnels in hard-soft heterogeneous ground, 2015, 35(2): 144―148. (in Chinese)
STUDY ON THE EFFECTS OF COMBINED SUPPORTS OF SEGMENTAL LININGS AND COMPRESSIBLE LAYERS IN DEEP-BURIED COMPOSITE GROUND
Abstract: The surrounding rock pressure of deep buried shield tunnels is mainly the deformation pressure produced by large extrusion type deformation of the surrounding rock. Its main feature is that the deformation lasts for a long time with repeatability. The pressure of the surrounding rock will keep increasing after the support is completed. Because it is unfeasible to restrain the deformation of surrounding rock by increasing the support rigidity, yieldable supports become a solution for the problem. Meanwhile, due to the complexity and variability of the surrounding rock condition and the rock mass structure, it is inevitable to pass through composite strata in shield tunnel construction. Based on the inclined shafts in two deep buried shield coal mines, comparison and analysis on the mechanical properties of segment linings with the segment lining + compressible layer combined supports in different composite stratum conditions are studied by means of similarity model tests and the finite element numerical method. The results indicate that the finite element method results are in good agreement with the experimental results when the model is correctly established and the parameter values are reasonable. Under the uniform formation condition, the compressible layer brings about 12.5%~19.9% decrease to the maximum bending moment and 14.2% decrease to the maximum axial force. The composite stratum causes obvious changes in the value and distribution of the segment bending moment, but has little effect on the segmental axial force, indicating that the bending moment is more sensitive to the resistance of the composite stratum while the axial force is relatively insensitive. With the compressible layer, the distribution of the segment internal force is more uniform in the composite stratum and there is little change in the axial force. Furthermore, the relative thickness of the composite stratum influences the maximum positive bending moment stably. It also greatly influences the maximum negative bending moment, causing deviation to the relative soft side of its generating position. The larger the relative thickness of the composite stratrum, the more obvious is the deviation. In an upper hard and lower soft composite stratum, the segment bending moment is more easily affected by the relative stiffness of the stratum.
Key words: shield (TBM) construction; model test; composite stratum; segmental lining; compressible layer; yieldable support
文章编号：1000-4750(2019)04-0062-10
中图分类号：TD262; U25
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.10.0760
收稿日期：2017-10-11；
修改日期：2019-01-02
基金项目：国家重点研发计划项目(2016YFC0802202)；国家自然科学基金项目(51878569，51578462，U1361210)
何 川(1964―)，男，重庆人，教授，博士，博导，主要从事隧道与地下工程方面的教学和研究工作(E-mail: chuanhe21@163.com);
彭祖昭(1993―)，男，广东人，硕士生，主要从事隧道与地下工程方面的研究工作(E-mail: 1101091692@qq.com);
汤 印(1991―)，男，四川人，硕士，主要从事隧道与地下工程方面的设计与研究工作(E-mail: 1530398460@qq.com);
代 聪(1988―)，男，山东人，博士，主要从事隧道与地下工程方面的研究工作(E-mail: dc_526@163.com).