
图1 扑翼气动力测试平台工作原理[25]
Fig.1 Working principle of the flapping wing aerodynamic force platform[25]
摘 要:昆虫、鸟类与蝙蝠等生物具有高超的飞行能力,是扑翼飞行器的主要模仿对象。近年来,扑翼空气动力学领域的研究取得了很大进展,该文主要对其主要研究成果进行综述,重点介绍扑翼空气动力学各研究方向的最新进展,包括昆虫、鸟类与蝙蝠扑翼的主要升力机制,翅膀形态学参数与微观结构、翅膀柔性与动态变形、翼-翼干扰、翼-身干扰、个体间干扰及地面效应等对扑翼气动特性的影响。同时还对仿生扑翼飞行器气动研究的新进展进行了介绍,并提出了扑翼空气动力学所面临的主要问题和挑战。
关键词:扑翼;空气动力学;昆虫;鸟类;蝙蝠
自然界有近100万种飞行昆虫、9000余种鸟类以及1000余种蝙蝠采用扑翼飞行。这些生物形态各异,其中很多物种具备高超的飞行能力,例如蜻蜓可以实现悬停、侧飞、倒飞等运动[1];沙漠蝗虫一天可以飞行数百公里,甚至会数以亿只组成集群飞越大西洋[2];而军舰鸟则可以完成3000 km的不间断迁徙飞行,并在飞行过程中睡眠[3]。自古至今,人类一直对扑翼生物的飞行机理抱有浓厚兴趣。早在公元15世纪,Leonardo da Vinci就根据自己对鸟类飞行的观察,绘制了人力驱动扑翼机的设计草图[4]。但真正从空气动力学角度研究扑翼飞行机理则只有百年历史。最初研究者采用定常及准定常分析方法对生物扑翼气动特性进行评估,很难得到正确的结果[5]。自20世纪80年代起,随着实验观测手段 进步以及计算流体力学(Computational Fluid Dynamics,CFD)发展,研究者开始从非定常角度研究扑翼空气动力学,并取得了一系列卓越成果[6-15]。
经过以上阶段发展,扑翼空气动力学形成了一套较完备的体系构架,但也提出了更多有趣且充满挑战性的问题,微小结构在扑翼飞行中的作用、集群飞行时的个体间气动干扰等问题研究正处于起步阶段。在这样的大背景下,本文对近年来有关扑翼空气动力学的研究进行综述,介绍扑翼气动研究的各研究方向最新进展,并指出未来可能的发展方向,以求对扑翼空气动力学研究及人造扑翼飞行器设计有所帮助与启发。
本文将首先介绍昆虫、鸟类与蝙蝠扑翼气动研究中所使用的主要研究方法及所发现的主要升力机理,随后依次讨论翅膀形态学参数对气动特性影响、翅膀微观结构、翅膀柔性与动态变形,翼-翼、翼-身、个体间干扰及地面效应。得益于理论进步,仿生扑翼飞行器研制近年来取得一系列突破,本文对仿生扑翼飞行器气动研究中的新进展与新问题进行了介绍。并在最后对扑翼空气动力学相关工作进行总结与展望。
昆虫、鸟类与蝙蝠在飞行过程中通过扑动翅膀以产生升力与推力,并依靠对翼面运动模式的快速动态调节实现出色的稳定性与机动性。复杂的扑翼运动与柔性的翅膀结构导致扑翼周围的流场具有强非定常与高度三维化特征。近年来,为研究这类复杂流动问题,多种数值与实验手段均有所应用。
扑翼气动实验的研究重点之一是扑翼气动力测量。现有的接触式力学测量方法难以对生物飞行时的扑翼气动力进行直接准确测量,目前扑翼气动力实验主要是采用测力天平测量人造扑翼飞行器[16-17]或扑翼机构[18-23]的气动力与力矩。在保持雷诺数(Reynolds Number,Re,惯性力与粘性力之比)不变的前提下,使用大尺寸的人造扑翼机构模拟真实[18-20]或简化[21-23]的生物扑翼运动,可实现对昆虫等小型生物的扑翼气动特性研究,这显著降低了对测力装置的性能要求,但在测量人造扑翼气动力时,需特别考虑去除扑翼惯性力的影响[24]。近期,Hightower等[25]成功研发了非接触式的扑翼气动力测试平台(图1),其主体为上下表面布置有多个测力点(图1中F1~F6点)的刚性空盒,当蜂鸟等小型扑翼生物在空盒内悬停飞行时,所产生扑翼气动力以压力波形式传递至空盒上下表面,并被测力点所记录,经处理即可获得小型扑翼生物自由飞行时的垂向气动力。这种非接触式的测力方法对生物飞行的干扰较小,为直接测量扑翼气动力提供了新思路。

图1 扑翼气动力测试平台工作原理[25]
Fig.1 Working principle of the flapping wing aerodynamic force platform[25]
扑翼气动实验的另一研究重点是对扑翼流场结构的观测分析。对生物扑翼[26-28]或人造扑翼[14]运动时的翼面周围与尾迹流场结构进行可视化与量化,并分析其中的涡流演变过程,可以解释扑翼气动力的产生与变化规律,揭示扑翼飞行的气动机理。早期的扑翼流场观测采用烟线法[28]、气泡法[14]等传统流场显示方法。粒子图像测速方法(Particle Image Velocimetry, PIV)由于可以实现对扑翼近场与远场流动更为准确细致的定性显示与定量测量,近年来成为扑翼流场实验观测的主流技术手段,包括层析PIV[20,29]与立体PIV[30-31]技术均有所应用,显著促进了昆虫、鸟类与蝙蝠扑翼空气动力学研究。
研究扑翼气动问题的另一利器是数值仿真。针对不同的扑翼气动研究需求,研究者们开发了大量不同的数值仿真方法。在研究扑翼气动机理时,需要获得尽可能真实细致的扑翼流场信息与气动力数据,相对应的数值研究方法主要是基于不可压缩Navier-Stokes (N-S)方程所开发的各类CFD算法,包括使用贴体网格的传统CFD算法[32-36]以及使用笛卡尔网格的浸入边界法[37-38]等。这些CFD算法可以求解获得扑翼流场在空间与时间尺度上的速度与压力分布,而这类信息目前还难以依靠气动实验完整获得。
虽然CFD方法在研究扑翼气动问题时可获得准确详细的仿真数据,但其需要消耗大量的计算机算时与算力。扑翼气动优化设计与扑翼飞行动力学建模研究对于扑翼气动计算的时效性要求较高,为此研究者们开发了多种扑翼气动力快速估算方法,包括扑翼气动准定常模型[39-41]、降阶模型方法[42]、片条理论方法[43]、非定常涡格法[44-45]等。但上述方法相比CFD方法,在准确性与适用性上尚有差距。建立更加准确高效、适用面更广的扑翼气动力快速估算方法,是目前扑翼气动研究的方向之一。
悬停飞行是扑翼运动中能耗最高的一种模式,同时悬停运动规律使用实验观测手段也相对容易获取,因此大多数有关昆虫飞行的研究围绕悬停飞行展开。以往研究从活体飞行观测、模型实验、数值仿真等多方面分析了昆虫悬停飞行的气动机理,并提出了延迟失速机制[7,14]、附加质量效应[12]、尾迹捕获机制[9]等多种昆虫扑翼高升力机制。其中:
延迟失速机制是指扑翼在上扑与下扑的大攻角平动阶段,边界层在前缘附近分离并卷起形成一个较强的前缘涡(Leading Edge Vortex,LEV,如图2所示),由于扑翼特殊的运动模式以及较低的雷诺数和展弦比,前缘涡可以在平动全程或大部分行程里保持依附并在上表面形成稳定的低压区,从而提供持续的升力贡献。延迟失速机制是昆虫扑翼飞行的最主要升力机制,其所产生的气动力占整个拍动周期中的大部分[46-47]。
附加质量效应指扑翼在突然起动以及扑动方向转换时存在快速加速和减速过程,这一过程会带动扑翼周围的空气进行快速加速与减速运动,结果导致作用于扑翼上的压力增加,投影至升力方向既形成了一定的升力增量。

图2 模型果蝇悬停飞行时的翅膀前缘涡(LEV)与翼尖涡(TV)[47]
Fig.2 The leading edge vortex and the wing tip vortex in fruit fly hovering flight[47]
尾迹捕获机制是指扑翼在扑动方向反转后,会与前一个拍动行程所产生的尾迹相遇,包含在尾迹中的部分能量会被扑翼重新捕获,从而提高整个周期的扑动效率。尾迹捕获被认为在合拢-打开过程中有较显著的增升效果[12]。但一般悬停飞行[48]以及近地面飞行[35]时,尾迹与扑翼之间的干扰受包含扑翼运动、形态在内的诸多参数影响,对于升力正向以及不利影响均有可能出现。
图3给出了甲虫翅膀模型在一个完整扑动周期内的垂向升力随时间变化历程,其中垂向升力采用CFD计算与机械模型测力实验两种方式获得,二者所得平均升力结果误差小于10%[19]。该模型在0.125 T~0.375 T、0.625T~0.875 T时间区间内处于平动阶段,期间的持续高升力即得益于延迟失速机制,而在0.375 T~0.625 T的翅膀转动过程中的较小升力峰值,则可视为附加质量效应与尾迹捕获机制的作用效果。
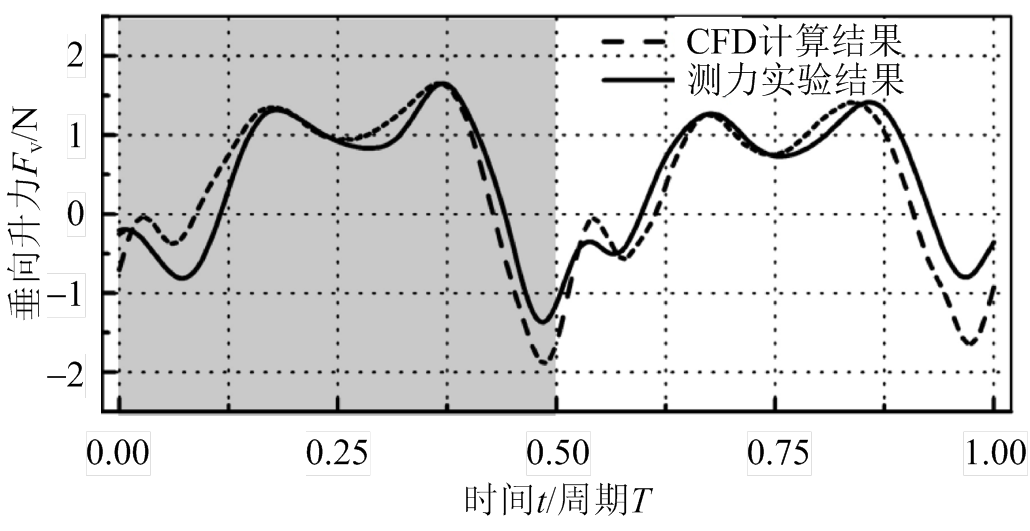
图3 甲虫翅膀模型在一个扑动周期内的垂向升力随时间变化历程[19]
Fig.3 Time courses of the vertical lift in one flapping cycle for a model beetle-wing[19]
昆虫扑翼高升力研究经过数十年发展,已经形成了较为系统的理论,以往多篇综述[49-52]对于上述机制进行了详细介绍。近年来对于昆虫扑翼升力机理的研究,从注重分析升阻力特性逐渐转向对扑翼近场及远场涡结构与演变过程的分析,前缘涡的稳定性问题是其中一个重要研究方向。以往研究表明,昆虫翅膀在扑动过程中存在从翅根到翅尖的轴向流,这一流动受离心力及科氏力驱动,不断将前缘涡中的涡量向翅尖输送并最终汇入下游。这种涡量输送避免了前缘涡增长过大以至于破裂、脱落,从而起到稳定前缘涡的作用[14]。但仿真分析表明,展向流强度受雷诺数影响,当Re<120时,展向流非常微弱[11,53]。此外Wojcik和Buchholz[54]对旋转平板的前缘涡涡量输运定量分析(Re≈2000)表明,尽管存在明显轴向流,但其作用并不足以完成所需的涡量输运。新的前缘涡稳定性机制仍有待发掘。
得益于近年高速摄影技术的进步,学者们开始对昆虫移动飞行时的扑翼运动进行研究。昆虫移动飞行的运动模式与悬停飞行不同,有的果蝇甚至会采用类似划桨的方式在空气中飞行[55],昆虫在不同移动速度下的扑翼运动模式也会有所不同[56-58]。昆虫移动飞行过程中的气动机理有待去发现。
鸟类与蝙蝠在快速飞行时经常采用滑翔的方式,而在慢飞时扑动翼面以获取足够支撑自重的升力。主动变形是鸟类和蝙蝠在扑翼飞行过程中提高升力与推力的一种常见方式。主动变形主要有两种形式:一类是变翼展,在下扑时伸展翅膀提高下扑升力,上扑过程中收缩翅膀降低上扬阻力,完整周期内产生正向升力和推力。低展弦比鸟类一般通过翅膀弯曲折叠来实现变翼展[59],蝙蝠则可以通过关节折叠加伸缩翼膜实现(如图4所示)。近年来也有学者通过数值[37,60]和实验[59]方法研究了生物变翼展飞行的气动特性;动态变形的另一类形式是翅膀扭转,钻石鸠[59]等大展弦比鸟类会以较大迎角下扑翅膀,在上扑时扭转翼尖以降低迎角[61-62],同时初级飞羽散开使气流从羽间缝隙穿过[61],升力与推力主要由下扑过程提供。
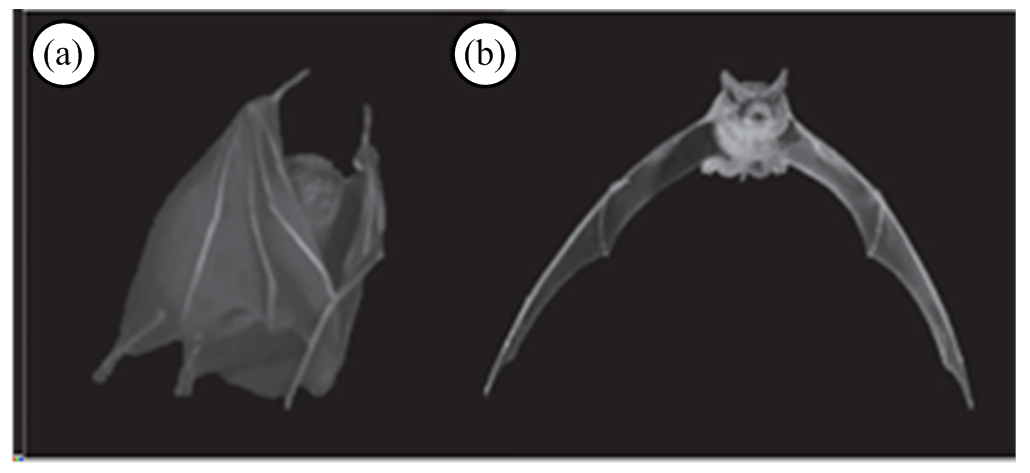
图4 巴西无尾蝙蝠的变翼展过程[63]
Fig.4 Changing wingspan process of the Brazilian free-tailed bat[63]
值得注意的是,具备高超悬停与机动飞行能力的蜂鸟[64]同样采用了主动扭转翅膀的方式飞行,但扭转方式跟其他鸟类不同。蜂鸟扑翼方式与昆虫更加类似,但也存在一定不同。比如蜂鸟可以通过翅膀肌肉与关节系统实现扑动过程中的迎角主动反转[65],而昆虫扑翼的迎角反转则主要靠翼根肌肉及翼面被动变形来综合实现[66],因此蜂鸟与昆虫的扑翼气动特性及升力机制并不完全一样。基于高速影像数据,对蜂鸟悬停时的三维CFD模拟[64]表明蜂鸟在整个扑翼周期内上扑与下扑存在显著的不对称性(参见图5);对蜂鸟前飞时的三维CFD模拟[67]表明其上扑与下扑均会产生推力,但只有下扑会产生升力。不论悬停还是前飞,蜂鸟的气动特性相比昆虫都有一定差异。
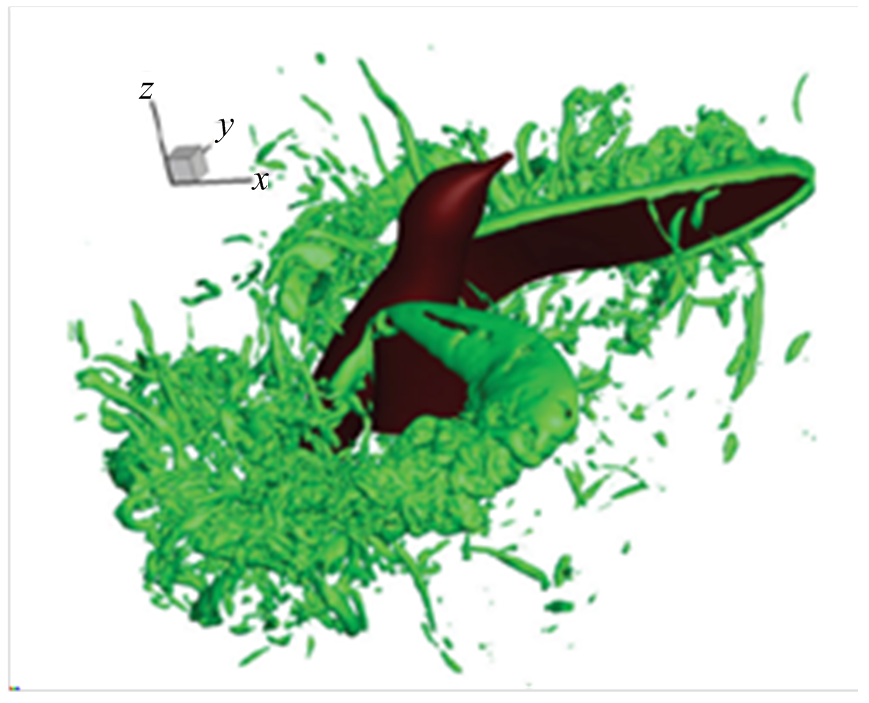
图5 蜂鸟悬停扑动的三维CFD模拟[64]
Fig.5 Three-dimensional CFD simulation of hummingbird’s hovering flight[64]
除了主动变形外,近年研究表明前缘涡同样在某些鸟类[14,68-69]与蝙蝠[37,70-71]飞行中起到显著的增升作用。但不同于昆虫翅膀的被动变形和三自由度扑动,鸟类与蝙蝠翅膀可以主动变形和多自由度运动(蝙蝠单侧翅膀关节数超过10,自由度超过20[72])。此类复杂变形与运动会对翅膀附近涡结构演变产生复杂的影响,其是否有助于稳定前缘涡以及延迟流动分离,是一个值得探寻的问题。以往研究在获取鸟类与蝙蝠飞行流场时多采用风洞结合粒子图像测速的手段[59,63,73-75],很难对扑翼近场涡结构进行细致的观察。得益于CFD以及高速摄像技术进步,如今可以对整只鸟或蝙蝠的自由飞行过程进行数值模拟[37,64,67]。针对不同鸟类与蝙蝠扑翼飞行的CFD仿真分析与涡结构分析是未来的发展方向之一。
展弦比(翼展与平均弦长之比)是对机翼形状进行分类的主要指标,同时也是衡量机翼性能的关键因素。飞机与直升机等所采用的大展弦比机翼有利于减小诱导阻力,提供更高的升阻比与飞行能量效率[76]。相比之下昆虫、蜂鸟等飞行生物具有灵活的慢飞、悬停能力,低展弦比翅膀是其显著的形态学特征。以往研究表明,前缘涡从翼根至翼尖尺寸逐渐增大,呈现锥状结构[47,77-79]。扑动过程中保持依附的前缘涡,使昆虫、蜂鸟等生物在高迎角时不失速[14]。
近年来研究者针对昆虫及蜂鸟翅膀展弦比对前缘涡结构的影响展开了诸多研究。一方面,展弦比变化会显著影响前缘涡与翼弦长的相对尺寸,在展向2倍弦长位置,前缘涡覆盖整个翼面,若展弦比大于2,翼尖附近的前缘涡将有一部分位于后缘之外[78-80]。另一方面,展弦比变化也会对前缘涡的结构产生影响,展弦比增加会使前缘涡演化出双涡或多涡结构,并在展向距离翼根超过4倍弦长区域出现破裂与脱落现象[78]。此外,在不同雷诺数、悬停或前飞运动中,前缘涡随展弦比的变化规律是类似的[80]。在确定扑翼最佳展弦比时,展弦比过小,上翼面易受到翼尖涡下洗气流影响;展弦比过大,前缘涡会出现大面积的破碎甚至脱落[81-82]。对于蜂鸟[83-84]、昆虫[82]的数值仿真研究表明,展弦比3~4.5时扑翼所产生的平均升力最高,这与蜂鸟、以及多数昆虫扑翼的真实展弦比相符。但多样化的飞行生物翅膀中也有与上述最佳展弦比偏离较远的,蝴蝶的翅膀展弦比只有1.5左右,宽大的翅膀导致蝴蝶的翅拍频较低(20 Hz左右),其在扑翼周期的不同阶段综合利用了延迟失速、尾迹捕获、合拢-打开等多种增升机制[85],同时蝴蝶飞行中身体的上下、俯仰震荡对其飞行起到重要的调节作用[56,86]。对于传统固定翼飞行器,采用大展弦比机翼意味着以牺牲机动性为代价来获得更高的升阻比。作为一个有趣的对比,展弦比相对较大的昆虫(如蜻蜓、蚊子)反而拥有极强的机动性,但这种机动性的直接原因并非大展弦比的翅膀。蜻蜓的机动性主要是源于其可以对四片细长翅膀进行单独控制[87],而蚊子的机动性则主要源于其800 Hz的极高扑翼频率[27]。
除展弦比外,也有学者针对鸟类和昆虫翅膀更细节的形状特征展开研究。鸟类的翅膀可以分为翼臂(Arm wing)和翼手(Hand wing)两部分。Thielicke等[88]研究了鸟类慢飞过程中,翼臂和翼手分别采用不同弯度和厚度时的气动特性,结果表明较薄较平的翼手有利于慢飞过程中前缘涡的形成;而较厚较弯的翼臂作用则更像飞机机翼,可以在快速飞行时提供升力。小翼羽(Alula)是位于翼臂和翼手之间的小型结构,由指骨和数片羽毛组成。Lee等[89]结合飞行实验与风洞测试手段,发现鸟类在慢飞过程中小翼羽可以起到类似涡流发生器的作用,在上翼面生成较强的流向涡,有效压制了翼面流动分离,从而起到增加升力、延迟失速的作用。
翅脉等结构的存在使昆虫翅具备皱褶特征。Meng等[90-93]对昆虫皱褶翼的气动性能进行了非常全面的研究,涵盖不同雷诺数(Re: O(101)~O(103))时的悬停[91]、前飞[90]、滑翔[93],以及翼面动态变形情况[92]。带皱褶翼与平板翼相比,升力降低约3%~16%,这主要是因为下翼面褶皱中所形成旋涡造成局部低压,而上翼面皱褶大多处于分离区中,不能产生类似强度的局部涡和低压区[93]。Brandt等[94]和Bomphrey等[87]分别对果蝇和蜻蜓的真实褶皱翅膀形态进行了三维重建,并采用CFD方法对比了褶皱翅膀与理想化平板翅膀所产生的气动力、压力分布及表面流场结构。上述两项研究同样表明褶皱并没有产生气动收益,反而会导致升阻比的下降。褶皱的存在更可能是为了以较小的重量、气动损失换取扑翼弯曲刚度的明显提高[95]。与昆虫翅膀皱褶相对应,鸟类翅膀由于羽毛的存在具备更复杂的起伏分层翅面形态,同时鸟类的飞行雷诺数更高(Re>10000),因此其翅膀周围的边界层对于这种起伏分层结构更敏感。Van Bokhorst等[96]研究了雨燕滑翔过程中翅面粗糙度对周围流场的影响,发现这种起伏突起可以促使流动转为紊流,从而降低翅面流动分离。
昆虫的翅膀具有多层次的结构,除了肉眼可见的展弦比、褶皱等宏观形态特征以外,还存在纤毛、鳞片等微观结构。以往研究认为这类微结构的作用主要有超疏水性、光学反射以及力学黏附[97],但这些翼面微结构对于扑翼飞行同样存在影响。此前对植物的空气动力学研究[98]探讨了植物表面纤毛对于边界层的影响,结果表明有纤毛存在时的边界层与光滑表面边界层并不相同。而对覆盖有纤毛层的圆柱的绕流气动分析表明,纤毛层的存在可以对涡脱落造成影响,进而减小升力波动与阻力[99]。Slegers等[100]采用高速摄像机对11组蝴蝶在正常飞行以及被抹去翼面鳞片后飞行时的表现进行了观察分析,被抹去翼面鳞片后,这些蝴蝶的拍幅平均降低7%,爬升效率平均降低32.2%。因此翼面微观结构对于扑翼气动的影响是不应被忽视的,这一领域尚有许多问题等待去解决。
Mymaridea和Trichogrammatidae科的一些微型寄生蜂体长小于0.3 mm,是已知最小的飞行生物[101]。不同于一般昆虫的膜翅,微型寄生蜂的翅膀呈现高度稀疏的梳子翼形态(如图6所示)。以往有关梳子翼的气动研究主要以体积相对更大一些的缨翅目昆虫“蓟马”为对象,研究者们采用缩比模型实验[22,102]及理论计算分析[103-105]的手段研究了蓟马前翅在平动及转动过程中的气动特性,认为梳子翼在极低雷诺数下可以凭借相对更小的翼面积实现接近于平板翼的气动力输出。近期,Jones等[106]研究了微型寄生蜂梳子翼的“突然打开”过程,认为梳子翼可以减小“突然打开”过程中的阻力。Lee等[107-108]采用油场实验与CFD的手段研究了不同刚毛密度的平动梳子翼在雷诺数O(101)~O(103)区间内的流场结构。由于微型寄生蜂体积甚小,要捕捉其飞行过程对高速摄影机的显微、高光、视野等性能指标要求极高,目前还没有完整的视频图像资料。生物学分析表明微型寄生蜂可能采用间接胸腔变形而非传统昆虫所采用的直接肌肉驱动来扑动翅 膀[109]。其在使用梳子翼飞行时可能存在不同于其他大型昆虫的扑动方式及升力机理,这方面的研究将有助于探寻生物扑翼飞行的极限。

图6 微型寄生蜂(Tinkerbella nana)显微图像[109]
Fig.6 Micrograph of micro-wasp (Tinkerbella nana)[109]
鸟类、蝙蝠在飞行过程中翅膀受肌肉关节驱动会出现显著的主动变形,相关数值研究都不会忽视这种大变形的影响[37,64,67,110]。相比之下,以往许多数值研究均将昆虫翅膀视为纯刚性,但实际上昆虫翅膀在扑动过程中受气动力、惯性力以及翅膀内力的影响,会出现一定的被动变形。研究者通过分析昆虫扑翼变形的高分辨率观测数据发现,如美洲斑潜蝇(Liriomyza sativae)这样的微小昆虫,扑动过程翅膀相对变形量很小,刚性翅假设是合理的[111]。但尺寸较大的昆虫在扑翼运动时会出现明显的弦向弯度变化与展向扭转变形,其中蝗虫翅膀的瞬时弦向弯度变化可达弦长的10%,瞬时扭转变形可达30°[112],蜂蝇翅膀的柔性变形更大,瞬时弦向弯度变化可达弦长的12%,瞬时扭转变形超过50°[113]。这种扑翼被动变形是否隐含新的扑翼升力机制是扑翼研究的热点与难点。Mountcastle和Combes[114]对活体大黄蜂的翅膀进行微加工处理,使用微型夹板固定翅膀静脉关节,使用载重实验对比测试了黄蜂使用不同刚度翅膀飞行时的垂向升力,发现大黄蜂翅膀关节被夹板固定后,所能产生的最大垂向升力降低了8.6%。但本实验存在太多的不确定因素,例如大黄蜂原本的扑翼运动规律是配套于原生的柔性翼结构的,翼刚度改变可能会引起大黄蜂的扑翼运动模式随之变化。
在使用数值方法研究扑翼柔性变形时,方法之一是观测得到真实昆虫翅膀随时间变形数据,据此定义数值仿真中的翅膀运动边界条件,进而求解动态变形扑翼气动特性。基于这种方法研究蝗虫[28]以及蜂蝇[115]扑翼动态变形,发现相比刚性翼,动态变形可以提高翅膀整周期的平均升力,同时降低飞行能耗。蝴蝶翅膀变形对其前飞气动特性的影响研究[116]表明,变形蝴蝶翼相比于刚性蝴蝶翼升力提升29%,升力与功率之比提升46%,这一增长幅度是一般昆虫柔性翅的三倍以上,说明翅膀相对面积较大的昆虫飞行过程中的翅膀被动变形不容忽视。除上述方法外,也有学者采用耦合求解N-S方程和结构动力学方程的流固耦合方法研究扑翼柔性的影响。周超英等[117]针对二维柔性扑翼模型的气动性能研究表明,适当的柔性变形有利于延迟前缘涡脱落,从而提高扑翼的推进效率。Dai等[118]研究了具备弦向柔性的矩形翼在做绕轴扑动过程中的气动力与效率,发现由翼柔性所引起的被动变形速率与相位会对扑翼气动特性产生显著影响,而这种被动变形则与扑翼刚度、质量比以及运动规律直接相关,当扑翼频率ω与矩形翼固有频率ωn之比ω/ωn≤0.3时,扑翼变形才能显著提升气动升力及效率,过度的变形则会产生不利影响。Nakata等[77,119-120]根据真实鹰蛾翅的实验测量数据构建了翅膀结构模型(如图7所示),研究了鹰蛾翼身整体做悬停飞行[77,119],以及单独翅膀加速旋转与匀速旋转[120]时的翅膀柔性变形及相应气动特性,三种运动仿真中柔性翼均出现了沿展向的扭转变形并使翼尖迎角降低,同时伴有弦向的正弯度,综合变形有利于提高升力与效率。
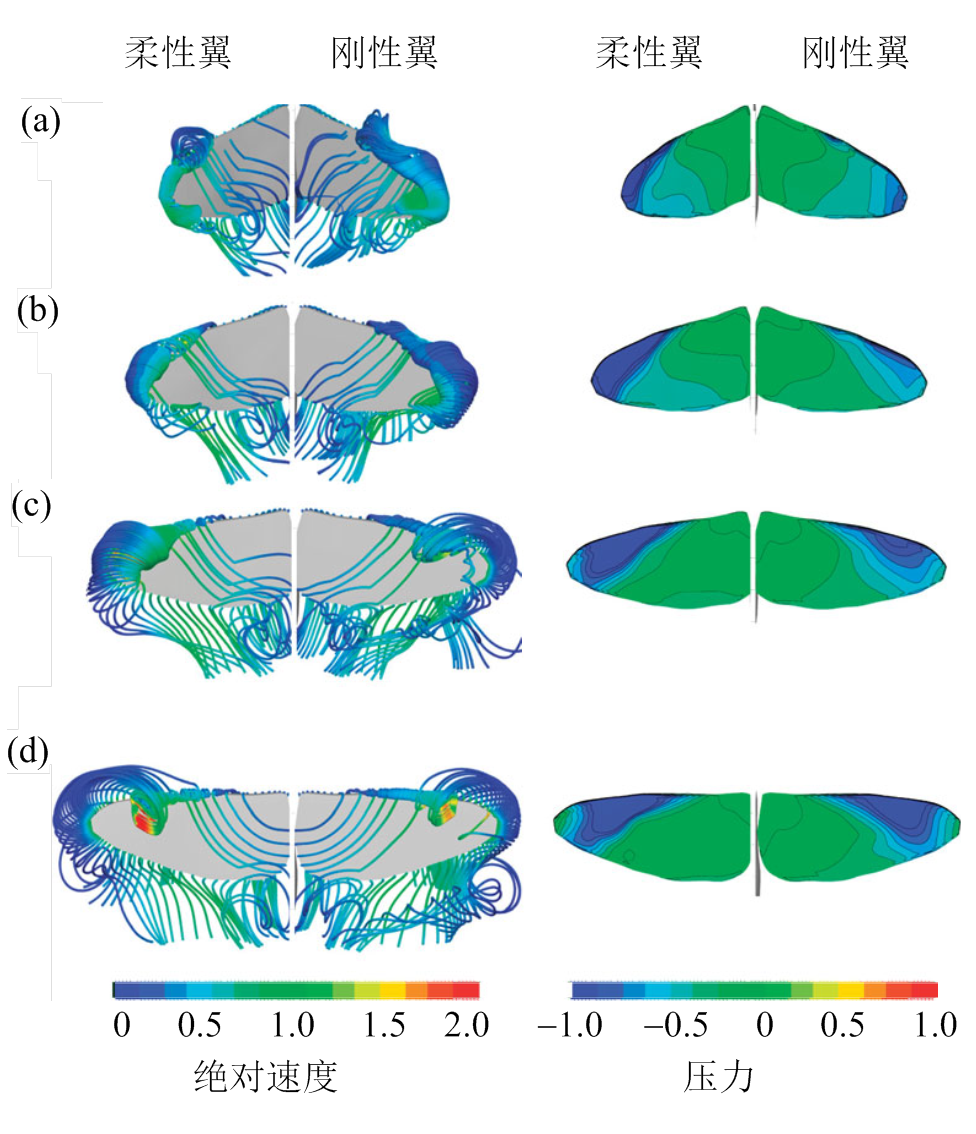
图7 柔性翅与刚性翅扑动时的流线与压强分布对比[77]
Fig.7 Streamlines and pressure contours on the flexible and rigid flapping wing [77]
值得注意的是,人们在使用仿生扑翼模型测试柔性影响时却得到了与数值方法不同的结论。Zhao等[24]使用动态扩比模型研究了Re=2000时刚性翼以及不同刚度的柔性翼的气动特性,发现当攻角小于50°时,刚性翼会产生最大平均升力。Tanaka等[121]使用微型压电扑动机构,比较了跟真实蜂蝇(Eristalis tenax)同尺寸的柔性聚合薄膜翼以及刚性碳纤维翼所产生的升力大小,其中的柔性扑翼具有与真实扑翼类似的翅脉结构、褶皱分布以及弯曲刚度,结果显示柔性翼和刚性翼分别能产生5.9×102 μN 和6.9×102 μN的升力。数值计算与仿生扑翼实验所得结果之间差异的产生原因值得进一步探索。
生物在飞行过程中,左右翅之间以及四翼昆虫前后翅之间会出现一定的气动干扰。这种干扰在特定情况下会对扑翼气动特性产生显著影响。情况之一是左右双翼合拢-打开运动,情况之二是蜻蜓前后串联翼扑动时的动态相位调整。
对于扑翼飞行,雷诺数过低(Re<100)时粘性显著增加,导致扑翼效率降低[122]。为了避免这一问题,微小昆虫进化出极高的扑翼拍频(不小于250 Hz[111,123])以尽可能提高飞行雷诺数。同时对于大多数完全变态昆虫而言,受自身固定的肌肉-胸腔结构限制,其翅膀拍频在飞行途中是基本稳定不变的,要调控飞行动力时主要采用改变扑翼拍幅的方式[124]。这些微型昆虫在飞行过程中通常会使用最大拍幅,这也就自然形成了左右翼面的合拢-打开运动(如图8所示)。这种运动最早由Weis-Forg在研究台湾小黄蜂时发现[125],后续对大多数微小昆虫的运动观察均发现了合拢-打开运动的存在[126]。实验、二维与三维数值仿真表明合拢-打开运动可以显著提高扑翼升力[127-129],这也被称为Weis-Fogh机制。该机制存在很多变体,包括部分合拢-打开[111],贴近合拢-打开[130]以及合拢-剥落[85,131]等。图9给出了一个扑动周期内模型果蝇在进行完整合拢-打开运动、部分合拢-打开运动以及不使用合拢-打开扑动时升阻力系数的时间变化历程,从中一方面可以看到合拢-打开机制的增升效果,另一方面合拢-打开机制在提升同时也造成了阻力的显著增加,而部分合拢-打开则可以对阻力增加起到一定缓解[133]。合拢-打开机制并非只限于微小昆虫,蝴蝶[85]、部分鸟类如斑胸草雀[59]在飞行中同样采用合拢-打开机制增加升力。最近的研究表明水生软体动物海蝴蝶Limacina helicina[134],罕见地采用合拢打开机制来增加游动动力,这是游动生物与飞行生物趋同进化的一项显著实例。生物界更多的合拢-打开运动及其变体等待去发现和研究。
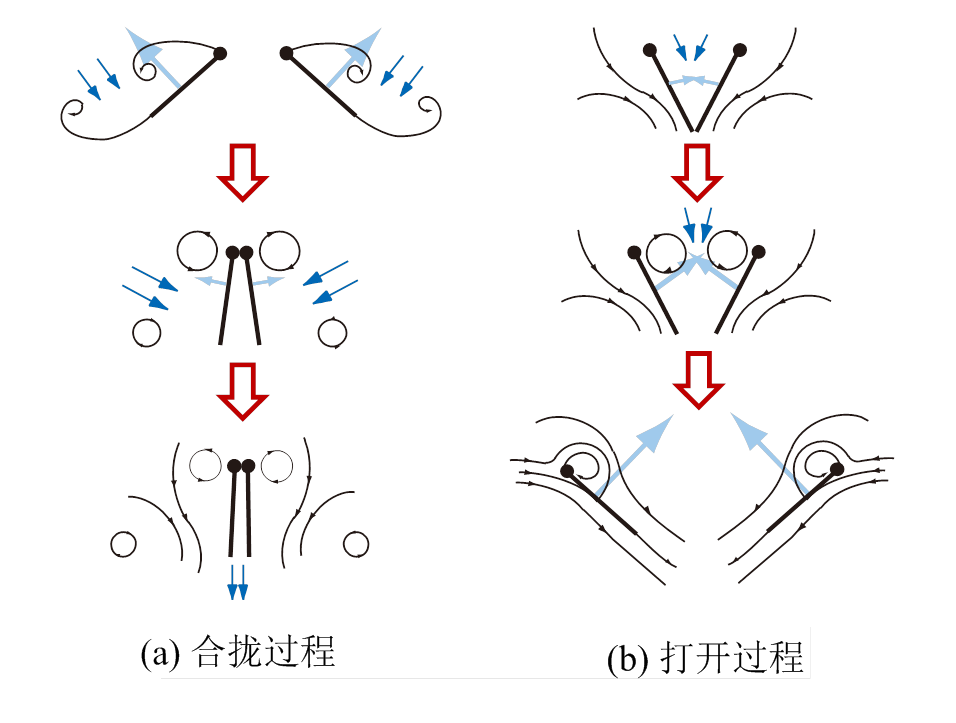
图8 合拢-打开机制[132]
Fig.8 Clap-and-fling mechanism[132]
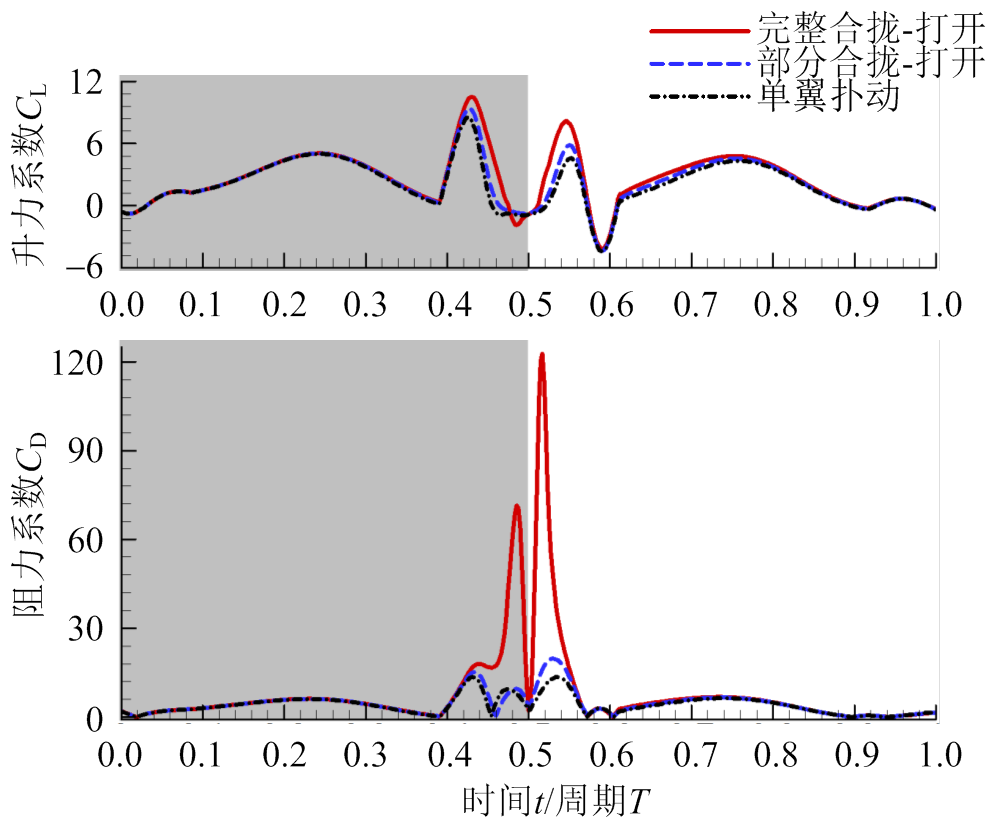
图9 模型果蝇在使用完整合拢-打开运动、部分合拢-打开运动以及不使用合拢-打开运动时一个扑动周期内的升阻力系数时间变化历程[133]
Fig.9 Time courses of the lift and drag coefficients in one flapping cycle of a model fruit fly using full clap-and-fling, partial clap-and-fling and don’t using clap-and-fling[133]
蜻蜓是机动能力最强的昆虫之一。两对大展弦比的前、后翅是其显著的形态特征,前翅与后翅间的运动相位差被认为是实现蜻蜓超机动飞行的关键所在。蜻蜓会在不同飞行状态时对前后翅运动规律进行动态调节,以获得更好的飞行效率与抵御突风能力[135]。当悬停飞行时,蜻蜓前后翅反相位拍动[1,34],这一状态有助于减少飞行能量消耗;当做起飞等加速飞行时,蜻蜓前后翅同相位拍动[34],以产生更大的加速度。以往对串联翼的研究多采用刚性翼,Zheng等[136]测试了不同柔性的蜻蜓串联翼模型在悬停及不同速度前飞时的升力及涡结构,发现适当的展向弯曲有利于悬停和前飞时前缘涡的附着,从而增加飞行气动力。
以往很多有关扑翼的数值研究均忽略了扑翼与身体之间的相互干扰,而单独研究扑翼的气动特性。近年来越来越多的扑翼数值研究开始综合考虑翼身整体的气动特性。一些学者通过数值仿真对翼身干扰的影响效果进行了评估,发现当果蝇悬停飞行时,翼身干扰可以引起2%以内的升力提升[47,137]。当果蝇以不同速度下前飞时,翼身干扰引起的整体升力变化小于7.5%[138]。有关蜂鸟的翼身整体扑翼研究亦显示其翼身干扰并不显著[64]。但也有一些飞行生物的翼身干扰效应非常显著。蝉的身体占整体的比例要比果蝇大很多,Liu等[38]基于高速影响数据,对蝉的前飞过程进行建模仿真,发现翼身干扰可以使翅膀升力增加约6.7%,身体升力增加超过7倍,总升力增加约18.7%。由于蝉独特的宽体结构,其在前飞时从胸部和尾部分别形成了两个脱落涡,这在其他昆虫飞行时并未观察到。其中胸部的脱落涡有利于增强扑翼的下洗气流,这可以被视为一种蝉特有的增升机制[38,139]。
除翼身干扰以外,飞行生物的一些非飞行器官由于体积占比较大,同样会对扑翼气动性能产生一定影响。蝙蝠的大耳朵可以增强其对回声的感知能力,以往有关蝙蝠与鸟类飞行能力的对比研究[140-141]认为,大耳朵的存在会降低蝙蝠身体所产生的升力,同时增加附加阻力。基于长耳蝙蝠(Plecotus auritus)飞行流场的观察与分析表明,蝙蝠耳朵本身可以产生一定升力,但耳朵所产生的尾涡与翼根涡相互干扰似乎会对翅膀气动性能产生不利影响[26]。
集群或编队飞行是常见于鸟类[142]、昆虫[143]、蝙蝠[144]的一种生物自组织行为。在集群飞行过程中,周围个体所产生的流场扰动必然会影响到扑翼飞行的气动性能。Portugal等[145]对秃鹮V字型编队飞行过程进行了观测,发现侧后方鸟正好处于理论气动模型所预测的最佳气动位置,其通过与前鸟之间的扑翼相位差,使整个周期内所捕捉到的上洗气流最大化。而当后鸟处于前鸟紧后方时(流向涡位置),其扑翼相位将与前鸟反向,这有利于将前鸟所产生下洗流的不利影响降至最低。相比大型鸟类的编队飞行,昆虫、蝙蝠以及小型鸟类密集飞行时机动剧烈,气动干扰复杂。Davidovich与Ribak[146]借助高速摄影观测分析了豆娘在交配飞行时的扑翼频率与幅度,发现雄性豆娘在雌、雄性交配飞行时提供了更大比例的气动力输出。当昆虫集群数量较多时,要对其中个体间干扰进行空气动力学分析难度较高,目前还未见相关研究成果,对集群飞行进行原理性的简化建模分析是未来可能的研究突 破口。
对于扑翼近地面悬停过程中的气动特性研究展开较早,结果表明从空间尺度观察,离地高度较小时(小于1倍~2倍翼弦长),地面效应使升力增大,高度增加地面效应导致升力降低;高度再增加,地面效应消失[23,147]。从时间尺度观察,地面效应在扑翼起动后前几个周期内效果显著,随后地面效应的影响越来越弱。
扑翼起飞过程中的地面效应研究只局限在少数几类昆虫和鸟类,但即便如此,这几类物种受地面效应的影响也有较明显的不同。对于果蝇(Drosophila virilis[148]),蜂蝇(Eristarlis tenax[149]),以及蝴蝶(Pieris rapae[150])的研究显示地面效应对起飞产生不利影响,而对甲虫(Trypoxylus dichotomus)的前两个周期扑动却有显著的增升效果[151]。Kolomenskiy等[35]通过耦合飞行力学求解器,综合研究了果蝇这一尺寸昆虫在起飞及悬停过程中地面效应对气动力的影响。结论显示,果蝇在以真实速度起飞过程中,地面效应存在负面影响;慢速起飞过程相比真实起飞过程,地面效应对气动力影响显著,但正面或负面的影响在不同情况时均会出现;果蝇悬停时,地面效应会对昆虫身体施加一个加大的托举力,尽管翅膀上的升力在部分时段出现减小,但翼身总升力增加。
上述研究表明地面效应受到尺寸、形态、飞行状态、离地距离等多参数影响,其所涉及的参数空间非常巨大。不同参数组合下,从地面反弹回来的脱落涡与翼扑动会形成不同的相互作用,从而对气动力产生正面或反面的影响。这与旋翼飞行器始终正面的地面效应存在很大不同。未来针对扑翼领域提出覆盖主要参数空间的统一地面效应理论是很有意义的。
近年来,得益于扑翼飞行器设计与控制理论、先进材料及加工制造技术进步,世界各国的研究人员、工程师以及民间爱好者推出了大量仿生扑翼飞行器。尽管这些飞行器受生物扑翼飞行启发而研制,但并非是对现有生物的完全复现。这些飞行器在形态、结构、运动、功能等方面与扑翼生物存在差异,这也导致了一些新的扑翼气动问题与研究热点产生。
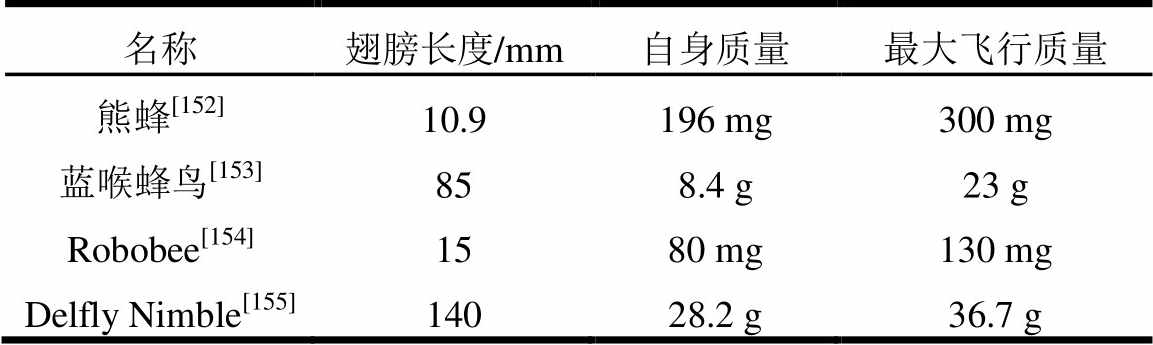
首先是扑翼飞行器的气动优化设计。气动设计是扑翼飞行器设计的重要组成,高升力的气动设计是提升扑翼飞行器飞行性能的关键。表1统计了两种扑翼生物与两款仿生扑翼飞行器的翅膀长度、自身质量与最大飞行质量,其中仿生扑翼飞行器选取了著名的哈佛大学Robobee压电驱动扑翼飞行器(图10)与代尔夫特理工大学Delfly Nimble电机驱动扑翼飞行器(图11)。根据与扑翼生物的翅膀长度及最大飞行质量对比,仿生扑翼飞行器在气动性能方面尚有较大的提升空间。以往扑翼飞行器在进行气动优化设计时,一般会选取一个或多个核心参数进行优化,但由于扑翼飞行器的气动强非线性、结构的大柔性以及飞行动力学的不稳定性,其气动优化设计存在一个高度耦合的多参数设计空间,如何快速准确地在这一设计空间中确定最优或较优气动设计方案,是扑翼飞行器气动研究的核心。
表1 飞行生物与微型扑翼飞行器的飞行载重能力对比
Table 1 Comparison of flight load capacity between flying creatures and flapping-wing micro air vehicle
名称翅膀长度/mm自身质量最大飞行质量 熊蜂[152]10.9196 mg300 mg 蓝喉蜂鸟[153]858.4 g23 g Robobee[154]1580 mg130 mg Delfly Nimble[155]14028.2 g36.7 g

图10 Robobee[154]
Fig.10 Robobee[154]

图11 Delfly Nimble[155]
Fig.11 Delfly Nimble[155]
在研制扑翼飞行器时,除直接模仿昆虫[154,156]、蜂鸟[157]、大型鸟类[16,158]以及蝙蝠[159]的扑翼形态与运动外,也有研究者在生物扑翼基础上进行了布局创新。例如以Delfly Nimble为代表的X型布局四翼飞行器,这类飞行器单侧的两片翅膀可以通过合拢-打开运动产生额外的高升力[155,160]。另一类颇具创新意义的设计是将扑翼布局与旋翼布局混合的扑旋翼飞行器[161-162],如图12所示。扑旋翼飞行器具有一对反对称扑翼,机翼扑动产生的力矩驱动机翼自身旋转,飞行过程中靠扑动与旋转两种运动同时提供升力,兼具扑翼、旋翼两种构型特点。这类创新布局仿生飞行器的气动机理及高效气动设计方案有待进一步探究,同时扑翼气动研究也将促进更多创新的仿生飞行器设计方案的出现。
除在布局上对扑翼飞行器进行创新设计以外,研究者同时也在拓展扑翼飞行器的功能与应用场景。自2013年实现稳定飞行[154]后,研究人员对Robobee扑翼飞行器进行了多处改良,2015年实现了该飞行器从空中向水中的单向跨介质飞行[163](图13),2017年借助电解原理制造微型爆炸,实现Robobee从水中向空中的弹射起飞[164]。Robobee是世界上首个可实现跨介质飞行的微型仿生飞行器。由于空气与水的密度与粘性不同,跨介质扑翼飞行器需针对两种流场介质设计两套扑翼运动模式[163,165]。此外,开发跨介质扑翼飞行器气动计算与实验方法,设计在水和空气两相流动中均具有较好推进性能的扑翼形态、结构,亦是未来的研究方向之一。

图12 北航微型扑旋翼飞行器室内飞行实验[162]
Fig.12 Indoor flight test of the flapping-wing rotor aerial vehicle developed by Beihang University[162]
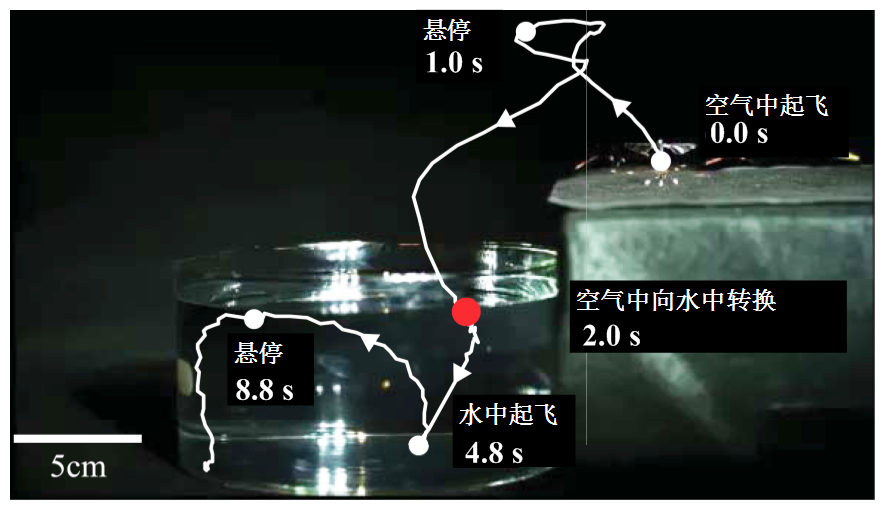
图13 Robobee的跨介质飞行过程[163]
Fig.13 The cross-media flight process of Robobee[163]
扑翼飞行器的另一特殊应用场景是火星。火星飞行器可以显著扩展地面火星车的探测范围,对崎岖复杂地形的适应性也更强。火星的重力加速度只有地球的三分之一,但其空气密度只有地球的1.3%[166]。在相同的形态尺寸、运动模式与运动速度下,火星飞行器的飞行雷诺数将只有地球飞行器的1.56%。对于低速的火星探测飞行任务而言,扑翼飞行器相比传统固定翼飞行器将更具优势。Bluman等[167]采用CFD仿真与飞行动力学结合的方式模拟了熊蜂在火星中的自由飞行,其结论表明熊蜂在火星上的飞行升力并不能承担其自身重量,但若保持熊蜂身体体积不变,将翅膀尺寸扩大3.5倍,振幅55.3°、频率63.1 Hz的扑翼运动是可以产生足够升力来维持自重的。这一研究结论体现出火星扑翼飞行器良好的应用前景,该领域气动研究属于起步阶段,尚有很多科学与技术问题等待探索。
扑翼空气动力学相关研究在近些年呈现不断增长的趋势,并形成了一套较系统的理论构架。总体来讲对于昆虫扑翼的气动研究相比鸟类和蝙蝠更加深入;对于刚性翼的气动研究相比柔性翼更加深入;对于扑翼宏观机制的研究相比微观机制更加深入;对于个体飞行的研究相比群体飞行更加深入;同时扑翼气动研究的相关成果近些年正不断应用于人造微型飞行器的设计当中。随着研究不断深入,扑翼空气动力学还有更多有趣且充满挑战性的问题等待去探索解决:
(1) 鸟类与蝙蝠扑翼气动机理的进一步研究。对于鸟类和蝙蝠扑翼过程的三维数值仿真在近几年才刚刚开始,不同种类鸟类与蝙蝠扑翼的气动特性等待去研究。
(2) 柔性翅的具体增升机制。目前仿生柔性扑翼在模仿昆虫运动时往往会导致升力降低,这与昆虫扑翼数值仿真的结果相矛盾。翅膀柔性对气动的影响规律仍需进一步探究。
(3) 微小昆虫的气动特性及翅膀微观结构的气动影响。一些微小昆虫的翅膀形态及运动规律与一般昆虫存在差异,这些昆虫可能存在独特扑翼机理。同时昆虫翼上纤毛、鸟类堆叠羽毛对边界层流动的影响有待进一步研究。
(4) 集群飞行时的个体间气动干扰。昆虫、鸟类、蝙蝠均存在集群飞行现象,生物是否会利用个体间气动干扰提升升力或飞行效率,是一个值得关注的问题。
(5) 近年来仿生飞行器对气动性能的需求不断提高,并在布局、功能与应用场景上不断创新,随之产生了许多不同于生物扑翼气动研究的新问题,开发更高效准确的扑翼飞行器气动设计方法,并构建成熟的扑翼飞行器设计体系与理论,是未来该领域的研究重点。
参考文献:
[1] Usherwood J R, Lehmann F O. Phasing of dragonfly wings can improve aerodynamic efficiency by removing swirl [J]. Journal of the Royal Society Interface, 2008, 5(28): 1303-1307.
[2] Lovejoy N R, Mullen S P, Sword G A, et al. Ancient trans-Atlantic flight explains locust biogeography: molecular phylogenetics of Schistocerca [J]. Proceedings of the Royal Society B-Biological Sciences, 2006, 273(1588): 767-774.
[3] Rattenborg N C, Voirin B, Cruz S M, et al. Evidence that birds sleep in mid-flight [J]. Nature Communications, 2016, 7: 12468. doi: 10.1038/ncomms12468.
[4] Shyy W, Aono H, Kang C-K, et al. An introduction to flapping wing aerodynamics [M]. Cambridge: Cambridge University Press, 2013.
[5] Ellington C P. The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms [J]. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 1984, 305(1122): 79-113.
[6] Dickinson M H, Gotz K G. Unsteady aerodynamic performance of model wings at low reynolds numbers [J]. The Journal of Experimental Biology, 1993, 174(1): 45-64.
[7] Ellington C P, Van Den Berg C, Willmott A P, et al. Leading-edge vortices in insect flight [J]. Nature, 1996, 384(6610): 626-630.
[8] Liu H, Ellington C P, Kawachi K, et al. A computational fluid dynamic study of hawkmoth hovering [J]. The Journal of Experimental Biology, 1998, 201(4): 461-477.
[9] Dickinson M H, Lehmann F-O, Sane S P. Wing rotation and the aerodynamic basis of insect flight [J]. Science, 1999, 284(5422): 1954-1960.
[10] Wang Z J. Two dimensional mechanism for insect hovering [J]. Physical Review Letters, 2000, 85(10): 2216-2219.
[11] Birch J M, Dickinson M H. Spanwise flow and the attachment of the leading-edge vortex on insect wings [J]. Nature, 2001, 412(6848): 729-733.
[12] Sane S P, Dickinson M H. The control of flight force by a flapping wing: Lift and drag production [J]. Journal of Experimental Biology, 2001, 204(15): 2607-2626.
[13] Sun M, Tang H. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion [J]. Journal of Experimental Biology, 2002, 205(1): 55-70.
[14] Lentink D, Dickinson M H. Rotational accelerations stabilize leading edge vortices on revolving fly wings [J]. Journal of Experimental Biology, 2009, 212(16): 2705-2719.
[15] Vanella M, Fitzgerald T, Preidikman S, et al. Influence of flexibility on the aerodynamic performance of a hovering wing [J]. Journal of Experimental Biology, 2009, 212(1): 95-105.
[16] Perez-Rosado A, Gehlhar R D, Nolen S, et al. Design, fabrication, and characterization of multifunctional wings to harvest solar energy in flapping wing air vehicles [J]. Smart Materials and Structures, 2015, 24(6): 065042. doi: 10.1088/0964-1726/24/6/065042.
[17] Nakata T, Liu H, Tanaka Y, et al. Aerodynamics of a bio-inspired flexible flapping-wing micro air vehicle [J]. Bioinspiration & Biomimetics, 2011, 6(4): 045002. doi: 10.1088/1748-3182/6/4/045002.
[18] Han J S, Chang J W, Kim S T. Reynolds number dependency of an insect-based flapping wing [J]. Bioinspiration & Biomimetics, 2014, 9(4): 046012. doi:10.1088/1748-3182/9/4/046012.
[19] Truong T V, Le T Q, Park H C, et al. Experimental and numerical studies of beetle-inspired flapping wing in hovering flight [J]. Bioinspiration & Biomimetics, 2017, 12(3): 036012. doi: 10.1088/1748-3190/aa6c79.
[20] Fu J J, Liu X H, Shyy W, et al. Effects of flexibility and aspect ratio on the aerodynamic performance of flapping wings [J]. Bioinspiration & Biomimetics, 2018, 13(3): 036001. doi: 10.1088/1748-3190/aaaac1.
[21] Wang Z J, Birch J M, Dickinson M H. Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments [J]. Journal of Experimental Biology, 2004, 207(3): 449-460.
[22] Sunada S, Takashima H, Hattori T, et al. Fluid-dynamic characteristics of a bristled wing [J]. Journal of Experimental Biology, 2002, 205(17): 2737-2744.
[23] Lu H, Lua K B, Lim T T, et al. Ground effect on the aerodynamics of a two-dimensional oscillating airfoil [J]. Experiments in Fluids, 2014, 55(7). doi:10.1007/s00348- 014-1787-4.
[24] Zhao L, Huang Q F, Deng X Y, et al. Aerodynamic effects of flexibility in flapping wings [J]. Journal of the Royal Society Interface, 2010, 7(44): 485-497.
[25] Hightower B J, Ingersoll R, Chin D D, et al. Design and analysis of aerodynamic force platforms for free flight studies [J]. Bioinspiration & Biomimetics, 2017, 12(6): 064001. doi: 10.1088/1748-3190/aa7eb2.
[26] Johansson L C, Hakansson J, Jakobsen L, et al. Ear-body lift and a novel thrust generating mechanism revealed by the complex wake of brown long-eared bats (Plecotus auritus) [J]. Scientific Reports, 2016, 6: 24886. doi: 10.1038/srep24886.
[27] Bomphrey R J, Nakata T, Phillips N, et al. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight [J]. Nature, 2017, 544(7648): 92-95.
[28] Young J, Walker S M, Bomphrey R J, et al. Details of insect wing design and deformation enhance aerodynamic function and flight efficiency [J]. Science, 2009, 325(5947): 1549-1552.
[29] Zheng Y Y, Wu Y H, Tang H. An experimental study on the forewing-hindwing interactions in hovering and forward flights [J]. International Journal of Heat and Fluid Flow, 2016, 59: 62-73.
[30] Phillips N, Knowles K, Bomphrey R J. Petiolate wings: effects on the leading-edge vortex in flapping flight [J]. Interface Focus, 2017, 7(1): 20160084. doi: 10.1098/rsfs. 2016.0084.
[31] Phillips N, Knowles K, Bomphrey R J. The effect of aspect ratio on the leading-edge vortex over an insect-like flapping wing [J]. Bioinspiration & Biomimetics, 2015, 10(5): 056020. doi: 10.1088/1748- 3190/10/5/056020.
[32] Trizila P, Kang C K, Aono H, et al. Low-reynolds- number aerodynamics of a flapping rigid flat plate [J]. Aiaa Journal, 2011, 49(4): 806-823.
[33] Cheng X, Sun M. Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force [J]. Journal of Fluid Mechanics, 2018, 855: 646-670.
[34] Wang Z J, Russell D. Effect of forewing and hindwing interactions on aerodynamic forces and power in hovering dragonfly flight [J]. Physical Review Letters, 2007, 99(14): 148101. doi: 10.1103/PhysRevLett.99. 148101.
[35] Kolomenskiy D, Maeda M, Engels T, et al. Aerodynamic ground effect in fruitfly sized insect takeoff [J]. Plos One, 2016, 11(3): 0152072. doi: 10.1371/journal.pone. 0152072.
[36] Liu H. Integrated modeling of insect flight: From morphology, kinematics to aerodynamics [J]. Journal of Computational Physics, 2009, 228(2): 439-459.
[37] Wang S Z, Zhang X, He G W, et al. Lift enhancement by bats' dynamically changing wingspan [J]. Journal of the Royal Society Interface, 2015, 12(113): 20150821. doi: 10.1098/rsif.2015.0821.
[38] Liu G, Dong H B, Li C Y. Vortex dynamics and new lift enhancement mechanism of wing-body interaction in insect forward flight [J]. Journal of Fluid Mechanics, 2016, 79(2016)5: 634-651.
[39] Nabawy M R A, Crowthe W J. A quasi-steady lifting line theory for insect-like hovering flight [J]. Plos One, 2015, 10(8): 0158929. doi: 10.1371/journal.pone.0158929.
[40] Nabawy M R A, Crowther W J. On the quasi-steady aerodynamics of normal hovering flight part II: model implementation and evaluation [J]. Journal of the Royal Society Interface, 2014, 11(94): 20131197. doi: 10.1098/ rsif.2013.1197.
[41] Nabawy M R A, Crowther W J. On the quasi-steady aerodynamics of normal hovering flight part I: the induced power factor [J]. Journal of the Royal Society Interface, 2014, 11(94): 20131196. doi: 10.1098/rsif. 2013.1196.
[42] Liu K, Li D C, Xiang J W. Reduced-order modeling of unsteady aerodynamics of a flapping wing based on the Volterra theory [J]. Results in Physics, 2017, 7(2017): 2451-2457.
[43] Hassanalian M, Throneberry G, Abdelkefi A. Wing shape and dynamic twist design of bio-inspired nano air vehicles for forward flight purposes [J]. Aerospace Science and Technology, 2017, 68(2017): 518-529.
[44] Nguyen A T, Kim J K, Han J S, et al. Extended unsteady vortex-lattice method for insect flapping wings [J]. Journal of Aircraft, 2016, 53(6): 1709-1718.
[45] Ghommem M, Collier N, Niemi A H, et al. On the shape optimization of flapping wings and their performance analysis [J]. Aerospace Science and Technology, 2014, 32(1): 274-292.
[46] Sun M, Du G. Lift and power requirements of hovering insect flight [J]. Acta Mechanica Sinica, 2003, 19(5): 458-469.
[47] Aono H, Liang F, Liu H. Near- and far-field aerodynamics in insect hovering flight: an integrated computational study [J]. Journal of Experimental Biology, 2008, 211(2): 239-257.
[48] Wu J H, Sun M. The influence of the wake of a flapping wing on the production of aerodynamic forces [J]. Acta Mechanica Sinica, 2005, 21(5): 411-418.
[49] Platzer M F, Jones K D, Young J, et al. Flapping-wing aerodynamics: Progress and challenges [J]. Aiaa Journal, 2008, 46(9): 2136-2149.
[50] Shyy W, Aono H, Chimakurthi S K, et al. Recent progress in flapping wing aerodynamics and aeroelasticity [J]. Progress in Aerospace Sciences, 2010, 46(7): 284-327.
[51] Sun M. Insect flight dynamics: Stability and control [J]. Reviews of Modern Physics, 2014, 86(2): 615-646.
[52] Chin D D, Lentink D. Flapping wing aerodynamics: from insects to vertebrates [J]. Journal of Experimental Biology, 2016, 219(7): 920-932.
[53] Shyy W, Lin H. Flapping wings and aerodynamic lift: The role of leading-edge vortices [J]. Aiaa Journal, 2007, 45(12): 2817-2819.
[54] Wojcik C J, Buchholz J H J. Vorticity transport in the leading-edge vortex on a rotating blade [J]. Journal of Fluid Mechanics, 2014, 743(2014): 249-261.
[55] Ristroph L, Bergou A J, Guckenheimer J, et al. Paddling mode of forward flight in insects [J]. Physical Review Letters, 2011, 106(17): 178103. doi: 10.1103/ PhysRevLett.106.178103.
[56] Fei Y H J, Yang J T. Importance of body rotation during the flight of a butterfly[J]. Physical Review E, 2016, 93(3): 033124. doi: 10.1103/PhysRevE.93.033124.
[57] Meng X G, Sun M. Wing and body kinematics of forward flight in drone-flies [J]. Bioinspiration & Biomimetics, 2016, 11(5): 056002. doi: 10.1088/1748- 3190/11/5/056002.
[58] 朱建阳. 扑动轨迹对扑翼气动特性影响的数值研究[J]. 工程力学, 2016, 33(1): 246-251.
Zhu J Y. Numerical study on the effect of kinematics of a flapping wing on its aerodynamic performance [J]. Engineering Mechanics, 2016, 33(1): 246-251. (in Chinese)
[59] Crandell K E, Tobalske B W. Kinematics and aerodynamics of avian upstrokes during slow flight [J]. Journal of Experimental Biology, 2015, 218(16): 2518-2527.
[60] Wang S Z, Zhang X, He G W, et al. Lift enhancement by dynamically changing wingspan in forward flapping flight [J]. Physics of Fluids, 2014, 26(6): 061903. doi: 10.1063/1.4884130.
[61] Crandell K E, Tobalske B W. Aerodynamics of tip-reversal upstroke in a revolving pigeon wing [J]. Journal of Experimental Biology, 2011, 214(11): 1867-1873.
[62] Ros I G, Bassman L C, Badger M A, et al. Pigeons steer like helicopters and generate down- and upstroke lift during low speed turns [J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(50): 19990-19995.
[63] Hubel T Y, Hristov N I, Swartz S M, et al. Changes in kinematics and aerodynamics over a range of speeds in Tadarida brasiliensis, the Brazilian free-tailed bat [J]. Journal of the Royal Society Interface, 2012, 9(71): 1120-1130.
[64] Song J L, Luo H X, Hedrick T L. Three-dimensional flow and lift characteristics of a hovering ruby-throated hummingbird [J]. Journal of the Royal Society Interface, 2014, 11(98): 20140541. doi: 10.1098/rsif.2014.0541.
[65] Hedrick T L, Tobalske B W, Ros I G, et al. Morphological and kinematic basis of the hummingbird flight stroke: scaling of flight muscle transmission ratio [J]. Proceedings of the Royal Society B-Biological Sciences, 2012, 279(1735): 1986-1992.
[66] Ennos A R. The inertial cause of wing rotation in diptera [J]. Journal of Experimental Biology, 1988, 140(1): 161-169.
[67] Song J L, Tobalske B W, Powers D R, et al. Three-dimensional simulation for fast forward flight of a calliope hummingbird [J]. Royal Society Open Science, 2016, 3(6): 160230. doi: 10.1098/rsos.160230.
[68] Warrick D R, Tobalske B W, Powers D R. Lift production in the hovering hummingbird [J]. Proceedings of the Royal Society B-Biological Sciences, 2009, 276(1674): 3747-3752.
[69] Muijres F T, Johansson L C, Hedenstrom A. Leading edge vortex in a slow-flying passerine [J]. Biology Letters, 2012, 8(4): 554-557.
[70] Muijres F T, Johansson L C, Barfield R, et al. Leading-edge vortex improves lift in slow-flying bats [J]. Science, 2008, 319(5867): 1250-1253.
[71] Florian T M, Johansson L C, York W, et al. Leading edge vortices in lesser long-nosed bats occurring at slow but not fast flight speeds [J]. Bioinspiration & Biomimetics, 2014, 9(2): 025006.
[72] Riskin D K, Willis D J, Iriarte-Diaz J, et al. Quantifying the complexity of bat wing kinematics [J]. Journal of Theoretical Biology, 2008, 254(3): 604-615.
[73] Hubel T Y, Riskin D K, Swartz S M, et al. Wake structure and wing kinematics: the flight of the lesser dog-faced fruit bat, Cynopterus brachyotis [J]. Journal of Experimental Biology, 2010, 213(20): 3427-3440.
[74] Henningsson P, Muijres F T, Hedenstrom A. Time-resolved vortex wake of a common swift flying over a range of flight speeds [J]. Journal of the Royal Society Interface, 2011, 8(59): 807-816.
[75] Hakansson J, Hedenstrom A, Winter Y, et al. The wake of hovering flight in bats [J]. Journal of the Royal Society Interface, 2015, 12(109): 20150357. doi: 10.1098/ rsif.2015.0357.
[76] Withers P C. An aerodynamic analysis of bird wings as fixed aerofoils [J]. Journal of Experimental Biology, 1981, 90(1): 143(1): 143-162.
[77] Nakata T, Liu H. Aerodynamic performance of a hovering hawkmoth with flexible wings: a computational approach [J]. Proceedings of the Royal Society B-Biological Sciences, 2012, 279(1729): 722-731.
[78] Harbig R R, Sheridan J, Thompson M C. Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms [J]. Journal of Fluid Mechanics, 2013, 717(2013): 166-192.
[79] Garmann D J, Visbal M R. Dynamics of revolving wings for various aspect ratios [J]. Journal of Fluid Mechanics, 2014, 748(2014): 932-956.
[80] Harbig R R, Sheridan J, Thompson M C. The role of advance ratio and aspect ratio in determining leading-edge vortex stability for flapping flight [J]. Journal of Fluid Mechanics, 2014, 751(2014): 71-105.
[81] Johansson L C, Engel S, Kelber A, et al. Multiple leading edge vortices of unexpected strength in freely flying hawkmoth [J]. Scientific Reports, 2013, 3(2013): 03264. doi: 10.1038/srep03264.
[82] Han J S, Chang J W, Cho H K. Vortices behavior depending on the aspect ratio of an insect-like flapping wing in hover [J]. Experiments in Fluids, 2015, 56(9): 181. doi: 10.1007/s00348-015-2049-9.
[83] Kruyt J W, Quicazan-Rubio E M, Van Heijst G F, et al. Hummingbird wing efficacy depends on aspect ratio and compares with helicopter rotors [J]. Journal of the Royal Society Interface, 2014, 11(99): 20140585. doi: 10.1098/ rsif.2014.0585.
[84] Kruyt J W, Van Heijst G F, Altshuler D L, et al. Power reduction and the radial limit of stall delay in revolving wings of different aspect ratio [J]. Journal of the Royal Society Interface, 2015, 12(105): 20150051. doi: 10.1098/rsif.2015.0051.
[85] Srygley R B, Thomas A L R. Unconventional lift-generating mechanisms in free-flying butterflies [J]. Nature, 2002, 420(6916): 660-664.
[86] Yokoyama N, Senda K, Iima M, et al. Aerodynamic forces and vortical structures in flapping butterfly's forward flight [J]. Physics of Fluids, 2013, 25(2): 021902. doi: 10.1063/1.4790882.
[87] Bomphrey R J, Nakata T, Henningsson P, et al. Flight of the dragonflies and damselflies [J]. Philosophical Transactions of the Royal Society B-Biological Sciences, 2016, 371(1704): 20150389. doi: 10.1098/rstb.2015. 0389.
[88] Thielicke W, Stamhuis E J. The influence of wing morphology on the three-dimensional flow patterns of a flapping wing at bird scale [J]. Journal of Fluid Mechanics, 2015, 768(2015): 240-260.
[89] Lee S I, Kim J, Park H, et al. The function of the alula in avian flight [J]. Scientific Reports, 2015, 5(2015): 9914. doi: 10.1038/srep09914.
[90] Meng X G, Sun M. Aerodynamic effects of corrugation in flapping insect wings in forward flight [J]. Journal of Bionic Engineering, 2011, 8(2): 140-150.
[91] Meng X G, Xu L, Sun M. Aerodynamic effects of corrugation in flapping insect wings in hovering flight [J]. Journal of Experimental Biology, 2011, 214(3): 432-444.
[92] Du G, Sun M. Aerodynamic effects of corrugation and deformation in flapping wings of hovering hoverflies [J]. Journal of Theoretical Biology, 2012, 300: 19-28.
[93] Meng X G, Sun M. Aerodynamic effects of wing corrugation at gliding flight at low Reynolds numbers [J]. Physics of Fluids, 2013, 25(7): 071905. doi: 10.1063/1. 4813804.
[94] Brandt J, Doig G, Tsafnat N. Computational aerodynamic analysis of a Micro-CT based bio-realistic fruit fly wing [J]. Plos One, 2015, 10(5): 0124824. doi: 10.1371/ journal.pone.0124824.
[95] Rajabi H, Ghoroubi N, Malaki M, et al. Basal complex and basal venation of odonata wings: Structural diversity and potential role in the wing deformation [J]. Plos One, 2016, 11(8): 0160610. doi: 10.1371/journal.pone.0160610.
[96] Van Bokhorst E, De Kat R, Elsinga G E, et al. Feather roughness reduces flow separation during low Reynolds number glides of swifts [J]. Journal of Experimental Biology, 2015, 218(20): 3179-3191.
[97] Watson G S, Watson J A, Cribb B W. Diversity of cuticular micro-and nanostructures on insects: properties, functions, and potential applications [J]. Annual Review of Entomology, 2017, 62(2017): 185-205.
[98] De Langre E. Effects of wind on plants [J]. Annual Review of Fluid Mechanics, 2008, 40(2008): 141-168.
[99] Favier J, Dauptain A, Basso D, et al. Passive separation control using a self-adaptive hairy coating [J]. Journal of Fluid Mechanics, 2009, 627(2009): 451-483.
[100] Slegers N, Heilman M, Cranford J, et al. Beneficial aerodynamic effect of wing scales on the climbing flight of butterflies [J]. Bioinspiration & Biomimetics, 2017, 12(1): 1-12.
[101] Polilov A A. Small is beautiful: features of the smallest insects and limits to miniaturization [J]. Annual Review of Entomology, 2015, 60(2015): 103-121.
[102] Takahashi H, Sato K, Nguyen M-D, et al. Characteristic evaluation of a bristled wing using mechanical models of a thrips wings with MEMS piezoresistive cantilevers [J]. Journal of Biomechanical Science and Engineering, 2015, 10(2): 14-00233-14-00233.
[103] Barta E, Weihs D. Creeping flow around a finite row of slender bodies in close proximity [J]. Journal of Fluid Mechanics, 2006, 551(2006): 1-17.
[104] Weihs D, Barta E. Comb wings for flapping flight at extremely low reynolds numbers [J]. Aiaa Journal, 2008, 46(1): 285-288.
[105] Davidi G, Weihs D. Flow around a comb wing in low-reynolds-number flow [J]. Aiaa Journal, 2012, 50(1): 249-253.
[106] Jones S K, Yun Y J J, Hedrick T L, et al. Bristles reduce the force required to 'fling' wings apart in the smallest insects [J]. Journal of Experimental Biology, 2016, 219(23): 3759-3772.
[107] Lee S H, Kim D. Aerodynamics of a translating comb-like plate inspired by a fairyfly wing [J]. Physics of Fluids, 29(8): 081902. doi: 10.1063/1.4998434.
[108] Lee S H, Lahooti M, Kim D. Aerodynamic characteristics of unsteady gap flow in a bristled wing [J]. Physics of Fluids, 2018, 30(7): 071901. doi: 10.1063/1.5030693.
[109] Huber J T, Noyes J S. A new genus and species of fairyfly, Tinkerbella nana (Hymenoptera, Mymaridae), with comments on its sister genus Kikiki, and discussion on small size limits in arthropods [J]. Journal of Hymenoptera Research, 2013, 32(2013): 17-44.
[110] 张云飞, 叶正寅, 谢飞. 展向柔性对扑翼推力影响原因的数值分析[J]. 工程力学, 2013, 30(2): 419-426.
Zhang Y F, Ye Z Y, Xie F. The numerical analysis of the reason for the effect of Spanwise flexibility on flapping wing thrust [J]. Engineering Mechanics, 2013, 30(2): 419-426. (in Chinese)
[111] Cheng X, Sun M. Wing-kinematics measurement and aerodynamics in a small insect in hovering flight [J]. Scientific Reports, 2016, 6(2016): 25706. doi: 10.1038/ srep25706.
[112] Walker S M, Thomas A L R, Taylor G K. Deformable wing kinematics in free-flying hoverflies [J]. Journal of the Royal Society Interface, 2010, 7(42): 131-142.
[113] Walker S M, Thomas A L R, Taylor G K. Photogrammetric reconstruction of high-resolution surface topographies and deformable wing kinematics of tethered locusts and free-flying hoverflies [J]. Journal of the Royal Society Interface, 2009, 6(33): 351-366.
[114] Mountcastle A M, Combes S A. Wing flexibility enhances load-lifting capacity in bumblebees [J]. Proceedings of the Royal Society B-Biological Sciences, 2013, 280(1759): 20130531. doi: 10.1098/rspb.2013. 0531.
[115] Du G, Sun M. Effects of wing deformation on aerodynamic forces in hovering hoverflies [J]. Journal of Experimental Biology, 2010, 213(13): 2273-2283.
[116] Zheng L X, Hedrick T L, Mittal R. Time-varying wing-twist improves aerodynamic efficiency of forward flight in butterflies [J]. Plos One, 2013, 8(1): 53060. doi: 10.1371/journal.pone.0053060.
[117] 周超英, 朱建阳, 汪超, 等. 柔性扑翼气动性能的数值研究[J]. 工程力学, 2013, 30(5): 13-18.
Zhou C Y, Zhu J Y, Wang C, et al. Numerical study on the effect of flexiblity of a flapping wing on its aerodynamic perforwing on its aerodynamic performancemance [J]. Engineering Mechanics, 2013, 30(5): 13-18.(in Chinese)
[118] Dai H, Luo H X, Doyle J F. Dynamic pitching of an elastic rectangular wing in hovering motion [J]. Journal of Fluid Mechanics, 2012, 693: 473-499.
[119] Nakata T, Liu H. A fluid-structure interaction model of insect flight with flexible wings [J]. Journal of Computational Physics, 2012, 231(4): 1822-1847.
[120] Noda R, Nakata T, Liu H. Effects of wing deformation on aerodynamic performance of a revolving insect wing [J]. Acta Mechanica Sinica, 2014, 30(6): 819-827.
[121] Tanaka H, Whitney J P, Wood R J. Effect of flexural and torsional wing flexibility on lift generation in Hoverfly flight [J]. Integrative and Comparative Biology, 2011, 51(1): 142-150.
[122] Jones S K, Laurenza R, Hedrick T L, et al. Lift vs. drag based mechanisms for vertical force production in the smallest flying insects [J]. Journal of Theoretical Biology, 2015, 384: 105-120.
[123] Santhanakrishnan A, Robinson A K, Jones S, et al. Clap and fling mechanism with interacting porous wings in tiny insect flight [J]. Journal of Experimental Biology, 2014, 217(21): 3898-3909.
[124] Sane S P. Neurobiology and biomechanics of flight in miniature insects [J]. Current Opinion in Neurobiology, 2016, 41: 158-166.
[125] Weis-Fogh T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production [J]. Journal of Experimental Biology, 1973, 59(1): 169.
[126] Miller L A, Peskin C S. Flexible clap and fling in tiny insect flight [J]. Journal of Experimental Biology, 2009, 212(19): 3076-3090.
[127] Sun M, Yu X. Aerodynamic force generation in hovering flight in a tiny insect [J]. Aiaa Journal, 2006, 44(7): 1532-1540.
[128] Kolomenskiy D, Moffatt H K, Farge M, et al. Two-and three-dimensional numerical simulations of the clap- fling-sweep of hovering insects [J]. Journal of Fluids and Structures, 2011, 27(5): 784-791.
[129] Arora N, Gupta A, Sanghi S, et al. Lift-drag and flow structures associated with the “clap and fling” motion[J]. Physics of Fluids, 2014, 26(7): 071906. doi: 10.1063/1. 4890221.
[130] GÖtz K G. Course-control, metabolism and wing interference during ultralong tethered flight in drosophila melanogaster [J]. Journal of Experimental Biology, 1987, 128(1): 35-46.
[131] Percin M, Hu Y, Van Oudheusden B W, et al. Wing flexibility effects in clap-and-fling [J]. International Journal of Micro Air Vehicles, 2011, 3(4): 217-227.
[132] Sane S P. The aerodynamics of insect flight [J]. Journal of Experimental Biology, 2003, 206(23): 4191-4208.
[133] Cheng X, Sun M. Aerodynamic forces and flows of the full and partial clap-fling motions in insects [J]. Peerj, 2017, 5(2017): 3002. doi: 10.7717/peerj.3002.
[134] Murphy D W, Adhikari D, Webster D R, et al. Underwater flight by the planktonic sea butterfly [J]. Journal of Experimental Biology, 2016, 219(4): 535-543.
[135] Lian Y. Numerical Study of a Flapping Airfoil in Gusty Environments [C]. San Antonio, U.S.: 27th AIAA Applied Aerodynamics Conference, 2009.
[136] Zheng Y Y, Wu Y H, Tang H. Force measurements of flexible tandem wings in hovering and forward flights [J]. Bioinspiration & Biomimetics, 2015, 10(1): 016021. doi: 10.1088/1748-3190/10/1/016021.
[137] Yu X, Sun M. A computational study of the wing-wing and wing-body interactions of a model insect [J]. Acta Mechanica Sinica, 2009, 25(4): 421-431.
[138] Liang B, Sun M. Aerodynamic interactions between wing and body of a model insect in forward flight and maneuvers [J]. Journal of Bionic Engineering, 2013, 10(1): 19-27.
[139] Wan H, Dong H, Gai K. Computational investigation of cicada aerodynamics in forward flight [J]. Journal of The Royal Society Interface, 2015, 12(102): 20141116. doi: 10.1098/rsif.2014.1116.
[140] Johansson L C, Wolf M, Hedenstrom A. A quantitative comparison of bird and bat wakes [J]. Journal of the Royal Society Interface, 2010, 7(42): 61-66.
[141] Muijres F T, Johansson L C, Bowlin M S, et al. Comparing aerodynamic efficiency in birds and bats suggests better flight performance in birds [J]. Plos One, 2012, 7(5): 37335. doi: 10.1371/journal.pone.0037335.
[142] Weimerskirch H, Martin J, Clerquin Y, et al. Energy saving in flight formation-Pelicans flying in a ‘V’ can glide for extended periods using the other birds' air streams [J]. Nature, 2001, 413(6857): 697-698.
[143] Sullivan R T. Insect swarming and mating [J]. The Florida Entomologist, 1981, 64(1): 44-65.
[144] Piksa K, Bogdanowicz W, Tereba A. Swarming of bats at different elevations in the Carpathian Mountains [J]. Acta Chiropterologica, 2011, 13(1): 113-122.
[145] Portugal S J, Hubel T Y, Fritz J, et al. Up wash exploitation and downwash avoidance by flap phasing in ibis formation flight [J]. Nature, 2014, 505(7483): 399-402.
[146] Davidovich H, Ribak G. Loaded flight in male Ischnura elegans and its relationship to copulatory flight [J]. Journal of Insect Physiology, 2018, 110: 44-56.
[147] Gao T, Lu X Y. Insect normal hovering flight in ground effect [J]. Physics of Fluids, 2008, 20(8): 087101. doi: 10.1063/1.2958318.
[148] Chen M W, Sun M. Wing/body kinematics measurement and force and moment analyses of the takeoff flight of fruitflies [J]. Acta Mechanica Sinica, 2014, 30(4): 495-506.
[149] Chen M W, Zhang Y L, Sun M. Wing and body motion and aerodynamic and leg forces during take-off in droneflies [J]. Journal of the Royal Society Interface, 2013, 10(89): 20130808. doi: 10.1098/rsif.2013.0808.
[150] Bimbard G, Kolomenskiy D, Bouteleux O, et al. Force balance in the take-off of a pierid butterfly: relative importance and timing of leg impulsion and aerodynamic forces [J]. Journal of Experimental Biology, 2013, 216(18): 3551-3563.
[151] Truong T V, Byun D, Kim M J, et al. Aerodynamic forces and flow structures of the leading edge vortex on a flapping wing considering ground effect [J]. Bioinspiration & Biomimetics, 2013, 8(3): 036007. doi: 10.1088/1748-3182/8/3/036007.
[152] Buchwald R, Dudley R. Limits to vertical force and power production in bumblebees (Hymenoptera: Bombus impatiens) [J]. Journal of Experimental Biology, 2010, 213(3): 426-432.
[153] Chai P, Millard D. Flight and size constraints: hovering performance of large hummingbirds under maximal loading [J]. The Journal of Experimental Biology, 1997, 200: 2757-2763.
[154] Ma K Y, Chirarattananon P, Fuller S B, et al. Controlled flight of a biologically inspired, insect-scale robot [J]. Science, 2013, 340(6132): 603-607.
[155] Karasek M, Muijres F T, De Wagter C, et al. A tailless aerial robotic flapper reveals that flies use torque coupling in rapid banked turns [J]. Science, 2018, 361(6407): 1089-1094.
[156] Zou Y, Zhang W P, Ke X J, et al. The design and microfabrication of a sub 100 mg insect-scale flapping-wing robot [J]. Micro & Nano Letters, 2017, 12(5): 297-300.
[157] Keennon M, Klingebiel K, Won H. Development of the Nano Hummingbird: A Tailless Flapping Wing Micro Air Vehicle[C]. Nashville, U.S.: 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2012.
[158] Mackenzie D. A flapping of wings [J]. Science, 2012, 335(6075): 1430-1432.
[159] Ramezani A, Chung S-J, Hutchinson S. A biomimetic robotic platform to study flight specializations of bats [J]. Science Robotics, 2017, 2(3): 2505. doi: 10.1126/ scirobotics.aal2505.
[160] Tay W B, Van Oudheusden B W, Bijl H. Numerical simulation of X-wing type biplane flapping wings in 3D using the immersed boundary method [J]. Bioinspiration & Biomimetics, 2014, 9(3): 036001. doi: 10.1088/ 1748-3182/9/3/036001.
[161] Wei X, Li D, Jiaqi J, et al. Experimental and numerical study of flapping wing rotary MAV [C]. 2017 IEEE International Conference on Unmanned Systems (ICUS), 2017: 23-28.
[162] Yi S, Li D, Jiaqi J, et al. Experimental and numerical study of flapping wing rotary MAV [C]. Beijing, China: 2017 IEEE International Conference on Unmanned Systems, 2017.
[163] Chen Y F, Helbling E F, Gravish N, et al. Hybrid aerial and aquatic locomotion in an at-scale robotic insect [C]. Hamburg, Germany: 2015 Ieee/Rsj International Conference on Intelligent Robots and Systems, 2015.
[164] Chen Y, Wang H, Helbling E F, et al. A biologically inspired, flapping-wing, hybrid aerial-aquatic microrobot [J]. Science Robotics, 2017, 2(11): 5619. doi: 10.1126/ scirobotics.aao5619.
[165] 杜晓旭, 张正栋. 四种扑动方式对水下扑翼推进性能影响数值分析[J]. 工程力学, 2018, 35(4): 249-256.
Du X X, Zhang Z D. Numerical analysis of influence of four flapping modes on propulsion performance of underwater flapping foils [J]. Engineering Mechanics, 2018, 35(4): 249-256. (in Chinese)
[166] Shrestha R, Benedict M, Hrishikeshavan V, et al. Hover performance of a small-scale helicopter rotor for flying on mars [J]. Journal of Aircraft, 2016, 53(4): 1160-1167.
[167] Bluman J E, Pohly J A, Sridhar M K, et al. Achieving bioinspired flapping wing hovering flight solutions on Mars via wing scaling [J]. Bioinspiration & Biomimetics, 2018, 13(4): 046010. doi: 10.1088/1748-3190/aac876.
RESEARCH PROGRESS AND APPLICATION OF FLAPPING WING AERODYNAMICS
Abstract: Insects, birds and bats have superb flying ability. They are the main imitators of a flapping-wing aircraft. In recent years, a great progress has been made in the field of flapping-wing aerodynamics. This paper summarized the main research results, and focus on the recent advances in flapping-wing aerodynamics, including the flapping-wings lift mechanism of insects, birds and bats, the effects of wing morphological parameters and microstructures, wing flexibility, dynamic deformation, wing-wing interference, wing-body interference, inter-individual interference, and ground effect on the flapping wing aerodynamics. We also introduced the research progress of aerodynamic research on bionic flapping-wing aircraft design. At the end, the main problems and challenges faced by flapping-wing aerodynamics are presented.
Key words: flapping wing; aerodynamics; insect; bird; bat
文章编号:1000-4750(2019)04-0008-16
中图分类号:V211.5
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.03.0175
收稿日期:2018-03-26;
修改日期:2019-01-26
基金项目:国家自然科学基金面上项目(11572023)
孙 毅(1978―),男,陕西人,工程师,博士生,从事无人机总体技术与微型飞行器设计研究(E-mail: 821522495@qq.com);
申 童(1993―),男,陕西人,博士生,从事微型扑翼气动特性研究(E-mail: shentong@buaa.edu.cn).