在高层建筑、大跨桥梁以及大型风力发电系统等结构中，风荷载往往是对结构安全性起控制作用的因素，因此长期以来对于风场的研究一直是众多学者关注的重点。通常，风速随着空间和时间而变化，因此空间不同位置处的风速往往处理为具有相关性的随机过程，并采用互功率谱密度函数矩阵刻画风场的特征[1－3]。随着对结构在风荷载作用下非线性效应的日益关注，脉动风速场的模拟，即如何根据给定的功率谱密度函数或矩阵生成脉动风速时程，是结构风振随机响应分析与可靠性设计中的关键环节之一。在许多实际工程中，一般只考虑空间中多个离散点的纵向分量的风速时程[4－5]。
谱表达方法是脉动风场模拟中应用最广泛的方法之一[5－9]。当只进行空间中给定单点的风速模拟时，其表达形式为一系列谐和分量的叠加[10－11]。当模拟空间中多个点的风速时，需要引入互功率谱矩阵以考虑空间相关性，一般需要对互功率谱矩阵进行Cholesky分解[12]或者本征正交分解[13]。由于该方法在模拟风场时，要对互功率谱矩阵在每个频率点处进行一次分解，当模拟的点数较多时，互功率谱矩阵维数非常高，分解效率很低，甚至可能由于出现矩阵奇异而难以实现。而当模拟的脉动风速时程为非平稳随机过程时，由于演变功率谱具有时变性，使得对互功率谱矩阵的分解次数大为增加[14－15]。不少学者对此进行了多方面改进[14－18]，但难以避免高维矩阵分解，因而该问题仍值得进一步研究。
事实上，脉动风速场是一个随时间和空间连续变化的随机场，由于对空间的人为离散，导致了上述对互功率谱矩阵的分解问题。而早在1971年，Shinozuka[5]在研究多维随机过程问题时，把沿一维空间分布的脉动风场考虑为一个二维随机过程，推导了其功率谱的表达形式，并给出了风场模拟的公式。遗憾的是，该方法长期没有得到关注。直到2013年以后，Benowitz[6]及Benowitz和Deodatis[7]采用了相同的思路，针对一维空间均匀脉动风场的模拟问题，将脉动风场考虑为沿时间和空间变化的随机过程，推导了其波数-频率联合功率谱的具体表达公式，并利用谱表达方法模拟了一维空间的均匀脉动风场。该方法原则上无需进行空间离散，也不需要Cholesky分解或本征正交分解，表达形式简单，同时可以采用二维FFT技术提高模拟效率。Peng等[19]在此基础上引入基于POD的插值方法，模拟了水平方向非等间距分布点的均匀脉动风场。刘章军等[20]基于此方法，引入标准正交随机变量集的随机函数表达，极大地降低了随机变量的个数，模拟了水平方向等间距分布点的均匀脉动风场。Peng等[21]进一步地引入“演变谱”的概念，将该方法拓展到一维空间非均匀脉动风场的模拟。然而，当模拟点为非等间距点时，基于波数和频率的非均匀脉动风场模拟方法无法使用FFT，因此模拟效率有待进一步提高。
本文基于一维空间非均匀脉动风场的波数-频率联合演变功率谱，引入“结构化”非均匀离散方法和“舍选法”的思想，建议了两类二维波数-频率域的非均匀离散策略，并给出了相应的谱表达形式。应用该方法，对某桥塔的非均匀脉动风场进行了数值模拟，验证了其有效性。
在工程应用中，脉动风速时程通常可以模拟为平稳随机过程。根据雷诺分解，在z高度处(本文仅研究一维空间的风场情况)总的风速时程X′(z,t)可以表示为[4]：
式中：U(z)为z高度处的平均风速；X(z,t)是z高度处的脉动风速，且E[X(z,t)] = 0，E(·)表示数学期望。在1z和z2高度处脉动风速X1(t)和X2(t)的互相关函数为：
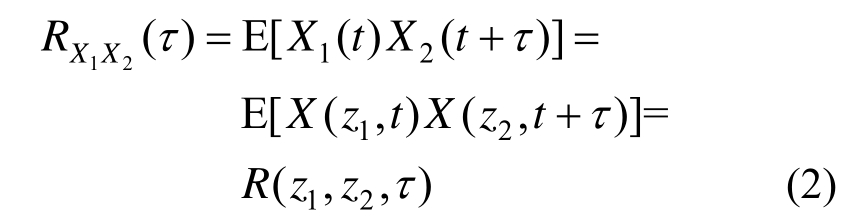
对式(2)关于时间间隔τ进行Fourier变换，可以得到空间两个不同点处脉动风速的互功率谱密度函数：
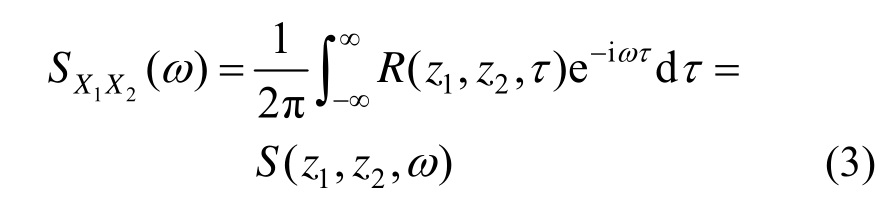
式中，ω/(rad/s)为圆频率。
当z1 =z2=z时，通过式(3)可以得到给定空间点z处脉动风速的自功率谱密度函数：
在实际工程中，互功率谱密度函数通常可以由自功率谱密度函数和相干函数得到：
其中，ρX1X2(ω)为脉动风的相干函数，常采用如下形式[4]：
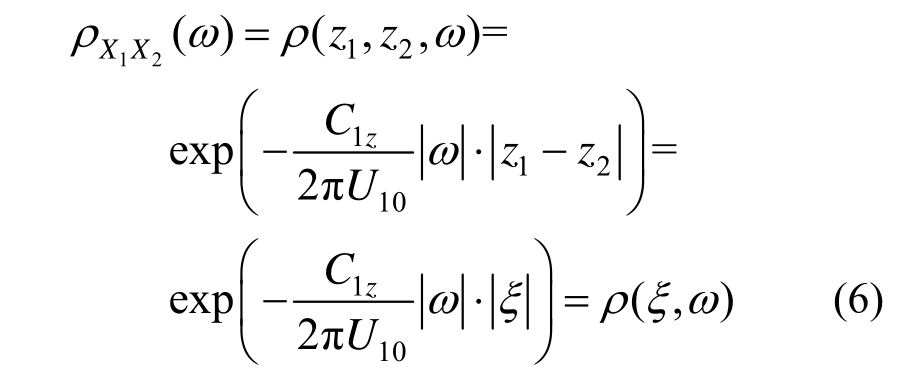
式中：C1z为常数，可取为7[19]；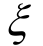
=z1 -z2为空间两点的坐标差；U10为10 m高度处的平均风速。
在实际工程中，有时采用与高度无关的脉动风速谱S0(ω)。例如在我国《建筑结构荷载规范》GB 50009－2012中采用Davenport脉动风速谱[2]。此时，脉动随机风场是空间均匀风场。针对一维问题，文献[6－7]给出了基本结果。事实上，这时式(5)可写为：
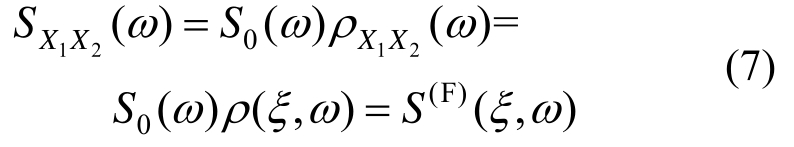
式中，上标“(F)”表示(F)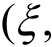
,)Sω为频域上的谱。
进一步地，对式(7)关于空间距离变量ξ进行Fourier变换，可得：
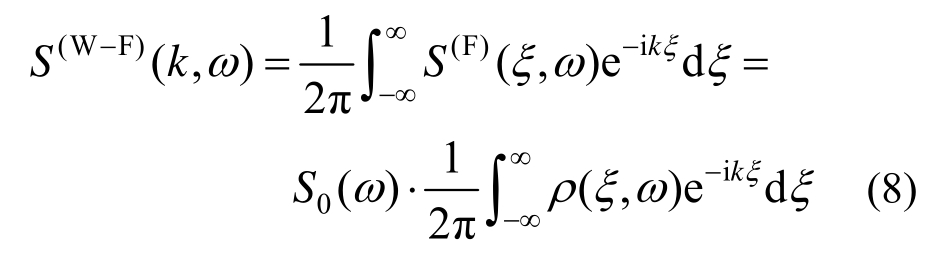
式中：k/(rad/m)表示波数；上标“(W-F)”表示S(W-F)(k,ω )是波数-频率域上的联合谱。
将式(6)代入式(8)，并利用下述积分公式[20,22]：
可得：
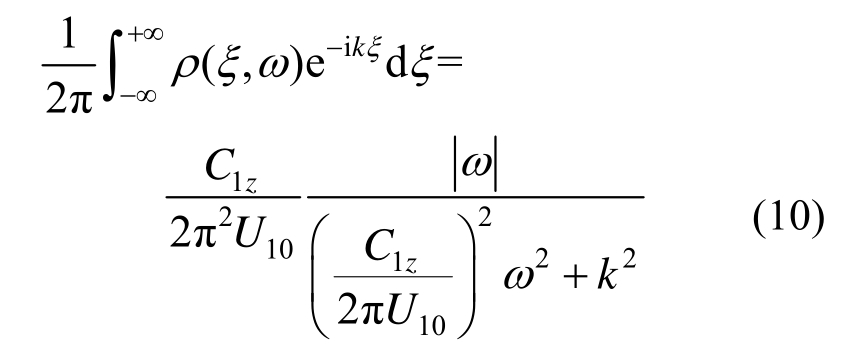
由此，可以得到一维空间均匀脉动风场的波数-频率联合功率谱：
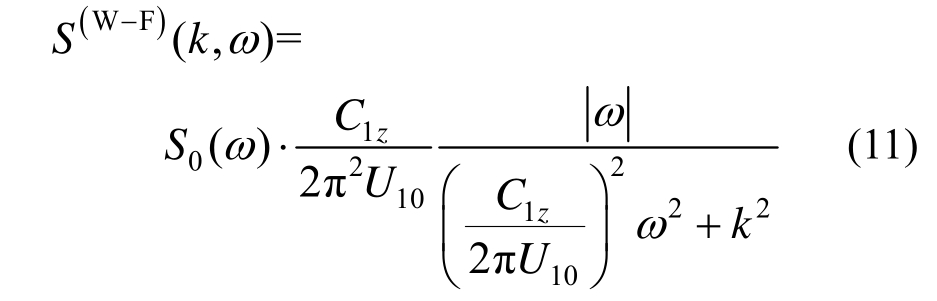
在此基础上，采用谱表达方法[10]，可得一维空间各点的脉动风速时程：
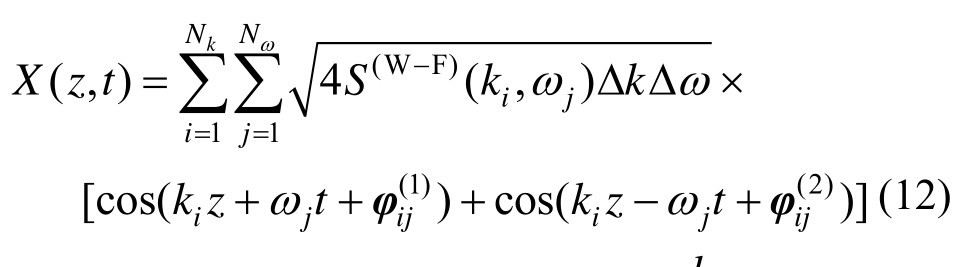
其中
是波数截断上限，Nk是波数的离散个数；类似地，在频域上也有
ωu是频率截断上限，Nω是频率的离散个数；
和
是两组在[0，2π]均匀分布且相互独立的随机相位。
实际工程中应用的脉动风速谱往往与高度有关，例如常用的Kaimal谱[3]，其双边谱形式如下：
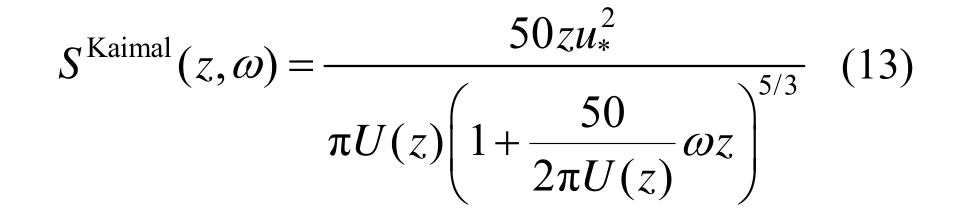
式中：u*表示剪切速度；U(z)表示z高度处的平均风速。
此时，一维空间脉动风场不再是均匀随机场。引入非平稳随机过程的演变谱概念，可将上述基本思想拓展至一维非均匀脉动风场之中[21]。
非平稳随机过程(场)可以看作是与之对应的平稳随机过程(场)在时域(空间)和频率(波数)上调制后得到的。相应地，随时间(空间)变化的功率谱密度函数成为演变功率谱密度函数[23－24]。
不失一般性，记A(t,ω)为关于时间和频率(空间和波数)的复调制函数。那么非均匀随机过程(场)Y(t)可以表示为：
其中，η(ω)是频域(波数域)内的正交随机过程，满足：
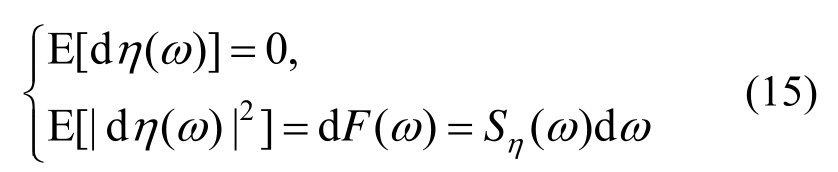
式中，Sη(ω)为对应的平稳随机过程(场)η(t)的功率谱密度函数。
那么，该非平稳随机过程(场)Y(t)的自相关函数为：
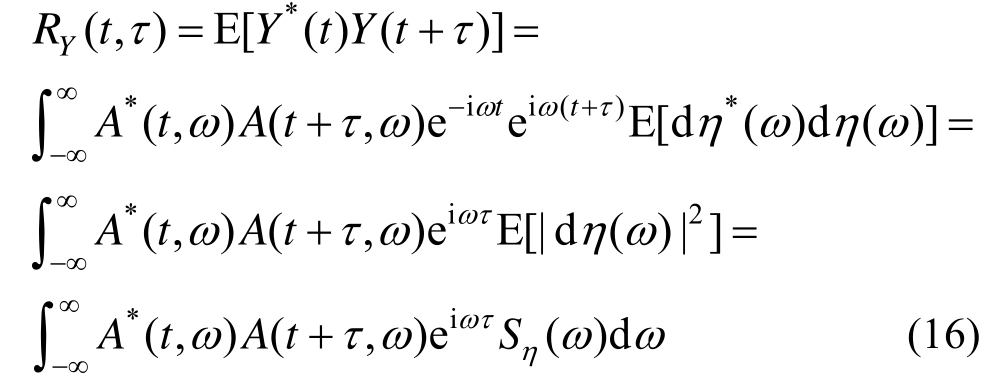
则Y(t)的方差为：
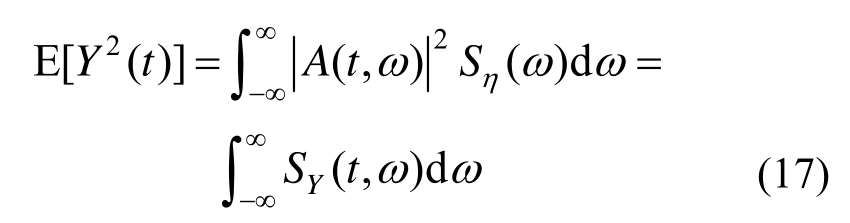
相应地，演变功率谱密度函数可以表示为：
现在考虑随高度变化的脉动风速功率谱密度函数，此时脉动风场是非均匀的。记z高度处脉动风速时程X(z,t)的自功率谱密度函数为SX(z,ω)，则不同高度处两点脉动风速时程X(z1,t)和X(z2,t)的互功率谱密度函数为：
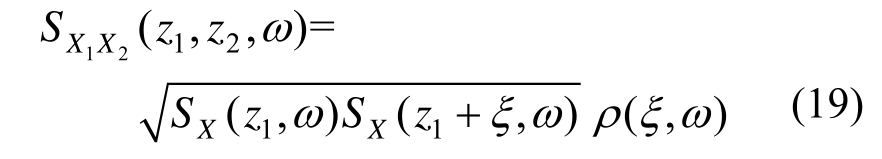
式中，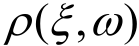
仍取式(6)的形式。
记在时间-空间域上的均匀随机场为Γ(z,t)，其功率谱密度函数和相关函数分别为SΓ (k,ω)和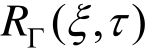
，且有：
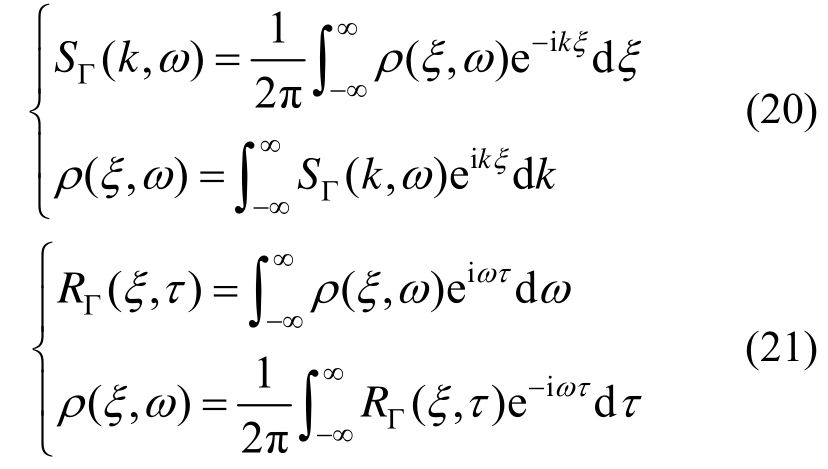
该均匀随机场可表示为：
其中，Γ(k,)ω为正交的随机场，且：
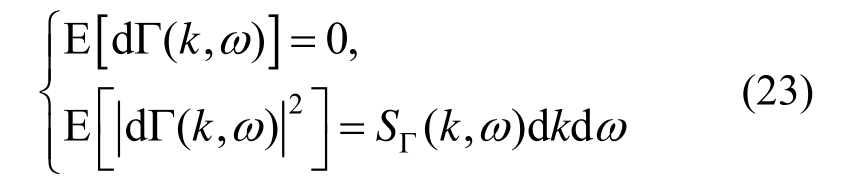
取调制函数为：
则可以得到非均匀随机场X0(z,t)为：
其相关函数为：
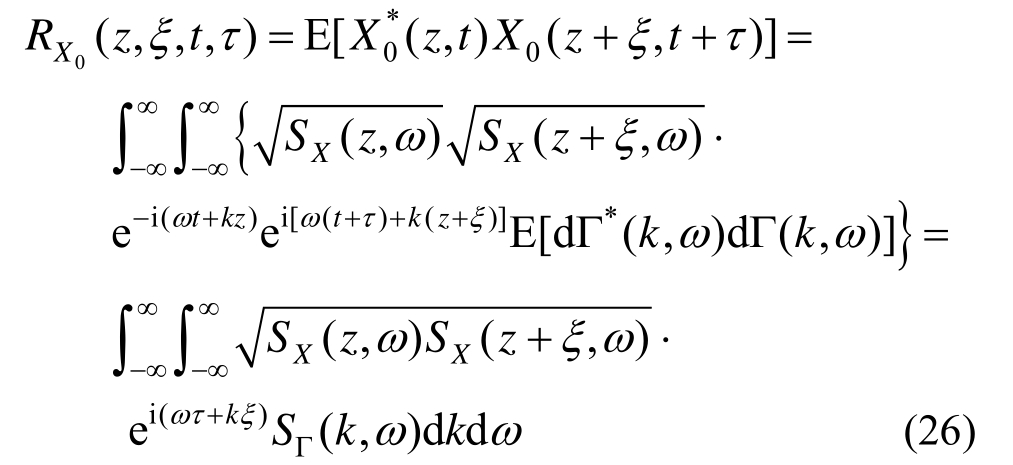
将式(20)中第2式代入式(26)，得：
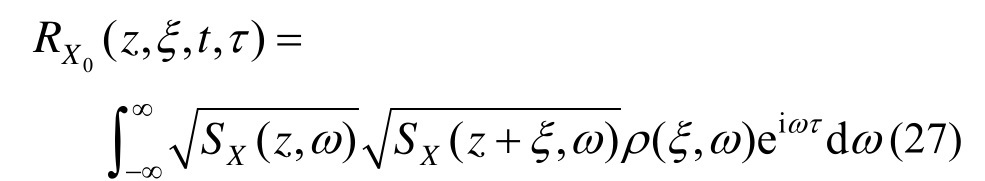
可以发现，对X(z,t)的功率谱密度函数，即式(19)进行Fourier变换后，正是式(27)，这说明由均匀随机场Γ(z,t)经过调制后得到的非均匀随机场X0(z,t)就是X(z,t)。
根据式(26)可得该非均匀随机场的方差函数为：
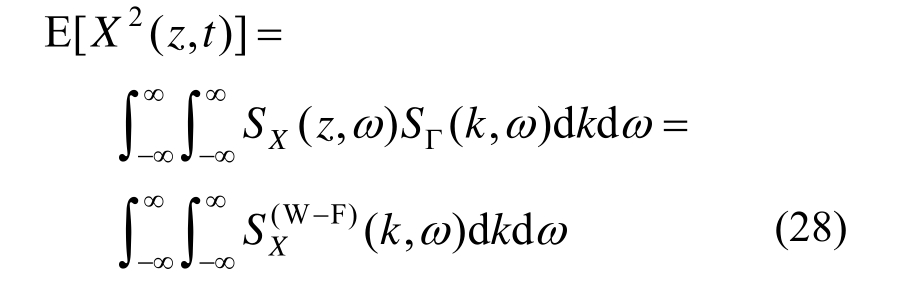
因此非均匀随机场X(z,t)的波数-频率联合演变功率谱的表达式为：
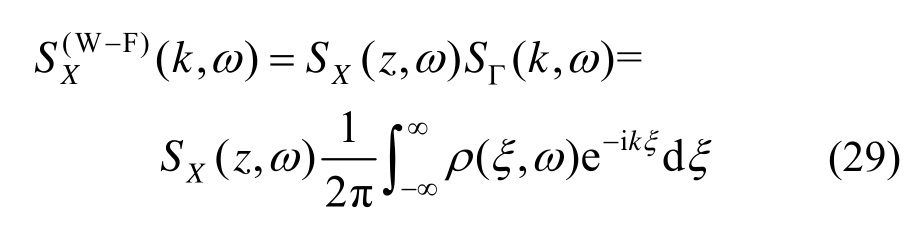
引入Kaimal谱，并根据式(10)，可得：
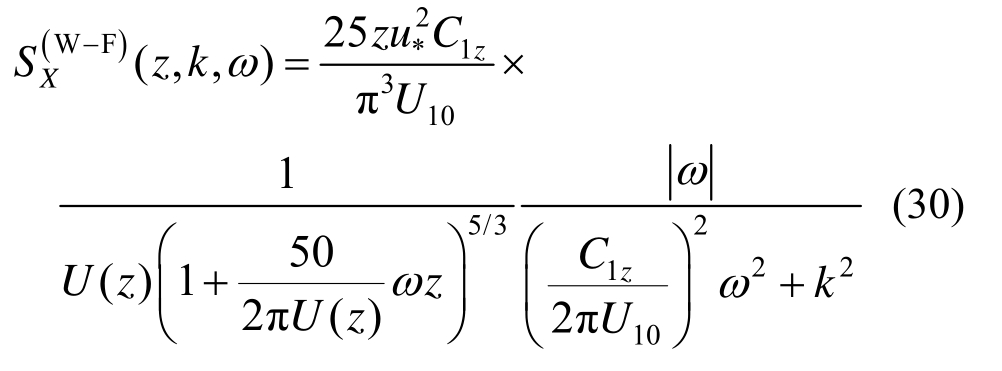
对于非均匀脉动风场的谱表达形式，只需将式中的波数-频率联合功率谱换为演变谱即可[25－27]，即：
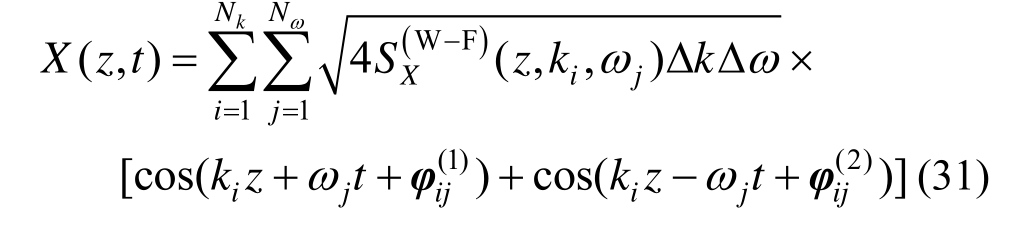
式中，其余各参数的意义与式(12)相同。
需要注意的是，式(31)是基于波数和频率两个方向均匀离散的结果。更重要的是，式(30)的联合功率谱，其能量主要分布在距原点较近的区域，且谱值变化很快，同时联合功率谱具有较长的尾部。且空间高度越高(z越大)，这一特征越明显。由于这些特征，在均匀离散时为了能够较为准确地刻画功率谱在频域-波数域上的能量分布情况，在频率方向上需要离散数目为 103量级的频率点，而在波数方向上需要离散量级近 104的波数点，因而总的点数达到 1 06 ～107量级，这导致了很大的计算量。为了进一步提高效率，可以采用非均匀离散的思想，即在联合功率谱谱值较大的区域离散点较为密集，而在其它区域则较为稀疏，由此可以显著减少总的离散点数，从而大大降低计算量。为此，本文提出“结构化”和“舍选法”思想的两种非均匀离散方式。
3.2.1 “结构化”非均匀离散
研究表明[28]，在两个方向进行非均匀离散常常可在保持精度相当的前提下极大地降低计算量。针对本文中的问题，在波数方向上，在(0,0.1] rad/m区域离散300个点，在(0.1,1.0] rad/m离散200个点，在(1.0,5.0] rad/m离散300个点，共计800个点。在频率方向，按照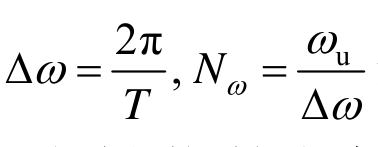
进行均匀离散，其中T为生成风速时程的时间长度，得到Nω=750。这样总的离散点数为800×750=6×105，较之式(31)表示的均匀离散方式降低了一个数量级。由于点数较多难以全部画出，图1(a)表示离散后点的示意图。
3.2.2 “舍选法”非均匀离散
舍选法常用来生成非均匀分布随机变量的样本[24]。这一思想可以引入波数-频率域的非均匀离散之中。为此，首先采用Sobol序列[29]在正方体[0,1]3内生成均匀散布的点集
然后，通过尺度变换
其中a＞max
将初始点集Mn′变换到长方体区域
之中，得到点集
。最后，对点集Mn进行如下舍选：若
，则剔除点ηi，将最终剩下来的点记为
进而，取
为二维波数-频率域内的离散点。利用这一方法进行下文算例中的波数-频率域离散，由于不同高度处的波数-频率联合功率谱不同，这里选取最高点的联合功率谱，即
“舍选法”过程中使用，由此共得到约1×105个离散点，如图1(b)所示。较之结构化非均匀离散，总点数又大为降低。
3.2.3 非均匀离散后的谱表达形式
对波数-频率二维区域进行非均匀离散后，式(31)的表达式不再适用。此时，式(31)可以改写为：
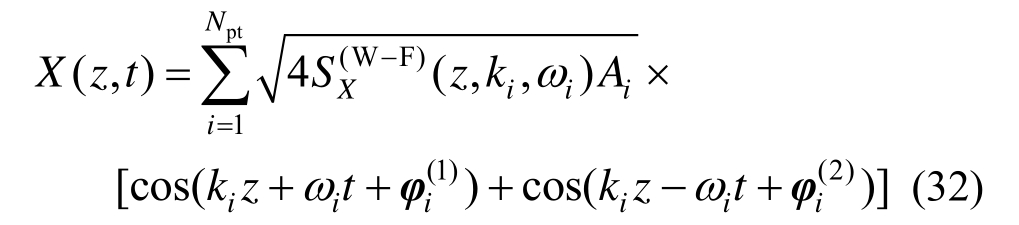
式中：Npt为离散点的个数；Ai为第i个离散点的代表面积(对于多维空间的波数-频率高维区域离散，Ai为第i个离散点的代表体积)，其计算方法可以类比计算Voronoi区域赋得概率的方法[24]；ki和ωi分别为第i个离散点对应的波数和频率；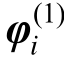
和
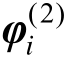是两组在[0,2π]均匀分布且相互独立的随机相位。
顺便指出，利用随机谐和函数方法[27]，上述离散点数还可以大大降低。限于篇幅，兹不赘述。
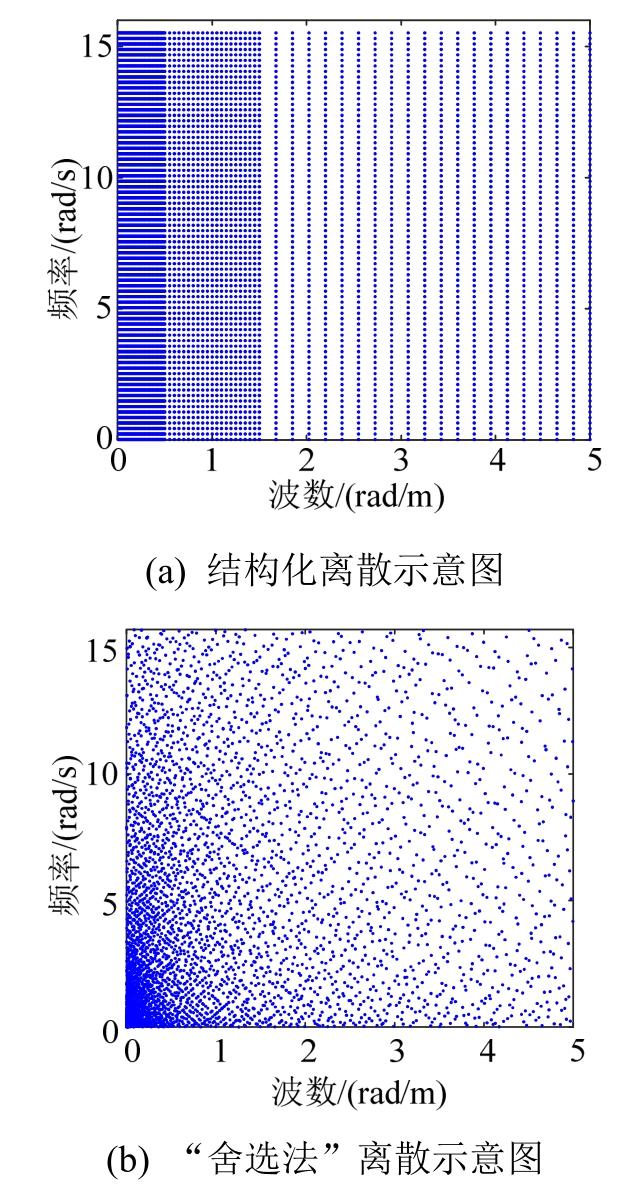
图1 两种非均匀离散方法得到的离散点
Fig.1 Discrete points obtained by two uneven discretization methods
参考某实际工程设计资料[30]，该桥址处10 m高度处10 min设计平均风速为31.88 m/s，该桥址处摩擦速度*u=1.691 m/s，地面粗糙度长度z0=0.005 m。在本算例中，对其中一个高度为170 m的桥塔的风场进行模拟，这里仅考察10 m高度、80 m高度和160 m高度处的脉动风速特征。
应注意到，在利用本文的方法模拟风场时首先要确定波数和频率的截断上限。通常，截断上限可按如下准则确定[10]：
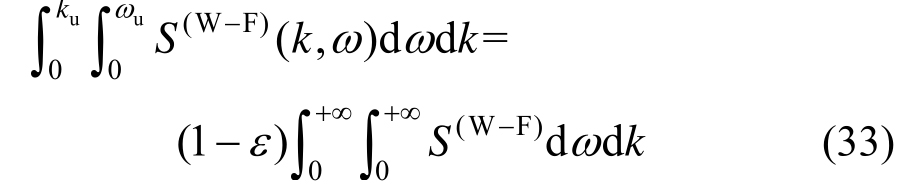
取
可使ε＜5%，即保证了95%的能量。
在生成脉动风速样本时程时，时间步长取为
4.2.1 结构化非均匀离散情况
基于本文方法，采用如图1(a)所示的60万个波数-频率离散点，生成了500个脉动风场样本，典型样本时程如图2所示。
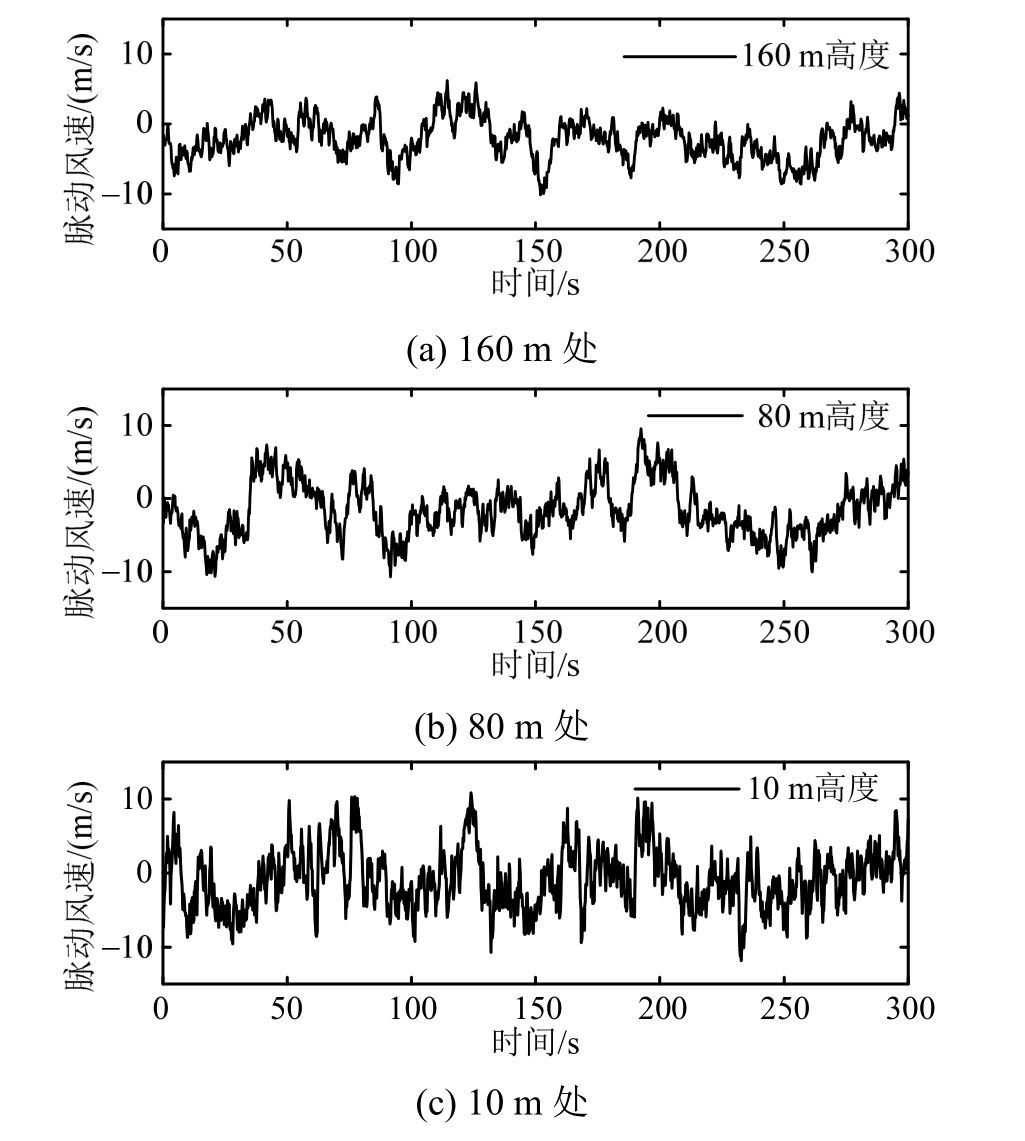
图2 不同高度处脉动风速样本时程(结构化离散)
Fig.2 Fluctuating wind speed histories for different height(structured discretization method)
自功率谱密度函数可以按下式估计[22]：
其中：FX (ω)是脉动风速样本时程X(t)的Fourier谱；T为样本时程长度。
基于生成的500个样本，估计了不同高度处的自功率谱，并与目标谱进行对比，结果如图3所示。可以看到，不同高度处的自功率谱估计值均与目标值吻合良好。
互相关函数的估计值
(τ)可通过式(2)获得，而互相关函数的目标值为：
式中，
由式(19)定义。
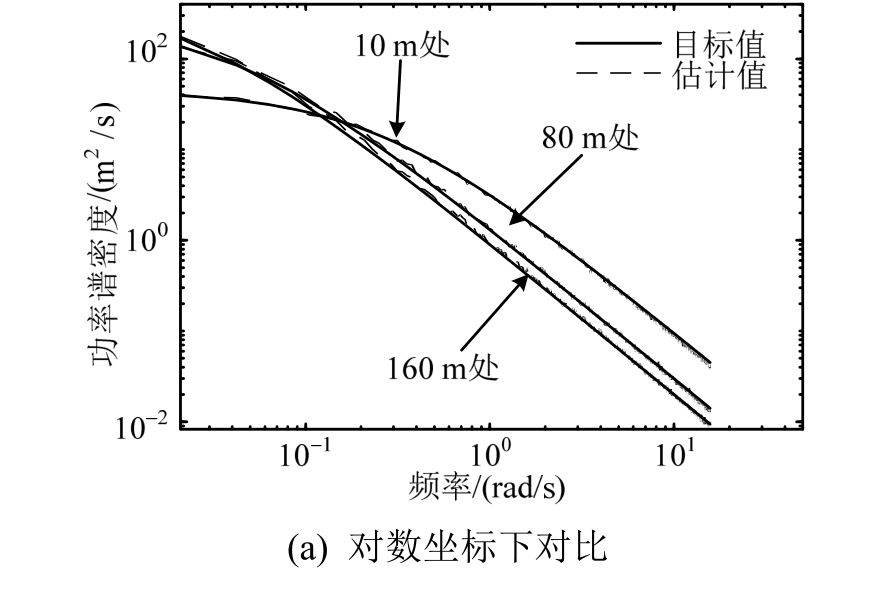
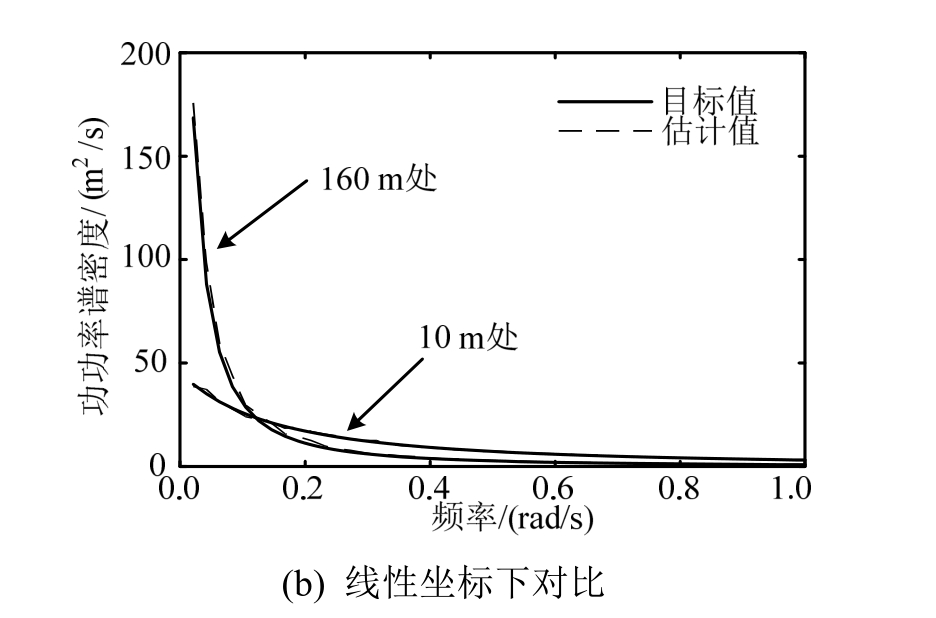
图3 不同高度功率谱估计值和目标值对比(结构化离散)
Fig.3 Comparisons of estimated and target auto-PSD for different height (structured discretization method)
同样基于500个样本，对两点之间的互相关函数进行了估计，并与目标值进行了对比，结果如图4所示，可见互相关函数的估计值和目标值也吻合良好。
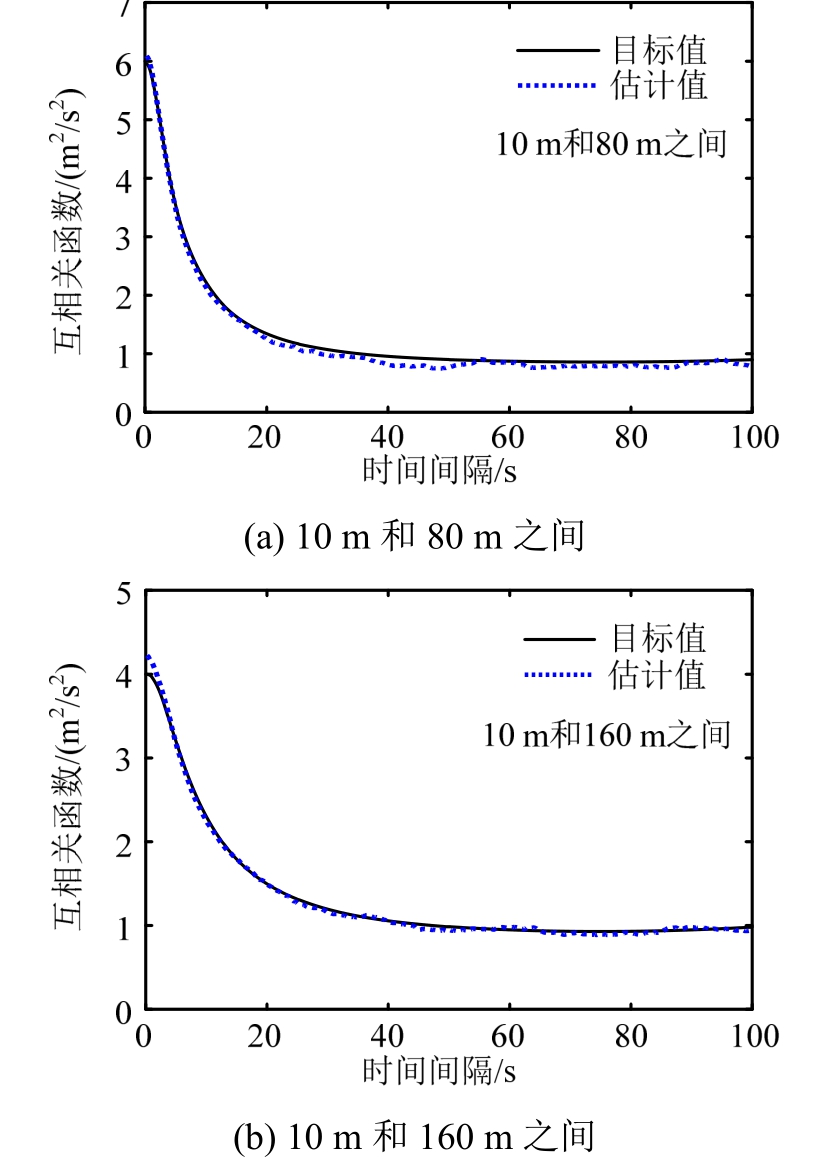
图4 互相关函数估计值和目标值对比(结构化离散)
Fig.4 Comparisons of estimated and target cross-correlation function (structured discretization method)
进而，利用上述数据进行如下相干函数估计。
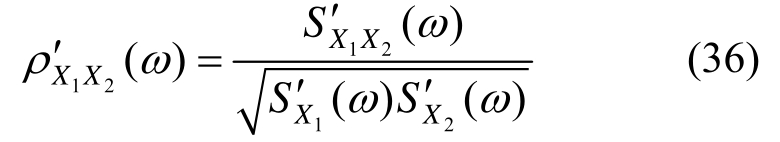
其中，
为互功率谱密度函数的估计值：
相干函数估计值与目标值的对比如图5所示。可以再次看到，相干函数估计值与目标值趋势一致，并在目标值附近波动，总体吻合良好。
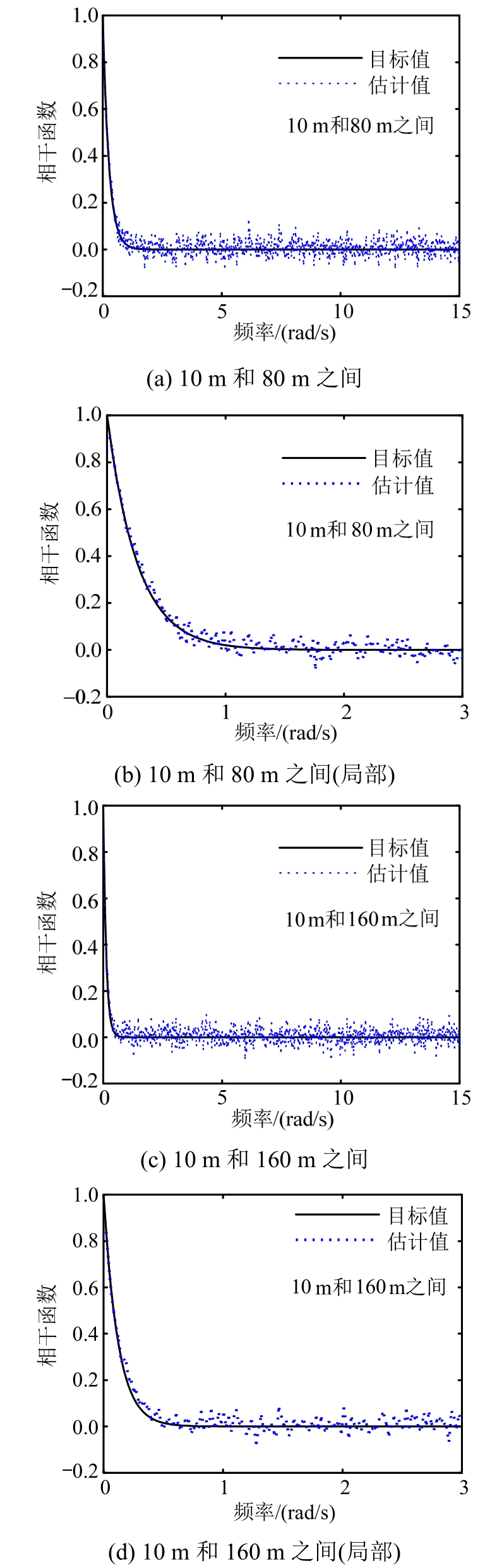
图5 相干函数估计值和目标值对比(结构化离散)
Fig.5 Comparisons of estimated and target coherence function (structured discretization method)
4.2.2 舍选法非均匀离散情况
基于“舍选”非均匀离散方法，采用图1(b)所示的约10万个波数-频率离散点，根据式(32)生成了500个样本，典型风速时程样本如图6所示。与前述方法类似，对样本的自功率谱密度函数、互相关函数和相干函数分别采用式(34)、式(2)和式(36)进行估计，并分别与目标值进行对比，结果如图7～图9所示。
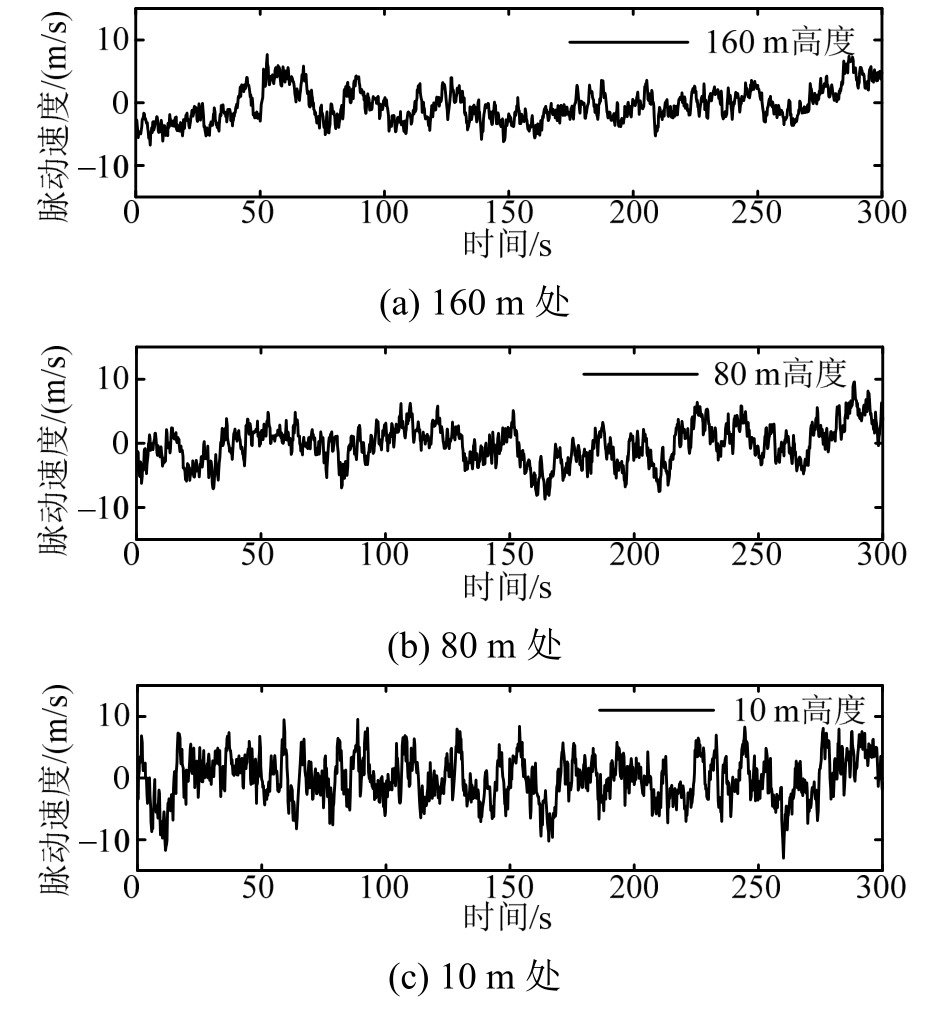
图6 不同高度处脉动风速样本时程(舍选法离散)
Fig.6 Fluctuating wind speed histories for different height(acceptance-rejection discretization method)
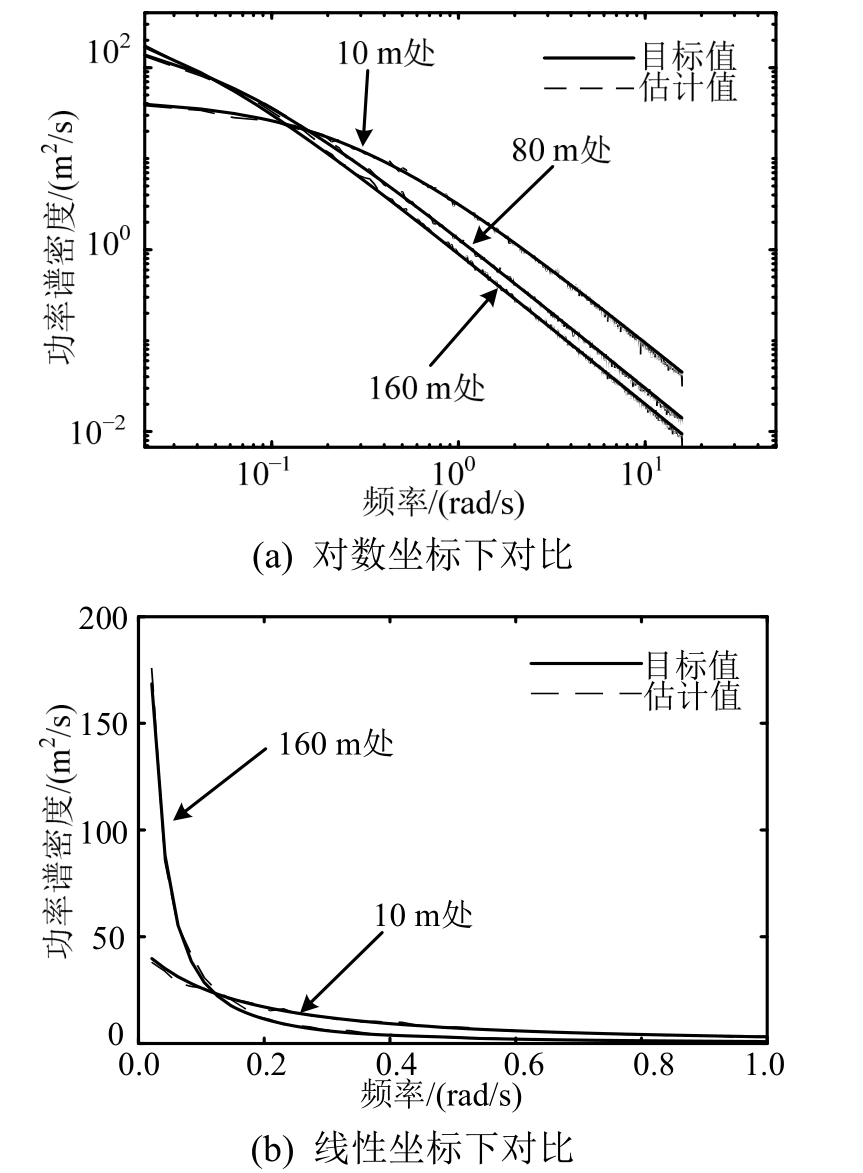
图7 不同高度功率谱估计值和目标值对比(“舍选法”离散)
Fig.7 Comparisons of estimated and target auto-PSD for different height (acceptance-rejection discretization method)
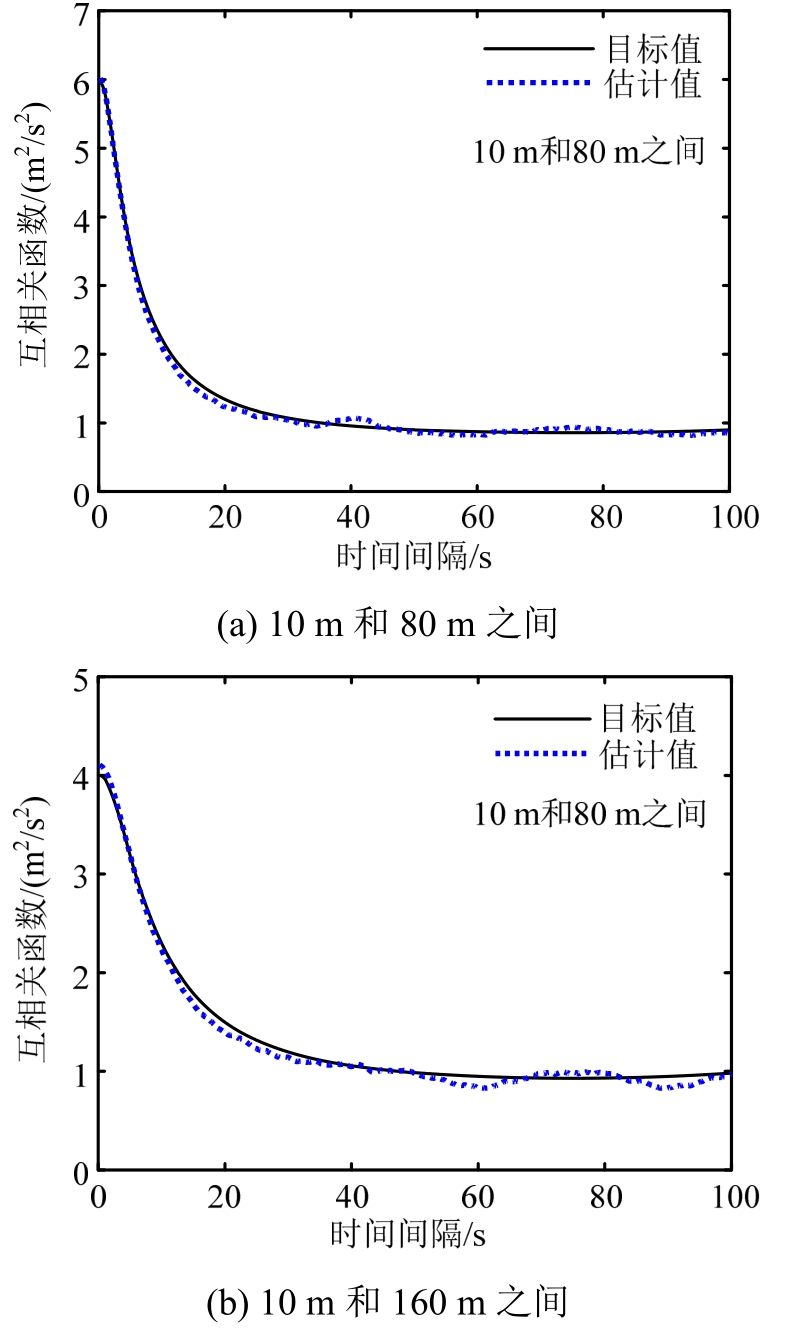
图8 互相关函数估计值和目标值对比(舍选法离散)
Fig.8 Comparisons of estimated and target cross-correlation function (acceptance-rejection discretization method)
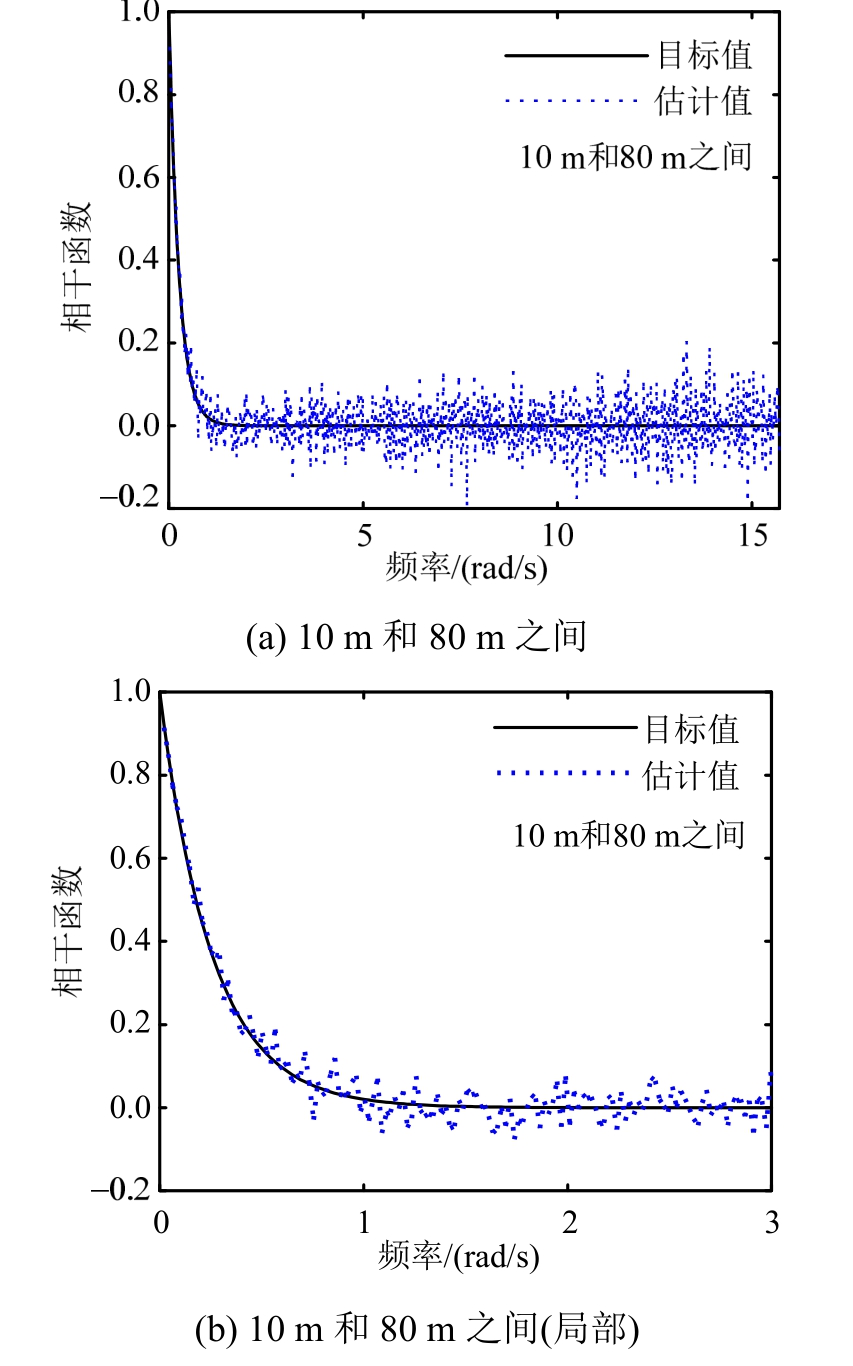
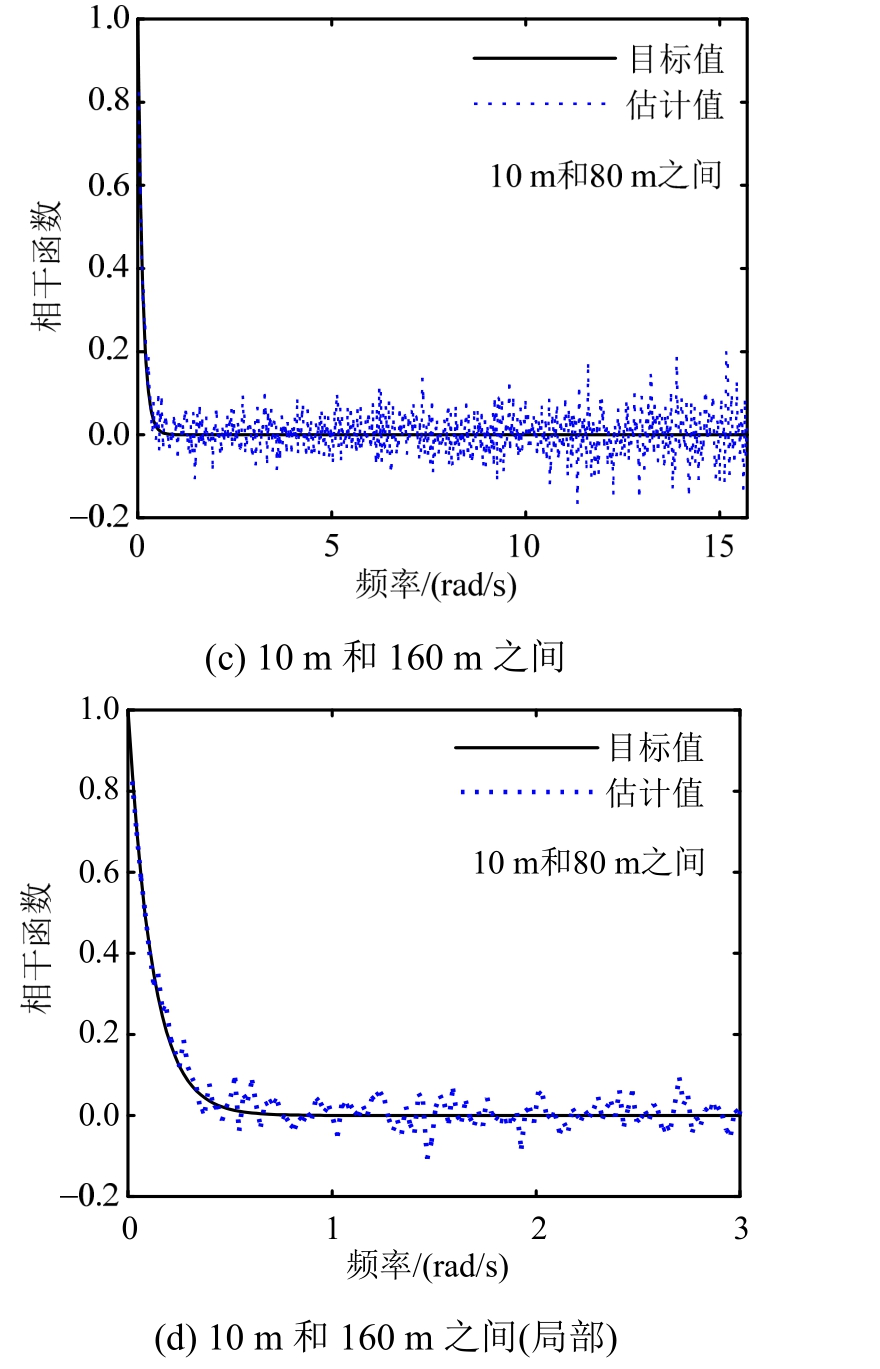
图9 相干函数估计值和目标值对比(“舍选法”离散)
Fig.9 Comparisons of estimated and target coherence function (acceptance-rejection discretization method)
可以看到，基于样本估计的自功率谱密度函数、互相关函数和相干函数与目标值均吻合良好，验证了本文建议方法的有效性。
进一步地，为了检验本文方法的模拟效率，分别计算了均匀离散方法和本文建议的两种非均匀离散方法的计算时间。对于均匀离散方法，在波数方向离散5000个点，在频率方向离散750个点(与上文算例相同)，风场模拟的其它参数也与上述算例一致，利用式(31)模拟空间中一个点处的脉动风速时程，耗时98.5 s；而采用本文建议的“结构化”非均匀离散和“舍选法”非均匀离散耗时分别为18.5 s和2.6 s。因此，本文建议的两种非均匀离散方法能够有效地提高模拟效率，其中“舍选法”非均匀离散的模拟效率更高。
上述基本思想可以推广到二维均匀与非均匀脉动随机风场的模拟之中[31－32]。
脉动风速场的模拟对于土木工程结构、特别是高层、高耸和大跨等柔性结构至关重要。谱表达方法是模拟风场时常用的方法。基于互功率谱矩阵分解的风场模拟方法由于需要Cholesky分解或POD分解，当模拟点数较多时，效率低下。本文基于波数-频率联合演变功率谱的方法，引入“结构化”非均匀离散和“舍选法”非均匀离散两种方法。通过某桥塔的一维非均匀脉动风场模拟，对方法进行了示例和验证。结论如下：
(1) 基于波数-频率联合演变功率谱的风场模拟方法，不需要引入互功率谱矩阵及其分解，具有理论基础严密、实施更为便捷的优点。
(2) 当空间模拟点为非等间距点时，该方法不能使用FFT技术，若直接进行波数-频率域规格化离散，将导致较大的计算量。通过引入“结构化”非均匀离散和“舍选法”非均匀离散两种方法，可以将计算工作量降低一到两个数量级，从而显著地提高模拟效率，且精度较高。
(3) 与“结构化”非均匀离散方法相比，基于“舍选法”的非均匀离散方法具有更小的计算量，且模拟的精度相差不大，因此在实际应用中推荐采用基于“舍选法”的非均匀离散方法。
值得指出，本文仅考察了一维空间上非均匀脉动风场的模拟问题，但其基本思想可以推广应用于二维空间均匀与非均匀脉动风场的模拟之中[31－32]。
[1] Panofsky H A,McCormick R A.Properties of spectra of atmospheric turbulence at 100 meters [J].Quarterly Journal of the Royal Meteorological Society,1954,80(346): 546－564.
[2] Davenport A G.The spectrum of horizontal gustiness near the ground in high winds [J].Quarterly Journal of the Royal Meteorological Society,1961,87(372): 194－211.
[3] Kaimal J C,Wyngaard J C,Izumi Y,et al.Spectral characteristics of surface-layer turbulence [J].Journal of Royal Meteorological Society,1972,98(417): 563－589.
[4] Simiu E,Scanlan R H.Wind Effects on Structures (The 3rd edition) [M].New York: John Wiley & Sons,1996.
[5] Shinozuka M.Simulation of multivariate and multidimensional random processes [J].Journal of the Acoustical Society of America,1971,49(1): 357－368.
[6] Benowitz B A.Modeling and simulation of random processes and fields in Civil Engineering and Engineering Mechanics [D].New York: Columbia University,2013.
[7] Benowitz B A,Deodatis G.Simulation of wind velocities on long span structures: A novel stochastic wave based model [J].Journal of Wind Engineering & IndustrialAerodynamics,2015,147: 154－163.
[8] 柯世堂,王同光,胡丰,等.基于塔架-叶片耦合模型风力机全机风振疲劳分析[J].工程力学,2015,32(8):36－41.Ke Shitang,Wang Tongguang,Hu Feng,et al.Wind-induced fatigue analysis of wind turbine system based on tower-blade coupled model [J].Engineering Mechanics,2015,32(8): 36－41.(in Chinese)
[9] 宫成,刘志文,谢钢,等.高墩大跨斜拉桥悬臂施工期风致振动控制[J].工程力学,2015，32(增刊1): 122－128.Gong Cheng,Liu Zhiwen,Xie Gang,et al.Control of wind-induced vibration in large span cable-stayed bridge with high piers during cantilever construction stages [J].Engineering Mechanics,2015,32(Suppl 1): 122－128.(in Chinese)
[10] Shinozuka M,Deodatis G. Simulation of multi-dimensional Gaussian stochastic fields by spectral representation [J].Applied Mechanics Reviews,1996,49(1): 29－53.
[11] Spanos P D,Zeldin B A.Monte Carlo treatment of random fields: a broad perspective [J].ASME.Applied Mechanics Reviews,1998,51(3): 219－237.
[12] Shinozuka M,Jan C M.Digital simulation of random processes and its applications [J].Journal of Sound &Vibration,1972,25(1): 111－128.
[13] Paola M D.Digital simulation of wind field velocity [J].Journal of Wind Engineering & Industrial Aerodynamics,1998,74/75/76(2): 91－109.
[14] Zhao N,Huang G Q.Fast simulation of multivariate nonstationary process and its application to extreme winds [J].Journal of Wind Engineering & Industrial Aerodynamics,2017,170: 118－127.
[15] Li Y L,Togbenou K,Xiang H Y,et al.Simulation of non-stationary wind velocity field on bridges based on Taylor series [J].Journal of Wind Engineering &Industrial Aerodynamics,2017,169: 117－127.
[16] Cao Y H,Xiang H F,Zhou Y.Simulation of stochastic wind velocity field on long-span bridges [J].Journal of Engineering Mechanics,2000,126(1): 1－6.
[17] 陶天友,王浩.基于Hermite插值的简化风场模拟[J].工程力学,2017,34(3): 182－188.Tao Tianyou,Wang Hao.Reduced simulation of the wind field based on Hermite interpolation [J].Engineering Mechanics,2017,34(3): 182－188.(in Chinese)
[18] Togbenou K,Xiang H Y,Li YL,et al.Improved spectral representation method for the simulation of stochastic wind velocity field based on fft algorithm and polynomial decomposition [J].Journal of Engineering Mechanics,2018,144(2)：04017171.
[19] Peng L L,Huang G Q,Kareem A,et al.An efficient space-time based simulation approach of wind velocity field with embedded conditional interpolation for unevenly spaced locations [J].Probabilistic Engineering Mechanics,2016,43: 156―168.
[20] 刘章军,叶永友,刘增辉.脉动风速连续随机场的降维模拟 [J].工程力学,2018,35(11): 8―16.Liu Zhangjun,Ye Yongyou,Liu Zenghui.Simulation of fluctuating wind velocity continuous stochastic filed by dimension reduction approach [J]. Engineering Mechanics,2018,35(11): 8―16.(in Chinese)
[21] Peng L L,Huang G Q,Chen X,et al.Simulation of multivariate nonstationary random processes: hybrid stochastic wave and proper orthogonal decomposition approach [J].Journal of Engineering Mechanics,2017,143(9): 04017064.
[22] Bendat J S,Piersol A G.Random data [M].4th ed.Hoboken: John Wiley & Sons,2010.
[23] Priestley M B.Evolutionary spectra and non-stationary processes [J].Journal of the Royal Statistical Society,1965,27(2): 204－237.
[24] Li J,Chen J B.Stochastic dynamics of structures [M].Singapore: John Wiley & Sons,2009.
[25] Shinozuka M,Deodatis G.Stochastic process models for earthquake ground motion [J].Probabilistic Engineering Mechanics,1988,3(3): 114－123.
[26] Liang J W,Chaudhuri S R,Shinozuka M.Simulation of nonstationary stochastic processes by spectral representation [J].Journal of Engineering Mechanics,2007,133(6): 616－627.
[27] Chen J B,Kong F,Peng Y B.A stochastic harmonic function representation for non-stationary stochastic processes [J].Mechanical Systems & Signal Processing,2017,96: 31－44.
[28] Gerstner T,Griebel M.Dimension-adaptive tensorproduct quadrature [J].Computing,2003,71(1): 65－87.
[29] Dick J,Pillichshammer F.Digital Nets and sequences:discrepancy theory and Quasi-Monte Carlo integration[M].New York: Cambridge University Press,2010.
[30] 李永乐,廖海黎,强士中.京沪高速铁路南京长江大桥桥址区风特性研究[J].桥梁建设,2002(4): 5－7.Li Yongle,Liao Haili,Qiang Shizhong.Research on the wind characteristics of the site of Nanjing Changjiang river bridge on Beijing-Shanghai high-speed railway [J].Bridge Construction,2002(4): 5－7.(in Chinese)
[31] Chen J B,Song Y P,Peng Y B,et al.Simulation of homogeneous fluctuating wind field in two spatial dimensions via a wavenumber-frequency joint power spectrum [J].Journal of Engineering Mechanics,2018,144(11): 04018100.
[32] Song Y P,Chen J B,Peng Y B,et al.Simulation of nonhomogeneous fluctuating wind speed field in two-spatial dimensions via an evolutionary wavenumberfrequency joint power spectrum [J].Journal of Wind Engineering & Industrial Aerodynamics,2018,179:250－259.
SIMULATION OF NONHOMOGENEOUS FLUCTUATING WIND FIELD IN ONE-DIMENSIONAL SPACE BY EVOLUTIONARY WAVENUMBER-FREQUENCY JOINT POWER SPECTRUM
宋玉鹏(1992―)，男，河南人，博士生，主要从事海上风电结构可靠度研究(E-mail: songyupeng@tongji.edu.cn).
陈建兵(1975―)，男，湖北人，教授，博士，博导，主要从事随机动力学和结构可靠度研究(E-mail: chenjb@tongji.edu.cn).