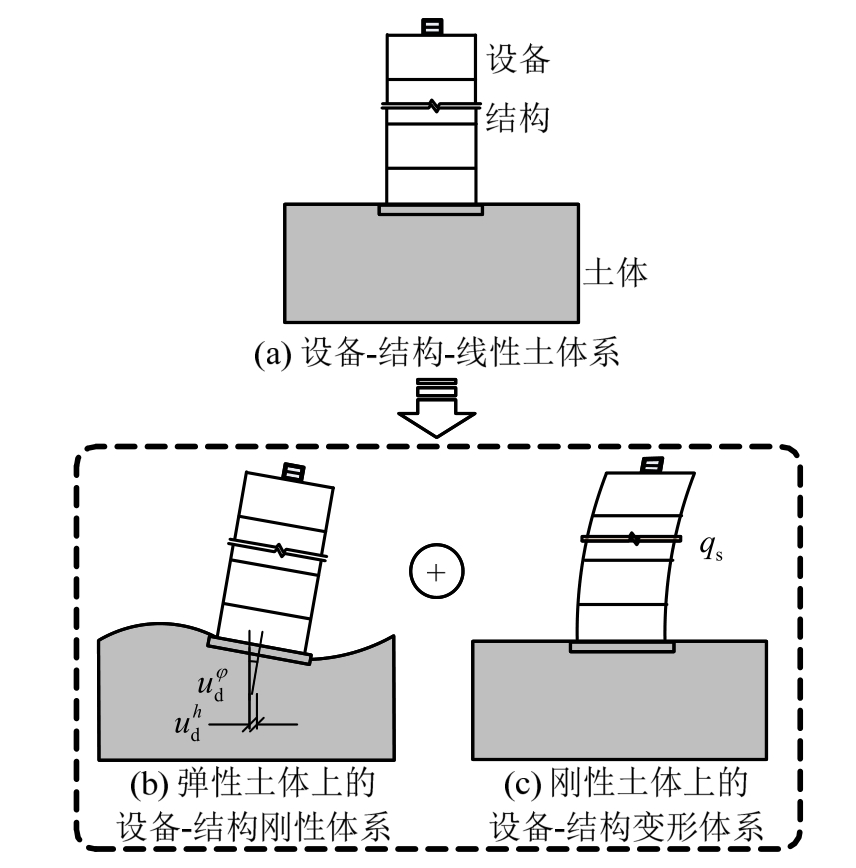
图1 设备-结构-线性土体系运动方程推导示意图
Fig.1 Schematic for motion equation of equipment-structure-linear soil system
由于土体介入将影响上部设备-结构体系真实的地震反应，土体对上部设备-结构体系抗震性能的研究逐渐成为研究热点。采用土箱模型放置在振动台[1―2]或离心机[3]模拟土-结构相互作用时，需要建造完整的试验模型，该类型试验能够同时得到结构与土体的地震反应，但试验造价以及技术要求较高。实时子结构试验方法的发展为设备-结构-土这种复杂相互作用体系试验提供了实现的途径，该方法首先由Nakashima等[4]提出，将整体模型划分为试验子结构和数值子结构两部分，将主要研究对象作为试验子结构由试验装置加载控制，其余部分作为数值子结构通过软件模拟计算，能够有效减小试验规模，降低试验难度。考虑土体影响的振动台实时子结构试验研究，通常将土体等作为数值子结构，上部结构作为试验子结构，两者之间实时数据交互，联合评估整个耦合体系的动力响应。由于该试验实时性的要求，数值子结构通常选择简化计算模型，例如Wang等[5]采用地基集总参数模型、李忠献等[6]采用改良彭津模型、唐贞云等[7]采用单自由度模型作为土体数值子结构。采用土体简化计算模型能够保证子结构试验中数值子结构计算效率的要求，但是对某些复杂土体模型的计算精度产生影响，而直接采用复杂的有限元模型又无法完成实时子结构试验。振动台实时子结构试验[8]基本原理根据试验子结构与数值子结构界面协调条件推导，例如Zhang等[9]对简单的剪切型结构推导振动台实时子结构试验涉及运动方程，公式推导过程较繁琐，因此采用一般方法推导设备-结构-土体系的计算公式难度更大。姜忻良等[10]采用分支模态子结构方法推导了土-结构相互作用运动方程，并且对土体进行了模态变换，有效地解决了土体的自由度冗余问题。
结合当前的研究成果，本文探讨设备-结构-土体系振动台实时子结构试验方法的可行性，其中设备-结构体系作为由振动台加载控制试验子结构，土体作为由仿真软件计算的数值子结构。首先基于文献[10]中的分支模态子结构方法，推导了设备-结构-线性土体系的运动方程，经变换后可用于振动台实时子结构试验。与线性阶段相比，强震作用下土体进入非线性阶段后土-结构相互作用对上部结构的地震反应影响将发生较大变化[11]。结合此时土体并非全部进入非线性阶段，提出采用线性-非线性混合约束子结构法[12]建立的局部非线性地基土模型作为子结构试验中数值子结构。限于试验条件，本文仅开展设备-结构-线性土体系振动台实时子结构试验，按照试验相似比原理设计了设备-结构-土相互作用缩尺模型，设备简化为单自由度模型模拟放置楼层的通信设备，结构为四层钢框架，土体是三类场地，同时搭建的振动台实时子结构试验系统，进行各地震动作用下的设备-结构-土体系振动台实时子结构试验研究。通过比较振动台实时子结构试验结果与数值计算结果验证本文试验方法可行性。
设备-结构-土体系包括设备、结构和土体三部分，设备-结构体系作为试验子结构由振动台加载控制，将土体作为数值子结构由仿真软件计算分析，两者之间进行实时数据交互。
按照分支模态子结构方法，将如图1(a)中设备-结构-线性土体系划分成图1(b)中分支d：弹性土体上的设备-结构刚性体系和图1(c)中分支s：刚性土体上的设备-结构变形体系。
图1 设备-结构-线性土体系运动方程推导示意图
Fig.1 Schematic for motion equation of equipment-structure-linear soil system
分支d的特征方程如式(1)所示，其中kd、md表示分支d中土体的刚度矩阵和质量矩阵，可求出由m阶模态组成分支d的模态变换矩阵Φd。
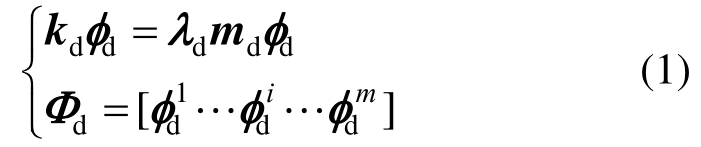
分支d模态变换后的计算矩阵如式(2)所示，ud表示分支d中土体物理坐标，qd表示分支d中土体模态坐标，cd表示分支d中土体阻尼矩阵，可由一般阻尼理论得到，fd表示分支d中土体荷载矩阵。
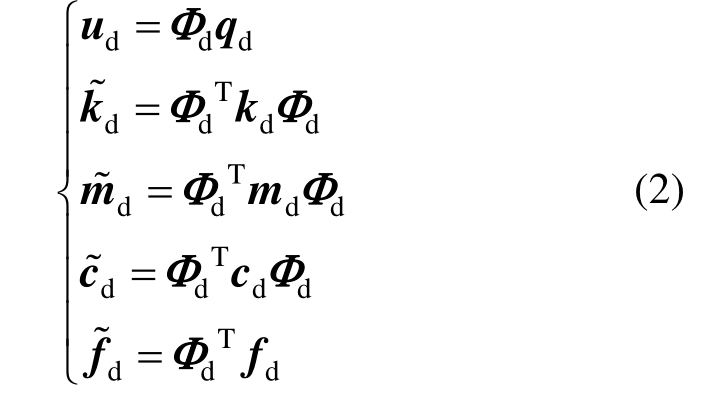
由于设备-结构体系自由度相对较少，不作模态变换，保留完整的计算矩阵。设备-结构体系的位移us由两部分组成，一是图1(b)中土体变形引起设备-结构体系的刚体位移，二是图1(c)中设备-结构体系本身的变形qs如式(3)所示：
其中，R可由分支d中土体变形产生的设备-结构体系刚体位移求得。现给出设备-结构体系和土体位移的关系并写成矩阵形式。
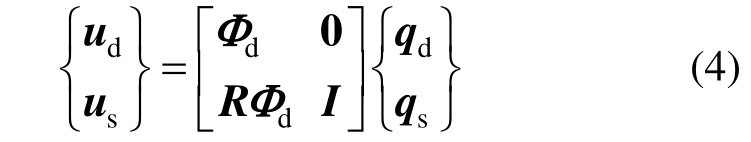
按变形协调关系并整理可得设备-结构-土体系的运动方程如式(5)所示：
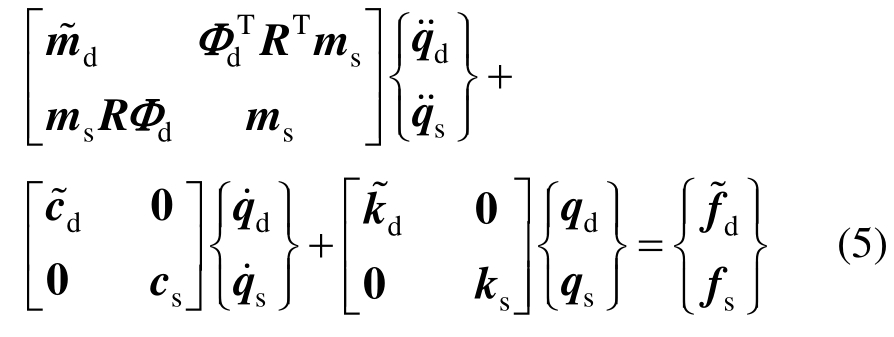
式中，ms、cs、ks和fs表示分支s中设备-结构体系的质量矩阵、阻尼矩阵、刚度矩阵和荷载矩阵。设备-结构-土体系总运动方程质量矩阵中耦合项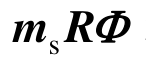
是连接设备-结构体系和土体之间的纽带。为了实现子结构试验，现将总运动方程中的耦合项相关项移动到方程右边，从而得到土体和设备-结构体系各自的运动方程如式(6)、式(7)所示：
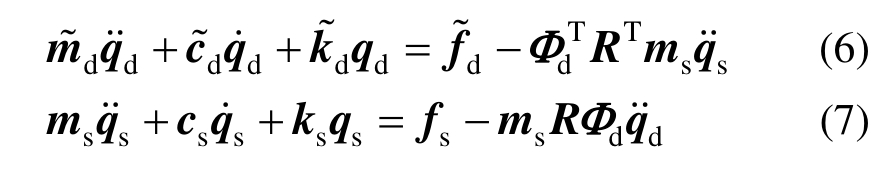
结合强震作用下土体并非全部进入非线性阶段的这一特点，提出在振动台实时子结构试验中引入线性-非线性混合约束模态子结构法建立的局部非线性土模型作为数值子结构，解决非线性土体的自由度冗余等问题。
如图2所示的设备-结构-非线性土体系运动方程推导示意图，土体包括线性土子结构α与非线性土子结构β两部分。先按照分支模态子结构法推导设备-结构-非线性土子结构β运动方程，划分为分支d：非线性土子结构β上设备-结构刚性体系与分支s：刚性非线性土子结构β上设备-结构变形体系。具体公式推导步骤如下。
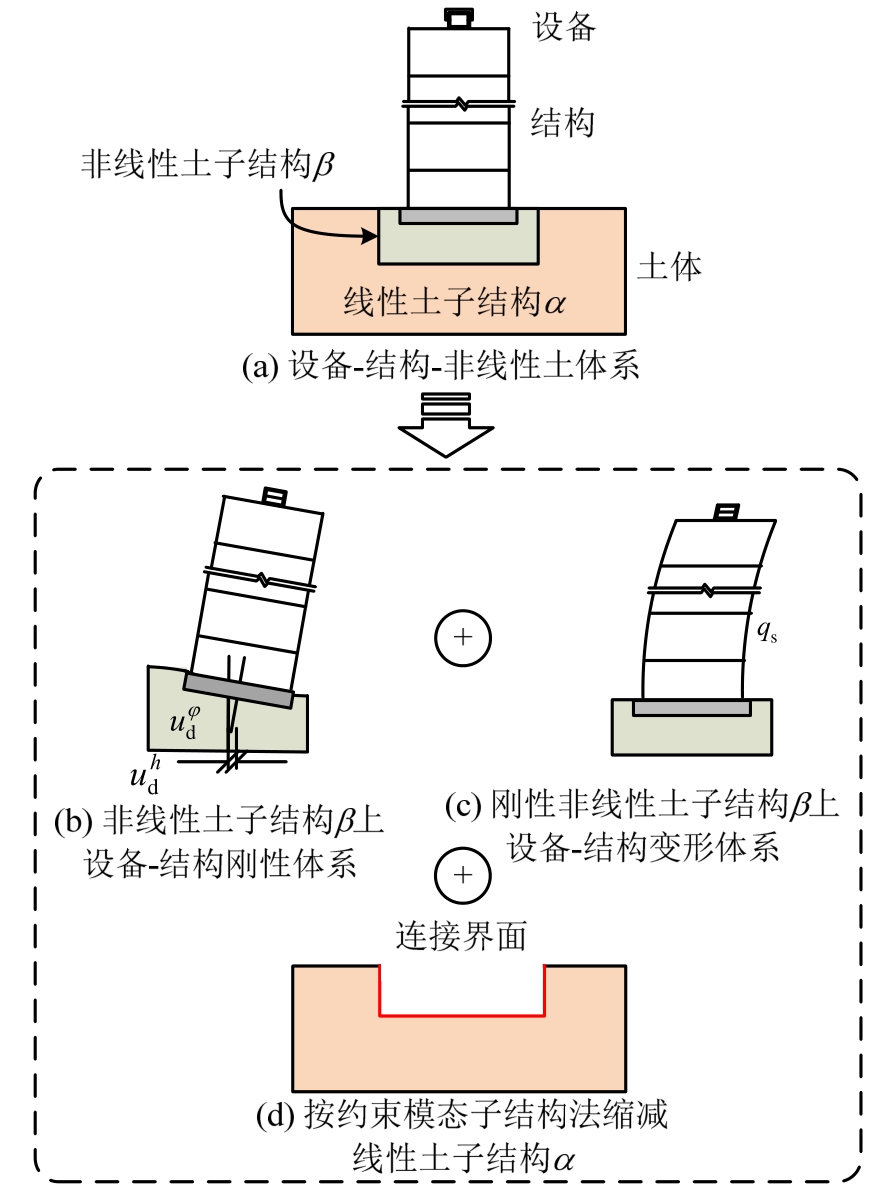
图2 设备-结构-非线性土体系运动方程推导示意图
Fig.2 Schematic for motion equation of equipment-structure-nonlinear soil system
由于强震作用下设备-结构体系与非线性土子结构β均需考虑非线性因素影响，保留设备-结构体系与非线性土子结构β完整的计算矩阵。设备-结构体系的位移us由两部分组成，一是图2(b)中非线性土子结构β变形引起设备-结构体系的刚体位移，二是图2(c)中设备-结构体系本身的位移qs，如式(8)所示：
式中，R可由分支d中非线性土子结构β变形产生的设备-结构体系刚体位移求得。现给出设备-结构体系和非线性土子结构β位移的关系并写成矩阵式如式(9)所示：
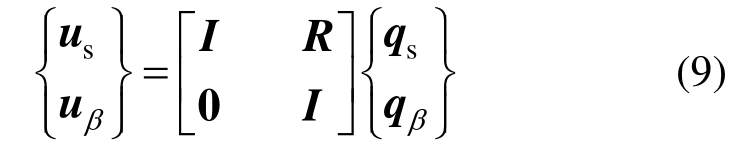
按分支模态子结构法惯性耦合的原理，整理可得到设备-结构-非线性土子结构β的运动方程如式(10)所示，其中只有质量矩阵存在耦合项，而刚度与阻尼矩阵均是解耦的。
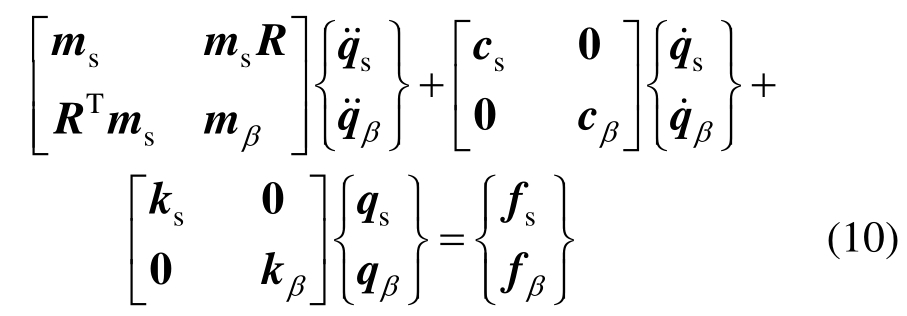
式中：ms、cs、ks和fs表示设备-结构体系的质量矩阵、阻尼矩阵、刚度矩阵和荷载矩阵；mβ、cβ、kβ和fβ表示非线性土子结构β的质量矩阵、阻尼矩阵、刚度矩阵和荷载矩阵。将式(10)非线性土子结构的计算矩阵按照内部自由度i和边界自由度b重新分块后的运动方程如式(11)所示，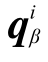
、
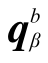分别表示非线性土子结构β的内部自由度和边界自由度对应的位移。
线性土子结构α计算矩阵按照内部自由度i和边界自由度b形式重新排列后按照约束模态子结构法进行自由度缩减。线性土子结构α自由度缩减的坐标变换矩阵T如式(12)中所示，由主模态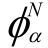
、约束模态
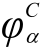以及单位向量和零向量组成。
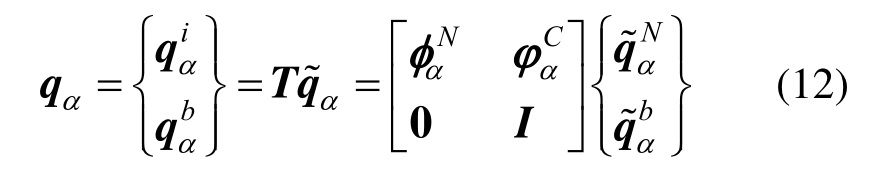
按照约束模态子结构法，经坐标变换后线性土子结构α的运动方程如式(13)所示：
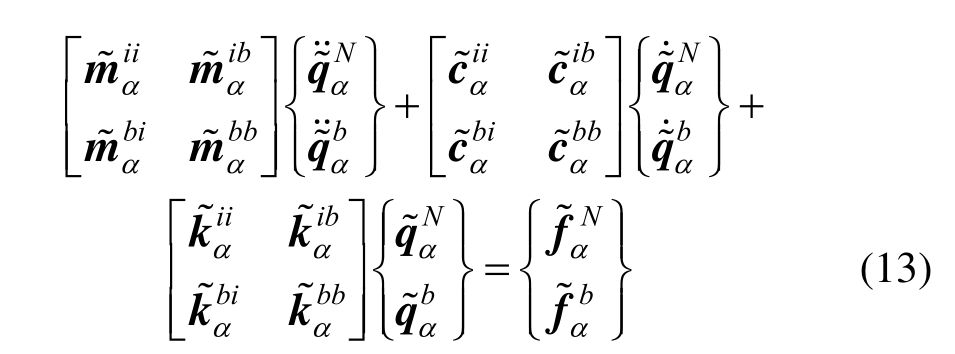
非线性土子结构β与线性土子结构α之间的界面协调满足如式(14)所示关系，再按照对号入座的方法，根据非线性土子结构β与线性土子结构α位移协调关系，综合线性与非线性土子结构的运动方程，最终得到设备-结构-土体系整体运动方程如式(15)所示：
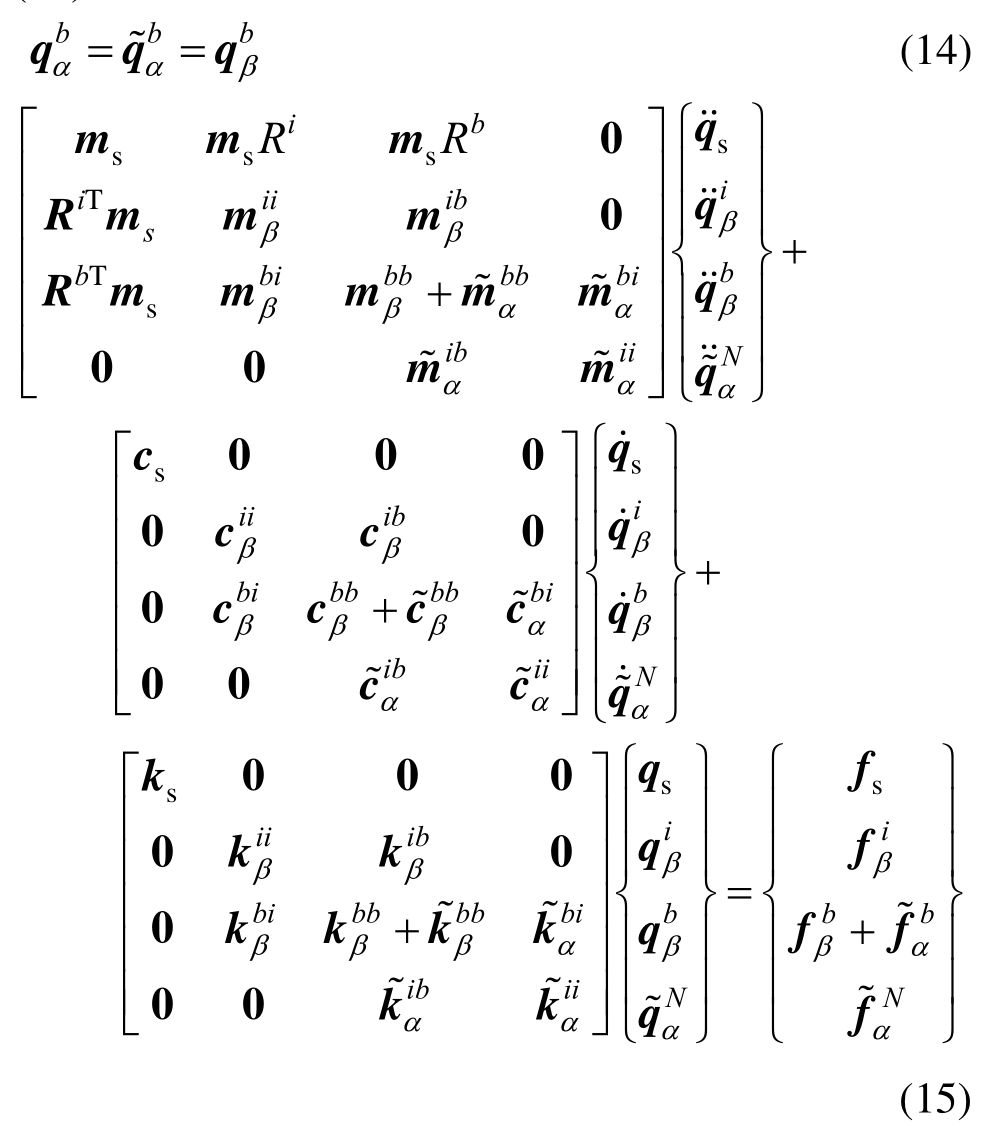
整体体系总运动方程质量矩阵中耦合项msRi、msRb是连接设备-结构体系和局部非线性土体之间的纽带。为了实现子结构试验，现将总运动方程中的耦合项相关的荷载移动到方程右边，从而得到设备-结构体系与局部非线性土体各自的运动方程如式(16)、式(17)所示。
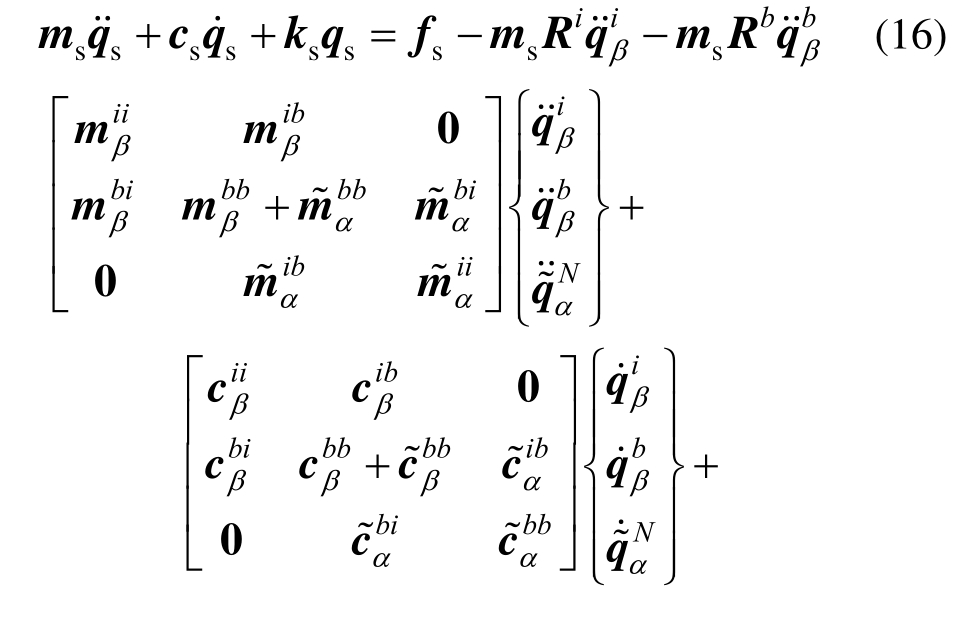
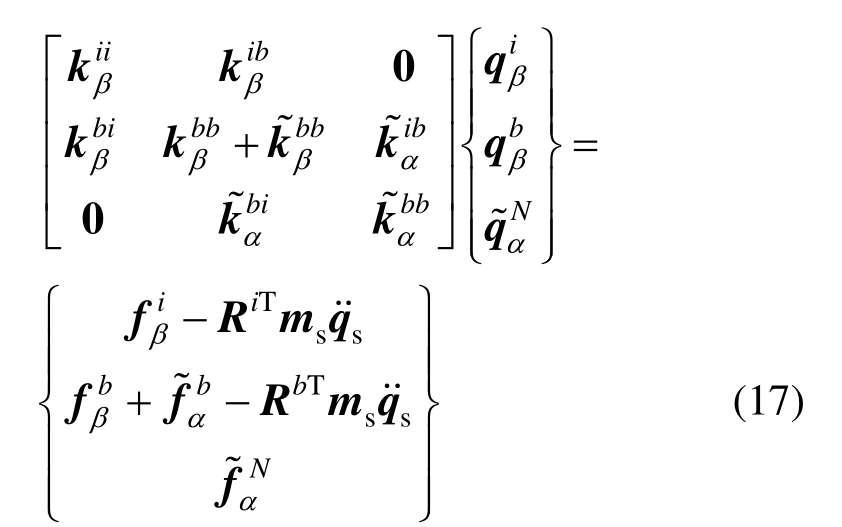
这里保留设备-结构体系与非线性土子结构β完整的计算矩阵能够考虑各自非线性因素的影响，而线性土子结构α进行自由度缩减后可显著提高地基土的计算效率。限于试验条件，本文仅实施设备-结构-线性土体系振动台实时子结构试验，其中试验中的设备是单自由度模型，钢框架可简化成四自由度剪切型模型，这样设备-结构体系就组成五自由度计算模型，所以R具体表达式如式(18)中所示，是一个5×n的矩阵，n表示土体自由度总数。
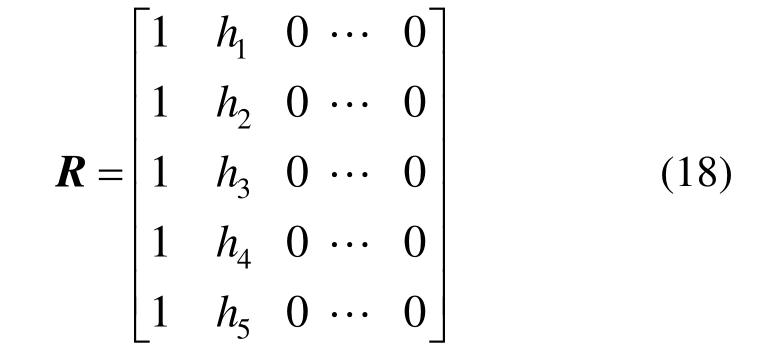
地震激励üg作用下设备-结构体系动力方程右边的外荷载和耦合项荷载如图3所示。
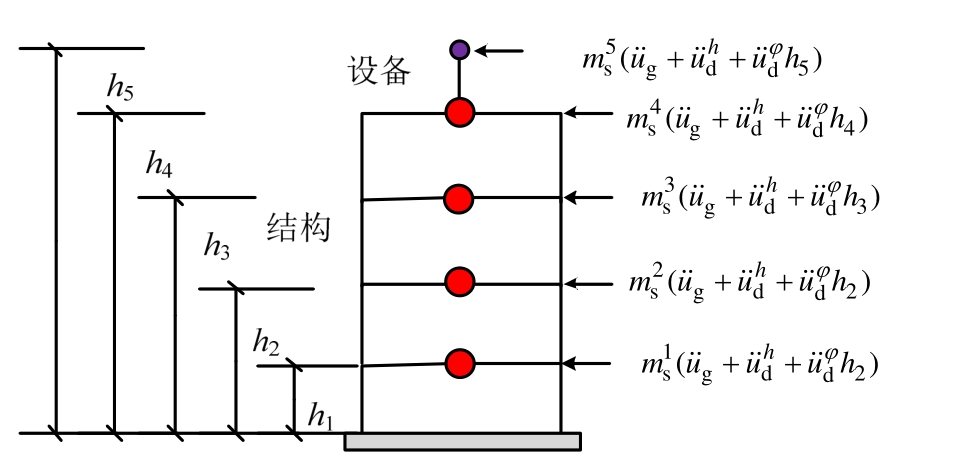
图3 等效荷载转化
Fig.3 Equivalent load transformation
由图中可以看到基础转动加速度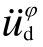
对设备-结构体系各自由度产生作用与高度有关，为了能使基础转动加速度在振动台上得以实现，将
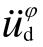按照水平荷载等效原理进行等效，近似考虑基础转动的影响，具体如式(19)与式(20)所示：
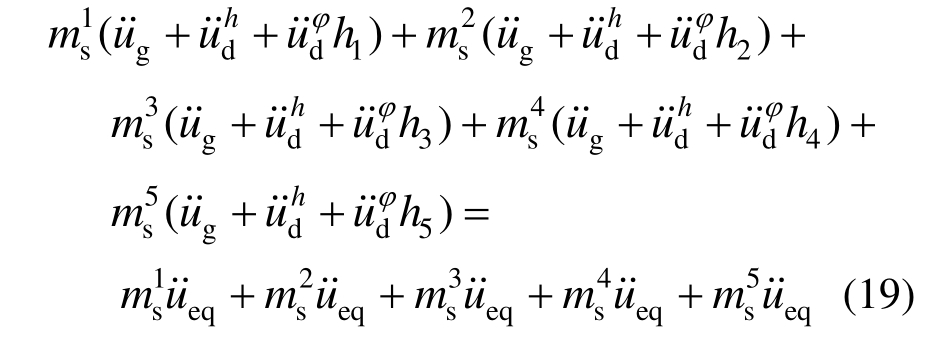
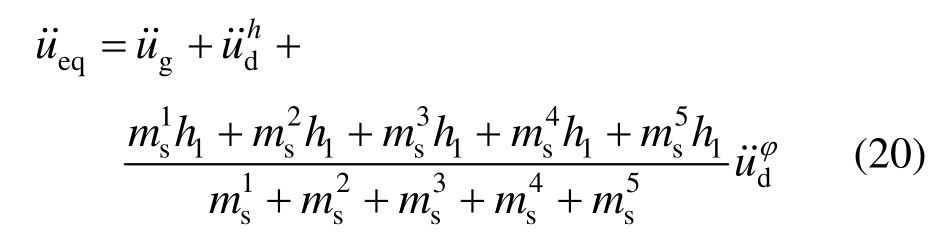
本文按照分支模态子结构法推导了设备-结构-土体系的运动方程，此时整体运动方程仅质量矩阵是耦合的(惯性耦合)。为了实施振动台实时子结构试验将整体运动方程拆分，并将质量矩阵中耦合项移至方程的右边以荷载项的形式出现。初始时假定土体的耦合项荷载为已知(可设为零)，而后将式(6)与式(7)的耦合项荷载来回传递，即可实现试验子结构与数值子结构交互的试验方法。
现给出设备-结构-土体系振动台实时子结构试验具体流程：1) 假定第i步土体受到的外荷载和耦合项荷载均已知；2) 按照式(6)数值计算得到土体在i+Δt步的加速度反应；3) 根据式(7)的右边项计算设备-结构体系受到的外荷载和耦合项荷载；4)根据荷载等效原理按式(19)计算等效加速度的大小，并将其作为新的指令驱动振动台，这样就通过振动台将上述荷载施加给试验子结构；5) 通过安装在设备-结构体系上的加速度测量数据以及地震激励计算在土体产生的作用力，并将其传递给土体，继续下一步数值计算，这样每一步振动台试验数据与仿真软件计算数据交互传递直到试验结束为止。
本文开展设备-结构-土体系振动台实时子结构试验，设计了设备-结构-土体系1/5缩尺模型，其中设备为放置在屋面的单自由度模型模拟通信设备，结构为四层钢框架，土体为三类场地。本试验在北京工业大学3 m×3 m的振动台上进行，选择适合三类场地分析的自然波El Centro、TianJin地震动和模拟的人工波PerSon地震动作为本试验的地震激励，本文采用是地面波，直接在地面上(基础下)施加地震激励，各地震动的加速度时程曲线如图4所示。结构与设备的加速度采集均使用941B传感器，该传感器是一种能够实现低频测量的多功能测量仪器。
如图5所示的设备-结构体系中结构模型采用统一型号的H型钢(HN100×45×6×8)，结构模型第1层高度0.68 m，其余各层高度均为0.63 m，纵横向跨度均为1.6 m；结构第1到第3层的总质量均为1700 kg，第4层的总质量1540 kg。设备模型高度0.5 m，采用圆形钢管设计，总质量90 kg。结构材料的弹性模量与屈服强度分别为202.0 GPa和339.6 MPa，设备材料的弹性模量与屈服强度分别为192.0 GPa和421.4 MPa。结构顶部中心处布置用于连接设备的钢板，试验时将设备用螺栓锚固在结构顶部的中心位置。
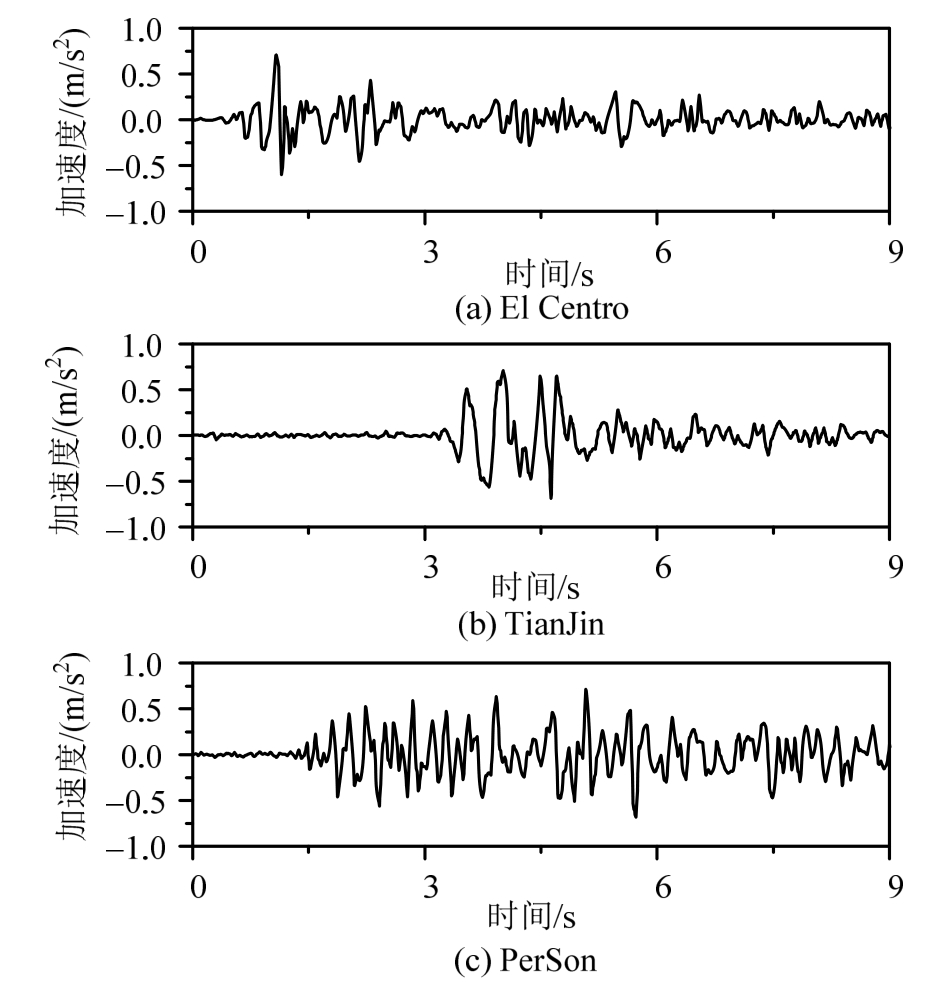
图4 试验地震动加速度时程曲线
Fig.4 Acceleration time history curves of ground motions
图5 试验子结构模型
Fi5 Model of the experimental substructure
基于卓越周期相似比方法[13]设计土体缩尺模型，使模型土保持原场地的主要特性。土体模型材料参数见表1，模型总尺寸30 m×15 m×15 m，埋置基础尺寸为2.2 m×2.2 m×0.4 m。采用通用有限元软件ANSYS按照试验设计要求建立如图6所示的土体有限元模型。土体有限元模型选择八节点实体单元，每个单元节点含有ux、uy、uz方向的自由度，其中单元划分原则取单元高度hmax=(0.200～0.125)λs，λs表示波长，单元的宽度不大于单元高度的5倍。由于试验子结构模型主要沿x方向作水平运动，引起土体模型的变形也以x向的平动变形为主，对土体有限元模型建立相关约束方程进行简化。定义刚性基础的约束方程方法，O点是基础面的中心点，S表示基础面上任意点，由于O点本身属于实体单元节点不具备转动自由度，故在O点处引入Mass21单元，此时O点具备沿x轴、y轴和z轴方向平动自由度和转动自由度，基础中心点O点与基础面其他任意点S的自由度满足如下关系式：
其中
分别表示点O与点S沿x轴方向位移，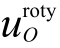
表示点O绕y轴方向转角，
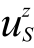表示点S沿z轴方向位移，xs表示点S在x轴方向坐标。边界条件土体底部固定，周边设置粘弹性边界。
表1 土体材料参数
Table 1 Parameters of soil material
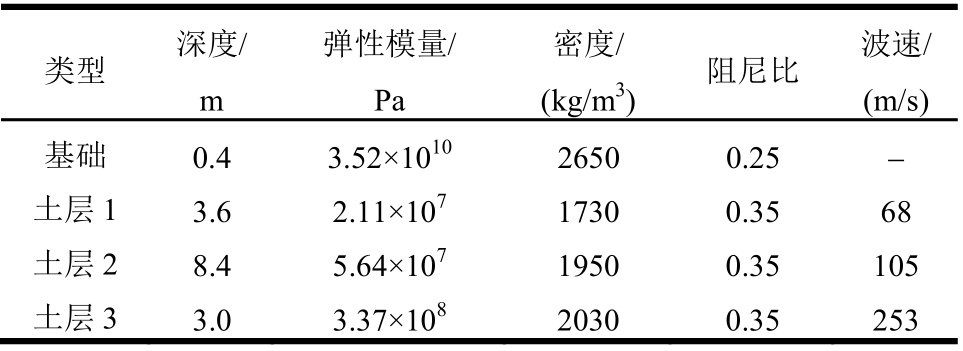
类型 深度/m弹性模量/Pa (kg/m3) 阻尼比 波速/(m/s)密度/基础 0.4 3.52×1010 2650 0.25 -土层1 3.6 2.11×107 1730 0.35 68土层2 8.4 5.64×107 1950 0.35 105土层3 3.0 3.37×108 2030 0.35 253
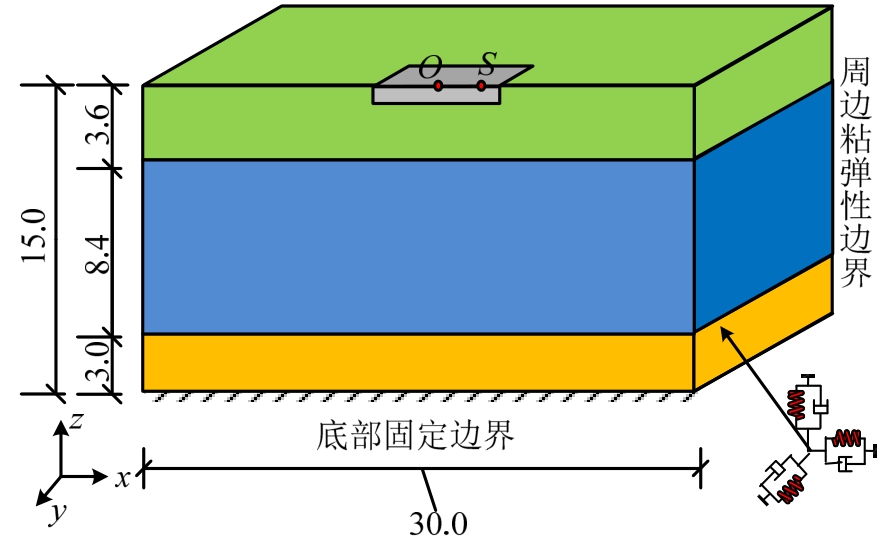
图6 数值子结构模型
Fig.6 Model of the numerical substructure
由于土体有限元模型自由度冗余，直接采用完整的土体有限元模型严重影响数值子结构计算效率，无法满足振动台实时子结构的实时性要求。本文将建立土体有限元模型，利用ANSYS命令流导出土体的计算矩阵，然后将土体的计算矩阵按照一定的方法导入到MATLAB编程软件中对该有限元模型进行自由度缩减。由于土体主模态分布离散，Li和Jiang[14]考虑外荷载与土体自身振动特性的对应关系，利用RITZ向量法计算土体模态向量，可以滤除对土体振动影响较小的振型。本文采用该方法进行土体的RITZ向量分析，计算得到土体每阶RITZ向量振型和频率，并与土体完整模态计算结果对比见表2。
表2 土体特征参数表
Table 2 Characteristic parameters of the soil
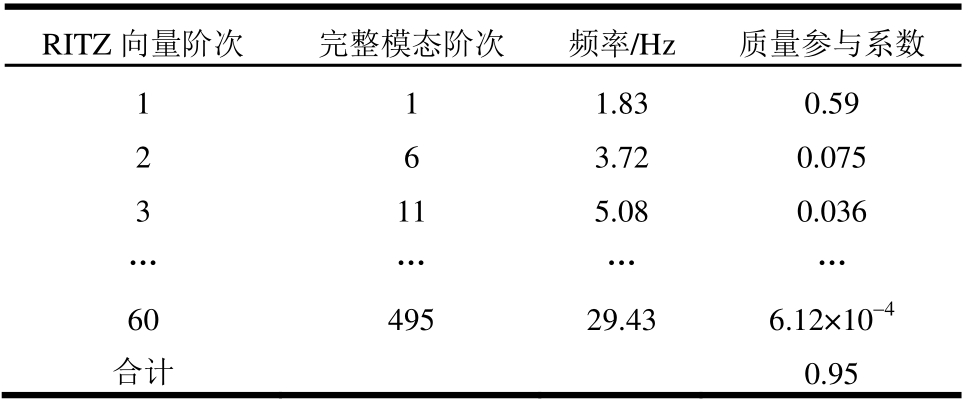
RITZ向量阶次 完整模态阶次 频率/Hz 质量参与系数1 1 1.83 0.59 2 6 3.72 0.075 3 11 5.08 0.036… … … …60 495 29.43 6.12×10-4合计 0.95
根据《建筑抗震设计规范》要求振型参与质量达到总质量的90%以上，本文计算土体每阶RITZ向量对应的质量参与系数，截取60阶计算结果，总的质量参与系数可达到0.95。按上述方法得到土体模型的模态变换矩阵Φd，根据式(2)可以计算得到土体有限元模型自由度缩减后的计算矩阵。上述方法针对土体模型较复杂时情况，需要先建立土体有限元模型再进行自由度缩减。当土体模型较简单时，可按照等效模量简化后提取计算刚度系数矩阵。
如图7所示为设备-结构-土体系振动台实时子结构试验系统组成，主要涉及三个方面：1) 实时通信；2) 控制器设计；3) 数值子结构计算。本试验采用专业工程控制计算机作为数值子结构计算的服务器，并安装SIMULINK仿真软件用于数值子结构计算和控制器设计。应用SIMULINK仿真软件“Real Time”工具箱可将计算模块编译成C代码在实时环境下运行。这样只需要一台计算机、一个编译器、一个I/O设备板，就能建立通路的实时子结构试验系统，为实时子结构试验交互提供了一种造价低廉并且行之有效的解决途径。
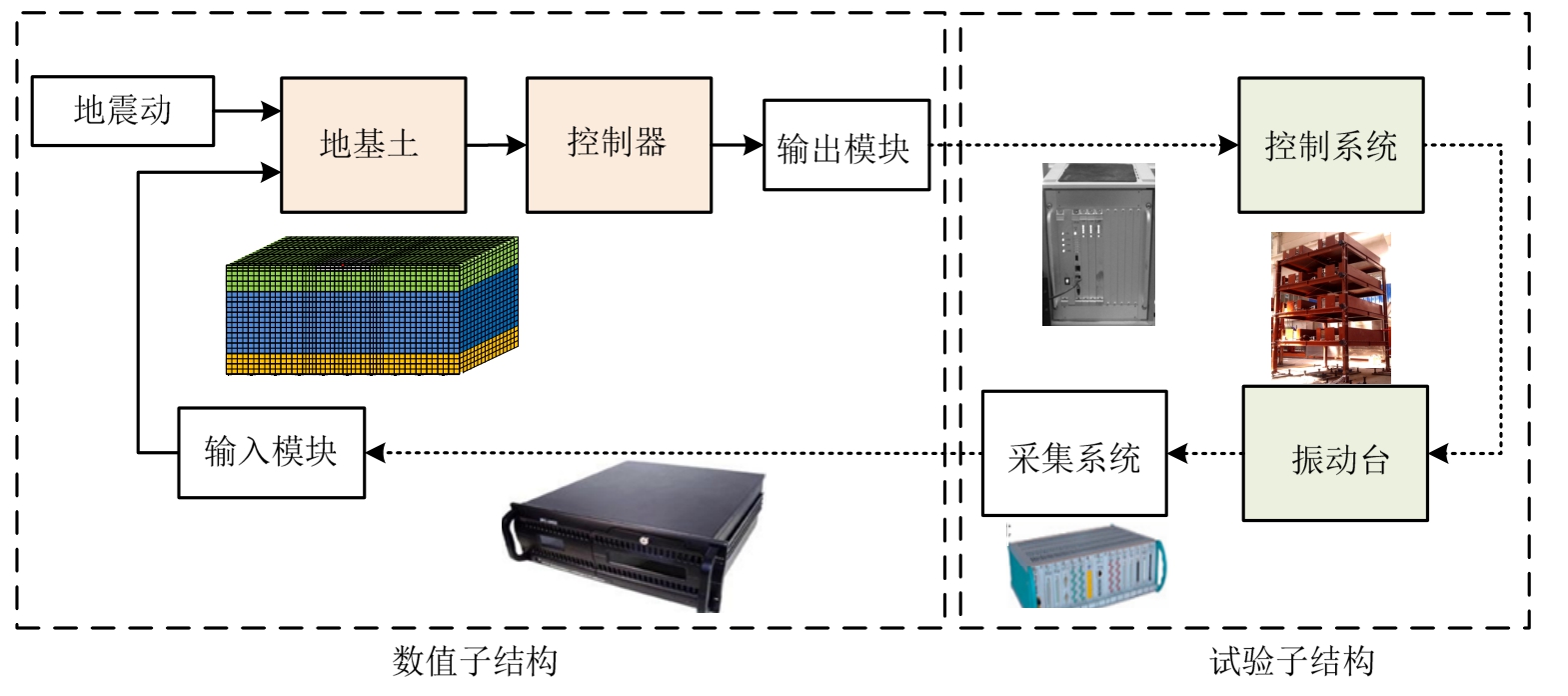
图7 试验系统组成
Fig.7 Schematic diagram of the experimental system
数值子结构采用SIMULINK状态空间方法进行求解，具体计算模块如图8所示。其中状态变量x由土体的模态位移和模态速度组成，输入变量u由土体外荷载和耦合项荷载组成，输出变量y是经过坐标变换后的土体物理加速度，然后通过“Selector”模块选择输出对应刚性基础的平动加速度和转动加速度，按照式(19)中的方法计算等效水平加速度，从而得到此时试验子结构受到的真实的地震激励，将其作为振动台的驱动命令。状态空间法参数A、B、C、D具体计算见图8中所示。
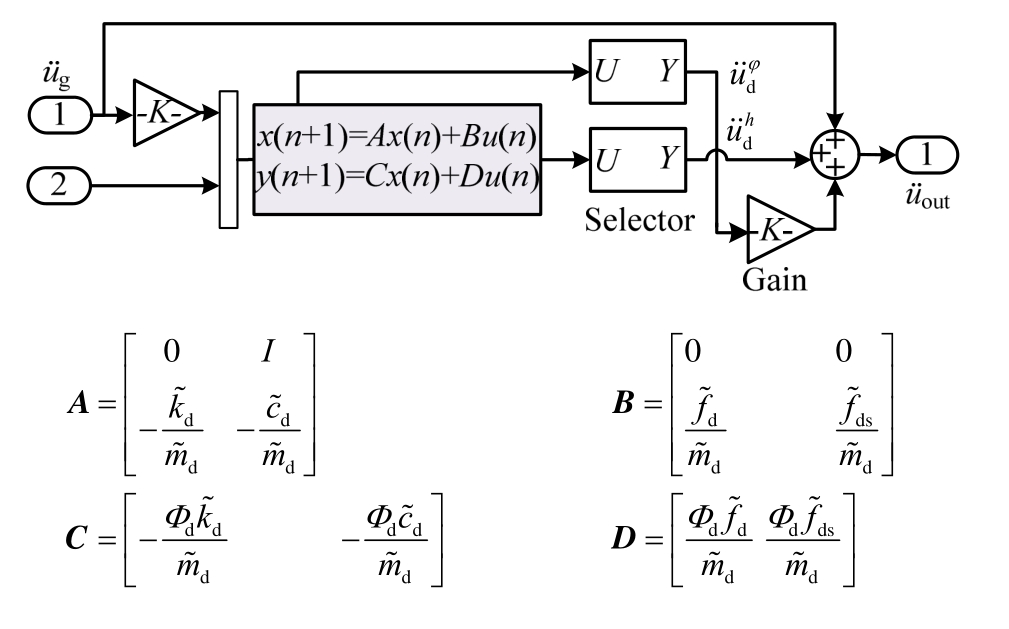
图8 数值子结构计算模块
Fig.8 Numerical substructure calculation module
为了更准确地追踪试验装置的性能，需要对振动台实时子结构试验系统进行补偿控制。其中时滞补偿控制通常将试验加载系统简化成一纯时滞系统，系统的时间滞后τ取常数，然后通过不同预测方法提前τ秒输出试验指令，从而保证试验加载系统的输入信号与输出信号是一致的。周惠蒙等[15]开展作动器类型实时子结构试验研究，并设计相应的控制器模块取得较好的控制效果。唐贞云等[16]建立振动台系统综合动力模型，对相关时滞假设方法分析，发现基于时滞简化给出的稳定性预测结果具有一定不确定性。
由于振动台动力特性更加复杂，简化成纯时滞系统无法完全补偿加载系统误差。逆动力补偿控制方法中输入信号r与输出信号y满足y=C(s)G(st)r。若能建立振动台准确的数学模型并求逆，这样就满足C(s)G(st)=1，就能完全补偿试验加载系统的幅值和相位误差。但是由于试验装置动力特性的复杂性以及外部环境等因素影响，导致该方法的实际补偿效果并不理想。Tagawa等[17]、Tang等[18]引入虚拟控制对象提出了基于仿真的逆动力补偿控制策略，能够避免噪声等外部信号的干扰。考虑到不确定因素等影响，本文采用闭环控制与基于仿真的实时逆动力补偿控制策略相结合方法控制实际的振动台，具体控制原理如图9所示。
图9 试验控制方法原理图
Fig.9 Principle of control technique
该方法对振动台可预测和不可预测动力特性进行两部分补偿控制。对于可数学模型描述的动力特性采用基于仿真的逆动力补偿，对于不可数学模型描述的因素则通过物理闭环进行补偿。应用正弦扫频信号对振动台进行系统辨识，并采用MATLAB中的“fminsearch”函数识别出振动台四阶传递函数G(n)如式(20)所示：
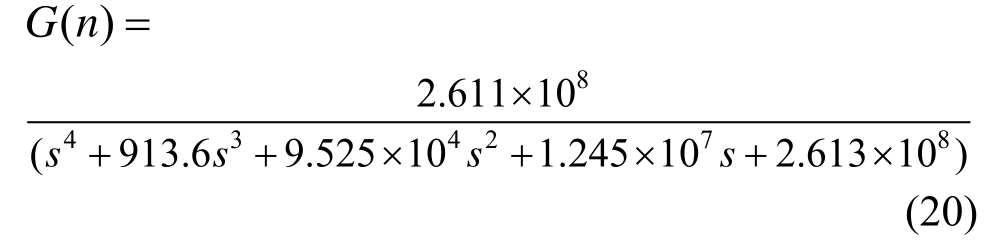
利用搭建的振动台实时子结构试验系统，进行设备-结构-土体系振动台实时子结构试验，按照8度抗震设防小震阶段要求输入地震动。为了验证本文振动台实时子结构试验方法的可行性，以设备顶部的加速度反应为指标，对比振动台实时子结构试验结果与数值计算结果的差异。数值计算时应用MATLAB按照式(5)建立的设备-结构-土体系运动方程，并按Newmark-β直接积分算法求解计算。土体计算矩阵按照2.2节计算得到。设备-结构体系简化为五自由度计算模型，由设计参数知结构第1、2、3层的质量m1=m2=m3=1700 kg，第4层的质量m4=1540 kg，计算得到结构第1层的刚度k1=2423080 N/m，第2层、3层、4层的刚度k2=k3=k4=3833120 N/m，第1层的阻尼c1=4463 N/(m/s)，第2层、3层、4层的阻尼c2=c3=c4=7061 N/(m/s)。设备的质量m5=90 kg，设备的刚度k5=93046 N/m，设备的阻尼c5=42 N/(m/s)。如图10所示的设备顶部加速度响应试验结果与数值计算结果对比图，与数值计算结果相比较，8度小震阶段El Centro、TianJin和PerSon地震动作用下振动台实时子结构试验中的设备顶部加速度的峰值反应分别减小6.0%、4.5%和3.8%，并且各地震动作用下，两种方法得到的设备顶部加速度时程曲线整体趋势基本吻合在一起，总体上能够满足试验精度的要求，证明本文提出的振动台实时子结构试验方法是可靠有效的。存在误差的原因，主要是振动台本身控制性能限制，以及数值计算中设备-结构体系的计算模型与实际模型存在差异。
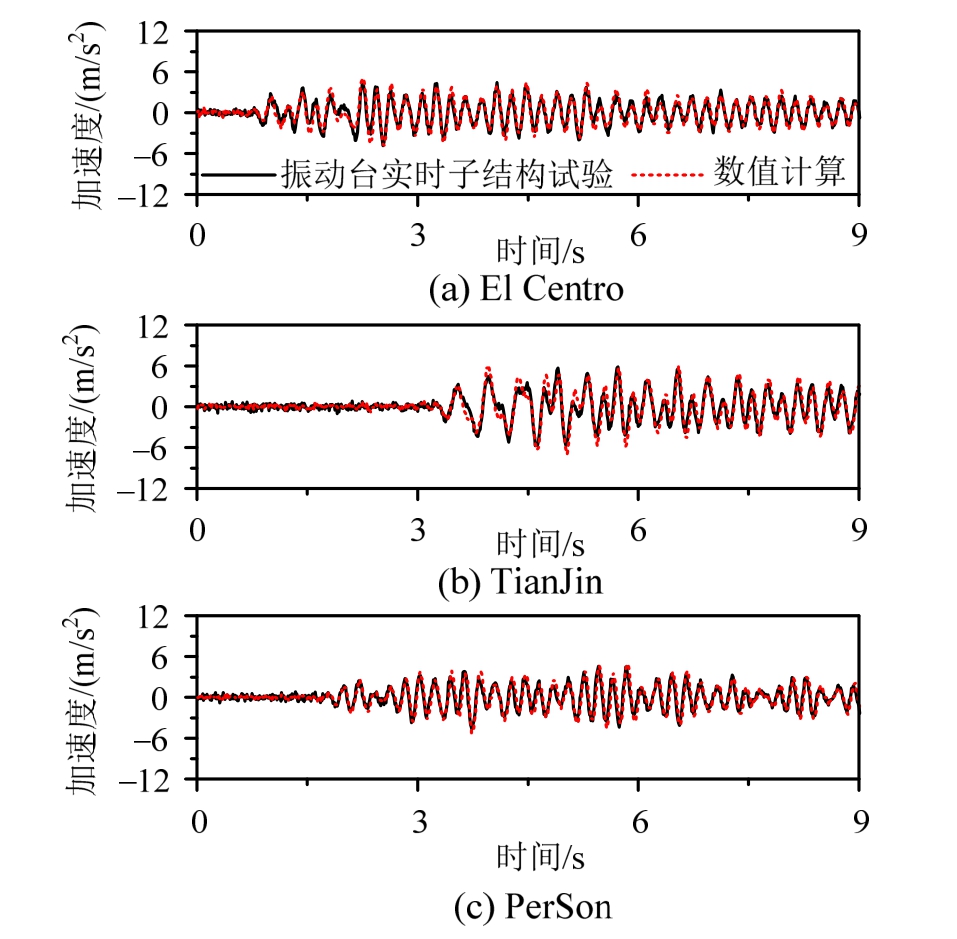
图10 试验与数值计算设备顶部加速度响应
Fig.10 Experimental and numerical acceleration responses of the equipment top
通过设备-结构体系作为试验子结构的振动台实时子结构试验，实现了考虑设备-结构-土相互作用整体试验的效果。该振动台实时子结构试验方法能够充分利用仿真软件的计算优势与试验装置联合试验，而且引入RITZ向量法建立复杂土体数值子结构模型，能够保证计算精度的前提下高效完成实时子结构试验，准确地反映线性土体对上部结构抗震性能的影响。这样既符合科学研究精细化建模要求，也适合在实际试验中推广应用，将进一步拓展实时子结构试验方法的应用范围。
本文探讨设备-结构-土体系振动台实时子结构试验的可行性，推导了设备-结构-土体系运动方程，并开展设备-结构-土体系振动台实时子结构试验研究，得到以下结论。
(1) 基于分支模态子结构方法，推导并变换了设备-结构-土体系运动方程，并将其应用于设备-结构-土相互作用振动台实时子结构试验，该方法具有概念清晰、使用方便等特点。
(2) 采用等效原则把基础转动加速度转化为作用于试验子结构上等效的水平加速度，实现了平动振动台实时子结构试验能考虑基础转动的因素影响，进一步提高了试验结果的精度。
(3) 试验系统应用实时数值控制与实时物理控制相结合的方法对实际的振动台补偿控制，能够较好地追踪和控制振动台轨迹满足试验精度的需要。
(4) 对比振动台实时子结构试验结果与数值计算结果，发现两种方法的结果尽管存在一定的误差，但整体的变化趋势基本吻合，说明该振动台实时子结构试验方法是可靠有效的。
本文基于分支模态子结构法实施的设备-结构-土体系振动台实时子结构试验，仅考虑了线性土体对设备与结构抗震性能的影响，对于更复杂相互作用体系特别是土体进入非线性阶段情况需要开展进一步的研究。
[1] 姜忻良,徐炳伟,焦莹.大型土-桩-复杂结构振动台模型试验研究[J].土木工程学报,2010,43(10): 98―105.Jiang Xinliang,Xu Bingwei,Jiao Ying.Analysis of shaking table test of large-scale soil-pile-complex structure interaction [J].China Civil Engineering Journal,2010,43(10): 98―105.(in Chinese)
[2] 尚守平,鲁华伟,邹新平,等.土与结构相互作用大比例模型试验研究[J].工程力学,2013,30(9): 41―46.Shang Shouping,Lu Huawei,Zou Xinping,et al.Experimental study on soil-structure interaction through large scale model tests [J].Engineering Mechanics,2013,30(9): 41―46.(in Chinese)
[3] Park H,Ha J,Kwon S,et al.Investigation of the dynamic behaviour of a storage tank with different foundation types focusing on the soil-foundation-structure interactions using centrifuge model tests [J].Earthquake Engineering and Structural Dynamics,2017,46(1):2301―2316.
[4] Nakashima M,Kato H,Takaoka E.Development of real-time pseudo dynamic testing [J].Earthquake Engineering and Structural Dynamics,1992,21(1): 79―92.
[5] Wang Q,Wang J,Jin F,et al.Real-time dynamic hybrid testing for soil-structure interaction analysis [J].Soil Dynamics and Earthquake Engineering,2011,31(12):1690―1702.
[6] 闫晓宇,李忠献,韩强,等.考虑土-结构相互作用的大跨度连续刚构桥振动台阵试验研究 [J].工程力学,2014,31(2): 58―65.Yan Xiaoyu,Li Zhongxian,Han Qiang,et al.Shaking tables test on a long-span rigid-framed bridge considering soil-structure interaction [J].Engineering Mechanics,2014,31(2): 58―65.(in Chinese)
[7] 郭珺,唐贞云,李易,等.基于子结构试验的土-结构相互作用实现研究[J].工程力学,2017,34(增刊1):214―219.Guo Jun,Tang Zhenyun,Li Yi,et al.The simulation of soil structure interaction based on substructuring testing[J].Engineering Mechanics,2017,34(Suppl 1): 214―219.(in Chinese)
[8] Lee S K,Park E C,Min K W,et al.Real-time substructuring technique for the shaking table test of upper substructures [J].Engineering Structures,2007,29(9): 2219―2232.
[9] Zhang R,Lauenstein P V,Phillips B M.Real-time hybrid simulation of a shear building with a uni-axial shake table [J].Engineering Structures,2016,119: 217―229.
[10] 姜忻良,严士超.分枝模态二步分析法及其在液体-结构-桩土体系中的应用[J].振动工程学报,1994,7(4):346―351.Jiang Xinliang,Yan Shichao.Two step method of the branched modal and its use for liquid-structure-pile-soil interaction system [J].Journal of Vibration Engineering 1994,7(4): 346―351.(in Chinese)
[11] Bolisetti C,Whittaker A S,Coleman J L.Linear and nonlinear soil-structure interaction analysis of buildings and safety-related nuclear structures [J].Soil Dynamics and Earthquake Engineering,2018,107: 218―233.
[12] 王菲,姜南.土-结构三维动力分析的线性-非线性混合子结构法[J].工程力学,2012,29(1): 155―161.Wang Fei,Jiang Nan.3D dynamic analysis of soil-structure interaction system based on mixed linear-nonlinear substructure method [J].Engineering Mechanics,2012,29(1): 155―161.(In Chinese).
[13] 姜忻良,徐炳伟,李竹.土-桩-结构振动台模型试验相似理论及其实施[J].振动工程学报,2010,23(2): 225―229.Jiang Xinliang,Xu Bingwei,Li Zhu.Similitude laws and its application in shaking table test of soil-pile-structure interaction system [J].Journal of Vibration Engineering,2010,23(2): 225―229.(in Chinese)
[14] Li Y,Jiang X L.Parametric analysis of eccentric structure-soil interaction system based on branch mode decoupling method [J].Soil Dynamics and Earthquake Engineering,2013,48(6): 63―70.
[15] 周惠蒙,吴斌,王涛,等.基于速度的显式等效力控制方法的研究[J].工程力学,2016,33(6): 15―22.Zhou Huimeng,Wu Bin,Wang Tao,et al.Explicit equivalent force control method based on velocity [J].Engineering Mechanics,2016,33(6): 15―22.(in Chinese)
[16] 唐贞云,陈适才,张金喜,等.基于振动台的实时动力子结构实验系统稳定性预测研究[J].工程力学,2016,33(12): 217―224.Tang Zhenyun,Chen Shicai,Zhang Jinxi,et al.Study on the stability prediction of real-time dynamic substructure system based on shaking table [J].Engineering Mechanics,2016,33(12): 217―224.(in Chinese)
[17] Tagawa Y,Tu J Y,Stoten D P.Inverse dynamics compensation via 'simulation of feedback control systems’ [J].Proceedings of the Institution of Mechanical Engineers Part I Journal of Systems and Control Engineering,2010,225(1): 137―153.
[18] Guo J,Tang Z Y,Chen S,et al.Control strategy for the substructuring testing systems to simulate soil-structure interaction [J].Smart Structures and Systems,2016,18(6): 1169―1188.
STUDY ON SHAKING TABLE REAL-TIME SUBSTRUCTURE EXPERIMENTAL METHODOLOGY OF EQUIPMENT-STRUCTURE-SOIL SYSTEM
张崇祥(1987―)，男，山东人，博士生，主要从事土-结构相互作用研究(E-mail: xcziby@tju.edu.cn);
姜 南(1980―)，男，浙江人，博士生，副教授，博士，主要从事土-结构相互作用与结构抗震研究(E-mail: jiangnan@tju.edu.cn);
罗兰芳(1988―)，女，四川人，博士生，主要从事土-结构相互作用研究(E-mail: lanfangluo@tju.edu.cn).