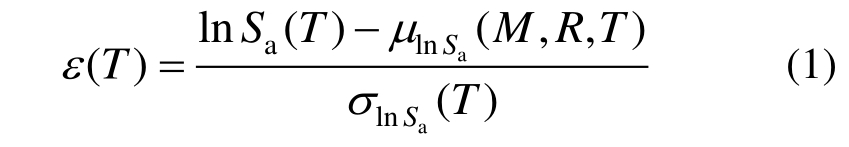
目前，许多国家的抗震规范已将时程分析方法作为静力设计方法的必要补充，针对超高层、大跨等特殊结构形式以及重要工程更是强制使用时程分析方法[1]。虽然规范中一般都要求选取的地震动要依据一定的地震信息并考虑结构特性，但过于笼统的规定以及地震动自身极强的不确定性，往往使得结构时程分析结果产生过大的离散性[2]。
以往由于实震记录匮乏，时程分析仅限于几条典型记录及人工波，如EL-Centro波、Taft波、迁安波、天津波等。而目前国内及世界范围内可获取的实震记录数据量已相当庞大，常见的数据库如美国的 COSMOS (Consortium of Organizations for Strong Motion Observations System)、PEER (Pacific Earthquake Engineering Research)和 SMDB(Southern California Strong Motion Database)，日本的 K-NET和KiK-NET，欧洲和中东的ISESD( European Strong-Motion Database)，我国建研院的EQDBMS和EQSS.88.1以及国家地震局的STRONGMOTION等，都为结构抗震时程分析提供了基础数据。然而，实际工程场地千差万别，找到与设定环境完全相同的地震记录绝非易事。那么如何有效利用这些数据，选取适于时程分析的强震记录，是研究人员面临的一项挑战。
选波研究主要是围绕两个问题：一是确定选波的评判指标(包括选波及调整方法)，另一个是确定样本容量[2]。关于地震动记录选取的研究可以追溯到20世纪末，Nau等[3]研究发现，相对于地震动峰值(加速度、速度、位移)，经反应谱值归一化后所得结构反应的离散性明显降低。如今，随着结构分析的目的由结构反应均值，逐渐发展到结构反应概率分布，强震记录选择及缩放方法也得到了相应地发展。选波的评判指标从地震信息(如震级、震中距、场地等)发展到目标反应谱(如：规范标准谱或设计谱、一致概率谱UHS (Uniform Hazard Spectrum)、条件均值谱CMS (Conditional Mean Spectrum)、位移目标谱、均值目标谱等，也包括考虑各种定义的地震动强度指标(如PGA、PGV、EPA、EPV、Arias强度、Housner强度等)。强震记录缩放的方法，从依据目标谱单点缩放，发展到考虑反应谱形的频段缩放。样本容量及分组方法的研究也不尽相同。本文旨在将近些年国内外学者提出以及各国规范所采用的选波研究方法进行归纳总结并加以评述，望对后续研究有所脾益。
对某一建筑的抗震设计，最好是选用建筑所在场地曾经记录到的地震加速度记录作为时程分析的输入，然而这种机会极少[4]。目前，应用最为广泛的方法是以震级、震中距、场地条件等地震信息为第一评判指标进行初选，再以目标反应谱为第二评判指标进行选波。应用最多的目标谱是设计加速度反应谱，而后又发展出一致概率谱、条件均值谱、位移目标谱、均值目标谱等诸多特定含义的反应谱。除了目标反应谱外，国内外学者已给出数十种与结构地震反应相关性密切的地震动强度指标，也可用作选波的评判指标。本节将重点介绍目标谱选波方法，并对基于地震信息及地震动强度指标的选波研究做简要介绍。
1.1.1 震级和震中距
震级和震中距对于选波的重要性认知不一。Shome等[5]研究认为除了受高阶振型影响较大的高层结构外，一般只要以结构基本周期处弹性反应谱值为匹配标准来选波及缩放，就能保证较好的结构反应估算精度，是否考虑震级和震中距并不重要。Iervolino和Cornell[6]研究了不同周期和延性系数的单自由度体系和多自由度钢筋混凝土抗弯钢框架结构的地震反应，并利用假设检验证明，选波时无需考虑震级和震中距影响，但必须满足一定条件(震级在6.4～7.4之间，缩放系数小于4，延性系数小于6)。Stewart等[7]则认为震级对于地震动的频率和持时都有重要影响，须保证选波的震级范围在±0.25 MW(MW为矩震级)内；Bommer和Acevedo[1]更是建议这一范围应控制在±0.2 MW内。对于震中距的研究，Bommer和Acevedo[1]采用4种衰减关系，对比了在相同震级(MW=7)下，震中距从5 km到50 km范围内，加速度反应谱形的变化，发现震中距对谱形并不敏感。选波时过于限制震中距往往使得选出波数量不足。因此，在严格限制震级的前提下可适当放宽对于震中距的限制。
1.1.2 场地
场地条件对强震动记录及反应谱的影响较为显著。目前国际上常以30 m覆盖层厚度范围内土层剪切波速VS,30作为场地类别划分指标，各国规范划分种类不尽相同。Bommer等[8]的研究表明，除震级和震中距外，增加场地类别这一限制，会明显减少可选波数量。因此，可适当放宽对于场地类别的限制，如采用相邻类别场地的记录。虽然这样做并不合理，但不失为一种较为实用的方法。
1.1.3 持时
目前对于持时的定义已超过30种[9－10]，其对于结构反应的影响程度并不明确。Bommer和Ruggeri[11]统计了33个抗震设计规范，仅有两个规范(法国和土耳其)对持时有明确的限制要求。ASCE4－98[12]和希腊抗震规范[13]也有考虑持时的要求。Hancock和Bommer[14]总结了百余篇关于持时与结构损伤的关系文献，认为当研究结构损伤是以能量的累积耗散为指标，持时的影响显著；若以结构的峰值反应为损伤指标，则与持时无明确的关联。国内学者的研究也与此认知相同[15－16]。
1.1.4 断层机制
虽然没有证据证明地震动与断层方向有何显著性联系，但垂直断层方向的地震动会产生较大的速度脉冲效应及幅值变化，这一观点已得到广泛认可。但目前断层机制对结构反应的影响研究还不成熟，考虑断层机制会大大减少可选波数量，相比于震级、震中距、场地等影响显著而明确的地震信息，一般不将断层类型作为选波的限制条件。
震级、震中距、场地条件是国内外学者及规范最为认可的三项限制选波的地震信息，一般不单独考虑，而是常与目标反应谱或其它地震动强度指标共同作为评判指标。如王亚勇等[16]较早时提出的标定设计反应谱，按一定权重分组选波的方法，主要依据的是近远震、场地类别、反应谱特征周期等信息，虽然对反应均值的估计误差较大，但结构反应离散性较小。ATC-58和ATC-63 (Applied Technology Council，2008)也是将震级、震中距、场地类别、PGA、PGV等参数加以限制，所选波数量较大，结构反应的均值估计较好，但离散性较大。虽然Baker和Cornell[17]以及Goulet等[18]将反应谱形参数作为地震信息限定之外的附加条件，也未能明显降低结构反应的离散性。因此，目前的研究以及各国的规范和标准，如：Eurocode 8(Design of structures for earthquake resistance)[19]、ASCE 7-05[20]、ASCE 4-98[12]、FEMA 规程[21]、新西兰标准[22]、意大利规范[23]和希腊抗震规范[13]，多是将震级、震中距及场地条件作为选波的初始条件。
以特定含义下的反应谱作为目标谱，选取反应谱与目标谱“一致”的实震记录的方法，即谱形匹配法，已成为最常采用的强震记录选取方法。目标谱法常与地震信息选波相结合，即以地震信息作为第一评判指标，以目标谱为第二评判指标[24]。
目标谱的定义不同，最为广泛使用的是设计加速度目标谱(即规范标准谱)，之后随着概率地震危险性分析的发展与应用，又发展出一致概率谱(UHS)、条件均值谱(CMS)、位移目标谱以及均值目标谱等。地震动记录从匹配确定性均值反应谱，发展为匹配概率含义的目标谱分布(即均值与方差)。
1.2.1 目标谱的确定
1) 设计加速度目标谱(或规范标准谱)
基于设计加速度目标谱(即规范标准谱或设计谱)的强震记录选取方法，是直接将强震记录反应谱与设计反应谱进行比较，选用更为接近的强震记录，由此来控制所选强震记录的频谱特性，是国内外规范及学者最常用的选波方法。
无论是我国抗震规范(GB 50011—2010)中的设计谱亦或是其它国家的设计谱，均是将反应谱简化为几段直线或曲线的公式表示的反应谱函数[25]。事实上，规范设计谱的谱形是经较多地震波反应谱统计平均(平台段抽象化)及适当人为修正(长周期)基础上确定的，其幅值满足一定的概率水准，如我国抗震规范(GB 50011－2010)的中震，符合50年超越概率10%。因此，规范设计谱的本质是经验公式抽象化的一致概率谱。
2) 一致概率谱(UHS)
一致概率谱(UHS，Uniform Hazard Spectrum)是由地震危险性概率分析得出的合成地震动反应谱。首先，对工程场地进行概率性地震危险性分析(PSHA，Probabilistic Seismic Hazard Analysis)；然后，根据结构重要性确定目标超越概率，对于任意周期的谱值对应的超越概率是一致的；最后，将这些谱值绘制在对应的周期点上即为一致概率谱UHS。
一致概率谱实质上是一种包络反应谱，并非源于某个实际地震。在不同的周期段，由不同的地震事件决定，一般认为高频段由小震近震决定，低频段由大震远震决定。众所周知，大地震出现概率低，小地震出现概率高，但大地震的地震动中长周期成份丰富，而小地震的地震动短周期成份丰富，有可能导致一致概率谱过高地估计了设计地震动的中长周期成分[26]，进而造成根据一致概率谱计算得到的结构反应偏于保守，不利于准确地评估结构的抗震性能[8,27－28]。
UHS最本质的局限在于，它认为各个周期点反应具有相同的超越概率，而这并不符合一次地震事件的概率分布特征，为了能够考虑不同周期点谱值间关系，弥补各周期点超越概率一致的缺陷，又能够利用既有规范(如ICC (International Code Council 2006))，Malhotra[29]提出了一种更为精确地运用UHS进行结构非线性分析的方法。他以美国规范反应谱为基准，考虑具有相同重现期的0.2 s和1.0 s处谱值的相关性，利用蒙特卡洛模拟和大量强震记录统计结果，建构了一种概率反应谱。这种概率反应谱可以近似描述一次地震中不同周期点反应谱值间的相关性。
3) 条件均值谱(CMS)
根据概率地震危险性的合成分解方法可以得到符合一致概率的反应谱均值和反应谱方差，但在指定的震级和震中距以及超越概率条件下，一次地震动反应谱值会与统计所得的均值反应有一定的差距，即ε参数[30](见式(1))。
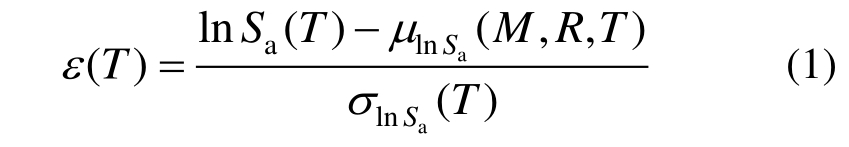
式中：lnSa(T)是指定周期点处加速度反应谱对数值；
分别是在一定震级和震中距下由衰减关系给出的某一周期点处的对数谱均值和对数标准差。
对于某一结构进行抗震设计时，结构基本周期对应的加速度反应谱值以及超越概率都应大于其它周期。结构基本周期点对应反应谱值采用此周期点处的UHS值是合理的，但在其它周期点不应采用具有相同超越概率的UHS值[31]。为反映不同周期点处谱值的差异与联系，Baker基于特定周期点T*(一般取结构基本周期点)的ε参数ε(T*)，并利用任意两个周期点处ε参数的相关系数ρ(Ti,T*)(地震动的固有特性)[30,32]来计算其它周期点Ti处的ε(Ti)(式(2))，从而确定其它周期点处反应谱值。
Baker正是考虑了任意两周期点ε参数的相关性，提出了具有合理的概率统计意义的条件均值谱(CMS，Conditional Mean Spectrum)[31]，其均值和方差可见式(3)和式(4)。
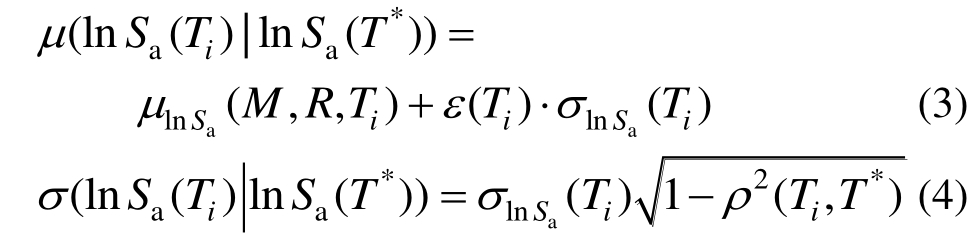
式中：
表示在条件
下反应谱在周期点Ti处的均值和方差
和
表示在无条件
或ε=0时的均值和方差。
CMS中ε参数除了可以定量地表达指定加速度反应谱与一定震级和震中距下衰减关系得到的谱均值之间的差别，还对CMS的谱形有重要影响[30]：当ε为正值时，其它周期点谱值均小于基本周期点谱值，CMS会在周期点处出现“尖峰”；若为负值时，则相反，CMS会在周期点处出现“低谷”。因此，常称ε为谱形系数(如图1)[33]。
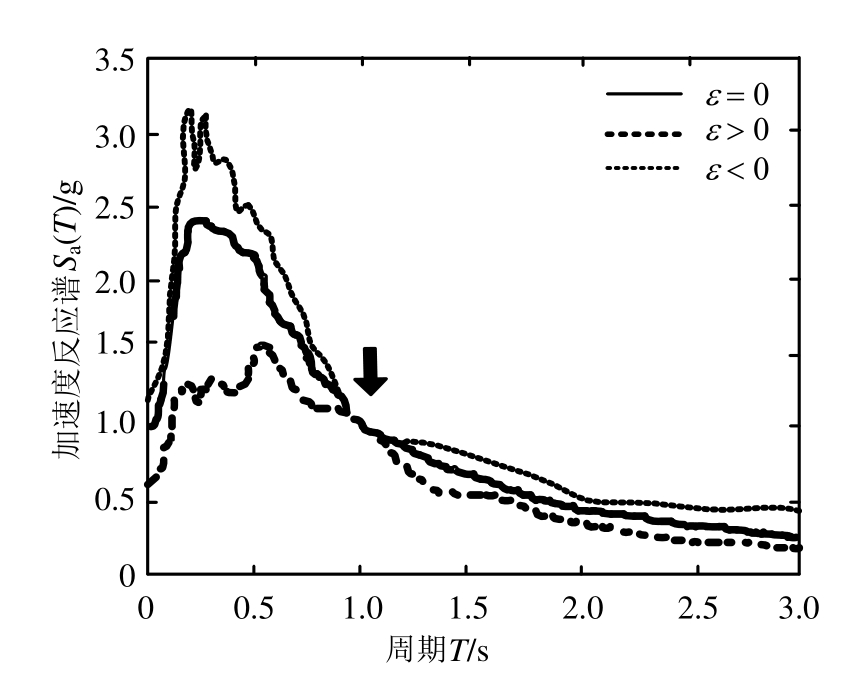
图1ε参数对谱形的影响[33]
Fig.1 Epsilon value effect on spectra shape
注：正负ε均缩放至相同Sa(T1),T1=1 s
正是由于Baker采用的ε参数能够反映反应谱形，从而使CMS法能够准确地估计多自由度体系的地震反应[34]。文献[34]中采用了14种地震动选择和调整方法，分析了4种钢筋混凝土框架和剪力墙结构，通过层间位移角的对比分析可见，CMS及其改进方法，对于结构反应均值和方差的估计精度都远高于其它方法。
条件均值谱在国外已得到了广泛的关注和应用，如NEHRP 2011、USGS2012和ASCE7-16(第一个正式采用CMS选波的规范)，并且基于CMS已研发出多个应用软件，如Wang等[35]研发的DGML，Marasco和Cimellaro[36]研发的OPENSIGNAL，Mahmoud[37]研发的软件QuakeManager等。Shantz[38]将弹性CMS位移反应谱乘以由函数CR(R,T,ε)确定的放大系数(CR(R,T,ε)是理想弹塑性单自由度体系的塑性位移反应与弹性位移反应之比)，便可得到基于CMS建立的非弹性位移表面IDS谱。该IDS是以周期T为x坐标，以位移延性系数μ为y坐标，以最大位移反应为z坐标的三维曲面谱。将IDS作为目标位移面，并考虑1阶和2阶振型影响，可使结构反应均值的估计非常准确，但离散性较大。Shantz方法适用于一阶振型为主的结构，且依赖于工程师的主观判断，以及确定目标位移面的形状和位置[38]。为更好地预测非线性结构反应，Mousavi等[39]在确定ε参数时，不仅考虑加速度反应谱Sa，还加入了PGV的影响，称为η参数(式(5))，记为E-CMS法。
式中：εSa和εPGV为Sa和PGV的ε参数；b为权重系数。
Mousavi[39]采用ε与η两种参数，对结构非线性反应中周期与延性的相关性进行研究。其结果表明，采用η参数可使它们的相关性更显著。从样本容量对比可见，CMS法对样本容量非常敏感，样本容量减小则估计的结构反应精度会明显降低；而E-CMS法即使取用较少量的强震记录，其反应谱也可与目标谱实现较好地匹配。对于长周期结构，两种方法相差不大；但对于中短周期结构，CMS法会出现低估结构反应的情况。
目前，国内学者对于条件均值谱的关注和研究尚处于起步阶段，陈波[40]在建筑结构非线性分析中采用此方法与UHS法以及仅考虑谱形系数ε的方法作对比，再次说明CMS方法的优越性；李琳等[25]也将CMS作为目标谱用于地震安全性评价；韩建平等[41]在地震动选择及调整时将CMS用作目标谱，在5层和11层钢筋混凝土框架时程分析中也得到了良好的效果。
条件均值谱的建立受衰减关系、震级M、距离R及各周期谱值间相关性(即相关系数ρ)等因素的影响。我国规范在地震动参数区划图制定中已建立了衰减关系，但与PSHA相关的地震危险性分析信息尚未很好地提供，将CMS与我国规范相结合用于选波工作，仍有多处细节需进一步深入研究。
4) 位移目标谱
上述目标谱均为加速度反应谱，但对于长周期结构，其一阶自振周期处于反应谱的长周期位移敏感区，用位移反应谱做目标谱则更有优势。Smerzini等[42]通过概率危险性分析，并利用加速度、速度及位移反应谱间的转换关系
建立了基于意大利规范及相关研究项目成果的位移目标谱(或称设计位移谱)，并研发了选波软件REXEL-DISP。该目标谱的适用频段范围广泛，既适用于短周期高频段，也适用于长周期低频段选波。
此外，上述目标谱均依据弹性反应谱建立，而某些情况下，如近断层地震动，采用弹性反应谱方法则准确性很难保证。Luco和Cornell[43]以及Tothong和Luco[44]均采用依据一阶振型所得的非弹性位移反应谱SdI以及二阶振型所得的弹性位移反应谱SdE组合而成的地震动强度指标IM1I,2E来选波，评判与目标谱的匹配程度时，采用分权重的方法，即核心区权重大，边缘区权重小。该种方法虽然比较准确，但必须给出指定地震动的非弹性位移与地震灾害平均发生概率间的衰减关系，未与目前主流的概率地震危险性分析(PHSA)相关联，其发展受到较大的限制[33]。
Kalkan和Chopra[45]提出了一种基于非弹性位移谱的选波方法，即MPS(Modal Pushover-based Scaling)法。MPS法考虑近断层地震动作用，将由21条近断层地震动位移反应谱的平均谱乘以非弹性位移比系数CR获得非弹性位移目标谱。结构反应按如下步骤进行计算：先初设缩放系数(可先取SF=1)，按结构Pushover分析得出的底部剪力与各层位移关系等效为非弹性单自由度体系的力-位移关系，输入单自由度运动方程，即可得出位移反应时程及反应峰值。能保证位移反应与目标位移值之差在允许范围内的SF为所选记录的缩放系数，选取SF最接近1的记录，将缩放后加速度记录输入结构做时程分析。具体计算流程如图2。Kalka和Chopra[45]将该法与ASCE 7-05方法做对比，其计算准确度明显高于ASCE 7-05。
文献[34]对比的14种选波方法中，非弹性位移反应谱方法具有很小的离散性，但其对结构反应均值的估计偏大。这有可能是因为对比参考的“真实反应”是依据加速度弹性反应谱Sa进行选波并输入结构进行时程分析统计得出的，而非弹性位移反应谱法依据的目标谱是非弹性位移谱Sd。参考的标准不同，使得多位学者研究得出的“非弹性位移反应谱法对结构均值反应高估”的结论不够可靠[33]。关于非弹性位移反应谱法的可靠度研究还有待深入。
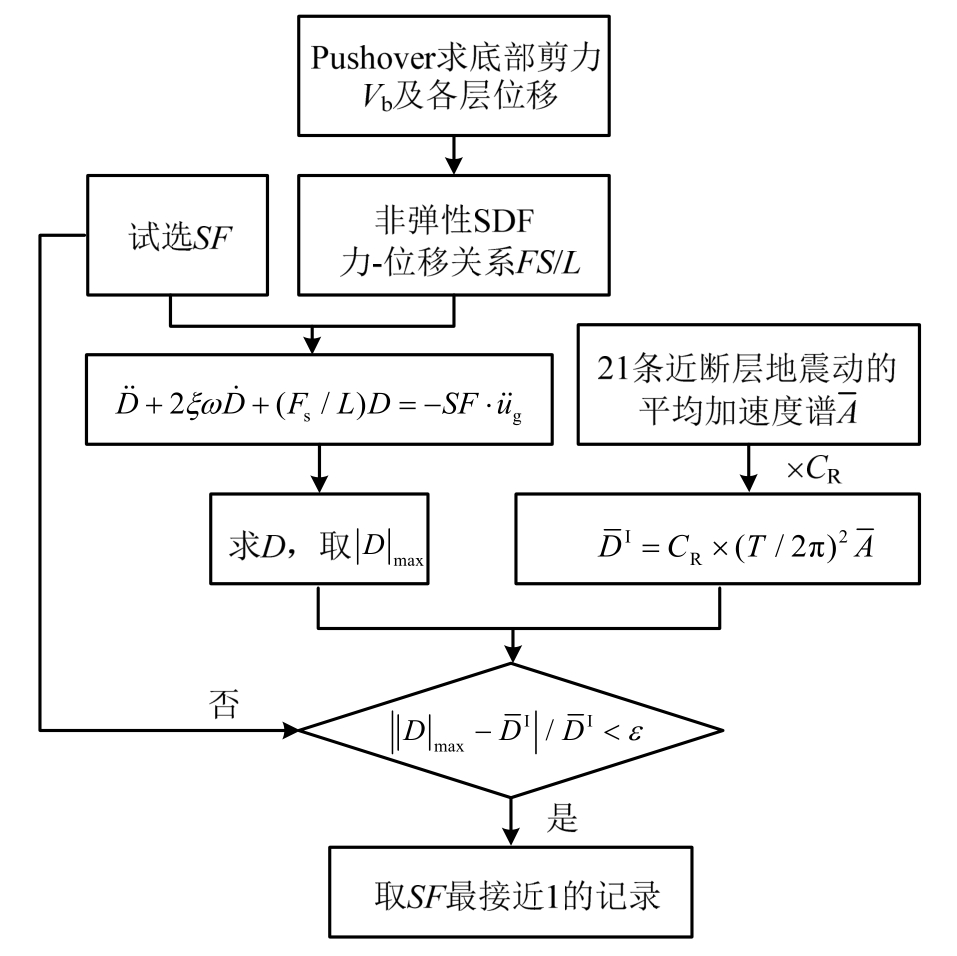
图2 MPS选波方法计算流程
Fig.2 Calculation flow diagram of MPS
5) 均值目标谱
考虑到研究的特定工况不同，很多学者在确定目标谱时常采用指定数据库中地震动反应谱(包括加速度、速度、位移反应谱)的均值谱作为目标谱。Youngs等[46]也将限定震级和震源距确定的记录数据库的平均反应谱作为目标谱，在匹配谱形选取记录时使用均方差MSE和斜率系数Slope两个匹配指标。Kalkan和Chopra[45]在MPS方法中所用的非弹性位移目标谱也是在21条近断层地震动加速度反应谱的平均谱的基础上建立的。
确定均值目标谱的记录数据库，常由研究人员结合工程需求确定，且可充分利用目前国内外庞大的实震记录数据库，确定的目标谱能更为准确地表现真实记录的反应谱特征。同时，由该数据库中记录所得结构反应的均值也可作为“目标反应”，即假定的“真实反应”，用于选波准确性的评判依据[46―48]。确定均值目标谱的数据库要依赖于现有强震动记录的数据量、震级和震中距的分组情况，有时为满足设计要求还要设置一定数量的人工波，如美国SAC Steel Project项目中50年超越概率2%工况下提出的部分记录即为人工模拟地震波。
1.2.2 目标谱均值匹配法及记录缩放方法
目前的选波研究主要是以目标谱均值作为匹配目标，本文1.2.1节中已将个别选波方法的匹配及缩放方法做了简要介绍，因匹配选波与缩放有时分步进行，有时又交织在一起，因此，本节将强震记录匹配及缩放方法同时进行介绍。
这里介绍的缩放方法主要为线性缩放。虽然小波技术等频率调整方法能使反应谱在很宽的周期范围内与目标谱达到很好的匹配，但计算所得结构反应却小于将真实记录线性缩放的结果[1,49]。可见，将真实地震记录线性缩放是一种简单而行之有效的缩放方法。
上述各种目标谱法均是要求选取与目标谱有较高匹配程度的反应谱对应的强震记录，只是判定匹配程度的误差参数，以及计算误差参数时覆盖的周期段有所差别，有的是单个周期点，有的是频段(如单频段、双频段以及多频段等)，现分述如下：
1) 单点匹配
单点匹配即是选取结构特征周期点(一般取结构一阶自振周期T1)对应反应谱值与设计谱值相差不超过一定范围的强震记录。Martinez-Rueda[50]、Kappos和Kyriakakis[51]以及Shome和Cornell[52]研究发现，以结构基本周期T1对应的反应谱值来调整地震动记录能够减小结构反应的离散性。多国规范及学者研究(Shome[5]；Watson-Lamprey和Abrahamson[53])均将
作为缩放系数，其中Sa(T1)为所选记录在结构基本周期T1处的加速度反应谱值，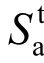
(T1 )为T1处的目标谱值。
但考虑到结构进入非线性阶段时基本周期T1会延长，Catalán等[54]认为将T1延长至1.1T1是较为合理的，并通过两个4层和8层框架在不同超越概率下的抗震结构统计分析得到了验证。Marasco和Cimellaro[36]则建议，对于受高阶振型影响显著的结构，应将T1替换为Tref(式(6))。
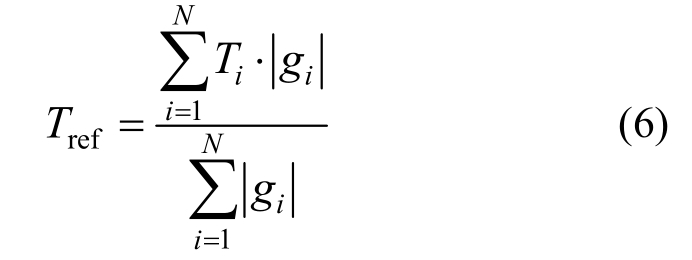
式中：Ti和gi表示第i阶自振周期及对应的振型参与系数；N为须考虑的前几阶自振周期数。
单点匹配方法虽操作简单，但该方法仅片面地强调某一周期点处的谱值匹配，无法反映反应谱形的匹配程度。
2) 单频段匹配
单频段匹配是保证在指定的一个周期段内，反应谱与目标谱有较好的匹配，匹配程度是控制反应谱均值与目标谱均值之差较小，即单频段均值匹配。如高学奎和朱晞[55]在近场地震动选波研究中控制加速度反应谱值在[0.1,Tg]平台段的均值，还另外引入了近场地震特征参数PGV/PGA，可减小计算结果的离散性且能够反应近场地震动的特性。
当频段较宽时，匹配程度常是控制频段内各个周期点对应反应谱值与目标谱值间的误差，即单频段多点匹配。误差参数及缩放系数的确定方法有很多。国外规范多是采用单频段多点匹配，单频段的范围由结构的基本周期T1确定。美国NIST2011计划中建议，抗弯框架结构可取0.2T1～3T1，框剪及剪力墙结构可取0.2T1～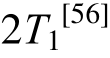
。Eurocode 8 (EC8)中规定此范围为0.2T1～2T1，Uniform Building Code 1997(UBC97)为0.2T1～1.5T1，ASCE 7-05则规定在0.2T1～1.5T1范围内，所选记录反应谱要大于设计谱。由于ASCE7-05中没有详细规定具体做法，Kalkan和Chopra[45]利用最小二乘法，采用经过缩放的反应谱与目标谱之差的平方和λ作为控制参数(式(7))，取dλ / dSF ≅ 0，得出能使得 λ最小的缩放系数SF(式(8))。
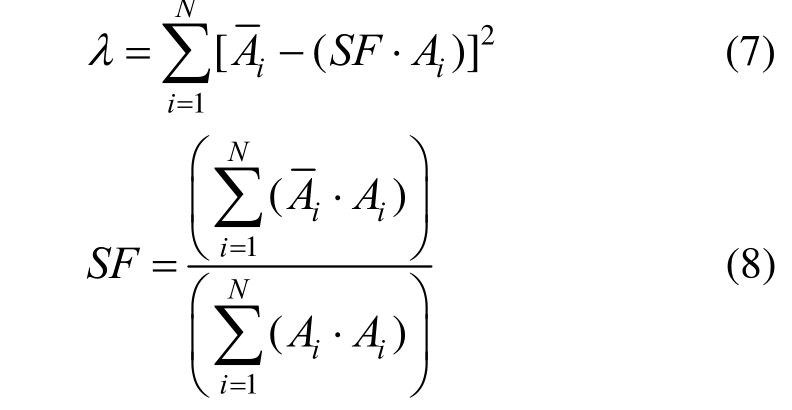
式中：N为周期点数量；Ai和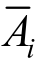
为记录在Ti周期点的加速度反应谱值和目标谱值；SF为缩放系数。
单频段起始点也可由结构的多个自振周期控制。Beyer和Bommer[57]则建议EC8中的频段范围应改为[Tm,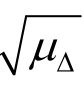
T1]，其中m为保证振型参与质量总和达90%需要考虑的最高阶振型数，μΔ为结构的位移设计值。Ambraseys等[58]通过欧洲强震数据库提出了参数Drms(式(9))。
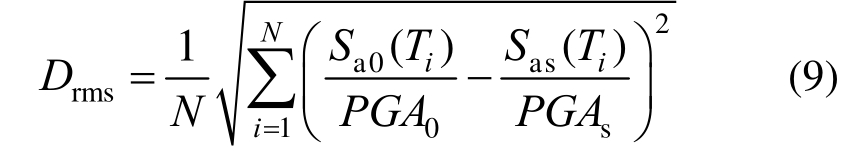
式中：Sa0(Ti )和Sas(Ti )为记录在周期点Ti处的加速度反应谱值和目标谱值；PGA0和PGAs分别为备选强震记录及确定目标谱所用强震记录的峰值加速度；N为周期点数。
Iervolino等[59]采用如下的误差参数δ(式(10))。
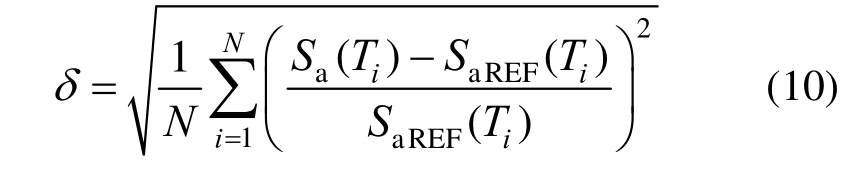
式中，Sa(Ti )和SaREF(Ti )分别是周期点Ti的加速度反应谱值和目标谱值。
式(9)和式(10)确定的误差参数，关注的是T1到TN频段的谱形匹配，或者说是关注结构前N阶振型的影响。进一步考虑，此频段的范围也可根据结构关注的频段或振型范围进行调整，当关注结构第j到第k阶振型影响时，可采用式(11)或标准化的式(12)[56]来计算误差参数。
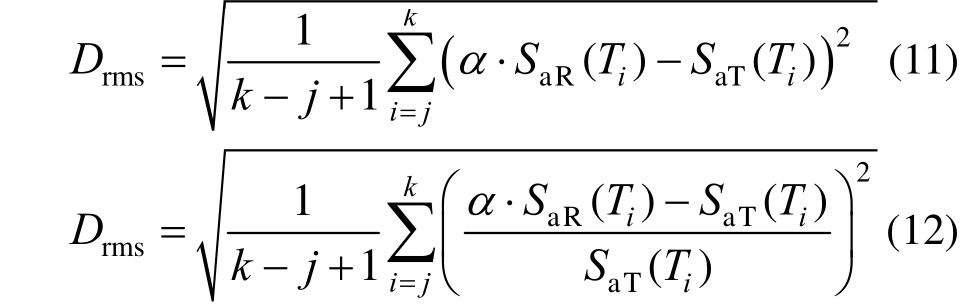
式中：SaR(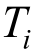
)和SaT(
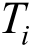)分别为反应谱与目标谱在Ti处的谱值；α为第i条波的缩放系数。
Reyes和Kalkan[60]则是在0.2T1～1.5T1范围内，令缩放后反应谱与目标谱对数值之差的欧氏范数最小，来确定缩放系数SF(如式(13))。
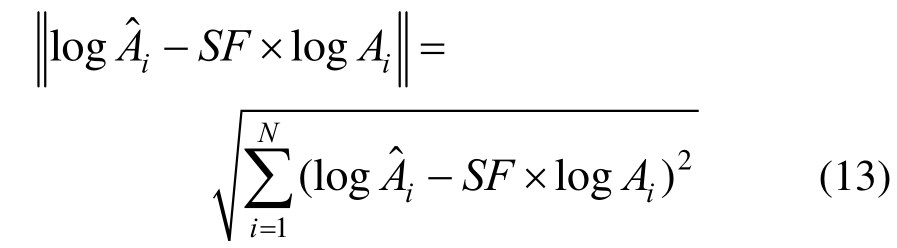
式中：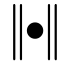
为欧氏范数；N为从0.2T1～1.5T1范围内取周期点数；
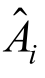和Ai分布为记录在i周期点处的加速度点目标谱值和反应谱值。
Naeim和Le[27]将遗传算法用于选波研究，以设计谱为目标谱，将选波与缩放两部分工作同时进行，从备选记录中选取误差参数(式(14))最小的一组(7条)强震记录。
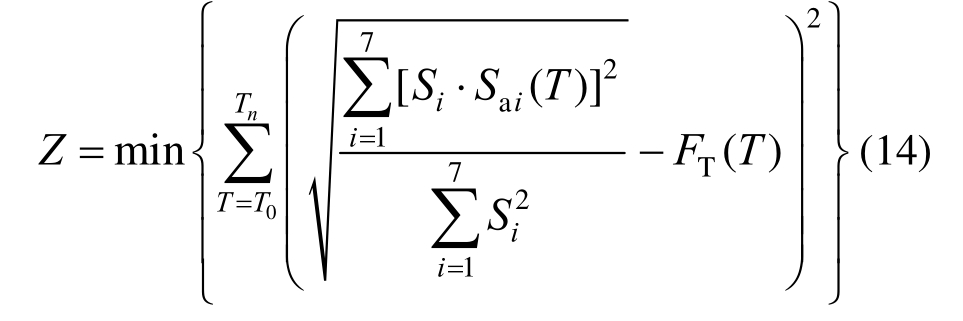
式中：Z代表误差参数；T为结构基本周期，其取值从一阶自振周期T0到n阶自振周期Tn；Si为第i条波的缩放系数；Sai(T )和FT(T)分别表示第i条波在周期T处的反应谱值及目标谱值。
我国工程人员在进行选波工作时，常采用的方法是控制结构前几阶自振周期点对应的反应谱值与设计谱值间误差之和在一定范围内(私人讨论结果)。此外，针对受高阶振型影响的高层结构，周颖和唐少将[61]将结构前几阶振型周期点对应的反应谱与设计谱值偏差，按各周期所对应的振型质量参与系数作加权平均，通过控制加权平均偏差值即可选取出满足要求的工程地震动。
单频段匹配方法的精度与设定的频段宽度有关，若频段较窄，即仅关注一阶周期点周围频段，则受高阶振型影响的结构的第二、三周期无法落入频段内，即不利于高柔结构反应评估；若频段设置较宽，则有必要在计算匹配误差时考虑各阶振型的不同贡献而匹配不同的权重。冀昆等[62]则是在[0.1 s,6.0 s]这样几乎是设计谱的全周期段的范围内，通过权重匹配目标谱，达到较好的选波效果。
3) 双频段匹配
双频段控制方法由杨溥等[63]提出以来得到较为广泛的关注和应用。它是在地震动记录数据库中直接挑选那些经调幅后其拟加速度反应谱在短周期段(如[0.1 s,Tg])和结构一阶自振周期附近([T1-ΔT1,T1+ΔT2])的反应谱均值与设计反应谱相差不超过10%的地震动记录，而不考虑震级、震中距、场地条件等地震信息限制的选波方法。其中，Tg为场地特征周期；T1为结构的一阶自振周期；ΔT1与ΔT2为周期控制范围。考虑到结构遭受地震损伤后周期会有所增大，一般ΔT2大于ΔT1，建议取ΔT1 = 0.2 s，ΔT2=0.5 s。双频段选波可保证所选波的反应谱与目标谱能达到较好的一致性，并考虑了结构基本周期的影响，从而使得时程分析结果较为准确。杨溥等[63]将该方法与基于场地、特征周期Tg以及反应谱Tg前后的面积选波方法进行了比较，证明双频段选波能够满足抗震规范对于底部剪力大于振型分解反应谱法80%的要求，且离散性远小于其他方法。
此外，考虑到双频段选波仅考虑了地震动三要素(即幅值、频谱、持时)中的加速度峰值和频谱特性，没有考虑持时和能量分布影响。肖明葵等[15]建议将地震动弹性总输入能反应作为补充指标，先按双频段选波，然后选择总输入能量反应相差10倍左右的两条波。这样能保证至少选到一条长持时或中等持时强震记录,可以考虑地震动持时对结构累积损伤的影响。刘良林等[64]以一个12层钢筋混凝土框架为例，再次证明此方法的有效性。
4) 多频段匹配
王东升等[65]在高墩桥梁的抗震设计中，在双频段匹配方法的基础上对第二频段误差指标进行了改进，引入归一化振型参与系数作为误差匹配权重系数，只是匹配范围由各个周期点扩展为各个周期点周围一定范围的多个频段，并在匹配之初依据震级、震中距、场地条件等确定备选数据库，以小样本实现了时程分析结果与设计谱结果在统计意义相符的抗震设计要求。王东升等[65]仅进行了高墩桥梁的线弹性时程分析和弹性反应谱的验证工作。张锐等[47]在王东升等[65]的方法的基础上，根据地震信息筛选出的20条强震记录的均值放大系数谱为目标谱，以美国SAC Steel Project中提出的9层和20层抗弯钢框架为Benchmark模型，以结构最大层间位移角为结构反应指标，验证了该方法在受高阶振型影响的结构非线性时程分析中的可行性，并与ASCE 7-05方法进行了对比，并且将该方法用于近断层地震动选波工作，同样得到了较为良好的效果[48]。Katsanos和Sextos[66]同样在匹配目标谱时引入了权重系数，所得结构分析结果的离散性降低，并提高了结构反应分析的可靠度。
叶献国和王德才[67]也认为，可以在多个频段内考虑反应谱与目标谱的匹配，并在Iervolino等[59]研究(式(10))的基础上，在误差参数δ计算时引入了权重系数wi，如式(15)所示：
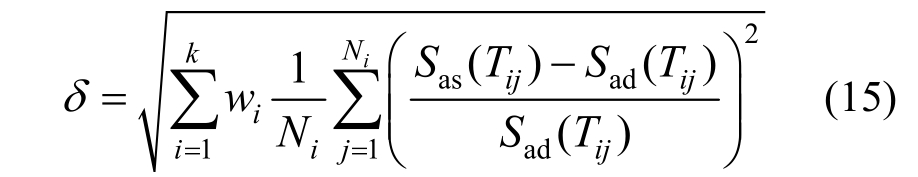
式中：k为控制周期段数；wi为第i个周期控制段的权重系数，可根据控制段的重要性确定；Ni为第i个控制周期范围内离散周期点数；Sas(Tij)和Sad(Tij)分别为第i个控制周期范围内第j个周期点Tij处实际地震动记录反应谱值和目标谱值。
上述各种匹配方法中，无论采用哪种形式的误差参数，其值越小，反应谱与设计谱的谱形越匹配，结构时程分析的结果可接受。因此，误差参数常被作为强震记录优选排序的依据。一般情况下，误差参数大小取决于地震记录数据库大小及选波数量[31]，同时也依赖于指定谱匹配的周期范围。
此外，对于两水平方向地震反应相差较大的结构(如大跨桥梁、不规则建筑等)进行选波时，目标谱和备选波反应谱都应反映两水平方向地震动的共同作用，其表达方式有多种，如采用两水平方向反应谱的几何均值、算数均值以及SRSS谱等[57]。
需要注意的是，虽然记录通过缩放能够达到减小结构反应离散性的目的，但过大的缩放会使得反应谱失真，进而使结构反应失真。因此，建议尽量选用缩放系数接近1的记录[7]。Krinitzsky和Chang[68]提出缩放系数不能大于4，对于液化场地，缩放系数更应限制在2以内[69]。而Luco和Bazzurro[70]强调了反应谱形的重要性，认为除非所选记录的谱形与目标谱存在严重差异，否则大调幅不会对结构非线性反应产生影响。Watson-Lamprey和Abrahamson[53]也认为，只要选择的地震动合适，缩放系数即使达到20，仍可获得较好的结构反应预估。目前，受记录数据量的限制，并没有对缩放系数做严格的限制，对其研究还没有形成统一的认识。
1.2.3 目标谱分布匹配法
目标谱除了匹配确定性的均值谱，还有匹配由目标均值和方差表示的具有概率含义的目标分布方法，即目标谱分布匹配法。
2011年美国国家标准协会(NIST)专门设立了项目，用于解决基于性能的结构非线性抗震分析中的强震记录选择与缩放问题，并提出在进行选波工作前必须要明确结构非线性研究的目的[56]。大多数研究只关心结构的均值反应，但随着基于性能的抗震设计理念的深入，地震危险性概率方法的逐渐完善，结构反应的概率分布也成为设计者们需要预测的反应指标。因此，很多研究在匹配目标谱均值的同时也兼顾目标谱的方差匹配。Kottke和Rathje[71]提出的半自动选波方法，即先匹配目标谱均值，再缩放强震记录以实现方差的匹配。但该方法不适于选波数量较大的情况，而且所选波必须经过缩放。Baker等[72]的研究则突破了这些限制，运用蒙特卡洛算法，依据目标谱(条件均值谱)的均值和方差，模拟出多条符合这些统计特征的反应谱作为目标谱组，打破了一条目标均值谱的局限。模拟的目标谱组的反应谱数量越多，匹配越准确。此时，评判所选波反应谱与目标谱的匹配程度，除了考虑均值外，还增加了方差的比较，并按照需要分配一定权重(由式(16)中的w权重系数体现)。误差参数SSSE如下公式：
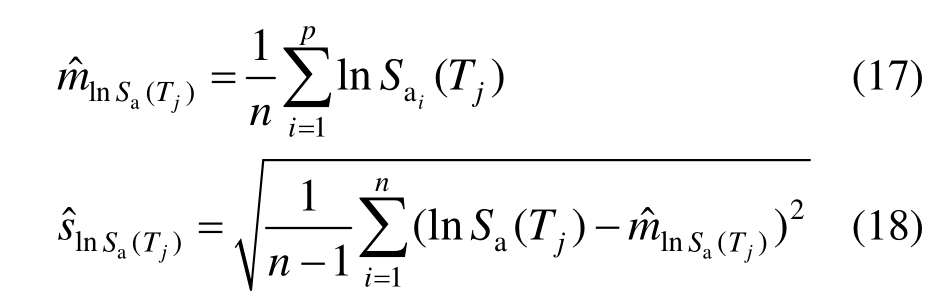
式中：n表示每组记录数；Sa(Tj)为备选记录在周期点Tj对应的强震动记录谱值；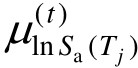
和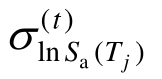
为周期点Tj对应的目标谱均值和方差。
Wang[73]基于CMS建立多个目标谱组成的目标谱组时，引入了误差指标Rt(式(19)～式(21))，其能够同时反映均值和方差的匹配程度，即通过误差指标选取最优的目标谱组。同样在强震记录选择时也同时考虑均值和方差的匹配，并且当目标谱组的误差较小时，选波的误差也能得到较好地控制。
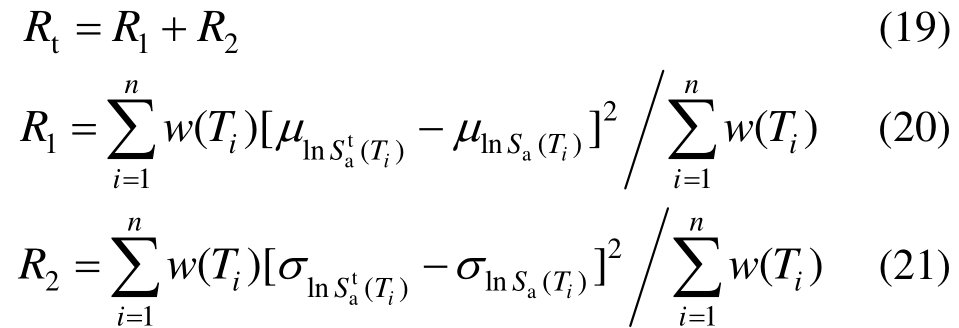
式中：R1和R2分别代表均值和方差的加权误差；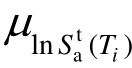
和
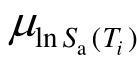分别表示Ti处目标谱和反应谱的对数均值；
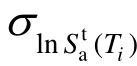和
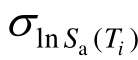分别表示Ti处目标谱和反应谱的对数方差；w(Ti )表示Ti的权重。
目前已有多个基于CMS建立的选波软件，如DGML[35]、OPENSIGNAL[36]和QuakeManager[37]等，均可方便地实现均值和方差的匹配，而且其目标谱设定也非常灵活，可以是设计反应谱也可以是用户自定义的反应谱。
鉴于遗传算法在大数据处理中的优势，常有学者将遗传原理用于反应谱分布的匹配，将选波与缩放过程同时进行。如Alimoradi等[74]开发的软件Genetic Search for Design Earthquakes。有时为达到更为理想的缩放效果，还会采用一些优化方法。Baker等[72]采用了贪婪算法使所选记录反应谱与目标谱更为吻合。叶献国和王德才[67]通过式(15)选出强震记录后，利用遗传算法确定参数，再利用贪婪算法对遗传算法确定的个体编码串进行修复，可限制反应谱与目标谱间误差在很小的范围内。
与仅匹配目标谱均值相比较，考虑目标谱方差不会影响到结构反应均值的估计，但会影响结构反应的方差及概率分布[66]。当结构反应非线性程度越大时，结构反应的离散性会越强。在选波中考虑这种概率计算需求，就显得非常必要。
多年来，国内外地震学者也一直在努力寻求与结构地震反应紧密相关的地震动强度指标。选用合理的地震动强度指标进行地震波标准化，是降低结构反应离散性的有效途径。Luco和Cornell[43]提出地震强度指标的选择既要考虑其充分性，也要考虑其有效性，充分性要求的目的是减少或消除动力分析对所选地震强度指标未能反映的其他地震动特性的依赖，而有效性要求的目的是降低地震波不同产生结构反应的离散性。PGA是最早采用的地震强度指标，而后发展出Housner谱强度[75]、Arias强度[76]等以地震动峰值和地震动谱峰值为依据衍生的复合强度指标。叶献国[77]针对20世纪七八十年代提出的8种典型的地震强度指标，探讨了结构地震破损与地震强度指标的相关性。智利学者Riddell等[78]总结了该时期发展的14种地震强度指标与单自由度体系的滞回耗能之间的相关性，认为无法采用单一地震强度指标在三个反应谱敏感区与结构反应之间均具有同样良好的相关性。
进入20世纪后，各种复合强度指标相继提出。发展至今，地震动强度指标已有四五十种，旨在体现地震动幅值、频谱和持时三要素的同时，更关注与结构反应的相关性。陈波[40]总结了50种地震动强度指标，按与PGA、PGV、PGD的相关性归为三类，认为与PGA有关的地震强度指标与短周期结构反应相关性最好；与PGV、PGD有关的地震强度指标与中长周期结构反应的相关性最好，这一结论与Riddell以及叶列平等[79]的研究基本一致。李英民等[80]分析了结构弹性和弹塑性反应(加速度、速度和位移)与6种幅值定义(峰值加速度(PGA)、峰值速度(PGV)、有效峰值加速度(EPA)、有效峰值速度(EPV)、Arias强度(IA)和谱强度(SI，阻尼比取0.02))间的相关系数谱，并认为除了PGV外，其他五种幅值均与结构反应具有良好的相关性。然而韩建平和周伟[81]基于汶川地震记录的研究表明，速度谱强度、Housner谱烈度与SDOF体系最大响应的相关性较好。卢啸等[82]对超高层结构反应的研究也认为，PGV与超高层结构的层间位移角响应具有较好的相关性。苏宁粉等[83]以普通框架、规则和不规则超高层结构的最大层间位移角为工程需求参数，对比分析了9种地震强度指标，认为反应谱参数的有效性均优于PGA；对超高层结构，PGV的有效性最好；对周颖等[84]提出的考虑高阶振型影响的地震动强度参数，当考虑振型数越多时，该参数有效性越高。
Kurama和Farrow[85]以7种缩放方法(即PGA、EPA、A95、EPV、MIV、Sa(T1)、Sa(T1→Tμ))，对比分析了单自由度和多自由度体系在不同场地、震中距、屈服强度、结构周期、滞回规则条件下，结构峰值位移反应的离散性。其中最大增值速度MIV，是指两个连续零加速度周期点之间的加速度时程曲线包含的面积的最大值。研究表明与PGV相关的MIV参数缩放方法，尤其对于近场地震动、软土场地、结构非线性程度较高等特殊情况下，优越性要明显高于以反应谱强度为依据的缩放方法。O’Donnel等[86]通过4种小缩尺比的钢框架结构720次的振动台试验，对比包括MIV在内的4种选波方法(即ASCE7-10、Sa(T1)、MIV、MPS)，以试验再次证明了MIV方法的优越性。认为MIV方法之所以优于其它选波方法，主要源于其不受结构特性的影响，当结构进入非线性阶段时基本周期会延长，而其它选波方法均依赖于难以准确估计的结构周期等特性。试验研究还表明“以Sa(T1)来缩放地震波能够减小结构反应的离散性”的结论在阻尼比较小(如5%)时是不成立的，只有当阻尼比较大(如10%～20%)时，这种优势才能显现出来，这与以往的经典结论有些不同。可见，选波研究很有必要采用试验研究的方式。限于选波研究试验量大，试件损耗大等客观条件限制，目前的选波研究多基于数值模拟结果。而O’Donnel等[86]则是在易于出现塑性铰的梁柱节点处设计反映结构损伤的摩擦阻尼连接件，能够使试件在非线性变形后具有自复位能力，从而使得以试验方法进行选波研究成为可能。
针对受高阶振型影响的高层结构，Tan等[87]提出了地震动强度指标S90(式(22))，可分权重考虑对结构反应起主要作用的前几阶振型的贡献。
式中，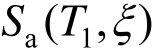
至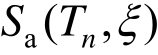
表示T1到Tn周期点加速度反应谱值(阻尼比为
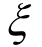)；α ,β,… ,θ表示各周期点谱值的权重。Luco和Cornell[43]提出了6个体现结构信息的强度指标IMS，其中4个涉及弹性、非弹性、等效和有效的一阶模态振动特性，其余两个考虑了一阶和二阶模态的共同作用效应，并以美国SAC Steel Project提出的3层、9层和20层抗弯钢框架结构[88]的非线性动力分析结果进行参数线性回归分析，以量化强度研究指标的有效性。Tothong和Luco[44]在抗震概率需求分析(PSDA)中提出了选波所用的地震动强度指标，可不必通过震级、震中距及ε参数进行初选，并指出对于近场地震动以及受高阶振型影响显著的结构，采用弹性加速度反应谱，甚至非弹性位移谱都不合适，而应采用综合性的地震动强度指标。
上述研究往往依据单个地震动强度指标，但毕竟地震动具有振幅、频率、持时三个要素，仅以某一个地震动强度指标来表征结构反应，不免过于片面。谢礼立和翟长海[89]提出一种基于潜在破坏势的综合评价方法。地震动潜在破坏势是综合考虑地震动本身、结构弹性及非弹性反应、破坏准则等因素经过适当的推导得出的，能全面反映地震动三要素及结构动力特性。该方法旨在选取能使结构的地震反应或结构的地震性态趋于最危险或最不利状态的地震动。曲哲等[90]将该法与基于地震信息和设计谱两种方法进行了比较。Bradley[91]认为条件均值谱CMS方法，仅能反映加速度反应谱特征，而对地震动特性中的持时和能量等特性考虑不够。Bradley[91]基于地震危险性概率分析PSHA，以强震记录的经验分布与理论分布间的拟合优度为误差参数，提出了一种综合性的选波方法(GCIM，generalized conditional intensity measure)，该方法可用于以任意种类及数量的地震动强度指标为评价指标的选波工作。
除了以结构位移反应为地震反应参数外，若以结构损伤、刚度退化以及滞回耗能为研究目的，选择与持时和地震动能量累积有关的地震动强度指标(如 70%能量持时、Ie、Arias强度、Housner强度、Riddell指标、Park-Ang指标)则更为合理。Angelo等[92]通过三种不同填充墙形式的框架结构地震反应发现，Housner强度与结构反应的相关性优于PGA、PGV、Sa、Sd等地震动强度指标。Marasco和Cimellaro[36]将反应谱划分成很小的频段，通过傅里叶变化求出每个频段的幅值，再平方和求能量项，以此能量项作为评判指标，对结构反应实现了较为准确的评估。
目前常用的以地震动强度指标为评价指标选波的研究，与目标谱选波法类似，仍多以地震信息(震级、震中距、场地等)为初选条件，再辅以一个或多个地震动强度指标为评价指标。地震动强度指标的选择主要依据结构反应参数指标及评估结构反应的目的来确定。强震记录的缩放多依据所选强震记录的地震动强度指标与目标参数相等为原则进行，也可与之前介绍的缩放方法综合使用。如Marasco和Cimellario[36]首先保证选波反应谱在周期点Tref(式(6))处与目标谱相等为原则确定缩放系数，再要求0.2Tref～2Tref范围内Housner谱强度与目标谱相等进一步修正缩放系数。其实基于目标谱选波法与基于地震动强度指标选波法往往是相辅相成、互相补充的：当所用地震动强度指标仅源于弹性反应(或相关)谱时，显然谱匹配方法包含了地震动强度指标的全部内容；但当地震动强度指标建立融入了更多因素，如地震动持时、结构损伤和非弹性反应等，则基于地震动强度指标选波会与谱匹配方法有所差别，但若目标谱建立也包括或逐步考虑这些因素时，二者又会趋于一致。
选取多少条记录来进行结构时程分析，也就是样本容量的确定，是强震记录选取研究中另一个主要考虑的问题。样本容量的确定要考虑诸多因素：预测结构反应的目标(均值或分布)及精度、结构倒塌概率、结构非线性程度等[93]。理想的样本容量，应该是能使结构分析准确性与计算成本之间达到一种相对的平衡，尤其对于复杂结构的时程分析，样本容量对计算成本的消耗影响很大。
Shome等[5]早在1998年就研究发现，以结构基本周期T1处反应谱值与目标谱相等为原则对强震记录进行缩放，对比于未经缩放的强震记录，产生结构反应的离散性更小，所需的强震记录数量更少，此后相关研究相继展开。Carballo[94]也发现，对结构反应均值进行估计时，采用匹配目标谱的方法，可以减少所需地震波数量。Stewart等[7]研究认为，如果采用3条地震波，则需调整反应谱的波峰波谷使其与设计谱实现较好的匹配，这样可使得结构反应不会受限于某一条地震波。Bommer和Acevedo[1]在2004年的研究中指出，7条是比较理想的选波数量，结构反应可取用7条结果的平均值，但是也不必拘泥于7条的结论；2008年，在其与Hancock等[93]的共同研究中，更为系统全面地分析了结构非线性动力分析所需的地震波数量，认为其与结构非线性反应可靠度以及所需估计的结构反应参数相关。如对结构反应均值估计的误差满足5%所需地震波数量就要是误差满足10%所需数量的4倍。相比于线性缩放，采用谱匹配小波调整方法进行缩放，可使结构反应离散性降低，从而所需地震波数量减少。文献[93]中还分析了结构反应估计的偏差，认为偏差主要来自于选择和匹配方法的不同，且与结构反应指标的选取有关，如结构峰值反应的估计所需样本容量就少于对结构损伤及能量消耗的估计。缩放系数对偏差没有影响，甚至可以取到10。
除伊朗抗震规范规定可用2条真实记录，国际标准委员会制定的海港工程抗震规范ISO/DIS 19901-2[95]要求至少4条强震记录外，多数国家的抗震设计规范，如EC8，UBC997，IBC2000/2006，CBC2007，ASCE/SEI 7 (ASCE，2005，2010)以及我国抗震规范，均规定至少选用3条记录，若少于7条，取用时程分析所得结构反应的最大值，若大于等于7条，则用时程分析所得结构反应的平均值。Reyes和Kalkan[60]将与结构反应真值对比的“准确性、有效性、一致性”作为评判记录样本容量的标准，将480组强震记录，按照从3～10不等的样本容量分组，对16种单自由度体系(4种基本周期、4种屈服强度系数)进行了时程分析的统计工作。研究表明，ASCE 7-05中对于“小于7条要取最大值”的规定过于保守；样本容量若小于7条，计算准确度难以保证；大于7条(如取7到10条)时，计算精度并未随着样本容量增大有明显提高。因此，建议7条为最合理的样本容量。但是该研究仅是基于单自由度体系，且记录缩放是基于弹性反应谱，对于多自由度结构体系非线性反应分析，该研究还有局限。
上述样本容量的确定主要是对结构反应均值的估计，若以结构反应概率分布为评估目标，则需更大的样本容量。Catalán等[54]认为符合正态及对数正态分布的结构反应可采用30条记录；若要求结构倒塌评估准确率达到90%，则需60条地震波。Wang[73]也认为30或60条地震波可以实现稳定性较好的结构反应方差估计。陈波[40]基于可靠度理论给出在不同置信水平和误差范围内建议取用的样本容量，并对比了几类强震记录缩放方法需取用的样本容量，发现选择合理的地震动缩放方法，对于缩小样本容量，降低结构反应的离散性有着积极的作用，这也正与Hancock等[93]的研究结论相吻合。
目前，国内外已建立多个数据量庞大的真实记录数据库，利用真实记录进行结构时程分析已成为必然趋势。选波研究中的两大主要问题——评判指标和样本容量会受到诸多因素的影响，如：结构分析的目标(结构反应均值或分布)、结构反应性能指标(如结构反应峰值、结构损伤耗能等)以及结构自身特点(如受高阶振型影响显著、不规则、双向刚度差异大等)等等。目前研究的选波方法，仍依据规则结构的均值反应居多，并常以结构的位移峰值反应作为参数指标，其它影响因素的研究仍不成熟。
地震动强度指标现已总结出四五十种，与之相关的选波的有效性认知还不统一。目前最为主流的是目标谱选波法。震级、震中距、场地等地震信息常作为第一评判指标，目标谱或其它地震动强度指标作为第二评判指标。目标谱除了应用最为广泛的设计加速度反应谱外，已发展出多种特定含义的目标谱。结构反应估计的准确性与反应谱与目标谱的谱形的匹配程度关系密切。条件均值谱(CMS)正因其能够实现良好的谱形匹配，并遵从一次地震事件的概率分布特点且考虑了不同周期点间的相关关系，使CMS能够实现对结构反应的高精度估计，成为目前最受关注的目标谱。将CMS与我国规范相结合用于选波工作，仍有多处细节需进一步深入研究。
随着基于性能的抗震设计理念的深入，地震危险性概率方法的逐渐完善，结构反应已不再局限于均值的估计，结构反应的概率分布也将成为设计者们需要预测的反应指标。这也将使确定反应谱与目标谱匹配程度的评价，由单一的谱均值间的误差估计，发展到均值加方差的综合评价误差指标。同时，评估结构反应概率分布时，样本容量也需比仅评估均值反应的数量大很多。目前，国内以结构反应概率分布为评估目标的选波研究还很有限。
[1] Bommer J J,Acevedo A.The use of real earthquake accelerograms as input to dynamic analysis [J].Journal of Earthquake Engineering,2004,8(1): 43―91.
[2] 李英民,赖明,白绍良.工程结构的地震动输入问题[J].工程力学,2003,20(増刊): 76―87.Li Yingmin,Lai Ming,Bai Shaoliang.Selection of earthquake records as input to dynamic analysis of structures [J].Engineering Mechanics,2003,20(Suppl):76―87.(in Chinese)
[3] Nau J M,Hall W J.Scaling methods for earthquake response spectra [J].Structure Engineering,1984,110(7): 1533―1548.
[4] 王亚勇.结构抗震设计时程分析法中地震波的选择[J].工程抗震,1988,12(4): 15―22.Wang Yayong.Selection of earthquake ground motion for structural time-history analysis [J].Earthquake Resistant Engineering,1988,12(4): 15―22.(in Chinese)
[5] Shome N,Cornell C A,Bazzurro P.et al.Earthquakes,records and nonlinear responses [J].Earthquake Spectra,1998,14(3): 469―500.
[6] Iervolino I,Cornell C A.Record selection for nonlinear seismic analysis of structures [J].Earthquake Spectra,2005,21(7): 685―713.
[7] Stewart J P,Chiou S J,Bray J D,et al.Ground motion evaluation procedures for performance-based design [R].Berkeley,U.S.: Pacific Earthquake Engineering Research Center,University of California,2001.
[8] Bommer J J,Scott S G,Sarma S K.Hazard-consistent earthquake scenarios [J].Soil Dynamics & Earthquake Engineering,2000,19 (4): 219―231.
[9] Bommer J J,Martínez-Pereira A.The effective duration of earthquake strong motion [J].Journal of Earthquake Engineering,1999,3(2): 127―172.
[10] Bommer J J,Martínez-Pereira A.Strong-motion parameters: definition,usefulness and predictability [C].Auckland,New Zealand: Proceedings of the Twelfth World Conference on Earthquake Engineering,2000:206.
[11] Bommer J J,Ruggeri C.The specification of acceleration time-histories in seismic design codes [J].European Earthquake Engineering,2002,16(1): 3―17.
[12] ASCE.Seismic analysis of safety-related nuclear structures and commentary.ASCE standardno.004-98[S].Reston,Virginia: American Society of Civil Engineers,2000.
[13] EPPO.Hellenic antiseismic code (EAK2000) [S].Athens,Greece: Ministry of Public Works,2000.
[14] Hancock J,Bommer J J.A state of knowledge review of the influence of strong motion duration on structural damage [J].Earthquake Spectra,2006,22(3): 827―845.
[15] 肖明葵,刘纲,白绍良.基于能量反应的地震动输入选择方法讨论[J].世界地震工程,2006,22(3): 90―96.Xiao Mingkui,Liu Gang,Bai Shaoliang.Some methods of selecting earthquake wave based on energy responses[J].World Information on Earthquake Engineering,2006,22(3): 90―96.(in Chinese)
[16] 王亚勇,刘小弟,程民宪.建筑结构时程分析法输入地震波的研究[J].建筑结构学报,1991,12(2): 51―60.Wang Yayong,Liu Xiaodi,Cheng Minxian.Study on the input of earthquake ground motion for time-history analysis of structures [J].Journal of Building Structures,1991,12 (2): 51―60.(in Chinese)
[17] Baker J W,Cornell C A.A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon [J].Earthquake Engineering & Structural Dynamics,2005,34(10): 1193―1217.
[18] Goulet C A,Haselton C B,Mitrani-Reiser Beck J L,et al.Evaluation of the seismic performance of a code-conforming reinforced concrete frame building from seismic hazard to collapse safety and economic losses [J].Earthquake Engineering and Structural Dynamics,2007,36(13): 1973―1997.
[19] CEN.Eurocode8: Design of structures for earthquake resistance.Part1: general rules,seismic actions and rules for buildings.Draft No.5,Document CEN/TC250/SC8/N317 [S]. Brussels,Belgium: European Committee for Standardization,2002.
[20] ASCE.Minimum design loads for buildings and other structures.ASCE standard no.007-05 [S].Reston,Virginia: American Society of Civil Engineers,2006.
[21] FEMA.NEHRP recommended provisions for seismic regulations for new buildings and other structures,2000 edition,Part1 FEMA368 [S].Washington,DC: Building Seismic Safety Council for the Federal Emergency Management Agency,2001.
[22] NZS1170.5.Structural design actions,Part5: earthquake actions—New Zealand code and supplement [S].Wellington,New Zealand: Standards New Zealand,2004.
[23] Ordinanza del Presidente del Consiglio dei Ministri(OPCM) n.3274.Norme tecniche per il progetto,la valutazione e l’adeguamento sismico degli edifici [S].Italy: Gazzetta Ufficiale della Repubblica Italiana,2003.
[24] Katsanos E I,Sextos A G,Manolis G D.Selection of earthquake ground motion records: A state-of-the-art review from a structural engineering perspective [J].Soil Dynamics and Earthquake Engineering,2010,30(4):157―169.
[25] 李琳,温瑞智,周宝峰,等.基于条件均值反应谱的特大地震强震记录的选取及调整方法[J].地震学报,2013,35(3): 380―389.Li Lin,Wen Ruizhi,Zhou Baofeng,et al.Selection and scaling of ground motion records for great scenario earthquakes based on the conditional mean spectrum [J].Acta Seismologica Sinica,2013,35(3): 380―389.(in Chinese)
[26] 崔江余,杜修力.重大工程设定地震动确定[J].世界地震工程,2000,16(4): 25―28.Cui Jiangyu,Du Xiuli.Determination of design ground motion for critical engineering project [J].World Information on Earthquake Engineering,2000,16(4):25―28.(in Chinese)
[27] Naeim F,Le M.On the use of design spectrum compatible time histories [J].Earthquake Spectra.,1995,11(1): 111―127.
[28] Reiter L.Earthquake hazard analysis: issues and insights[M].New York,U.S: Columbia University Press,1990.
[29] Malhotra P K.Seismic response spectra for probabilistic analysis of nonlinear systems [J].Journal of Structural Engineering,2011,137(11): 1272―1281.
[30] Baker J W,Cornell C A.Spectral shape,epsilon and record selection [J].Earthquake Engineering & Structural Dynamics,2006,35(9): 1077―1095.
[31] Baker J W.Conditional mean spectrum: tool for ground-motion selection [J].Journal of Structural Engineering,2011,137(3): 322―331.
[32] Baker J W,Jayaram N.Correlation of spectral acceleration values from NGA ground motion models [J].Earthquake Spectra,2008,24(1): 299―317.
[33] Ghafory-Ashtiany M,Azarbakht A,Mousavi M.State of the art: structure-specific strong ground motion selection by emphasizing on spectral shape indicators [C].Lisbon,Portugal: Proceedings of the 15th World Conference on Earthquake Engineering,2012.
[34] Haselton C B.Evaluation of ground motion selection and modification methods: predicting median interstory drift response of buildings [R].Berkeley,U.S.: Pacific Earthquake Engineering Research Center College of Engineering,2009.
[35] Wang G,Youngs R R,Power M,Li Z.Design ground motion library: an interactive tool for selecting earthquake Ground Motions [J]. Earthquake Spectra,2015,31(2): 617―635.
[36] Marasco S,Cimellaro G P.A new energetic based ground motion selection and modification algorithm [C].Santiago,Chile: Proceedings of the 16th World Conference on Earthquake Engineering,2017.
[37] Mahmoud M H.Quake Manager: A software framework for ground motion record management,selection,analysis and modification [C].Beijing,China:Proceedings of the 14th World Conference on Earthquake Engineering,2008.
[38] Shantz T.Selection and scaling of earthquake records for nonlinear dynamic analysis of first mode dominate bridge structures [C].San Francisco.Oakland,California: Earthquake Engineering Research Institute,Proceedings of the 8th National Conference on Earthquake Engineering,2006.
[39] Mousavi M,Ghafory-Ashtiany M,Azarbakht A.A new indicator of elastic spectral shape for the reliable selection of ground motion records [J].Earthquake Engineering & Structural Dynamics,2011,40(2): 1403―1416.
[40] 陈波.结构非线性动力分析中地震动记录的选择和调整方法研究[D].哈尔滨: 中国地震局地球物理研究所,2013.Chen Bo.Ground motion selection and modification methods for performing nonlinear dynamic analysis of buildings [D].Harbin: Institute of Geophysics,China Earthquake Administration,2013.(in Chinese)
[41] 韩建平,魏世龙,张鑫.地震动记录选择与调整对RC框架结构地震响应影响研究[J].土木工程学报,2016,49(增刊): 43―48.Han Jianping,Wei Shilong,Zhang Xin.Investigation on selection and modification of ground motion records for the influence of seismic responses of RC frames [J].China Civil Engineering Journal,2016,49(Suppl): 43―48.(in Chinese)
[42] Smerzini C,Galasso C,Iervolino I,et al.Ground motion record selection based on broadband spectral compatibility [J].Earthquake Spectra,2014,30(4):1427―1448.
[43] Luco N,Cornell C A.Structure-specific scalar intensity measures for near-source and ordinary earthquake motions [J].Earthquake Spectra,2007,23 (2): 357―392.
[44] Tothong P,Luco N.Probabilistic seismic demand analysis using advanced ground motion intensity measures [J].Earthquake Engineering & Structural Dynamics,2007,36(13): 1837―1860.
[45] Kalkan E,Chopra A K.Practical guidelines to select and scale earthquake records for nonlinear response history analysis of structures [R].Berkeley,U.S.: Earthquake Engineering Research Institute,2010.
[46] Youngs R R,Power M S,Chin C C.Design ground library [C].San Francisco,CA: Proceedings of the 8th National Conference on Earthqake Engineering,2006.
[47] 张锐,成虎,吴浩,等.时程分析考虑高阶振型影响的多频段地震波选择方法研究[J].工程力学,2018,35(6): 162―172.Zhang Rui,Cheng Hu,Wu Hao,et al.Multi-band matching method for selection of ground motions in time-history analysis considering higher modes effects[J].Engineering Mechanics,2018,35(6): 162―172.(in Chinese)
[48] 张锐,成虎,吴浩,等.考虑高阶振型影响选波方法对近断层地震动输入适用性研究[J].沈阳建筑大学学报,2018,34(3): 439―448.Zhang Rui,Cheng Hu,Wu Hao,et al.Applicability of records selection method considering higher modes effects for near-fault ground motions [J].Journal of Shenyang Jianzhu University,2018,34(3): 439―448.(in Chinese)
[49] 王德才,华贝,叶献国.匹配目标谱模拟地震动记录时频特征对比分析 [J].工程抗震与加固改造,2016,38(6): 122―128,135.Wang Decai,Hua Bei,Ye Xianguo.Comparison of time-frequency characteristics of spectrum-compatible ground motion records [J].Earthquake Resistant Engineering and Retrofitting,2016,38(6): 122―128,135.(in Chinese)
[50] Martinez-Rueda J E.Scaling procedure for natural accelerograms based on a system of spectrum intensity scales [J].Earthquake Spectra,1998,14(1): 135―152.
[51] Kappos A J,Kyriakakis P.A re-evaluation of scaling techniques for natural records [J].Soil Dynamics and Earthquake Engineering,2000,20(1/2/34): 111―123
[52] Shome N,Cornell C A.Probabilistic seismic demand analysis of nonlinear structures [R].Stanford,U.S:Stanford University,1999.
[53] Watson-Lamprey J A,Abrahamson N A.Selection of ground motion time series and limits on scaling [J].Soil Dynamics and Earthquake Engineering,2006,26(5):477―482.
[54] Catalán Ariel,Amadeo Benavent-Climent,Xavier Cahís.Selection and scaling of earthquake records in assessment of structures in low-to-moderate seismicity zones [J].Soil Dynamics and Earthquake Engineering,2010,30(1/2): 40―49.
[55] 高学奎,朱晞.近场地震动输入问题的研究[J].华北科技学院学报,2005,2(3): 80―83.Gao Xuekui,Zhu Xi.Study on selecting inputting waves for seismic response analysis excited by near-fault earthquakes [J].Journal of North China Institute of Science & Technology,2005,2(3): 80―83.(in Chinese)
[56] Haselton C B ,Whittaker A S,Hortacsu A,et al.Selecting and scaling earthquake ground motions for performing response-history analyses [C].Lisboa,Portugal : Proceedings of the 15th World Conference on Earthquake Engineering,2012.
[57] Beyer K,Bommer J J.Selection and scaling of real accelerograms for bi-directional loading: a review of current practice and code provisions [J].Journal of Earthquake Engineering,2007,11(Suppl): 13―45.
[58] Ambraseys N N,Douglas J,Rinaldis D,et al.Dissemination of European strong-motion data,vol.2,CD-ROM collection [C].Engineering and Physical Sciences Research Council,UK,2004.
[59] Iervolino I,Galasso C,Cosenza E.REXEL: computer aided record selection for code-based seismic structural analysis [J].Bulletin of Earthquake Engineering,2010,8(2): 339―362.
[60] Reyes J C,Kalkan E.Required number of records for ASCE/SEI 7 ground motion scaling procedure [R].U.S.:Geological Survey Open-File Report,2011.
[61] 周颖,唐少将.考虑高阶振型的工程地震动选取方法[J].地震工程与工程振动,2014,34(增刊): 69―75.Zhou Ying,Tang Shaojiang.A method of engineering ground motion selection considering higher modes [J].Earthquake Engineering and Engineering Dynamics,2014,34(Suppl): 69―75.(in Chinese)
[62] 冀昆,温瑞智,任叶飞.适用于我国抗震设计规范的天然强震记录选取[J].建筑结构学报,2017,38(12):57―67.Ji Kun,Wen Ruizhi,Ren Yefei.Ground motion recordings selection for seismic design code [J].Journal of Building Structures,2017,38 (12): 57―67.(in Chinese)
[63] 杨溥,李英民,赖明.结构时程分析法输入地震波的选择控制指标[J].土木工程学报,2000,33(6): 33―37.Yang Pu,Li Yingmin,Lai Ming.A new method for selecting inputting waves for time-history analysis [J].China Civil Engineering Journal,2000,33(6): 33―37.(in Chinese)
[64] 刘良林,王全凤,沈章春,等.基于弹性总输入能的地震波选择方法[J].华侨大学学报,2009,30(2): 192―194.Liu Lianglin,Wang Quanfeng,Shen Zhangchun,et al.The selection method of seismic wave based on elastic total input energy [J].Journal of Huaqiao University(Natural Science) ,2009,30(2): 192―194.(in Chinese)
[65] 王东升,岳茂光,李晓莉,等.高墩桥梁抗震时程分析输入地震波选择[J].土木工程学报,2013,46(增刊):209―213 Wang Dongsheng,Yue Maoguang,Li Xiaoli,et al.Selections of real ground motions in seismic history analysis for bridges with high columns [J].China Civil Engineering Journal,2013,46 (Suppl): 209―213.(in Chinese)
[66] Katsanos E I,Sextos A G.Structure-specific selection of earthquake ground motions for the reliable design and assessment of structures [J].Bulletin of Earthquake Engineering,2018,16(2): 583―611.
[67] 叶献国,王德才.结构动力分析实际地震动输入的选择与能量评价[J].中国科学: 科学技术,2011,41(11):1430―1438.Ye Xianguo,Wang Dongcai.Selection of real earthquake accelerograms for structural dynamic analysis and energy evaluation [J].Science China: Technology Science,2011,54: 2878―2885.(in Chinese)
[68] Krinitzsky E L,Chang F K.Specifying peak motions for design earthquakes [R]. Vicksburg,Mississippi:State-of-the-Art for Assessing Earthquake Hazards in the United States.US Army Corps of Engineers,1977.
[69] Vanmarcke E H.Representation of earthquake ground motion: Scaled accelerograms and equivalent response spectra [R].Vicksburg,Mississippi: State-of-the-Art for Assessing Earthquake Hazards in the United States.US Army Corps of Engineers,1979.
[70] Luco N,Bazzurro P.Does amplitude scaling of ground motion records result in biased nonlinear structural drift responses? [J].Earthquake Engineering and Structural Dynamics,2007,36(13): 1813―1835.
[71] Kottke A R,Rathje E M.A semi-automated procedure for selecting and scaling recorded earthquake motions for dynamic analysis [J].Earthquake Spectra,2008,24(4):911―932.
[72] Baker J W,Lee C.An improved algorithm for selecting ground motions to match a conditional spectrum [J].Journal of Earthquake Engineering,2018,22(4): 708―723.
[73] Wang Gang.A ground motion selection and modification method capturing response spectrum characteristics and variability of scenario earthquakes [J].Soil Dynamics and Earthquake Engineering.2011,31(4): 611―625.
[74] Alimoradi A,Pezeshk S,Naeim F,et al.Fuzzy pattern classification of strong ground motion records [J].Journal of Earthquake Engineering,2005,9(3): 307―332.
[75] Housner G.W.Spectrum intensities of strong motion earthquakes [C].California,U.S.: Proceedings of the Symposium on Earthquake and Blast Effects on Structures,EERI,1952.
[76] Arias A.A measure of earthquake intensity,inseismic design for nuclear power plants [R].Cambridge,Massachusetts: MIT Press,1970.
[77] 叶献国.地震强度指标定义的客观评价[J].合肥工业大学学报:自然科学版,1998,21(6): 7―11.Ye Xianguo.Objective evaluation on definition of earthquake intensity index [J].Journal of Heffei University of Technology,1998,21(6): 7―11.(in Chinese)
[78] Riddell R,Garcia E J.Hysteretic energy spectrum and damage control [J] .Earthquake Engineering and Structure Dynamics,2001,30(12): 1791―1816.
[79] 叶列平,马千里,缪志伟.结构抗震分析用地震动强度指标的研究[J].地震工程与工程振动,2009,29(4):9―22.Ye Lieping,Ma Qianli,Miao Zhiwei.Study on earthquake intensities for seismic analysis of structures[J].Journal of Earthquake Engineering and Engineering Vibration,2009,29(4): 9―22.(in Chinese)
[80] 李英民,丁文龙,黄宗明.地震动幅值特性参数的工程适用性研究[J].重庆建筑大学学报,2001,23(6):16―21.Li Yingmin,Ding Wenlong,Huang Zongming.Study on the suitability of amplitude definitions of strong ground motions for engineering purpose [J].Journal of Chongqing Jianzhu University,2001,23(6): 16―21.(in Chinese)
[81] 韩建平,周伟.基于汶川地震记录的地震动强度指标与SDOF体系响应的相关性[J].土木工程学报,2010,43(增刊): 10―15.Han Jianping,Zhou Wei.Correlation between ground motion intensity indices and SDOF system responses based on the data of Wenchuan earthquake [J].China Civil Engineering Journal,2010,43(Suppl): 10―15.(in Chinese)
[82] 卢啸,陆新征,叶列平.超高层建筑地震动强度指标探讨[J].土木工程学报,2012,45(增刊): 292―296.Lu Xiao,Lu Xinzheng,Ye Lieping.Discussion on the ground motion intensity measures for super high-rise buildings [J].China Civil Engineering Journal,2012,45(Suppl): 292―296.(in Chinese)
[83] 苏宁粉,周颖,吕西林,等.增量动力分析中地震动强度参数的有效性研究[J].西安建筑科技大学学报(自然科学版),2016,48(6): 846―852.Su Ningfen,Zhou Ying,Lü Xilin,et al.Study on the efficiency of intensity measures for incremental dynamic analysis [J].Journal of Xi’an University of Architecture and Technology (Natural Science Edition),2016,48(6):846―852.(in Chinese)
[84] 周颖,苏宁粉,吕西林.高层建筑结构增量动力分析的地震动强度参数研究[J].建筑结构学报,2013,34(2): 53―60.Zhou Ying,Su Ningfen,Lü Xilin.Study on intensity measure of incremental dynamic analysis for high-rise structures [J].Journal of Building Structures,2013,34(2): 53―60.(in Chinese)
[85] Kurama Y,Farrow K.Ground motion scaling methods for different site conditions and structure characteristics[J].Earthquake Engineering and Structural Dynamics.2003,32(15): 2425―2450.
[86] O’Donnell A P,Kurama Y C,Kalkan E,et al.Experimental evaluation of four ground-motion scaling methods for dynamic response-history analysis of nonlinear structures [J].Bulletin of Earthquake Engineering,2017,15(5): 1899.
[87] Tan Q,Li Y M,Qin Y,et al.A spectral intensity index of ground motions for input selection with consideration of higher modes effect for super high-rise buildings [C].Santiago,Chile: Proceedings of the 16th World Conference on Earthquake Engineering,2017.
[88] FEMA 355C.State of the art report on systems performance of steel moment frames subject to earthquake ground shaking [R].CA: SAC Joint Venture,Sacra- mento,2000.
[89] 谢礼立,翟长海.最不利设计地震动研究[J].地震学报,2003,25(3): 250―261.Xie Lili,Zhai Changhai.Study on the severest real ground motion for seismic design and analysis [J].Acta Seismologica Sinica,2003,25(3): 250―261.(in Chinese)
[90] 曲哲,叶列平,潘鹏.建筑结构弹塑性时程分析中地震动记录选取方法的比较研究[J].土木工程学报,2011,44(7): 10―21.Qu Zhe,Ye Lieping,Pan Peng.Comparative study on methods of selecting earthquake ground motions for nonlinear time history analyses of building structures [J].China Civil Engineering Journal,2011,44(7): 10―21.(in Chinese)
[91] Bradley B A.A generalized conditional intensity measure approach and holistic ground-motion selection [J].Earthquake Engineering & Structural Dynamics,2010,39(12): 1321―1342.
[92] Angelo M,Marco V,Marco M.Selection of natural and synthetic accelerograms for seismic vulnerability studies on reinforced concrete frames [J].Journal of Structural Engineering,2011,137(3): 367―378.
[93] Hancock J,Bommer J J,Stafford P J.Numbers of scaled and matched accelerograms required for inelastic dynamic analyses [J].Earthquake Engineering and Structural Dynamics,2008; 37(4): 1585―1607.
[94] Carballo J E.Probabilistic seismic demand analysis spectrum matching and design [D].Stanford University,CA,2000.
[95] ISO/DIS 19901-2,Petroleum and natural gas industries-Specific requirements for offshore structures- Part 2:Seismic design procedures and criteria [S].International Organization for Standardization,1990.
SELECTION AND SCALING OF REAL ACCELEROGRAMS AS INPUT TO TIME-HISTORY ANALYSIS OF STRUCTURES: A STATE-OF-THE-ART REVIEW
张 锐(1978―)，女，辽宁人，博士生，主要从事结构抗震和防灾减灾研究(E-mail: zhangrui@djtu.edu.cn);
王东升(1974―)，男，内蒙古库伦旗人，教授，博士，博导，主要从事结构抗震和防灾减灾研究(E-mail: dswang@hebut.edu.cn);
成 虎(1989―)，男，江苏人，博士生，主要从事结构工程抗震研究(E-mail: hoocheng@163.com).