增量动力分析(Incremental Dynamic Analysis,IDA)方法最早由 Bertero于 1977年提出,于 2000年被美国FEMA350、FEMA351所采用,之后被广泛应用于性能化地震工程中。马千里等[1]利用IDA对Pushover分析的加载模式进行研究,建议采用多种侧向力模式对结构进行 Pushover分析以全面评价结构不同楼层的抗震性能。杨成等[2]利用弹塑性反应谱替代弹性反应谱作为 IDA方法中的地震强度指标,通过算例分析表明此方法能很好体现结构的非线性反应特征。卜一等[3]采用IDA方法对高层混合结构的性能水准进行研究,给出了控制结构抗震目标的四个性能水准。吕大刚等[4]采用IDA方法对结构进行倒塌分析,提出“折半取中”的原则来确定倒塌极限状态点,通过分析指出钢筋屈服后强化特性对结构倒塌能力具有显著影响。李宁等[5]考虑结构偏心对动力反应的影响,将结构等效为平动-扭转的双自由度体系,提出了一种简化的 IDA方法。Alembagheri等[6]采用 IDA方法对混凝土拱坝进行损伤分析,建议了简化的拱坝损伤指标,通过算例表明建议的损伤指标能够正确的反映坝体在不同强度地震下的损伤情况。韩庆华等[7]采用自定义钢材本构关系,考虑压杆失稳后的力学性能,对格构式拱结构进行IDA,得到结构的薄弱位置及倒塌破坏极限位移。吴巧云等[8]提出一种基于随机IDA来确定结构屈服和倒塌水平能力限值的方法。Khorami等[9]采用IDA方法对屈曲约束支撑框架和同心支撑框架的抗震性能进行比较,结果表明前者具有较高的抗震性能。Soleimani等[10]在基于能量的双向Pushover分析基础上提出了一种双分量的IDA方法。有些学者将IDA和模态Pushover分析相结合,提出了模态IDA方法(Han和Chopra[11],Zarfam等[12],Moon等[13]),即运用模态等效单自由度(SDOF)体系替代原结构进行IDA,独立分析后再将各模态结果进行组合,这种简化方法可大大缩短分析时间,且具有一定的准确性。
近年来许多学者将 IDA应用于地震易损性分析中。陆新征等[14]通过对两个算例结构的IDA和倒塌易损性分析,指出仅考虑地震动单一水平分量的IDA分析会高估结构抗倒塌安全性。吕西林等[15]针对复杂的高层结构,采用IDA获得不同地震强度的结构损伤参数,并建立易损性曲线以评估结构损伤,Hossein等[16]采用IDA方法和遗传算法优化技术来估计结构在地震作用下的失效概率,分析表明该方法可大大减少用于失效概率分析的地震记录数量。徐骏飞等[17]采用IDA方法针对一实际结构进行地震易损性分析,对设置与不设置支撑对主余震协同作用下的结构失效概率、初始投资和生命周期总费用进行了比较。周奎等[18]基于IDA方法,利用OpenSees平台输入地震数据,计算结构倒塌概率,并拟合了倒塌概率易损性曲线。张海等[19]针对不同类型的砌体结构进行IDA和地震易损性分析,考虑场地条件、高宽比等因素的影响,给出了砌体结构的一些抗震建议。卢杰志等[20]考虑材料、荷载和地震动参数的随机性,利用OpenSees平台对PC框架结构模型进行基于IDA的地震易损性分析,并根据分析结果对设计参数取值给出修订建议。梁丹等[21]采用IDA方法对不同参数的RC框架结构进行倒塌易损性分析,建立了简化的抗倒塌性能评估指标。Emami等[22]针对一42层RC核心筒结构模型进行倒塌IDA,以研究强震下该类型结构的易损性参数关系和倒塌概率。陈力波等[23]采用IDA方法建立公路斜交梁桥地震易损性模型,研究斜交角和易损性参数之间的关系,给出公路斜交梁桥地震易损性简化计算方法。
目前,基于IDA的性能化抗震设计研究已经取得了一定量的成果。然而,由于IDA方法要采用一定数量的地震动作为结构激励,原模型结构的IDA计算量很大、耗时很长,在实际使用中很不方便。为此,本文提出了一种基于简化IDA的结构地震损伤评估方法。首先建议一种简化IDA方法,然后基于该方法进行结构的地震易损性分析,给出结构的地震损伤分布结果,最后通过计算损伤指数期望来分析结构在地震下的损伤状况,评估结构的抗震性能。
多层房屋结构在水平方向地震动作用下的运动方程表示为:
对于楼层不多的房屋结构,第1振型对侧向位移模式起主导作用,结构可按第1振型等效为SDOF体系,运动方程表示为:
式中:q1(t)为等效 SDOF体系的位移反应;![]() 其中φ1和γ1分别为标准化的第1振型向量(顶层振型值为 1)和第 1振型的振型参与系数。根据等效SDOF体系推导过程,通过式(2)计算出q1(t)后,代入u(t)=q1(t)φ1γ1可以得到结构各楼层的位移反应。设结构等效SDOF体系在地震动作用下的最大位移反应为qm,通过式(3)可以得到结构的最大顶层位移反应urm:
其中φ1和γ1分别为标准化的第1振型向量(顶层振型值为 1)和第 1振型的振型参与系数。根据等效SDOF体系推导过程,通过式(2)计算出q1(t)后,代入u(t)=q1(t)φ1γ1可以得到结构各楼层的位移反应。设结构等效SDOF体系在地震动作用下的最大位移反应为qm,通过式(3)可以得到结构的最大顶层位移反应urm:
但在等效SDOF体系假设中,运用弹性振型φ1来表示不断变化的侧向位移分布存在不合理性。为了缩小偏差,本文建议通过Pushover分析获得结构进入塑性反应阶段后的标准化第 1振型向量φ1p(t)(顶层值为 1)。由于是推覆到某一顶层位移值时对应的结构第 1振型向量,所以这里φ1p(t)是时间的函数。用φ1p(t)替代φ1,有:
式中:up(t)为结合Pushover分析方法得到的结构位移反应向量;γ1p为对应φ1p(t)的振型参与系数。
抗震设计规范给出了对应不同设防烈度下小震和大震的峰值加速度(PGA),以及小震和大震下的结构弹性和弹塑性的层间位移角限值[θ],所以在IDA中可将PGA作为地震动强度参数,最大层间位移角θm作为结构性能参数。
本文建议的简化IDA方法的具体步骤如下:
绘制结构等效SDOF体系的IDA能力曲线。
1) 计算标准化的结构第1振型向量φ1和振型参与系数γ1。
2) 按照式(5)建立Pushover侧向力模式,进行Pushover分析,建立“顶层位移-基底剪力”格式的Pushover能力曲线,并简化为双线性形式。
3) 将双线性形式的“顶层位移-基底剪力”关系转换为结构等效SDOF体系的“位移-力”单调关系,并基于此给出等效SDOF体系的恢复力模型。
4) 选择一条地震动记录,将地震动的PGA由小到大进行调幅,然后对等效SDOF体系进行激励逐级增加的动力时程分析,得到对应不同 PGA的最大位移qm,并绘制等效SDOF体系qm-PGA格式的IDA能力曲线。
绘制结构体系的IDA能力曲线。
5) 将等效SDOF体系IDA能力曲线中的qm代入式(3)中得到对应不同PGA的urm。
6) 再次对结构进行 Pushover分析,推覆到每一个PGA对应的urm(步骤5))为止,然后确定此时的塑性第1振型向量φ1p,并代入式(4)中得到结构位移向量up,进而确定每一个urm对应的θm,即每一个PGA对应的θm。
7) 绘制θm-PGA格式的结构IDA能力曲线。
在采用多条地震动作用的 IDA中,θm的平均值表示为μθm,对μθm-PGA格式平均能力曲线的横纵坐标分别取对数得到 ln(μθm)-ln(PGA)格式曲线,一般来说该曲线可以近似表示为[24]:
式中,a和b为常数。在某强度的地震动作用下,结构的θm达到或超过[θ]的条件失效概率表示为Pf。当θm和[θ]均服从对数正态分布时,结构的抗震失效概率Pf可由下式计算得到[24]:
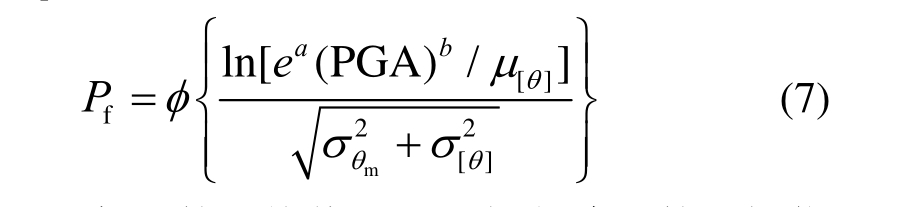
式中:μ[]θ为[θ]的平均值,可取规范给出的层间位移角限值;σθm和σ[θ]分别为θm和[θ]的对数标准差,参数a和b由式(6)进行回归分析得到。
本文考虑钢筋混凝土结构。将结构在地震动作用下的损伤状态划分为 5个等级,根据文献[25]并结合《建筑抗震设计规范》中的大震下层间位移角限值给出对应各损伤等级的结构θm的范围。定义损伤指数R来表示结构的地震损伤状况,R∈(0,1),按结构地震损伤状况的比例取值,R值越大结构地震损伤越严重。表1中给出了抗震三水准、地震损伤等级、R和θm范围的对应关系。
表1 抗震水准、损伤等级和最大层间位移角的对应关系
Table 1 The correspondence of seismic levels, damage grades and maximum story drift ratios
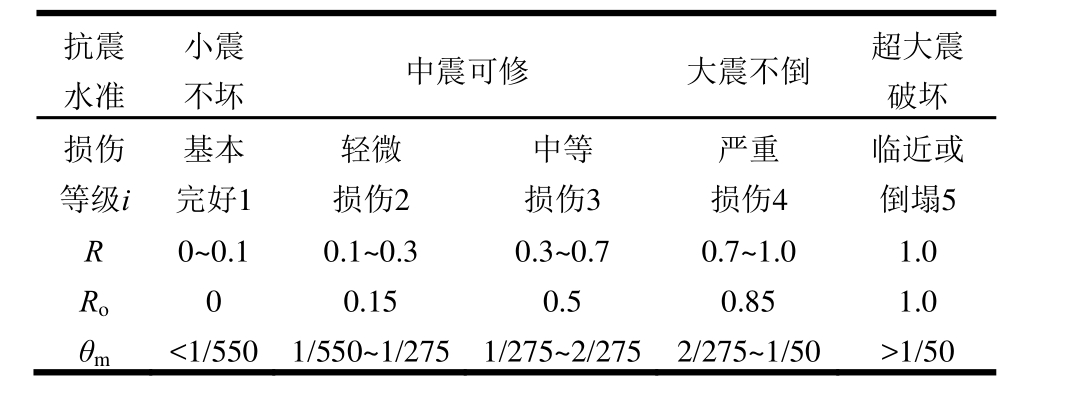
注:Ro为对应各损伤等级的损伤指数计算值。
抗震水准小震不坏 中震可修 大震不倒 超大震破坏损伤等级i基本完好1轻微损伤2中等损伤3严重损伤4临近或倒塌5R0~0.1 0.1~0.3 0.3~0.7 0.7~1.0 1.0Ro0 0.15 0.5 0.85 1.0θm<1/550 1/550~1/275 1/275~2/275 2/275~1/50 >1/50
对于不同的PGA,将结构第i损伤等级的失效概率值Pf,i代入式(8)中,可计算出结构在地震动下发生第i损伤等级的概率Pi。
当i=1时,Pf,0=1。
由以上可知,针对某一PGA值,各损伤指数R都对应着相应的概率P,且概率之和为 1。通过以下全概率公式可计算出结构的损伤指数期望值Re:
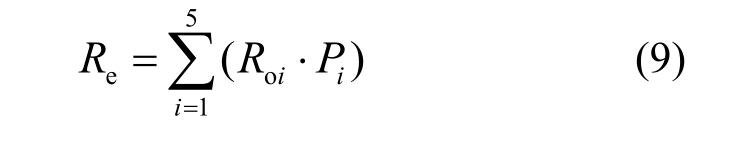
式中,第i损伤等级的损伤指数计算值Roi的取值见表1。
本文建议的基于简化 IDA的结构地震损伤评估方法步骤如下:
1) 通过简化IDA方法绘制结构的μθm-PGA格式的平均能力曲线,并计算出![]()
2) 对μθm-PGA 平均能力曲线的纵、横坐标分别取自然对数,并代入式(6)中,回归出参数a和b。
3) 取某一PGA值,由式(7)计算结构不同地震损伤等级的Pf,式中μ[]θ取表1中各损伤等级对应的θm的上限值,![]() 根据文献[26]取0.399。
根据文献[26]取0.399。
4) 将结构第i损伤等级的Pf,i代入式(8)中,计算出结构第i损伤等级的Pi。
5) 将各损伤等级对应的P和Ro代入式(9)中,计算出对应该PGA的结构损伤指数期望值Re。
6) 重复步骤3)~步骤5),计算出对应不同PGA的Re,并将Re与表1中R值进行对照,判断结构在不同 PGA的地震动激励下的损伤情况,进而评估结构是否符合抗震性能水准要求。
按照场地类别I0、II和IV设计三幢六层的结构模型:结构1、结构2和结构3。设计地震分组为第三组,设防烈度为7度。三幢结构模型的层高均为 3.6 m;沿楼层的侧向剪切刚度为均匀分布;设层间阻尼为瑞雷阻尼,阻尼比均为 5%;基本周期均为0.61 s。
本算例的结构模型可以简化为多自由度(MDOF)体系。这三个MDOF体系的层间滞回关系均采用修正的Clough模型,屈服刚度系数取0.024,刚度退化系数取 0.2。表 2中列出了三幢结构模型的层间剪切强度,楼层荷载代表值及振型。
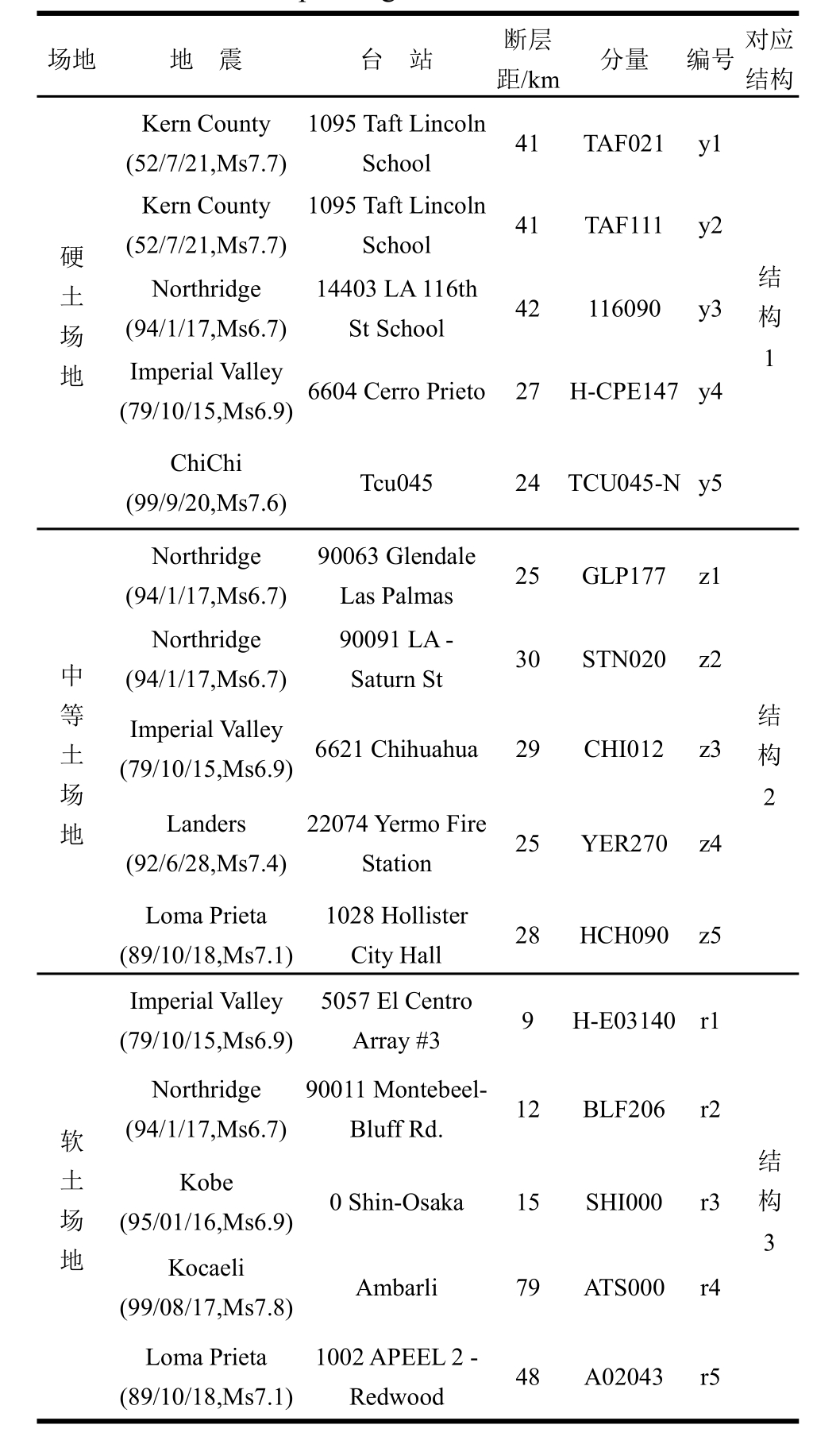
对应结构1、结构2和结构3,分别按硬土、中等土和软土三种场地类别,共选择 15条地震加速度记录作为三个结构模型的地震动激励。相关信息如表3所示。
表2 结构模型的主要参数
Table2 The parameters of the structural models
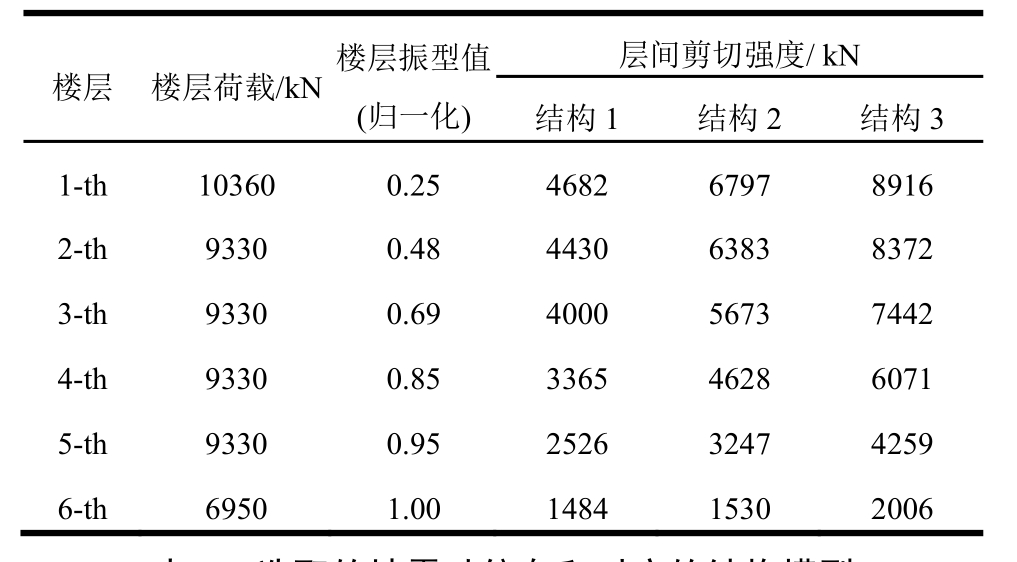
楼层 楼层荷载/kN楼层振型值(归一化)层间剪切强度/ kN结构1 结构2 结构3 1-th 10360 0.25 4682 6797 8916 2-th 9330 0.48 4430 6383 8372 3-th 9330 0.69 4000 5673 7442 4-th 9330 0.85 3365 4628 6071 5-th 9330 0.95 2526 3247 4259 6-th 6950 1.00 1484 1530 2006
表3 选取的地震动信息和对应的结构模型
Table 3 The selected ground motion records and the corresponding structural models
场地 地 震 台 站 断层距/km 分量 编号 对应结构Kern County(52/7/21,Ms7.7)1095 Taft Lincoln School 41 TAF021 y1硬土场地Kern County(52/7/21,Ms7.7)1095 Taft Lincoln School 41 TAF111 y2 Northridge(94/1/17,Ms6.7)14403 LA 116th St School 42 116090 y3 Imperial Valley(79/10/15,Ms6.9)6604 Cerro Prieto 27 H-CPE147 y4结构1 ChiChi(99/9/20,Ms7.6) Tcu045 24 TCU045-N y5 Northridge(94/1/17,Ms6.7)90063 Glendale Las Palmas 25 GLP177 z1中等土场地Northridge(94/1/17,Ms6.7)90091 LA -Saturn St 30 STN020 z2 Imperial Valley(79/10/15,Ms6.9)6621 Chihuahua 29 CHI012 z3结构2 Landers(92/6/28,Ms7.4)22074 Yermo Fire Station 25 YER270 z4 Loma Prieta(89/10/18,Ms7.1)1028 Hollister City Hall 28 HCH090 z5 Imperial Valley(79/10/15,Ms6.9)5057 El Centro Array #3 9 H-E03140 r1软土场地Northridge(94/1/17,Ms6.7)90011 Montebeel-Bluff Rd. 12 BLF206 r2 Kobe(95/01/16,Ms6.9) 0 Shin-Osaka 15 SHI000 r3结构3 Kocaeli(99/08/17,Ms7.8) Ambarli 79 ATS000 r4 Loma Prieta(89/10/18,Ms7.1)1002 APEEL 2 -Redwood 48 A02043 r5
图1给出3个结构模型分别在相应的多条地震动作用下采用简化 IDA方法绘制的θm-PGA格式IDA能力曲线和μθm-PGA格式IDA能力曲线。图2给出分别采用传统的IDA方法和简化IDA方法绘制的μθm-PGA格式IDA能力曲线的比较图。由图2可知,对于结构1和结构2,当大约PGA<0.8g时,简化IDA方法得到的θm偏大;而对于结构3,当大约PGA<0.6g时,简化IDA方法得到的θm偏大。由于通常强震的PGA不会超过0.6g,所以说明一般情况下采用简化IDA方法偏于安全。
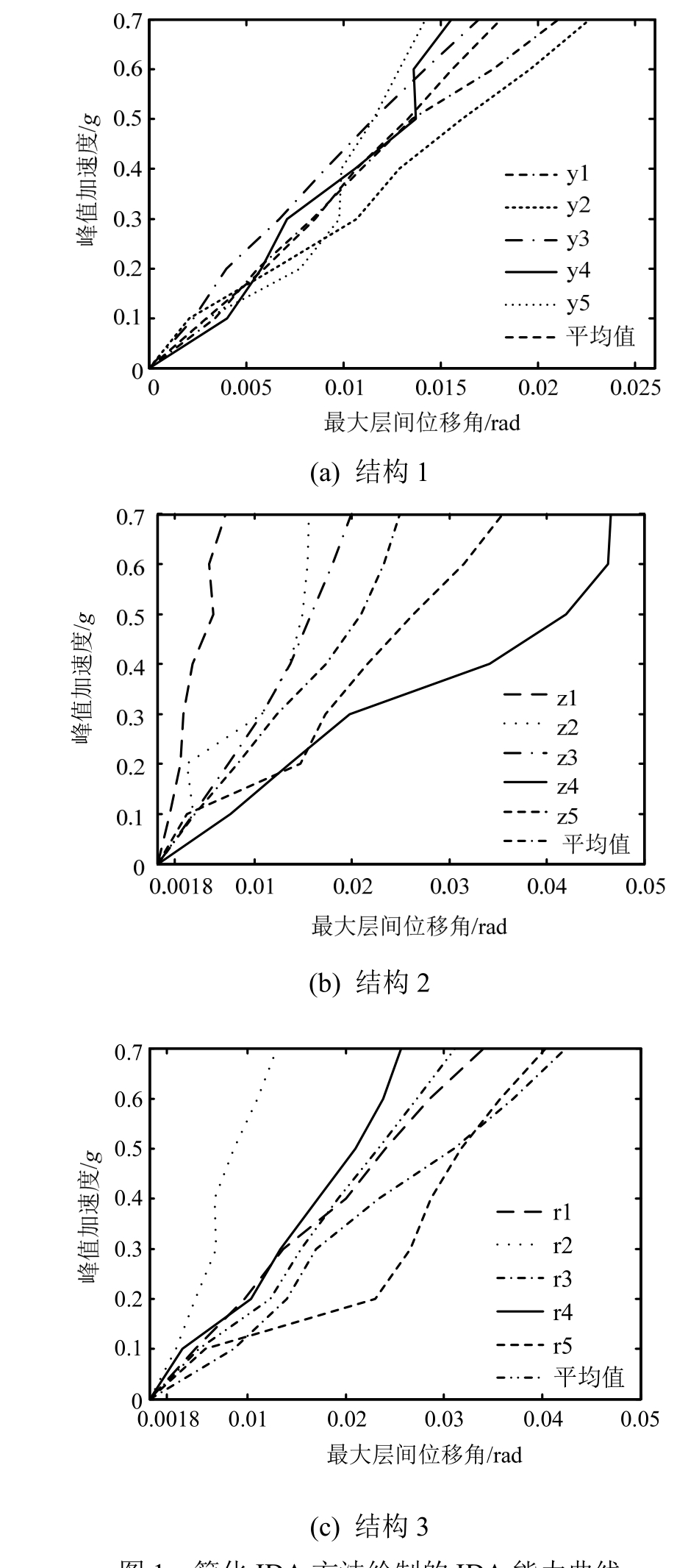
图1 简化IDA方法绘制的IDA能力曲线
Fig.1 IDA capacity curves based on the simplified IDA method
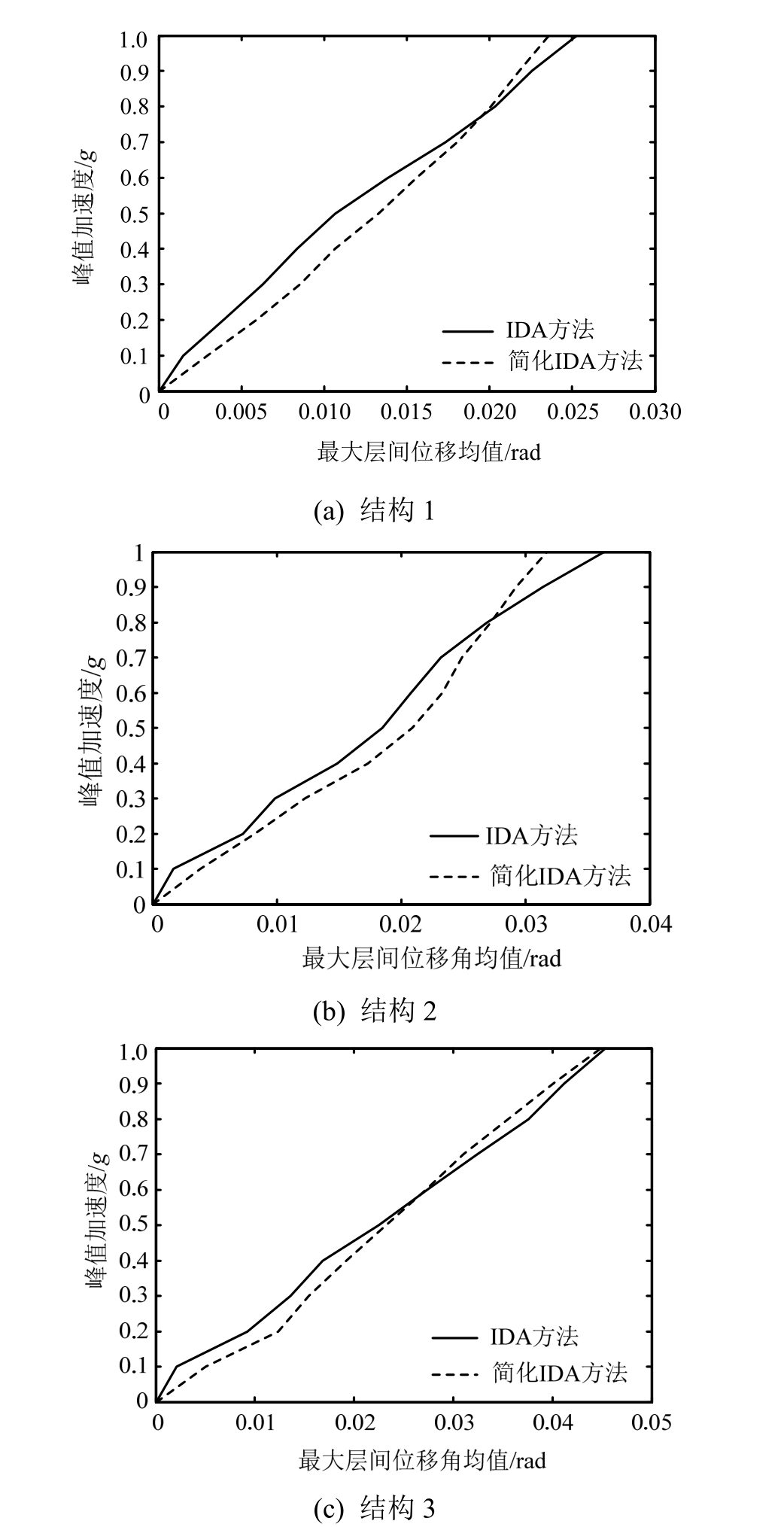
图2 两种方法绘制的IDA能力曲线比较
Fig.2 Comparison of the IDA capacity curves between two IDA methods
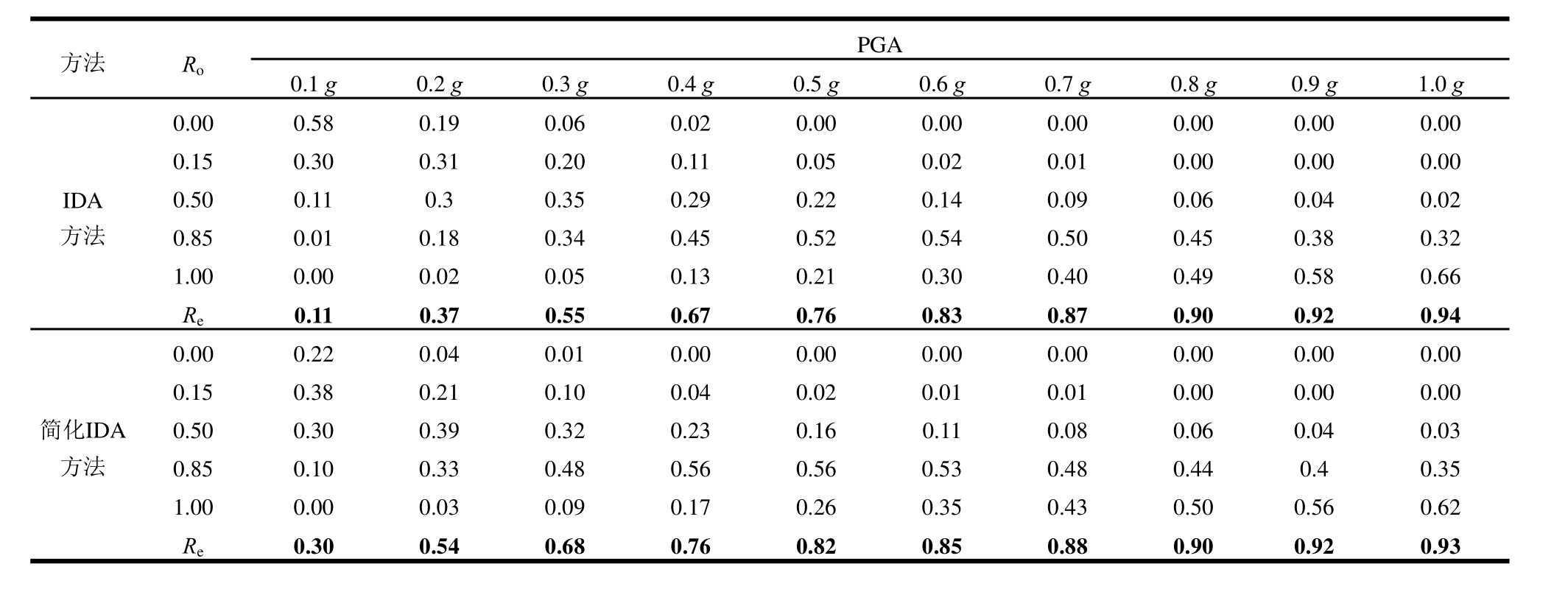
通过式(6)、式(7)和式(8)计算得到结构在不同地震强度下发生不同损伤等级的震害概率矩阵,并通过式(9)求解出对应不同 PGA的结构损伤指数期望值Re。表4给出结构1的震害概率矩阵及损伤指数期望Re。由于论文篇幅原因,结构2、结构3的相关数据没有在此列出。
以Re为纵坐标,PGA为横坐标,绘制PGA-Re曲线,见图3。通过PGA-Re曲线可以较直观地判断不同地震强度下结构是否满足抗震性能要求。将通过简化 IDA方法和传统 IDA方法得到的 PGA-Re曲线进行比较可知,相同强度的地震作用下,通过简化IDA方法计算得到的结构地震损伤等级较高,但随着PGA的增加,这种差异会逐渐减小,当PGA增长到大约 0.7g之后两者非常接近。由此说明,PGA大约在0g~0.7g之间,通过简化IDA方法得到的结构地震损伤偏重,进一步说明该方法结果偏于安全。
比较三个结构模型的 PGA-Re曲线可知,结构1(对应硬土场地)随着PGA的增加,Re开始阶段增加比较缓慢,在PGA>0.7g后增加进一步减缓,但仍有上升趋势;结构2(对应中等土场地)和结构3(对应软土场地)与结构1不同,随着PGA的增加,Re的增加相比迅速,且在PGA>0.7g后曲线接近水平。由以上现象说明,相比结构2和结构3,结构1的抗震能力较强,随着 PGA的增加,其地震损伤增加较为缓慢。
表4 结构1的震害概率矩阵及损伤指数期望值Re
Table 4 Earthquake damage probability matrix and damage index expectationsReof the structure 1
方法RoPGA 0.1g0.2g0.3g0.4g0.5g0.6g0.7g0.8g0.9g1.0g0.00 0.58 0.19 0.06 0.02 0.00 0.00 0.00 0.00 0.00 0.00 IDA方法简化IDA方法0.15 0.30 0.31 0.20 0.11 0.05 0.02 0.01 0.00 0.00 0.00 0.50 0.11 0.3 0.35 0.29 0.22 0.14 0.09 0.06 0.04 0.02 0.85 0.01 0.18 0.34 0.45 0.52 0.54 0.50 0.45 0.38 0.32 1.00 0.00 0.02 0.05 0.13 0.21 0.30 0.40 0.49 0.58 0.66Re0.11 0.37 0.55 0.67 0.76 0.83 0.87 0.90 0.92 0.94 0.00 0.22 0.04 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.15 0.38 0.21 0.10 0.04 0.02 0.01 0.01 0.00 0.00 0.00 0.50 0.30 0.39 0.32 0.23 0.16 0.11 0.08 0.06 0.04 0.03 0.85 0.10 0.33 0.48 0.56 0.56 0.53 0.48 0.44 0.4 0.35 1.00 0.00 0.03 0.09 0.17 0.26 0.35 0.43 0.50 0.56 0.62Re0.30 0.54 0.68 0.76 0.82 0.85 0.88 0.90 0.92 0.93

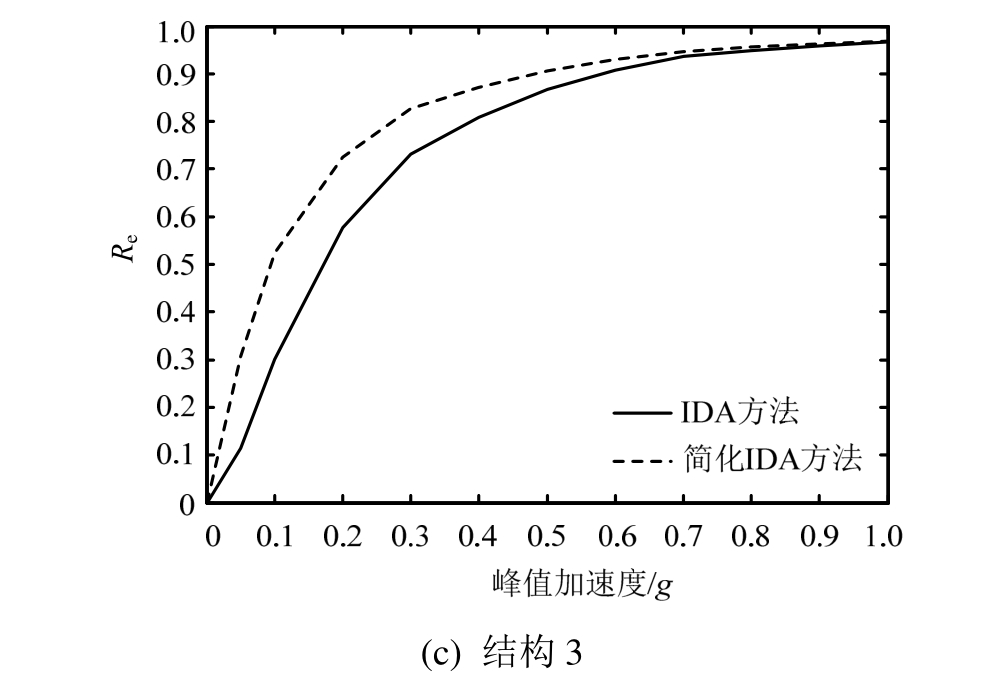
图3 结构模型的Re与PGA的关系曲线
Fig.3 The relationship curves betweenReand PGA of the structure models
设简化IDA方法和IDA方法得到的Re的比值等于β。比值β反映了采用简化IDA方法对算例结构模型进行地震损伤评估的保守程度,β越大说明简化方法的评估结果越偏于保守,而β越接近于1则说明越接近实际。将对应不同场地的三个结构模型的β列于表5中。由表5可知,PGA较小时基于简化IDA方法得到的损伤值很大,即损伤评估的保守程度高,特别是硬土场地下的结构1;而随着PGA增大,基于简化IDA方法得到的损伤值与传统IDA方法逐渐接近。
表5 算例结构模型的β值
Table 5βfor the example structural models
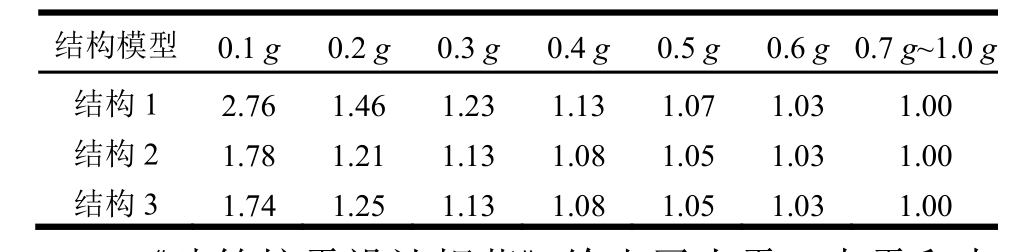
结构模型 0.1g0.2g0.3g0.4g0.5g0.6g0.7g~1.0g结构1 2.76 1.46 1.23 1.13 1.07 1.03 结构2 1.78 1.21 1.13 1.08 1.05 1.03结构3 1.74 1.25 1.13 1.08 1.05 1.03
结构2 1.78 1.21 1.13 1.08 1.05 1.03结构3 1.74 1.25 1.13 1.08 1.05 1.03
《建筑抗震设计规范》给出了小震、中震和大震下的地震动 PGA值,本算例的三个结构模型均为7度设防,按照规范PGA分别取为0.036g、0.10g和0.22g。将对应这三个PGA值的Re值与抗震水准相对应的R取值范围(见表 1)进行对照,评估算例的结构模型是否符合三水准的抗震性能要求,并将评估结果列于表6中。由表6可知:
1) 对于结构1,两种方法的评估结果一致,模型结构均符合三水准的抗震性能要求,特别是在大震作用下,结构震损较小,均没有超过中震对应的结构损伤等级。
2) 对于结构2和结构3,当采用传统的IDA方法时,两个模型结构均符合三水准的抗震性能要求;但当采用简化IDA方法时,得到的结构地震损伤指数偏大,在小震下就超过了结构反应限值,但在中震和大震下符合相应水准的抗震性能要求。
3) 比较两种方法,总体来说基于简化 IDA方法得到的结构地震损伤等级较高,说明这种方法进行结构抗震评估偏于保守。
表6 结构模型的地震损伤评估
Table 6 Seismic damage assessment of the structural models

注:图中★、▲分别表示传统的IDA方法和简化IDA方法的地震损伤评估结果
结构模型 抗震水准 小震不坏 中震可修 大震不倒R= 0~0.1R=0.1~0.7R=0.7 ~1.0小震 0.036g★ ▲结构1中震 0.100g★ ▲大震 0.224g★ ▲小震 0.036g★ ▲结构2中震 0.100g★ ▲大震 0.224g★ ▲小震 0.036g★ ▲结构3中震 0.100g★ ▲大震 0.224g★ ▲
本文首先建议了一种简化的IDA方法,即通过结构的等效SDOF体系假设近似计算结构顶层最大位移,再结合Pushover分析计算出结构的最大层间位移角,求解结构抗震性能指数与逐级增加的地震强度之间的对应关系。然后,给出结构在不同地震强度下的失效概率计算公式,并推导出结构地震损伤概率公式。最后,定义损伤指数R来表示结构的地震损伤状况,并建议了R与θm范围、地震损伤等级和抗震三水准的对应关系,在此基础上提出了通过计算损伤指数期望值Re来估计结构在不同强度地震下的损伤状况,进而评估结构抗震性能的地震损伤评估方法。
为了检验和演示本文所提出的方法,按照硬土、中等土和软土场地设计了三幢结构模型,并按不同场地各选取了五条典型地震动记录作为模型结构的地震动激励。在算例分析中,首先将简化IDA方法与传统IDA方法的IDA能力曲线进行了比较,通过比较发现在一般情况下采用简化 IDA方法得到的结构反应值较大,说明计算结果偏于安全。在此基础上,分别针对两种方法得到的结构反应与地震强度关系进行地震易损性分析,计算出结构地震损伤概率矩阵和对应不同地震强度的地震损伤指数,给出简化IDA方法相对于传统方法得到的损伤指数的放大值,并根据损伤指数期望值向量评估结构的抗震性能。通过算例分析表明:基于简化IDA的结构地震损伤评估方法计算量小、简单易于操作,但得到的结构抗震评估结果偏于安全。
[1]马千里, 叶列平, 陆新征, 等. 采用逐步增量弹塑性时程方法对 RC 框架结构推覆分析侧力模式的研究[J].建筑结构学报, 2008, 29(2): 132―140.Ma Qianli, Ye Lieping, Lu Xinzheng, et al. Study on lateral load patterns of pushover analysis using incremental dynamical analysis for RC frame structure[J]. Journal of Building Structure, 2008, 29(2): 132―140. (in Chinese)
[2]杨成, 徐腾飞, 李英民, 等. 应用弹塑性反应谱对 IDA方法的改进研究[J]. 地震工程与工程振动, 2008,28(4): 64―69.Yang Cheng, Xu Tengfei, Li Yingmin, et al. Research on modified IDA method by inelastic response spectrum [J].Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(4): 64―69. (in Chinese)
[3]卜一, 吕西林, 周颖, 等. 采用增量动力分析方法确定高层混合结构的性能水准[J]. 结构工程师, 2009,25(2): 77―84.Bo Yi, Lü Xilin, Zhou Ying, et al. Studies on the multi-levels of hybrid structures using incremental dynamic analysis [J]. Structural Engineers, 2009, 25(2):77―84. (in Chinese)
[4]吕大刚, 于晓辉, 王光远. 单地震动记录随机增量动力分析[J]. 工程力学, 2010, 27(I): 53―58.Lü Dagang, Yu Xiaohui, Wang Guangyuan. Singlerecord random incremental dynamic analysis [J].Engineering Mechanics, 2010, 27(I): 53―58. (in Chinese)
[5]李宁, 翟长海, 谢礼立. 单向偏心结构的简化增量动力分析方法[J]. 工程力学, 2011, 28(5): 8―12.Li Ning, Zhai Changhai, Xie Lili. Simplified incremental dynamic analysis method for uniaxial plan-asymmetric structures [J]. Engineering Mechanics, 2011, 28(5): 8―12. (in Chinese)
[6]Alembagheri M, Ghaemian M. Damage assessment of a concrete arch dam through nonlinear incremental dynamic analysis [J]. Soil Dynamics and Earthquake Engineering, 2013, 44(1): 127―137.
[7]韩庆华, 芦燕, 徐颖, 等. 基于IDA的格构式拱结构抗倒塌性能分析[J]. 土木工程学报, 2015, 48(3): 1―7.Han Qinghua, Lu Yan, Xu Ying, et al. Analysis on collapse-resistant performance of spatial latticed steel arches based on IDA method[J]. China Civil Engineering Journal, 2015, 48(3): 1―7. (in Chinese)
[8] 吴巧云, 朱宏平. 基于随机 IDA的结构量化指标限值求解方法[J]. 工程力学, 2014, 31(4): 61―68.Wu Qiaoyun, Zhu hongping. Solving method of structural quantitative indicators based on random IDA[J]. Engineering Mechanics, 2014, 31(4): 61―68. (in Chinese)
[9]Khorami M, Alvansazyazdi M, Shariati M, et al. Seismic performance evaluation of buckling restrained braced frames (BRBF) using incremental nonlinear dynamic analysis method (IDA) [J]. Earthquakes and Structures,2017, 13(6): 531―538.
[10] Soleimani S, Aziminejad A, Moghadam A S.Approximate two-component incremental dynamic analysis using a bidirectional energy-based pushover procedure [J]. Engineering Structures, 2017, 157: 86―95.
[11] Han S W, Chopra A K. Approximate incremental dynamic analysis using the modal pushover analysis procedure [J]. Earthquake Engineering and Structural Dynamics, 2006, 35(15): 1853―1873.
[12] Zarfam P, Mofid M. On the modal incremental dynamic analysis of reinforced concrete structures, using a trilinear idealization model [J]. Engineering Structures,2011, 33(4): 1117―1122.
[13] Moon K H, Han S W, Lee T S, et al. Approximate MPA-based method for performing incremental dynamic analysis [J]. Nonlinear Dynamics, 2012, 67(4): 2865―2888.
[14] 陆新征, 施炜, 张万开, 等. 三维地震动输入对IDA倒塌易损性分析的影响[J]. 工程抗震与加固改造, 2011,33(6): 1―7.Lu Xinzheng, Shi Wei, Zhang Wankai, et al. Influence of three-dimensional ground motion input on IDA-based collapse fragility analysis [J]. Earthquake Resistant Engineering and Retrofitting, 2011. 33(6): 1―7. (in Chinese)
[15] 吕西林, 苏宁粉, 周颖. 复杂高层结构基于增量动力分析法的地震易损性分析[J]. 地震工程与工程振动,2012, 32(5): 19―25.Lü Xilin, Su Ningfen, Zhou Ying. IDA-based seismic fragility analysis of a complex high-rise structure [J].Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(5): 19―25. (in Chinese)
[16] Hossein K, Alireza A, Mohsen G A. Estimating the annual probability of failure using improved progressive incremental dynamic analysis of structural[J]. Structural Design of Tall and Spectral Buildings, 2013, 22(17):1279―1295.
[17] 徐骏飞, 陈隽, 丁国. 基于 IDA 的主余震序列作用下RC框架易损性分析与生命周期费用评估[J]. 地震工程与工程振动, 2015, 35(4): 206―212.Xu Junfei, Chen Jun, Ding Guo. Fragility analysis and life cycle cost assessment of RC frame under mainshock aftershock seismic sequences through IDA [J].Earthquake Engineering and Engineering Dynamics,2015, 35(4): 206―212. (in Chinese)
[18] 周奎, 林杰, 祝文. 基于增量的动力分析(IDA)方法的地震易损性工程实例分析[J]. 地震工程与工程振动,2016, 36(1): 135―140.Zhou Kui, Lin Jie, Zhu Wen. Case study of seismic fragility analysis based on the incremental dynamic analysis (IDA) method [J]. Earthquake Engineering and Engineering Dynamics, 2016, 36(1): 135―140. (in Chinese)
[19] 张海, 孟亚翠, 田丽媛. 基于 IDA 砌体结构地震易损性影响因素研究[J]. 防灾减灾工程学报, 2017, 37(1):49―53.Zhang Hai, Meng Yacui, Tian Liyuan. Seismic vulnerability factors analysis of masonry structure based on IDA [J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(1): 49―53. (in Chinese)
[20] 卢杰志, 张耀庭, 郭宗明, 等. 多层预应力混凝土框架结构基于IDA的地震易损性分析[J]. 工程力学, 2017,34(6): 109―119.Lu Jiezhi, Zhang Yaoting, Guo Zongming, et al. Seismic fragility analysis of multi-storey PC frame structures using incremental dynamic analysis [J]. Engineering Mechanics, 2017, 34(6): 109―119. (in Chinese)
[21] 梁丹, 梁兴文. RC框架结构抗倒塌性能评估的简化方法[J]. 工程力学, 2017, 34(2): 102―110.Liang Dan, Liang Xingwen. A simplified method for collapse-resistant performance evaluation of RC frame structures [J]. Engineering Mechanics, 2017, 34(2):102―110. (in Chinese)
[22] Emami A R, Halabian A M. Incremental dynamic collapse analysis of RC core-wall tall buildings considering spatial seismic response distributions [J].Structural Design of Tall and Special Buildings, 2017,26(15): e1383.
[23] 陈力波, 王嘉嘉, 上官萍. 公路斜交桥地震易损性模型研究[J]. 工程力学, 2018, 35(1): 160―171.Chen Libo, Wang Jiajia, Shangguan Ping. Research of seismic vulnerability model for skew highway girder bridge [J]. Engineering Mechanics, 2018, 35(1): 160―171. (in Chinese)
[24] [24] 韩淼, 那国坤. 基于增量动力法的剪力墙结构地震易损性分析[J]. 世界地震工程, 2011, 27(3): 108―113.Han Miao, Na Guokun. Seismic fragility analysis of shear wall structure by using incremental dynamic method [J].World Earthquake Engineering, 2011, 27(3): 108―113.(in Chinese)
[25] [25] 吕大刚, 李晓鹏, 王光远. 基于可靠度和性能的结构整体地震易损性分析[J]. 自然灾害学报, 2006,15(2): 107―114.Lü Dagang, Li Xiaopeng, Wang Guangyuan. Global seismic fragility analysis based on reliability and performance [J]. Journal of Natural Disasters, 2006,15(2): 107―114. (in Chinese)
[26] [26] 李刚, 程耿东. 基于性能的抗震设计-理论、方法与应用[M]. 北京: 科学出版社, 2004.Li Gang, Cheng Gengdong. Seismic design theory method and application based on the performance [M].Beijing: Science Press, 2004. ( in Chinese)
SEISMIC DAMAGE ASSESSMENT PROCEDURE OF STRUCTURES BY USING SIMPLIFIED IDA