表1 数值模型骨料参数
Table 1 Aggregate parameters of the numerical model

尺寸/mm 小石/粒 中石/粒 5 mm网格数量150×150×150 32 313 29791 300×300×546 500×500×910 700×700×1274 472 2187 6002 4563 21123 57961 409310 1830000 4998000
随着我国城市化进程的加快,现代建筑向超高层、大跨度、重载工业厂房和地下建筑方向发展,框架柱承担的竖向荷载越来越大,但在实际工程中,为了满足轴压比限制的要求,设计人员常常又不得不增大柱子的截面尺寸,从而容易形成短柱(剪跨比小于2),甚至是超短柱(剪跨比小于1.5)[1],如高层或超高层建筑底部的钢筋混凝土柱、支承大型锅炉或煤斗等设备的柱子以及房屋设有夹层、错层出现的框架短柱等。钢筋混凝土短柱的特点在于刚度大、延性差、耗能量小[2―4],难以在抗震工程中得到应用。在水平地震力作用下,钢筋混凝土框架柱同时承受着轴力、弯矩和剪力,是一种偏压剪构件,以至于地震作用中,短柱往往首先发生剪切脆性破坏,从而导致整个结构受到灾难性破坏[5―7]。
至今,国内外学者针对轴压比对钢筋混凝土柱的受力性能和破坏机理进行了大量的研究,分析其破坏过程和破坏现象。但以轴压比为变化参数的试验研究还很不系统,存在诸多问题:1) 采取的轴压比均比较低[8―10];2) 轴压比变化幅值不大,试验对比少;3) 研究多集中在剪跨比大于2的长柱[11―14];而高轴压比作用下的压剪短柱,其试验研究却很少;4) 轴压比超限问题还有待于研究[15]。
同时,由于 1) 混凝土材料本身的非均质性及其力学非线性,以及2) 钢筋/混凝土相互作用的高度复杂性,从而导致钢筋混凝土短柱脆性压-剪破坏还受到尺寸效应(Size effect)的影响[16―17]。20世纪80年代至90年代,国内外对钢筋混凝土短柱的抗震性能的研究工作主要集中在截面尺寸为300以下的小尺寸试件[3,18-20]。近年来,试验研究中截面尺寸有所扩大,如何世钦等[21]进行 4个截面尺寸为700 mm×700 mm的钢筋混凝土柱的拟静力试验,但轴压比较小(仅为 0.05)。总体来说,对大尺寸钢筋混凝土短柱特别是在高轴压比作用下的抗震性能及尺寸效应依然还缺乏深入研究。
目前,限于大尺寸物理试验的复杂性,随着数值模拟技术日渐成熟与完善,数值模拟已经成为研究混凝土及钢筋混凝土构件的断裂破坏过程和宏观力学性能的有效途径[22―23],尤其是基于细观数值手段来研究混凝土材料及构件层面的尺寸效应,已成为近年来研究者关注的重要方法之一。
本文拟借助细观数值模拟方法,以钢筋混凝土短柱尤其是大尺寸钢筋混凝土短柱为研究对象,主要研究轴压比及截面尺寸对钢筋混凝土短柱的抗震性能的影响机制与规律。
解咏平[24]采用相似关系设计了6组钢筋混凝土短柱,选取3种截面尺寸,分别为300 mm×300 mm,500 mm×500 mm和700 mm×700 mm;配箍形式、配箍率、纵筋配筋率、纵筋布置形式、剪跨比等试验参数保持不变;而纵筋直径、纵筋间距、箍筋直径、箍筋间距、混凝土保护层厚度按照3∶5∶7的原则进行设计,开展3种尺寸在轴压比为0.4和0.6下的钢筋混凝土短柱压剪破坏的物理试验,分析研究钢筋混凝土短柱在水平反复加载下其受剪性能的尺寸效应规律。
在细观尺度范围内,混凝土材料往往被视为由骨料颗粒,砂浆基质以及界面过渡区(ITZ)[25―27]组成的三相复合材料。参同文献[28]工作,骨料假定为球形,采用二级配混凝土,即小石等效粒径为12 mm,中石等效粒径为30 mm,骨料体积分数约为 30%。采用表 1所示的骨料物理参数[29],根据Walraven公式[30],基于 Monte-Carlo方法,采用Fortran编程将骨料颗粒随机投放到砂浆中。考虑到计算量的影响,将连接骨料和砂浆的界面过渡区厚度设置为1 mm[23],首先建立起素混凝土短柱3D细观模型。将有限元网格投影到骨料结构上,然后根据各相组分在网格中的位置判定单元类型(如:骨料单元、砂浆基质单元及界面单元),并在此基础上插入钢筋,再将其导入商业软件ABAQUS,建立钢筋混凝土短柱三维细观模型(典型试件尺寸为:300 mm×300 mm×546 mm),如图1所示。其中,混凝土各组分采用八节点六面体减缩积分单元进行划分,钢筋采用梁单元进行离散,网格单元平均尺寸为5 mm。
表1 数值模型骨料参数
Table 1 Aggregate parameters of the numerical model

尺寸/mm 小石/粒 中石/粒 5 mm网格数量150×150×150 32 313 29791 300×300×546 500×500×910 700×700×1274 472 2187 6002 4563 21123 57961 409310 1830000 4998000
结合解咏平[24]的工作,本文在试验轴压比 0.4和0.6的基础上,分别对3种尺寸拓展模拟了轴压比为0,0.2,0.4的工况,共计12组不同尺寸、不同轴压比下的钢筋混凝土短柱,其相关几何参数如
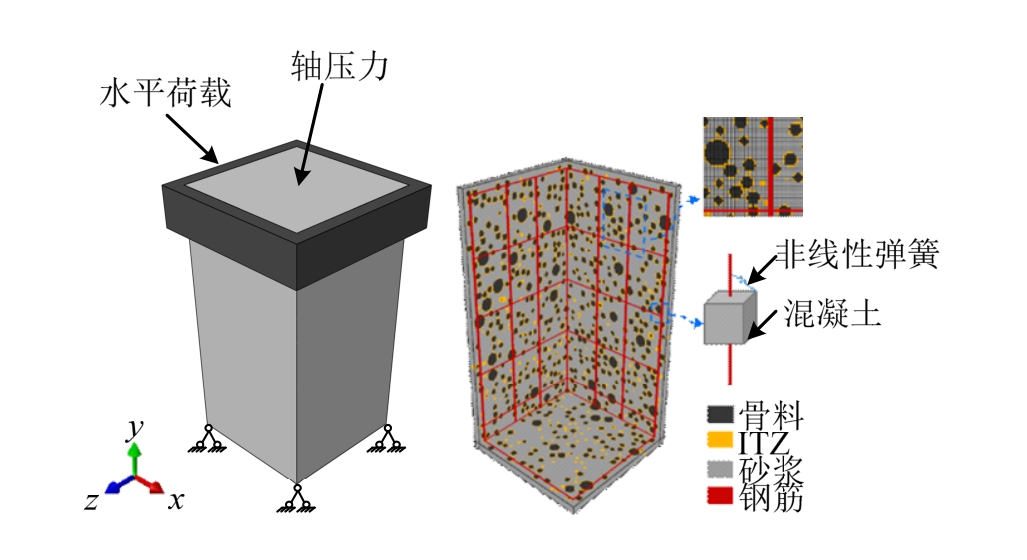
图1 钢筋混凝土柱三维细观数值模型及加载设置
Fig.1 3D meso-scale simulation model of RC column and loading schematic diagram
表2所示。表2试件名称中,第一个字母“C”代表 Cyclic loading(循环加载),第二个字母“C”代表Column(柱)。数字“3、5和7”分别代表柱子的横截面尺寸为 300 mm×300 mm,500 mm×500 mm和700 mm×700 mm;数字“0、0.2、0.4、0.6”分别代表轴压比;所有柱子的剪跨比均为2.0。试验采用的混凝土抗压强度为30.2 MPa。纵筋采用HRB400级钢筋,其平均屈服强度为426 MPa,配筋率为 1.51%,箍筋采用 HPB300级钢筋,其平均屈服强度为 390 MPa,其配箍率为0.338%。
表2 钢筋混凝土柱几何参数
Table 2 Geometrical parameters of the RC columns
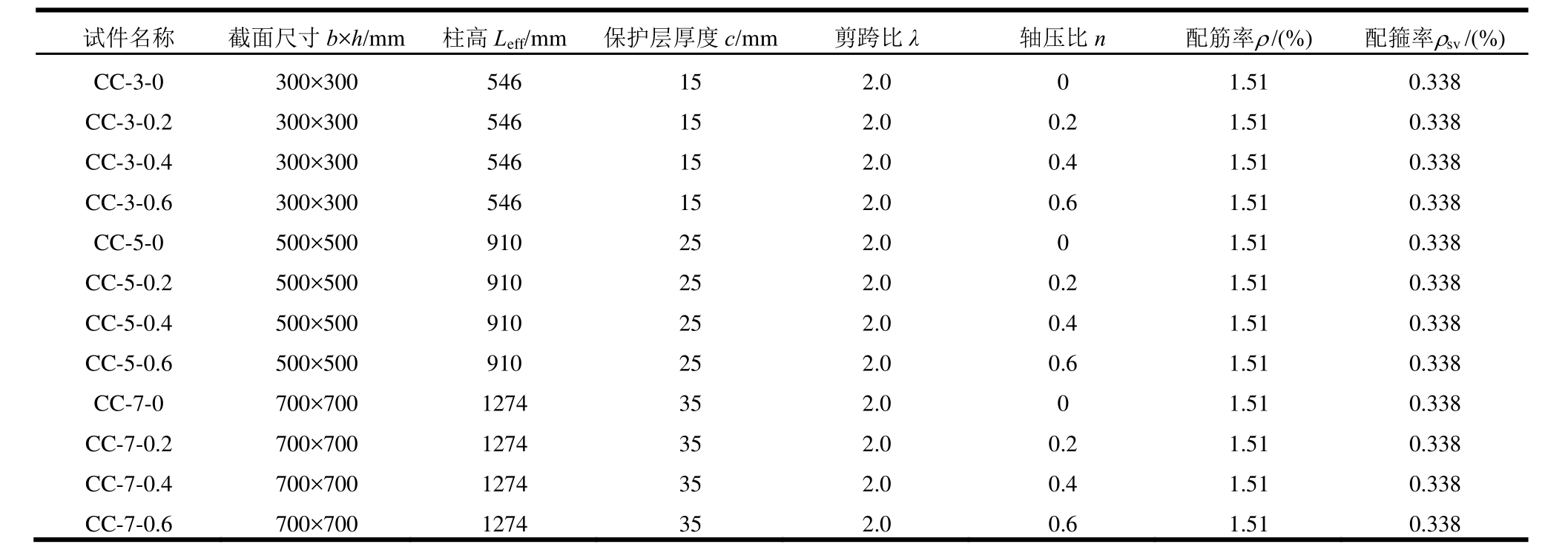
试件名称 截面尺寸b×h/mm 柱高Leff/mm 保护层厚度c/mm 剪跨比λ轴压比n配筋率ρ/(%) 配箍率ρsv/(%)CC-3-0 300×300 546 15 2.0 0 1.51 0.338 CC-3-0.2 300×300 546 15 2.0 0.2 1.51 0.338 CC-3-0.4 300×300 546 15 2.0 0.4 1.51 0.338 CC-3-0.6 300×300 546 15 2.0 0.6 1.51 0.338 CC-5-0 500×500 910 25 2.0 0 1.51 0.338 CC-5-0.2 500×500 910 25 2.0 0.2 1.51 0.338 CC-5-0.4 500×500 910 25 2.0 0.4 1.51 0.338 CC-5-0.6 500×500 910 25 2.0 0.6 1.51 0.338 CC-7-0 700×700 1274 35 2.0 0 1.51 0.338 CC-7-0.2 700×700 1274 35 2.0 0.2 1.51 0.338 CC-7-0.4 700×700 1274 35 2.0 0.4 1.51 0.338 CC-7-0.6 700×700 1274 35 2.0 0.6 1.51 0.338
骨料颗粒由于强度较高,在静力加载下一般不会产生大的变形,因此将骨料设定为弹性体。对于砂浆基质及界面过渡区,参照Majewski等[31]的工作,采用塑性损伤本构模型[32]来描述其力学性能。钢筋由于材料较均质,故采用理想弹塑性本构模型来描述其力学行为。本文采用《混凝土结构设计规范》(GB 50010—2010)[33]推荐的钢筋-混凝土粘结滑移(τ-s)本构关系模型,即通过非线性弹簧单元来描述钢筋与混凝土之间的粘结滑移,如图2所示。各关键点的确定方法见表3。这里需要说明的是,模型中钢筋与混凝土的粘结行为是一种宏观均质特性,即没有考虑细观组分与钢筋之间的粘结性能。
3种细观组分及钢筋力学参数,包括单轴压缩强度fc、单轴拉伸强度ft、弹性模量E、泊松比ν等参数见表 4。其中,“*”数据所示的骨料颗粒及砂浆基质的力学参数为实测数据,“^”所示的界面力学参数(特别是材料弹性模量和强度)无法通过试验测得。这里,通过开展大量对边长为150 mm的标准立方体混凝土试块单轴压缩试验来反演确定界面力学参数[26],其他力学数据均为默认值。基于该方法模拟到的混凝土单轴抗压强度是 30.1 MPa,与试验值30.2 MPa基本吻合。
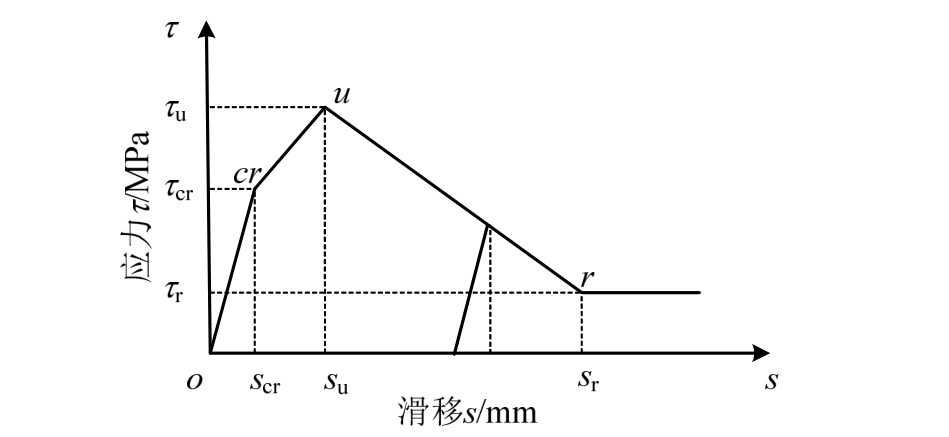
图2 钢筋混凝土粘结应力-滑移模型
Fig.2 The bond stress-slip model between steel and concrete
表3 粘结-滑移本构模型中参数
Table 3 Parameters utilized in the bond-slip model

关键点 开裂(cr) 峰值(u) 残余(r)应力τ/MPaτcr=2.5ftτu=3ftτr=ft滑移s/mmscr,l=0.025dsu,l=0.04dsr,l=0.55d
底端固定,对柱施加轴向荷载预定值,再对柱侧面顶部区域施加水平循环往复荷载,如图1所示。水平荷载采用位移控制加载方式。
表4 3种细观成分及钢筋的力学参数
Table 4 Mechanical parameters of the three meso-components of concrete and reinforcing bars utilized
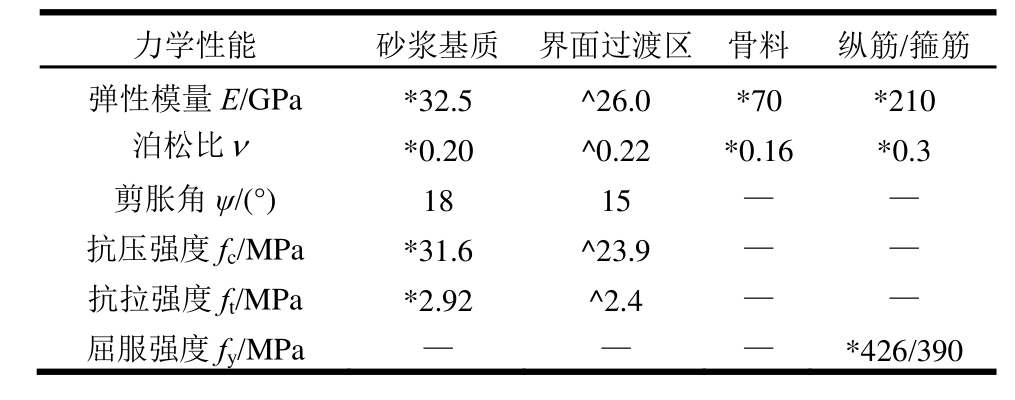
力学性能 砂浆基质 界面过渡区 骨料 纵筋/箍筋弹性模量E/GPa *32.5 ^26.0 *70 *210泊松比ν*0.20 ^0.22 *0.16 *0.3剪胀角ψ/(°) 18 15 — —抗压强度fc/MPa *31.6 ^23.9 — —抗拉强度ft/MPa *2.92 ^2.4 — —屈服强度fy/MPa — — — *426/390
为了验证利用的钢筋混凝土短柱细观数值模型来分析结构尺寸对钢筋混凝土短柱抗震性能影响的合理性和可靠性,对解咏平[24]开展的物理试验进行数值模拟对比。
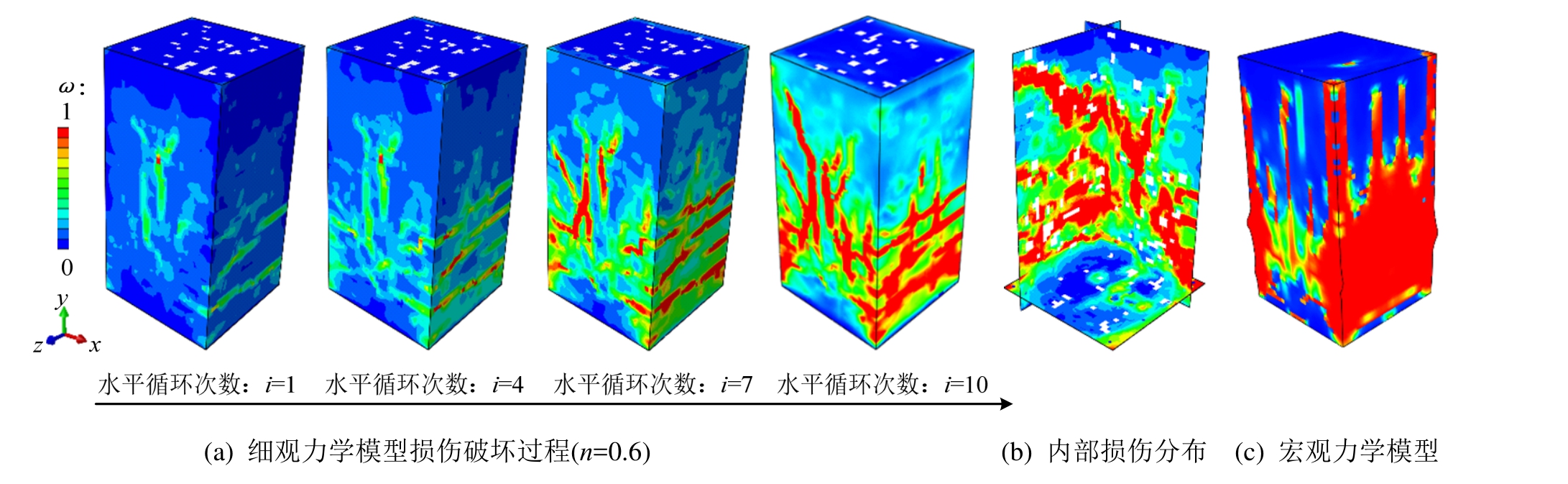
图3 钢筋混凝土柱CC-3-0.6损伤破坏过程
Fig.3 The damage process of the RC column CC-3-0.6

图4 尺寸为300 mm×300 mm×546 mm (n=0.6) 短柱模拟结果
Fig.4 Simulation results of a short RC column sized of 300 mm×300 mm×546 mm (n=0.6)
以试件CC-3-0.6为例,研究细观尺度下,柱子内部的裂缝开展过程,最终破坏模式,以及得到的滞回曲线。如图 3(a)所示(损伤因子ω=0表示完好无损,ω=1表示完全破坏),在弹性阶段,柱子根部出现了不是很明显的水平弯曲裂缝,同时,由于轴力的存在,出现了早期劈拉裂缝。随着荷载的增加,裂缝分布由柱子的根部快速向上发展,两侧水平裂缝向斜下方延伸,并接近中和轴。之前的根部裂缝沿水平方向不断延伸扩展,同时裂缝的宽度不断增大,当钢筋屈服,滞回曲线出现残余变形,试件开始进入弹塑性阶段。最后,当循环荷载达到极限荷载时,裂缝数量不断增多,在柱根部及加载点间出现了贯通的主斜裂缝,保护层脱落,发生脆性剪切破坏。图3(b)给出钢筋混凝土短柱试件内部的细观损伤分布云图,可以看出:损伤(裂缝)在细观层次上主要发生于力学性能相对于薄弱的界面过渡区中,并且受材料非均质性的影响,损伤较为分散。本文还给出了试件 CC-3-0.6的宏观力学模型模拟结果,如图3(c)所示。对比图3(c)和图3(a)、图3(b)发现,宏观力学模型虽然也能在一定程度上模拟裂缝的发展过程及其破坏模式,但损伤分布结果对称,不能表征混凝土材料力学性能的离散性和非均质性。而细观尺度模型能够充分体现混凝土材料的非均质性,如骨料颗粒的随机分布、细观组分力学性质的离散性等。对比图4(a)模拟最终破坏模式和图4(b)试验最终破坏模式发现,破坏模式基本相同,两者都是因为最后形成两条剪切裂缝而被破坏。图4(c)给出的是模拟和试验得到的滞回曲线。从图中可以看出,模拟结果和试验结果吻合良好。图4(d)所示的是钢筋笼的Mises应力云图。从图中可以看到,在水平循环往复荷载作用下,靠近根部的纵筋发生屈服,同时屈服的纵筋和力施加的方向一致。
综上所述,无论是在破坏模式上,还是在承载力等方面,本文采用的细观模型模拟的结果较宏观模型与试验结果更加吻合,可以更真实地反映钢筋混凝土构件受荷载作用的破坏过程和破坏模式,说明该方法的合理性和可靠性。
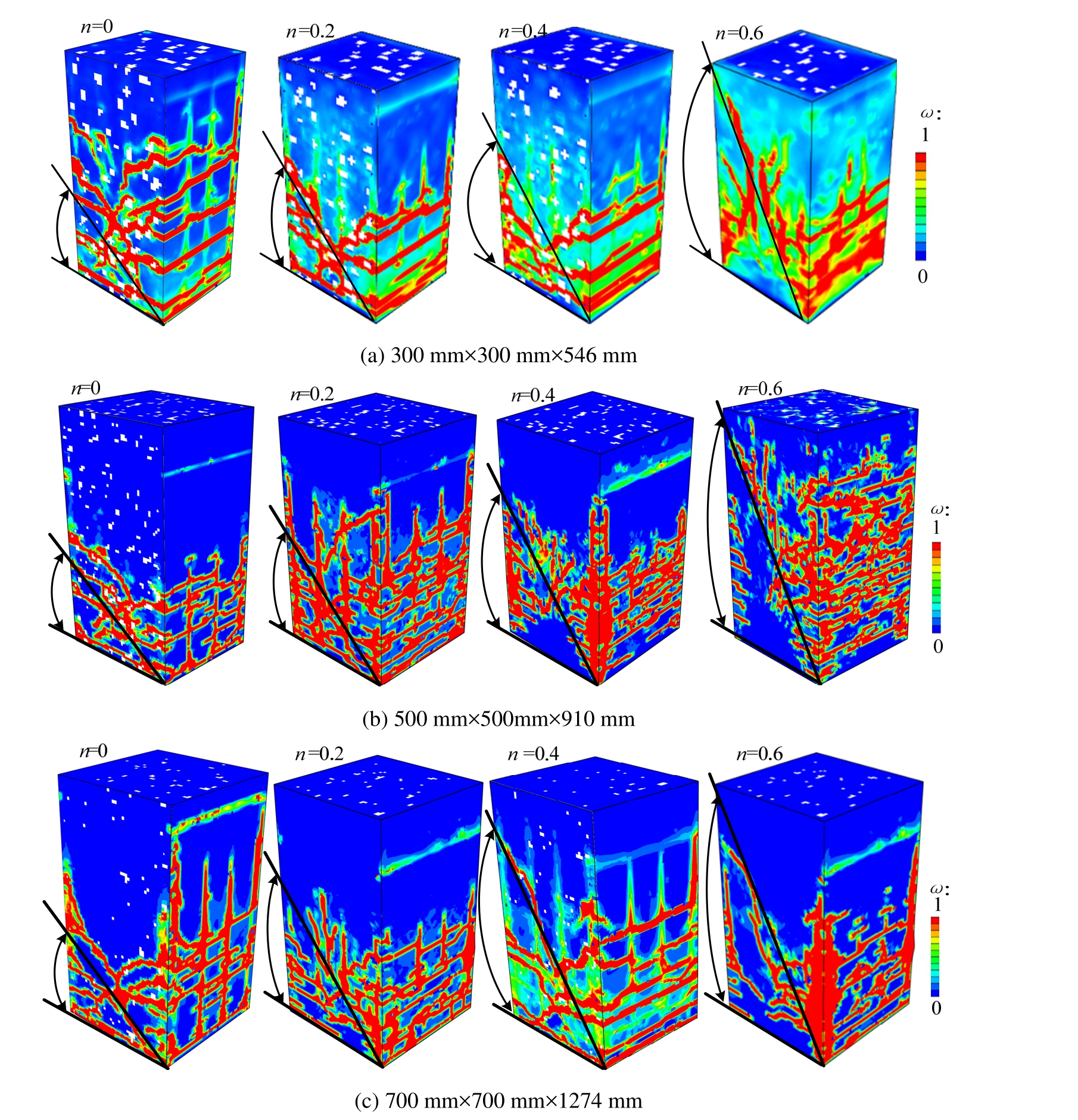
图5 不同尺寸柱子在不同轴压比下的最终破坏模式
Fig.5 The ultimate failure pattern of the RC columns with different structural sizes and axial compression ratios
不同尺寸(300 mm×300 mm、500 mm×500 mm、700 mm×700 mm),不同轴压比(n=0、n=0.2、n=0.4、n=0.6)下钢筋混凝土短柱在水平循环往复荷载作用下的最终破坏模式如图5所示。根据试件破坏的的形态特点,所有试件都属于剪切破坏,不过具体又可分为剪压破坏和斜压破坏两种破坏形态。以截面尺寸为300 mm×300 mm为例,轴压比较小时发生剪压破坏,其特点是首先出现水平裂缝,其次出现斜裂缝,接着主斜裂缝形成并开始屈服,同时,剪压区混凝土酥碎压裂,最后试件破坏。当轴压比较大时发生斜压破坏,在施加水平荷载之前,竖向荷载引起一定的初始损伤,能够改变主拉应力分布,从而导致裂缝的开展过程、发展角度产生变化,水平弯曲裂缝与剪切裂缝交替出现,并最终导致构件受剪破坏形态发生改变。此外,主裂缝的斜率随轴压比的增大而增大。不同尺寸的构件在相同轴压比情况下,其裂缝开展路径类似,最后出现大量斜裂缝,且这些斜裂缝基本上是相互平行的,伴随着大面积混凝土脱落。
图 6分别为截面尺寸为 300 mm×300 mm、500 mm×500 mm、700 mm×700 mm 试件在不同轴压比下的水平荷载-位移位移关系滞回曲线。可以看出,加载初期,试件处于弹性工作阶段,加载曲线的斜率变化小,正反向加卸载一次所形成的滞回环不明显,试件的滞回环面积很小且基本重合,试件刚度基本不变。随着位移和循环次数的增加,滞回曲线的斜率逐渐减小,刚度开始退化,残余变形逐渐增大。屈服后表现尤为明显,刚度出现明显的退化。加载至极限荷载后,荷载几乎没有减小而试件就突然发生剪切性破坏。随着轴压比的增大,试件的最大水平承载力逐渐提高,但增加的趋势随轴压比的增大而减小。极限荷载所对应的位移减小,同时,峰值荷载的下降段变陡。滞回曲线的形状由梭形向弓形过渡,滞回环的面积逐渐变小,捏拢效应愈加明显,耗能能力及延性逐渐减弱。因此,在实际工程中,提高钢筋混凝土短柱的抗剪承载力不宜过度依赖轴压比的增加。
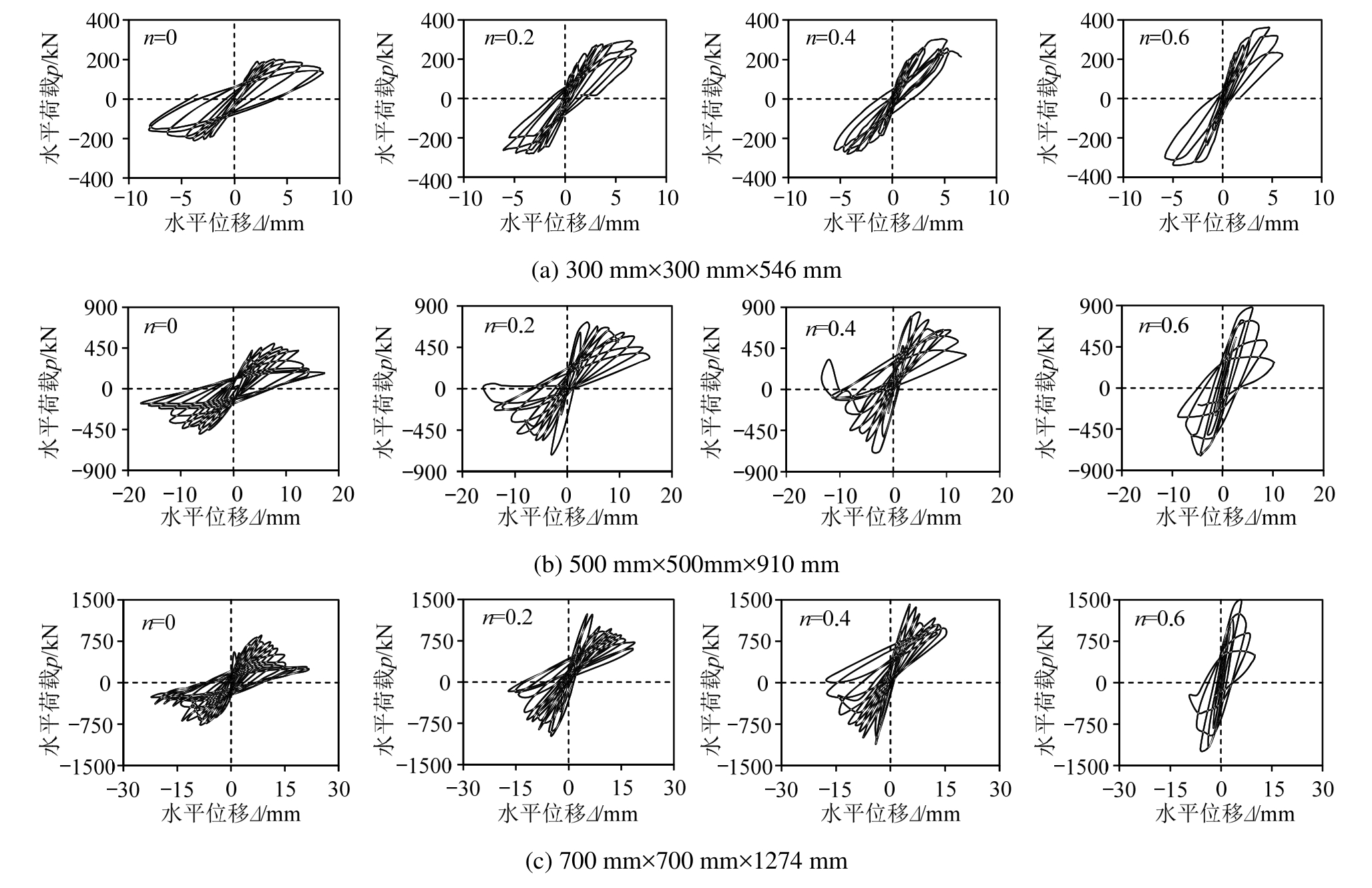
图6 12组试件在不同轴压比下的滞回曲线
Fig.6 Hysteretic curves of the twelve RC columns under different axial compression ratios
采用位移延性系数来反映试件的延性性能,位移延性系数定义为试件的极限位移和屈服位移的比值,即μ=Δu/Δy,Δu为极限位移,Δy为用能量等值法求得的屈服位移[34]。轴压比和结构截面尺寸是影响构件延性的主要因素。
图7给出的是不同轴压比下,截面尺寸与位移延性系数的关系。从图中可以看出,相同轴压比下,位移延性系数随钢筋混凝土短柱截面尺寸的增大而减小,但减小的趋势随轴压比的增大而增大。构件 截 面 尺 寸 由 300 mm×300 mm 增 加 到700 mm×700 mm,当n=0时,位移延性系数减小了14.5%,而当n=0.6时,位移延性系数减小了20%。
相同截面尺寸下,位移延性系数随轴压比的增加而减小,值得注意的是,减小趋势随轴压比的增加而减小,以截面尺寸 300 mm×300 mm为例,当轴压比n由0增大到0.2,0.2增大到0.4,0.4增大到0.6,位移延性系数依次减小了24.9%,14.7%,8.9%。由此可知,随着轴压比和截面尺寸的增加,试件的延性明显减弱,变形能力降低。
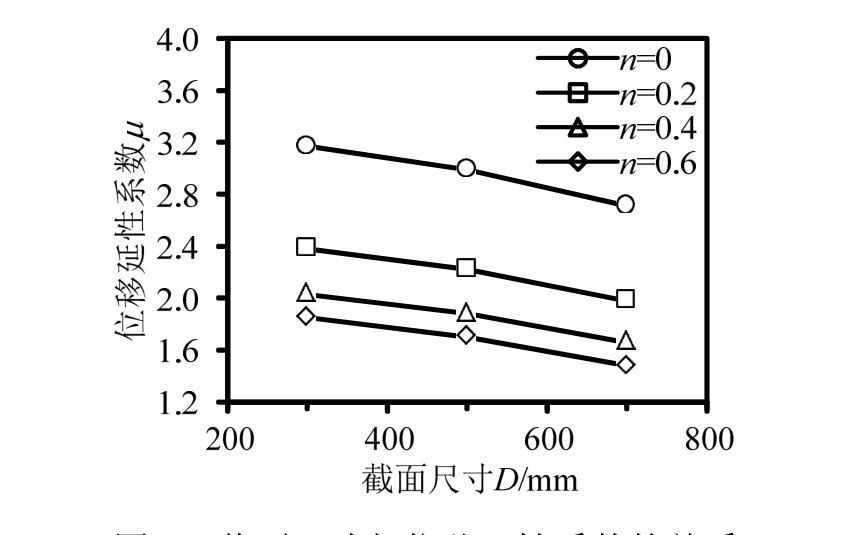
图7 截面尺寸与位移延性系数的关系
Fig.7 The relationship between structure size and displacement ductility coefficient
构件的耗能能力是对其抗震性能评价的一个重要指标。一般文献都是采用等效黏滞阻尼系数he来评价构件的耗能能力。由于试件破坏时极限位移角随试件截面尺寸的变化而不同,故等效黏滞阻尼系数与试件截面尺寸的关系不太明确,本文引入梁书亭等[35]的平均耗能系数的概念,来反映构件的耗能能力,即μe=E/(mEy)。其中E为试件屈服后至破坏前的各滞回曲线面积的总和,Ey为名义弹性能量,用Ey=VyΔy/2来表示,Vy为屈服荷载,Δy为屈服位移,m为试件屈服后循环次数。图8给出的是不同轴压比下,截面尺寸与平均耗能系数的关系。从图中可以看出,相同轴压比下,平均耗能系数随钢筋混凝土短柱截面尺寸的增大而减小,但减小的趋势随轴压比的增大而增大。构件截面尺寸由300 mm×300 mm 增加到 700 mm×700 mm,当n=0时,平均耗能系数减小了9.6%,而当n=0.6时,平均耗能系数减小了14.7%。
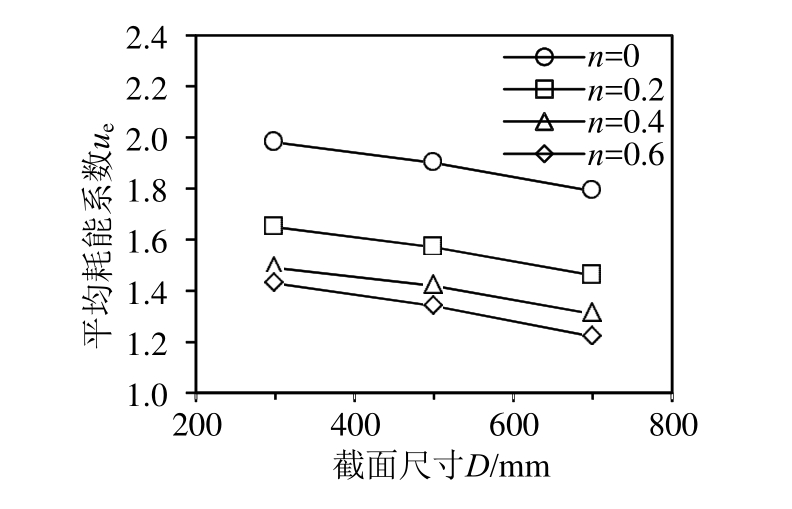
图8 截面尺寸与平均耗能系数的关系
Fig.8 The relationship between structure size and average energy consumption coefficient
相同截面尺寸下,平均耗能系数随轴压比的增加而减小,值得注意的是,减小趋势随轴压比的增加而减小,以截面尺寸 300 mm×300 mm为例,当轴压比n由0增大到0.2,0.2增大到0.4,0.4增大到0.6,平均耗能系数依次减小了16.7%,9.7%,4%。由此可知,轴压比和截面尺寸是影响钢筋混凝土短柱耗能能力的主要因素,随着轴压比和截面尺寸的增加,钢筋混凝土短柱的耗能能力减弱。
图9给出的是在不同轴压比下,12根钢筋混凝土短柱模型名义抗剪强度(σNu=V/bh0)同截面尺寸的关系。从图9中明显可以看到,在压弯剪作用下,钢筋混凝土短柱的抗剪承载力随着截面尺寸的增加而减小,尺寸效应明显。值得注意的是,相同截面尺寸下,名义抗剪强度随轴压比的增加而增大,但增大的趋势减小。通过对比可以发现,轴压比较大的构件,其名义抗剪强度降低趋势增强。而实际上,构件破坏时脆性越大,尺寸效应越明显。轴压比较大时,竖向荷载引起初始损伤,加上在反复荷载作用下,试件裂缝的开展与闭合使混凝土受到较多损伤,继而致使构件的脆性更大,最终导致构件表现出更明显的尺寸效应。
Bažant基于断裂力学理论给出了适用于混凝土材料及构件的尺寸效应理论公式(SEL)[36]:
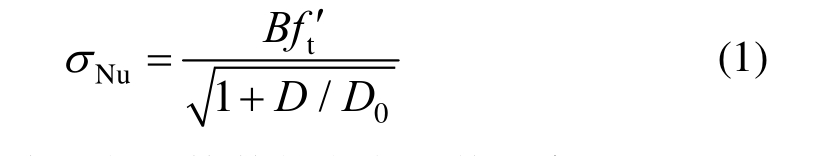
式中:σNu为混凝土构件的名义抗剪强度;B和D0为经验系数;D为混凝土构件的特征尺寸(这里即为柱子截面尺寸);ft′为混凝土抗拉强度。
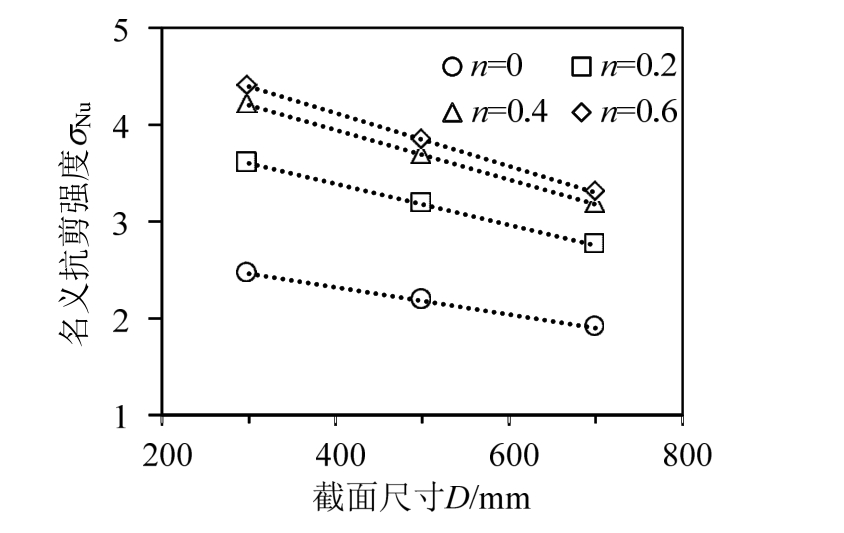
图9 试件名义抗剪强度与截面尺寸的关系
Fig.9 Nominal strength vs structure size of specimen
大量的试验研究工作[17,23,37―38]表明:Bažant尺寸效应律不仅可以很好地描述混凝土材料层次破坏的尺寸效应,还可以较好地描述钢筋混凝土构件层次破坏的尺寸效应规律。鉴于此,本文尝试探讨Bažant尺寸效应律是否可以描述钢筋混凝土短柱压剪破坏的尺寸效应规律。
对模拟数据进行回归分析后,可得到钢筋混凝土短柱名义强度随构件变化的双对数曲线,如图10所示。同时,还将模拟结果同 Bažant尺寸效应律(Bažant’s SEL)、线弹性断裂力学理论(LEFM,针对完全脆性材料)以及塑性强度(Strength criterion:针对塑性材料,不考虑尺寸效应)进行拟合对比,拟合相关系数R2为0.98,说明钢筋混凝土短柱尺寸效应结果与Bažant尺寸效应律吻合良好。从图10还可以看到,轴压比较大的数据点比轴压比小的更接近准脆性的曲线,即斜率为-1/2的直线,说明轴压比大的构件,其尺寸效应更明显。

图10 名义强度随构件尺寸变化的对数曲线
Fig.10 Logarithmic curve of nominal strength vs structure size
我国现行《混凝土结构设计规范》(GB 50010—2010)[33]柱斜截面抗剪承载力Vu计算公式:
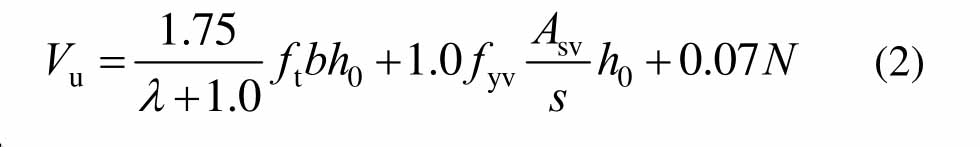
式中:λ为剪跨比;ft为混凝土抗拉强度设计值;fyv为箍筋抗拉强度设计值;Asv为配置在同一截面内各肢的全部截面面积;s沿构件长度方向箍筋的间距;N为与剪力设计值V相应的轴向压力设计值;当N>0.3fcA时,取N=0.3fcA;A为构件的截面面积。
从式(2)可以看出,规范建议的承载力设计公式不能反映结构尺寸的影响,即名义抗剪强度为恒定值,这与第3节分析结果相悖。因此,需要对该承载力设计公式进行修正。
为分析截面尺寸高度对钢筋混凝土柱抗剪承载力的影响,将模拟结果与式(2)计算得到的结果进行比较,从而得出安全储备系数(Vt/Vc)与截面尺寸高度的关系,如图 11所示。其中,Vt为模拟值,Vc为按照规范获得的计算值。
从图 11可以看出,虽然计算值偏于保守,但随截面尺寸的增加,柱子承载力安全储备系数呈降低趋势,而且当n=0.6,截面尺寸从300 mm增加到700 mm时,安全储备系数降低可以达到24.9%。本质上来说,该安全储备系数的降低是由于规范计算理论中未考虑尺寸效应这一因素。
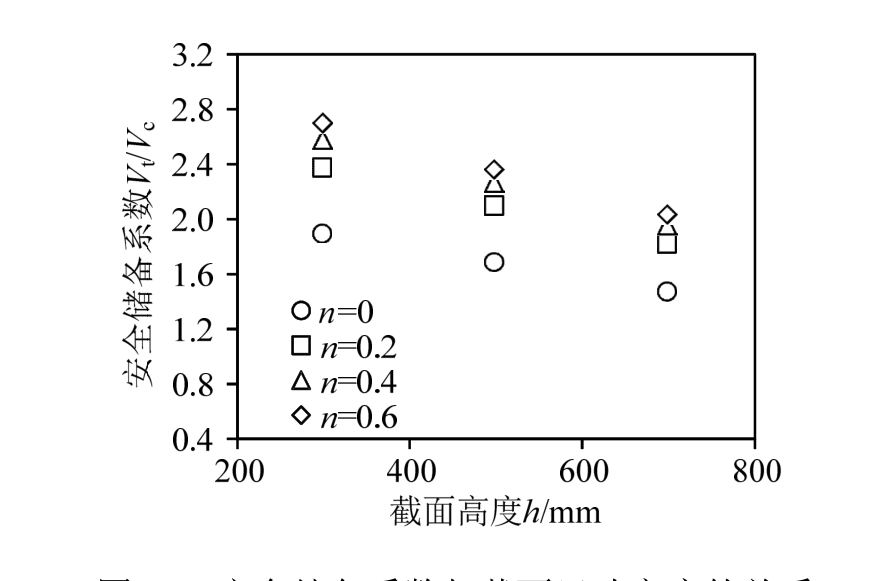
图11 安全储备系数与截面尺寸高度的关系
Fig.11 The relationship between safety coefficient and cross section height
实际上,钢筋混凝土柱斜截面抗剪承载性能的尺寸效应行为源于两个方面,即为:1) 混凝土材料本身的尺寸效应;2) 箍筋与周围混凝土间复杂的非线性相互作用。鉴于此,针对式(2)右侧3项的贡献,提出柱斜截面受剪承载力Vu的修正公式为:
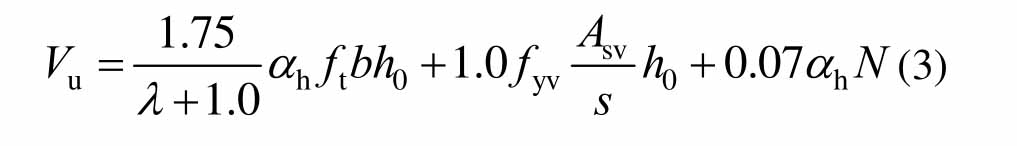
式中:αh(<1)为截面尺寸效应影响系数(应是为与截面尺寸相关的函数),反映的是由于尺寸效应而带来的承载力的减弱。借鉴Bažant基于裂缝带模型给出的适用于混凝土尺寸效应理论公式,假定αh可满足如下形式:
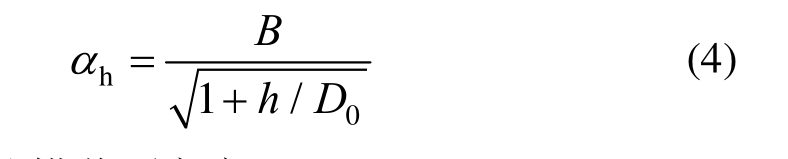
式中:h为柱横截面高度。
由于混凝土强度存在尺寸效应,而N=nfcA,若仍用轴心抗压强度值计算出的轴力会偏大,从而会高估构件的抗剪承载力,所以需要对轴心抗压强度值计算出来的轴力进行修正,并且大尺寸构件轴力对抗剪承载力的影响可采用与混凝土强度影响相同的修正系数来考虑。
通过将模拟数据线性拟合回归分析后,得出B=4.4,D0=17.31,考虑到αh的性质及小尺寸试件实际情况,且由式(4)可知:D=318 mm 时,αh=1.0,因此建议当h≤300 mm 时,αh=1.0。进而得到αh与h的关系曲线,如图12所示。图12中的试验数据是收集的解咏平[24]作试验的数据。
图 13为考虑尺寸效应影响系数的钢筋混凝土柱抗剪承载力的计算结果,修正后安全储备系数随截面高度的增加趋于一条水平线,即大小试件的安全储备系数趋于一致。
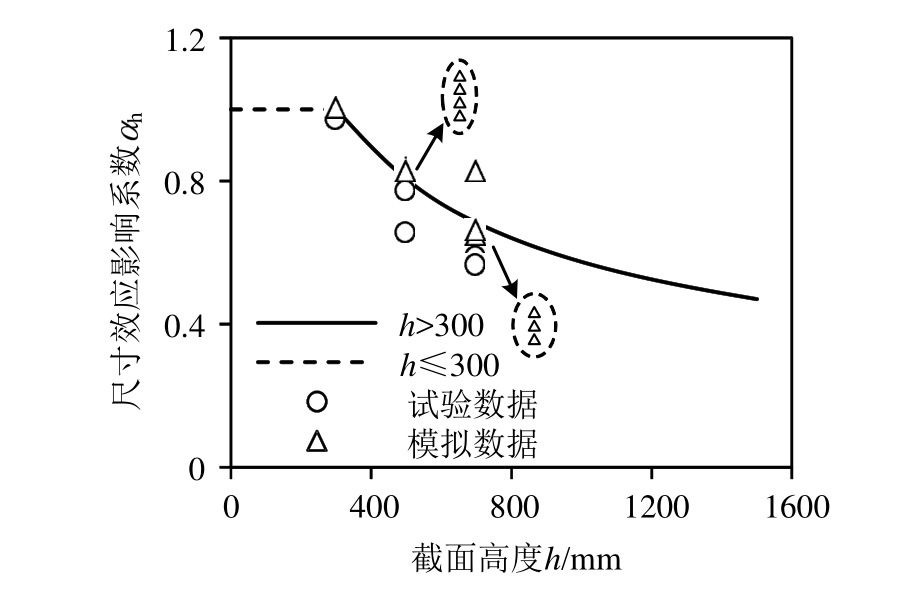
图12 尺寸效应影响系数与截面高度的关系
Fig.12 The relationship between size effect coefficient and cross section height
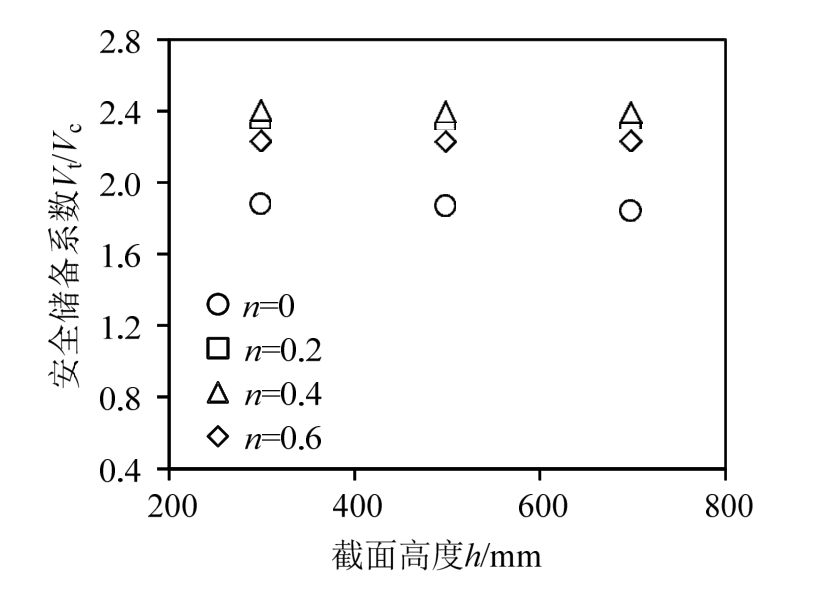
图13 新算法的安全储备系数与截面尺寸高度的关系
Fig.13 The relationship between safety coefficient and cross section size based on new theory
将混凝土视为有骨料颗粒、砂浆基质以及界面过渡区组成的三相复合材料,考虑钢筋与混凝土之间的非线性粘结滑移行为,建立了钢筋混凝土短柱在压-剪作用下的细观尺度力学分析模型。首先通过现有的试验结果进行对比来验证模型的合理性及可靠性。继而在试验的基础上,拓展模拟了不同轴压比下,横截面尺寸为300 mm×300 mm,500 mm×500 mm和700 mm×700 mm钢筋混凝土短柱在水平荷载和竖向荷载联合作用下的剪切破坏行为,研究了轴压比对钢筋混凝土短柱抗震性能的影响。最后,基于相关试验及模拟数据,提出了能反映尺寸效应的柱抗剪承载力计算理论公式。结果表明:
(1) 随着轴压比的增大,柱的抗剪承载力增强,但柱的变形能力随之减弱。
(2) 钢筋混凝土短柱的抗剪强度、位移延性系数、耗能能力等抗震性能指标均随结构尺寸的增加而降低,表现出明显的尺寸效应。
(3) 轴压比越大,柱破坏越具脆性,柱的压剪破坏行为尺寸效应越为显著。
(4) 提出的钢筋混凝土柱抗剪承载力计算公式反映了尺寸效应的影响,使不同尺寸钢筋混凝土短柱抗剪承载力的安全储备系数基本一致。
值得注意的是,Bažant尺寸效应律是Bažant根据断裂力学理论推导出来适用于素混凝土材料的尺寸效应规律。而钢筋混凝土构件层次的尺寸效应,既包含混凝土材料层次的尺寸效应,还包含钢筋与混凝土之间复杂的非线性相互作用问题。本质上说,Bažant尺寸效应律难以全面解释钢筋混凝土构件层次的尺寸效应规律,因此还需进行深入的研究。
[1]Ding H, Liu Y, Han C, et al. Seismic performance of high-strength short concrete column with high-strength stirrups constraints [J]. Transactions of Tianjin University, 2017, 23(4): 360―369.
[2]史庆轩, 王朋, 王秋维. 钢筋混凝土柱剪切粘结破坏影响因素分析[J]. 工程力学, 2013, 30(11): 136―142.Shi Qingxuan, Wang Peng, Wang Qiuwei. Analysis of the influencing factors for the shear-bond failure of RC columns [J]. Engineering Mechanics, 2013, 30(11):136―142. (in Chinese)
[3]Colomb F, Tobbi H, Ferrier E, et al. Seismic retrofit of reinforced concrete short columns by CFRP materials [J].Composite Structures, 2008, 82(4): 475―487.
[4]Promis G, Ferrier E, Hamelin P. Effect of external FRP retrofitting on reinforced concrete short columns for seismic strengthening [J]. Composite Structures, 2009,88(3): 367―379.
[5]马颖, 张勤, 贡金鑫. 钢筋混凝土柱弯剪破坏恢复力模型骨架曲线[J]. 建筑结构学报, 2012, 33(10): 116―125.Ma Ying, Zhang Qin, Gong Jinxin. Skeleton curves of restoring force model of reinforced concrete columns failed in flexure-shear [J]. Journal of Building Structures,2012, 33(10): 116―125. (in Chinese)
[6]Thanh N T C, Li B. Ultimate displacement of reinforced concrete columns with light transverse reinforcement [J].Journal of Earthquake Engineering, 2013, 17(2): 282―300.
[7]Huang L, Xu L, Chi Y, et al. Experimental investigation on the seismic performance of steel–polypropylene hybrid fiber reinforced concrete columns [J].Construction and Building Materials, 2015, 87(1-2):16―27.
[8]殷小激, 黄小坤, 田春雨, 等. 配置大间距高强纵筋的钢筋混凝土柱抗震性能试验研究[J]. 建筑结构学报,2016, 37(8): 41―47.Yin Xiaoji, Huang Xiaokun, Tian Chunyu, et al.Experimental study on seismic behavior of RC columns with large spacing and high strength longitudinal reinforcements [J]. Journal of Building Structures, 2016,37(8): 41―47. (in Chinese)
[9]Aboutaha R S, Machado R I. Seismic resistance of steel-tubed high-strength reinforced-concrete columns[J]. Journal of Structural Engineering, 1999, 125(5):485―494.
[10] Li Y A, Huang Y T, Hwang S J. Seismic response of reinforced concrete short columns failed in shear [J]. ACI Structural Journal, 2014, 111(4): 945―954.
[11] 顾祥林, 蔡茂, 林峰. 地震作用下钢筋混凝土柱受力性能研究[J]. 工程力学, 2010, 27(11): 160―165.Gu Xianglin, Cai Mao, Lin Feng. Study on behavior of RC columns subjected to earthquake [J]. Engineering Mechanics, 2010, 27(11): 160―165. (in Chinese)
[12] Sezen H, Moehle J P. Seismic tests of concrete columns with light transverse reinforcement [J]. ACI Structural Journal, 2006, 103(6): 842―852.
[13] Brachmann I, Browning J A, Matamoros A B. Drift dependent confinement requirements for reinforced concrete columns under cyclic loading [J]. ACI Structural Journal, 2004, 101(5): 669―677.
[14] 解咏平, 李振宝, 杜修力, 等. 低周反复荷载作用下钢筋混凝土柱抗震性能尺寸效应试验研究[J]. 建筑结构学报, 2013, 34(12): 86―93.Xie Yongping, Li Zhenbao, Du Xiuli, et al. Experimental study on size effect of seismic behavior for reinforced concrete columns under low cycle reversed loading [J].Journal of Building Structures, 2013, 34(12): 86―93. (in Chinese)
[15] 张国军, 吕西林, 刘伯权. 钢筋混凝土框架柱在轴压比超限时抗震性能的研究[J]. 土木工程学报, 2006,39(3): 47―54.Zhang Guojun, Lü Xilin, Liu Boquan. Seismic behavior of reinforced concrete frame columns with excessive axial compression ratios [J]. China Civil Engineering Journal, 2006, 39(3): 47―54. (in Chinese)
[16] 李冬, 金浏, 杜修力. 钢筋混凝土柱轴心受压性能及尺寸效应的细观数值研究[J]. 水利学报, 2016, 47(2):209―218.Li Dong, Jin Liu, Du Xiuli. A meso-scale numerical study on the axial compression performance and size effect of reinforced concrete columns [J]. Journal of Hydraulic Engineering, 2016, 47(2): 209―218. (in Chinese)
[17] Li D, Jin L, Du X, et al. Size effect tests of normal-strength and high-strength RC columns subjected to axial compressive loading [J]. Engineering Structures,2016, 109: 43―60.
[18] Nojavan A, Schultz A E, Chao S H, et al. Influence of cross-sectional size on seismic performance of reinforced concrete columns [J]. ACI Structural Journal, 2017,114(2): 311―321.
[19] Zhou X, Liu J. Seismic behavior and strength of tubed steel reinforced concrete (SRC) short columns [J].Journal of Constructional Steel Research, 2010, 66(7):885―896.
[20] Ma H, Xue J, Liu Y, et al. Cyclic loading tests and shear strength of steel reinforced recycled concrete short columns [J]. Engineering Structures, 2015, 92: 55―68.
[21] 何世钦, 安雪晖, 小原孝之, 等. 低周反复荷载下夹式钢筋对钢筋混凝土柱破坏形态的影响[J]. 土木工程学报, 2009, 42(2): 17―23.He Shiqin, An Xuehui, Taku M, et al. Effects of clip reinforcement on failure modes of reinforced concrete columns under low cycle reversed loading [J]. China Civil Engineering Journal, 2009, 42(2): 17―23. (in Chinese)
[22] Hoover C G, Bažant Z P. Cohesive crack, size effect,crack band and work-of-fracture models compared to comprehensive concrete fracture tests [J]. International Journal of Fracture, 2014, 187(1): 133―143.
[23] Jin L, Li D, Du X, et al. Experimental and numerical study on size effect in eccentrically loaded stocky rc columns [J]. Journal of Structural Engineering, 2017,143(2): 04016170.
[24] 解咏平. 钢筋混凝土柱抗震性能尺寸效应研究[D]. 北京: 北京工业大学, 2013.Xie Yongping. Size effect on seismic behavior of reinforced concrete columns [D]. Beijing: Beijing University of Technology, 2013. (in Chinese)
[25] Rios R D, Riera J D. Size effects in the analysis of reinforced concrete structures [J]. Engineering Structures,2004, 26(8): 1115―1125.
[26] 杜敏, 金浏, 李冬, 等. 骨料粒径对混凝土劈拉性能及尺寸效应影响的细观数值研究[J]. 工程力学, 2017,34(9): 54―63.Du Min, Jin Liu, Li Dong, et al. Mesoscopic simulation study of the influence of aggregate size on mechanical properties and specimen size effect of concrete subjected to splitting tensile loading [J]. Engineering Mechanics,2017, 34(9): 54―63. (in Chinese)
[27] 杜修力, 金浏. 细观分析方法在混凝土物理/力学性质研究方面的应用[J]. 水利学报, 2016, 47(3): 355―371.Du Xiuli, Jin Liu. Applications of meso-scale analysis methods on the study of the physical/mechanical properties of concrete [J]. Journal of Hydraulic Engineering, 2016, 47(3): 355―371. (in Chinese)
[28] 金浏, 杜修力. 钢筋混凝土构件细观数值模拟分析[J].水利学报, 2012, 43(10): 1230―1236.Jin Liu, Du Xiuli. Meso numerical simulation of reinforced concrete members [J]. Journal of Hydraulic Engineering, 2012, 43(10): 1230―1236. (in Chinese)
[29] GB/T 50081—2002, 普通混凝土力学性能试验方法标准[S]. 北京: 中国建筑工业出版社, 2003.GB/T 50081—2002, Standard for test method of mechanical properties on ordinary concrete [S]. Beijing:China Architecture & Building Press, 2003. (in Chinese)
[30] Walraven J C, Reinhardt H W. Theory and experiments on the mechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading [J].HERON, 1981, 26 (1A): 1―68.
[31] Majewski T, Bobinski J, Tejchman J. FE analysis of failure behaviour of reinforced concrete columns under eccentric compression [J]. Engineering Structures, 2008,30(2): 300―317.
[32] Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, 1998, 124(8): 892―900.
[33] GB 50010—2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50010—2010, Code for design of concrete structures[S]. Beijing: China Architecture & Building Press, 2010.(in Chinese)
[34] 王全凤, 沈章春, 杨勇新, 等. HRB400级钢筋混凝土短柱抗震试验研究[J]. 建筑结构学报, 2008, 29(2):114―117.Wang Quanfeng, Shen Zhangchun, Yang Yongxin, et al.Seismic behavior of HRB400 reinforcement concrete short columns [J]. Journal of Building Structures, 2008,29(2): 114―117. (in Chinese)
[35] 梁书亭, 丁大钧, 陆勤. 钢筋混凝土复合配箍柱铰的延性和抗震耗能试验研究[J]. 工业建筑, 1994(11):16―20.Liang Shuting, Ding Dajun, Lu Qin. Experimental study of earthquake-resistant energy-dissipation and ductility of reinforced concrete column hinge with composite stirrups [J]. Industrial Construction, 1994(11): 16―20.(in Chinese)
[36] Bažant Z P. Size effect in blunt fracture: concrete, rock,metal [J]. ASCE Journal of Engineering Mechanics,1984, 110(4): 518―535.
[37] Syroka-Korol E, Tejchman J. Experimental investigations of size effect in reinforced concrete beams failing by shear [J]. Engineering Structures, 2014, 58(7): 63―78.
[38] Barbhuiya S, Choudhury A M. A study on the size effect of RC beam–column connections under cyclic loading[J]. Engineering Structures, 2015, 95: 1―7.
EFFECT OF STRUCTURAL SIZE ON SEISMIC PERFORMANCE OF REINFORCED CONCRETE SHORT COLUMNS—A MESO-SCALE STUDY