
图1 腐蚀试件示意图
Fig.1 Schematic diagram of corrosion test
钢结构具有质轻高强、结构多样化等优点,广泛地应用于大型桥梁、海上采油平台、工业与民用建筑。现有规范认为钢结构在服役期间结构性能保持不变,可以通过防护措施等保证钢结构的耐久性[1-3]。但在现实情况中,许多处于腐蚀环境下的钢结构工程,会出现较严重的锈蚀问题,导致材料及结构性能逐渐退化,其耐久性难以得到保证,地震作用下结构发生破坏的概率也将增大。
徐善华等[4-7]发现锈蚀不仅导致构件截面面积减小,而且导致钢材强度和延性降低。Albrecht等[8]发现随着锈蚀程度的增加,钢梁的疲劳寿命呈迅速下降趋势,点蚀对疲劳寿命的影响远高于全面锈蚀。郑山锁等[9-10]发现随锈蚀程度的增大,锈蚀钢框架柱的极限承载力和耗能能力显著下降,强度和刚度退化明显。锈蚀导致钢框架的力学性能指标下降。对不同锈蚀程度的钢框架结构,未锈蚀的指标限值已不能用来评估锈蚀结构的抗震性能,因此需要对锈蚀钢结构的抗震性能水平进行重新定义,进而可以准确评估不同锈蚀程度的钢结构抗震性能。
本文选用层间位移角作为评价结构抗震能力的指标,提出一种有效评估锈蚀钢结构地震响应的易损性评定方法。通过静力弹塑性分析方法得到不同龄期的钢框架结构最大层间位移角限值。以PGA为地震动强度指标,以最大层间位移角θmax为地震需求指标,运用IDA方法得到不同龄期的钢框架地震易损性曲线。并基于不同修正限值,对最大层间位移角的易损性曲线进行比较,探讨锈蚀钢结构的“修正限值”对评估结构抗震能力的影响。
采用中性盐雾室内加速试验法加速Q235钢材的腐蚀速度,并将加速腐蚀时间通过腐蚀量相同的原则,等效为钢结构最有可能处于的典型大气环境中的腐蚀时间,参考表2 ISO12944-2[11],此处环境类别取C3典型大气环境。
试验采用YWX/Q-020型号盐雾箱。腐蚀溶液为质量分数5% NaCl溶液,pH值为6.2~7.2。试件固定在与水平面成30º角的方向,保证钢板两面腐蚀情况一致。图1为腐蚀试件示意图,试件在盐雾箱内摆放如图2所示。
盐雾箱内的环境见文献[12]。喷雾方式采用间隙喷雾,12个小时为一个周期,总试验时间为4200 h。每一组试件中按照 ISO8407[13]的规定,试验前进行酸洗除锈、烘干,通过失重率测定其锈蚀程度。

图1 腐蚀试件示意图
Fig.1 Schematic diagram of corrosion test

图2 试件盐雾箱内摆放图
Fig.2 Test pieces in salt spray box
本文采用锈蚀率来评定试件的腐蚀程度,对于评定局部腐蚀仅作为参考数据。定义失重率Dw为:
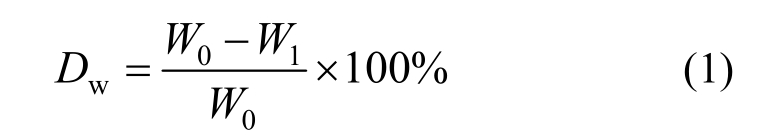
式中:Dw为锈蚀率;W0为未锈试件的质量;W1为锈蚀试件的质量。
通过对8 mm钢板进行为期4200 h的加速腐蚀试验,得到8 mm厚度钢材的锈蚀率和厚度损失如表1所示。研究发现处于相同环境中的钢材腐蚀速率基本相等,因而在相同条件下钢材腐蚀后的厚度损失相等[14],可以把8 mm钢板加速腐蚀的腐蚀速率和厚度损失量推广应用到本文计算模型中的构件。
另外钢材的室内加速腐蚀试验的腐蚀时间换算成大气腐蚀年限的关系式为[14]:

式中:T为换算成的大气腐蚀年限;D为8 mm钢板腐蚀厚度;K为大气环境腐蚀速率。
根据表2中环境分类可以看出,大部分钢结构基本都处在C2~C3大气环境中。按照研究目的及国际标准化组织对环境的分类可以认为结构处于 C3典型环境中。根据文献[14]中不同城市的腐蚀速率数据,以广州为例,腐蚀速率K取40 µm/a。
按照腐蚀损伤量相同的原则,将表1中的盐雾加速腐蚀造成的钢板腐蚀厚度与表2所示的腐蚀环境中Q235钢在大气中的腐蚀速率进行比较,可以得到盐雾加速腐蚀时间折合成 ISO12944-2腐蚀大气环境下的腐蚀时间,如表3所示。
表1 8 mm钢板厚度损失量
Table 1 Thickness loss of 8 mm steel plates

加速腐蚀时间/h 0 350 700 1000 1400 1700 2000 2800 3300 4200锈蚀率/(%) 0 3.82 4.26 5.83 7.24 7.61 8.42 9.64 11.14 11.54厚度损失/µm 0 310 340 470 580 610 670 770 890 920
表2 国际标准化组织ISO 12944-2
Table 2 International organization for standardization ISO 12944-2

注:表中a表示时间单位“年”,下表同义。
腐蚀类别腐蚀速率典型环境K/(µm/a) 室外室内C1 ≤1.3 加热的建筑内部,空气洁净C2 1.3~25 大气污染较低、大部分是乡村地区 未加热的建筑内部,可能发生冷凝C3 25~50 城市和工业大气、中等的二氧化硫污染、低盐度沿海区域 高湿度和有一定空气污染的生产场所C4 50~80 高盐度的工业区和沿海地区 化工厂、游泳池、船厂等
表3 钢材在盐雾箱与典型大气环境腐蚀时间对比
Table 3 Comparison of corrosion time of steel in salt spray chamber and typical atmospheric environment
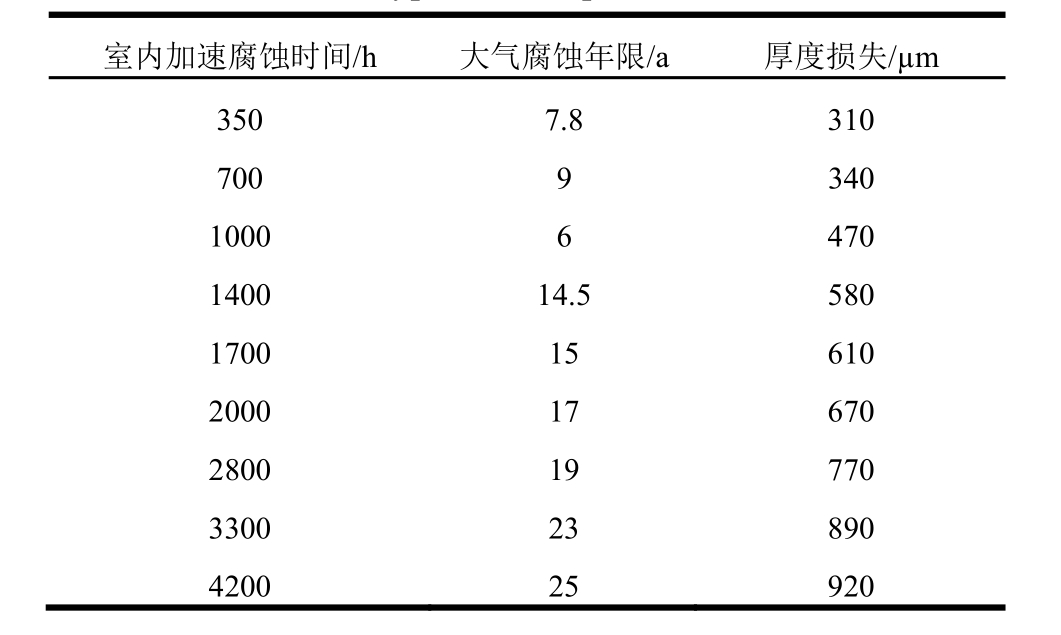
室内加速腐蚀时间/h 大气腐蚀年限/a 厚度损失/µm 350 7.8 310 700 9 340 1000 6 470 1400 14.5 580 1700 15 610 2000 17 670 2800 19 770 3300 23 890 4200 25 920
根据平截面假定,截面曲率延性系数μφ可用截面极限曲率与屈服曲率的比值来表示,即可按式(3)进行计算:

式中:uφ为极限曲率;yφ为屈服曲率。
考虑由锈蚀造成截面的损失和力学性能指标的降低,并以H500×220×16×20为例,分别计算室内加速腐蚀时间为 0 h、350 h、700 h、1000 h、1400 h、1700 h、2000 h、2800 h、3300 h及 4200 h截面的曲率延性系数,并通过软件Origin8.5对数据进行线性拟合,见图3所示。通过图3看出,截面的延性随着锈蚀程度的增加呈逐渐降低趋势,锈蚀对钢材的延性有较大影响。
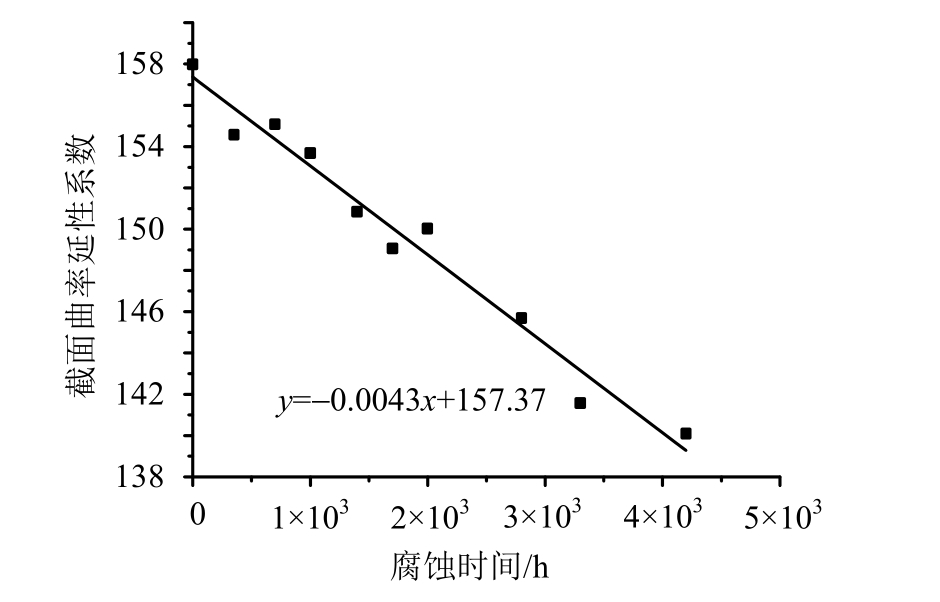
图3 曲率延性系数与腐蚀时间的关系
Fig.3 Relationship between curvature ductility factor and corrosion time
通过对锈蚀钢材进行单调拉伸力学试验,如图4所示,研究腐蚀对钢材的力学性能指标的影响。从图5可以发现随着钢材锈蚀程度不断增加,钢材的名义强度均呈下降趋势,屈服平台长度逐渐变短甚至消失,极限应变值减小。

图4 钢材力学性能试验
Fig.4 Testing of mechanical properties of steel

图5 部分钢材的应力-应变曲线
Fig.5 Stress-strain curves of some steels
名义强度为实际荷载和相应钢板公称截面面积的比值。名义屈服强度和名义极限强度随着锈蚀率变化的关系式如式(4)、图6所示。
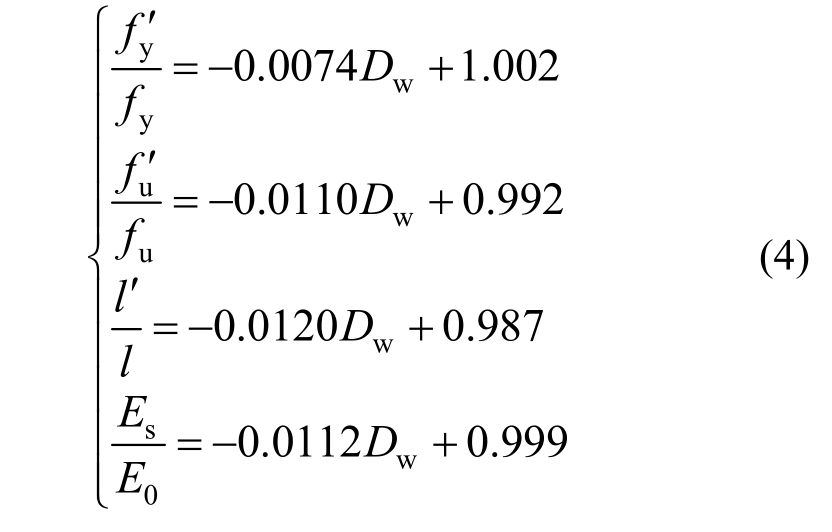
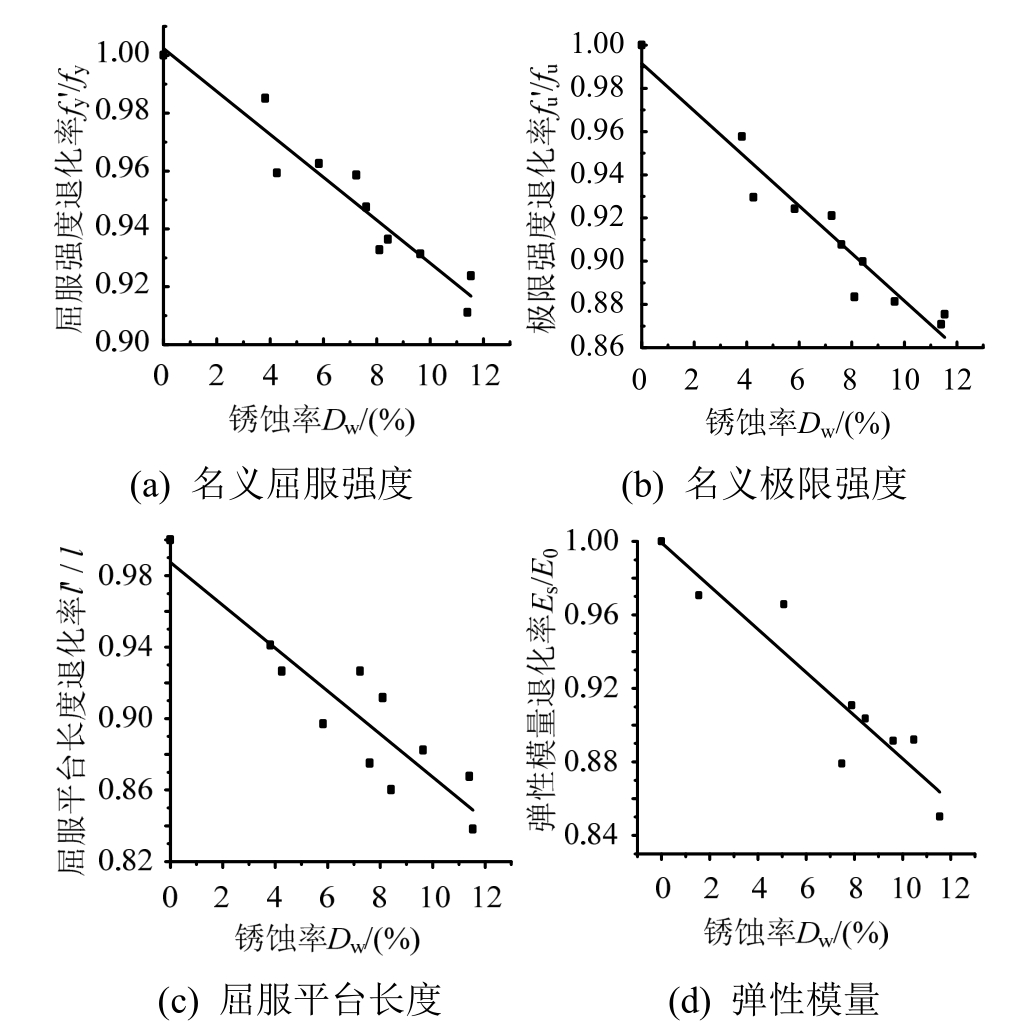
图6 钢材力学性能指标与锈蚀率的回归分析
Fig.6 Regression analysis of mechanical properties and corrosion rate of steel
综合国内外关于结构性能水平的划分[15―16],将结构的抗震性能划分为正常使用(NO)、立即使用(IO)、生命安全(LS)及防止倒塌(CP)性能水平,如表4所示。结构的极限破坏状态定义见表5所示。
表4 结构性能水平及其限值
Table 4 Level of structural performance and its limits

性能水平 正常使用(NO)立即使用(IO)生命安全(LS)防止倒塌(CP)具体要求 无损坏或损坏较小需要少量的修复具有一定的的安全储备破坏在一定范围内,且不倒塌性能水平限值 LS1 LS2 LS3 LS4
表5 结构的极限破坏状态
Table 5 Ultimate failure state of structures

极限破坏状态 具体要求正常使用 构件屈服立即使用 10%以下的承重构件破坏轻微生命安全 10%以下的承重构件破坏严重,或10%~50%的承重构件破坏轻微,结构刚度下降防止倒塌 50%以上的承重构件破坏严重,或结构局部形成机构,不倒塌
本文引用文献[17]5层 3跨钢框架,层高均为3.6 m,跨度7.2 m。钢框架梁、柱均为Q235焊接H型钢,截面尺寸见表 8所示,屋面恒载标准值为5.0 kN/m2,楼面恒载标准值为 4.7 kN/m2,屋面及楼面活载标准值均为2.0 kN/m2。由于结构平面布置规则,选取一榀框架进行分析。
为了探究锈蚀对钢框架抗震性能的影响,运用SAP2000有限元软件,考虑锈蚀对构件力学性能的影响。创建模型时,梁、柱均采用框架单元,假定楼盖为刚性板。本文利用Xtract软件计算塑性铰属性。采用自定义的塑性铰,基于平截面假定的纤维模型法,计算不同材料属性(对应不同锈蚀率)梁的截面属性和柱的截面轴力-弯矩屈服曲线。
在运行重力荷载工况的基础上,选用第1振型荷载分布的侧向荷载工况,对大气腐蚀龄期为0年、9年、17年、25年的5层钢框架进行Pushover分析。不同龄期的钢框架结构的基底剪力-顶点位移曲线见图7。
由图7可以看出,钢框架结构基底剪力-顶点位移曲线在线弹性阶段斜率,随着锈蚀程度的增加呈降低趋势,而曲线斜率反映了结构整体的抗侧刚度。所以随着锈蚀程度的增加,结构的整体抗侧刚度呈降低趋势,结构的抗震性能也逐渐减弱。
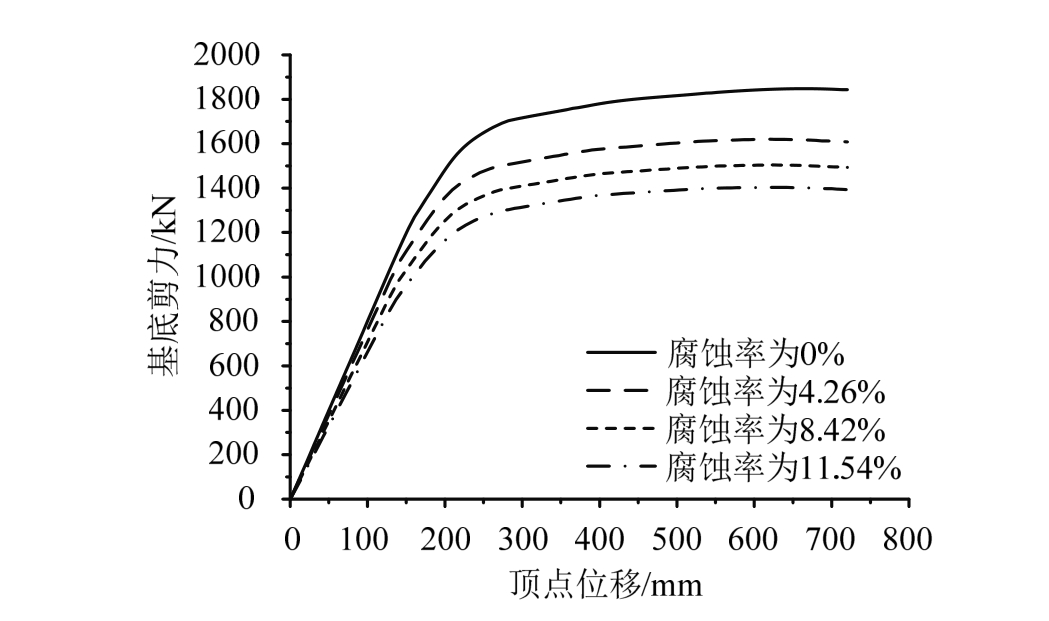
图7 锈蚀钢框架基底剪力-顶点位移曲线
Fig.7 Shear-vertex displacement curve of steel frame base
我国现行建筑抗震设计规范和 FEMA356[14]均采用结构层间变形衡量地震作用下结构变形能力与抗震设防水准的关系。但是锈蚀对结构中不同的构件的截面特性带来不同程度的损伤,导致锈蚀钢框架层间位移角增长幅度不一致,而且锈蚀后钢框架结构的薄弱层也可能会发生变化。
本文采用第1振型荷载分布的侧向荷载对不同锈蚀程度的5层钢框架进行Pushover分析,得到不同锈蚀程度的5层钢框架结构在多遇、罕遇地震作用下的层间位移角曲线分别如图8所示。
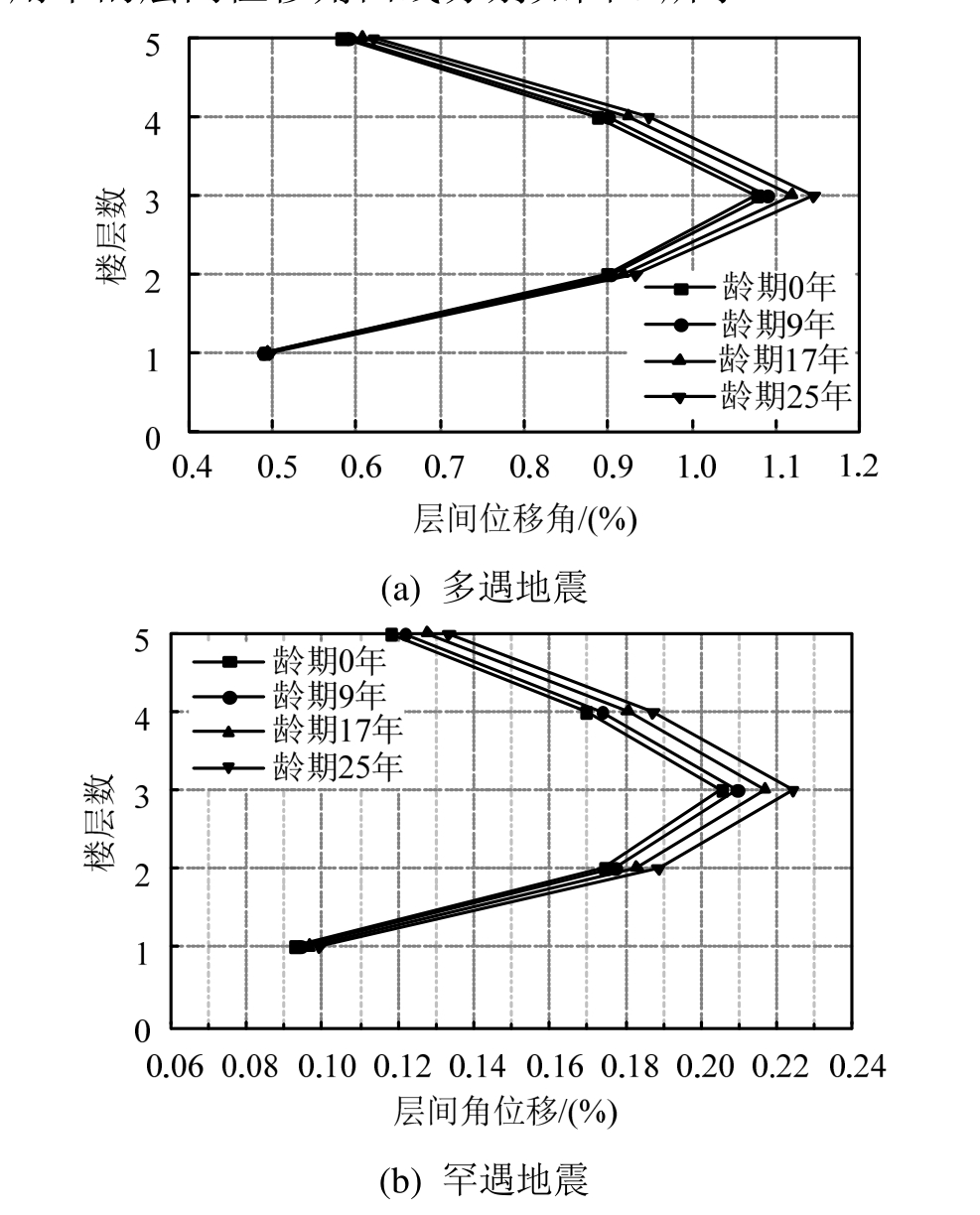
图8 不同龄期的钢框架结构层间位移角曲线
Fig.8 Inter story displacement angle curves of steel frame structures at different ages
图8容易看出,对于5层锈蚀钢框架结构,相比于未锈蚀结构在多遇和罕遇地震作用下的结构层间位移曲线,底层及顶层的层间位移角发生较小的变化;第3层的层间位移角变化较大。薄弱层位置没有变化,仍在第3层。
最大层间位移角不仅与节点转动、楼层层间变形能力直接相关,而且能更好地反映结构的层间位移延性和结构的整体位移延性,故适用于描述框架结构的损伤情况,可以让研究人员更加全面的了解结构性能[18-19]。图 8也可以看出随着锈蚀率的增加,层间位移角不断增大,反映锈蚀对钢结构抗震性能的影响,因此本文采用最大层间位移角表征结构体系的抗震能力。
通过对锈蚀钢框架静力弹塑性分析,得到4种极限状态的量化指标限值。介于篇幅限制,仅列出龄期为 25年时的钢框架静力弹塑性分析过程。图中●点表示铰达到弹性极限状态;█点代表构件达到极限承载力; 、
、 及◆点代表塑性铰的性能水平,分别对应立即使用、生命安全和防止倒塌,如表6、图9所示。
及◆点代表塑性铰的性能水平,分别对应立即使用、生命安全和防止倒塌,如表6、图9所示。
表6 龄期25年的钢框架极限破坏状态量化指标
Table 6 Limit failure state of steel frames in age of 25 years
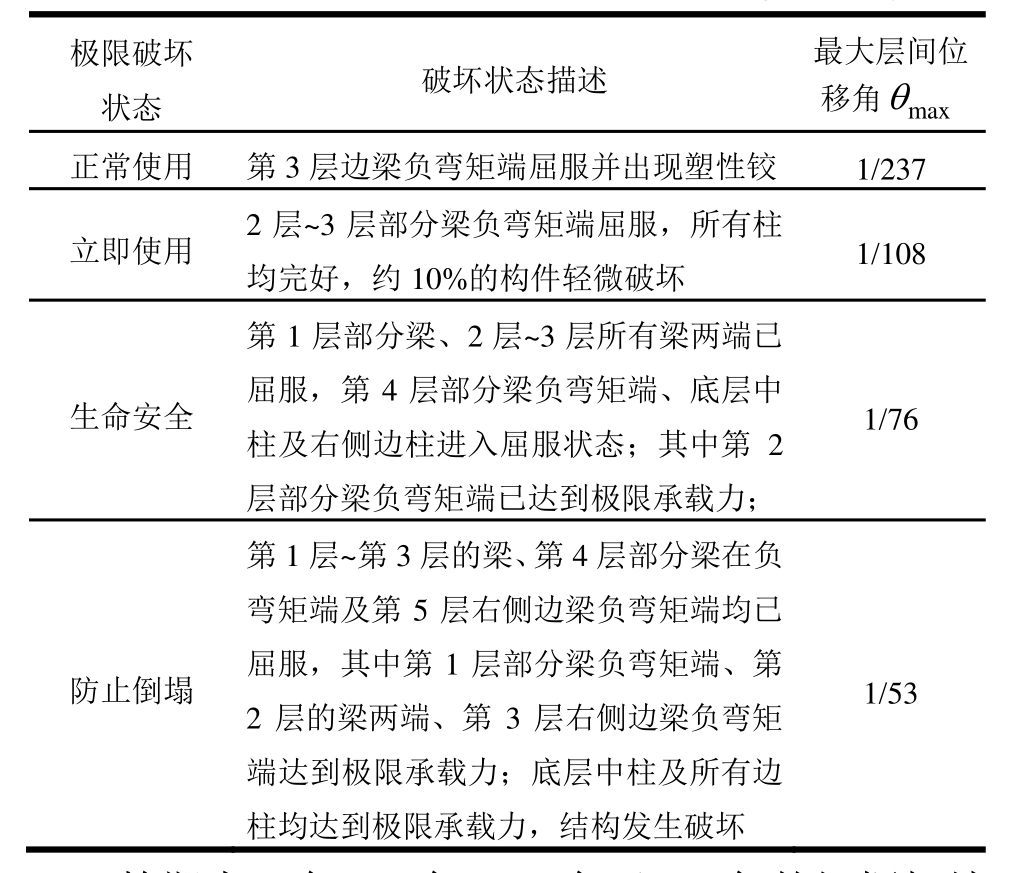
极限破坏状态 破坏状态描述 最大层间位移角θmax正常使用 第3层边梁负弯矩端屈服并出现塑性铰 1/237立即使用 2层~3层部分梁负弯矩端屈服,所有柱均完好,约10%的构件轻微破坏 1/108生命安全第1层部分梁、2层~3层所有梁两端已屈服,第4层部分梁负弯矩端、底层中柱及右侧边柱进入屈服状态;其中第 2层部分梁负弯矩端已达到极限承载力;1/76防止倒塌第1层~第3层的梁、第4层部分梁在负弯矩端及第5层右侧边梁负弯矩端均已屈服,其中第1层部分梁负弯矩端、第2层的梁两端、第3层右侧边梁负弯矩端达到极限承载力;底层中柱及所有边柱均达到极限承载力,结构发生破坏1/53
龄期为0年、9年、17年及25年的钢框架结构,极限状态时对应的量化指标限值如表7所示。
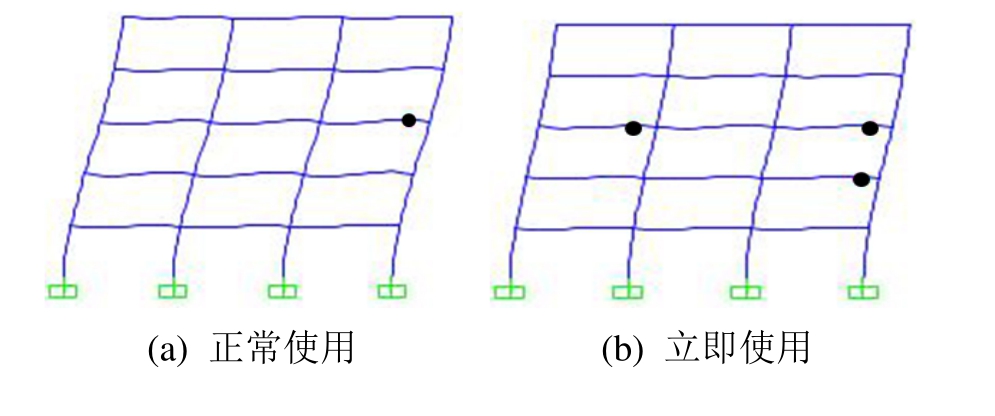

图9 龄期25年的钢框架极限破坏状态
Fig.9 Ultimate failure state of steel frame in 25 years
表7 钢框架极限破坏状态量化指标取值
Table 7 Values of quantitative indexes for ultimate failure state of steel frames
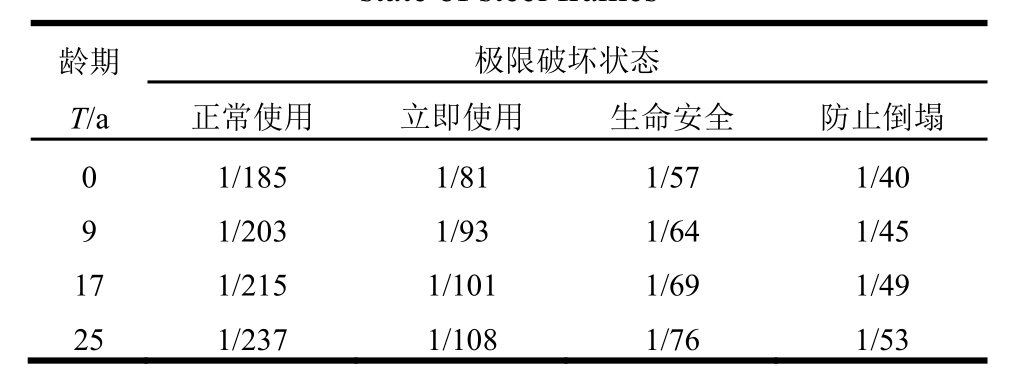
龄期T/a极限破坏状态正常使用 立即使用 生命安全 防止倒塌0 1/185 1/81 1/57 1/40 9 1/203 1/93 1/64 1/45 17 1/215 1/101 1/69 1/49 25 1/237 1/108 1/76 1/53
计算模型采用4.1节的5层钢框架结构,抗震设防烈度为8度,场地土类别为II类,设计地震分组为第1组,层高均为3.6 m,跨度7.2 m,钢材等级为Q235B,梁柱截面尺寸见文献[12],楼层重量按照(1.0×恒载+0.5×活载)进行折算。
利用 ABAQUS软件建模时,计算模型采用杆系模型,梁采用B21梁单元,柱采用B22梁单元,网格划分时取网格长度为0.5 m,阻尼比取为0.05,模型各构件连接形式为刚接,结构底端采用固定端约束。考虑结构锈蚀时,采用名义强度,不削弱截面。采用随动强化模型,退化规律式(4)采用钢材锈蚀本构关系。
结合文献的研究,为了精确评估结构的地震需求,选择合理有效的地震动强度指标时,一般选择10条~20条地震动记录。结构模型的场地类别为二类,设防烈度为8度,地震分组为第1组,因此参照文献[21―22]选波原则,挑选20条满足要求的地震记录[20]。
结构的易损性曲线表示不同强度的地震作用下,结构反应D超过破坏阶段定义的结构能力参数C的概率,可以按下式进行计算:

令Z=C-D,即![]() 由于C、D均服从正态分布,且为独立随机变量,Z也服从正态分布。
由于C、D均服从正态分布,且为独立随机变量,Z也服从正态分布。
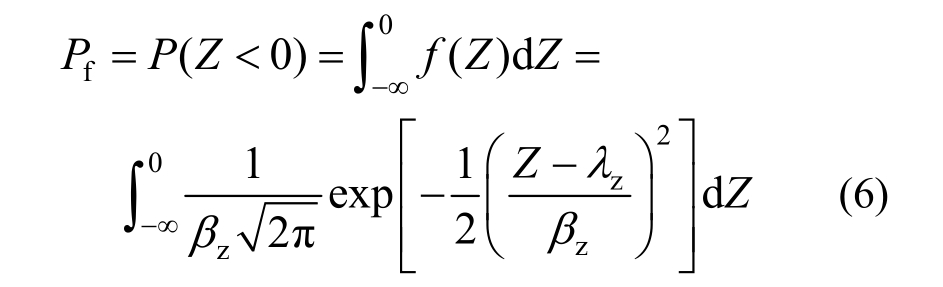
标准正态化后,式(6)变成:
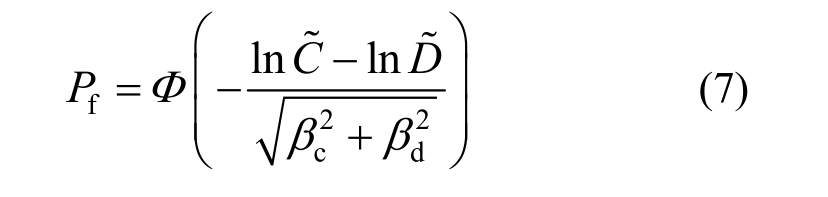
其中,~C为不同性能水平所对应的最大层间位移角限值,见表6;式(7)中的cβ和dβ可以根据设计规范HAZUS99[23]取值。当易损性曲线以PGA为自变量时![]()
Φ(x)为标准正态分布:

根据相关研究[24],地震需求参数的对数中位值为D~和地震动参数IM服从指数关系:
对上式两边同时取对数,则有:
结构损伤指标和地震动强度指标分别为θmax和PGA。通过对不同龄期的结构进行动力增量分析,并根利用式(10)对进行对数线性拟合。分析结果如图10所示,拟合公式如下:

将式(9)代入式(7),得式(12):
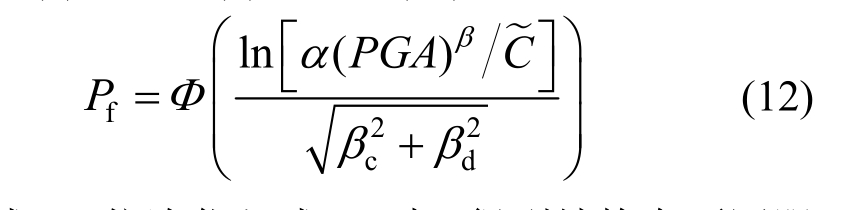
将式(11)依次代入式(12)中,得到结构在不同服役时间的地震易损性曲线。
根据式(12),得到不同锈蚀程度的钢框架结构在正常使用(NO)、立即使用(IO)、生命安全(LS)及防止倒塌(CP)状态下的地震易损性曲线,如图 11所示。

图10 不同锈蚀率的结构最大层间位移角回归分析
Fig.10 Regression analysis of maximum storey displacement angle with different corrosion rates

图11 地震易损性曲线
Fig.11 Seismic fragility curves
从图11可以看出,随着地震动加速度PGA的增加,结构超越极限状态的概率不断提高,即结构易损性增大;在同一地震动强度下,随着龄期的增大,结构构件截面减小和材料力学性能衰减,导致结构抗震能力降低,结构超越极限状态的概率也逐渐增大。例如倒塌极限状态下,当地震动加速度为0.4g时,随着龄期的增加,结构超越极限状态的概率逐渐变大,分别为56%、72%、81%、89%。
锈蚀后结构的指标限值与未锈蚀时的指标限值是有差异的,但是现有研究者对结构易损性曲线的绘制均是基于规范规定的未锈蚀结构的抗震性能水平指标限值,这种方法会放大或缩小了结构超越不同极限状态的概率。
应用本文提出的评估锈蚀钢框架地震响应的易损性评定方法,可以通过对不同锈蚀率的结构基于不同修正限值的易损性曲线的对比分析(图12所示),揭示其具体的变化特征。

图12 不同龄期的结构基于不同修正限值的易损性曲线
Fig.12 Vulnerability curves of different age structures based on different correction limits
从图12可以发现,对于5层钢框架结构,在相同龄期的情况下,不同极限状态的结构超越极限状态的概率的变化不同:不同修正限值的曲线在倒塌极限状态下的差距较大,而在正常使用极限状态下的差距较小,说明锈蚀对于正常使用极限状态影响较小,而对于倒塌极限状态下影响较为明显。
当结构龄期为9年、17年及25年时,基于“未修正限值”的超越极限状态的概率小于基于“修正限值”,说明对于锈蚀的钢框架结构,若使用“未修正限值”会高估锈蚀后的钢框架结构的抗震性能,验证了本文提出的评估锈蚀钢结构地震响应的易损性评定方法的有效性。因此,在高烈度地区进行钢结构抗震性能评估时,应充分考虑锈蚀损伤对结构的不利影响,避免抗震设计偏于不安全。
本文采用动力增量分析方法对锈蚀钢结构进行地震易损性分析,主要结论如下:
(1) 随着龄期增加,锈蚀钢框架整体抗侧刚度逐渐减小,抗震性能逐渐减弱;底层及顶层的层间位移角发生较小的变化;第3层的层间位移角变化较大。薄弱层位置没有变化,仍在第3层。
(2) 相同龄期情况下,修正的层间位移角限值对于不同极限状态的结构超越概率影响不同:不同修正限值的曲线在倒塌极限状态下的差距较大,而在正常使用极限状态下的差距较小,说明锈蚀对于正常使用极限状态影响较小,而对于倒塌极限状态下影响较为明显。
(3) 随着龄期增加,结构超越极限状态的概率逐渐增大。当龄期相同时,基于“未修正限值”的钢框架结构超越极限状态的概率小于基于“修正限值”,若不修正层间位移角限值会高估锈蚀钢框架抗震性能。
[1]GB 50017—2003, 钢结构设计规范[S]. 北京:中国计划出版社, 2003.GB 50017—2003, Code for design of steel structures [S].Beijing, China Planning Press, 2003. (in Chinese)
[2]American Institute of Steel Construction, Inc. Load and resistance factor design specification for structural steel buildings [M]. Chicago, AISC, 1986:1―10.
[3]GB 50046—2008, 工业建筑防腐蚀设计规范[S]. 北京:中国计划出版社, 2008.GB 50046—2008, Code for anticorrosion design of industrial constructions [S]. Beijing: China Planning Press, 2008. (in Chinese)
[4]徐善华, 王皓, 薛南. 锈蚀钢材偏心受压钢柱承载性能退化规律[J]. 哈尔滨工业大学学报, 2016, 48(6):157―163.Xu Shanhua, Wang Hao, Xue Nan. Deterioration law of bearing properties for corroded eccentric steel columns[J]. Journal of Harbin Institute of Technology, 2016,48(6): 157―163. (in Chinese)
[5]Zhu P, Cao X, Wang W, et al. An investigation on microstructure and pitting corrosion behavior of 316L stainless steel weld joint [J]. Journal of Materials Research, 2017, 32(20): 1―8.
[6]邱斌, 徐善华. 锈蚀钢板力学性能的退化规律[J].机械工程材料, 2014, 38(10): 60―63.Qiu Bin, Xu Shanhua. Deterioration law of mechanical properties of corroded steel plates [J]. Materials for Mechanical Engineering, 2014, 38(10): 60―63. (in Chinese)
[7]郑山锁, 左英, 张晓辉, 等. 酸性大气环境下多龄期平面钢框架结构抗震性能试验研究[J]. 工程力学, 2017,34(9): 73―82.Zheng Shansuo, Zuo Ying, Zhang Xiaohui, et al.Experimental research on the seismic behavior of multi-aged planar steel frames under acidic atmospheric environment [J]. Engineering Mechanics, 2017, 34(9):73―82. (in Chinese)
[8]Albrecht P, Lenwari A. Fatigue strength of trolley bridge stringers made of ASTM A7 steel [J]. Journal of Bridge Engineering, 2008, 13(1): 67―74.
[9]郑山锁, 张晓辉, 王晓飞. 近海大气环境下多龄期钢框架柱抗震性能的试验研究[J]. 土木工程学报, 2016,49(4): 69―77.Zheng Shansuo, Zhang Xiaohui, Wang Xiaofei.Experimental research on seismic behaviors of multi-aged steel frame columns in the offshore atmospheric environment [J]. China Civil Engineering Journal, 2016, 49(4): 69―77. (in Chinese)
[10] 郑山锁, 王晓飞, 韩言召. 酸性大气环境下锈蚀钢框架柱双参数地震损伤模型研究[J]. 工程力学, 2016,33(7): 129―135.Zheng Shansuo, Wang Xiaofei, Han Yanzhao. Study on dual-parameter seismic damage model of corroded steel frame columns in acidic environments [J]. Engineering Mechanics, 2016, 33(7): 129―135. (in Chinese)
[11] ISO 12944-2, Paints and varnishes-corrosion protection of steel structures by protective paint systems-part2:classification of environments [S]. Switzerland:International Organization for Standardization, 1998: 8―10.
[12] 位龙虎. 锈蚀钢结构地震易损性分析[D]. 陕西: 西安建筑科技大学, 2015.Wei Longhu. Seismic vulnerability analysis of corroded steel structure [D]. Shaanxi: Xi’an University of Architecture and Technology, 2015. (in Chinese)
[13] ISO 8407, Corrosion of metal and alloys―removal of corrosion products from corrosion test specimens [S].Switzerland: the International Organization for Standardization, 2009: 2―5.
[14] 史炜洲, 童乐为, 陈以一, 等. 腐蚀对钢材和钢梁受力性能影响的试验研究[J]. 建筑结构学报, 2012, 33(7):53―60.Shi Weizhou, Tong Lewei, Chen Yiyi. et al. Experimental study on influence of corrosion on behavior of steel material and steel beams [J]. Journal of Building Structures, 2012, 33(7): 53―60. (in Chinese)
[15] 张耀庭, 杜晓菊, 杨力. RC框架结构基于构件损伤的抗震性能评估研究[J]. 湖南大学学报(自科版), 2016,43(5): 9―21.Zhang Yaoting, Du Xiaoju, Yang Li. Research on Seismic Performance Assessment Based on Component Damage for RC Frame Structure [J]. Journal of Hunan University(Natural Sciences), 2016, 43(5): 9―21. (in Chinese)
[16] FEMA356, Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington D C, Federal Emergency Management Agency, 2000: 55―57.
[17] 孙国华, 顾强, 何若全. 基于能量反应谱的抗弯钢框架结构能量计算[J]. 土木工程学报, 2012, 45(5): 43―46.Sun Guohua, Gu Qiang, He Ruoquan. Evaluation of seismic energy of steel frames based on energy spectrums [J]. China Civil Engineering Journal, 2012,45(5): 43―46. (in Chinese)
[18] 蒋伟, 徐龙军, 张进国. 框架结构抗震性态设计分析[J]. 地震工程与工程振动, 2013, 33(5): 93―99.Jiang Wei, Xu Longjun, Zhng Jinguo. Analysis of performance-based seismic design of frame structures[J]. Earthquake Engineering and Engineering Vibration,2013, 33(5): 93―99. (in Chinese)
[19] Vamvatsikos D. Seismic performance, capacity and reliability of structures as seen through incremental dynamic analysis [D]. California, Stanford university,2002: 73―74.
[20] Luco N, Cornell C A. Effects of connection fractures on SMRF seismic drift demands [J]. Journal of Structural Engineering, 2000, 126(1): 127―136.
[21] 徐龙河, 单旭, 李忠献. 强震下钢框架结构易损性分析及优化设计[J]. 工程力学, 2013, 30(1): 175―179.Xu Longhe, Shan Xu, Li Zhongxian. Vulnerability analysis and optimization design for steel frame structure under strong earthquakes [J]. Engineering Mechanics,2013, 30(1): 175―179.
[22] 吴小峰, 孙启国, 狄杰建, 等. 抗震分析反应谱法和时程分析法数值仿真比较[J]. 地震工程学报, 2011,33(3): 275―278.Wu Xiaofeng, Sun Qiguo, Di Jiejian, et al. A numerical simulation comparison between response analysis and time history analysis [J]. China Earthquake Engineering Journal, 2011, 33(3): 275―278. (in Chinese)
[23] FEMA, Earthquake loss estimation methodology technology manual: HAZUS99 [S]. Washington DC,Federal Emergency Management Agency, 1999: 45―46.
[24] Baker J W, Cornell C A. Vector-valued intensity measures for pulse-like near-fault ground motions [J].Engineering Structures, 2008, 30(4): 1048―1057.
A METHOD FOR THE SEISMIC VULNERABILITY ASSESSMENT OF CORRODED STEEL STRUCTURES