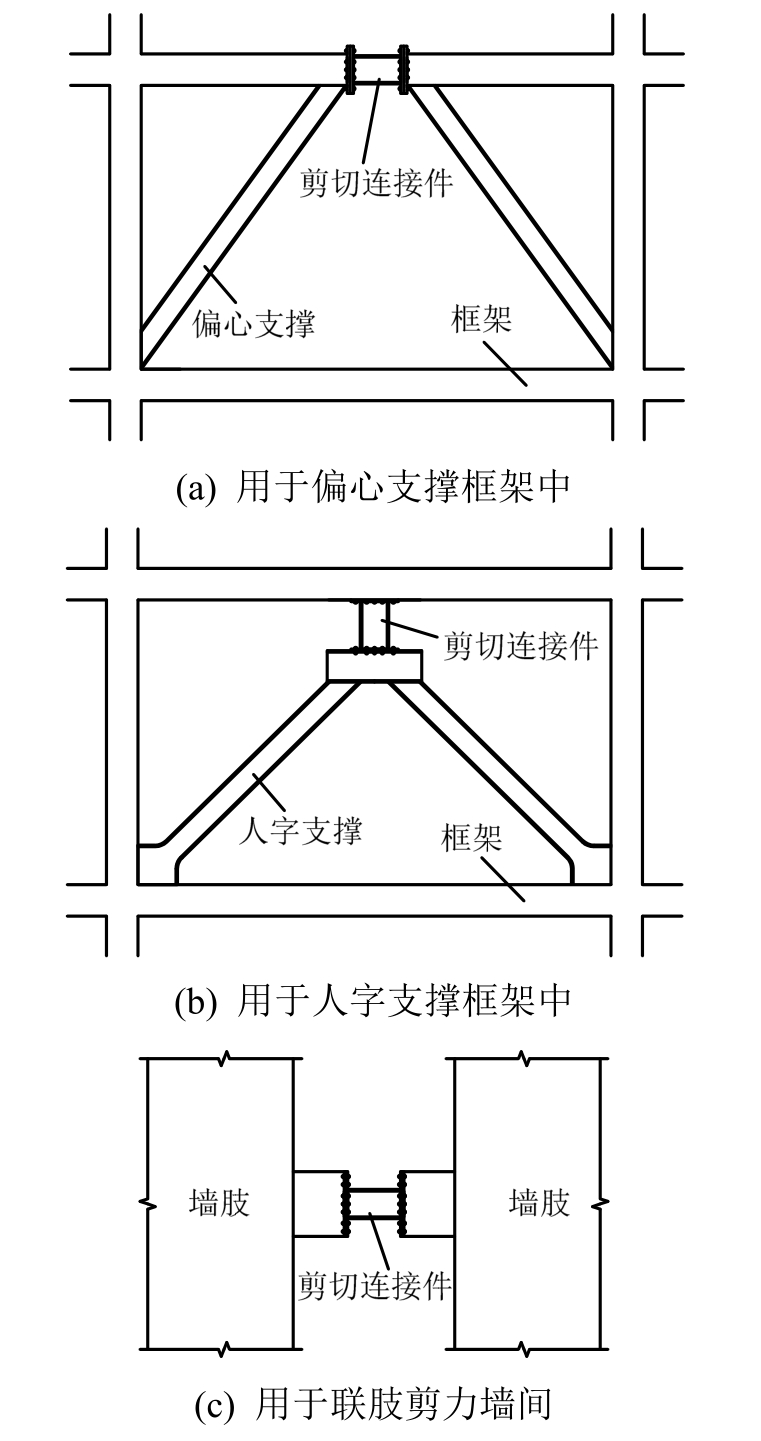
图1 剪切连接件的典型应用示意图
Fig.1 Typical applications of shear link devices
被动消能减振技术作为结构振动控制的一种有效方法，已经受到广泛关注并被普遍应用于工程实践[1]。地震中，大量的能量被输入到结构中，通过在结构中安装被动耗能装置，一部分输入结构的能量将转移到这些装置中被耗散掉，从而将有效地降低结构自身的地震响应、减小结构本身的破坏[2]。近年来将剪切连接件(shear link device，SLD)用于结构耗能减震成为了结构工程领域的研究热点，其中包括：偏心支撑框架中的可更换剪切耗能梁段[3－5](如图 1(a)所示)；人字支撑框架结构中的剪切耗能件[6－9](如图 1(b)所示)；联肢剪力墙间的可更换剪切耗能连梁[10](如图1(c))；连柱框架体系中的柱间剪切耗能元件[11－12]和桥梁主塔中的剪切耗能减震装置[13－15]等。剪切连接件通常在小震作用下处于弹性工作状态，在中震及大震作用水平下通过剪切屈服耗散输入的能量，从而有效减小结构的地震响应。
图1 剪切连接件的典型应用示意图
Fig.1 Typical applications of shear link devices
剪切连接件具有滞回耗能性能优良，受外界环境影响小，制作、安装及更换方便快捷等诸多优点。基于其上述优点，剪切连接件具有广阔的发展和工程应用前景。为进一步研究剪切连接件的受力机理及相关力学性能，对剪切连接件的设计及工程应用提供有效参考，本文着重从理论研究的角度出发，基于剪切连接件的典型构造形式，建立等效力学模型，应用弹性力学半逆解法对其腹板应力分布进行求解，对其各项力学性能指标进行理论分析，提出一种基于Bouc-Wen模型和模拟退火算法的等效屈服点确定方法，最后通过单调拟静力加载试验进行相关验证。
如图 2(a)所示为剪切连接件的典型构造形式，主要由两块连接端板、两块侧翼缘板和一块腹板构成。在剪切连接件中，腹板是提供刚度及耗能工作的核心部件，侧翼缘的主要作用是为腹板提供边界约束以抑制其面外屈曲，连接端板上通常开设螺栓孔以便于装置与结构的连接。剪切连接件的几何尺寸参数如图2(b)所示，主要包括：腹板的高度hw、宽度bw、厚度tw，侧翼缘板的高度hf、宽度bf、厚度tf，其中hw=hf=h，h为剪切连接件的高度。剪切连接件的截面积为A0=bwtw+2bftf，腹板的截面积为Aw=bwtw，单个侧翼缘的截面积为Af=bftf。
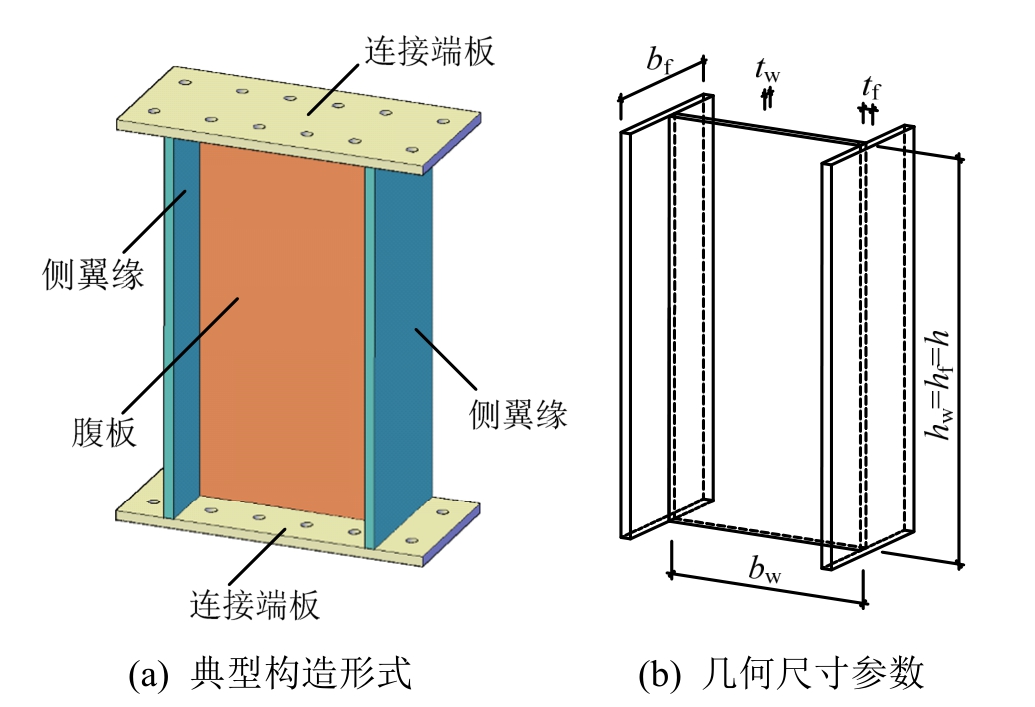
图2 剪切连接件的基本构造形式
Fig.2 Typical structure of shear link device
在地震作用下，剪切连接件两端随结构变形发生平行的相对错动，因此可简化为如图3所示的力学模型，其两端分别受到反对称的弯矩M和剪力V的作用，且有：
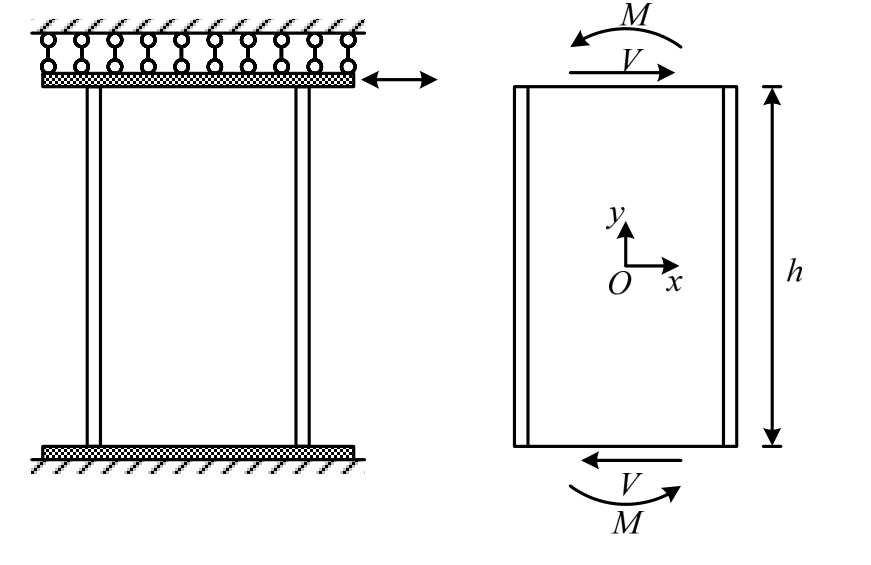
图3 等效力学模型
Fig.3 Equivalent mechanical model
基于图3所示的剪切连接件计算简图，将腹板中心取为原点O，高度方向设为y方向，宽度方向设为x方向。可见剪切连接件的力学模型是典型的对称结构受到反对称荷载作用的问题，且相应的对称轴为y=0(即x轴)，因此其应力分布也相应地关于对称轴y=0成反对称分布，只需求出其对称轴一侧的应力分布，即可相应得到另一侧的应力分布。现以剪切连接件的上半部分(y＞0)为研究对象，可以得到剪切连接件的内力分布：
式中：FV(y)为沿高度各横截面的剪力值；M(y)为沿高度各横截面的弯矩值。
采用弹性力学中的半逆解法[16－17]对剪切连接件腹板的各应力分量进行求解。令σy表示y向正应力，σx表示x向正应力，τxy表示切应力。考虑到腹板无x向挤压应力(σx=0)，且需满足变形协调方程，故设应力函数为Φ=Ax3y+Bx2y+Cxy+Dx3+Hx2，可求得各应力分量的表达式：
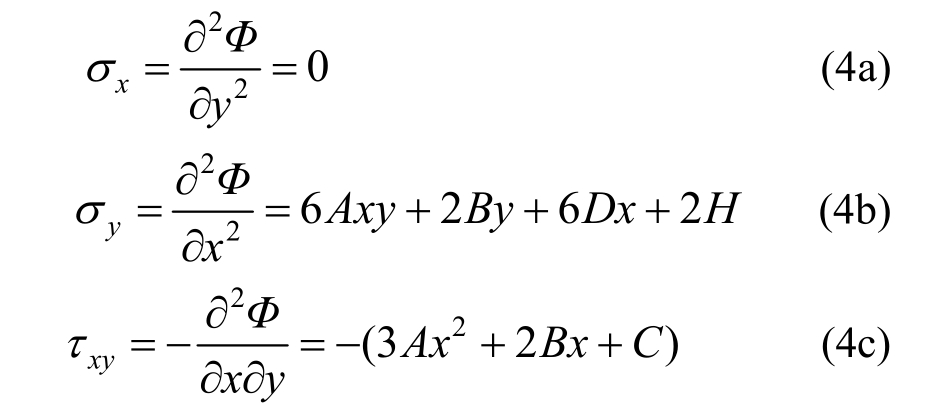
式中的各待定系数需要进一步通过边界条件求解。
基于目前对剪切连接件的试验研究及工程应用[3－15]，其腹板高度hw通常明显大于腹板宽度bw，因此将腹板与侧翼缘的交界线定义为主要边界，将腹板与连接端板的交界线定义为次要边界。
将侧翼缘约束的主要边界转化为应力边界条件，如图4所示，可以得到腹板两侧边界处的切应力值为：
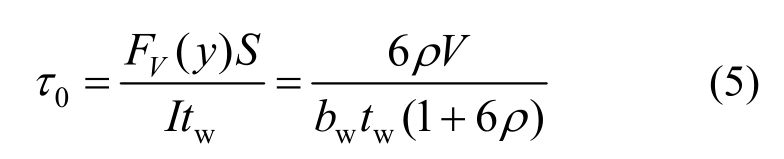
式中：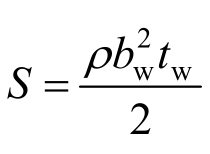
为侧翼缘对中性轴的面积矩；
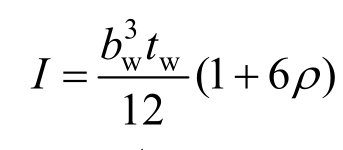为剪切连接件的横截面惯性矩；
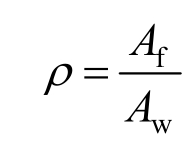为侧翼缘截面积与腹板截面积之比。
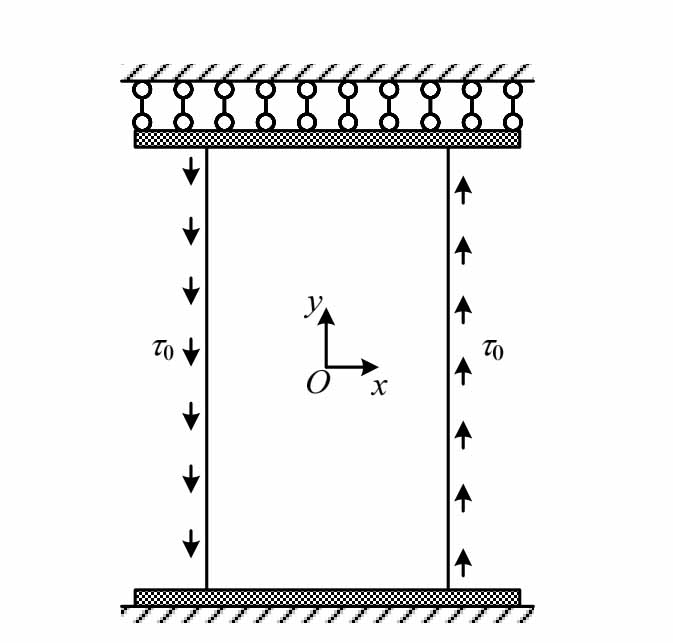
图4 腹板计算简图
Fig.4 Analytical diagram for web plate
在x=bw/2和x=-bw/2两个主要边界上，需满足应力边界条件：
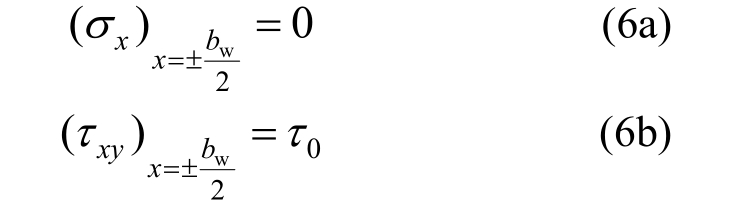
在次要边界y=h/2上，τxy合成的剪力为V；同时考虑腹板及侧翼缘对主矢和主矩的贡献，σy合成的主矢和主矩分别为0和M。根据圣维南原理，得到积分边界条件：
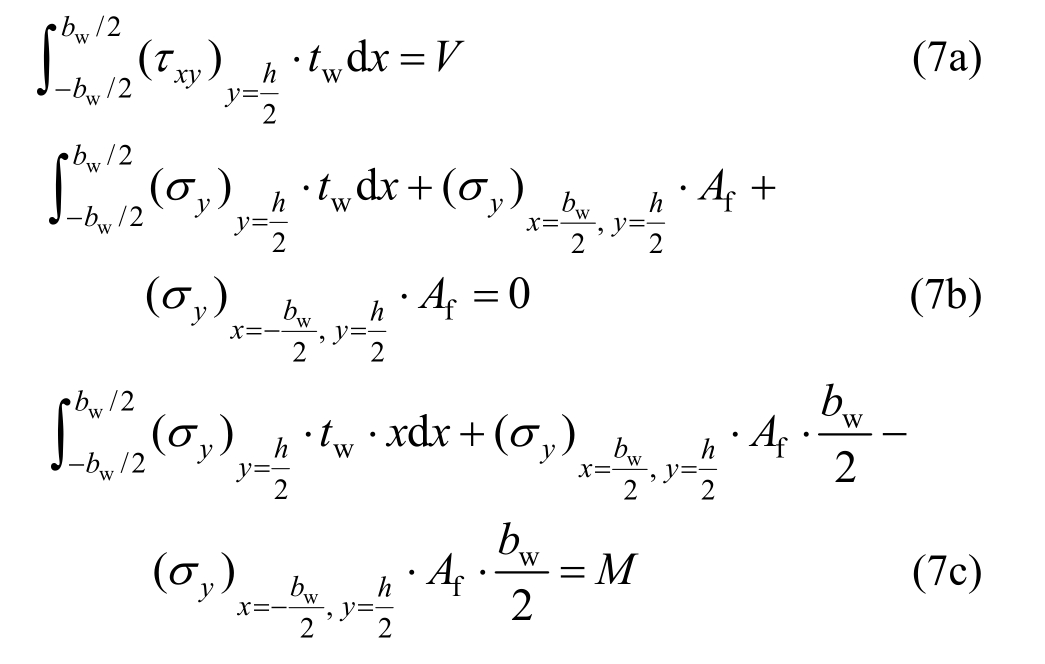
将式(4)、式(6)、式(7)联立可以解得应力分量表达式中的各系数为：
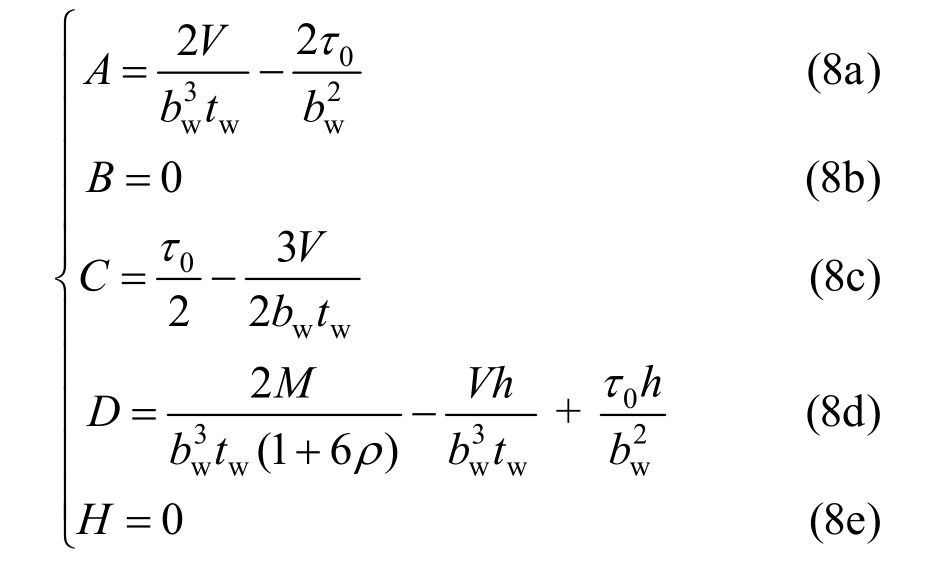
将式(1)、式(5)、式(8)代入式(4)即可得到各应力分量的计算公式：
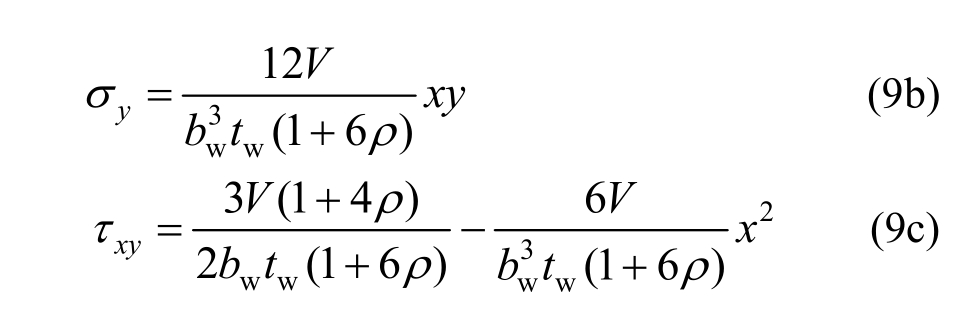
此外，由于剪切连接件的横截面剪力沿全高保持不变，故各横截面由于剪力引起的翘曲程度相同，即不会由于不均匀翘曲而引起附加的y向正应力[18－20]，因此式(9b)无需再附加翘曲正应力分项。式(9)求出的是剪切连接件腹板上半部分(y≥0)的应力分布函数，根据反对称性，可知下半部分(y＜0)的应力分布函数仍为式(9)。基于式(9)采用MATLAB绘制腹板的应力分布情况如图5所示。
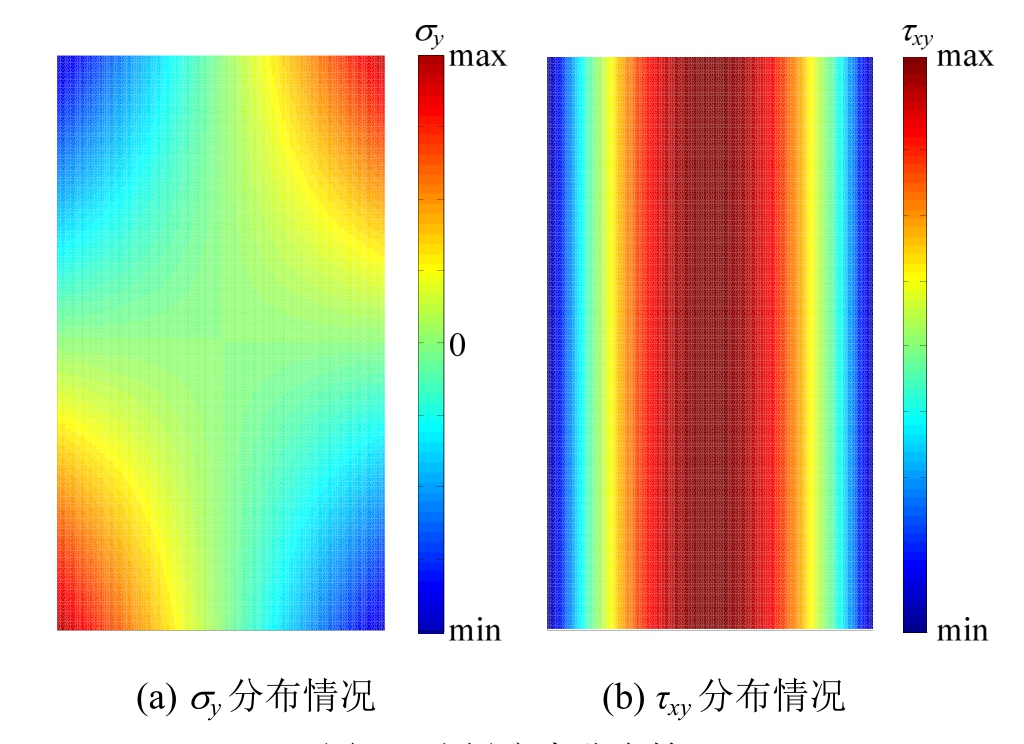
图5 腹板应力分布情况
Fig.5 Stress distribution in web plate
设剪切连接件上、下连接端板沿x向的相对错动变形为u，相应施加的x向荷载即恢复力为F，其中F的大小等于剪切连接件受到的剪力V。在剪切连接件的工程设计及性能评估中常要用到的关键性能指标为初始刚度K、屈服后刚度K′、屈服荷载Fy及屈服位移uy。
当u较小时，整个剪切连接件保持弹性工作，其初始刚度K为：
在小位移弹性范围内，剪切连接件的变形u主要由弯曲变形和剪切变形引起[21]：
其中，uM与uV分别为剪切连接件的弯曲变形和剪切变形引起的侧移量，可分别由下式计算：
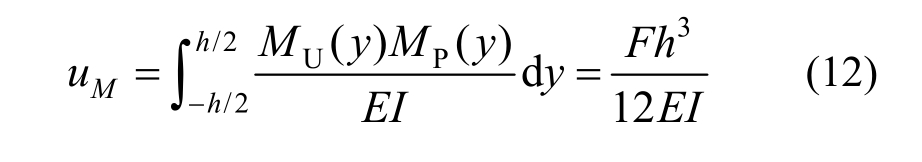
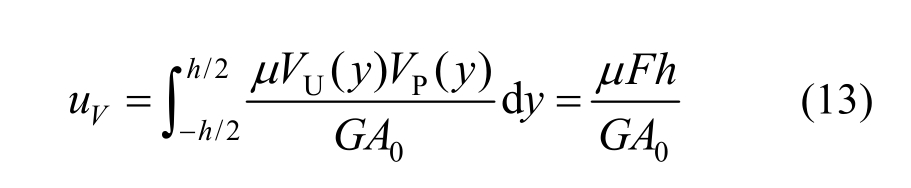
式中：E、G分别为钢材的弹性模量和剪切模量；ν为钢材泊松比，且G=E/[2(1+ν)]≈0.4E，H 形截面的剪应力分布不均匀系数μ=A0/Aw[21]。将式(11)～式(13)代入式(10)可得剪切连接件的初始刚度：
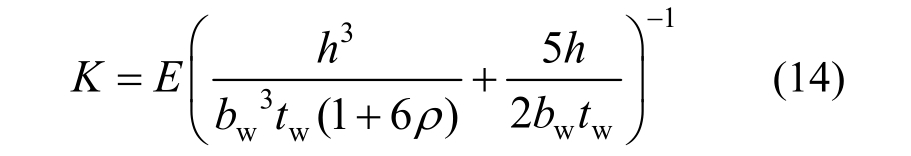
为进一步分析弯曲变形与剪切变形各自所占的比例，将式(12)与式(13)相比可得：
其中：β=hw/bw，为腹板的高宽比。ρ的常见取值范围为0.5～1.5，β的常见取值范围为1～3，因此一般情况下uV＞uM，即剪切变形一般占主要成分。
当剪切连接件屈服后，腹板几乎完全进入塑性，而翼缘板则基本保持弹性。设钢材的切线模量为E′，屈服后折减系数α=E′/E，可以根据等效截面法计算得到剪切连接件的屈服后刚度为：
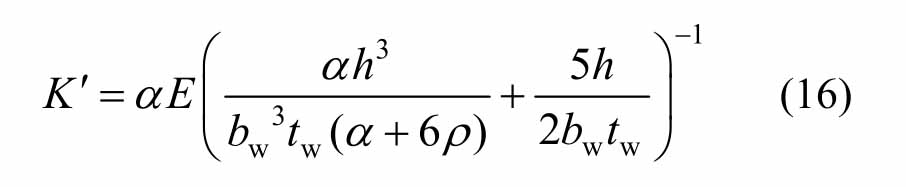
将腹板中部截面达到全截面剪切屈服时的水平剪力定义为屈服荷载Fy，即：
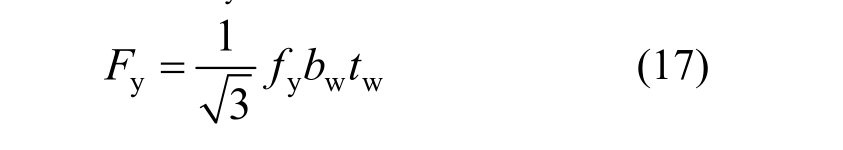
其中，fy为腹板钢材的屈服强度。由uy=Fy/K可以得到相应的屈服位移为：
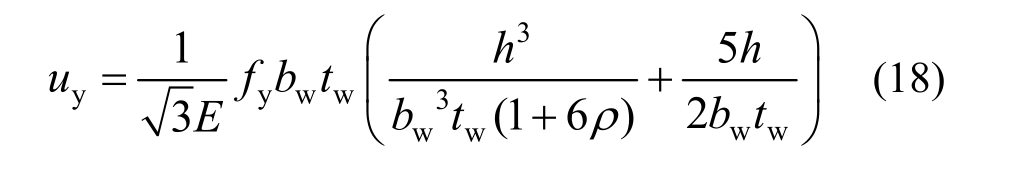
剪切连接件的屈服点是联系上述各项力学性能指标的关键节点，其对于剪切连接件的性能评估及工程应用是至关重要的。剪切连接件的实际屈服点一般可通过单调加载试验曲线并结合适当的确定方法得到，目前主要有基于观察法的屈服点确定方法和基于双线性模型的屈服点确定方法等，本节将提出一种更加合理的屈服点确定方法。
基于观察法的屈服点确定方法[22]是直接将单调加载曲线刚开始出现明显刚度改变的点指定为屈服点Y，如图6所示。这是最简单的一种屈服点确定方法，但该方法具有较大的主观性，并且不与任何一种具体的滞回模型相对应。
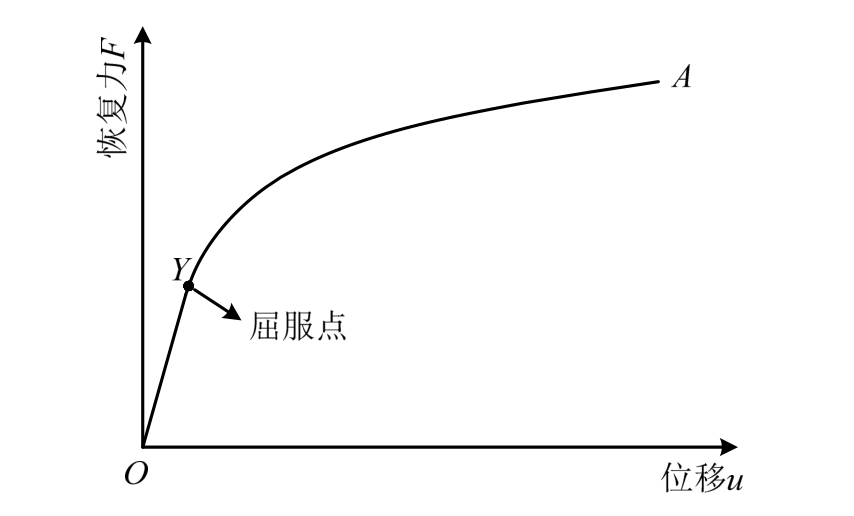
图6 基于观察法的屈服点确定方法
Fig.6 Yield point determination based on observation method
基于双线性模型的屈服点确定方法[23]是过单调加载曲线的原点O和最大位移点A作双折线，并使得双折线与横坐标轴所包络的面积与单调加载曲线与横坐标轴所包络的面积相等，从而确定双折线的转折点即为等效屈服点Y，如图7所示。该方法采用双线性模型基于等面积(能量)原则得到等效屈服点，具有一定的合理性，但双线性模型以直线代替曲线，在某些情况下仍存在较大误差。
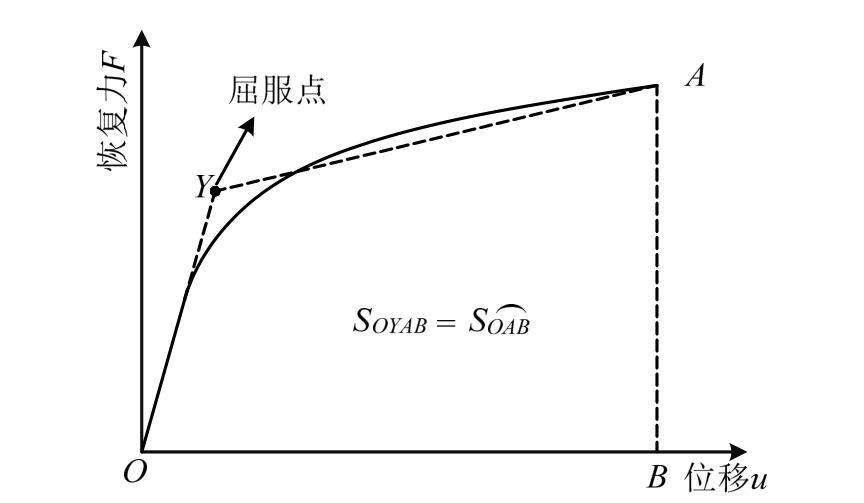
图7 基于双线性模型的屈服点确定方法
Fig.7 Yield point determination based on bilinear model
为解决上述传统屈服点确定方法所存在的不足，现提出一种基于Bouc-Wen模型和模拟退火算法的屈服点确定方法。
Bouc-Wen模型是一种用于描述滞回力学行为的经典模型，由Bouc首先提出[24]，并由Wen进一步推广[25]。为方便Bouc-Wen模型的工程应用，在结构分析软件SAP2000中也引入了基于Bouc-Wen模型的非线性连接单元[26]，其表达式为：
其中：F为恢复力；u为位移(变形)；z为内部迟滞变量；Fy为屈服荷载；K为初始刚度，K′为屈服后刚度，γ=K′/K为屈服后刚度比。Bouc-Wen模型与双线性模型不同，其具有圆滑的弹塑性过渡段，参数n即为控制弹塑性过渡段圆滑程度的参数。当n较小时，过渡段较长；当n较大时，过渡段较短；当n趋近于无穷大时，过渡段消失，转变为双线性模型。相应的滞回曲线形状如图8所示，其中点0为原点，过原点作切线与塑性段交于点 1，该点即为等效屈服点，相应的纵坐标和横坐标分别为屈服荷载Fy和屈服位移uy，直线
的斜率即为初始刚度K。点2和点3分别为最大正、负向工作位移点，直线
的斜率即为屈服后刚度K′。曲线
即为Bouc-Wen模型所描述的单调加载曲线，并且对于该段曲线，有u˙z＞0，因此式(19)可以进一步简化为：
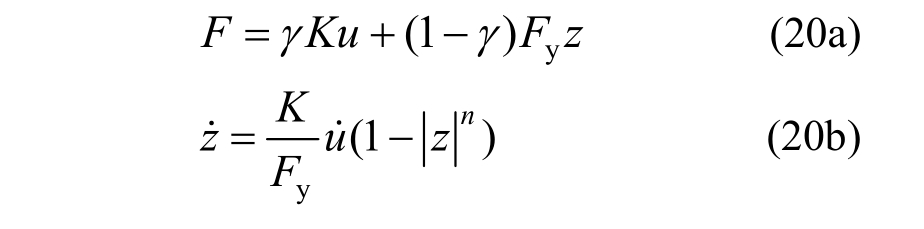
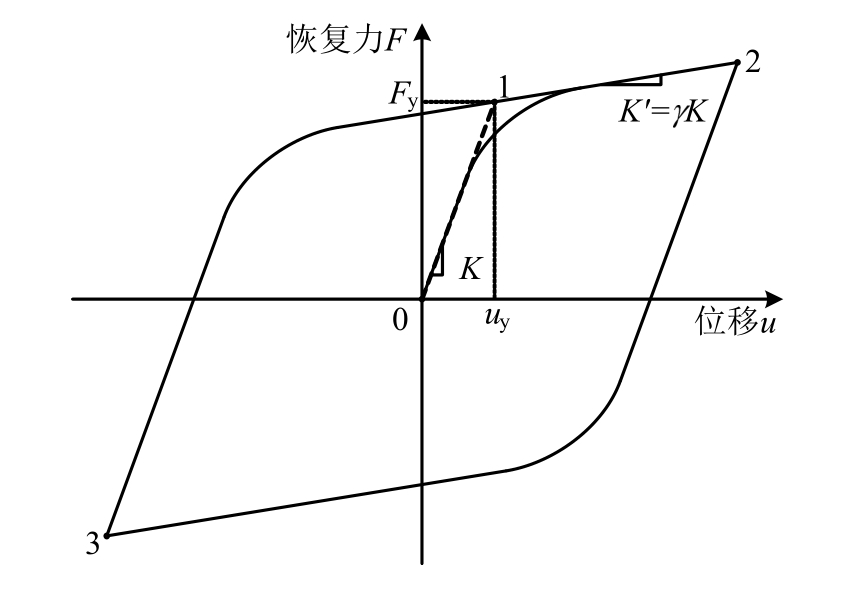
图8 Bouc-Wen模型滞回曲线
Fig.8 Hysteresis curves of Bouc-Wen model
可见只需采用式(20)对剪切连接件的单调加载曲线进行拟合，即可得到相应的等效屈服点及相关的力学性能指标。设单调加载曲线共有N个采样点，每个采样点对应的横坐标、纵坐标分别为ui、Ft,i，其中i=1,2,…,N。根据式(20)可以得到相应横坐标处的拟合荷载值为Fm,i。为了实现拟合曲线与原始单调加载曲线尽量吻合，需要使得拟合曲线与原始单调加载曲线的均方根误差(RMSE)最小化，因此拟合的目标可以表达为：
上述拟合问题实质上是一个以均方根误差(RMSE)为目标函数的非线性优化问题，可以采用模拟退火算法进行求解。模拟退火算法(simulated annealing, SA)是一种典型的随机优化算法，由Kirkpatrick等首先提出[27]，它模拟高温金属降温的热力学过程，具有较强的鲁棒性、全局收敛性和隐含并行性，可广泛应用于解决各领域的优化问题[28]。采用该算法进行优化求解时，先设定初始温度Tmax，从一个初始解X(0)开始迭代，并考察当前解X(i)的目标函数值J(X(i))；接着对当前解进行邻域扰动生成新解X(i+1)，并计算新解的目标函数值J(X(i+1))；然后基于Metropolis接受准则，以概率1接受较好解，以概率
接受较差解作为当前解，并逐步实施降温，直到系统冷却至指定的低温Tmin。另外，MATLAB中也已加入模拟退火优化算法工具箱[29]，因此可以直接使用MATLAB实施模拟退火算法编程。
为了进一步提高拟合优化效率，初始刚度K可以直接通过对剪切连接件单调加载曲线起始段进行线性拟合得到，因此最终采用模拟退火算法进行优化求解时的待拟合参数为{Fy,γ,n}。
综上所述，基于Bouc-Wen模型和模拟退火算法的屈服点确定方法具体操作步骤可以概括为：
1) 对剪切连接件单调加载曲线起始段采用最小二乘法线性拟合得到初始刚度K；
2) 将K代入式(20)，并将{Fy,γ,n}作为待求解变量，利用MATLAB模拟退火工具箱对式(20)所示的 Bouc-Wen模型基于式(21)所示的均方根误差目标函数进行优化求解，得到参数{Fy,γ,n}的拟合值。
完成拟合后，可以得到等效屈服点的坐标(uy,Fy)，剪切连接件各项基本力学参数{K,K′,Fy,uy}的拟合值，以及相应的Bouc-Wen模型表达式。相对传统的基于观察法和基于双线性模型的屈服点确定方法，采用本方法确定出的屈服点与 Bouc-Wen模型曲线相对应，具有明确的物理意义，并且拟合出的曲线能够较为准确地模拟曲线的过渡段，与单调加载试验曲线更加贴近，能够更加准确地描述剪切连接件的力学行为。
本文对一个缩尺的剪切连接件进行了单调拟静力加载试验验证。试验装置示意图及照片分别如图9、图10所示。剪切连接件的基本几何尺寸参数为h=hw=hf=280 mm，bw=160 mm，tw=5 mm，bf=90 mm，tf=8 mm。对剪切连接件的腹板和翼缘钢材进行了常温拉伸试验，如表1所示。为验证本文推导的剪切连接件应力分布弹性力学解，在剪切连接件腹板上布置应变花如图 11所示，其中R1～R13为应变花编号。此外，采用通用有限元软件ANSYS进行数值模拟，建模时采用的各项几何及材料参数均与试验构件相一致。
表1 钢材常温拉伸力学性能试验结果
Table 1 Results of tensile test at room temperature
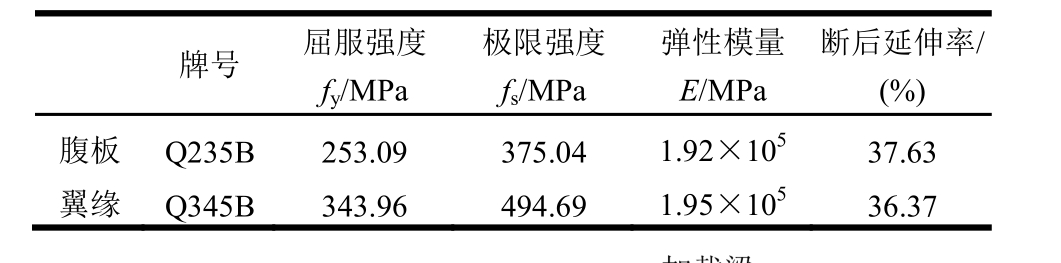
牌号 屈服强度fy/MPa极限强度fs/MPa弹性模量E/MPa断后延伸率/(%)腹板 Q235B 253.09 375.04 1.92×10537.63翼缘 Q345B 343.96 494.69 1.95×10536.37
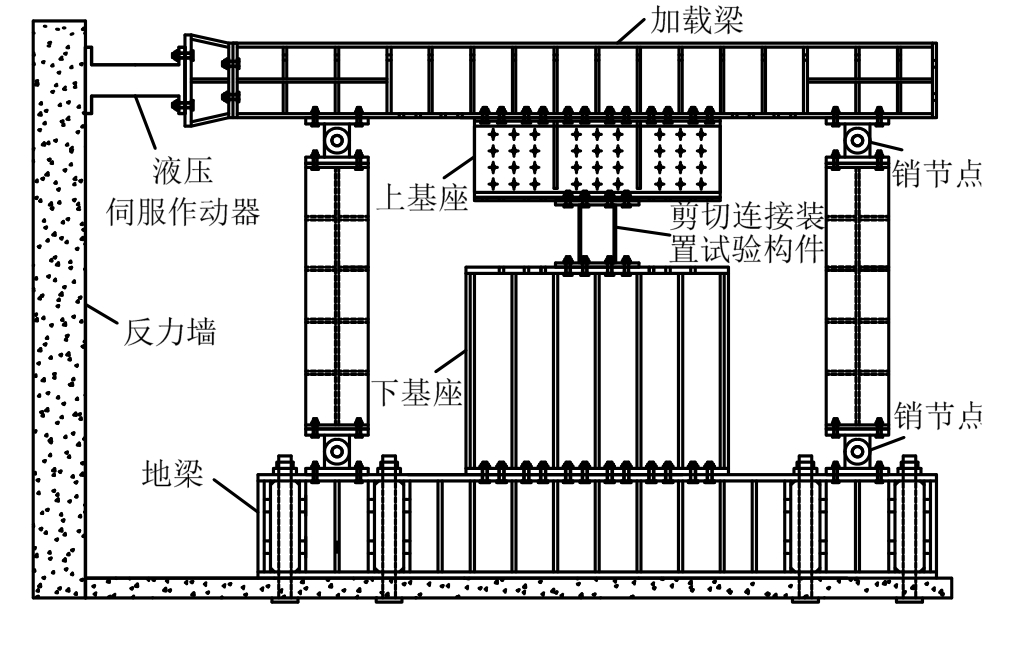
图9 试验装置示意图
Fig.9 Diagram of test setup
图10 试验照片
Fig.10 Picture of test
试验得到剪切连接件的单调加载曲线如图 12中的实线所示。根据本文提出的基于Bouc-Wen模型和模拟退火算法的屈服点确定方法，首先对试验单调加载曲线的起始段进行最小二乘拟合，可以得到初始刚度拟合值K=174.48 kN/mm；然后采用MATLAB 模拟退火工具箱对参数{Fy,γ,n}进行拟合，并结合K′=γK及uy=Fy/K，最终可以得到其等效屈服点坐标为(uy,Fy)=(0.69 mm, 121.26 kN)，相关的各项力学性能指标的拟合值{K,K′,Fy,uy} ={174.48 kN/mm, 2.60 kN/mm, 121.26 kN, 0.69 mm}，相应的拟合曲线如图 12中的虚线所示，可见拟合曲线与试验曲线能够良好吻合。将力学性能指标的试验拟合值与根据第 3节式(14)、式(16)～式(18)得到的理论计算值和有限元分析结果对比见表 2，可见三者能够较好吻合。此外，图 12中还给出了基于双线性模型的拟合曲线(见图中点划线)及基于观察法得到的屈服点(见图中实心点)。可见，双线性模型曲线无法与试验曲线形成良好贴合，因此导致双线性模型曲线与原始试验曲线的均方根误差达到RMSE=15.37 kN，而基于本文所提出方法的Bouc-Wen模型拟合曲线与试验曲线的均方根误差仅为RMSE=3.15 kN。采用传统的观察法，取试验曲线初始阶段刚度开始发生偏离的点作为屈服点，得到的屈服点坐标为(uy,Fy)=(0.19 mm, 30.81 kN)，可见该方法明显低估了屈服位移uy和屈服力Fy，且无法获得一个相应的理论模型。本文提出的屈服点确定方法优于以往的两种传统方法。
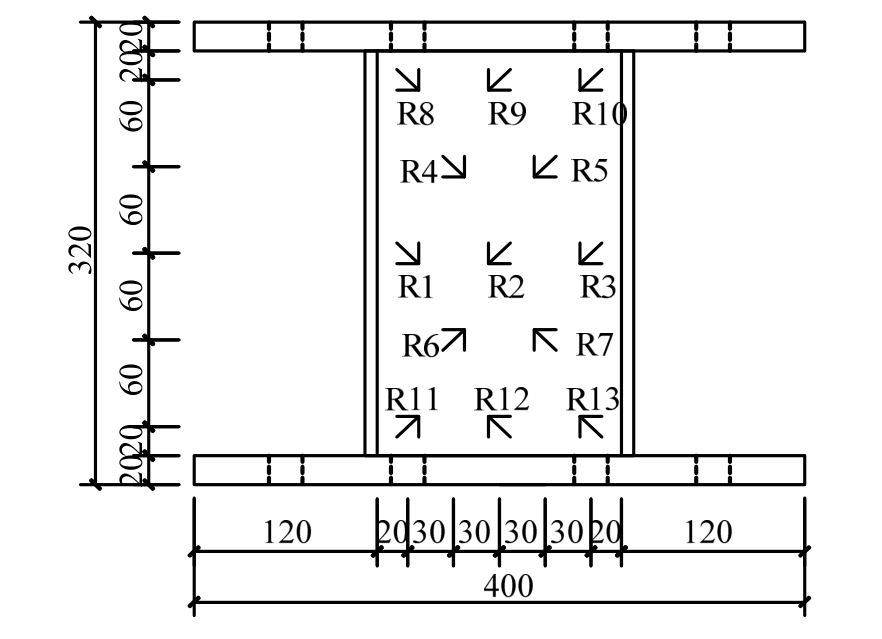
图11 应变花布置图
Fig.11 Layout of strain rosettes
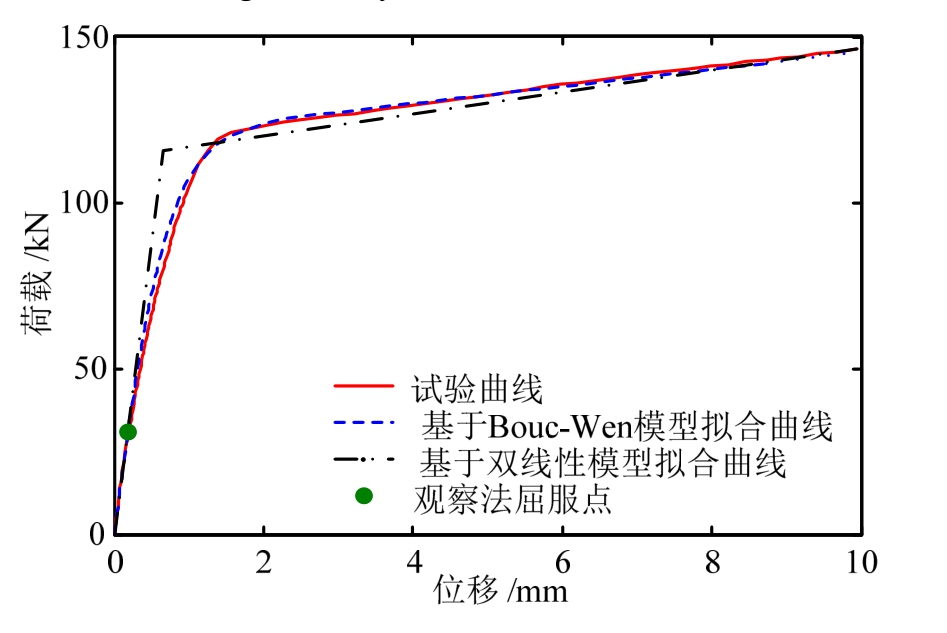
图12 单调加载试验曲线
Fig.12 Monotonic loading curve by test
表2 力学性能指标对比
Table 2 Comparison of mechanical performance parameters
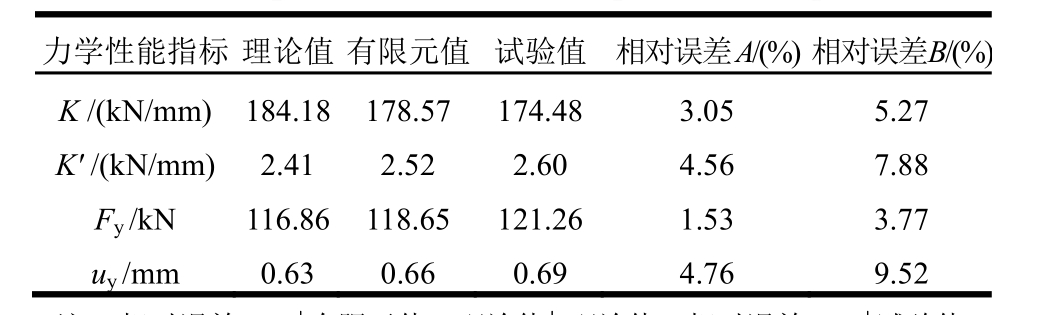
注：相对误差A＝|有限元值－理论值|/理论值，相对误差B＝|试验值－理论值|/理论值。
力学性能指标 理论值有限元值 试验值 相对误差A/(%)相对误差B/(%)K/(kN/mm)K′/(kN/mm)Fy/kNuy/mm 184.18 2.41 116.86 0.63 178.57 2.52 118.65 0.66 174.48 2.60 121.26 0.69 3.05 4.56 1.53 4.76 5.27 7.88 3.77 9.52
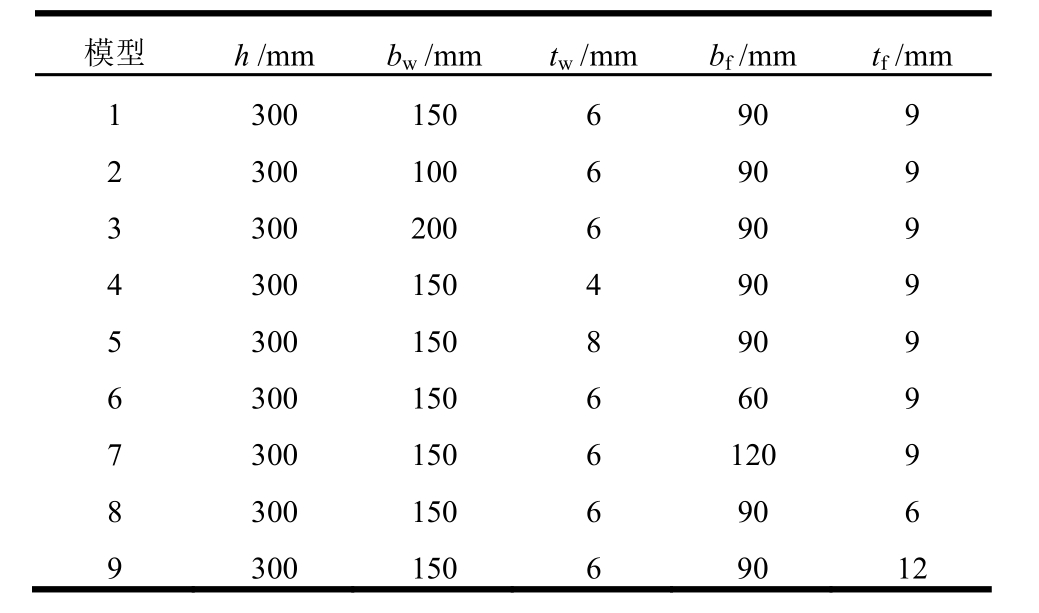
表3 有限元分析模型
Table 3 Models for finite element analysis
模型h/mmbw/mmtw/mmbf/mmtf/mm 1 300 150 6 90 9 2 300 100 6 90 9 3 300 200 6 90 9 4 300 150 4 90 9 5 300 150 8 90 9 6 300 150 6 60 9 7 300 150 6 120 9 8 300 150 6 90 6 9 300 150 6 90 12
表4 分析结果对比
Table 4 Comparison of analysis results
注：平均相对误差为9个模型同一项性能指标的相对误差平均值。
平均模型 性能指标K/(kN/mm)K′/(kN/mm)uy/mmFy/kN有限元解 178.35 2.57 0.75 132.94 2 理论解 110.06 1.68 0.80 87.64有限元解 106.12 1.80 0.85 89.93 3 理论解 260.73 3.37 0.67 175.28有限元解 249.45 3.14 0.71 177.63 4 理论解 130.63 1.69 0.67 87.64有限元解 126.93 1.80 0.71 90.38 5 理论解 233.29 3.36 0.75 175.28有限元解 224.50 3.30 0.78 175.87 6 理论解 170.94 2.52 0.77 131.46有限元解 165.46 2.45 0.79 131.25 7 理论解 192.78 2.53 0.68 131.46有限元解 184.23 2.69 0.73 135.03 8 理论解 170.94 2.52 0.77 131.46有限元解 162.84 2.41 0.80 130.37 9 理论解 192.78 2.53 0.68 131.46有限元解 188.21 2.71 0.73 137.96相对误差/(%) 3.61 4.94 5.45 1.91 1 理论解 184.32 2.53 0.71 131.46
除试验构件外，本文还对表3所示的一组具有代表性的剪切连接件进行有限元参数化分析。其中模型1为基准模型，模型2～模型9为对比模型，分别为通过改变基准模型的腹板高宽比、腹板高厚比(宽厚比)及翼缘尺寸而得到。结果对比见表 4，其中理论解为根据第3节公式得到，有限元解为采用本文提出的屈服点确定方法对有限元分析得到的单调加载曲线进行拟合得到。各项性能指标理论解与有限元解的平均相对误差均在5.50%以内，理论解与有限元解能够良好吻合。
为验证本文推导的剪切连接件腹板应力分布弹性力学解，取试验中荷载达到F=60 kN时由应变花采集数据得到的腹板应力，并与相应的理论值和有限元分析值对比，将部分具有代表性的测点数据列举见表5。可见，对于腹板高度中部附近的测点，三者吻合良好，但对于靠近上、下端板的测点，理论计算值与有限元分析值及试验值之间的误差略见增大。其原因是，推导应力分布弹性力学解式(9)时，腹板与连接端板相交处的边界条件采用了圣维南原理进行简化，因此在计算靠近该边界的应力时可能存在一定误差。
表5 腹板应力对比
Table 5 Comparison of stress in web plate
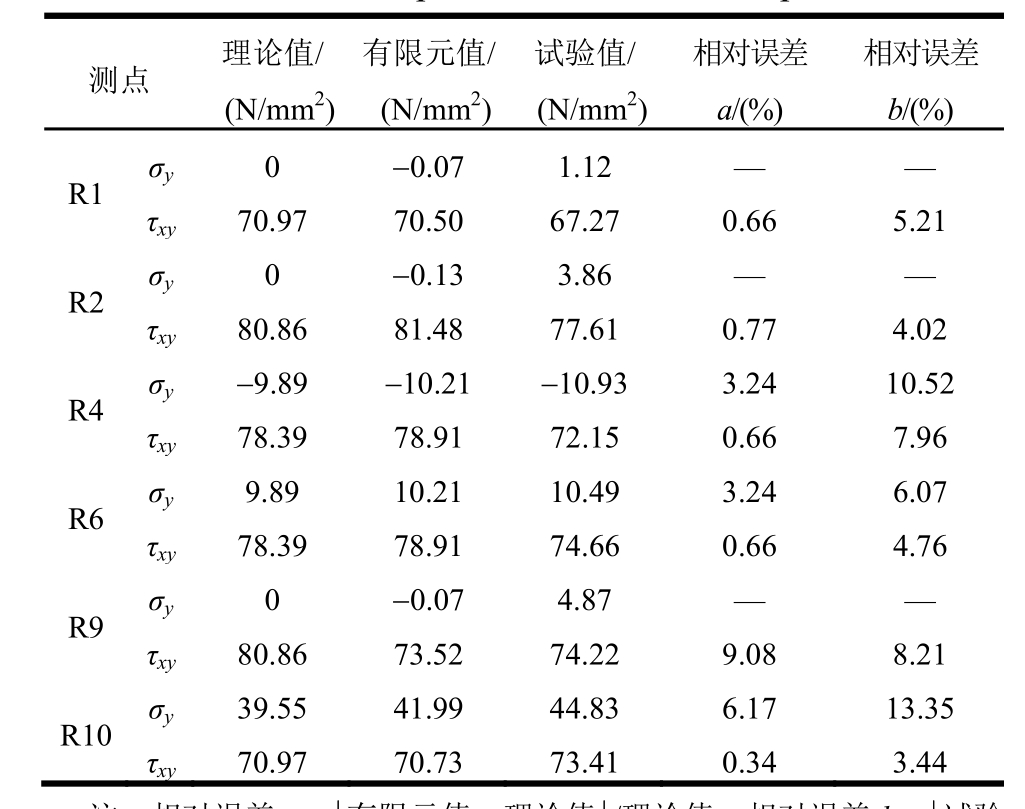
注：相对误差a＝|有限元值－理论值|/理论值，相对误差b＝|试验值－理论值|/理论值。
测点 理论值/(N/mm2)有限元值/(N/mm2)试验值/(N/mm2)相对误差a/(%)相对误差b/(%)R1σyτxy0 70.97-0.07 70.50 1.12 67.27—0.66—5.21 R2σyτxy—4.02 R4σyτxy0 80.86-0.13 81.48 3.86 77.61—0.77 10.52 7.96 R6σyτxy-9.89 78.39-10.21 78.91-10.93 72.15 3.24 0.66—8.21 R10σyτxy6.07 4.76 R9σyτxy9.89 78.39 10.21 78.91 10.49 74.66 3.24 0.66 0 80.86-0.07 73.52 4.87 74.22—9.08 39.55 70.97 41.99 70.73 44.83 73.41 6.17 0.34 13.35 3.44
本文对剪切连接件的受力机理进行了理论研究与试验验证。研究结果表明，剪切连接件的腹板应力分布理论解及各项力学性能指标的理论解均与相应的有限元分析结果及试验结果吻合较好。采用本文提出的屈服点确定方法能够有效实现对剪切连接件试验曲线的拟合及对其关键力学性能指标的识别，且拟合效果明显优于以往基于观察法及双线性模型的屈服点确定方法。相关研究成果可以为剪切连接装置的工程设计、性能评估及后续研究提供理论参考。
[1]Housner G W, Bergman L A, Soong T T, et al. Structural control past, present, and future [J]. Journal of Engineering Mechanics, 1997, 123(9): 897―971.
[2]Soong T T, Spencer B F. Supplemental energy dissipation: State-of-the-art and state-of-the-practice [J].Engineering Structures, 2002, 24(3): 243―259.
[3]Mansour N, Christopoulos C, Tremblay R. Experimental validation of replaceable shear links for eccentrically braced steel frames [J]. Journal of Structural Engineering, 2011, 137(10): 1141―1152.
[4]周云, 何志明, 张超. 可更换剪切钢板阻尼器偏心支撑框架分析[J]. 地震工程与工程振动, 2015, 35(5):68―78.Zhou Yun, He Zhiming, Zhang Chao. Structure analysis of replaceable shear link eccentrically brace with steel shear panel damper [J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(5): 68―78. (in Chinese)
[5]Najafi L H, Tehranizadeh M. Equation for achieving efficient length of link-beams in eccentrically braced frames and its reliability validation [J]. Journal of Constructional Steel Research, 2017, 130: 53―64.
[6]Durucan C, Dicleli M. Analytical study on seismic retrofitting of reinforced concrete buildings using steel braces with shear link [J]. Engineering Structures, 2010,32(10): 2995―3010.
[7]Mazzolani F M. Innovative metal systems for seismic upgrading of RC structures [J]. Journal of Constructional Steel Research, 2008, 64(7): 882―895.
[8]连鸣, 苏明周, 李慎. Y形高强钢组合偏心支撑框架结构基于性能的塑性设计方法研究[J]. 工程力学, 2017,34(5):148―162.Lian Ming, Su Mingzhou, Li Shen. Performance-based plastic design method for Y-type high strength steel composite eccentrically braced frames [J]. Engineering Mechanics, 2017, 34(5): 148―162. (in Chinese)
[9]Vetr M G, Ghamari A, Bouwkamp J. Investigating the nonlinear behavior of eccentrically braced frame with vertical shear links (V-EBF) [J]. Journal of Building Engineering, 2017, 10: 47―59.
[10] 纪晓东, 马琦峰, 王彦栋, 钱稼茹. 钢连梁可更换消能梁段抗震性能试验研究[J]. 建筑结构学报, 2014,35(6): 1―11.Ji Xiaodong, Ma Qifeng, Wang Yandong, Qian Jiaru.Structure analysis of replaceable shear link eccentrically brace with steel shear panel damper [J]. Journal of Building Structures, 2014, 35(6): 1―11. (in Chinese)
[11] Iwai R, Dusicka P. Development of linked column frame system for seismic lateral loads [C]// Structures Congress 2007: Structural Engineering Research Frontiers, ASCE,2007: 1－13.
[12] Malakoutian M, Berman J W, Dusicka P. Seismic response evaluation of the linked column frame system[J]. Earthquake Engineering & Structural Dynamics,2013, 42(6): 795―814.
[13] Uang C M, Seible F, McDaniel C, et al. Performance evaluation of shear links and orthotropic bridge deck panels for the new San Francisco–Oakland Bay Bridge[J]. Earthquake Engineering & Structural Dynamics,2005, 34(4/5): 393―408.
[14] McDaniel C C, Seible F. Influence of inelastic tower links on cable-supported bridge response [J]. Journal of Bridge Engineering, 2005, 10(3): 272―280.
[15] McDaniel C C, Uang C M, Seible F. Cyclic testing of built-up steel shear links for the new bay bridge [J].Journal of Structural Engineering (ASCE), 2003, 129(6):801―809.
[16] Timoshenko S P, Goodier J N. Theory of elasticity [M].3rd ed. New York: McGraw-Hill, 1970: 11―28.
[17] 徐芝纶. 弹性力学[M]. 第四版. 北京: 高等教育出版社, 2006: 9―35.Xu Zhilun. Elasticity [M]. 4th ed. Beijing: Higher Education Press, 2006: 9―35. (in Chinese)
[18] 刘计良, 王正中, 韩彦宝, 等. 均布荷载作用下工字形截面单跨超静定深梁应力计算方法研究[J]. 工程力学,2010, 27(3):174―179.Liu Jiliang, Wang Zhengzhong, Han Yanbao, et al. Study on stress calculation method for hyperstatic deep beams with single span and i section subjected to uniform load[J]. Engineering Mechanics, 2010, 27(3):174―179. (in Chinese)
[19] 王正中, 朱军祚, 谌磊, 等. 集中力作用下深梁弯剪耦合变形应力计算方法[J]. 工程力学, 2008, 25(4): 115―120.Wang Zhengzhong, Zhu Junzuo, Chen Lei, et al. The stress calculation method of deep beam with shear-bending coupling distortion under concentrated force [J]. Engineering Mechanics, 2008, 25(4):115―120. (in Chinese)
[20] 王正中, 沙际德. 深孔钢闸门主梁横力弯曲正应力与挠度计算[J]. 水利学报, 1995, 9: 40―46.Wang Zhengzhong, Sha Jide. Calculation of normal stress and deflection in transverse bending of main beam in outlet gate [J]. Journal of Hydraulic Engineering,1995, 9: 40―60. (in Chinese)
[21] Gere J M. Mechanics of materials (sixth edition) [M].Belmont: Brooks/Cole-Thomson Learning, 2004.
[22] Chan R W K, Albermani F. Experimental study of steel slit damper for passive energy dissipation [J].Engineering Structures, 2008, 30(4): 1058―1066.
[23] 孙国华, 顾强, 齐永胜, 等. 钢板剪力墙结构的剪切变形分析[J]. 沈阳建筑大学学报(自然科学版), 2013,29(2): 205―214.Sun Guohua, Gu Qiang, Qi Yongsheng, et al. Shear deformation analysis of steel plate shear walls [J].Journal of Shenyang Jianzhu University (Natural Science), 2013, 29(2): 205―214. (in Chinese)
[24] Bouc R. Forced vibration of mechanical systems with hysteresis [C]// Proceedings of the Fourth Conference on Nonlinear Oscillation. Prague, Czechoslovakia, 1967.
[25] Wen Y K. Method for random vibration of hysteretic systems [J]. Journal of Engineering Mechanics Division(ASCE), 1976, 102(2): 249―263.
[26] 北京金土木软件技术有限公司. SAP2000中文版使用指南[M]. 第二版. 北京: 人民交通出版社, 2012: 60.Beijing Civil King Software Technology Co., Ltd.SAP2000 user guide [M]. 2nd ed. Beijing: China Communications Press, 2012: 60. (in Chinese)
[27] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simulated annealing [J]. Science, 1983, 220(4598):671―680.
[28] Ingber L. Simulated annealing: practice versus theory [J].Mathematical and Computer Modelling, 1993, 18(11):29―57.
[29] Math Works. Optimization toolbox: user’s guide [M].Natick, MA, USA: MathWorks, 2016.
THEORETICAL STUDY AND EXPERIMENTAL VERIFICATION OF THE MECHANICAL MECHANISM OF SHEAR LINK DEVICES