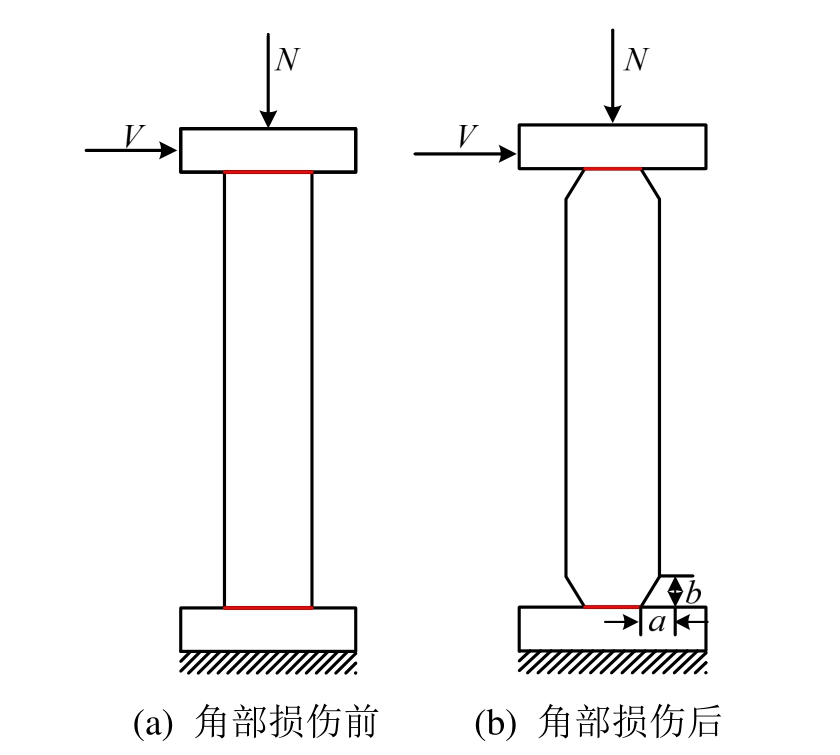
图1 损伤前后摇摆构件
Fig.1 Rocking elements before and after being damaged
摇摆结构自被提出以来[1]，已经有了多种实现方式，包括摇摆块体、摇摆桥墩、摇摆框架、摇摆墙等。摇摆结构通过放松结构与基础或构件之间的约束，允许结构或构件在地震作用下发生摇摆，并利用摇摆引起的局部集中变形将损伤控制在摇摆界面上，减少结构主体的损伤。
各国学者对摇摆结构进行了不同的理论分析和试验研究[2―5]。一些学者将摇摆构件简化为刚体，分析其在脉冲作用下的倾覆性能[6]，以及在碰撞时的能量耗散[7]。另一些学者考虑到实际摇摆结构不是刚体，荷载位移曲线不能近似为线性强化刚塑性，为了更合理地分析摇摆体的运动状态，关注了其在转动前的弹塑性变形[8]。Mander等[9]在摇摆桥墩的研究中将其抗侧刚度分为摇摆前和摇摆后两部分，Roh和Reinhorn[10―12]在摇摆柱的分析中将摇摆前的变形细分为了接触面分离和屈服两个过程。
摇摆构件在摇摆前的变形过程中由于端部接触面的变化具有明显的非线性特征。传统结构的弹塑性变形分析采用集中塑性模型或者弥散塑性模型，Roh等[13]对此进行了总结并优化了一种幂弥散塑性模型，并借鉴传统结构弥散塑性模型的方法提出了摇摆构件的分析模型[10]和简化的弥散塑性模型[11―12]。Belleri等[14]比较了实体单元、纤维梁单元、受压弹簧模型、集中转动弹簧模型在有限元分析中的差异。Avgenakis等[15]通过将摇摆单元端部应力拆分为普通弯曲梁叠加自平衡应力，通过自平衡应力产生的变形来考虑非线性影响。
Preti等[16]在摇摆墙转动导致角部混凝土损伤剥落后，用高性能纤维增强混凝土在原墙体破坏位置进行修补后再次试验。Roh等[12]注意到摇摆构件在摇摆运动中支撑点会出现破坏，因此分析模型考虑了初始摇摆柱和破坏稳定后的摇摆柱两种情况，在桥墩的分析模型中也考虑了角部的缺失[17]。
需要注意的是，Roh等[10―12]通过改变有效刚度系数来考虑损伤前后的不同，而角部损伤后的摇摆柱比无损伤摇摆柱的有效刚度系数大，这种方式值得商榷。为了更合理地解释角部损伤摇摆构件在摇摆前的变形，本文参考Roh等[10]精细模型分析完整摇摆构件摇摆前变形的方法，引入一个损伤影响系数来考虑角部缺陷对损伤后摇摆构件摇摆前刚度的影响，并通过 ABAQUS实体有限元模型和已有的试验对提出的分析模型进行验证。
摇摆构件受轴压力N和顶部逐渐增大的水平力V作用，如图1所示，假定其与上、下梁接触面间切向无滑动，法向硬接触，且上梁在变形中保持平动，则摇摆构件两端的受力与变形是反对称的，摇摆前的端部正应力分布随水平力增大的变化如图2所示。Roh等[11―12]在简化塑性弥散模型中定义摇摆体的摇摆前运动过程时，认为接触面边缘正应力为0的状态为分离点；接触面边缘正应力到屈服应力的状态为屈服点；正应力全部到达屈服应力的状态为摇摆起始点，且摇摆运动的转动中心在应力分布区间的中点。
图1 损伤前后摇摆构件
Fig.1 Rocking elements before and after being damaged
图2 正应力分布变化
Fig.2 Variation of normal stress distribution
摇摆构件同时受剪力V、弯矩M0和轴压力N作用的接触面，正应力分布随弯矩的变化规律与轴压比n相关。轴压比大于0.5时，如图2(a)所示，弯矩增大的过程中接触面先后经历屈服点和分离点，最后开始转动；轴压比等于0.5时，如图2(b)所示，弯矩增大的过程中接触面的分离和屈服点相同，最后开始转动；轴压比小于0.5时，如图2(c)所示，弯矩增大的过程中接触面先后经历分离点和屈服点，最后开始转动。考虑到转动点靠近截面中心时不易进行摇摆运动，Roh等[11]摇摆柱试验的轴压比最大为 0.2，因此本文分析的摇摆构件轴压比均小于 0.5，正应力分布的变化和相应关系如图 3所示，假定轴压比为n，端部截面宽度为L，变形过程中的接触面宽度mL，正应力合力N偏离端部截面中心距离xL，正应力合力N偏移到接触面中心时为Nc，产生的弯矩为mc，可确定以下关系式：
当摇摆体弹性模量较大，变形较小，不考虑P-Δ效应时：
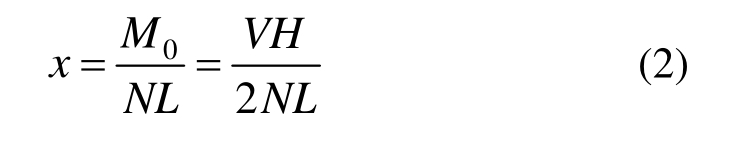
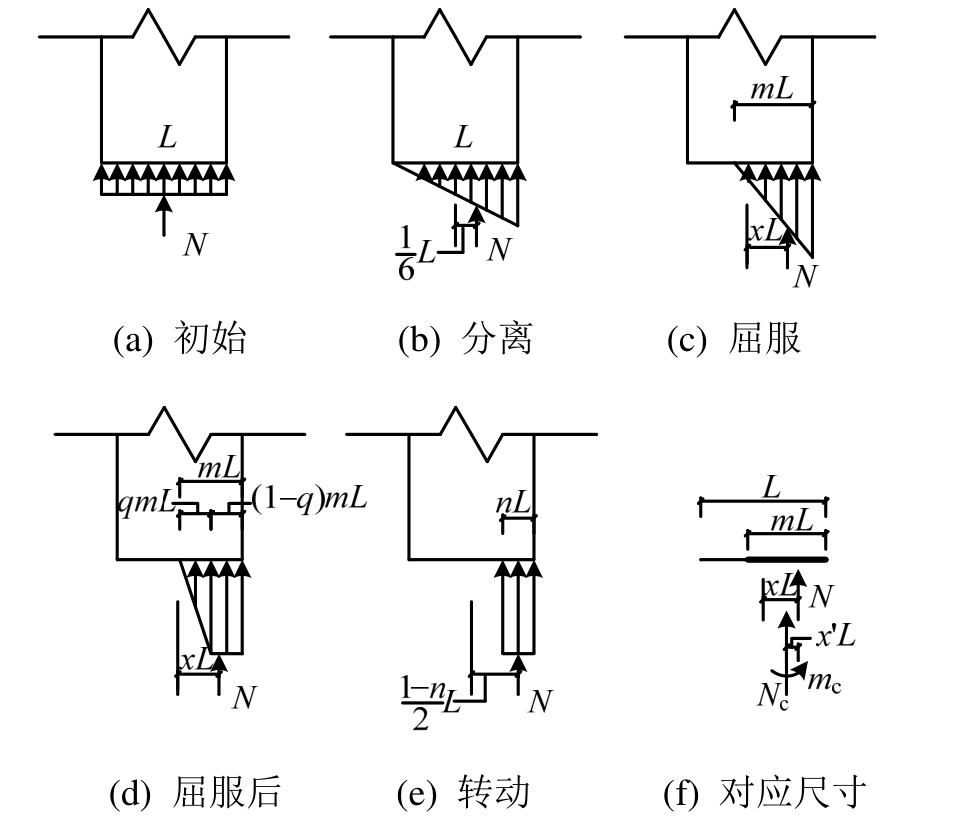
图3 正应力分布计算
Fig.3 Calculation of normal stress distribution
当
时：
当
时：
当
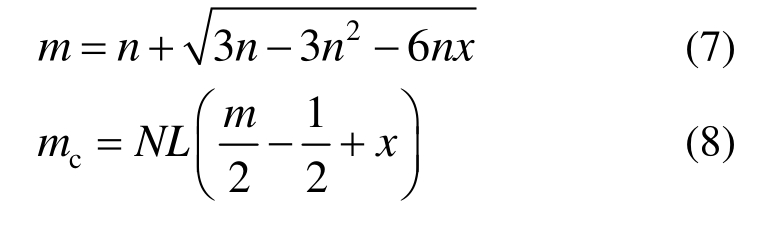
摇摆构件顶部水平力增大的过程中，如图4所示，上、下端部由完全接触开始分离，在摇摆构件接触面附近的高度形成了非线性分布区域。构件沿高度的有效截面及其刚度特性变化如图5所示。Roh等[10]在精细化模型中以正应力的扩散范围确定非线性截面的区间，在弥散塑性简化模型中以开裂弯矩的位置确定非线性范围[11―12]。为方便计算，本文也采用开裂弯矩的位置确定非线性区间。
图4 非线性区间形成过程
Fig.4 Development of nonlinear area
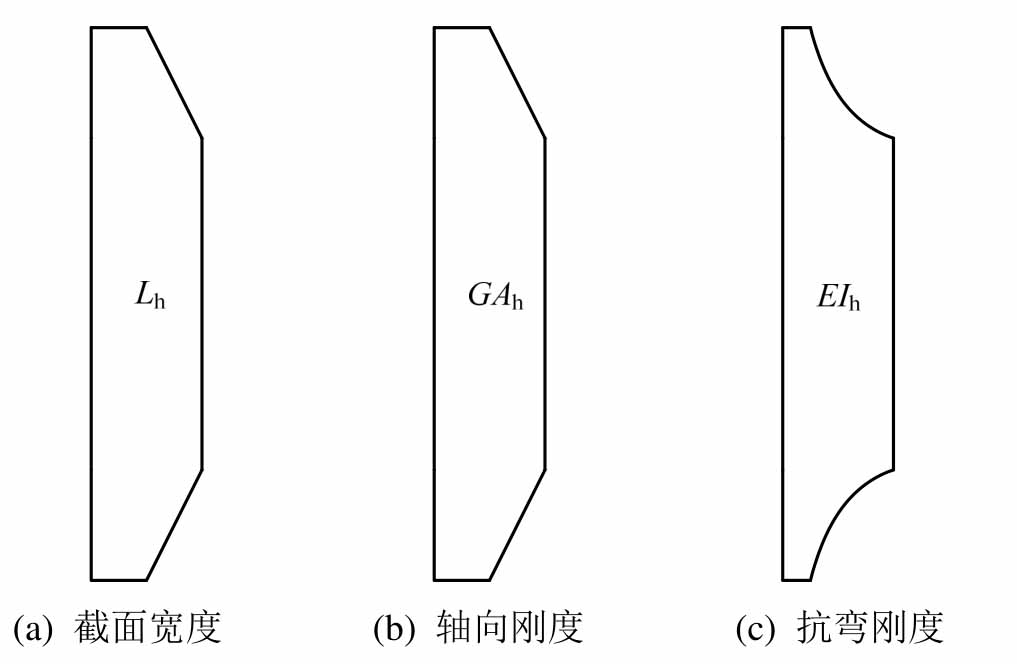
图5 截面几何特性
Fig.5 Sectional properties
无损伤摇摆构件分离前的受力如图6所示，达到分离状态后到摇摆起始点的受力和截面尺寸变化如图7所示，摇摆构件高度H，损伤后的端部截面宽度L0，端部截面面积A0，端部截面惯性矩I0，非线性区间的比例α按式(9)确定：
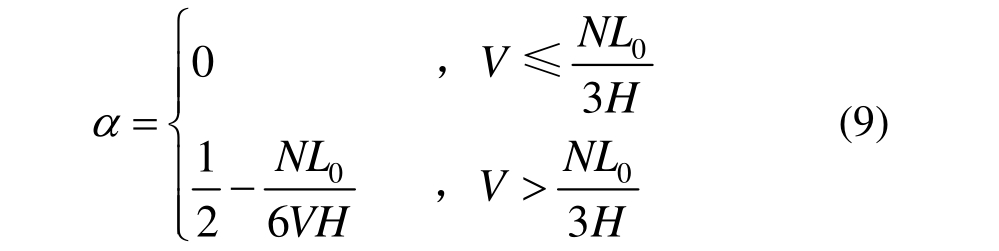
图6 分离前内力分布
Fig.6 Distribution of internal force before separation
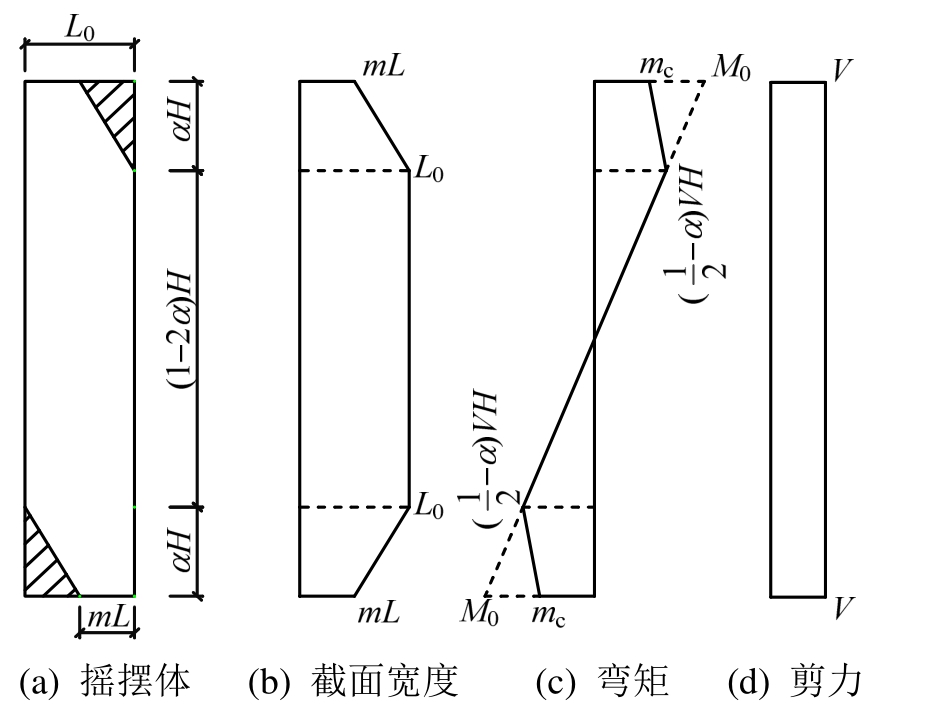
图7 分离后内力分布
Fig.7 Distribution of internal force after separation
截面宽度Lh、面积Ah、惯性矩Ih沿高度变化如式(10) ~式(12)所示：
实际弯矩和剪力如式(13)、式(14)所示：
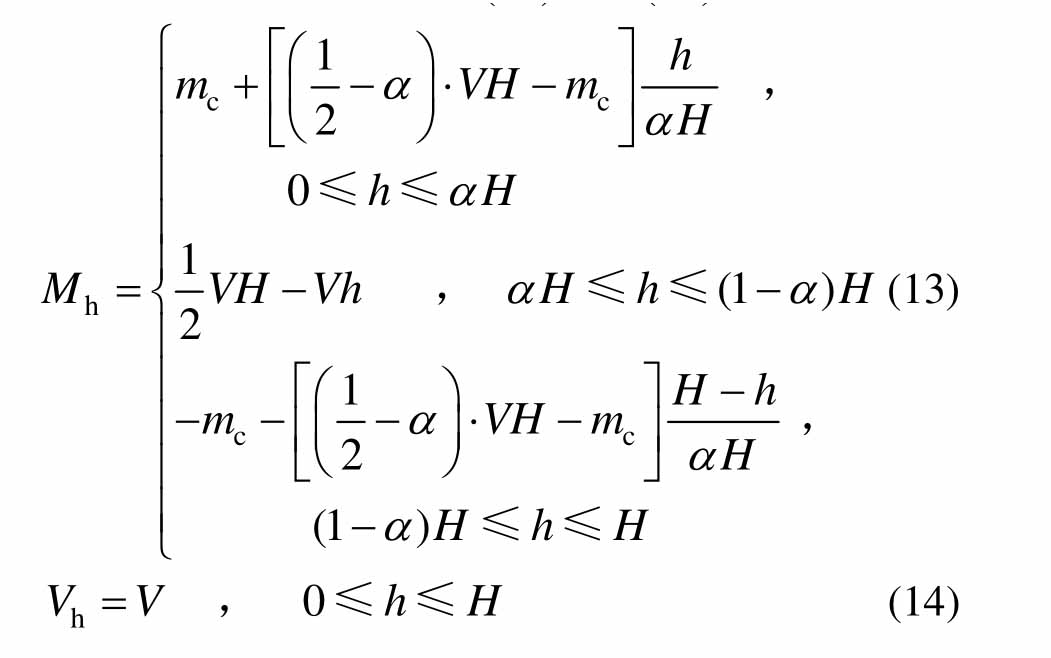
如图8所示，采用单位力法对摇摆构件的水平变形u进行计算分析，则单位力作用下相应的弯矩和剪力如式(15)、式(16)所示：
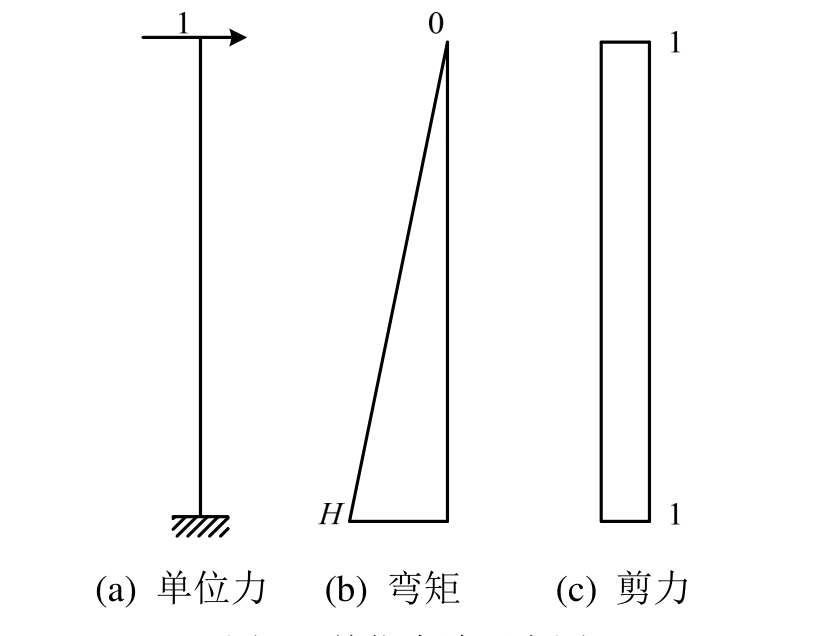
图8 单位力法示意图
Fig.8 Unit force method diagram
相应的计算公式为：α= 0：
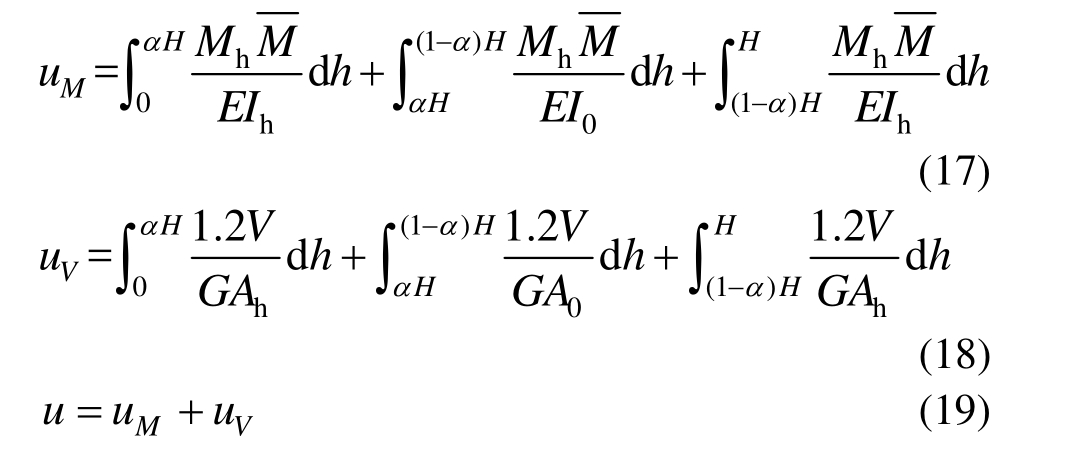
如图6所示，当摇摆构件未分离时，即m=1，
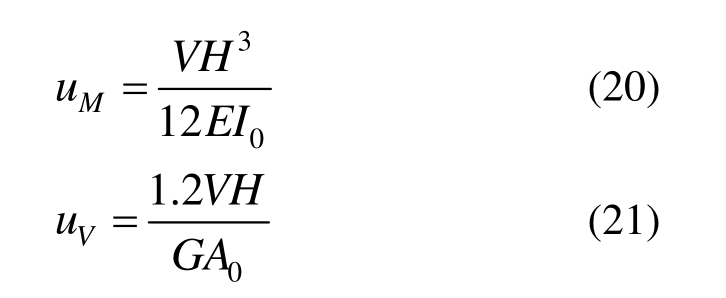
如图7所示，构件分离后到摇摆前，即m＜1，α＞ 0：
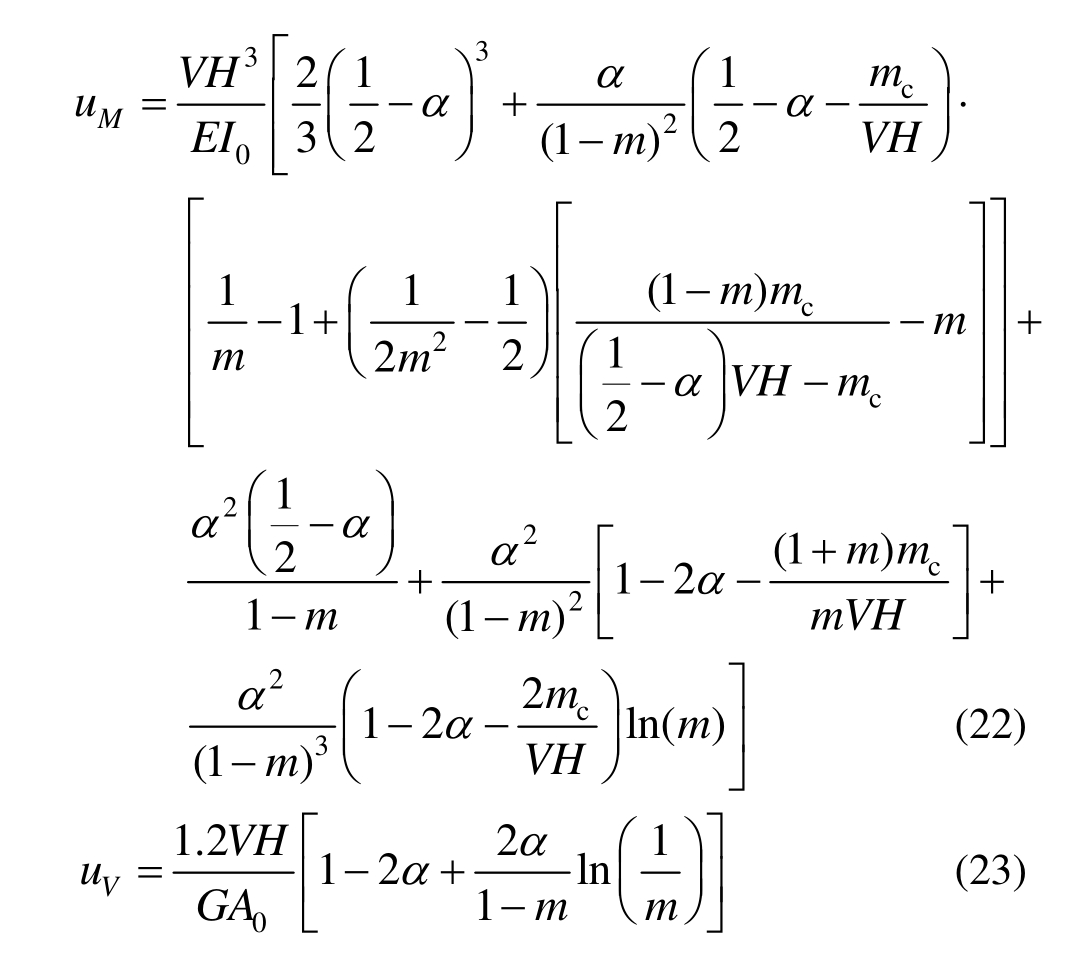
如图1(b)所示的角部损伤摇摆构件，假定损伤稳定后的四个缺角尺寸：宽度a、高度b。其顶部水平力增大的过程和无损伤摇摆构件相似，上、下端部由完全接触到分离屈服，最后摇摆构件转动。角部损伤摇摆构件引入损伤影响系数β考虑角部缺陷，假定摇摆构件在初始状态下接触面附近βH高度内有效截面尺寸线性变化，在接触面分离后又在此基础上发展新的非线性分布区域。如图 9~图11所示，构件高度H，损伤后的端部截面宽度L，端部截面面积A，端部截面惯性矩I，未损伤截面宽度RL，初始有效截面非线性范围βH大于等于角部破坏高度b，在变形过程中，非线性区间αH从接触面分离前的0逐渐增大到超过βH。此处采用开裂弯矩的位置确定变形过程中的非线性区间，沿构件高度的开裂弯矩Mcr按式(24)确定：
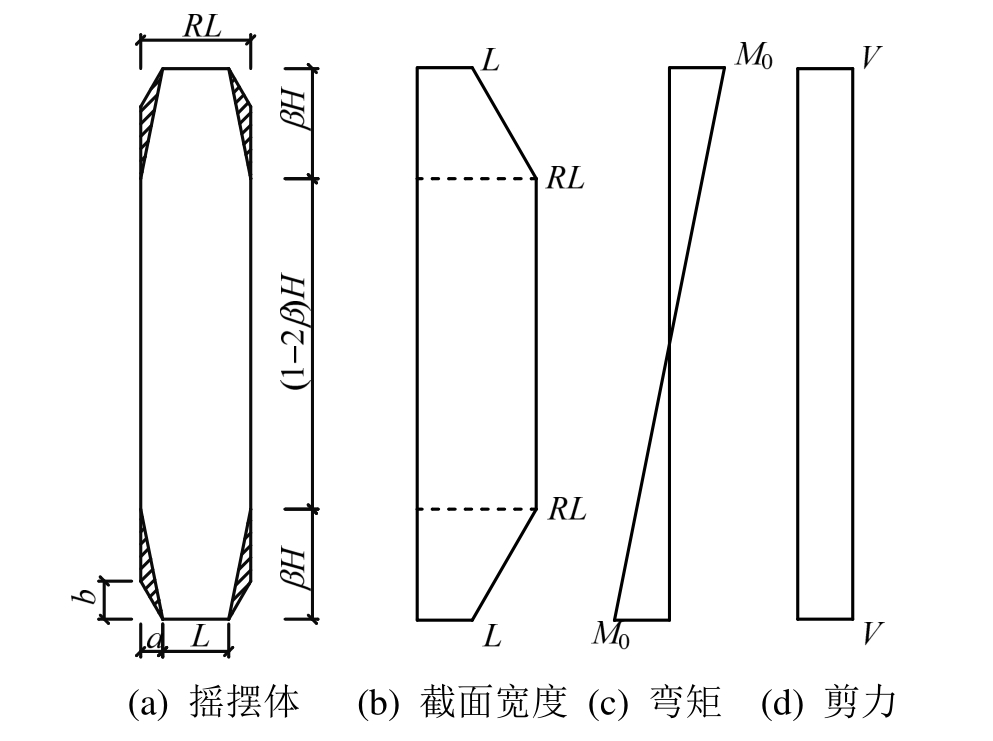
图9 分离前内力分布
Fig.9 Distribution of internal force before separation
图10 分离初期内力分布
Fig.10 Distribution of internal force at early stage of separation
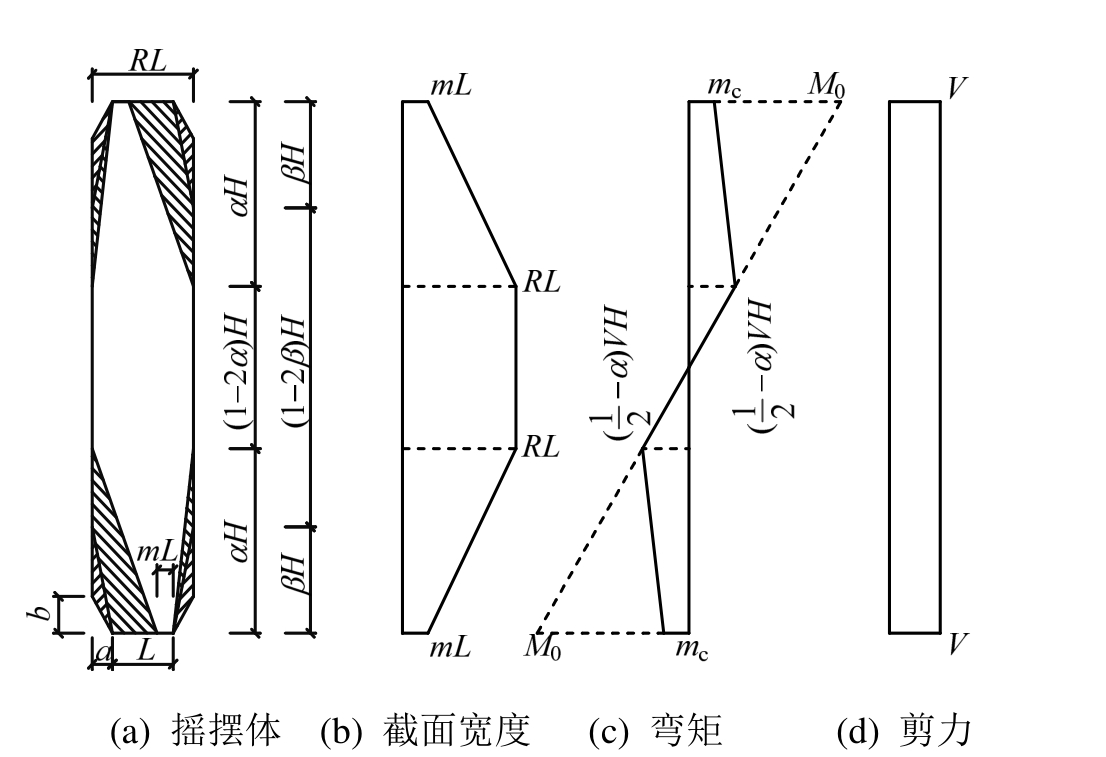
图11 分离后期内力分布
Fig.11 Distribution of internal force at later stage of separation
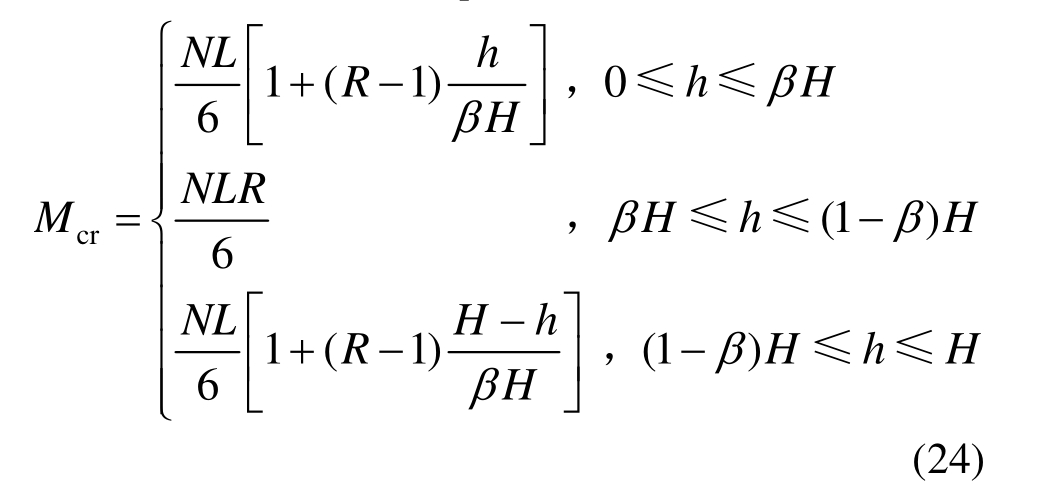
非线性区间的比例系数α按式(25)确定：
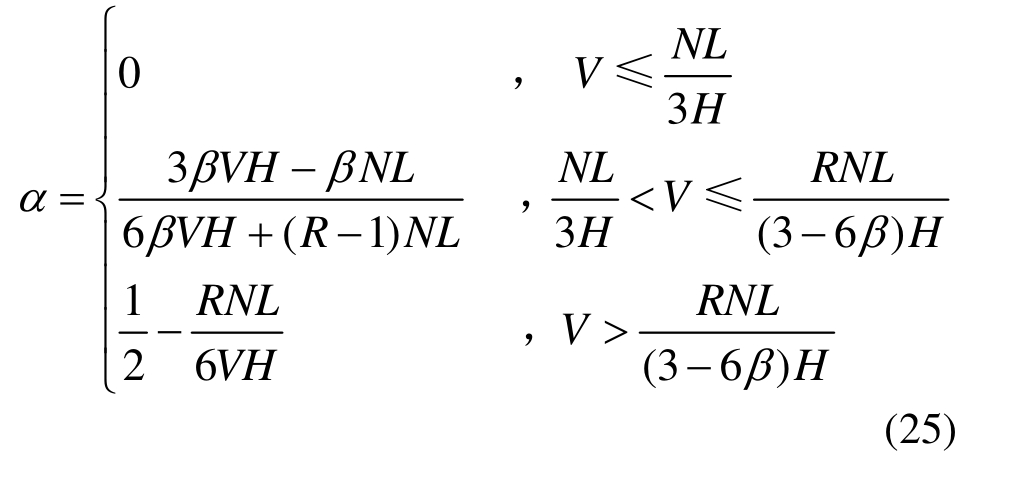
采用单位力法对角部损伤摇摆构件的水平变形进行计算分析，则单位力作用下相应的弯矩和剪力同式(15)、式(16)，水平变形u的计算公式同式(19)，但损伤后的摇摆构件在每一阶段的有效截面和内力分布都不相同。
如图9所示，当摇摆构件未分离时，即m=1，α= 0：
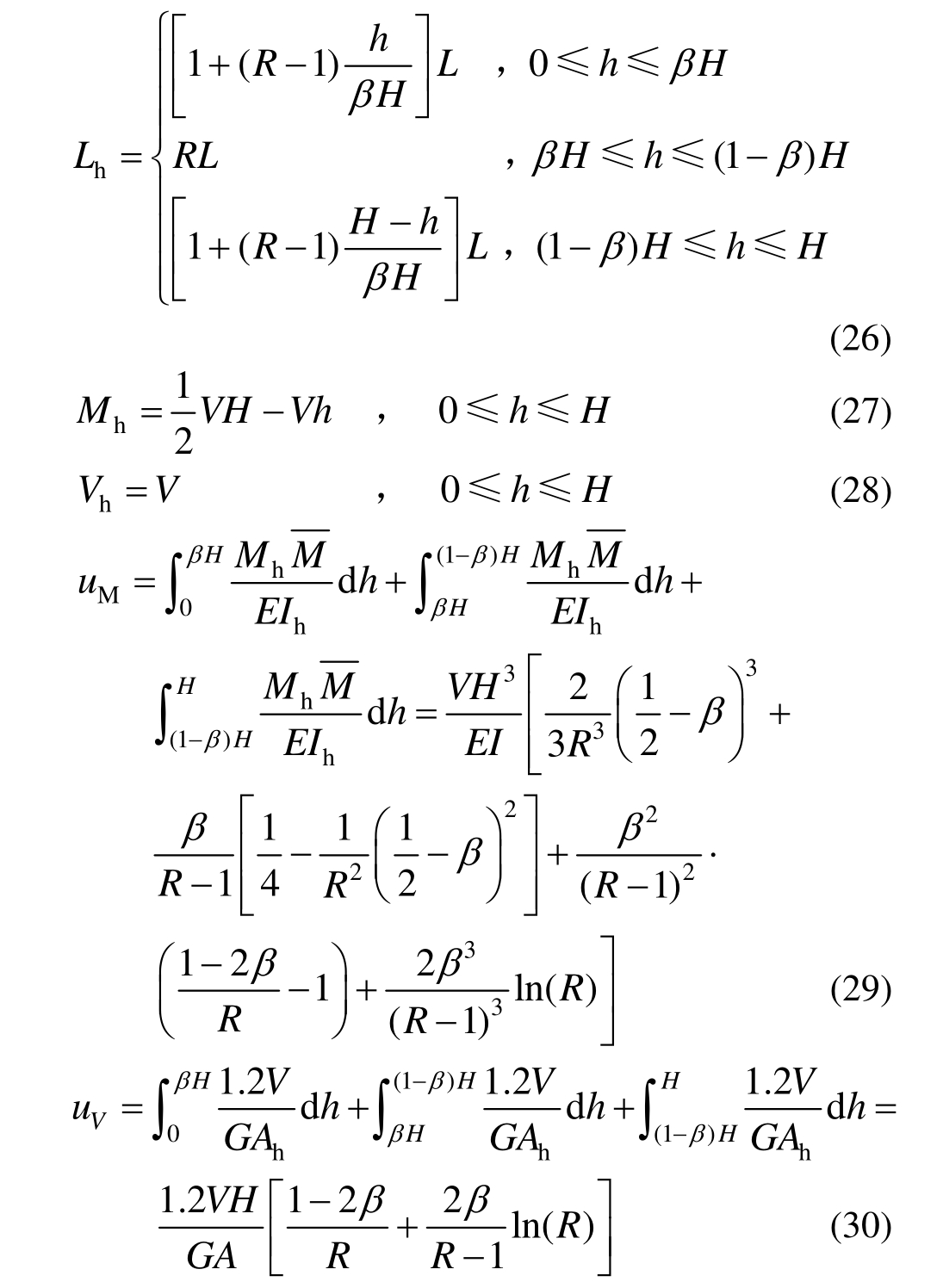
如图 10所示，当摇摆构件刚开始分离时，即0＜α＜β，m＜1：
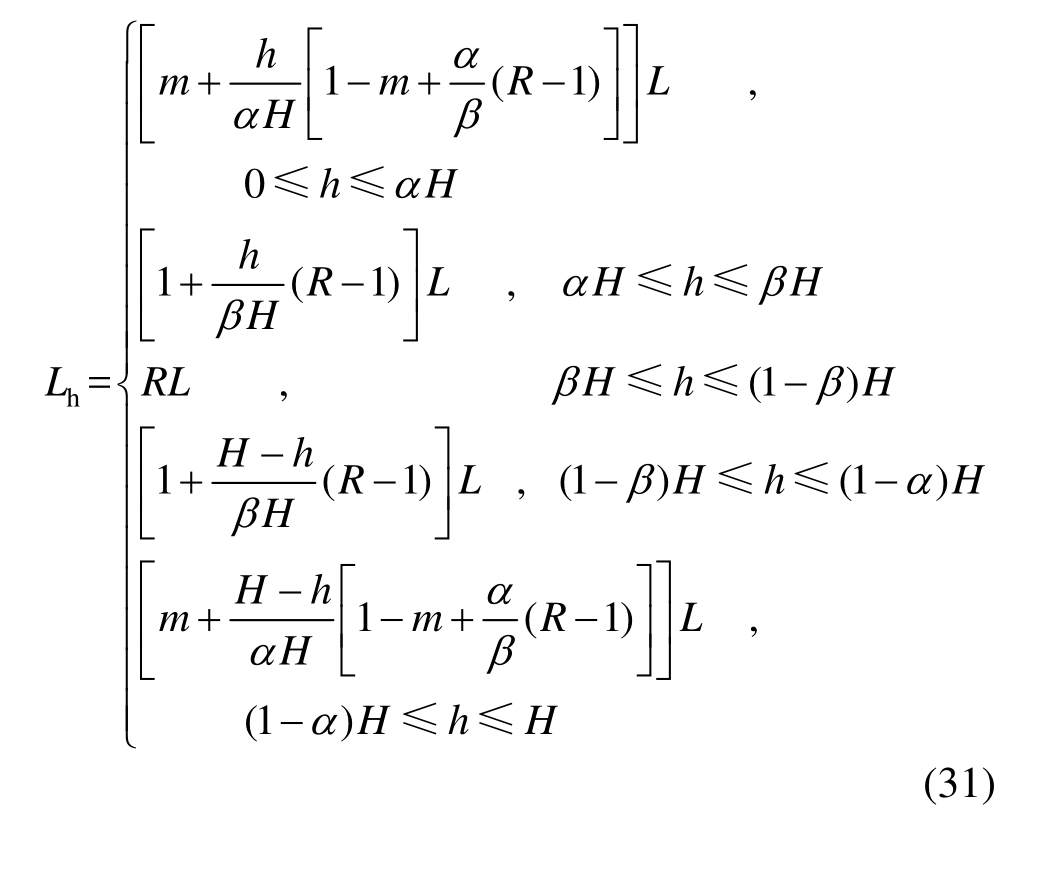
如图 11所示，当摇摆构件刚分离到接近摇摆时，即α≥β，m＜1：
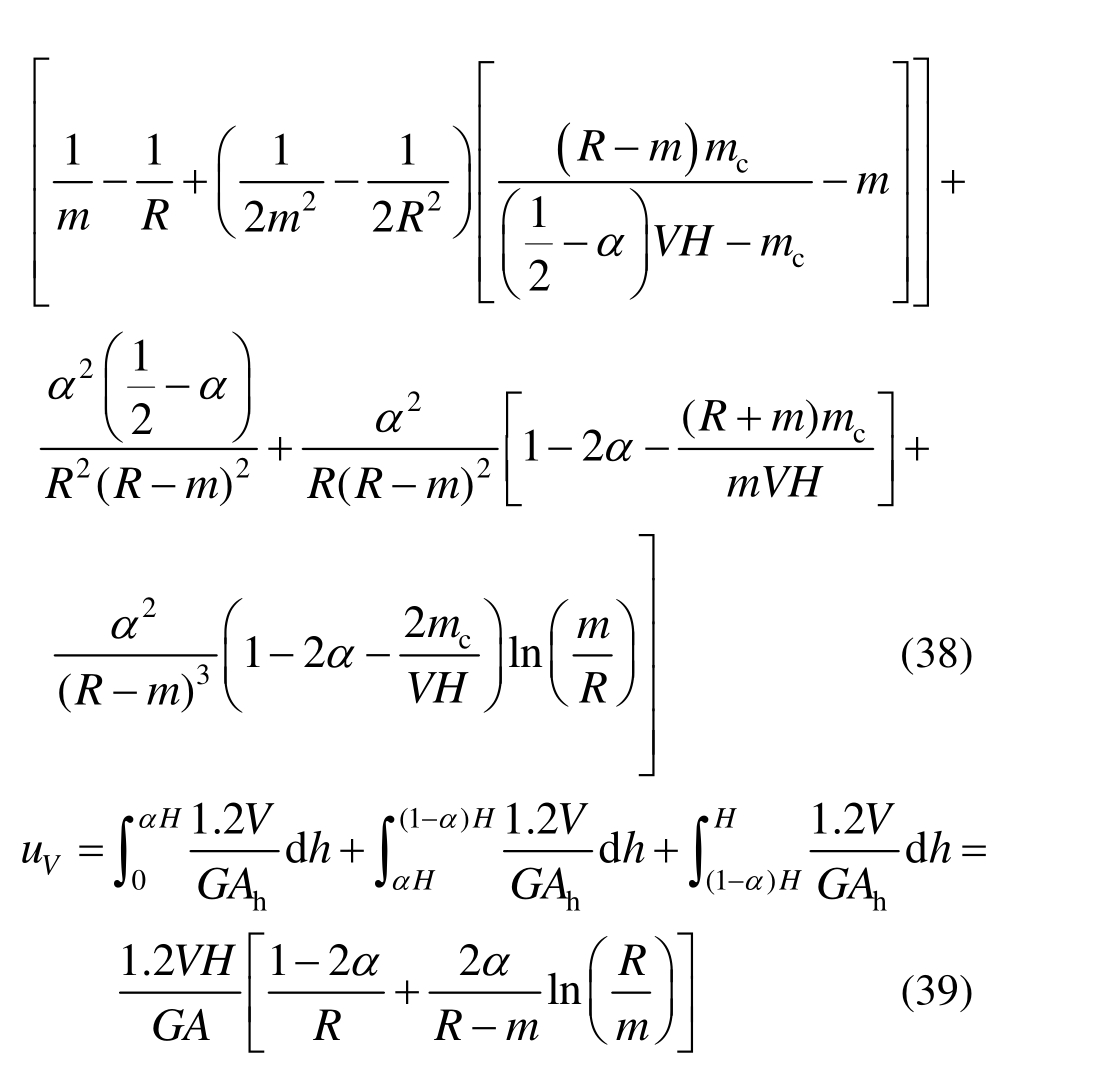
上述损伤前后摇摆构件摇摆前的变形计算均基于弹性变形理论，而在接触面进入屈服位置后，如图3(d)所示，正应力按比例分为弹性段q和屈服段1-q两部分，其中q取2-2n/m。因此在使用弹性变形理论计算时应考虑截面有效抗弯刚度的折减。参照 Park等[18]和Priestley等[19]的理论，开裂普通钢筋混凝土柱的有效抗弯刚度系数基于弯矩与轴力的变化范围为0.25~1.0。Mander等[9]在计算摇摆桥墩摇摆前抗侧刚度时未调整端部有效截面尺寸，而是基于普通混凝土柱乘以有效抗弯刚度系数0.5进行调整。Roh等[10]提出参照上述方式，在精细化分析模型对比试验结果时认为应乘以有效抗弯刚度系数0.7等；在简化弥散塑性模型对比角部无损伤试验构件时乘以有效抗弯刚度系数0.5[11]，在角部损伤后有效抗弯刚度系数反而增大至0.63和 0.75[12]，这种方式值得商榷。Roh等[10―12]和本文的计算模型本身已经考虑了有效截面，只需要在进入屈服点出现弹塑性变形后考虑进一步的修正折减，本文提出有效刚度修正系数为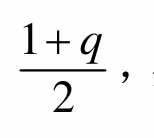
其值随内力增大由1.0减少至0.5。在计算时剪切刚度不调整，有效抗弯刚度取：
为了验证所提出分析模型的准确性，用ABAQUS对一系列无损伤和有损伤摇摆构件的摇摆前变形进行了模拟。参照Roh等[10]的方法建模，采用C3D8R单元，理想弹塑性材料，弹性模量E=30 GPa，泊松比ν=0.2，屈服强度fy=40 MPa，构件厚度t=500 mm，相关尺寸如表 1所示。其中表 1中的完整构件A与Roh[10]文中构件C-3完全相同。
不同轴压比下完整摇摆构件的有限元模型与理论计算模型的对比如图12(a)~图12(c)所示，理论计算包括使用原始抗弯刚度EIh和式(40)修正有效抗弯刚度EIeff。轴压比0.1作用下的不同摇摆构件在不同损伤下的有限元分析与不同损伤影响系数β下的理论计算比较如图 12(d)~图 12(u)所示，理论计算公式均使用有效刚度EIeff，其中，为考虑某些平缓缺角的侧面参与受力，将端部截面宽度调整增大，即缺角宽度a的尺寸缩小5 mm或10 mm。
表1 摇摆构件相关尺寸
Table 1 Dimensions of different rocking elements
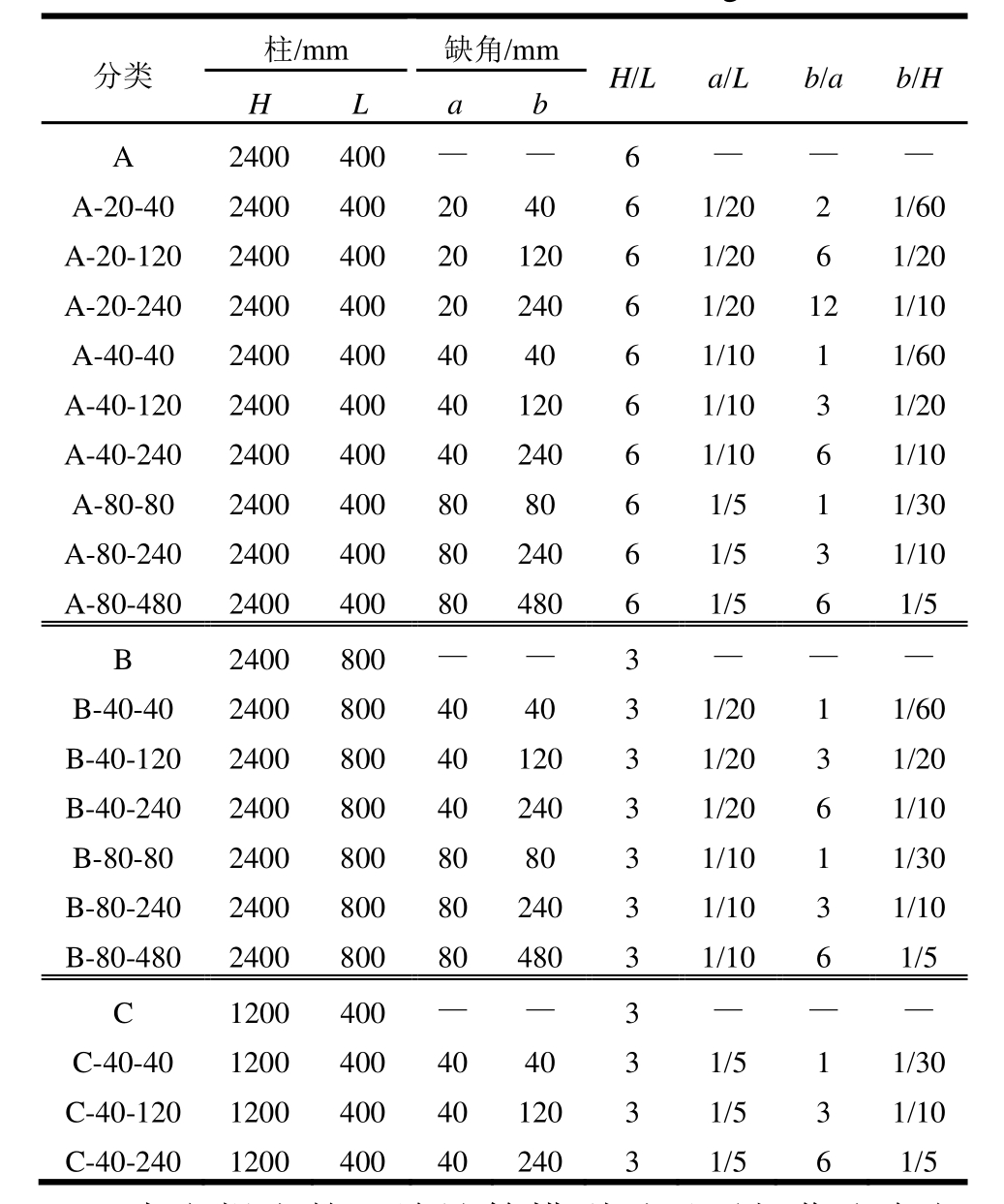
分类 柱/mm 缺角/mmH/La/Lb/ab/H HLabA 2400 400 — — 6 — — —A-20-40 2400 400 20 40 6 1/20 2 1/60 A-20-120 2400 400 20 120 6 1/20 6 1/20 A-20-240 2400 400 20 240 6 1/20 12 1/10 A-40-40 2400 400 40 40 6 1/10 1 1/60 A-40-120 2400 400 40 120 6 1/10 3 1/20 A-40-240 2400 400 40 240 6 1/10 6 1/10 A-80-80 2400 400 80 80 6 1/5 1 1/30 A-80-240 2400 400 80 240 6 1/5 3 1/10 A-80-480 2400 400 80 480 6 1/5 6 1/5 B 2400 800 — — 3 — — —B-40-40 2400 800 40 40 3 1/20 1 1/60 B-40-120 2400 800 40 120 3 1/20 3 1/20 B-40-240 2400 800 40 240 3 1/20 6 1/10 B-80-80 2400 800 80 80 3 1/10 1 1/30 B-80-240 2400 800 80 240 3 1/10 3 1/10 B-80-480 2400 800 80 480 3 1/10 6 1/5 C 1200 400 — — 3 — — —C-40-40 1200 400 40 40 3 1/5 1 1/30 C-40-120 1200 400 40 120 3 1/5 3 1/10 C-40-240 1200 400 40 240 3 1/5 6 1/5
本文提出的理论计算模型对于无损伤和角部损伤的摇摆构件摇摆前的变形预测与有限元模型的结果几乎相同。可以看出使用有效抗弯刚度EIeff的理论公式更好地符合了有限元摇摆模型的变形情况。通过比较不同尺寸的有损伤摇摆构件可发现：由于损伤区域的宽度a已经在有效截面中体现，a/L对损伤影响系数β的取值影响不大；损伤区域的b/H越大，损伤影响系数β取值越大；损伤区域的b/a越小，角部损伤区域的宽度a调整减小的值越大。通过调整损伤影响系数β和端部截面宽度可以预测不同程度角部损伤的摇摆构件变形情况。本文中β取 0.3保守预测了算例中损伤摇摆构件的变形。
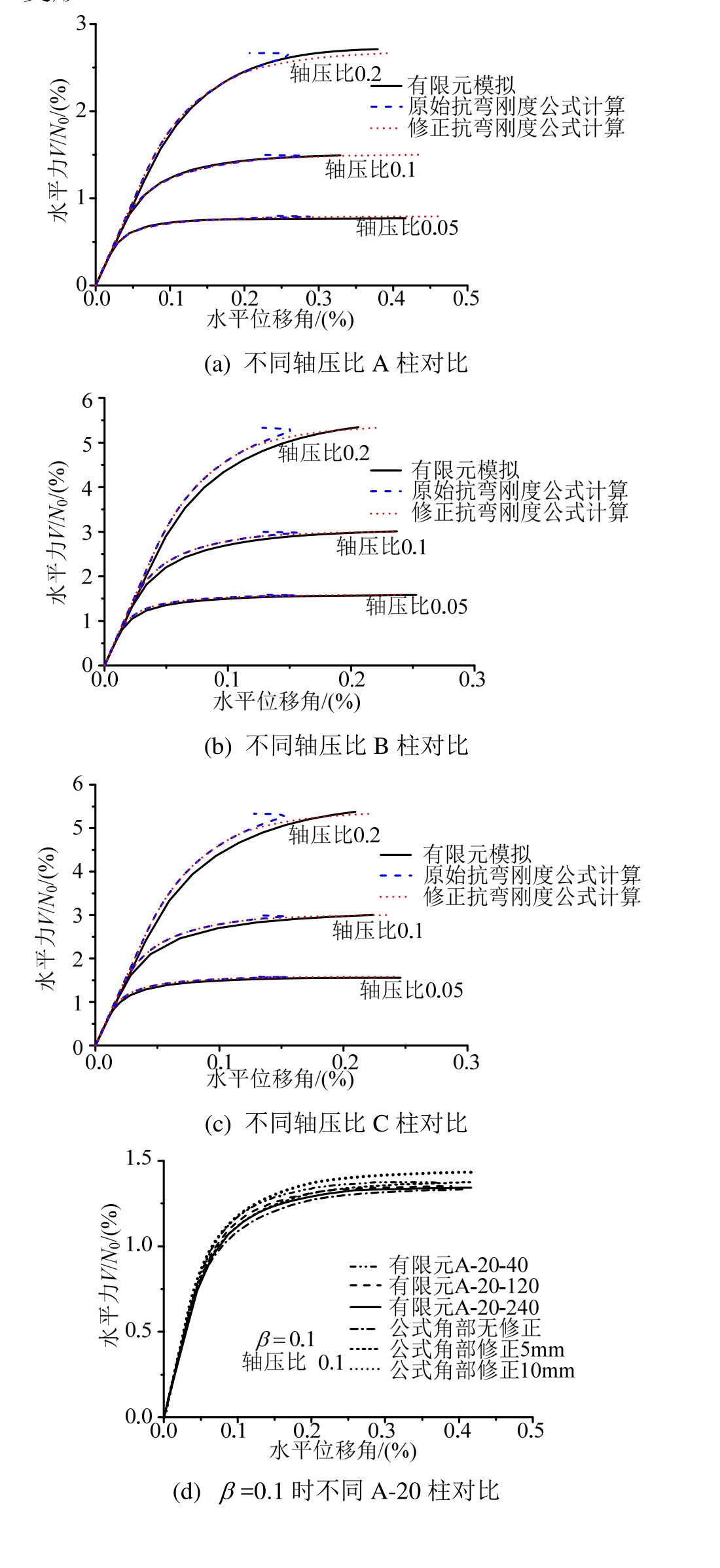
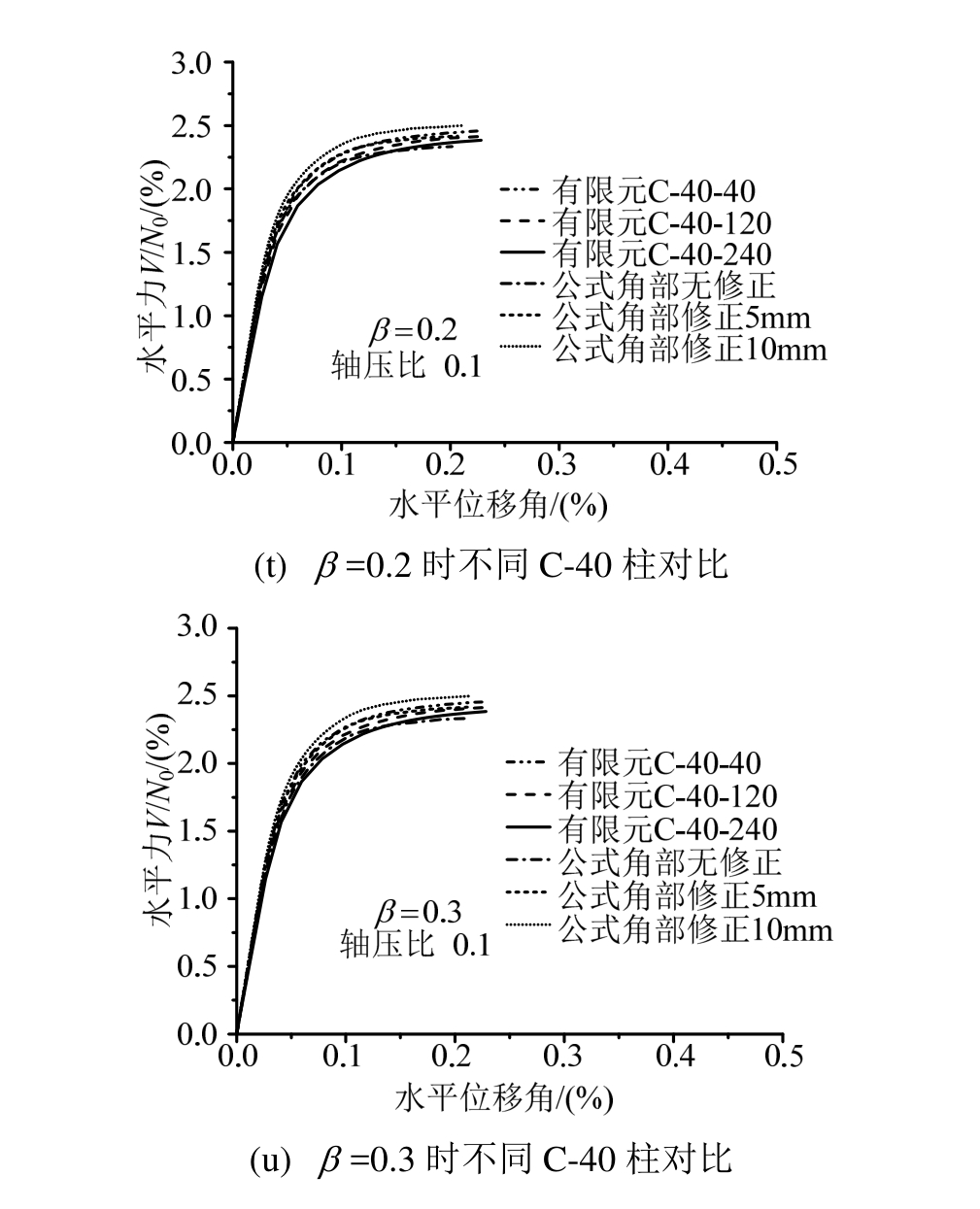
图12 有限元和理论模型对比
Fig.12 Comparison of finite element model and analytical model
本文进一步将理论模型与 Roh等[12]试验的摇摆柱(CY-5、CY-10)和对应的简化ABAQUS模型进行了对比，如图11和图12中分别所示，图中恢复力较大的曲线代表摇摆柱初始无损伤状态下的荷载位移关系，恢复力较小的曲线代表摇摆柱在一个循环加载后角部出现损伤后的荷载-位移关系。
试验构件混凝土强度fc′=36.12 MPa，屈服应变yε=0.0024，钢筋屈服强度257.8 MPa。摇摆柱高H=1219 mm，厚度t=178 mm，完整宽度L0=178 mm。
理论模型计算时将摇摆体弹性模量设置为E=15.05 GPa，屈服强度fc′=36.12 MPa，泊松比ν=0.2，不考虑钢筋的作用。使用有效刚度系数对抗弯刚度进行修正，损伤影响系数β=0.3，损伤后不考虑端部截面的宽度调整。根据 Roh等[12]的相关计算公式：
施加轴压比 4.65%压力后损伤稳定的L=136.6 mm，施加轴压比5.41%压力后损伤稳定的L=129.9 mm；施加轴压比9.28%压力后损伤稳定的L=95.4 mm，施加轴压比10.91%压力后损伤稳定的L=80.9 mm。
有限元模拟时端部接触面采用法向硬接触切向无滑动定义。混凝土与钢筋均采用理想弹塑性材料，混凝土屈服强度36.12 MPa，弹性模量15.05 GPa；钢筋屈服强度257.8 MPa，弹性模量200 GPa。混凝土采用C3D8R单元，钢筋采用TRUSS单元，钢筋嵌入混凝土。有限元模拟时不考虑往复过程中轴压比不同造成的缺角差别，根据公式和试验图片估算，5%轴压比损伤的缺角宽度a=22.5 mm，b= 50 mm；10%轴压比损伤的缺角宽度a=45 mm，b= 75 mm。
理论计算公式与有限元模拟的结果几乎相同，损伤后荷载位移曲线存在的部分差别主要是由于有限元模型的缺角根据设计轴压比设置的固定值，而理论计算则根据往复过程中的轴压比变化进行了调整，并在计算中忽略了钢筋的作用。理论计算在整体上可以准确预测出试验的结果，但分离状态前的抗侧刚度略大于试验值。注意到一般高强混凝土初始的弹性模量在30 MPa附近，而ABAQUS模拟和理论计算中理想弹塑性的混凝土采用的弹性模量值仅为实际中混凝土的 1/2，理论计算中甚至未考虑钢筋的作用，并且理论计算和有限元模型中均排除了滑移的影响，如果试验构件未发生滑动，其初始的抗侧刚度应当高于有限元模拟与理论计算，因此试验与理论模型和有限元模型的差异可能来自于试验过程中出现的滑移。
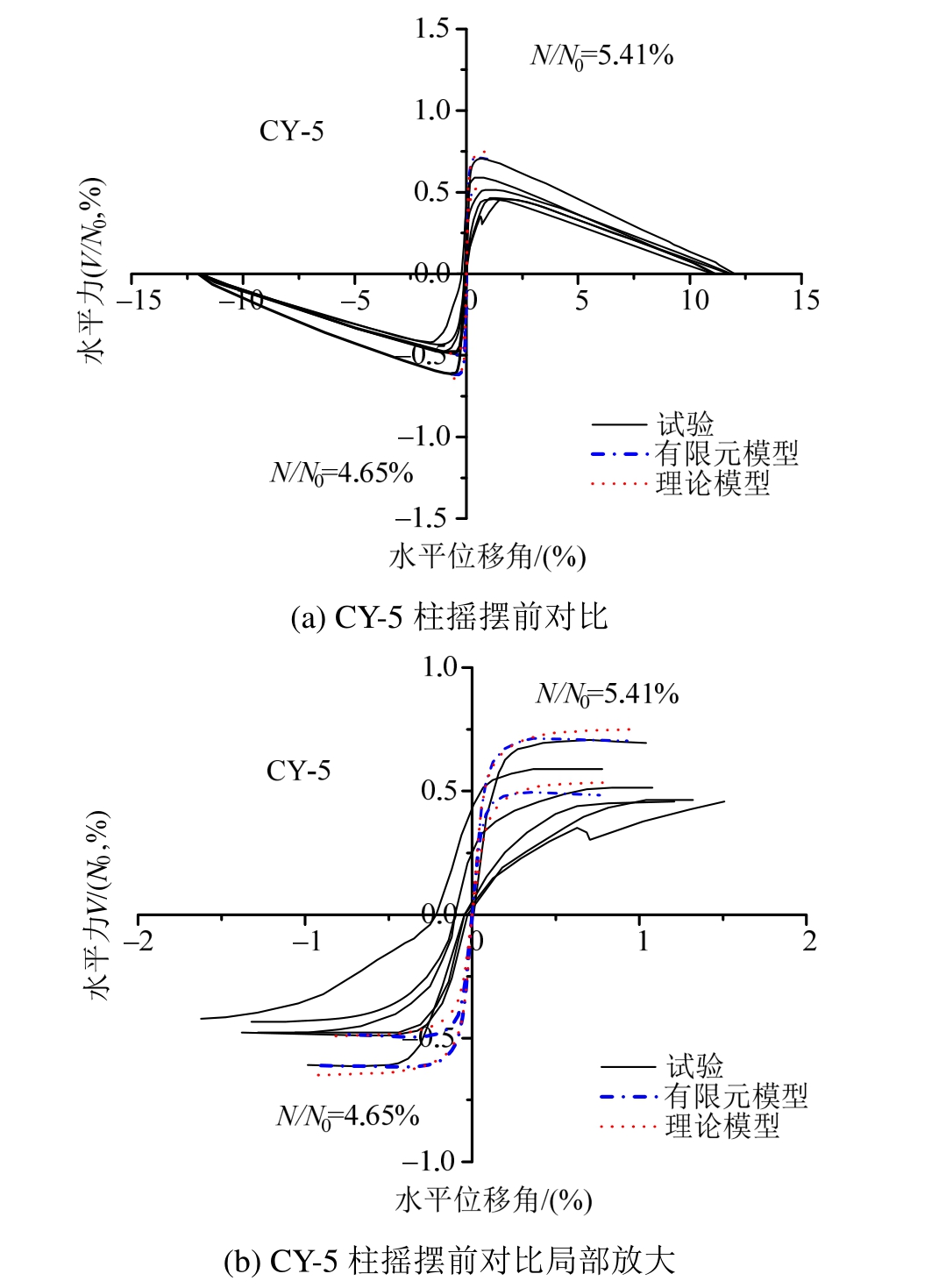
图13 CY-5柱理论模型、有限元与试验对比
Fig.13 Comparison of analytical model, finite element model and experiment of CY-5
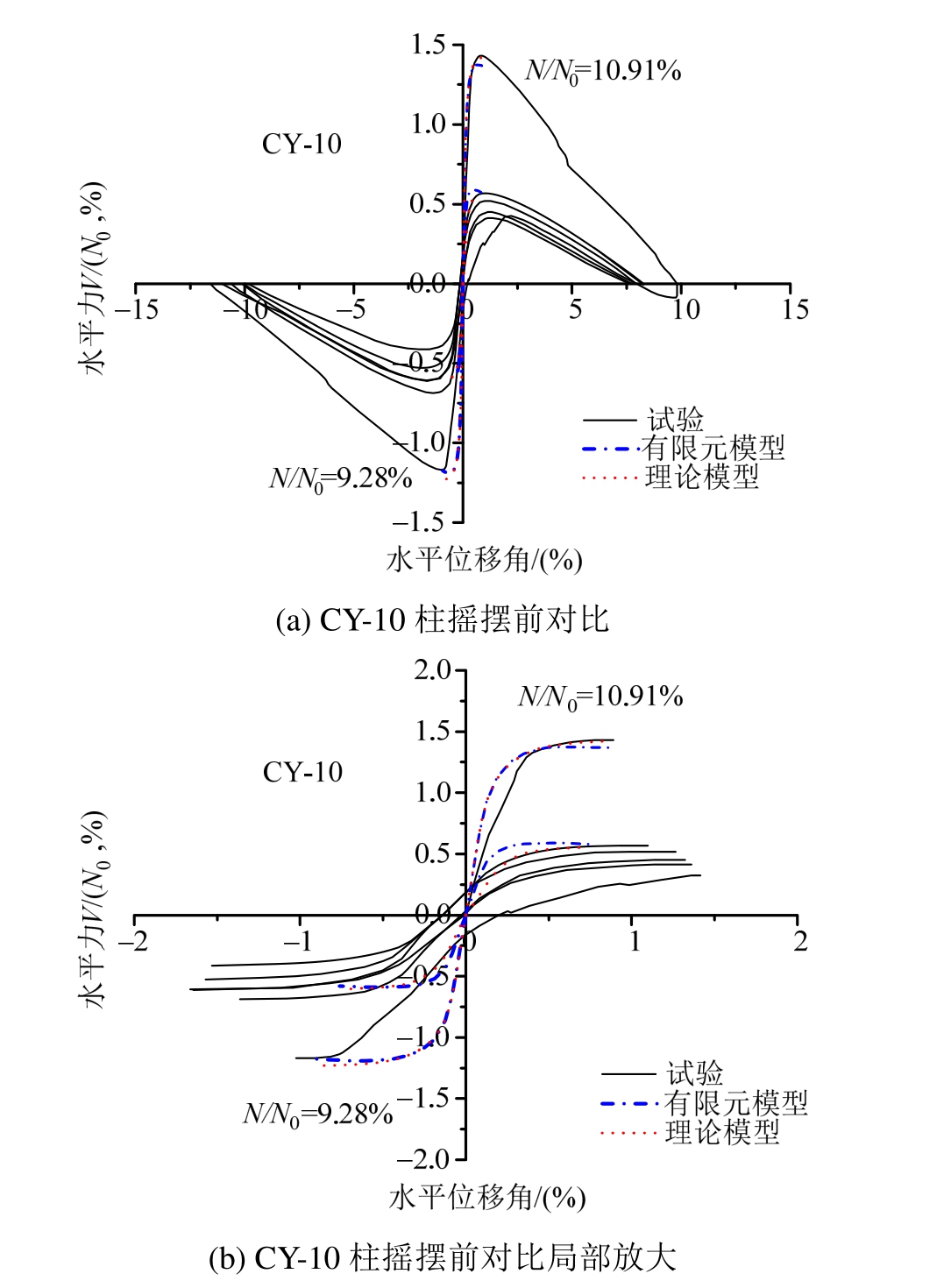
图14 CY-10柱理论、有限元与试验对比
Fig.14 Comparison of analytical model, finite element model and experiment of CY-10
本文结合已有的类似弥散塑性模型计算无损伤摇摆构件摇摆前变形的方法，建立了新的损伤后摇摆构件分析模型，分析了损伤前后摇摆构件的端部非线性段内力和截面特性变化，采用新的有效刚度计算方法，基于虚功原理提出了计算其摇摆运动前水平弹塑性变形的理论公式。通过 ABAQUS实体有限元模型和既有试验对分析模型进行的验证表明，本文提出的摇摆前分析模型能够准确预测损伤前后的摇摆构件在摇摆前的变形情况。本文使用的随接触面正应力分布而变化的有效刚度系数经验证适用于损伤前后摇摆构件摇摆运动前变形的分析。通过调整本文提出的损伤影响系数可以合理地反映出不同的角部损伤程度对摇摆构件刚度的影响。损伤角部所占比例越大，损伤影响系数越大，摇摆构件的抗侧刚度越小。损伤角部平缓时可在计算中增大端部截面宽度，也可偏保守不进行调整。
[1]Housner G W. The behavior of inverted pendulum structures during earthquakes [J]. Bulletin of the Seismological Society of America, 1963, 53(2): 403―417.
[2]Sritharan S, Aaleti S, Henry R S, et al. Precast concrete wall with end columns (PreWEC) for earthquake resistant design [J]. Earthquake Engineering & Structural Dynamics, 2015, 44(12): 2075―2092.
[3]Perez F J, Pessiki S, Sause R. Experimental lateral load response of unbonded post-tensioned precast concrete walls [J]. ACI Structural Journal, 2013, 110(6): 1045.
[4]胡晓斌, 贺慧高. 往复荷载作用下自复位墙受力机理研究[J]. 工程力学, 2013, 30(11): 202―206.Hu Xiaobin, He Huigao. Study on the mechanical behavior of self-centering wall under cyclic loading [J].Engineering Mechanics, 2013, 30(11): 202―206. (in Chinese)
[5]朱冬平, 周臻, 孔祥羽, 等. 往复荷载下带竖向阻尼器自复位墙滞回性能分析[J]. 工程力学, 2017, 34(3):115―123.Zhu Dongping, Zhou Zhen, Kong Xiangyu, et al.Hysteretic performance analysis of self-centering walls with vertical dampers under cyclic loads [J]. Engineering Mechanics, 2017, 34(3): 115―123. (in Chinese)
[6]Zhang J, Makris N. Rocking response of free-standing blocks under cycloidal pulses [J]. Journal of Engineering Mechanics, 2001, 127(5): 473―483.
[7]Kalliontzis D, Sritharan S, Schultz A. Improved coefficient of restitution estimation for free rocking members [J]. Journal of Structural Engineering, 2016,142(12): 06016002.
[8]Meek J W. Dynamic response of tipping core buildings[J]. Earthquake Engineering & Structural Dynamics,1978, 6(5): 437―454.
[9]Mander J B, Cheng C T. Seismic resistance of bridge piers based on damage avoidance design [R]. Technical Report MCEER-97-0014. Buffalo: University at Buffalo,The State University of New York. Multidisciplinary Center for Earthquake Engineering Research, 1997.
[10] Roh H, Reinhorn A M. Analytical modeling of rocking elements [J]. Engineering Structures, 2009, 31(5):1179―1189.
[11] Roh H, Reinhorn A M. Nonlinear static analysis of structures with rocking columns [J]. Journal of Structural Engineering, 2009, 136(5): 532―542.
[12] Roh H, Reinhorn A M. Modeling and seismic response of structures with concrete rocking columns and viscous dampers [J]. Engineering Structures, 2010, 32(8): 2096―2107.
[13] Roh H, Reinhorn A M, Lee J S. Power spread plasticity model for inelastic analysis of reinforced concrete structures [J]. Engineering Structures, 2012, 39(8): 148―161.
[14] Belleri A, Torquati M, Riva P. Finite element modeling of“Rocking Walls” [C]// Proceedings of the 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering. Kos Island, Greece, 2013: 2831―2848.
[15] Avgenakis E, Psycharis I N. Modeling of rocking elastic flexible bodies under static loading considering the nonlinear stress distribution at their base [J]. Journal of Structural Engineering, 2017, 143(7): 04017051.
[16] Preti M, Meda A. RC structural wall with unbonded tendons strengthened with high-performance fiberreinforced concrete [J]. Materials and Structures, 2015,48(1/2): 249―260.
[17] Roh H, Reinhorn A M. Hysteretic behavior of precast segmental bridge piers with superelastic shape memory alloy bars [J]. Engineering Structures, 2010, 32(10):3394―3403.
[18] Park R, Paulay T. Reinforced concrete structures [M].Wiley-Interscience Publication, John Wiley & Sons,1975.
[19] Priestley M J N, Seible F, Calvi G M. Seismic design and retrofit of bridges [M]. New York: John Wiley & Sons,1996.
ANALYTICAL MODEL OF ROCKING ELEMENTS BEFORE ROCKING