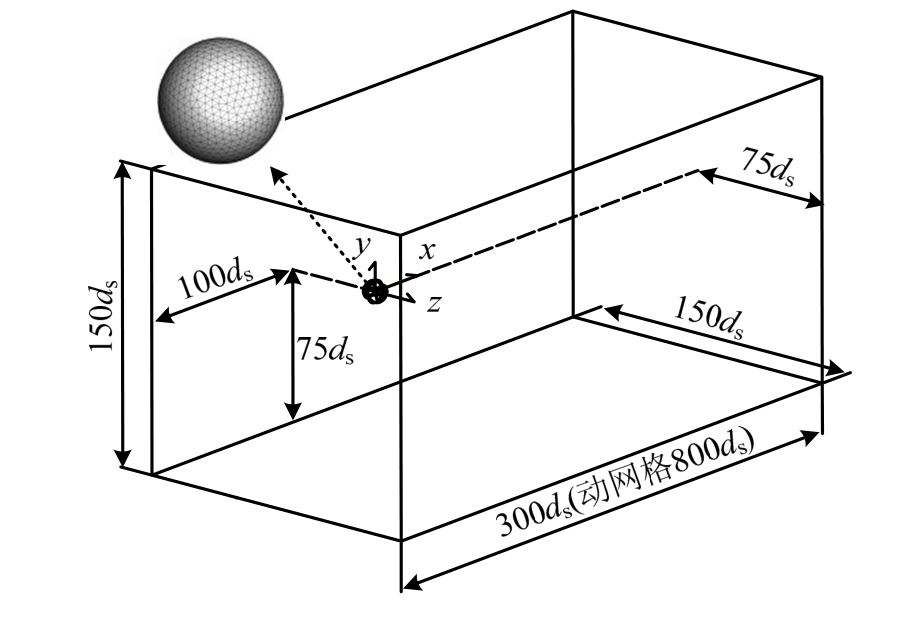
图1 计算域及颗粒网格离散
Fig.1 Computational domain and grid discretization
地表初始积雪在风的作用下发生搬运，运动形态包含蠕移、跃移及悬移。其中，跃移与悬移颗粒因离地滞空，且输运量、迁移距离均较大，是形成风雪流及显著积雪重分布的主要原因[1]。
过去有关风吹雪空间传质及地表二次积雪问题的研究多以实测或实验为主[2－3]，这是基于宏观条件下对现象最表面、直观的认识。近年来，伴随数值风洞技术的兴起，该类问题有望得以高效求解，但受制于当前的认知水平，数值模型建立时多相流理论的调用、基本参数的确立及模型的简化与假定等仍缺乏足够的理论支撑。如当前用于解决风雪课题的主流模型[4－5]：欧拉框架的VOF模型、混合模型、欧拉双流体模型，及拉格朗日框架的离散颗粒轨迹模型等，它们在被调用时大多需要对雪相的受力规则或运动行为进行指定[6－7]，而国内外学者对其相关参数如颗粒终端速度、相间滑移速度等的取值仍存在较大差异或难以追溯来源[8－9]。加之不同多相流模型均存在各自的局限性及适用范围，这些问题都成了影响数值模拟求解精度甚至结果可靠性的关键因素。
要解决上述问题，需要从微观层面对雪相的输运本质进行研究，主要包括滞空颗粒的受力特性、运动行为及小时间空间尺度下的弛豫效应等。而雪颗粒因尺寸较小，往往难以通过实测或实验对其运动状态下的非线性气动信息进行全面、系统的捕获。因此，建立微观层面的三维动网格颗粒运动数值模型，有助于从小时空尺度对不同来流环境(颗粒雷诺数Res)下的颗粒运动机理进行参数化研究。本文基于风吹雪稀疏流假定，采用商用 CFD软件Fluent，对不同粒径及密度参数的单个理想球形雪颗粒进行了静止空气与梯度流场下的受力及运动行为模拟，考察了颗粒运动初期的非线性变速自由沉降及强迫运动过程，研究了颗粒与流场介质间的互馈机制及引起颗粒终端速度差异的主要原因。
雪颗粒一旦滞空，其运动行为直接取决于所受各外力。就稀疏流体系下的悬移颗粒而言，一般可近似忽略颗粒间由于碰撞引起的能量交换。根据介质与颗粒的相互关系，这些气动外力主要包括Stokes粘阻力、附加质量力、Basset力、Saffman力及Magnus力等[10]。经典颗粒运动学理论虽已对上述部分介质力进行了数学描述，但因其解析式大多过于复杂，且主要针对低雷诺数(Res＜1)条件，实际风雪流问题中难以对其建立完整的颗粒运动学方程并直接加以求解。
考虑到滞空跃移或悬移雪颗粒已历经蠕移或多次起跳、磨蚀，外形近似球体，并根据Schmidt[11]等对风雪流颗粒粒径分布规律的实测统计结果，这里认为滞空雪粒粒径在50 μm～350 μm，计算选取粒径ds为 100 μm、150 μm 及 200 μm 三种情况。雪粒密度在新雪表观与冰的真实密度间选取，参考已有风致积雪漂移沉积数值模拟后[12－13]，令其取值分别为150 kg/m3、500 kg/m3及900 kg/m3。空气密度取为1.225 kg/m3，动力粘性系数取为μ=17.89×10-6Pa·s。
假设颗粒位于无界流场中且弛豫效应及变速过程均属于小时间空间尺度问题。对于静风气动力验证工况，根据粒径确定的计算域尺寸为x×y×z=300ds×150ds×150ds；对于颗粒自由沉降及强迫运动模拟工况，建立计算域为x×y×z= 800ds×150ds×150ds。初始状态颗粒均位于坐标原点，其形心距迎风边界100ds，距各侧面边界均75ds，计算域尺寸设置如图 1。对于静风计算工况，入口边界设置为速度进口，出口边界设置为压力出口，四周设为对称边界；对于运动颗粒的动网格模拟，由于颗粒与流场存在互馈现象，分别采用两套边界条件进行无界场验证：所有边界均设为对称边界(Bdr.1)；原入口边界设为压力出口，出口边界设为无滑移壁面，四周设置为对称边界(Bdr.2)。
球形颗粒采用多面网格逼近，不同粒径下壁面面网格分块数在 1.6×103～1.8×103不等。颗粒周边40ds范围内建立了数值耗散相对较低的prism棱柱型边界层网格域，贴壁面体网格高度统一取为1 μm，法向增长率为 1.2。动网格执行时，边界层网格域随颗粒同步运动且不发生网格的变形与重构。外层空间网格采用TGrid方式下的Tet/Hybrid单元离散，动网格执行时根据颗粒位置的改变发生网格的时变与重构。不同粒径工况下动网格模型体网格总量在 1×104～1.2×104不等，颗粒网格划分如图1所示。
考虑到单个颗粒粒径在微米量级且空气粘性较小，这里假设颗粒在不同来流风速下的绕流行为大致服从Stokes流条件，选用laminar模型进行计算。迭代时间步的选择应尽量满足不同Res要求并取其较小值，经过多次试算后，统一采用时间步长 1×10-5s。压力—速度耦合采用PISO算法，压力场采用二阶格式离散，动量方程采用二阶迎风格式离散。
图1 计算域及颗粒网格离散
Fig.1 Computational domain and grid discretization
验证主要包含两部分内容：Stokes流下的静风阻力系数求解，用于确保不同粒径下，网格划分精度与时间离散步长等参数对Res变化的适应性及模拟结果的有效性；静止空气中颗粒以对应风速进行匀速运动，该工况主要用于考察网格弹簧变形及分裂合并是否对模拟结果产生显著影响。
由于Res随相间相对速度改变，对于静止至完全加速的颗粒，Res遍历范围可能较大，这里选取Res为0.5、1.5、2.5、150、350、550六种情况进行计算，颗粒粒径均取为150 μm。计算不同Res下的颗粒气动阻力时程
如图2所示。
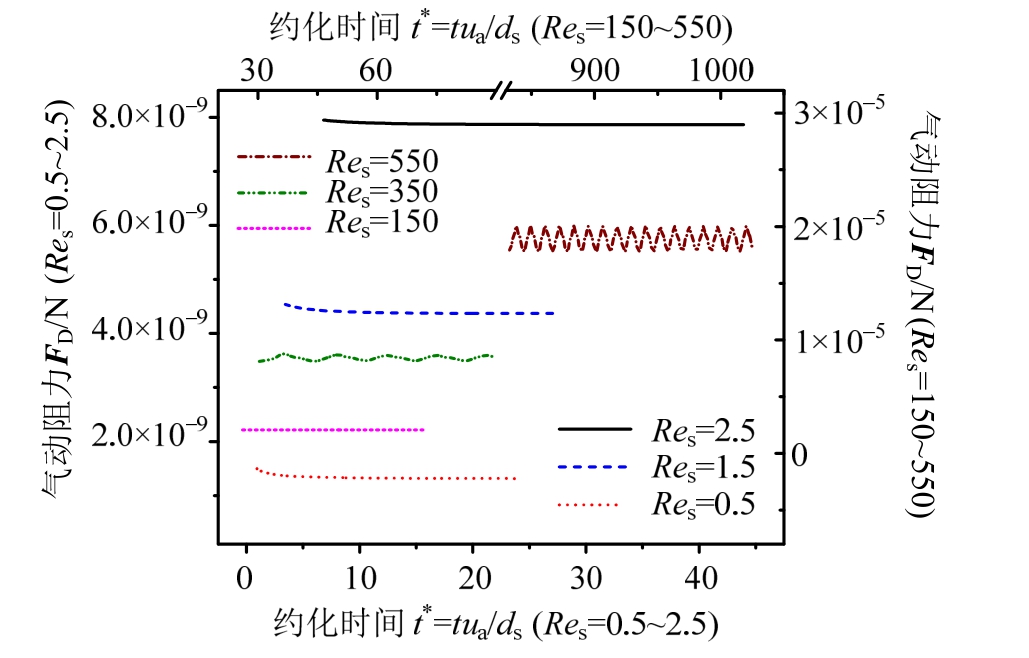
图2 计算颗粒静风气动阻力
Fig.2 Particle drag forces in differentRes
如图所示，当Res在0.5～150，计算静风气动阻力在达到稳定状态时恒为常数，当Res超过350时，计算稳定的气动阻力开始出现周期性振荡，表明该Res下的介质绕流可能不再完全服从 Stokes层流行为，且随着Res的继续增大，来流对确定粒径颗粒的周期性激励频率增大，计算平均气动阻力也单调递增。
两种Res状态下计算颗粒附近流场迹线分布如图3所示。对于近似处于层流状态的低Res情况，介质流经颗粒时总是贴壁面通过，最后在背风侧汇聚后以几乎平行于来流的方式分离，粘性效应是形成气动阻力的主要原因。较高Res情况下，流线在壁面背风侧提前分离，分离位置随时间周期性移动，形成显著特征湍流，背风侧回流漩涡尺度大约为1倍颗粒直径ds。与典型钝体绕流相似，由于高Res下背风漩涡引起了负压面积的增大，惯性效应是形成气动阻力的主要原因，换算颗粒阻力系数CD随Res的增大有所减小。
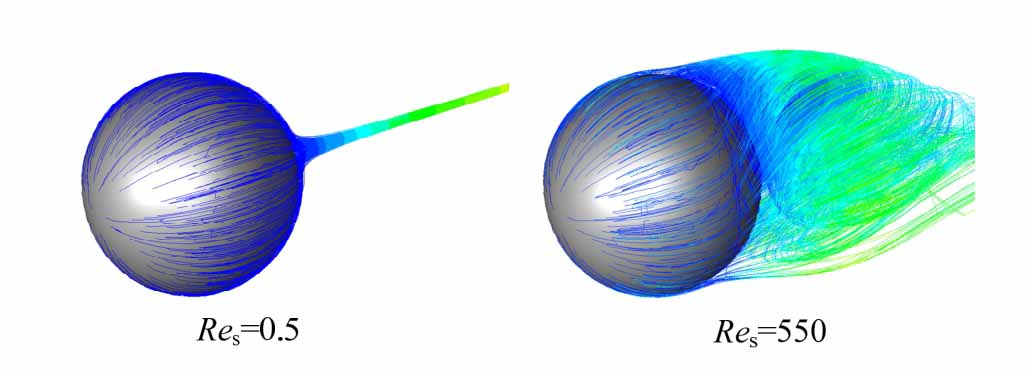
图3 颗粒周边绕流迹线分布
Fig.3 Ambient flows around particles
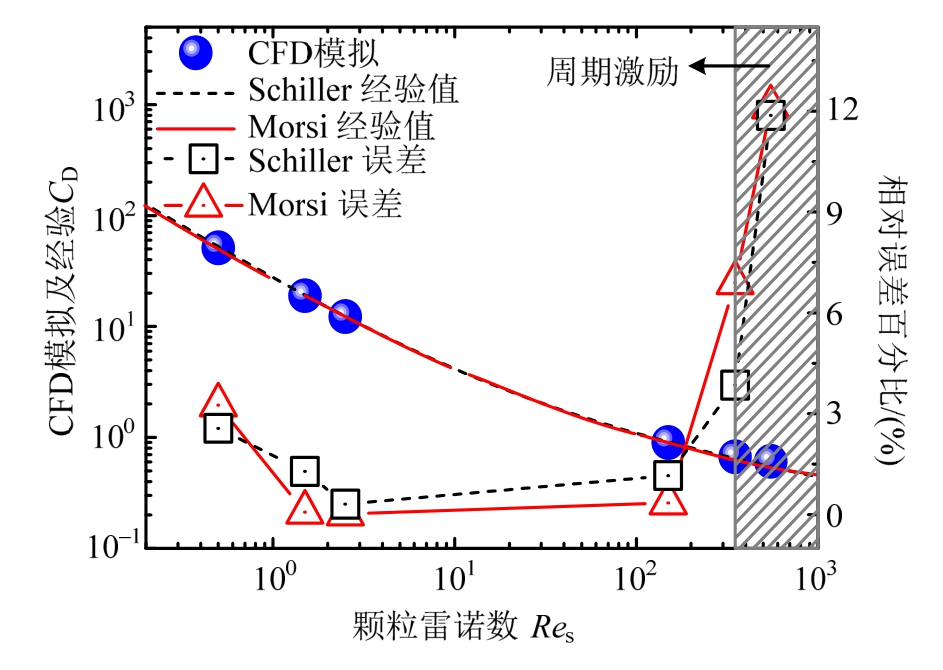
图4 计算阻力系数与经验曲线
Fig.4 Particle drag coefficients versus empirical values
将图2的计算颗粒气动阻力时程按Res换算后并与Schiller等和Morsi等[14]的经验阻力系数曲线进行对比，结果如图4所示。可见，CFD模拟结果与两种经验分布值在低Res区间内几乎没有任何差异，但对于较高Res情况，模拟结果较Schiller等与Morsi等的分段拟合值均略为偏大，总体上，计算颗粒阻力系数随Res的变化规律与两种经验函数较为一致。同时，就模拟结果与经验值的相对偏差来看，当Res＜150时，相对误差均在5%以内，而当Res超过350后，误差迅速增大，这可能与计算所选用的流场模型为 laminar层流模型有关。但针对一般风吹雪问题，由于颗粒粒径多在微米量级，均匀流下Res达到350时，介质与颗粒的相对流速已超过34 m/s，因此，这里近似认为研究所选用的流场模型及参数设置对模拟常规风雪流滞空颗粒的运动行为基本有效。
图5为Res=2.5时，颗粒的静风绕流与颗粒在静止空气中以对应风速进行匀速直线运动的静压场及介质矢量模拟结果，其中，流场与颗粒的运动方向均为从左至右。理论上，对于低Res情况，当计算流场扰动完全稳定时，两种情况下的颗粒气动力应完全相同。当颗粒静止时，介质速度矢量在颗粒壁面附近达到最小值，静压在颗粒迎风侧达到极大值，最大压强为0.12 Pa。流场静止时，由于颗粒初速度对周边静止空气产生扰动并携带其以相同速度运动，风速矢量在颗粒周边达到极大值，静压在相对迎风侧(颗粒右侧)达到最大，颗粒附近压强分布规律与静风工况完全相同，但方向相反。
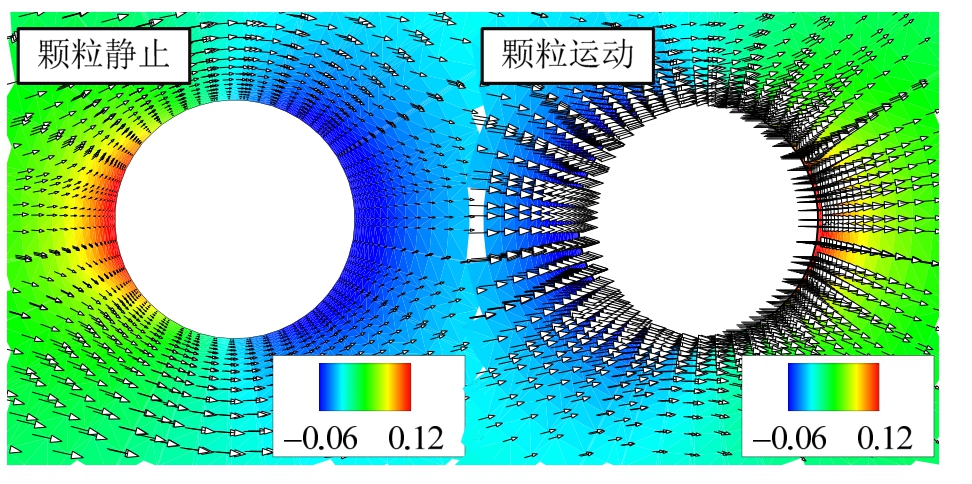
图5 静压场及风速矢量分布(计算稳定) /Pa
Fig.5 Static pressures and wind velocity vectors
图6同时给出了两种边界条件下匀速运动颗粒与颗粒静风工况的气动力计算结果，不同工况下颗粒所受稳定气动力几乎没有任何差异，表明求解采用的动网格设置可有效的模拟颗粒自由及强迫沉降运动，计算域基本满足无解场要求。
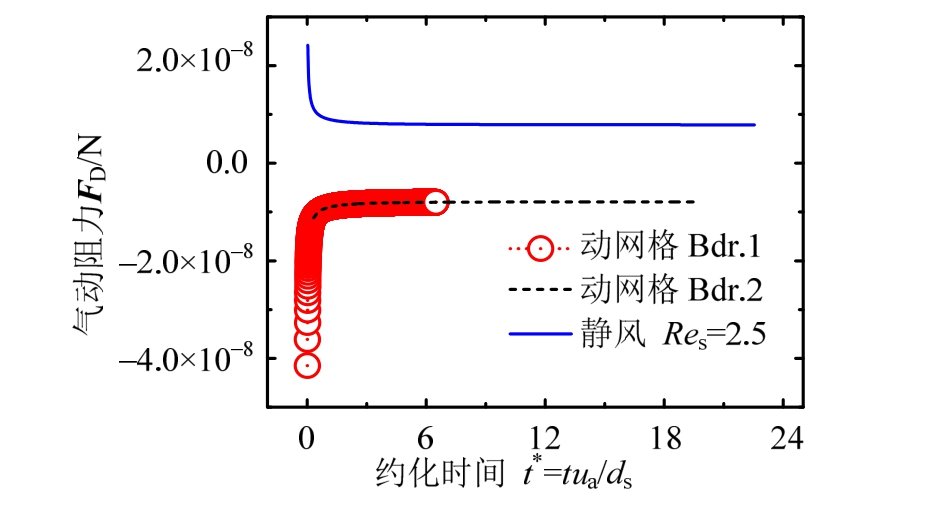
图6 无界流边界条件无关性
Fig.6 Independent verification for unbounded flow field
为更真实的反映当前网格条件下颗粒的实际受力情况，自由沉降计算中同时考虑了由于颗粒壁面初始离散缺陷及数值耗散等因素对模拟结果的影响，即同时计入颗粒侧向漂移及旋转效应。设重力加速度方向为+x方向(图 1)，则颗粒在介质中所受浮力为-x方向，旋转方向按右手法则规定。模拟三种密度下(150 kg/m3、500 kg/m3及 900 kg/m3)，粒径ds=150 μm颗粒在静止空气中发生自由沉降的运动行为如图7所示。
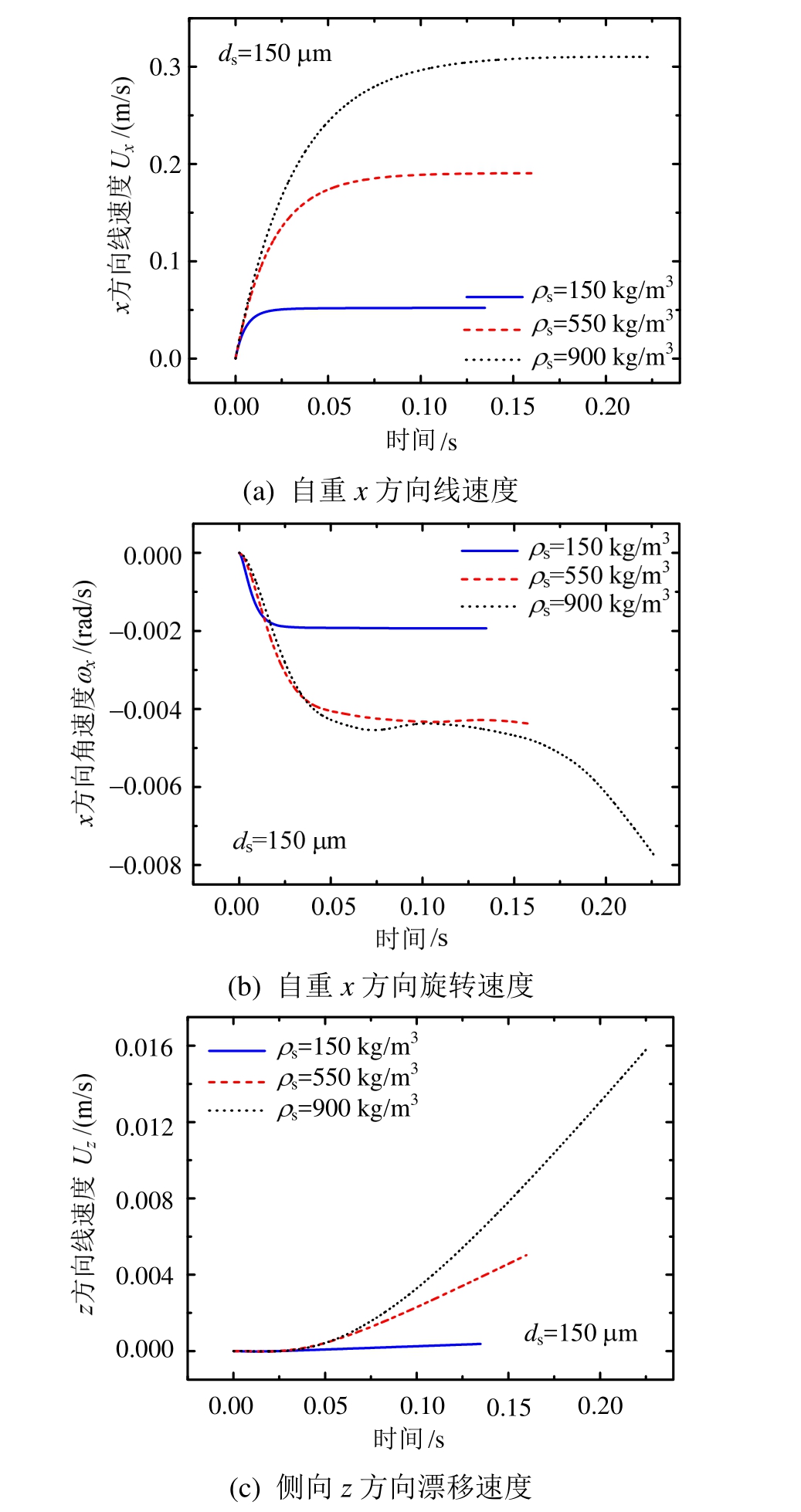
图7 计算不同密度颗粒自由沉降速度时程
Fig.7 Calculating particle velocities in different densities
如图7(a)所示，粒径ds=150 μm的颗粒在完全均匀介质条件下，自由沉降x方向终端线速度分别约为0.31 m/s、0.19 m/s及0.05 m/s，速度随颗粒密度单调变化。根据各曲线达到水平稳定所需最短时间，可大致对各密度颗粒的弛豫效应进行判断，即密度较小的颗粒松弛时间较短，可能存在更好的流场跟随性，且受到与流场相对变速运动有关的附加质量力与Basset效应历时更短。总体来讲，不同密度颗粒的自沉线速度均在0.2 s内达到稳定，因此，相对于大时间尺度下的积雪搬运二次堆积过程，颗粒的变加速阶段可近似忽略。
图7(b)与图7(c)分别为计算颗粒重力x方向自旋转角速度与侧向z方向漂移线速度。如图7(b)所示，由于颗粒非绝对中心对称，在受到微小非均匀气动效应干扰时，颗粒将发生空间旋转，产生Magnus加速效应，并进一步对周边流场及颗粒横漂线速度产生影响。各气动效应在微观时空层面的相互作用最终形成了颗粒的时变速度场及流场分布。另外，对于较小密度颗粒，角速度总是首先达到稳定，且量值小于大密度颗粒，这主要与不同密度下颗粒质量所提供的转动惯量差异有关。颗粒旋转速度所反映的弛豫效应随密度的变化规律与颗粒自沉线速度情况完全一致。如图7(c)所示，就同一颗粒网格模型而言，计算横漂运动方向均为z轴负方向，且线速度随颗粒密度的增大而增大，但量值总体在自沉x方向线速度的1%以内。对于完全对称的拟无界场条件，横漂速度同样由颗粒壁面网格的初始离散缺陷所致，同时，由于现实中并不存在理想球体，这一模拟结果可被接受并与文献[15]的实验规律保持一致。
图8为计算三种密度颗粒在x轴向的无量纲位移
—时间t关系。可见，各密度颗粒在自重方向的相对位置主要在t=0.01 s后发生改变，这是由于运动接近稳定时，首先以低密度颗粒(ρs=150 kg/m3)在t1=0.05 s时与介质趋于相对匀速运动，其后受力以定常的重力、空气粘性阻力为主；而逐渐稳定的其他密度颗粒由于所受重力效应更为显著，随后的位移增量也相对剧烈。若以t1=0.05 s、t2=0.1 s及t3=0.2 s分别作为各密度颗粒的沉降速度稳定时间，则ds= 150 μm颗粒在非定常气动力影响下的自由沉降位移尺度分别约为1.5ds、10ds及35ds。因此，对于大空间尺度的风雪流自重沉降现象而言，颗粒的变加速阶段同样可近似忽略。
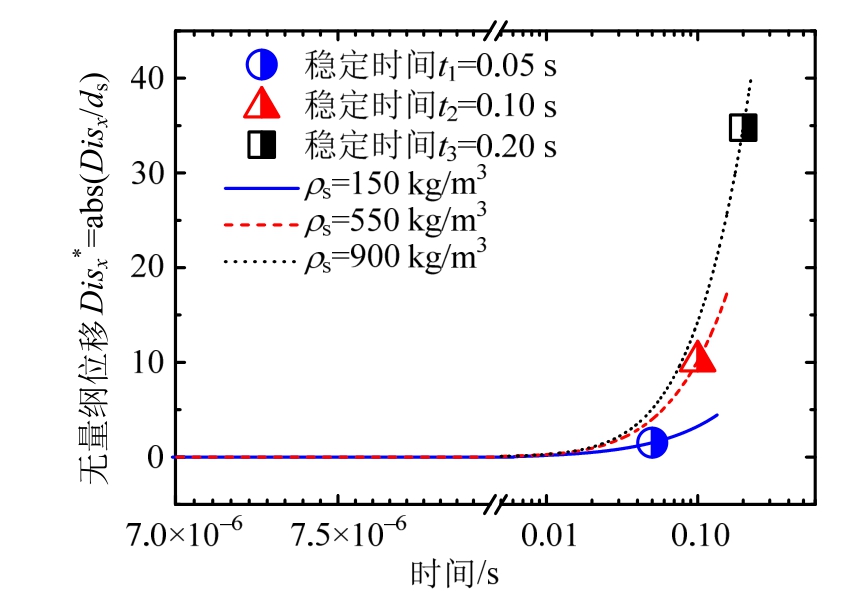
图8 颗粒自由沉降无量纲位移-时间关系(ds=150 μm)
Fig.8 Calculating particle displacements in different densities
图 9为计算密度 150 kg/m3的三种粒径(ds= 100 μm 、ds= 150 μm 、ds= 200 μm)颗粒在发生自由沉降时，重力x方向的线速度时程分布规律。如图所示，在颗粒密度确定的情况下，随着粒径的增大，计算稳定沉降终端速度单调递增，表明粒径的增大虽造成了迎风面积的增大，对阻力系数产生影响，但其效应远不及颗粒自重增量对运动加速产生的影响。
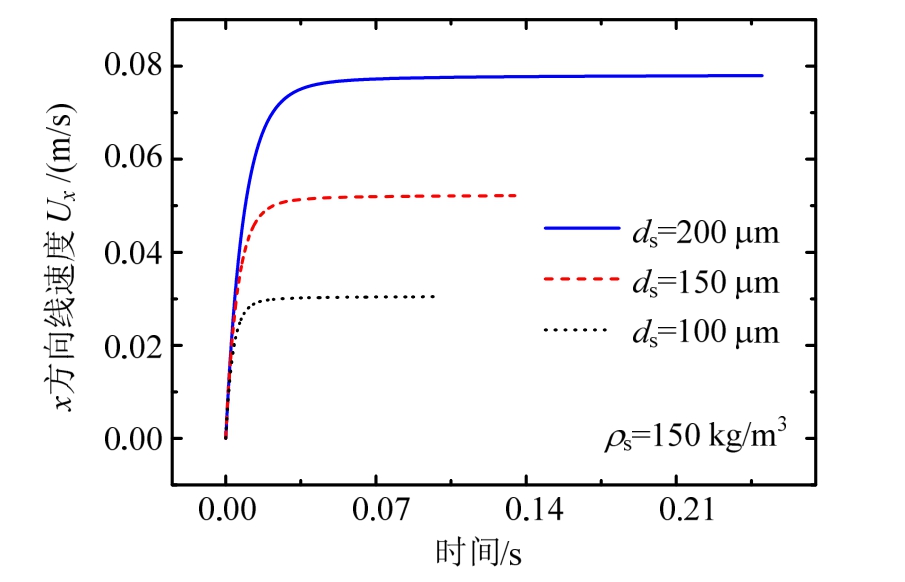
图9 计算不同粒径颗粒自由沉降方向线速度时程
Fig.9 Calculating particle velocities in different sizes
颗粒非线性自由沉降过程的力学机理可通过壁面压强等指标间接反映。图 10为计算密度
的颗粒，由运动加速初期直至x方向沉降线速度接近稳定时的6种不同时刻下，颗粒壁面的静压等值线(虚线)分布、附面流迹线及以此确定的介质驻点、分离点静压值模拟结果。可见，该参数颗粒在整个沉降过程中均满足介质的贴壁绕流，未出现高雷诺数情况下的分离点前移现象(如图 3：Res=550)，表明本研究采用laminar模型计算自由沉降问题基本有效。
另外发现，颗粒运动时，由贴壁流线发展方向及源、汇点共同确定的驻点、分离点位置，与静止颗粒在流场中达到绝对稳定时，由介质相对运动方向所确定的驻点、分离点位置(如图 5所示)完全相反，这一现象反映了颗粒在变加速运动初期就对周边气流产生了加速“携带”效应，从而使得相对迎风面出现了“非稳定状态”下的负静压情况。当颗粒自沉线速度接近终端速度时，加速气流在颗粒相对背风面的回流重附着使其壁面静压改变为正值，并逐渐增大趋于平稳，而相对迎风壁面静压逐渐减小至稳定。此时，颗粒所受介质粘性效应主要表现为克服其自重x方向的加速运动。
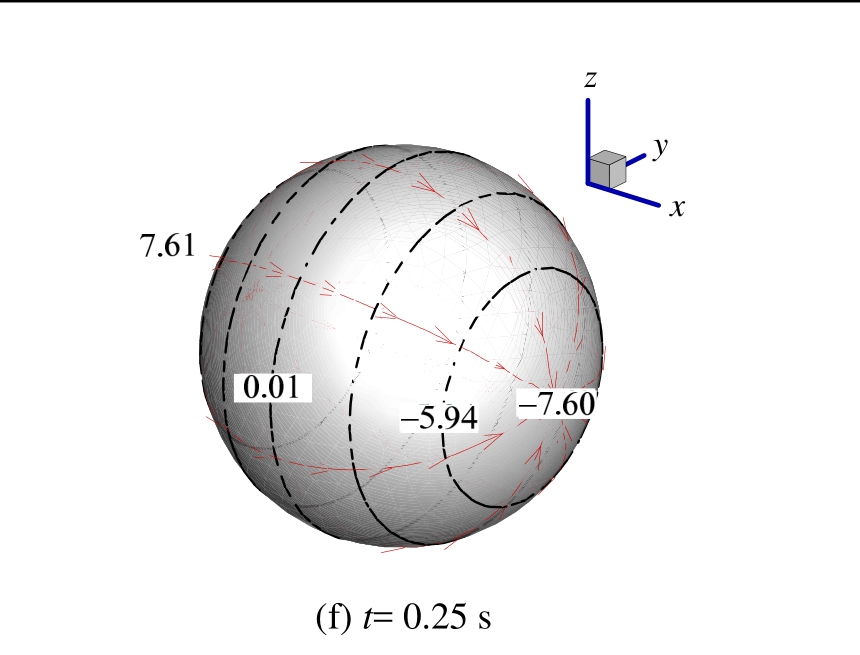
图10 计算不同时刻自由沉降颗粒壁面静压分布
Fig.10 Calculating particle static pressures on wall boundary
对不同时刻下驻点及分离点静压变化速率进行分析后还发现，颗粒受介质非定常气动力的影响时间大致在t= 0.15 s以内，之后尽管颗粒x方向沉降线速度变化率已小于 1‰，但壁面驻点与分离点的静压值仍发生轻微改变。这一现象表明气、固两相间的非线性气动效应并非在颗粒运动速度接近终端沉降速度时立即消失，其后较长时期内，各气动外力间的协调变化都是维持颗粒在当前运动方向下，线速度保持不变的主要外因。
由于存在相对变加速度，这里也采用包含动压指标q的压力系数Cp对非线性气动效应进行分析。Cp按式(1)定义，其中p为颗粒壁面绝对静压，pref为参考静压，根据远场值取为 0 Pa。qref为参考动压，按式(2)定义，参考密度ρref取为空气密度1.225 kg/m3。考虑颗粒运动速度的时变性，这里给出两种定义方式下的参考速度uref：其中uref,1统一取值1 m/s；uref,2按当前颗粒运动时刻所对应的x方向沉降线速度Ux取值(如图7(a))，并规定初始时刻静止颗粒Cp,2=0。
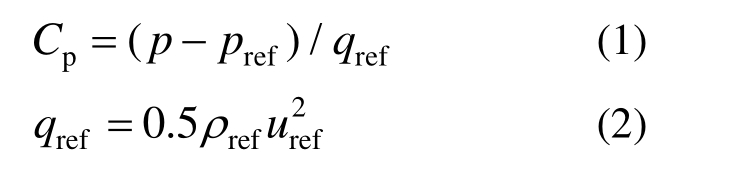
图11为提取颗粒壁面与z*=(z-zcenter)/ds=0平面相交线上不同时刻的相对压力系数Cp,1分布，其中zcenter为颗粒形心z坐标。可见，在颗粒加速初期(t=0.01 s)，壁面环线上Cp,1总体为负值，根据压力系数定义方式及流场在该阶段的对称性，颗粒周边气流总体以远离壁面运动为主。随着颗粒的加速沉降，相对背风侧壁面Cp,1逐渐呈现正值分布，且量值总是略大于对应位置迎风侧壁面，x*=0平面大致为Cp,1正负取值分界面。当t=0.15 s时，颗粒运动速度接近稳定，Cp,1不再发生明显改变。
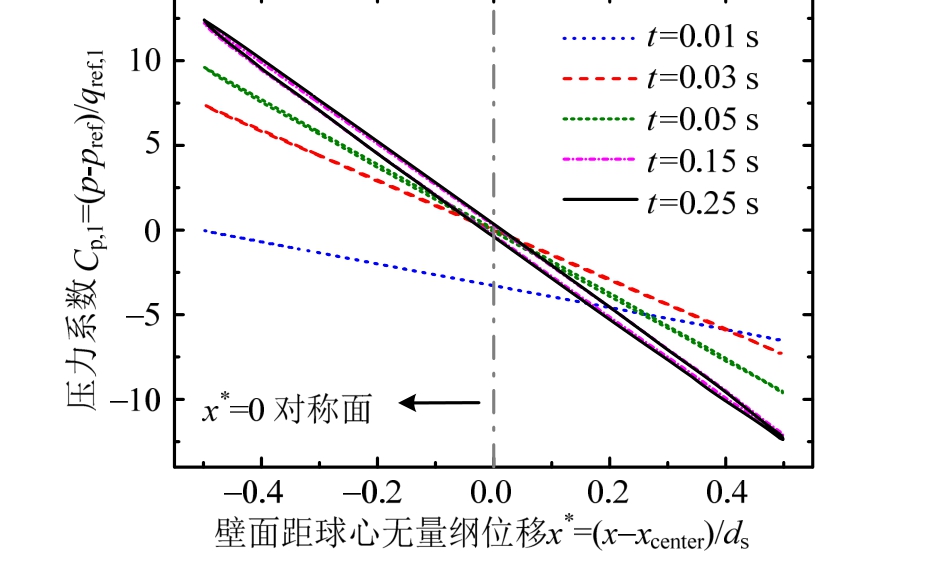
图11 颗粒壁面环线压力系数 (z*= 0)
Fig.11 Calculating particle pressure coefficients on loop line
图 12为提取颗粒驻点及分离点绝对压力系数Cp,2随时间的变化规律。由于采用颗粒当前沉降速度计算qref，Cp,2在相对低速的运动初期取值最大。t=0.01 s时，背风端点x*=-0.5处Cp,2量值显著小于迎风端点x*=0.5处量值且同为负值，这一现象与Cp,1完全一致。表明在t=0.01 s以前，颗粒受自重作用加速沉降所“携带”的迎风气流回流尚未完全“抵达”背风壁面，介质的运动及发展部分滞后于颗粒，进而呈现出复杂的非线性气动特征。
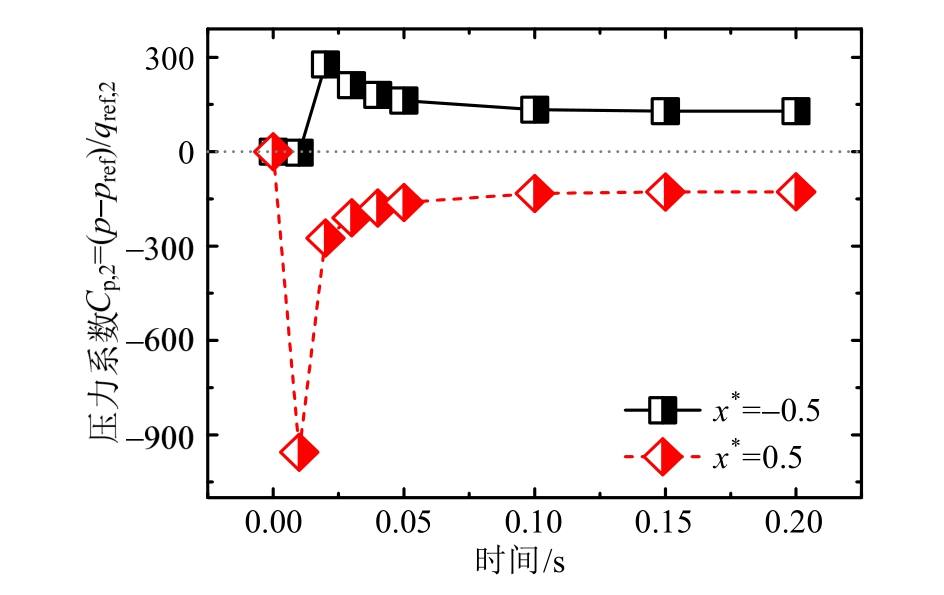
图12 颗粒壁面驻点及分离点压力系数
Fig.12 Pressure coefficients at stagnation and separation point
实际风雪流总伴随环境风作用，颗粒在气流驱动下一方面发生强迫运动，另外也受到与空气相对速度无关的浮力及重力等效应影响。就处于大气边界层内的风吹雪现象，风场结构受地表粗糙度及地物绕流影响表现为复杂、各向异性的梯度流，此时的颗粒将在风速梯度及压力梯度下表现出更为复杂的旋转效应(Magnus)及非线性变加速特性。
建立计算域尺寸为x×y×z=0.16 m×0.06 m×0.02 m，垂直于x轴方向两边界分别设为速度入口及压力出口，垂直于z轴方向两边界及+y轴方向边界均设为对称边界，垂直于-y轴方向边界设为壁面边界，以模拟风速为0 m/s的无滑移地表(参考图1)。颗粒位于坐标原点，距离出口边界0.15 m，距离+y轴及+z轴方向边界均为0.01 m。
计算颗粒直径取为 150 μm，密度取为
考虑6种情况的风速梯度条件Ugrad,，y其中，引起颗粒发生强迫运动的来流沿x轴正方向运动，风速梯度在y方向线性改变，侧向z方向无梯度变化，设置重力方向为-y方向，则浮力指向+y方向。
Ugrad,y按式(3)定义，分别取值 1 s-1、 10 s-1、25 s-1、 50 s-1、 100 s-1、 200 s-1，式中
表示y处来流平均风速，则颗粒初始形心位置所受平均风速大小分别为 0.05 m/s、0.5 m/s、1.25 m/s、2.5 m/s、5 m/s、10 m/s。首先计算风场至完全稳定(如图 13所示)，则不同Res条件下的颗粒均受到初始定常的外力作用，然后以静止颗粒作为初始状态模拟颗粒在不同梯度流下的强迫运动。
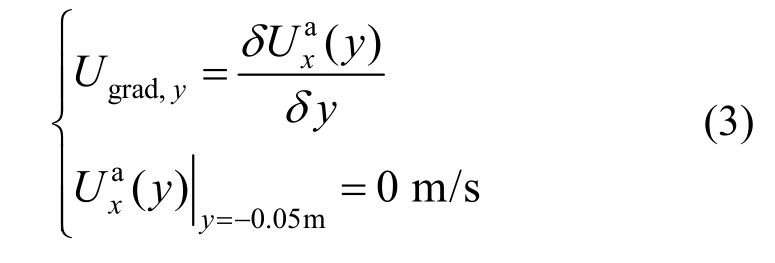
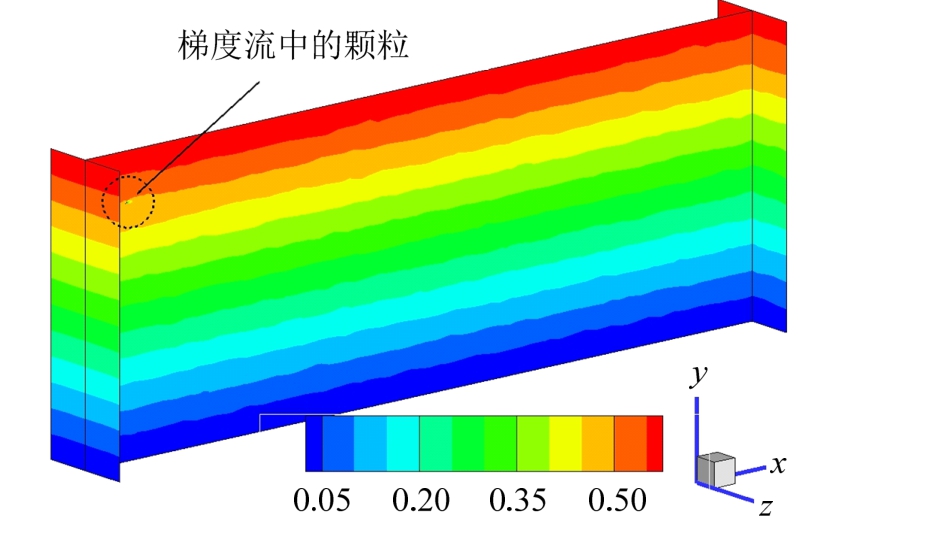
图13 梯度风场平均流速(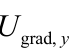
= 10 s-1) /(m/s)
Fig.13 Contour of gradient wind fields
计算同样选用 laminar层流模型并忽略背景湍流的影响，则颗粒因自重及风速梯度等效应发生的竖向(y方向)运动将使颗粒遍历水平x轴方向下强度时变的来流驱动力，用于反映边界层颗粒强迫运动的一般性。
图14为模拟不同梯度风下颗粒在x方向的强迫运动线速度Ux及所受无量纲气动拖曳力
时程，其中，
采用颗粒自重G约化得到
并规定重力方向为负值。如图14(a)所示，当风速梯度
时，该参数颗粒在水平x方向的线速度呈现多次往复波动，首次+x方向加速持续时长在0.01 s左右。随后，颗粒发生x方向减速并逆风加速的运动，当-x方向线速度达到极大值后，Ux再次减小至0 m/s并重现顺风向加速，第二次+x方向加速所能达到的最大速度Ux大于首次加速最大值。当风速梯度Ugrad,y＞100 s-1后(图14(b)、图14(c))，初始静止颗粒在来流驱动下呈现Ux的单调递增并基本保持稳定，对应线速度分别约为4.5 m/s及10.2 m/s。对比颗粒初始位置所受平均风速5 m/s及10 m/s，两者差异不大。
图14 来流方向颗粒线速度及气动外力时程(ds= 150 μm ，ρs= 150 kg/m3)
Fig.14 Calculating particle linear velocities and aerodynamic forces in approaching direction
图15为颗粒自重沉降y方向的运动线速度Uy及该方向无量纲合外力时程
对于
的情况(图 15(a))，初始静止颗粒在自重作用下首先发生加速沉降，
随后，Uy逐渐减小至0 m/s并发生克服自重的向上加速运动，这与小风速梯度下x方向的强迫运动规律相似。当
后，同一时刻下颗粒的瞬时沉降加速度总体随风速梯度单调递减，且在当前模拟的小时间尺度范围内，沉降速度与时间几乎呈线性关系。
图15 自重方向颗粒沉降线速度及合外力时程(ds= 150 μm ，ρs= 150 kg/m3)
Fig.15 Calculating particle linear velocities and resultant forces in gravity direction
对x、y两方向的运动线速度时程进行综合分析可知，小风速梯度下(Ugrad,y=1 s-1)，滞空颗粒运动初期主要表现为全局坐标系下x-y平面内的顺时针螺旋运动，且根据颗粒在两方向的第二次加速所获得的最大速度大于首次加速值，可大致推测运动初期的颗粒平均绕行轨迹半径逐渐增大。当
100 s-1后，颗粒两方向线速度均随时间总体不减，此时的运动表现为向前“抛射”，并且根据Ux在加速后期的平稳保值，颗粒运动轨迹将呈现开口向下的抛物线形态。
颗粒气动力性能方面，任意方向颗粒运动线速度达到局部极大值时，对应方向颗粒气动力总是穿越0值点，气动力与运动速度对应关系一致。如图14(a)所示的小风速梯度工况，颗粒在x方向主要受气动拖曳力作用，该力变化规律直接影响颗粒在x方向线速度的改变。运动初期，颗粒由静止发生加速，水平方向相间相对速度逐渐减小，同时，伴随颗粒的下沉，当前位置所受入口风速较初始位置有所减弱，气动阻力
衰减较为迅速。而运动颗粒受弛豫效应影响，水平方向速度Ux的增大滞后于前进气流相对速度的减小，在大约0.015 s时，颗粒运动速度大于来流风速，气动力
反向，颗粒发生减速，并在大约0.05 s时，
达到极大值。与此同时(0.05 s)，如图15(a)所示，下沉颗粒在y方向受Saffman升力影响完全克服自重，
在约 0.12 s时减速至0 m/s并向上加速，随后所处位置对应入口风速有所增大，导致颗粒气动阻力
在x正方向的增大。大约0.29 s时，Ux经历第二次加速后再次达到正方向极大值，
反向，同时，颗粒发生下沉，Uy向下增大，Ux逐渐减小。可见，对于低
情况，颗粒在x、y两方向所受气动力的增大与减小交替呈现且相互影响，运动速度总体滞后于竖向梯度下空间变化的来流风速。
对于图14、图15中两种大速梯风度工况，颗粒所受x方向气动力
及y方向合外力
几乎不随时间出现较大程度改变，且随着
的增大，
将更快趋于0并达到稳定，反映了初始强风条件下的颗粒将具有更好的顺风向流场跟随性；而运动后期
的平均值总体大于1，表明自重方向的大风速梯度可能加剧颗粒的沉降。但随着
增大至
有所减小，也反映出上述效应将随流场梯度的增大而减弱。
因来流梯度仅存在于y方向，这里认为颗粒将主要发生绕其形心并指向z轴的自旋转。图16为模拟颗粒z方向角速度zω及所受合外力矩Mz时程，其中Mz采用颗粒浮力及直径进行无量纲处理
由于风速梯度的存在，颗粒顶面所受流场切应力总是大于底面，初始状态颗粒将受到一-z方向力矩而旋转。随后，各
下颗粒力矩均迅速增大，引起了zω的增大，较短时间内，
即达到局部极大值，且随Ugrad,y的增大而增大。与颗粒线速度及气动外力间的关系相似，受弛豫效应影响，最大旋转速度总是滞后于最大合外力矩出现，对于小
情况(图16(a))，颗粒在运动初期将经历加速—减速—再次加速旋转至稳定的过程。而对于
的大梯度情况，颗粒所受合外力矩及旋转速度将在较短时间内(t＜0.02 s)趋于稳定，且随着
的增大，稳定的zω总体有所减小。该参数颗粒在运动初期的旋转效应主要在小梯度风环境下更为显著。
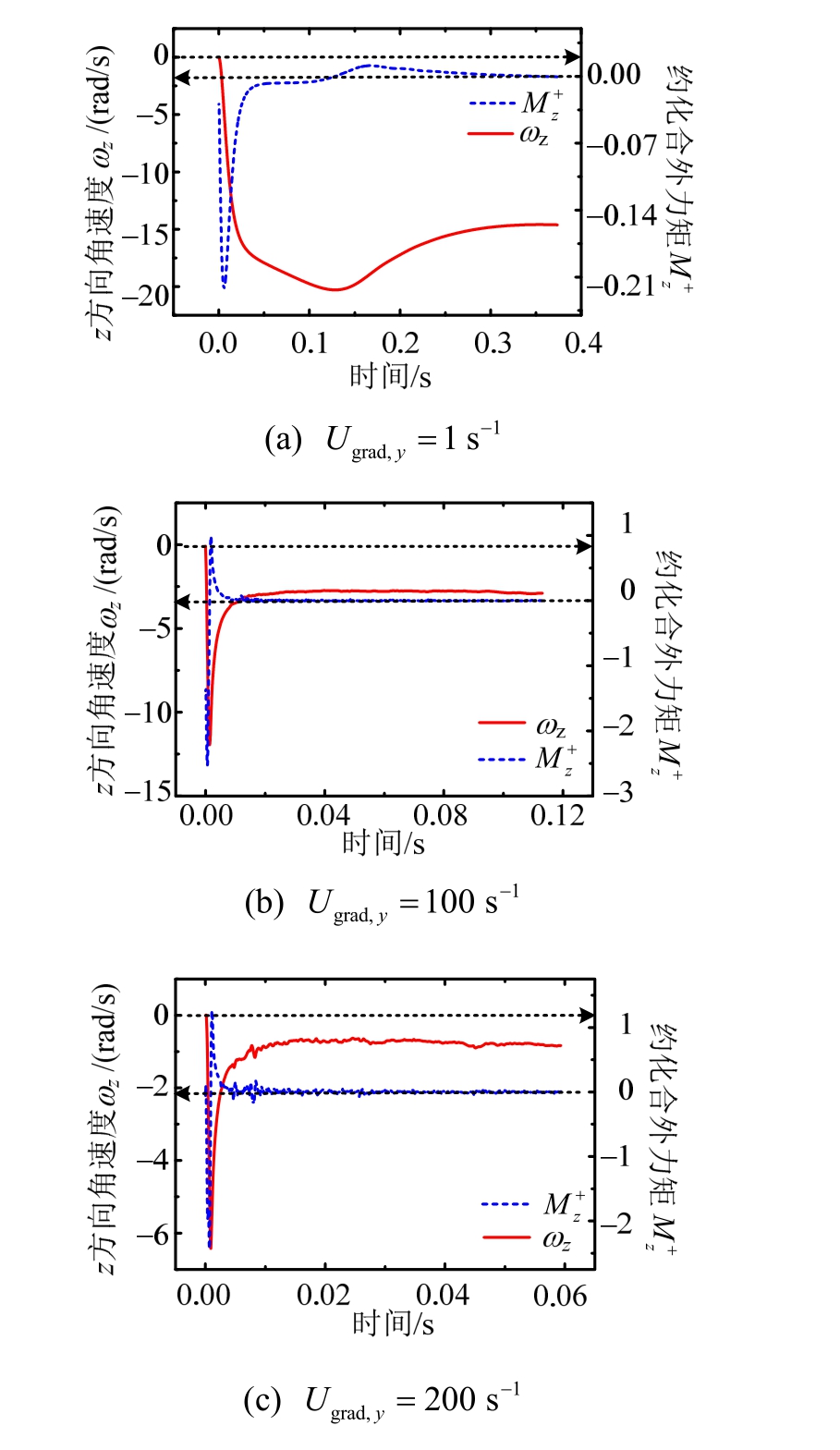
图16 水平方向颗粒旋转速度及合外力矩时程
(ds= 150 μm ，ρs= 150 kg/m3)
Fig.16 Calculating particle angular velocities and external moments in lateral direction
本文通过对理想雪颗粒建立微观层面的数值计算模型，求解了不同相对雷诺数(Res)下滞空颗粒的空间绕流、非线性变加速运动与受力行为。研究主要得出以下结论：
(1) 当
时，滞空雪颗粒绕流行为近似服从斯托克斯层流；当
时，颗粒存在明显特征湍流。对于常规大气环境下的风吹雪现象，可近似忽略颗粒运动对流场湍流成分的贡献。
(2) 雪颗粒在静止空气中发生自由沉降所能达到的最大终端速度与颗粒粒径及密度直接相关。当粒径(密度)不变时，随着颗粒密度(粒径)的增大，终端速度及其达到稳定所需时长均单调增大。雪颗粒的自由沉降过程属于小时间尺度问题。
(3) 受非线性气动外力影响，当雪颗粒粒径不变时，相同时间内大密度颗粒自重沉降距离更远。雪颗粒的变速沉降过程属于小空间尺度问题。
(4) 雪颗粒自由沉降的非线性变速阶段相对于大时空尺度的风致积雪漂移及沉积过程可忽略不计。该问题满足多相流混合单流体模型理论的局部短时空尺度均衡假定。
(5) 由不同时刻自由沉降雪颗粒壁面驻点及分离点静压分布值可知，非线性气动效应并非在颗粒速度接近稳定沉降速度时立即消失，各气动力将在短期内轻微、协调变化以维持终端速度的不变。
(6) 雪颗粒在梯度风下的强迫运动非线性变速阶段仍可视为小时空尺度问题。对于较高风速情况，颗粒在来流方向具有更好的流场跟随性。颗粒自重及主旋转方向的运动行为也近似满足混合单流体模型理论的局部短时空尺度均衡条件。
[1]Dyunin A K, Anfilofiyev B A, Istrapilovich M G, et al.Strong snow-storms, their effect on snow cover and snow accumulation [J]. Journal of Glaciology, 1977, 19(81):441－449.
[2]Oikawa S, Tomabechi T, Ishihara T. One-day observations of snowdrifts around a model cube [J].Journal of Snow Engineering of Japan, 2009, 15(4):283－291. (in Japanese)
[3]Iversen J D, Wang W P, Rasmussen K R, et al. The effect of a roughness element on local saltation transport [J].Journal of Wind Engineering & Industrial Aerodynamics,1990, 36(1/2/3): 845－854.
[4]Figueiredo M A T, Jain A K. Unsupervised Learning of Finite mixture models [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(3): 381－396.
[5]Marocco L, Inzoli F. Multiphase euler–lagrange CFD simulation applied to wet flue gas desulphurisation technology [J]. International Journal of Multiphase Flow,2009, 35(2): 185－194.
[6]李雪峰, 周晅毅, 顾明, 等. 立方体模型周边风致积雪飘移的数值模拟[J]. 同济大学学报(自然科学版),2010, 38(8): 1135－1140.Li Xuefeng, Zhou Xuanyi, Gu Ming, et al. Numerical simulation on snow drifting around a cube model [J].Journal of Tongji University (Natural Science Edition),2010, 38(8): 1135－1140. (in Chinese)
[7]周晅毅, 刘长卿, 顾明, 等. 拉格朗日方法在风雪运动模拟中的应用[J]. 工程力学, 2015, 32(1): 36－42.Zhou Xuanyi, Liu Changqing, Gu Ming, et al.Application of Lagrangian method to snowdrift model[J]. Engineering Mechanics, 2015, 32(1): 36－42. (in Chinese)
[8]Beyers J H M, Sundsbø P A, Harms T M. Numerical simulation of three-dimensional, transient snow drifting around a cube [J]. Journal of Wind Engineering &Industrial Aerodynamics, 2004, 92(9): 725－747.
[9]Tominaga Y, Okaze T, Mochida A. CFD modeling of snowdrift around a building: An overview of models and evaluation of a new approach [J]. Building &Environment, 2011, 46(4): 899－910.
[10] Lukerchenko N, Kvurt Y, Keita I, et al. Drag force, drag torque, and magnus force coefficients of rotating spherical particle moving in fluid [J]. Particulate Science& Technology, 2012, 30(1): 55－67.
[11] Schmidt R A. Measuring particle size and snowfall intensity in drifting snow [J]. Cold Regions Science &Technology, 1984, 9(2): 121－129.
[12] Alhajraf S. Computational fluid dynamic modeling of drifting particles at porous fences [J]. Environmental Modelling & Software, 2004, 19(2): 163－170.
[13] 刘多特, 李永乐, 汪斌. 风雪绕流数值模拟的积雪预测模型研究[J]. 工程力学, 2016, 33(8): 121－131.Liu Duote, Li Yongle, Wang Bin. A numerical prediction model for snow accumulation caused by ambient snowdrift [J]. Engineering Mechanics, 2016, 33(8):121－131. (in Chinese)
[14] Morsi S A, Alexander A J. An investigation of particle trajectories in two-phase flow systems [J]. Journal of Fluid Mechanics, 1972, 55(2): 193－208.
[15] 库建刚, 何逵, 徐露, 等. 重力沉降法测定流体中颗粒运动阻力系数及其验证 [J]. 矿冶工程, 2015, 35(1):31－34.Ku Jiangang, He Kui, Xu Lu, et al. Measurement and validation of drag coefficient of particles in fluid by gravity settling method [J]. Mining and Metallurgical Engineering, 2015, 35(1): 31－34. (in Chinese)
A NUMERICAL SIMULATION ON AERODYNAMIC FORCES AND MOTION BEHAVIORS OF SNOW GRANULES IN AIR