。另外，增大翼腹比可有效提高短剪切型消能梁段腹板受剪屈服后的承载力，但改变翼缘强度和跨高比对其性能无明显影响。胡淑军1,2，熊进刚1,2，王 湛3
(1．南昌大学建筑工程学院，江西，南昌 330031；2．江西省近零能耗建筑工程实验室，江西，南昌 330031；3．华南理工大学亚热带建筑科学国家重点实验室，广东，广州 510640)
摘 要：已有研究表明，长度比小于1.0的短剪切型消能梁段与普通剪切型消能梁段的超强系数和塑性转角存在较大差异。该文基于Q235和Q345钢材，设计108个考虑加劲肋间距、翼缘与腹板面积比、翼缘强度和跨高比等因素的模型，并采用与已有试验结果对比验证的有限元分析方法，详细研究短剪切型消能梁段的力学性能及各因素的影响规律。结果表明，短剪切型消能梁段的超强系数和塑性转角分别能达到1.90和0.13，加劲肋间距系数和翼缘宽厚比可分别放宽至40和。另外，增大翼腹比可有效提高短剪切型消能梁段腹板受剪屈服后的承载力，但改变翼缘强度和跨高比对其性能无明显影响。
关键词：短剪切型消能梁段；加劲肋间距；翼缘宽厚比；超强系数；塑性转角
偏心支撑结构是一种抗震性能良好的结构体系，地震作用下主要通过消能梁段的非弹性变形耗散能量[1―3]。消能梁段的延性和耗能能力越强，结构的抗震性能越好[4―7]。消能梁段的长度比 ρ=eVp/Mp，其中，e、Vp和Mp分别是消能梁段的长度、塑性剪力和塑性弯矩。当ρ≤1.6，属于剪切型耗能梁；当ρ≥2.6，属于弯曲型耗能梁；当1.6＜ρ＜2.6，属于弯剪型耗能梁[8―9]。由于剪切型消能梁段在延性和耗能能力等方面均优于弯曲型和弯剪型消能梁段，在偏心支撑结构中被推荐使用[3,10]。
剪切型消能梁段的力学性能主要包括超强系数和塑性转角，规范建议值分别为1.50和0.08[8―9]。然而，对长度比小于 1.0的短剪切型消能梁段，McDaniel等[4]研究表明，构件平均超强系数为1.90，但腹板与加劲肋连接处的焊缝提前破坏，其塑性转角未能满足要求；Dusicka等[5]研究表明，最大超强系数和塑性转角为1.90和0.20；纪晓东等[11]研究表明，构件的腹板会发生全截面受剪屈服，随后由翼缘、加劲肋和受剪屈服的腹板组成的子框架继续承受荷载，其超强系数和塑性转角分别达到1.99和0.15。另外，Azad和Topkaya[3]提出，该种剪切型消能梁段与普通剪切型消能梁段的力学性能有较大差异，将其应用于偏心支撑结构中会严重影响结构的抗震性能，并使结构产生非预期破坏。
纪晓东等[11]研究表明，加劲肋间距对剪切型消能梁段超强系数和塑性转角的影响非常明显，且适当放宽加劲肋间距限值后，其力学性能仍能满足要求；Mohebkhah和Chegeni[12]研究发现，减小加劲肋间距会使消能梁段的超强系数增大 15%～20%。对长度比小于1.0的短剪切型消能梁段，其腹板发生受剪屈服后的子框架承载能力受加劲肋间距的影响明显，如何进一步细化加劲肋间距对该种消能梁段的影响及其规律，以及是否允许适当放宽加劲肋间距的限值等，是当前研究的重要内容之一。
增大翼缘面积可提高翼缘对腹板的约束作用。然而，当翼缘宽厚比过大时，端部弯矩的增大可能使得翼缘容易发生屈曲，对消能梁段产生不利影响。Okazaki等[10]、Richards和 Uang[13]研究采用A992钢所设计构件表明，对剪切型消能梁段的翼缘宽厚比限值可放宽至 0.38(E/fy)1/2。《建筑抗震设计规范》[8]中规定，消能梁段翼缘的外伸部分宽厚比限值是8ε，其中，
，fy是钢材的屈服强度。与普通框架梁相比，该限值相对保守，消能梁段可能需通过增大翼缘厚度来满足该值，这将直接增大结构中梁、柱和支撑的截面。同时，许多轧制型钢由于无法满足该要求而不能用作消能梁段。胡淑军和王湛[14]研究表明，对剪切型消能梁段，其翼缘宽厚比可放宽至10ε。对长度比小于1.0的短剪切型消能梁段，其承载力达到极限状态时两端的弯矩仍较小，翼缘宽厚比限值和翼腹比对其性能所带来的影响需进行深入分析。
在剪切型消能梁段中，翼缘强度的提高可以增大翼缘对腹板的约束作用和翼缘的抗弯承载能力[11]，由此影响子框架和剪切型消能梁段的力学性能。另外，当剪切型消能梁段的长度和腹板面积相同时，截面高度的变化对其承载能力和塑性变形能力影响也不得而知。因此，必需进一步研究翼缘强度和跨高比两种因素对构件的影响。
以上分析表明，加劲肋间距、翼腹比、翼缘强度和跨高比等参数是影响长度比小于1.0的短剪切型消能梁段的主要因素。因此，本文基于Q235和Q345钢材，设计了四组共 108个模型来分析该种消能梁段的力学性能及各因素的影响规律，为该种剪切型消能梁段及相应结构的设计和分析提供可靠的理论保障，促进偏心支撑结构体系的发展。
目前，规范中对剪切型消能梁段的超强系数和塑性转角均采用统一的标准[8―9]。然而，对于部分较短的剪切型消能梁段，其规范值可能过于保守，无法应用于这类剪切型消能梁段中[4―5,11]。
McDaniel和 Uang[4]，Dusicka 等[5]和纪晓东等[11]对基于多种钢材所设计的剪切型消能梁段进行试验研究，取 C345、L225、type1、type3、L11、L21、Q11和Q21八个长度比小于1.0的消能梁段为研究对象。
当消能梁段长度比小于1.0时，腹板将发生全截面受剪屈服，且子框架有较大的承载能力，使其超强系数的最小值为1.80，平均值为1.90，大于规范建议值1.50。此外，由于消能梁段长度较短，当其剪力达到极限状态时的端弯矩M与塑性弯矩Mp的比值小于0.90，平均值为0.70，如图1所示。
剪切型消能梁段的端部剪力V与弯矩M的关系可表示为：
基于图1中的已有试验研究结果，可得该类型消能梁段的最大弯矩值为 0.90 Mp，最小剪力值为1.80 Vp，并代入式(1)中可得：
此时，长度比 ρ=1.0。因此，定义长度比小于1.0的消能梁段为短剪切型消能梁段，其力学性能与普通剪切型消能梁段存在较大差异[4―5]。
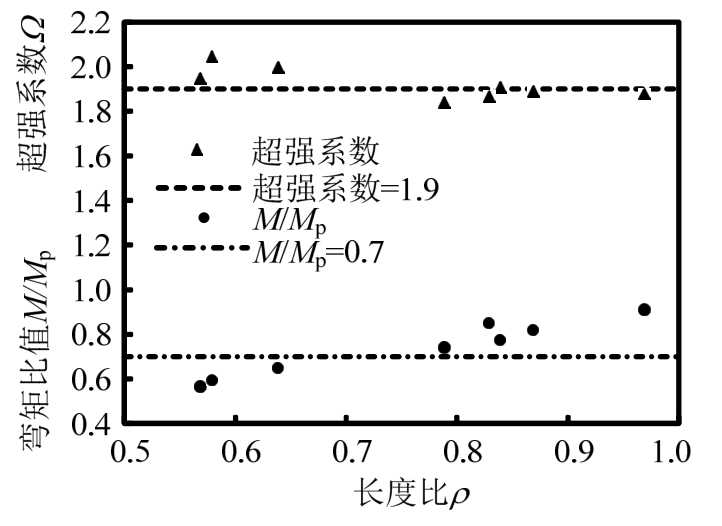
图1 已有试验数据中超强系数和弯矩比值与长度比图
Fig.1 Overstrength coefficient, M/MPversus length ratio for experimental data
为研究往复荷载下加劲肋、翼腹比、翼缘强度和跨高比等因素对短剪切型消能梁段性能的影响，设计多组模型并采用 ANSYS软件进行有限元分析。通过与已有试验结果对比，验证有限元分析的准确性，并对所设计的各组模型进行分析。
设计和分析短剪切型消能梁段模型时，以H型截面H400×200×10×14和H474×330×14×22为基础，通过改变相应截面参数和构件长度，以考虑各种因素的影响并得到相应的力学性能。所有构件的加劲肋均对称布置，且厚度取ta=10 mm，在考虑单个因素影响时构件的其他参数均应满足规范[9]要求。
试件分析时需采用的Q235和Q345钢材，其性能采用文献[11]中的数据，如表1所示。钢材的弹性模量E=1.95×105N/mm2，泊松比ν =0.3。ANSYS模拟时采用多线性随动强化和von Mises屈服准则，以考虑往复荷载作用下钢材的屈服。然而，钢材在单调和往复加载下的力学性能有一定差异[15―16]。
为研究Q235和Q345钢材在低周反复加载下的力学性能，石永久等[15]对 50个模型进行试验研究和有限元分析，得到了两种钢材在单调和反复加载时的本构关系，如图2所示。往复加载下钢材的屈服强度与单调加载时相同，但钢材的硬化导致其极限强度大于单调加载时的极限强度。此外，往复加载会使构件出现疲劳破坏，使得构件在达到极限强度时的应变提前，且最大伸长率偏小。
表1 钢材性能[11]
Table 1 Material properties for steel[11]
图2 钢材单调及往复加载曲线对比图[15]
Fig.2 Comparative of monotonic and hysteresis curves of steel[15]
由于剪切型消能梁段在往复荷载下翼缘和腹板不会发生明显的屈曲和局部失稳，且各板件会产生较大的应变硬化，有限元分析时钢材的本构关系宜采用考虑循环加载影响的力学模型[16]。因此，本文对剪切型消能梁段的有限元分析时，Q235和Q345钢材均采用以上模型。
ANSYS软件中有多种实体单元和壳单元可模拟消能梁段，本文选用Solid185单元。该单元用于构造三维固体结构，并通过8个节点来定义，每个节点有3个沿着x、y、z方向平移的自由度，具有超弹性、应力钢化、蠕变、大变形和大应变能力[14]。分析时，不考虑钢材的疲劳和残余应力的影响。
在消能梁段的有限元分析中，合理选择边界条件和加载方式是非常重要的。纪晓东等[11]在对短剪切型消能梁段的试验研究时，仅在试件上端施加竖直方向的剪力。有限元分析时，下端截面各方向都进行约束；上端截面约束平面外位移，但允许截面在竖向和和水平方向运动，但截面上各点的竖向和水平位移需分别相等，如图3所示，与试验方案相同。
各模型进行分析时，采用 AISC[17]中的加载方式，如图4所示。将转角转换成水平位移施加在上端截面上，并按照循环次数加载，直至构件破坏。
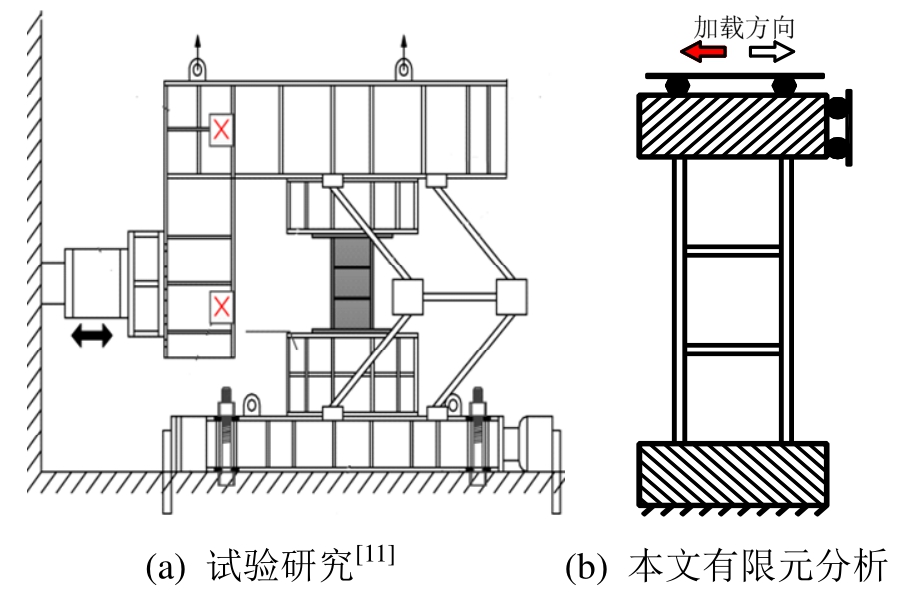
图3 边界条件
Fig.3 Boundary condition
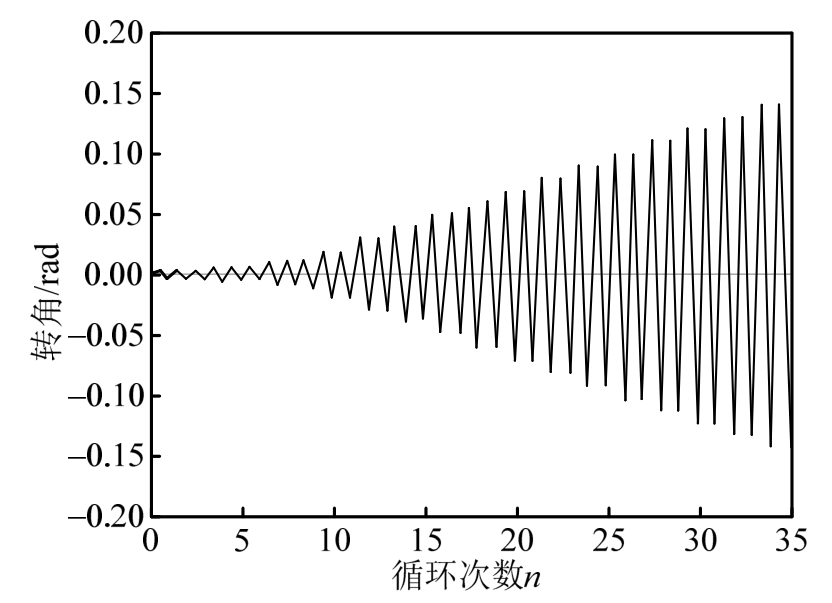
图4 加载方式
Fig.4 Loading protocols
本文通过分析纪晓东等[11]试验研究中的试件Q11、Q13和 Q21，以验证有限元分析方法的准确性。各模型截面均为H400×180×10×14，其中，Q11和 Q13的长度是 660 mm，加劲肋间距分别为220 mm和330 mm，ρ=0.97；Q21长度是440 mm，加劲肋间距为220 mm，ρ=0.64。各试件的加劲肋均对称布置，翼缘采用Q345钢，腹板和加劲肋采用Q235钢，钢材的力学性能如2.2节所述。
图5中各试件试验及有限元分析所得的剪力-转角曲线均相近。试件Q11的试验及有限元分析所得最大塑性转角均为0.13，剪力分别为1107 kN和1092 kN，超强系数分别为1.87和1.85；试件Q13的试验及有限元分析所得最大塑性转角均为0.11，剪力分别为 970 kN和 1002 kN，超强系数分别为1.64和1.69，有限元结果略大于试验结果，可能是由于试验加载后期出现屈曲转换现象，而在有限元分析中仅出现屈曲现象。另外，试件Q13加载后期出现承载力下降的现象，主要是由于加劲肋间距超出规范允许值，腹板已发生较大非弹性屈曲，降低构件后期的承载能力；试件Q21的试验及有限元分析所得最大塑性转角为均0.15，剪力分别为1180 kN和1149 kN，超强系数分别为1.99和1.95。由于该截面的加劲肋最大允许间距为220 mm[8]，当加劲肋间距放宽至330 mm时，其腹板发生较大屈曲，对构件的超强系数影响明显，但仍满足要求。
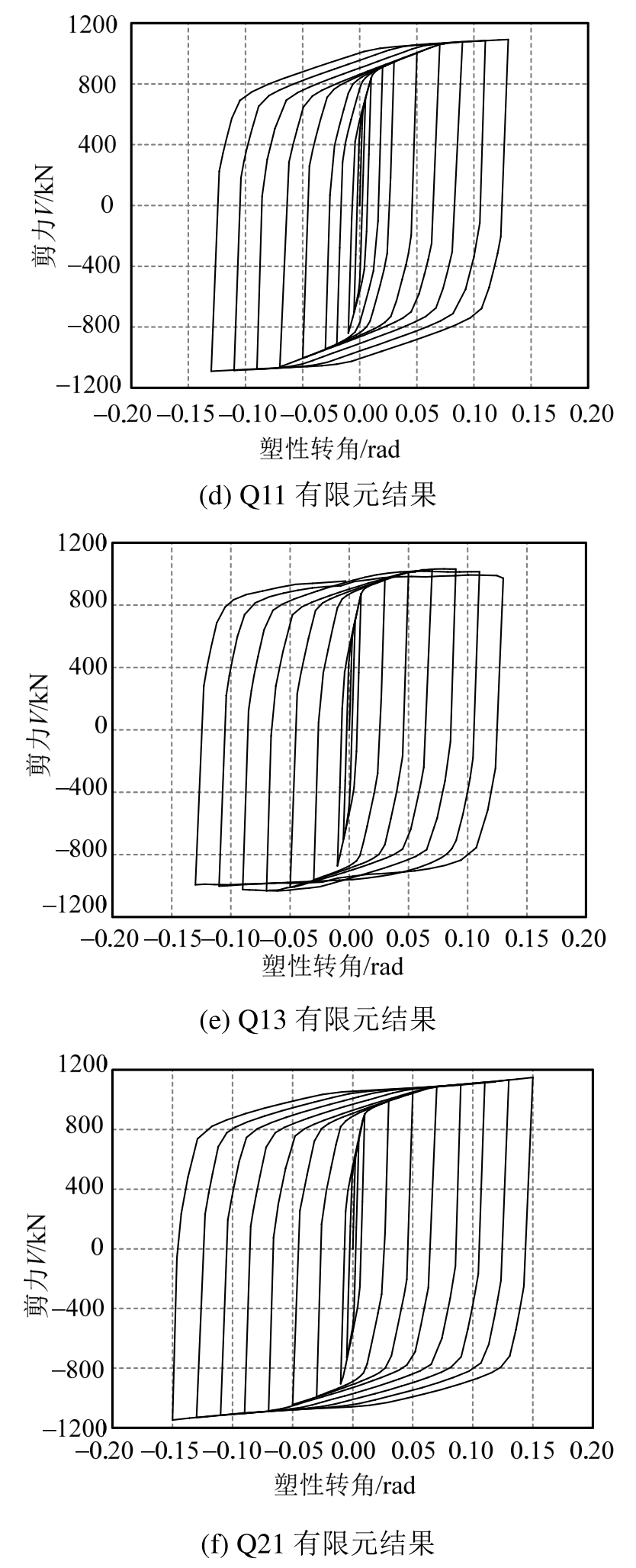
图5 试件Q11、Q13和Q21的剪力-塑性转角曲线对比
Fig.5 Comparison of shear versus inelastic rotation hysteresis for specimen Q11, Q13 and Q21
由于有限元分析时未考虑焊缝及板件断裂的影响，仅从应力最大处反应可能发生的破坏[14]。试验分析结果表明，试件Q11和Q21的破坏模式为翼缘与端板连接处的焊缝被破坏，如图6(a)所示；试件Q13的破坏模式为腹板与加劲肋交接处的腹板断裂。有限元分析结果表明，试件Q11和Q21的翼缘与端板连接处的应力最大，如图6(b)所示；Q13在腹板与加劲肋交接处应力集中严重，即认为有限元分析所得的破坏模式与试验分析结果基本吻合。
基于试验与有限元分析结果，可对比以上三个试件的滞回曲线、塑性转角、极限剪力和破坏模式，验证了本文有限元分析方法的准确性。因此，该有限元分析方法可用于短剪切型消能梁段的分析中。
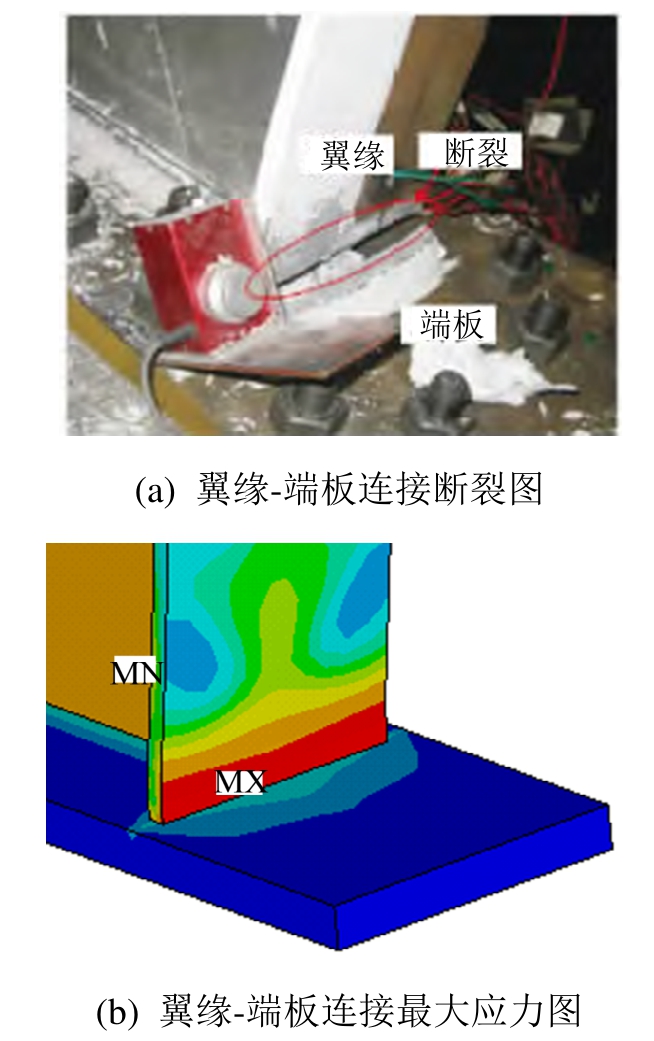
图6 试件Q11的破坏模式
Fig.6 Failure mode for specimen Q11
对2.1节中所述的H400×200×10×14截面，其长度l分别取480 mm、510 mm、540 mm、570 mm、600 mm、630 mm和660mm；对H474×330×14×22截面，长度l分别取720 mm、760 mm、800 mm、840 mm、880 mm、920 mm和960 mm。各长度下均设计两个不同加劲肋间距的模型，共设计 28个模型，以考虑加劲肋间距的影响。所有腹板、翼缘和加劲肋均采用Q235钢材。
对各模型进行有限元分析，可得到往复荷载下的滞回曲线，提取每次循环所得最大位移和所对应的力，并得到相应的骨架曲线。骨架曲线中强度折减处所对应的点，即为最大超强系数Ωmax和塑性转角 γmax；若曲线强度无折减段，则所施加的最大超强系数和塑性转角即为所求[14]。
往复荷载下，短剪切型消能梁段的加劲肋间距、长度比和超强系数的关系如图7所示。图中填充和未填充的方形分别为加劲肋间距满足和超出规范要求时的超强系数值。当加劲肋间距满足规范要求时，其超强系数值随长度比的增大而减小，且在长度比接近1.0时，超强系数值仍能达到1.90，比规范值高出26.7%；当加劲肋间距超出规范值时，其最小超强系数为1.70，仍高于规范值1.50。对比相同长度的消能梁段，加劲肋间距对超强系数的影响明显，主要是放宽加劲肋间距会增大短构件腹板的屈曲和减小腹板受剪屈服后子框架的承载能力。
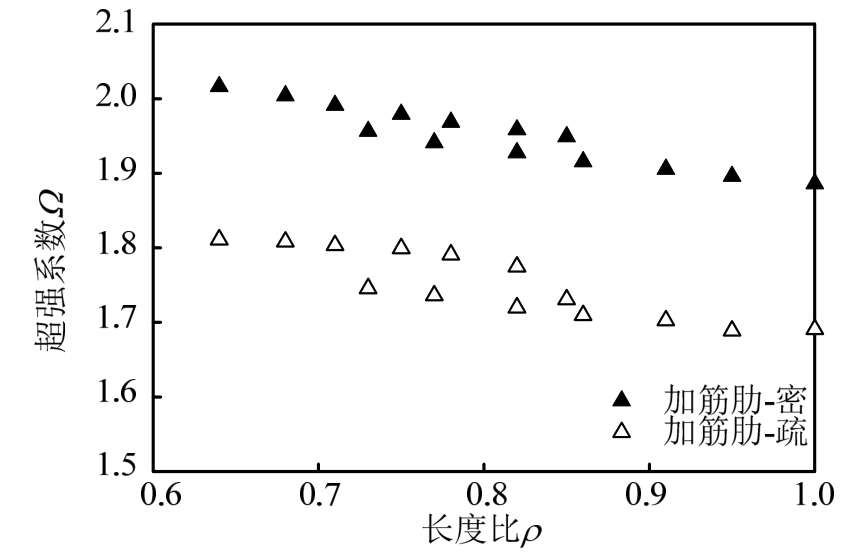
图7 短剪切型消能梁段加劲肋间距、长度比和超强系数关系
Fig.7 Relationship between stiffener spacing, length ratio and overstrength coefficient for short shear links
Kasai和Popov[1]通过对剪切型消能梁段研究，得到了腹板变形角、腹板宽高比和高厚比之间的关系：
式中：a为加劲肋间距；CB为加劲肋间距系数。《建筑抗震设计规范》[8]规定，剪切型消能梁段的加劲肋间距不应大于(30tw－h/5)，即CB=30。
图8为加劲肋间距系数与超强系数的关系图。当加劲肋间距系数小于规范值 30时，最小超强系数为1.90，平均值为1.95；当加劲肋间距系数放宽至40时，最小的超强系数值1.70，平均值为1.75。因此，放宽加劲肋间距系数至 40会对其超强系数有所影响，但仍能满足规范要求。
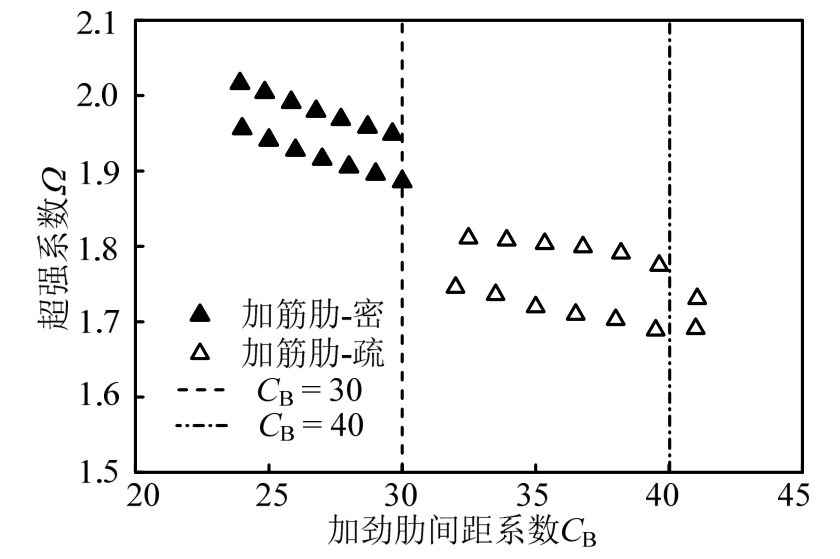
图8 短剪切型消能梁段的加劲肋间距系数与超强系数关系
Fig.8 Stiffener spacing coefficient versus overstrength coefficient for short shear links
往复荷载下，短剪切型消能梁段的加劲肋间距、长度比和塑性转角关系如图9所示。对于加劲肋间距满足规范[8]要求时，其塑性转角值随长度比的增大而减小，当长度比小于0.8时，塑性转角值能达到0.15；当其长度比接近1.0时，塑性转角值仍能达到0.13。对于加劲肋间距超出规范要求时，其塑性转角有所减小，当构件长度比小于0.8时，塑性转角值最大值为 0.13；当构件长度比接近 1.0时，超强系数最小值为0.11，高于规范值0.08[8]。对比相同长度比的短剪切型消能梁段，可知加劲肋间距对其塑性转角有一定影响，主要是放宽加劲肋间距会增大腹板的屈曲和减小子框架的变形能力。
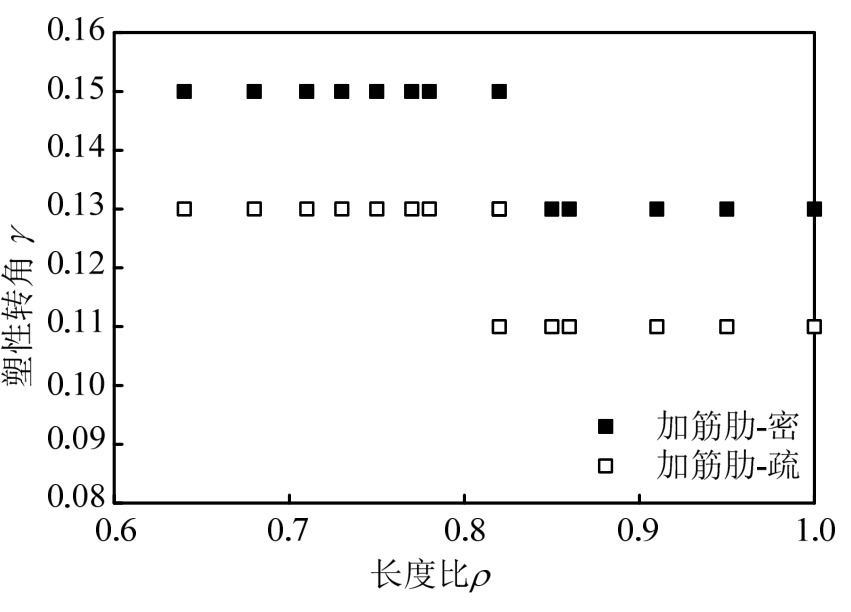
图9 短剪切型消能梁段加劲肋间距、长度比和塑性转角关系
Fig.9 Relationship between stiffener spacing, length ratio and inelastic rotation for short shear links
图10为加劲肋间距系数与塑性转角的关系图。当加劲肋间距系数小于规范允许值 30时，最小超强系数为 0.13；当加劲肋间距系数放宽至 40时，最小的塑性转角值为0.11，均大于规范要求值0.08。因此，对于短剪切型消能梁段，将其加劲肋系数放宽至40，其超强系数仍能满足规范要求。
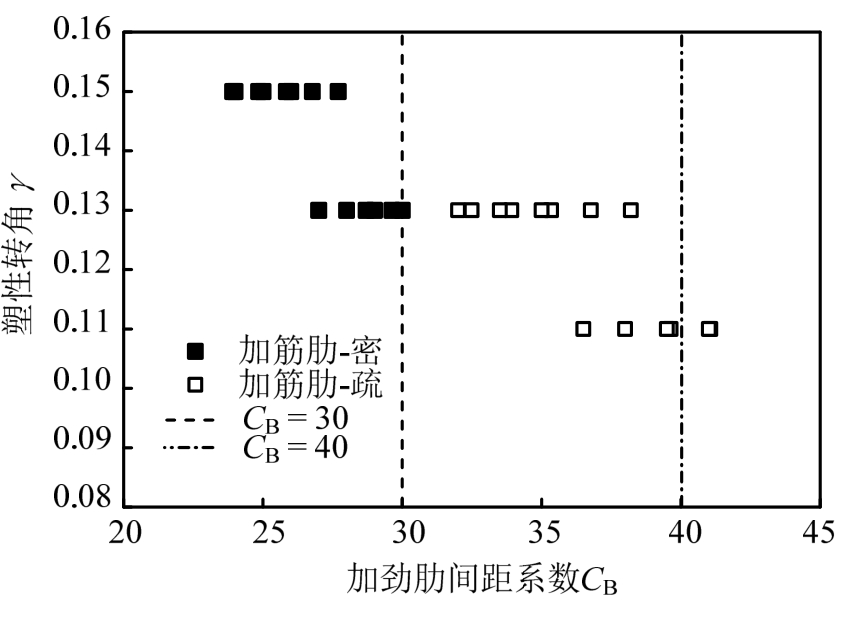
图10 短剪切型消能梁段的加劲肋间距系数与塑性转角关系
Fig.10 Stiffener spacing coefficient versus inelastic rotation for short shear links
基于以上分析加劲肋间距对短剪切型消能梁段超强系数和塑性转角的影响，可知当加劲肋间距满足规范要求时，短剪切型消能梁段的超强系数最小值为1.90，塑性转角也能达到0.13；当放宽加劲肋系数至 40时，超强系数和塑性转角的最小值仍至少能达到1.70和0.11。因此，对短剪切型消能梁段，可考虑将加劲肋间距系数CB放宽至40，即加劲肋间距需不应大于(40tw－h/5)。
对H400×bf×10×14截面，长度分别取440 mm、540 mm、600 mm 和 660 mm，各长度下翼缘宽厚bf分别取200 mm、220 mm、240 mm和260 mm；对 H474×bf×14×22截面，长度分别取 840 mm、900 mm 和 960 mm，各长度下翼缘宽厚 bf分别取300 mm、330 mm、360 mm 和 400 mm，共设计 28个分析模型，以研究翼缘宽厚比的影响。每种长度下的四个翼缘宽度包括满足规范[8]要求和超出规范[8]限值。所有腹板、翼缘和加劲肋均采用Q235钢材。
往复荷载下，短剪切型消能梁段的翼缘宽厚比、长度比和超强系数关系如图11所示。图中填充和未填充的三角形分别为翼缘宽厚比满足规范要求和超出规范值时的超强系数值。截面仅增大翼缘宽度时会增大其塑性模量，从而导致其长度比的减小。短剪切型消能梁段的超强系数随其长度比的增大而略微减小，超强系数的平均值为1.95，翼缘宽厚比对构件超强系数的影响不明显。
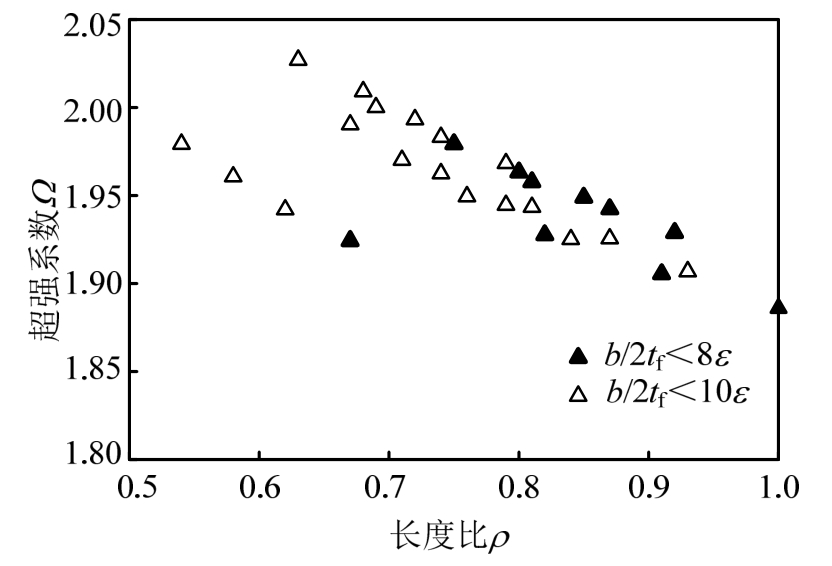
图11 短剪切型消能梁段翼缘宽厚比、长度比和超强系数关系
Fig.11 Relationship between flange width-thickness ratio,length ratio and overstrength coefficient for short shear links
图12为短剪切型消能梁段的翼缘宽厚比与超强系数的关系图。左边竖直虚线是允许的翼缘宽厚比bf/ 2tf= 8ε，右边虚线的bf/ 2tf=10ε。当翼缘宽厚比满足规范要求时，其超强系数的最小值为1.90；放宽翼缘宽厚比至 10ε时，翼缘面积的增大会提高翼缘对腹板的约束作用和子框架的承载能力。另外，由于构件端部弯矩较小，增大翼缘宽度不会引起翼缘屈曲，使其超强系数有所增大，均不小于1.92。
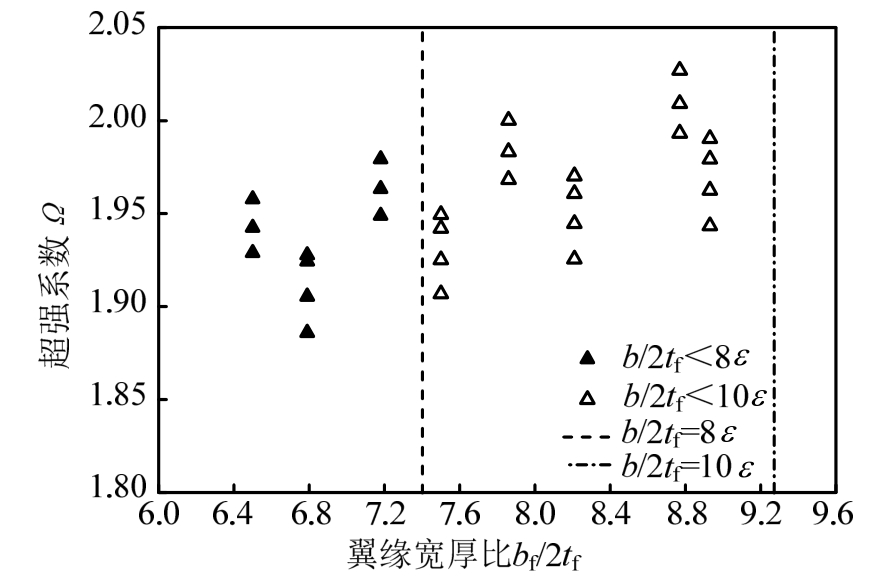
图12 短剪切型消能梁段的翼缘宽厚比与超强系数关系
Fig.12 Flange width-thickness ratio versus overstrength coefficient for short shear links
往复荷载下，短剪切型消能梁的翼缘宽厚比、长度比和塑性转角关系如图13所示。图中填充和未填充的三角形分别为翼缘宽厚比满足规范和超出规范值时的塑性转角。当构件长度比小于0.8时，塑性转角值能达到0.15；当构件长度比接近1时，超强系数值仍能达到0.13，高于规范值0.08。
图13 短剪切型消能梁翼缘宽厚比、长度比和塑性转角关系
Fig.13 Relationship between flange width-thickness ratio,length ratio and inelastic rotation for short shear links
图14为翼缘宽厚比与塑性转角的关系图，左、右两条虚线分别是翼缘宽厚比等于8ε和10ε。从图中可知，构件的最小塑性转角为0.13，放宽翼缘宽厚比值至 10ε，可提高翼缘对腹板的约束作用，由此提高部分构件的变形能力，增大其塑性转角。
因此，将短剪切型消能梁段的翼缘宽厚比放宽至 10ε，可提高构件的超强系数和塑性转角，最小值分别为1.92和0.13。另外，放宽翼缘宽厚比限值可增大消能梁段和非消能梁段的抗弯承载力，在允许的情况下，其翼缘宽厚比应尽量取大值。
图14 短剪切型消能梁段翼缘宽厚比与塑性转角关系
Fig.14 Flange width-thickness ratio versus inelastic rotation for short shear links
根据4.1节中对翼缘宽厚比的影响研究，进一步分析翼腹比对短剪切型消能梁段性能的影响。
往复荷载作用下，短剪切型消能梁段的翼腹比与超强系数关系如图15所示。翼腹比的增大可提高构件的超强系数。由于短消能梁段在达到极限塑性转角时，腹板已经发生全截面受剪屈服。对于腹板屈服后的子框架，在翼缘宽厚比从8ε增大至10ε时，其承载力可提高近20%，即增大翼腹比可明显提高子框架的承载能力。
由于短剪切型消能梁段在达到极限受剪承载力时的端弯矩较小，放宽其翼缘宽厚比限值后不会发生屈服，且翼缘面积的增大可有效提高翼缘对腹板的约束作用。因此，增大翼腹比(即放宽翼缘宽厚比后)有利于提高短剪切型消能梁段的超强系数和塑性转角，设计时应尽量增大该值。
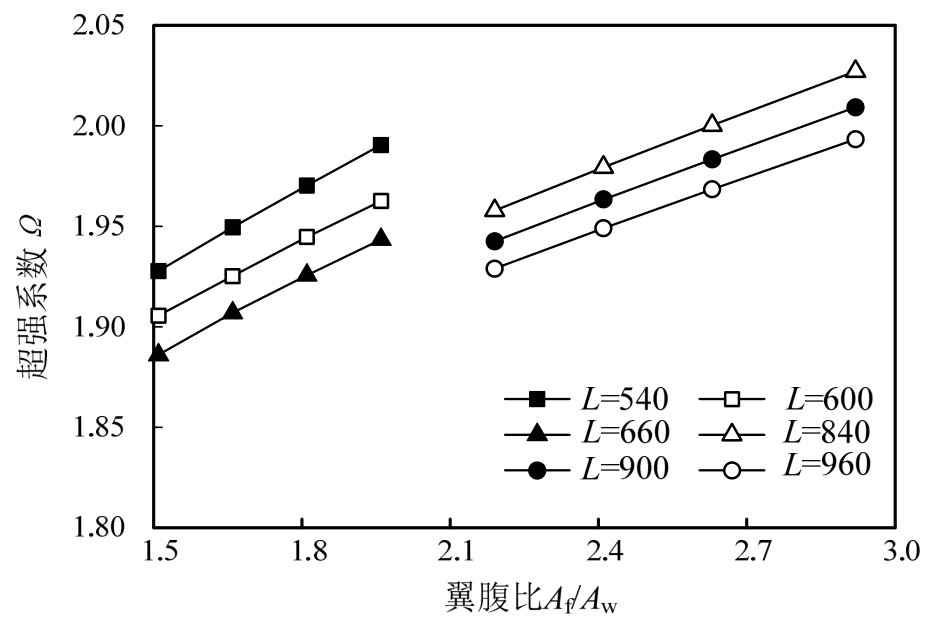
图15 短剪切型消能梁段的翼腹比和超强系数关系
Fig.15 Ratio of flange over web area versus overstrength coefficient for short shear links
为研究翼缘强度对短剪切型消能梁段的影响，采用 3.1节中考虑加劲肋间距满足规范[8]要求时的分析模型，且各模型中翼缘强度分别采用Q235和Q345钢材。基于不同长度和翼缘强度，设计28个分析模型并进行分析，以得到相应的结果。
往复荷载下，短剪切型消能梁段的翼缘强度、长度和超强系数关系如图16所示。对相同长度、截面和加劲肋布置的短剪切型消能梁段，腹板全截面受剪屈服后，翼缘强度从Q235提高至Q345，其子框架承载能力和构件超强系数仅能分别提高 8%和1.5%，即增大翼缘强度对其子框架的影响有限。
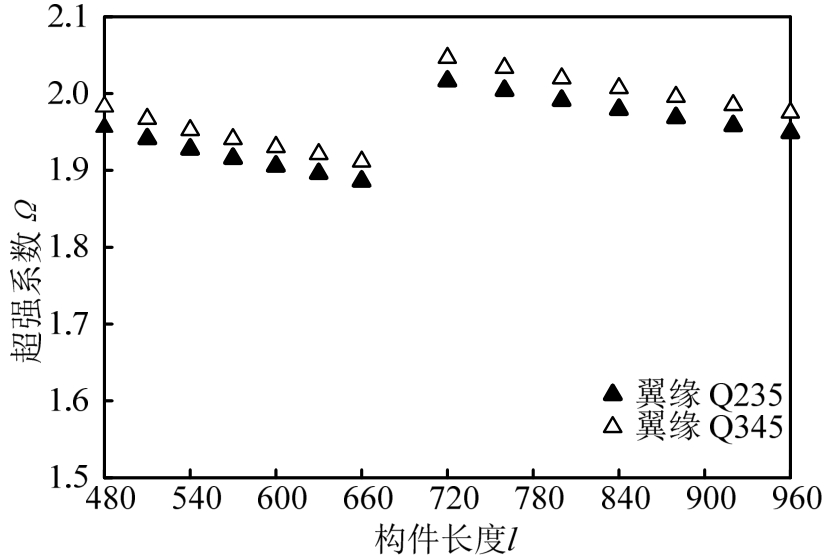
图16 短剪切型消能梁段翼缘强度、长度和超强系数关系
Fig.16 Relationship between flange strength, length and overstrength coefficient for short shear links
另外，短剪切型消能梁段的翼缘强度、长度和塑性转角关系如图17所示。提高翼缘强度将增大构件翼缘对腹板的约束作用，并增大子框架的变形能力和塑性转角。另外，考虑翼缘强度时，所得塑性转角最小值为0.13，大于规范值0.08。
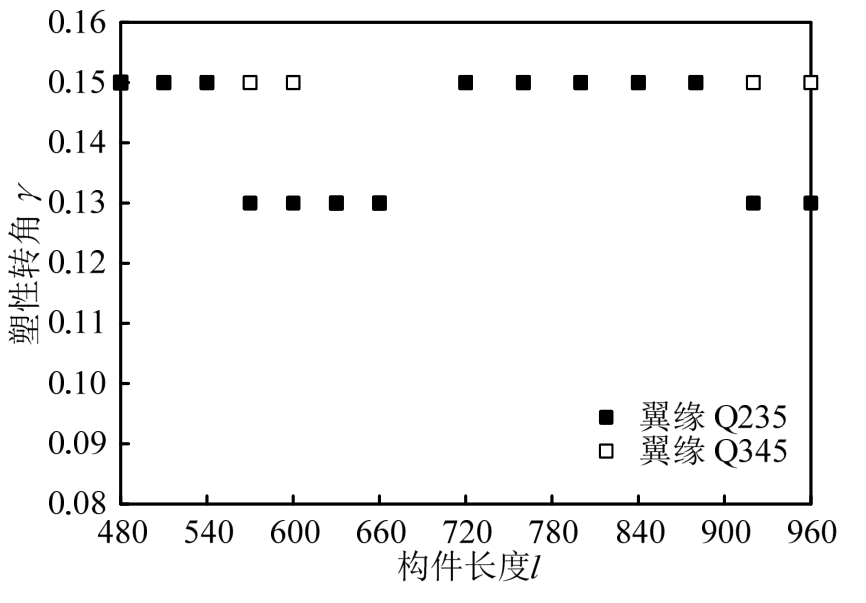
图17 短剪切型消能梁段翼缘强度、长度和塑性转角关系
Fig.17 Relationship between flange strength, length and inelastic rotation for short shear links
尽管增大翼缘强度可提高翼缘对腹板的约束作用，但对超强系数和塑性转角的提高能力有限，且对翼缘和腹板采用不同强度钢材，会增加施工难度。因此，对于短剪切型消能梁段，设计时仍建议采用腹板与翼缘等强度。
对H h×200×tw×14截面，h是截面高度，tw是腹板厚度，下同。长度分别取480 mm、540 mm、600 mm和 660 mm，各长度下 tw分别取 10 mm、9 mm和8 mm；对H h×330×tw×22截面，长度分别取720 mm、800 mm、880 mm和960 mm，各长度下tw分别取14 mm、13 mm和12 mm，共设计24个模型，以考虑跨高比对构件性能的影响。所有腹板、翼缘和加劲肋均采用Q235钢材。每个长度下所对应的三个模型的腹板面积相等，以保证各截面具有相同的塑性剪力，但截面高度的变化会影响其长度比和跨高比。
往复荷载下，短剪切型消能梁的跨高比、长度比和超强系数关系如图18所示。对相同塑性剪力和长度的模型，由跨高比引起的长度比变化对其超强系数的影响不大。对于相同长度和不同截面的短剪切型消能梁段，由于端弯矩较小，端部翼缘的屈曲后于腹板的屈曲，且腹板面积、加劲肋和翼缘截面均相同，在腹板完全屈服后翼缘和加劲肋所能达到的塑性弯矩也相等，使得该类构件产生相同的极限剪力和超强系数。
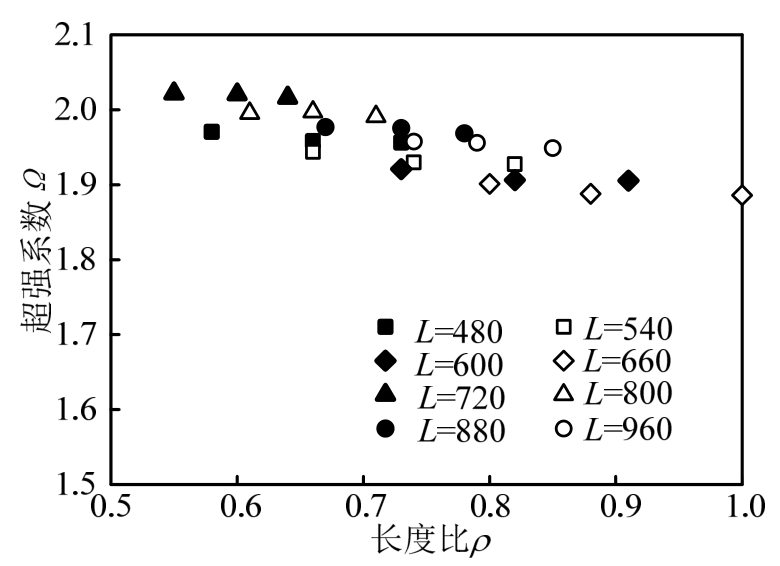
图18 短剪切型消能梁的跨高比、长度比和超强系数关系
Fig.18 Relationship between ratio of length and depth, length ratio and overstrength coefficient for short shear links
往复荷载下，短剪切型消能梁的跨高比、长度比和塑性转角关系如图19所示。对相同塑性剪力和长度的模型，由跨高比引起的长度比变化对其塑性转角无明显影响。因此，改变跨高比对构件力学性能无明显影响。由于增大跨高比可提高构件的塑性模量和抗弯承载力，设计时宜尽量提高其跨高比。
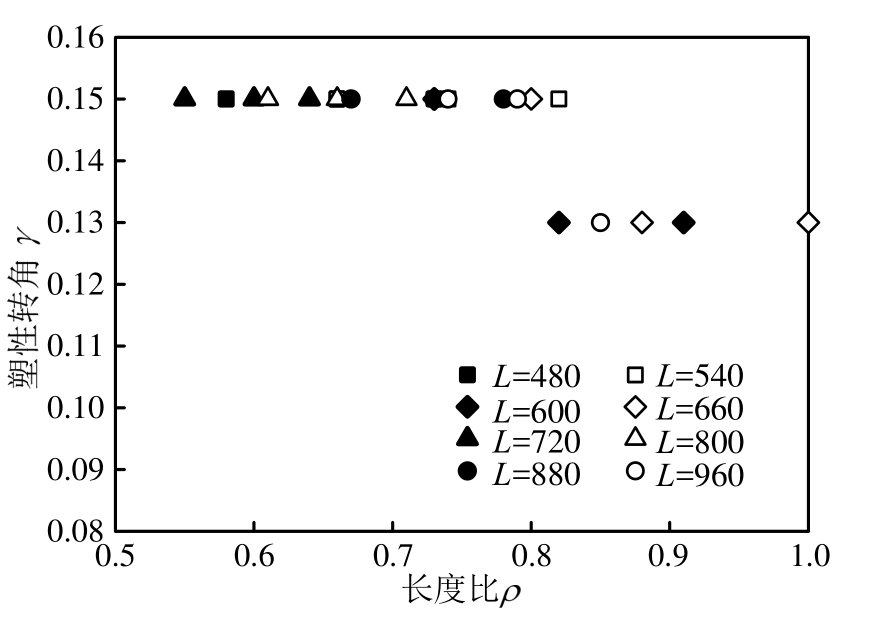
图19 短剪切型消能梁的跨高比、长度比和塑性转角关系
Fig.19 Relationship between ratio of length and depth, length ratio and inelastic rotation for short shear links
对考虑加劲肋间距、翼腹比、翼缘强度和跨高比等多种因素影响的短剪切型消能梁段的超强系数进行总结，如图20所示。当加劲肋间距系数小于 30时，考虑多种因素影响下构件的超强系数最小值为1.90，平均值为1.95；对加劲肋间距系数放宽至 40时，其超强系数最小值为 1.70，平均值为1.75，均大于规范值1.50。
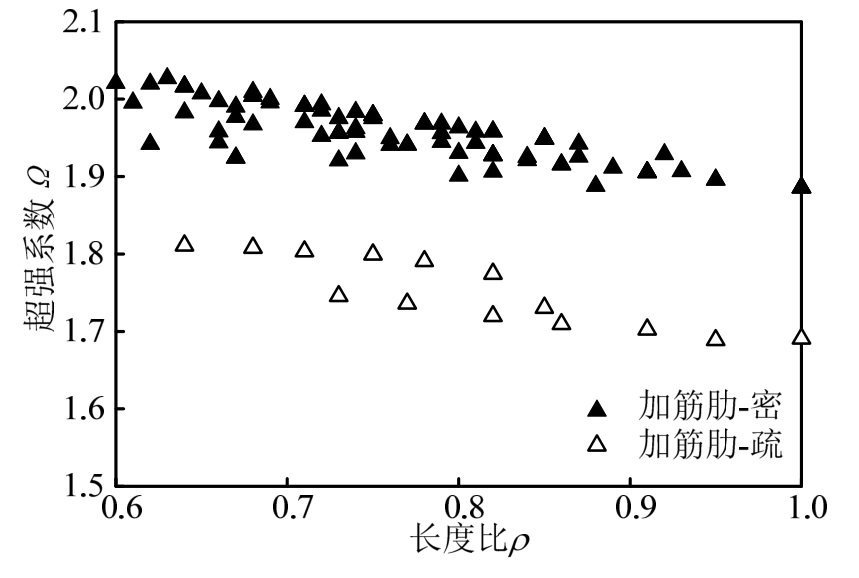
图20 短剪切型消能梁的长度比和超强系数关系图
Fig.20 Length ratio versus overstrength coefficient for short shear links
另外，考虑多种因素影响时短剪切型消能梁段的长度比与塑性转角关系如图21所示。从图中可知，长度比和加劲肋间距是影响其塑性转角的主要因素。当加劲肋间距系数满足规范要求时，考虑多种因素影响下构件的塑性转角最大值为 0.15，最小值为0.13；放宽加劲肋间距系数至40时，其塑性转角最大值为0.13，最小值为0.11，大于规范值0.08。
基于以上研究可知，当加劲肋间距系数满足要求时，其超强系数和塑性转角分别取1.90和0.13；当放宽加劲肋间距系数至 40时，其超强系数和塑性转角分别取1.70和0.11。因此，考虑多种因素影响时短剪切型消能梁段的力学性能与普通剪切型消能梁段有较大差异。
图21 短剪切型消能梁的长度比和塑性转角关系
Fig.21 Length ratio versus inelastic rotation for short shear links
基于加劲肋间距、翼腹比、翼缘强度和跨高比等因素对短剪切型消能梁段力学性能的影响分析，可得到以下结论：
(1)放宽加劲肋间距会降低短剪切型消能梁段的超强系数和塑性转角，但仍高于规范值。对短剪切型消能梁段，其加劲肋间距系数可放宽至40。
(2)短剪切型消能梁段的翼缘宽厚比限值可放宽至
。另外，增大翼腹比可提高翼缘对腹板的约束能力和子框架的承载和变形能力，构件设计时宜尽量增大翼缘面积。
(3)翼缘强度的提高仅能小幅增大短剪切型消能梁段超强系数和塑性转角，建议翼缘与腹板采用等强度钢材；跨高比对其性能无明显影响，但满足规范要下可尽量增大截面高度，以提高消能梁段和非消能梁段的抗弯承载力。
(4)对加劲肋间距系数满足规范要求的短剪切型消能梁段，其超强系数和塑性转角建议分别取1.90和0.13；当放宽加劲肋间距系数至40时，其超强系数和塑性转角分别取1.70和0.11。
参考文献：
[1]Kasai K, Popov E P. Cyclic web buckling control of shear link beams [J]. Journal of Structural Engineering,ASCE, 1986, 112(3): 505―523.
[2]杨文侠, 顾强, 宋振森, 等. Y形偏心支撑钢框架的地震反应折减系数和超强系数[J]. 工程力学, 2012,29(10): 129―136.Yang Wenxia, Gu Qiang, Song Zhensen, et al.Response modification factor R and overstrength factor of Y-eccentrically braced steel frames [J]. Engineering Mechanics, 2012, 29(10): 129―136. (in Chinese)
[3]Azad S K, Topkaya C. A review of research on steel eccentrically braced frames [J]. Journal of Constructional Steel Research, 2017, 128: 53―73.
[4]McDaniel C C, Uang C M, Seible F. Cyclic testing of built-up steel shear links for the new bay bridge [J].Journal of Structural Engineering, 2003, 129(6): 801―809.
[5]Dusicka P, Itani A M, Buckle I G. Cyclic behavior of shear links of various grades of plate steel [J]. Journal of Structural Engineering, ASCE, 2010, 136(4): 370―378.
[6]Hu S J, Wang Z. Study of an optimum design method for links [J]. Open Civil Engineering Journal, 2014, 8(1):335―343.
[7]连鸣, 苏明周, 李慎. Y形高强钢组合偏心支撑框架结构基于性能的塑性设计方法研究[J]. 工程力学, 2017,34(5): 148―162.Lian Ming, Su Mingzhou, Li Shen. Performance-based plastic design method for Y-type high strength steel composite eccentrically braced frames [J]. Engineering Mechanics, 2017, 34(5): 148―162. (in Chinese)
[8]GB 50010―2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50010―2010, Code for seismic design of buildings[S]. Beijing, China Architecture & Building Press, 2010.(in Chinese)
[9]AISC 341―10, Seismic provisions for structural steel buildings [S]. Chicago, Illinois: American Institute of Steel Construction, 2010.
[10]Okazaki T, Engelhardt M D. Cyclic loading behavior of EBF links constructed of ASTM A992 steel [J]. Journal of Constructional Steel Research, 2007, 63(6): 751―765.
[11]纪晓东, 马琦峰, 王彦栋, 等. 钢连梁可更换消能梁段抗震性能试验研究[J]. 建筑结构学报, 2014, 35(6): 1―11.Ji Xiaodong, Ma Qifeng, Wang Yandong, et al. Cyclic tests of replaceable shear links in steel coupling beams[J]. Journal of Building Structures, 2014, 35(6): 1―11.(in Chinese)
[12]Mohebkhah A, Chegeni B. Overstrength and rotation capacity for EBF links made of European IPE sections[J]. Thin-Walled Structures, 2014, 74(3): 255―260.
[13]Richards P W, Uang C M. Effect of flange width-thickness ratio on eccentrically braced frames link cyclic rotation capacity [J]. Journal of Structural Engineering, 2005, 131(10): 1546―1552.
[14]胡淑军, 王湛. 翼缘宽厚比对耗能梁性能的影响研究[J]. 中南大学学报(自然科学版)，2015, 46(9): 3405―3414.Hu Shujun, Wang Zhan. Influence of flange width-thickness ratio on behavior of links [J]. Journal of Central South University (Science and Technology),2015, 46(9): 3405―3414. (in Chinese)
[15]Shi Y J, Wang M, Wang Y Q. Experimental and constitutive model study of structural steel under cyclic loading [J]. Journal of Constructional Steel Research,2011, 67(8): 1185―1197.
[16]Corte G D, Aniello M D. Analytical and numerical study of plastic overstrength of shear links [J]. Journal of Constructional Steel Research, 2013, 82(2): 19―32.
[17]AISC 341―02. Seismic provisions for structural steel buildings [S]. Chicago, Illinois: American Institute of Steel Construction, 2002.
STUDY OF MECHANICAL PROPERTIES AND ITS INFLUENCE FACTORS FOR SHORT SHEAR LINKS
HU Shu-jun1,2, XIONG Jin-gang1,2, WANG Zhan3
(1. School of Civil Engineering and Architecture, Nanchang University, Nanchang, Jiangxi 330031, China;2. Jiangxi Provincial Engineering Laboratory of Nearly Zero Energy Building, Nanchang, Jiangxi 330031, China;3. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou, Guangdong 510640, China)
Abstract:Recent researches on the performance of short shear links with length ratio smaller than 1.0 have shown that the overstrength and inelastic rotation are much greater than the requirements of current specification.In order to re-evaluate the mechanical properties of short shear links, an analytical study is conducted to investigate the influence factors on the overstrength and inelastic rotation, which are based on the material properties of Q235 and Q345 steel. Finite element models are verified by comparison of theoretical results with experiments results, which are then used to investigate the performance of 108 short shear links, including the stiffener spacing, flange to web area ratio, flange strength and link length to depth ratio. The results indicate that the overstrengh coefficient and inelastic rotation of short shear links can reach 1.90 and 0.13 respectively.Furthermore, the normalized stiffener spacing and flange width-thickness ratio can be relaxed to 40 and
. Increase of the flange to web area ratio can effectively improve the short shear link strength after the web is fully yielded in shear, but the flange strength and link length to depth ratio have very limited difference on the behavior of short shear links.
Key words:short shear links; stiffener spacing; flange width-thickness ratio; overstrength coefficient; inelastic rotation
中图分类号：TU352.11
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.04.0306
文章编号：1000-4750(2018)08-0144-10
收稿日期：2017-04-24；修改日期：2017-08-06
基金项目：国家自然科学基金项目(51378219，51768044)；江西省博士后科研择优资助项目(2015KY49)；江西省自然科学基金项目(20161BAB216114)
通讯作者：熊进刚(1970―)，男，江西人，教授，博士，主要从事结构抗连续性倒塌、结构优化等方面研究(E-mail: xiongjingang@ncu.edu.cn).
作者简介：
胡淑军(1985―)，男，江西人，讲师，博士，主要从事钢结构消能减震技术、结构优化等方面研究(E-mail: hushujun@ncu.edu.cn);
王 湛(1958―)，男，广东人，教授，博士，主要从事钢结构、组合结构和结构优化等方面的研究(E-mail: wangzhan@scut.edu.cn).