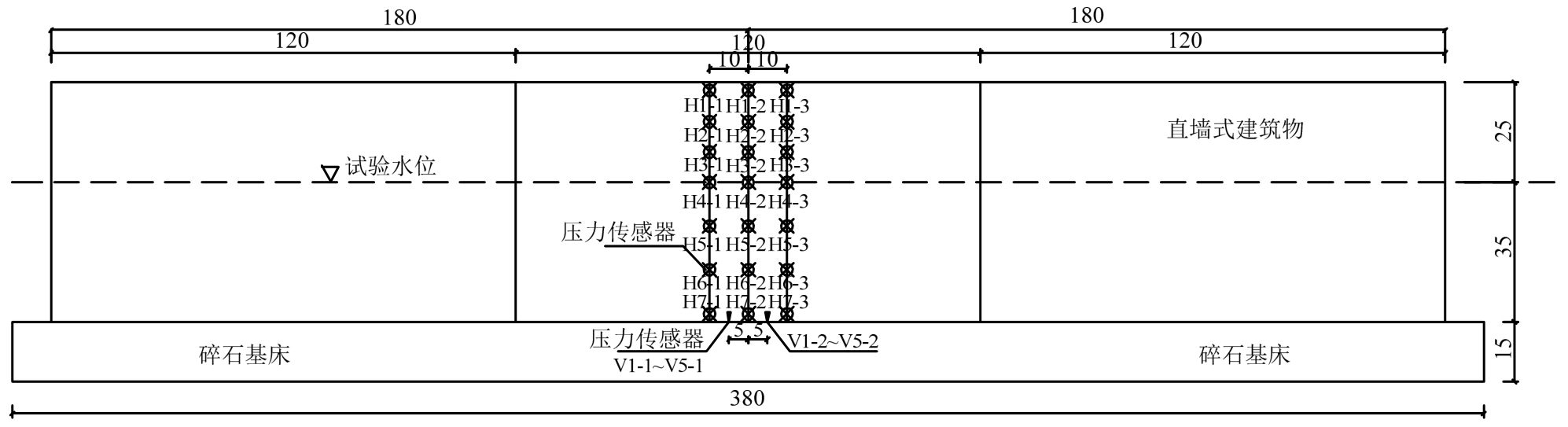
图1 波压力传感器在防波堤立面上的布置 /cm
Fig.1 Wave pressure sensors layout on the elevation of breakwater
王浩霖1,张华昌2,董 胜1
(1.中国海洋大学工程学院,山东,青岛 266100;2.海军工程设计研究院工程综合试验研究中心,山东,青岛 266100)
摘 要:为了研究在不同入射波向时直立堤上的波压力,基于FLOW-3D,该文建立了三维数值波浪水池,并进行了物理模型试验。模型采用推板造波及孔隙消波的方法形成稳定的波浪场,数值模拟结果与试验结果吻合较好。研究表明:墙面测点的波压力与波吸力均随入射角度的增大而增大;墙底各测点浮托力的变化规律较为复杂,合田公式不能准确描述;墙面波压力的分布与合田公式基本相符;墙底浮托力的分布并不是合田公式描述的三角形,而是近似梯形分布;斜向波作用下的墙面波吸力分布图相似于正向入射时的分布。研究结论可为防波堤设计提供参考依据。
关键词:海岸工程;数值波浪水池;直立堤;斜向波;波压力;合田公式;FLOW-3D
防波堤是保护沿海地区免遭潮、浪袭击的重要工程措施,防波堤的破坏将导致严重的后果。直立堤是防波堤中的重要结构型式。由于直立堤消浪差,所受波浪力较大,为确保其安全,故应对其所受波浪力进行研究,以确定合理的设计方案。目前设计直立堤时,多按单向波正向击堤时计算波浪力[1]。但在自然界中,波浪常斜向击堤。对于斜向波与建筑物的相互作用,Goda[2]在其提出的公式中考虑了波浪入射角的影响,计算得到波浪力随波向角增大而单调减小;Battjes[3]基于线性理论给出了斜向波作用时单元堤上的水平波浪力沿单元堤纵向折减系数的计算公式;Fenton[4]基于Hsu短峰波理论,提出了作用在直墙上的波浪力和力矩的改进三阶公式,并经过数值计算,认为作用在直墙上的最大波浪力是由斜向波产生的;Franco等[5]通过分析波浪对直堤的试验研究,认为作用在直堤上的总波浪力随波向角的增大而减小,并指出在长峰波情况下,当入射角小于40°时,合田公式能较好的预测单位堤长上波浪力随角度的变化,且直墙上波压力的分布形状基本不随波向角的变化而变化;Madrigal[6]通过分析深水非破碎海域中斜向和多向波对沉箱防波堤作用的试验研究,指出在入射角小于40°时,单位堤长上的波浪力随波向角的增大而增大,而若考虑单元堤长度影响,则堤上总波力以正向入射时最大;Tzang和Liaw[7]在Fenton短峰波近似理论的基础上研究了正向及45°斜向波与直立堤的相互作用,证实最大波压力并不出现在正向入射时,并提出了一种用于深水直立堤的短峰波力计算模型;李玉成等[8―9]通过斜向规则波或斜向不规则波与直墙相互作用的实验研究,分别给出了每延米及考虑单元堤长时的斜向波浪力与正向力之比的折减系数,并得出斜向波的反射系数和正向波时相同;俞聿修等[10]试验得出实测斜向波作用于直立堤上的单位堤长波力在规则波和波陡较小的不规则波时随入射角的增大而增大,且常在45°时达最大值;李本霞等[11]通过斜向随机波与直立堤相互作用的试验研究,讨论了直立堤上波浪力与波浪入射角度、单元堤长等因素的关系,并总结出了波浪力纵向分布系数和折减系数与相对堤长的关系式;胡金鹏等[12]通过试验和数值模拟得出任意波向下单位堤长波浪力随相对波高的增大而增大,且波浪力与波高不成线性关系;陈汉宝[13]通过试验对合田公式及《港口与航道水文规范》中的波浪力计算公式进行了修正,通过数值模拟得出建筑前的最大波高随入射角的增大而减小,并经分析后得出波浪入射角度与建筑物相对长度是影响波浪力的两个重要因素。除上述论述外,近年来如Liu[14]、Mandal[15]、Umeda[16]等诸多学者对斜向波做了多方面研究,丰富了斜向波的理论及工程应用体系。
随着计算机技术的发展,利用CFD技术建立数值水槽成为研究波浪与海上结构物相互作用的重要手段。Lin等[17]提出了基于N-S方程,将附加质量源添加到连续方程的质量源造波方法,并对规则波与不规则波进行了模拟;李宏伟[18]基于Fluent研究了仿物理造波及纯数值造波技术,探讨了三维数值波浪水池的构建及斜向波的生成;张博杰和张庆河[19]基于OpenFOAM,采用质量源造波及阻尼消波的方法,结合VOF法建立了二维无反射数值波浪水槽,较好地模拟了行进波和立波;丁阳等[20]利用FLOW-3D软件,采用质量源造波及海绵层消波的方法建立三维波流数值水槽,能够形成稳定的波流场用于研究波流对结构的联合作用;马小舟等[21]应用完全非线性Boussinesq方程数值模型,研究了不规则波浪在缓坡潜堤上传播时非线性参数的变化;唐晓成等[22]应用修正SPH数值方法研究了波浪与开孔沉箱相互作用时的动应力响应问题。
本文在物理试验的基础上,基于FLOW-3D软件建立了三维数值波浪水池,采用推板造波及孔隙消波的方法实现稳定的波浪场,并通过改变堤轴线来实现不同入射角度波浪与直立堤的相互作用,进而研究堤面及堤底波浪力的变化规律。采用物理模型试验对数模结果进行验证,结果吻合较好。
试验在海军工程设计研究院工程综合试验研究中心的长59 m、宽37 m、深1.2 m的室内水池中进行。水池装有“L”型造波机,能产生多向不规则波和规则波,造波范围涵盖180°。造波机推板单宽0.5 m,两侧造波总宽度分别为30m和26 m。采用DS-30系统测量波高和波压力,采样间隔为0.012 s,可以满足试验数据的采集及处理需求。
试验模型比尺为50。试验模型的直墙部分用铁板制作,总长度360cm,分为三段,每段长120cm、宽30cm、高60cm。碎石基床采用级配块石(块石原型重量10kg~100kg)。块石筛选时,先用水冲洗保证碎石的干净,从而保证其透水性良好,再保证不同重量范围块石的数量,从而保证碎石的级配。
压力传感器安装在模型的中间位置,距离模型两端约180cm。模型垂直墙面上安装了3列、7排共计21个测点,每排三个测点代表一个测量位置,自上而下测量位置以H1~H7命名,其中H4位于水位线上。模型底部安装了2列、5排共计10个测点,自前而后以V1~V5命名。波压力传感器在防波堤立面上和横断面的布置分别如图1和图2所示。

图1 波压力传感器在防波堤立面上的布置 /cm
Fig.1 Wave pressure sensors layout on the elevation of breakwater
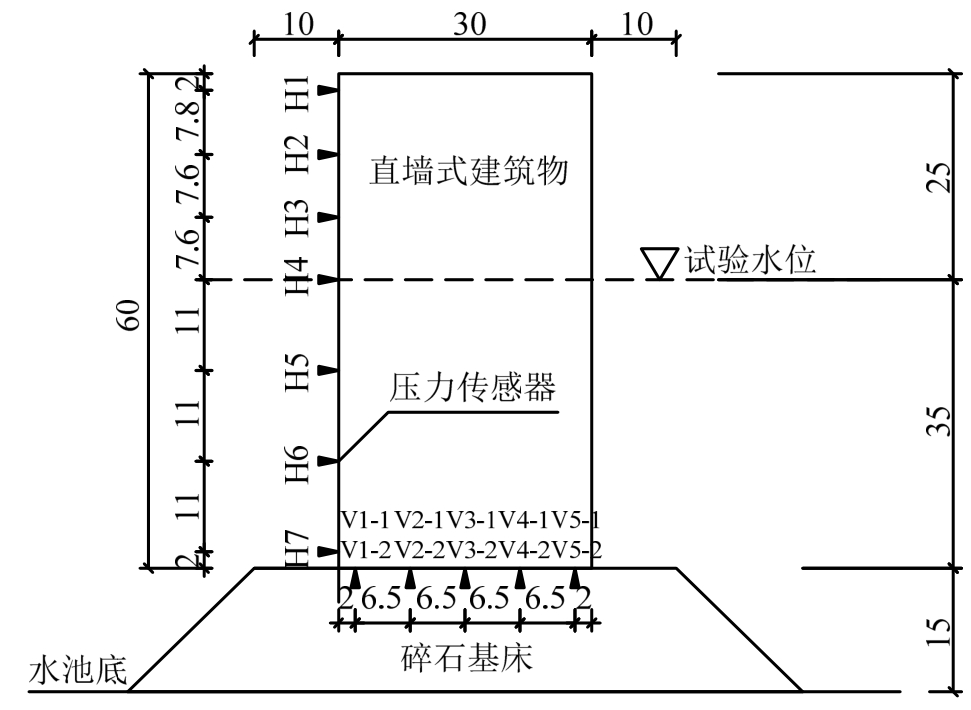
图2 波压力传感器在防波堤横断面上的布置 /cm
Fig.2 Wave pressure sensors layout on breakwater cross section
建筑物模型放置在各方向波浪共同的有效作用区域内,建筑物距两有效边界各为2 m左右,周边放置消波结构。模型在水池内的平面布置情况如图3所示,试验布置实况如图4所示。
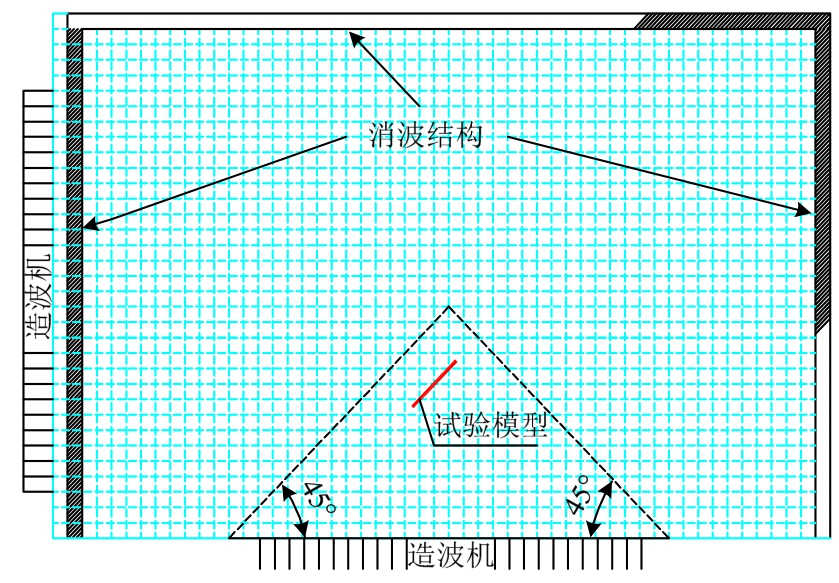
图3 试验模型在水池中的布置 /m
Fig.3 Arrangement of physical model in wave basin

图4 试验布置实况
Fig.4 Layout of experiment
试验水深d=0.5 m,试验采用规则波,波高H=0.1 m,周期T=1.7 s。试验中入射波向包括10个,分别与建筑物直墙面成0°~90°(本文中入射波与建筑物的夹角均指墙面与波向线间的夹角),各方向波浪要素相同。
造波时,待堤处波况平稳后,开始采集波面和波压力数据,规则波的采样间隔为0.012 s。试验时每个工况重复5~6遍,以各试验工况的平均值作为最终结果。试验过程中,各试验工况均不发生越浪。
数值建模采用连续性方程和不可压缩黏性流体运动的Navier-Stokes方程作为流体运动的控制方程。连续性方程为:
动量方程为:
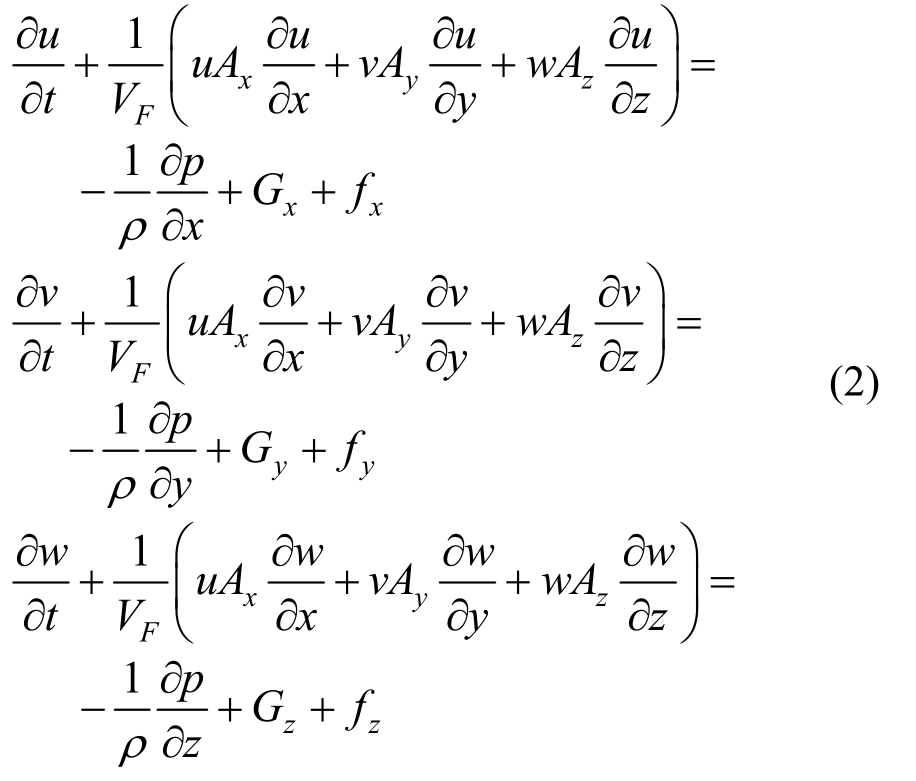
式中:ρ为流体密度;p为压力;u、v、w为对应x,y,z方向的速度分量;Ax、Ay、Az和VF分别为与FLOW-3D中FAVOR网格技术相关的x、y、z方向可流动的面积分数和可流动的体积分数;Gx、Gy、Gz为物体在x、y、z三个方向的重力加速度;fx、fy、fz为x、y、z方向的黏滞力加速度。
本文所建立的三维数值波浪水池要模拟波浪与建筑物的相互作用,波浪会出现剧烈的变形破碎,因此采用RNGk-ε模型作为湍流模型效果较好。湍动能kT和其耗散率εT的方程表达式如下:
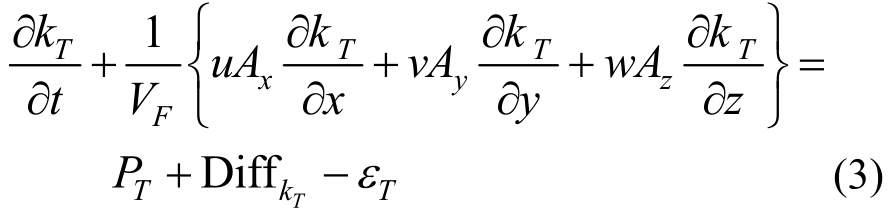
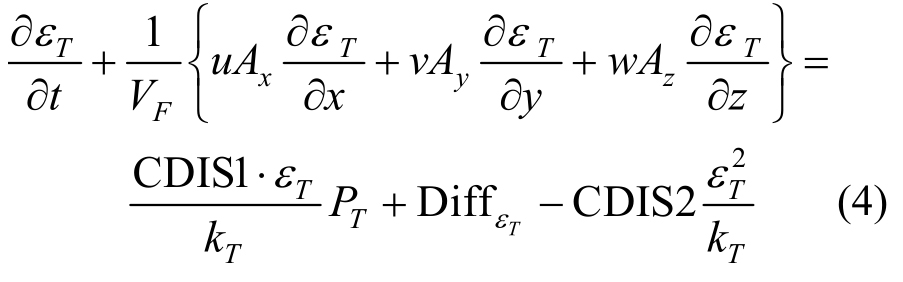
式中:PT为剪切效应引起的湍动能产生项;DiffkT和DiffεT为扩散项;CDIS1和CDIS2为模型参数。
为了与试验条件相一致,本文采用推板造波的仿物理造波法。通过在数值水池一端添加一GMO(general moving object)模型组分模拟推板。根据朱萍等[23]对造波机参数的研究,确定推板参数与波浪要素之间的关系,即目标波高H与行程S之比为:
式中:k为波数,即k=2π/L,L为波长;d为水深。推波板做来回往复直线运动时的速度表达式为:
式中:ω=2π/T为波浪的圆频率。据此,在FLOW-3D的用户子程序mvbvel_usr.f中通过添加推板运动的表达式来实现规则波的模拟。
数值水池的消波采用孔隙结构进行处理。水流遇到孔隙结构会发生紊动,能量耗散巨大,从而产生消波效果。文献[24]建议选取孔隙率为0.8,斜坡坡度为1∶3,材料粒径为0.1 m,高为1 m的斜坡式孔隙结构作为消波设施,其结构形式如图5所示。

图5 孔隙结构示意图
Fig.5 Schematic diagram of pore structure
三维数值模型的边界条件如图6所示。使用推板造波及孔隙消波的方法,水池在x轴向上的两端(即前端和末端)设为壁边界;水池底面同样设为壁边界;在自由表面上压力需要满足动力学边界条件,ps=pa,pa为大气压,因此顶部设为压力边界;剩余两面设为对称边界,可避免波浪反射的影响。
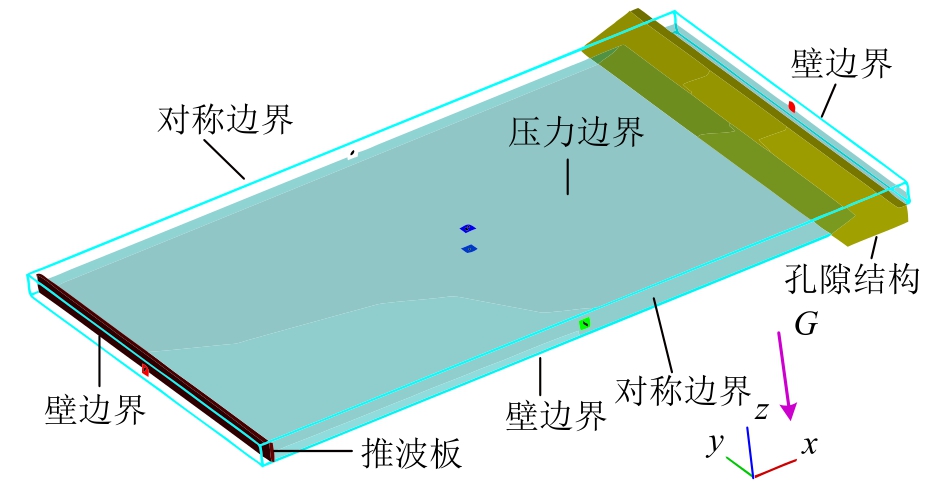
图6 边界条件示意图
Fig.6 Schematic diagram of boundary conditions
初始条件:在计算域内,压强设定为静水压强;添加一水深为0.5 m的流体区域,其范围设定为推板至水池末端;初始波面设为静水水面。
按照物理模型试验建立三维数值波浪水池,其两侧边界分别与模型的两端相距12 m;造波端与消波端的距离及数值水池的高与试验水池相同,分别为37 m和1.2 m。通过改变结构的轴线方向来实现波浪不同角度的入射。图7为波浪正向入射模型。
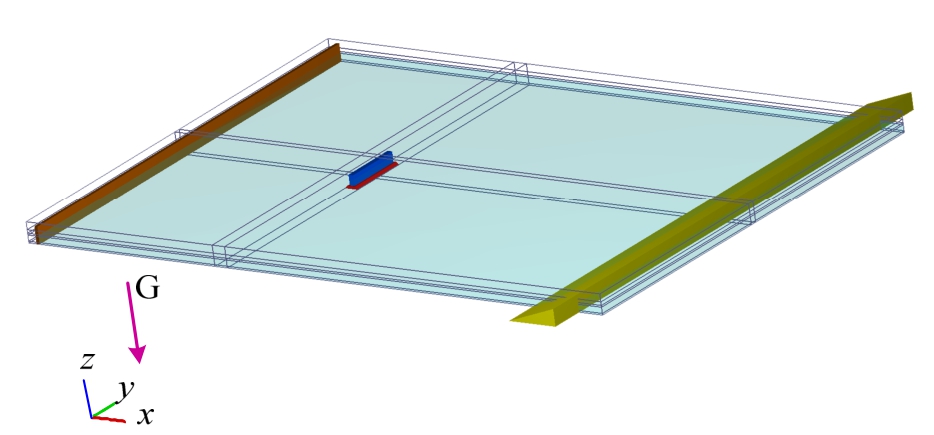
图7 模型示意图
Fig.7 Schematic diagram of model
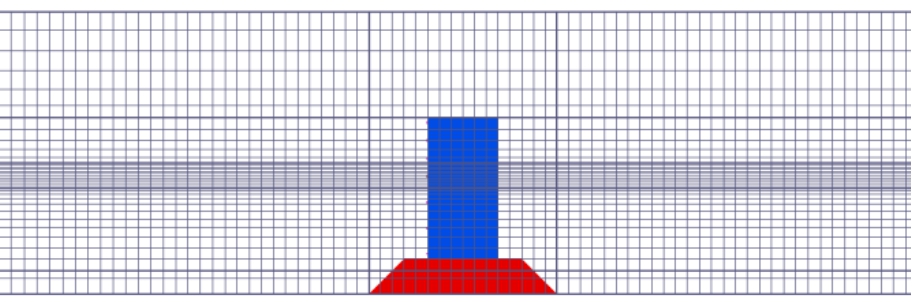
图8 模型网格划分示意图
Fig.8 Schematic diagram of model meshes
基于以上建立的三维数值波浪水池模型,以试验波浪要素对数值模型进行验证,将数值解与理论解进行比较。
图9分别给出了无直立堤时距直立堤前一倍波长(x=L)和直立堤前(x=0)两个位置处的波面历时曲线。由图可见,与理论波面曲线比较,数值水池可以生成稳定的波浪,数值解与理论解吻合较好。
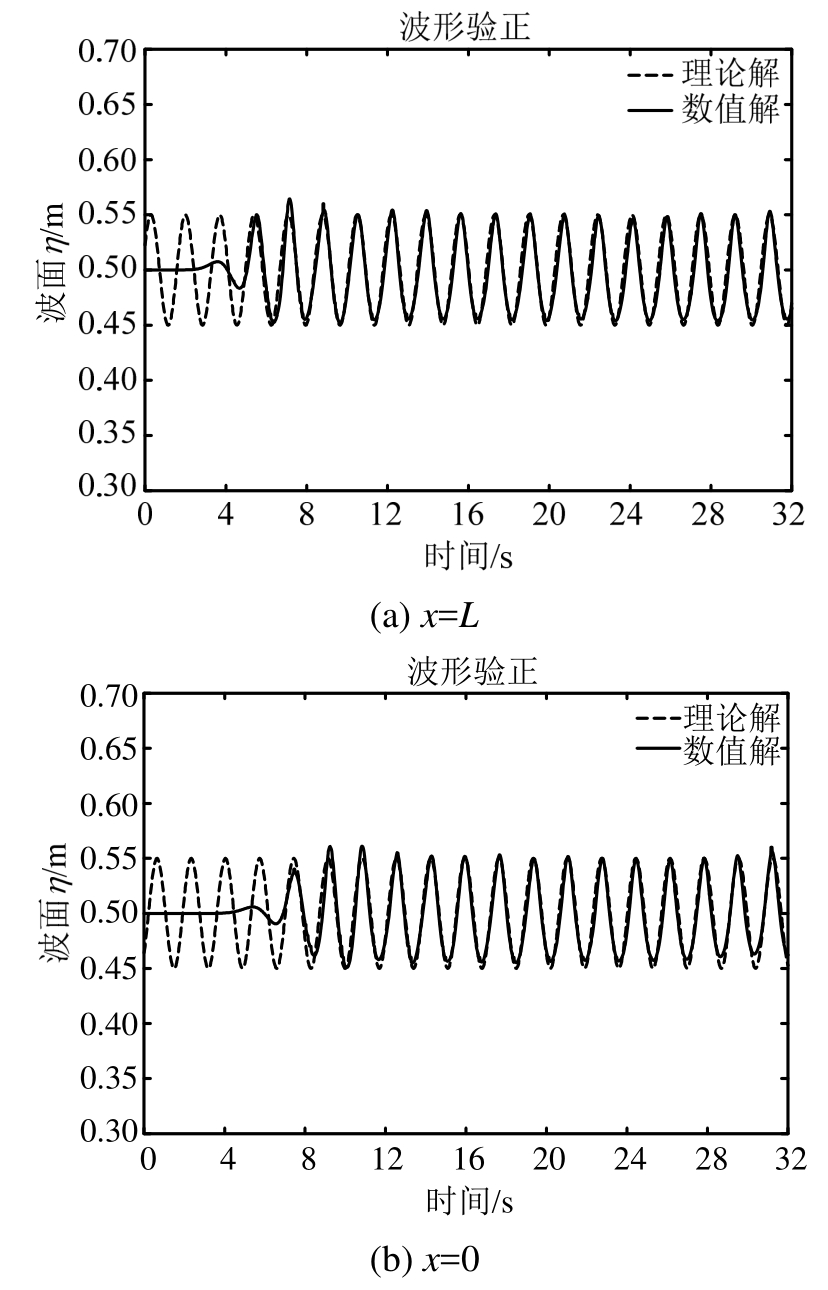
图9 不同位置处的波面历时曲线(无结构物)
Fig.9 Time series of wave surface at different locations(without structure)
图10给出了直立堤存在时的波面历时曲线,可见由于直立堤的存在使波浪的非线性增强。

图10 不同位置处的波面历时曲线(有结构物)
Fig.10 Time series of wave surface at different locations(with structure)
为了解各测量位置的波浪力随波向的变化规律,以及物模与数模结果的吻合情况,将各测点在不同方向波浪作用时的试验数据与数值结果绘制在同一图中。图中波浪力皆为动水压力,其中正值代表波压力,负值代表波吸力。由于H1、H2两点位于建筑物顶部,在所有工况中,波浪力值均较小甚至无波浪力产生,所以在分析中忽略不计。
由于考虑了斜向波的作用,在设计直立堤时,常用合田公式计算波压力。本文将数模、物模及合田公式的结果放在同一图中进行比较分析。
如图11和图12所示,数值计算各点波压力随波向的变化与试验结果吻合较好。由图11可知:①墙面各测点的波压力总体上随入射角度的增大而逐渐增大,0°时最小,90°时最大;②由合田公式计算的结果在总的变化趋势上与试验及数值结果相同,但其压力值普遍小于物模和数模的结果,说明合田公式在一定程度上低估了墙面波压力;③试验和数值结果不像合田公式随入射角单调增加,在某些角度压力值会发生突变,设计时要给予重视。
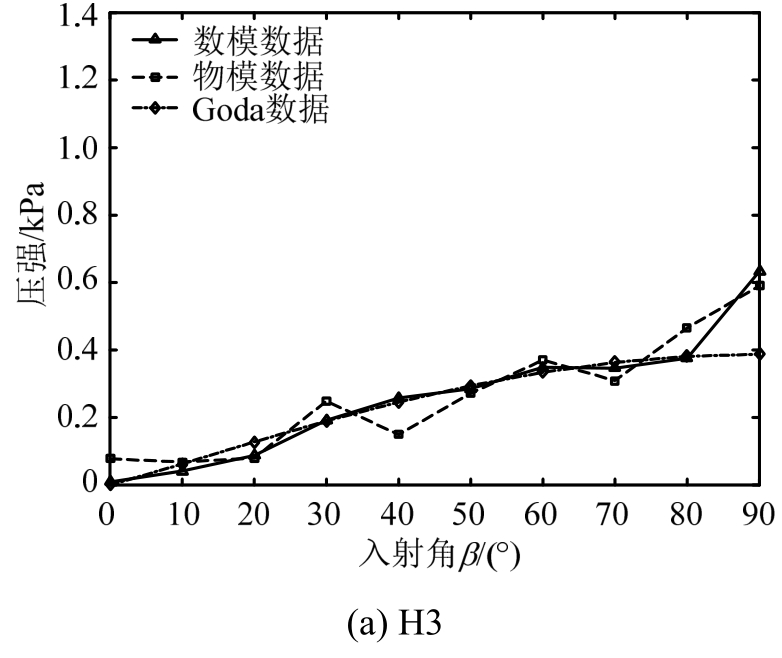
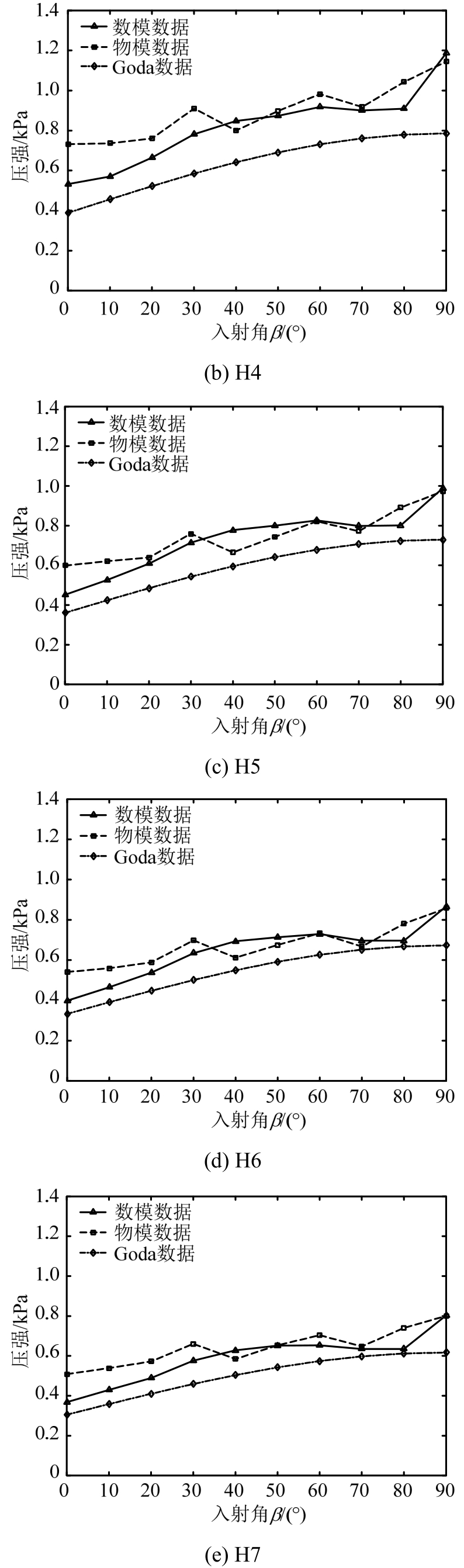
图11 墙面测点在不同方向波浪作用时的波压力分布曲线
Fig.11 Wave pressure distribution curve of measuring points on the wall in different wave directions
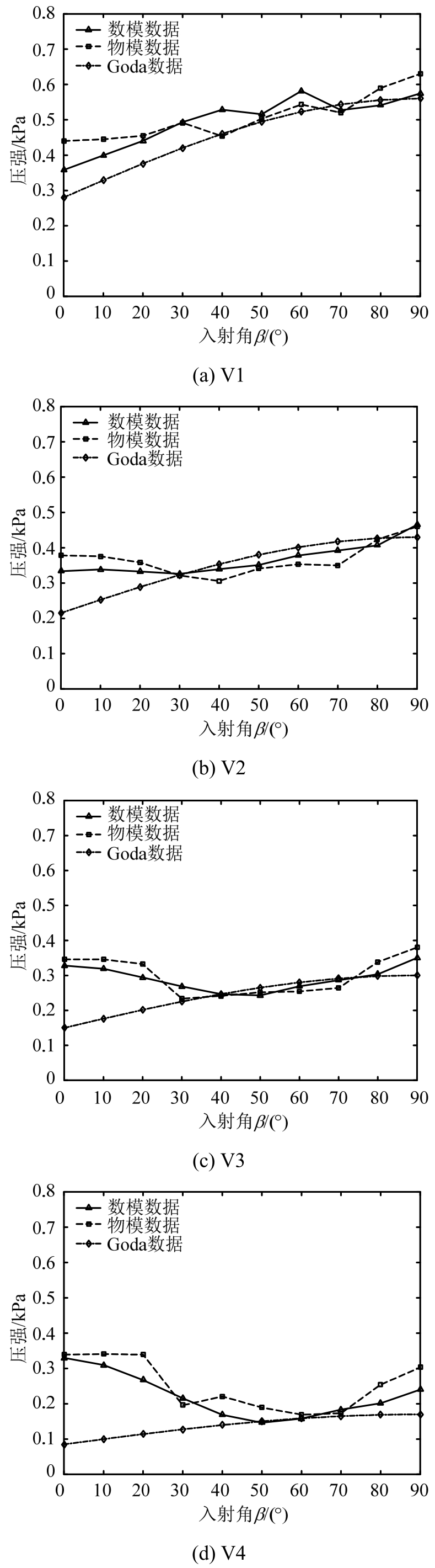
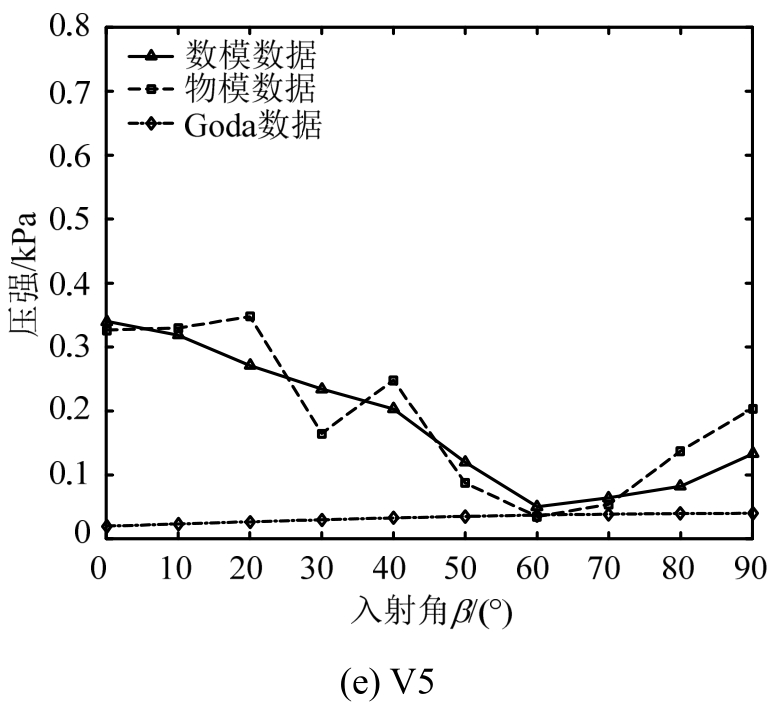
图12 墙底测点在不同方向波浪作用时的浮托力分布曲线
Fig.12 Uplifting pressure distribution curve of measuring points at bottom of the wall in different wave directions
对于墙底波压力即浮托力的变化规律,由图12可知:①墙底各点浮托力随入射角度变化的趋势并不相同,V1及V2两测点整体上呈逐渐增大的趋势,在90°时浮托力最大,但其余三点呈先减小后增大的趋势,测点V3在0°和90°时的浮托力大小相近,V4、V5两点的最大值均出现在0°时,后三测点在50°或60°时浮托力最小;②合田公式在测点V1处的变化趋势与试验和数值符合较好,但总体上其对墙底浮托力随入射角变化趋势的描述不符合试验及数值结果,说明按合田公式设计墙底浮托力时不够安全。
波吸力是由波谷作用于直立堤时产生的指向外海侧的负压力。合田公式不适用于求解波吸力,在此不再与之比较。在各种工况下,H3、H4两点处产生的波吸力较小,可忽略不计。其余测点随波向变化的波吸力曲线如图13和图14所示。
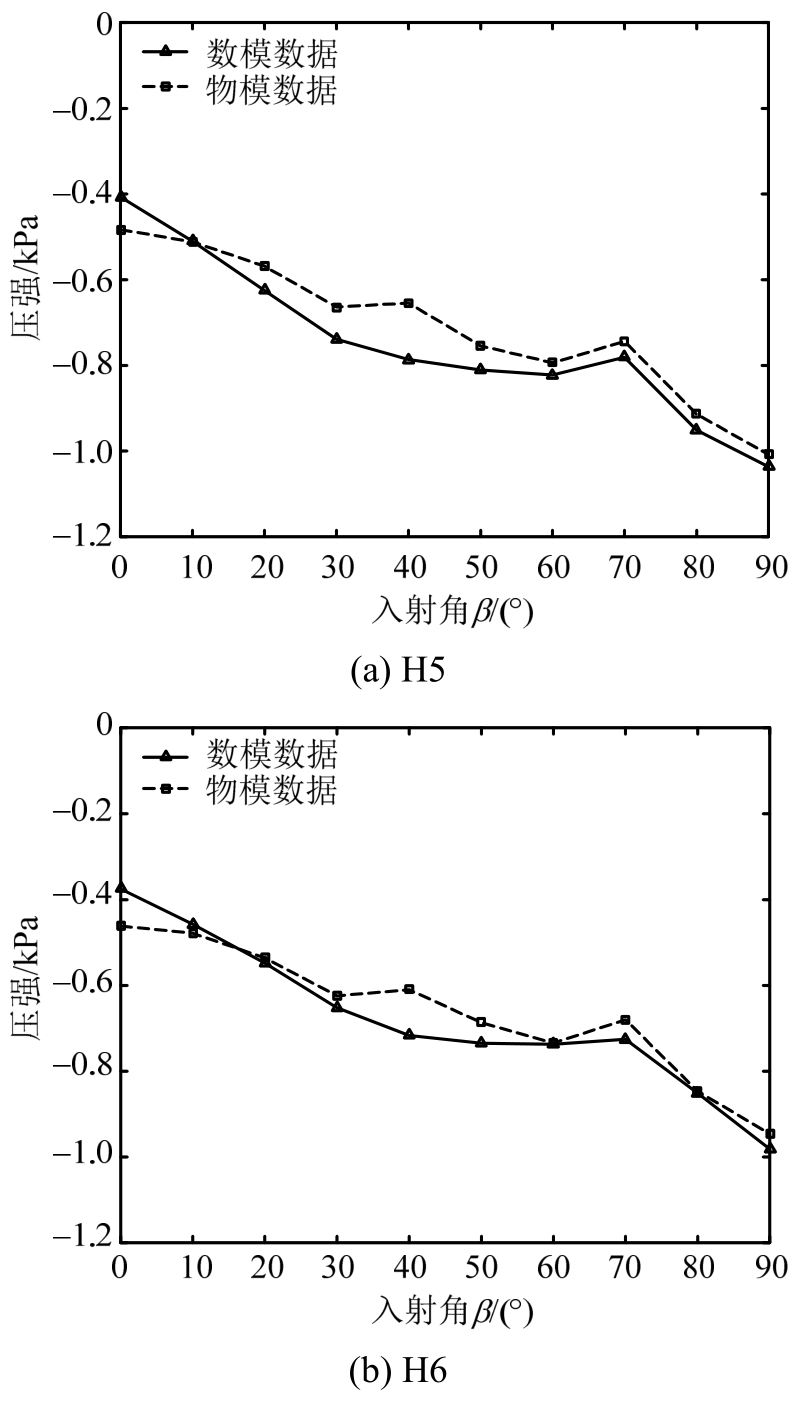
由图13可知,墙面各测点波吸力随波向变化的数值结果与试验结果吻合较好。①总体上,墙面各测点波吸力随入射角的增大而增大,0°时最小,90°时最大;②测点波吸力在70°时发生突变,产生较小的波吸力,在设计时要注意。
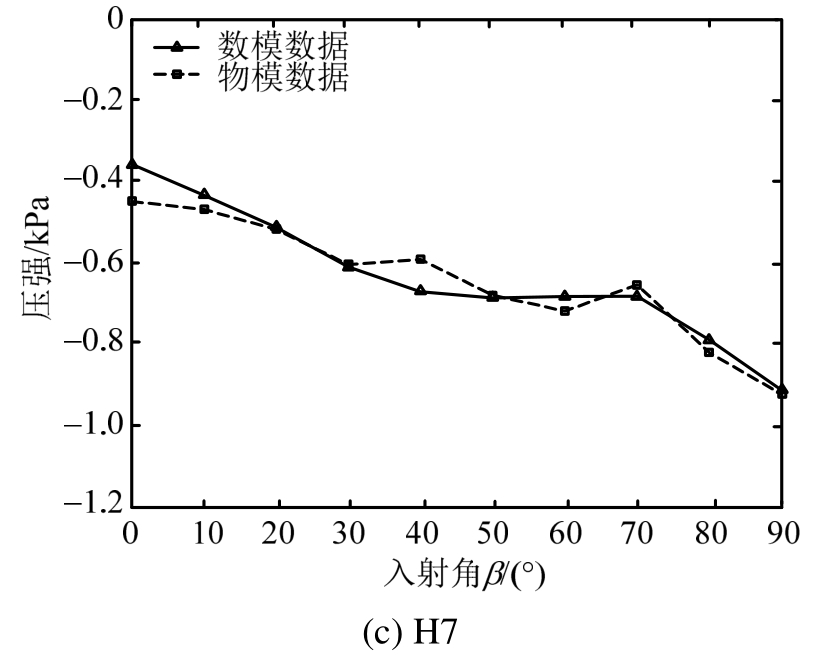
图13 墙面测点在不同方向波浪作用时的波吸力分布曲线
Fig.13 Negative wave pressure distribution curve of measuring points on the wall in different wave directions
由图14可知,数值计算的墙底测点波吸力的变化与试验结果的吻合程度不如墙面测点好。①V1、V2两点的变化趋势总体上与试验结果吻合较好,波吸力随入射角的增大而增大,90°时有最大值;②V3、V4两点试验结果的趋势是先减小后增大,0°与90°时的波吸力值相近,数值结果呈先增大后减小再增大的趋势,最大值出现在90°或40°时;③V5点的试验及数值结果在总趋势上呈“勺子”形变化,在20°或30°时波吸力最大。墙底波吸力试验与数值结果吻合稍差的可能性分析结果为:墙底各点受波浪绕射的影响,距迎浪面越远的点所受影响越大,绕射程度受到波向的影响;其次,试验中基床抛石粒径大小不一,而数值中基床颗粒按照均匀进行考虑。
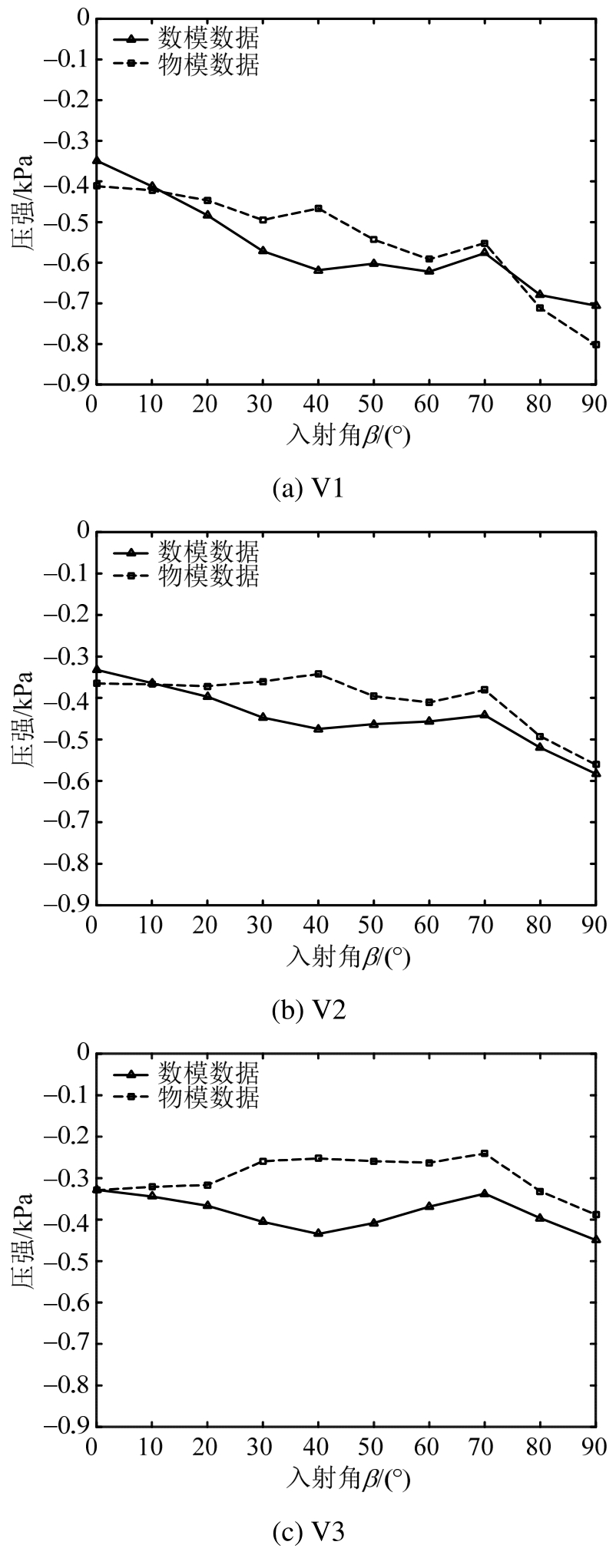
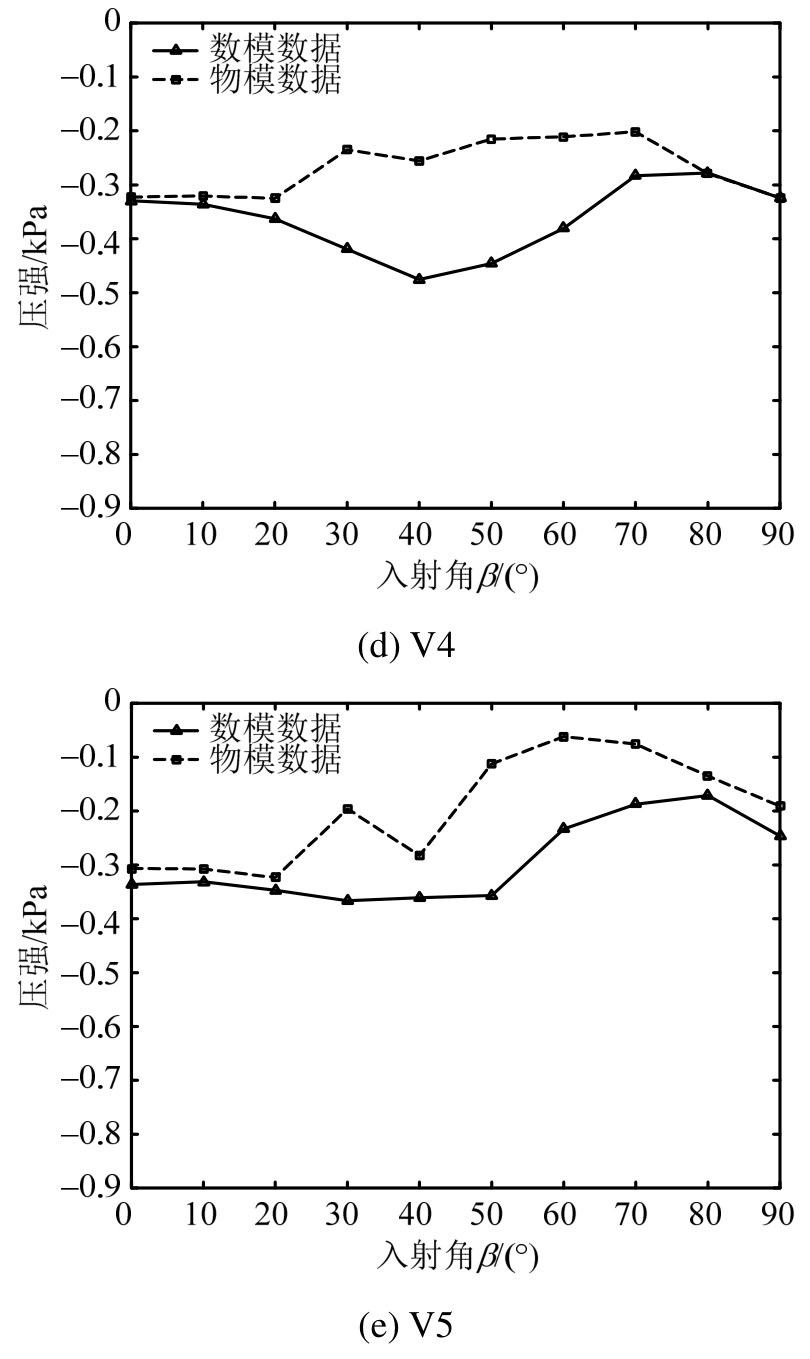
图14 墙底测点在不同方向波浪作用时的波吸力分布曲线
Fig.14 Negative wave pressure distribution curve of measuring points at bottom of the wall in different wave directions
由于篇幅所限,本文仅给出入射角为10°、60°及90°时试验和数值的波压力及波吸力分布图。如图15和图16所示,波压力及波吸力分布的试验与数值结果吻合较好。同时为了便于读者阅读,给出了10°工况时墙面及墙底的波压力分布示意图,如图17所示。
由图15可知,由试验和数值得到的墙面波压力的分布基本上与合田公式给出的图示相符,仅在量值上有一些差别;本文中墙底浮托力近似呈梯形分布,而不是合田公式表述的三角形分布。
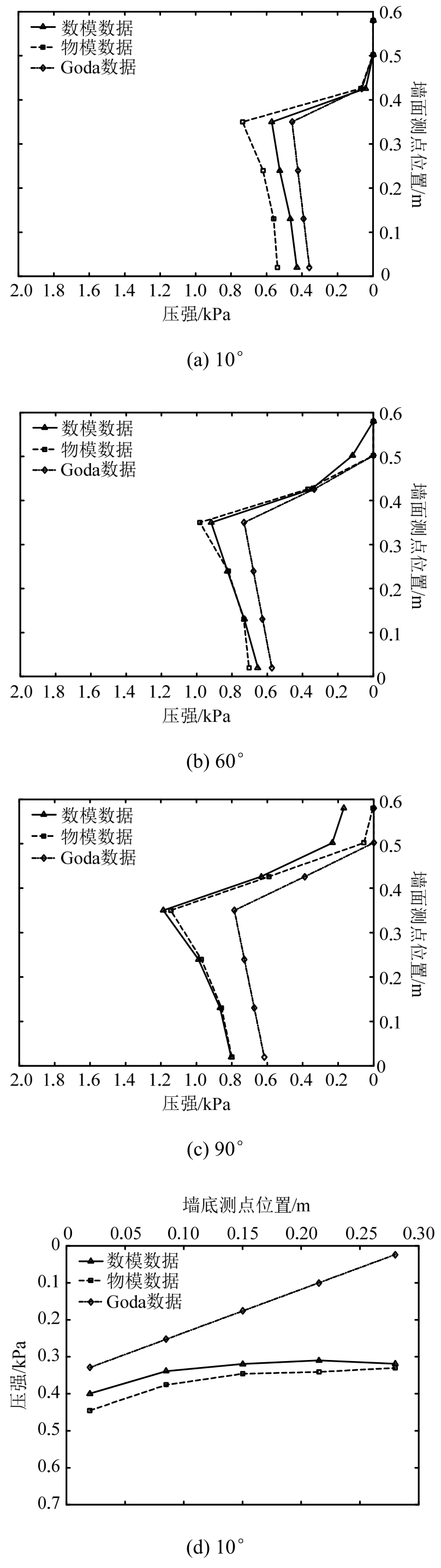
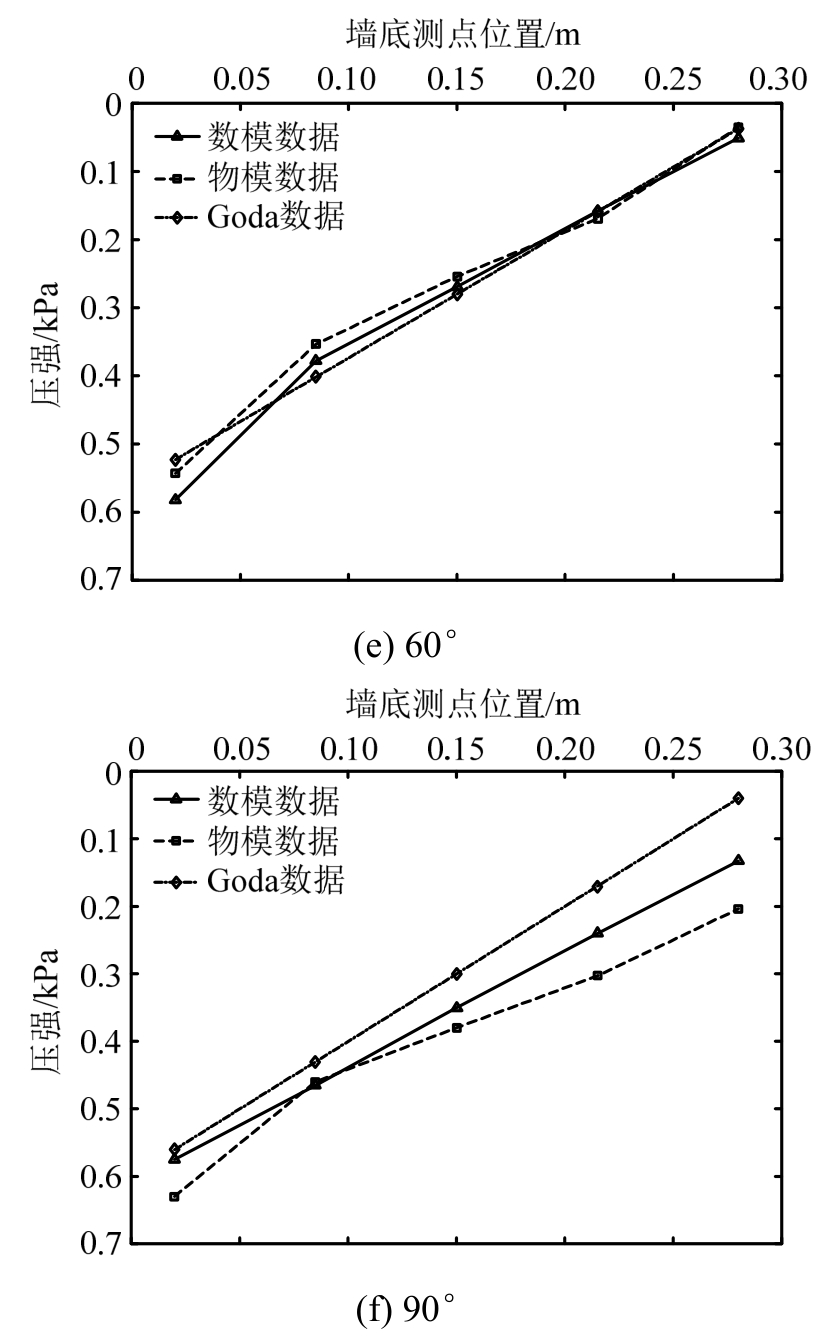
图15 波压力分布示意图
Fig.15 Schematic diagram of wave pressure distribution
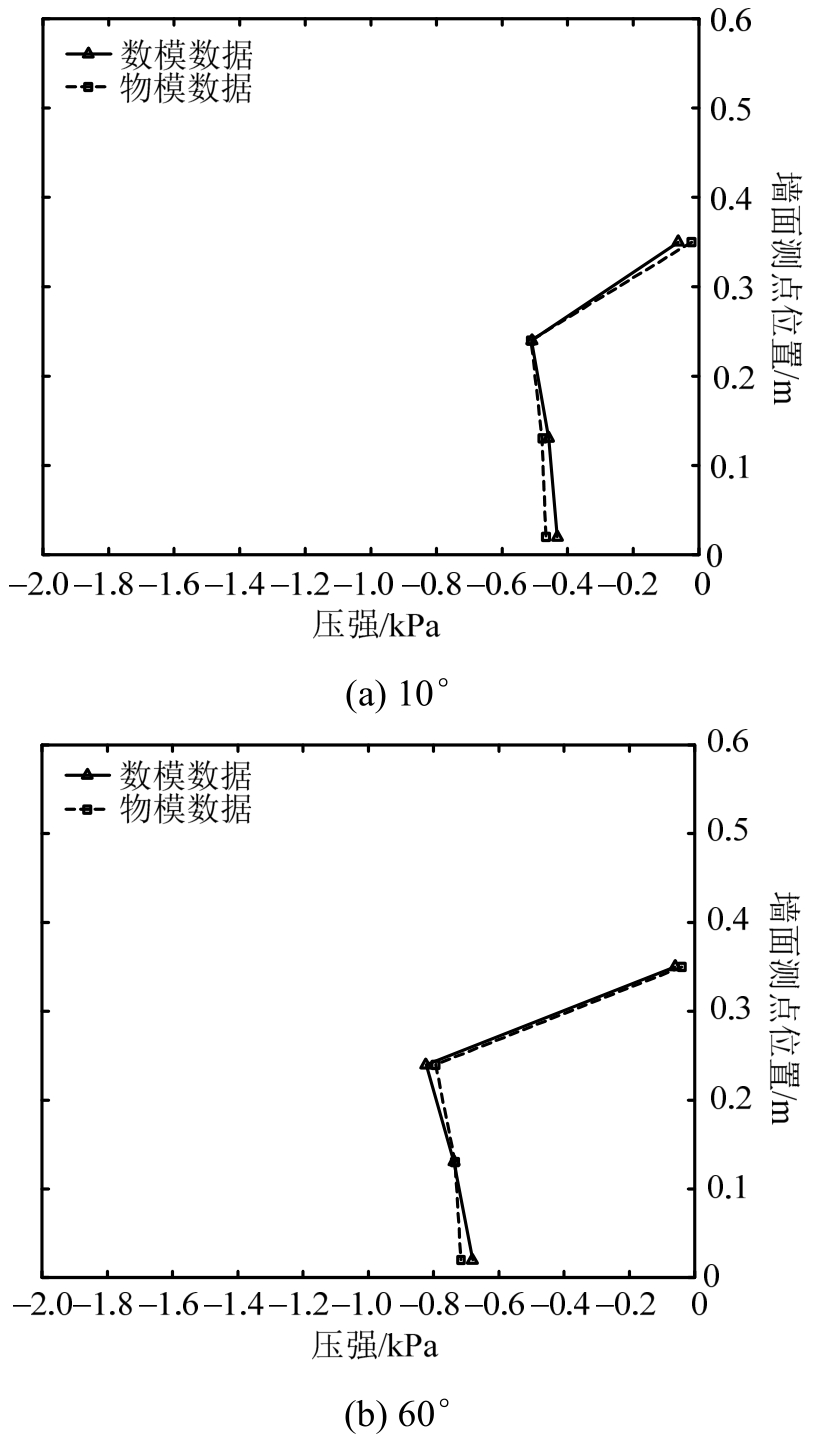
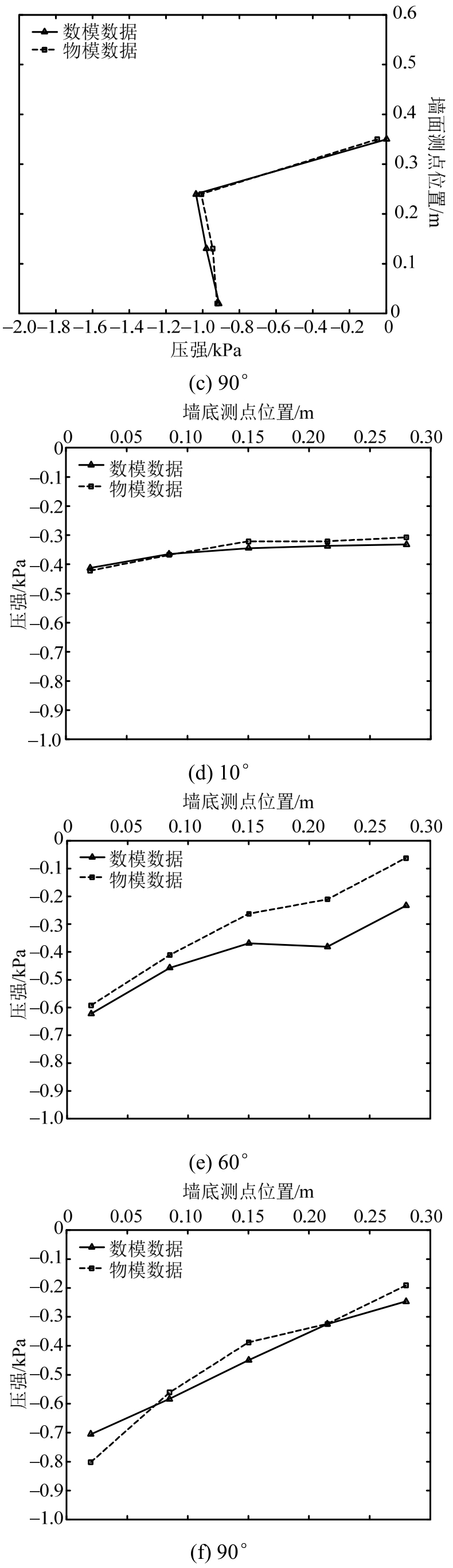
图16 波吸力分布示意图
Fig.16 Schematic diagram of negative wave pressure distribution
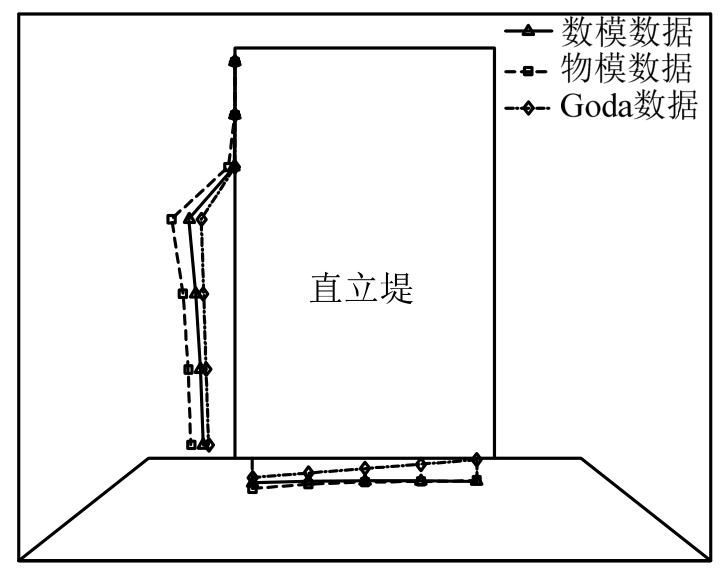
图17 直立堤波压力分布示意图(工况10°)
Fig.17 Schematic diagram of wave pressure distribution on vertical breakwater(case 10°)
由图16可知,斜向波作用下墙面波吸力的分布图相似于正向入射时的分布;墙底处波吸力的分布同样近似梯形,且随入射角度的增大,其分布图形的斜率越大。
通过上述试验与数值结果的对比分析,可以得出如下结论:
(1)墙面各测点波压力分布的总体趋势与合田公式相符,压力值随入射角度的增大而增大,正向入射时有最大值,但合田公式在一定程度上低估了墙面波压力值。对于墙底浮托力,V1及V2测点整体上呈逐渐增大的趋势,在90°时浮托力最大,其余三点均呈先减小后增大的趋势,测点V3在0°和90°时的浮托力大小相近,V4、V5两点的最大值出现在0°时;合田公式对墙底浮托力随入射角变化趋势的描述不符合试验及数值结果,在设计时需要注意。
(2)在总体趋势上,墙面各测点波吸力随入射角的增大而增大。墙底测点波吸力变化的数值和试验结果吻合程度稍差,V1、V2测点处的波吸力总体上随入射角的增大而增大,90°时有最大值;V3、V4测点试验结果的趋势是先减小后增大,数值结果呈先增大后减小再增大的趋势,V5测点试验及数值结果在总趋势上呈“勺子”形;试验和数值吻合稍差可能是由于波浪绕射或试验与数值在基床组成上的差别导致的。
(3)墙面波压力的分布基本上与合田公式相符;墙底浮托力的分布并不是合田公式描述的三角形,而是近似梯形分布。
(4)斜向波作用下的墙面波吸力的分布图相似于正向入射时的分布;墙底处波吸力近似梯形分布。
综上所述,本文所建立的数值模型与试验结果符合较好,对防波堤工程设计具有一定的指导作用。
参考文献:
[1]JTS 145―2015,港口与航道水文规范[S].北京:人民交通出版社,2015.JTS 145―2015,Code of hydrology for Harbor and Waterway[S].Beijing:China Communications Press,2015.(in Chinese)
[2]Goda Y.Random seas and design of maritime structures[M].Singapore:World Scientific Publishing Co Pte Ltd.,2000:132―141.
[3]Battjes J A.Effects of short-crestedness on wave loads on long structures[J].Applied Ocean Research,1982,4(3):165―172.
[4]Fenton J D.Wave forces on vertical walls[J].Journal of Waterway,Port,Coastal,and Ocean Engineering,1985,111(4):693―718.
[5]Franco C,Van Der Meer J W,Franco L.Multidirectional wave loads on vertical breakwaters[M]// Billy L.Edge.Coastal Engineering 1996.New York,ASCE.1997:2008―2021.
[6]Madrigal B G.Loads on caisson breakwaters in multidirectional random non-breaking seas[C]//Proceedings of 5th International Conference on Coastal and Port Engineering in Developing Countries.Cape Town,South Afric,1999:1314―1326.
[7]Tzang S Y,Liaw S R.A design short-crested wave force model for vertical deep-water breakwaters[M]// Billy L.Edge.Coastal Engineering 1996.New York,ASCE,1997:2494―2507.
[8]李玉成,董国海,孙昭晨,等.斜向规则波与直墙相互作用的实验研究[J].中国海洋平台,2001,16(4):1―6.Li Yucheng,Dong Guohai,Sun Zhaochen,et al.An investigation on the interaction between diagonal regular waves and vertical wall[J].China Offshore Platform,2001,16(4):1―6.(in Chinese)
[9]李玉成,孙昭晨,董国海,等.斜向不规则波与直墙相互作用的实验研究[J].海洋工程,2002,20(1):57―63.Li Yucheng,Sun Zhaochen,Dong Guohai,et al.Investigation of the action of diagonal irregular waves and vertical wall[J].The Ocean Engineering,2002,20(1):57―63.(in Chinese)
[10]俞聿修,胡金鹏,李本霞,等.斜向波作用于直立堤上的单位堤长波浪力[J].港工技术,2003,40(2):6―8.Yu Yuxiu,Hu Jinpeng,Li Benxia,et al.Wave forces on unit length of vertical breakwater under oblique wave attack[J].Port Engineering Technology,2003,40(2):6―8.(in Chinese)
[11]李本霞,俞聿修,张宁川.斜向随机波对直立堤作用的试验研究[J].水利水运工程学报,2003(2):1―6.Li Benxia,Yu Yuxiu,Zhang Ningchuan.Experimental investigation of oblique random wave load on vertical breakwaters[J].Hydro-Science and Engineering,2003(2):1―6.(in Chinese)
[12]胡金鹏,俞聿修,朱良生.单位堤长斜向波浪力的短峰波计算方法及试验验证[J].港工技术,2004,41(3):1―4.Hu Jinpeng,Yu Yuxiu,Zhu Liangsheng.Numerical calculation based on short-wave model and laboratory data test for wave forces on unit length of vertical breakwater under oblique wave attack[J].Port Engineering Technology,2004,41(3):1―4.(in Chinese)
[13]陈汉宝.斜向波与直立式防波堤相互作用研究[D].天津:天津大学,2004.Chen Hanbao.Investigation of the action of diagonal waves and vertical breakwater[D].Tianjin:Tianjin University,2004.(in Chinese)
[14]Liu Y,Li Y,Teng B.Interaction between oblique waves and perforated caisson breakwaters with perforated partition walls[J].European Journal of Mechanics B/Fluids,2016,56:143―155.
[15]Mandal S,Behera H,Sahoo T.Oblique wave interaction with porous,flexible barriers in a two-layer fluid[J].Journal of Engineering Mathematics,2016,100(1):1―31.
[16]Umeda N,Sakai M,Fujita N,et al.Numerical prediction of parametric roll in oblique waves[J].Ocean Engineering,2016,120:212―219.
[17]Lin P,Liu P L F.Internal wave-maker for Navier-Stokes equations models[J].Journal of Waterway,Port,Coastal,and Ocean Engineering,1999,125(4):207―215.
[18]李宏伟.数值水池造波方法研究[D].哈尔滨:哈尔滨工程大学,2009.Li Hongwei.The research of wave-generating method in numerical tank[D].Harbin:Harbin Engineering University,2009.(in Chinese)
[19]张博杰,张庆河.基于OpenFOAM开源程序的无反射数值波浪水槽[J].中国港湾建设,2012,32(5):1―3,18.Zhang Bojie,Zhang Qinghe.2D Numerical wave flume without reflection based on OpenFOAM[J].China Harbour Engineering,2012,32(5):1―3,18.(in Chinese)
[20]丁阳,马瑞,李宁.三维波流耦合水槽模拟模型[J].工程力学,2015,32(10):68―74.Ding Yang,Ma Rui,Li Ning.A simulation model for three-dimensional coupled wave-current flumes[J].Engineering Mechanics,2015,32(10):68―74.(in Chinese)
[21]马小舟,马玉祥,朱小伟,等.波浪在潜堤上传播的非线性参数分析[J].工程力学,2016,33(9):235―241.Ma Xiaozhou,Ma Yuxiang,Zhu Xiaowei,et al.Analysis of wave nonlinear parameters for waves transformation over a submerged bar[J].Engineering Mechanics,2016,33(9):235―241.(in Chinese)
[22]唐晓成,姜峰,陈洪洲,等.波浪作用下开孔沉箱动应力时域特性数值研究[J].工程力学,2017,34(9):184―192.Tang Xiaocheng,Jiang Feng,Chen Hongzhou,et al.Time-domian study of the dynamic stress of perforated caisson under wave action[J].Engineering Mechanics,2017,34(9):184―192.(in Chinese)
[23]朱萍,黄晶华,赵丽君.水槽造波机的参数确定及结构设计[J].现代电力,2011,28(4):44―48.Zhu Ping,Huang Jinghua,Zhao Lijun.Parameters determination and structure design for basin wave-maker[J].Modern Electric Power,2011,28(4):44―48.(in Chinese)
[24]张婷.波浪的三维数值模拟及其应用[D].天津:天津大学,2009.Zhang Ting.Three-dimensional numerical simulation of waves and its application[D].Tianjin:Tianjin University,2009.(in Chinese)
A STUDY ON ARBITRARY INCIDENT WAVE PRESSURE ON VERTICAL BREAKWATERS
WANG Hao-lin1,ZHANG Hua-chang2,DONG Sheng1
(1.College of Engineering,Ocean University of China,Qingdao 266100,China;2.Experiment Research Center,Navy Engineering Design and Research Institute,Qingdao 266100,China)
Abstract:In order to study the wave pressure acting on the vertical breakwater with various incident wave directions,a 3-D numerical wave pool is established based on FLOW-3D software,and a corresponding physical model test is carried out for the validation of the numerical model.The numerical model uses apiston-type plate to generate waves and a pore structure to absorb waves.The results of numerical simulation agree well with the experimental results.The comparison analysis shows that both wave pressure and wave suction of measuring points on the wall increase with the incident angle increasing.At the bottom of the wall,the change trend of the uplifting pressure is more complex,which is no longer applicable described by the Goda’s formula.The distribution of wave pressure on the wall is basically consistent with the Goda’s formula.And the distribution shape of the uplifting pressure at the bottom of the wall is similar to a trapezoid rather than a triangle described by the Goda’s formula.The negative wave pressure distribution under oblique waves is similar to that at forward incidence on the wall.The results can provide a reference for the breakwater design in costal engineering.
Key words:coastal engineering;numerical wave pool;vertical breakwater;oblique wave;wave pressure;Goda’s formula;FLOW-3D
中图分类号:P751;TV139.2
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.01.0020
文章编号:1000-4750(2018)05-0246-11
收稿日期:2017-01-05;修改日期:2017-10-17
基金项目:国家自然科学基金委员会-山东省人民政府联合基金项目(U1706226);国家重点研发计划课题项目(2016YFC0802301)
通讯作者:董 胜(1968―),男,山东青岛人,教授,博士,博导,从事海洋工程环境及其与结构相互作用研究(E-mail:dongsh@ouc.edu.cn).
作者简介:王浩霖(1992―),男,山东济宁人,硕士生,主要从事海岸工程及其与海洋环境的相互作用研究(E-mail:wanghaolin1062@163.com);
张华昌(1966―),男,山东寿光人,高工,硕士,从事海岸工程建筑物设计及波浪物理模型试验研究(E-mail:zhanghuachang306@ 126.com).