图1 发生于欧洲铁路的轻度钢轨隐伤
Fig.1 Squats occurred in a European railway
赵小罡，赵 鑫，温泽峰，金学松
(西南交通大学牵引动力国家重点实验室，四川，成都 610031)
摘 要：采用ANSYS/LS-DYNA建立了含有钢轨直裂纹的三维显式有限元模型，考虑了高速条件下轮轨间的瞬态滚动接触和裂纹面之间的滑动接触，于时域内分析了轮轨滚滑作用下裂纹面之间的瞬态法、切向接触和裂尖动态应力场强度因子。轮轨接触和裂纹面间的接触，均采用“面-面”接触算法定义，切向接触满足库伦摩擦定律。裂尖应力场强度因子采用虚拟闭合法计算，不考虑裂纹面之间的间隙，即两个裂纹面上的离散节点完全重合。牵引工况的计算结果表明，滚滑状态下的轮轨法、切向接触力不随轮轨黏着系数的增加而变化，但裂纹面间的最大法、切向接触力却随黏着系数的增加而不断减小。车轮滚到裂纹时，钢轨的弯曲变形使得两个裂纹面相互挤压闭合，即KI值为0，而KII最大值约为KIII最大值的8.1倍左右。这意味着钢轨表面的直裂纹，如果可以扩展，其在无横移牵引工况下的扩展应该以II型撕裂为主导。随着粘着系数由0.1增至0.5时，无横移牵引工况下KII最大值仅增大3.98%，而KIII最大值反而降低20.8%。
关键词：轮轨滚滑；滚动接触疲劳；直裂纹；轮轨黏着；动态应力场强度因子；显式有限元法
近几十年来，滚动接触疲劳逐渐成为国内外钢轨的主要损伤形式之一。一般而言，轮轨滚动接触疲劳是由车轮载荷循环导致的萌生于接触区附近的轮轨表面和浅表层裂纹，若不及时处理，裂纹持续扩展通常会导致轮轨表面的材料剥离，某些极端情况下也会导致断轨和崩轮，严重威胁行车安全[1]，例如，2000年英国一列车以185 km/h的速度过曲线时发生脱轨事故，调查发现其原因是外侧钢轨轨矩角处的滚动接触疲劳斜裂纹导致了断轨[2]。我国第一条准高速线广深线刚开始运营时，在曲线段外轨轨距角也发生了大量斜裂纹[3]。与斜裂纹一样广泛发生的另一类钢轨滚动接触疲劳是萌生于接触带中心的钢轨隐伤(Squat类滚动接触疲劳)，图1展示了一个发生在欧洲的钢轨隐伤。该研究旨在分析轮轨滚滑作用下钢轨裂纹的瞬态扩展行为，为理解滚动接触疲劳的扩展机理和优化其防治措施提供支撑。
图1 发生于欧洲铁路的轻度钢轨隐伤
Fig.1 Squats occurred in a European railway
利用MTS试验机，王文健和刘启跃[4]测试了常温下PD3和U71Mn两种钢轨钢的疲劳裂纹扩展行为，并确定了适用于Paris公式的疲劳裂纹扩展速率。利用WR-1轮轨滚动磨损试验机，黄育斌等[5]试验了不同轮轨垂向力、横向力和冲角等载荷下车轮表面疲劳裂纹的萌生与扩展，并对试验结果做出了解释。虽然实验可以更加直接地观察钢轨材料表面疲劳裂纹的萌生和扩展等，但鉴于疲劳试验往往是比例试验，无法精确模拟现场曲线线路、车体振动等实际参数，且研究耗费较大。因此，更多国内外学者利用数值仿真手段来研究和表征滚动接触疲劳。
就断裂力学所关注的裂尖应力场强度因子而言，目前存在多种算法。刘明尧等[6]采用逐节点建模和实体建模两种方法建立了含裂纹的有限元薄板模型，并将1/4节点法、位移外推法和虚拟裂纹闭合法三种算法的计算结果与理论解进行对比，发现均能达到较高精度，但虚拟裂纹闭合法效率最高。
针对裂纹几何、作用应力和断裂韧性三大断裂判断基本要素[7]的影响分析，文献中多有报道。李煦等[8]建立了二维斜裂纹有限元模型，采用移动荷载法研究了纯滚动下裂纹长度对钢轨疲劳裂纹扩展的影响。李士一等[9]建立了二维直裂纹有限元模型，将轮轨间作用应力以移动接触载荷形式施加于钢轨表面，研究了轴重对U71Mn钢轨表面微裂纹扩展的影响。Pletz等[10]建立二维准静态有限元模型来研究车轮和带裂纹钢轨的接触响应，分析了钢轨塑性变形的影响。邓永果等[11]研究了钢轨焊接接头处二维斜裂纹的裂尖应力场强度因子KI和应力场强度因子范围ΔKII，发现焊接接头处表面斜裂纹以II型剪切型扩展模式占主导。Makino等[12]建立二维有限元模型来模拟车轮与带疲劳裂纹钢轨间的滚动接触。以上研究均针对单个裂纹工况，但现场中表面微裂纹均是多条近似平行呈带状分布。针对此问题，李伟等[13]通过热机耦合有限元法分析了多裂纹在轮轨滚动接触下的相互作用，计算了不同裂纹数量下的裂尖应力场强度因子KI和应力场强度因子范围ΔKII，发现均随裂纹数量增多而降低。
总结以上文献不难发现，大多数学者将轮轨间作用力以移动Hertz载荷的形式施加于钢轨表面，从而实现准静态或稳态下二维裂纹的动态扩展行为模拟，此类方法不能考虑到实际的轮轨接触几何，难以模拟车轮滚过裂纹缺陷时的瞬态行为，从而无法准确估计裂纹的扩展能力，且通常忽略了接触斑内的黏滑分布。
学术界极少对轮轨真实滚滑载荷作用下的裂纹扩展行为开展详细研究，也忽略了钢轨离散支持的影响，尤其缺少针对高速工况的研究。该文基于赵鑫等[14]建立的三维瞬态滚动接触模型，进一步考虑了钢轨直裂纹，文献[15]已对三维直裂纹的有限元建模方法开展了初步研究，该文将着重分析轮轨黏着系数对钢轨裂纹处瞬态法、切向接触和裂尖应力场强度因子分布的影响。
图2展示了利用ANSYS/LS-DYNA建立的三维轮轨瞬态滚动接触有限元模型，模型考虑了国内某高速线路的车辆-轨道结构，车轮踏面廓形为LMa，轮径860mm，钢轨廓形为CN60，轨底坡1∶40，具体模型尺寸和材料参数见表1。模型考虑了直线段轨道，由钢轨、扣件、轨道板和砂浆层组成，不考虑轮对横移，所以仅包含了轮对和轨道的一半。模型中轮、轨、轨道板和砂浆层采用8节点恒应力单元离散，轮轨接触采用“面-面”接触算法求解，切向接触满足库伦摩擦定律。由于裂纹处的瞬态行为属于高频范畴，一系悬挂以上的车体和构架因其影响很小而简化为质点。为保证裂尖求解精度，同时尽可能减少网格规模，对钢轨裂纹区网格进行了局部细化，最小网格尺寸0.25 mm，而其他区域最小网格尺寸1 mm，满足轮轨接触求解要求。模型中建立了满足右手定则的笛卡尔坐标系，如图2所示，其中x代表横向，y代表垂向，z代表纵向，更多模型细节见文献[14]。
表1 模型材料参数
Table1 Model material parameters
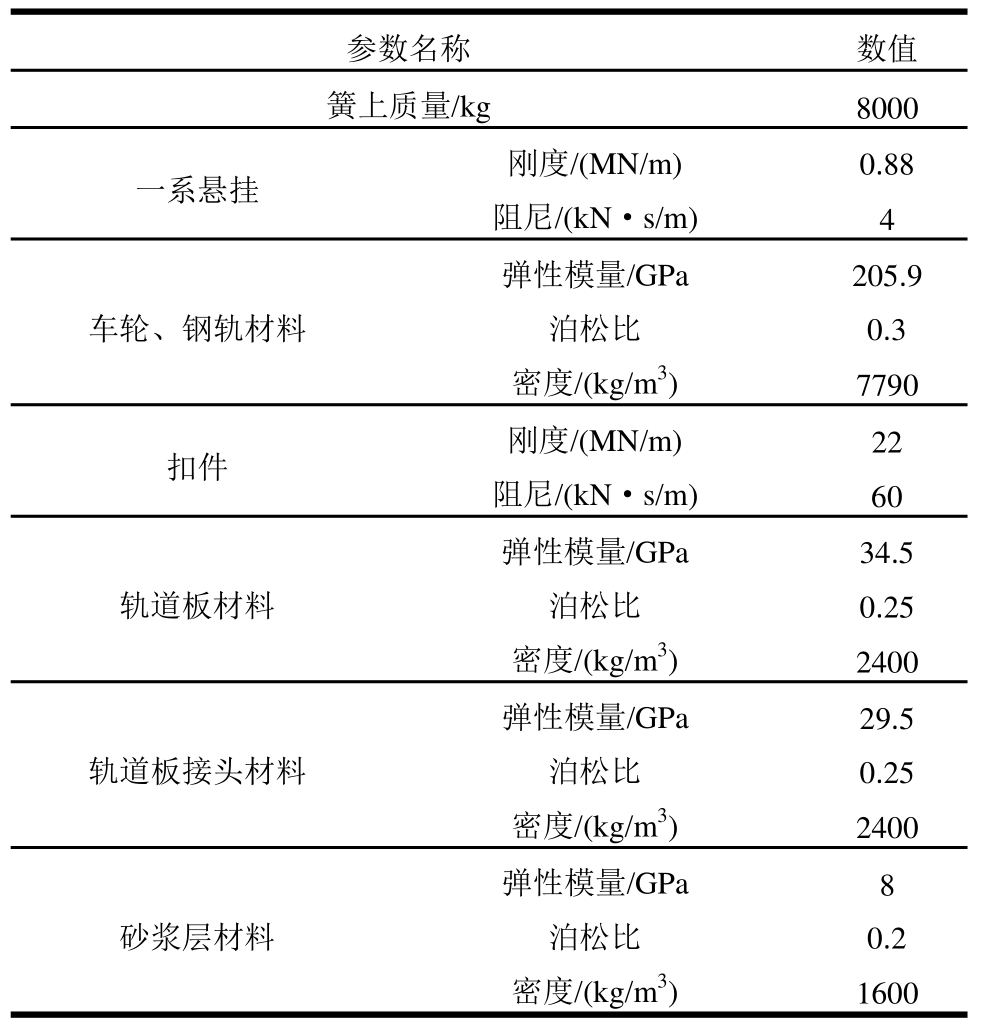
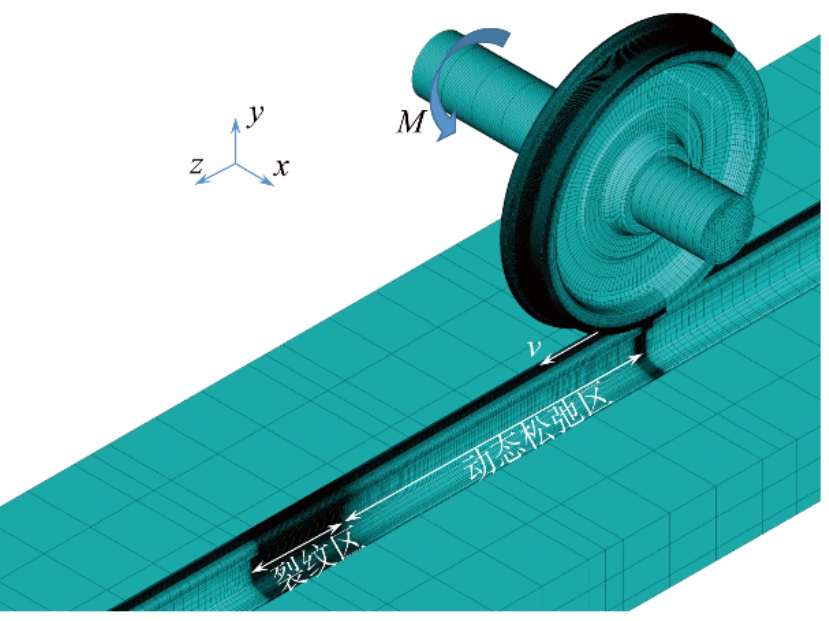
图2 三维轮轨瞬态滚动接触有限元模型
Fig.2 A 3D finite element model of wheel-rail transient rolling contact
由于裂纹区网格尺寸与其他区域差异较大，在裂纹区纵向两端采用了不连续网格，图3中虚线为裂纹区一侧分界面。计算中，在该边界设置了沿x、y和z三个方向上的耦合约束，以保证车轮可顺利滚过，而影响可以忽略，即实现了边界上连续材料的模拟。计算结果表明，上述边界面的影响很小(见3.1节)，即上述耦合方法可以满足要求。
该文所模拟的直裂纹施加在裂纹区的中间，即z=1.3 m。其创建方法如下：在裂纹施加位置选择一组节点作为一个裂纹面，而在相同位置上复制上述节点组以构建另一个裂纹面，即两个裂纹面及其上的节点均重合，上述两组节点在钢轨内部的边界构成裂尖。图4展示了本文所模拟的直裂纹，其中“°”代表裂纹面内的节点，“·”代表的节点属于未开裂材料，裂尖用黑色实线表示。裂纹面间接触也由面-面接触算法求解，切向接触同样满足库伦摩擦定律。所施加裂纹面近似为半椭圆，裂纹宽度为15 mm，深度为2 mm，轮轨接触斑几乎可以全部覆盖裂纹。因为当裂纹尺寸大于0.5 mm时，线弹性断裂力学可精确表征其断裂行为[16]，所以该文的轮轨材料均采用了线弹性模型来模拟，具体数值见表1。需说明，由于节点离散及显示比例的问题，图中裂纹面与完美椭圆有一定差距。为了方便展示应力场强度因子沿裂尖的分布，在裂纹面上建立如图4所示的局部极坐标系O'(rθ)，坐标极点O'位于裂纹表面节点的中间，极轴与整体坐标系x轴方向一致，规定极径r为极点O'到裂尖的距离，极角θ为极轴绕极点逆时针转动的角度。
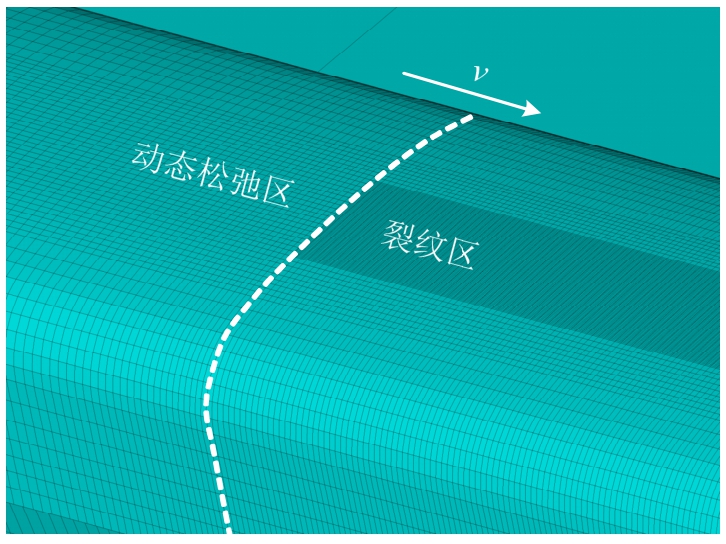
图3 裂纹区边界面网格
Fig.3 Mesh on the boundary of the crack zone
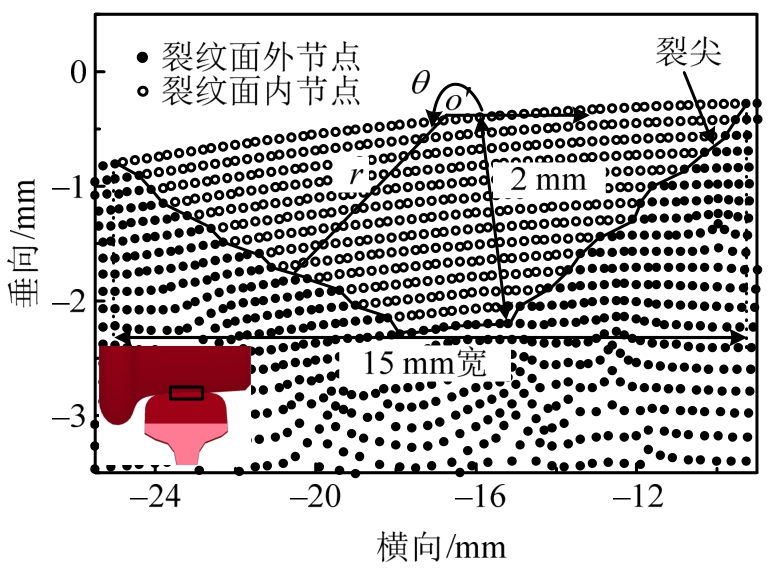
图4 裂纹定义
Fig.4 Definition of the crack
该文采用虚拟裂纹闭合法计算裂尖应力场强度因子，它是由Rybicki和KANNIMEN[17]首先提出，早期用于求解二维裂纹问题，后来被Shivakumar等[18]拓展到三维裂纹。图5展示了裂尖节点附近的网格示意图，裂尖节点处沿三个方向的应变能释放率GI、GII和GIII分别按式(1)～式(3)由裂尖附件的应力场和位移场算得。由图5可见，h1、h2、l1和l2为裂尖节点i附近的网格尺寸，j和j*是距离i最近的裂纹面内两个重合节点。
式中：模型修正量A=(h1l1+h1l2)/2；Fxi、Fyi和Fzi为裂尖节点i在三个方向的节点力；Δux(j，j*)、Δuy(j，j*)和Δuz(j，j*)为重合节点j和j*在三个方向的位移之差。
算得应变能释放率后，裂尖应力场强度因子KI、KII和KIII可由式(4)～式(16)计算：
式中：E为钢轨弹性模量；ν为泊松比。
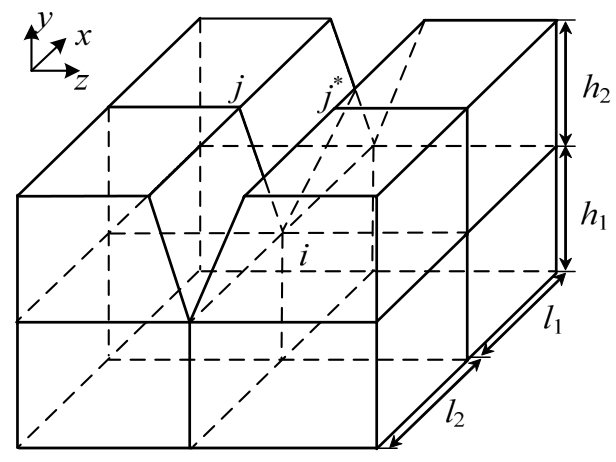
图5 三维裂尖网格示意图
Fig.5 Schematic diagram of three-dimensional crack tip mesh
该节分析中，车轮滚动速度取为我国高铁的典型速度300km/h，牵引系数取动车组运行中高值0.15，而黏着系数取0.1、0.2、0.3和0.5等系列值以研究其影响。另外，以往研究发现，裂纹面摩擦系数减小会促进裂纹扩展[15]，所以该节中裂纹面摩擦系数取为0，即模拟最恶劣工况。需说明，该文仅考虑了牵引系数为正值的工况，对应着列车牵引，而未考虑牵引系数为负值的制动工况。
图6展示了不同黏着系数下轮轨间法、切向接触力结果，图中纵坐标为不同时刻下车轮的纵向位置，具体分析时取轮轨接触斑中心的位置。因为该文未考虑轮对的横向位移，所以图6(a)所示的法向力基本上等于垂向力，图6(b)中切向轮轨力基本上等于纵向力(横向力相对纵向力而言要小很多)。由图6(a)可以看出，法向轮轨力在耦合边界位置(即z=1.137 m 处)存在一个峰值(幅值约101.5 kN)，而切向力在相同位置上的变化因黏着系数而异，黏着系数为0.1时出现一个峰值，而取其他值时出一个谷值，见图6(b)，其原因均是裂纹区的耦合边界。在裂纹处(z=1.3 m)，车轮已远离耦合边界，且轮轨力已趋于稳定，所以耦合边界对裂纹结果的影响可以忽略。对比不同黏着系数的结果(耦合边界之外)，可以看出，黏着系数对轮轨法向接触力的影响可以忽略；当黏着系数由0.2变到0.5时，切向力稍稍增大，但幅值依然可以忽略，而当黏着系数由0.1增至0.2时，切向力存在一个跃升，这是因为黏着系数为0.1时轮轨间切向接触力只能达到0.1FN，虽然牵引系数为0.15，即车轮处于全滑动状态，接触斑内全为滑移区；而当黏着系数大于设定的牵引系数时，切向轮轨力大小取决于牵引系数，即0.15FN，不受黏着系数影响。
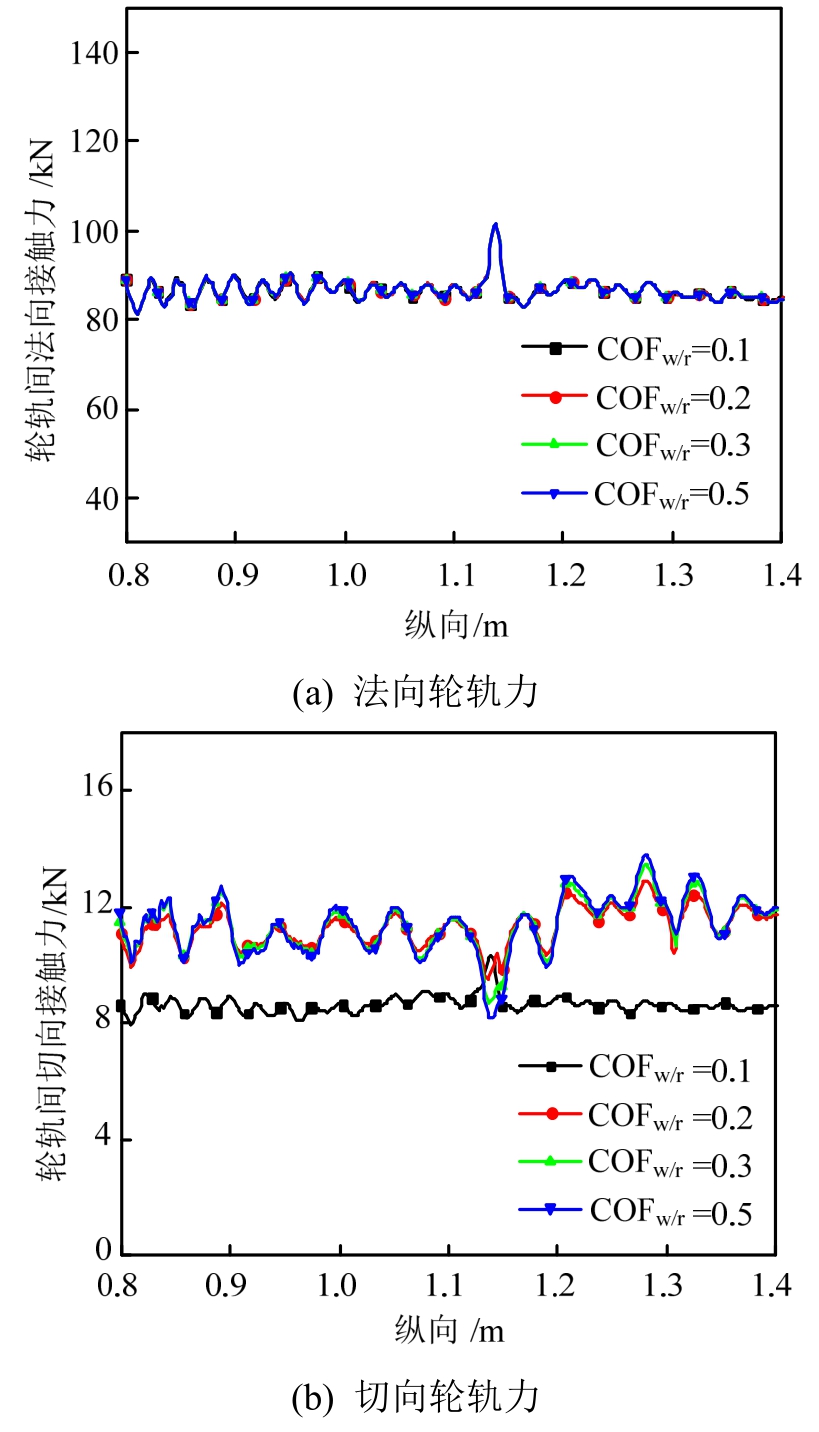
图6 不同黏着系数下的轮轨力结果
Fig.6 Wheel-rail force results under different adhesion coefficients
图7展示了是不同黏着系数下裂纹面的法、切向接触力结果，图中纵坐标与图6相同。从图7(a)可知，车轮滚过裂纹时(即z=1.3 m)的裂纹面法向接触力均为负值，这意味着两个裂纹面始终处于相互挤压的接触状态，即该裂纹处于闭合状态。进一步发现，裂纹面间的最大法、切向接触力均随着黏着系数的增加而不断减小。这是因为黏着系数增大时，接触斑中的黏着区变大，而滑移区变小，从而导致车轮相对于钢轨的切向滑动变小，而该轮轨间切向运动反映到裂纹面时，刚好表征了裂纹面的法向运动，即两个裂纹面间的法向相互渗透量的减小，从而使得裂纹面法向接触力减小。此外切向轮轨力作用点在接触斑内的相对位置后移，轮轨间总的相对滑动量变小，使得轮轨间切向接触力变小，相应的裂纹面间切向接触力也随之变小。
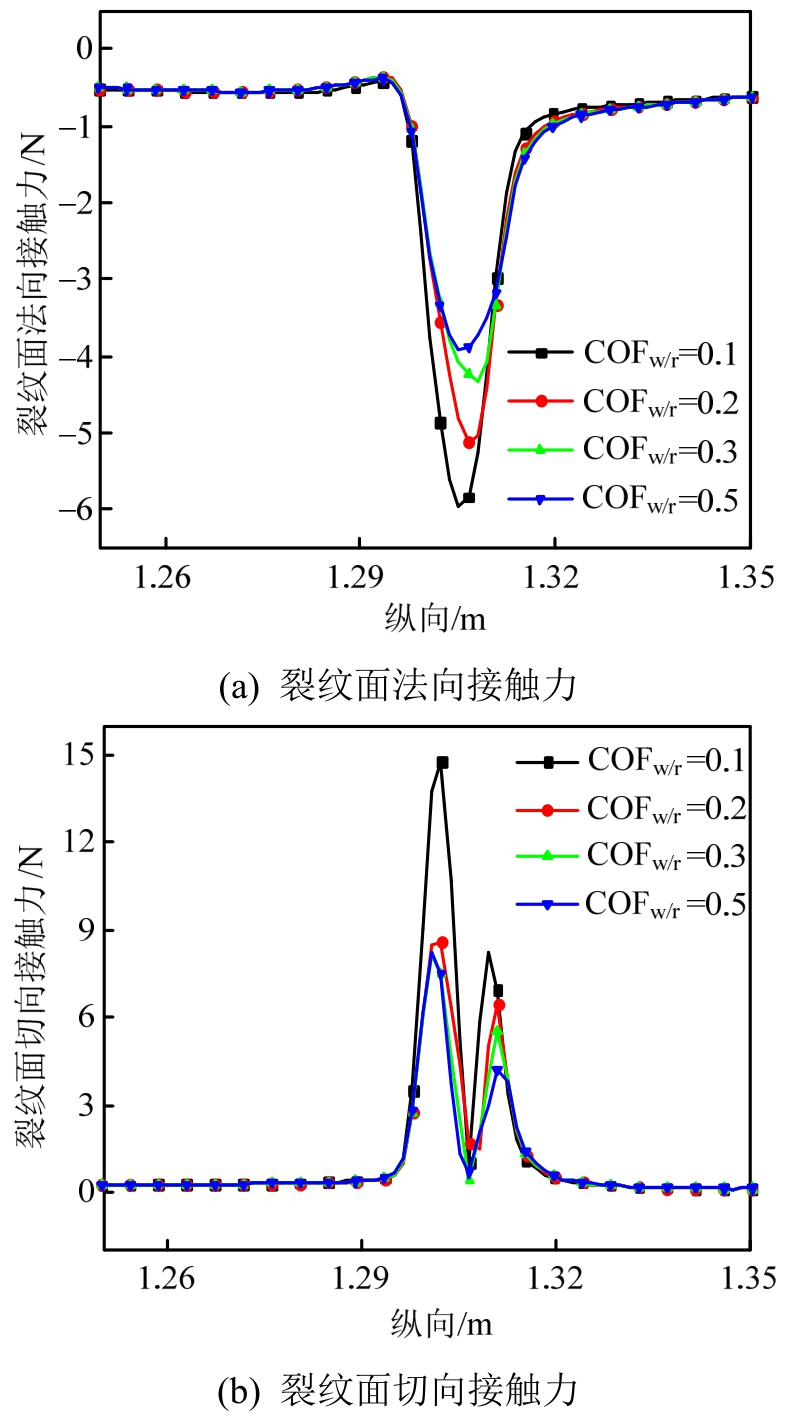
图7 不同黏着系数下的裂纹面接触力结果
Fig.7 Contact forces on crack surfaces under different adhesion coefficients
为展示车轮滚过直裂纹时的瞬态过程，该文输出了车轮在裂纹附近时7个时刻的结果，它们所对应的接触斑纵向位置如图8所示。可见，7个时刻所对应的接触斑中心与裂纹的纵向距离分别为-3a、-2a、-a、0、a、2a、3a(a为轮轨接触斑半长)。为避免相互重叠造成的视觉混淆，图8中将7个时刻的接触斑分两行排列于坐标轴两侧。
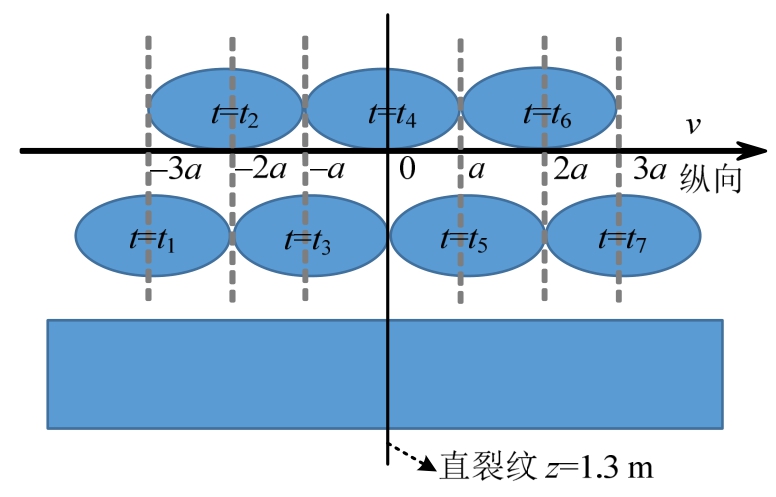
图8 不同时刻轮轨接触斑与裂纹的位置
Fig.8 The position of wheel-rail contact patch and crack mouth at different instants
以黏着系数0.5的工况结果为例，图9展示了上述7个不同时刻的应力场强度因子分布结果，其中采用了前面定义的局部极坐标系
来展示结果。因为在所有选取时刻KI沿整个裂尖均为0，即裂纹始终处于闭合状态，故其结果未展出。KII和KIII分布均随着载荷移动而呈现出明显变化，t4时刻的结果在所选7个时刻中最大，即接触斑中心刚好位于裂纹之上。KII值在t1～t4时刻为正，在t5～t7时刻为负，表明在车轮中心滚过裂纹面的瞬间，裂纹面之间沿y轴的错动方向发生了变化，即II型撕裂的方向变化。此现象很好理解，轮载在车轮滚过裂纹前施加在裂纹左边，而之后施加于裂纹右边。KIII值较KII值要小很多，这主要是因为该文忽略了轮对横移、横向力很小的缘故。KIII撕裂方向沿裂尖发生了变化(数值有正有负)，说明了应力场沿钢轨横向的复杂分布形式。需指出，图9中裂尖应力场强度因子分布曲线存在较多局部波动，其来源应该是有限元法不可避免的离散误差和截断误差等。
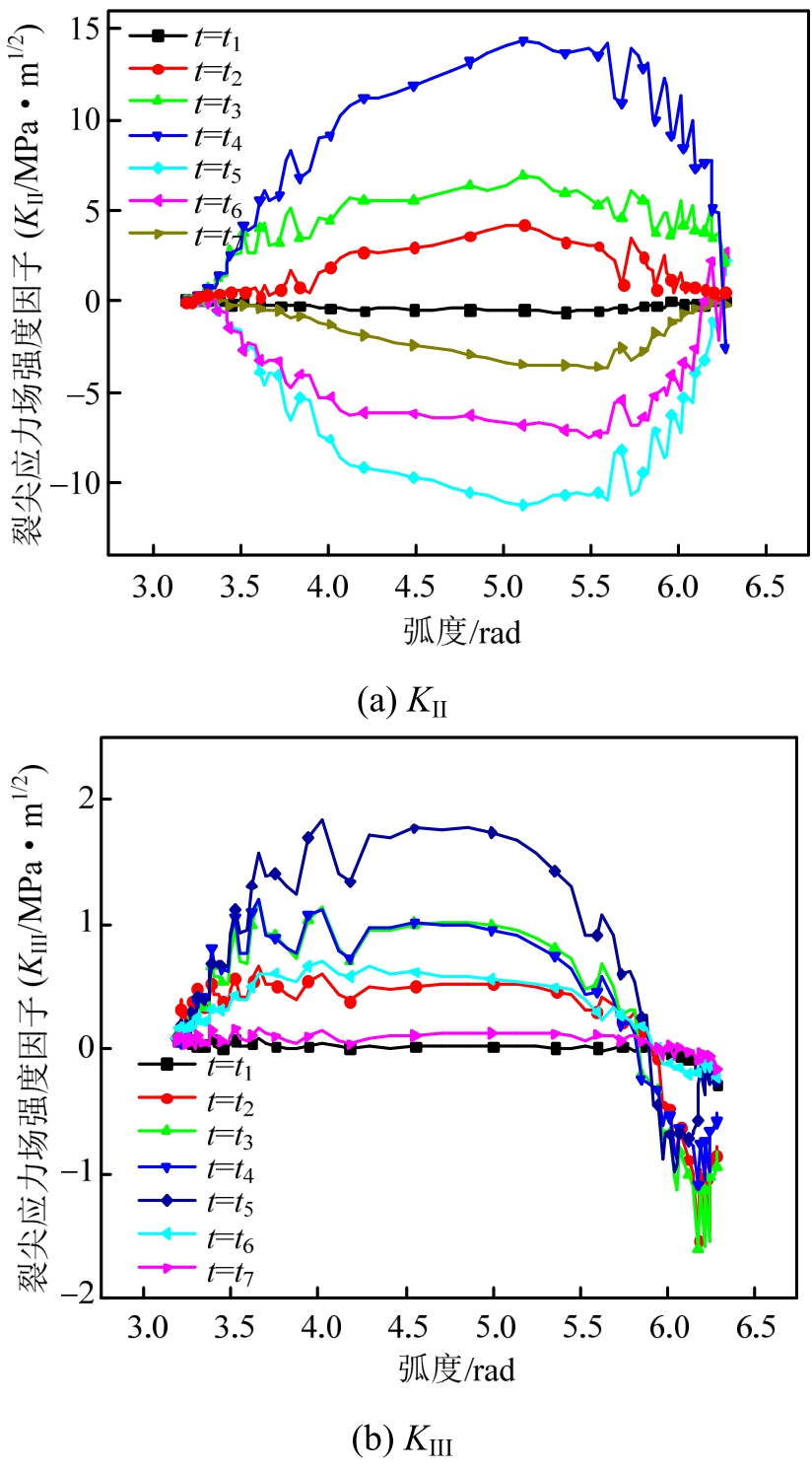
图9 黏着系数0.5的裂尖应力场强度因子瞬态变化
Fig.9 Transient variations of SIFs with adhesive coefficient 0.5
图10展示了不同黏着系数下裂尖应力场强度因子的对比结果。为方便对比，图中显示了裂尖各节点最大值的分布，此值为裂尖每一个节点在整个滚动过程中所经历的绝对值最大的应力场强度因子，很明显，不同节点的最大值可能发生在不同的时刻。KI在不同黏着系数下依然为0，故没有展出相关结果。从图10(a)可以发现，黏着系数由0.1变化到0.5仅造成了KII最大值3.98%的波动，而且KII最大值并非随黏着系数增大单调变化，而是在黏着系数取0.2时达到最大。其解释如下：黏着系数主要影响轮轨间切向作用，即沿x向和z向，而KII值体现的是裂纹沿y方向的错动，故影响很小。相对而言，当黏着系数增大时，KIII最大值不断减小，该结果与上小节所示裂纹面切向接触力结果一致。但需强调，KIII明显小于KII。
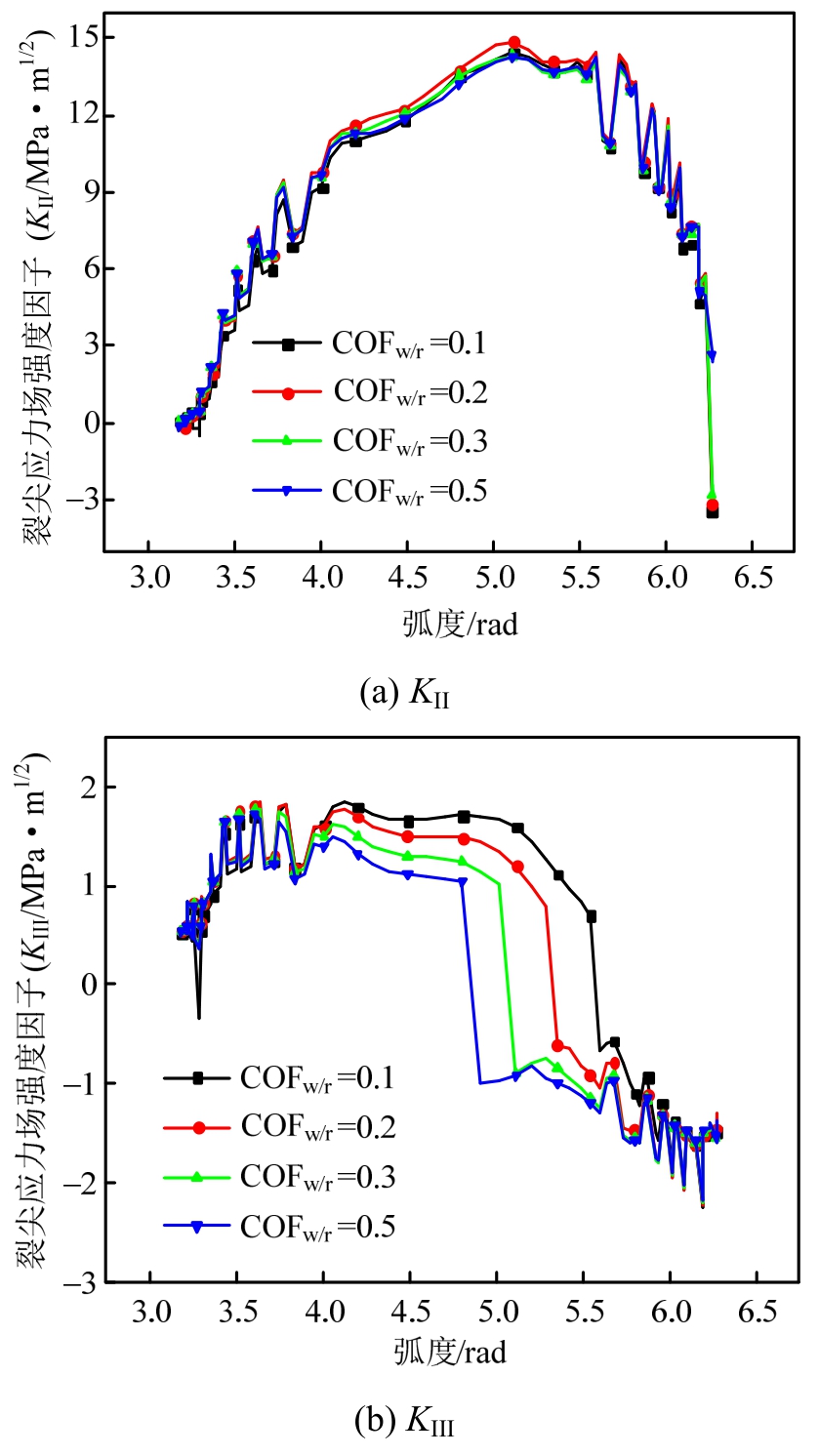
图10 不同黏着系数下裂尖应力场强度因子
Fig.10 SIFs under different adhesion coefficients
该文所考虑的载荷工况可以在一定程度上适用于萌生于接触光带中心且与轮轨横向作用基本无关的Squats类滚动接触疲劳，但现实中Squats类疲劳呈现出斜裂纹的特点[19]，该文裂纹模型差异明显。
采用ANSYS/LS-DYNA建立了带直裂纹的三维轮轨瞬态滚动接触模型，分析了高速牵引状态下车轮滚过钢轨表面直裂纹时轮轨间和裂纹面间的法、切向瞬态接触和裂尖应力场强度因子。基于不同轮轨黏着系数下结果对比，可以得到以下结论：
(1)滚滑状态下，黏着系数对于轮轨间法、切向接触力基本无影响，当黏着系数低于牵引系数时，车轮因出现打滑现象而导致切向力降低。
(2)随着黏着系数的增加，裂纹面最大法、切向接触力均略微减小。
(3)车轮滚过钢轨表面直裂纹时，裂纹均处于闭合状态，即KI值为0；KII最大值约为KIII的8.1倍左右，表明该裂纹如果开裂的话，其扩展应该以II型撕裂为主导。
(4)黏着系数的增加仅造成KII最大值3.98%的变化，而KIII最大值相应地降低20.8%。
(5)该文建议对车辆安装撒沙装置，减少车轮打滑现象发生，同时也减少裂纹扩展的可能。
参考文献：
[1]金学松，温泽峰，张卫华，等.世界铁路发展状况及其关键力学问题[J].工程力学，2004，21(增刊 l):90―104.Jin Xuesong，Wen Zefeng，Zhang Weihua，et al.Development status of world railway and its key mechanics problems[J].Engineering Mechanics，2004，21(Suppl 1):90―104.(in Chinese)
[2]Grassie S L.Rolling contact fatigue on the British railway system:treatment[J].Wear，2005，258(7):1310―1318.
[3]赵雪芹，王文健，郭俊，等.广深线PD3与U71Mn钢轨斜裂纹形成特性[J].润滑与密封，2007，32(3):35―42.Zhao Xueqin，Wang Wenjian，Guo Jun，et al.An investigation on formation characteristic of oblique crack of PD3 and U71Mn in Guangzhou-Shenzhen railway[J].Lubricat Ion Engineering，2007，32(3):35―42.(in Chinese)
[4]王文健，刘启跃.PD3和U71Mn钢轨疲劳裂纹扩展速率研究[J].机械强度，2007，29(6):1026―1029.Wang Wenjian，Liu Qiyue.Study on fatigue crack growth rate of PD3 and U71Mn rail steel[J].Journal of Mechanical Strength，2007，29(6):1026―1029.(in Chinese)
[5]黄育斌，何成刚，马蕾，等.干态下车轮材料表面疲劳裂纹萌生试验研究[J].摩擦学学报，2016，36(2):194―200.Huang Yubin，He Chenggang，Ma Lei，et al.Experimental study on initiation of surface fatigue crack of wheel material under dry condition[J].Tribology.2016，36(2):194―200.(in Chinese)
[6]刘明尧，柯孟龙，周祖徳，等 裂纹尖端应力强度因子的有限元计算方法分析[J].武汉理工大学学报，2011，33(6):116―121.Liu Mingyao，Ke Menglong，Zhou Zude，et al.Analysis of finite element calculation methods for crack-tip stress intensity factor[J].Journal of Wuhan University of Technology，2011，33(6):116―121.(in Chinese)
[7]陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社，2001.Chen Chuanyao.Faigue and fracture[M].Wuhan:Huazhong University of Science and Technology Press，2001.(in Chinese)
[8]李煦，曹世豪，文良华，等.裂纹长度对钢轨裂纹扩展的影响[J].应用数学和力学，2014，35(S):131―135.Li Xu，Cao Shihao，Wen Lianghua，et al.The influence of crack length on the propagation of rail crack[J].Applied Mathematics and Mechanics，2014，35(S):131―135.(in Chinese)
[9]李士一，肖华磊，江晓禹.轮轨接触表面微裂纹的扩展[J].钢铁研究学报，2013，25(6):35―39.Li Shiyi，Xiao Hualei，Jiang Xiaoyu.Growing of micro-crack on wheel/rail contact surface[J].Journal of Iron and Steel Research，2013，25(6):35―39.(in Chinese)
[10]Pletz M，Daves W，Yao W，et al.Multi-scale finite element modeling to describe rolling contact fatigue in a wheel-rail testing[J].Tribology International，2014，80(12):147―155.
[11]邓永果，李伟，温泽峰，等.轮滚相互作用下钢轨焊接接头表面裂纹扩展分析[J].应用力学学报，2013，30(4):624―629.Deng Yongguo，Li Wei，Wen Zefeng，et al.Analysis of crack propagation on rail weld surface under wheel/rail interaction[J].Chinese Journal of Applied Mechanics，2013，30(4):624―629.(in Chinese)
[12]Makino T，Kato T，Hirakawa K.The effect of slip ratio on the rolling contact fatigue property of rail way wheel steel[J].International Journal of Fatigue，2012，36(1):68―79.
[13]李伟，温泽峰，金学松，等.轮轨摩擦接触下钢轨多裂纹相互作用[J].工程力学，2012，29(11):295―301.Li Wei，Wen Zefeng，Jin Xuesong，et al.A study of multiple crack interaction in rail under wheel-rail friction contact[J].Engineering Mechanics，2012，29(11):295―301.(in Chinese)
[14]赵鑫，温泽峰，王衡禹.三维高速轮轨瞬态滚动接触有限元模型及其应用[J].机械工程学报，2013，49(18):1―7.Zhao Xin，Wen Zefeng，Wang Hengyu.A 3-D transient finite element model for high-speed wheel-rail in rolling contact and its application[J].Chinese Journal of Mechanical Engineering，2013，49(18):1―7.(in Chinese)
[15]Zhao X，Zhao X G，Liu C，et al.A study on dynamic stress intensity factors of rail cracks at high speeds by a 3D explicit finite element model of rolling contact[J].Wear，2016，366―367(11):60―70.
[16]Ringsberg J W.Shear mode growth of short surface-breaking RCF cracks[J].Wear，2005，258(7):955―963.
[17]Rybicki E F，Kannimen M F.A finite element calculation of stress intensity factors by a modified crack closure integral[J].Engng.Fracture Mech，1977，9(4):931―938.
[18]Shivakumar K N，Tan P W，Newman J C.A virtual crack-closure technique for calculating stress intensity factors for cracked three dimensional bodies[J].International Journal of Fracture，1988，36(3):R43―R50.
[19]Grassie S L.Squats and squat-type defects in rails:the understanding to date[J].Journal of Rail and Rapid Transit，2012，226(3):235―242.
INFLUENCE OF WHEEL-RAIL ADHESION COEFFICIENT ON TRANSIENT PROPAGATION OF A VERTICAL RAIL CRACK
ZHAO Xiao-gang，ZHAO Xin，WEN Ze-feng，JIN Xue-song
(State Key Laboratory of Traction Power，Southwest Jiaotong University，Chengdu，Sichuan 610031，China)
Abstract:A 3D explicit finite element model has been established with ANSYS/LS-DYNA to simulate the high-speed transient rolling contact between a wheelset and a cracked rail，for which a vertical rail crack is considered.By defining another contact pair，the normal as well as tangential contact forces between the crack faces and the resulted dynamic stress intensity factors(SIFs)at the crack tip are analyzed in the time domain.The virtual crack closure technique is employed to calculate the SIFs，so that the discrete nodes on the two crack surfaces are kept coincident.No gap between the crack faces has been considered.The wheel-rail contact and the contact between crack faces are both defined by a ‘surface-to-surface’ contact algorithm，and the Coulomb’s law of friction is implemented to treat tangential contact problems for both contact pairs.The results under traction have shown that the normal and tangential contact forces between the wheel and rail do not change with the adhesion coefficient，while those between crack faces decrease correspondingly.As the wheel reaches the crack，the two faces are pressed against each other due to rail bending under wheel loading，i.e.，the crack is closed andKIis zero value，while the maximum ofKIIis 8.1 times that ofKIII.This means that mode II shear probably dominates the propagation of the vertical crack，if it can，under traction conditions and without lateral shift.Withthe increase of the adhesion coefficient from 0.1 to 0.5，the maximum ofKIIincreases by only 3.98% under traction conditions and without lateral shift，while the maximum ofKIIIdecreases by 20.8%.
Key words:wheel-rail rolling;rolling contact fatigue;vertical crack;wheel-rail adhesion;dynamic stress intensity factor;explicit finite element method
中图分类号：U211.5
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0090
文章编号：1000-4750(2018)05-0239-07
收稿日期：2017-01-23；修改日期：2017-11-27
基金项目：国家自然科学基金项目(51305361，51675444)；牵引动力国家重点实验室自主课题(2015TPL_T09)
通讯作者：赵 鑫(1981―)，男，山东人，副研究员，博士，从事轮轨关系研究及轮轨滚动接触损伤(E-mail:xinzhao@home.swjtu.edu.cn).
作者简介：赵小罡(1992―)，男，江苏人，硕士生，从事轮轨滚动接触力学和伤损研究(E-mail:xiaog_z@163.com);
温泽峰(1976―)，男，广西人，研究员，博士，博导，从事轮轨关系和伤损研究(E-mail:zfwen@home.swjtu.edu.cn);
金学松(1956―)，男，江苏人，教授，博士，博导，从事高速轮轨关系及高速列车减振降噪研究(E-mail:xsjin@home.swjtu.edu.cn).