孙小云1，2，韩建平1，2，党 育1，2，周 颖3
(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室，甘肃，兰州 730050；2.兰州理工大学 防震减灾研究所，甘肃，兰州 730050；3.同济大学 土木工程防灾国家重点实验室，上海200092)
摘 要：地震动持时对非弹性结构的累积损伤和破坏有较大影响，但目前抗震分析设计中对地震动持时的规定是不明确的。从美国太平洋地震工程研究中心地震动数据库中选择具有不同持时和加速度峰值的60条地震动记录(PEER)中选取具有不同持时和加速度峰值的60条地震动记录，并划分为长、短持时两组各30条。利用OpenSees分析软件建立了一钢筋混凝土框架-填充墙结构教学楼的三维空间模型。分别以梁柱节点区不考虑非弹性变形、梁柱节点区考虑钢筋黏结滑移、梁柱节点区考虑钢筋黏结滑移和剪切变形三种工况来依次模拟节点区的破坏模式。以此60条地震动记录为输入进行结构的地震易损性分析，得到在五种损伤水平下，对应于不同工况两组持时记录的结构地震易损性曲线，进而评估地震动持时对考虑节点区不同破坏模式结构抗震性能的影响。分析结果表明，相对于短持时地震动记录，长持时地震动记录使结构在相应损伤水平和工况下的超越概率明显提高；同一损伤水平下，按照梁柱节点区不考虑非弹性变形，考虑钢筋黏结滑移，同时考虑钢筋黏结滑移和剪切变形的顺序，长、短持时地震动记录作用下其超越概率均显著提高，且长持时地震动记录对节点区考虑钢筋黏结滑移和剪切变形结构的影响更为明显。
关键词：重要持时；钢筋混凝土(RC)框架；抗震性能；损伤水平；易损性曲线
目前抗震设计中多采用的振型分解反应谱法，并不能反映地震动持时特性对结构地震反应的影响。而地震动持时对结构破坏的影响已引起相关人员的足够重视，尤其在2010年智利8.8级地震和2011年日本东北地震中，由于长持时引起的结构破坏更为明显[1]。一般认为对于具有刚度和强度退化特性的结构，地震动持时对其破坏具有一定的影响[2]。但地震动持时对结构破坏的影响程度还存在一定的争议，在抗震分析设计中如何考虑持时的影响也不明确[3]。
近几年有研究表明：虽然地震动持时对结构的峰值反应影响不大，但它与结构积累损伤和疲劳破坏有较大的相关性[4－6]，尤其会显著影响结构的残余位移和抗倒塌能力[7－8]。而梁柱节点作为框架结构的关键受力部位和抗震的薄弱环节，关于持时对考虑节点区不同破坏模式的RC框架结构抗震性能影响的研究甚少。大量震后研究表明地震作用下结构节点区非弹性变形主要为钢筋黏结滑移和节点剪切变形，而非弹性变形的发展程度不同也会导致结构以不同的破坏模式失效[9－11]。在目前的数值分析中，经常选用的纤维单元模型可以精确地模拟轴力和弯矩的作用，但无法考虑会导致结构发生非弹性变形的钢筋黏结滑移和节点剪切变形。因此，在研究持时对结构抗震性能的影响时，较为准确地考虑节点的非弹性变形及其可能造成的结构破坏模式是非常必要的。
建筑结构的地震易损性(Seismic Fragility)是指在不同强度地震作用下结构达到或超过某种极限状态的条件概率，是对建筑物所有极限状态的概率分布的描述，通过易损性曲线或易损性矩阵表示。它从概率的意义上定量地刻画了工程结构的抗震性能，从宏观的角度描述了地震动强度与结构破坏程度之间的关系，目前已经成为地震工程和结构工程的热点研究领域[12－13]。结构的地震易损性分析对于评估结构抗震性能、进行结构抗震设计及加固和维修决策等具有重要应用价值[14－15]。
该文选取具有不同持时和峰值加速度的60条地震动记录，为减小频谱特性对结构地震响应的影响，对此60条地震动记录进行了基于规范谱的拟加速度谱的匹配。以60条地震动记录的5%～95%重要持时为依据，将其分为短持时和长持时地震动记录各30条。以一按GB 50011—2010《建筑抗震设计规范》设计的8度(0.2 g)设防的某小学钢筋混凝土框架-填充墙教学综合楼为算例，考虑填充墙平面内外相互作用建立三维空间数值模型。框架梁柱节点分为不考虑非弹性变形(以下简称“工况1”)、考虑钢筋黏结滑移(以下简称“工况2”)、同时考虑钢筋黏结滑移和剪切变形(以下简称“工况3”)的三种情况模拟。选用上述 60条地震动记录，采用OpenSees分析软件对该结构进行地震易损性分析(Seismic Fragility Analysis)，进而通过易损性曲线，评估地震动持时对考虑节点区不同破坏模式RC框架结构抗震性能的影响。
本文选用重要持时Ds(Significant Duration)的计算方法来定义持时指标。重要持时是用地震动加速度记录的能量累积达到两个不同的阈值之间的时间段来定义的。如Trifunac和Brady[16]给出的90%重要持时即为从地震动能量达到总能量的5%开始至达到总能量95%为止所经历的时间。能量的积累过程由地面运动的加速度的积分平方表示。对加速度的平方积分，就可以得到如式(1)所示的Arias强度IA(t)。同时，归一化的Arias强度A(t)可以用式(2)表示。
式中：a(t)为地震加速度记录；g为重力加速度。
归一化的Arias强度记为：
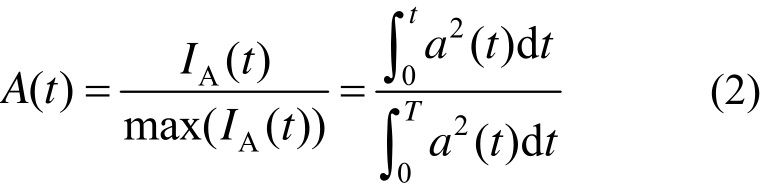
式中：T为加速度记录a(t)的总持续时间；A(t)为一个值域为0～1的函数。
目前，5%～95%重要持时是在工程实践中应用最广泛的持时。Kempton和Stewart[17]指出，绝大多数持时预测方程都采用5%～95%重要持时作为研究对象，而5%～75%重要持时一般情况下只包含体波的能量，可为不同类型地震动的区分提供依据。
为了尽可能消除峰值加速度和频谱特性的影响，仅考虑持时特性对结构抗震性能的影响，该文对表1所示的60条地震动记录进行了基于规范谱的拟加速度谱的匹配，并采用5%～95%重要持时Ds5%-95%作为地震动持时指标。以Eq.12地震记录为例，其5%～95%重要持时的计算如图1所示。
对所选取的60条地震动记录，以Ds5%-95%=30s为界线划分长持时记录和短持时记录，则长持时记录和短持时记录各为30条。以2010规范设计反应谱为目标谱进行谱匹配，目标谱和60条匹配谱周期均从0.02s～6.00s，时间间隔为0.02s。
对于60条地震动记录基于规范谱匹配的比较，以Eq.28地震动记录(Ds5%-95%=20.47s)和Eq.51地震动记录(Ds5%-95%=103.95s)为例，短持时地震动记录和长持时地震动记录谱匹配后拟加速度反应谱、位移反应谱的比较分别如图2(a)和图2(b)所示。
表1 选取的地震动记录
Table1 Selected ground motion records
续表
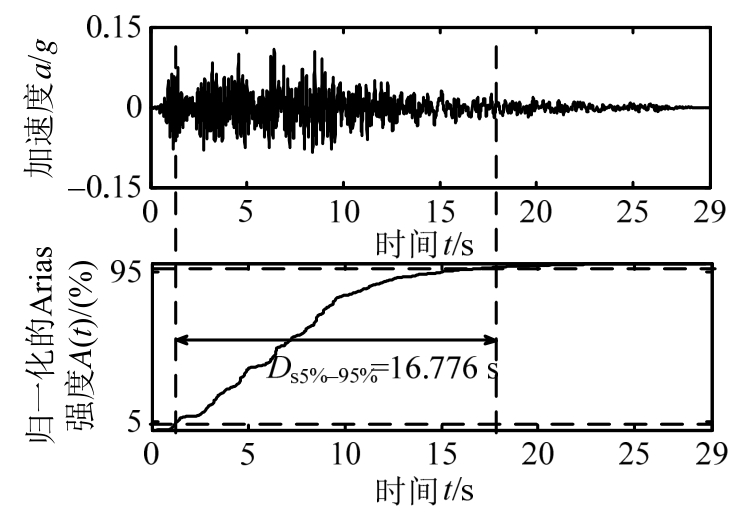
图1 Eq.12地震动记录5%～95%重要持时的计算
Fig.1 Computation of 5%～95% significant duration of Eq.12 ground motion record
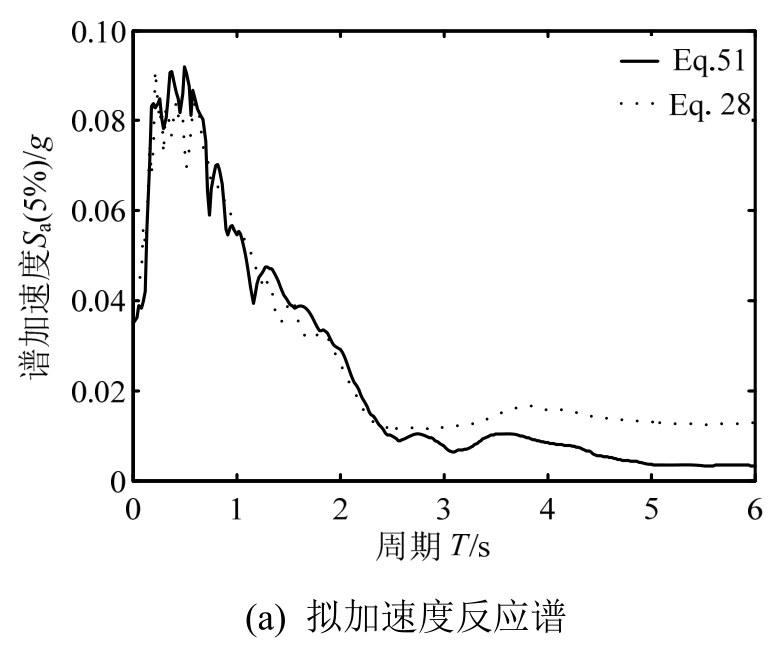
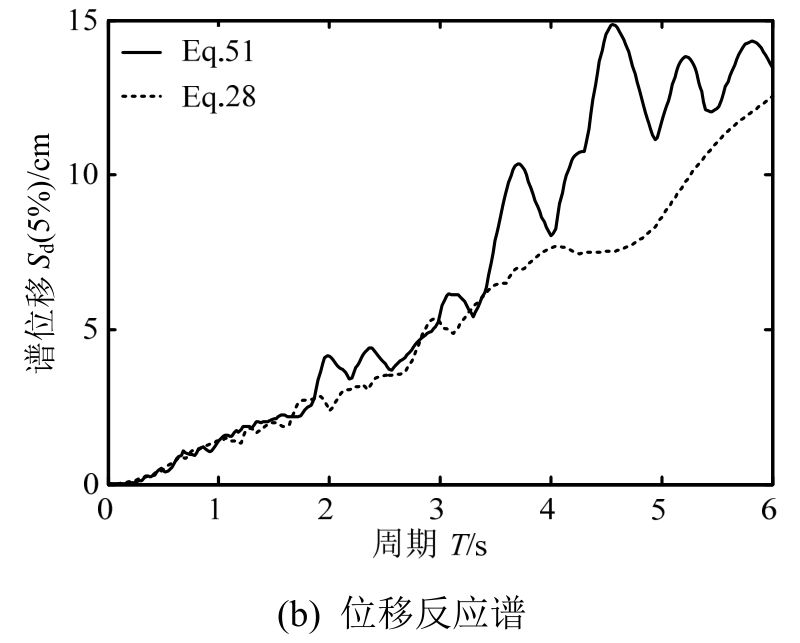
图2 谱匹配后长、短持时地震动记录反应谱的比较
Fig.2 Comparison of response spectra of spectrally matched ground motion records with long and short durations
图3所示为某小学教学综合楼结构平面布置图。
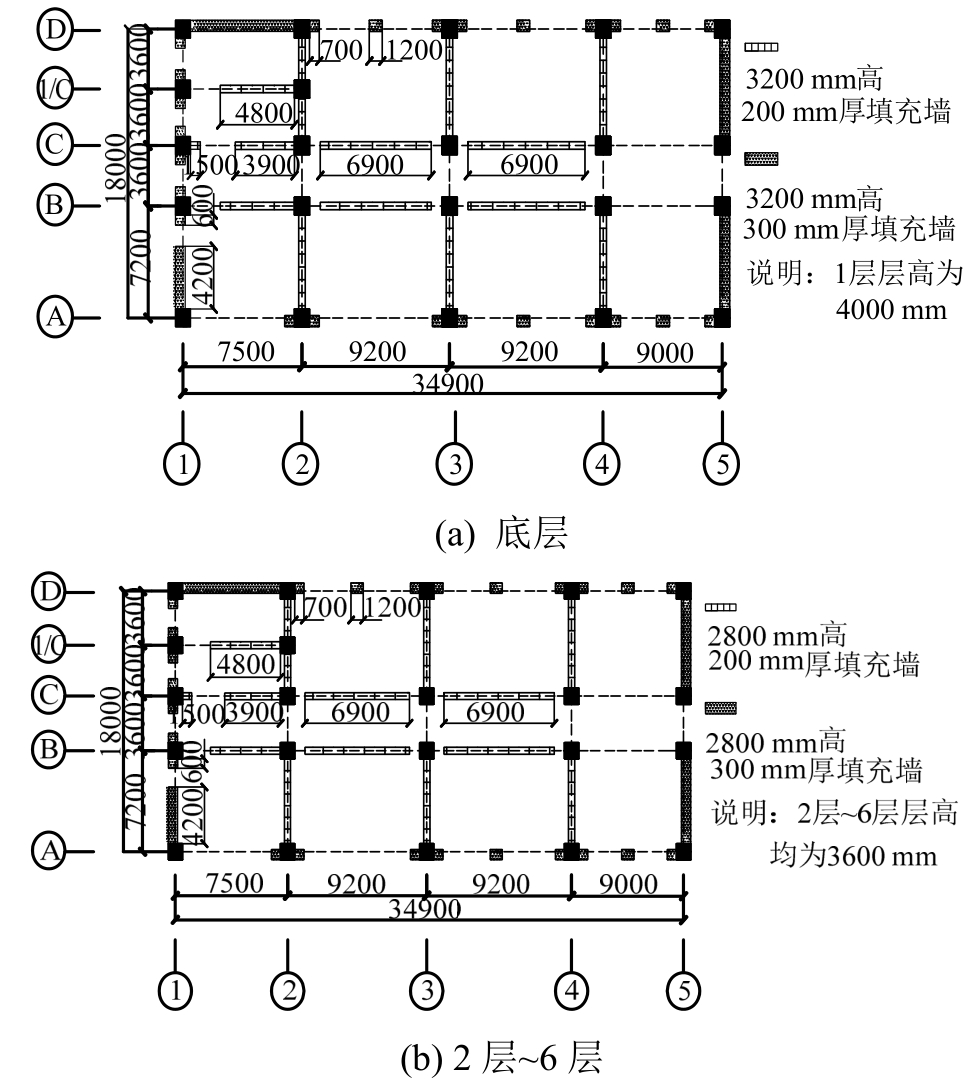
图3 6层RC框架-填充墙结构平面布置
Fig.3 Floor plans of 6-story infilled RC frame structure
该工程共六层，1层层高4 m，其它层层高均为3.6 m。填充墙采用加气混凝土砌块，容重≤800kg/m3，砌体砂浆采用M5混合砂浆，砌筑质量等级为B级。楼板采用厚为270mm的空心楼板，框架柱与框架梁均采用C40混凝土，楼板采用C30混凝土。梁柱受力主筋均采用HRB400钢筋，箍筋采用HPB300钢筋。工程所在地抗震设防烈度为8度，设计基本地震加速度值为0.2g，场地类别为Ⅱ类，设计地震分组为第三组，场地设计特征周期为0.45 s，建筑抗震设防类别为重点设防类。
以OpenSees为计算分析平台，混凝土本构采用Concrete02，并考虑核心区混凝土的约束效应，分别对核心区混凝土和保护层混凝土的本构进行定义[18－19]。钢筋本构采用ReinforcingSteel，已考虑钢筋后期强度退化。采用梁柱纤维单元建立整体框架的分析模型[18－20]。梁、柱均采用基于位移的梁柱单元(Displacement-Based Beam-Column Element)。柱的几何坐标转换选用P-Δ转换器(P-ΔTransformation)，以考虑结构侧移引起的二阶弯矩效应[21]。填充墙采用可以考虑填充墙平面内外相互作用的纤维离散化梁-柱单元模型，用两个带塑性铰的梁单元模拟[21]。
如图4所示在梁柱单元端部附加一个零长度截面单元以考虑钢筋黏结滑移。钢筋黏结滑移本构关系如图5所示[22]。
图4 黏结滑移的零长度截面单元
Fig.4 Zero-length section element of bond-slip
图5 钢筋黏结滑移本构关系
Fig.5 Constitutive relationship of bar-slip
直线部分：
曲线部分：
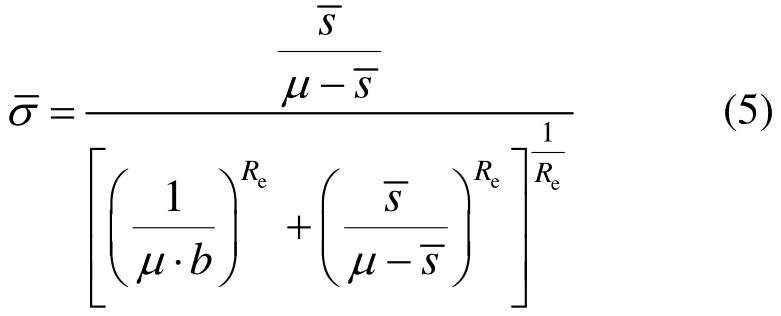
式中：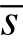
=(s-sy)/sy为标准化的钢筋滑移；μ=(su-sy)/sy为延性系数；b为刚度折减系数，其代表刚开始屈服时曲线段的初始斜率与弹性区斜率k的比值；fy和fu分别为钢筋的屈服强度和极限强度，而sy和su则分别为当钢筋应力为fy和fu时加载端的滑移。系数Re的取值决定循环往复加载下曲线的捏笼效应，其值通常取0.5～1.0，Re越小，捏笼效应越明显。
在梁柱节点区，沿垂直柱轴向用一个与梁柱单元串联的剪切弹簧模拟柱的弯-剪耦合，剪切弹簧选用Shear Limit Curve和Limit State Material材料模型定义；沿柱轴向用一个与梁柱单元串联的轴向弹簧模拟柱的轴向变形，轴向弹簧选用Axial Limit Curve和Limit State Material材料模型定义。该模型考虑了轴-剪-弯三者的耦合，如图6所示。剪切弹簧和轴向弹簧分别满足式(6)和式(7)所示的极限曲线[23]。
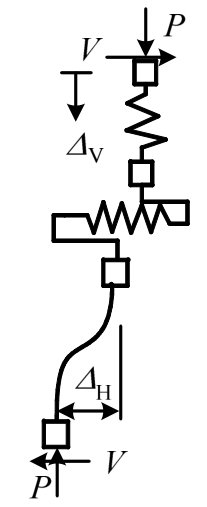
图6 考虑轴-剪-弯耦合的串联模型
Fig.6 Series model considering axial-shear-flexure interaction
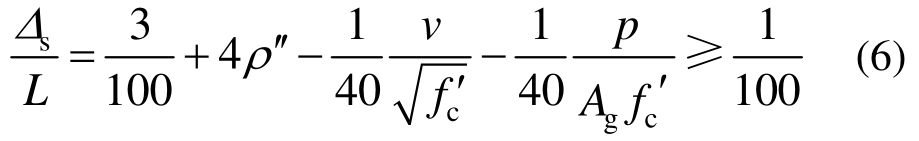
式中：
为发生剪切破坏时的位移角；
为横向钢筋配筋率；v为名义剪切应力；
为混凝土抗压强度；p为柱上的轴向荷载；Ag为总的横截面积。
式中：dc为柱截面核心区高度；s为箍筋间距；Ast和fyt分别为横向箍筋的面积和屈服强度；θ为剪切裂缝与水平方向所成的夹角，通常取65°。
该文为了体现节点区在地震中可能出现的实际破坏模式，分以下三种工况进行节点模型的建立。
工况1：梁柱单元节点区不考虑非弹性变形，即不考虑梁柱节点区的钢筋黏结滑移和剪切变形。
工况2：在梁柱单元节点处串联一零长度截面单元考虑梁柱节点区钢筋黏结滑移。
工况3：在梁柱单元节点区既考虑钢筋黏结滑移又考虑剪切变形。
结构的地震易损性定义为给定强度地震作用下，预定状态失效的条件概率。其中，在基于性能抗震设计中，“失效”指的是结构不能满足某种预定的性能水平。根据地震易损性的定义，其数学表达式为：
式中：FR为地震易损性；P[·]为失效概率；A为地震动强度指标，可取地面峰值加速度PGA、地面峰值速度PGV、阻尼比5%的结构基本周期对应的加速度谱值Sa(T1，5%)等；fR|A[r|a]为地震动强度A=a时，结构反应的条件概率密度。
改变式(8)中a的数值，计算结构达到或超过破坏状态的地震易损性FR，然后采用某种统计分布的方法进行曲线拟合，得到光滑的曲线称为“地震易损性曲线”，其意义为在某一特定的地震烈度作用下，结构遭受特定损伤状态的概率[24]。
在地震易损性分析中，通常将建筑结构在地震作用下的破坏程度分为若干等级，该文结合2010版抗震设计规范给出的钢筋混凝土框架结构竖向构件对应于不同破坏状态的最大层间位移角参考控制目标：基本完好(1/550)、轻微破坏(1/250)、中等破坏(1/120)和不严重破坏(1/60)以及弹塑性层间位移角限值(1/50)[25]，将结构在地震作用下的破坏程度划分为五种损伤水平，且根据易损性分析结果给出了五种损伤水平下，对应于不同持时地震动记录和考虑节点区不同破坏模式三种工况的易损性曲线，如图7～图16所示。图7～图16中横坐标Sa(T1，5%)表示阻尼比为5%、结构基本周期对应地震动加速度谱值，纵坐标Pf表示不同损伤水平下的超越概率。
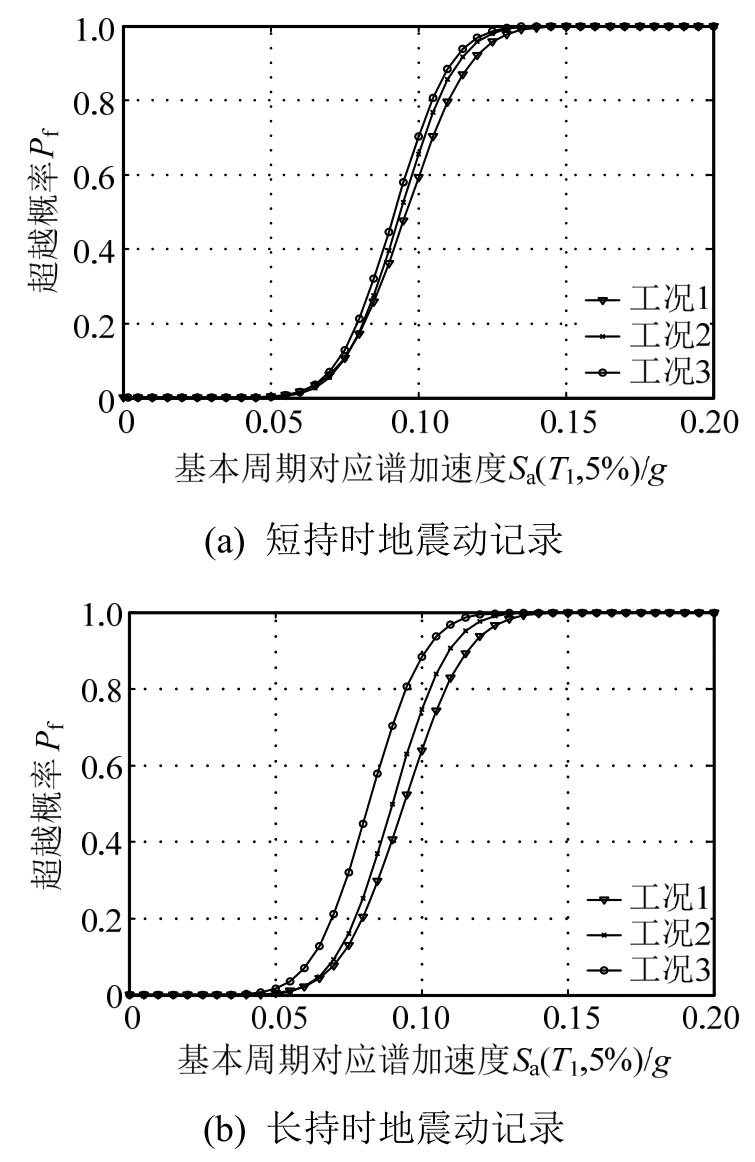
图7 基本完好状态对应的地震易损性曲线
Fig.7 Seismic fragility curves of well preservation state
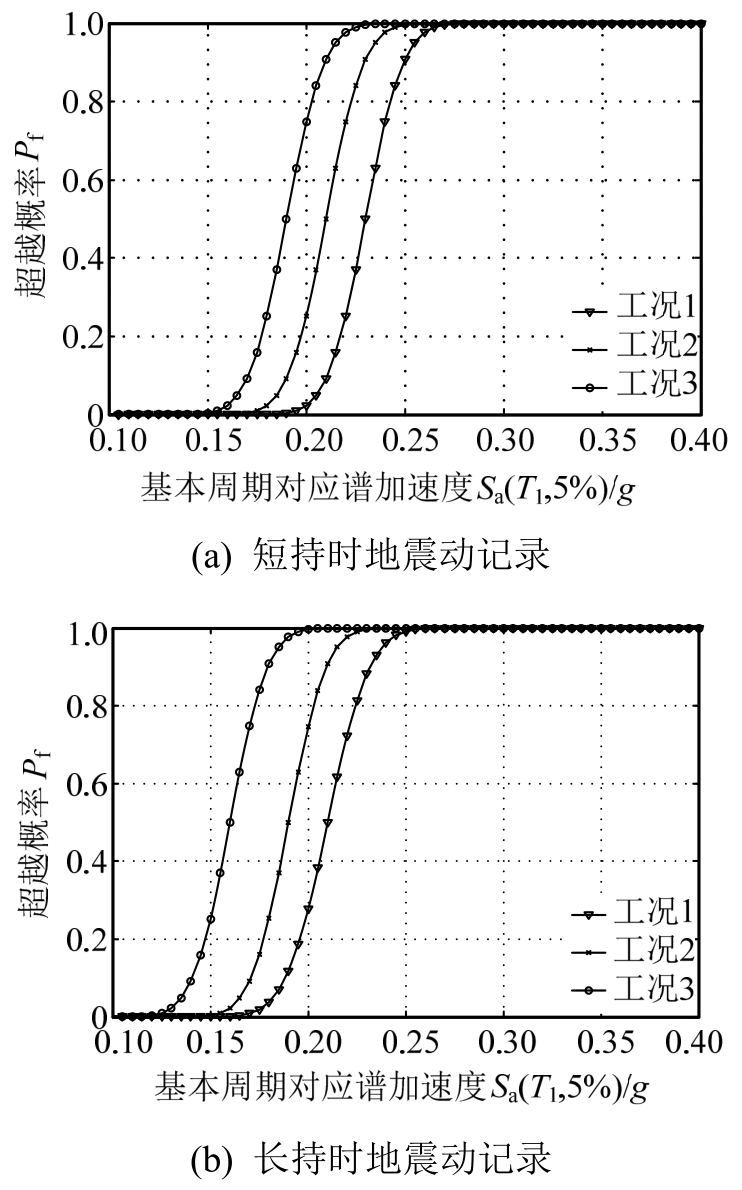
图8 轻微破坏状态对应的地震易损性曲线
Fig.8 Seismic fragility curves of slight damage state
图7～图11表示同为长持时或短持时记录作用下，对应于节点区不考虑非弹性变形、节点区考虑钢筋粘结滑移以及节点区同时考虑粘结滑移和剪切变形三种工况下的易损性曲线比较。
图9 中等破坏状态对应的地震易损性曲线
Fig.9 Seismic fragility curves of moderate damage state
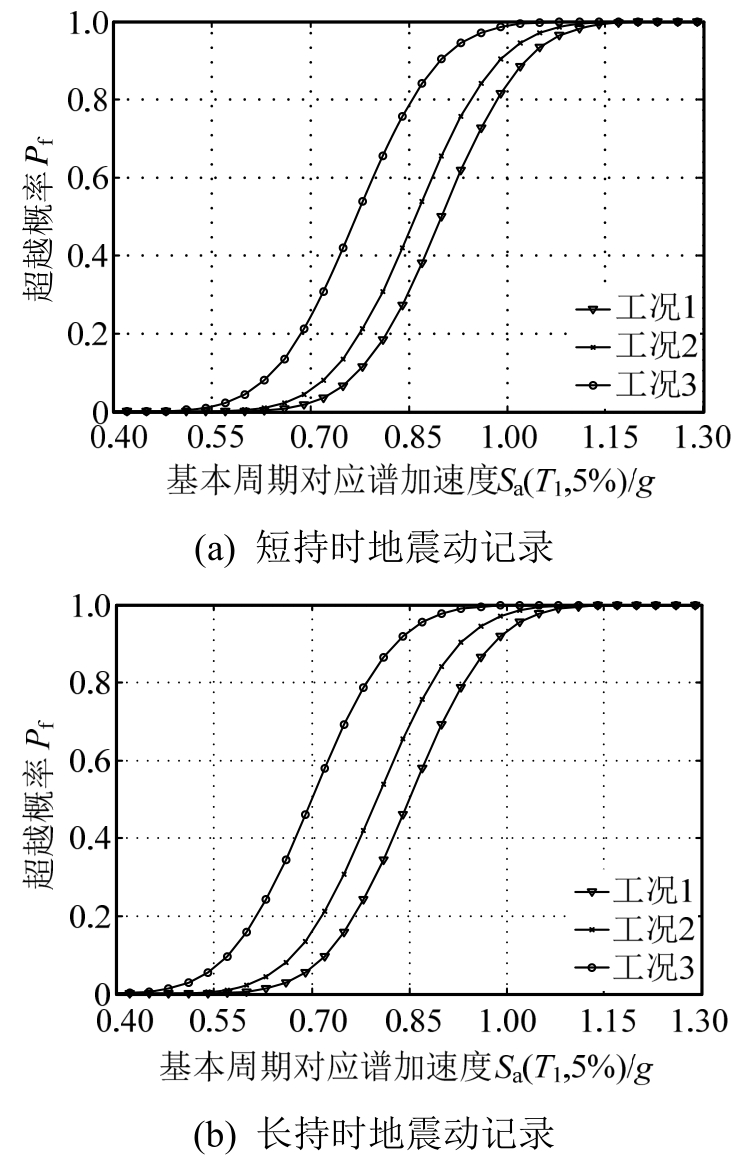
图10 不严重破坏状态对应的地震易损性曲线
Fig.10 Seismic fragility curves of no severe damage state
图11 弹塑性层间位移角限值状态对应的地震易损性曲线
Fig.11 Seismic fragility curves of inelastic inter-story drift limit state
图7～图11结果表明，在基本完好性能水平下，由于结构变形处于弹性范围，工况1、工况2和工况3易损性曲线切线斜率基本接近，虽然工况1、工况2、工况3下超越概率依次增大，但增大幅度不是很明显；随着损伤不断积累，如结构逐渐进入轻微破坏、中等破坏、不严重损伤状态甚至临近结构弹塑性层间位移角限值状态，工况1、工况2、工况3下结构易损性曲线中的斜坡段切线斜率明显增大，超越概率依次增大的幅度更加明显。总体上，在5种损伤水平下，无论是长持时还是短持时记录，工况3各损伤状态的超越概率最大，工况2次之，工况1最小；工况3相对于工况2超越概率的提高幅度均大于工况2相对于工况1超越概率的提高幅度，而且在长持时地震动记录作用下这种差别更加明显。在同一损伤水平下，长持时记录导致三种工况超越概率的变化幅度明显高于短持时记录导致三种工况超越概率的变化幅度，而且随着结构损伤不断积累增大，差异更加明显。即结构由于节点区剪切变形造成的破坏明显高于节点区钢筋滑移变形造成的破坏。
图12～图16表示在三种节点区破坏模式下，长持时与短持时记录作用下结构的易损性曲线比较。
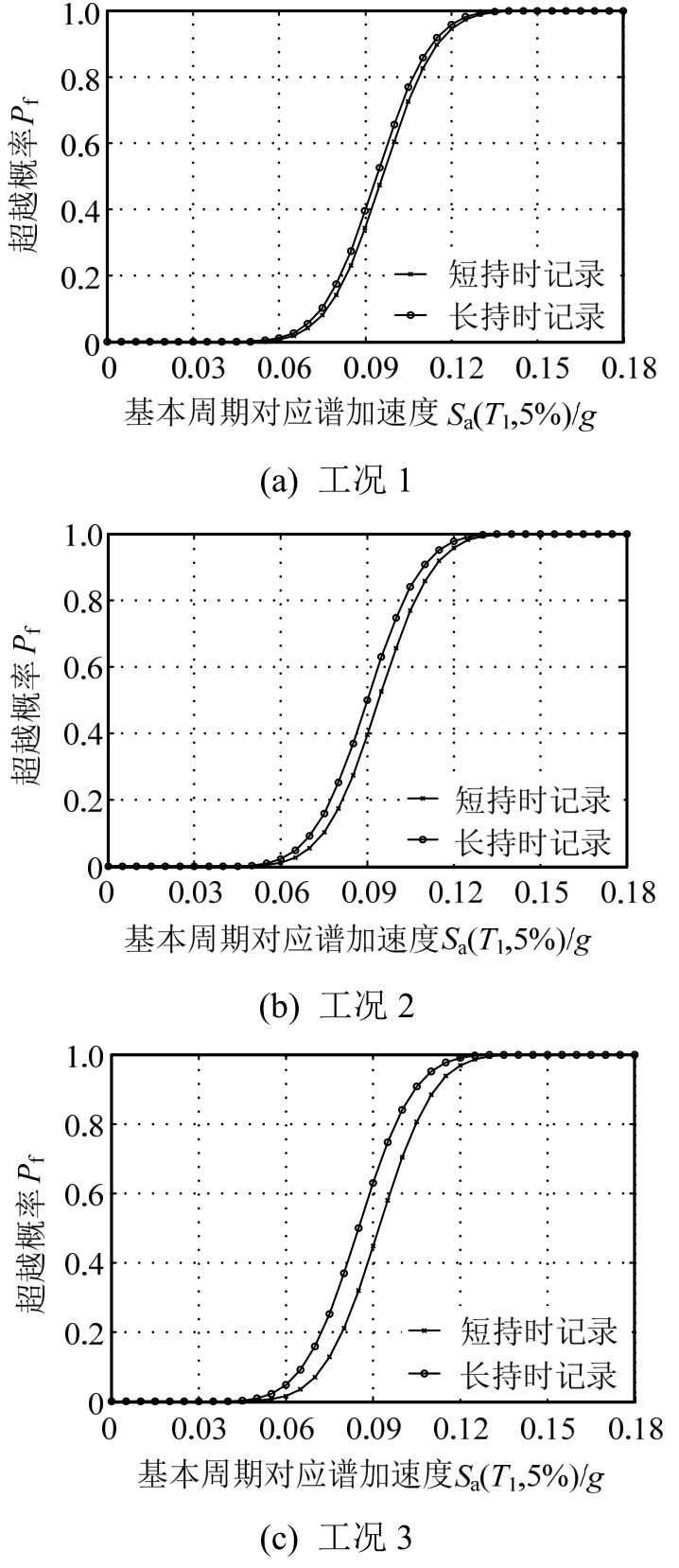
图12 基本完好状态对应的地震易损性曲线
Fig.12 Seismic fragility curves of well preservation state
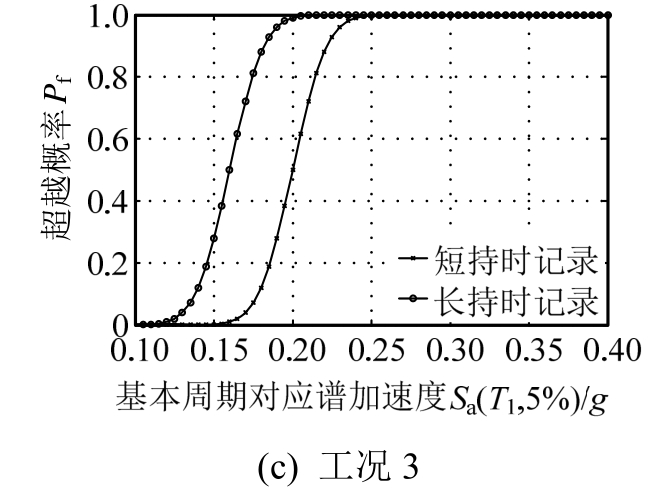
图13 轻微破坏状态对应的地震易损性曲线
Fig.13 Seismic fragility curves of slight damage state
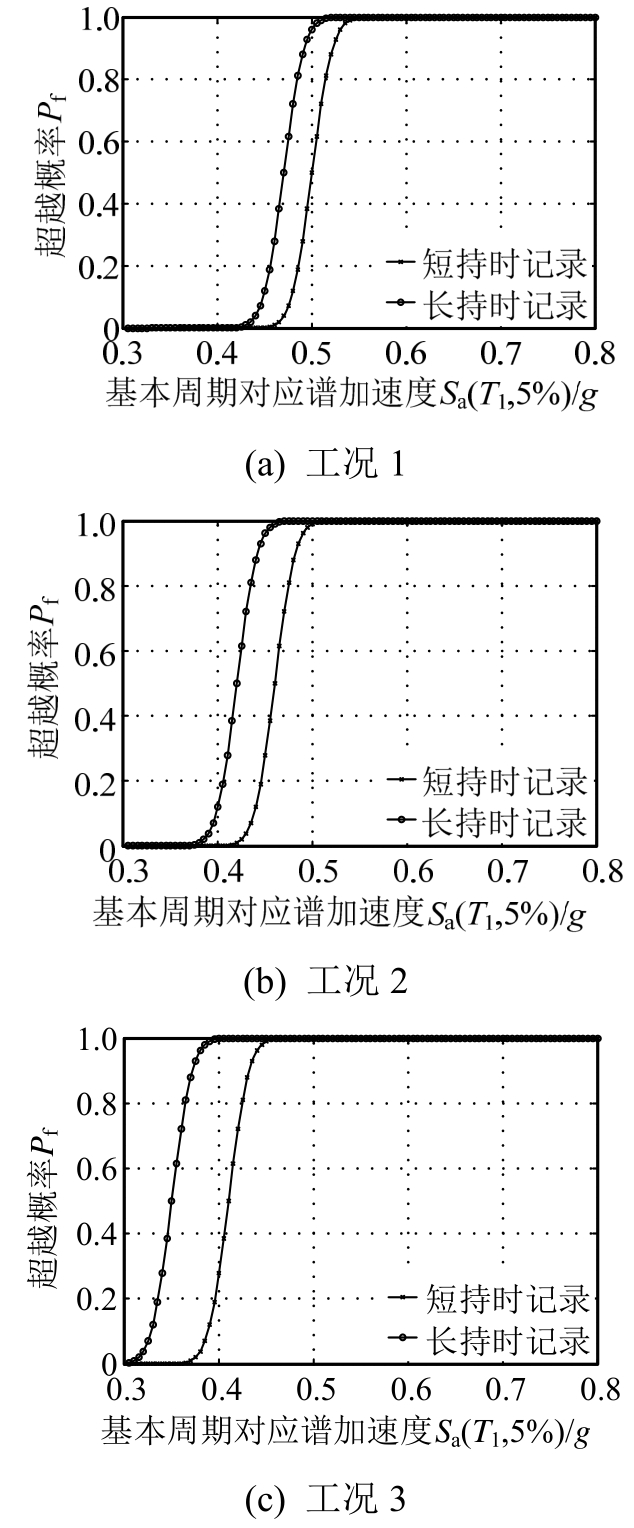
图 14 中等破坏状态对应的地震易损性曲线
Fig.14 Seismic fragility curves of moderate damage state
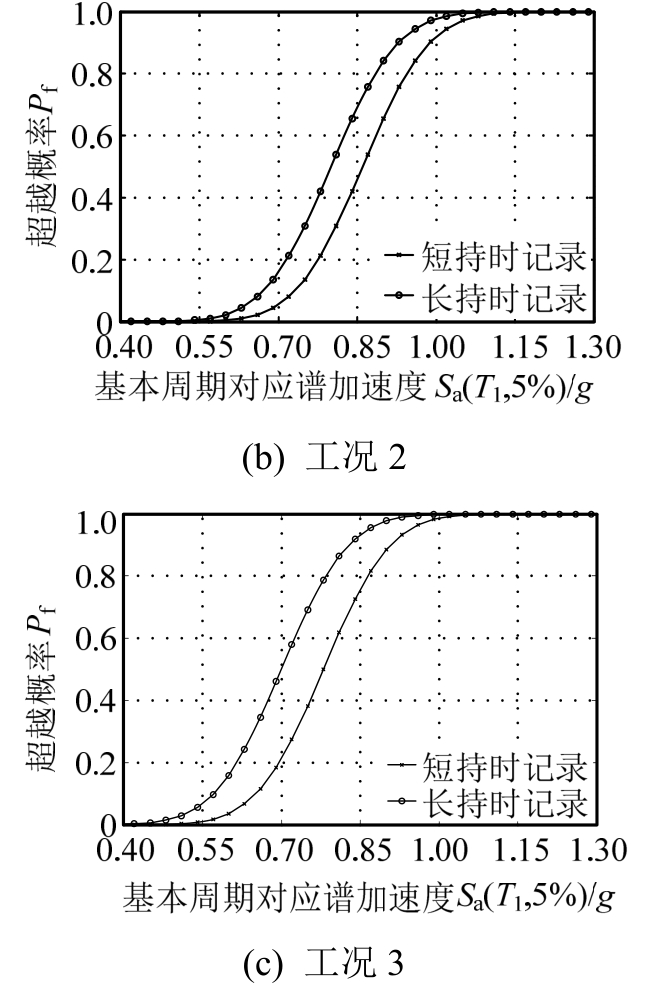
图15 不严重破坏状态对应的地震易损性曲线
Fig.15 Seismic fragility curves of no severe damage state
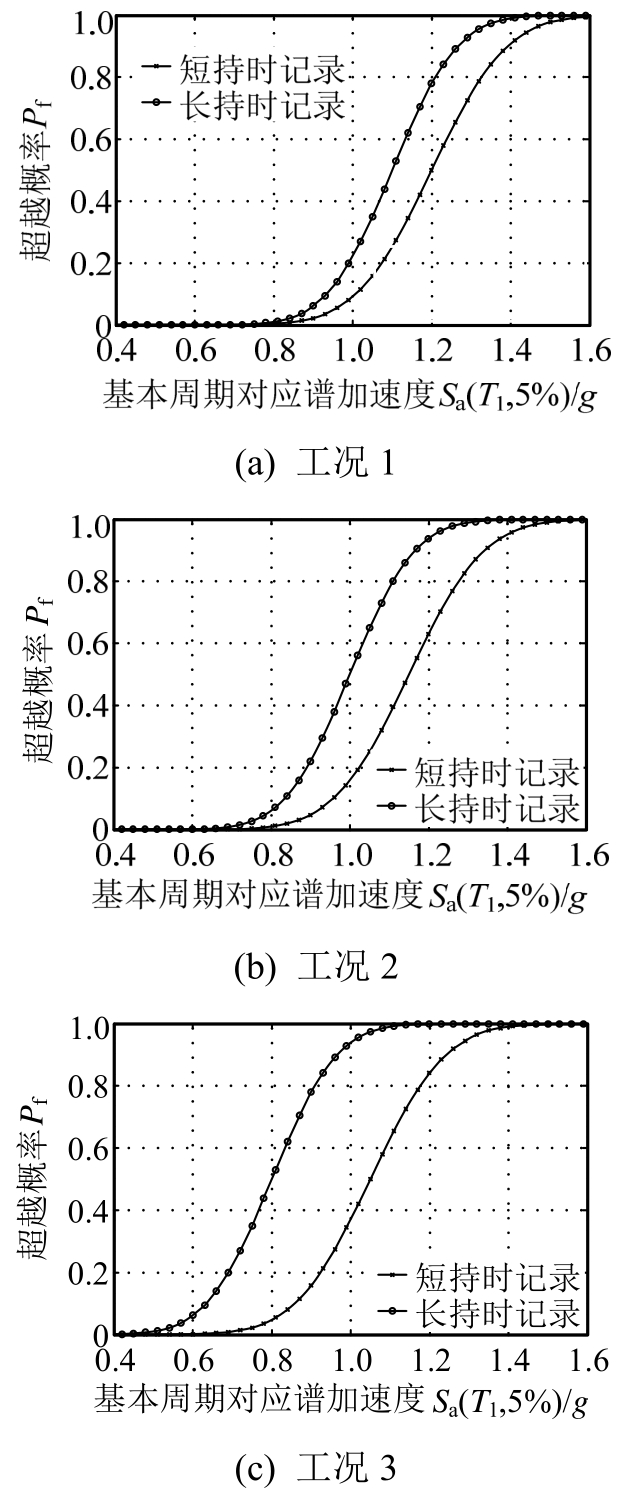
图16 弹塑性层间位移角限值状态对应的地震易损性曲线
Fig.16 Seismic fragility curves of inelastic inter-story drift limit state
图12～图16结果表明，在不同的损伤水平下，与短持时地震动记录相比，长持时地震动记录使每种工况的结构在该损伤水平的超越概率均会提高，且随着损伤不断积累，如结构逐渐进入轻微破坏、中等破坏、不严重损伤状态甚至临近结构弹塑性层间位移角限值状态，这种提高幅度愈加明显，且不论是短持时地震动记录还是长持时地震动记录，均会使每种工况下结构的超越概率依次增大。
基于OpenSees分析软件，为考虑梁柱节点区在地震中常见的破坏模式，建立了三种不同工况下的梁柱节点破坏模型，对一6层钢筋混凝土框架-填充墙结构进行了地震易损性分析，结果表明：
(1)在同一损伤水准下，随着RC框架结构节点区不考虑非弹性变形，考虑钢筋黏结滑移，以及同时考虑钢筋黏结滑移和剪切变形，短持时和长持时地震动记录作用下相应结构响应的超越概率均有所提高，即节点的复杂非弹性变形和破坏模式对结构损伤有重要影响。并且与节点区考虑黏结滑移相比，考虑剪切变形的破坏模式使其提高幅度均较大，即节点区剪切变形比钢筋滑移变形对结构抗震性能的影响更加明显。
(2)随着RC框架结构节点区非弹性变形逐步发展和损伤不断积累，长持时地震动记录作用下结构超越概率的提高幅度明显大于短持时地震动记录作用下结构超越概率的提高幅度，即长持时地震动记录对结构剪切变形和钢筋滑移变形的影响明显高于短持时地震动记录对其产生的影响。
(3)随着损伤不断积累，长持时地震动更易使结构发生不同程度的损伤。即长持时地震动记录对结构抗震性能的影响更为明显。
参考文献：
[1]Midorikawa S，Miura H，Si H.Preliminary analysis for characteristics of strong ground motion from gigantic earthquakes[C]// Proceedings of the 15th World Conference on Earthquake Engineering.Lisboa，Portugal:International Association for Earthquake Engineering，2012.
[2]李杰，李国强.地震工程学导论[M].北京:地震出版社，1992:51―53.Li Jie，Li Guoqiang.Introduction to earthquake engineering[M].Beijing:Seismological Press，1992:51―53.(in Chinese)
[3]Bommer J J，Magenes G，Hancock J，et al.The influence of strong motion duration on the seismic response of masonry structures[J].Bulletin of the Seismological Society of America，2004，2(1):1―26.
[4]Reagan C，Baker J W，Deierlein G G，et al.Hazard-consistent ground motion duration:calculation procedure and impact on structural collapse risk[C]//Proceedings of the 10th U.S.National Conference on Earthquake Engineering.Alaska:Earthquake Engineering Research Institute，2014.
[5]Foschaar J C，Baker J W，Deierlein G G.Preliminary assessment of ground motion duration effects on structural collapse[C]// Proceedings of the 15th World Conference on Earthquake Engineering.Lisboa，Portugal:International Association for Earthquake Engineering，2012.
[6]Lin L，Naumoski N，Saatcioglu M，et al.Effects of strong-motion duration on the response of reinforced concrete frame buildings[C]// Proceeings of the 9th U.S.National and 10th Canadian Conference on Earthquake Engineering.Toronto，Canada:Canadian Association for Earthquake Engineering，2010.
[7]Raghunandan M，Liel A B.Effect of ground motion duration on earthquake-induced structural collapse[J].Structural Safety，2013，41:119―133.
[8]韩建平，孙小云，周颖.基于规范谱拟合的人工地震动持时对RC框架结构抗倒塌能力影响[J].建筑结构学报，2016，37(7):121―126.Han Jianping，Sun Xiaoyun，Zhou Ying.Effect of code-spectrum-matched artificial ground motion duration on collapse resistance capacity of RC frame[J].Journal of Building Structures，2016，37(7):121―126.(in Chinese)
[9]Zhao B，Taucera F，Rossettob T.Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China[J].Engineering Structures，2009，31(8):1707―1723.
[10]杨红，莫林辉，陈进可，等.钢筋混凝土梁柱节点区非弹性变形的改进模型研究[J].建筑结构学报，2014，35(3):128―137.Yang Hong，Mo Linhui，Chen Jinke，et al.Study on modified models for inelastic deformation of reinforced concrete beam-column joints[J].Journal of Building Structures，2014，35(3):128―137.(in Chinese)
[11]朱绩超，王响，张勤.考虑粘结-滑移与剪切作用的钢筋混凝土柱侧向变形分析[J].工程力学，2015，32(7):128―135.Zhu Jichao，Wang Xiang，Zhang Qin.Lateral deformations analysis of reinforced concrete columns incorporating bond-slip and shear effects[J].Engineering Mechanics，2015，32(7):128―135.(in Chinese)
[12]于晓辉，吕大刚，王光远.土木工程结构地震易损性分析的研究进展[C]//第二届结构工程新进展国际论坛论文集.北京:中国建筑工业出版社，2008:763―774.Yu Xiaohui，Lü Dagang，Wang Guangyuan.Seismic fragility analysis of civil engineering structures:state-of-the-art[C]// Proceedings of 2nd International Forum on Advances in Structure Engineering.Beijing:China Architecture and Building Press，2008:763―774.(in Chinese)
[13]何益斌，李艳，沈蒲生.基于性能的高层混合结构地震易损性分析[J].工程力学，2013，30(8):142―147.He Yibin，Li Yan，Shen Pusheng.Performance-based seismic fragility analysis of tall hybrid structures[J].Engineering Mechanics，2013，30(8):142―147.(in Chinese)
[14]姜绍飞，杨博，党永勤.易损性分析在结构抗震及健康监测中的应用[J].建筑科学与工程学报，2008，25(2):15―23.Jiang Shaofei，Yang Bo，Dang Yongqin.Application of vulnerability analysis in structural seism and health monitoring[J].Journal of Architecture and Civil Engineering，2008，25(2):15―23.(in Chinese)
[15]于晓辉，吕大刚.HAZUS相容的钢筋混凝土框架结构地震易损性分析[J].工程力学，2016，33(3):152―160.Yu Xiaohui，Lü Dagang.HAZUS-compatible seismic fragility analysis for RC frame structures[J].Engineering Mechanics，2016，33(3):152―160.(in Chinese)
[16]Trifunac M D，Brady A G.A study on the duration of strong earthquake of ground motion[J].Bulletin of the Seismological Society of American，1975，65(3):581―626.
[17]Kempton J J，Stewart J P.Prediction equations for significant duration of earthquake ground motions considering site and near-source effects[J].Earthquake Spectra，2006，22(4):985―1013.
[18]韩建平，杨军平.考虑结构构件退化特性评估大震下RC框架抗整体性倒塌能力[J].地震工程与工程振动，2012，32(6):111―122.Han Jianping，Yang Junping.Investigation on global collapse resistance capacity of RC frame under severe earthquake considering deterioration characteristic of structural components[J].Earthquake Engineering and Engineering Vibration，2012，32(6):111―122.(in Chinese)
[19]Mazzoni S，McKenna F，Fenves G L.The OpenSees getting started manual[EB/OL].[2015-03-31].http://opensees.berkeley.edu，2007.7.1.
[20]Kunnath S K，Heo Y A，Mohle J F.Nonlinear uniaxial material model for reinforcing steel bars[J].ASCE Journal of Structural Engineering，2009，135(4):335―343.
[21]韩建平，黄林杰，孙小云.考虑填充墙平面内外相互作用评估 RC框架-填充墙结构抗整体性倒塌能力[J].工程力学，2016，33(9):146―154.Han Jianping，Huang Linjie，Sun Xiaoyun.Global collapse resistance capacity investigation of infilled RC frame considering in-plane and out-of-plane interaction of infill walls[J].Engineering Mechanics，2016，33(9):146―154.(in Chinese)
[22]Zhao J，Sritharan S.Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J].ACI Structural Journal，2007，104(2):133―141.
[23]Elwood K J，Moehle J P.Dynamic collapse analysis for a reinforced concrete frame sustaining shear and axial failures[J].Earthquke Engineering and Structural Dynamics，2008，37(7):991―1012.
[24]吴巧云，朱宏平，樊剑.基于性能的钢筋混凝土框架结构地震易损性分析[J].工程力学，2012，29(9):117―124.Wu Qiaoyun，Zhu Hongping，Fan Jian.Performancebased seismic fragility analysis of RC frame structures[J].Engineering mechanics，2012，29(9):117―124.(in Chinese)
[25]GB 50011—2010，建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.GB 50011—2010，Code for seismic design of buildings[S].Beijing:China Architecture and Building Press，2010.(in Chinese)
EFFECT OF GROUND MOTION DURATION ON SEISMIC FRAGILITY OF RC FRAMES WITH DIFFERENT BEAM-COLUMN JOINT FAILURE MODES
SUN Xiao-yun1，2，HAN Jian-ping1，2，DANG Yu1，2，ZHOU Ying3
(1.Key Laboratory of Disaster Prevention and Mitigation in Civil Engineering of Gansu Province，Lanzhou University of Technology，Lanzhou，Gansu 730050，China;2.Institute of Earthquake Protection and Disaster Mitigation，Lanzhou University of Technology，Lanzhou，Gansu 730050，China;3.State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China)
Abstract:Ground motion duration has great influence on the cumulative fragility and damage of inelastic structures，but the consideration of duration is not clear in current seismic analysis and design.60ground motion records with different durations and peak ground accelerations were selected from the PEER strong ground motion database，and categorized as 30 long-and 30 short-duration records.A three-dimensional model of aninfilled RC frame teaching building was built via OpenSees.In order to simulate the different failure modes of the beam-column joints，three models were taken，which are the beam-column joints without considering inelastic deformation，with considering the bar bond-slip，and with considering both the bar bond-slip and the shear deformation.Seismic fragility analysis was carried out on the three models under the 60 ground motion records，and the fragility curves for two the kinds of records under different cases were obtained corresponding to five damage levels.Furthermore，the influence of ground motion duration on structural seismic behavior considering the different failure modes of beam-column joints was evaluated.The analytical results show that comparing with the short-duration records，the long-duration records can increase the structural exceedance probability obviously for the corresponding damage levels and beam-column joint cases.Comparing with the case without considering inelastic deformation of beam-column joints，both long-and short-duration records can increase the structural exceedance probability clearly under the same damage level when considering the bar bond-slip or considering both the bar bond-slip and the shear deformation.The effect of long-duration ground motion records on structural seismic performance considering the bar bond-slip and the shear deformation of the beam-column joints is more obvious.
Key words:significant duration;RC frame;seismic performance;fragility level;fragility curves
中图分类号：TU375.4
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0089
文章编号：1000-4750(2018)05-0193-11
收稿日期：2017-01-23；修改日期：2017-06-25
基金项目：国家自然科学基金项目(51578273，51268036)；教育部长江学者和创新团队发展计划项目(IRT13068)
通讯作者：韩建平(1970―)，男，甘肃宕昌人，教授，博士，博导，主要从事结构抗震与减震控制、结构健康监测与损伤诊断研究(E-mail:jphan@lut.cn).
作者简介：孙小云(1988―)，女，甘肃会宁人，博士生，主要从事工程结构抗震研究(E-mail:sxyhuining@163.com);
党 育(1976―)，女，甘肃正宁人，副教授，博士，主要从事工程结构抗震研究(E-mail:dangdangyu@sohu.com);
周 颖(1978―)，女，甘肃古浪人，教授，博士，博导，主要从事工程结构抗震、高层建筑抗震、动力试验方法与技术研究(E-mail:yingzhou@tongji.edu.cn).