表1 试件设计参数
Table1 Test design parameters of specimens
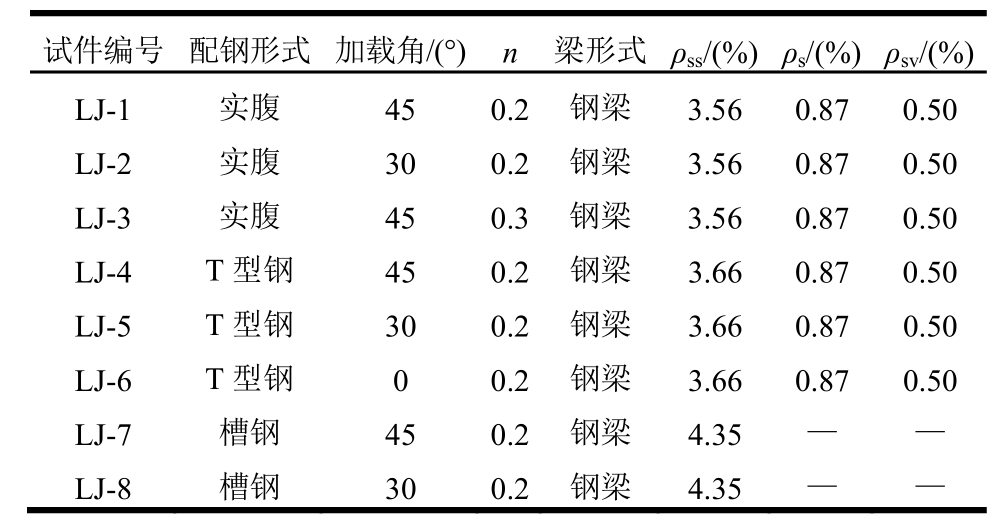
注:n为轴压比,n=N/(fcAc+fyAss),N为轴压力,fc为混凝土轴心抗压强度,Ac、Ass分别为柱中混凝土与型钢的截面面积,fy为型钢屈服强度;ρss为型钢含钢率,包括纵向型钢和水平腹杆;ρs为纵筋配筋率;ρsv为体积配箍率。
王 妮1,陈宗平2,3,陈宇良2
(1.长安大学环境科学与工程学院,陕西,西安 710064,2.广西大学土木建筑工程学院,广西,南宁 530004,3.广西大学工程防灾与结构安全教育部重点实验室,广西,南宁 530004)
摘 要:为研究型钢混凝土L形柱空间角节点的抗震性能,对8个节点试件进行低周反复荷载试验和有限元模拟,二者结果吻合较好。基于此考虑了柱配钢形式、轴压比和加载角度3个变化参数,通过ABAQUS非线性有限元模拟,分析了变化参数对其峰值荷载、耗能和延性的影响规律,并提出可供工程设计参考的建议。研究结果表明,型钢混凝土L形柱空间角节点破坏形态以剪切斜压和弯曲破坏为主,扭转伴随黏结破坏为辅;实腹配钢试件综合抗震性能最好,其峰值荷载较空腹配钢试件提高了10%;随轴压比的增加,不同配钢形式试件的位移延性下降程度不同,实腹配钢试件下降缓慢,建议轴压比限值设计值为0.5;45°加载角度以内,随着加载角度的增加,峰值荷载增加,耗能和延性逐渐降低,45°加载试件与0°平面节点相比,峰值荷载提高了约30%,延性系数降低约10%,最不利加载方向为0°加载。
关键词:型钢混凝土;L形柱;空间角节点;抗震性能;有限元分析
随着国民经济水平的提高,消费者对建筑的宽敞、美观有了更高的要求,钢筋混凝土异形柱结构其柱肢厚度与框架填充墙一致,具有节约空间、美观适用等优点,但特殊的截面形状和配筋形式导致其承载力低、抗震性能差、施工困难等等,这些都限制其在抗震设防高烈度区及高层建筑中的应用,将型钢内置于钢筋混凝土异形柱结构中形成型钢混凝土异形柱结构,能够很好地克服上述缺点,具有广阔的应用前景,有关学者对此进行了研究[1-4]。
节点作为结构的重要组成部位,对保证结构整体安全至关重要。但目前关于型钢混凝土异形柱节点的研究成果主要集中在平面节点[5-6],对其空间节点的抗震性能研究极少[7],而对其他组合空间节点抗震性能的研究较多并取得了一些成果[8-10],但以上空间节点的抗震试验主要采用梁端加载,此方式不能反映柱子P-Δ效应,与工程结构的实际受力不太接近,柱端加载可以解决这一问题,特别是它能研究加载角度对空间节点抗震性能的影响规律。
课题组前期进行了型钢混凝土十、T及L形柱空间节点的柱端加载抗震试验及受力性能研究,取得了较好的成果[11-13],该文结合L形柱空间节点试验数据,利用ABAQUS软件对其进行有限元模拟和参数分析,为异形柱结构的工程设计提供参考。
试件选取多层多跨框架角节点两梁与上、下柱反弯点之间的梁柱组合体为研究对象,考虑配钢形式、轴压比和加载角度(即水平荷载与柱截面形心之间的夹角)3个变化参数。试件按1/2缩尺比设计,肢厚均为240mm,肢高厚比为3,柱中型钢钢筋采用贯通的方式,柱反弯点间距为1400mm,梁反弯点到梁柱交接处的距离为1050mm,试件按“强构件弱核心”的原则设计。各试件的设计参数见表1,试件几何尺寸及配钢如图1所示。
表1 试件设计参数
Table1 Test design parameters of specimens

注:n为轴压比,n=N/(fcAc+fyAss),N为轴压力,fc为混凝土轴心抗压强度,Ac、Ass分别为柱中混凝土与型钢的截面面积,fy为型钢屈服强度;ρss为型钢含钢率,包括纵向型钢和水平腹杆;ρs为纵筋配筋率;ρsv为体积配箍率。
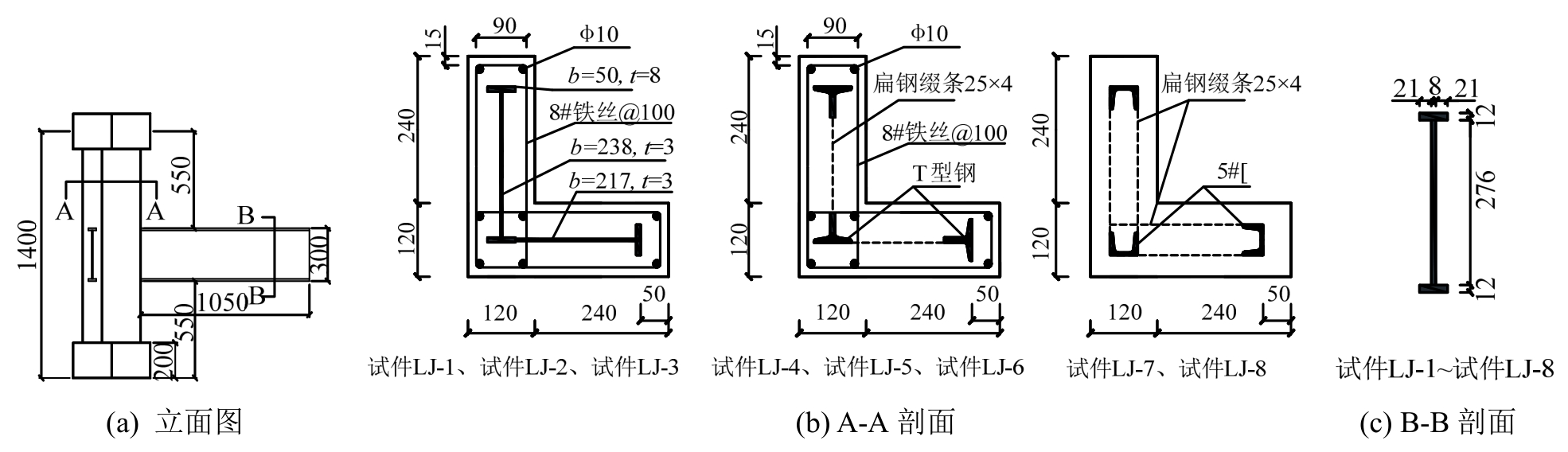
图1 试件几何尺寸及配钢图
Fig.1 Geometrical dimensions and steel reinforcement details of specimens
型钢-钢梁骨架采用相应规格的钢板焊接而成,T型钢桁架通过单侧焊接水平腹杆连接,槽钢桁架通过双侧焊接水平腹杆连接。对于实腹配钢与T型钢桁架的试件,柱中配有相应规格的构造纵筋和箍筋。构件采用C30混凝土立式浇筑,立方体抗压强度为30MPa。实测钢材与钢筋材料属性见表2。
表2 钢材材料性能
Table2 Properties of steel
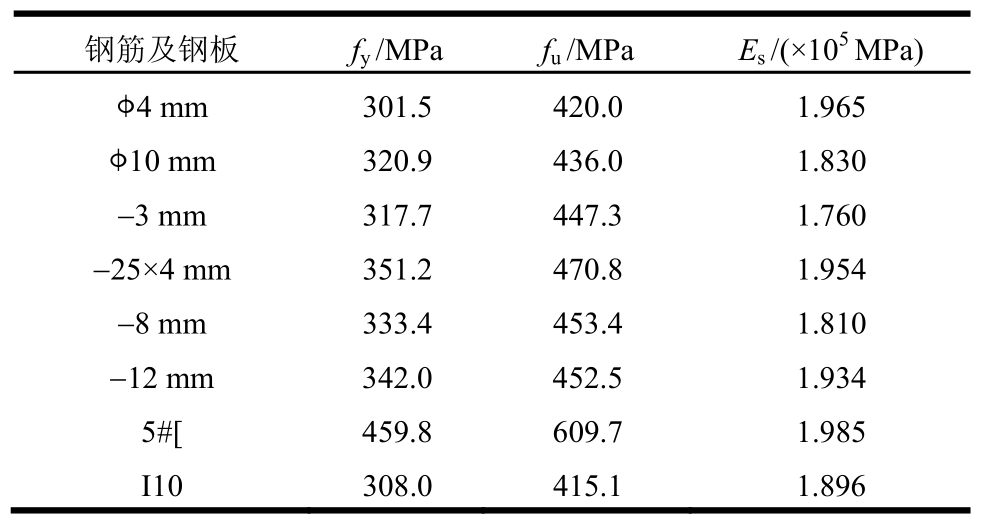
图2所示为试验的加载装置,采用柱顶水平加载的方式不仅能够反映较大轴压力下不可忽视的P-Δ效应,从而模拟实际空间节点的受力特征,而且能够反映不同加载角度对空间节点抗震性能的影响。底端采用自制的单向铰支座,梁端部采用一对滚动轴近似模拟该反弯点处仅能水平移动而不能发生竖向移动的特点。试验开始时,首先通过油压千斤顶施加竖向轴力,然后由电液伺服作动器施加水平往复荷载(千斤顶与反力梁之间设置滚轮装置,使千斤顶随柱顶保持水平移动),持续加载到试件承载力下降至最大荷载的85%时结束试验。
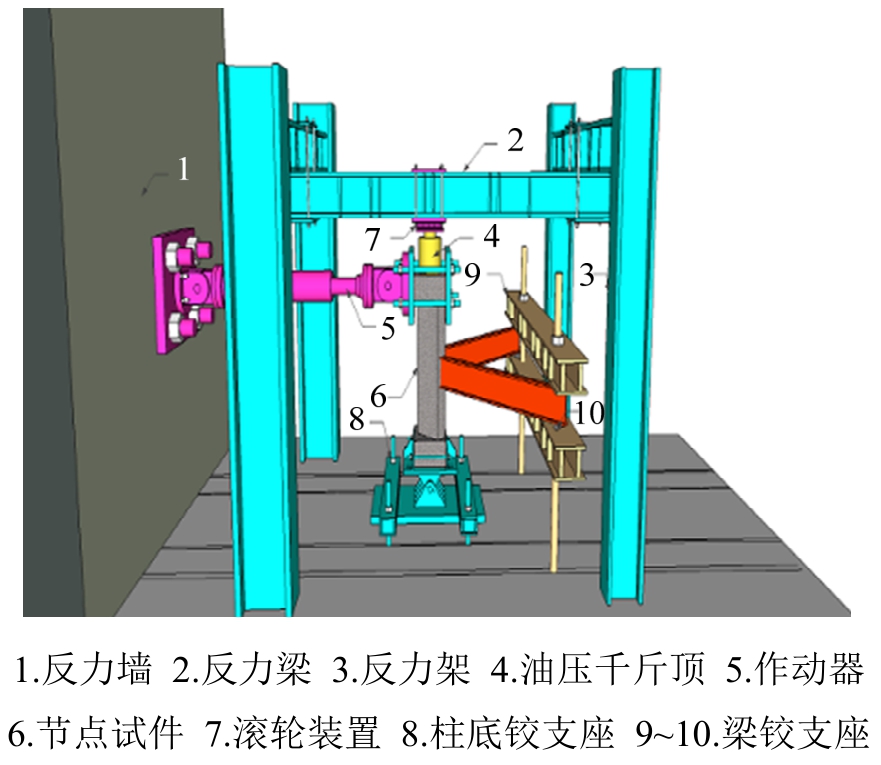
图2 加载装置图
Fig.2 Loading setup
试验先采用荷载控制加载至试件屈服,随后采用位移控制加载,控制位移取屈服位移Δy的倍数,每一级控制位移下水平荷载循环3次。
为了对型钢混凝土L形柱空间角节点进行更深入的研究,该文采用通用有限元软件Abaqus进行非线性分析,并将计算结果与试验结果进行对比。
型钢与混凝土均采用8节点六面体二次缩减积分单元,即C3D8R单元,钢筋采用三维线性桁架单元,即T3D2单元。型钢、钢筋与混凝土之间相互作用采用embed来定义,忽略钢材与混凝土之间的粘结滑移。构件有限元模型见图3。
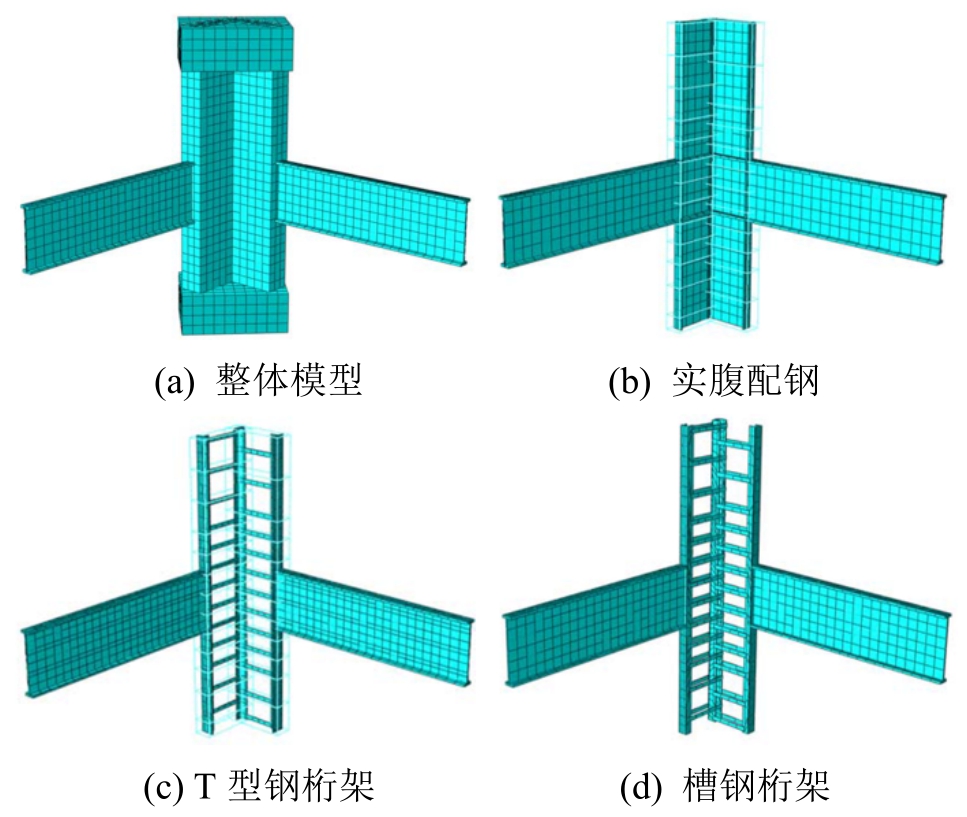
图3 构件有限元模型
Fig.3 Finite element models of specimens
混凝土采用塑性损伤本构模型,应力-应变关系采用GB 50010—2010《混凝土结构设计规范》推荐的曲线,如图4所示。图4(a)中,x=ε/εfc表示混凝土压应变与轴压强度对应应变的比值,y=σ/σfc表示混凝土压应力与轴压强度的比值。图4(b)中,x=ε/εf表示混凝土拉应变与轴拉强度对应应变的比值,y=σ/σf表示混凝土拉应力与轴拉强度的比值。受拉、受压应力-应变曲线方程和损伤方程见式(1)~式(6)。
单轴受拉应力-应变曲线方程:
单轴受拉损伤方程:
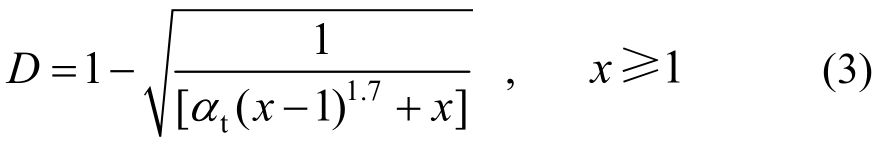
同理混凝土单轴受压的应力-应变曲线方程可按下列公式确定:
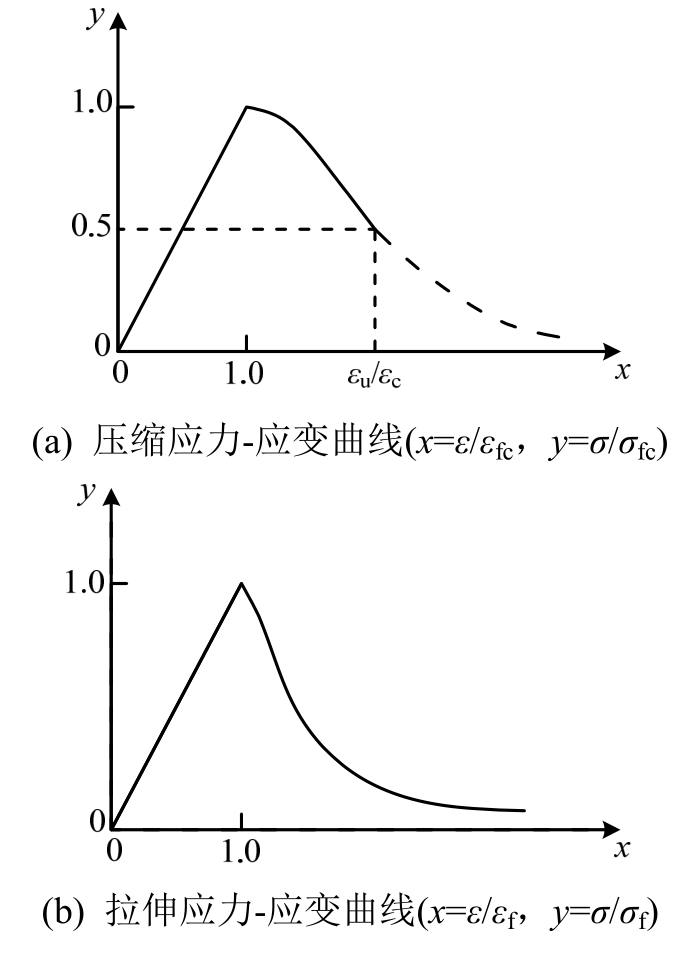
图4 混凝土应力-应变曲线
Fig.4 Stress-strain curves of concrete
当x≥1时 ,
单轴受压损伤方程:
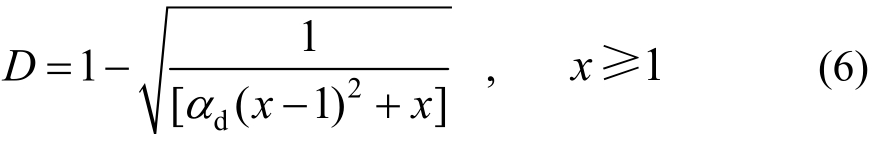
式中:![]()
型钢采用韧性金属损伤模型,通过定义Damage initiation来判定型钢发生初始损伤的条件,初始损伤通过定义断裂应变、应力三轴度和应变率三个参数来实现,根据等效塑形位移来定义Damage evolution来反映型钢在低周反复力作用下损伤的发展过程,参考课题组文献[14],钢筋采用线性强化模型。
在ABAQUS中设置两步施加荷载,第一步在构件柱顶形心处施加轴向力,第二步在试件的端头侧面形心处,以位移控制模式施加水平荷载。为避免柱子端头局部变形过大,将其设置为刚性,将形心设置为参考点,将参考点与加载面耦合,虽然荷载是加载在参考点上,但实际上荷载是以面荷载的形式加在施加面的各个节点上。轴向力和水平荷载施加位置可参考图2中千斤顶和作动器所施加面的形心位置。
2.2.1 破坏形态对比分析
图5是加载角度分别为45°、30°和0°的试件L3、L2和L6破坏时混凝土应力云图与试验结果对比,可以看出,试件受负方向极限荷载时,沿试件高度500mm~550mm(钢梁与柱肢交汇处)和850mm~900mm范围(两肢交汇处,内核)附近,混凝土应力达到最大,并且破坏范围向核心区扩散,具有剪切斜压特点,试验试件核心区有斜向交叉裂缝和水平裂缝,沿柱型钢保护层厚度有粘结裂缝,30°和0°的试件还出现扭转变形。与内核相比,两柱肢的配钢量较小,并且钢梁的约束较大,故柱肢相对薄弱,破坏严重。
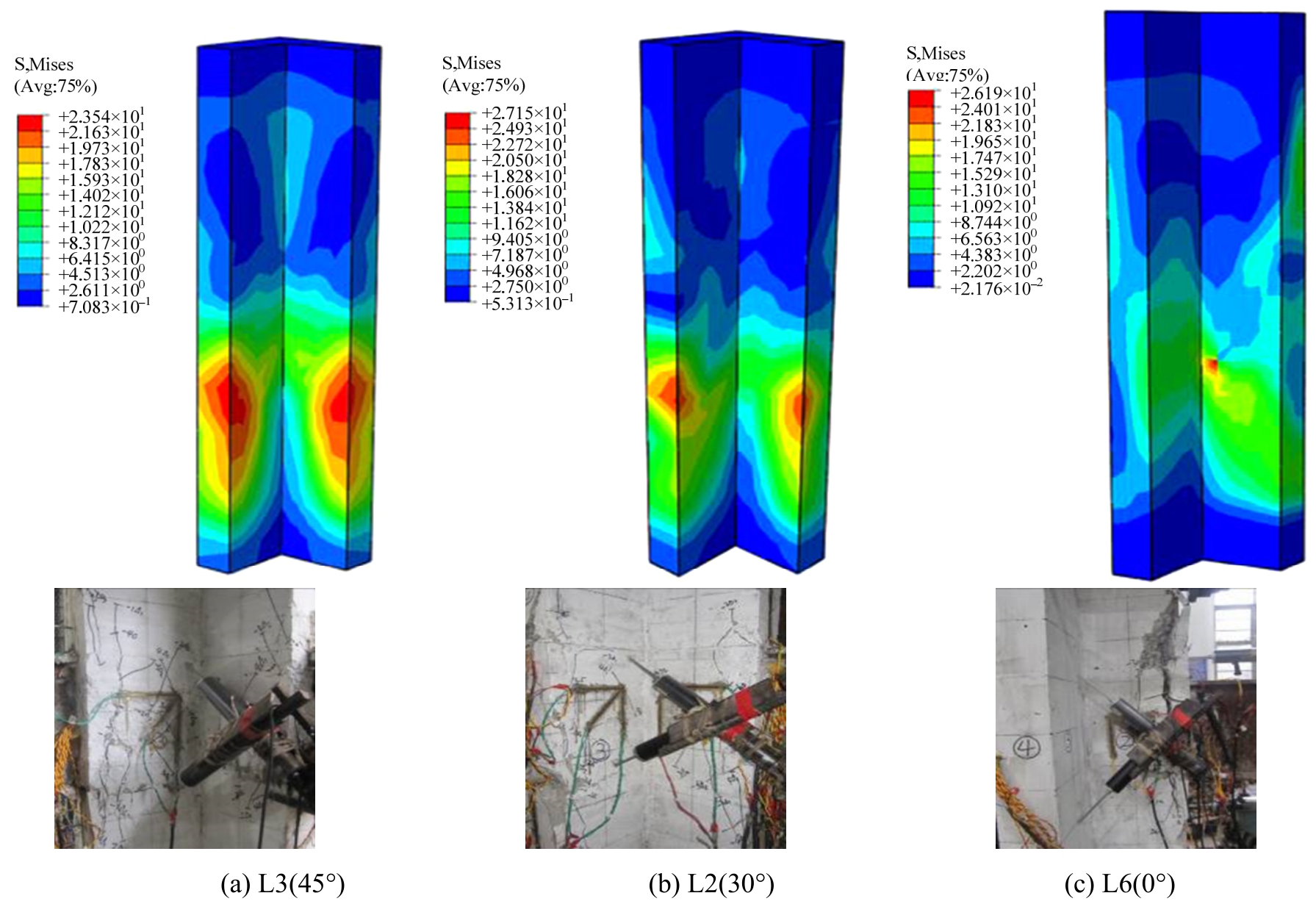
图5 混凝土应力云图与试验破坏形态
Fig.5 Stress contour of concrete and test failure pattern
图6分别给出了45°加载试件L1和30°加载试件L2在正向极限荷载时内部型钢骨架的Mises应力云图。可以看出节点核心区腹板大部分屈服。与柱肢交汇处的核心区内部钢梁根部上、下基本已屈服,纵向型钢只有局部接近屈服,钢梁大部分未屈服。对于45°加载试件,两柱肢及钢梁的应力分布基本对称,对于30°加载试件,30°柱肢对应的节点核心区内部型钢与钢梁屈服范围大于60°柱肢。
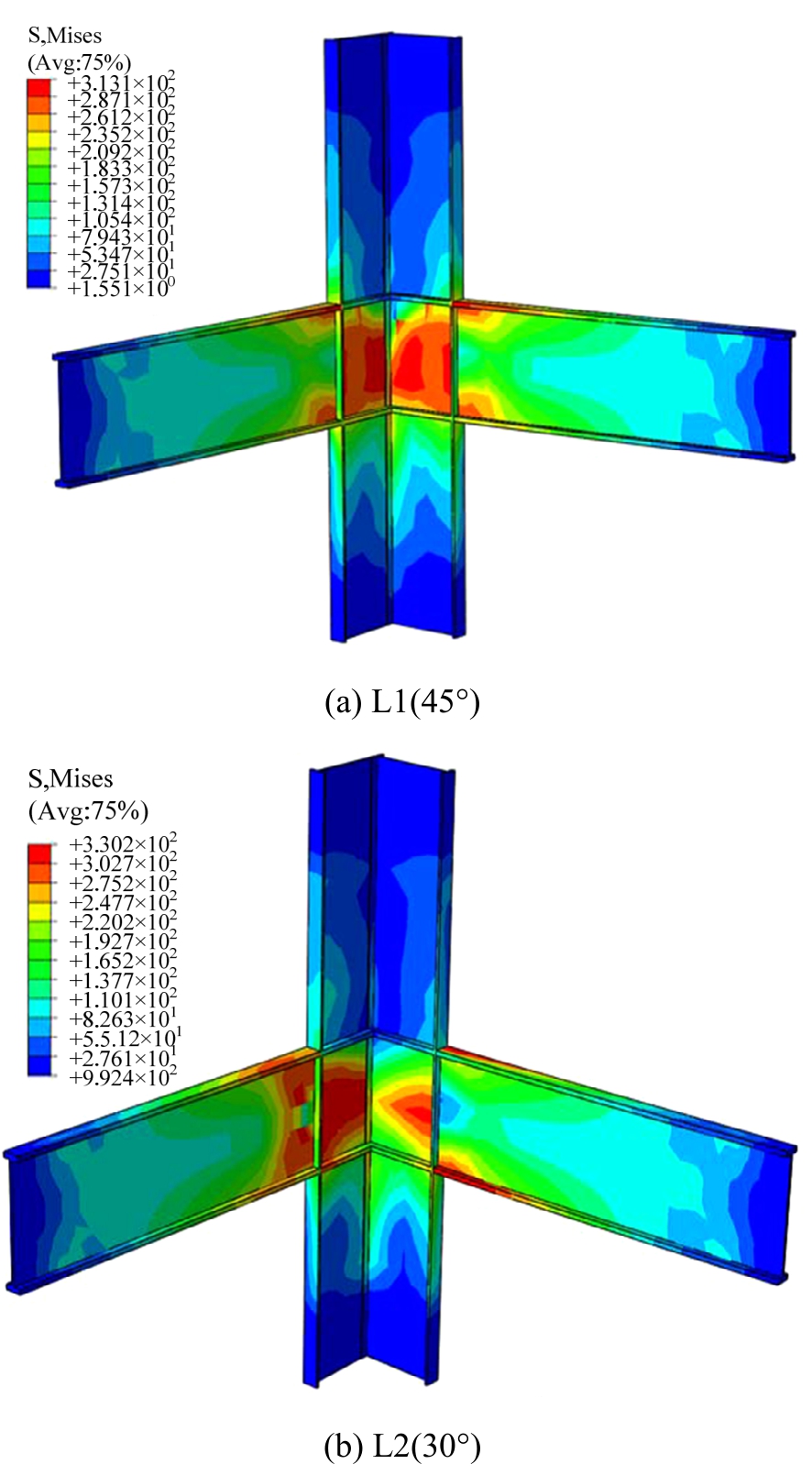
图6 型钢骨架应力云图
Fig.6 Stress contour of steel skeleton
2.2.2 试件变形图
试件从初始阶段到破坏阶段的变形图放大8倍后如图7所示。图中浅色、深色部分分别表示试件的初始状态和破坏后的变形。由图7可见,试件不只在xz、yz面发生弯曲和剪切变形,在xy平面,节点核心存在张开和闭合弯矩,这种受力状态与顶层平面角节点在各加载角度下的受力状态相似。另外,可以看出30°和0°加载试件存在扭转变形,这是由于水平荷载通过截面形心,但不经过截面的弯曲中心所致,因此加载角度对试件变形影响显著。
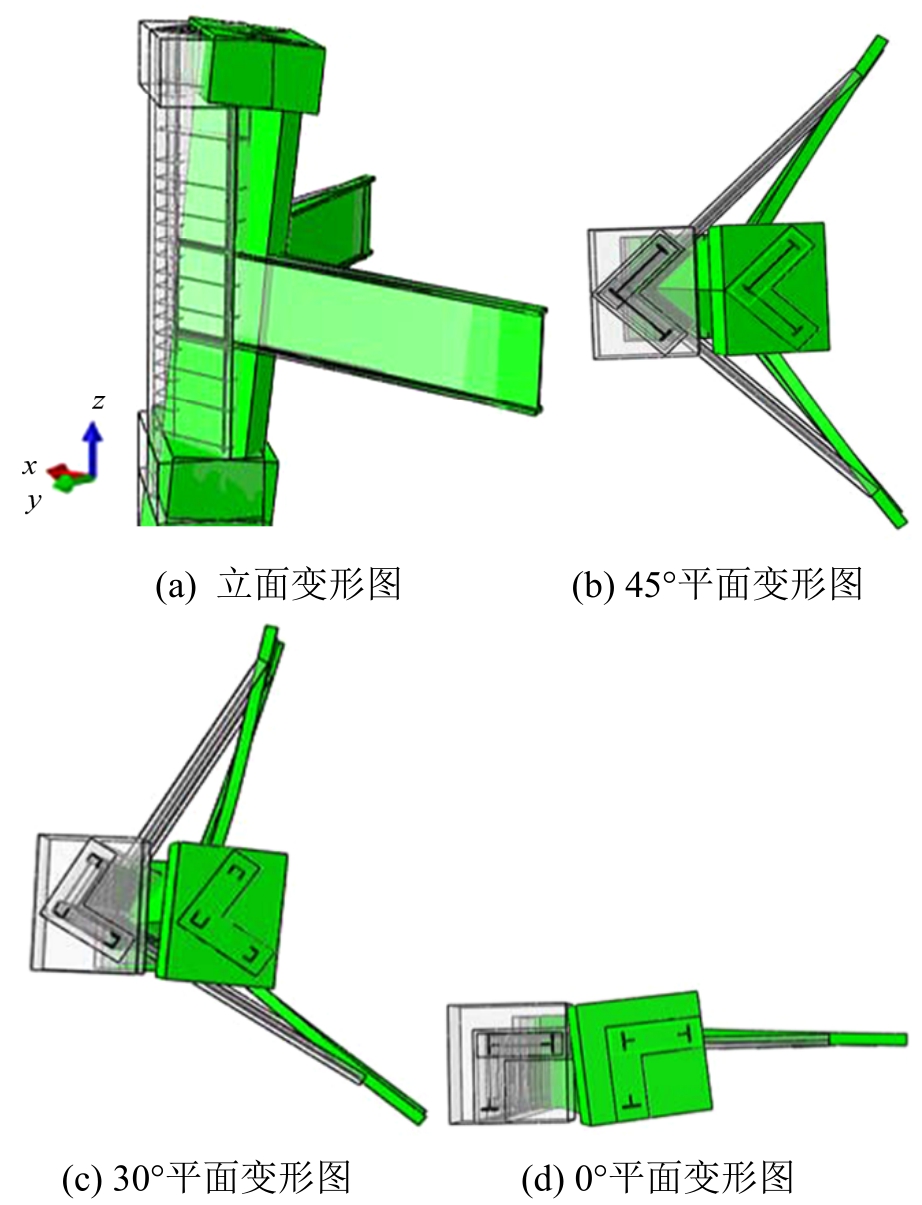
图7 放大后的试件变形图
Fig.7 Scaled deformation diagram of specimens
2.2.3 滞回曲线对比分析
基于Abaqus计算的滞回曲线与试验曲线对比如图8所示。由图可见,每个循环的正向峰值点与试验基本一致,加载及卸载的刚度基本吻合。计算所得滞回曲线正负方向基本对称,滞回曲线的负向与试验结果偏差较大,这是由于有限元分析钢梁的边界条件与试验存在误差。该文仅取其正向荷载进行对比分析如表3所示,计算值与试验值误差基本在10%以内,计算获得的滞回曲线更加饱满,曲线不存在捏拢效应,主要原因有两点:该计算模型中忽略了型钢与混凝土的共同作用与黏结滑移。
2.2.4 耗能能力对比分析
取部分试件计算与试验的等效黏滞阻尼系数he,绘制出he-Δ/Δy曲线进行对比,如图9所示。由图可见,加载初期,计算值小于试验值。这主要是因为计算过程忽略了力控阶段,导致加载初期滞回环面积的计算值小于试验值,从而得出的等效黏滞阻尼系数he计算值较试验值小。

图8P-Δ滞回曲线对比
Fig.8 Comparison ofP-Δhysteretic curves
表3 峰值点处计算值与试验值的对比
Table3 Comparison of FEM and test results on peak points
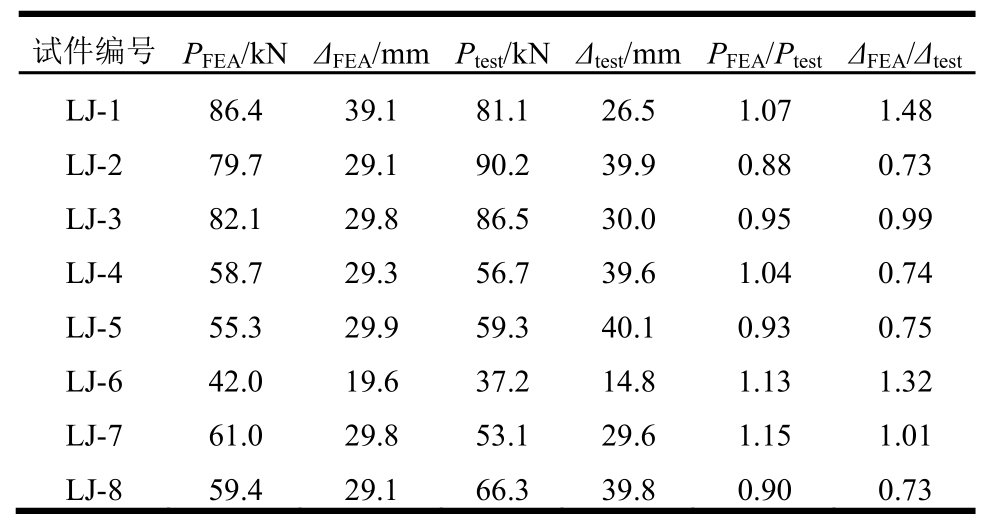
注:PFEA是峰值点对应的荷载计算值;ΔFEA是峰值点对应的位移计算值;Ptest是峰值点对应的荷载试验值;Δtest是峰值点对应的位移试验值。
2.2.5 延性系数对比分析
图10为延性系数的计算值与试验值的对比图。可以看出计算值较试验值略偏大,这也是因为滞回曲线的下降段计算值较试验值更加平缓,使其极限位移较试验值增加,从而导致位移延性系数较试验值更大,但误差基本在10%以内,可见该文基于试验建立的有限元模型计算其抗震性能是可行的。
为了深入研究影响该新型节点抗震性能的各种因素,采用单因素设计方法,细化柱截面配钢形式、轴压比、加载角度3个变化参数,共设计29个足尺节点进行抗震性能有限元分析。

图9 部分试件的各级位移下的he值对比
Fig.9 Comparison ofheof part of specimens at displacement of all levels
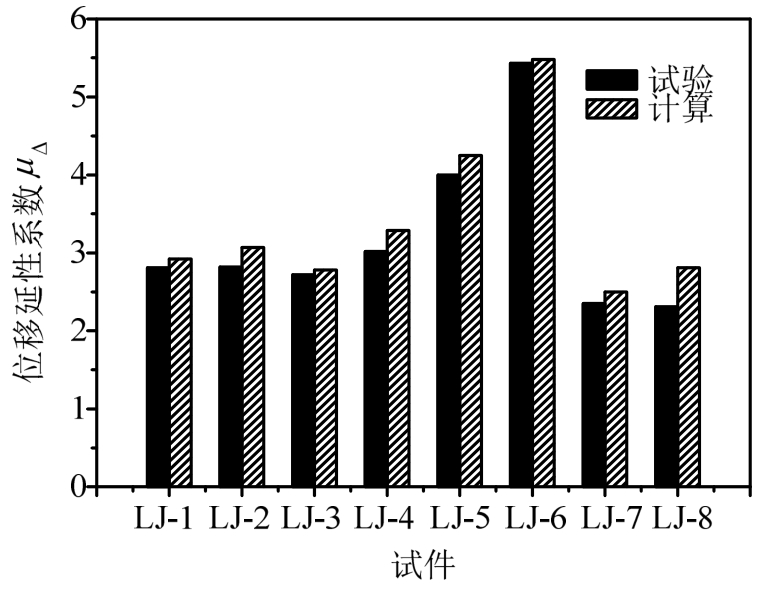
图10 位移延性系数对比
Fig.10 Comparison of displacement ductility factors
3.1.1 试件参数设计
选取3种不同配钢形式:实腹配钢、T型钢桁架、槽钢桁架,截面尺寸及配钢形式详见图11。沿45°角加载,轴压比取0.2,肢高厚比为3,柱反弯点高度3000mm,梁长2400mm。试件设计参数详见表4。

图11 试件截面尺寸及配钢形式
Fig.11 Sectional dimensions and steel forms of specimens
表4 试件参数设计及主要计算结果
Table4 Specimen design parameters and main calculation results

注:ρss为纵向型钢含钢率;ρsw为腹杆配钢率;ρs为纵筋配筋率;ρsv为体积配箍率。
3.1.2 滞回曲线
三种配钢形式下试件的滞回曲线见图12。由图可见滞回曲线正负向基本对称,与空腹配钢试件(配T型钢桁架和配槽钢桁架)相比,实腹配钢试件的滞回曲线更加饱满,峰值荷载较高、刚度较大、耗能能力较好。在含钢率基本相同的条件下,实腹配钢试件的综合抗震性能优于空腹配钢试件,配T型钢桁架较槽钢桁架试件更加饱满。
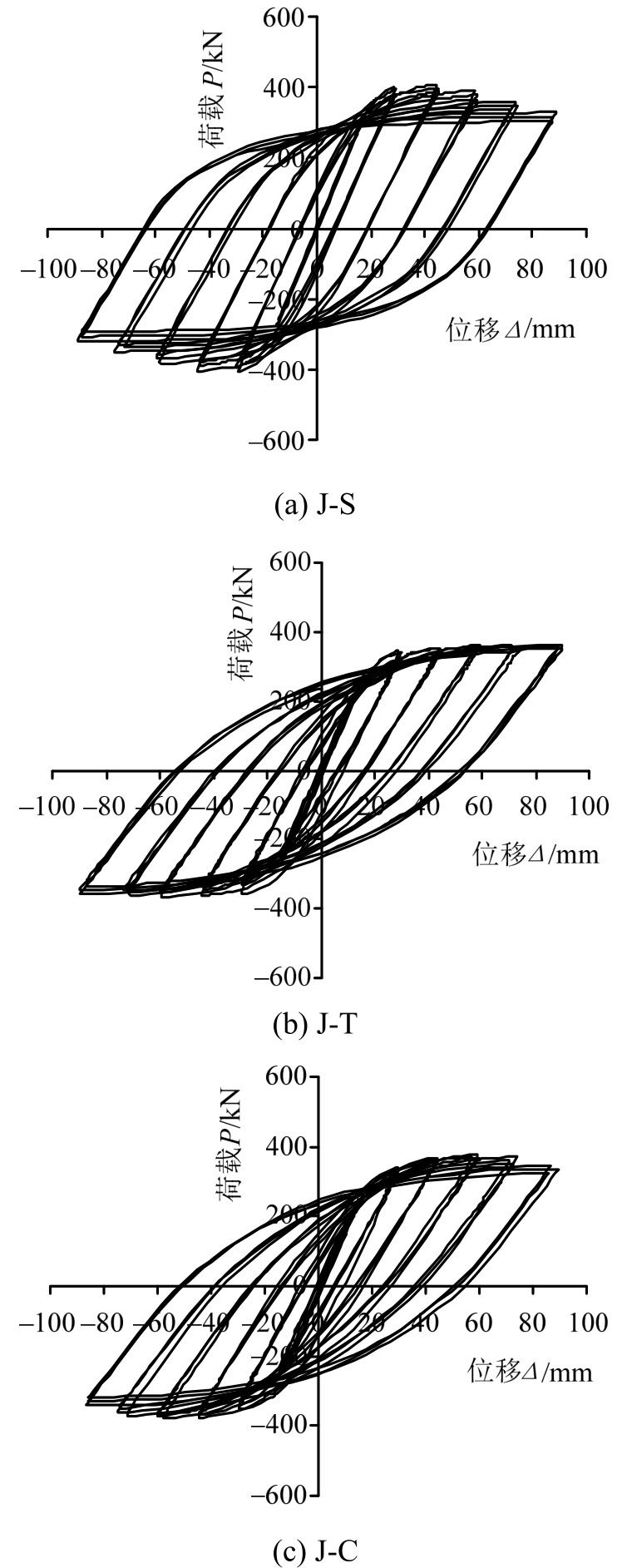
图12 不同配钢形式下试件P-Δ滞回曲线
Fig.12P-Δhysteretic curves of specimens under different steel forms
3.1.3 峰值荷载、耗能及延性
三种配钢形式下试件的骨架曲线、耗能和延性对比见图13、图14和图15。由图13可见,与空腹配钢试件相比,实腹配钢试件峰值荷载可提高10%以上,抗震承载能力最好。由图14可见,随着位移的增加,试件耗能逐渐增加,破坏时的he基本在0.30~0.35之间,可看出三种配钢形式下的试件耗能较普通钢筋混凝土(RC)节点均更好,并且实腹配钢试件的整体耗能优于空腹配钢试件。由图15可见,三种配钢形式试件的位移延性介于3.22~3.74之间,且均大于3,有较好的变形能力,且配T型钢桁架试件的延性最好,这与试验结果一致。

图13 骨架曲线对比
Fig.13 Skeleton curve comparison
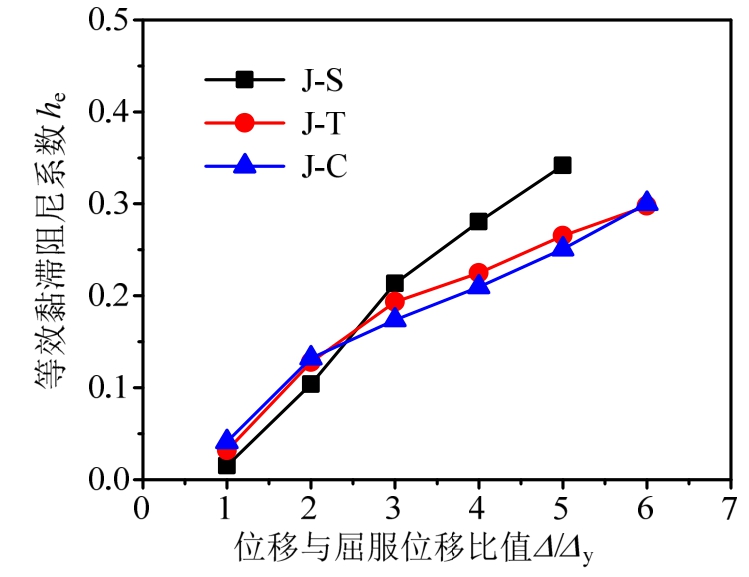
图14 配钢形式与he值的关系
Fig.14 Relationship of steel form andhe
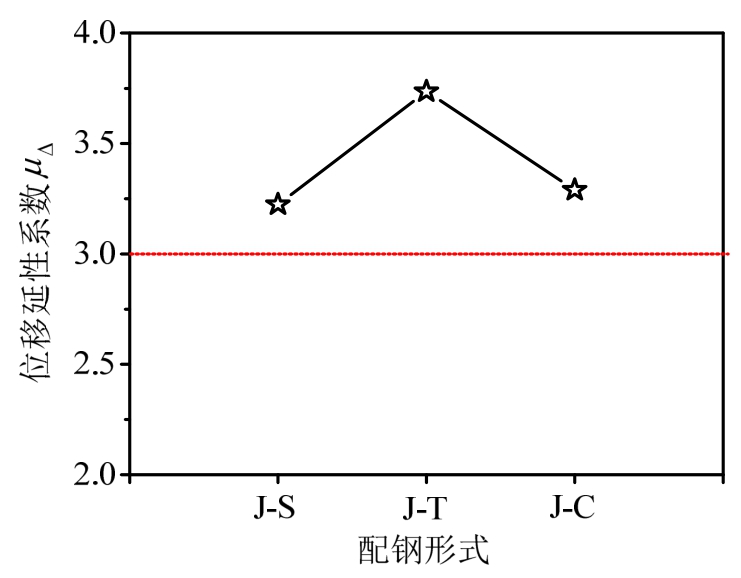
图15 配钢形式与位移延性的关系
Fig.15 Relationship of steel form andμΔ
综合承载能力、耗能和延性3个抗震指标,工程设计中优先选用实腹配钢形式,若对延性要求较高者还可选用T型钢桁架的配钢形式。
3.2.1 试件参数设计
由于构件的承载力及延性受轴压比影响较大,该文分别以J-S、J-T和J-C试件为研究对象,加载角度采用45°,选取5种实际轴压比:0.2~0.6(中间极差0.1),对其进行数值计算。试件设计参数详见表4,试件截面尺寸及配钢形式见图11。
3.2.2 滞回曲线
三种配钢形式的部分试件在不同轴压比下的P-Δ滞回曲线如图16所示。由图可见,轴压比的变化对不同配钢形式试件的滞回曲线有显著影响。随着轴压比的增加,实腹配钢试件的滞回环更加饱满,后期强度下降较快,而空腹配钢试件的极限位移逐渐变小,后期强度下降更快,延性较差。这是由于实腹配钢试件内置的型钢腹板能承受部分轴压力,而空腹配钢试件内部水平腹杆不能承受轴向力,因此在较高轴压比时(特别是0.5以后),空腹配钢柱轴力产生的二级效应更加显著,节点一旦破坏,试件很快失去承载能力。

图16 不同轴压比下试件P-Δ滞回曲线
Fig.16P-Δhysteretic curves of specimens under different axial compression ratios
3.2.3 峰值荷载、耗能及延性
三种配钢形式下不同轴压比下试件的骨架曲线、耗能和延性的对比图见图17、图18和图19。由图17可见,随着轴压比的增加,试件的峰值荷载逐渐降低,并且峰值荷载的下降幅度依次为配槽钢桁架试件>配T型钢桁架试件>实腹配钢试件。由图18可见,试件的耗能能力随轴压比的增加而增加,并且实腹配钢试件的整体耗能优于空腹配钢试件。由图19可见,随着轴压比的增加,三种配钢形式的试件的位移延性都有所下降,当轴压比为0.2~0.4时,试件的延性系数均大于3,轴压比超过0.4以后试件延性大幅下降。
关于型钢混凝土(SRC)结构轴压比限值的确定,认为当位移延性系数μ满足μ≥3时,其对应的轴压比限值是可行的[15],日本SRC规范[16]则以柱子极限侧移角满足0.01弧度来确定柱子的轴压比限值。该文认为同时满足以上两个条件时,试件对应的轴压比限值较为安全。将该文试验轴压比0.4换算成设计轴压比后为0.68,此时试件对应的位移延性约为3,并且对应的极限转角均大于0.01弧度,结合试验的延性系数与轴压比的关系,偏于安全考虑,建议型钢混凝土L形柱空间角节点的轴压比限值设计值为0.5。
3.3.1 试件参数设计
以J-S为研究对象,选取最有代表性的加载角(0°~180°,极差10°)进行分析,加载角度示意如图20所示,O为试件L形柱的截面形心。
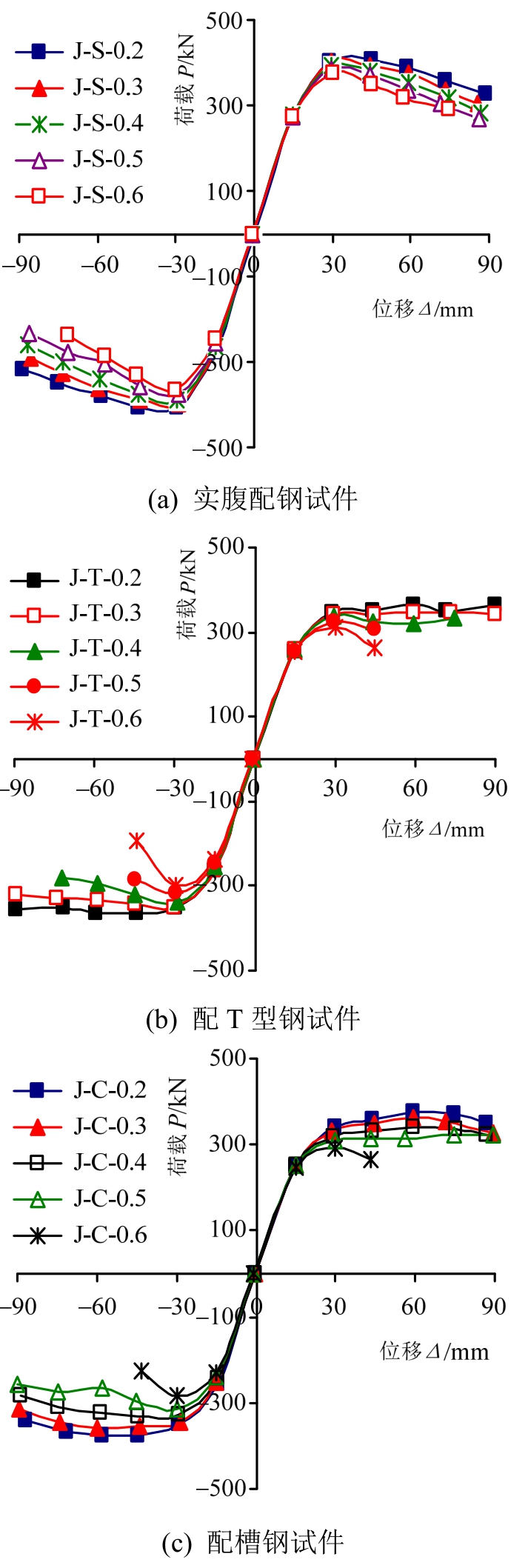
图17 骨架曲线对比
Fig.17 Skeleton curve comparison
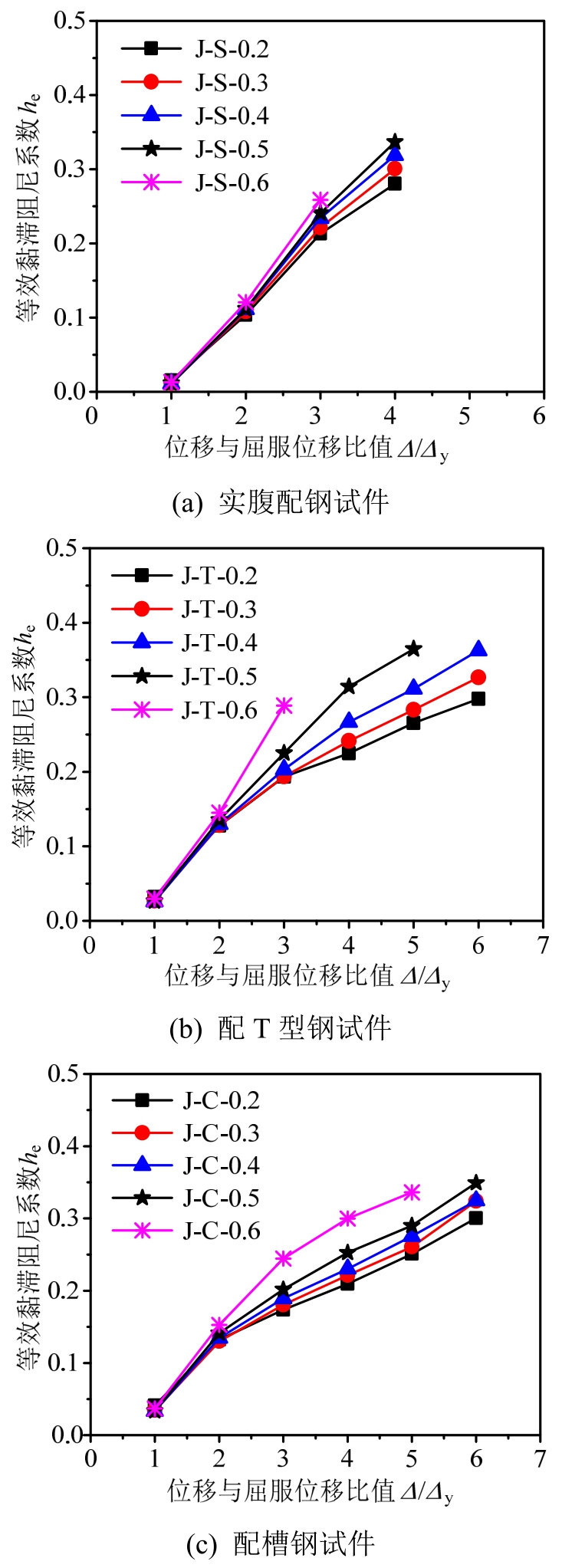
图18 轴压比与he值的关系
Fig.18 Relationship of axial compression ratio andhe

图19 轴压比与位移延性的关系
Fig.19 Relationship of axial compression ratio andμΔ
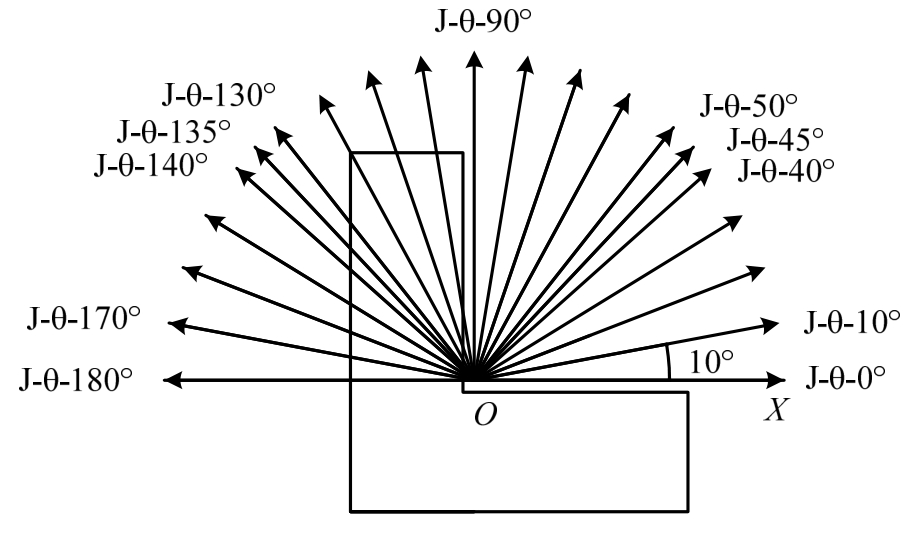
图20 试件加载角度示意图
Fig.20 Load angle diagram of specimen
3.3.2 滞回曲线
选取部分试件的滞回曲线见图21。可见加载角度同是 0°的空间节点J-θ-0°和平面节点J-θ-0P的滞回曲线相似。当0°≤θ≤45°时,加载角为θ与90°-θ的试件滞洄曲线相似,同理当90°≤θ≤135°时,加载角为θ与270°-θ的试件滞洄曲线相似。这是由于试件柱肢关于y=x对称。
3.3.3 峰值荷载、耗能及延性
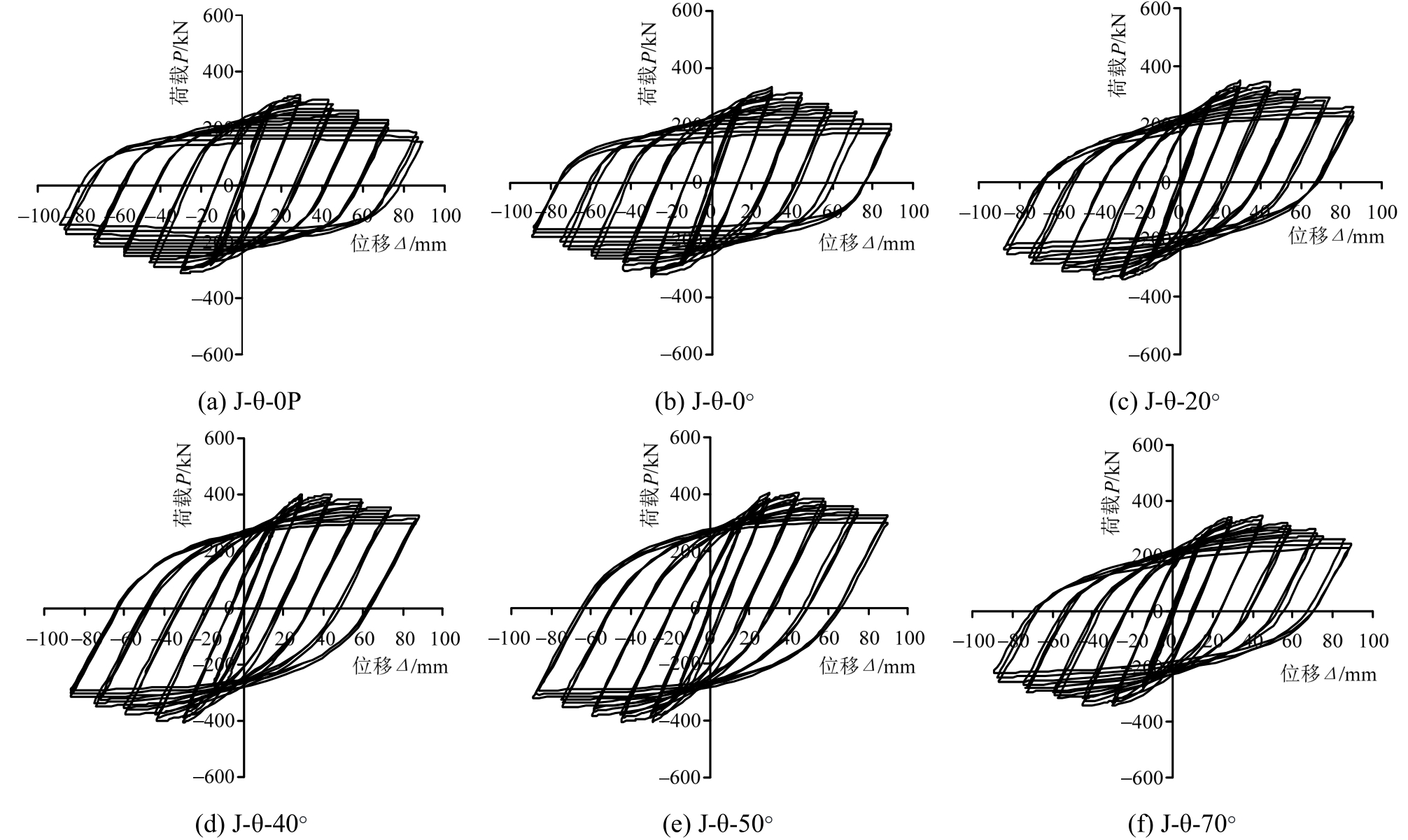
图21 不同加载角度下试件P-Δ滞回曲线
Fig.21P-Δhysteretic curves of specimens under different load angles
将峰值荷载与加载角度绘制在直角坐标系中如图22(a),与平面节点相比,45°加载试件的峰值荷载提高了约30%。第二象限的峰值荷载略高于第一象限,由于计算所得滞回曲线基本对称,可推算出1、3象限曲线相似,2、4象限曲线相似。补充3、4象限数据,将直角坐标系转化为极坐标系,如图22(b),该曲线经过拟合可得:
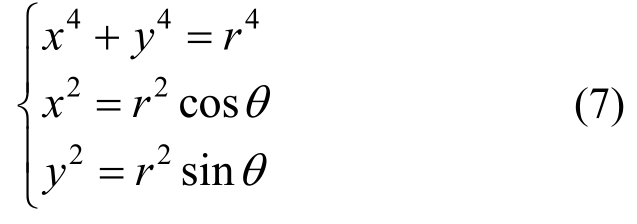
式中:r为0°加载试件峰值荷载;θ为加载角。该公式可为试件抗剪承载力计算提供依据。
不同加载角度下试件的耗能和延性对比图见图23和图24。由图23可见,在各级位移下,随着加载角度的增加,试件的等效黏滞阻尼系数he值逐渐降低,这是由于加载角度越小,试件的扭转效应越明显,扭转虽使试件承载力降低,但同时吸收部分能量,因此试件的耗能能力越好。
由图24可见,试件的位移延性均介于3.22~3.58之间,有较好的变形能力,并且试件的延性随加载角度的增加而降低,45°加载试件较平面节点延性系数降低约10%,这表明双向加载对结构延性不利。
综合承载能力、耗能和延性3个抗震指标,工程设计中按平面节点计算极限承载力偏于安全,但也要考虑双向加载对试件延性的不利影响。
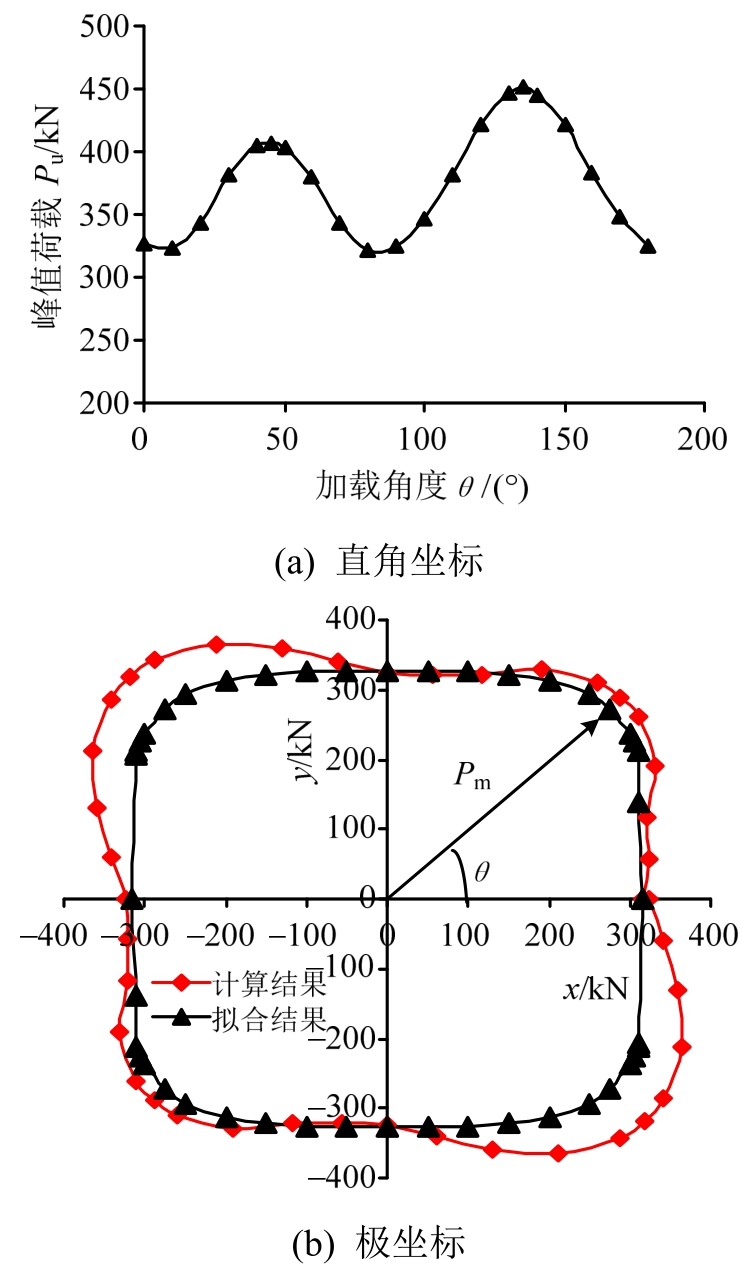
图22 不同加载角度下试件峰值荷载
Fig.22 Peak loads of specimens under different load angles
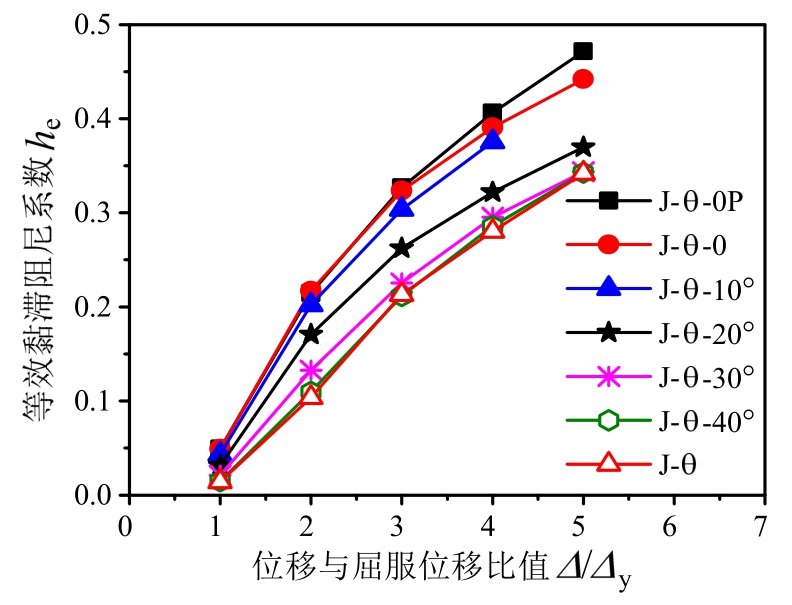
图23 加载角度与he值的关系
Fig.23 Relationship of load angle andhe
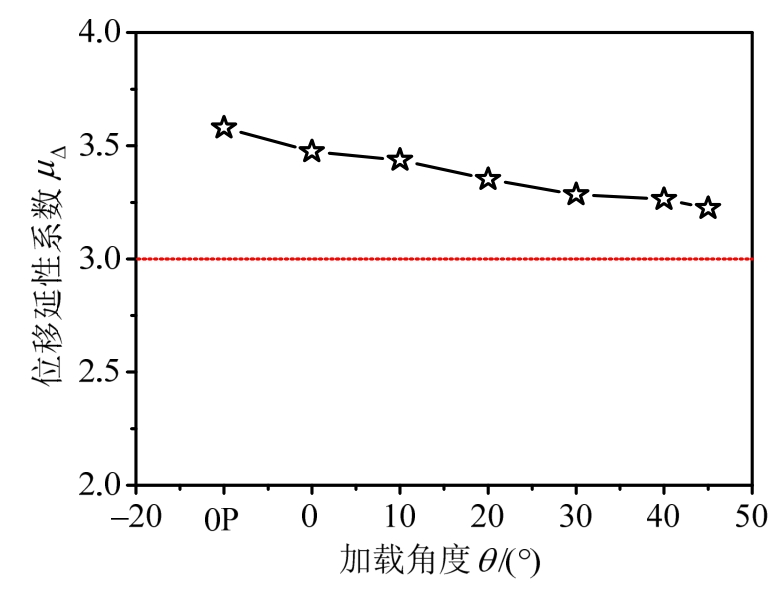
图24 加载角度与位移延性的关系
Fig.24 Relationship of load angle andμΔ
(1)型钢混凝土L形柱空间角节点的破坏模式和滞回曲线的计算结果与试验结果基本吻合,破坏形态以剪切斜压和弯曲破坏为主,扭转伴随黏结破坏为辅。该文有限元建模是合理的。
(2)不同配钢形式下的滞回曲线形状不同。实腹配钢试件呈梭形,滞回环饱满;空腹配钢试件的滞回曲线呈弓形。
(3)配钢形式对该节点抗震性能有显著影响。实腹配钢试件承载能力和耗能最好,其峰值荷载较空腹配钢试件提高了10%,配T型钢桁架试件的延性最好,建议优先选用实腹配钢试件。
(4)轴压比对该节点抗震性能有一定影响。随着轴压比的增加,试件的峰值荷载逐渐降低,并且配槽钢桁架试件下降幅度最大;试件的耗能能力随轴压比的增加而增加,实腹配钢试件的整体耗能最优;随轴压比的增加,三种配钢形式试件的位移延性下降程度不同,实腹配钢试件下降缓慢,建议轴压比限值设计值为0.5。
(5)加载角度对该节点抗震性能有较大影响。45°加载角度以内,随着加载角度的增加,峰值荷载增加,耗能和延性降低,45°加载试件与0°平面节点相比,峰值荷载提高了约30%,延性系数降低约10%。设计中按平面节点计算极限承载力偏于安全,需考虑双向加载对试件延性的不利影响。
参考文献:
[1]李哲,张小峰,郭增玉,等.钢骨混凝土T形截面短柱力学性能的试验研究[J].土木工程学报,2007,40(1):1―5.Li Zhe,Zhang Xiaofeng,Guo Zengyu,et al.Experimental study on the mechanical property of steel reinforced concrete short columns of T-shaped cross-section[J].China Civil Engineering Journal,2007,40(1):1―5.(in Chinese)
[2]柯晓军,陈宗平,薛建阳,等.反复荷载下型钢混凝土异形柱粘结滑移性能研究[J].工程力学,2013,30(2):211―218.Ke Xiaojun,Chen Zongping,Xue Jianyang,et al.Study on bond slip behavior of SRC special-shaped columns under cyclic reversed loading[J].Engineering Mechanics,2013,30(2):211―218.(in Chinese)
[3]陈宗平,薛建阳,赵鸿铁,等.型钢混凝土异形柱抗震性能试验研究[J].建筑结构学报,2007,28(3):53―61.Chen Zongping,Xue Jianyang,Zhao Hongtie,et al.Experimental research on seismic behavior of steelreinforced concrete special-shaped columns[J].Journal of Building Structures,2007,28(3):53―61.(in Chinese)
[4]Tokgoz S,Dundar C.Tests of eccentrically loaded L-shaped section steel fibre high strength reinforced concrete and composite columns[J].Engineering Structures,2012,38(5):134―141.
[5]薛建阳,刘义,赵鸿铁,等.型钢混凝土异形柱框架节点抗震性能试验研究[J].建筑结构学报,2009,30(4):69―77.Xue Jianyang,Liu Yi,Zhao Hongtie,et al.Experimental research on seismic behavior of steel reinforced concrete special-shaped column-beam joints[J].Journal of Building Structures,2009,30(4):69―77.(in Chinese)
[6]Rong X,Zhang J X,Li Y Y.Seismic behavior of shaped column joints with X-shaped reinforcement[J].Transactions of Tianjin University,2013,19(2):110―117.
[7]邓志恒,唐光暹,向平,等.钢骨混凝土T形截面柱节点抗震性能研究[J].建筑结构,2010,40(6):44―47.Deng Zhiheng,Tang Guangxian,Xiang Ping,et al.Experimental study on seismic behavior of SRC T-shaped column joints under low cyclic reversed loading[J].Building Structures,2010,40(6):44―47.(in Chinese)
[8]Li L M,Mander J B,Dhakal R P.Bidirectional cyclic loading experiment on a 3D beam-column joint designed for damage avoidance[J].Journal of Structural Engineering,2008,134(11):1733―1742.
[9]樊健生,周慧,聂建国,等.双向荷载作用下方钢管混凝土柱-组合梁空间节点抗震性能试验研究[J].建筑结构学报,2012,33(6):50―58.Fan Jiansheng,Zhou Hui,Nie Jianguo,et al.Research on seismic responses of 3D joints with CFT column and composite beam under bi-directional loading[J].Journal of Building Structures,2012,33(6):50―58.(in Chinese)
[10]薛伟辰,姜东升,陈以一,等.预应力混凝土空间节点抗震性能试验研究[J].建筑结构学报,2007,28(1):43―51.Xue Weichen,Jiang Dongsheng,Chen Yiyi,et al.Experimental study of seismic performance of prestressed concrete spatial joints[J].Jourmal of Building Structures,2007,28(1):43―51.(in Chinese)
[11]陈宗平,徐金俊,薛建阳.型钢混凝土异形柱-钢梁空间边节点的抗震性能及影响因素分析[J].工程力学,2015,32(2):105―113.Chen Zongping,Xu Jinjun,Xue Jianyang.Seismic behavior and influence factor analysis on 3D side joints composed of steel reinforced concrete special-shaped columns and steel beams[J].Engineering Mechanics,2015,32(2):105―113.(in Chinese)
[12]王妮,陈宗平,张士前,等.型钢混凝土异形柱中节点受力性能试验及有限元分析[J].建筑结构学报,2013,34(s1):102―109.Wang Ni,Chen Zongping,Zhang Shiqian,et al.Experimental research and FEA on mechanical behavior of steel interior joint between SRC special shaped column and steel beam[J].Journal of Building Structures,2013,34(s1):102―109.(in Chinese)
[13]王妮,陈宗平,陈宇良,等.反复荷载下型钢混凝土异形柱空间角节点破坏机理及损伤分析[J].工程力学,2015,32(3):140―150.Wang Ni,Chen Zongping,Chen Yuliang,et al.Failure mechanism damage analysis of space corner joint of SRC L-shaped columns under cyclic loading[J].Engineering Mechanics,2015,32(3):140―150.(in Chinese)
[14]徐金俊.型钢混凝土T形柱-钢梁空间节点的震损机制与计算理论[D].南宁:广西大学,2016.Xu Jinjun.Seismic damage mechanism and calculation theory for T-shaped steel reinforced concrete column-steel beam 3D joints[D].Nanning:Guangxi University,2016.(in Chinese)
[15]贾金青,姜睿,厚童.钢骨超高强混凝土框架柱抗震性能的试验研究[J].土木工程学报,2006,39(8):14―18.Jia Jinqing,Jiang Rui,Hou Tong.An experimental study on the seismic performance of steel reinforced super high-strength concrete columns[J].China Civil Engineering Journal,2006,39(8):14―18.(in Chinese)
[16]鉄骨鉄筋コンクーリト構造計算規準.同解說[S].第5版.东京:日本建築学会,2001.Standard for structural calculation about steel reinforced concrete.Commentary[S].5th ed.Tokyo:Japanese Architecture Institute,2001.(in Japanese)
ANALYSIS ON SEISMIC PERFORMANCE OF STEEL REINFORCED CONCRETE L-SHAPED COLUMN SPACE CORNER JOINTS
WANG Ni1,CHEN Zong-ping2,3,CHEN Yu-liang2
(1.School of Environmental Science and Engineering,Chang’an University,Xi’an,Shaanxi 710064,China;2.College of Civil Engineering and Architecture,Guangxi University,Nanning 530004,China;3.Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education,Guangxi University,Nanning,Guangxi 530004,China)
Abstract:In order to study the seismic performance of steel reinforced concrete L-shaped column space corner joints,low-cycle reversed loading tests and finite element simulations for 8 specimens were carried out.It indicated that the results of the numerical analysis exhibited a good agreement with those of experiments.While considering three parameters based on the above results,which were the column section steel form,load angle and axial compression ratio,the influences of the three parameters on the seismic performance indicators including the peak load,energy dissipation capacity and displacement ductility were analyzed by using Abaqus nonlinear finite element simulation.Suggestions for engineering design reference were proposed.The results indicated that the failure pattern of steel reinforced concrete L-shaped column space corner joints is dominated by compression-shear and flexural failure,followed by torsion and bond failure.The overall seismic performance of the solid web steel specimen is the best,with its peak load increased by 10% as compared with hollow steel specimens.While increasing the axial compression ratio,the displacement ductility of the specimens withdifferent forms of steel was decreased by different degrees,with solid web steel specimens declining slowly.A value of 0.5 was suggested for the axial compression ratio limit for design.Moreover,when the load angle is less than 45°,the peak load increased while the energy dissipation and ductility decreased gradually with the increase of the load angle.The peak load and the ductility coefficient of the 45° loading specimens were increased by about 30% and decreased by 10% as compared with the 0° loading specimens,which is the most disadvantageous loading direction.
Key words:steel reinforced concrete;L-shaped column;space corner joint;seismic performance;finite element analysis
中图分类号:TU398
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.01.0081
文章编号:1000-4750(2018)05-0180-13
收稿日期:2017-01-19;修改日期:2017-06-14
基金项目:中央高校基本科研业务费专项资金项目(310829161011,310829161013,310821171011);广西防灾减灾与结构安全重点实验室开放课题项目(2014ZDK0011);广西高等学校高水平创新团队及卓越学者项目(桂教人[2017]38号)
通讯作者:陈宗平(1975—),男,广西人,教授,博士,博导,主要从事钢-混凝土组合结构受力性能研究(E-mail:zpchen@gxu.edu.cn).
作者简介:王 妮(1985—),女,陕西人,讲师,博士,主要从事钢-混凝土组合结构受力性能研究(E-mail:wangnivviv@163.com);
陈宇良(1987―),男,广西人,博士生,主要从事钢-混凝土组合结构受力性能研究(E-mail:ylchen616@163.com).