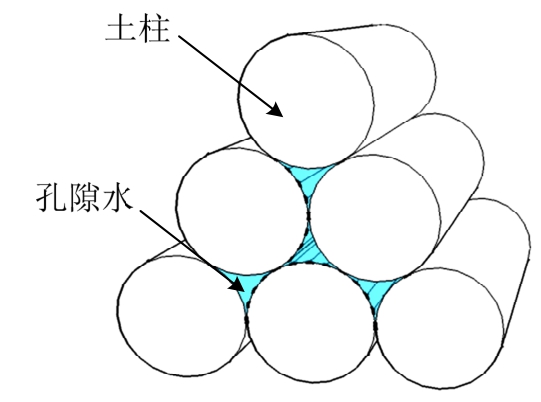
图1 一维热传导模型
Fig.1 One dimensional model of heat conduction
夏锦红1，陈之祥2，3，夏元友1，李顺群2，3
(1.武汉理工大学土木工程与建筑学院，武汉 430070；2.天津城建大学土木工程学院，天津 300384；3.天津市软土特性与工程环境重点实验室，天津 300384)
摘 要：基于饱和冻土的三相组成和导热系数量纲定义，将冻土简化为由土柱、液态水、冰柱组成的混合物，进而建立了冻土导热系数的几何模型。考虑实际冻土中三相组成的含量随温度变化而不断变化的事实，给出了随温度变化的水柱和冰柱体积计算与演变规律。在此基础上，利用并联体系导热效果的叠加原理，给出了随温度变化的冻土导热系数计算模型。基于热流传递过程中并联与串联同时进行的耦合特性，建立了考虑固-液界面的导热系数计算模型。将预测值与瞬态探针法的实测结果和Johansen法的计算结果对比后发现，该类计算方法能有效模拟不同负温条件下冻土的导热系数，并且具有概念清晰、方法简单等特点。
关键词：岩土工程；冻土；导热系数模型；未冻水；固-液界面
冻土导热系数是表征土体在负温下传导热量的能力，是冻土区天然温度场研究和土木建筑热工计算的基础指标[1―2]。近年来，随着冻结法施工的普遍应用和大面积推广，冻土导热系数已成为联络通道施工和抢险方案设计的关键参数[3]。
冻土是由土颗粒、冰、未冻水和气构成的复杂多相体，即使总的含水量不变，不同负温条件下冻土中水/冰含量也不相同[4]。由于水与冰的物理力学性质相去甚远，因此不同水/冰含量的冻土，其力学和热学参数往往存在较大差异[5―6]。可见，冻土的物理力学性质严重依赖其所处的温度和液态水含量。
冻土的比热容和导热系数是冻结法设计和施工过程中最基本的热工参数。比热容是与质量相关的标量，它只影响土体达到稳态传热所需的时间。因此，只有准确确定相关岩土的导热系数，才能对某时刻冻土温度场的分布进行科学预测，从而合理设计冷冻功率和进行隔热层设计等工作。
由于工程的广泛性和应用的迫切性，国内外科研工作者从不同角度对冻土的导热系数进行了研究。Johansen[7]基于经验法和回归分析法，从土中各相体积含量的角度出发，提出了一种预估土体导热系数的方法。原喜忠等[8]考虑冻土的非饱和性，提出了一种适用于非饱和冻土导热系数计算的经验模型。洪涛等[9]对冻土导热系数与温度、含水率及干密度之间的关系进行了回归分析，提出了应用于黄河源区多年冻土的导热系数评价模型。陶兆祥和张景森[10]从比较法的角度，给出了一种冻土导热系数的测试装置，并用该装置测定了五种不同冻土的导热系数。刘为民等[11]在研究了多种因素对冻土导热系数的影响后，给出了一种半理论半经验的导热系数算法。陈琳等[12]采用微结构分析方法，研究了青藏高原冻土区风积沙的导热系数变化机理。
可见，既有的岩土体导热系数研究一般是建立在统计学基础之上的[7―12]。基于传热学理论，从土的组成和微观结构出发，研究冻土导热系数随不同负温的变化机理并建立相应的计算模型尚不多见。
基于冻土的固相颗粒、孔隙水和孔隙冰三相组成，依据导热系数的量纲定义，建立了冻土导热系数的几何模型。考虑实际冻土中三种成分的含量随温度变化而不断变化的事实后，给出了随温度变化的冻土导热系数计算模型。基于土柱模型热流传递过程中并联与串联同时进行的耦合特性，建立了考虑固-液界面的导热系数计算模型，并将该类方法预测值与Johansen法计算值和瞬态探针法实测数据进行了对比。
基于冻土的土颗粒、孔隙水和孔隙冰圆柱体模型假设，可得到土体冻结过程中的一些普遍性规律。
基于理想假设，该模型骨架由等径的土柱叠合而成，如图1所示。可见，该土柱堆积模式是最紧密堆积。由图1的模型可看出，三个土柱是彼此相切的，而孔隙柱体存在于土柱之间。假设该模型是饱和的，则孔隙柱体中充满孔隙水。
图1 一维热传导模型
Fig.1 One dimensional model of heat conduction
根据土的冻结试验研究成果可知，远离土颗粒的水受颗粒化学、矿物成分和双电层的影响较小，故其首先冻结[13]。即孔隙冰首先在图1中孔隙柱体的中央出现，并随着冻结的深入逐渐向四周扩展。也就是说，未冻水总是尽可能存在于靠近土颗粒的位置[14]。可见，随冻结温度的不断降低，冻结冰柱将不断扩大并由与土柱相离逐渐发展至与土柱相切，甚至相交，直至冻结冰体充满整个孔隙柱体。
根据图1模型在不同冻结阶段土柱、冰柱、水柱的几何关系，可以计算出该模型对应的土柱、冰柱、水柱体积比例关系。进一步，根据土、水、冰三种材料的导热系数，采用复合体的导热系数计算方法，可以综合评价土体的等效导热系数。
土柱、冰柱、水柱的几何关系演变，实际上反映了图1模型中土体的冻结过程。根据冰柱与土柱之间的位置关系，可以将冻结过程分为两个阶段。第一阶段，土柱与冻结冰柱相离无接触阶段，此时模型中含冰量较低，属于冻结初始阶段。此时，模型的导热系数由对应的冰柱体积、未冻水柱体积和土柱体积确定。第二阶段，土柱与冻结冰柱相切、相交等接触阶段。此时，冻结冰柱可扩展至两个土柱之间的狭小角隅。由于冰柱净体积增长缓慢，导热系数的变化亦趋缓，模型的导热系数可由冰柱、角隅未冻水柱和土柱的体积共同决定。
根据土中水冻结的一般规律，冻结从C点开始发生，如图2(a)所示。设冻结冰体圆柱半径为r/mm，土柱半径为R/mm。在初始冻结阶段，即当冻结冰体圆柱较小时，它与土柱是相离的，冻结冰体圆柱的截面积为：
式中，r为结冰体圆柱半径，且应满足：
图2 冻结冰体圆柱与土柱的位置关系
Fig.2 Position relationship among frozen ice and soil columns
导热系数表征的是温度梯度为1 K/m时，单位时间内通过单位面积土体的热量[15]。取1 m3冻土进行导热系数各相比例的确定，取立方体截面中心为某土柱截面的圆心，依次排列土柱从而进行计算数量的确定。由图3可知，单元截面范围内首排完整土柱数量应为1000/2R个，可知每一横排两相邻土柱的围合区域数量为1000/R个；共计1000/2R+1排土柱交接面。
图3 某微小截面单元的土柱分布
Fig.3 Soil column distribution of a micro section
3个土柱围合成的单个完整封闭区域面积S为：
单元体内完整封闭区域的个数n为：
单元体内完整封闭区域内自由水的总体积Vf为：
单元体积内土柱所占的体积Vs为：
假设任意时刻冻结柱的体积为Vi，则此刻土体中的未冻水体积含量Vu为：
结合式(1)及式(4)可知初始冻结阶段任意时刻冻结柱的体积Vi为
式中，r为结冰体圆柱的半径，且应满足式(2)。
考虑水冻结后的体积增量，冻土中各相在不同冻结阶段所占冻土的体积比例为：
式中：γj为冻土中j相所占的体积比例；γi为冻土中冰体所占的体积比例。
当冻结冰体圆柱逐渐增大至与土柱相交后，如图2(b)所示，冻结进入接触阶段。此后，冻结柱半径在同等增速情况下，冻结冰柱体积增大的趋势逐渐趋缓。复合体系的导热系数增速受有效冰柱体积增长缓慢的影响而减缓。此时，冻结冰体圆柱截面面积可依据图4建立的坐标系进行求解。
图4(a)中阴影部分的面积S1为冰体截面积，即：
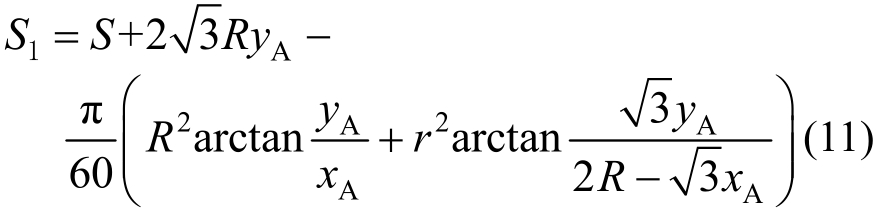
式中，S1为图4(a)中阴影部分的面积，即为冰体截面积，且有：
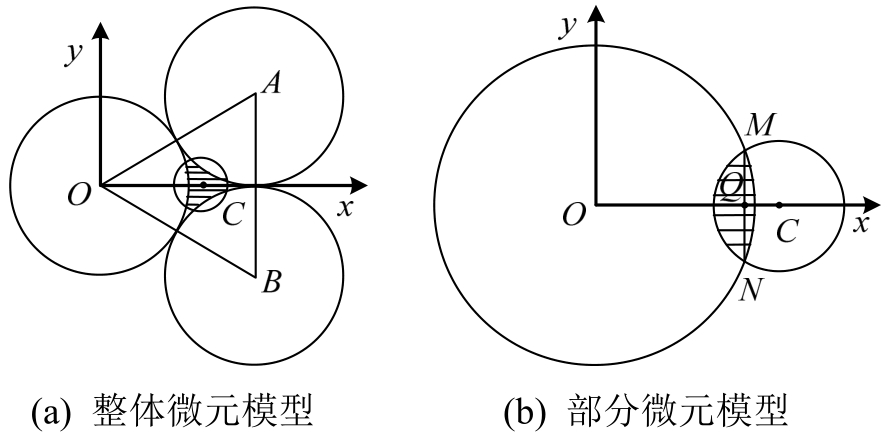
图4 冻结圆柱与土柱相交时的计算模型
Fig.4 Calculation model when frozen column intersects with soil column
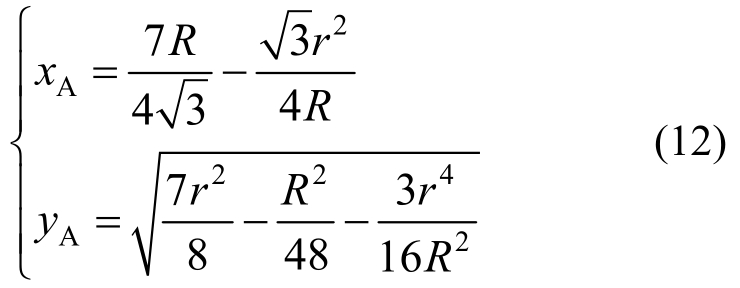
式中，r为冻结冰体圆柱半径且应满足：
结合式(11)及式(4)可知，接触冻结阶段任意时刻冻结柱的体积Vi为：
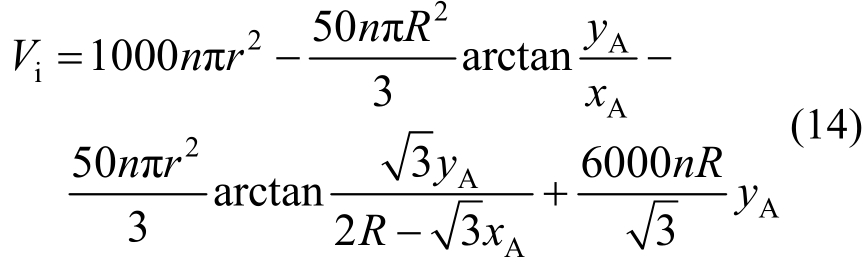
导热系数与其组成各相的体积含量相关，依据何种方式解读冻土的热源传递形式是进行导热系数计算的关键。分别基于Johansen法、流量比拟法和考虑固-液界面的方法进行冻土导热系数的确定。
Johansen[7]建议用广义的几何平均法估算土体的导热系数λ，即：
且有：
式中：
为第j种矿物的导热系数；xj为该种矿物占全部土体的体积分数。徐学祖等[15]基于Johansen估算法提出了考虑冻土中未冻水含量的导热系数λf计算方法，即：
式中：λs为土体矿物的平均导热系数，可依据土中各固体矿物的组成及体积含量加权计算；φ为冻土中冰和未冻水所占的总体积比例；Δφ为冻土中未冻水所占的体积比例。
依据式(5)～式(10)和式(14)计算冻土中各相所占总体积的比例，结合表1中材料的导热系数，利用式(17)即可计算冻土的导热系数。因土质等条件不同，表1中未标明土中固体矿物的导热系数。
表1 不同材料的导热系数
Table1 Thermal conductivity of different materials
冻土是由土颗粒、孔隙水、孔隙冰组成的多相体，孔隙水和孔隙冰随温度的变化保持变化且两者始终保持动态的平衡。导热系数实质上是由不同导体并联或混联组成的体系，基于此，提出一种冻土的流量比拟理论模型，如图5所示。
图5 流量比拟理论模型
Fig.5 Flow analogy theory model
由图5可知，流量比拟模型中因各相组成含量不同，其热源传递所相邻断面大小也不同。在传递长度一致的前提下，将单位体积冻土中的不同成分分配为大小不同的断面，基于断面比例叠加计算冻土的导热系数。具体计算式为：
式中：λw、λi分别为孔隙水和孔隙冰的导热系数，取值如表1所示；Vs、Vw、Vi分别为不同时刻冻土中土颗粒、未冻水和冰体的体积。
由于冻土中不同相体之间的导热系数差异，土柱模型的热流传播模式并非图5所示的平行传输模式。也就是说，热流除了平行传递外，在不同相间也会进行传递，如图6(a)所示。热传导条件下，模型中的热流会在土柱-水、冰柱-水、土柱-冰柱之间传递，并最终达到热流平衡。因此，导热系数理论计算中，除依据图5所示的各相不同的体积来分配传输的热量外，还需考虑各相导热系数不同带来的传输问题。考虑土、水、冰之间的导热系数差异，土柱模型的典型热流传递形式如图6(b)所示。
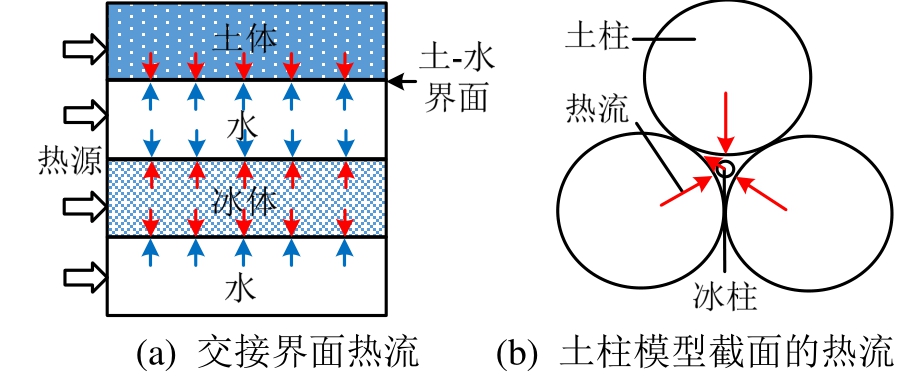
图6 固-液界面的热流形式
Fig.6 Heat flow pattern of solid-liquid interface
由图6(b)结合表1可知，土和冰的导热系数较大，同等时间下，某土柱截面上固相土和冰中的热流较早到达。此时热流会沿着土-水、冰-水交接界面向液态水中传播。土柱模型截面的热流除在方向上产生变化外，不同相间交接界面的导热系数应为两相的均值。
考虑固-液界面的冻土导热系数必然存在：1)土柱截面不同相之间的热流传输；2)交接界面处的导热系数加权计算。考虑固-液交接界面特性的导热系数计算模型，如图7所示。
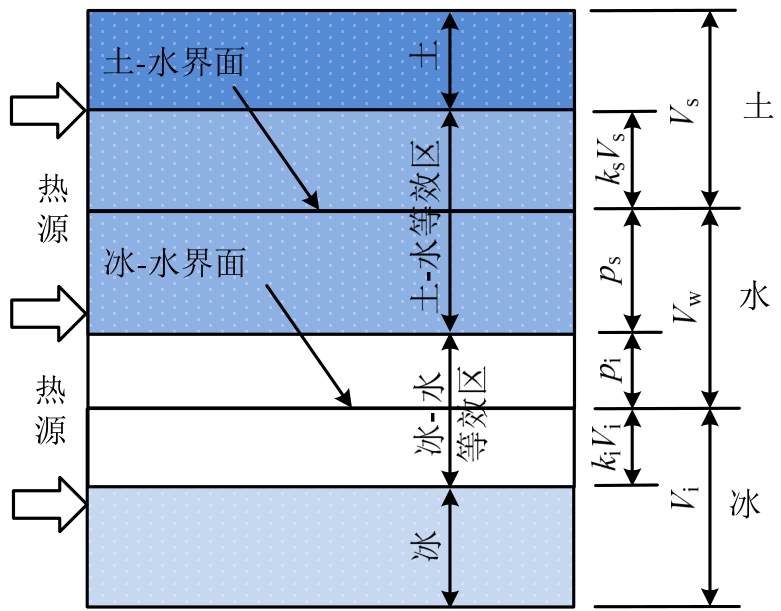
图7 考虑固-液界面的计算模型
Fig.7 Computational model considering solid-liquid interface
在图7中，将冻土未冻水依据固体土颗粒和冰占固相的比例分为两部分，一部分与土颗粒进行热流传递，另一部分与固态冰进行热流传递，即：
在同一时间下，体积为ps的液态水需要一定体积的土颗粒与其达到热流平衡。该区域与其导热系数之积与一定体积土颗粒和土颗粒导热系数之积相等，即：
同样，冰体与水之间满足：
式中，ks、ki分别为导热系数差异引起的土颗粒和冰的体积等效系数。
不难想象，(ps+ksVs)部分与(Vs-ksVs)部分之间仍存在导热系数差别引起的热流传递现象，如图7所示。也就是说，各相导热系数差别引起的热流横向传递持续存在，直至各相材料达到热流的平衡。若考虑(ps+ksVs)部分与(Vs-ksVs)部分之间仍存在导热系数差别，二次进行传递后的等效区域服从：
式中：α为土-水混合物和土导热系数差异引起的体积等效系数；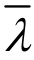
为土-水混合物的等效导热系数。
前文所述，固-液界面上的导热系数为土颗粒与水导热系数的平均值，则导热系数应从固-液界面向两侧线性变化。为简化计算量，本文以考虑固-液仅传递一次为例，进行导热系数计算方法的说明，如图8所示。
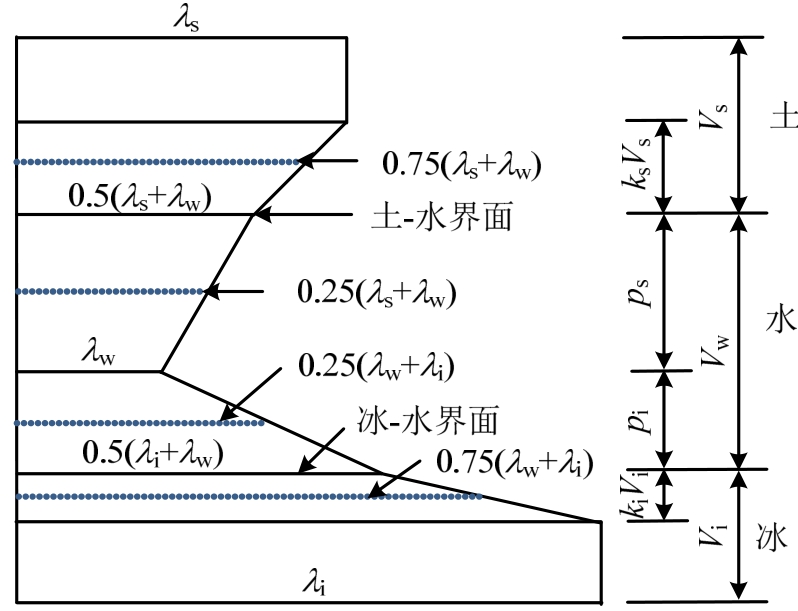
图8 考虑固-液界面的计算示意图
Fig.8 Sketch of calculation of solid-liquid interface
饱和冻土是由土颗粒、水和冰组成的三相体，由于水的导热系数显著小于土颗粒和冰的导热系数，冰首先产生于远离土颗粒的液态水中，加之固相间接触产生的Kapitza阻抗较大[16]。因此，在冻结初期可认为饱和冻土中的冰体与土颗粒不直接接触，据此可依据土、冰所占固体的体积分配等效体积，建立的考虑固-液界面的导热系数计算公式为：
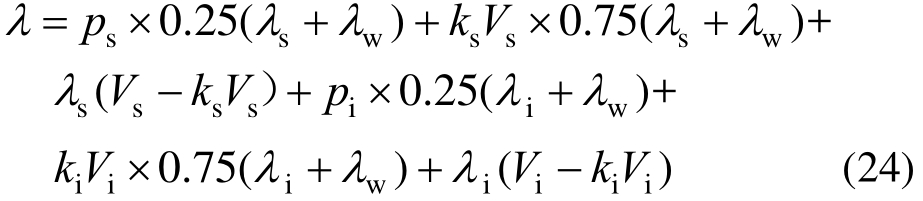
将式(19)～式(22)引入式(24)，消去含有动态变量的ksVs和kiVi，得到考虑固-液界面一次传递的导热系数计算式为：
依据式(25)和冻土中各相的组成，可计算获取冻土在不同负温下的导热系数。
将原状粉质黏土烘干碾碎后，重塑成不同干密度的饱和试样。之后采用探针法对不同温度下的冻土导热系数进行测定[17]，获取的不同干密度饱和黏土的导热系数和冻结温度，如表2所示。
表2 饱和粉质黏土导热系数和冻结温度试验结果
Table2 Test results of thermal conductivity and frozen temperature of saturated silty clay
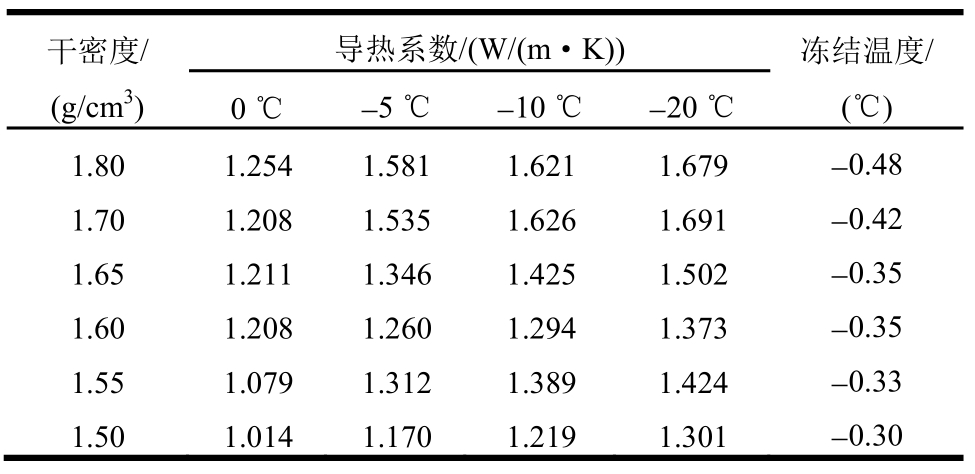
由表2可知，随着冻结温度的降低，土体的导热系数逐渐增大，且在高温冻土区间变化明显，这与实际情况是吻合的[14，16]。同时发现，同一温度情况下，随着土样干密度的增大，其导热系数增速并不显著，甚至有减小的趋势。这是由于土体干密度增大的实质是一定体积内孔隙水含量的减少，土颗粒将孔隙水分割为更多的单元，孔隙水量的减少决定了水的相变总量，更多的孔隙水单元使得冰体难以连续，因而土体的导热系数变化趋缓。同样，从不同干密度土体的冻结温度可看出，随着饱和土样干密度的增大，其冻结温度呈现逐渐降低趋势，这与冻土导热系数随温度的变化趋势是吻合的。
基于提出的导热系数几何模型，用Johansen的土体导热系数预估方法、冻土流量比拟计算法和考虑固-液界面的方法对冻土导热系数进行计算，并将三种计算模型的计算值与瞬态探针法实测值进行了比较。
基于Johansen[7]和徐学祖等[15]提出并完善的冻土导热系数计算方法，结合提出的冻土导热系数几何模型，对试验获得的数据进行对比和分析。以半径1 mm的土柱为例，进行导热系数理论模型的计算，得到不同冻结阶段饱和冻土导热系数的变化趋势，如图9所示。依据不同半径土柱的几何模型在不同冻结时刻的导热系数，得到饱和冻土干密度与冻土导热系数的关系，如图10所示。
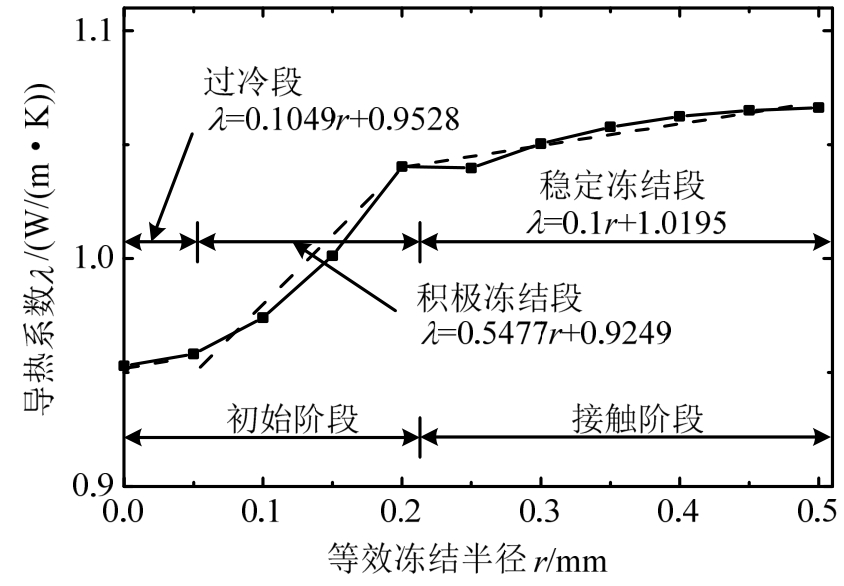
图9 理论模型的导热系数演变趋势
Fig.9 Thermal conductivity evolution trend of theoretical model
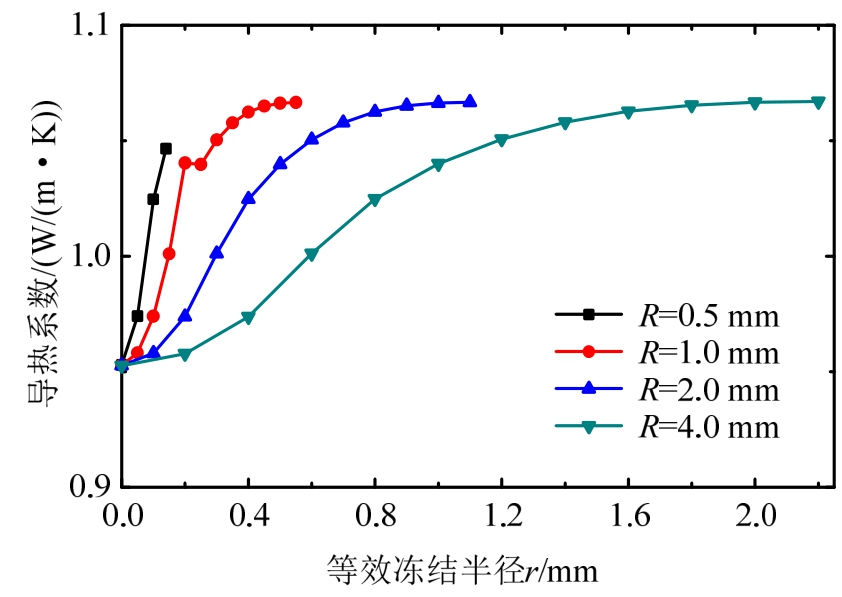
图10 不同半径土柱的导热系数
Fig.10 Thermal conductivity of soil columns with different radius
由图9可知，随着冻土中等效冻结半径(冰柱)的增大，其导热系数逐渐增大，且初始阶段导热系数增速大于接触阶段的导热系数增速。反映出冻土的导热系数增长趋势与不同负温相关，这与实际情况是相符的[8，15]。冻土导热系数在积极冻结阶段变化明显，并随着冻土未冻水含量的稳定，其导热系数也趋于平缓。土柱模型能够较好地反映土体在冻结过程中的过冷、积极冻结和稳定冻结等阶段。
由图10可看出，冻结半径增速均匀情况下土体导热系数变化与冻土中土颗粒含量相关。随着土柱半径的增大，即土体干密度的相对增大，饱和土体的导热系数变化越平缓。究其原因是冻土中土颗粒含量的相对增多，使得土体的导热系数变化更多的受到土颗粒因素的制约，土中水相变成冰后导热系数增大约四倍，而土颗粒的导热系数变化受温度影响较小。也就是说，同等冰体含量下，饱和土体的干密度越小，冻土的导热系数变化越敏感，这与表2中土体冻结温度的试验结果是吻合的。
基于流量比拟模型的加权计算方法，结合提出的冻土导热系数几何模型，对试验获得的数据进行对比分析。以半径1 mm的土柱为例进行导热系数理论计算，获取的导热系数曲线如图11所示。
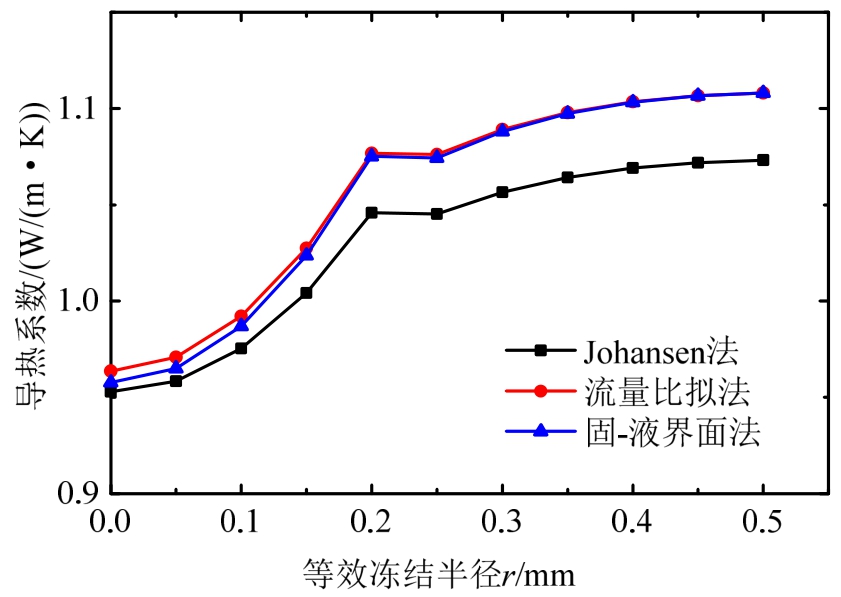
图11 不同方法计算的导热系数值
Fig.11 Numerical values of thermal conductivity calculated by different methods
由图11可看出，流量比拟法与Johansen法计算模型的导热系数变化趋势较为相似。总体看来两者之间的差别微小，均是随着冻土温度的下降，冻土导热系数上升，这与实际情况是吻合的[14―15]。
考虑固-液界面的导热系数计算方法，将传输过程中因各相导热系数差异引起的热流传输预测差别降到了最低。也就是说该模型考虑了热流一维传播过程中垂直方向的影响。以半径1 mm的土柱为例进行导热系数理论计算，获取的考虑固-液界面方法的导热系数，如图11所示。
由图11可看出，在冻结初期，固-液界面法计算获取的冻土导热系数位于Johansen法和流量比拟法之间。随着冻结的深入，冻土中冰体含量增多，固-液界面法与流量比拟法计算获取的数据基本一致，这与土体冻实后冰体连续导致的导热系数增大现象是一致的。
饱和土体的干密度与体积比之间可用式(26)换算，即：
式中：Vs为土体中土颗粒所占的体积；V为土体总体积；ρd为土体干密度；ds为土颗粒相对密度。测定了干密度为1.8和1.55的粉质黏土在不同负温下的未冻水含量，具体方法参考文献[18]。结合Johansen法、流量比拟法和固-液界面法，计算得到了不同负温下的冻土导热系数，并将其与表2中的实测数据进行了对比，结果如表3所示。
表3 不同方法获取的导热系数计算值和实测值
Table3 Calculated and measured values of thermal conductivity by different methods
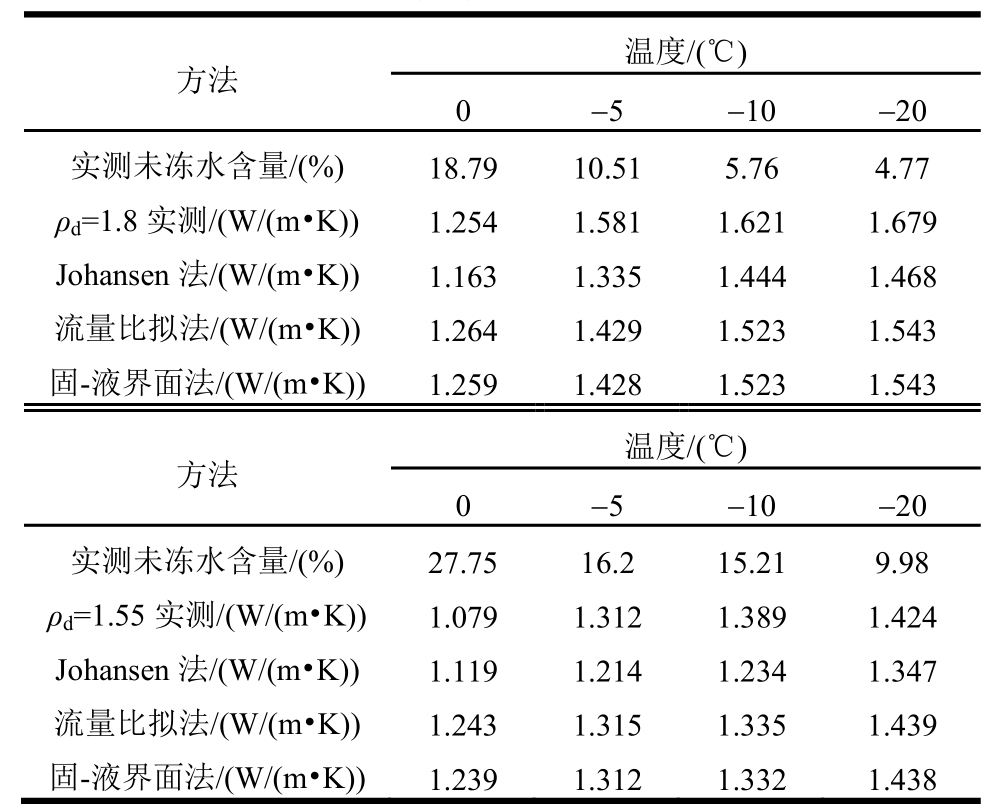
由表3可知，依据未冻水含量测试结果，获取的不同负温下冻土导热系数的计算值与实测值并不相等，甚至存在一定差距。总体而言，Johansen法和流量比拟法以及固-液界面法均能预测冻土导热系数随不同负温的变化趋势。相较于流量比拟法，固-液界面法预测的冻结初期导热系数更逼近于实测值，冻结后期其预测值与流量比拟法预测值基本一致。
计算值与实测值存在一定误差的原因可从以下方面分析：1)土中固相矿物的导热系数测试存在误差，土中一些矿物离子特别是随温度变化敏感离子使得计算结果存在误差。2)导热系数测试存在误差，探针法的插针位置对干密度较小的土体测试结果影响较大[19―21]。土体在冻结过程中，水分迁移等情况持续发生，因而存在一些数据点的离散，最终测试结果失真，这也为冻结法设计与施工埋藏了隐患[22―23]。提出的冻土导热系数几何模型，适用于Johansen法、流量比拟法以及提出的固-液界面法，能够为冻土导热系数的预测提供理论依据。
基于冻土的固相颗粒、孔隙水和孔隙冰三相组成，依据导热系数的量纲定义，建立了冻土导热系数的几何模型。考虑实际冻土中三种成分的含量随温度变化而不断变化的事实后，给出了随温度变化的水柱和冰柱体积计算与演变规律。同时提出了考虑固-液界面的导热系数计算模型，并与Johansen法计算值和瞬态探针法实测数据进行了对比。主要研究结论如下：
(1)提出的几何模型直观表达了土体冻结过程中的导热系数变化趋势，丰富了考虑土体微观组成的导热系数模型研究。
(2)提出的理论土柱模型能够揭示土体在冻结过程中导热系数的演变规律，印证了冻土导热系数随不同负温变化的主要原因是受其未冻水含量的影响。
(3)基于土柱模型热传导形式的并联和串联耦合特性，建立的考虑固-液界面的导热系数计算模型，考虑了复合介质热传导过程中的方向性，且能够较好地预测土体冻结初期的导热系数。
(4)建立能反映土体冻结过程的导热系数计算模型具有理论可行性，但高精度预测冻土导热系数取值仍具一定难度。
参考文献：
[1]Tian Z，Lu Y，Horton R，et al.A simplified de Vries-based model to estimate thermal conductivity of unfrozen and frozen soil[J].European Journal of Soil Science，2016，67(5):564―572.
[2]朱志武，宁建国，马巍.土体冻融过程中水、热、力三场耦合本构问题及数值分析[J].工程力学，2007，24(5):138―144.Zhu Zhiwu，Ning Jianguo，Ma Wei.Constitutive model and numerical analysis for the coupled problem of water，temperature and stress fields in the process of soil freeze-thaw[J].Engineering Mechanics，2007，24(5):138―144.(in Chinese)
[3]Han L，Ye G，Li Y，et al.In-situ monitoring of frost heave pressure during cross passage construction using ground freezing method[J].Canadian Geotechnical Journal，2016，53(3):1―10.
[4]毛卫南，刘建坤.不同离散化方法在正冻土水热耦合模型中的应用[J].工程力学，2013，30(10):128―132.Mao Weinan，Liu Jiankun.Different discretization method using in coupled water and heat transport model for soil under freezing conditions[J].Engineering Mechanics，2013，30(10):128―132.(in Chinese)
[5]武建军，韩天一.饱和正冻土水-热-力耦合作用的数值研究[J].工程力学，2009，26(4):246―251.Wu Jianjun，Han Tianyi.Numerical research on the coupled process of the moisture-heat-stress fields in saturated soil during freezing[J].Engineering Mechanics，2009，26(4):246―251.(in Chinese)
[6]马悦，朱志武，马巍，等.冻土冲击动态应力-应变曲线特征及汇聚现象分析[J].工程力学，2015，32(10):52―59.Ma Yue，Zhu Zhiwu，Ma Wei，et al.Characteristics of stress-strain curves and convergence phenomenon of frozen soil under dynamic loading[J].Engineering Mechanics，2015，32(10):52―59.(in Chinese)
[7]Johansen O.Thermal conductivity of soils[D].Trondheim，Norway:University of Trondheim，1975.
[8]原喜忠，李宁，赵秀云，等.非饱和(冻)土导热系数预估模型研究[J].岩土力学，2010，31(9):2689―2694.Yuan Xizhong，Li Ning，Zhao Xiuyun，et al.Study of thermal conductivity model for unsaturated unfrozen and frozen soils[J].Rock and Soil Mechanics，2010，31(9):2689―2694.(in Chinese)
[9]洪涛，梁四海，孙禹，等.黄河源区多年冻土热传导系数影响因素分析及其在活动层厚度模拟中的应用[J].冰川冻土，2013，35(4):824―833.Hong Tao，Liang Sihai，Sun Yu，et al.Analyzing the factors that impact on the heat conductivity coefficient and applying them to simulate the depth of permafrost active layer in the headwaters of the Yellow River[J].Journal of Glaciology and Geocryology，2013，35(4):824―833.(in Chinese)
[10]陶兆祥，张景森.大含水(冰)量融冻土导热系数的测定研究[J].冰川冻土，1983，5(2):75―80.Tao Zhaoxiang，Zhang Jingsen.The thermal conductivity of thawed and frozen soils with high water(ice)content[J].Journal of Glaciology and Geocryology，1983，5(2):75―80.(in Chinese)
[11]刘为民，何平，张钊.土体导热系数的评价与计算[J].冰川冻土，2002，24(6):770―773.Liu Weimin，He Ping，Zhang Zhao.A calculation method of thermal conductivity of soils[J].Journal of Glaciology and Geocryology，2002，24(6):770―773.(in Chinese)
[12]陈琳，喻文兵，杨成松，等.基于微观结构的青藏高原风积沙导热系数变化机理研究[J].冰川冻土，2014，36(5):1220―1226.Chen Lin，Yu Wenbing，Yang Chengsong，et al.Conductivity of aeolian sand on the Tibetan Plateau based on microstructure[J].Journal of Glaciology and Geocryology，2014，36(5):1220―1226.(in Chinese)
[13]Kozlowski T.A simple method of obtaining the soil freezing point depression，the unfrozen water content and the pore size distribution curves from the DSC peakmaximum temperature[J].Cold Regions Science & Technology，2016，122(122):18―25.
[14]з·д.叶尔绍夫.冻土学原理[M].第二册.刘经仁，等译.兰州:兰州大学出版社，2015.з·д.Ершов.Principles of geocryology[M].2nd ed.Translated by Liu Jingren，et al.Lanzhou:Lanzhou University Press，2015.(in Chinese)
[15]徐学祖，王家澄，张立新.冻土物理学[M].北京:科学出版社，2010.Xu Xuezu，Wang Jiacheng，Zhang Lixin.Physics of frozen soil[M].Beijing:Science Press，2010.(in Chinese)
[16]Dietze G F.On the Kapitza instability and the generation of capillary waves[J].Journal of Fluid Mechanics，2016，789:368―401.
[17]陈之祥，李顺群，王杏杏，等.热参数对温度场的影响及敏感性分析[J].水利水电技术，2017，48(5):136―141.Chen Zhixiang，Li Shunqun，Wang Xingxing，et al.Analysis on impact and sensitivity of thermal parameters on frozen soil temperature field[J].Water Resources and Hydropower Engineering，2017，48(5):136―141.(in Chinese)
[18]Kruse A M，Darrow M M.Adsorbed cation effects on unfrozen water in fine-grained frozen soil measured using pulsed nuclear magnetic resonance[J].Cold Regions Science & Technology，2017，142:42―54.
[19]黄建华.考虑卸压孔卸荷作用的人工冻土冻胀特性研究[J].工程力学，2010，27(12):141―148.Huang Jianhua.Research on frost heaving characteristics of artificial frozen soil based on unloading effect by discharge holes[J].Engineering Mechanics，2010，27(12):141―148.(in Chinese)
[20]郑先昌，郑伟锋.中国南极中山站区冻土融沉和冻胀模拟试验及基础对策研究[J].工程力学，2010，27(增1):154―158.Zheng Xianchang，Zheng Weifeng.Freeze-thaw and freeze-heaving experiment and foundamental countermeasure of the China Zhongshan station in the south pole[J]Engineering Mechanics，2010，27(Suppl 1):154―158.(in Chinese)
[21]孙斌祥，徐学祖，赖远明，等.青藏高原铁路多年冻土路堤的碎石层高度[J].工程力学，2006，23(6):127―134.Sun binxiang，Xu Xuezu，Lai Yuanming，et al.Ballast layer height of railway embankment in Qinghai-Tibet Plateau permafrost region[J].Engineering Mechanics，2006，23(6):127―134.(in Chinese)
[22]梁波，陈兴冲.青藏铁路的重要意义、技术难点及力学问题[J].工程力学，2004，21(增1):139―149.Liang Bo，Chen Xingchong.The significance，the key technical problem and the mechanical problem of Qinghai-Tibetan Railway[J].Engineering Mechanics，2004，21(Suppl 1):139―149.(in Chinese)
[23]陈兴冲，高峰，吴少海.冻土层对桥梁地震反应的影响[J].工程力学，2007，24(3):120―125.Chen Xingchong，Gaofeng，Wu Shaohai.Effect on frozen layer on seismic response of bridges[J].Engineering Mechanics，2007，24(3):120―125.(in Chinese)
THEORETICAL MODEL AND EXPERIMENTAL VERIFICATION ON THERMAL CONDUCTIVITY OF FROZEN SOIL UNDER DIFFERENT NEGATIVE TEMPERATURE CONDITIONS
XIA Jin-hong1，CHEN Zhi-xiang2，3，XIA Yuan-you4，LI Shun-qun2，3
(1.School of Civil Engineering and Architecture，Wuhan University of Technology，Wuhan 430070，China;2.School of Civil Engineering，Tianjin Chengjian University，Tianjin 300384，China;3.Tianjin Key Laboratory of Soft Soil Characteristics and Engineering Environment，Tianjin 300384，China)
Abstract:A geometric model of frozen soil thermal conductivity is established based on a simplified definition of frozen soil as a mixture of soil column，liquid water and ice column according to the three-phase composition and the definition of thermal conductivity of saturated frozen soil.The volume calculation and evolution law of water and ice column variation with temperature is established considering the fact that the contents of the three phases in the frozen soil change with the temperature.Based on the superposition principle of the thermal effect of the parallel system，the calculation model of frozen soil thermal conductivity is established.In view of the coupling characteristics of parallel connection and series connection in the heat transfer process，a calculation model of thermal conductivity considering the effect of solid-liquid interface is established.The comparisons among the calculation results，the experimental results with transient probe method and the results by Johansen’smethod indicate that those methods can effectively simulate the thermal conductivity of frozen soil under different negative temperature conditions with clear concepts and simple procedures.
Key words:geotechnical engineering;frozen soil;thermal conductivity model;unfrozen water;solid-liquid interface
中图分类号：TU752
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0048
文章编号：1000-4750(2018)05-0109-09
收稿日期：2017-01-12；修改日期：2017-11-09
基金项目：国家自然科学基金项目(41472253)；天津市自然科学基金重点项目(16JCZDJC39000)；天津市建设系统科学技术项目发展计划项目(2016-25)
通讯作者：陈之祥(1990―)，男，河南濮阳人，硕士生，主要从事环境岩土工程方面的研究(E-mail:chen_zhixiang@126.com).
作者简介：夏锦红(1966―)，女，河南卫辉人，教授，博士，主要从事岩土工程和结构工程方面的教学与研究(E-mail:yantugc@yeah.net);
夏元友(1965―)，男，安徽庐江人，教授，博士，博导，主要从事岩土工程教学与研究(E-mail:xiayy1965@126.com);
李顺群(1971―)，男，河南卫辉人，教授，博士，硕士，主要从事岩土工程教学与研究(E-mail:lishunqun@yeah.net).