袁修开，朱海燕，张保强
(厦门大学航空航天学院，福建，厦门 361005)
摘 要：在工程结构的可靠性优化过程中，求解的效率和精度是优化方法的关键。该文提出一种针对解耦优化的融合策略。所提方法在优化迭代解耦所用的失效概率函数为前几次迭代设计点构建的局部失效概率函数的加权融合形式。在对原可靠性优化问题进行解耦后，结合序列近似优化方法进行迭代求解。相比于常规的仅使用当次局部建立的失效概率函数而言，所提融合策略最大限度利用了各次迭代中产生的信息用于优化解耦求解，能够提高失效概率函数的近似精度，从而间接达到减少迭代次数和计算量的目的。最后给出了屋架和十杆结构的可靠性优化算例，验证该文方法的正确性和可行性。
关键词：可靠性优化；解耦；融合策略；失效概率函数；序列近似优化
在工程结构设计中，基于可靠性的优化设计是极具优势的设计方法[1－3]。但其包括优化求解与可靠性估计[4－5]的嵌套求解结构，这两者都需要多次对结构的响应值进行计算，而有些复杂结构问题的结构响应值计算往往需要进行耗时的有限元分析。并且工程对分析及优化的精度也提出了更高的要求。因此，可靠性优化广泛应用到实际工程问题中还存在很大的困难和挑战[2]。可靠性优化求解的效率和精度决定了整个设计过程的可行与否。常用的可靠性优化求解方法有双循环[6]、单循环[7]和解耦优化方法[8－10]。双循环、单循环常常与可靠性分析方法中效率较高的一类方法相结合，如近似解析方法。但是随着工程问题越来越复杂，对结构设计精度的要求也不断提高，这类方法因为存在计算精度低以及适用性差的问题，已不能满足工程需求。解耦方法[8－10]是解决可靠性优化问题的一个高效可行的方法，它通过建立关于设计参数的显式表达式来近似可靠性优化问题中包含的概率约束，从而将包含嵌套求解结构的原问题解耦成常规的确定性优化问题，然后就可通过一般的优化算法对该问题进行求解。其中，概率约束的近似表达，也就是失效概率函数的求解是方法的关键。目前已有多种构建失效概率函数的方法，如灵敏度信息法[9－10]、贝叶斯方法[11]和加权策略法[12－13]，其中加权策略法通过“加权因子”仅需进行单次可靠性估计就可以得到局部近似的失效概率函数，大大提高了优化效率。但由于此失效概率函数为局部近似，在优化过程中会存在某些精度的问题导致优化迭代的次数较多，从而影响可靠性优化求解的效率。
为了进一步提高可靠性优化求解的精度和效率，本文针对可靠性优化的解耦方法，提出一种融合策略。所提策略将当前次迭代的失效概率函数取为前几次设计点建立的失效概率函数的加权融合形式。该策略可以提高优化结果的精度，进而减少迭代次数，提高可靠性优化设计的效率，在工程上具有重要的意义。
本文讨论的可靠性优化问题可定义为在给定的可靠性约束和确定性约束下最小化结构成本，可用式(1)所示数学表达式来描述：
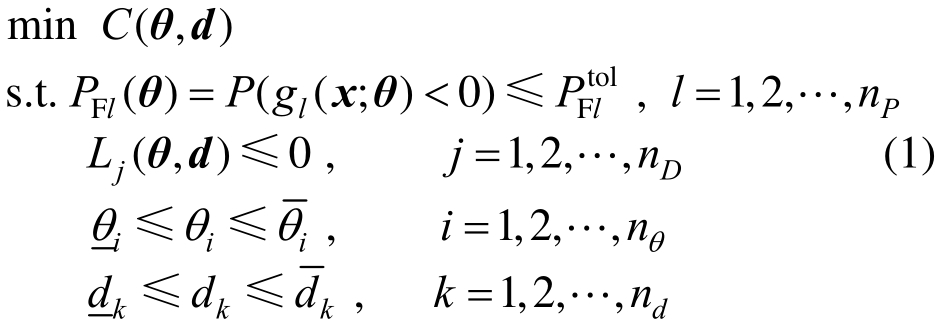
式中：C(θ，d)为目标函数，d=[d1，d2，…，dn]为确定性设计参数，θ=[θ1，θ2，…，θnθ]为设计参数向量；PFl(θ)=P(g(x;θ)＜0)是第l个失效概率约束(也即可靠性约束)，称之为失效概率函数；gl(x;θ)为结构第l个极限状态函数，x为基本随机变量向量；在本文中，考虑θ为变量x的分布参数的情形(如均值)；
为相应的失效概率约束阀值；Lj(θ，d)为第j个确定性约束。
所提优化求解策略包含了解耦及序列近似优化两个部分：1)解耦过程，即通过融合策略来构建近似失效概率函数，将原可靠性优化问题转化成一般的确定性优化问题；2)序列近似优化[14－15]过程，为保证获得原问题的最优解，将原问题转换成一系列的优化子问题来进行求解。本文所提的融合策略即是针对序列近似优化过程的特点，提出的一种改进的策略，即充分利用各次迭代过程中的信息于下一次的寻优，从而提高求解的精度和效率。
由于解耦方法中往往获得的是局部近似的失效概率函数估计，因此常常将其与序列近似优化方法[15]相结合来进行可靠性优化的求解，即通过一系列的子区域上的确定性优化的迭代求解来逼近原问题的最优解。但在实际求解中发现，在迭代解不断逼近最优解的过程中，每次迭代所建立的局部失效概率函数实际上是存在相互重叠的区域，因此，综合利用每次建立的信息(失效概率函数)，而不仅仅是当前次迭代的信息，是切实可行且具有提高优化求解精度、加快优化进程的意义。本文针对序列近似优化过程的特点提出一种融合策略，其充分而综合地利用各次迭代过程的信息用于下一次的寻优，从而提高求解的精度和效率。
假定当前为第k次迭代过程，本文所提的融合策略下的失效概率函数
表示为前k次近似失效概率函数的加权和形式，即：
式中：
为第i(i=1，2，…，k)次迭代中围绕优化解(设计值)θ(i)新建立的失效概率函数的近似估计；ri为对应的权重。
的建立失效概率函数近似估计的建立目前已有多种方式，如基于灵敏度的方法[9－10]以及基于抽样模拟改造的方法[11，16]；本文采用文献[16]所提的加权重要抽样方法为例进行探讨，其他构建方法可以纳入本文所提策略中。详细如下。
首先对于设计参数θ，失效概率函数可表达为：
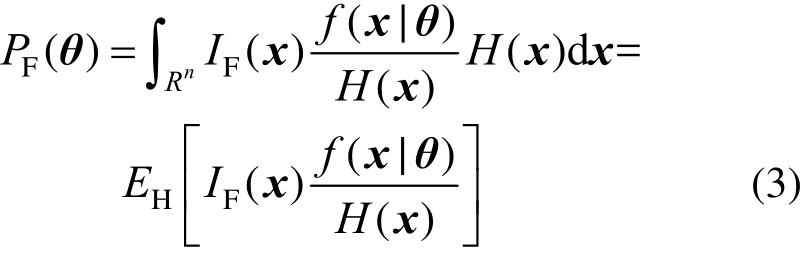
式中：Rn为n维变量空间；IF(x)为失效域的指示函数，当x∈F，IF(x)=1，反之为0；H(x)为辅助重要抽样函数；f(x|θ)为变量x的概率密度函数(依赖于设计参数θ)。
依照式(3)，即可在第i次迭代中依据当前设计值
选择合适的辅助重要抽样函数H(x)，再从H(x)中抽取样本x(j)(j=1，2，…，N)。由式(3)可知，相应的局部近似失效概率函数可以由式(4)来估计：
辅助重要抽样函数H(x)的选取在一定程度上影响失效概率函数的求解效率和精度，其选取可以类比于一般情形(常规失效概率计算)下重要抽样函数的选取，即既可通过优化方法获得最优抽样函数的近似，亦可以通过简单的基于自适应的[13]或基于设计点[12]的方式来构建。区别在于这里的辅助抽样函数要兼顾到不同取值参数下失效概率的近似程度。本文采用最简单易行的基于设计点的正态密度函数形式的辅助抽样函数的选取方法。
在优化迭代过程中，基于设计点的辅助重要确定抽样函数对应的选取方法有两种。一种是依据每次优化迭代的设计值来重新确定重要抽样函数对应的抽样中心；另外一种是仅在第一次优化迭代中求解当θ=θ(1)时对应的极限状态的设计点值x*(1)，在后续迭代过程中，将迭代得到的新的设计参数代替原设计点值x*(1)中的对应设计参数，其他参数保持不变。本文采用计算量较少的第二种方法：首先按与设计参数的关系将随机变量分为两类，与设计参数θ有关的记为xd=[x1，x2，…，xnθ]，其他的记为xr=[xnθ+1，xnθ+2，…，xnθ+nr]。将x相应的分布参数取为设计初值θ=θ(1)时，对应概率密度函数为f(x|θ(1))，求解此时的设计点为
。则在第k次迭代中的辅助抽样密度H(k)(x)的抽样中心设为
。在后续迭代过程中，亦可根据重要抽样得到的失效概率估计的变异系数等，考虑对xr*(1)进行更新。详细可参考文献[12，16]。
最直接而又易于实现的融合策略是对各次所得的局部失效概率函数进行加权平均，其关键在于加权权重的确定。由于局部失效概率函数是基于当前迭代设计值而建立的，如在本文中，设计值被用于辅助抽样密度的中心的构建，故权重应依设计值而定。本文提出如下两种权重确定的策略：
1)静态权重策略
考虑到当前新建立的与前几次建立的局部失效概率函数，对当前优化贡献程度是不一样的，故将加权因子分为两部分来分别对待。一部分，将当前次(记为k)获得的失效概率函数的权重设为α∈[0，1]，如取0.5～0.8。另一部分，前几次(i=1，2，…，k-1)失效概率函数的总权重为1-α，且第i次的权重值与该次优化设计值θ(i)到第k次优化设计值θ(k)的正则化距离di成反比，即：
式中，σj为参数θj对应的随机变量的方差。
2)动态权重策略
考虑到融合的目标为保证下一次迭代的精度，故可将各次函数的权重设定为随θ取值的变化而变化。此时权重值取为与参数点θ到各次优化设计值(建立失效概率函数的点)θ(i)(i=1，2，…，k)的正则化距离成反比：
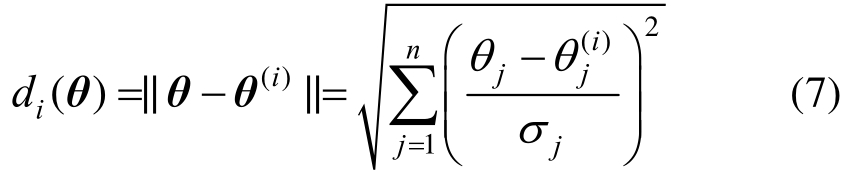
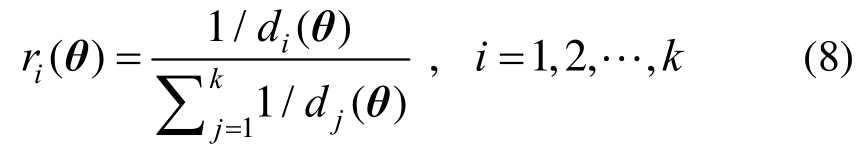
在确定权重之后，代入式(2)所示的融合的失效概率函数
表达式中即可得到其估计。需要指出的是，上述加权融合能够保留原估计的特性，如本文式(4)估计的无偏性。
上述两种权重确定策略各有特点：静态权重将各次局部失效概率函数按照抽样中心确定其权重值，而动态权重方法则按照设计取值来动态确定。第一种仅需计算k次即可，而第2种每次计算不同设计值的
时都需要重新计算权重值。
通过式(2)构建近似失效概率函数之后，原可靠性优化问题将被解耦为如下确定性优化问题：
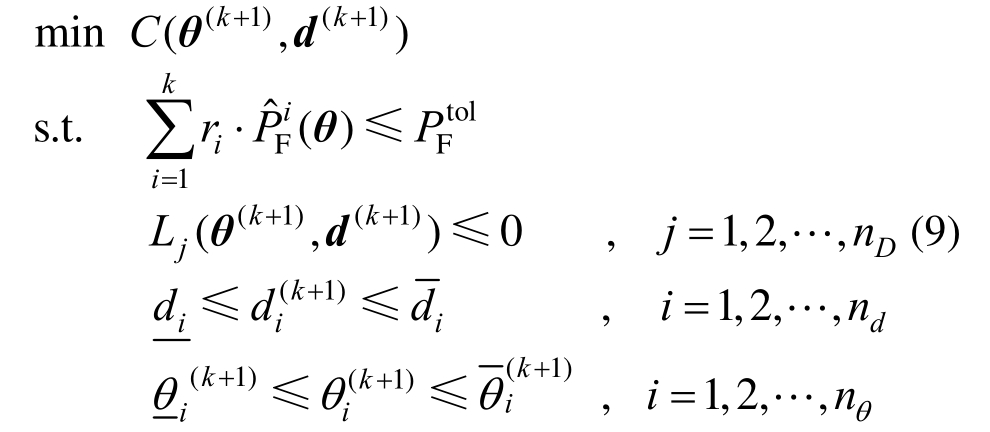
求解该确定性优化子问题可得出下一次迭代优化设计值
。然后基于
重复上述加权融合求解过程，可得到一系列的备选优化解序列
该序列将逼近原可靠性优化问题的最优解。式(9)中
表示局部优化区域的上下界，本文采用如下方式[12]选取：
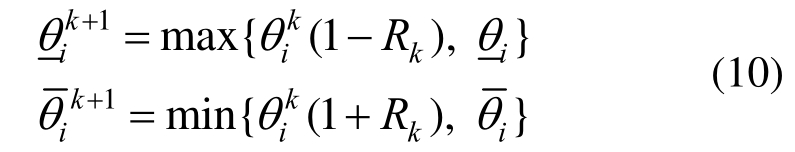
式中，Rk控制局部优化区间的大小。为确保失效概率函数的近似精度，采用一种渐变策略：
式中：01r＜＜为缩减因子；0R为初始值，一般取20%左右。同时设定收敛准则为
或
，其中Ctol和εtol为预先给定的阀值。
综上，采用本文所提基于融合策略的解耦方法进行可靠性优化求解的具体流程如图1所示。
如图2所示的屋架，屋架的上弦杆和其他拉杆采用钢筋混凝土杆，下弦杆和其他拉杆采用钢杆。设屋架承受均布载荷q作用，将均布载荷q化成节点载荷后有P=ql/4。结构力学分析可得C点沿垂直地面方向的位移为：
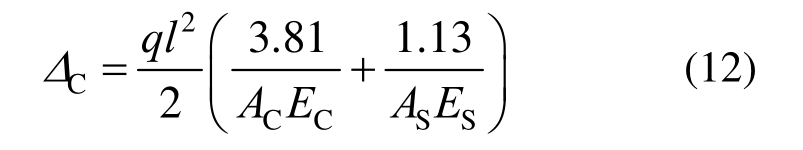
式中，AC、EC、AS、ES、l分别为混凝土和钢杆的横截面积、弹性模量、长度。考虑屋架的安全性和适用性，以屋架顶端C点的向下挠度不大于5cm为约束条件。根据约束条件可得到结构极限状态函数
，其中6个随机变量为：
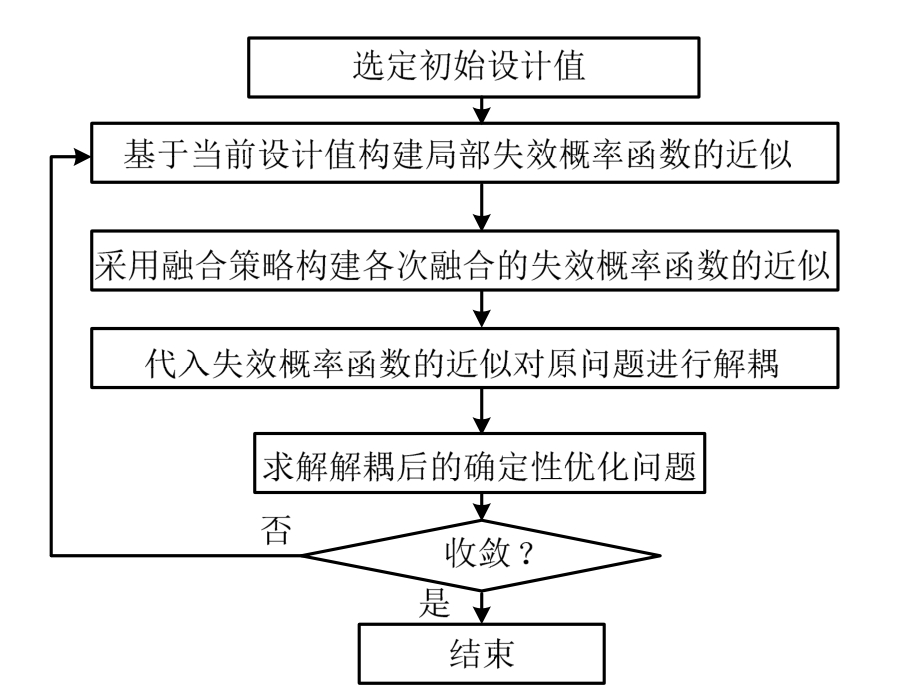
图1 所提优化方法流程图
Fig.1 Flow chart of proposed method
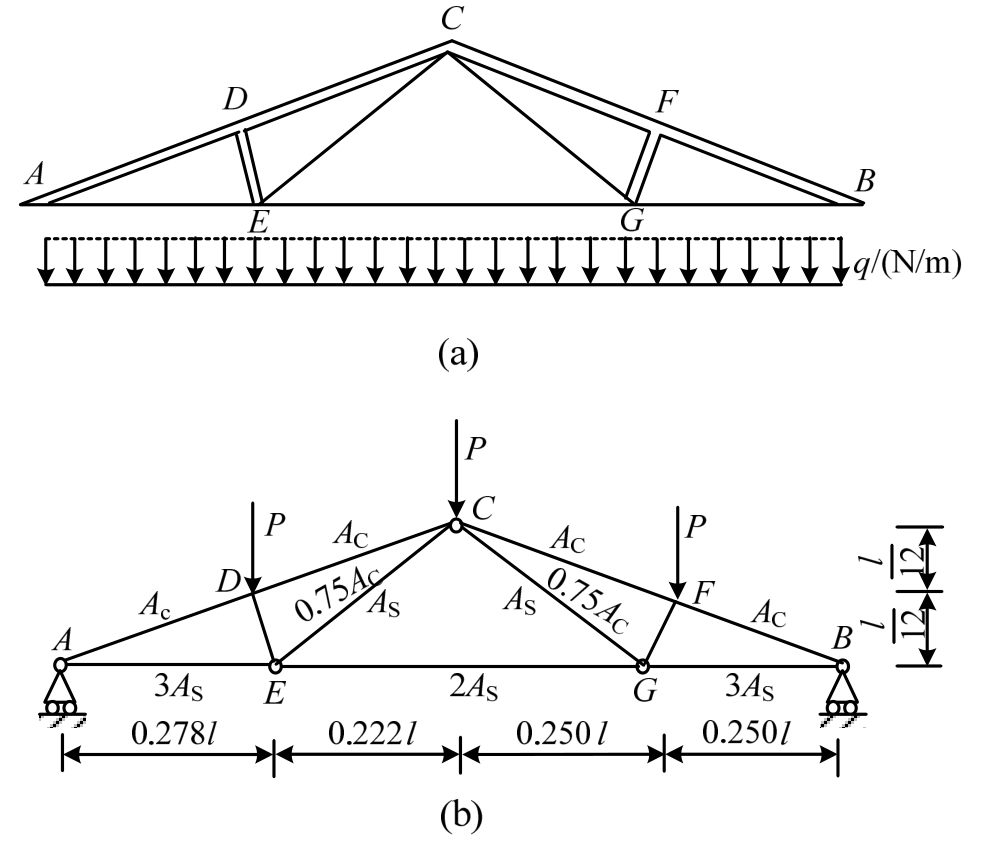
图2 屋架算例简单示意图
Fig.2 Simple sketch of roof truss
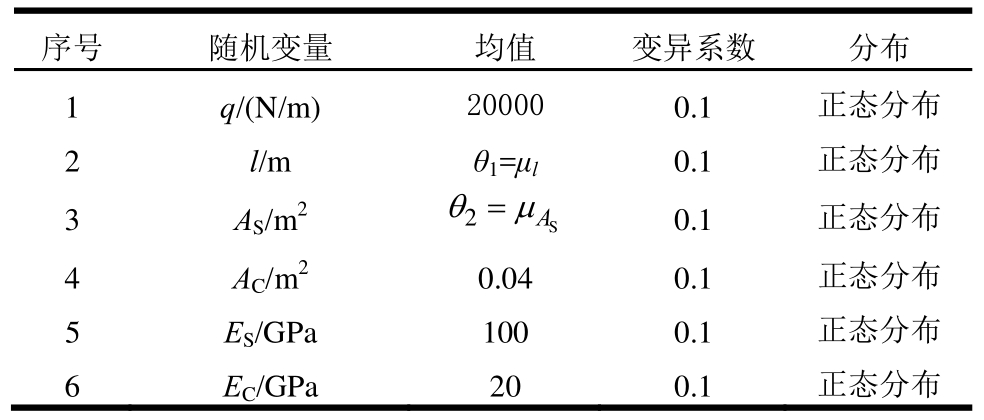
假设所有随机变量均服从独立的正态分布，它们的分布参数参见表1。将l和AS的均值视为设计变量，即
，设计区间
该可靠性优化问题的数学模型如下：
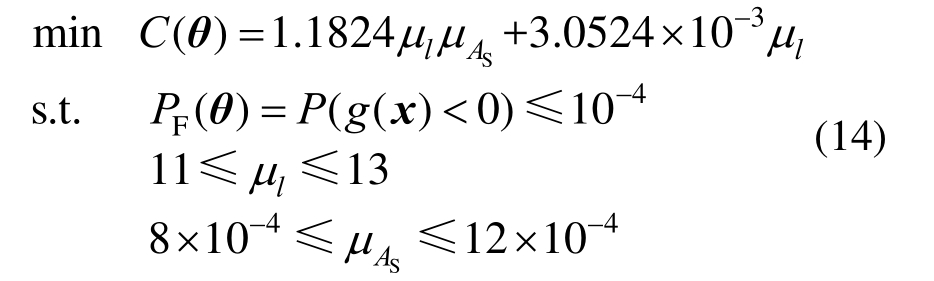
式中：目标函数C(θ)表示与屋架的重量及造价直接相关的各拉杆总体积；PF(θ)表示设计参数的失效概率函数。
表1 算例1随机变量的分布信息
Table1 Distributed information of random variables in example 1
分别采用本文所提两种融合策略来求解上述优化问题，其中，静态权重策略预设α=0.7。每次解耦过程采用N=2500个重要抽样点来获得迭代点θ(k)附近的近似失效概率函数。初始设计值取为θ(1)=[12，9.82×10-4]mm，其对应的设计点中与设计参数有关的为
其他不相关变量的为
在后续迭代过程中，取
为辅助密度函数的抽样中心，相应的标准差为抽样中心与变异系数的乘积。选取相应的局部优化区域参数为：R0=20%，r=0.95。设置收敛条件为Ctol=0.0001。
为了说明所提融合方法的精确度，图3和图4给出了由各种方法得出的第2次优化迭代时的失效概率曲线对比图。(No integration)为非融合方法，即重要抽样加权方法；Weighted Important Sampling(WIS)表示重要加权方法[12]；Integrated Approach (Static)(简记 IA(S))表示本文所提静态权重融合方法；Integrated Approach(Dynamic)(简记为IA(D))表示动态权重融合方法。由图3和图4可看出，采用本文方法融合所得的失效概率函数估计相对于重要加权方法的结果，更加接近真实失效概率函数(精确结果由直接蒙特卡罗方法(DMCS)采用样本数107个计算所得)，说明本文所提融合方法能够提高失效概率函数的求解精度，并且可以看出动态权重方法比静态权重方法精度要高，这将保证优化过程的快速收敛。
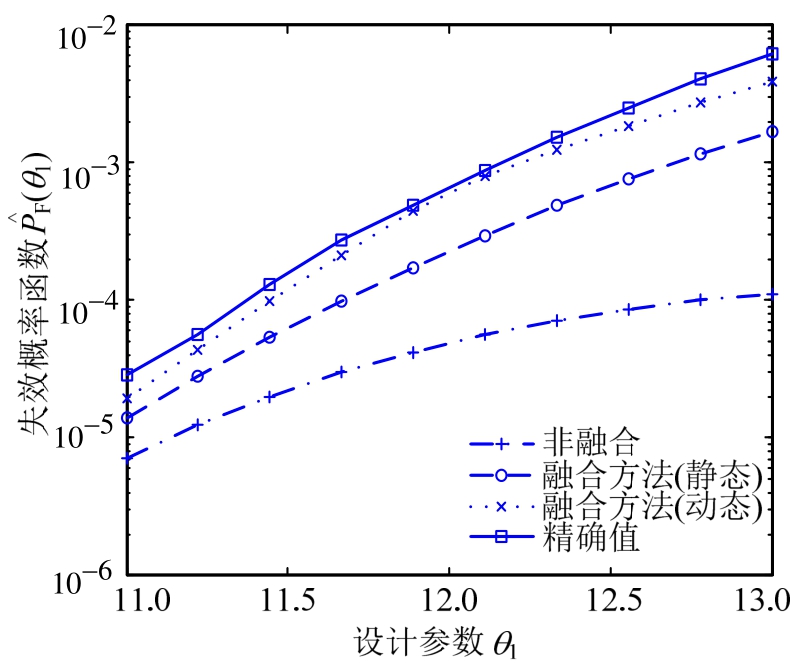
图3 第2次迭代失效概率曲线对比图
Fig.3 Comparison diagram of failure probability curve in 2nd iteration
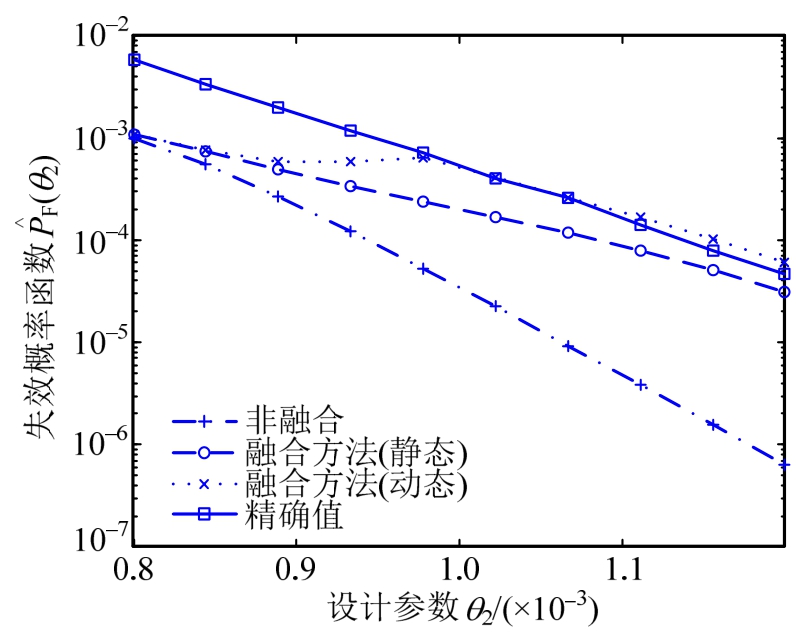
图4 第2次迭代失效概率曲线对比图
Fig.4 Comparison diagram of failure probability curve in 2nd iteration
表2给出了各方法的优化结果。由表2可以看出，本文所提动态权重方法优化迭代次数最少，静态权重方法次之。结果表明本文所提融合方法相比于非融合方法具有更高的求解效率。
表2 算例1的优化结果
Table2 Optimization result of example 1
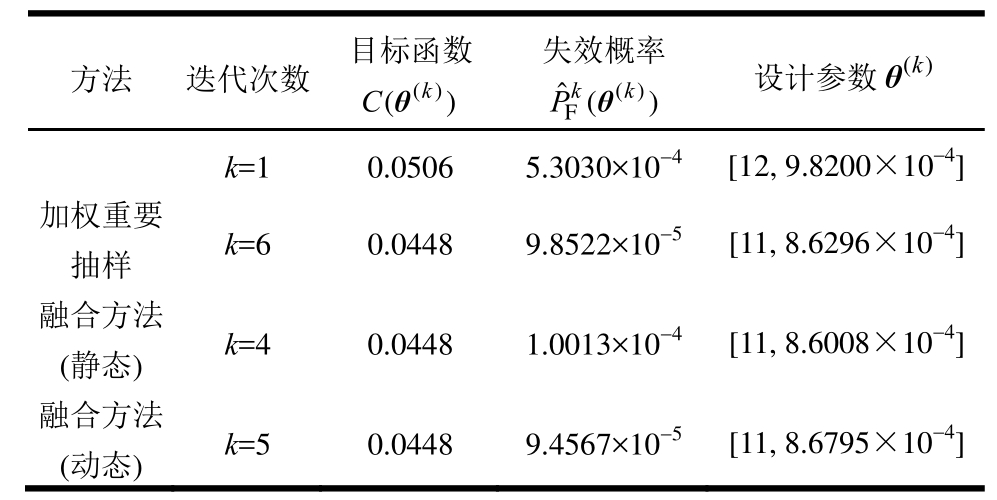
图5和图6给出了在预先给定迭代次数niter=10次迭代过程中目标函数值及失效概率值的变化历程。从图中可以看出，融合方法更快地收敛到最优点附近，并且动态权重融合方法在优化过程中具有更好的稳健性，证明所提方法的策略是有效的。
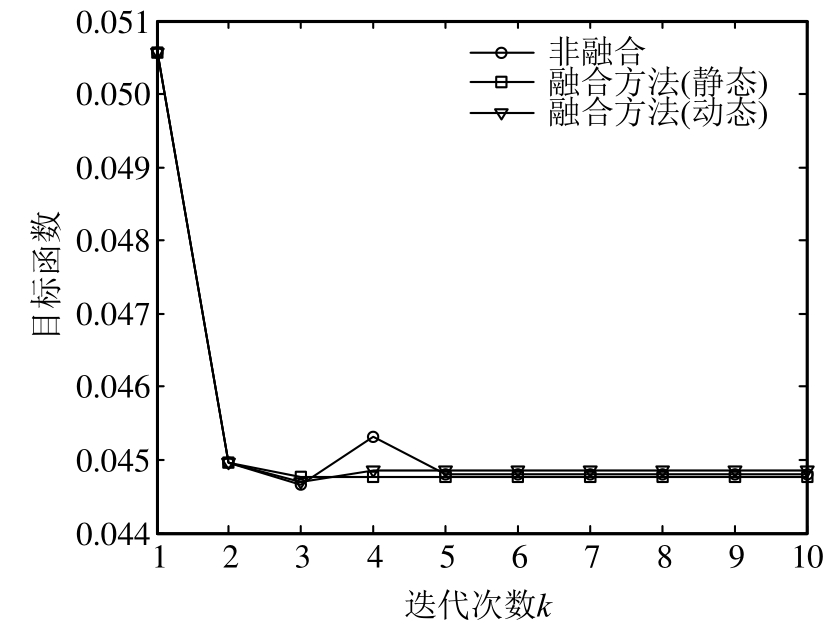
图5 算例1目标函数优化历程
Fig.5 Optimization routine of objective function of example 1
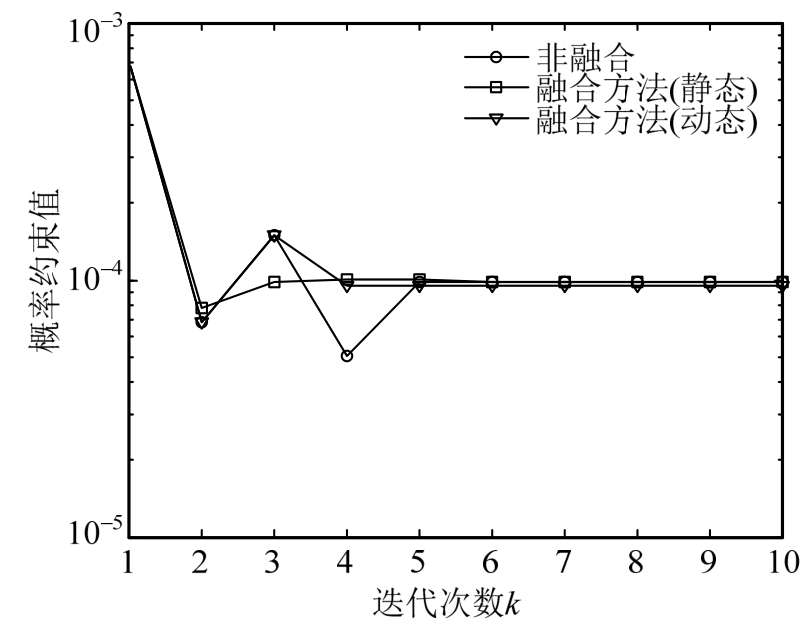
图6 算例1失效概率约束优化历程
Fig.6 Optimization routine of probabilistic constraint of example 1
如图7所示的十杆结构。所有水平杆和垂直杆的长度均为L。Pi(i=1，2，3)为集中载荷。每个杆的截面积和弹性模量分别为
和E，因此共有15个基本随机变量，即：
本例中15个随机变量的分布信息见表3，其中Ai(i=1，2，…，10)的均值被设为设计参数，即：
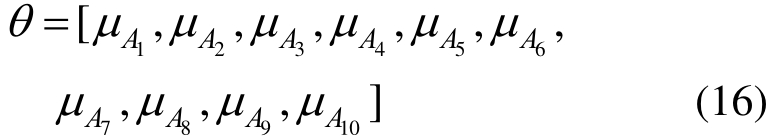
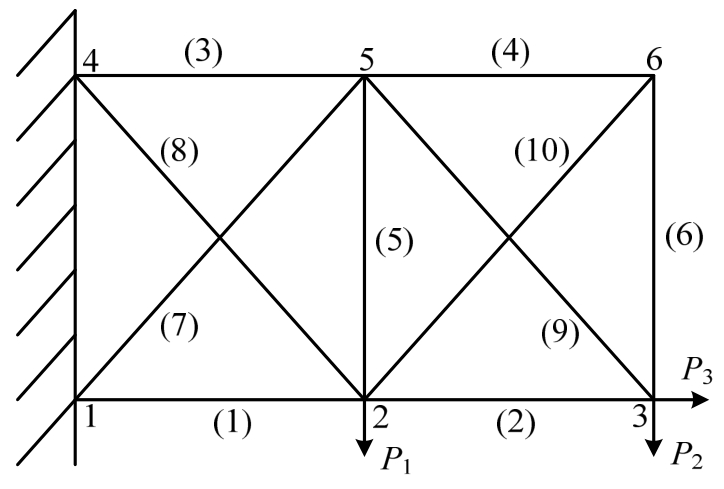
图7 十杆结构示意图
Fig.7 Schematic diagram of ten-bar structure
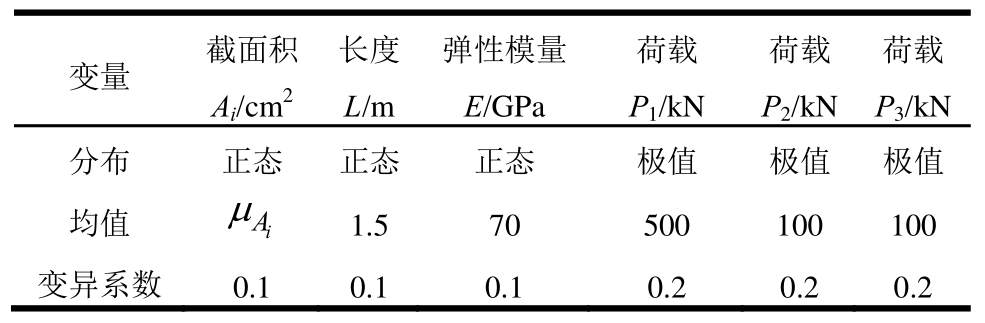
表3 十杆结构随机变量的分布信息
Table3 Distributed information of random variables of ten-bar structure
该算例的优化模型为：
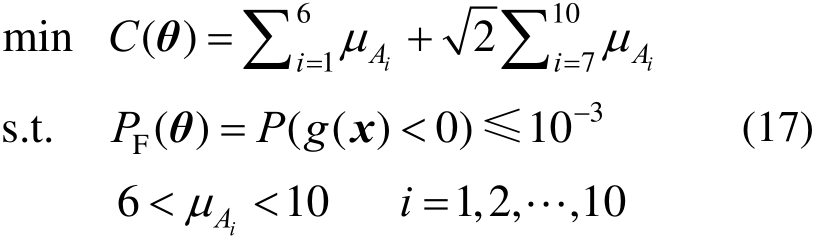
式中：g(x)=D-dy(x)是极限状态函数，dy(x)是节点3的垂直方向的位移，可以通过有限元分析求得。失效定义为节点3的垂直位移超过允许阈值D=0.1 m。目标函数C(θ)表示与十杆结构总重相关的量。所选材料属性为弹性模量E=70GPa。单元类型为LINK1。有限元模型受力变形图如图8所示。
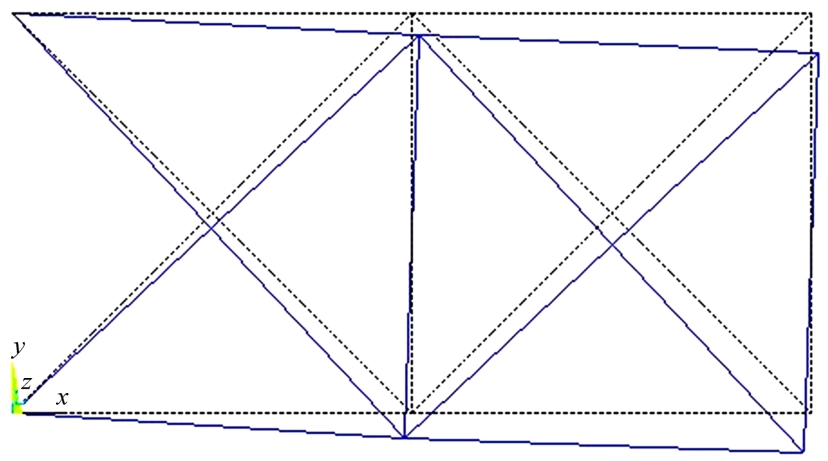
图8 十杆结构有限元模型
Fig.8 Finite element model of ten-bar structure
取初始点为θ(1)=[8，8，8，8，8，8，8，8，8，8]，当设计变量取初始点值时求解相应的设计点MPP。忽略设计点中相关设计参数部分，非相关随机变量的MPP点为xr*(1)=[1.717，55.31，604.0，115.3，98.15]。在后面每一步迭代中辅助密度函数的抽样中心设置为
，每次抽取5000个样本点来获得失效概率函数FPF的局部近似，进而获得可靠性优化问题的解耦。选择相应的局部优化区域参数为R0=20%，r=0.9。设定收敛准则为Ctol=0.1，得到优化设计结果如表4所示。图9和图10给出了目标函数和失效概率在迭代过程中的变化历程曲线。从图中容易可以看出融合策略在一定程度上加快了收敛，从而提高了优化求解的效率，因此所提方法是有效的。
表4 十杆结构优化结果
Table4 Optimization result of ten-bar structure
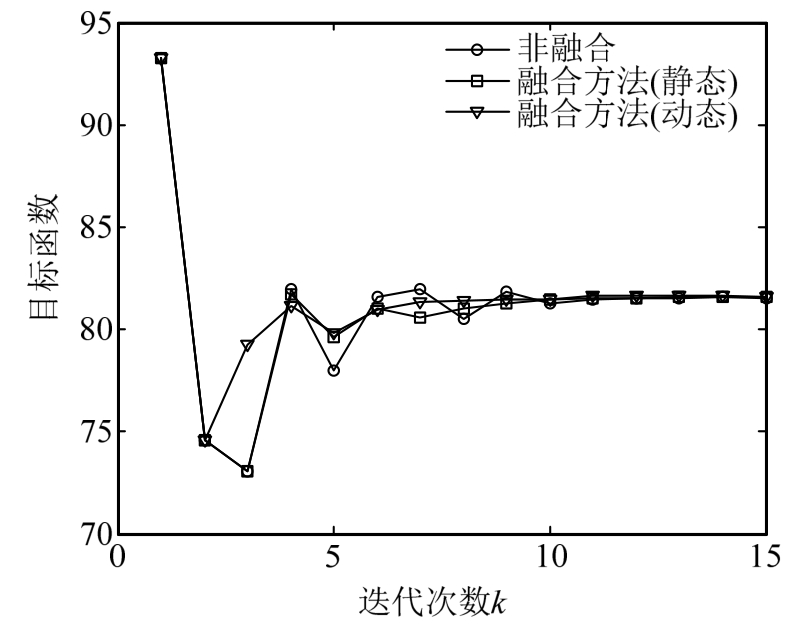
图9 算例2的目标函数的优化历程图
Fig.9 Optimization routine of objective function of example 2
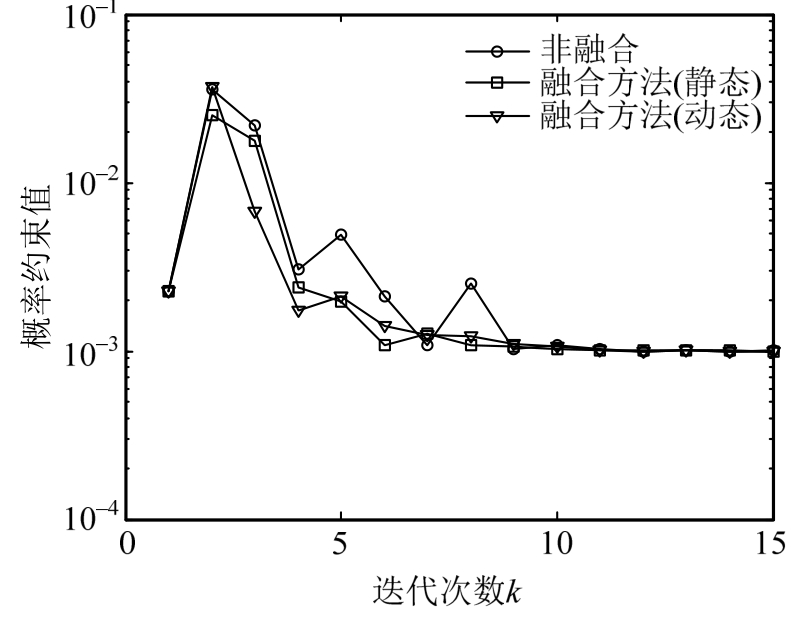
图10 算例2的失效概率的优化历程图
Fig.10Optimization routine of failure probability of example 2
针对工程中的可靠性优化问题，提出了一种融合策略的解耦求解方法。所提策略针对可靠性优化的解耦方法，提出用于解耦的失效概率函数取为前几次新建立的失效概率函数的加权融合形式，使得优化迭代求解的精度提高。文中提出了两种融合策略：静态加权融合和动态加权融合，并给出算例对所提融合策略进行了论证和说明。算例结果表明，融合求解策略的确能够在一定程度上提高失效概率函数近似的精度，借此保证了优化算法的稳健性和精度，进而达到了进一步提高可靠性优化求解的效率。
参考文献：
[1]张义民，刘仁云，于繁华.基于计算智能技术的结构系统可靠性优化设计[J].工程力学，2007，24(8):27―31.Zhang Yiming，Liu Renyun，Yu Fanhua.Computational intelligence-based reliability design optimization for structral system[J].Engineering Mechanics，2007，24(8):27―31.(in Chinese)
[2]Valdebenito M A，Schuëller G I.A survey on approaches for reliability-based optimization[J].Structural and Multidisciplinary Optimization，2010，42(5):645―663.
[3]Bobby S，Suksuwan A，Spence S M J，et al.Reliabilitybased topology optimization of uncertain building systems subject to stochastic excitation[J].Structural Safety，2017，66:1―16.
[4]赵宽，陈建军，曹鸿钧，等.随机参数双连杆柔性机械臂的可靠性分析[J].工程力学，2015，32(2):214―220.Zhao Kuan，Chen Jianjun，Cao Hongjun，et al.Reliability analysis on two-link flexible robot manipulator with random parameters[J].Engineering Mechanics，2015，32(2):214―220.(in Chinese)
[5]袁修开，吕震宙，许鑫.基于马尔科夫链模拟的支持向量机可靠性分析方法[J].工程力学，2011，28(2):36―43.Yuan Xiukai，Lü Zhenzhou，Xu Xin.Support vector machine reliability analysis method based on markov chain simulation[J].Engineering Mechanics，2011，28(2):36―43.(in Chinese)
[6]Tu J，Choi K K，Park Y H.A new study on reliability-based design optimization[J].Journal of Mechanical Design，1999，121(4):557―564.
[7]Kuschel N，Rackwitz R.Two basic problems in reliability-based structural optimization[J].Mathematical Methods of Operations Research，1997，46(3):309―333.
[8]Jensen H A，Catalan M A.On the effects of non-linear elements in the reliability-based optimal design of stochastic dynamical systems[J].International Journal of Non-Linear Mechanics，2007，42(5):802―816.
[9]朱海燕，袁修开.基于灵敏度的可靠性优化解耦方法[J].航空学报，2015，36(3):881―888.Zhu Haiyan，Yuan Xiukai.A decoupling method of reliability optimization based on sensitivity[J].Chinese Journal of Aeronautics，2015，36(3):881―888.(in Chinese)
[10]Zou T，Mahadevan S.A direct decoupling approach for efficient reliability-based design optimization[J].Structural and Multidisciplinary Optimization，2006，31(3):190―200.
[11]Ching J，Hsieh Y.Local estimation of failure probability function and its confidence interval with maximum entropy principle[J].Probabilistic Engineering Mechanics，2007，22(1):39―49.
[12]Yuan X K，Lü Z.Efficient approach for reliability-based optimization based on weighted importance sampling approach[J].Reliability Engineering and System Safety，2014，132:107―114.
[13]Yuan X K，Zeng L.Weighted simulation for failure probability function estimation[C]// Second International Conference on Vulnerability and Risk Analysis and Management(ICVRAM2014).Liverpool，England，2014.
[14]Schueller G I，Valdebenito M A.Efficient strategies for reliability-based optimization involving non-linear，dynamical structures[J].Computer and Structures，2010，89(19―20):1797―1811.
[15]Jacobs J H，Etman L F P，van Keulen F，et al.Framework for sequential approximate optimization[J].Struct Multidisc Optim，2004，27(5):384―400.
[16]Yuan X K.Local estimation of failure probability function by weighted approach[J].Probabilistic Engineering Mechanics，2013，34:1―11.
A DECOUPLING-INTEGRATED APPROACH FOR STRUCTURAL RELIABILITY-BASED DESIGN OPTIMIZATION
YUAN Xiu-kai，ZHU Hai-yan，ZHANG Bao-qiang
(School of Aeronautics and Astronautics，Xiamen University，Xiamen，Fujian 361005，China)
Abstract:In engineering structural design，the accuracy and efficiency of the reliability-based design optimization(RBDO)are the key issues.A decoupled method based on an integrating approach is proposed for RBDO.In the proposed method，the approximated function for decoupling in the current iteration is a weighted integration of the failure probability functions(FPFs)obtained in previous iterations.After the original reliability-based optimization problem is decoupled，it is solved within the sequence approximation optimization framework.Compared to the traditional approach that only uses the currently built FPF for decoupling，the proposed approach utilizes all the information generated in previous iterations to solve the problem.It results in a more reasonable and accurate approximation of the FPF，leading to the reduction of the number of iterations and the computational cost.Examples of roof truss and ten-bar structure are given to validate the efficiency and robustness of the proposed method.
Key words:reliability-based optimization;decoupling;integration approach;failure probability function;sequential approximation optimization
中图分类号：TU318+.1;TB114.3
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0047
文章编号：1000-4750(2018)05-0102-07
收稿日期：2017-01-11；修改日期：2017-09-28
基金项目：国家自然科学基金委员会-中国工程物理研究院NSAF联合基金项目(U1530122)；国家自然科学基金青年科学基金项目(51505398)
通讯作者：袁修开(1981―)，男，湖北黄石人，副教授，博士，主要从事结构可靠性分析及优化研究(E-mail:xiukaiyuan@xmu.edu.cn).
作者简介：朱海燕(1991―)，女，江西上饶人，硕士，主要从事可靠性优化研究(E-mail:601256420@qq.com);
张保强(1982―)，男，山东人，助理教授，博士，主要从事结构力学及分析研究(E-mail:bqzhang@xmu.edu.cn).