表1 混凝土材料配合比
Table1 Concrete mixture proportions
金 浏1，杜 敏1，2，杜修力1，李振宝1
(1.北京工业大学城市减灾与防灾防护教育部重点实验室，北京 100124；2.防灾科技学院防灾工程系，河北，三河 065201)
摘 要：开展了12组不同尺寸几何相似的箍筋约束混凝土圆柱轴心受压破坏试验，试验的工况参数为：配箍率为1.26%和2.89%；圆柱尺寸(直径)相似比为1∶1.5∶2.25，圆柱最大直径为576 mm；圆柱长细比为3。根据试验结果探讨了箍筋约束作用混凝土圆柱破坏模式及轴压强度尺寸效应的影响规律。基于Bažant尺寸效应律思想，提出了能反映尺寸影响的箍筋约束混凝土圆柱轴压承载力计算理论，与试验结果的良好吻合证明了修正承载力计算理论的合理性。最后，建立了钢筋混凝土柱破坏行为及尺寸效应模拟的3D细观尺度数值分析方法，在模拟结果与试验结果吻合良好的基础上，扩展模拟了更大尺寸圆柱的破坏行为。
关键词：箍筋约束混凝土；圆柱；轴压强度；箍筋率；尺寸效应；承载力；细观数值模拟
约束混凝土构件(包括：箍筋、FRP、CFRP、GFRP及钢管等约束方式)被广泛应用于建筑工程中。约束混凝土是指利用外部约束，改善混凝土自身原有受压特性，以提高其抗压强度及变形能力。约束混凝土是一个比较经典的结构课题，也是现代结构工程界最基本的研究领域之一，国内外学者对此进行了大量的研究[1]。
对于箍筋约束混凝土，Richart等[2]利用液体围压以及圆形箍筋对承受轴压作用下的混凝土施加横向约束作用，不仅分析了液体围压对混凝土圆柱轴心受压性能的影响，还提出了关于计算约束混凝土轴心抗压强度以及峰值应变的理论公式。Chan[3]开展了方形箍筋约束混凝土试验研究，由于箍筋间距较大，试验结果显示矩形箍筋约束作用只能提高混凝土的峰值应变而无法提高峰值强度。Soliman和Yu[4]针对箍筋直径、间距、体积配箍率等因素，开展了混凝土方柱抗弯试验，其试验结果表明矩形约束箍筋能够提高混凝土的宏观强度。Sheikh和Uzumeri[5]亦开展了矩形箍筋约束混凝土试验研究，其试验结果与Soliman和Yu结果相同；此外，他们首次提出了有效约束区的概念。Mander等[6]改进了有效约束区的概念，并以有效约束系数乘以配箍特征值作为唯一约束指标，提出约束混凝土力学模型。除此之外，史庆轩等[1，7]、钱稼茹等[8]、郑文忠和侯翀驰[9]及Jonathan等[10]提出了关于箍筋约束混凝土的承载力计算理论方法。虽然取得了丰硕的研究，但目前关于箍筋约束混凝土试验研究及承载力计算理论均基于小尺寸构件，未考虑尺寸效应的影响；同时，我国《混凝土结构设计规范》[11]亦未考虑尺寸效应对钢筋混凝土柱轴压承载力的影响。
实际上，已有的大量试验研究表明：在轴压加载下，钢筋混凝土柱名义轴压强度随着构件尺寸增大而降低。如Bažant和Kwon[12]、Němeček和Bittnar[13]、Sener等[14]、车轶等[15]及Li等[16]工作均印证了这一事实。杜修力等[17―18]亦对混凝土材料及混凝土工程结构的尺寸效应开展了评述。相关的钢筋混凝土柱的破坏试验及数值模拟工作中，主要针对钢筋混凝土方柱，典型的如：杜敏和金浏等[19]针对箍筋约束混凝土方柱，采用细观数值模拟方法研究了箍筋约束作用下混凝土柱轴压破坏的尺寸效应行为。
本文以圆形约束钢筋混凝土柱为研究对象，主要目的为：1)基于试验研究，揭示大尺寸箍筋约束混凝土圆柱轴压破坏的尺寸效应规律；2)建立能考虑尺寸影响的箍筋约束混凝土圆柱轴压承载力计算方法；3)建立能反映钢筋混凝土构件尺寸效应行为模拟的数值分析理论。
鉴于此，本文开展了12组最大截面尺寸(直径)为576 mm的箍筋约束混凝土圆柱轴压大变形破坏试验，讨论了箍筋约束作用对尺寸效应的影响规律。基于试验结果，提出了能考虑尺寸影响的圆柱轴压承载力计算理论。最后，构建了箍筋约束混凝土柱破坏行为模拟的三维细观尺度数值模型，开展了更大尺寸圆柱破坏行为的数值模拟工作。
所有试件的混凝土均采用同批次C30商品混凝土，混凝土密度为2434 kg/m3，混凝土塌落度在160mm～180mm之间，水灰比为0.4，混凝土材料的配合比见表1。粗骨料(碎石)的最大粒径约为25 mm，其弹性模量为70.1 GPa，泊松比为0.2。在同等养护条件(28 d)下，测得的标准混凝土立方体试块(尺寸为150mm)的抗压强度为42.8 MPa，标准棱柱体(长与宽均为150mm，高为300mm)抗压强度为35.0MPa，劈裂抗拉强度为2.90MPa，弹性模量为34.8 GPa。纵筋和箍筋均采用HRB400级带肋钢筋，实测钢筋屈服强度的均值为477 MPa，极限强度的均值为664 MPa。
表1 混凝土材料配合比
Table1 Concrete mixture proportions
为揭示箍筋约束作用对混凝土圆柱轴压破坏行为尺寸效应的影响，按照1∶1.5∶2.25比例共设计12根几何相似的最大截面尺寸为576 mm(为柱子的横截面直径)箍筋约束混凝土圆柱。箍筋率及箍筋间距均会直接影响箍筋约束混凝土柱的力学性能及尺寸效应规律。本文试验中，箍筋的直径、间距和约束混凝土柱的构件几何尺寸均按照1∶1.5∶2.25的比例尺寸进行设计。其具体几何参数及配筋情况如图1所示。所有柱子的纵筋率均为0.28%，根据体积配箍率将箍筋约束混凝土柱分为CA和CB两个系列。符号C代表圆柱体；A和B表示不同的体积配箍率ρsv，分别为1.26%和2.89%。试件编号中的S、M和L分别代表小、中和大三种构件尺寸，1和2代表样本个数。需要注意的是，在试件上下两端1/6柱高范围内，对箍筋进行了加密布置，以防试件在加载过程中端部过早发生破坏。试验中所有试件的长细比λ均为3。
图1 箍筋约束混凝土柱几何参数与钢筋布置/mm
Fig.1 Geometrical configuration and reinforcement layout of stirrup-confined RC columns
箍筋约束混凝土柱轴压加载试验在北京工业大学工程结构实验中心开展，使用4×104kN多功能电液伺服试验机进行加载，如图2(a)所示。柱子变形由安装在试件上的位移计测得，测量标距为2H/3(H为试件高度)。试验测试参数包括：轴向荷载p、轴向压缩变形Δ以及箍筋应变。加载方式为不间断轴向单调加载，在荷载值达到试件极限承载力之前，采用力控加载，之后通过位移控制加载，直至试件压溃。试验加载装置及数据采集设备如图2(a)和图2(b)所示。
图2 加载装置及数据采集
Fig.2 Loading arrangement and measuring instruments
轴向压缩荷载作用下，两组不同配箍率下不同尺寸箍筋约束混凝土圆柱的破坏模式分别如图3(a)和图3(b)所示。可以看出：受压柱的破坏模式呈典型的压缩剪切破坏形态，箍筋断裂根数及断裂的位置相近，同一系列内三种尺寸试件的最终破坏形态基本相似。较大尺寸试件的横向膨胀变形相对较小，剪切破坏面与试件纵轴线的夹角略有减小。
图3 约束混凝土柱体破坏模式
Fig.3 Failure patterns of the confined RC columns
相比于CA系列柱，对于含箍率更高的CB系列柱，由于受到更充分的箍筋约束作用，试件在受荷过程中聚集了更多的应变能，核心区混凝土裂缝更加分散，横向膨胀变形增大，试验结束时产生的酥松混凝土量以及被拉断箍筋的根数也更多，这表明箍筋的约束作用促进了混凝土塑性的发展，且随着约束作用的增大，这种塑性发展愈加充分。因此，箍筋约束作用的增强，一方面增强了柱的轴向压缩承载力，同时也提高了柱轴向加载的变形能力。
12根约束混凝土圆柱的轴向应力-应变关系曲线如图4所示。这里，轴向名义应力σ为轴向荷载P与柱横截面面积的比值，即为：
名义轴压强度σNu为轴向荷载达到峰值荷载Pu时的名义应力值。名义应变ε为柱端产生的竖向位移Δ与柱高H的比值，即ε=Δ/H。
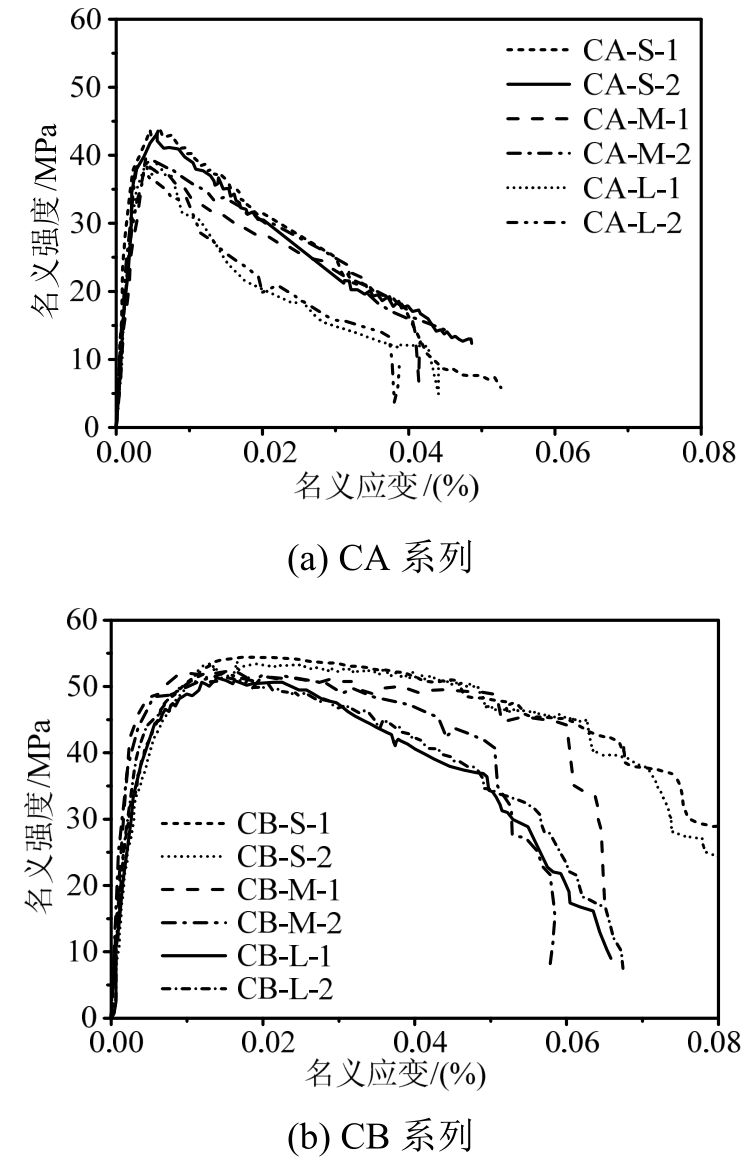
图4 约束混凝土圆柱的名义应力-应变曲线
Fig.4 Nominal compressive stress-strain curves for the 12 groups of stirrups-confined RC circular columns
由图4可见，对于两组配箍率混凝土试件，随着构件尺寸的增大，约束混凝土柱的名义轴压强度均随之降低。另外，柱尺寸越大，其反应达到峰值后软化曲线下降斜率越大，表现出更脆的特征。
对于CA系列柱(ρsv=1.26%)，其轴压应力-应变曲线具有明显的转折点，峰值强度过后曲线急剧降低，因此柱子的破坏具有较为明显的脆性。而具有更高配箍率的CB系列柱(ρsv=2.89%)，获得的轴压应力-应变曲线没有明显的拐点，柱子承载力达到峰值后，名义强度随名义应变的增大呈现出缓慢减小的趋势，表现出很强的延性特征。
箍筋约束混凝土柱名义轴压强度和应变测试结果见表2所示。σNu、εcc为名义轴压强度及其对应的峰值应变；ε85是试件承载力下降到85%Pu时的轴向名义应变；延性系数为u=ε85/εcc，其反映了构件破坏的变形性能。
表2 箍筋约束混凝土圆柱测试结果
Table2 Test results for the stirrup-confined concrete columns
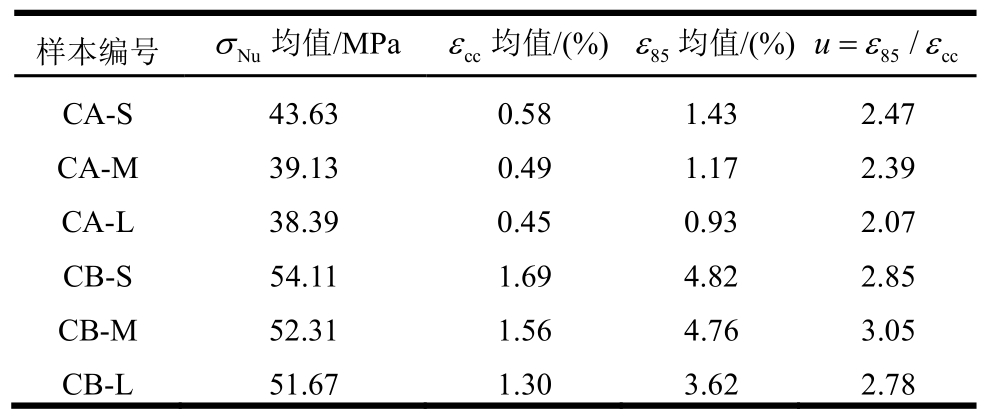
由表2可见，小、中和大三种尺寸下高配箍率CB系列柱的峰值应力比低配箍率CA样本的峰值应力分别提高了19.9%、33.68%和34.60%。而对应的峰值应变εcc则分别提高了191.4%、218.4%和188.9%。另外，试件承载力下降到85%时的应变ε85及柱子破坏的延性系数u值也明显提高。
图5为箍筋约束混凝土圆柱的名义轴压强度σNu与构件截面尺寸D(即为柱子的横截面直径)之间的关系。从图5可以看出：1)随着构件截面尺寸的增加，两组配箍率下柱的名义压缩强度表现出不同程度的下降趋势；2)虽然柱子名义强度随尺寸增大而降低，但降低的趋势却随配箍率的增大而减弱；说明增大配箍率可以削弱尺寸效应对名义轴压强度的影响；3)CB系列柱子的名义轴压强度明显大于CA系列的柱，说明增大构件的配箍率，可以增强箍筋对构件的约束作用，从而提高其名义轴压强度。对比于CB系列柱，由于CA系列柱配箍率较低，致使约束作用较弱，发生破坏时更具有脆性，因而其表现出更为明显的尺寸效应行为。
图5 约束混凝土柱名义强度与结构尺寸关系
Fig.5 Nominal compressive strength vs.structural size
Bažant[20]基于断裂能释放的断裂力学理论，推导并提出了符合混凝土类准脆性材料的尺寸效应统一表达式：
式中：σNu为混凝土名义强度；B、D0为经验系数；D是试件特征尺寸(这里即为柱直径)；
为混凝土材料劈裂抗拉强度；β是反映材料脆性大小的参数。为了得到常数项
和D0。具体操作如下，将式(2)改写成线性方程：
式中：
通过对试验数据进行回归分析后，得到尺寸效应参数，如表3所示，进而可以绘制钢筋混凝土柱名义强度随构件变化的双对数曲线(图6)。
表3 Bažant尺寸效应理论拟合参数
Table3 Fitting parameters of Bažant’s size effect law
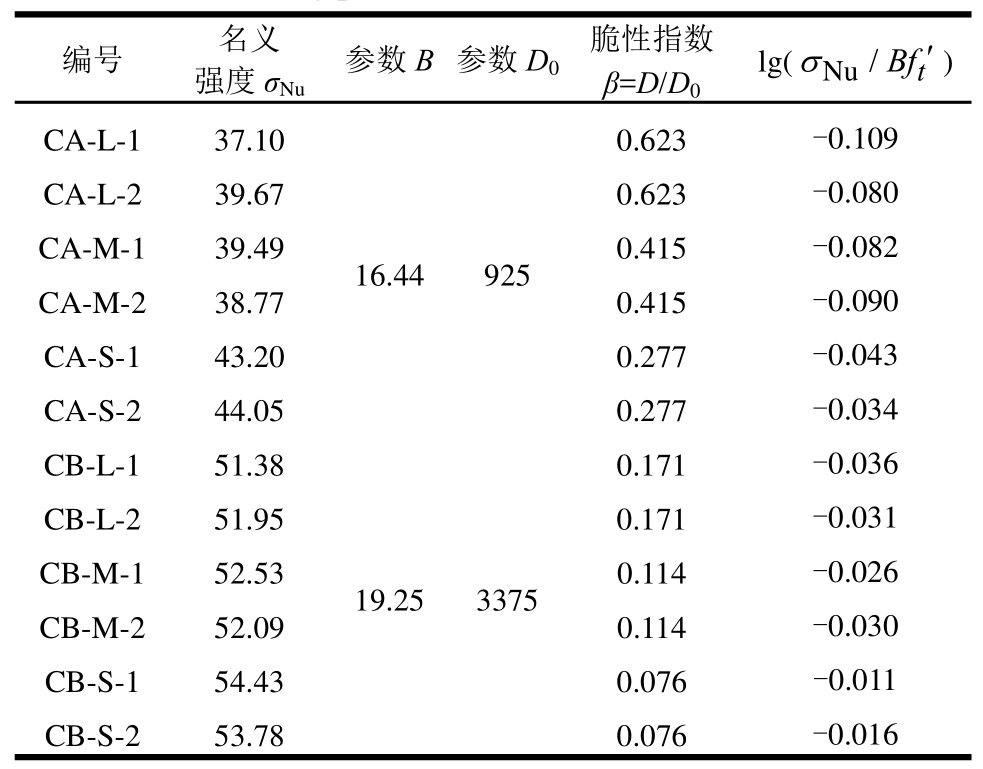
图6 约束混凝土柱试验数据回归分析
Fig.6 Test data regression analysis of confined RC columns
由表3可知，体积配箍率越低，脆性参数β越大，即约束混凝土柱破坏的脆性越大。图6给出了本文试验结果与Bažant尺寸效应理论结果、塑性理论模型(即强度准则)和脆性理论模型(即线弹性断裂力学理论)的对比情况。可以看出Bažant尺寸效应理论能很好的反映约束混凝土柱轴压强度的尺寸效应规律(拟合系数R2=0.87)。另外，可看出图中所有数据点都远离线弹性断裂力学理论线和强度准则线，说明约束混凝土柱的破坏介于纯脆性材料和塑性材料之间，小尺寸柱的强度数据接近于塑性材料的理论公式，大尺寸试件的强度数据更接近于脆性材料的理论公式。相比于CB系列，含更低配箍率的CA系列柱的强度数据点最趋近于线弹性断裂力学理论线，即斜率为-1/2的直线，因而其尺寸效应现象更为显著。实际上，正如前文所分析，配箍率越大，约束作用越明显，柱子破坏表现出更弱的脆性，因而表现出较弱的尺寸效应行为。
关于箍筋约束混凝土柱的力学行为研究方面，国内外众多研究者，如Park等[21]、Mander等[6]及Legeron和Paultre[22]等开展了大量的研究工作。Richart等[2]利用液体围压以及圆形箍筋对承受轴压作用下的混凝土施加横向约束作用，定量地研究了液体围压对混凝土圆柱体轴压性能的影响，并提出约束混凝土核心区抗压强度计算公式：
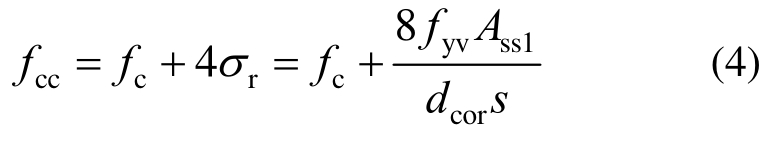
式中：fcc、fc分别为约束混凝土核心区及素混凝土轴心抗压强度；σr为螺旋箍筋对核心区混凝土产生的被动压应力；fyv是箍筋屈服应力；Ass1为螺旋箍筋的截面面积；dcor为核心区混凝土直径；s为箍筋间距。受压构件配箍特征值λt为：
式中：Vs为钢筋体积；Vc为混凝土体积；ρsv为体积配箍率。将式(5)代入式(4)，可得：
因此，约束混凝土圆柱的轴压承载力Nu为：
式中：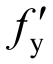
和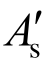
分别为纵筋的屈服应力及横截面面积；Acor为核心混凝土横截面面积。
图7给出了两组配箍率下混凝土圆柱的实测承载力与理论承载力(基于式(7)获得)的对比情况。可以发现：当构件尺寸较小时，理论计算结果与试验数据吻合较好；而随着构件尺寸的增大，理论承载力明显高于试验测量数据。实际上，这是由于式(7)给出的承载力计算方法未考虑构件尺寸对承载力的影响而造成的。
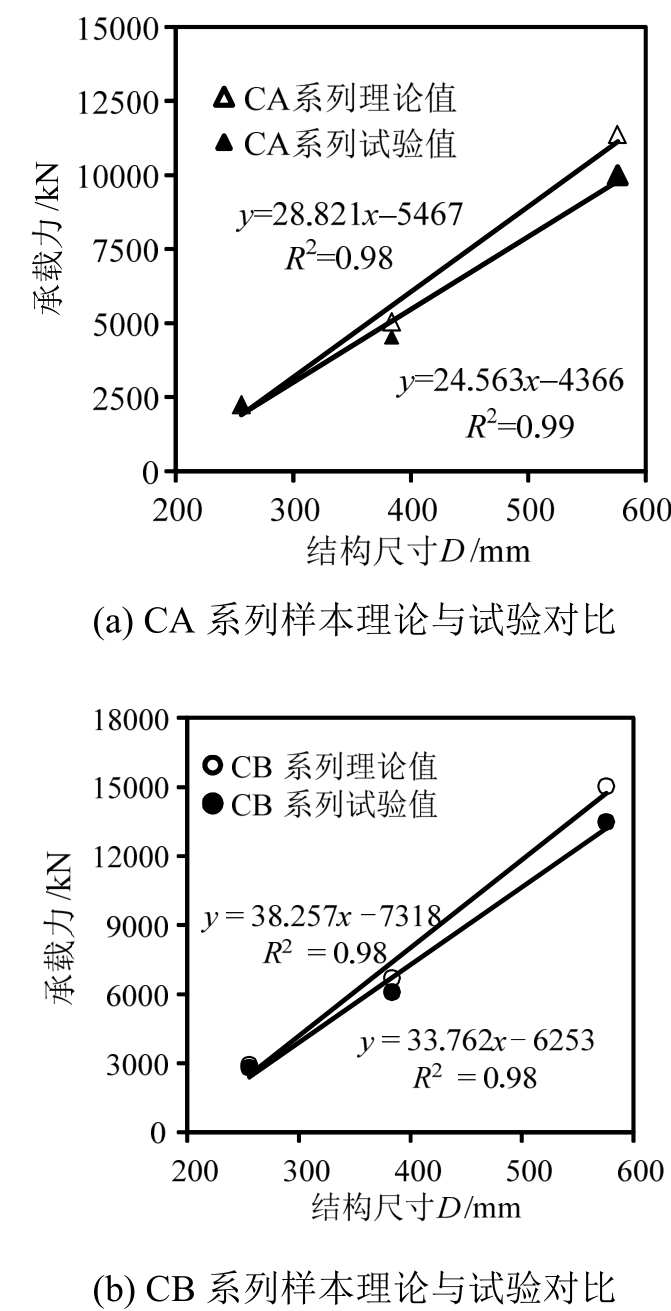
图7 承载力理论计算值与试验数据对比
Fig.7 Comparisons of theoretical and experimental data
实际上，箍筋约束混凝土柱轴压破坏尺寸效应行为，主要源于[23]：1)混凝土自身的尺寸效应；2)箍筋/混凝土间复杂的相互作用。
考察式(7)，可知：为反映构件尺寸对承载力的影响，应修正式(7)等式右侧的第一项“fccAcor”。从式(6)得知，实际上该项反映了素混凝土部分(fc)及箍筋约束作用(2ρsvfsv)对约束混凝土柱承载力的贡献。本质上来说，正是该两方面的作用导致了约束混凝土柱轴压强度的尺寸效应。
鉴于此观点及理念，对混凝土核心区的强度fcc进行修正，提出如下修正公式：
式中，α(D)和γ(D)分别反映素混凝土及箍筋/混凝土相互作用部分的尺寸效应系数，它们均是结构尺寸D的函数。借鉴Bažant尺寸效应律[17]，设定α(D)和γ(D)满足如下形式：
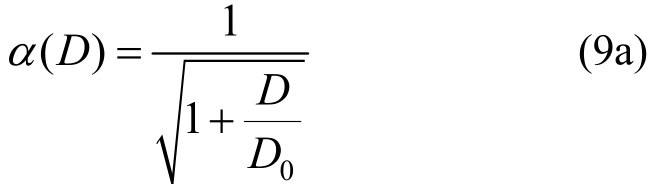
式中：D0为待定拟合参数。另外，箍筋间距s＜2D时，认为存在约束作用；而当s≥2D时，γ(D)=0，认为箍筋约束作用消失，这与Sheikh和Uzumeri[24]的研究结果一致。这本质上是考虑了箍筋间距对约束作用强弱的影响。将式(8)代入式(7)，即可得到修正的箍筋约束混凝土圆柱承载力计算公式：
通过与本文试验结果的拟合对比，确定待定参数D0的最优取值为2960。图8(a)为不考虑尺寸效应影响的约束混凝土柱承载力(式(6)计算)与试验结果(6组实测承载力)的残差值，而图8(b)为修正后的理论公式与试验结果的残差值。这里，残差值=理论计算值-试验实测值均值。
图8 承载力理论计算结果与试验数据对比
Fig.8 Comparisons of theoretical results and experimental data
对比图8(a)和图8(b)可知，修正后的计算公式能很好地反映结构尺寸对箍筋约束混凝土柱承载力的影响，与试验结果吻合良好。
正如前述，钢筋混凝土构件尺寸效应源于两个方面[23]：1)混凝土及钢筋材料本身的尺寸效应—非均质性；2)钢筋/混凝土复杂的非线性相互作用。因此，合理的钢筋混凝土构件数值分析模型应能反映该两方面的全部“特征”。本文结合前人[20，25]的工作，采用混凝土细观尺度数值分析方法来模拟混凝土材料及钢筋混凝土构件尺寸效应行为。
在细观尺度范围内，混凝土材料往往被视为由骨料颗粒、砂浆介质和界面过渡区(ITZ)组成。骨料颗粒假定为球体，最大等效骨料粒径为30mm。基于经典的“取-放”方法[23，26]，建立了与试验试件尺寸相同的三组3D混凝土圆柱，即圆柱直径为256 mm、384 mm和576 mm。另外，扩展构建了一更大尺寸(直径为864 mm)的钢筋混凝土圆柱。4个试件中，骨料的体积分数均为35%，界面过渡区厚度设为4 mm，网格划分尺寸为4 mm。建立的4根混凝土圆柱的细观结构形式如图9(a)～图9(d)所示。
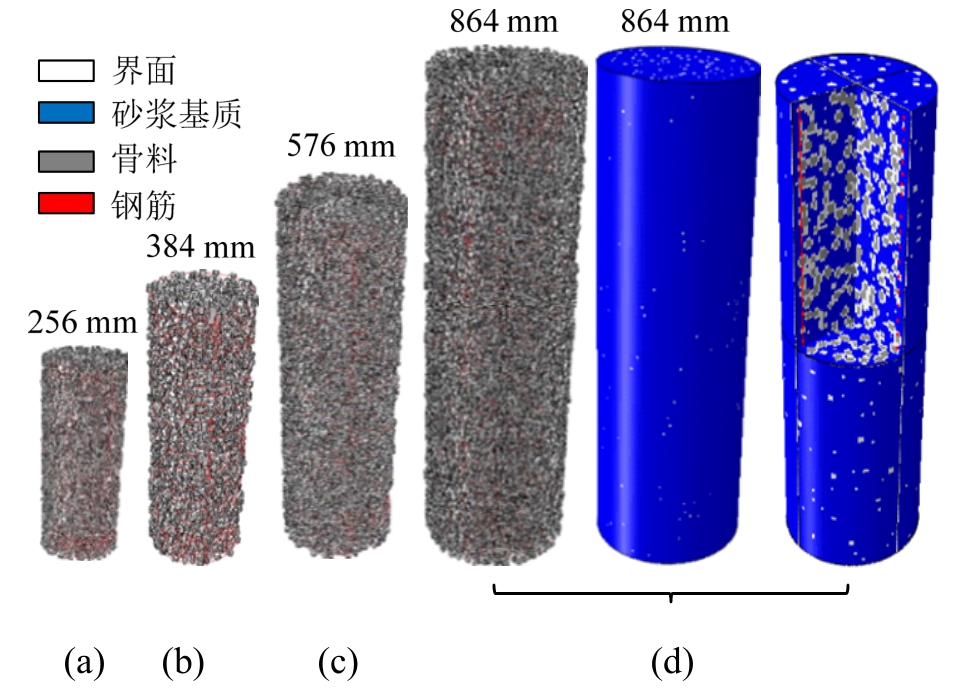
图9 约束混凝土柱细观尺度数值模型
Fig.9 Meso-scale mechanical models of confined RC columns
将建立的钢筋笼嵌入到混凝土中，其中，混凝土各组分采用八节点六面体减缩积分单元进行划分，钢筋采用梁单元进行离散，进而采用我国《混凝土结构设计规范》[11]推荐的钢筋-混凝土粘结滑移本构关系模型，即通过非线性弹簧单元来描述钢筋与混凝土之间的粘结滑移。关于该粘结界面的本构关系模型及模型中参数的选取问题详见前文的工作[23，27]。同前文[23，27]，骨料颗粒强度较高，故假定不破坏，设定为弹性体，砂浆基质和界面过渡区采用塑性损伤本构模型来描述其力学性能；钢筋材料力学性能较均匀，采用理想弹塑性本构模型描述钢筋的力学行为。
混凝土细观组分及钢筋的主要力学参数见表4所示。表4中，“*”数据所示的力学参数为实测数据，“^”所示的界面力学参数(尤其是弹性模量及单轴拉/压强度)无法通过试验测得，本文通过开展大量立方体试块(边长为150mm，如图10所示)单轴压缩数值试验来反演确定界面过渡区的力学参数，即通过反复试算而确定的。基于该方法模拟得到的混凝土单轴压缩强度为42.6 MPa(与试验测得的42.8 MPa接近)，说明了参数选取的合理性。
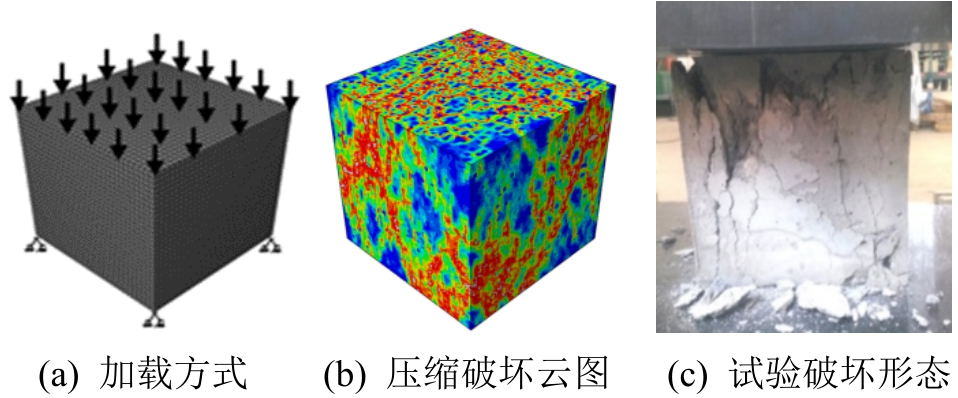
图10 试件模拟与试验破坏形态对比
Fig.10 Comparison of the numerical and experimental results
基于提出的细观数值模拟方法，对4组不同尺寸的配箍率为ρsv=2.89%的圆柱轴压破坏行为进行模拟。每组尺寸的试件数量为2，各试件中骨料的体积分数相同，仅空间随机分布不同。考虑到篇幅所限，本文在此不列出配箍率ρsv=1.26%情况下钢筋混凝土圆柱轴压破坏模拟结果。
表4 混凝土细观组分及钢筋力学参数
Table4 Mechanical parameters of meso components
图11为直径为576 mm约束混凝土圆柱的轴压破坏模拟结果与试验破坏模式的对比。从混凝土柱的损伤变化过程(图11(a))可以看出，轴向加载下，损伤裂缝首先发生在柱中位置，随着荷载增加，混凝土受压损伤区域扩大，最终形成一条主剪切斜裂缝，呈典型的压-剪破坏形态。在混凝土柱横向膨胀过程中，箍筋开始约束混凝土横向形变，随荷载增加，箍筋应变不断增大，部分箍筋达到屈服强度后发生颈缩断裂，如图11(b)所示。由图11(a)和图11(b)与试验结果图11(c)的对比可知，本文采用的数值模拟结果可以更真实地反映能约束混凝土柱在轴向加载下的破坏行为。
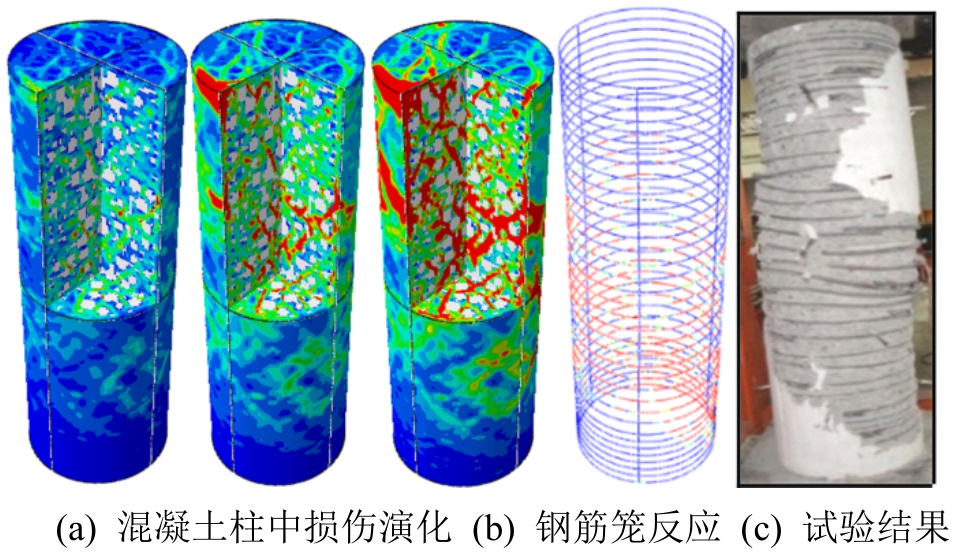
图11 约束混凝土柱(直径为576 mm)损伤破坏
Fig.11 Failure process of the confined RC columns having the cross-sectional diameter of 576 mm
图12为模拟获得的4根不同尺寸约束混凝土柱最终破坏模式图。从图12可以看出：结构尺寸(直径)小于384 mm时，约束混凝土柱中发生压缩破坏；而对于结构尺寸较大的混凝土柱，其发生典型的压-剪破坏形式，其特点为柱子表面有一条明显的主剪切斜裂缝，这与试验结果亦吻合良好。
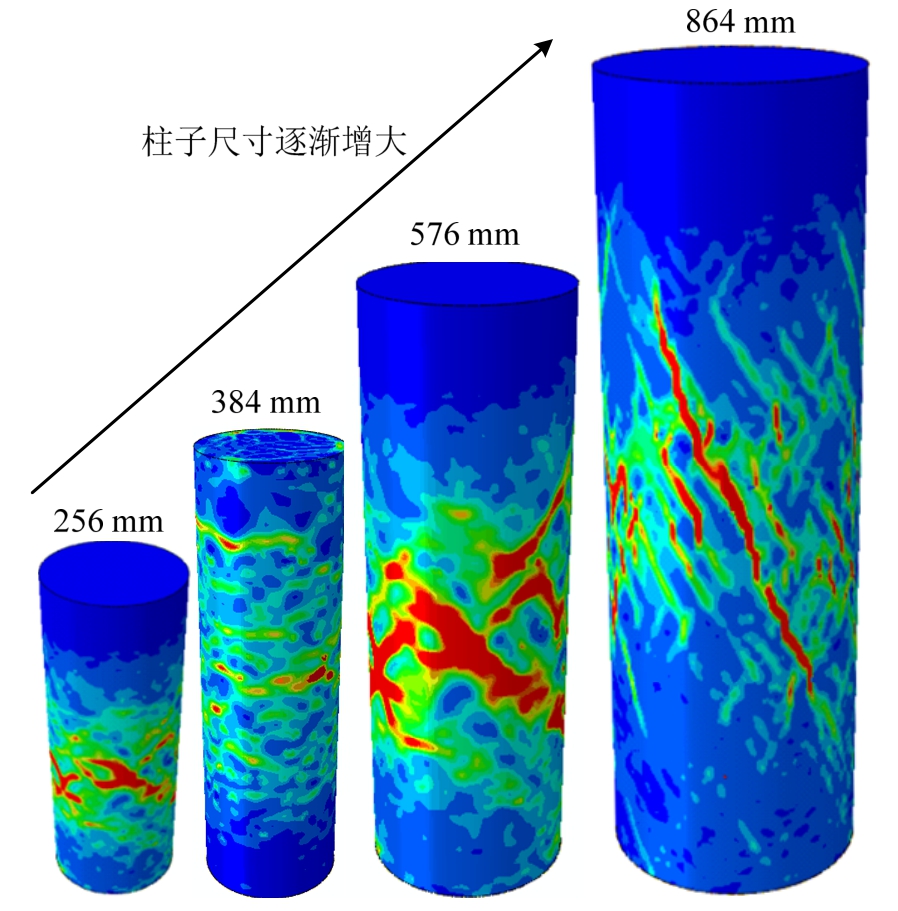
图12 4根不同尺寸约束混凝土柱破坏模式
Fig.12 Failure patterns of the four stirrup-confined RC columns having the same stirrup ratios of 2.89%
表5为箍筋约束混凝土柱的名义轴压强度值(数值解和试验结果)。可以看出，数值模拟结果均能与试验结果吻合良好(误差不超过5%)，再次说明了该模拟方法的合理性和可靠性。另外，模拟得到了更大尺寸(即CB-U，直径为864 mm)、配箍率为2.89%圆柱的名义轴压强度均值为48.79 MPa。
表5 数值模拟结果和试验结果对比
Table5 Comparisons of the simulation results and test data
总言之，与试验结果的吻合良好证明了数值方法的合理性与可靠性，继而可以在后续工作中，基于该套数值分析方法，分析不同因素，如柱子截面形式、配箍率、混凝土强度等级及钢筋屈服强度等对箍筋约束混凝土柱尺寸效应的定量影响。
本文开展了体积配箍率1.26%和2.89%，12根几何相似的箍筋约束混凝土圆柱轴心受压破坏试验；提出了能反映尺寸影响的箍筋约束混凝土圆柱轴压承载力计算公式；建立了钢筋混凝土柱破坏行为及尺寸效应模拟的3D细观尺度数值分析方法。研究获得的主要结论如下：
1)本文试验工况下，即体积配箍率在0～2.89%内，直径在256 mm～576 mm之间的箍筋约束混凝土圆柱的轴压强度存在较为明显的尺寸效应规律。箍筋率越低，约束作用越弱，破坏更具脆性，尺寸效应更显著。
2)针对本文试验工作，Bažant尺寸效应律能很好地描述箍筋约束混凝土圆柱轴压破坏的尺寸效应规律。
3)提出的箍筋约束混凝土圆柱轴压承载力修正计算理论能够反映结构尺寸对承载力的影响，且理论结果与试验结果吻合良好。
4)构建的钢筋混凝土柱细观数值分析模型能很好地描述结构尺寸对构件破坏行为以及名义强度的影响。
需要说明的是，轴压强度对应的峰值应变、轴压强度后的变形与轴压强度一样，都是该柱轴压破坏行为的重要指标。后续的研究中，将对这些工作开展深入讨论。
参考文献：
[1]史庆轩，侯炜，张兴虎，姜维山.箍筋约束混凝土结构及其发展展望[J].建筑结构学报，2009，30(增刊 2):109―114.Shi Qinxuan，Hou Wei，Zhang Xinghu，Jiang Weishan.Development and prospects of hoop reinforceement confined concrete[J].Journal of Building Structures，2009，30(Suppl 2):109―114.(in Chinese)
[2]Richart F E，Brandtzaeg A，Brown L R.A study of thefailure of concrete under combined compressive stresses[R].Urbana，university of Illinois，1928:82―95.
[3]Chan W W L.The Ultimate Strength and Deformation of Plastic Hinges in Reinforced Concrete Frameworks[J].Magazine of Concrete Research，1955，7(21):121―132.
[4]Soliman M T M，Yu C W.The flexural stress-strain relationship of concrete confined by rectangular transverse reinforcement[J].Magazine of Concrete Research，1967，19(61):223―238.
[5]Sheikh S A，Uzumeri S M.Analytical model for concrete confined in tied Columns[J].ASCE Journal of the Structural Division，1982，108(12):2703―2722.
[6]Mander J B，Priestley M J N，Park R.Observed stress-strain behavior of confined concrete[J].ASCE Journal of Structural Engineering，1988，114(8):1827―1849.
[7]史庆轩，杨坤，刘维亚，等.高强箍筋约束高强混凝土轴心受压力学性能试验研究[J].工程力学，2012，29(1):141―149.Shi Qingxuan，Yang Kun，Liu Weiya，et al.Experimental study on mechanical behavior of high strength concrete confined by high-strength stirrups under eccentric loading[J].Engineering Mechanics，2012，29(1):141―149.(in Chinese)
[8]钱稼茹，程丽荣，周栋梁.普通箍筋约束混凝土柱的中心受压性能[J].清华大学学报，2002，42(10):1369―1373.Qian Jiaru，Cheng Lirong，Zhou Dongliang.Behavior of axially loaded concrete columns confined with ordinary hoops[J].Journal of Tsinghua University，2002，42(10):1369―1373.(in Chinese)
[9]郑文忠，侯翀驰.不同强度等级箍筋约束混凝土柱设计方法[J].建筑结构学报，2016，37(12):74―82.Zheng Wenzhong，Hou Chongchi.Design method for confined concrete column with different yield strength stirrups[J].Journal of Building Structures，2016，37(12):74―82.(in Chinese)
[10]Jonathan West，Ahmed Ibrahim，Riyadh Hindi.Analytical compressive stress-strain model for high-strength concrete confined with cross-spirals[J].Engineering Structures，2016，113:362―370.
[11]GB 50010―2010，混凝土结构设计规范[S].北京:中国建筑工业出版社，2010.GB 50010―2010，Code for design of concrete structures[S].Beijing:China Architecture & Building Press，2010.(in Chinsese)
[12]Bažant Z P，Kwon Y W.Failure of slender and stocky reinforced concrete columns:tests of size effect[J].Materials and Structures，1994，27(2):79―90.
[13]Němeček J，Bittnar Z.Experimental investigation and numerical simulation of post-peak behavior and size effect of reinforced concrete columns[J].Materials and Structures，2004，37(3):161―169.
[14]Sener S，Barr B I G，Abusiaf H F.Size effect in axially loaded reinforced concrete columns[J].ASCE Journal of Structural Engineering，2004，130(4):662―670.
[15]车轶，王铁东，班圣龙，宋玉普.箍筋约束混凝土轴心受压性能尺寸效应研究[J].建筑结构学报，2013，34(3):118―123.Che Yi，Wang Tiedong，Ban Shenglong，Song Yupu.Size effect on behavior of concrete confined by stirrups under axial compression[J].Journal of Building Structures，2013，34(3):118―123.(in Chinese)
[16]Li D，Jin L，Du X，Fu J，Lu A.Size effect tests of normal-strength and high-strength RC columns subjected to axial compressive loading[J].Engineering Structures，2016，109:43―60.
[17]杜修力，金浏，李冬.混凝土与混凝土结构尺寸效应述评：(I)材料层次[J].土木工程学报，2017，50(9):28―45.Du Xiuli，Jin Liu，Li Dong.A state-of-the-art review on the size effect of concretes and concrete structures(I):concrete materials[J].China Civil Engineering Journal，2017，50(9):28―45.(in Chinese)
[18]杜修力，金浏，李冬.混凝土与混凝土结构尺寸效应述评：(II)构件层次.土木工程学报，2017，50(11):24―44.Du Xiuli，Jin Liu，Li Dong.A state-of-the-art review on the size effect of concretes and concrete structures(II):RC members[J].China Civil Engineering Journal，2017，50(11):24―44.(in Chinese)
[19]杜敏，金浏，杜修力，李冬，张帅.箍筋约束混凝土方柱轴压破坏尺寸效应细观数值研究[J].中国科学:技术科学，2017，47(10):1057―1066.Du Min，Jin Liu，Du Xiuli，Li Dong，Zhang Shuai.Mesoscopic simulation of size effect on stirrup-confined concrete columns under axial compression[J].Scientia Sinica Techbologica，2017，47(10):1057―1066.(in Chinese)
[20]Bažant Z P.Scaling theory for quasibrittle structural failure[J].Proceedings of the National Academy of Sciences of the United States of America，2004，101(37):13400―13407.
[21]Park R，Priestley M J，Gill W D.Ductility of squareconfined concrete columns[J].ASCE Journal of the Structural Division，1982，108(4):929―950.
[22]Legeron F，Paultre P.Uniaxial confinement model for normal and high strength concrete columns[J].ASCE Journal of Structural Engineering，2003，129(2):241―252.
[23]Jin Liu，Li Dong，Du Xiuli，et al.Experimental and numerical study on size effect in eccentrically loaded stocky RC columns[J].ASCE Journal of Structural Engineering，2017，143(2):04016170.
[24]Sheikh S A，Uzumeri S M.Analytical model for concrete confinement in tied columns[J].ASCE Journal of Structural Division，1982，108(12):2703―2722.
[25]Unger J F，Eckardt S.Multiscale modeling of concrete[J].Archives of computational Methods in Engineering，2011，18(3):341―393.
[26]Wrigger P，Moftah S O.Mesoscale models for concrete:homogenisation and damage behavior[J].Finite Elements in Analysis and Design，2006，42(7):623―636.
[27]李冬，金浏，杜修力，等.钢筋混凝土轴压柱长细比效应的细观数值研究[J].中国科学:技术科学，2016，46(9):1―9.Li Dong，Jin Liu，Du Xiuli，et al.Mesoscopic numerical investigations on the slenderness effect of reinforced concrete column under axial compression[J].Scientia Sinica Technologica，2016，46(9):1―9.(in Chinese)
SIZE EFFECT ON THE FAILURE OF STIRRP-CONFINED REINFORCED CONCRETE COLUMNS UNDER AXIAL COMPRESSION
JIN Liu1，DU Min1，2，DU Xiu-li1，LI Zhen-bao1
(1.The key laboratory of Urban Security and Disaster Engineering，Beijing University of Technology，Beijing 100124，China;2.Department of Disaster Prevention Engineering，Institute of Disaster-prevention Science and Technology，Sanhe，Hebei 065201，China)
Abstract:A total of 12 geometric similar stirrup-confined circular reinforced concrete(RC)columns subjected to axial compression were designed and tested.In the tests，two stirrup ratios of 1.26% and 2.89% were utilized.The structural similarity ratio of the columns was 1∶1.5∶2.25.The maximum cross-sectional diameter was 576 mm，and the slenderness ratio was 3.The confinement effect on the failure patterns and the axial compressive strength of the stirrup-confined columns was explored.Moreover，based on the basic theory of the Size Effect Law(SEL)proposed by Bažant，a modified formula for evaluating the bearing capacity of stirrup-confined RC columns was developed，which can reflect the effect of structural size.Good agreement between the theoretical results and the test results indicated the reasonability of the modified formula.Finally，a 3D meso-scale numerical method for the simulation of the failure behavior and size effect of RC members was established.The simulated results were consistent with the tested ones，and the meso-scale simulation method was then extended to model the failure of circular RC columns with larger structural dimensions.
Key words:stirrup-confined concrete;circular column;axial compressive strength;stirrup ratio;size effect;bearing capacity;meso-scale simulation
中图分类号：TU528
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0036
文章编号：1000-4750(2018)05-0093-09
收稿日期：2017-01-09；修改日期：2017-04-17
基金项目：国家自然科学基金创新研究群体项目(51421005)；国家自然科学基金项目(51408127)；教育部创新团队项目(IRT13044)
通讯作者：杜修力(1962―)，男，四川人，教授，博士，博导，主要从事地震工程学领域研究工作(E-mail:duxiuli@bjut.edu.cn).
作者简介：金 浏(1985―)，男，江苏人，教授，博士，博导，主要从事混凝土与混凝土工程结构领域研究工作(E-mail:jinliu@bjut.edu.cn);
杜 敏(1978―)，女，辽宁人，副教授，博士，主要从事混凝土尺寸效应方面工作(E-mail:dumin2001@163.com);
李振宝(1962―)，男，山东人，教授，博士，博导，主要从事混凝土工程结构方面研究工作(E-mail:lizb@bjut.edu.cn).