姚 博1，2，全 涌2，顾 明2，聂 铭1
(1.广东电网有限责任公司电力科学研究院，广东，广州 510080；2.同济大学土木工程防灾国家重点实验室，上海 200092)
摘 要：在混合风气候地区，不同类型风气候(如台风、良态风)的极值风速概率分布特性各不相同，如果直接采用单一概率分布模型对混合极值风速进行拟合，往往会造成较大的分析误差。目前常采用将台风和良态风数据分离后分别分析的方法进行极值风速分析，但这种方法在分析良态风时存在难以将台风记录从气象部门长期观测数据中分离出来的问题，在台风蒙特卡罗模拟研究中存在台风参数概率分布信息收集困难的问题。该文基于混合函数构建混合风气候地区极值风速的概率密度函数，采用加权最小二乘法拟合分布函数和权重函数的参数，并对各参数进行优化得到更为精确的计算结果。最后采用蒙特卡罗模拟结果和长期观测数据验证了该文方法的准确性和实用性。
关键词：混合气候；极值风速；良态风；台风；概率分布；蒙特卡罗模拟
极值风速分析在高层建筑结构风荷载的评估中起着十分重要的作用，极值风速分析准确与否将影响着风荷载的最终评估结果。然而，无论沿海混合气候地区还是内陆良态风影响区域，极值风速的大小、方向和分布特性都有着明显的不同。混合气候极值风速由台风和良态风数据共同组成，且二者的概率分布各不相同，如果直接对混合气候极值风速进行取样并采用单一的概率分布模型进行拟合，则拟合结果通常不能反映极值风速的真实概率分布。因此需要对混合气候区的极值风速分析进行深入研究。
到目前为止，良态风极值风速的分析方法研究已发展地较为充分。Fisher等[1]提出的渐进极值理论成为极值分析的重要基础。Gumbel[2]通过引入三种渐进极值分布概念，促使极值分析被广泛应用。若采用年最大风速作为分析对象则会使样本数据太少，为此，研究者提出了多种提高风速观测数据利用率的方法，如穿越分析法[3]、跨阈值法[4]等。同时，用于分布函数参数拟合的方法也在不断更新，如Harris[5]基于次序统计理论给每个统计量分配权重，并采用加权最小二乘方法进行拟合；后来，Harris[6]又针对该方法实用性差的缺点提出了计算折减变量的改进方法。传统的极值分析方法可能会因为采用了不合理的概率值而低估统计结果，为此Makkonen[7]提出经验分析方法。在国内，张秉超和全涌等[8]采用改进的独立风暴法进行取样，并结合极值统计理论提出了一种可以考虑风向效应的良态风极值风速估计新方法，分析结果表明该算法具有非常良好的精度；董胜等[9]基于风速风向玫瑰图提出了建立风速风向联合分布模型的新方法，分析结果表明，新的模型可以更好的反映相邻方向间风速分布的相关性，且克服了传统风速风向玫瑰图仅有16个风向的不足。与此同时，用于台风模拟的各种研究方法也逐渐趋于成熟。Meng等[10]建立了适用于工程分析的台风模型；Rusell[11]和Fujii等[12]分别提出了采用蒙特卡罗模拟台风的数值分析方法。雷鹰等[13]根据厦门地区50年的台风历史资料得到台风关键参数统计模型，并基于Yan Meng台风模型模拟得到厦门地区的极值风速。与实测结果吻合较好，证明了台风模拟的可行性和有效性。
在混合风气候极值风速研究方面，Gomes等[14]基于各种气候类型风速的概率分布特点，给出雷暴、飓风和龙卷风等混合气候的复合极值风速分析方法，并进行极值风速估计。Cook[15]对该方法进行了改进，并分析了混合风气候极值风速的置信区间，但是由于台风数据不易获取，因而暂未出现考虑风向的混合风气候极值风速的分析方法。Cook[16]基于建筑表面风压的指数尾的偏斜高斯分布，提出了适用于描述建筑风压分布的偏斜高斯指数混合模型，该模型可以很好地拟合概率分布的主体和尾部分布，并产生具有恒定相对误差的所需指数尾；Vrac等[17]发展了用于降水量预测的混合概率分布模型方法，但由于研究对象、使用范围等均不同且无法考虑风的相关特性，因此并不适用于极值风速分析。总之，目前对混合气候极值风速进行分析的一般思路是分别分析台风和良态风的概率特性，再联立得到混合气候的概率分布规律，最后再计算给定重现期极值风速。但这种方法存在一定的缺陷：首先甄别各种类型的风气候数据计较困难，工作量大；另外，台风模拟过程较为复杂，受各种参数概率分布非常敏感，且这些参数的概率分布难以准确给出。
综上可知，传统极值方法在分析混合气候极值风速时存在诸多不足。本文基于混合函数构建台风和良态风混合气候的极值风速概率密度函数，通过借鉴良态风极值分析中成熟的数据处理方法并考虑影响极值分布的多种因素采用加权最小二乘法求解各个参数并对参数进行优化，最后采用蒙特卡罗模拟等方法验证了本文方法的有效性。与传统方法相比，本文方法更简便实用，容易被工程实践采纳。
东南沿海地区的风气候通常会受到台风和良态风的共同影响，不同气象系统的极值风速概率分布各不相同。Van等[18]研究表明，这种气候的风速满足混合分布。Frigessi等[19]最早提出采用混合函数的思想来处理服从不同分布的随机过程的混合数据，但实际应用时仍采用传统拟合方法，这使得计算过程复杂且无法得到满意的结果。针对目前混合气候风速分析中存在的问题，本文首先区分不同类型的极值风速数据，然后构建混合气候极值风速的概率密度函数，再基于加权最小二乘法求解参数并进行优化，最终精确计算极值风速。
不同气候类型的风速数据满足不同的概率分布，因此以往混合气候极值风速的分析，通常需要从气象记录中将各种类型的风速数据分离再分析。Gomes等[3]和Cook[15]等基于一定判据将各种类型的风速数据分别分离，最后求解整个混合气候的极值风速。这种方法的一个弊端就是需要从气象站的风速风向长期观测记录中甄别不同类型的风速数据，过程受人为因素影响很大，难以实现程序化处理。本文根据混合气候中极值风速和折减变量间的关系，基于加权最小二乘原理识别良态风主导范围(良态风数据占主导，同时含有很少的台风数据，对下尾部分布影响较小)和台风主导范围，以代替传统风速类型的识别方法。
混合气候中台风和良态风数据通常满足不同的概率分布函数，折减变量与极值风速的关系曲线往往并不是一条直线，因此无法采用单一函数进行拟合得到混合气候极值风速的概率分布函数。本文首先采用分部拟合的方式分别得到各个主导区的概率分布函数，再构建混合分布函数。
气象站的风速记录为每日风速风向信息，考虑到有些日最大风速较小，不便于极值分析，同时为了得到尽可能多的数值较大的极值风速样本，本文采用观测时矩为8 d的阶段极值法对最大风速进行抽样。对所有样本进行从小到大排序，则n个极值风速样本中第m个样本的不超越概率为
然后基于Harris极值理论[20]求解折减变量
由于折减变量在上尾部具有很大的离散性，不同的变量对拟合结果贡献并不相同，因此再对各个样本分配权重，权重值wm取为极值风速方差的倒数[21]。最后采用左截断方法得到N个极值风速样本。识别良态风主导范围数据和台风主导范围数据并分别拟合时，首先选择最少的极值样本组(i=2)，并基于式(1)所示的极值I型分布函数和对应的权重系数进行加权最小二乘拟合，得到上部台风主导范围的分布函数；同时对余下的N-i组极值样本采用式(2)所示的分布函数和对应的权重值进行加权最小二乘拟合，得到下部良态风主导范围的概率分布函数。最后计算误差函数值ss2(i)，如式(3)所示。
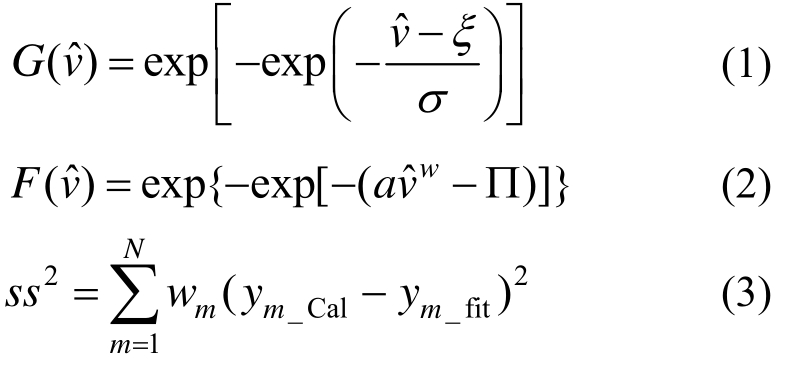
式中：N为用于函数拟合的极值风速样本数目；vˆ为极值风速；wm为拟合权重因子；ym_Cal为采用极值理论得到的折减变量均值；ym_fit为拟合函数对应的折减变量；ξ和σ为G函数参数；a、w和∏为F函数参数。同理，逐渐增加上部台风主导范围极值样本的数量i=i+1，再分别进行极值拟合和计算对应的加权最小二乘误差函数值，如此反复。最后，选择误差函数最小值ss2_min对应的极值风速样本数量作为识别良态风主导范围和台风主导范围的依据，进而得到各主导范围如式(1)和式(2)所示的概率分布函数。分析流程如图1所示。
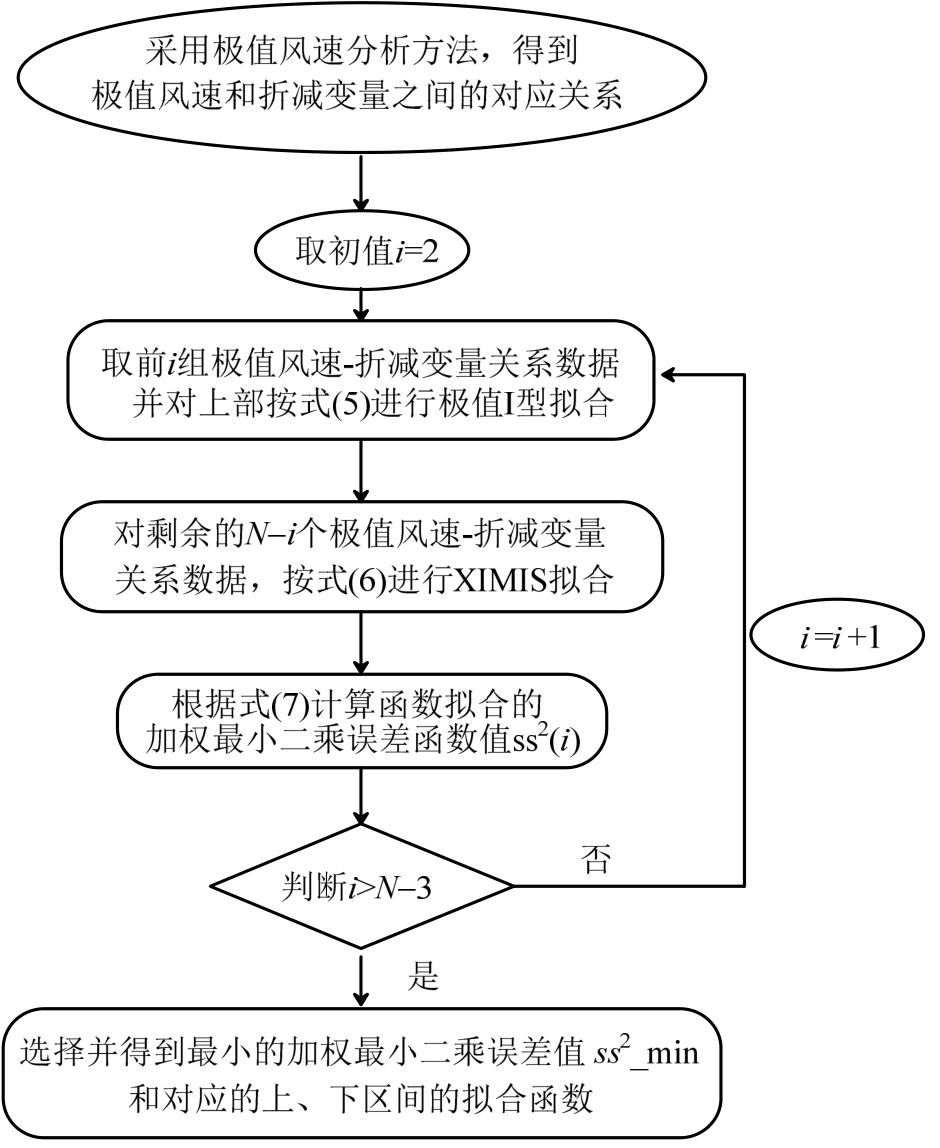
图1 混合模型的分布参数拟合流程
Fig.1 The fitting process of distributed parameter
由上述分析可知，混合气候区极值风速无法采用单一概率分布函数进行拟合，基于折减变量和极值风速的关系可将风速数据分为良态风主导区和台风主导区，并分别拟合得到相应的概率分布函数。在此基础上进一步构建如式(4)所示的用于描述混合气候区极值风速的概率密度函数：
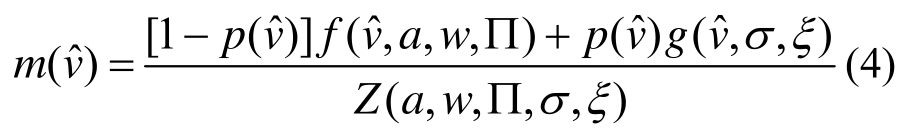
式中：g(vˆ，σ，ξ)为台风主导区极值风速概率密度函数可由式(1)拟合得到；f(vˆ，a，w，∏)为良态风主导区极值风速概率密度分布函数可由式(2)拟合得到；Z(a，w，∏，σ，ξ)为归一化函数；p(vˆ)为权重函数，其值介于(0，1)之间，当风速逐渐增大时权重函数取值趋向于1，也就意味着当风速较大时混合函数m(vˆ)上尾部主要由函数g(vˆ，σ，ξ)决定，风速较小时下尾部主要由函数f(vˆ，a，w，∏)决定。权重函数p(vˆ)表达式为：
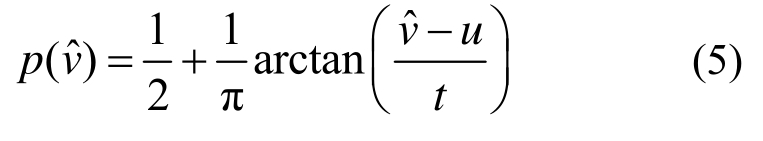
式中：u为位置参数，是一个大于0的常数；t为形状参数，通常取值在0～10。权重函数的几何属性可以理解为提供一种平滑过渡来连接良态风主导区和台风主导区的极值风速概率分布函数。基于上述良态风极值风速分布函数、台风极值风速分布函数和权重函数，可推导出归一化常数Z的表达式为：
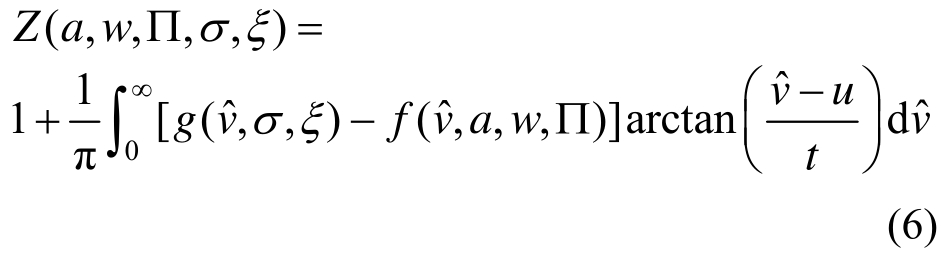
基于式(1)和式(2)得到的良态风主导区极值风速概率分布函数和台风主导区极值风速概率分布函数可分别表示为：
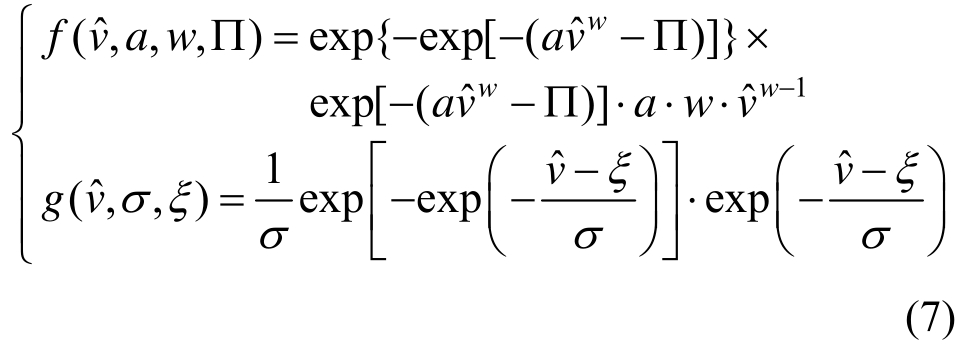
将式(7)概率密度函数代入式(6)得到归一化常数Z；然后将各极值风速概率密度函数、权重函数和归一化函数代入式(4)得到混合气候的极值风速概率密度函数；最后再对极值风速密度函数进行积分得到概率分布函数，进而可计算得到N年重现期的极值风速。
1.2 节构建了适用于混合气候区极值风速的概率分布函数，但精确计算极值风速还需要准确确定各个参数值，这里采用加权最小二乘原理对各参数进行拟合求解和优化。
1.3.1 权重函数参数
权重函数有两个重要参数—位置参数u和形状参数t需要确定。位置参数u的物理含义代表了极值风速—折减变量关系中台风主导范围和良态风主导范围的分界位置，因此可由2.1节临界风速值来确定。形状参数直接反映了台风主导范围和良态风主导范围不同分布函数曲线的过渡规律。形状参数可基于混合函数与原极值样本的拟合程度来确定，即：首先给出一个较小的初始形状参数值t(如，取t=0.01)，得到式(5)所示的权重函数，进而根据式(6)计算其归一化常数Z，再由式(4)得到混合分布函数m(vˆ)，最后联合各风速样本的权重值并由式(3)计算t对应的加权最小二乘误差函数值；改变t值，重复相同过程，并计算下一组拟合函数对应的加权最小二乘误差函数值，直到选出最优的形状参数t和对应的混合分布函数m(vˆ)。流程如图2所示。
图2 混合模型权函数的形状参数求解流程
Fig.2 The fitting process of shape parameter
1.3.2 参数优化
1.3.1 基于加权最小二乘原理来求解概率分布函数参数和形状参数。这种方法一方面可使计算过程较为简便，但另一方面由于分布函数参数和权重函数参数是分别分析计算的，这就有可能使得给出的结果并非最优解。假定真实的精确结果不会大范围偏离上述过程结果，在上述拟合结果附近对拟合参数进行优化，得到更精确的结果。
选取多组受台风和良态风共同影响的沿海城市风气候数据和仅受良态风影响的内陆城市风气候数据，气象记录数据来源于中国气象数据网。将采用本文方法给出的分析结果与蒙特卡罗模拟方法、传统极值分析方法和气象站长期观测结果进行对比，以检验本文方法的精确性和适用性。
在气象数据中除去台风数据，并基于良态风极值风速处理方法对剩余数据进行拟合得到良态风16个方向极值风速的概率分布函数[22]，然后再采用蒙特卡罗方法模拟良态风分布，即：基于每个风向的年极值风速分布随机抽取一个样本，得到一个1×16的数列，表示一年中各个风向的年极值风速，重复该过程1×106次，得到一个表示该地区106年内各个风向年极值风速的16×106数据阵列。
选取合适的台风模型和关键台风参数来模拟台风过程。Meng等[10]基于径向压力梯度、向心力、Coriolis力和摩擦力来建立扰动平衡方程，并在二维极坐标网格内推导了梯度层和边界层的风速分布关系，使得台风模拟过程得到了大大的简化。台风模拟所需数据源于中国气象局提供的台风年鉴以及国家海洋局第一海洋研究所。基于Meng等[10]提出的台风模型和肖玉凤[23]等给出的台风关键参数统计模型可模拟每年台风发生个数和每个台风的风速时程。最后取一年中各个台风作用下各方向风速最大值作为该向台风风速极值，重复该过程106次，得到一个与良态风极值风速相对应的16×106台风极值风速数据阵列。
最后，将良态风极值风速数据阵列和台风极值风速数据阵列的各元素一一对应，并取相同位置较大值作为极值风速，这样就得到一个新的16×106的混合区极值风速数据阵列。该方法常用于无气象记录地区的极值风速分析，因涉及台风参数统计和台风模拟，计算成本高于其他极值分析方法。
考虑到蒙特卡罗模拟受台风关键参数统计精确程度影响以及实测数据受观测年限影响的限制，本文在以上海、广州、海口和厦门等多个东南沿海地区混合气候的极值风速分析为例进行分析时，将对本文方法拟合结果、蒙特卡罗方法模拟结果、传统的极值I型概率分布模型拟合结果和观测结果进行综合对比分析对比，结果如图3所示。
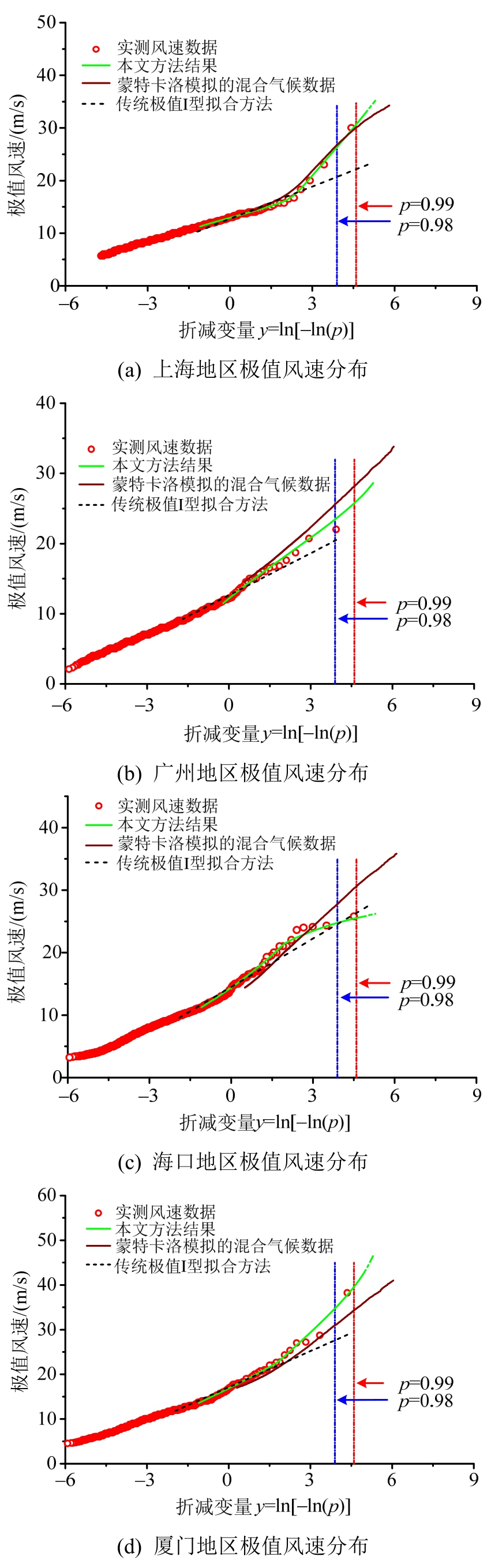
图3 沿海地区混合气候极值风速分析结果
Fig.3 The analysis results of extreme wind speed in mixed climate areas
图3(a)～图3(b)较为典型地反映了混合气候极值风速的概率分布特性，其中蓝线和红线分别对应于50年(保证率p=0.98)和100年(p=0.99)重现期极值风速。以图3(a)上海地区极值风速分析为例，本文方法与Monte Carlo模拟方法和实测数据吻合较好，而传统的极值I型拟合方法在低速良态风主导范围与实测结果吻合较好，而在重现期较高的台风主导范围该方法不再适用。这是因为，上海地区低速的良态风极值风速概率分布和高速的台风极值风速概率分布差异较大，使得尾部分布偏离较为明显，采用单一分布函数的传统作法不再有效。针对100年重现期极值风速，采用本文混合概率分布方法给出的结果为30.65 m/s，与蒙特卡罗方法模拟结果30.06 m/s非常接近，分析误差低于2%；而传统的极值风速分析方法给出的结果为22.14 m/s，大大低于上述两种方法的结果；对厦门地区极值风速分布研究表明，采用本文分析方法得到的50年和100年一遇极值风速分别为34.78 m/s和39.58 m/s，雷鹰等[24]专门针对厦门地区极值风速进行研究给出50年和100年一遇极值风速分别为35.81 m/s和41.13 m/s，二者相对误差分别为2.9%和3.8%。对广州、海口等更多沿海地区风气候的分析结果表明，混合气候极值风速的尾部分布表现出不同程度的偏离，传统分析方法将产生一定的计算误差，而本文方法计算精度是较高。
基于上述多种方法对内陆地区良态风气候的极值风速进行分析，结果如图(4)所示。由图可知，内陆地区几乎不受台风影响，极值风速样本源于单一的良态风气候，因此极值风速和折减变量之间满足很强的线性关系，尾部分布并未出现明显的偏离，这与混合气候极值风速的概率分布有明显的区别。此时，采用本文方法得到的结果与蒙特卡罗模拟方法、传统分析方法得到结果一致且均具有很高的计算精度。
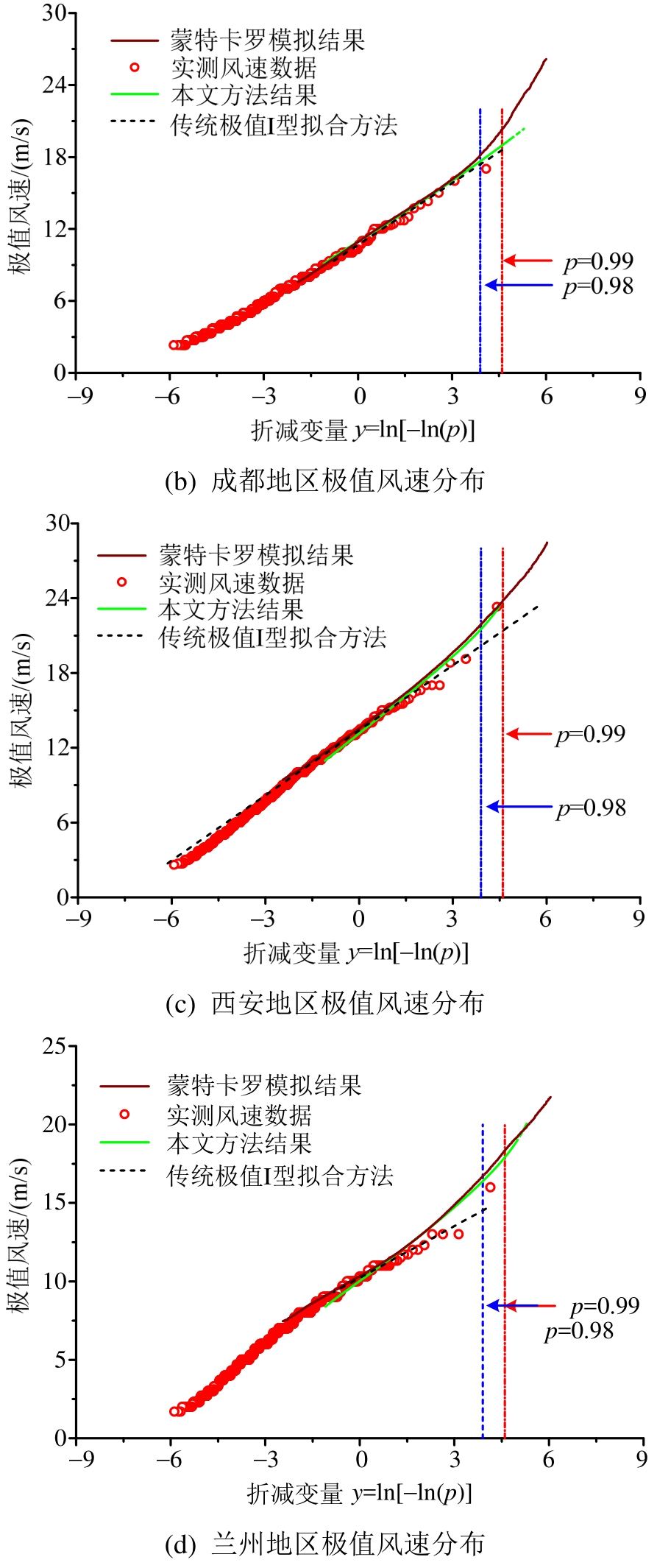
图4 内陆良态风气候极值风速分析结果
Fig.4 The analysis results of extreme wind speed in normal wind climate areas
本文基于混合函数构建台风和良态风混合气候地区的极值风速概率密度函数，通过采取左截断取样、改进简化变量和分配权重等多种措施，并采用加权最小二乘法求解各个参数，最后对参数进行优化得到精度更高的概率分布函数。通过对混合风气候极值风速的研究，得到如下结论。
(1)内陆良态风气候区，极值风速样本源于单一风气候，尾部分布未出现明显偏离，因此采用传统极值I型分布即可获得精度满意的计算结果。
(2)沿海混合气候区，极值风速源于台风和季风这种具有不同概率分布的气候类型，尾部分布偏离较为明显，此时若仍采用传统的极值风速分析方法，则会造成不同程度的误差。
(3)本文方法无论是对良态风气候还是对混合气候，均具有很好的适用性；与采用极值I型分布函数的传统分析方法相比，本文方法使用范围更广、精度更好；相较于蒙特卡罗模拟方法，本文方法无需专门收集台风关键参数和进行复杂的模拟运算，更适于工程应用。
参考文献：
[1]Fisher R A，Tippett L H C.Limiting forms of the frequency distribution of the largest or smallest member of a sample[C]// Mathematical Proceedings of the Cambridge Philosophical Society.Cambridge University Press，1928，24(02):180―190.
[2]Gumbel E J.Statistics of extremes[M].New York:Columbia University Press，1958.
[3]Gomes L，Vickery B J.On the prediction of extreme wind speeds from the parent distribution[J].Journal of Wind Engineering and Industrial Aerodynamics，1977，2(1):21―36.
[4]Weiss L.Asymptotic inference about a density function at an end of its range[J].Naval Research Logistics Quarterly，1971，18(1):111―114.
[5]Harris R I.Improvements to the method of independent storms'[J].Journal of Wind Engineering and Industrial Aerodynamics，1999，80(1):1―30.
[6]Harris R I.XIMIS.A penultimate extreme value method suitable for all types of wind climate[J].Journal of Wind Engineering and Industrial Aerodynamics，2009，97(5):271―286.
[7]Makkonen L.Problems in the extreme value analysis[J].Structural Safety，2008，30(5):405―419.
[8]张秉超 全涌 顾明.考虑风向的良态风极值风速估计方法[J].工程力学，2017(9):119―124.Zhang Bingchao，Quan Yong，Gu Ming.A method for estimating directional extreme wind speeds in zones of normal climates[J].Engineering Mechanics，2017(9):119―124.
[9]董胜，林逸凡.固定测站的风向风速联合分布研究[J].工程力学，2016，33(6):234―241.Dong Sheng，Lin Yifan.Study of joint probabilistic distribution of wind speed and direction at a fixed observation station[J].Engineering Mechanics，2016，33(6):234―241.
[10]Meng Y，Matsui M，Hibi K.An analytical model for simulation of the wind field in a typhoon boundary layer[J].Journal of Wind Engineering and Industrial Aerodynamics，1995，56(2):291―310.
[11]Russell L R.Probability distributions for hurricane effects[J].Journal of the Waterways，Harbors and Coastal Engineering Division，1971，97(1):139―154.
[12]Fujii T，Mitsuta Y.On prediction of occurrence probability of severe wind by a typhoon，prediction of the sea-surface wind[J].Japan Society for Natural Disaster Science，1992，11(3):125―144.
[13]雷鹰，李涛，张建国，等.厦门地区台风风场特性的数值模拟[J].工程力学，2014，31(1):122―128.Lei Ying，Li Tao，Zhang Jianguo，et al.Numerical simulation of the characteristics of typhoon wind-field in XIiamen region[J].Engineering Mechanics，2014，31(1):122―128.
[14]Gomes L，Vickery B J.Extreme wind speeds in mixed wind climates[J].Journal of Wind Engineering and Industrial Aerodynamics，1978，2(4):331―344.
[15]Cook N J.Confidence limits for extreme wind speeds in mixed climates[J].Journal of Wind Engineering and Industrial Aerodynamics，2004，92(1):41―51.
[16]Cook N J.Short communication:on the Gaussian-Exponential Mixture Model for pressure coefficients[J].Journal of Wind Engineering & Industrial Aerodynamics，2016，153:71―77.
[17]Vrac M，Naveau P.Stochastic downscaling of precipitation:From dry events to heavy rainfalls[J].Water Resources Research，2007，43(7):W07402.
[18]Van den Brink H W，Können G P，Opsteegh J D.Statistics of extreme synoptic-scale wind speeds in ensemble simulations of current and future climate[J].Journal of Climate，2004，17(23):4564―4574.
[19]Frigessi A，Haug O，Rue H.A dynamic mixture model for unsupervised tail estimation without threshold selection[J].Extremes，2002，5(3):219―235.
[20]Harris R I.Gumbel re-visited-a new look at extreme value statistics applied to wind speeds[J].Journal of Wind Engineering and Industrial Aerodynamics，1996，59(1):1―22.
[21]Plackett R L.Some theorems in least squares[J].Biometrika，1950，37(1/2):149―157.
[22]张秉超.建筑围护结构极值风压的全概率分析方法研究[D].上海:同济大学，2014.Zhang Bingchao.Research on the fully probabilistic method of the extreme wind pressure on buildings[D].Shanghai:Tongji University，2014.(in Chinese)
[23]肖玉凤.基于数值模拟的东南沿海台风危险性分析及轻钢结构风灾易损性研究[D].哈尔滨:哈尔滨工业大学，2011.Xiao Yufeng.Typhoon wind hazard analysis based on numerical simulation and fragility of light-gauge steel structure in southeast china coastal regions[D].Harbin:Harbin Institute of Technology，2011.(in Chinese)
[24]雷鹰，李涛，张建国，等.厦门地区极值风速预测[C]//第十四届全国结构风工程学术会议论文集(上册)，中国:北京，2009:63―68.Lei Ying，Li Tao，Zhang Jianguo，et al.The prediction of extreme wind speed in Xiamen area[C]// Proceedings of the 14th National Symposium on Structural Wind Engineering(1)，China:Beijing.2009:63―68.
STUDY ON THE ANALYSIS METHOD OF EXTREME WIND SPEED IN MIXED CLIMATE AREAS
YAO Bo1，2，QUAN Yong2，GU Ming2，NIE Ming1
(1.Electric Power Research Institute of Guangdong Power Grid Co.，Ltd，Guangzhou，Guangdong 510080，China;2.State Key Laboratory for Disaster Deduction in Civil Engineering，Tongji University，Shanghai 200092，China)
Abstract:The probability distribution of extreme wind speed for different wind climate，such as typhoon and normal wind，are different from each other in the region of mixed wind climate.Large analytical error/deviation would be generated if only one probability distribution model is used to fit the extreme wind speed of mixed wind climate.At present，in the analysis of extreme wind speed for mixed climate，the method to separate the wind data into typhoon and normal wind and analyze them individually is commonly applied.However，when using this method，it is difficult to distinguish the typhoon records from the long-term observation wind data of meteorological department.Moreover，it is hard work to collect the probability distribution information of the key parameters of typhoon for the Monte Carlo simulation.In present study，a probability density function of extreme wind speed for mixed wind climate is proposed based on a mixed function.The parameters of the distribution function and the weight function are fitted through the weighted least square method.Then optimization has been made for these parameters to obtain more accurate simulation results.Finally，the simulation results from Monte Carlo method，the results of the proposed method and the long-term observation data are compared to verify the accuracy and practicability of the proposed method.
Key words:mixed climate;extreme wind speed;normal wind;typhoon;probability density function;Monte Carlo simulation
中图分类号：P444
文献标志码：A
doi:10.6052/j.issn.1000-4750.2016.12.1000
文章编号：1000-4750(2018)05-0086-07
收稿日期：2016-12-27；修改日期：2017-08-28
基金项目：广东电网公司重点科技项目(GDKJQQ20153009)
通讯作者：全涌(1972―)，男，重庆人，教授，博士，博导，主要从事风工程研究(E-mail:quanyong@tongji.edu.cn).
作者简介：姚博(1986―)，男，河南商丘人，博士，从事结构风工程研究(E-mail:lixue05-116@163.com);
顾明(1957―)，男，江苏人，教授，博士，博导，主要从事结构风工程方面研究(E-mail:minggu@tongji.edu.cn);
聂铭(1973―)，男，湖南人，教授级高工，硕士，主要从事结构工程方向研究(E-mail:nieming@gddky.csg.cn).