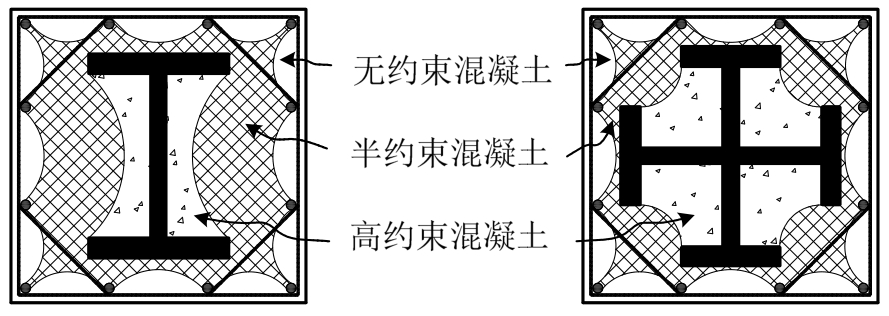
图1 SRC柱截面区域划分
Fig.1 Regions for SRC composite sections
赵宪忠1，2，温福平2
(1.同济大学土木工程防灾国家重点实验室，上海 200092；2.同济大学土木工程学院，上海 200092)
摘 要：目前，钢骨混凝土(SRC)柱的试验结果与数值分析结果之间多无法良好吻合；究其原因，在于缺乏对钢骨约束混凝土的约束机制认识及与之相应的钢骨约束混凝土模型的建立。为此，该文在以往钢骨约束混凝土试验基础上，深入研究了带翼缘十字形钢骨对混凝土的约束机制，提出了钢骨对混凝土产生的实际侧向约束应力的简化分布形式，并以此将钢骨约束混凝土划分为钢骨强约束混凝土、钢骨弱约束混凝土和钢骨无约束混凝土。同时，通过计算有效侧向约束应力，确定了各钢骨约束区域可表征钢骨约束作用强弱的混凝土强度提高系数；借鉴经典的Mander模型，通过修正模型关键参数方法以建立各钢骨约束区域混凝土的应力-应变模型。引入该应力-应变模型的有限元分析和试验对比结果表明，该文所提出的钢骨约束混凝土的约束机制和所建立的钢骨约束混凝土应力-应变模型是合理且有效的。
关键词：钢骨约束混凝土；约束机制；区域划分；有效侧向约束应力；应力-应变模型
钢骨混凝土柱(简称SRC柱)为内嵌钢骨的钢筋混凝土构件，其受力时钢骨与混凝土之间相互作用，即混凝土可以防止钢骨局部屈曲，使钢材强度充分发挥、延缓构件刚度降低；钢骨可对混凝土提供约束作用，提高混凝土的强度和延性[1]。因此，SRC柱以其良好的承载性能、防火性能和抗震性能，被广泛应用于高层、超高层建筑和复杂建筑结构中。
目前，已有大量学者对SRC柱的受力性能进行了系统深入的试验研究和数值模拟，考察了钢/混凝土材料强度组合、钢骨截面形式、含钢率、配箍率、栓钉设置、轴压比等因素对其性能的影响[2－10]，基本把握了SRC构件的静动力受力性态。但已有研究表明，无论对于SRC构件截面承载力N-M相关曲线[4]还是压弯状态下的滞回性能模拟[6]，理论或数值分析结果与试验结果之间仍无法良好吻合。究其原因，主要在于缺乏对钢骨约束混凝土的约束机制认识，研究中未考虑钢骨对混凝土的有效约束作用或约束混凝土应力-应变模型选取不当，即未准确划分SRC构件中无约束混凝土、半约束混凝土(钢筋约束混凝土)、高约束混凝土(钢骨和钢筋共同约束混凝土)的作用区域(图1)并赋予其相应的混凝土应力-应变模型。
图1 SRC柱截面区域划分
Fig.1 Regions for SRC composite sections
为此，文献[11]对钢骨约束混凝土的约束机制进行了相关试验研究，明确了混凝土约束效应的影响因素；同时，结合有限元数值模拟，确定了钢骨约束混凝土强度和延性的提高系数，通过回归分析得到提高系数与相关影响因素之间的函数关系；最后基于Mander模型[12]，给出了带翼缘十字形钢骨约束混凝土应力-应变关系的建议公式。
文献[11]的研究弥补了钢骨约束混凝土试验研究的不足，为后续钢骨约束混凝土的研究奠定了基础。但该文所建立的钢骨约束混凝土应力-应变模型主要是基于试验结果的现象学公式，其中钢骨与约束混凝土面积比Ass/Ach这一参数与钢骨约束混凝土作用机制之间没有明确的联系，不能从机理角度直接解释钢骨对混凝土产生的约束效应强弱。鉴于此，本文在文献[11]试验研究和应力-应变模型基础上，从钢骨约束混凝土作用机理角度出发，借鉴Mander模型，提出一种适用性广泛的钢骨约束混凝土应力-应变模型。
钢筋混凝土构件、钢管混凝土构件或SRC构件在轴压荷载作用下将发生轴向压缩变形，由于泊松效应，混凝土受压横向膨胀，钢筋、钢管或钢骨会抑制混凝土的膨胀变形，从而对混凝土产生侧向约束作用，提高混凝土的强度和延性。钢筋或钢管截面封闭，因此通过环向受拉，对核心混凝土产生连续封闭的侧向约束作用[12－13]，参见图2。然而，SRC柱中内置的钢骨通常为开口截面形式，钢骨不会因混凝土横向膨胀变形而环向连续受拉，因此也不会对混凝土产生连续封闭的侧向约束作用。
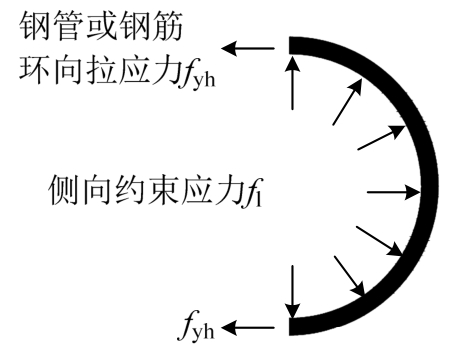
图2 钢管或钢筋约束混凝土作用机理
Fig.2 Constraint mechanism of concrete confined by hoops or steel tube
文献[11]为探究开口截面形式钢骨约束混凝土的约束机制，进行了20个带翼缘十字形钢骨混凝土芯柱轴压试验。如图3所示，在柱身二分之一高度处沿钢骨翼缘布置了12个横向位移计，每个侧面布置3个，且每一侧面的中间位移计布置于钢骨翼缘与腹板的交接处，其余两个位移计布置于翼缘外边缘。
截面横向膨胀位移差是指布置于钢骨翼缘边缘的8个位移(图3中测点D5、D7、D8、D10、D11、D13、D14、D16)所测值的平均值减去布置于钢骨翼缘中间的4个位移(图3中测点D6、D9、D12、D15)所测值的平均值，其可表示钢骨翼缘外伸部分由于抑制混凝土横向膨胀变形产生的弯曲变形。截面横向膨胀位移差值越大，钢骨对混凝土的约束作用越强。
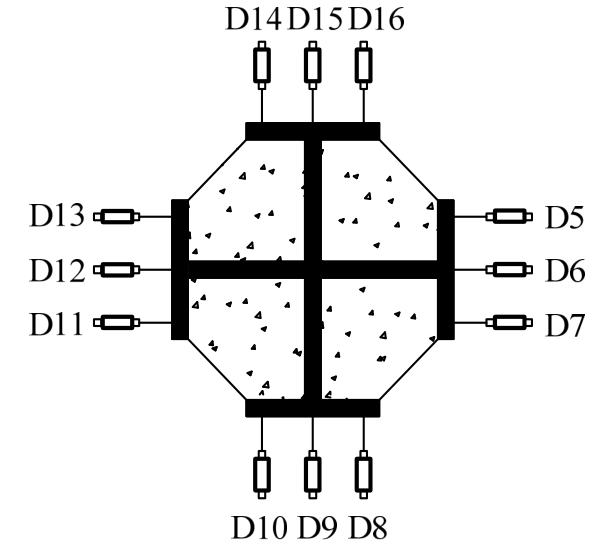
图3 位移计布置[11]
Fig.3 Arrangement of displacement transducers
图4为试件的轴压荷载-截面横向膨胀位移差曲线，图中，Ny和Np分别表示试件的屈服承载力和全截面塑性承载力。
由图4可知，所有试件当其承受外荷载小于构件屈服承载力Ny时，截面横向膨胀位移差很小，钢骨翼缘外伸部分没有发生明显的弯曲变形，钢骨翼缘外伸部分对混凝土的约束作用很弱；试件所受外荷载超过其屈服承载力Ny时，截面横向膨胀位移差开始逐渐增大，钢骨对混凝土的约束作用逐渐增强，混凝土的轴向强度也不断提高，直到试件荷载达到全截面塑性承载力Np时，混凝土受钢骨翼缘外伸部分的约束作用达到最大；试件所受外荷载超过全截面塑性承载力Np时，钢骨翼缘外伸部分进入塑性，弯曲变形迅速增大，因而不能再对混凝土的横向膨胀变形起到足够的抑制作用。因此，钢骨对混凝土的约束作用开始逐渐减弱，混凝土的轴向强度也逐渐降低。
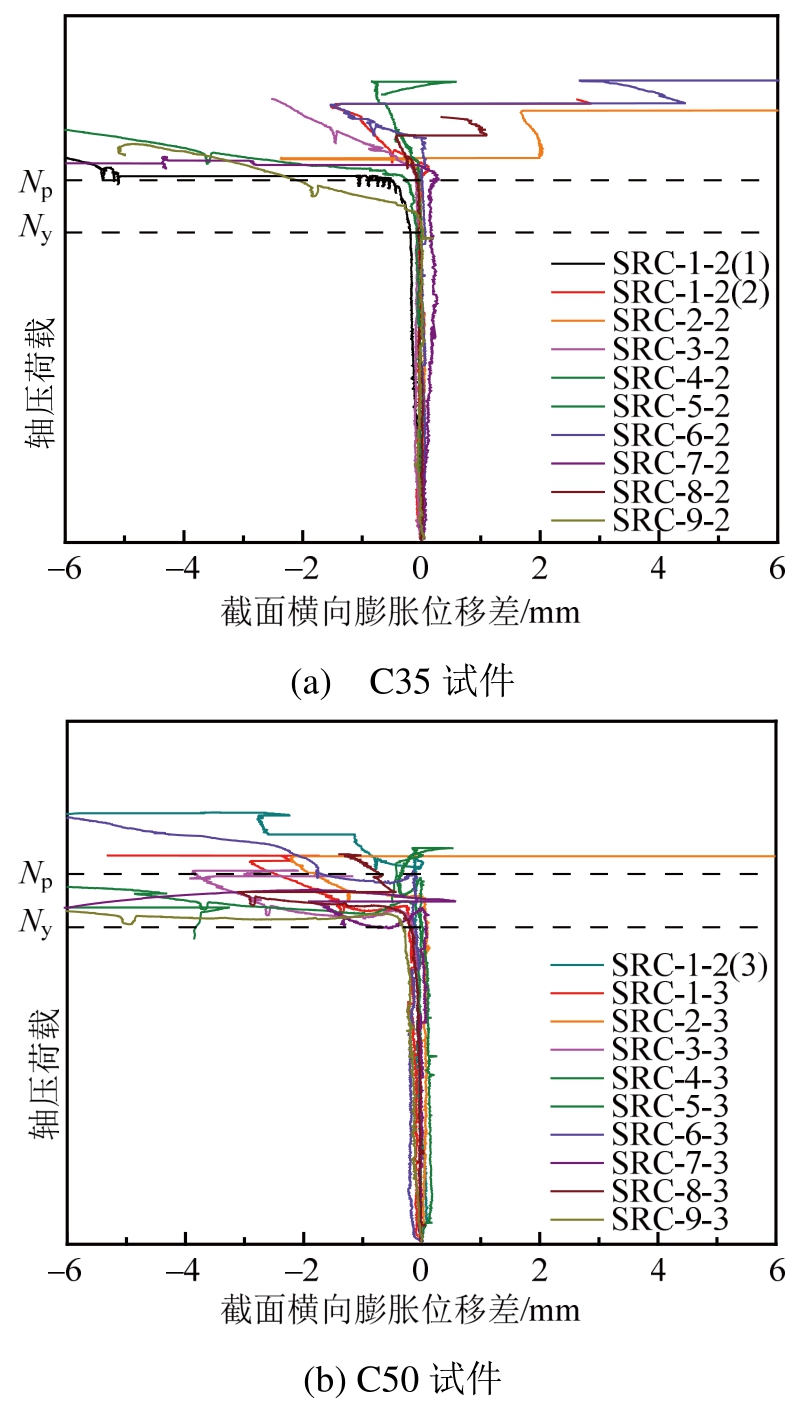
图4 荷载-截面膨胀位移差曲线[11]
Fig.4 Force-section dilation displacement curves
综上可知，带翼缘十字形钢骨是依靠钢骨翼缘外伸部分的平面外弯曲变形而抑制混凝土的横向膨胀，对混凝土产生侧向约束作用，提高了混凝土的强度[11，14]。
以往的SRC构件受力性能研究中，高约束混凝土(钢骨和钢筋共同约束混凝土)的应力-应变模型一般都是在经典的Park模型[15－16]或Mander模型[12]等钢筋约束混凝土应力-应变模型的基础上通过修正模型参数建立的。例如，Mirza[17]进行细长钢骨混凝土组合构件强度分析时，高约束混凝土采用Park模型，并考虑到高约束混凝土受钢骨和钢筋的共同约束作用，从而假定高约束混凝土达到峰值强度后强度不再下降。伍佩等[18]采用有限元方法模拟内置十字型钢骨混凝土圆柱轴压试验时，高约束混凝土采用Kent-Park模型，并增大了混凝土下降段的刚度。El-Tawil等[19]和Chen等[20]对SRC柱受力性能进行理论研究时，高约束混凝土均采用了Mander应力-应变模型。El-Tawil讨论了H型钢约束混凝土作用机理，认为高约束混凝土所受约束作用是钢筋和H型钢骨约束作用的线性迭加；Chen定义了高约束混凝土的强度提高系数，并通过试验结果进行了校正。可见，除文献[19]外，以上学者所建立的高约束混凝土应力-应变模型均缺乏钢骨约束混凝土作用的机理解释；文献[19]也仅是提供了H型钢约束混凝土作用机理的理论依据。因此，针对于带翼缘十字形钢骨截面形式，有待提出一种从受力机理角度出发的钢骨约束混凝土应力-应变模型的建立方法。
Mander模型以钢筋对混凝土产生的有效侧向约束应力
为出发点，通过大量试验数据回归分析得到有效侧向约束应力与混凝土强度提高系数之间的函数关系，进而建立钢筋约束混凝土应力-应变模型。本文延续Mander模型的建立思路，将钢骨约束混凝土划分为不同约束区域，然后计算不同约束区域钢骨对混凝土产生的有效侧向应力，进而计算不同约束区域混凝土的强度提高系数k，最终分别建立各约束区域混凝土的应力-应变关系曲线。
带翼缘十字形钢骨混凝土柱截面双轴对称，可选取其四分之一截面(即区域Z1)进行讨论(图5)。
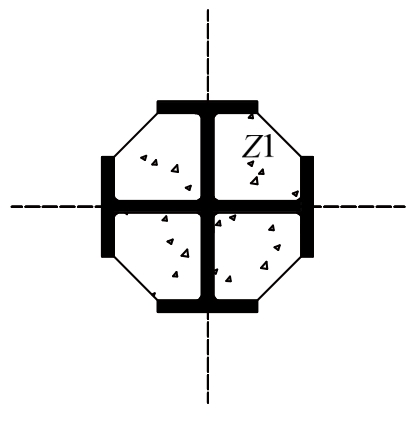
图5 钢骨混凝土芯柱截面示意图[11]
Fig.5 Cross section of SRC core column
由平衡条件及有限元分析结果可知，区域Z1混凝土受到钢骨有效侧向约束应力的实际分布如图6(a)阴影部分所示。由于x、y两个方向相邻钢骨翼缘外伸部分并不相交，钢骨不会对区域Z1混凝土产生环向连续等大的侧向约束作用。此外，钢骨翼缘产生的实际侧向约束应力主要分布在与之相邻的腹板一侧；钢骨腹板产生的实际侧向约束应力主要分布在钢骨腹板相交处。因此，区域Z1混凝土各处受钢骨约束状态差异较大，不能将该区域混凝土看作受到钢骨均匀约束作用。虽然如此，但可以通过适当简化钢骨产生的侧向约束应力的分布形式，直接反映该区域混凝土受钢骨的约束作用特征。
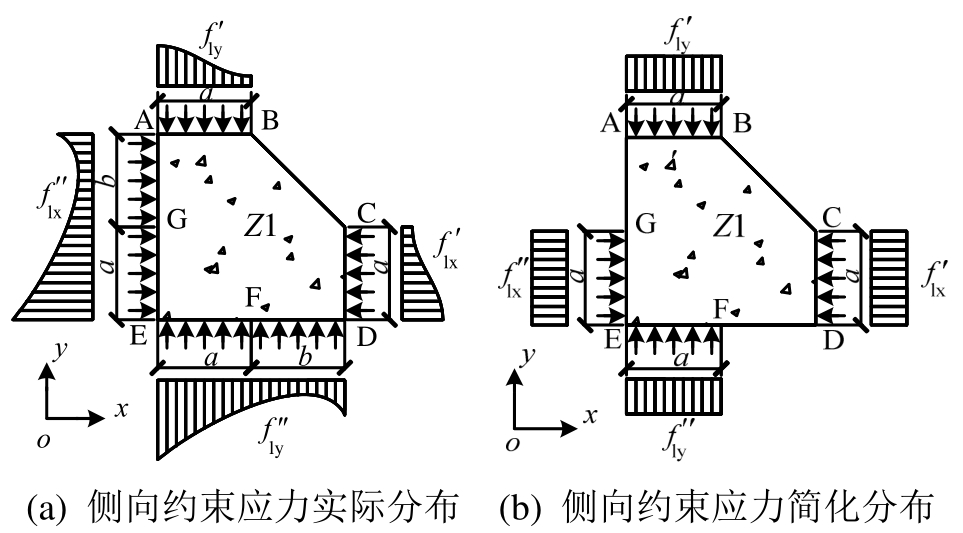
图6 侧向约束应力分布
Fig.6 Distribution of lateral confining stress
El-Tawil[19]在探究H型钢约束混凝土的约束机理时，认为混凝土仅受一个方向钢骨的侧向约束作用，并将钢骨侧向约束应力的分布形式简化为矩形分布，如图7中阴影部分所示。此外，由图6(a)可知，钢骨腹板AG与FD一侧产生的实际侧向约束应力较钢骨腹板GE和DC一侧相对较小。因此，为明确区域Z1混凝土受钢骨的约束作用特征，借鉴El-Tawil提出的H型钢产生的侧向约束应力的简化分布形式，并忽略钢骨腹板AG与FD一侧产生的侧向约束应力，将区域Z1混凝土的侧向约束应力分布进行简化，如图6(b)所示。图中，
和
分别表示钢骨翼缘外伸部分在x方向和y方向产生的侧向约束应力；和分别表示钢骨腹板在x方向和y方向产生的侧向约束应力，侧向约束应力值的求解方法见2.3节。
图7 侧向约束应力分布
Fig.7 Distribution of lateral confining stress
由前述可知，区域Z1各处混凝土受钢骨约束的应力状态不同，为进一步明确带翼缘十字形钢骨对混凝土产生的约束效应，这里将区域Z1混凝土按照钢骨侧向约束应力的简化分布形式(图6(b))划分为三类约束区共4个区域，如图8所示。
区域I混凝土为钢骨强约束混凝土，可看作受到双向钢骨的侧向约束作用(图9(a))；区域II和区域III混凝土为钢骨弱约束混凝土，可看作仅受到单向钢骨的侧向约束作用(图9(b)、图9(c))；区域IV混凝土为钢骨无约束混凝土，可看作不受到钢骨的侧向约束作用(图9(d))。
El-Tawil[19]认为，在计算钢骨对混凝土产生的有效侧向约束应力时，可将钢骨翼缘外伸部分看作是悬臂梁，并将有效侧向约束应力分布形式简化为矩形分布，即有效侧向约束应力在钢骨翼缘外伸部分各处等大。当SRC柱达到极限强度时，认为翼缘外伸部分根部截面边缘处的应力达到屈服强度(图10)，翼缘的内力抵抗矩与翼缘所受混凝土挤压的侧向外力矩相平衡，同时考虑钢骨有效约束系数
后的内力平衡表达式如式(1)所示，有效约束应力的表达式如式(2)所示。
图8 约束区域划分方式
Fig.8 Regions for sections of concrete confined by steel
图9 各约束区域混凝土简化约束状态
Fig.9 Simplified stress state of each confined concrete region
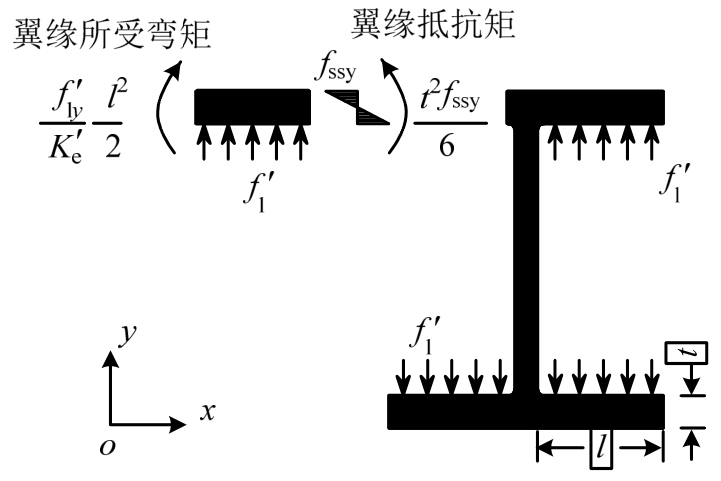
图10 H型钢约束混凝土作用机理[19]
Fig.10 Mechanism of H-shaped steel confined concrete
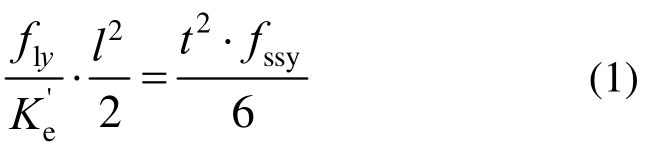
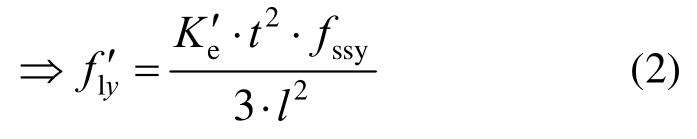
式中：t为钢骨外伸翼缘厚度；l为钢骨翼缘外伸部分的长度；fssy表示钢骨翼缘屈服强度；为有效约束系数，其表达式如下：
定义钢骨有效约束混凝土区域时，Mirza和Skrabek[17]认为，H型钢翼缘外伸部分对混凝土产生的侧向约束应力在试件横截面内以抛物线形式扩散，抛物线在型钢翼缘自由端处的切线倾角为45°(图11)。
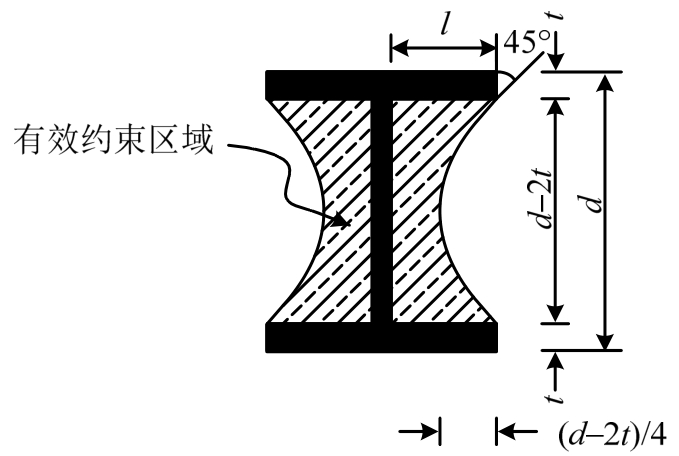
图11 H型钢混凝土有效约束区域[17]
Fig.11 Region for H-shaped steel effectively confined concrete
此外，在定义方钢管有效约束混凝土区域时，蔡健[21]认为应考虑钢管管壁各处的侧向变形能力。由于截面中部的钢管壁抗侧刚度较小，因而对混凝土约束作用较小。进而假定钢骨无效约束混凝土区域的形状是起角为45°的抛物线(图12)。
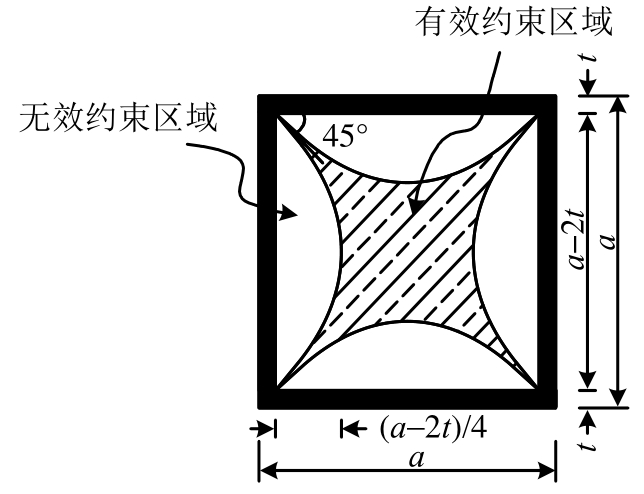
图12 方钢管混凝土有效约束区域[21]
Fig.12 Region for square steel tube effectively confined concrete
因此，本文定义H形钢骨有效约束混凝土区域时，在文献[17]提出的有效约束应力分布趋势呈抛物线的基础上，还应借鉴文献[19]的有效约束区域划分方法，即考虑钢骨翼缘各处抗侧刚度不同对钢骨约束混凝土作用的影响，假定钢骨翼缘无效约束混凝土区域的形状是终角为45°的抛物线(图13)。
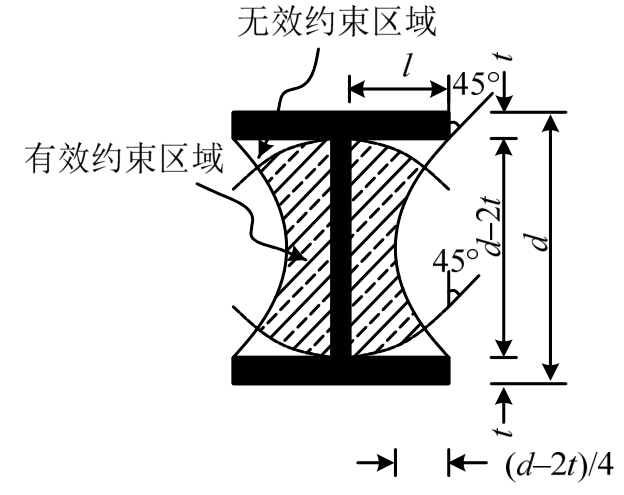
图13 混凝土有效约束区域
Fig.13 Region for effectively confined concrete
类同于H型钢依靠钢骨翼缘外伸部分发生平面外弯曲变形对核心混凝土产生侧向约束作用[18]，带翼缘十字形钢骨对核心混凝土的侧向约束作用如图14所示，且其翼缘外伸部分对核心混凝土产生的有效侧向约束应力可由式(2)表达。但是计算有效侧向约束应力时，需按照约束区域划分方式分别计算不同约束区域的有效约束系数，然后代入式(2)，从而确定不同约束区域钢骨产生的有效侧向约束应力。
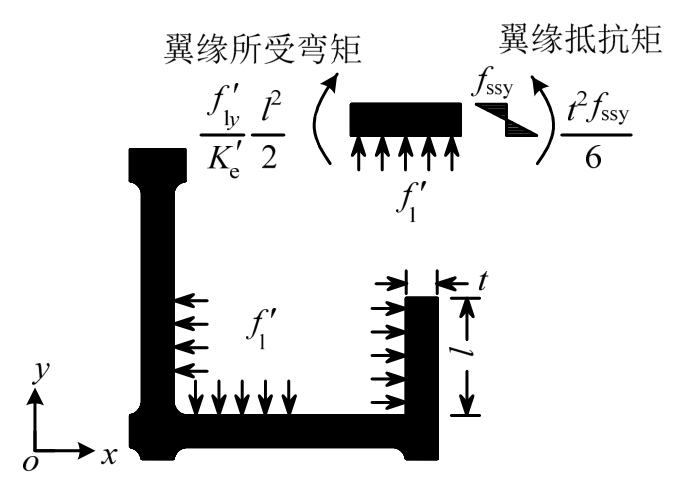
图14 带翼缘十字型钢骨约束混凝土作用机理
Fig.14 Mechanism of concrete confined by cross-shaped steel with flanges
2.3.1 钢骨强约束混凝土有效约束系数
钢骨强约束混凝土简化约束状态示意图如图15所示(黑色区域表示等效钢骨约束)。GE边与EF边对应钢骨腹板传来的等效钢骨约束；GO边与OF边对应钢骨翼缘外伸部分传来的等效钢骨约束。
钢骨腹板位于截面对称轴上，所以不会发生弯曲变形，然而钢骨翼缘外伸部分会因抑制混凝土受压后的横向膨胀而发生弯曲变形。因此，依据图13表示的混凝土有效约束区域划分方法，钢骨强约束混凝土有效约束区域划分示意图如图16所示。此外，按照式(3)可计算得到钢骨强约束混凝土有效约束系数，其表达式参见式(4)。
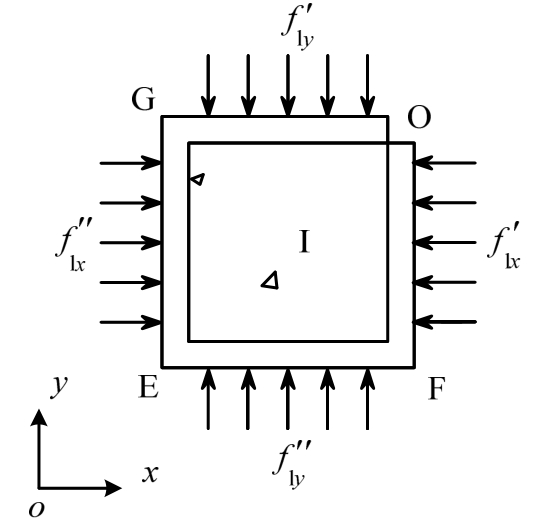
图15 钢骨强约束混凝土简化约束状态
Fig.15 Simplified stress state of strong steel confined concrete
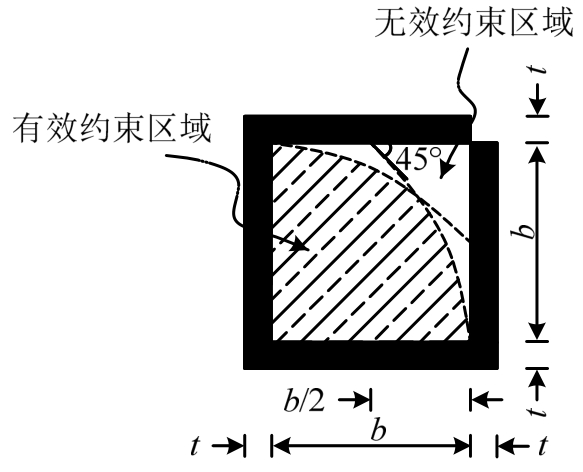
图16 钢骨强约束混凝土有效约束区域
Fig.16 Effectively confined region for strong steel confined concrete
2.3.2 钢骨弱约束混凝土有效约束系数
钢骨弱约束混凝土简化的约束状态示意图如图17所示(黑色区域表示等效钢骨约束)。AB边对应钢骨翼缘外伸部分传来的等效钢骨约束；AG边对应钢骨腹板传来的等效钢骨约束；GO边对应钢骨强约束混凝土传来的约束。
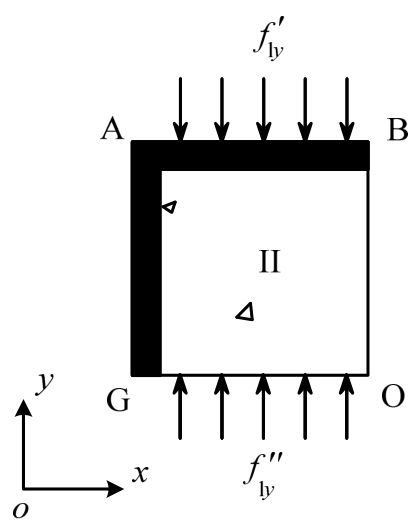
图17 钢骨弱约束混凝土简化约束状态
Fig.17 Simplified stress state of weak steel confined concrete
由图17可知，钢骨弱约束混凝土仅受单向钢骨约束作用，当AB边与GO边对该区域混凝土产生约束作用后，AB边会发生平面外的弯曲变形，而GO边由于周边存在其他区域混凝土抑制其变形，因此可认为GO边不发生弯曲变形。参考图13表示的有效约束区域划分方法，钢骨弱约束混凝土有效约束区域划分示意图如图18所示。钢骨弱约束混凝土的有效约束系数表达式如式(3)所示。
图18 钢骨弱约束混凝土有效约束区域
Fig.18 Effectively confined region for weak steel confined concrete
2.3.3 钢骨无约束混凝土有效约束系数
钢骨无约束混凝土不受钢骨的侧向约束作用，因此，钢骨无约束混凝土的有效约束系数=0。
约束混凝土强度提高系数k表征了由于受到钢筋或钢骨的侧向约束作用混凝土强度提高的程度。Mander[12]在建立约束混凝土应力-应变模型时，给出了表述约束混凝土受到两个水平方向的有效侧向约束应力fl1和fl2
与强度提高系数k之间关系的三轴图(图19)。
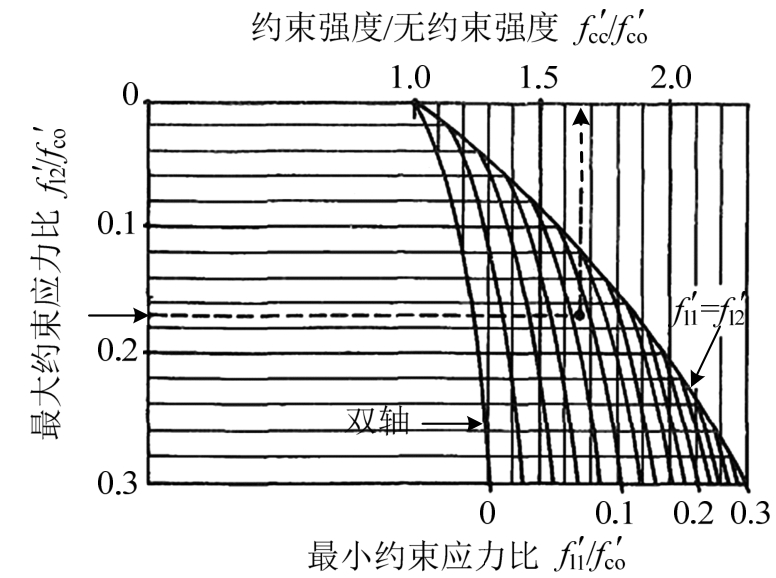
图19 侧向约束应力与强度提高系数关系[11]
Fig.19 Relationships between lateral confining stress and coefficient of strength enhancement
基于图19，EI-Tawil[19]给出了对应的数学函数关系表达式。约束混凝土强度提高系数k的上限解kh和下限解kl分别对应以下两种情况[19]：
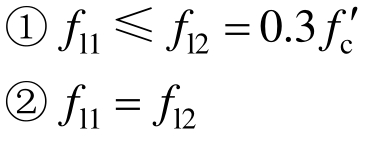
对于情况①，强度提高系数上限解kh表达式如下：
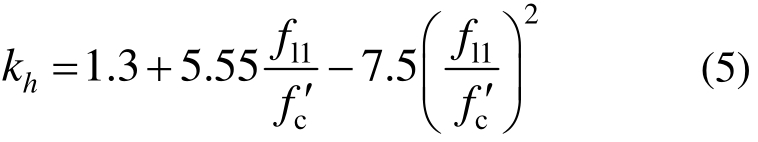
对于情况②，强度提高系数下限解kl表达式如下：
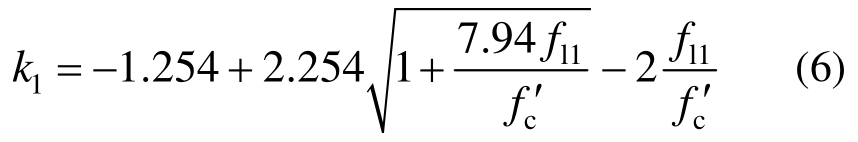
最后同时考虑强度提高系数上限解kh与下限解kl从而确定强度提高系数k，表达式如下：
对于受不同截面形式钢骨约束的混凝土，可从本文给出的钢骨约束混凝土的约束机制出发，确定可对混凝土产生约束作用的钢骨翼缘外伸部分，进而按照本文分析方法，划分不同钢骨约束混凝土区域，并基于Mander模型分别建立各钢骨约束区域混凝土的应力-应变关系曲线，具体步骤如下：
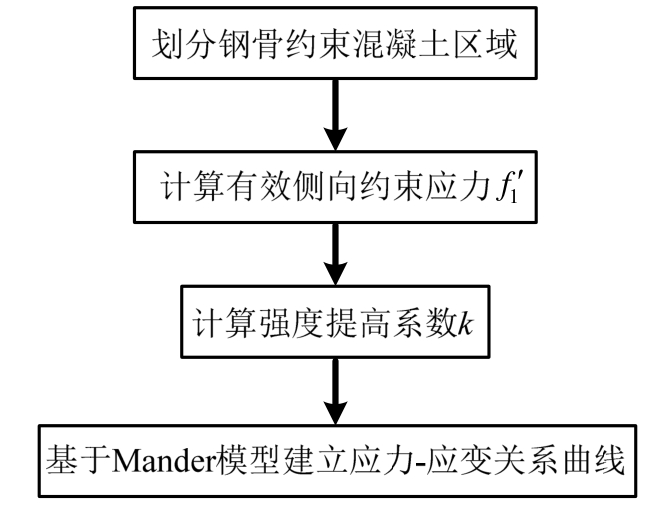
首先，按照钢骨约束混凝土的简化约束状态，将钢骨约束混凝土划分为钢骨强约束混凝土、钢骨弱约束混凝土和钢骨无约束混凝土(图20)。
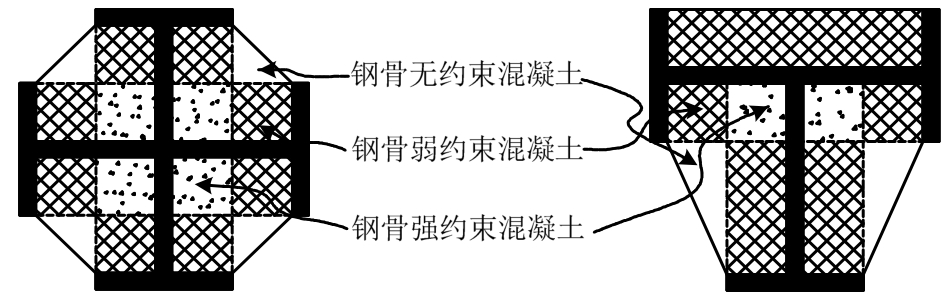
图20 不同截面形式的SRC芯柱截面区域划分
Fig.20 Regions for SRC core columns with different kinds of steel sections
然后，分别计算各钢骨约束区域的有效侧向约束应力，其统一表达式如下：
式中：为有效约束系数；f1为侧向约束应力。以带翼缘十字形钢骨约束混凝土芯柱为例，结合本文2.3节分析可知，钢骨强约束混凝土受到两个方向等大的钢骨侧向约束作用，即
钢骨弱约束混凝土仅受到一个方向的钢骨侧向约束作用，即
；钢骨无约束混凝土不受到钢骨侧向约束作用，即fl1=fl2=0。进而，可由式(5)、式(6)和式(7)计算各钢骨约束区域混凝土的强度提高系数。
最后，基于Mander模型，通过修正混凝土强度提高系数k，建立各钢骨约束区域混凝土的应力-应变关系曲线，如图21所示。图中，kw和kf分别表示钢骨强约束混凝土和钢骨弱约束混凝土的强度提高系数；εcw和εcf分别表示钢骨强约束混凝土和钢骨弱约束混凝土的峰值应变。由于钢骨翼缘外伸部分可对混凝土产生持续的约束作用，提高了混凝土的强度和延性。因此，假定钢骨强约束混凝土的极限压应变εcwu取为混凝土强度退化至0.7kw
时对应的应变；钢骨弱约束混凝土的极限压应变εcfu取为混凝土强度退化至0.5kf时对应的应变(图21)。
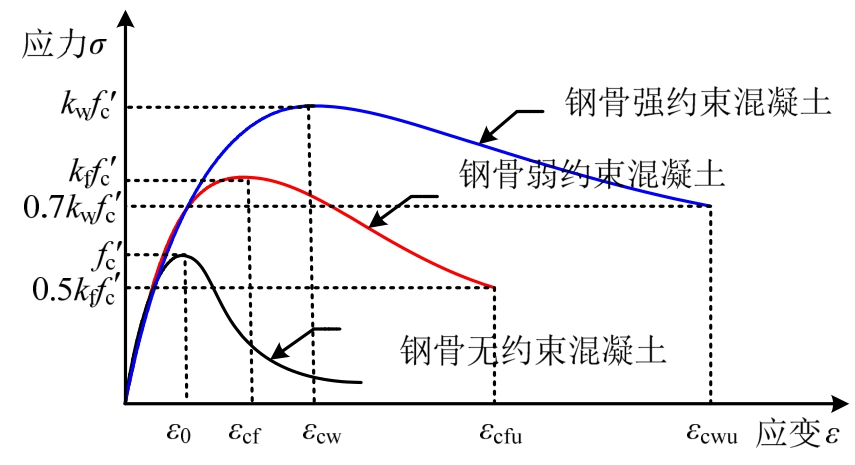
图21 各区域约束混凝土理论应力-应变曲线
Fig.21 Theoretical stress-strain curves of each steel confined concrete region
各钢骨约束区域混凝土统一的应力-应变模型表达式如下：
式中：
、εc分别表示无约束混凝土圆柱体抗压强度和对应峰值应变；
、εcc分别为钢骨约束混凝土抗压强度和对应峰值应变；k表示混凝土强度提高系数。
采用前述建立的钢骨约束混凝土应力-应变模型，对文献[11]完成的20个带翼缘十字形钢骨混凝土柱芯柱的轴压试验进行有限元模拟，从而验证本文提出的带翼缘十字形钢骨约束混凝土的约束作用机理以及钢骨约束混凝土应力-应变模型建立方法的准确性。
3.1.1 混凝土材料应力-应变关系
有限元分析模型中混凝土材料模型选用ABAQUS自带的混凝土塑性损伤模型，相关参数设置见表1。钢骨约束混凝土应力-应变模型选用本文建立的应力-应变曲线，圆柱体混凝土强度材性数据参见文献[11]。混凝土的弹性模量取为Ec=
泊松比取为0.2。
表1 混凝土参数设置
Table1 Parameter settings of concrete
3.1.2 钢材材料应力-应变关系
钢材材料选用材性试验得到的真实应力-应变关系曲线，钢材的屈服强度和抗拉强度参见文献[11]。钢材弹性模量取Es=206 GPa，泊松比取为0.3。
3.1.3 单元选择及网格划分
有限元分析对象均按照文献[11]试验试件的实际尺寸建立，钢骨、混凝土部分均采用C3D8R单元。钢骨混凝土柱截面材料定义时分为5部分，即钢骨翼缘、钢骨腹板、钢骨强约束混凝土、钢骨弱约束混凝土和钢骨无约束混凝土，如图22所示。有限元模型的单元尺寸均为20mm，单元尺寸与试件实际高度之比为1∶60。
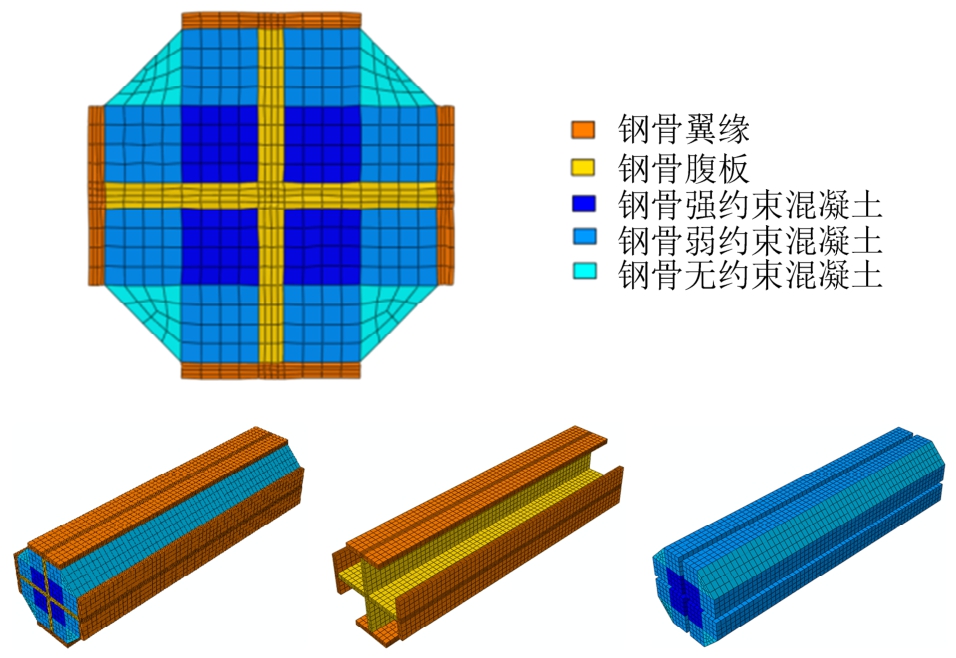
图22 有限元分析模型
Fig.22 Finite element model
3.1.4 界面处理和边界条件
试件制作过程中，钢骨腹板与翼缘内侧并未布置栓钉，因此需要进行钢骨与混凝土之间接触的定义，接触面法线方向为硬接触，切线方向的摩擦系数取为0.25[23]。
有限元模型的边界条件与试件实际加载边界条件一致，顶端固接，由底端向顶端施加轴向竖向荷载。
3.1.5 初始几何缺陷
试验构件在制作和安装过程中存在偏差，因此建立有限元分析模型时需引入初始几何缺陷，初始几何缺陷取为l/1000[24](l为芯柱长度)。
选取代表性试件SRC-1-2(1)的有限元分析结果进行说明。当轴压荷载达到全截面塑性承载力时(图23中蓝色圆圈处)，芯柱截面中钢骨水平方向的位移云图和应力云图如图24、图25所示。
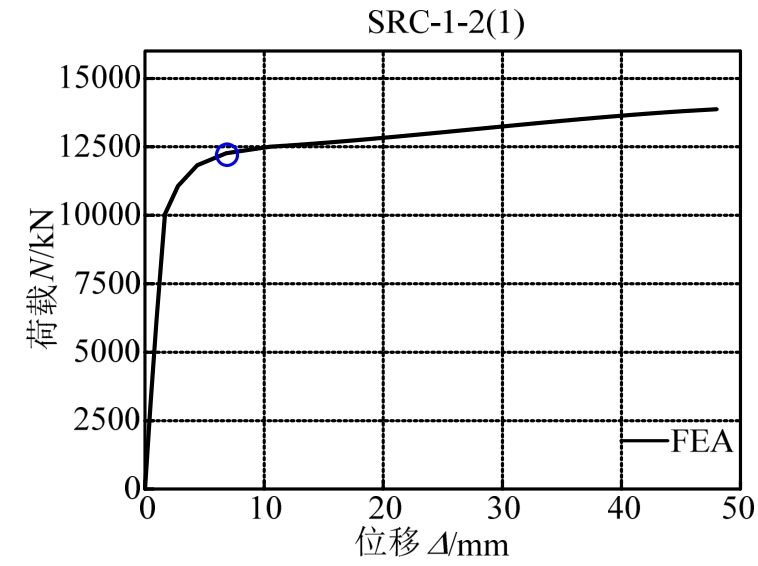
图23 试件SRC-1-2(1)荷载-位移曲线
Fig.23 Force-deformation curve for SRC-1-2(1)
由图24可知，钢骨翼缘外伸部分在U1方向或U2方向的位移值明显大于与之相交的钢骨腹板的位移值。此外，从翼缘与腹板连接处到翼缘自由端，钢骨翼缘外伸部分平面外的水平位移逐渐增大。由上可知，钢骨翼缘外伸部分发生了明显的平面外弯曲变形。究其变形本质，是因为钢骨翼缘抑制了混凝土轴向受压后产生的横向膨胀变形。
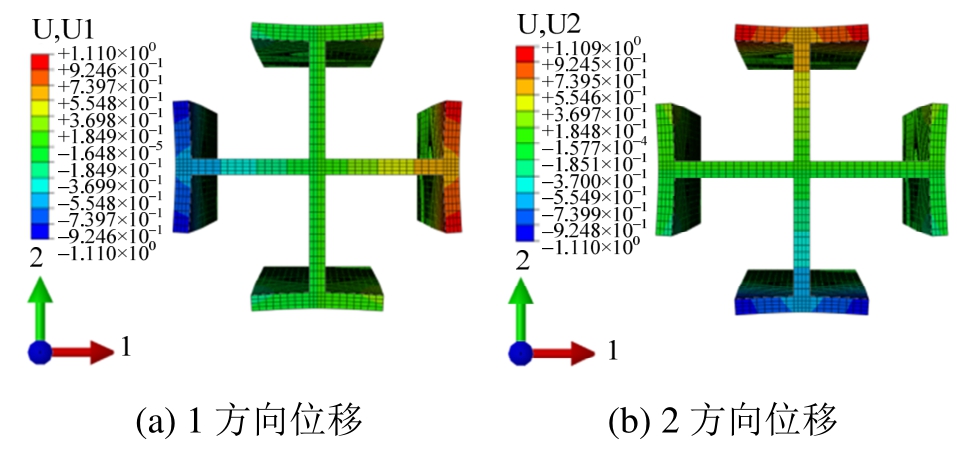
图24 钢骨水平位移云图
Fig.24 Lateral displacement of steel
由图25可知，在钢骨翼缘的切线方向，由翼缘边缘至翼缘中性轴，翼缘外伸部分的根部截面(图中蓝色箭头所指位置)的水平应力值逐渐降低。此外有限元分析得到的根部截面的水平应力分布形式与钢骨翼缘外伸部分发生弯曲变形后同位置处的应力理论分布形式一致(图25)。
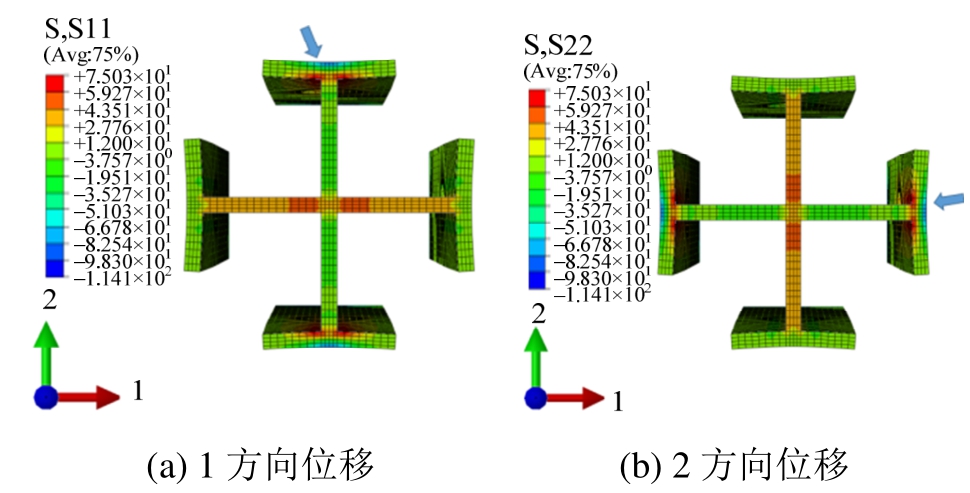
图25 Mises应力云图
Fig.25 Mises stress of steel
由上述有限元分析结果可知，本文提出的带翼缘十字形钢骨约束混凝土的约束机制是合理的。
3.3.1 试件变形特征
所有试件采用有限元分析得到的变形特征和破坏形态与试验结果基本一致，这里仅列出代表性试件SRC-9-3的对比结果，如图26所示。由此可知，有限元分析得到的破坏形态与试验结果吻合良好。
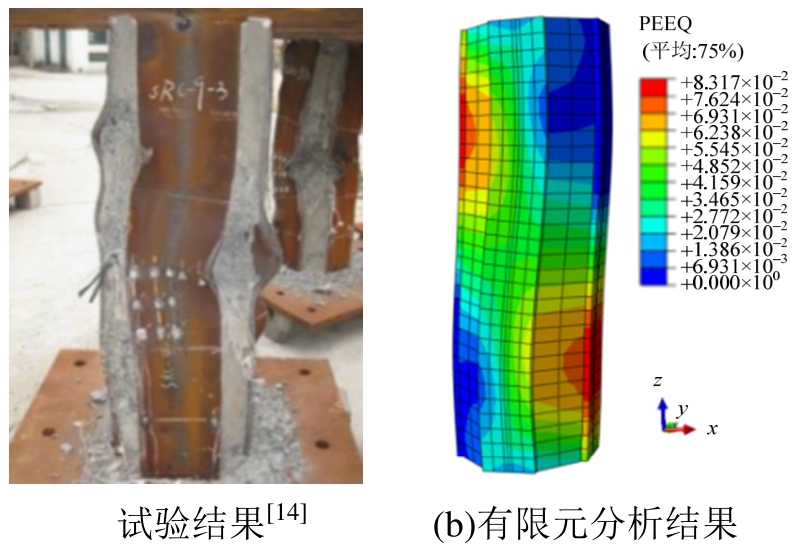
图26 试件SRC-9-3试验变形与有限元分析对比
Fig.26 Comparison of deformation between test and FEA for SRC-9-3
3.3.2 混凝土轴向应力分布
所有试件采用有限元分析得到的半高截面处混凝土的轴向应力(S33)云图分布形式均相类似，这里仅列出代表性试件SRC1-2(1)轴压荷载达到全截面塑性承载力时的轴向应力云图进行说明，如图27所示。轴向压应力整体呈现从试件中心至边缘逐渐降低的趋势。结合本文2.2节钢骨约束区域的划分方式可知，不同钢骨约束区域混凝土的轴向应力不同，即混凝土受到钢骨的约束作用程度不同。钢骨强约束区域约束作用最强，钢骨弱约束区域次之，钢骨无约束区域不存在约束作用。
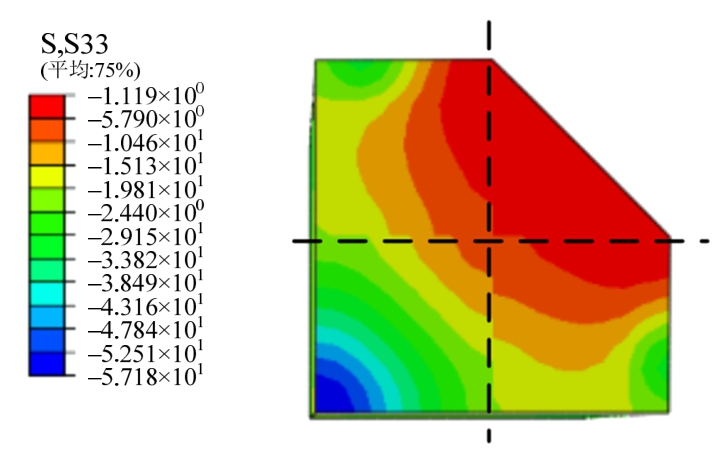
图27 钢骨约束混凝土轴向应力云图
Fig.27 Mises stress of steel confined concrete
此外，各钢骨约束区域混凝土有效约束区域的划分与混凝土的轴向应力分布也吻合良好。由此判定，本文给出的有效约束系数计算方法是合理的。
3.3.3 荷载-位移曲线
图28给出了试验与有限元分析得到的轴压荷载-轴向位移曲线的对比结果，试件编号与文献[10]对应，图中N和Δ分别表示试件的轴压荷载和轴向位移；fsyf、fsyw和f分别表示相应构件的钢骨翼缘屈服强度、钢骨腹板屈服强度和无约束混凝土圆柱体抗压强度。
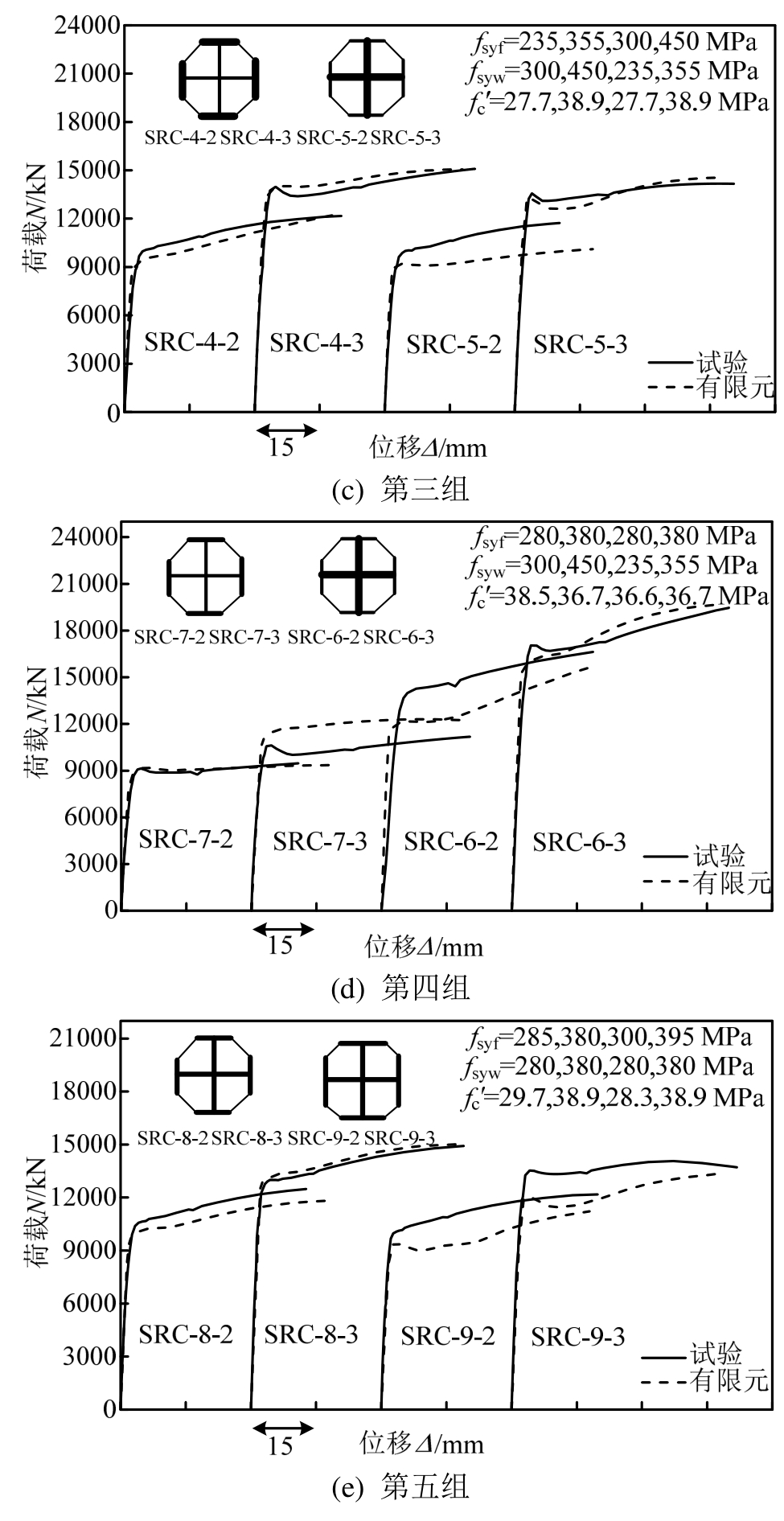
图28 试验与有限元荷载-位移曲线对比
Fig.28 Comparison of force-deformation curves between tests and FEA
由图可知，在构件的初始刚度、全截面塑性承载力以及承载性能强化段等方面，有限元分析结果与试验结果均吻合良好。
综上可见，采用本文推荐的钢骨约束混凝土应力-应变模型对带翼缘十字形钢骨混凝土芯柱试件进行有限元分析时，能更好的模拟试件的真实受力性态和变形性态。
本文基于钢骨约束混凝土的约束机制，借鉴Mander模型，以计算得到有效侧向约束应力为出发点，提出了适用于带翼缘十字形钢骨约束混凝土应力-应变模型的建立方法，并通过ABAQUS软件对已有的SRC芯柱轴压试验进行了模拟与验证。结论如下：
(1)带翼缘十字形钢骨依靠钢骨翼缘外伸部分平面外的弯曲变形对混凝土产生侧向约束作用，从而提高了混凝土的强度和延性。
(2)根据简化约束应力状态的不同，将钢骨约束混凝土划分为钢骨强约束混凝土、钢骨弱约束混凝土和钢骨无约束混凝土等三类钢骨约束区域混凝土，并可定量的表示各约束区域混凝土受钢骨约束作用的强弱。
(3)基于Mander模型，根据约束区域的划分，提出了带翼缘十字形钢骨约束混凝土应力-应变模型的建立方法。并通过有限元与试验结果的对比分析，验证了上述应力-应变模型建立方法的有效性。
参考文献：
[1]赵鸿铁.钢与混凝土组合结构[M].北京:科学出版社，2001.Zhao Hongtie.Composite structures of steel and concrete[M].Beijing:Science Press，2001.(in Chinese)
[2]叶列平，方鄂华.钢骨混凝土柱的轴压力限值[J].建筑结构学报，1997，18(5):43―50.Ye Lieping，Fang Ehua.Axial load limit for steel reinforced concrete columns[J].Journal of Building Structures，1997，18(5):43―50.(in Chinese)
[3]叶列平，方鄂华.钢骨混凝土构件的受力性能研究综述[J].土木工程学报，2000，33(5):1―12.Ye Lieping，Fang Ehua.State of the art of study on the behaviors of steel reinforced concrete structure[J].China Civil Engineering Journal，2000，33(5):1―12.(in Chinese)
[4]胡敬礼，陈以一，赵宪忠，等.高含钢率SRC 柱轴压承载性能研究[J].建筑结构学报，2008，29(3):24―30.Hu Jingli，Chen Yiyi，Zhao Xianzhong，et al.Ye Lieping，Fang Ehua.Study on loading capacity of high steel ratio SRC columns under axial compression[J].Journal of Building Structures，2008，29(3):24―30.(in Chinese)
[5]陈以一，王海生，赵宪忠，等.高含钢率SRC 压弯柱滞回性能试验研究[J].建筑结构学报，2008，29(3):31―39.Chen Yiyi，Wang Haisheng，Zhao Xianzhong，et al.Experimental study on hysteretic behavior of SRC columns with high ratio of core steel[J].Journal of Building Structures，2008，29(3):31―39.(in Chinese)
[6]王海生.高含钢率钢骨混凝土柱滞回性能研究[D].上海:同济大学，2008.Wang Haisheng.Research on hysteretic behavior of steel reinforced concrete columns with high ratio of core steel[D].Shanghai:Tongji University，2008.(in Chinese)
[7]殷小溦，吕西林，卢文胜.配置十字型钢的型钢混凝土柱恢复力模型[J].工程力学，2014，31(1):97―103.Yin Xiaowei，Lu Xilin，Lu Wensheng.Resilience model of SRC columns with corss-shaped encase steel[J].Engineering Mechanics，2014，31(1):97―103.(in Chinese)
[8]秦浩，赵宪忠.高含钢率钢骨混凝土柱的滞回数值分析[J].结构工程师，2014，30(4):25―31.Qin Hao，Zhao Xianzhong.Numerical analysis of composite columns with high steel ratio under cyclic loading[J].Structural Engineers，2014，30(4):25―31.(in Chinese)
[9]赵宪忠，杨笑天，陈以一.钢骨截面延展性对高含钢率SRC柱静力性能的影响研究[J].土木工程学报，2016，49(1):31―41.Zhao Xianzhong，Yang Xiaotian，Chen Yiyi.Effect of shape distribution of encased steel section on static performance of steel reinforced concrete columns with high steel ratio[J].China Civil Engineering Journal，2016，49(1):31―41.(in Chinese)
[10]赵宪忠，杨笑天，陈以一.钢骨截面延展性对高含钢率SRC柱滞回性能的影响研究[J].土木工程学报，2016，49(3):80―90.Zhao Xianzhong，Yang Xiaotian，Chen Yiyi.Effect of shape distribution of encased steel section on hysteretic performance of steel reinforced concrete columns with high steel ratio[J].China Civil Engineering Journal，2016，49(3):80―90.(in Chinese)
[11]赵宪忠，秦浩，陈以一.十字形截面钢骨约束混凝土本构模型试验研究[J].建筑结构学报，2014，35(4):268―279.Zhao Xianzhong，Qin Hao，Chen Yiyi.Experimental and constitutive model study of steel confined concrete in SRC columns with cruciform steel section[J].China Civil Engineering Journal，2014，35(4):268―279.(in Chinese)
[12]Mander J B，Priestley M J N，Park R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering，1988，114(8):1804―1826.
[13]Schneider S P.Axially loaded concrete-filled steel tubes[J].Journal of Structural Engineering，1998，124(10):1125―1138.
[14]秦浩.高含钢率钢骨混凝土柱力学性能及恢复力模型研究[D].上海:同济大学，2013.Qin Hao.Performance and hysteretic model of SRC columns with high encased steel ratio[D].Shanghai:Tongji University，2013.(in Chinese)
[15]Park R，Priestley M J N，Gill W D.Ductility of square-confined concrete columns[J].Journal of the Structural Division，1982，108(4):929―950.
[16]Kent D C，Park R.Flexural members with confined concrete[J].Journal of the Structural Division，1971，97(7):1969―1990.
[17]Mirza S A，Skrabek B W.Statistical analysis of slender composite beam-column strength[J].Journal of Structural Engineering，1992，118(5):1312―1332.
[18]Chen S W，Wu P，Liu Q，et al.Studies on axially compressed SRC column using Q460high-strength steel[C]// Proceedings of the 8th International Conference on Behavior of Steel Structures in Seismic Area.Shanghai:Science Press，2015:131―132.
[19]EI-Tawil S M，Deierlein G G.Fiber element analysis of composite beam-column cross-sections[G].New York:Cornell University，1996.
[20]Chen C C，Lin N J.Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns[J].Journal of Constructional Steel Research，2006，62(5):424―433.
[21]蔡健，孙刚.方形钢管约束下核心混凝土的本构关系[J].华南理工大学学报:自然科学版，2008，36(1):105―109.Cai Jian，Sun Gang.Constitutive relationship of concrete core confined by square steel tube[J].Journal of South China University of Technology(Natural Science Edition)，2008，36(1):105―109.(in Chinese)
[22]318 A C.Building code requirements for structural concrete(ACI 318M-11)and commentary[M].Farmington Hills，Mich:American Concrete Institute，2011.
[23]Ellobody E，Young B.Numerical simulation of concrete encased steel composite columns[J].Journal of Constructional Steel Research，2011，67(2):211―222.
[24]GB 50017—2003，钢结构设计规范[S].北京:中国计划出版社.2003.GB 50017—2003，Code for design of steel structures[S].Beijing:China Planning Press，2003.(in Chinese)
THEORETICAL STUDY ON CONFINEMENT MECHANISM AND STRESS-STRAIN MODEL FOR STEEL CONFINED CONCRETE IN SRC COLUMNS
ZHAO Xian-zhong1，2，WEN Fu-ping2
(1.State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China;2.College of Civil Engineering，Tongji University，Shanghai 200092，China)
Abstract:Results from experimental and numerical analysis on SRC columns generally do not agree well at present.The main reason may be the lack of understanding on the confinement mechanism，as well as the application of corresponding stress-strain model for steel confined concrete.In this paper，the confinement mechanism of concrete by cross-shaped steel with flanges is studied in depth based on previous experimental results on steel confined concrete.Firstly，a simplified distribution of lateral stress imposed by steel confinement to concrete is proposed，based on which steel confined concrete was divided into three regions，including strong steel confined concrete，weak steel confined concrete and steel non-confined concrete.Confinement factors reflecting the confining level of steel to concrete for each region of the confined concrete were determined by calculating the effective lateral confining pressure.Based on Mander’s model for stress-strain relationship of concrete considering the confining effect from spiral stirrup reinforcement，a unified stress-strain model for steel confined concrete is developed by modifying the key parameters of Mander’s model.It is proved by comparingthe results from experiment and numerical simulation utilizing the proposed stress-strain model that the confinement mechanism and the constitute model for steel confined concrete established in this paper are reasonable and effective.
Key words:steel confined concrete;confinement mechanism;region division;effective lateral confining pressure;stress-strain model
中图分类号：TU398.9
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.02.0109
文章编号：1000-4750(2018)05-0036-11
收稿日期：2017-02-14；修改日期：2017-07-27
基金项目：科技部国家重点实验室基金项目(SLDRCE15-B-01)
通讯作者：赵宪忠(1972―)，男，吉林桦甸人，教授，博士，主要从事钢结构研究(E-mail:x.zhao@tongji.edu.cn).
作者简介：温福平(1993―)，男，辽宁大连人，博士，主要从事组合结构研究(E-mail:fpwen2014@163.com).