表1 试件设计参数
Table1 Design parameters of specimens
刘祖强,薛建阳,韩 琛,杨青峰
(西安建筑科技大学土木工程学院,西安 710055)
摘 要:为研究实腹式型钢混凝土T形柱的抗震性能,进行了10个试件的水平加载试验,考虑了加载制度、轴压比和配钢率的影响,观察了试件的受力过程和破坏形态,分析了荷载-位移曲线、侧移角、延性、强度、刚度及耗能等力学性能。结果表明,试件均发生弯曲破坏,但不同加载制度下试件的破坏形态不同;试件的滞回曲线饱满,极限侧移角介于1/36~1/9,位移延性系数介于3.97~12.11,破坏时等效粘滞阻尼系数介于0.319~0.374,体现出良好的变形和耗能能力;随着加载循环次数的增多和轴压比的增大,试件的延性降低,强度衰减和刚度退化加快;随着配钢率的增大,试件的延性提高,强度衰减和刚度退化变缓。
关键词:型钢混凝土;异形柱;实腹式配钢;抗震性能;加载制度
型钢混凝土异形柱是指在混凝土异形(L形、T形、十形等)截面中主要配置型钢,并配有适量纵向钢筋和箍筋形成的一种新型结构柱。它不仅柱肢与填充墙等厚,柱棱在室内不凸出,房间使用面积大,便于家具布置和室内装饰,而且承载能力高、抗震性能好,能够应用于高层及高抗震烈度区的建筑[1]。根据配钢形式的不同,型钢混凝土异形柱分为空腹式和实腹式两类[2]。
T形柱为异形柱的一种,主要用于框架边柱[3-4]。目前,对于型钢混凝土T形柱受力性能的研究相对较少。徐亚丰等[5]对实腹式T形柱进行了双向小偏压试验,分析了配钢率对构件承载力的影响;李哲等[6]对空腹式T形短柱进行了低周反复加载试验,考察了剪跨比、轴压比、配箍率和配钢率的影响,提出了构件抗剪承载力计算公式;蒋丽娜[7]对空腹式T形柱进行了低周反复加载试验,分析了轴压比和配钢率对构件抗震性能的影响;薛建阳等[8]对不同配钢形式的T形柱进行了低周反复加载试验,分析了配钢形式、轴压比、剪跨比和加载角度对构件抗震性能的影响。上述研究结果表明,与空腹式相比,实腹式型钢混凝土T形柱的受力性能更为优越,在工程应用中应优先考虑,但对于该类构件的研究尚不够系统,尤其是抗震性能方面的研究。
鉴于此,本文通过10个实腹式型钢混凝土T形柱的水平加载试验,分析不同加载方式、轴压比和配钢率对构件抗震性能的影响,为该类构件的工程应用和理论分析提供依据。
以肢厚为240mm、肢高肢厚比为3的T形柱为原型,按1/2比例缩尺,共设计10个型钢混凝土T形柱试件。试件均为实腹式配钢,剪跨比为2.5,变化参数包括加载制度、轴压比和配钢率。加载制度取单调加载、变幅循环和单调混合加载、常幅循环加载和变幅循环加载;轴压比取0.2、0.4和0.6;配钢率取6.18%、7.09%和8.01%。试件编号及主要设计参数如表1所示,外形尺寸及截面配钢如图1所示。
表1 试件设计参数
Table1 Design parameters of specimens


图1 试件外形尺寸及截面配钢
Fig.1 Geometry and steel layout of specimens
钢筋均为HPB300级,纵筋采用8 10,配筋率为0.873%;箍筋沿柱全长按
10,配筋率为0.873%;箍筋沿柱全长按 6@60布置,体积配箍率为1.41%。型钢由不同厚度的Q235级钢板焊接而成(图2)。箍筋制作成U型或非封闭的矩形焊接在型钢上,并将纵筋与箍筋绑扎在一起形成钢骨架(图3)。钢筋和钢板的物理力学性能如表2所示。
6@60布置,体积配箍率为1.41%。型钢由不同厚度的Q235级钢板焊接而成(图2)。箍筋制作成U型或非封闭的矩形焊接在型钢上,并将纵筋与箍筋绑扎在一起形成钢骨架(图3)。钢筋和钢板的物理力学性能如表2所示。

图2 型钢
Fig.2 Shaped-steel

图3 钢骨架
Fig.3 Steel skeleton
表2 钢筋、钢板的力学性能
Table2 Mechanical properties of steel

混凝土采用立式分段浇筑,先浇筑下端头,然后浇筑试验段和上端头。实测混凝土的立方体抗压强度为34.5MPa。
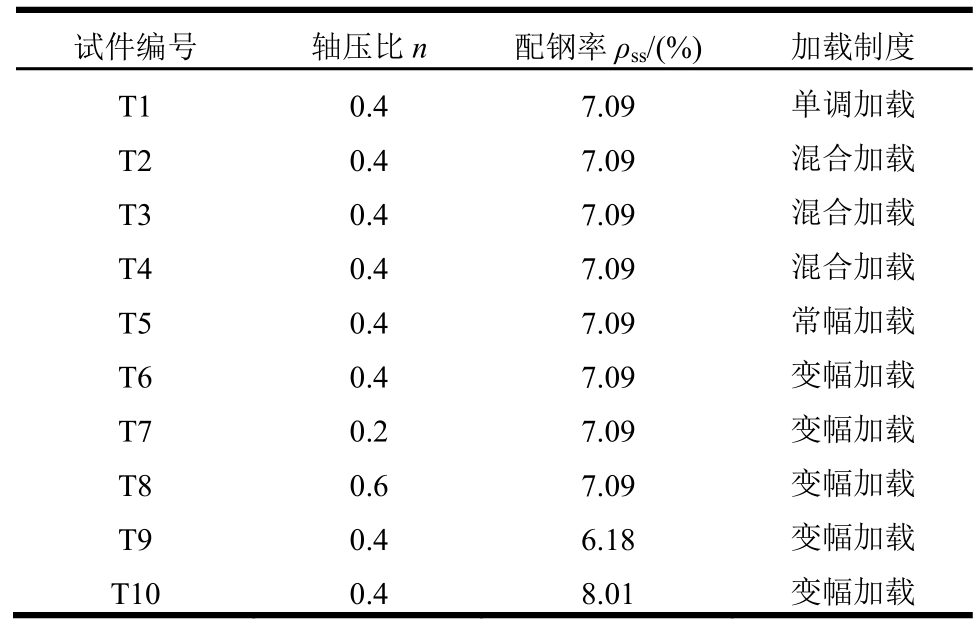
试验在西安建筑科技大学结构工程与抗震教育部重点实验室进行。首先在柱顶施加竖向荷载,并保持恒定,然后施加水平荷载。为更好地模拟异形柱的实际边界条件和真实受力状态,采用建研式的加载装置[9],如图4所示。该装置能够保证截面不对称的T形柱在推、拉两个方向的受力相同,得到的性能指标便于比较分析。

图4 加载装置
Fig.4 Test set-up
水平加载时沿异形柱腹板方向(图5),采用荷载和位移混合控制的方式,试件屈服前采用荷载控制,每级荷载增量为20kN;屈服后采用位移控制,每级位移增量为一倍的屈服位移,直至荷载下降到峰值荷载的85%时停止加载。具体加载制度为:
单调加载,如图6(a)所示,试件屈服前采用荷载控制单调递增,屈服后采用位移控制单调递增。试件T1采用该加载制度。
混合加载,如图6(b)所示,试件屈服前采用荷载控制,每级荷载循环一次;屈服后采用位移控制,每级位移循环三次,并在完成一定的循环加载级数后改为单调加载。试件T2、T3和T4采用该加载制度,分别在完成一级、两级和三级位移循环加载后进行单调加载。
常幅加载,如图6(c)所示,试件屈服前采用荷载控制单调递增;屈服后采用位移控制单调递增,当完成一定的单调加载级数后保持位移幅值不变,改用循环加载。试件T5采用该加载制度,在完成两级位移单调加载后进行循环加载。
变幅加载,如图6(d)所示,试件屈服前采用荷载控制,每级荷载循环一次;屈服后采用位移控制,每级位移循环三次。试件T6~T10采用该加载制度。
为监测应力变化,在柱上、下端的型钢和纵筋上分别布置应变片,距柱端面为30mm,具体位置如图7所示,其中S表示型钢应变片,B表示纵筋应变片。为测量试件的变形,在上端头、柱中和下端头分别布置位移计,如图5所示。
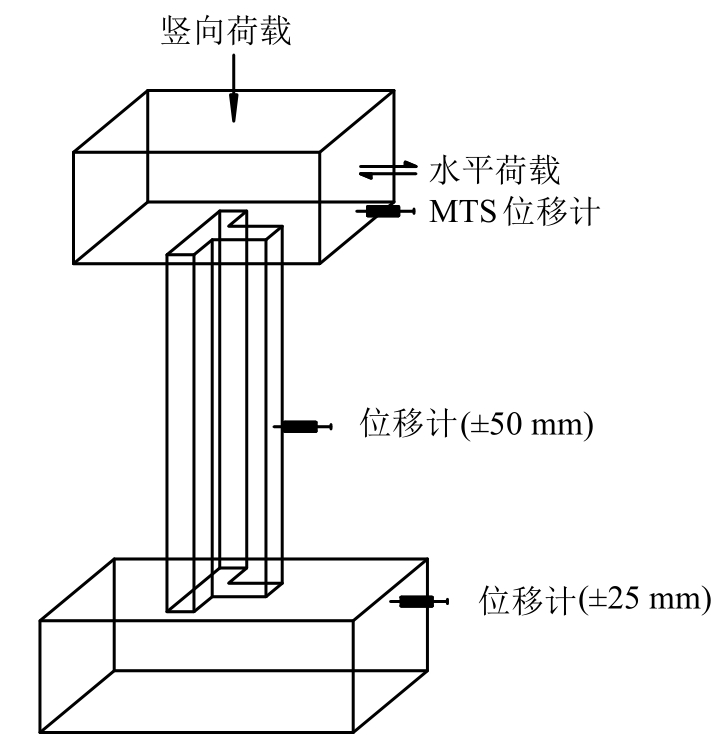
图5 加载方向示意
Fig.5 Schematics of loading direction
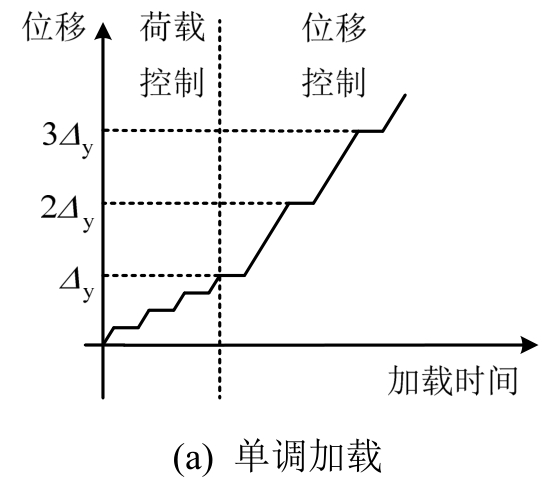
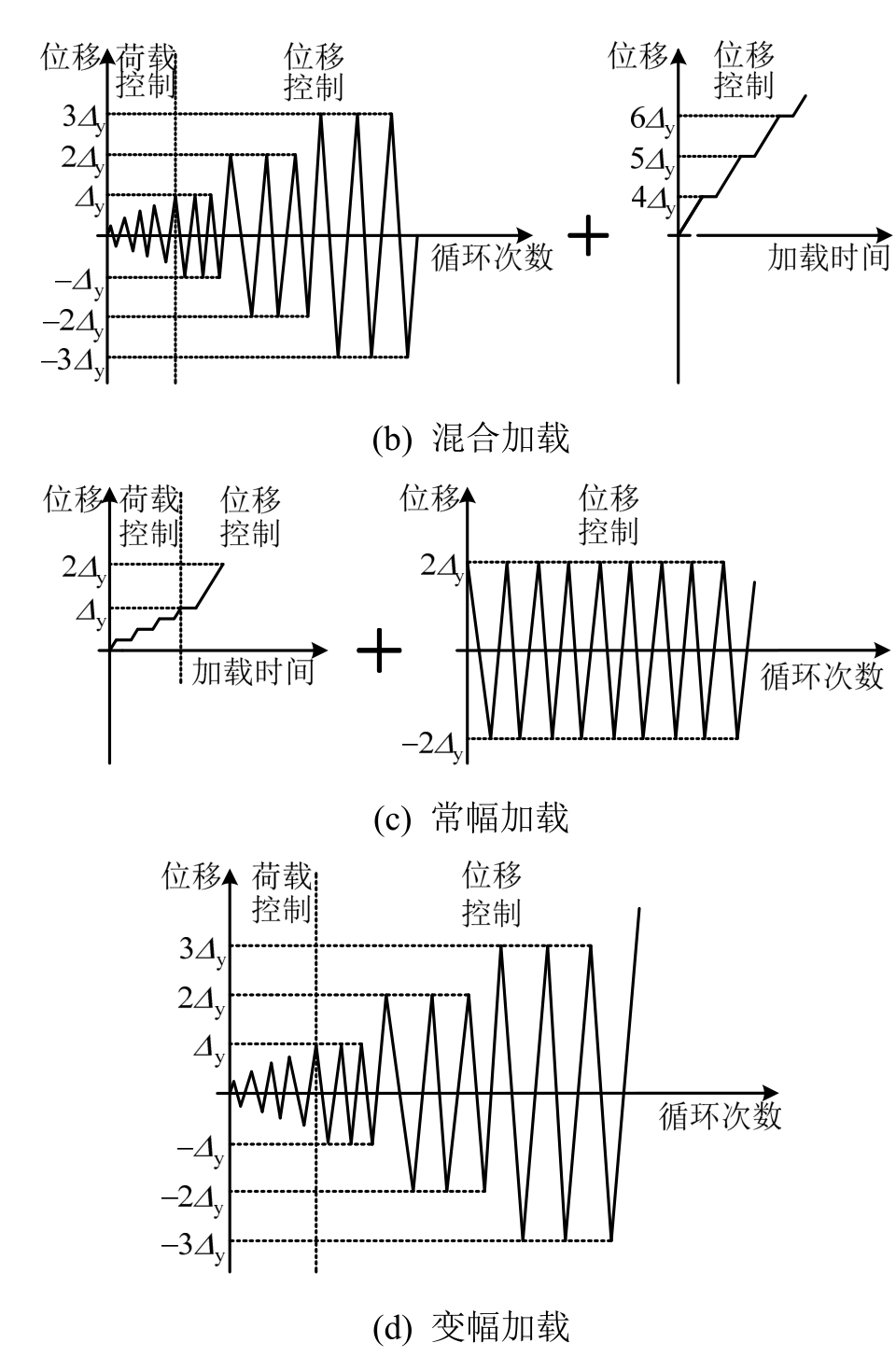
图6 加载制度
Fig.6 Loading procedure
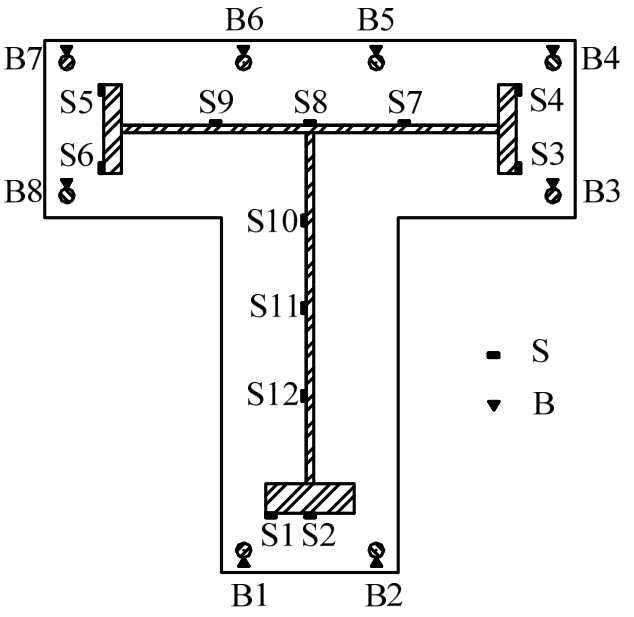
图7 应变片布置
Fig.7 Arrangement of strain gages
试件均发生典型的弯曲破坏,其破坏过程大致为:加载初期,试件上下两端首先出现弯曲水平裂缝;随着荷载增大,上下两端的水平裂缝不断发展并贯通,纵筋和型钢相继发生屈服(图8),同时柱中腹板两侧产生少量竖向裂缝。进入位移控制阶段后,上下两端的混凝土开始起皮剥落,且破坏区域逐渐扩大,箍筋、纵筋、型钢相继外露;随着位移幅值的增大,纵筋压曲外凸,上下两端的混凝土被压碎脱落,此后荷载持续下降,试件破坏。具体破坏形态如图9所示。
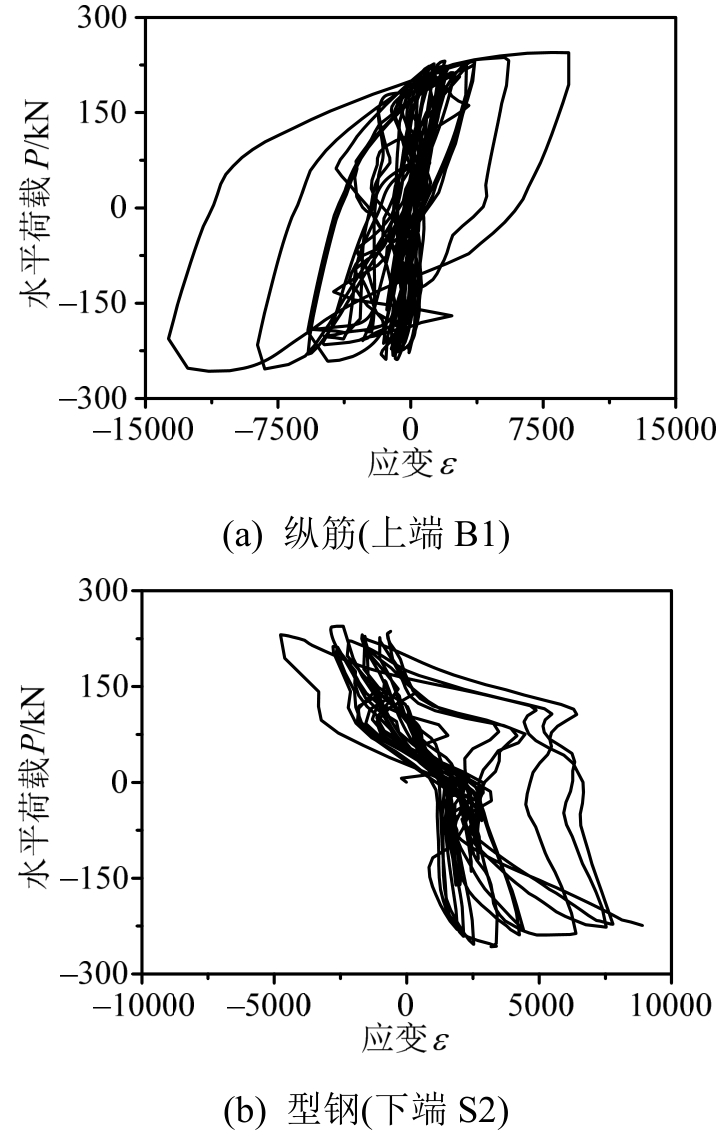
图8 纵筋和型钢应变(T9)
Fig.8 Strain of reinforcement and shaped-steel(T9)

图9 试件的破坏形态
Fig.9 Failure patterns of specimens
试件在加载过程中承担压弯剪作用,但从试件的破坏过程可知,压弯为主要作用。加载开始阶段,端部弯矩较小,轴向压力的偏心距也较小,试件处于小偏心受压状态;随着加载的进行,端部弯矩不断增大,轴向压力的偏心距也相应增大,试件逐渐由小偏心受压转变为大偏心受压;之后,由于轴向压力相对较小,起控制作用的是端部弯矩,试件最终发生弯曲破坏。
试件T1~T4在加载后期均为单调加载,因此其上下两端的破坏形态不同,一端为腹板(受压)破坏相对严重,另一端为翼缘(受压)破坏相对严重;试件T5的位移幅值为两倍的屈服位移,比其他试件小得多,因此破坏相对轻微;试件T6~T10均为低周反复加载,其上下两端破坏形态类似,破坏相对严重。
试件端部腹板的破坏比翼缘严重,这主要是由于本试验的水平加载沿腹板方向,腹板的配钢和受力面积均比翼缘小得多,从而在相同弯矩作用下腹板的破坏更为严重。试件破坏时,纵筋大部分被压曲,型钢未发现压屈现象,且被压碎的混凝土主要发生在箍筋外侧,箍筋内侧的混凝土破坏轻微。
图10所示为实测试件的荷载-位移曲线,其中P、Δ分别表示柱上端的水平荷载和位移。由图可知:
1)加载初期,试件处于弹性阶段,荷载-位移曲线近似呈线性变化;随着荷载增大,试件进入屈服阶段,曲线逐渐向位移轴倾斜;在位移控制加载阶段,随着位移幅值的递增,曲线倾斜愈加明显,试件的刚度和强度不断退化。
2)与直接进行单调加载的试件T1相比,试件T2、T3、T4分别在完成Δy、2Δy、3Δy控制下的循环加载后进行单调加载,随着循环次数的递增,试件的损伤不断累积,承载能力和极限变形能力依次降低。
3)试件T5~T10的滞回曲线正反方向基本对称,滞回环饱满,呈梭形,体现出较强的耗能能力。
4)其他参数相同时,常幅(2Δy)控制加载的试件T5与变幅循环控制加载的试件T6相比,前者的强度退化幅度较小,且比较缓慢,残余变形小,刚度退化现象不显著,而后者在位移为2Δy的循环加载过程中强度和刚度退化均相对较大,这主要是由于变幅循环控制加载除了使试件的循环次数增加外,位移幅值也不断递增,使得试件的累积损伤加重。当位移幅值增加到较大时,混凝土不断压碎脱落而退出工作,导致退化现象愈加明显。
5)其他参数相同而轴压比不同的试件T6、T7和T8相比,轴压比越大,试件的强度和刚度退化越快,极限变形越小,滞回曲线越不稳定。这主要是由于大轴压比试件在水平荷载作用下,P-Δ效应影响更为显著,试件损伤累积更快。
6)其他参数相同而配钢率不同的试件T6、T9和T10相比,配钢率越大,试件的滞回环相对饱满,承载能力高,极限变形大,耗能能力强。
各试件的骨架曲线如图11所示,不同阶段的承载力和位移如表3所示。
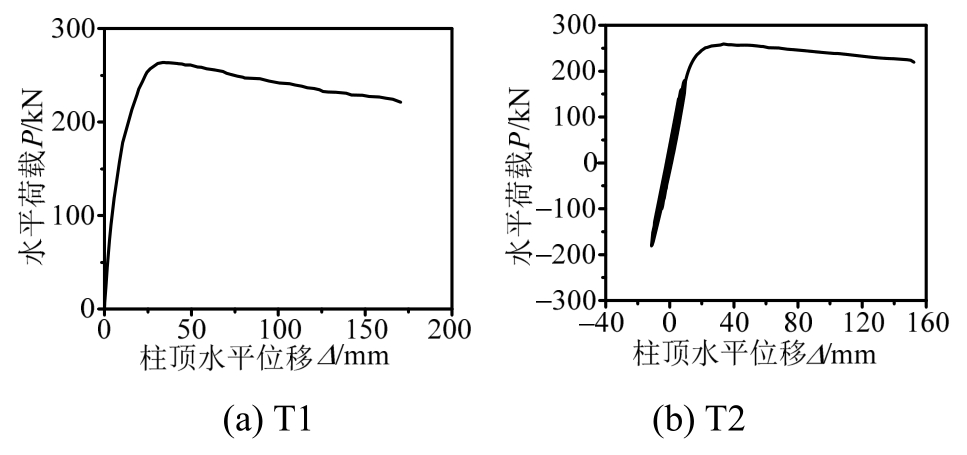
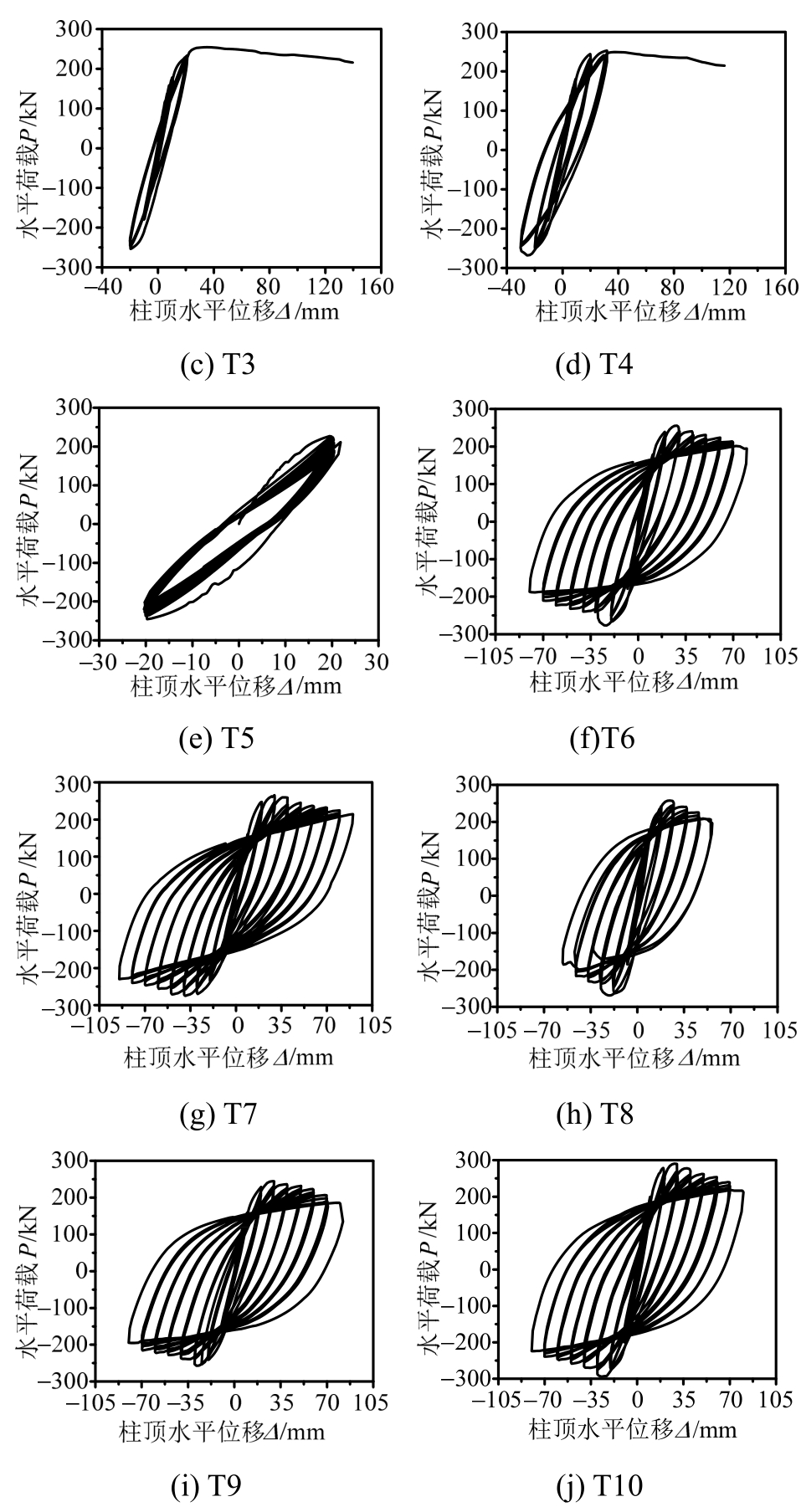
图10 水平荷载-位移曲线
Fig.10 Curves of horizontal load and displacement
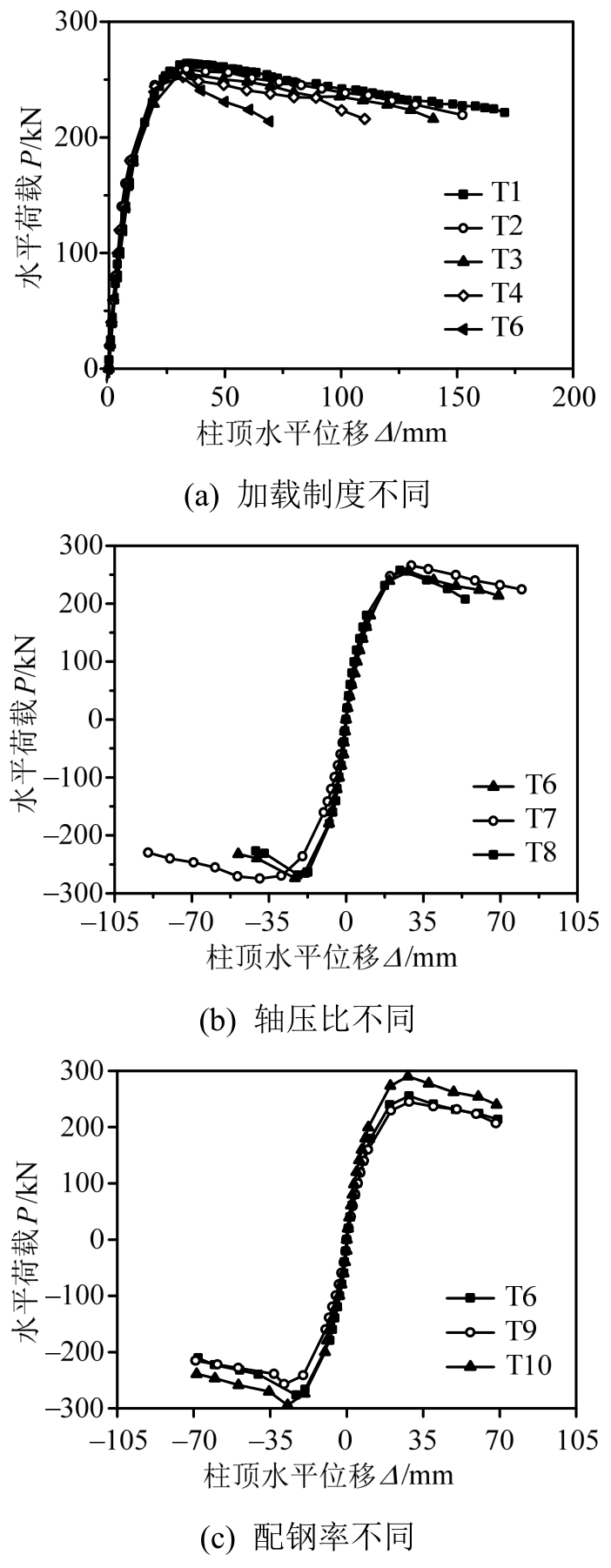
图11 骨架曲线
Fig.11 Skeleton curves
表3 试件各阶段试验结果
Table3 Experimental results of specimens at different stages

续表

注:Pcr为开裂荷载;Py为屈服荷载,由“通用屈服弯矩法”确定[10];Pm为峰值荷载;Pu为破坏荷载,取峰值荷载下降到85%时对应的值;Δcr、Δy、Δm、Δu分别为开裂荷载、屈服荷载、峰值荷载、破坏荷载对应的位移。
根据(GB 50010―2010)《建筑抗震设计规范》[11]的要求,为防止发生倒塌,结构在罕遇地震作用下的层间侧移角要低于规定的限值(钢筋混凝土框架为1/50)。表4所示为实测各试件的极限侧移角θu,根据θu=Δu/H确定,其中H为试件的高度。由表可知,试件的极限侧移角介于1/36~1/9,远大于1/50,表明实腹式型钢混凝土T形柱具有较强的抗倒塌能力。
表4 试件的极限侧移角和位移延性系数
Table4 Maximum drift angle and ductility coefficients of specimens
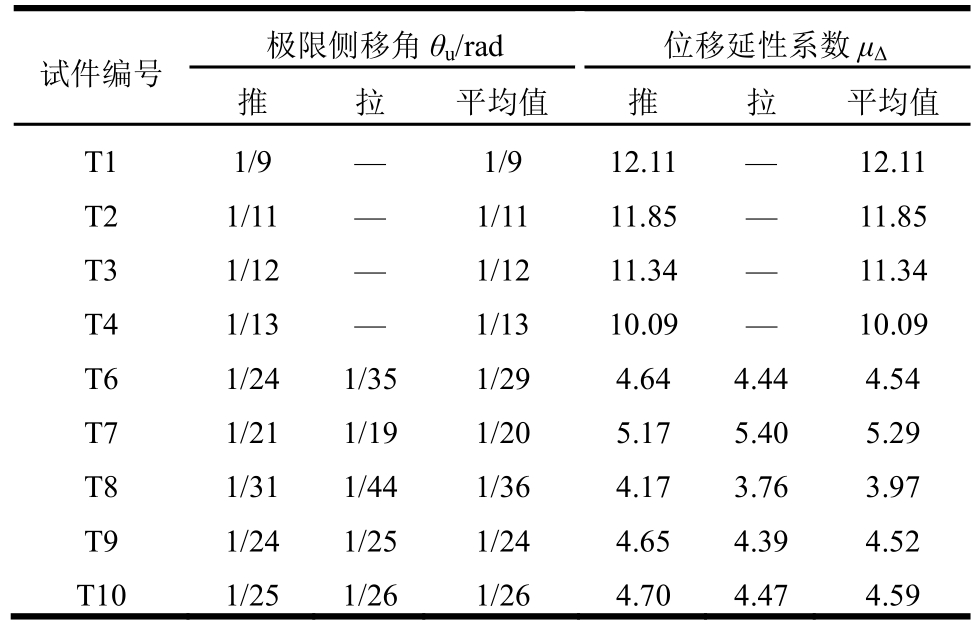
采用位移延性系数μ△来表示试件的延性,根据μ△=Δu/Δy确定,如表4所示。由表可知,除轴压比较大的试件T8(位移延性系数为3.97)外,其余试件的位移延性系数均大于4,最大的达到12.11,表明实腹式型钢混凝土T形柱具有良好的变形能力。
图12(a)所示为不同加载制度对试件延性的影响。由图可知,单调加载的试件延性最好,混合加载的次之(试件T2、T3和T4的延性依次减小),变幅加载的最差,且后者延性系数比前两者小得多。主要原因是,随着循环加载次数的增多,试件的累积损伤加重,强度衰减较快,变形能力变差。
图12(b)所示为不同轴压比对试件延性的影响。由图可知,轴压比越大,试件的延性越差。主要原因是加载后期,试件侧移较大,轴压比越大,P-Δ效应的影响越显著,附加弯矩将加快强度衰减,导致试件延性变差。同时,试件外表面混凝土几乎全部剥落,实际轴压比较设计轴压比更大,进一步加大了P-Δ效应。
图12(c)为不同配钢率对试件延性的影响。由图可知,随着配钢率的提高,试件的延性逐渐增大,但增大幅度较小。
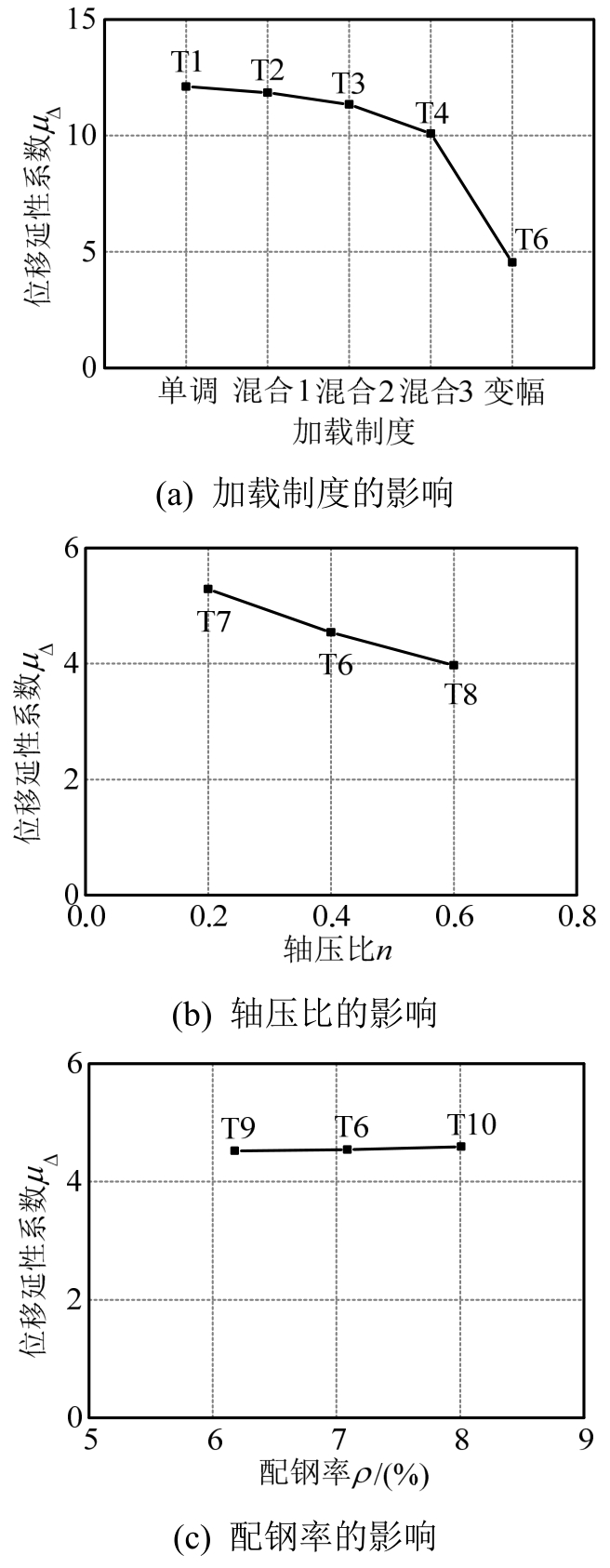
图12 不同影响因素下延性的变化规律
Fig.12 Relationship between ductility coefficients and different influence factors
随着损伤的发展和弹塑性变形的增大,试件的强度发生衰减。
图13(a)为不同加载制度下试件的强度随循环次数的变化规律,其中N为循环次数。由图可知,常幅加载的试件T5从第二次位移循环开始,强度发生衰减,但在整个破坏过程,强度衰减较为缓慢,P-N曲线近似呈斜率很小的直线。变幅加载的试件T6在一倍屈服位移的三次循环加载中,强度衰减不明显;从二倍屈服位移开始,随着裂缝的开展延伸、纵筋和型钢逐渐屈服,试件强度衰减明显变大,尤其是三倍屈服位移下的第三循环,P-N曲线甚至出现了陡降,其主要原因是柱两端混凝土大部分被压碎,同时也体现出混凝土的脆性性质。此后,由于位移幅值的增大及循环次数的增加,混凝土逐渐退出工作,荷载主要由型钢承担,P-N曲线趋于平缓。
图13(b)所示为不同轴压比下试件强度随循环次数的变化规律。由图可知,轴压比对试件强度衰减的影响较突出。对于轴压比为0.2的试件T7,强度衰减幅度小,P-N曲线下降缓慢。对于轴压比为0.6的试件T8,后期强度的衰减幅度尤为显著,衰减速率不断变大。轴压比为0.4的试件T6,P-N曲线介于上述两者之间。
图13(c)所示为不同配钢率下试件强度随循环次数的变化规律。由图可知,配钢率越大,强度衰减越平缓。因此,在型钢混凝土T形柱的工程设计中,可适当提高配钢率,以减缓强度衰减的速率。
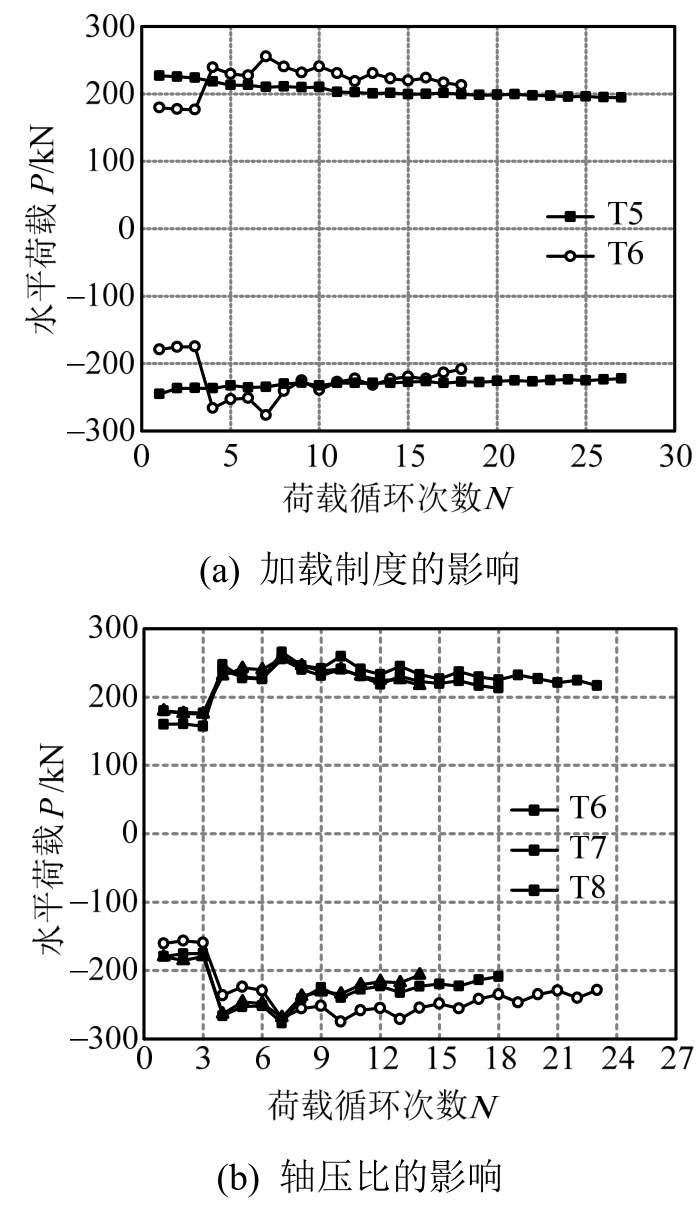
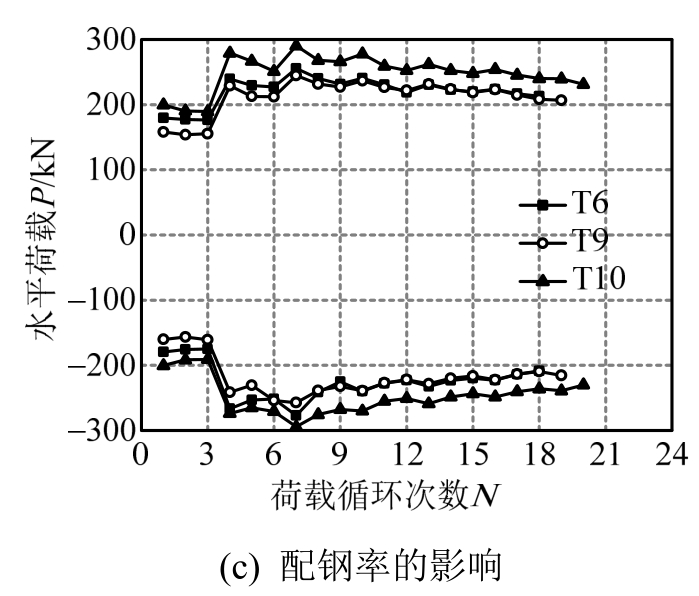
图13 不同影响因素下强度随荷载循环次数的变化规律
Fig.13 Relationship between strength and load cycles under different influence factors
图11所示的骨架曲线表明,试件屈服后,刚度随着损伤的发展一直在退化,尤其达到峰值荷载后,残余变形增大,试件刚度退化速率加快。图14所示为不同加载制度、轴压比和配钢率时割线刚度[12]与循环次数的关系。由图可知:
1)屈服荷载与峰值荷载之后,试件的刚度分别出现明显陡降,呈现出两个拐点,表明累积损伤发展到一个新的阶段,导致刚度突变。峰值荷载过后刚度退化变缓。
2)常幅加载下,试件的刚度退化缓慢,幅度较小,而变幅加载下,刚度退化显著。
3)轴压比越大,试件的初始刚度越大,但整体刚度退化速率越快。对于轴压比大的试件,在同一位移的三次循环中,后一循环的刚度比前一循环退化明显,而轴压比小的试件,第三次循环较第二次循环刚度退化不显著。

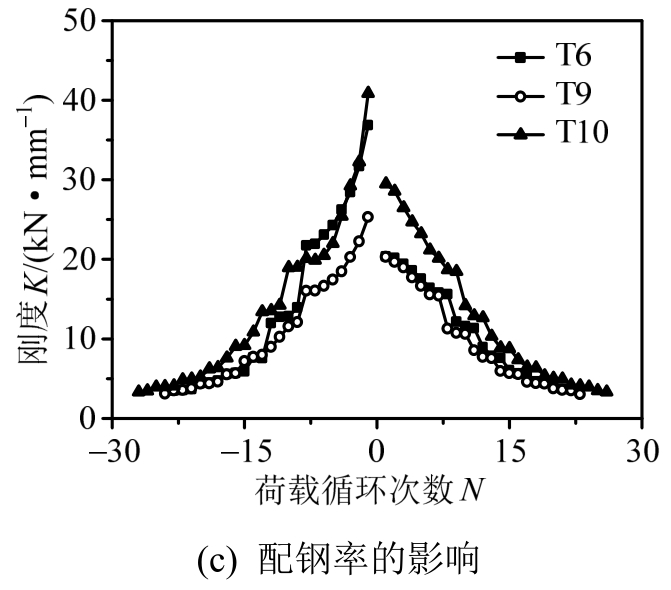
图14 不同影响因素下刚度随荷载循环次数的变化规律
Fig.14 Relationship between stiffness and load cycles under different influence factors
4)配钢率越大,试件的初始刚度越大,相同循环次数后的残余刚度越大。在加载后期,配钢率越大,试件的刚度退化越缓慢。
耗能能力采用等效粘滞阻尼系数he表示[13]。试件对应不同阶段的he如表5所示。由表可知,试件破坏时的he介于0.319~0.374,而钢筋混凝土T形柱试件破坏时he小于0.2[14],说明截面中加入实腹式型钢后,T形柱的耗能能力得到明显改善。
表5 试件的等效粘滞阻尼系数
Table5 Equivalent viscous damping coefficients of specimens
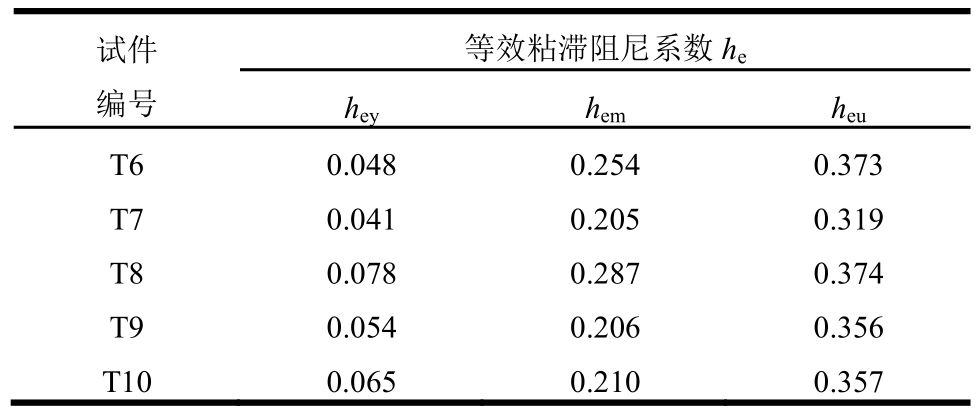
注:hey、hem、heu分别表示试件达到屈服荷载、峰值荷载和破坏荷载时的等效粘滞阻尼系数。
通过实腹式型钢混凝土T形柱的水平加载试验,得到以下主要结论:
(1)剪跨比为2.5的试件均发生典型弯曲破坏。单调和混合加载时,试件上下两端的破坏形态不同;而等幅和变幅加载时,试件上下两端的破坏形态类似,但变幅加载时试件的破坏比等幅加载时严重得多。
(2)型钢混凝土T形柱滞回曲线饱满,呈梭形,耗能能力优于钢筋混凝土T形柱。
(3)随着循环次数的增加,试件的承载能力和极限变形能力降低,延性变差。
(4)与变幅加载相比,等幅加载时试件的强度衰减和刚度退化均较为缓慢。
(5)随着轴压比增大,试件的延性变差,强度衰减和刚度退化速率加快。
(6)随着配钢率增大,试件的延性逐渐增大,但幅度较小,强度衰减和刚度退化减缓。
参考文献:
[1]刘祖强,薛建阳,赵鸿铁.型钢混凝土异形柱框架滞回性能分析[J].工程力学,2016,33(7):73―83.Liu Zuqiang,Xue Jianyang,Zhao Hongtie.Analysis on hysteretic behavior of steel reinforced concrete frame with special-shaped columns[J].Engineering Mechanics,2016,33(7):73―83.(in Chinese)
[2]陈宗平,赵鸿铁,薛建阳,等.型钢混凝土异形柱截面配钢分析[J].哈尔滨工业大学学报,2005,37(S):128―131.Chen Zongping,Zhao Hongtie,Xue Jianyang,et al.Shape steel layout analysis of SRC special-shaped columns[J].Journal of Harbin Institute of Technology,2005,37(S):128―131.(in Chinese)
[3]Liu Z Q,Xue J Y,Zhao H T,et al.Cyclic test for solid steel reinforced concrete frames with special-shaped columns[J].Earthquakes and Structures,2014,7(3):317―331.
[4]陈宗平,徐金俊,薛建阳.型钢混凝土异形柱-钢梁空间边节点的抗震性能及影响因素分析[J].工程力学,2015,32(2):105―113.Chen Zongping,Xu Jinjun,Xue Jianyang.Seismic behavior and influence factor analysis on 3D side joints composed of steel reinforced concrete special-shaped columns and steel beams[J].Engineering Mechanics,2015,32(2):105―113.(in Chinese)
[5]徐亚丰,李晓丽,佟雪伟,等.钢骨混凝土T形柱双向小偏压试验[J].沈阳建筑大学学报(自然科学版),2009,25(5):863―870.Xu Yafeng,Li Xiaoli,Tong Xuewei,et al.Experimental research on T-shaped steel reinforced concrete columns under biaxial eccentric pressure[J].Journal of Shenyang Jianzhu University(Natural Science),2009,25(5):863―870.(in Chinese)
[6]李哲,张小锋,郭增玉,等.钢骨混凝土T形截面短柱力学性能的试验研究[J].土木工程学报,2007,40(1):1―5.Li Zhe,Zhang Xiaofeng,Guo Zengyu,et al.Experimental study on the mechanical property of steelreinforced concrete short columns of t-shaped cross-section[J].China Civil Engineering Journal,2007,40(1):1―5.(in Chinese)
[7]蒋丽娜.钢骨混凝土T形截面异形柱抗震性能试验研究[D].南宁:广西大学,2006.Jiang Lina.Experimental research on seismic behavior of steel reinforced concrete special-shaped column[D].Nanning:Guangxi University,2006.(in Chinese)
[8]Xue J Y,Chen Z P,Zhao H T,et al.Shear mechanism and bearing capacity calculation on steel reinforced concrete special-shaped columns[J].Steel and Composite Structures,2012,13(5):473―487.
[9]陈宗平,薛建阳,赵鸿铁,等.型钢混凝土异形柱抗震性能试验研究[J].建筑结构学报,2007,28(3):53―61.Chen Zongping,Xue Jianyang,Zhao Hongtie,et al.Experimental study on seismic behavior of steel reinforced concrete special-shaped columns[J].Journal of Building Structures,2007,28(3):53―61.(in Chinese)
[10]Tao M X,Fan J S,Nie J G.Seismic behavior of steel reinforced concrete column-steel truss beam hybrid joints[J].Engineering Structures,2013,56:1557―1569.
[11]GB 50011―2010,建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.GB 50011―2010,Code for seismic design of buildings[S].Beijing:China Architecture & Building Press,2010.(in Chinese)
[12]Ma H,Xue J Y,Zhang X C,et al.Seismic performance of steel-reinforced recycled concrete columns under low cyclic loads[J].Construction and Building Materials,2013,48:229―237.
[13]Chou C C,Uang C M.Cyclic performance of a type of steel beam to steel-encased reinforced concrete column moment connection[J].Journal of Constructional Steel Research,2002,58(5/6/7/8):637―663.
[14]郝贵强.聚丙烯纤维增强异形柱框架抗震性能的研究[D].天津:天津大学,2008.Hao Guiqiang.Research on seismic performance of RC frames with specially-shaped columns reinforced by polypropylene fiber[D].Tianjin:Tianjin University,2008.(in Chinese)
EXPERIMENTAL STUDY ON ASEISMIC PERFORMANCE OF SOLID STEEL REINFORCED CONCRETE T-SHAPED COLUMN
LIU Zu-qiang,XUE Jian-yang,HAN Chen,YANG Qing-feng
(College of Civil Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China)
Abstract:In order to investigate the aseismic performance of the solid steel reinforced concrete T-shaped column,ten specimens were tested under horizontal loading,considering various loading procedures,axial compression ratios,and steel ratios.The failure process and patterns were observed.The mechanical behaviors were analyzed,such as load-displacement curves,drift angle,ductility,loading capacity,stiffness and energy dissipation.Test results show that:bending failure occurred for all specimens,and the failure pattern is different when the load was applied to the specimen according to different loading procedures.The hysteretic loops are in a plump-shape.The maximum drift angle is between 1/36 and 1/9,the displacement ductility coefficient is between 3.97 and 12.11,and the equivalent viscous damping coefficient is about 0.319 to 0.374 as the specimen failed,indicating good capacity of deformation and energy dissipation.With the increase of the number of cyclic loading and the axial compression ratio,the ductility of the specimen is reduced,and the speed of the strength and stiffness degradation tend to fast.With the increase of steel ratio,the ductility of the specimen is improved,and the speed of the strength and stiffness degradation tend to slow.
Key words:steel reinforced concrete;special-shaped column;solid steel;aseismic performance;loading procedure
中图分类号:TU398.2
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.03.0211
文章编号:1000-4750(2018)05-0017-10
收稿日期:2017-03-17;修改日期:2017-09-18
基金项目:国家自然科学基金项目(51308444);陕西省自然科学基础研究基金项目(2014JQ7288);西安建筑科技大学创新团队资助计划和青年科技基金项目(QN1408)
通讯作者:薛建阳(1970―),男,河南洛阳人,教授,博士,博导,主要从事钢与混凝土组合结构及工程结构抗震研究(E-mail:jianyang_xue@163.com).
作者简介:刘祖强(1984―),男,山东青岛人,副教授,博士,主要从事钢与混凝土组合结构及工程结构抗震研究(E-mail:liuzuqiang0081@126.com);
韩 琛(1990―),男,江苏无锡人,硕士,主要从事型钢混凝土异性柱结构研究(E-mail:164499656@qq.com);
杨青峰(1989―),男,陕西渭南人,硕士,主要从事型钢混凝土异性柱结构研究(E-mail:316335855@qq.com).