王 珊
(北京航天微系统研究所,北京 100094)
摘 要:对于含穿透裂纹的板结构,裂纹尖端应力场及应力强度因子的计算精度对评估板的安全性具有非常重要的影响。基于含裂纹Kirchhoff板弯曲问题中裂纹尖端场的辛本征解析解,该文提出了一个提高裂纹尖端应力场计算精度的有限元应力恢复方法。首先利用常规有限元程序对含裂纹板弯曲问题进行分析,得到裂纹尖端附近的单元节点位移;然后根据节点位移确定辛本征解中的待定系数,得到裂纹尖端附近应力场的显式表达式。数值结果表明,该方法给出的应力分析精度得到较大提高,并具有良好的数值稳定性。
关键词:有限元;辛本征解;Kirchhoff板;裂纹;应力恢复;应力强度因子
板是工程中常见的一种结构形式,广泛应用于诸多工程领域。对于含有裂纹的板件,一般难以获得断裂参量的解析解。有限元法是结构分析中常用的一种数值方法,形成了许多通用的有限元软件。这些程序系统大多采用基于最小势能原理的位移元,可以给出单元节点位移的高精度结果[1-2],但单元应力的精度会大大降低,特别是对板弯曲问题。另外,对于具有应力奇异性的问题,常规有限单元需要在奇点附近划分非常稠密的网格,以保证求解精度,这样显然会降低求解效率。而且在求解应力强度因子等断裂参数时通常需借助后处理的手段,例如应力外推法,其求解精度也主要取决于有限元应力计算结果。
为改善有限元应力场的求解精度,出现了一些应力磨平方法。Oden和Reddy[3]提出了一种局部应力磨平的近似方法,Hinton和Campbell[4]基于最小二乘法提出了全局及局部的有限元应力磨平方法。Mota和Abel[5]提出了基于混合有限元的应力恢复方法。Ahmed和Singh[6]提出了基于应力恢复技术的板料成形过程自适应有限元分析方法。钟万勰和孙雁[7]通过解析求解位移和应力的影响函数,利用功的互等定理计算应力值。在求解裂纹问题方面,也出现了一些应力磨平方法。Xiao和Karihaloo等[8-9]利用移动最小二乘法对有限元求得的裂纹尖端场进行应力磨平,并且提出了扩展有限元的应力磨平方法。钟万勰等[10-14]将辛对偶体系的求解方法引入弹性力学,使以往很多难以求解的弹性力学问题获得了解析解或半解析解[15]。辛本征解析解的获得为有限元应力磨平提供了新途径,比如,基于极坐标辛对偶体系所提供的平面弹性力学解析辛本征展开解的应力磨平方法得到了较为满意的结果[16]。
本文利用有限元法给出的Kirchhoff板裂纹尖端附近区域节点位移,以辛对偶体系提供的环扇形板辛本征解析通解为插值函数,提出了一个用于Kirchhoff板裂纹问题的应力恢复方法,并通过应力强度因子与辛本征解中奇异项展开系数之间的关系直接计算其大小。由于不存在位移导数带来的精度降阶问题,且回避了常规有限元分析应力奇异性问题的局限性,这使得裂纹尖端域内应力场及应力强度因子具有较高的精度。
内外半径分别为R1和R2的环扇形板如图1所示,(ρ,φ)代表极坐标,环扇形板张开半角度为α(-α<φ<α)。
极坐标系下板的曲率-挠度关系为:
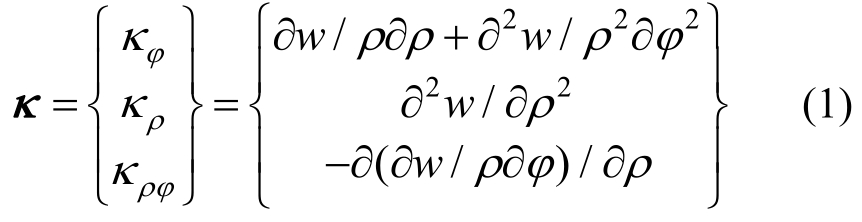
其中,κ、w分别表示板的曲率向量与挠度。
通过引入变换:
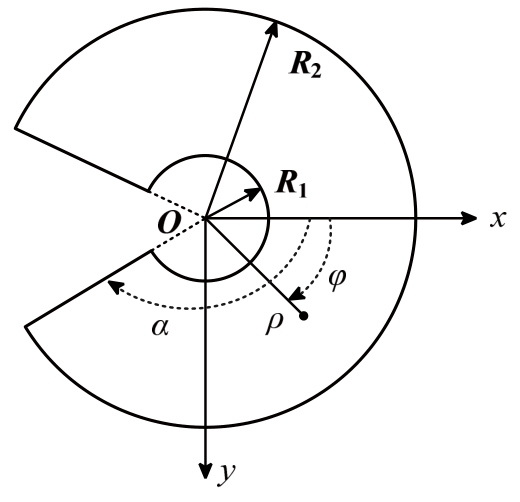
图1 环扇形板
Fig.1 Annular sector plate
板弯曲极坐标系的H-R变分原理可写为:
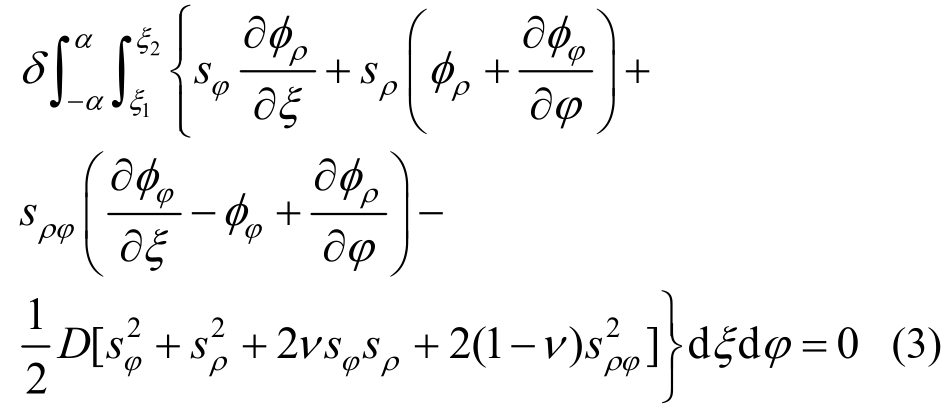
式中,D和ν分别代表板的弯曲刚度和泊松比。将ξ模拟为哈密顿体系的时间坐标,并记(˙)=∂/∂ξ。执行式(3)对sρ变分可得到:
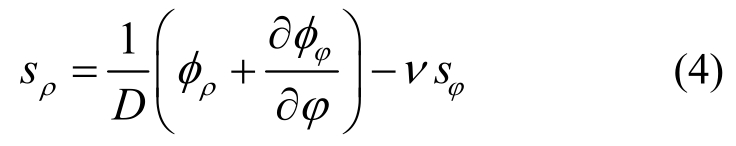
再将其代入式(3)并消去sρ得:
其中:
而哈密顿函数为:
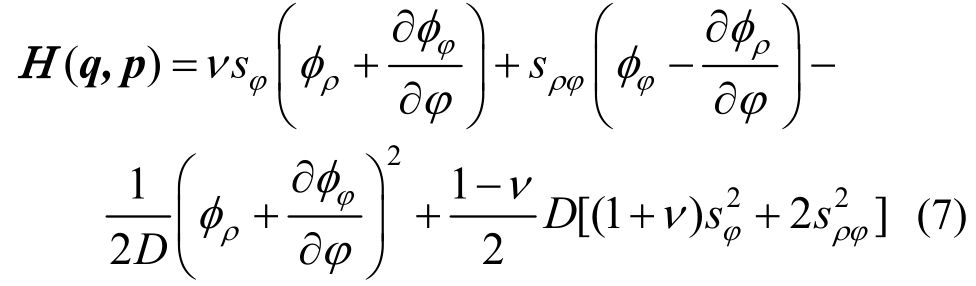
式(5)对q、p变分即得到对应面内无体力项的板弯曲辛对偶方程组:
其中,v为对偶向量:
哈密顿算子矩阵为:

φρ、φφ为弯矩函数。弯矩函数与弯矩的关系为:
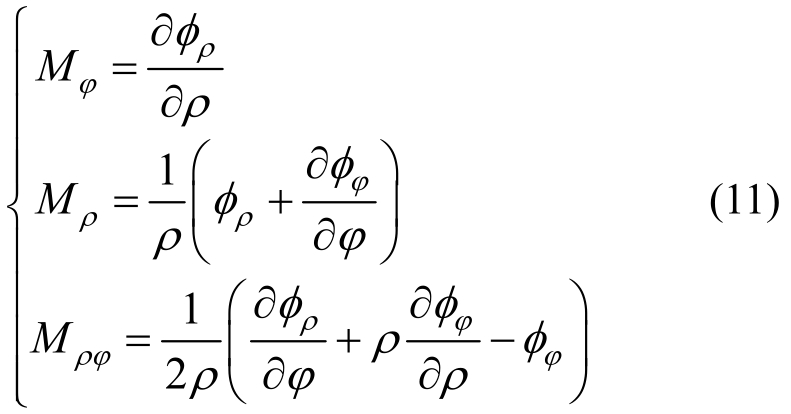
式(8)可以利用分离变量法进行求解,即令:
其中:μ是本征值;ψ(φ)是本征函数向量,它只是φ的函数。
对于两直边为自由边界条件的环扇形板,其辛本征解可分成相互解耦的两组,分别代表关于x轴为对称变形和反对称变形。对称变形的非零辛本征值超越方程为:
相应的本征解为:

该解的挠度为:
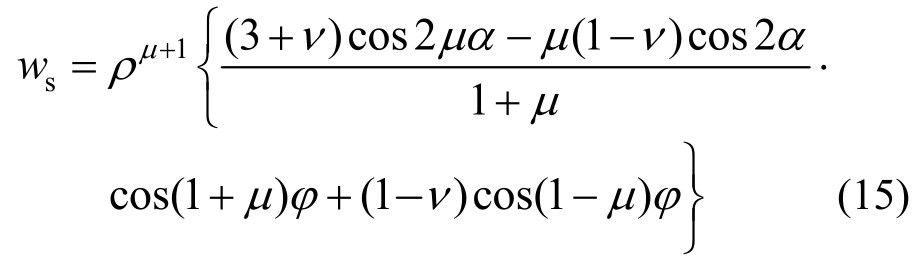
反对称变形的非零辛本征值超越方程为:
相应的本征解为:
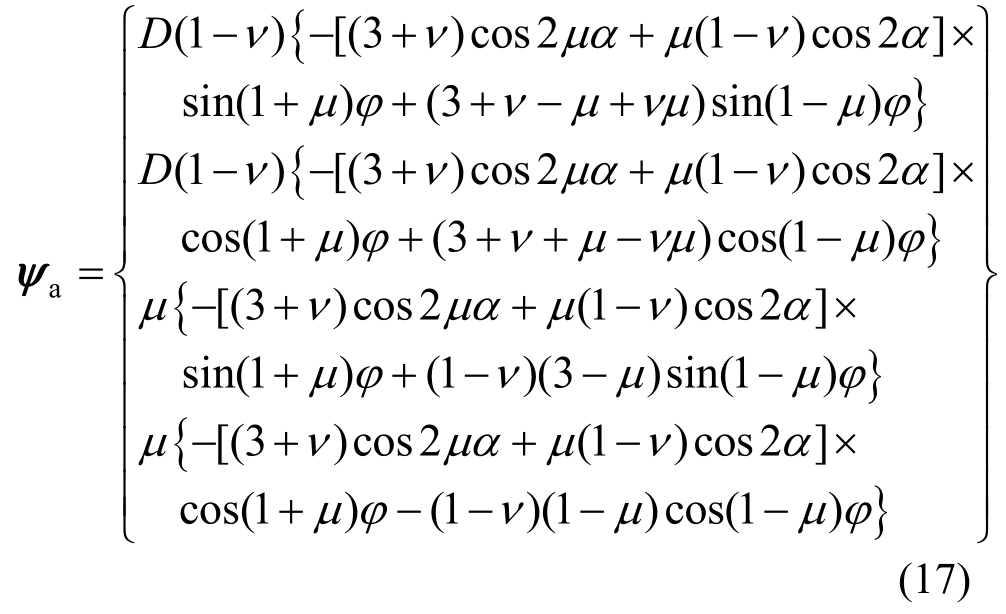
该解的挠度为:

以上的辛本征解仅与板的弯曲刚度D、泊松比ν、以及半顶角α有关。式(15)和式(18)对应的解在两直边延长线交点(即坐标原点)形成一个平衡力系。除对称与反对称变形解,两直边自由环扇形板还有六个具有特殊物理意义的解,它们与本文无关,在此不做详述。
由式(15)和式(18)的挠度表达式,环扇形板的位移场可近似表示为:

其中:R是某一特征长度,用于ρ坐标的无量纲化;Ns和Na是对称变形与反对称变形模式各取的项数;ci(i=1,2,…,Ns)、dj(j=1,2,…,Na)以及b1,b2,b3是待定常数;Fi(φ)、Gj(φ)分别为对称变形与反对称变形模式的角分布函数:
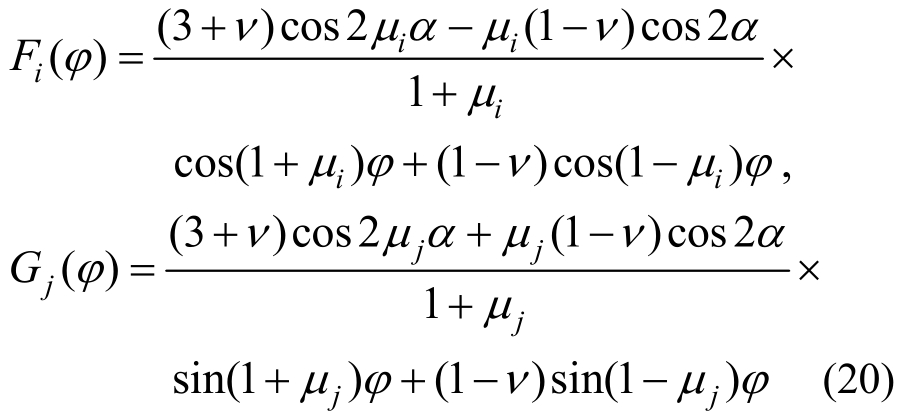
后三项是板的三个刚体位移解。
当R1=0,α=π时,上节给出的解对应就是裂纹问题的辛本征解。令式(13)、式(16)中α=π可给出裂纹尖端对称与反对称变形的非零辛本征值超越方程为:
由此得到辛本征值:
裂纹尖端附近总应变能必须有限,因此略去了i≤0的解。其中,介于0、1之间的辛本征值1/2表征了裂纹尖端的应力奇异性阶次,即ρ-1/2。将式(22)的本征值代入式(19)即得到裂纹尖端关于x轴为对称变形和反对称变形的挠度表达式。因此,裂纹尖端的位移场可表示为:
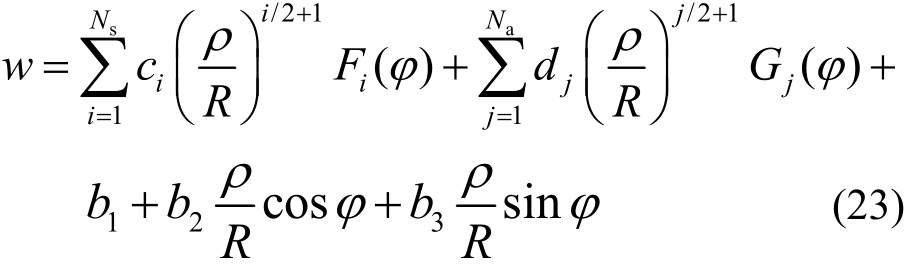
相应地,角分布函数Fi(φ)、Gj(φ)分别为:
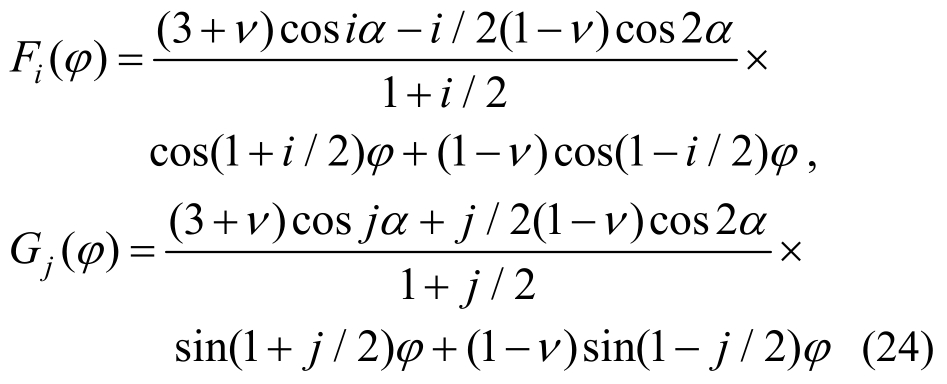
式(23)是无体力作用薄板断裂问题裂纹尖端位移场通解,它满足域内的所有微分方程和两直边自由的边界条件,而其中待定常数ci(i=1,2,…,Ns)、dj(j=1,2,…,Na)以及b1,b2,b3则可由环向边界的位移确定。对裂纹尖端附近区域,通过有限元分析可获得节点位移,问题则归结为求解环向边界为给定位移边界条件的不规则扇形区域问题的解析展开式。在确定了所有待定常数后,就确定了域内位移场,进而可给出解析形式的应力场,至此完成裂纹尖端应力场重构。通过首项应力奇异项的展开系数可直接计算应力强度因子。由于在裂纹尖端采用了解析通解,且有限元得到的位移场精度较高,因此重构后的裂纹尖端应力场也具有较高的精度。
为保证数值计算精度,应合理选取边界插值节点。数值试验证明,与文献[16]类似,当选取的插值节点沿参考区域边界分布状况较为规则时,应力重构的数值效果较好。根据这个原则,本文提出了一种适用于裂尖问题的边界插值节点选择方法。
1)应力重构参考区域的选择。以裂纹尖端为圆心选择一个适当大小扇形域(-π<φ<π的扇形域)作为应力重构的参考区域,如图2(a)所示。这里记其裂纹尖端为O,扇形参考区域半径为R,其边界记为Γp。
2)参考节点的确定。选取扇形参考区域边界Γp穿过的全部单元,这些单元的所有节点中位于扇形参考区域以外的即作为参考节点。参考节点的选取如图2(a)所示,参考节点在图中表示为白色三角形,将参考节点总数记为Nref。
3)插值节点数N的确定。统计所有相邻参考节点与裂纹尖端O连线的夹角,其中的最大值记为Δθ。取插值节点数N=min(2π/Δθ+1,αNref),其中α是为避免插值节点数过多而预先设定的筛选比,用以限制插值节点数在参考节点总数的占比。
4)N个插值节点的确定。以裂纹尖端O点为起点,延裂纹表面反向延长线(即φ=0)方向作射线,记为OP1。以裂纹尖端O点为起点,以射线OP1为基准,分别沿逆时针与顺时针方向作余下N-1条关于裂纹表面对称且等分扇形参考区域的射线,记为OP2,OP3,…,OPN。在所有Nref个参考节点中依次选取距离每条射线最近的节点作为一个插值节点,共选取N个插值节点。插值节点筛选过程如图2(b)所示,筛选后得到的插值节点用黑色三角形表示。
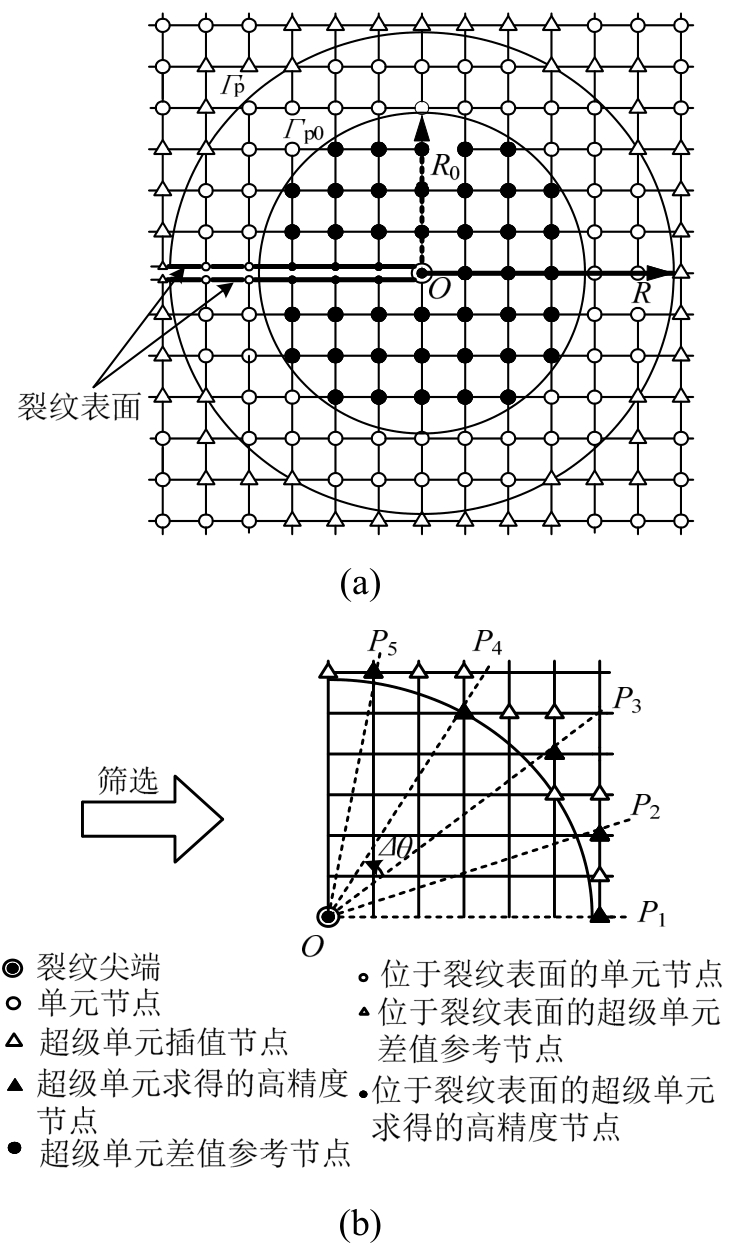
图2 插值节点筛选示意图
Fig.2 Schematic diagram of present method
确定了全部N个插值节点,就可利用有限元提供的这N个插值节点的位移来确定解析解中的待定常数ci(i=1,2,…,Ns)、dj(j=1,2,…,Na)以及b1,b2,b3,从而确定裂纹尖端场。待定常数的确定可采用最小二乘拟合以及等额配点法等方法,本文选用等额配点法。假定每个有限元节点上有三个位移参数,包括节点挠度w与节点处中面法线在直角坐标系下的转角θx和θy。
所选取的N个插值节点每个节点有三个独立节点位移,则插值节点位移向量为:
由式(23)可给出插值节点位移向量d与广义位移向量a之间的关系:
其中,T即为节点位移向量d到广义位移向量a之间的变换矩阵:
取Ns+Na+3=3N,则式(27)给出的转换矩阵T为3n阶可逆方阵,于是式(26)可改写为:
求得了广义位移向量a就可根据裂纹尖端解析表达式得到参考区域内的应力场。这里需要注意,因有边界效应,在参考区域内距离边界有一定距离的区域内给出的应力场数值结果是更理想的,该区域即图2(a)中的虚线圆区域ρR0<。
利用首项奇异项展开式即可得到薄板裂纹问题的应力强度因子。I型和II型变形模式的切口应力强度因子可以定义为:
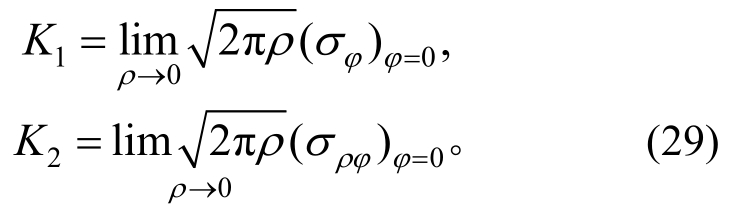
算例1.考虑如图3所示的含中心裂纹方形板,板的边长为l,板厚为h,中心裂纹长度为2a。板的泊松比取为ν=0.3,板的上下两条边承受均布弯矩m作用。有限元分析中采用三角形常应变单元(ANSYS中shell63单元退化而来),l=4a时的有限元网格划分如图4所示。本文分析时取扇形参考区域半径为R=0.5a,含中心裂纹方形板应力强度因子计算结果见表1。作为对比,表中还列出了Jiang和Cheung[17],以及Yao和Wang[18]给出的数值结果。若方形板边长l→∞,即归结为含中心裂纹无限大板对边承受均布弯矩的问题,中心裂纹无限大板应力强度因子的解析解为![]()
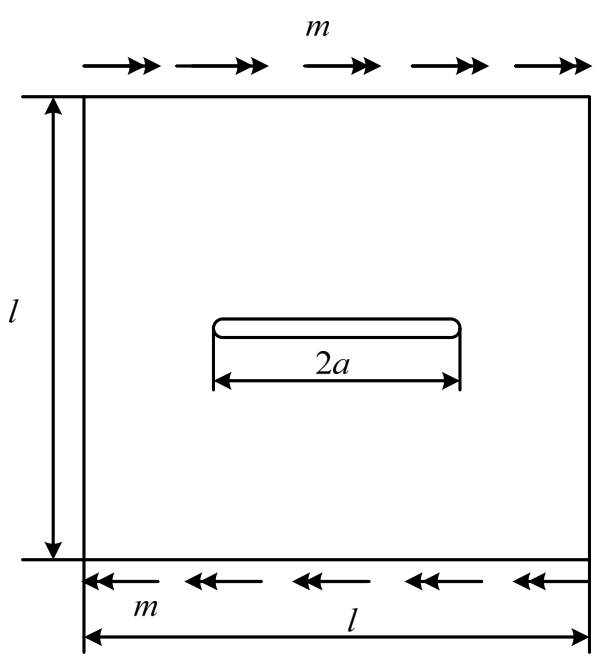
图3 承受对边均布弯矩的含中心裂纹方形板
Fig.3 A thin plate containing a central crack and subjected to uniform bending moment on opposite sides
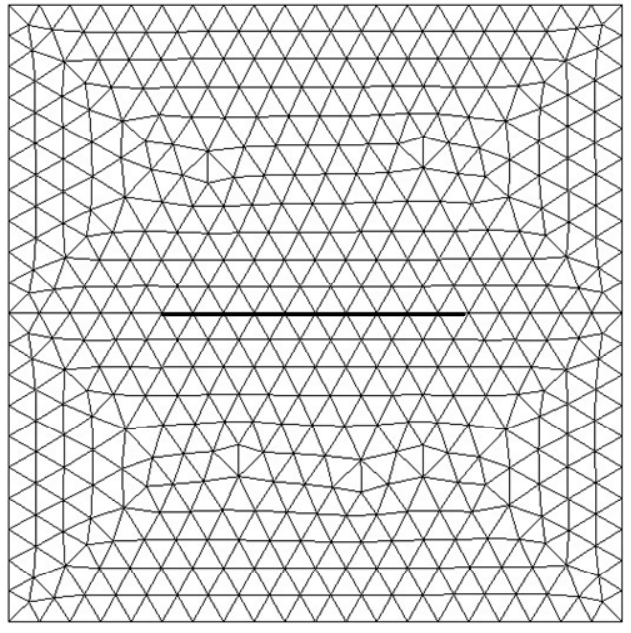
图4l=4a时采用的有限元网格
Fig.4 Meshes for thin plate whilel=4a
表1 含中心裂纹薄板I型应力强度因子![]()
Table1 Mode I SIFs![]() of thin plate with a central crack
of thin plate with a central crack

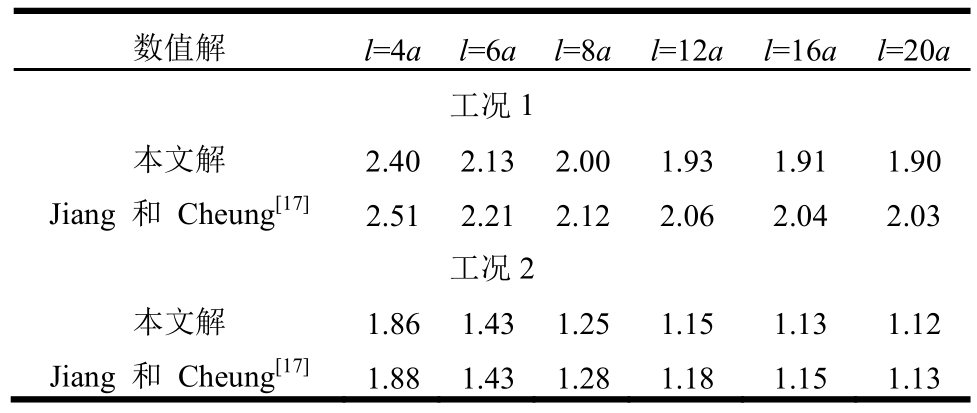
算例2.考虑算例1的含中心裂纹板,板所受的荷载分别为:1)工况1:板的裂纹上下表面中点承受一对方向相反的集中弯矩M作用(见图5(a));2)工况2:板面上承受一对方向相反的集中弯矩M作用(见图5(b))。有限元分析中仍采用三角形常应变单元,l=4a时的有限元网格划分如图4所示。本文分析时取扇形参考区域半径为R=0.5a,含中心裂纹方形板应力强度因子计算结果见表2。作为对比,表中还列出了Jiang和Cheung[17]给出的数值结果。若方形板边长l→∞,即归结为含中心裂纹无限大板承受集中弯矩作用的问题,工况1与工况2的应力强度因子解析解分别为![]()
![]()
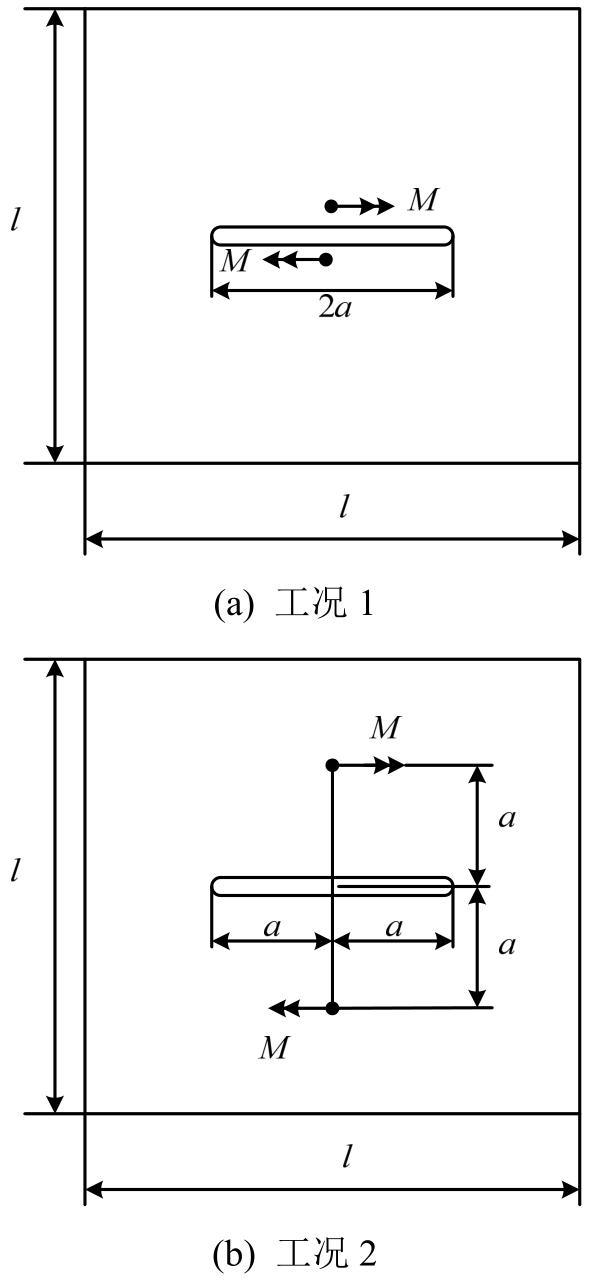
图5 承受集中弯矩的含中心裂纹方形板
Fig.5 A thin plate containing a central crack and subjected to concentrated moments
表2 含中心裂纹薄板I型应力强度因子![]()
Table2 Mode I SIFsK1![]() of thin plate witha central crack
of thin plate witha central crack
算例3.考虑如图6所示的含双边裂纹方形板,板的边长为l,板厚为h,板中间未开裂部分长度为2a。板的泊松比取为ν=0.3,板面上承受一对方向相反的集中弯矩M作用。有限元分析中仍采用三角形常应变单元,l=4a时的有限元网格划分如图7所示。本文分析时取扇形参考区域半径为R=0.5a,含双边裂纹方形板应力强度因子计算结果见表3。
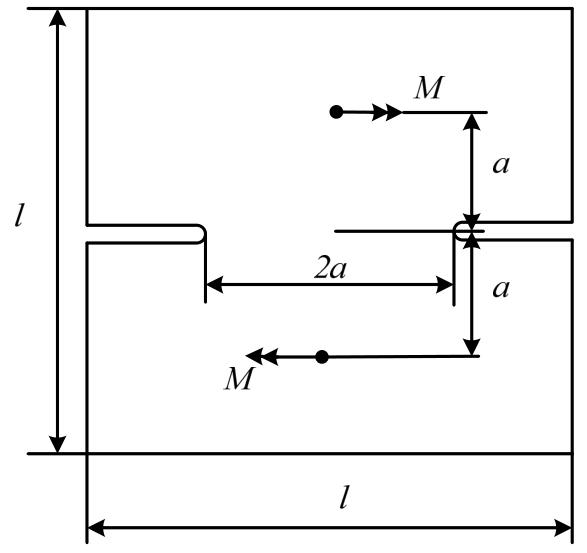
图6 承受集中弯矩的含双边裂纹方形板
Fig.6 A thin plate containing double edge cracks and subjected to concentrated moments
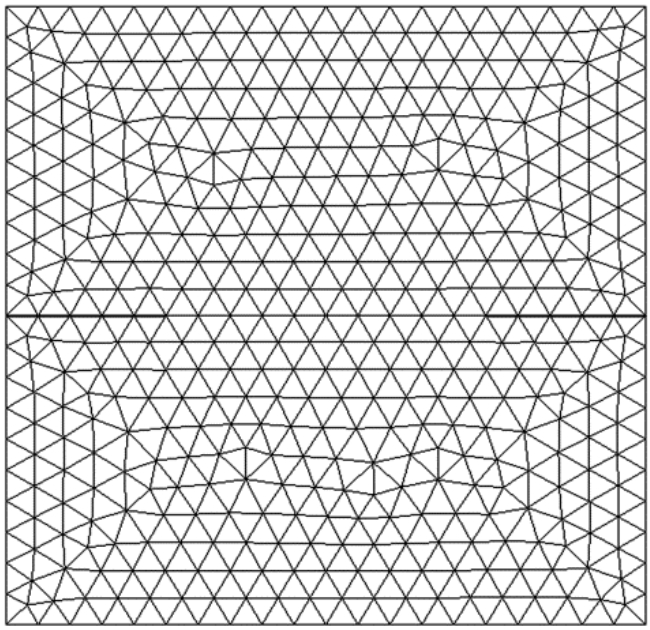
图7l=4a时采用的有限元网格
Fig.7 Finite element mesh for thin plate whilel=4a
表3 含双边裂纹薄板I型应力强度因子![]() K1
K1
Table3 Mode I SIFsK1![]() of thin plate with double edge cracks
of thin plate with double edge cracks

作为对比,表中还列出了Jiang和Cheung[17]给出的双边裂纹薄板I型应力强度因子的数值结果。这里要提及的是,当边长l→∞时,问题即为板面承受集中弯矩作用的含双边裂纹的无限大板,其应力强度因子的解析解为![]() =1.587。显然本方法所求得的应力强度因子的变化趋势与文献所提供的数值解以及解析解非常吻合。
=1.587。显然本方法所求得的应力强度因子的变化趋势与文献所提供的数值解以及解析解非常吻合。
需要说明的是,本文提出的有限元应力恢复方法对复杂几何形状和加载条件下的此类问题都是适用的。
基于含裂纹Kirchhoff板弯曲问题中裂纹尖端场的辛本征解析解,利用有限元方法提供的节点位移确定出辛本征解中的待定系数,重构裂纹尖端应力场,提出了一个提高裂纹尖端应力场计算精度的有限元应力恢复方法。与传统方法相比,该方法采用Kirchhoff板裂纹尖端辛本征解析解作为插值函数,规避了对位移求导损失的计算精度,又可反映裂纹尖端真实应力场,因此可以获得精度与有限元位移场相媲美的应力强度因子。由于应力恢复的精度依赖于有限元位移的精度,因此应尽可能提高有限元位移场的精度。数值算例结果表明,本方法给出的应力分析精度得到较大提高,并具有良好的数值稳定性,是一种计算Kirchhoff板弯曲问题应力强度因子的有效数值方法。
参考文献:
[1]Zienkewicz O C,Taylor R L.The finite element method[M].42th ed.N Y:McGraw2Hill,1989.
[2]王勖成.有限单元法[M].北京:清华大学出版社,2003.Wang Xucheng.Finite element method[M].Beijing:Tsinghua University Press,2003.(in Chinese)
[3]Oden J T,Reddy J N.Note on an approximate method for computing consistent conjugate stresses in elastic finite elements[J].International Journal for Numerical Methods in Engineering,1973,6(1):55―61.
[4]Hinton E,Campbell J S.Local and global smoothing of discontinuous finite element functions using a least squares methods[J].International Journal for Numerical Methods in Engineering,1974,8(3):461―480.
[5]Mota A,Abel J F.On mixed finite element formulations and stress recovery techniques[J].International Journal for Numerical Methods in Engineering,2015,47(1-3):191―204.
[6]Ahmed M,Singh D.Stress recovery based h-adaptive finite element simulation of sheet forming operations[J].Journal of the Institution of Engineers,2016,97(3):451―467.
[7]孙雁,钟万勰.影响函数与有限元应力计算[J].计算力学学报,2010,27(1):1―7.Sun Yan,Zhong Wanxie.Influence function and finite element stress calculation[J].Journal of Computational Mechanics,2010,27(1):1―7.(in Chinese)
[8]Xiao Q Z,Karihaloo B L.Statically admissible stress recovery for crack problems[C].Turin,Italy:Proceedings of ICF11,March,2005:20―25.
[9]Xiao Q Z,Karihaloo B L.Improving the accuracy of XFEM crack tip fields using higher order quadrature and statically admissible stress recovery[J].International Journal for Numerical Methods in Engineering,2006,66(9):1378―1410.
[10]钟万勰.弹性力学求解新体系[M].大连:大连理工大学出版社,1995.Zhong Wanxie.A new systematic methodology for theory of elasticity[M].Dalian:Dalian University of Technology Press,1995.(in Chinese)
[11]钟万勰,徐新生,张洪武.弹性曲梁问题的直接法[J].工程力学,1996,13(4):1―8.Zhong Wanxie,Xu Xinsheng,Zhang Hongwu.On a direct method for the problem of elastic curved beams[J].Engineering Mechanics,1996,13(4):1―8.(in Chinese)
[12]马坚伟,徐新生,杨慧珠,等.基于哈密顿体系求解空间粘性流体问题[J].工程力学,2002,19(3):1―5.Ma Jianwei,Xu Xinsheng,Yang Huizhu,et al.Solution of spatial viscous flow based on Hamiltonian system[J].Engineering Mechanics,2002,19(3):1―5.(in Chinese)
[13]赵岩,项盼,张有为,等.具有不确定参数车轨耦合系统随机振动灵敏度分析[J].工程力学,2013,30(4):360―366.Zhao Yan,Xiang Pan,Zhang Youwei,et al.Random vibration sensitivity analysis for coupled vehicle-track systems with parameter uncertainties[J].Engineering Mechanics,2013,30(4):360―366.(in Chinese)
[14]Yao W A,Zhong W X,Lim C W.Symplectic elasticity[M].Singapore:World Scientific,2009.
[15]王承强,郑长良.平面裂纹应力强度因子的半解析有限元法[J].工程力学,2005,2(1):33―37.Wang Chengqiang,Zheng Changliang.Semi-analytical finite element method for plane crack stress intensity factor[J].Engineering Mechanics,2005,22(1):33―37.(in Chinese)
[16]徐小明,张盛,姚伟岸,等.基于辛弹性力学解析本征函数的有限元应力磨平方法[J].计算力学学报,2012,29(4):511―516.Xu Xiaoming,Zhang Sheng,Yao Weian,et al.A stress recovery method based on the analytical eigenfunctions of symplectic elasticity[J].Chinese Journal of Computational Mechanics,2012,29(4):511―516.(in Chinese)
[17]Jiang C P,Cheung Y K.A special bending crack tip finite element[J].International Journal of Fracture,1995,71:55―69.
[18]Yao W A,Wang S.An analytical singular element for Kirchhoff plate bending with V-Shaped notches[J].J.Applied Mechanics,Transactions ASME,2012,79(5):051016.
A STRESS RECOVERY METHOD FOR CRACKS IN KIRCHHOFF PLATE BASED ON THE SYMPLECTIC EIGENSOLUTIONS NEAR THE CRACK TIPS
WANG Shan
(Beijing Aerospace Institute of Microsystems,Beijing 100094,China)
Abstract:For a plate structure with through cracks,the calculation accuracy of the stress field and the stress intensity factor near the crack tips has important influence on the safety evaluation of the plate.Based on the analytical symplectic eigen-solutions of the crack tip field in the Kirchhoff plate bending problem with cracks,a finite element stress recovery method is proposed to improve the calculation accuracy of the stress field near the crack tips.Firstly,the bending problem of the cracked plate is analyzed by using the conventional finite element program,and the nodal displacements near the crack tip are obtained.Secondly,the undetermined coefficients in the symplectic eigen-solutions are determined by using nodal displacements,and the explicit expression of the stress field near the crack tip is obtained.The numerical results show that the present approach can present the stress results with more precision and has good numerical stability.
Key words:finite element method;symplectic eigen-solution;Kirchhoff plate;crack;stress recovery;stress intensity factor
中图分类号:O343.4
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.01.0082
文章编号:1000-4750(2018)05-0010-07
收稿日期:2017-01-20;修改日期:2017-12-15
通讯作者:王珊(1981―),女,大连市人,高工,博士,主要从事计算固体力学、断裂力学研究(E-mail:wangshan1981@163.com).