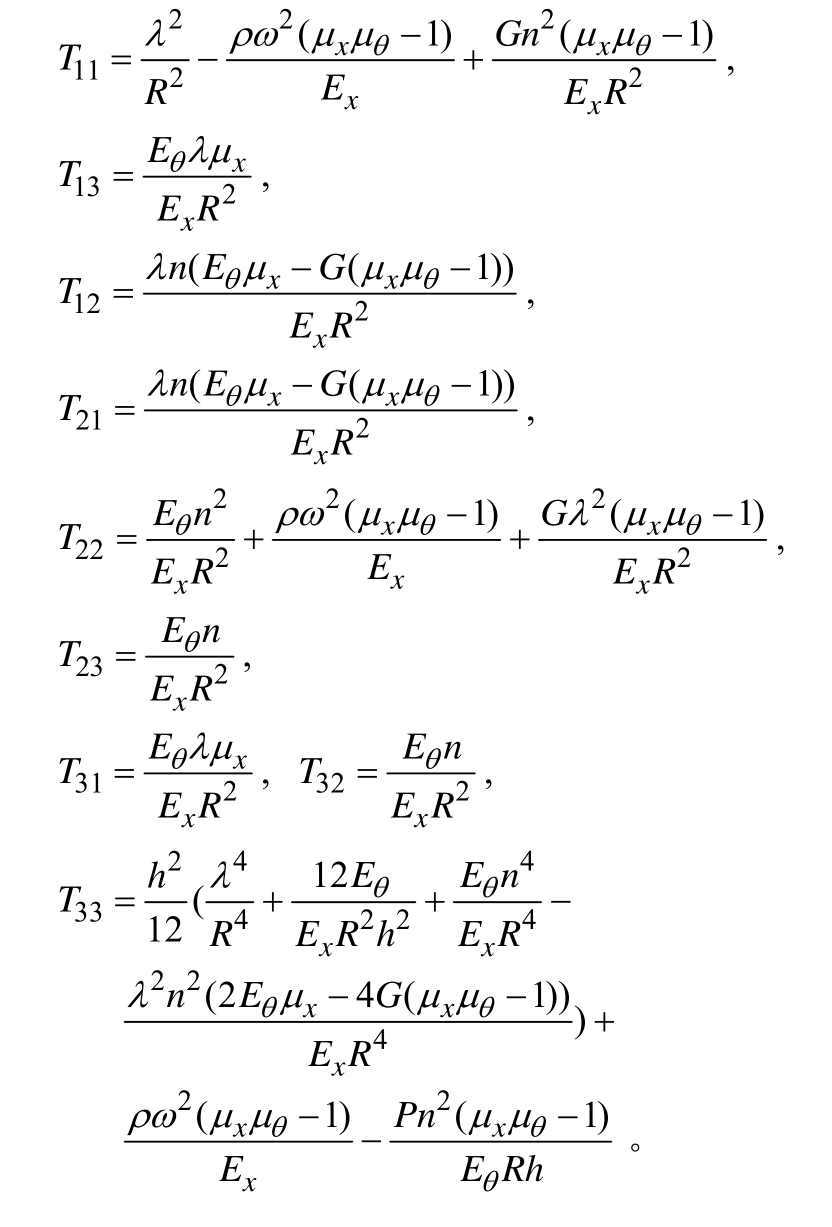圆柱壳作为一种简单、高效的结构形式，在工程实际中得到了广泛应用，如火箭、飞机、导弹、潜艇、轮胎、车轮、高压容器等结构。对圆柱壳结构的研究已持续一个世纪，以简支、固支及其组合等经典边界条件为主的各向同性圆柱壳的振动问题尤其受到关注，已有深厚的研究基础[1-3]。但在实际工程中会涉及到非经典边界条件下的圆柱壳或复合材料圆柱壳问题，比如轮胎等，属于复合材料制成的复杂结构件[4-6]。使用经典边界条件下的圆柱壳结构模型来处理此类部件会存在误差较大等问题。而采用弹性基础上的正交各向异性圆柱壳模型来处理此类问题则是其中一种可行方法，但目前的有关研究仍存在误差较大或计算程序繁琐等一些问题，亟待进一步研究。
圆柱壳振动问题的有关理论丰富，常用经典理论包括 Sanders[7]理论、Love[8]理论、Flügge[7,9]理论、Donnell-Mushtari[7,10]理论、Reissner-Naghdi-Berry[11]理论、Goldenveizer-Novozhilov[11]理论等。Leissa[11]对大量圆柱壳振动研究文献进行了综述，总结了众多经典文献的主要研究成果。近年研究则在已有研究基础上致力于解决更多复杂情况下圆柱壳振动的具体问题。Jafari等[12]利用 Love理论针对固支-自由边界条件下的复合材料圆柱壳的自由和强迫振动特性进行了研究，进一步丰富了复合材料圆柱壳在特定边界下振动特性的研究。Zhang[13-14]针对旋转层合复合材料圆柱壳的自由振动进行了分析研究，通过引入波传播方法提高了计算效率。Lam和Loy[15]基于Love理论并采用Ritz方法针对边界条件和纤维走向对正交各向异性层合圆柱壳的自由振动频率的影响进行了分析，为工程实践提供了有益指导。李学斌[16]从Flügge薄壳理论出发，推导出正交各向异性圆柱壳在简支边界条件下壳体自由振动特征方程，分析了正交各向异性圆柱壳的自由振动特性及稳态响应并针对静水压力对其自由振动频率的影响进行了讨论，仍属经典简支边界条件问题。
关于弹性边界条件下圆柱壳振动问题，可简单分为连续弹性基础和两端弹性基础等2类。Paliwal等[17―18]先后采用多种方法针对连续弹性基础上各向同性和正交各向异性圆柱壳的自由振动特性进行研究。Jin等[19]，利用瑞利利兹方法，基于Reissner-Naghdi线性圆柱壳理论，结合其提出的标准傅里叶余弦级数及其辅助函数方法，给出了两端弹性基础上层合复合材料圆柱壳的固有频率精确解。Zhou等[20]基于Flügge经典薄壳理论，通过直接解法给出圆柱壳振动波数的具体表达式，求得了两端弹性基础上圆柱壳的自由振动频率。马旭等[21]在波传播分析方法基础上采用改进傅里叶级数方法，研究了两端弹簧支撑圆柱壳的自由振动及其响应。Torkaman-Asadi和Firouz-Abadi[22]则基于Love理论，采用一种精确的级数扩展方法针对部分连续弹簧基础上的圆柱壳振动问题展开研究，与完全连续弹性边界条件问题有相似性。
综合以上研究发现，有关文献中应用广泛的波传播方法忽略了圆柱壳轴向和周向振动的耦合效应，虽简单易行，但有时会产生较大计算误差[9]。多种改进位移函数的求解方法及直接解法等一些方法的适用范围广，但表达式较繁琐，且有关公式随条件变化需进行改变。有关两端弹性基础上正交各向异性圆柱壳自由振动的研究尚比较欠缺，弹性基础刚度和内压力等因素的变化对正交各向异性圆柱壳固有频率影响规律的研究还不够充分。
本文针对两端弹性基础上的有均布径向预压力(以下简称内压力)的正交各向异性薄壁圆柱壳，参考经典文献[11,23]，基于 Donnell-Mushtari圆柱壳理论和Hamilton原理，得出系列表达式，并通过二分法对圆柱壳的自由振动频率进行了求解。由于在Donnell-Mushtari理论基础上未再引入其他假设，且本文方法充分考虑了八阶振动特征方程所有的可能解，避免了如文献[23]所指出的漏解问题，这种方法的求解精度和求解效率较高。研究结果表明，弹性基础的刚度会影响圆柱壳的固有振动频率，且随着振动阶次的不同而有区别。内压力也会对圆柱壳的固有频率造成影响，当薄壁圆柱壳内压力较小时，对于圆柱壳的振动特性影响较小，而当内压力持续增加，会造成薄壁圆柱壳固有频率的显著增大。本文方法既可用以解决弹簧支撑边界条件下考虑内压力的正交各向异性薄壁圆柱壳的自由振动问题，还可通过调整弹簧刚度来用于解决一般边界条件下的普通圆柱壳振动问题。
2 模型分析
为便于建模研究，可对轮胎等实际工程部件进行抽象，简化为如图1所示的结构，即在两端弹簧支撑边界条件下的薄壁圆柱壳。
在圆柱壳上建立柱坐标系(θ,x,r)，如图1所示，x、θ、r分别表示其轴向、周向和径向的坐标轴，u、v、w分别表示圆柱壳中面上任一点的轴向、周向和径向位移，φ表示壳体两端的扭转变形，圆柱壳的长度为L，厚度为h，平均半径为R，ku、kv、kw、kφ依次为均布在圆柱壳两端的轴向、周向、径向和扭转弹簧的刚度，壳体内壁均布有沿壳体径向作用的内压力P。
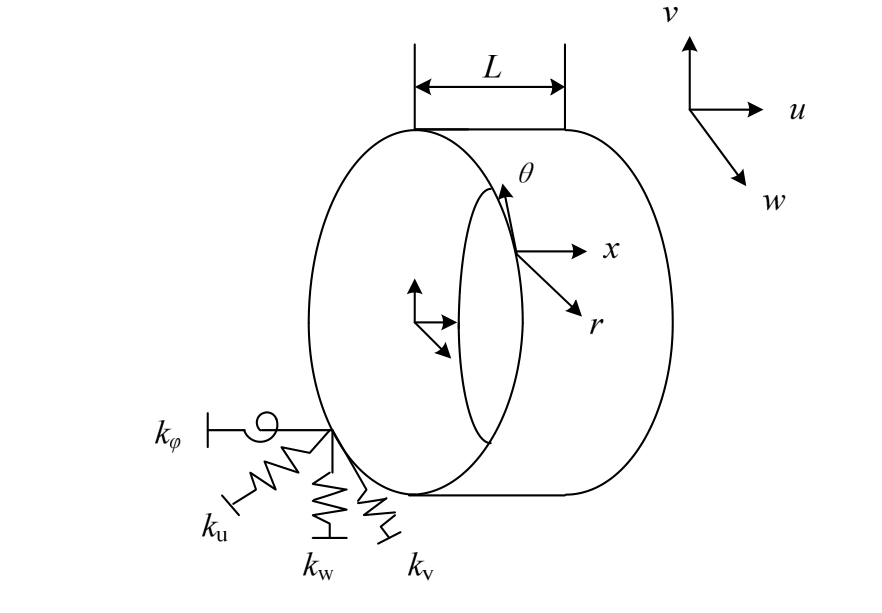
图1 弹性基础上圆柱壳结构及坐标系示意图
Fig.1 A cylindrical shell on elastic foundation and its corresponding coordinate system
基于Donnell-Mushtari理论[11]，壳体的应变表达式：
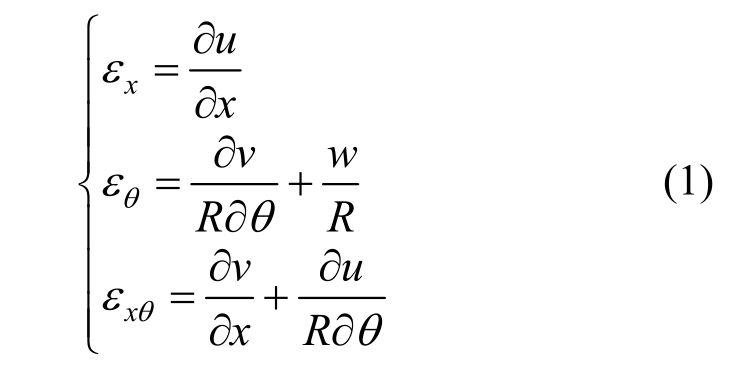
系统势能U包含2部分，U1为壳体应变能，U2是两端支撑弹簧的弹性势能：
式中：0σ是由于压力P作用所产生的初始预应力；
为内压力P引发的初始应变：
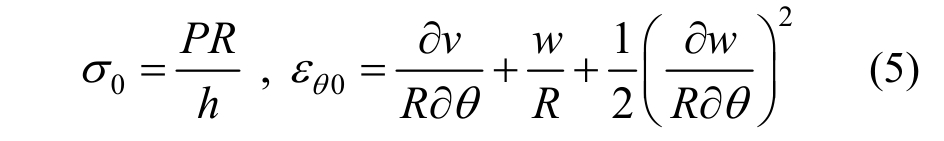
系统动能T：
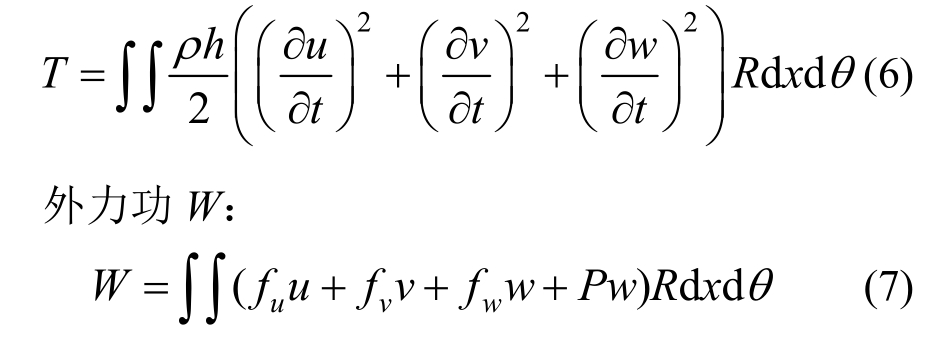
式中，fu、fv、fw分别为u、v、w方向的外力。
基于Hamilton原理：
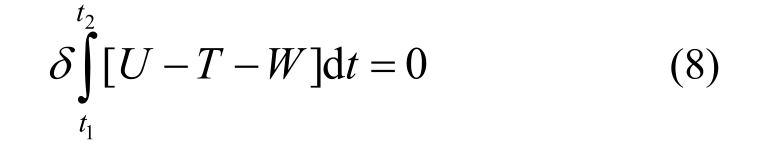
整理上述表达式，并令fu、fv、fw均为0，得到振动微分方程式(9)和对应的边界条件表达式(10)、式(11)：
式中各变量具体表达式见附录，下同。
对于周向封闭的圆柱壳，假设振型表达式为：
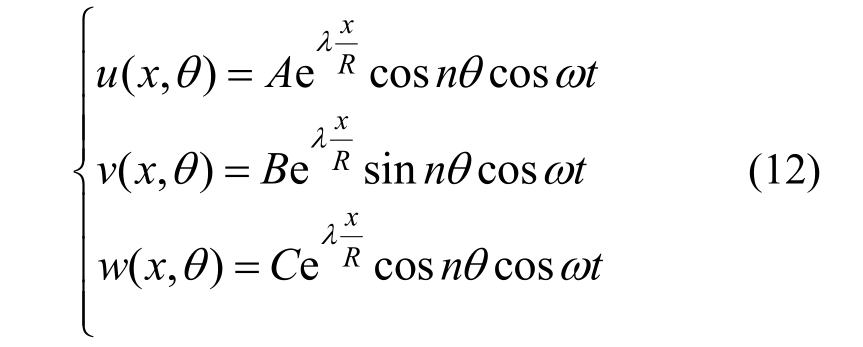
式(12)中：A、B、C为各方向的振幅参数；λ用来表示轴向波动；n代表周向波数；ω为圆柱壳的圆频率。将振型表达式代入到振动微分方程式(9)中，可得到下述表达式：
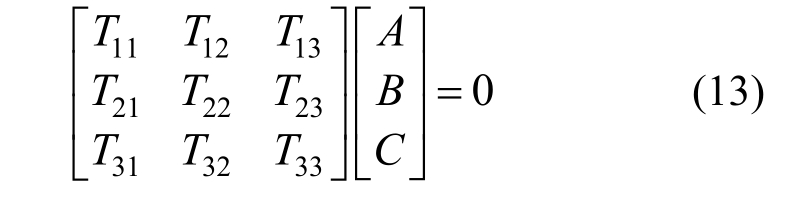
若式(13)有任意非零解，则左侧矩阵行列式值为零，整理可得下述表达式：
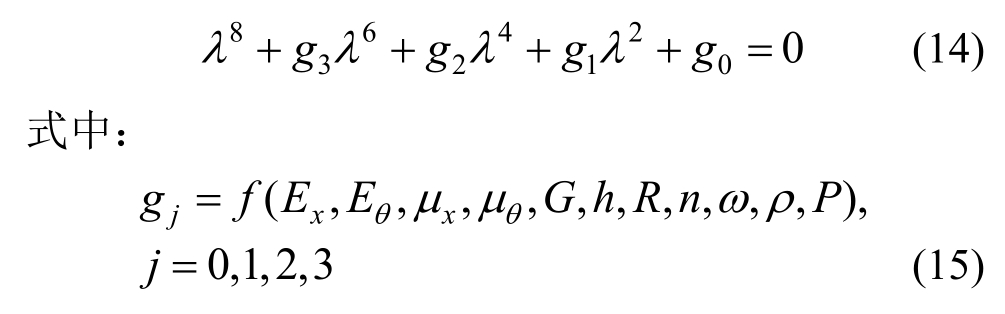
特征方程式(14)是一个关于无量纲轴向波动参数λ的8次方程，有正负 2类共 8个解
可能的形式有实数、虚数和复数3种，iλ为纯实数时代表轴向的传播波，iλ为纯虚数时为轴向的近场波，iλ为复数时代表沿轴向的传播衰减驻波。任何一支波都存在起始频率，在起始频率以下，该波不传播能量。在周围无流体介质时，传播波最多只会有 3支(对某阶周向模态而言)；除弯曲近场波以外，其他近场波都有起始和截止频率，一般来讲，截止频率是某支传播波的起始频率，起始频率是某支衰减驻波的截止频率[24]。
随着圆柱壳参数值等多种因素的变化，特征方程式(14)所对应的8个根的形式将随之变化，不同形式的根组合构成不同的一组解，共计存在9组不同的解。不应简单假定方程的解为一组特定形式根值的组合，如常用的1对纯实根、1对纯虚根和2对复根的组合，或有些文献中所提到的8种组合形式[25]，否则可能会出现漏解等问题。式(14)的可能解共包括如下9组：
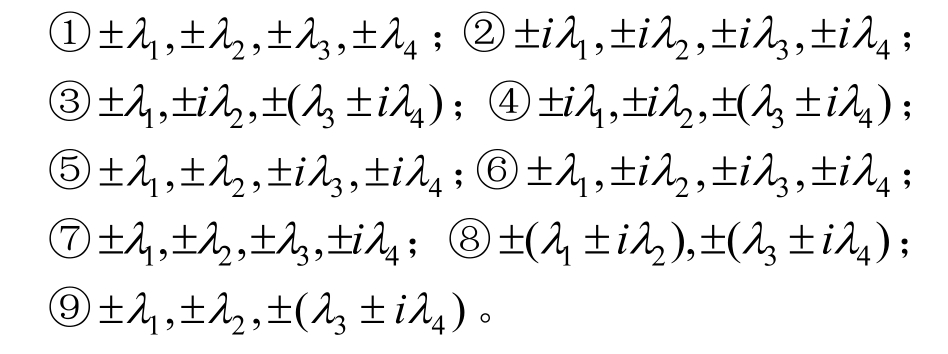
得到特征方程式(14)的根值，代入方程组式(13)，求得相应的振幅比系数iη和iε表达式：
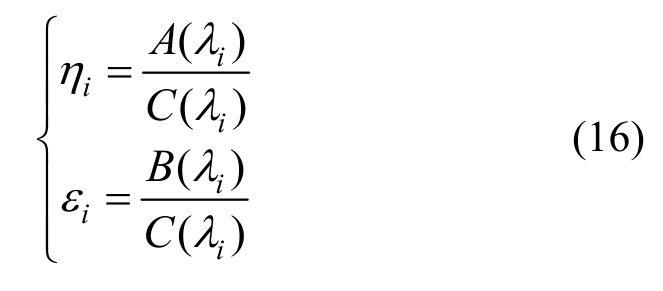
求得λ表达式，后计算得到幅值比表达式，带回位移表达式(12)中，得到具体的位移表达式。
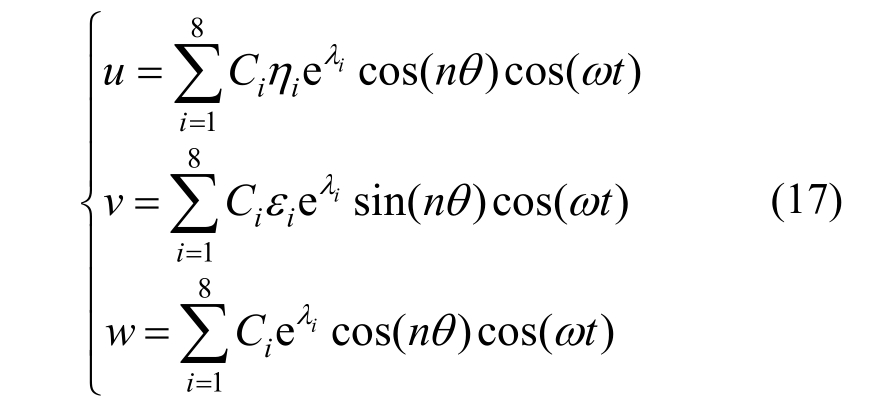
将式(17)代入式(10)和式(11)中，整理之后得到关于
的八元齐次代数方程组：
式中，
若方程组式(18)存在非零解，则系数矩阵行列式的结果为0，得：
如式(19)所示，系数矩阵行列式是n、λ、ω等3个未知变量的函数，同时n、λ、ω等3个变量还需满足等式(14)，因此求得式(14)与式(19)构成的方程组的解即可求得符合边界条件的圆柱壳固有频率等结果。
可使用MATLAB编写程序对方程组进行求解，详细求解流程如下：
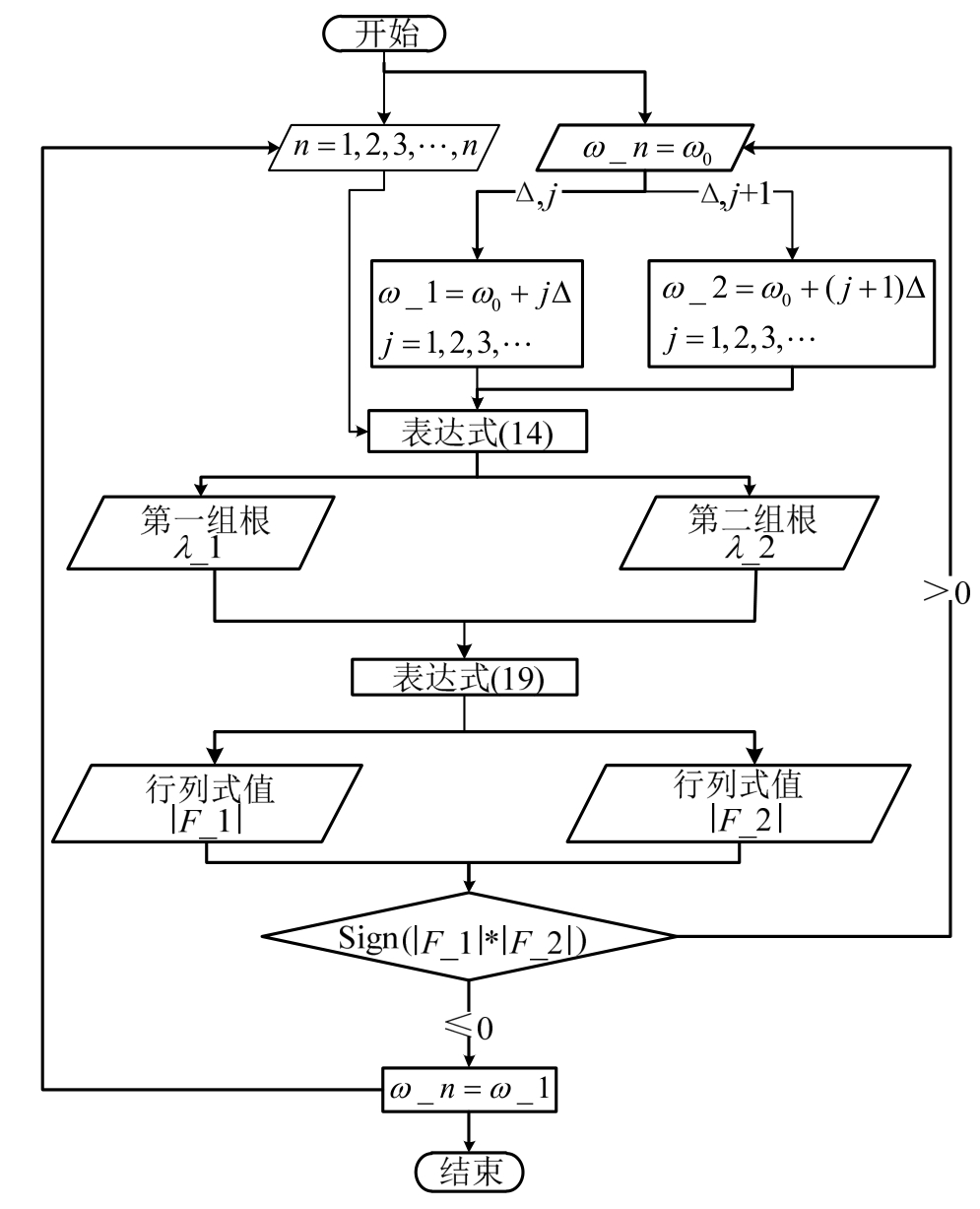
图2 固有频率计算流程图
Fig.2 Flow chart of natural frequency calculation
图2中，0ω是计算时给定的初始固有圆频率值，Δ为计算时采用的搜索步长值，ω_n即为对应的n阶固有频率。基于上述计算方法，可求得圆柱壳任意阶次固有频率及其模态振型。本文中的求解方法，完整覆盖了特征方程所对应的所有可能形式根值，可用于计算不同规格和边界条件下的正交各向异性薄壁圆柱壳固有振动特性及其变化，且不必像有些文献中那样需要针对对称和反对称振型 2种情况分别计算[26]。由于求解方法没有在Donnell-Mushtari圆柱壳理论基础上再做简化，因此所得结果是基于本文理论所能得到的精确计算结果，具体计算精度取决于流程图中的搜索步长值Δ。
另外，本文方法还可用于解决一般边界条件下的圆柱壳振动问题。自由、固支等一般边界条件可视为两端支撑弹簧的刚度极小、极大或组合时的情况，即通过调整圆柱壳两端支撑弹簧的刚度可实现对一般边界条件问题的求解。如调整径向弹簧刚度
极大，周向弹簧刚度kv极大，轴向弹簧刚度ku为0，扭转弹簧刚度kφ为0时，即可近似简支边界条件。其他边界条件问题同样进行对应调整即可。
3 算例分析
3.1 理论结果与文献中结果对照
为验证理论模型部分所提出计算方法的准确性，将本文计算方法所得结果与之前已发表文献中的数据进行对照。
表1所示即所用算例的圆柱壳的材料属性，圆柱壳的边界条件为两端简支。文献结果和采用本文方法计算所得结果如表2所示(壳体参数：L/R=2，h/R=0.01，轴向半波数m=1。无量纲固有频率表达式为：
表1 圆柱壳的材料属性
Table 1 Material properties of cylindrical shell
表2 圆柱壳无量纲固有频率参数的理论计算结果与文献中结果对照
Table 2 Comparison of non-dimensional frequencies of a cylindrical shell between results from theoretical calculation and literature
文献[16]采用 Flügge经典薄壳理论，文献[27]中使用了含有横向剪切应变的应变-位移表达式，并沿用Novozhilov壳体理论计算得到表中结果。表中的最大误差项是指本文计算结果与两组文献中结果比较时所得误差的最大值。结合表中的误差值不难看出，本文方法计算所得结果与两组文献中的计算结果相比，总体上误差很小，计算精度较高。
为验证本文求解方法相对于波传播方法的计算精度，将本文计算方法所得结果和文献中采用波传播方法所得的结果与文献中的有限元计算结果进行对比，如表3所示(圆柱壳参数：L=0.8 m，内直径Di=0.3048 m，h=0.0011016 m，E=64.73 GPa，μ=0.3285，密度ρ=2700 kg/m3，两端固支边界条件，轴向半波数m=5)。
表3 固有频率的理论计算结果与文献中结果对照
Table 3 Comparison between frequency obtained by theoretical calculation and results from literature
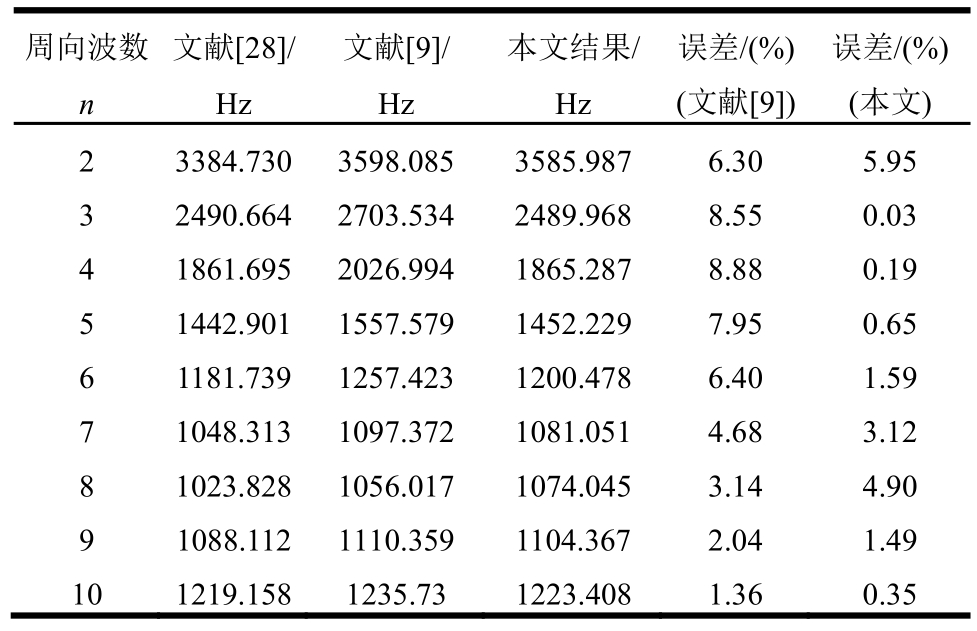
文献[28]采用的是有限元分析方法，文献[9]采用了波传播方法。2组误差分别指的是文献[9]和本文所得结果与文献[28]中有限元方法所得结果的误差值，对比2组误差结果可看出，本文方法所得结果相比较波传播方法所得结果误差更小，计算精度更高。
3.2 参数分析与讨论
为分析特征方程式(14)的解的变化情况，本节针对下面的算例进行讨论。
以各向同性材料圆柱壳为例，某圆柱壳的有关参数为：E=1.01×107Pa，μ=0.33，R=1.12 m，L=1.24 m，h=0.011 m，ρ=3010 kg/m3。边界条件为两端固支。利用本文所提出的方法，计算得到如表4所示的结果。
从表4的算例计算结果可看出，随着模态阶次的变化，圆柱壳的特征方程式(14)对应出现不同形式的解，对应不同的模态频率。但表中没有给出
等3种解所对应的固有频率结果，这是由于在一般边界条件下，圆柱壳的自由振动中不会出现上述3组解所对应的振型。上述3组不同形式的解分别对应至少4组传播波、4组近场波和4组衰减驻波的模态，在圆柱壳与流体耦合等复杂作用条件下将可能出现[24]。但无论从数学角度还是工程实际角度，本文给出振动特征方程的所有可能解，将有助于在解决此类问题时考虑所有可能形式的解，而不是简单的假定为某特定类型的解，进而导致可能出现的漏解等问题。
表4 圆柱壳的固有振动频率及其对应的特征方程解的形式
Table 4 Natural vibration frequency of cylindrical shell and corresponding forms of solutions of characteristic equation
另外，为分析讨论弹性基础即两端支撑弹簧的刚度对正交各向异性圆柱壳固有频率的影响，采用表5所示的圆柱壳参数进行计算分析(圆柱壳的尺寸参数为：L=2 m，R=1 m，h=0.01 m，轴向半波数m=1)。以轴向支撑弹簧和径向支撑弹簧的影响为例进行讨论，不断变化支撑弹簧的刚度来计算不同阶次的圆柱壳固有频率。
表5 圆柱壳的材料参数
Table 5 Material property of cylindrical shell
图3所示为轴向支撑弹簧刚度对圆柱壳固有频率的影响，图4所示为径向支撑弹簧刚度对圆柱壳固有频率的影响。
图3 弹性基础刚度ku对圆柱壳固有频率的影响
Fig.3 Influence of stiffnesskuon frequency of cylindrical shell
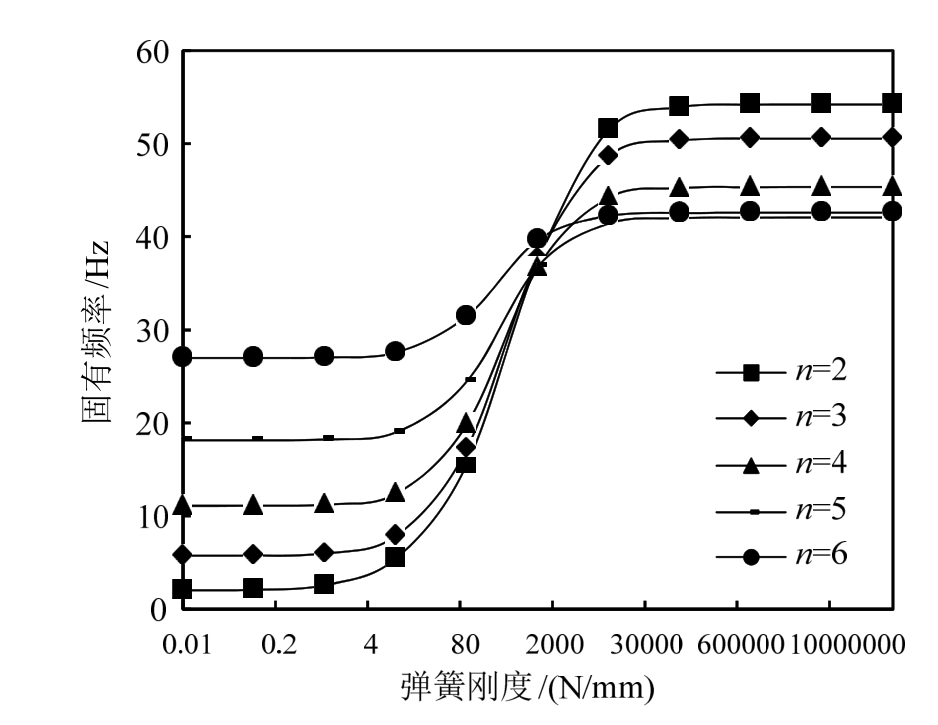
图4 弹性基础刚度kw对圆柱壳固有频率的影响
Fig.4 Influence of stiffnesskwon frequency of cylindrical shell
从以上2幅线图可得到以下几点结论：1) 总体上，随着弹性基础刚度的增加，圆柱壳固有频率呈现先增大后保持稳定的趋势；2) 随着阶次的升高，弹性基础刚度对于圆柱壳固有频率的影响程度逐渐变小；3) 轴向弹性基础和径向弹性基础对圆柱壳固有频率的影响规律有所不同。对轴向弹性基础，阶次越高，圆柱壳固有频率首次出现显著变化的刚度值越大；而对径向弹性基础，则基本没有随着阶次升高而变化。
上述现象的产生是由于支撑弹簧刚度的变化改变了圆柱壳的边界条件，进而影响和改变了圆柱壳的固有频率。以轴向弹簧为例，两端支撑弹簧的刚度从很小变化到很大，相当于圆柱壳的边界条件从轴向自由变为轴向固定，进而导致固有频率的升高。另外，参考有关文献[29]可知，圆柱壳的变形能可分为2类，弯曲变形能和薄膜变形能，它们的分配和振型波数及几何尺寸有关。在轴向半波数m值较小且不变的条件下，当n值较小时，薄膜变形能占主要成份，随着n值的增大，周向弯曲变形能逐渐增大，薄膜变形能的占比越来越小，相应的，与之相关的轴向和径向支撑弹簧的影响逐渐变小。
3.3 内压力的影响
本文方法可以考虑圆柱壳内压力对圆柱壳振动频率的影响，为便于计算，本文以各向同性圆柱壳为例进行分析。为验证本文方法的计算精度，分别采用有限元方法和本文方法对圆柱壳的固有频率进行计算，表6所示即为2种方法计算结果的对比。
表6结果显示，本文计算方法所得结果与有限元方法所得计算结果相比，总体误差控制在 1%左右，可部分证明本文计算方法的精确性(模型的基本参数如下，R=0.5 m，h=0.01 m，L=4 m，E=1.5×1011Pa，μ=0.3，ρ=7000 kg/m3。圆柱壳两端的径向均布弹簧的刚度为1000 N/m，内压力P=1×105Pa)。
为考察圆柱壳内压力对圆柱壳振动特性的影响，本文对不同内压力作用下的圆柱壳固有频率进行了计算，除内压力外，其余参数值与表6中算例相同，可得到如图5所示的变化规律。
表6 薄壁圆柱壳固有频率的理论计算结果与有限元仿真计算结果的对照(轴向半波数m=1)
Table 6 Comparison of theoretical results of natural frequency and results from finite element analysis of thin wall cylindrical shell (number of axial half-wavem=1)
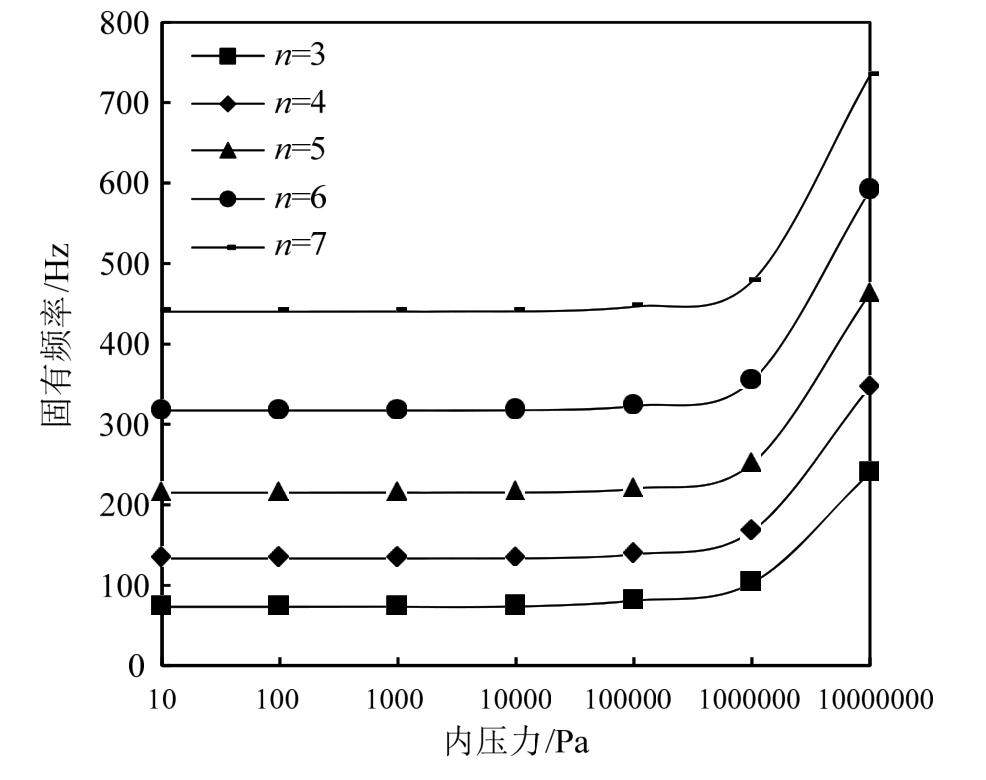
图5 内压力对弹性基础上的圆柱壳的固有振动频率的影响
Fig.5 Influence of internal pressure on vibration frequency of cylindrical shell on elastic foundations
从图5可以看出，薄壁圆柱壳内压力会使得其固有频率增大，但内压力较小的时候，固有频率变化并不显著；但随着内压力的逐渐增大，圆柱壳固有频率会在预压力的作用下产生显著变化，迅速增加。这主要是由于内压力的升高增大了圆柱壳的刚度，进而影响圆柱壳的固有频率。内压力较小的时候，对圆柱壳刚度的影响不显著，因此对固有频率的影响不显著，而当内压力导致的刚度变化逐渐增大接近圆柱壳自身刚度时，对频率的影响便开始变得显著。若不考虑圆柱壳结构的失效，圆柱壳的刚度会随着内压力的增大而不断增大，相应的，固有频率也将不断增大。
4 结论
基于Donnell-Mushtari圆柱壳理论和Hamilton原理，推导出了弹性基础上有径向预压力作用的正交各向异性圆柱壳振动微分方程，并针对圆柱壳固有频率提供了一种半解析计算方法，完整覆盖了振动特征方程所对应的理论根值，与文献及有限元计算结果相比，误差很小，并基于文中方法针对弹性基础和内压力对圆柱壳振动频率的影响规律进行了讨论。
(1) 圆柱壳两端支撑弹簧的刚度会影响圆柱壳的自由振动频率。随着弹簧刚度的增大，圆柱壳固有频率呈现先增加后保持不变的规律，但弹簧刚度对固有频率的影响程度随着阶次的升高而逐渐降低。
(2) 薄壁圆柱壳内的径向压力会使得其固有频率增大，内压力较小的时候，固有频率变化并不显著，随着压力的增大，圆柱壳固有频率逐渐增大。
本方法不仅可用于弹性支承边界条件下的考虑内压力的正交各向异性圆柱壳固有频率问题的计算，还可应用于各向同性材料圆柱壳及其他一般边界条件的圆柱壳固有频率计算，具有避免漏解、精确可靠、适用性强的优点，为这类工程结构的振动分析提供了可靠的方法和工具。
参考文献：
[1]朱大同.充液弹性薄壳的自振分析[J].工程力学,1988(1): 62―68.Zhu Datong.Study of free vibration of an elastic thin shell containing liquid [J].Engineering Mechanics.1988(1): 62―68.(in Chinese)
[2]梁斌, 刘小宛, 李戎, 等.充液环肋圆柱壳耦合振动的波动解[J].工程力学, 2016, 33(6): 9―14.Liang Bin, Liu Xiaowan, Li Rong,et al.Study on vibration of fluid-filled cylindrical shells with ring-stiffener using wave propagation approach [J].Engineering Mechanics.2016, 33(6): 9―14.(in Chinese)
[3]卿光辉, 王喆, 刘艳红.壁厚不连续不对称圆柱壳和开口壳的自由振动分析[J].工程力学, 2006, 23(Suppl 1): 25―29.Qing Guanghui, Wang Zhe, Liu Yanhong.Free vibration analysis of cylindrical shells and open shells with thickness discontinuity and dissymmetry [J].Engineering Mechanics.2006, 23(Suppl 1): 25―29.(in Chinese)
[4]Alibeigloo A, Jafarian H.Three-dimensional static and free vibration analysis of carbon nano tube reinforced composite cylindrical shell using differential quadrature method [J].International Journal of Applied Mechanics,2016, 8(3): 1650033-1―1650033-23.
[5]Ribeiro P.Linear modes of vibration of cylindrical shells in composite laminates reinforced by curvilinear fibres[J].Journal of Vibration and Control, 2016, 22(20):4141―4158.
[6]Florence S J K, Renji K.Modal density of thin composite cylindrical shells [J].Journal of Sound and Vibration,2016, 365(2016): 157―171.
[7]Dym C L.Some new results for the vibrations of circular cylinders [J].Journal of sound and Vibration, 1973,29(2): 189―205.
[8]Soedel W.Simplified equations and solutions for the vibration of orthotropic cylindrical shells [J].Journal of Sound and Vibration, 1983, 87(4): 555―566.
[9]Wang C, Lai J C S.Prediction of natural frequencies of finite length circular cylindrical shells [J].Applied acoustics, 2000, 59(4): 385―400.
[10]El-Mously M.Fundamental natural frequencies of thin cylindrical shells: a comparative study [J].Journal of sound and vibration, 2003, 264(5): 1167―1186.
[11]Leissa A W.Vibration of shells [M].New York:Acoustical Society of America, 1993.
[12]Jafari A A, Khalili S M R, Azarafza R.Transient dynamic response of composite circular cylindrical shells under radial impulse load and axial compressive loads [J].Thin-Walled Structures, 2005, 43(11): 1763―1786.
[13]Zhang X M.Parametric analysis of frequency of rotating laminated composite cylindrical shells with the wave propagation approach [J].Computer Methods in Applied Mechanics and Engineering, 2002, 191(19): 2057―2071.
[14]Zhang X M.Vibration analysis of cross-ply laminated composite cylindrical shells using the wave propagation approach [J].Applied Acoustics, 2001, 62(11): 1221―1228.
[15]Lam K Y, Loy C T.Influence of boundary conditions and fibre orientation on the natural frequencies of thin orthotropic laminated cylindrical shells [J].Composite Structures, 1995, 31(1): 21―30.
[16]李学斌.正交各向异性圆柱壳静动态特性分析及比较研究[D].武汉: 华中科技大学, 2004.Li Xuebin.Analysis and comparative study of static and dynamic characteristics of orthotropic circular cylindrical shells [D].Wuhan:Huazhong University of Science and Technology, 2004.(in Chinese)
[17]Paliwal D N, Pandey R K.The free vibration of a cylindrical shell on an elastic foundation [J].Journal of Vibration and Acoustics, 1998, 120(1): 63―71.
[18]Paliwal D N, Pandey R.Free vibrations of an orthotropic thin cylindrical shell on a Pasternak foundation [J].AIAA journal, 2001, 39(11): 2188―2191.
[19]Jin G, Ye T, Chen Y, et al.An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions [J].Composite Structures, 2013, 106(): 114―127.
[20]Zhou H, Li W, Lv B, et al.Free vibrations of cylindrical shells with elastic-support boundary conditions [J].Applied Acoustics, 2012, 73(8): 751―756.
[21]马旭, 杜敬涛, 杨铁军, 等.基于波传播方法的边界条件对圆柱壳振动特性的影响分析[J].振动工程学报,2009, 22(6): 608―613.Ma Xu, Du Jingtao, Yang Tiejun, et al.Analysis of influence of boundary conditions on cylindrical shell dynamics based on wave propagation approach [J].Journal of Vibration Engineering, 2009, 22(6): 608―613.(in Chinese)
[22]Torkaman-Asadi M A, Firouz-Abadi R D.Free vibration analysis of cylindrical shells partially resting on an elastic foundation [J].Meccanica, 2016, 51(5): 1113―1125.
[23]Smith B L, Vronay D F.Free vibration of circular cylindrical shells of finite length [J].AIAA Journal,1970, 8(3): 601―603.
[24]陈正翔, 张维衡.充液圆柱管壳中振动波的频散特性[J].船舶力学, 2000, 4(5): 60―67.Chen Zhengxiang, Zhang Weiheng.Frequency dispersion of vibrational waves in cylindrical shells filled with fluid[J].Journal of Ship Mechanics, 2000, 4(5): 60―67.(in Chinese)
[25]Alujevi? N, Campillo-Davo N, Kindt P, et al.A simplified tire model based on a rotating shell [C]// 4 th International Tyre Colloquium, 2015.
[26]邢誉峰，刘波.板壳自由振动的精确解[M].北京: 科学出版社, 2015.Xing Yufeng, Liu Bo.Exact solutions of free vibrations of plates and shells [M].Beijing: Science Press, 2015.(in Chinese)
[27]Warburton G B, Soni S R.Resonant response of orthotropic cylindrical shells [J].J.Sound Vib.1977, 53:1―23.
[28]Santiago J M, Wisniewski H L.Convergence of finite element frequency prediction for a thin walled cylinder[J].Computers and Structures, 1989, 32(3/4): 745―759.
[29]曹志远.板壳振动理论[M].北京: 中国铁道出版社,1989.Cao Zhiyuan.Vibration of plate and shell [M].Beijing:China railway Publishing House, 1989.(in Chinese)
